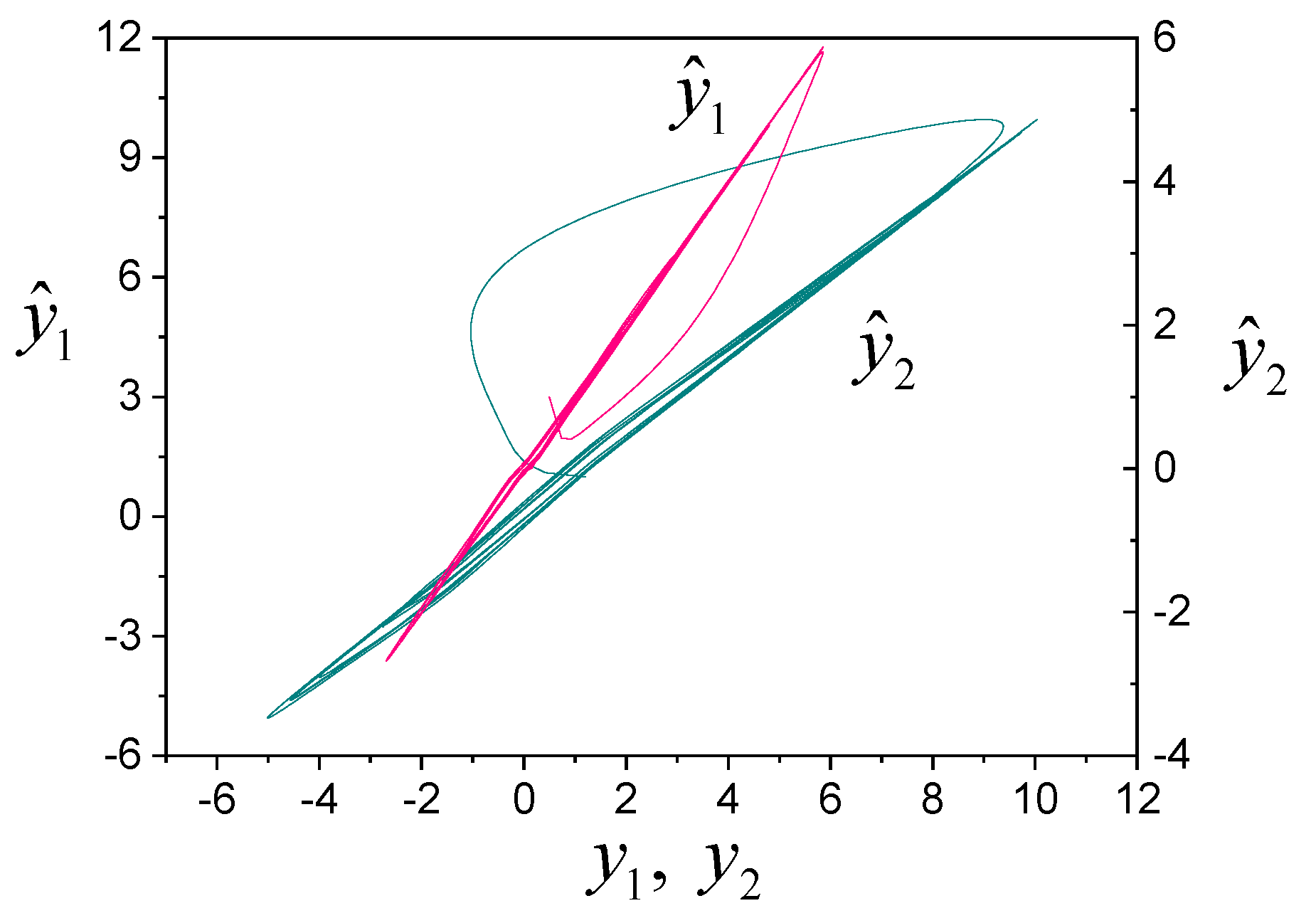Synthesis of Adaptive Algorithms with Given Quality

1. Introduction

The integrated adaptive algorithm (IAA) is widely used in control systems:

$$\dot{\widehat{A}}=-\mathsf{\Gamma }{E}^{T}RX,$$

(1)

where $\widehat{A}\in {ℝ}^n$ is vector of tuning parameters; $E\in {ℝ}^q$ is an error in estimating system output; $X\in {ℝ}^n$ is vector of observed variables (input, control); $\mathsf{\Gamma }\in {ℝ}^{n\times n}$ is positive definite gain matrix; $R=R^T>0$ is the matrix of the loss function (optimisation criteria).

Equation (1) describes the IAA class, which determined by minimising the quadratic loss function, consider heuristic assumptions, or ensuring the stability of the identification system (see, for example, [1,2,3,4,5,6,7,8,9,10]).

In [6], the system is considered

$$X^{(n)}=F\left(X^{(n-1)}\right)+\Delta F\left(X^{(n-1)}\right)+H^T\left(X^{(n-1)}\right)A+L\left(X^{(n-1)}\right)U,$$

(2)

where $X\in {ℝ}^m,U\in {ℝ}^m$ are vectors of state and control; $F\left(X^{(n-1)}\right)\in {ℝ}^r$ is a continuous vector function; $H\left(X^{(n-1)}\right)\in {ℝ}^{m\times r}$ and $L\left(X^{(n-1)}\right)\in {ℝ}^{r\times r}$ are continuous matrix functions, $\Delta F\left(X^{(n-1)}\right)\in {ℝ}^r$ is an undefined function; $A(t)\in {ℝ}^m$ is an unknown parameter vector. A preliminary estimate $A_0=A_0(t)\in {ℝ}^m$ is known for $A$.

A robust adaptive algorithm (AA) [6] is proposed:

$$\begin{array}{l}\dot{\widehat{A}}=H{P}_L^T(A)X-\left(\mu +1\right)\left(\widehat{A}-A_0\right)+{\dot{A}}_0,\\ U_a=H^{T}X\widehat{A},\end{array}$$

(3)

where $\widehat{A}$ is estimation of the $A$ vector, $U_a$ is control, $\mu >0$, $P_L^T(A)$ is a matrix that determines the quality of control.

The algorithm (3) implementation under uncertainty is difficult, since the current evaluation of the adaptation quality is not considered. Modification (3) and its simplifications are proposed in [6].

In [10], IAA (1) and its proportional $\sigma$-modification were considered [11]

$${\dot{\widehat{A}}}_i=\mathsf{\Gamma }\left(E_i^T{R}_i{X}_i-\sigma {\widehat{A}}_i\right),$$

(4)

where $\sigma >0$ guarantees damping of the tuning process.

A generalization of the $\sigma$-modification, if the condition of constant excitation is not fulfilled, is given in [12]. In [12], the design of AA is based on the requirements for the derivative of Lyapunov function (LF).

An adaptive law for the first-order system is proposed in the form

$${\dot{\widehat{A}}}_1=-e_1{X}_1-\gamma \left|e_1\right|{\widehat{A}}_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma >0,$$

(5)

where ${\dot{e}}_1=-k_m{e}_1+\Delta A_1^T{X}_1$, $e_1\in ℝ$ is error in predicting system output, $X_1\in {ℝ}^m$ is generalised system input, $k_m>0$. AA is introduced intuitively without synthesis formalization method.

Projection variants of IAA are proposed in [13]. Modifications of IAA are considered in [15,16,17,18]. A normalized version of the algorithm (1) (projection algorithm) is proposed in [16]

$$\dot{\widehat{A}}=-{\displaystyle \frac{\mathsf{\Gamma }{E}^{T}RX}{1+{‖X‖}^2}},$$

(6)

where ${‖X‖}^2=X^{T}X$. Various projection AA is considered in [19].

Regardless of [12], in [20], an analytical method is proposed for the synthesis of adaptive algorithms, considering functional limitations.

Remark 1. Sometimes, signalling adaptation (SA) [21] algorithms are used. As shown in [20], the SA use in adaptive identification systems is not always effective.

The analysis shows that the IAA is obtained based on the least squares method and its modifications, and the LF, are mainly used. Gradient algorithms based on numerical optimisation methods are often implemented. The AA parameters are selected to ensure the stability of the adaptive process.

In this paper, we generalise the approach proposed in [20] for the formalised synthesis of AA. The properties of the adaptive identification system (AIS) are investigated using the example of a decentralised system.

2. Problem Statement

Consider AIS

$$S_X:\left\{\begin{array}{l}\dot{X}=AX+Bu\\ y=C^{T}X\end{array}\right.,$$

(7)

where $X\in {ℝ}^n$ is the state vector, $A\in {ℝ}^{n\times n}$ is a matrix with constant elements, $B\in {ℝ}^n$, $C\in {ℝ}^n$, $y\in ℝ$ is system output.

Set of experimental data

$${\mathbb{I}}_o=\left\{y(y),\hspace{0.17em}\hspace{0.17em}u(t),\hspace{0.17em}\hspace{0.17em}t\in {\mathbb{J}}_t=\left[t_0,\hspace{0.17em}{t}_k\right]\right\}.$$

The model for evaluating elements $(A,B)$

$$S_A:\left\{\begin{array}{l}\dot{\widehat{X}}=-K\left(\widehat{X}-X\right)+\widehat{A}\widehat{X}+\widehat{B}u\\ \widehat{y}=C^T\widehat{X}\end{array}\right.,$$

(7)

where $K\in {ℝ}^{n\times n}$ is the Hurwitz matrix, $\widehat{X}\in {ℝ}^n$ is the model state vector, $\widehat{A}\in {ℝ}^{n\times n}$ and $\widehat{B}\in {ℝ}^n$ are tuning matrices.

Problem: find the tuning laws of the matrices G1 and K2 such that:

$$\underset{t\to \infty }{\lim }\left|e(t)\right|=\underset{t\to \infty }{\lim }\left|\widehat{y}(t)-y(t)\right|\le {\delta }_e,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\delta }_e\ge 0.$$

3. The Constant Excitation Condition

Consider the requirements for $\left(X,u\right)$. The estimation of system parameters (1) depends on the $S_X$-system identifiability. This property is guaranteed if the condition of constant excitation (CE) is satisfied for ${\mathbb{I}}_o$.

Let $u(t)$ satisfy the condition CE

$$\mathcal{E}{\mathcal{C}}_{{\underset{¯}{\alpha }}_u,{\overline{\alpha }}_u}:{\underset{¯}{\alpha }}_u\le u^2(t)\le {\overline{\alpha }}_u\hspace{0.17em}\hspace{0.17em}\forall t\in \left[t_0,t_0+T\right]\hspace{0.17em}\mathrm{or} u(t)\in \mathcal{E}{\mathcal{C}}_{{\underset{¯}{\alpha }}_u,{\overline{\alpha }}_u},$$

(8)

where ${\underset{¯}{\alpha }}_u>0,{\overline{\alpha }}_u>0$, $T>0$. If $u(t)$ does not have the CE property, then we will write $u(t)\notin \mathcal{E}{\mathcal{C}}_{{\underset{¯}{\alpha }}_u,{\overline{\alpha }}_u}$ or $u_i(t)\notin \mathcal{E}\mathcal{C}$.

Remark 2. If a nonlinear System is considered, then condition (8) is transformed [22].

4. AA Synthesis Based on LF

The error equation for the system (1), (7):

$$\dot{E}=-KE+\Delta AX+\Delta Bu,$$

(9)

where $E=\widehat{X}-X$; $\Delta A=\widehat{A}-A,\hspace{0.17em}\hspace{0.17em}\Delta B=\widehat{B}-B$ are parametric residuals.

Let a functional constraint $\chi \left(E,\Delta A,\Delta B\right)\ge 0$ be imposed on the system (9), where $\chi (\cdot )$ is a continuously differentiable function reflecting the tuning process quality. The task is reduced to meeting the target condition $\underset{t\to \infty }{\lim }\left|e(t)\right|=\underset{t\to \infty }{\lim }\left|\widehat{y}(t)-y(t)\right|\le {\delta }_e,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\delta }_e\ge 0$.

Introduce LF

$$V(E,\Delta A,\Delta B,t)=0.5E^T(t)PE(t)+0.5\mathrm{tr}\left(\Delta A^T{\mathsf{\Gamma }}_A^{-1}\Delta A\right)+0.5\Delta B^T{\mathsf{\Gamma }}_B^{-1}\Delta B,$$

(10)

where $P=P^T$ is symmetric positive definite matrix, $\mathrm{tr}$ is the trace of the matrix, ${\mathsf{\Gamma }}_A={\mathsf{\Gamma }}_A^T>0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathsf{\Gamma }}_B={\mathsf{\Gamma }}_B^T>0$ are diagonal matrices.

The $V$ derivative:

$$\dot{V}=-E^{T}QE+\mathrm{tr}\left[\left(PE{X}^T+\Delta {\dot{A}}^T{\mathsf{\Gamma }}_A^{-1}\right)\Delta A\right]+\left(E^{T}Pu+\Delta {\dot{B}}^T{\mathsf{\Gamma }}_B^{-1}\right)\Delta B,$$

(11)

where $K^{T}P+PK=-Q$, $Q=Q^T$ is symmetric positive definite matrix. From $\dot{V}\le 0$ we obtain AA

$$\begin{array}{l}\Delta \dot{A}=-{\mathsf{\Gamma }}_{A}XP{E}^T\\ \Delta \dot{B}=-{\mathsf{\Gamma }}_{B}PEu\end{array},$$

(12)

So, the IAA synthesized from the stability condition of the system (9). AIS is stable in the space $\left(t,E\right)$. This is a classic AA synthesis scheme.

Remark 3. In [18], a quadratic condition is imposed on $\dot{V}$ to develop a control algorithm. Functional restrictions (FR) for obtaining AA are not considered.

5. FR and AA Structure

Consider LF $V(E,\Delta A,\Delta B,t)$ and apply the approach [20]. Let FR imposes on the AIS

$$\dot{V}\le -\chi (E,\Delta A,\Delta B),$$

(13)

where $\chi \left(E,\Delta A,\Delta B\right)$ is a quality function of processes in the adaptive system.

Describe the approach to AA synthesis using the example of the matrix $A$ identification for the $S_X$-system. Let $V_{\Delta }\triangleq V(E,\Delta A,t)$. Consider examples of functions $\chi \left(E,\Delta A\right)$.

1. $\chi \triangleq {\chi }_{\Delta }={\alpha }_{\Delta }\mathrm{Sp}\left(\Delta A^T\Delta A\right)$, where ${\alpha }_{\Delta }>0$. Let ${\eta }_{\Delta }={\dot{V}}_{\Delta }+{\chi }_{\Delta }$. Then:

$${\eta }_{\Delta }=-E^{T}QE+E^{T}R\Delta AX+\mathrm{tr}\left(\Delta {\dot{A}}^T\Delta \dot{A}\right)+\mathrm{tr}\left(\Delta A^T\Delta \ddot{A}\right)+{\alpha }_{\Delta }\mathrm{tr}\left(\Delta A^T\Delta A\right).$$

(14)

From condition ${\eta }_{\Delta }\le 0$, we obtain

$$\Delta \ddot{A}=-\Delta \dot{A}-{\alpha }_{\Delta }\Delta A-{\mathsf{\Gamma }}_{A}RE{X}^T.$$

(15)

Let $\Delta A=Z_1$. We get the representation for equation (15) in the state space

$$S_{AA}:\left\{\begin{array}{l}{\dot{Z}}_1=Z_2,\\ {\dot{Z}}_2=-{\alpha }_{\Delta }{Z}_1-Z_2-{\mathsf{\Gamma }}_{A}RE{X}^T.\end{array}\right.$$

(16)

So, if FR is imposed on AIS, then AA is described by the system $S_{AA}$. In this form, to apply of the system (16) is difficult. Therefore, the system structural modification is necessary (16).

Remark 4. There are various modifications to the $S_{AA}$-system that depend on FR.

2. ${\chi }_{e,\Delta }={\alpha }_{e,\Delta }\underset{t}{\min }‖E‖\mathrm{tr}\left(\Delta A^T\Delta \dot{A}\right)$ и ${\eta }_{e,\Delta }={\dot{V}}_{\Delta }+{\chi }_{e,\Delta }$. Then we get the ${\mathcal{A}}_{\chi }$-algorithm:

$$\Delta \dot{A}=-{\mathsf{\Gamma }}_{A}RE{X}^T-{\tilde{\alpha }}_{e,\Delta }{\mathsf{\Gamma }}_{\dot{A}}\Delta \dot{A},$$

(17)

where ${\tilde{\alpha }}_{e,\Delta }={\alpha }_{e,\Delta }\underset{t}{\min }‖E‖$, $‖E‖=\sqrt{E^{T}E}$ is the Euclidean norm of the vector $E$.

Modifications of the ${\mathcal{A}}_{\chi }$-algorithm:

(a) integral ${\mathcal{A}}_{\chi }^I$-algorithm

$$\Delta \dot{A}=-M^{-1}{\mathsf{\Gamma }}_{A}RE{X}^T,$$

(18)

where $M=I_n+{\tilde{\alpha }}_{e,\Delta }{\mathsf{\Gamma }}_{\dot{A}}$, ${\mathsf{\Gamma }}_{\dot{A}}={\mathsf{\Gamma }}_{\dot{A}}^T>0$;

(b) ${\mathcal{A}}_{\chi }$-algorithm as a delayed system (modification (17)):

$$\Delta \dot{A}(t)=-{\mathsf{\Gamma }}_{A}RE(t)X^T(t)-{\omega }_e{\mathsf{\Gamma }}_{\dot{A}}\left(\Delta A(t)-\Delta A(t-\tau )\right),$$

(19)

where ${\omega }_{e,\Delta }={\tilde{\alpha }}_{e,\Delta }\hspace{0.17em}{\tau }^{-1}$, $\tau >0$ is time lag;

(c)

$$\Delta \dot{A}=-{\mathsf{\Gamma }}_{A}RE{X}^T-{\alpha }_{e,\Delta }D\left(\left|e_i\right|\right){\mathsf{\Gamma }}_{\dot{A}}\Delta \dot{A}.$$

(20)

Remark 5. The AA (17) implementation and its modifications is depended on the identified system and the properties of the set $\left\{X(t),u(t)\right\}$. At the beginning of the adaptation, apply variant (17). If the initial conditions can be chosen successfully, then apply algorithms (18)–(20).

3. ${\chi }_{E,\Delta }={\alpha }_{E,\Delta }\mathrm{Sp}\left(\Delta A^{T}D\left(\left|e_i\right|\right)\Delta A\right)$, where ${\alpha }_{E,\Delta }>0$, $D\left(\left|e_i\right|\right)$ is the diagonal matrix of the vector $E$ elements. ${\chi }_{E,\Delta }$ corresponds to the ${\mathcal{A}}_E$-algorithm

$$\Delta \dot{A}=-{\mathsf{\Gamma }}_{A}RE{X}^T-{\alpha }_{E,\Delta }D\left(\left|e_i\right|\right)\Delta A.$$

(21)

Remark 5 is valid for (21). Modifications and simplifications of the G2 algorithm are possible. As a special case, algorithm (5) follows from (20).

Remark 6. FR can have a different form. Above, we have considered only some examples of restrictions $\chi \left(E,\Delta A\right)$ for adaptive identification of matrix $A$. The described approach is valid for the vector $B$ identification. If in variant (2b) ${\chi }_{X,\Delta }={\alpha }_{X,\Delta }\mathrm{Sp}\left(\Delta A^{T}D\left(\left|x_i\right|\right)\Delta A\right)$, then we get of the algorithm (18) analog from (20), a special case of which is equation (6).

6. AIS Properties

We will evaluate the limitations of AIS trajectories using algorithms (19) and

$$\Delta \dot{B}(t)=-{\mathsf{\Gamma }}_{B}RE(t)u(t)-{\omega }_e{\mathsf{\Gamma }}_{B_1}\left(\Delta B(t)-\Delta B(t-\tau )\right)$$

(22)

Theorem 1. Let: 1) $A\in \mathcal{H}$ is the Hurwitz matrix; 2) Lyapunov functions $V_{\Delta }(t)=0.5\mathrm{tr}\left(\Delta A^T{\mathsf{\Gamma }}_A^{-1}\Delta A(t)\right)+0.5\Delta B^T{\mathsf{\Gamma }}_B^{-1}\Delta B(t)$ and $V_E=0.5E^{T}RE$ assume an infinitesimal upper limit, where ${\mathsf{\Gamma }}_A,{\mathsf{\Gamma }}_B$ are diagonal matrices with positive diagonal elements; 3) $X(t)\in \mathcal{E}{\mathcal{C}}_{{\underset{¯}{\alpha }}_X,{\overline{\alpha }}_X}$, $u(t)\in \mathcal{E}{\mathcal{C}}_{{\underset{¯}{\alpha }}_u,{\overline{\alpha }}_u}$; 4) 4) exists $\upsilon >0$ such that the condition

$$\mathrm{tr}\left(\Delta A^T{\mathsf{\Gamma }}_{\dot{A}}^{-1}{\mathsf{\Gamma }}_{A}ER{X}^T\right)=\upsilon \left[\left(\mathrm{tr}\left(\Delta A^T{\mathsf{\Gamma }}_{\dot{A}}^{-1}{\mathsf{\Gamma }}_A\Delta A\right)+E^T{R}^{2}E{‖X‖}^2\right)\right]$$

(23)

is performed at sufficiently large $t$ in some neighbourhood of $\mathbb{O}(0)$ zero. Then the trajectories of the system (9), (19), (22) are bounded on some set of initial conditions if

$${‖\Delta A(t-\tau )‖}^2\le \eta V_{\Delta }-\upsilon {\displaystyle \frac{2{\sigma }_e}{3{\sigma }_{\Delta }}}{V}_E,$$

(24)

where $\eta ={\underset{¯}{\lambda }}_{{\mathsf{\Gamma }}_{\dot{A}}}\left(1+{\displaystyle \frac{3}{4}}\upsilon {\sigma }_{\Delta }\right)$, ${\sigma }_e={\underset{¯}{\alpha }}_{X}2{\underset{¯}{\lambda }}_R$${\sigma }_{\Delta }={\underset{¯}{\lambda }}_{{\mathsf{\Gamma }}_{\dot{A}}}{\underset{¯}{\lambda }}_{{\mathsf{\Gamma }}_A}$, ${\underset{¯}{\lambda }}_{{\mathsf{\Gamma }}_{\dot{A}}}$ is the minimum eigenvalue of the matrix.

The proof of Theorem 1 is presented in Appendix A.

Theorem 1 confirms the limited trajectories in the system (9), (19), (22) and the possibility of local identifiability of model parameters. These statements are valid for some set of initial conditions, since AIS is a system with the delay.

Consider the system (9), (15). To simplify the results, we assume that the vector $\widehat{B}$ of the model (7) is precisely tuned (i.e., $\Delta B=0$), and:

$$\dot{E}=-KE+\Delta AX,$$

(25)

Present the algorithm (15) in the form (see Appendix B)

$$\Delta \dot{A}=-\upsilon \Delta A-d^{-1}{\mathsf{\Gamma }}_{A}ER{X}^T-\overline{\kappa }\Delta A(t-\tau ),$$

(26)

In (26), the argument $t$ is omitted, and $t-\tau$ is used to emphasise the delay.

Consider FL $V_E=0.5\left(E^{T}RE\right)$ and the Lyapunov

$$V_{\Delta ,\upsilon ,\tau }=V_{\Delta ,\upsilon }+V_{\Delta ,\tau }=0.5\mathrm{tr}\left(\Delta A^T\Delta A\right)+c{\displaystyle \underset{-\tau }{\overset{0}{\int }}\mathrm{tr}\left(\Delta A^T(t+s)\Delta A(t+s)\right)ds}$$

(27)

depending on initial conditions for $A(t-\tau )$.

Theorem 2. Let the theorem 1 conditions be fulfilled, where the functional (26) is used instead of $V_{\Delta }$, and 1) exists $\omega >0$ such that the condition

$$\mathrm{tr}\left(\Delta A^T\Delta A\left(t-\tau \right)\right)=\omega \left(\mathrm{tr}\left(\Delta A^T\Delta A\right)+\mathrm{tr}\left(\Delta A^T\left(t-\tau \right)\Delta A\right)\right)$$

is performed at sufficiently large $t$ in some neighbourhood of $\mathbb{O}(0)$ zero; 2) the system of inequalities

$$\underset{\dot{W}}{\underbrace{\left[\begin{array}{c}{\dot{V}}_E\\ {\dot{V}}_{\Delta ,\upsilon ,\tau }\end{array}\right]}}=\left[\begin{array}{cc}-{\mu }_E& {\overline{\alpha }}_X\tilde{\rho }\\ {\displaystyle \frac{{\overline{\lambda }}_{{\mathsf{\Gamma }}_A}^2{\overline{\alpha }}_X{\overline{\lambda }}_R}{8\upsilon d^2}}& -2{\omega }_{\Delta }\end{array}\right]\underset{W}{\underbrace{\left[\begin{array}{c}{V}_E\\ V_{\Delta ,\upsilon ,\tau }\end{array}\right]}}$$

(28)

is fair, where $\tilde{\rho }>0,$ ${\omega }_{\Delta }>0$ are numbers depending on the parameters of the adaptive system; 3) the upper solution for the Lyapunov vector function $W={\left[V_E\hspace{0.17em}\hspace{0.17em}{V}_{\Delta ,\upsilon ,\tau }\right]}^T$ satisfies the comparison system ${\dot{S}}_W=A_W{S}_W$ if $s_{W,k}\left(t_0\right)\ge w_{W,k}\left(t_0\right)$, where $s_{W,k}\left(t_0\right),\hspace{0.17em}\hspace{0.17em}{w}_{W,k}\left(t_0\right)$ are initial conditions for elements of corresponding vectors, $k=E,\left(\Delta ,\upsilon ,\tau \right)$. Then the adaptive system (25), (19), (26) is exponentially stable with the estimate

$$W_D\left(t_0\right)\le e^{A_D\left(t-t_0\right)}{S}_D\left(t_0\right)$$

If $\left({\mu }_E,{\omega }_{\Delta }\right)>0$, $2{\mu }_E{\omega }_{\Delta }>{\overline{\alpha }}_X\tilde{\rho }{\overline{\lambda }}_{{\mathsf{\Gamma }}_A}^2{\overline{\alpha }}_X{\overline{\lambda }}_R/8\upsilon d^2$, $\overline{\lambda }$ are the maximum eigenvalue of the matrix, $\tilde{\rho }>0$.

The proof of Theorem 1 is presented in Appendix C.

Theorem 2 proofs the exponential stability of the adaptive system (AS) with algorithm (26). We apply the Lyapunov functional (27) to prove this property.

Remark 7. Consider the tuning algorithm $\widehat{B}$ (26) does not change the statement of Theorem 2. In this case, the system of inequalities is valid (28).

So, we have proved the applications of AA as a dynamic system. These algorithms improve the quality of tuning process for model parameters.

Consider AIS (9), (21) with the algorithm

$$\Delta \dot{B}=-{\mathsf{\Gamma }}_{B}REu$$

(29)

where ${\mathsf{\Gamma }}_B={\mathsf{\Gamma }}_B>0$ is the diagonal matrix.

Theorem 3. Let conditions 1-3 of Theorems 1 be fulfilled and 1) exists ${\upsilon }_u>0$ such that the condition $\Delta B^{T}REu=0.5{\upsilon }_u\left(\Delta B^T\Delta B+2‖REu‖\right)$ is performed at sufficiently large $t$ in some neighbourhood of $\mathbb{O}(0)$ zero; 2) the system of inequalities

$$\underset{\dot{\mathsf{\Xi }}}{\underbrace{\left[\begin{array}{c}{\dot{V}}_E\\ {\dot{V}}_{\Delta }\end{array}\right]}}\le \underset{A_{\mathsf{\Xi }}}{\underbrace{\left[\begin{array}{cc}-{\mu }_E& \rho \\ {\eta }_u& -\stackrel{⌣}{\kappa }\end{array}\right]}}\underset{\mathsf{\Xi }}{\underbrace{\left[\begin{array}{l}{V}_E\\ V_{\Delta }\end{array}\right]}}$$

(30)

is fair, where ${\mu }_E$, $\tilde{\rho }$, $\stackrel{⌣}{\kappa }$ are positive numbers depending on the parameters of the adaptive system; 3) the upper solution for the Lyapunov vector function $W_{\mathsf{\Xi }}={\left[V_E\hspace{0.17em}\hspace{0.17em}{V}_{\Delta }\right]}^T$ $W={\left[V_E\hspace{0.17em}\hspace{0.17em}{V}_{\Delta ,\upsilon ,\tau }\right]}^T$ satisfies the comparison system ${\dot{S}}_{\mathsf{\Xi }}=A_{\mathsf{\Xi }}{S}_{\mathsf{\Xi }}$ if $s_{\mathsf{\Xi },k}\left(t_0\right)\ge w_{\mathsf{\Xi },k}\left(t_0\right)$, where $s_{W_{\mathsf{\Xi }},k}\left(t_0\right),\hspace{0.17em}\hspace{0.17em}{w}_{W_{\mathsf{\Xi }},k}\left(t_0\right)$ are initial conditions for elements of correspond vectors, $k=E,\Delta$. Then the adaptive system (9), (21), (29) is exponentially stable with the estimate:

$$W_{\mathsf{\Xi }}\left(t_0\right)\le e^{A_{\mathsf{\Xi }}\left(t-t_0\right)}{S}_{\mathsf{\Xi }}\left(t_0\right)$$

if ${\mu }_E>0,\hspace{0.17em}\hspace{0.17em}\stackrel{⌣}{\kappa }>0$, ${\eta }_u={\displaystyle \frac{{\overline{\alpha }}_X{\overline{\lambda }}_R}{8\tilde{\alpha }}}-{\upsilon }_u{\underset{¯}{\alpha }}_u{\underset{¯}{\lambda }}_R$ and ${\mu }_E\stackrel{⌣}{\kappa }\ge \rho {\eta }_u$.

Remark 8. Properties of IAA obtained without restrictions depend on the CE condition fulfilment.

7. Simulation Results

Consider the system

$$\begin{array}{l}{S}_1:\left\{\begin{array}{l}\hspace{0.17em}\left[\begin{array}{l}{\dot{x}}_{11}\\ {\dot{x}}_{12}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -a_{21}& -a_{22}\end{array}\right]\left[\begin{array}{l}{x}_{11}\\ x_{12}\end{array}\right]+\left[\begin{array}{l}0\\ {\overline{a}}_1\end{array}\right]x_2+\left[\begin{array}{l}0\\ b_1\end{array}\right]u_1+\left[\begin{array}{l}0\\ c_1\end{array}\right]f_1\left(x_{11}\right),\\ y_1=x_{11},\end{array}\right.\hspace{0.17em}\\ \hspace{0.17em}{S}_2:\hspace{0.17em}\left\{\begin{array}{l}{\dot{x}}_2=-a_2{x}_2+{\overline{a}}_2{x}_{11}+b_2{u}_2+c_2{f}_1\left(x_{11}\right),\\ y_2=x_2,\end{array}\right.\end{array}$$

(31)

where $X_1={\left[x_{11}\hspace{0.17em}\hspace{0.17em}{x}_{12}\right]}^T$, $y_1$ are state vector and output of the subsystem $S_1$; $u_1$ is input (control); $f_1\left(x_{11}\right)=\mathrm{sat}\left(x_{11}\right)$ is saturation function; $f_2\left(x_2\right)=\mathrm{sign}\left(x_2\right)$ is the sign function; $y_2$ is output of the subsystem $S_2$, $b_1=1$, $a_{21}=2,\hspace{0.17em}\hspace{0.17em}{a}_{22}=3$, ${\overline{a}}_1=1.5$, $b_1=1$, $c_1=1$, $a_2=1.25,$ ${\overline{a}}_2=0.2$, $b_2=1$, $c_2=0.25$. $u_i(t)$ inputs were sinusoidal.

The subsystem $S_1$ equation is represented [17] as:

$${\dot{y}}_1=-{\alpha }_1{y}_1+{\alpha }_2{p}_{y_1}+{\beta }_{12}{p}_{x_2}+b_1{p}_{u_1}+c_1{p}_{f_1},$$

(32)

where ${\alpha }_1$, ${\alpha }_2$, ${\beta }_{12}$, $b_1,\hspace{0.17em}\hspace{0.17em}{c}_1$ are estimated coefficients; $\mu >0$,

$$\begin{array}{c}{\dot{p}}_{y_1}=-\mu p_{y_1}+y_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\dot{p}}_{x_2}=-\mu p_{x_2}+x_2,\hspace{0.17em}\hspace{0.17em}\\ {\dot{p}}_{u_1}=-\mu p_{u_1}+u_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\dot{p}}_{f_1}=-\mu p_{f_1}+f_1.\end{array}.$$

(32)

Models for the system (31)

$${\dot{\widehat{y}}}_1=-k_1{e}_1+{\widehat{a}}_{11}{y}_1+{\widehat{a}}_{12}{p}_{y_1}+{\widehat{\beta }}_{12}{p}_{x_2}+{\widehat{b}}_1{p}_{u_1}+{\widehat{c}}_1{p}_{f_1},$$

(33)

$${\dot{\widehat{y}}}_2=-k_2{e}_2+{\widehat{a}}_2{y}_2+{\widehat{\overline{a}}}_2{y}_1+{\widehat{b}}_2{u}_2+{\widehat{c}}_1{f}_2,$$

(34)

where $k_1,k_2>0$, $e_1={\widehat{y}}_1-y_1$, $e_2={\widehat{y}}_2-y_2$, ${\widehat{a}}_i,\hspace{0.17em}{\widehat{\overline{a}}}_i,\hspace{0.17em}{\widehat{b}}_i,\hspace{0.17em}{\widehat{c}}_i$ are tuning parameters.

Adaptive algorithms

$$\begin{array}{c}{\dot{\widehat{a}}}_{11}=-{\gamma }_{a_{11}}{e}_1{y}_1+{\overline{\gamma }}_{a_{11}}{\widehat{a}}_{11}(t-\tau ),\hspace{0.17em}\hspace{0.17em}{\dot{\widehat{a}}}_{12}=-{\gamma }_{a_{12}}{e}_1{p}_{y_1},\hspace{0.17em}\hspace{0.17em}{\dot{\widehat{\beta }}}_{12}=-{\gamma }_{{\beta }_{12}}{e}_1{p}_{x_2},\\ {\dot{\widehat{b}}}_1=-{\gamma }_{b_1}{e}_1{p}_{u_1},\hspace{0.17em}\hspace{0.17em}{\dot{\widehat{c}}}_1=-{\gamma }_{c_1}{e}_1{p}_{f_1}+{\overline{\gamma }}_{c_1}{\widehat{c}}_1(t-\tau ),\end{array}$$

(35)

$${\dot{\widehat{a}}}_2=-{\gamma }_{a_2}{e}_2{y}_2,\hspace{0.17em}{\dot{\widehat{\overline{a}}}}_2=-{\gamma }_{{\overline{a}}_2}{e}_2{y}_1,\hspace{0.17em}\hspace{0.17em}{\dot{\widehat{b}}}_2=-{\gamma }_{b_2}{e}_2{u}_1,\hspace{0.17em}\hspace{0.17em}{\dot{\widehat{c}}}_2=-{\gamma }_{c_2}{e}_2{f}_2,$$

(36)

where ${\gamma }_{a_{11}}=0.026\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\gamma }_{{\beta }_{12}}=0.025,\hspace{0.17em}{\gamma }_{b_1}=0.002,\hspace{0.17em}{\gamma }_{c_1}=0.05,\hspace{0.17em}{\overline{\gamma }}_{c_i}=0.03,\hspace{0.17em}{\overline{\gamma }}_{a_{11}}=0.5$.

Results are shown in Figure 1, Figure 2 and Figure 3. s 1 reflects the adequacy of the models (33), (34).

Figure 1. Adequacy of models (33) and (34): 1 is model (33), 2 is model (34).

Figure 1. Adequacy of models (33) and (34): 1 is model (33), 2 is model (34).

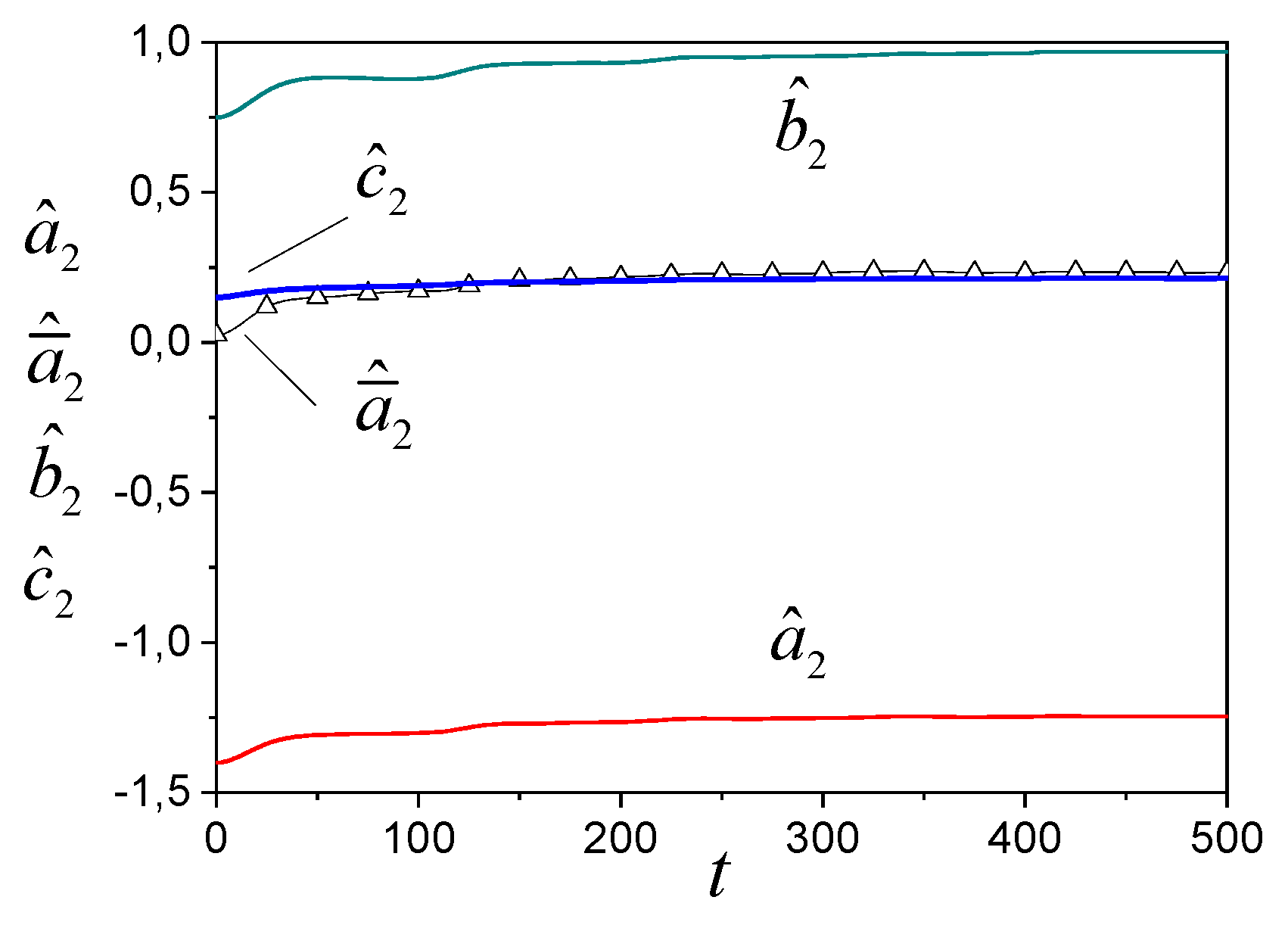
Results of tuning parameters for models (33) and (34) are shown in Figure 2 and Figure 3.

Figure 2. Tuning parameters of model (33).

Figure 2. Tuning parameters of model (33).

Figure 3. Tuning parameters of model (34).

Figure 3. Tuning parameters of model (34).

Simulation results confirm the proposed AA performance. (35) and (36). Tuning process can be linear or nonlinear. Efficiency is determined by properties of the adaptive system and the parameters of signals.

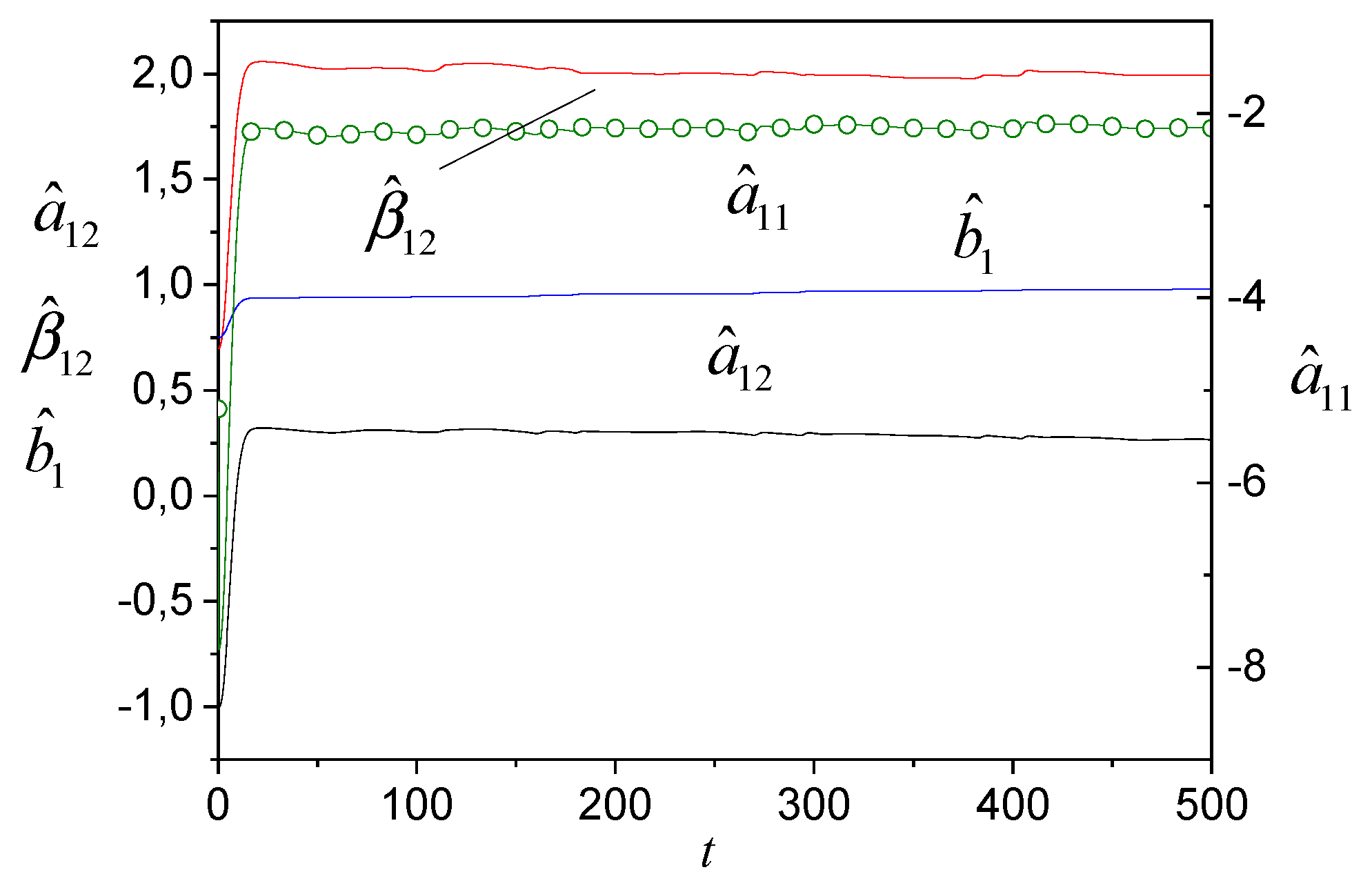
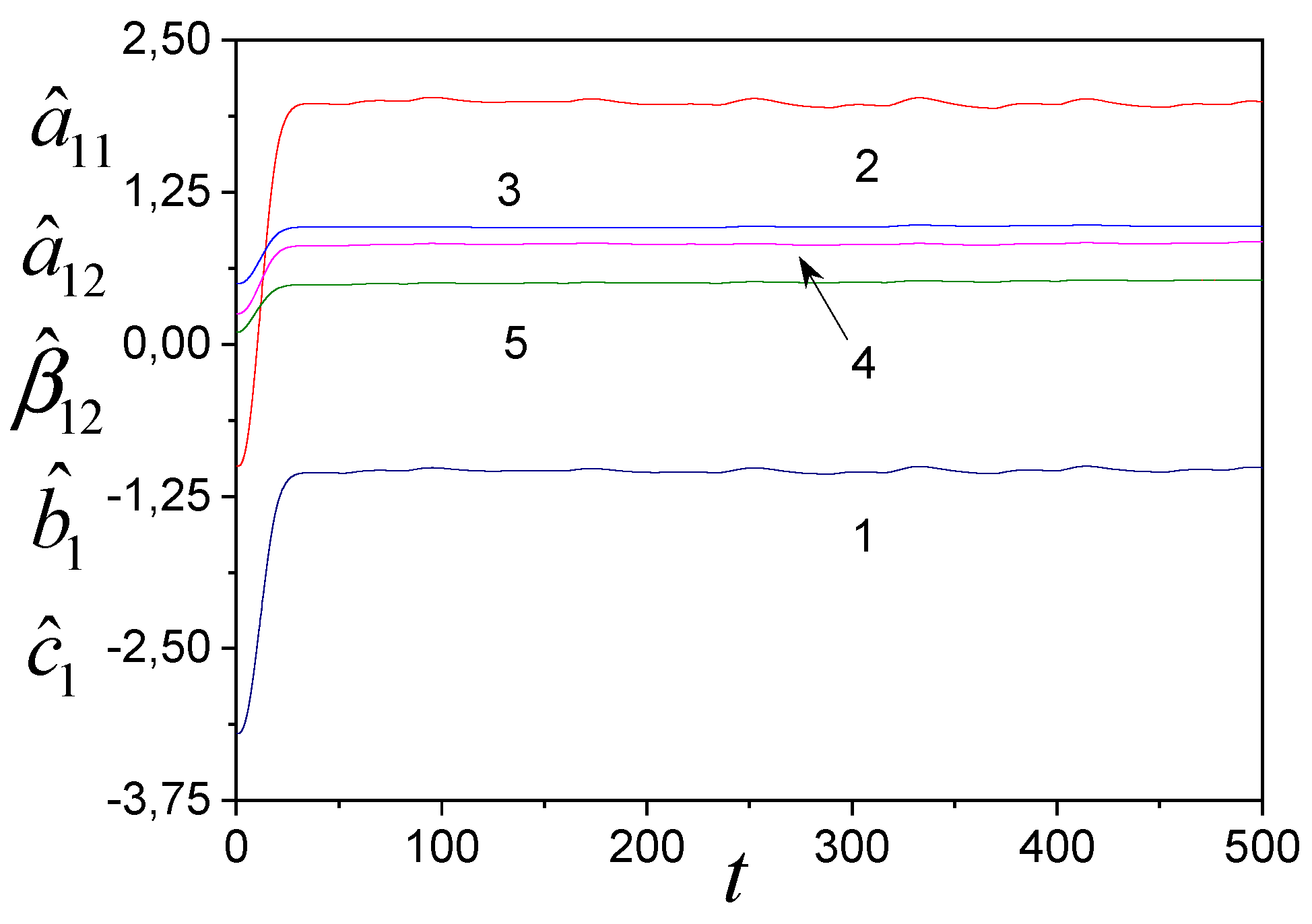
In Figure 4, Figure 5 and Figure 6, we present identification results of the system (31) with algorithms (35), (36), where algorithms for tuning ${\widehat{a}}_{11}$ and ${\widehat{c}}_1$ in (35) have the form

$$\begin{array}{c}{\dot{\widehat{a}}}_{11}=\left\{\begin{array}{c}\left(1-{\overline{\gamma }}_{a_{11}}\left|e_1\right|\right)-{\gamma }_{a_{11}}{e}_1{y}_1,\hspace{0.17em}\hspace{0.17em}\mathrm{if}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|e_1\right|/\left|y_1\right|>0.1,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{a}}_{11}-{\gamma }_{a_{11}}{e}_1{y}_1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{if}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left|e_1\right|/\left|y_1\right|\le 0.1,\end{array}\right.\\ {\dot{\widehat{c}}}_1=-{\gamma }_{c_1}{e}_1{p}_{f_1}.\end{array}$$

To ensure the system (31) S-synchroniability, we changed parameters $b_1=2.9$ and $b_2=1.4$. Tuning parameters for models (33) and (34) are shown in Figure 4 and Figure 5. The adequacy of the models is reflected in Figure 6.

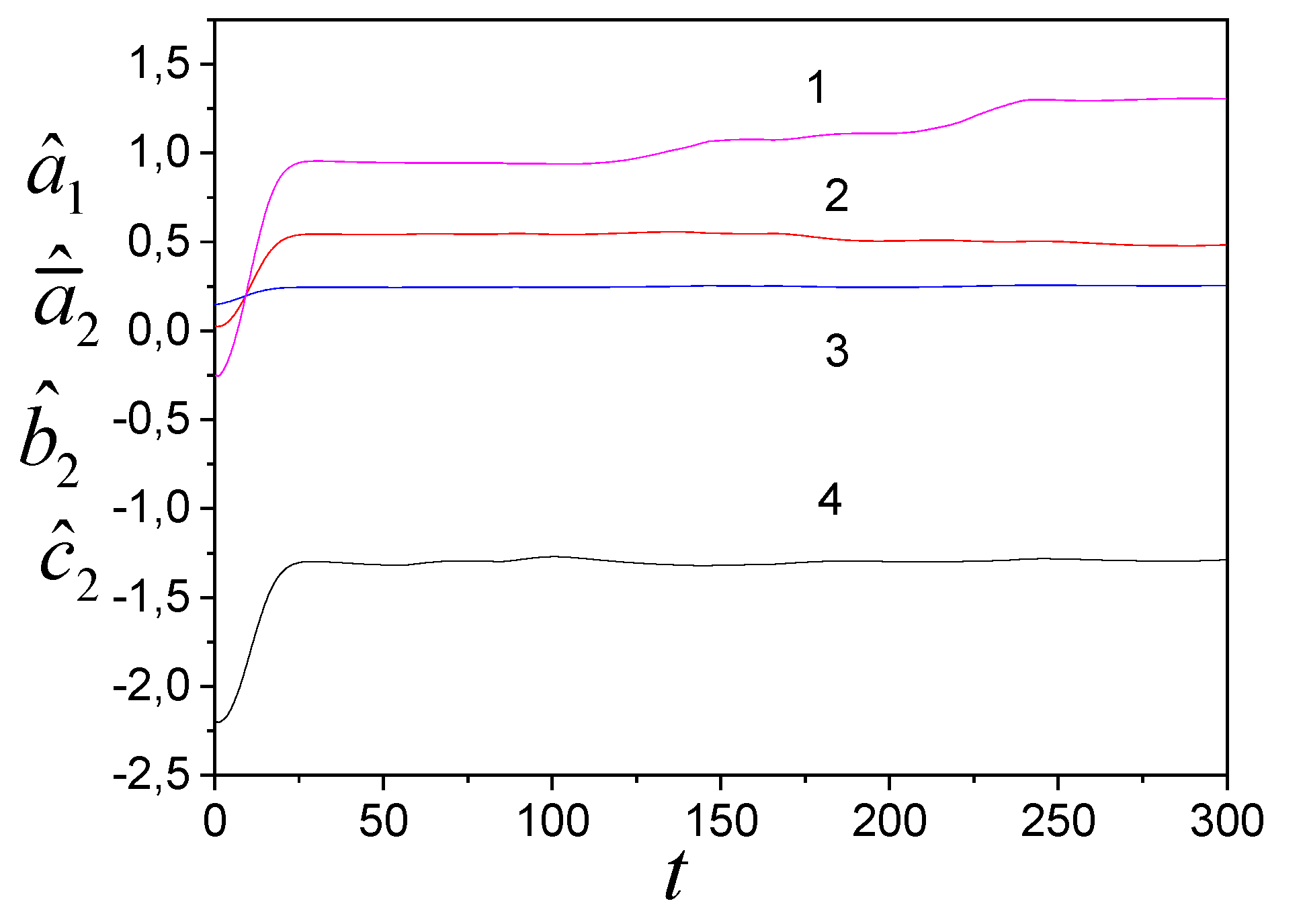
Figure 4. Tuning parameters of model (33): 1– ${\widehat{a}}_{11}$, 2 – ${\widehat{a}}_{12}$, 3 – ${\widehat{\beta }}_{12}$, 4 – ${\widehat{b}}_1$, 5 – ${\widehat{c}}_1$.

Figure 4. Tuning parameters of model (33): 1– ${\widehat{a}}_{11}$, 2 – ${\widehat{a}}_{12}$, 3 – ${\widehat{\beta }}_{12}$, 4 – ${\widehat{b}}_1$, 5 – ${\widehat{c}}_1$.

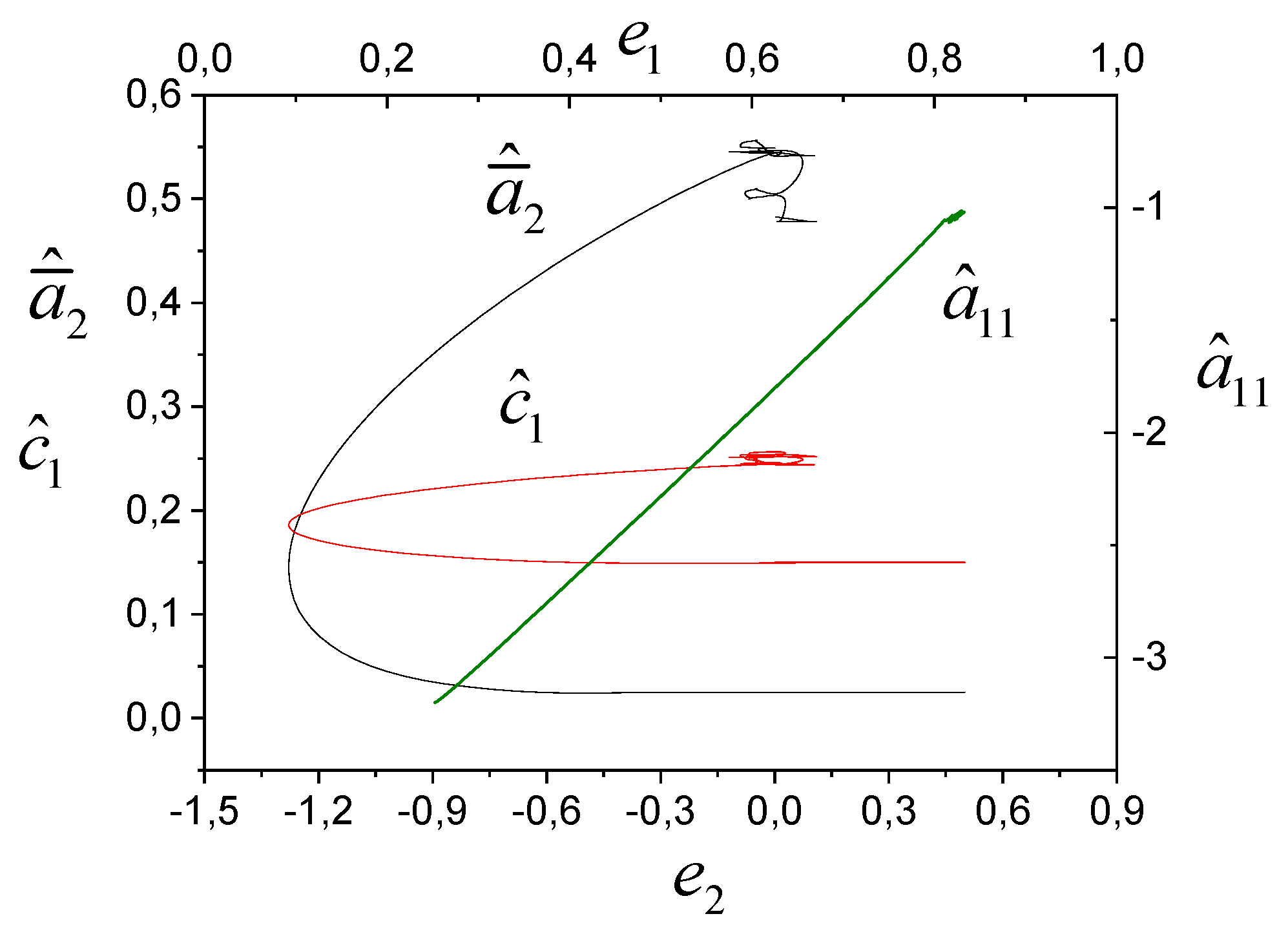
Figure 5. Tuning parameters of model (34): 1 is ${\widehat{b}}_2$, 2 is ${\widehat{a}}_1$, 3 is ${\widehat{c}}_2$, 4 is ${\widehat{\overline{a}}}_2$.

Figure 5. Tuning parameters of model (34): 1 is ${\widehat{b}}_2$, 2 is ${\widehat{a}}_1$, 3 is ${\widehat{c}}_2$, 4 is ${\widehat{\overline{a}}}_2$.

Figure 6. Adequacy of models (33) and (34).

Figure 6. Adequacy of models (33) and (34).

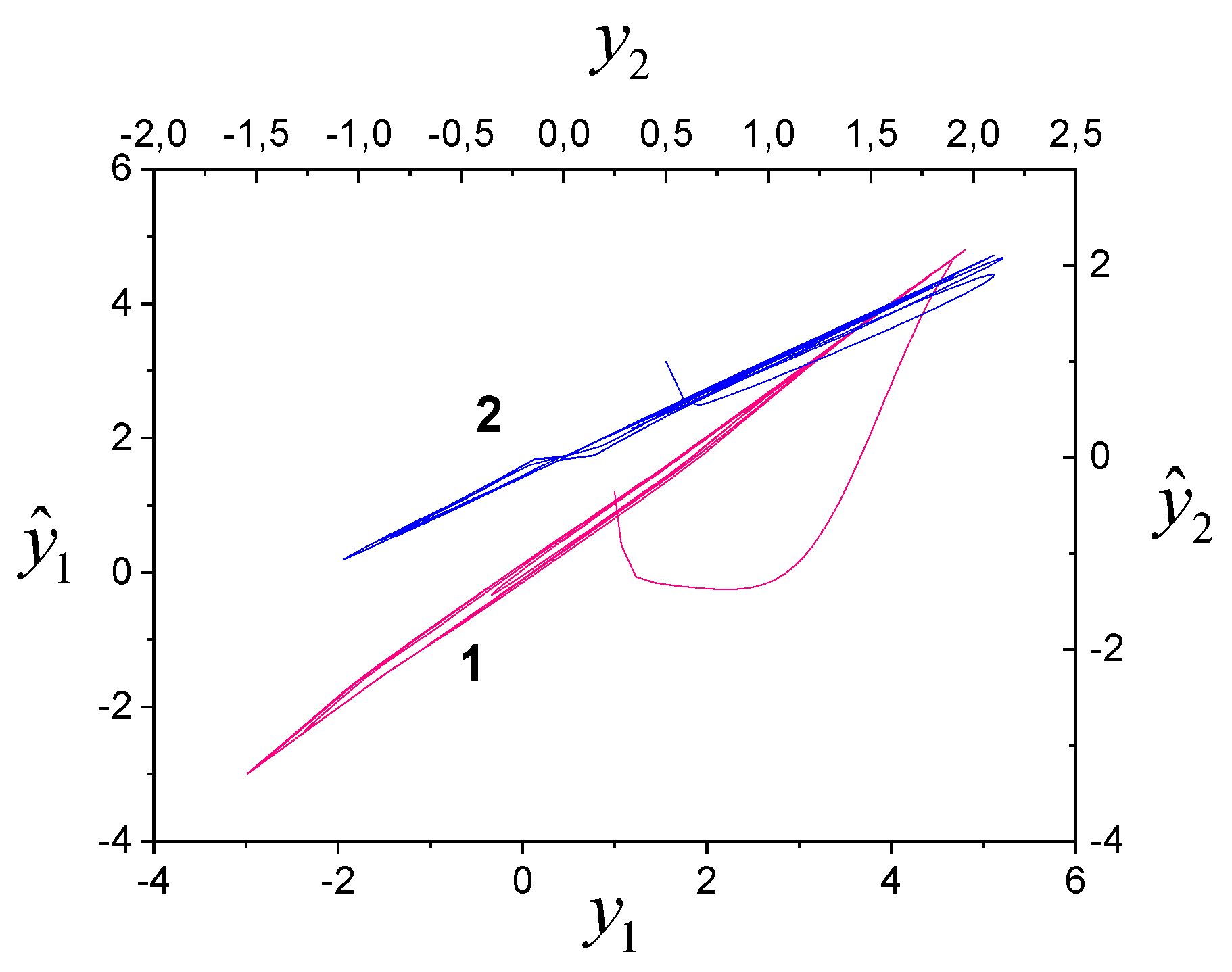
We see that the outputs of subsystems affect adaptation processes.

Figure 7 shows phase portraits in AIS in spaces $\left(e_1,{\widehat{a}}_{11}\right)$ и $\left(e_2,{\widehat{с}}_1\right)$, $\left(e_2,{\widehat{\overline{a}}}_2\right)$. We see that adaptation processes for $S_2$ are nonlinear, and they are almost linear for the $S_1$ system.

Figure 7. Phase portraits of AIS in spaces $\left(e_1,{\widehat{a}}_{11}\right)$, $\left(e_2,{\widehat{с}}_1\right)$ and $\left(e_2,{\widehat{\overline{a}}}_2\right)$.

Figure 7. Phase portraits of AIS in spaces $\left(e_1,{\widehat{a}}_{11}\right)$, $\left(e_2,{\widehat{с}}_1\right)$ and $\left(e_2,{\widehat{\overline{a}}}_2\right)$.

So, the simulation results confirm the proposed algorithms.

8. Conclusion

The approach to the synthesis of adaptive algorithms based on requirements for the adaptation process is proposed. These requirements are presented as functional constraints (FR). It is shown that, for the considered class of FR, the adaptive algorithm is described by the system in the state space. Special cases of FR are considered and the corresponding AA are obtained. For one class of adaptive algorithms, a representation is presented as the dynamic system with an aftereffect. Properties of adaptive systems of identification are studied, and the limited of trajectories and exponential stability are proved. Simulation results confirm the efficiency of adaptive algorithms.