Rotational Contraction Effects on Hawking–Bekenstein Entropy in Kerr and Schwarzschild Black Holes

1. Introduction

Length contraction, a consequence of special relativity, describes how objects moving at relativistic speeds appear shortened along their direction of motion. While originally formulated for linear motion, analogous contraction-like effects may conceptually extend to rotational motion in relativistic regimes such as Kerr black holes.

Rotating black holes are characterized by mass and angular momentum. The rotation significantly distorts spacetime near the event horizon, giving rise to phenomena like frame-dragging and the formation of an ergosphere. These modifications suggest that angular velocity might induce relativistic geometric effects, potentially influencing the thermodynamic properties of the black hole.

The Bekenstein–Hawking entropy relates entropy to the surface area of the event horizon. We hypothesize that relativistic rotation contracts the effective horizon geometry, reducing its area and thereby decreasing entropy. Though our contraction model is heuristic, it aligns qualitatively with observed geometric behavior in rotating spacetime metrics.

2. Theoretical Background

Schwarzschild Black Hole: For a non-rotating black hole of mass$M$The event horizon radius is$r_s=2GM$, and the surface area is:

$$A_{Sch}=16\pi G²M²$$

Corresponding entropy:

$$S_{Sch}=k{A}_{Sch}/\left(4ħG\right)$$

A rotating black hole with mass and angular momentum, and the angular parameter can be defined as follows,

$$J=a.M;$$

The outer horizon radius is:

$$r_{+}=M+\surd (M²-a²)$$

The surface area of the event horizon is:

$$A_{Kerr}=8\pi M(M+\surd (M²-a²\left)\right)$$

As $a\to M$ (extremal limit), The horizon area shrinks.

$$S_{Kerr}=A_{Kerr}.{\left(4ħG\right)}^{-1}$$

3. Heuristic Contraction Analogy

Inspired by special relativity, we propose a contraction factor analogous to the Lorentz factor γ, applied heuristically to the rotating horizon. This yields an effective reduction in horizon area and, hence, in entropy. Though not formally derived from general relativity, this analogy offers an intuitive bridge between motion and geometry:

$$A_{eff}=A_{Kerr}/\gamma ²\left(a\right)\Rightarrow S_{eff}<S_{Sch}$$

4. Comparison of Schwarzschild and Kerr Entropy

For equal mass M:

Schwarzschild entropy:

$$S_{Sch}={\displaystyle \frac{4\pi kG{M}^2}{\mathrm{ħ}}}$$

Kerr entropy:

$$S_{Kerr}=\left(k8\pi M\left(M+\sqrt{M^2-a^2}\right)\right).{\left(4\mathrm{ħ}G\right)}^{-1}$$

$S_{Kerr}<S_{Sch}$ ,if $a>0$.

5. Main Theoretical Claims

Claim I:

Kerr black hole entropy is reduced due to relativistic contraction induced by rotation.

Claim II:

For fixed mass, Schwarzschild black holes exhibit maximal entropy.

Claim III:

Horizon geometry is sensitive to angular momentum, shaping the entropy landscape.

These claims highlight the interdependence of motion, geometry, and thermodynamics.

6. Conclusion and Future Outlook

This study shows how rotational effects in Kerr black holes lead to reduced event horizon areas and, hence, reduced entropy. While our contraction analogy is heuristic, it conceptually mirrors the geometric evolution of rotating spacetimes.

Future research directions include:

- Numerical simulations of rotating black holes to visualize horizon deformation with spin.

- Quantum corrections to black hole entropy under high angular momentum.

- Entropy transport mechanisms involving the ergosphere and Penrose process.

- Exploring entanglement entropy perspectives linked to horizon geometry.

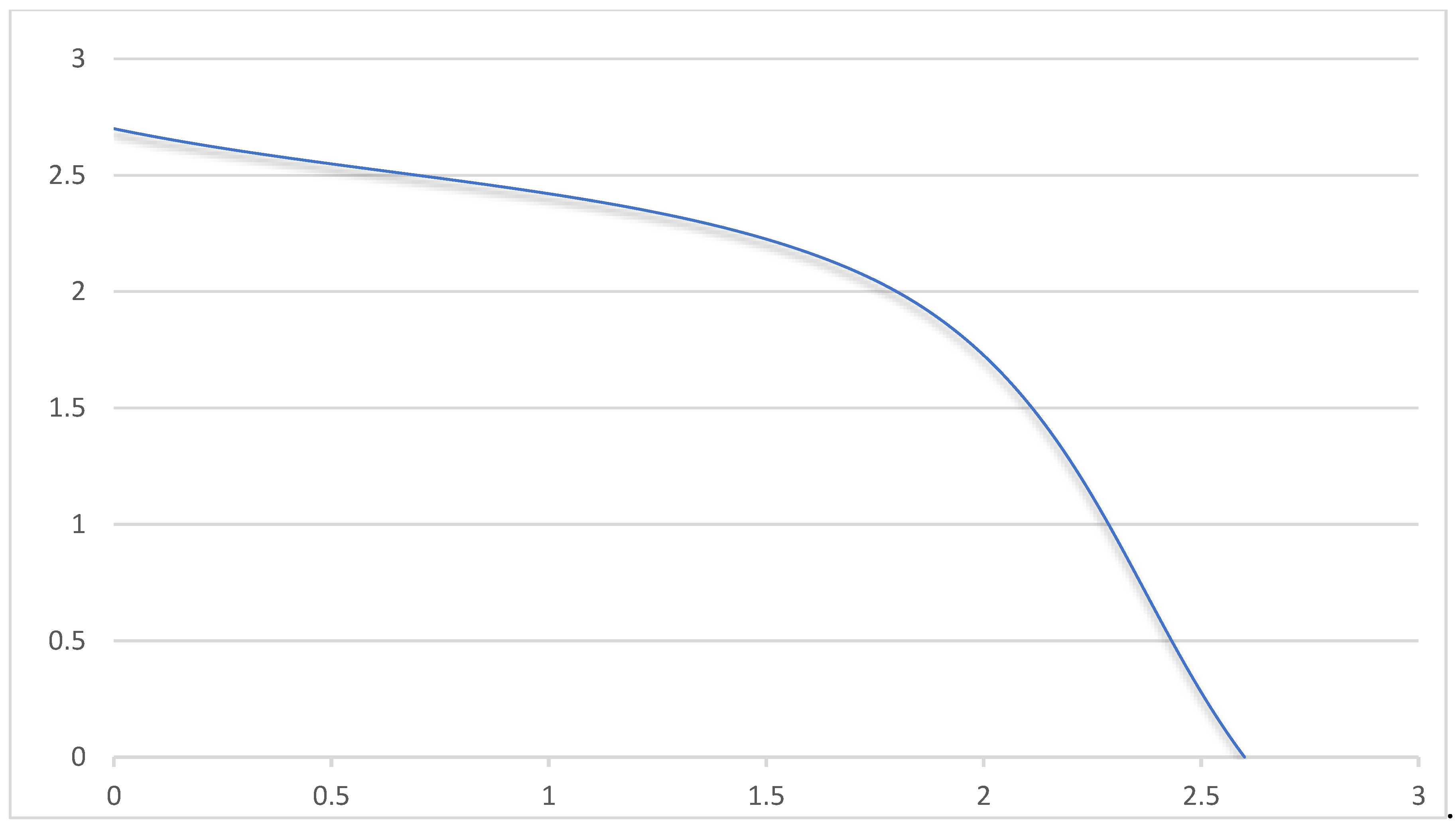
Figure 1. Entropy vs. spin parameter ${\displaystyle \frac{a}{M}}$.

Figure 1. Entropy vs. spin parameter ${\displaystyle \frac{a}{M}}$.

This plot illustrates the decrease in Kerr entropy as the spin parameter increases.