Ricci Flow and Schwarzschildʹs Metric

Rohit Dhormare

doi:10.20944/preprints202504.0527.v1

Submitted:

05 April 2025

Posted:

07 April 2025

You are already at the latest version

Abstract

This paper delves into the intriguing intersection between the Ricci low and the Schwarzschild metric, focusing primarily by applying these concepts to time-dependent metrics for spherical bodies, such as stars. By exploring the dynamic nature of the Schwarzschild metric through the lens of Ricci low, we aim to provide insights into the evolving geometry of space-time surrounding massive objects. Our study seeks to enhance the understanding of how massive bodies, like stars, influence the fabric of space-time over time, potentially impacting theories of gravity and cosmology.

Keywords:

Ricci flow

;

Schwarzschild metric

;

curvature tensor

Subject:

Physical Sciences - Theoretical Physics

Introduction

The Schwarzschild metric, introduced by Karl Schwarzschild in 1916, represents a significant milestone in the field of general relativity. It provides a solution to Einstein's field equations in the vacuum outside a spherical mass. The elegance of this metric lies in its simplicity and its ability to describe the gravitational field outside a spherical, non-rotating, uncharged mass such as a planet, star, or black hole. The metric is expressed as:

{d s}^{2} (t) = - (1 - \frac{2 G m (r)}{r}) d t^{2} + {(1 - \frac{2 G m (r)}{r})}^{- 1} d r^{2} + r^{2} d Ω^{2} .

where ( G ) is the gravitational constant, ( m ) is the mass of the object, and ( r ) is the radial coordinate from the center of the mass.

In this paper, we extend the Schwarzschild metric to incorporate time dependence, drawing upon the principles of Ricci flow. The Ricci flow, an equation introduced by Richard S. Hamilton, describes the process of deforming the metric of a Riemannian manifold in a way that "smooths out" irregularities in its shape.

The flow is defined as:

[g_{i j} ⟨t⟩ = - 2 \frac{\partial R}{\partial t}]

Where ( R ) is the Ricci tensor and (

g_{i j}

) is the metric tensor. By applying Ricci flow to the Schwarzschild metric, we explore how the space-time geometry around massive objects evolves. More advanced and detailed study appears in the [3].

Time-Dependent Schwarzschild Metric

The time-dependent Schwarzschild metric is formulated as:

d s^{2} (t) = - (1 - \frac{2 G m (t)}{r (t)}) d t^{2} + {(1 - \frac{2 G m (t)}{r (t)})}^{- 1} d r^{2} {+ r}^{2} d Ω^{2} .

This formulation allows for the mass ( m ) and radial coordinate ( r ) to vary with time, reflecting the dynamic nature of celestial bodies. The components of the time-dependent covariant metric are given by:

{1 . g}_{t t} (t) = - (1 - \frac{2 G m (t)}{r (t)});

{2 . g}_{r r} (t) = {(1 - \frac{2 G m (t)}{r (t)})}^{- 1};

{3 . g}_{Ѳ Ѳ} (t) = r^{2} (t);

{4 . g}_{φ φ} (t) = r^{2} (t) \sin^{2} Ѳ (t);

These components highlight the influence of Ricci flow on space-time geometry, suggesting a continuous deformation process akin to the evolution of shapes in geometry.

Time-dependent Curvature and Ricci Tensor

The Ricci flow not only influences the metric components but also affects the curvature of spacetime. The time-dependent curvature and Ricci tensor are expressed as:

[g_{i j} ⟨t⟩ = - 2 \frac{\partial R}{\partial t}]

With specific expressions for each component:

g_{t t} ⟨t⟩ = - 2 \frac{\partial R^{t t} . - 1 - \frac{2 G M}{r}}{\partial t}

(1)

g_{r r} ⟨t⟩ = - 2 \frac{\partial R^{r r} {(1 - \frac{2 G m (t)}{r (t)})}^{- 1}}{\partial t}

(2)

g_{Ѳ Ѳ} ⟨t⟩ = - 2 \frac{\partial R^{Ѳ Ѳ} . r^{2}}{\partial t}

(3)

g_{φ φ} ⟨t⟩ = - 2 \frac{\partial R^{φ φ} . r^{2} \sin^{2} Ѳ}{\partial t}

(4)

(As time ( t ) approaches infinity, these components trend towards zero, indicating a flattening of the space-time curvature around massive bodies. This suggests that over immense periods, the distortions in space-time caused by massive objects may diminish, potentially leading to a more uniform geometry. An important note is that we don’t provide a clear picture of the components of the Ricci tensor of the black hole’s metric. It’s easy to obtain.

Conclusions

The study of time-dependent metrics through Ricci flow provides valuable insights into the dynamic nature of space-time around massive objects. By understanding how these metrics evolve, we gain a deeper comprehension of the complex interplay between geometry and gravity. This understanding is crucial for advancing our knowledge of cosmology and the behavior of stars, galaxies, and black holes over time.

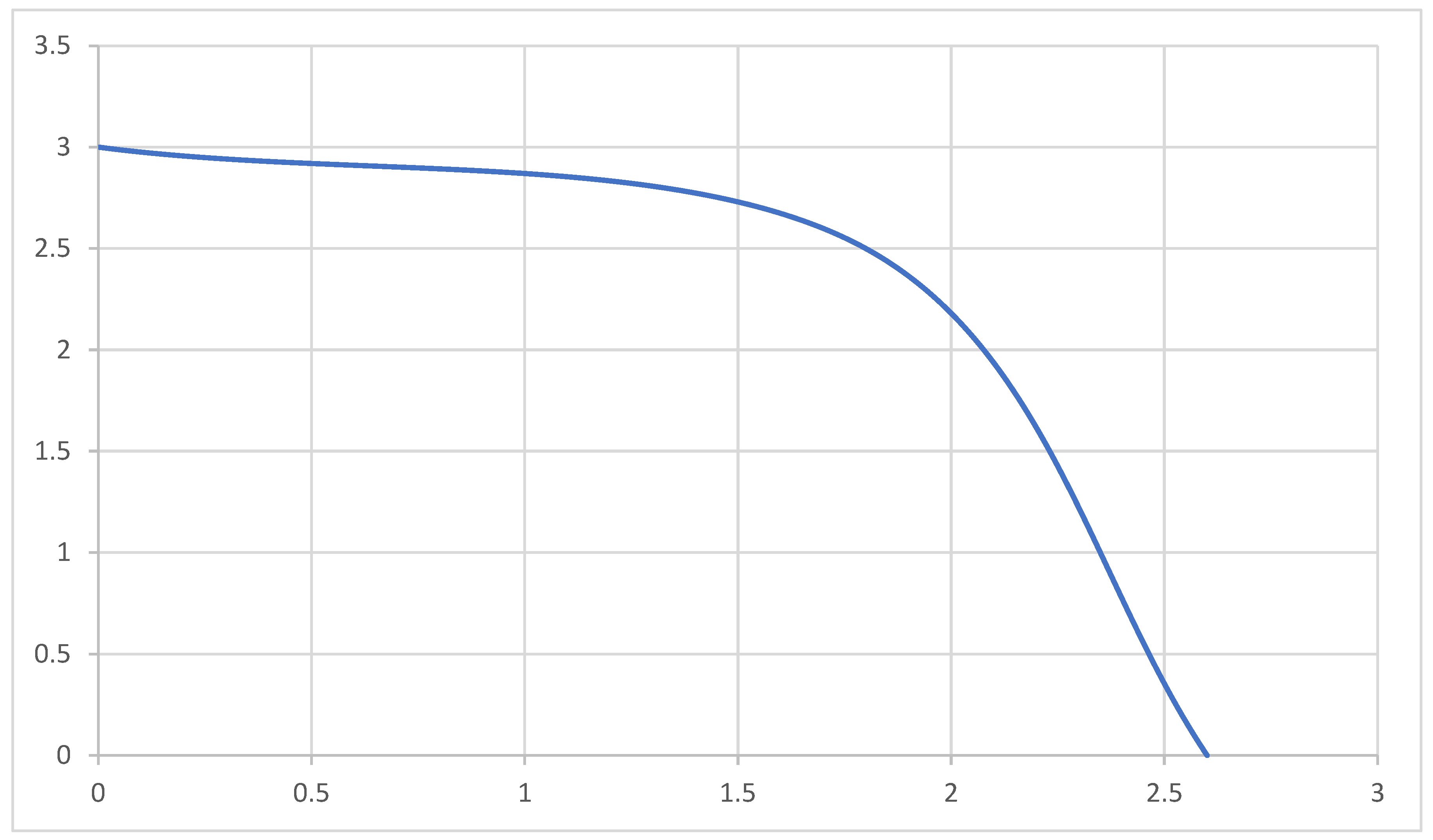
Figure A

Figure A. Graphical representation of (

g

_tt ,

g

_rr,

g_{θ θ}, g_{φ φ})

As t approaches zero.

Figure A. Graphical representation of (

g

_tt ,

g

_rr,

g_{θ θ}, g_{φ φ})

As t approaches zero.

Author’s statement

There is no commercial funding received for this research. There is no conflict of interest for this issue.

References

The Formal Foundation of the General Theory of Relativity by A. Einstein (October 29, 1914).
On the Gravitational Field of a Mass Point according to Einstein’s Theory † by K. Schwarzschild (12 may, 1999.
Hamiltonian Ricci flow by Bennett chow, peng Lu, lei Ni (volume 77).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.