Submitted:
23 April 2025
Posted:
24 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
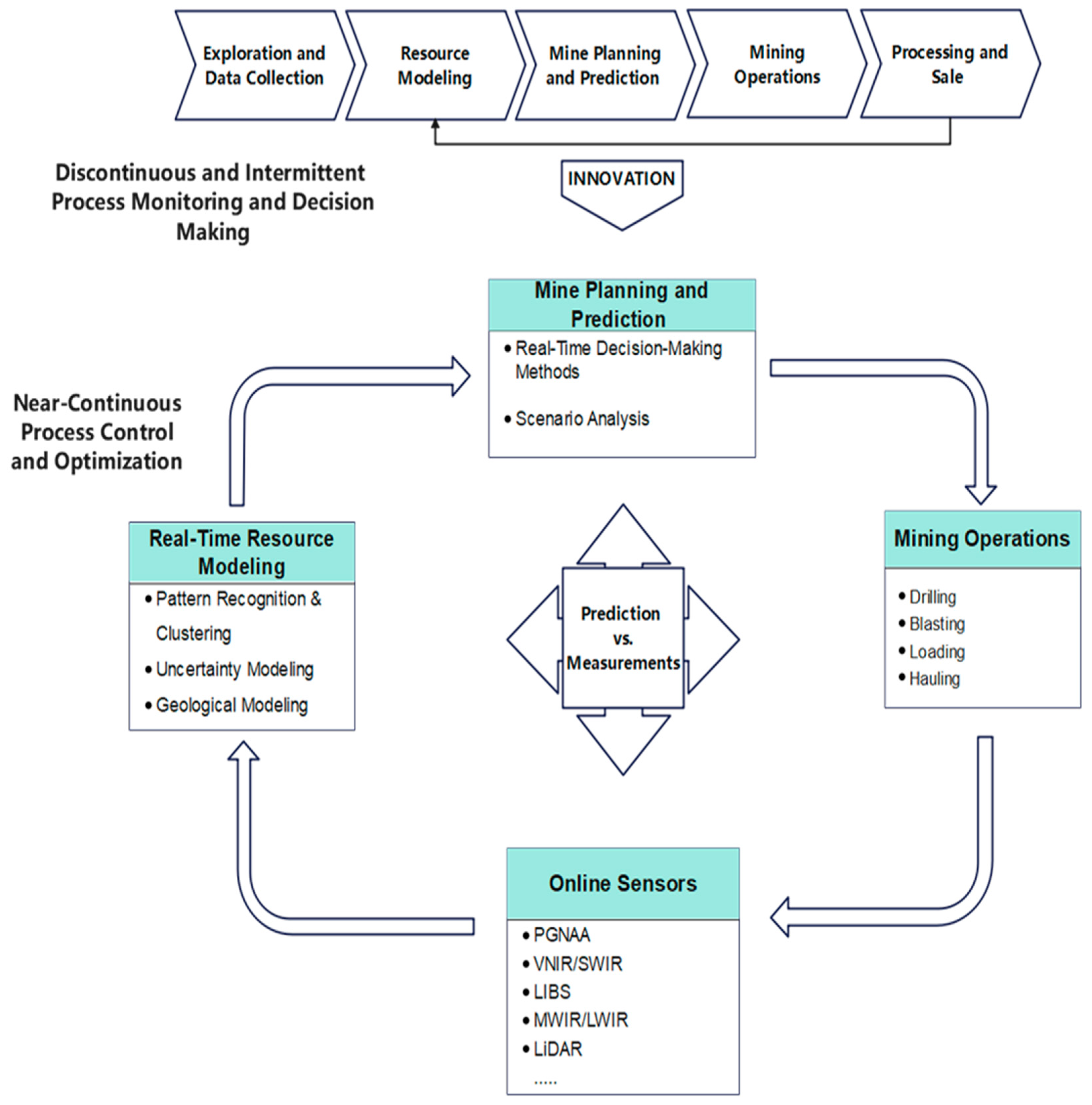
2. The RTM Concept
3. Transformation in Mining Operations Through Sensors
4. Mine Planning and Optimization
4.1. Long-Term Mine Planning: Strategic Production Scheduling and Ultimate Pit Definition
4.2. Short-Term Mine Planning: Detailed Scheduling, Production Control, and RTM
4.3. Stochastic and Deterministic Approaches in Mine Planning
4.4. Optimization Approaches
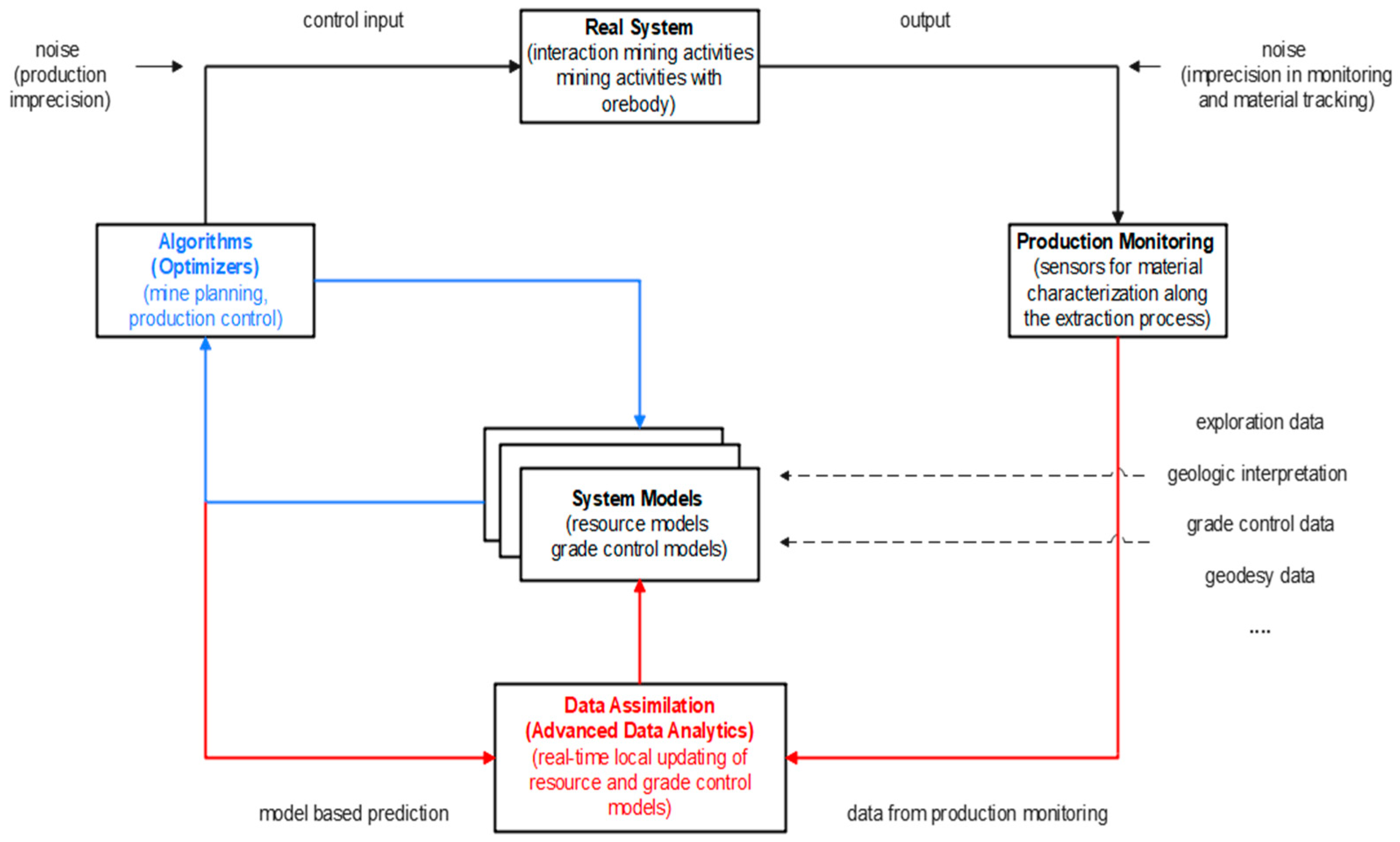
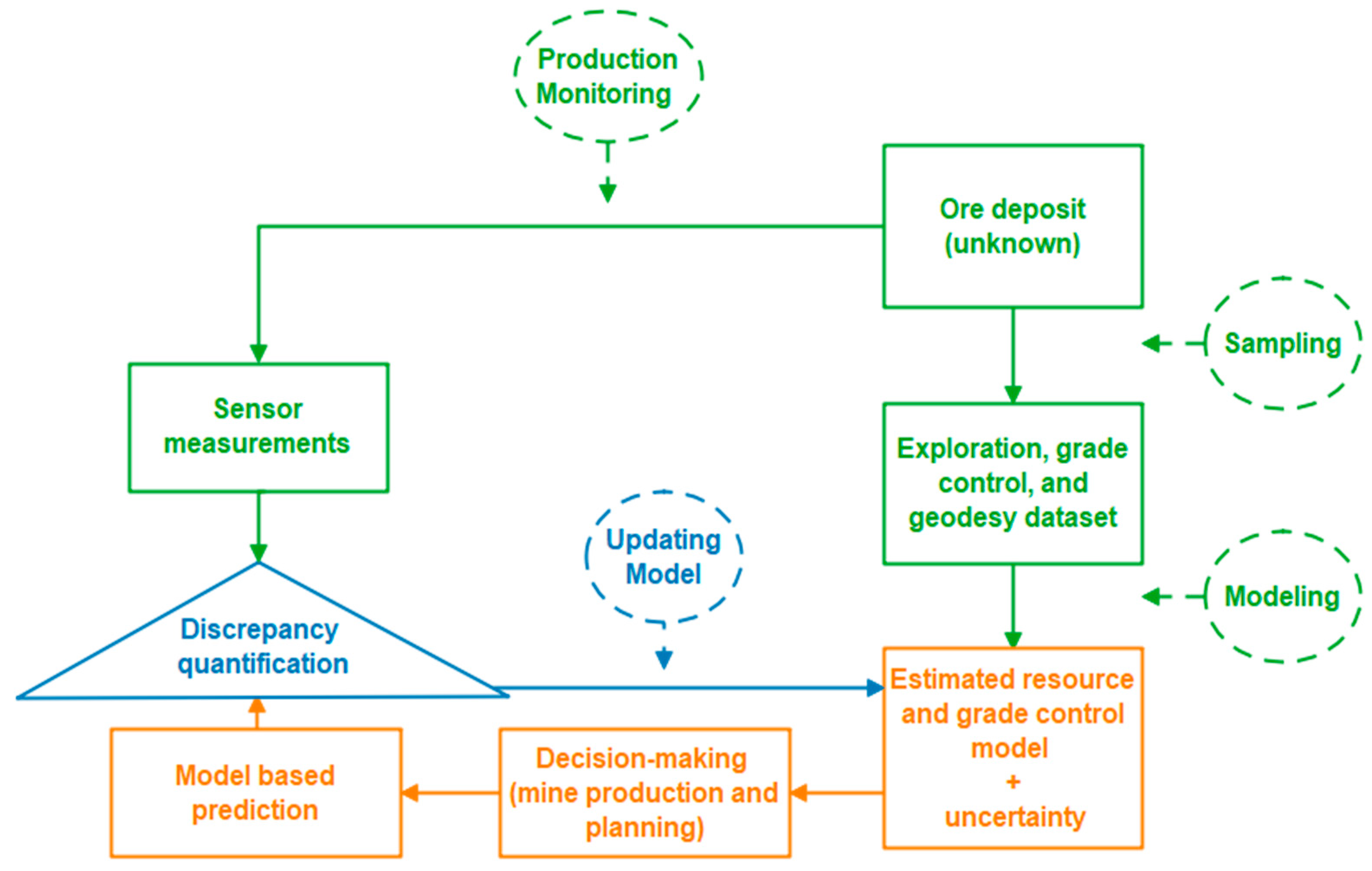
5. Data Assimilation in Closed-Loop RTM Management
5.1. Methods for Updating Data Assimilation in RTM Concept
5.2. Applications of Updating Data Assimilation in RTM Concept
- Forecast Step: The EnKF-based SEOD begins with a forecast step, where the forward model G is used to propagate the current ensemble of state vectors x_(i,j)^a to the next time step (Eq. (6)):
- 2.
- Optimal Sampling Design: The SEOD framework aims to determine the optimal locations for collecting new measurements, which is achieved by maximizing the relative entropy (RE) between the prior and posterior distributions. For a Gaussian distribution, RE is given by Eq. (7):
- 3.
- Analysis Step: After determining the optimal sampling strategy, the analysis step is performed to assimilate the collected data and update the state vector by Eq. (9):
6. Bridging RTM Implementation Gaps with Advanced Data Analytics
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AE | Absolute Error |
| AI | Artificial Intelligence |
| CLRM | Closed-Loop Mineral Resource Management |
| DCT | Discrete Cosine Transform |
| DE-XRT | Dual Energy X-Ray Transmission |
| DDPG | Deep Deterministic Policy Gradient |
| EnKF | Ensemble Kalman Filter |
| GA | Genetic Algorithm |
| GC | Grade Control |
| InDA | Indicator-Based Data Assimilation |
| IoT | Internet of Things |
| LIBS | Laser-Induced Breakdown Spectroscopy |
| LiDAR | Light Detection and Ranging |
| LWIR | Long-Wave Infrared |
| M2M | Mine-to-Mill |
| MWD | Measurement While Drilling |
| MWIR | Mid-Wave Infrared |
| NS-EnKF | Normal-Score Ensemble Kalman Filter |
| NPV | Net Present Value |
| OPS | Open-Pit Production Schedule |
| P-Field | Probability Field (in EnKF/P-Field simulation) |
| PGNAA | Prompt Gamma Neutron Activation Analysis |
| PSO | Particle Swarm Optimization |
| RL | Reinforcement Learning |
| RMSE | Root-Mean-Square Error |
| RTM | Real-Time Mining |
| SEOD | Sequential Ensemble-Based Optimal Design |
| SWIR | Short-Wave Infrared |
| TPG | Truncated Plurigaussian |
| TRL | Technology Readiness Level |
| VNIR | Visible-Near Infrared |
| WAI | Wide Area Illumination |
References
- Watari, T.; Nansai, K.; Nakajima, K. Major metals demand, supply, and environmental impacts to 2100: A critical review. Resources, Conservation and Recycling 2021, 164, 105107. [Google Scholar] [CrossRef]
- ICA. Copper - The pathway to net zero; International Copper Association: 2023; p. 41.
- Pickens, N.; Joannides, E.; Laul, B. Red metal, green demand - Copper’s critical role in achieving net zero; 2022.
- Franken, G.; Schütte, P. Current trends in addressing environmental and social risks in mining and mineral supply chains by regulatory and voluntary approaches. Mineral Economics 2022, 35, 653–671. [Google Scholar] [CrossRef]
- Yu, H.; Zahidi, I.; Fai, C.M.; Liang, D.; Madsen, D.Ø. Elevating community well-being in mining areas: the proposal of the mining area sustainability index (MASI). Environmental Sciences Europe 2024, 36, 71. [Google Scholar] [CrossRef]
- Benndorf, J. Closed loop management in mineral resource extraction: turning online geo-data into mining intelligence; Springer Nature: 2020.
- Anvari, K.; Mousavi, A.; Sayadi, A.R.; Sellers, E.; Salmi, E.F. Automatic detection of rock boundaries using a hybrid recurrence quantification analysis and machine learning techniques. Bulletin of Engineering Geology and the Environment 2022, 81, 398. [Google Scholar] [CrossRef]
- Masoumi, I.; Kamali, G.; Asghari, O.; Emery, X. Assessing the impact of geologic contact dilution in ore/waste classification in the Gol-Gohar Iron Ore Mine, Southeastern Iran. Minerals 2020, 10, 336. [Google Scholar] [CrossRef]
- Aghahadi, M.H.; Jozanikohan, G.; Asghari, O.; Hosseini, S.T.; Emery, X.; Rezaei, M. Geochemical anomaly separation based on geology, geostatistics, compositional data and local singularity analyses: a case study from the Kuh Panj copper deposit, Iran. Applied Geochemistry 2024, 173, 106135. [Google Scholar] [CrossRef]
- Antje Matthäus, M.D. Peter Graham, Amilcar Soares. Real-time optimization of extraction and the logistic process in highly complex geological and selective mining settings; 2017. [CrossRef]
- Kumar, A. Artificial intelligence algorithms for real-time production planning with incoming new information in mining complexes; McGill University (Canada): 2020.
- Blom, M.; Pearce, A.R.; Stuckey, P.J. Short-term planning for open pit mines: a review. International Journal of Mining, Reclamation and Environment 2019, 33, 318–339. [Google Scholar] [CrossRef]
- Dominy, S.C.; Noppé, M.A.; Annels, A.E. Errors and uncertainty in mineral resource and ore reserve estimation: The importance of getting it right. Exploration and Mining Geology 2002, 11, 77–98. [Google Scholar] [CrossRef]
- Lindi, O.T.; Aladejare, A.E.; Ozoji, T.M.; Ranta, J.-P. Uncertainty Quantification in Mineral Resource Estimation. Natural Resources Research 2024, 1–24. [Google Scholar] [CrossRef]
- Ullah, G.W.; Nehring, M.; Kizil, M.; Knights, P. Environmental, Social, and Governance Considerations in Production Scheduling Optimisation for Sublevel Stoping Mining Operations: a Review of Relevant Works and Future Directions. Mining, Metallurgy & Exploration 2023, 40, 2167–2182. [Google Scholar] [CrossRef]
- Benndorf, J.; Buxton, M.; Nienhaus, K.; Rattmann, L.; Korre, A.; Soares, A.; deJong, A.; Jeannee, N.; Graham, P.; Gehlen, S. Real-time mining-Moving towards continuous process management in mineral resource extraction. In Proceedings of the 3rd international future mining conference, Sydney, Austalia; 2015; pp. 1–10. [Google Scholar]
- Buttgereit, D.; Bitzen, S.; Benndorf, J.; Buxton, M. Real-time mining: grade monitoring und control cockpit; Universitätsbibliothek der RWTH Aachen: 2016.
- Sánchez, F.; Hartlieb, P. Innovation in the mining industry: Technological trends and a case study of the challenges of disruptive innovation. Mining, Metallurgy & Exploration 2020, 37, 1385–1399. [Google Scholar] [CrossRef]
- Young, A.; Rogers, P. A review of digital transformation in mining. Mining, Metallurgy & Exploration 2019, 36, 683–699. [Google Scholar]
- Aznar-Sánchez, J.A.; Velasco-Muñoz, J.F.; Belmonte-Ureña, L.J.; Manzano-Agugliaro, F. Innovation and technology for sustainable mining activity: A worldwide research assessment. Journal of Cleaner Production 2019, 221, 38–54. [Google Scholar] [CrossRef]
- Buxton, M.; Benndorf, J. The use of sensor derived data in optimization along the Mine-Value-Chain. In Proceedings of the Proceedings of the 15th international ISM congress, Aachen, Germany; 2013; pp. 324–336. [Google Scholar]
- Desta, F. Sensing and data fusion opportunities for raw material characterisation in mining: Technology and data-driven approach. 2021. [Google Scholar] [CrossRef]
- Lessard, J.; de Bakker, J.; McHugh, L. Development of ore sorting and its impact on mineral processing economics. Minerals Engineering 2014, 65, 88–97. [Google Scholar] [CrossRef]
- Corrigan, C.C.; Ikonnikova, S.A. A review of the use of AI in the mining industry: Insights and ethical considerations for multi-objective optimization. The Extractive Industries and Society 2024, 17, 101440. [Google Scholar] [CrossRef]
- Jackson, J. Enabling short interval control using spatial dense geoscience info beyond grade. 2020. Available online: https://smi.uq.edu.au/event/session/6543.
- Anvari, K.; Mousavi, A.; Sayadi, A.R.; Afzal, P.; Sellers, E.; Salmi, E.F. A Hybrid Recurrence Analysis and Wavelet Transformation for Rock Boundary Identification. Available at SSRN: https://ssrn.com/abstract=5049654 (accessed on 14 December).
- Aghahadi, M.H.; Jozanikohan, G.; Asghari, O.; Anvari, K.; Hosseini, S.T. Spatial Clustering of Primary Geochemical Halos Using Unsupervised Machine Learning in Sari Gunay Gold Deposit, Iran. Mining, Metallurgy & Exploration 2024, 1–20. [Google Scholar] [CrossRef]
- Dalm, M. Sensor-based sorting opportunities for hydrothermal ore deposits: Raw material beneficiation in mining. 2018. [Google Scholar] [CrossRef]
- Guatame-Garcia, A.; Buxton, M. Framework for monitoring and control of the production of calcined kaolin. Minerals 2020, 10, 403. [Google Scholar] [CrossRef]
- Wambeke, T.; Benndorf, J. A study of the influence of measurement volume, blending ratios and sensor precision on real-time reconciliation of grade control models. Mathematical Geosciences 2018, 50, 801–826. [Google Scholar] [CrossRef]
- Benndorf, J.; Restrepo, D.A.; Merkel, N.; John, A.; Buxton, M.; Guatame-Garcia, A.; Dalm, M.; de Waard, B.; Flores, H.; Möllerherm, S. TRIM4Post-Mining: Transition Information Modelling for Attractive Post-Mining Landscapes—A Conceptual Framework. Mining 2022, 2, 248–277. [Google Scholar] [CrossRef]
- Wambeke, T.; Benndorf, J. A simulation-based geostatistical approach to real-time reconciliation of the grade control model. Mathematical Geosciences 2017, 49, 1–37. [Google Scholar] [CrossRef]
- Benndorf, J. Making use of online production data: sequential updating of mineral resource models. Mathematical Geosciences 2015, 47, 547–563. [Google Scholar] [CrossRef]
- de Carvalho, J.P.; Dimitrakopoulos, R. Integrating short-term stochastic production planning updating with mining fleet management in industrial mining complexes: an actor-critic reinforcement learning approach. Applied Intelligence 2023, 53, 23179–23202. [Google Scholar] [CrossRef]
- Kumar, A.; Dimitrakopoulos, R. Updating geostatistically simulated models of mineral deposits in real-time with incoming new information using actor-critic reinforcement learning. Computers & Geosciences 2022, 158, 104962. [Google Scholar] [CrossRef]
- Prior, Á.; Tolosana-Delgado, R.; van den Boogaart, K.G.; Benndorf, J. Resource model updating for compositional geometallurgical variables. Mathematical Geosciences 2021, 53, 945–968. [Google Scholar] [CrossRef]
- Bisschoff, R.; Grobbelaar, S. Evaluation of data-driven decision-making implementation in the mining industry. South African Journal of Industrial Engineering 2022, 33, 218–232. [Google Scholar] [CrossRef]
- Benndorf, J.; Buxton, M. A Special Issue on Geomathematics for Real-Time Mining. Mathematical Geosciences 2019, 51, 845–847. [Google Scholar] [CrossRef]
- Jansen, J.-D.; Douma, S.; Brouwer, D.R.; Van den Hof, P.; Bosgra, O.; Heemink, A. Closed-loop reservoir management. In Proceedings of the SPE Reservoir Simulation Conference? 2009; p. SPE-119098-MS. [Google Scholar] [CrossRef]
- Babaei Khorzoughi, M.; Hall, R.; Apel, D. Rock fracture density characterization using measurement while drilling (MWD) techniques. International Journal of Mining Science and Technology 2018. [CrossRef]
- Babaei Khorzoughi, M.; Hall, R. Processing of measurement while drilling data for rock mass characterization. International Journal of Mining Science and Technology 2016, 26, 989–994. [Google Scholar] [CrossRef]
- Sellers, E.J.; Salmi, E.F.; Usami, K.; Greyvensteyn, I.; Mousavi, A. Detailed Rock Mass Characterization – A Prerequisite for Successful Differential Blast Design. In Proceedings of the YSRM2019 - The 5th ISRM Young Scholars’ Symposium on Rock Mechanics and REIF2019 - International Symposium on Rock Engineering for Innovative Future - An ISRM Specialized Conference, Okinawa, Japan; 2019. [Google Scholar]
- Usami, K.; Salmi, E.F.; Sellers, E.J. Genetic Algorithm to Optimise Rock Fragmentation in Selective Blasting for Grade Engineering. In Proceedings of the The 26th International Mining Congress and Exhibition of Turkey, Belek, Antalya, Turkey; 2019; pp. 359–372. [Google Scholar]
- McKee, D. Understanding mine to mill: The Cooperative Research Centre for Optimising Resource Extraction, Brisbane, AU, 96 p. 2013.
- Salmi, E.; Mousavi, A.; Usami, K.; Sellers, E. Value chain optimization for grade engineering by mine-wide frag-mentation optimisation. In Rock fragmentation by blasting; Wang, X.G., Ed.; 2022. [Google Scholar]
- Salmi, E.F.; Sellers, E.J. A review of the methods to incorporate the geological and geotechnical characteristics of rock masses in blastability assessments for selective blast design. Engineering geology 2021, 281, 105970. [Google Scholar] [CrossRef]
- Kurth, H. Measuring ore quality using real-time on-belt elemental analysis—More than grade control. In Proceedings of the Proceedings of the International Mining Geology Conference, Hobart, Australia, 2017; pp. 20–22.
- Charbucinski, J.; Malos, J.; Rojc, A.; Smith, C. Prompt gamma neutron activation analysis method and instrumentation for copper grade estimation in large diameter blast holes. Applied Radiation and Isotopes 2003, 59, 197–203. [Google Scholar] [CrossRef]
- Clarkson, L.; Williams, D. Critical review of tailings dam monitoring best practice. International Journal of Mining, Reclamation and Environment 2020, 34, 119–148. [Google Scholar] [CrossRef]
- Jawhari, T.; Roid, A.; Casado, J. Raman spectroscopic characterization of some commercially available carbon black materials. Carbon 1995, 33, 1561–1565. [Google Scholar] [CrossRef]
- Lintvedt, T.A.; Andersen, P.V.; Afseth, N.K.; Wold, J.P. In-line Raman spectroscopy for characterization of an industrial poultry raw material stream. Talanta 2024, 266, 125079. [Google Scholar] [CrossRef] [PubMed]
- Dalm, M.; Sandtke, M. Geochemical mapping of drill core samples using a combined LIBS and XRF core scanning system. In Proceedings of the Proceedings of the Real-Time Mining Conference, Freiberg, Germany, 2019; pp. 26–27.
- Lawley, C.J.; Somers, A.M.; Kjarsgaard, B.A. Rapid geochemical imaging of rocks and minerals with handheld laser induced breakdown spectroscopy (LIBS). Journal of geochemical exploration 2021, 222, 106694. [Google Scholar] [CrossRef]
- Díaz Pace, D.M.; Gabriele, N.A.; Garcimuño, M.; D’Angelo, C.A.; Bertuccelli, G.; Bertuccelli, D. Analysis of minerals and rocks by laser-induced breakdown spectroscopy. Spectroscopy Letters 2011, 44, 399–411. [Google Scholar] [CrossRef]
- Guo, L.-B.; Zhang, D.; Sun, L.-X.; Yao, S.-C.; Zhang, L.; Wang, Z.-Z.; Wang, Q.-Q.; Ding, H.-B.; Lu, Y.; Hou, Z.-Y. Development in the application of laser-induced breakdown spectroscopy in recent years: A review. Frontiers of Physics 2021, 16, 1–25. [Google Scholar] [CrossRef]
- Palleschi, V. Laser-induced breakdown spectroscopy: principles of the technique and future trends. ChemTexts 2020, 6, 1–16. [Google Scholar] [CrossRef]
- Benndorf, J. Geomonitoring und Markscheidewesen als integrativer Teil des Umweltmanagements in der Rohstoff-und Energiebranche–zukünftige Aufgaben. Allgemeine Vermessungsnachrichten 2021, 7, 237–247. [Google Scholar]
- Andreas Gunke, S.J. Derivation of Mine from correlates ALS, TLS and RGB Data. In Proceedings of the In 19. Geokinematischer TU Bergakademie Freiberg, Department of Mine Surveying and Geodesy, Freiberg, Germany; 2018; pp. 79–86. [Google Scholar]
- Martienßen, T.; Geier, A.; Wand, R. Untersuchungen zur Entfernungsmessung terrestrischer Long-Range Laserscanner. 2016.
- Donner, R.; Rabel, M.; Scholl, I.; Ferrein, A.; Donner, M.; Geier, A.; John, A.; Köhler, C.; Varga, S. Die Extraktion bergbaulich relevanter Merkmale aus 3D-Punktwolken eines untertagetauglichen mobilen Multisensorsystems. 2019. [Google Scholar] [CrossRef]
- Köhler, C.; Donner, M.; Donner, R. Semantische Klassifizierung von 3D-Punktwolken. 2018. [Google Scholar]
- Chen, Y.; Jiang, C.; Hyyppä, J.; Qiu, S.; Wang, Z.; Tian, M.; Li, W.; Puttonen, E.; Zhou, H.; Feng, Z. Feasibility study of ore classification using active hyperspectral LiDAR. IEEE Geoscience and Remote Sensing Letters 2018, 15, 1785–1789. [Google Scholar] [CrossRef]
- Naseri, A.; Rezaei Nasab, A. Automatic identification of minerals in thin sections using image processing. Journal of Ambient Intelligence and Humanized Computing 2023, 14, 3369–3381. [Google Scholar] [CrossRef]
- Desta, F.; Buxton, M. Evaluation of sensor technologies for on-line raw material characterization in “Reiche Zeche” underground mine-outcomes of RTM implementation. In Proceedings of the 2019 REAL TIME MINING-Conference on Innovation on Raw Material Extraction; 2019; pp. 32–47. [Google Scholar]
- Riley, D.N.; Hecker, C.A. Mineral mapping with airborne hyperspectral thermal infrared remote sensing at Cuprite, Nevada, USA. In Thermal infrared remote sensing: sensors, methods, applications; Springer, 2013; pp. 495–514. [Google Scholar] [CrossRef]
- Prabhavathy, P.; Tripathy, B.; Venkatesan, M. Unsupervised learning method for mineral identification from hyperspectral data. In Proceedings of the Innovations in Bio-Inspired Computing and Applications: Proceedings of the 10th International Conference on Innovations in Bio-Inspired Computing and Applications (IBICA 2019) held in Gunupur, Odisha, India during December 16-18, 2019 10, 2021; pp. 148–160. [CrossRef]
- Neubert, K.; Wotruba, H. Investigations on the detectability of rare-earth minerals using dual-energy X-ray transmission sorting. Journal of Sustainable Metallurgy 2017, 3, 3–12. [Google Scholar] [CrossRef]
- Noriega, R.; Pourrahimian, Y. A systematic review of artificial intelligence and data-driven approaches in strategic open-pit mine planning. Resources Policy 2022, 77, 102727. [Google Scholar] [CrossRef]
- Whittle, D. Open-pit planning and design. SME mining engineering handbook 2011, 1, 877–901. [Google Scholar]
- Askari-Nasab, H.; Frimpong, S.; Szymanski, J. Modelling open pit dynamics using discrete simulation. International Journal of Mining, Reclamation and Environment 2007, 21, 35–49. [Google Scholar] [CrossRef]
- Albor Consuegra, F.; Dimitrakopoulos, R. Stochastic mine design optimisation based on simulated annealing: pit limits, production schedules, multiple orebody scenarios and sensitivity analysis. Mining Technology 2009, 118, 79–90. [Google Scholar] [CrossRef]
- Moosavi, E.; Gholamnejad, J.; Ataee-Pour, M.; Khorram, E. A hybrid augmented Lagrangian multiplier method for the open pit mines long-term production scheduling problem optimization. Journal of Mining Science 2014, 50, 1047–1060. [Google Scholar] [CrossRef]
- Both, C.; Dimitrakopoulos, R. Joint stochastic short-term production scheduling and fleet management optimization for mining complexes. Optimization and Engineering 2020, 21, 1717–1743. [Google Scholar] [CrossRef]
- Mousavi, A.; Kozan, E.; Liu, S.Q. Comparative analysis of three metaheuristics for short-term open pit block sequencing. Journal of Heuristics 2016, 22, 301–329. [Google Scholar] [CrossRef]
- Mousavi, A.; Kozan, E.; Liu, S.Q. Open-pit block sequencing optimization: A mathematical model and solution technique. Engineering Optimization 2016, 48, 1932–1950. [Google Scholar] [CrossRef]
- Benndorf, J.; Jansen, J.D. Recent developments in closed-loop approaches for real-time mining and petroleum extraction. Mathematical Geosciences 2017, 49, 277–306. [Google Scholar] [CrossRef]
- Goodfellow, R.; Dimitrakopoulos, R. Simultaneous stochastic optimization of mining complexes and mineral value chains. Mathematical Geosciences 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Lamghari, A.; Dimitrakopoulos, R.; Ferland, J.A. A hybrid method based on linear programming and variable neighborhood descent for scheduling production in open-pit mines. Journal of Global Optimization 2015, 63, 555–582. [Google Scholar] [CrossRef]
- Guyaguler, B.; Horne, R.N.; Rogers, L.; Rosenzweig, J.J. Optimization of well placement in a Gulf of Mexico waterflooding project. SPE Reservoir Evaluation & Engineering 2002, 5, 229–236. [Google Scholar] [CrossRef]
- Yeten, B.; Durlofsky, L.J.; Aziz, K. Optimization of nonconventional well type, location, and trajectory. SPE Journal 2003, 8, 200–210. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R.; Keutchayan, J. Simultaneous stochastic optimization of an open-pit mining complex with preconcentration using reinforcement learning. Applied Soft Computing 2023, 138, 110180. [Google Scholar] [CrossRef]
- Noriega, R.; Boisvert, J. Optimization of underground mining production layouts considering geological uncertainty using deep reinforcement learning. Engineering Applications of Artificial Intelligence 2025, 139, 109493. [Google Scholar] [CrossRef]
- Noriega, R.; Pourrahimian, Y.; Askari-Nasab, H. Deep Reinforcement Learning based real-time open-pit mining truck dispatching system. Computers & Operations Research 2025, 173, 106815. [Google Scholar] [CrossRef]
- Pendharkar, P.C.; Rodger, J.A. Nonlinear programming and genetic search application for production scheduling in coal mines. Annals of Operations Research 2000, 95, 251–267. [Google Scholar] [CrossRef]
- Leite, A.; Dimitrakopoulos, R. Stochastic optimisation model for open pit mine planning: application and risk analysis at copper deposit. Mining Technology 2007, 116, 109–118. [Google Scholar] [CrossRef]
- Sayadi, A.R.; Fathianpour, N.; Mousavi, A.A. Open pit optimization in 3D using a new artificial neural network. Archives of Mining Sciences 2011, 56, 389–403. [Google Scholar] [CrossRef]
- Souza, M.J.; Coelho, I.M.; Ribas, S.; Santos, H.G.; Merschmann, L.H.d.C. A hybrid heuristic algorithm for the open-pit-mining operational planning problem. European Journal of Operational Research 2010, 207, 1041–1051. [Google Scholar] [CrossRef]
- Shishvan, M.S.; Benndorf, J. Simulation-based optimization approach for material dispatching in continuous mining systems. European Journal of Operational Research 2019, 275, 1108–1125. [Google Scholar] [CrossRef]
- Lamghari, A.; Dimitrakopoulos, R. Hyper-heuristic approaches for strategic mine planning under uncertainty. Computers & Operations Research 2020, 115, 104590. [Google Scholar] [CrossRef]
- LaRoche-Boisvert, M.; Dimitrakopoulos, R. An application of simultaneous stochastic optimization at a large open-pit gold mining complex under supply uncertainty. Minerals 2021, 11, 172. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R. Connecting planning horizons in mining complexes with reinforcement learning and stochastic programming. Resources Policy 2023, 86, 104136. [Google Scholar] [CrossRef]
- Levinson, Z.; Dimitrakopoulos, R. A reinforcement learning approach for selecting infill drilling locations considering long-term production planning in mining complexes with supply uncertainty. Mining Technology 2024, 25726668241244930. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. 1960. [Google Scholar] [CrossRef]
- Li, Y.; Sepúlveda, E.; Xu, C.; Dowd, P. A rapid updating method to predict grade heterogeneity at smaller scales. Mathematical Geosciences 2021, 53, 1237–1260. [Google Scholar] [CrossRef]
- Yüksel, C.; Benndorf, J.; Lindig, M.; Lohsträter, O. Updating the coal quality parameters in multiple production benches based on combined material measurement: a full case study. International Journal of Coal Science & Technology 2017, 4, 159–171. [Google Scholar] [CrossRef]
- Yüksel, C.; Thielemann, T.; Wambeke, T.; Benndorf, J. Real-time resource model updating for improved coal quality control using online data. International Journal of Coal Geology 2016, 162, 61–73. [Google Scholar] [CrossRef]
- Avalos, S.; Ortiz, J.M. Multivariate Geostatistical Simulation and Deep Q-Learning to optimize mining decisions. Mathematical Geosciences 2023, 55, 673–692. [Google Scholar] [CrossRef]
- Kumar, D.; Srinivasan, S. Ensemble-based assimilation of nonlinearly related dynamic data in reservoir models exhibiting non-Gaussian characteristics. Mathematical geosciences 2019, 51, 75–107. [Google Scholar] [CrossRef]
- Ma, W.; Jafarpour, B. Integration of soft data into multiple-point statistical simulation: re-assessing the probability conditioning method for facies model calibration. Computational Geosciences 2019, 23, 683–703. [Google Scholar] [CrossRef]
- Talesh Hosseini, S.; Asghari, O.; Benndorf, J.; Emery, X. Real-time uncertain geological boundaries updating for improved block model quality control based on blast hole data: A case study for Golgohar iron ore mine in Southeastern Iran. Mathematical Geosciences 2023, 55, 541–562. [Google Scholar] [CrossRef]
- Hu, L.; Zhao, Y.; Liu, Y.; Scheepens, C.; Bouchard, A. Updating multipoint simulations using the ensemble Kalman filter. Computers & geosciences 2013, 51, 7–15. [Google Scholar] [CrossRef]
- Jafarpour, B.; McLaughlin, D.B. History matching with an ensemble Kalman filter and discrete cosine parameterization. Computational Geosciences 2008, 12, 227–244. [Google Scholar] [CrossRef]
- Prior, Á.; Benndorf, J.; Mueller, U. Resource and grade control model updating for underground mining production settings. Mathematical Geosciences 2021, 53, 757–779. [Google Scholar] [CrossRef]
- Lan, T.; Shi, X.; Jiang, B.; Sun, Y.; Wu, J. Joint inversion of physical and geochemical parameters in groundwater models by sequential ensemble-based optimal design. Stochastic Environmental Research and Risk Assessment 2018, 32, 1919–1937. [Google Scholar] [CrossRef]
- Nejadi, S.; Trivedi, J.; Leung, J.Y. Estimation of facies boundaries using categorical indicators with P-Field simulation and ensemble Kalman filter (EnKF). Natural Resources Research 2015, 24, 121–138. [Google Scholar] [CrossRef]
- Oliver, D.S.; Chen, Y. Data assimilation in truncated plurigaussian models: impact of the truncation map. Mathematical Geosciences 2018, 50, 867–893. [Google Scholar] [CrossRef]
- Zhou, H.; Gomez-Hernandez, J.J.; Franssen, H.-J.H.; Li, L. An approach to handling non-Gaussianity of parameters and state variables in ensemble Kalman filtering. Advances in Water Resources 2011, 34, 844–864. [Google Scholar] [CrossRef]
- Avalos, S.; Kracht, W.; Ortiz, J.M. Machine learning and deep learning methods in mining operations: A data-driven SAG mill energy consumption prediction application. Mining, Metallurgy & Exploration 2020, 37, 1197–1212. [Google Scholar] [CrossRef]
- Ortiz, J.M.; Avalos, S.; Riquelme, A.I.; Leuangthong, O.; Madani, N.; Frenzel, M. Uncertainty and value: optimising geometallurgical performance along the mining value chain. Elements 2023, 19, 377–383. [Google Scholar] [CrossRef]
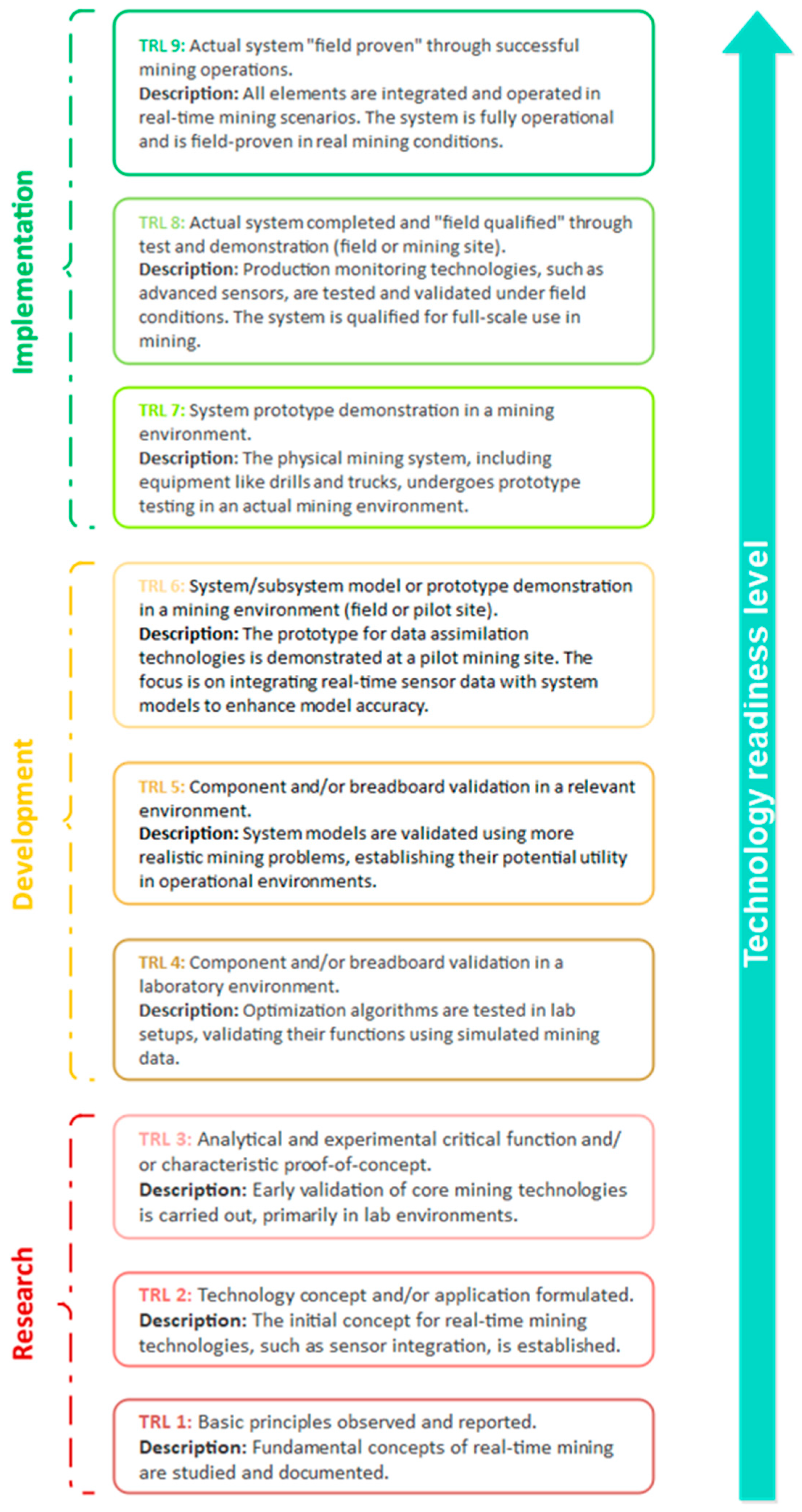
- Clay, R.L.; Shneider, M.S.; Marburger, S.; Trucano, T.G. Modeling and simulation technology readiness levels; Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA …: 2006. [CrossRef]
- Héder, M. From NASA to EU: the evolution of the TRL scale in Public Sector Innovation. The Innovation Journal 2017, 22, 1–23. [Google Scholar]
- Manning, C.G. Technology Readiness Levels. Available online: https://www.nasa.gov/directorates/somd/space-communications-navigation-program/technology-readiness-levels/ (accessed on 21 November).
| Mine Stage | Sensor Effects | Advantages of Sensors |
|---|---|---|
| Exploration | Sensors replace physical sampling and provide real-time data for resource definition (e.g., grade, geometry). | - Reduce costs and time for sampling. - Provide immediate data for decision-making. - Eliminate extensive need for offline laboratory analysis. |
| Production & Grade Control | Sensors monitor ore grade and material properties at the face to influence real-time extraction decisions. | - Improve compliance with mining plans. - Reduce misclassification of ore and waste. - Optimize production sequencing and equipment allocation. |
| Pre-sorting/Pre-upgrading | Sensors sort material before crushing, controlling dispatch to specific destinations (e.g., waste or stockpile). | - Reduce material variability. - Increase product homogeneity. - Improve efficiency by removing waste early. |
| Post-stockpile & Pre-processing | Sensors further refine material by removing residual variability in grade and chemistry. | - Increase feed quality for processing plants. - Enhance process control. - Improve precision of material characteristics. |
| Post-processing & Quality Control | Sensors ensure final product quality by analyzing the material stream in real time. | - Maintain product specifications. - Provide immediate feedback for process adjustments. - Eliminate off-line quality control analysis. |
| Sensor Technology | Application in Mining | Strengths | Weaknesses | Opportunities |
|---|---|---|---|---|
| Measurement While Drilling (MWD) | Blast optimization, rock mass blastability analysis | Provides real-time geomechanical data, enables M2M optimization |
Limited to drilling data, high setup cost | Enhanced bench characterization, integration with M2M systems |
| Prompt Gamma Neutron Activation Analysis (PGNAA) |
Elemental analysis of primary crushed ore | Real-time ore composition, high accuracy | Expensive, radiation safety concerns | In-situ metal grade estimation, reduced sampling errors |
| Hyperspectral Imaging (VNIR/SWIR) | Mineral identification, ore-waste discrimination |
High spectral resolution, rapid, non-contact | Sensitive to environmental conditions (dust, moisture) | Potential for in-situ sorting, dynamic technology |
| Mid-Wave Infrared (MWIR)/Long-Wave Infrared (LWIR) | Ore-waste discrimination, mineral classification | Effective for rock analysis, high classification rates | Limited instrument development, weak spectral features |
Automation potential, integration with chemometric tools |
| Raman Spectroscopy | Mineral identification | Detailed fingerprints, in-situ handheld instruments | Fluorescence interference, limited elemental correlation |
Real-time applications, expanded mineral libraries |
| Laser-Induced Breakdown Spectroscopy (LIBS) |
Raw material characterization, elemental analysis | No sample prep, effective for major/trace elements | Limited detection range, affected by environmental factors |
In-situ exploration, micro-scale spatial analysis |
| Light Detection and Ranging (LiDAR) | Raw material geometry, mineral mapping |
Provides 3D spatial data, operates in various conditions |
Limited spectral data, expensive equipment | Multispectral LiDAR for mineral classification |
| RGB Imaging | Mineral mapping, fragmentation analysis |
Portable, rapid data processing, non-destructive | Limited to surface characteristics, affected by dust | Enhanced imaging, ruggedized systems |
| Electromagnetic Sensors | Mineral density detection, ore-waste separation |
Effective for physical property measurement |
Affected by mineral mixture complexity | Improved accuracy, expanded detection range |
| Dual Energy X-Ray Transmission (DE-XRT) | Pre-concentration, ore-waste separation | Accurate density-based discrimination | Limited to specific mineral densities | Application in automated sorting processes |
| Author(s) | Method | Case Study | Result | Advantages |
|---|---|---|---|---|
| Pendharkar and Rodger [84] | Nonlinear programming and genetic search | Coal mines (Illinois, Virginia, Pennsylvania) | Improved production scheduling under cost and geological constraints | Potential to enhance decision support for coal production and blending |
| Leite and Dimitrakopoulos [85] | Stochastic optimization, simulated annealing | Copper deposit | 26% increase in NPV | Efficient scheduling with risk analysis; reduced likelihood of production target deviations compared to conventional methods |
| Askari-Nasab, Frimpong and Szymanski [70] | Discrete stochastic simulation | Iron ore deposit | $422 million NPV vs $414 million (conventional) | Better optimization of pit limit using a stochastic production simulator, outperforming Lerchs-Grossmann algorithm |
| Albor Consuegra and Dimitrakopoulos [71] | Simulated annealing | Copper deposit | 17% larger pit limits, 10% higher NPV | Integration of uncertainty to derive optimal pit limits and production schedule improvements |
| Sayadi, et al. [86] | Artificial neural network | Esfordi phosphate mine (Iran) | Generated pit with higher profit under impurity constraints | Improved pit limit classification and profitability compared to Lerchs-Grossmann algorithm |
| Moosavi, Gholamnejad, Ataee-Pour and Khorram [72] | Hybrid augmented Lagrangian relaxation and genetic algorithm | Long-term production scheduling | Better feasible solutions than traditional linearization method | Effective for large-scale problems; faster convergence than standard methods |
| Souza, et al. [87] | Hybrid heuristic (GRASP and GVNS) | Open-pit mining operational planning | Near-optimal solutions (less than 1% gap) | Dynamic truck allocation, minimized number of trucks while meeting production goals; efficient computing time |
| Mousavi, Kozan and Liu [75] | Hybrid branch-and-bound and simulated annealing | Short-term open-pit block sequencing | Optimized extraction sequences over short intervals | Efficient in solving short-term sequencing under machine capacity and precedence constraints |
| Mousavi, Kozan and Liu [74] | Comparative analysis of metaheuristics | Short-term open-pit sequencing | Hybrid TS-SA was superior to SA and TS | Enhanced performance and feasibility for real-scale open-pit problems |
| Goodfellow and Dimitrakopoulos [77] | Two-stage stochastic mixed integer nonlinear programming | Mining complexes | Improved production targets and NPV compared to deterministic methods | Joint optimization of extraction, blending, processing, and transportation under uncertainty |
| Both and Dimitrakopoulos [73] | Stochastic mixed integer programming | Real-world mining complex | 56% reduction in shovel movement costs and 3.1% reduction in truck costs | Improved short-term production scheduling and fleet management by integrating shovel relocation, truck allocation, and uncertainty management |
| Shishvan and Benndorf [88] | Simulation-based optimization | Continuous mining system | Minimized idle time, improved material dispatching | Integrated deterministic optimization and stochastic simulation for adaptive material dispatching |
| Lamghari, Dimitrakopoulos and Ferland [78] | Hybrid method (linear programming and variable neighborhood descent) | Open-pit mine scheduling | New best-known solutions for benchmark instances | Efficient and superior in computational performance compared to recent literature methods |
| Lamghari and Dimitrakopoulos [89] | Hyper-heuristic with reinforcement learning and tabu search | Generic mining operations | Comparable or better results than state-of-the-art methods | Robust against problem-specific details, effective for complex scheduling involving multiple processing streams |
| LaRoche-Boisvert and Dimitrakopoulos [90] | Simultaneous stochastic optimization | Open-pit gold mining complex | Maximized NPV; SAG mill identified as bottleneck | Integrated production scheduling across three mines and stockpiles under supply uncertainty |
| Levinson and Dimitrakopoulos [91] | Stochastic programming and reinforcement learning |
Copper mining complex | Jointly optimized short- and long-term schedules | Reduced risk of misalignment across timescales, enhanced operational feasibility |
| Levinson and Dimitrakopoulos [92] | Reinforcement learning and stochastic optimization | Copper mining complex | Improved production schedule using infill drilling data | Reduced uncertainty in production schedule, optimized drilling location selection |
| Methodology | Strengths | Weaknesses | Opportunities |
|---|---|---|---|
| Kalman Filter | Simple and effective for linear systems; well-established methodology for parameter estimation | Assumes linearity and Gaussianity; struggles with non-linear relationships | Use in systems with predominantly linear relationships and smaller-scale updates |
| EnKF | Widely used for sequential data assimilation; handles non-linear problems reasonably well |
Limited by Gaussian assumptions; can fail with strongly non-Gaussian or discontinuous variables | Hybridize with other non-linear techniques for improved assimilation of complex datasets |
| Normal-Score EnKF | Addresses non-Gaussian characteristics by transforming variables into Gaussian distributions | Transformation may not ensure joint multi-Gaussianity; requires multiple transformations | Use in settings with moderate non-Gaussianity where the linear update assumption mostly holds |
| Indicator-Based Data Assimilation | Suitable for non-Gaussian relationships; effective for transforming model parameters | Limited in handling very complex relationships; covariance-based association may be insufficient |
Extend the approach to hybrid models using additional non-linear statistics |
| EnKF with Compositional Data | Suitable for geometallurgical variables; uses transformations to maintain compositional consistency |
Log-ratio transformations add complexity; requires careful handling of relationships between variables | Apply in compositional geoscience models where maintaining data consistency is crucial |
| MPS with EnKF | Maintains geological realism in facies models; handles complex spatial patterns effectively | Computationally expensive; requires careful calibration to maintain geological realism | Improve computational algorithms to allow for faster and more efficient assimilation in realistic models |
| MPS with Soft Data Integration | Enhances facies model calibration by incorporating soft data; maintains geological continuity |
Sensitive to initial conditions; computationally intensive | Utilize for integrating additional soft data in highly uncertain geological environments |
| EnKF with P-Field Simulation | Enhances facies modeling by incorporating probability maps; better integrates geological information | Requires additional assimilation steps; increased computational requirements | Useful for complex geological settings where standard EnKF struggles to reproduce accurate facies |
| EnKF with TPG Models | Assimilates data while maintaining facies realism; handles categorical variables through truncation maps |
Difficult to handle non-monotonic truncation maps; requires derivative adjustments for accurate data matching | Use in channel facies modeling where categorical boundaries are critical |
| EnKF with DCT | Helps reduce dimensionality and improves history matching for high-dimensional problems | Increases computational complexity; sensitive to non-Gaussian data distributions | Apply for history matching in high-dimensional geological models where data compression is critical |
| SEOD with EnKF | Provides optimized sampling strategies and enhances model parameter estimation | Time-consuming optimization; computational overhead when dealing with complex geological data |
Combine with simpler methods to balance accuracy and computational efficiency |
| EnKF with DWT | Helps reduce geological boundary uncertainty; enhances real-time data assimilation |
High computational requirement; depends on quality of initial realizations | Extend application for sensor-based geological boundary identification |
| Reinforcement Learning (DDPG) | Learns adaptively in complex environments; able to handle dynamic, high-dimensional datasets | Requires extensive training data; computationally intensive and relies on strong computational resources |
Apply in dynamic mining environments where adaptive decision-making is beneficial |
| Actor-Critic Reinforcement Learning | Learns adaptively in dynamic environments; can self-optimize based on incoming data | Computationally heavy; requires large datasets for effective learning | Use in industrial-scale mining for optimizing resource extraction and adaptive decision-making |
| Author(s) | Method | Case Study | Result | Advantages |
|---|---|---|---|---|
| Jafarpour and McLaughlin [102] | EnKF with DCT | Synthetic Reservoirs | Reduced dimensionality, preserved geological realism | Reduced computational cost; better preservation of channel connectivity |
| Zhou, Gomez-Hernandez, Franssen and Li [107] | Normal-Score EnKF | Synthetic Bimodal Aquifer | Preserved non-Gaussian distributions, improved characterization | Preserved complex spatial features; enhanced quality of real-time geological models |
| Hu, Zhao, Liu, Scheepens and Bouchard [101] | MPS with EnKF | Fluvial Reservoir | Maintained geological consistency, effective history matching | Maintained geological features; effective in real-time history matching |
| Benndorf [33] | Kalman Filter | Synthetic Data | Reduced MSE, improved prediction accuracy | Improved decision-making by incorporating real-time sensor data; reduced uncertainty even with blending |
| Nejadi, Trivedi and Leung [105] | EnKF with P-Field Simulation | Reservoir Models | Improved facies boundary characterization | Preserves statistical properties; prevents overfitting; ensures ensemble diversity |
| Yüksel, Thielemann, Wambeke and Benndorf [96] | EnKF | Garzweiler Lignite Mine | Up to 70% reduction in model uncertainty | Direct incorporation of real-time measurements; better decision-making and quality control |
| Yüksel, Benndorf, Lindig and Lohsträter [95] | EnKF | Lignite Mining with Multiple Benches | Error reduction up to 73% | Practical and less computationally intensive; improved model predictions |
| Wambeke and Benndorf [32] | EnKF | Grade Control Reconciliation | Enhanced accuracy, practical for complex scenarios | Improved operational efficiency; reduced uncertainties; better resource extraction |
| Wambeke and Benndorf [30] | EnKF | Analysis of System Parameters | RMSE reduction up to 74%, improved model alignment | Mitigated discrepancies; enhanced production processes |
| Lan, Shi, Jiang, Sun and Wu [104] | SEOD with EnKF | Groundwater Models | Reduced uncertainty, improved predictions | Optimal sensor data collection; efficient computational performance; better model accuracy |
| Oliver and Chen [106] | EnKF with TPG Models | Synthetic Reservoir | Improved data match, reduced uncertainty | Handled nonlinearity and non-monotonic relationships; robust in complex geological environments |
| Kumar and Srinivasan [98] | Indicator-Based Data Assimilation | Synthetic Reservoir | Preserved non-Gaussian distributions, accurate spatial features | Overcomes EnKF limitations; maintains geological features; accurate in non-Gaussian contexts |
| Ma and Jafarpour [99] | MPS with Soft Data Integration | Facies Model Calibration | Improved consistency with training images and data | Maintains geological consistency; integrates soft data; effective framework |
| Li, Sepúlveda, Xu and Dowd [94] | Kalman Filter | Synthetic Dataset | Improved model accuracy, better mining selectivity | Integrates sensed data without complex methods; computational efficiency; practical for rapid decision-making |
| Prior, Benndorf and Mueller [103] | EnKF | Underground Mining (Reiche-Zeche) | Improved prediction accuracy for ore grade and vein thickness | Improved mining selectivity; effective even with sparse initial data |
| Prior, Tolosana-Delgado, van den Boogaart and Benndorf [36] | EnKF with Compositional Data | Bauxite Deposit | Accurate updates, preserved compositional characteristics | Reduced uncertainty; improved accuracy for decision-making |
| Kumar and Dimitrakopoulos [35] | Reinforcement Learning (DDPG) | Synthetic Dataset | Dynamic model updates, accounted for high-order statistics | Integrates new information dynamically; suitable for complex mining operations |
| Talesh Hosseini, Asghari, Benndorf and Emery [100] | EnKF with DWT | Golgohar Iron Ore Mine | Improved geological boundary accuracy, high compatibility | Enhances block model quality control; reduces spatial uncertainty; preserves statistical parameters |
| de Carvalho and Dimitrakopoulos [34] | Actor-Critic Reinforcement Learning | Copper Mining Complex | 47% improvement in cash flow | Dynamic fleet allocation and production scheduling based on real-time data. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





