Probability Representation of Quantum States: Tomographic Representation in Standard Potentials And Peres–Horodecki Criterion for Probabilities

1. Introduction

The United Nations have declared 2025 as the International Year of Quantum Science and Technologies [1]. Given this especial celebration, we want to emphasize a history of collaboration between the Lebedev Institute and the research group at UNAM in Mexico. This collaboration has taken place now for more than 30 years and is an example of the multiculturalism in the development of physics and, in particular, quantum science. There are many various topics discussed in this special collaboration. For example, one can mention some developments in the study of superpositions of coherent states and the tomographic representation of quantum systems along with different geometrical representations of quantum systems. We briefly mention some of the results of this joint research.

1.1. Brief Review of Lebedev Institute–Mexico Collaboration

The time-dependent integrals of motion $\widehat{I}$ ($d\widehat{I}/dt=0$), together with the quantum propagator are very useful tools to study the time evolution and the quasiprobability distribution functions of Wigner and Husimi related to optical quantum systems. As for example, the quantum propagator of a quadratic Hamiltonian in position and momentum can be obtained by solving the linear differential equation to obtain the integrals of motion. By using these advantages, the time evolution of the even and odd linear combinations of correlated states in the two-dimensional generalized oscillator were obtained. This time evolution, model the nonstationary Casimir effect with similar qualitatively properties to the case of the creation of photon and quadrature squeezing in a resonator with moving boundaries at constant velocity [2].

As an extension of the construction of even and odd coherent states of the electromagnetic field oscillator, the states carrying the irreducible representations of cyclic point groups $C_n$ were established. These states were called crystallized Schrödinger cat states, and their symmetry properties associated to the n-sided polygon were visualized by means of the determination of the Wigner and Husimi functions [3].

The linear time-dependent invariants of quadratic in position and momentum Hamiltonians can be obtained by means of a Noetherian symmetry transformation that follows the classical trajectory. Besides, one is able to show that the dynamical symmetry algebra of stationary and nonstationary quantum systems can be obtained by applying Nöther’s theorem to the classical Lagrangian or Hamiltonian formalisms. The procedure is the following: determine the time-independent symmetry variations of the coordinates, which suggest the time-dependent infinitesimal transformations, which yield the constants of the motion. As examples, the pseudo-Coulomb Hamiltonian and the generalized two dimensional nonstationary harmonic oscillator were considered [4,5].

To test many of the fundamental concepts of modern quantum optics, the study of ion traps provides precise measurements in the laboratory. For this reason, the evolution of Schrödinger-cat states in Paul and Penning traps were determined. For an ${}^{198}\mathrm{Hg}^{+}$ ion moving in a Paul trap, the Hamiltonian can be rewritten as a time-dependent harmonic oscillator, where the frequency is a function of the static and alternating quadrupole fields [6]. For an ion moving in an asymmetric Penning trap, the time-dependent Schrödinger equation is solved by means of their linear time-dependent invariants [7].

The tomographic methods can be used in classical statistical mechanics, which can be extended to define a new formulation of conventional quantum mechanics, based on the probability distribution function of a quantum state [8]. The probability distribution for the spin projection in a rotated reference frame is presented as the modulus squared of the matrix element of the $SU\left(2\right)$-group irreducible representation. Various properties related to this tomographic representation for discrete and continuous variable systems were also presented. The relation between the Heisenberg–Weyl and $su\left(2\right)$ algebras in the limit of high spins can be used to show that the spin tomograms in this limit become the tomograms of harmonic-oscillator states. The explicit expressions for the kernels, which determine the delta-function for the spin-tomographic symbols and the star-product of the symbols are determined [9].

A Hamiltonian for N two-level atoms in a cavity interacting with a classical electromagnetic field can be written in terms of the linear combination of angular momentum operators, whose time-dependent constants of motion can be obtained, and used to define the tomographic symbol of the Hamiltonian. This tomogram depends on the projection of the angular momentum m along the rotated reference frame given by the Euler angles. The solutions of the time-dependent Schrödinger equation are given in terms of the generalized Dicke states. When the classical field is sinusoidal, the Hamiltonian describes the Rabi’s problem. Additionally, the inverse problem, i.e., given a complete set of integrals of motion determine the corresponding Hamiltonian, is solved in this case. However, the procedure can also be applied to Hamiltonians quadratic in multimode field quadratures related to the $Sp(2N,\mathbb{R})$ symplectic group [10].

For quantum states of light, the photon number probability functions depending on a scaling factor and a rotation angle can be obtained for one mode of the electromagnetic field, which define the squeezed tomograms. These tomograms can be related to the Wigner function, the density matrix, and the symplectic tomograms by integral transforms. Extensions of the approach of squeeze tomography to the multimode case were shown. The evolution of squeezed tomograms were explicitely calculated for an oscillator with time-dependent frequency and for damped oscillator [11].

The density matrix of a quantum system of continuous variables can be discretized by means of a nonlinear positive map. By considering the two-mode electromagnetic field with density matrix $\varrho (x,y;x^{\prime },y^{\prime })$, the discretization leads to a density matrix depending on two discrete modes. This density matrix is used to calculate the entanglement between the two modes. We propose the discretization of the density matrix as a nonlinear positive map for systems with continuous variables. We use this procedure for calculating the entanglement between two modes through different criteria, such as Tsallis entropy, von Neumann entropy, and linear entropy, as well as the logarithmic negativity. As an example, we study the dynamics of entanglement for the two-mode squeezed-vacuum state in the parametric amplifier and show good agreement with the analytic results. Also we address the loss of information on the system state due to the discretization of the density matrix [12].

The linear time-dependent constants of motion of the parametric amplifier are obtained to determine the evolution of a general two-mode Gaussian state in the tomographic-probability representation. Some qubit separability criteria can be used to describe the entanglement of continuous variable systems, as the discretization procedure that maps a continuous system to a discrete one. Furthermore, any discrete system can define a qubit system. This discretization is called the qubit portrait of a continuous system and defines a $4\times 4$ density matrix from the continuous density matrix $\varrho (x,y;x^{\prime },y^{\prime })$. In general, this qubit portrait is obtained by dividing each mode two-dimensional subspace ($x,x^{\prime }$ and $y,y^{\prime }$) into four non-overlapping regions, the by integrating the density matrix in all the 16 combinations of the regions one obtains a well defined $4\times 4$ discrete density matrix which contains the separability information of the original continuous state. This procedure lead us to new different inequalities to describe the separability of continuous variable systems using properties of their qubit portrait [13].

Actually, the experimental studies in quantum optics are closely related to the quantum information theory; v.g. cryptography, teleportation, and dense coding protocols. Having in mind this motivation, we investigate finite d-dimensional density matrices, representing an information system of qudits, together with entropic bounds. An algebraic method is established to find extremal density matrices for a qudit Hamiltonian system, for pure and mixed states. The procedure mainly uses stationary solutions of the von Neumann equation of motion, orbits of the Hamiltonian, and the positivity conditions of the density matrix; this can be extended to any Hermitian operator [14,15].

For a given qudit system Hamiltonian, new inequalities connecting the mean value of the Hamiltonian and the entropy of an arbitrary state are found. These inequalities were defined using the relative entropy $S(\widehat{\rho },\widehat{\sigma })=-\mathrm{Tr}(\widehat{\rho }ln\widehat{\rho }-\widehat{\rho }ln\widehat{\sigma })$, between two different density matrices $\widehat{\rho }$ and $\widehat{\sigma }$ [16]. By using a similar method, upper and lower bounds for the subtraction of the relative entropy between two thermal equilibrium states are determined, whose bounds are given in terms of the expectation values of the Hamiltonian, number operator, and temperature of the two systems [17]. The analysis of the relative entropy between two thermal equilibrium states leads to the inequality relating the internal energy U, the entropy S, and the Helmholtz free energy F of the system. Applications of these inequality for a qubit and general Gaussian states are given. In particular, these inequalities for the thermal and parametric amplifier are investigated for different temperatures [18].

Classical probabilities can be used to describe quantum states; in particular, to understand quantum entanglement. The definition of the three Malevich squares associated to the probabilities to obtain a $+1/2$ for ${\widehat{S}}_x$, ${\widehat{S}}_y$, ${\widehat{S}}_z$ in a spin system and their areas provides a geometric approach to describe the qudit. This probabilistic construction of quantum mechanics is used to study the linear entropy $1-\mathrm{Tr}{\widehat{\rho }}^2$ of general qubit and qutrit systems [19].

A method to study the evolution of an open qubit system is established in terms of a general unitary transformation in three dimensions, yielding a non-unitary evolution for the system of qubits. With this procedure, we investigate the phase-damping and spontaneous-emission quantum channels, addressing its possible experimental realization [20]. An arbitrary qudit state can be represented by a qubit system, which was called the qubit representation, to study quantum correlations and state reconstruction. This qubit representation leads us to a graphical representation of a d-dimensional qudit quantum state, which is done by means of a quorum of Bloch vectors ($d(d-1)/2$ qubit states) [21].

This short review help us as an introduction to present new results in some of the areas mentioned above. In section 2, a new tomographic representation of wave functions related to standard quantum mechanical problems are presented. Also, separability criteria for bipartite, asymmetrical, real states are then discussed in section 3, using its momentum probability distributions. Finally, a summary of the results and some concluding remarks are given.

2. Tomographic Representation of Common Quantum-Mechanical Wave Functions

In quantum mechanics and in classical mechanics developed during the last century, the basic notion of position and velocity (momentum) of systems like a sole particle was defined and extensively used; this notion is intuitively different for classical mechanics and for quantum mechanics, while the notion of time is common for both type of systems. The development of quantum mechanics during the last century provides the possibility to employ the basic notion of the particle state – the common idea of the probability distribution of a particle position and momentum. This idea looked very attractive, there were many attempts to find this probability, but there were difficulties like the Robertson–Schrödinger uncertainty relations of the position and momentum, which were considered as arguments to forbidden the possibility of such an idea.

We discuss some examples to realize this possibility and present a short review of probability distributions describing states of the particle moving in some potential wells. In the conventional formulation of quantum mechanics, the wave function satisfying the Schrödinger equation [22,23] and the density matrix introduced by Landau [24] and von Neumann [25]; Tombesi et al. showed that both the wave function and the density matrix can be invertible mapped [26] onto conventional probability distributions (tomograms) describing the quantum states, density operators, and density matrices [27]. The quasi-distributions, such as the Wigner function [28] and the Husimi function [29], are also used to determine quantum tomograms. The pure quantum spin-1/2 states can also be described by the probability distribution [30]. The probability description of quantum states is useful for developing quantum technologies and quantum information processing.

The tomographic probability representation can be obtained from a standard wave function $\psi \left(x\right)$ as the following integral

$$\mathcal{W}\left(X\right|\mu ,\nu )={\displaystyle \frac{1}{2\pi \left|\nu \right|}}{\left|{\int }_{-\infty }^{\infty }\psi \left(x\right)e^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-i{\displaystyle \frac{X}{\nu }}x}dx\right|}^2,$$

(1)

where the variable X is interpreted as a rotation and rescaling of the phase space variables $(x,p)$ of a quantum system, i.e., $X=\mu x+\nu p$, with $\mu =scos\theta$ and $\nu =s^{-1}sin\theta$, where $s,\theta$ are re-scaling and rotation factors respectively.

The tomographic distribution of a state is a normalized probability distribution, which provides information of a combination of the position and momentum variables. Additionally, the tomogram can be used to obtain or reconstruct any quantum system as, in general, the density matrix is represented by

$$\widehat{\rho }={\displaystyle \frac{1}{2\pi }}\int \mathcal{W}\left(X\right|\mu ,\nu )exp\left[i\left(X\widehat{I}-\mu \widehat{x}-\nu \widehat{p}\right)\right]dXd\mu d\nu .$$

(2)

Below, we use properties of this definition to study the tomographic representation of different standard quantum systems.

2.1. Free Motion

Now we discuss the probability representation of free motion of a particle with the wave function $\psi \left(t\right)$, where its evolution is described by the Hamiltonian $\widehat{H}={\widehat{p}}^2/2$; we assume the units with $\hslash =1$ and $m=1$. The wave function of the particle $\psi \left(t\right)$ satisfies the Schrödinger equation

$$i{\displaystyle \frac{\partial \psi (x,t)}{\partial t}}=\widehat{H}\psi (x,t),$$

(3)

where the time evolution of the wave function can be described by the Green function $G(x,x^{\prime },t)$, which is the matrix element of the evolution operator $\widehat{U}\left(t\right)=exp(-i\widehat{H}t)$; in the position representation, it reads [31]

$$G(x,x^{\prime },t)={\displaystyle \frac{1}{\sqrt{2\pi it}}}exp\left({\displaystyle \frac{i{(x-x^{\prime })}^2}{2t}}\right),$$

(4)

and one has

$$\psi (x,t)=\int G(x,x^{\prime },t)\psi (x^{\prime },t=0)d{x}^{\prime }.$$

(5)

The initial value of the wave function can be taken as a normalized function satisfying the normalization condition

$$\int {\left|\psi (x^{\prime },t=0)\right|}^{2}d{x}^{\prime }=1,$$

(6)

and since the evolution operator is a unitary one, the normalization equality is the same for any value of time t. This means that the density operator ${\widehat{\rho }}_{\psi }{\left(t\right)}_{x{x}^{\prime }}=\psi (x,t){\psi }^{*}(x^{\prime },t)$ satisfies the normalization condition $Tr{\widehat{\rho }}_{\psi }\left(t\right)=1$; due to this, we can calculate the tomographic probability representation of the particle, in view of the following formula:

$$\mathcal{W}(X\mid \mu ,\nu ,t)=Tr\left({\widehat{\rho }}_{\psi }\left(t\right)\delta \left(X\widehat{I}-\mu \widehat{q}-\nu \widehat{p}\right)\right),$$

(7)

expressed in terms of the wave function as given by Eq. (1). Taking into account equation (7), ${\widehat{\rho }}_{\psi }\left(t\right)=\widehat{U}\left(t\right){\widehat{\rho }}_{\psi }\left(0\right){\widehat{U}}^{†}\left(t\right)$, and properties of the trace operator $\mathrm{Tr}\left(\widehat{A}\widehat{B}\widehat{C}\right)=\mathrm{Tr}\left(\widehat{C}\widehat{A}\widehat{B}\right)$, we arrive at the equality

$$\mathcal{W}(X\mid \mu ,\nu ,t)=Tr\left(\widehat{\rho }\left(0\right)\delta \left(\widehat{X}\widehat{I}-\mu {\widehat{q}}_H\left(t\right)-\nu {\widehat{p}}_H\left(t\right)\right)\right)=Tr\left(\widehat{\rho }\left(0\right)\delta \left(\widehat{X}\widehat{I}-\mu \widehat{q}-(\nu +\mu t)\widehat{p}\right)\right),$$

(8)

which means that

$$\mathcal{W}(X\mid \mu ,\nu ,t)=\mathcal{W}\left(X\mid {\mu }_H\left(t\right),{\nu }_H\left(t\right),t=0\right),$$

(9)

where ${\mu }_H\left(t\right)$ and ${\nu }_H\left(t\right)$ are parameters determined by the Heisenberg operators ${\widehat{q}}_H\left(t\right)$ and ${\widehat{p}}_H\left(t\right)$ of the free particle motion

$$q_H\left(t\right)=\widehat{q}+\widehat{p}t,p_H\left(t\right)=\widehat{p}.$$

(10)

Thus, we obtain the equality for tomographic evolution; it is

$$\mathcal{W}(X\mid \mu ,\nu ,t)=\mathcal{W}\left(X\mid {\mu }_H\left(t\right),{\nu }_H\left(t\right),t=0\right),$$

(11)

allowing us to predict the tomographic probability distribution for any time t, if we take the tomogram for the free particle $\mathcal{W}(X\mid {\mu }_H\left(t\right),{\nu }_H\left(t\right),t=0)$ and replace the parameters $\mu$ and $\nu$ by ${\mu }_H\left(t\right)=\mu$ and ${\nu }_H\left(t\right)=\nu +\mu t$.

2.1.1. Free Evolution of a Wave Packet.

In this section, we obtain the tomographic representation of a wave packet freely evolving. As it is known, the unidimensional free particle has the following wave function

$$\psi \left(x\right)=Aexp\left(ikx\right)+Bexp(-ikx),k=p/\hslash ,$$

(12)

which can be used to define a normalizable wave packet of the form

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{\infty }\varphi \left(k\right)e^{i(kx-\omega t)}dk,\mathrm{where}\varphi \left(k\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-\infty }^{\infty }\psi (x,0)e^{-ikx}dx,$$

(13)

with $\omega =\hslash k^2/\left(2m\right)$ and $\psi (x,0)$ is the initial envelopment of the wave packet. The tomographic representation of this wave packet can be obtained, using Eq. (1) and the imaginary Gaussian integral [32,33]

$${\int }_{-\infty }^{\infty }{e}^{i(C{x}^2-Dx)}dx=(1+i)\sqrt{{\displaystyle \frac{\pi }{2C}}}{e}^{-i{\displaystyle \frac{D^2}{4C}}},C,D\in \mathbb{R}.$$

(14)

Defining $C=\mu /2\nu$ and $D=(X/\nu )+k$, we arrive at the following general expression for the tomogram of any wave packet:

$$\mathcal{W}\left(X\right|\mu ,\nu )={\displaystyle \frac{1}{2\pi \left|\mu \right|}}{\int }_{-\infty }^{\infty }{e}^{{\displaystyle \frac{i}{2\mu }}(k-k^{\prime })(2X+(k+k^{\prime })\nu )}{e}^{i({\omega }^{\prime }-\omega )t}\varphi \left(k\right){\varphi }^{*}\left(k^{\prime }\right)dkd{k}^{\prime },{\omega }^{\prime }=\hslash k^{\prime 2}/\left(2m\right).$$

(15)

As an example, for a Gaussian wave packet with initial form $\psi (x,0)={\left({\displaystyle \frac{2a}{\pi }}\right)}^{1/4}{e}^{-a{x}^2}$, one has the following $\left(\varphi \left(k\right)={\displaystyle \frac{1}{{\left(2\pi a\right)}^{1/4}}}{e}^{-k^2/\left(4a\right)}\right)$ time-dependent wave function

$$\psi (x,t)={\left({\displaystyle \frac{2a}{\pi }}\right)}^{1/4}{\displaystyle \frac{\sqrt{m(m-2ia\hslash t)}exp\left(-\frac{am{x}^2(m-2ia\hslash t)}{m^2+4a^2{h}^2{t}^2}\right)}{\sqrt{m^2+4a^2{\hslash }^2{t}^2}}},$$

(16)

which defines the following tomographic probability distribution:

$$\mathcal{W}(X,t|\mu ,\nu )={\displaystyle \frac{1}{\sqrt{2\pi \sigma \left(t\right)}}}{e}^{-X^2/2\sigma \left(t\right)},\sigma \left(t\right)={\displaystyle \frac{{\mu }^2}{4a}}+{\displaystyle \frac{a{(\hslash \mu t+m\nu )}^2}{m^2}}.$$

(17)

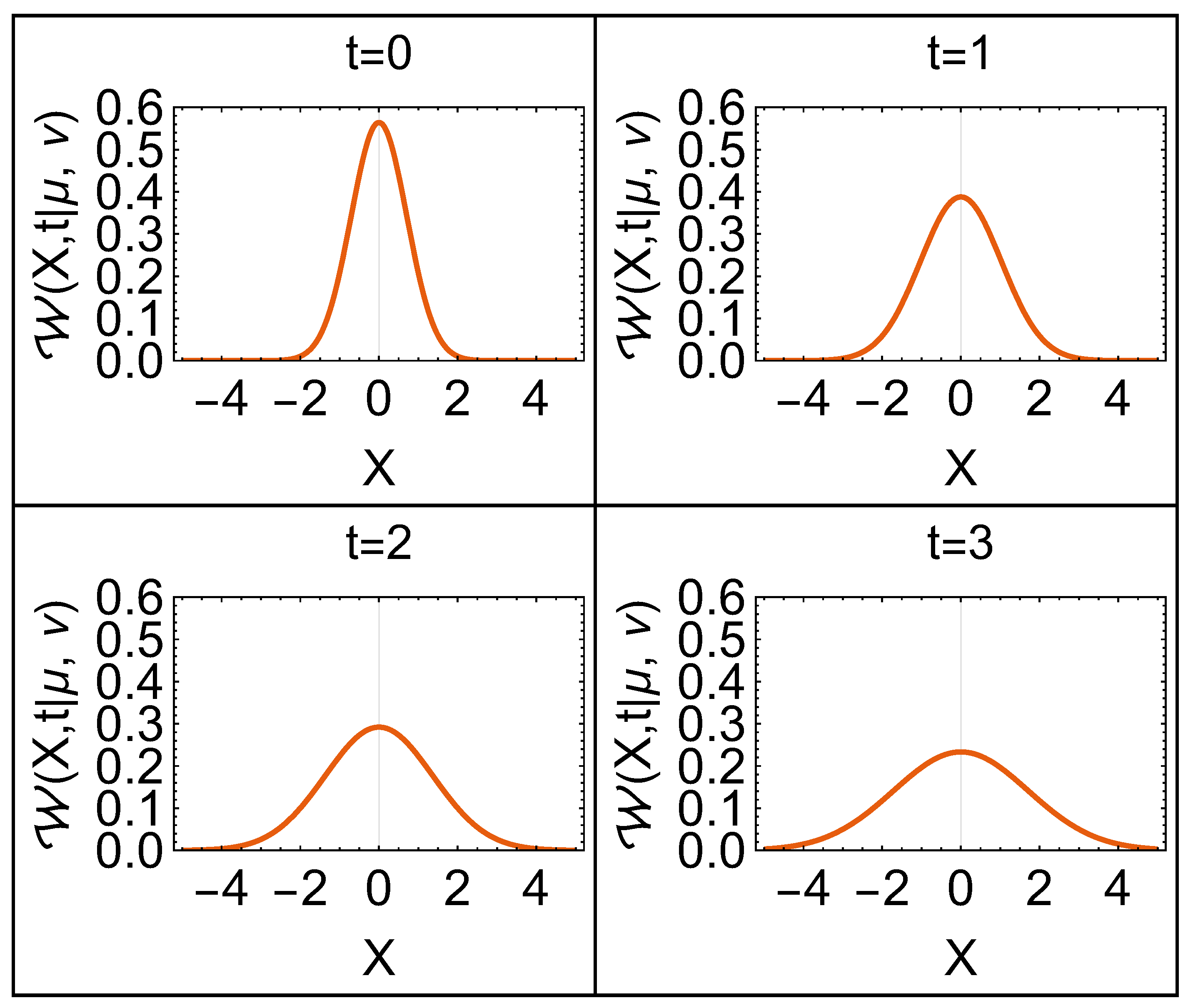
In Figure 1, the evolution of a Gaussian wave packet at different times is shown. One can see the spreading of the packet along the space as time increases. One can notice that the time dependence of the variance $\sigma \left(t\right)$ is quadratic, implying a linear standard deviation $\sqrt{\sigma \left(t\right)}$ for large t. This is an interesting property, since it can help to evaluate time differences by measuring the standard deviations of the system at different times.

2.2. Finite Potential Well

Another example, where we can obtain the tomographic representation, is the finite potential well; it is a potential given by the function

$$V\left(x\right)=\{\begin{array}{c}-V_0,-L<x<L,\\ 0,x\le -L,\mathrm{or}x\ge L,\end{array}$$

(18)

with $V_0$ being a positive constant. This problem allows one to obtain odd and even solutions given the symmetry of the potential well. The general solutions are usually obtained for three regions in the position space: $x\le -L$, $-L<x<L$, and $x\ge L$; they read

$${\psi }_{\mathrm{odd}}\left(x\right)=\left\{\begin{array}{c}A{e}^{k_{1}x},x\le -L,\\ Bsin\left(k_{2}x\right),-L<x<L,\\ -A{e}^{-k_{1}x},x\ge L,\end{array}\right.{\psi }_{\mathrm{even}}\left(x\right)=\left\{\begin{array}{c}{A}^{\prime }{e}^{k_{1}x},x\le -L,\\ Bcos\left(k_{2}x\right),-L<x<L,\\ A^{\prime }{e}^{-k_{1}x},x\ge L.\end{array}\right.$$

(19)

For all the eigenfunctions, one has the relations $k_1=\sqrt{{\displaystyle \frac{2m\left|E\right|}{{\hslash }^2}}}$ and $k_2=\sqrt{{\displaystyle \frac{2m(V_0-|E\left|\right)}{{\hslash }^2}}}$, while for odd (even) solutions, the parameters $k_1=-k_{2}cot\left(k_{2}L\right)$ ($k_1=k_{2}tan\left(k_{2}L\right)$). Additionally, the normalization constants A, $A^{\prime }$, and B are defined as

$$\begin{array}{c}\hfill A=-\sqrt{{\displaystyle \frac{k_1}{1+k_{1}L}}}sin\left(k_{2}L\right)e^{k_{1}L},A^{\prime }=\sqrt{{\displaystyle \frac{k_1}{1+k_{1}L}}}cos\left(k_{2}L\right)e^{k_{1}L},B=\sqrt{{\displaystyle \frac{k_1}{1+k_{1}L}}}.\end{array}$$

(20)

To obtain the tomographic representation of the wave functions, we separate the tomogram integral of Eq. (1) in three regions: $(-\infty ,-L]$, $[-L,L]$, and $[-L,\infty )$. For the odd wave functions, one obtains the following integrals:

$$A{\int }_{-\infty }^{-L}{e}^{k_{1}x}{e}^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx+B{\int }_{-L}^{L}sin\left(k_{2}x\right)e^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx-A{\int }_L^{\infty }{e}^{-2k_{1}x}{e}^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx,$$

(21)

and an analogous expression is found for the even states. The following integrals can be obtained for the regions outside of the barrier

$$\begin{array}{c}\hfill {\int }_{-\infty }^{-L}{e}^{k_{1}x}{e}^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx={\displaystyle \frac{i{e}^{-\frac{i{\left(X+i{k}_1\nu \right)}^2}{2\mu \nu }}{\left(\pi \nu \right)}^{1/2}{e}^{i\pi /4}}{{\left(2\mu \right)}^{1/2}}}\left(1+\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(i{k}_1\nu +\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\right),\\ \hfill {\int }_L^{\infty }{e}^{-k_{1}x}{e}^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx=\sqrt{{\displaystyle \frac{\pi }{2\mu }}}{e}^{{\displaystyle \frac{i{\left(k_1\nu +iX\right)}^2}{2\mu \nu }}}{e}^{i\pi /4}\left(1+i\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(i{k}_1\nu +\mu L-X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\right),\end{array}$$

(22)

while, inside the barrier, one has the following expressions for the even states:

$$\begin{array}{c}\hfill {\int }_{-L}^{L}cos\left(k_{2}x\right)e^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx={\displaystyle \frac{{\left(\pi \nu \right)}^{1/2}{e}^{\frac{3i\pi }{4}-\frac{i{\left(k_2\nu +X\right)}^2}{2\mu \nu }}}{2{\left(2\mu \right)}^{1/2}}}\left[e^{{\displaystyle \frac{2i{k}_{2}X}{\mu }}}\right\{\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(-k_2\nu -\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\\ \hfill -\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(-k_2\nu +\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\}+\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(k_2\nu -\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\\ \hfill -\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(k_2\nu +\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)],\end{array}$$

(23)

and this integral for odd states, inside the barrier

$$\begin{array}{c}\hfill {\int }_{-L}^{L}sin\left(k_{2}x\right)e^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx=-{\displaystyle \frac{{\left(\pi \nu \right)}^{1/2}{e}^{\frac{i\pi }{4}-\frac{i{\left(k_2\nu +X\right)}^2}{2\mu \nu }}}{2{\left(2\mu \right)}^{1/2}}}[\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(k_2\nu -\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\\ \hfill +e^{{\displaystyle \frac{2i{k}_{2}X}{\mu }}}\left\{\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(-k_2\nu +\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)+\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(k_2\nu +\mu L-X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\right\}\\ \hfill -\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(k_2\nu +\mu L+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)].\end{array}$$

(24)

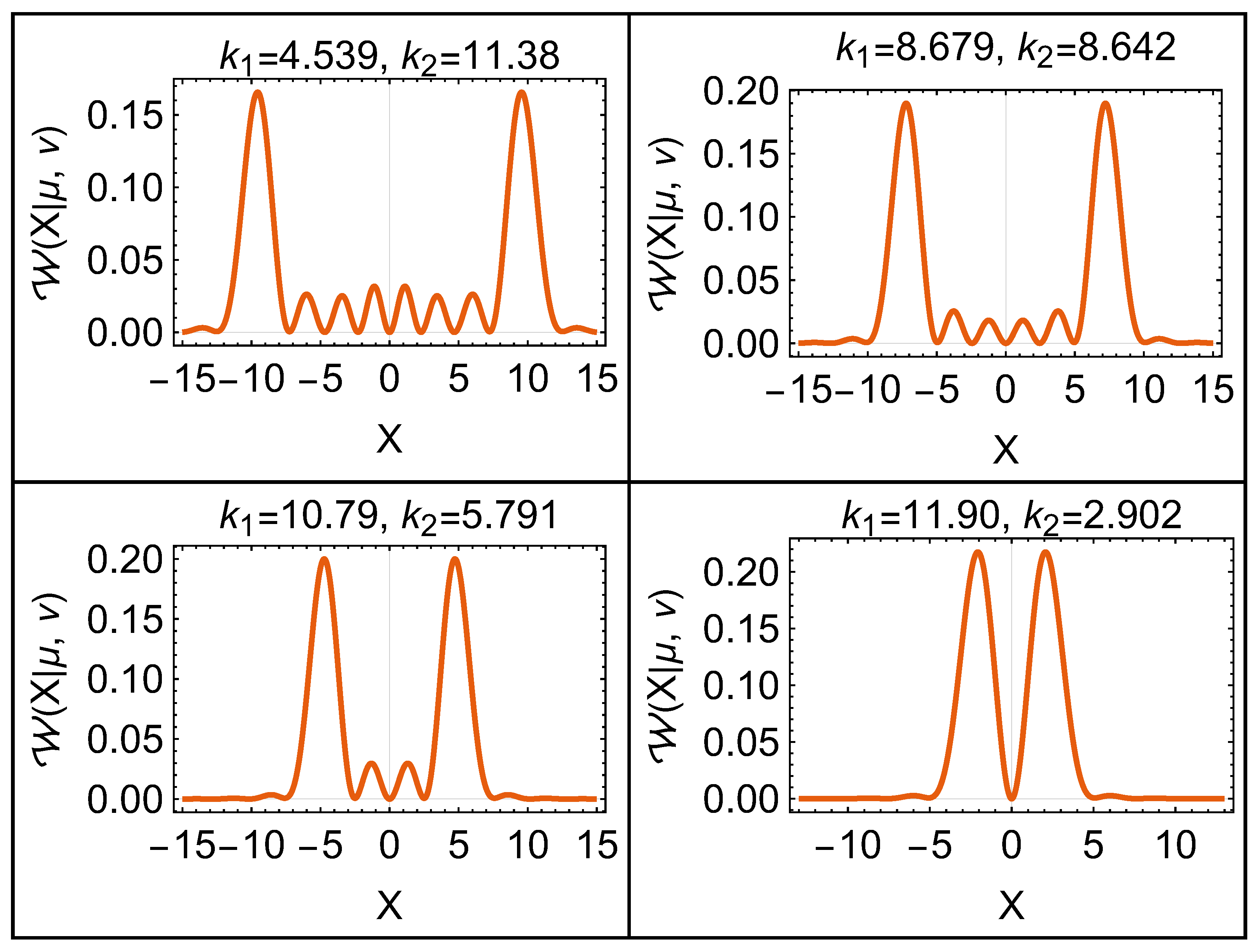
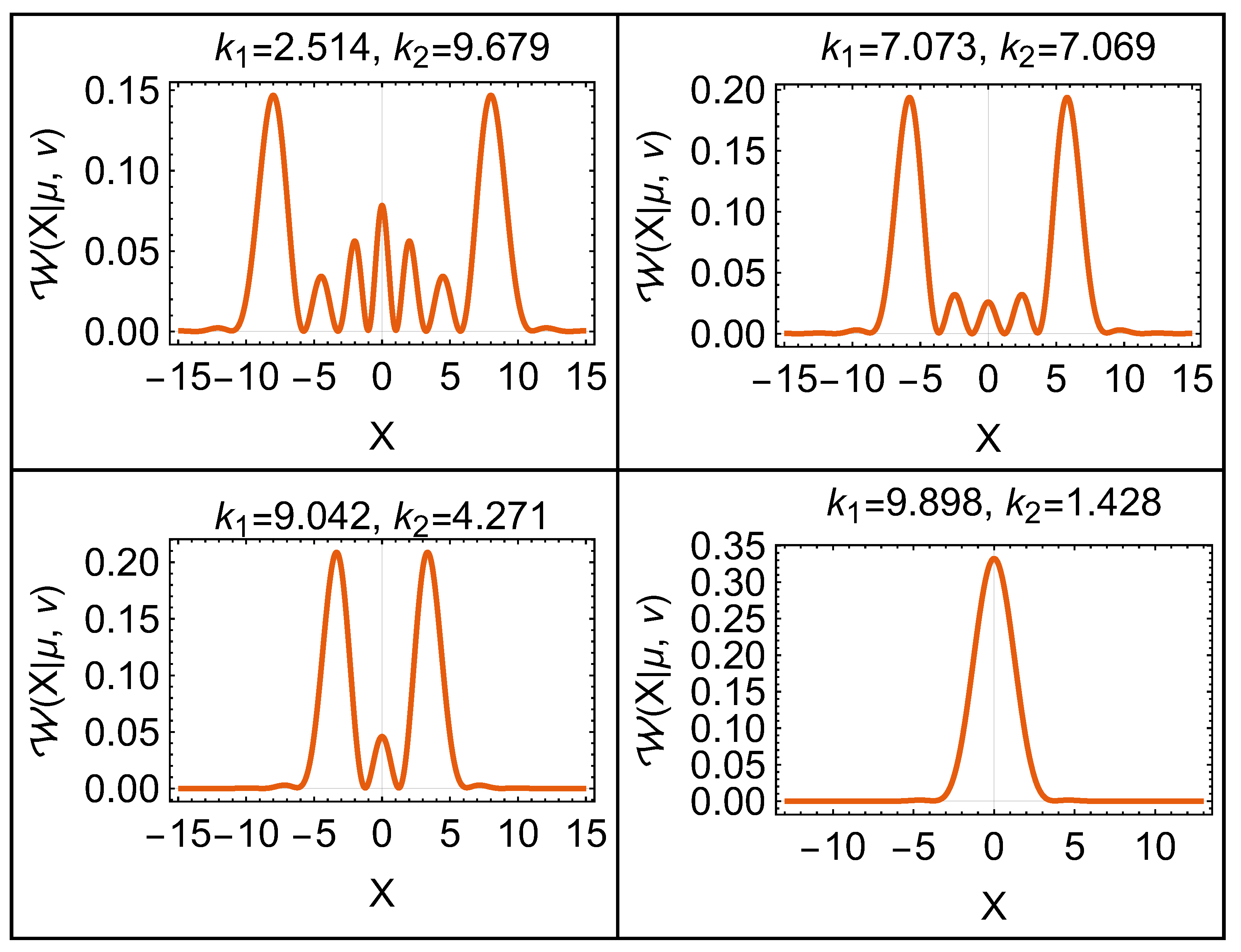
Then, using Eqs. (1), (23), and (24), one can plot the tomographic representation of the even and odd states of the finite potential well. In Figure 2 and Figure 3, we show the behavior of tomograms for the even and odd solutions of the problem. In these figures, one can see the combination of the position and momentum probability distributions. These tomograms have maxima around the well borders as in the momentum probability distribution and local maxima at the origin and other localized points inside the well as in the position probability distribution.

2.3. Infinite Potential Well

Another interesting example is the non-symmetrical infinite potential well. In this case, the problem is defined by the potential

$$V\left(x\right)=\left\{\begin{array}{c}\infty ,x<0,\mathrm{or}x>L,\\ 0,0\le x\le L,\end{array}\right.$$

(25)

which defines the following asymmetrical eigenfunctions of the system:

$${\psi }_n\left(x\right)=\sqrt{{\displaystyle \frac{2}{L}}}sin\left({\displaystyle \frac{n\pi x}{L}}\right).$$

(26)

In view of this expression, we obtain the tomographic representation which, in this case, can be determined using the following integral:

$$\begin{array}{c}\hfill f(b,x_0,x_1,X)={\int }_{x_0}^{x_1}{e}^{bx}{e}^{{\displaystyle \frac{i\mu }{2\nu }}{x}^2-{\displaystyle \frac{iX}{\nu }}x}dx={\displaystyle \frac{(1-i)}{2}}{\left({\displaystyle \frac{\pi \nu }{\mu }}\right)}^{1/2}{e}^{-i{\displaystyle \frac{{(X+ib\nu )}^2}{2\mu \nu }}}\\ \hfill \times \left\{\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(ib\nu -\mu x_0+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)-\mathrm{erfi}\left({\displaystyle \frac{\left(\frac{1}{2}+\frac{i}{2}\right)\left(ib\nu -\mu x_1+X\right)}{{\mu }^{1/2}{\nu }^{1/2}}}\right)\right\},\end{array}$$

(27)

expressed in terms of the imaginary error function. Using Eqs. (1), (26), and (27), the result is given by the following equation:

$$\mathcal{W}\left(X\right|\mu ,\nu )={\displaystyle \frac{1}{4\pi \left|\nu \right|L}}|f\left({\displaystyle \frac{in\pi }{L}},0,L,X\right)-f\left(-{\displaystyle \frac{in\pi }{L}},0,L,X\right){|}^2.$$

(28)

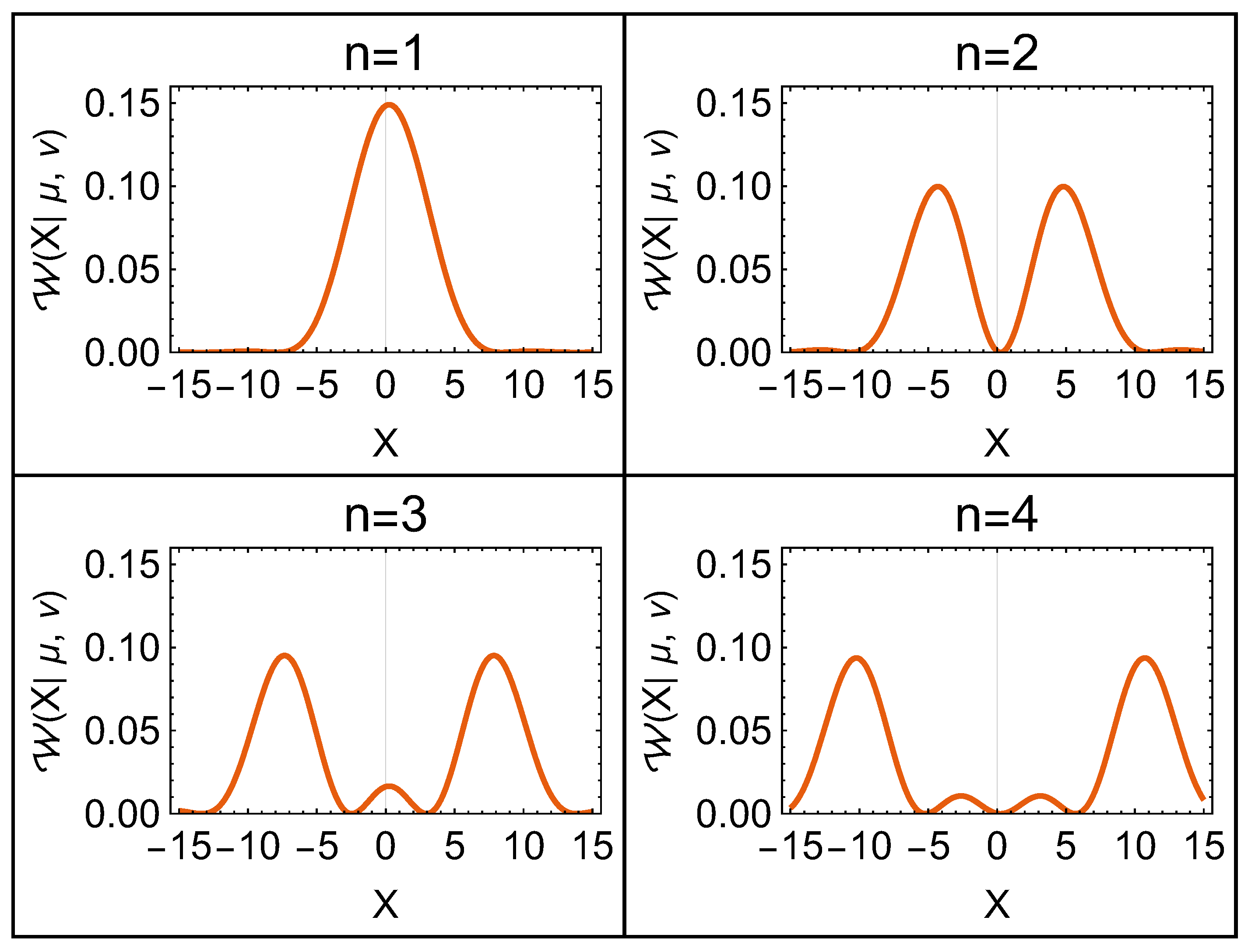
In Figure 4, we show the tomographic representation of the first four wave functions for the infinite well. One can see that, in the finite potential well, a combination of the momentum and position probability distributions, where the momentum probability has maxima at the borders of the potential and the position probability has maxima at localized points related to the quantum number n. In contrast with the solutions in the position representation which should be zero at $x=0,L$, the tomographic representation goes asymptotically to zero as the variable X goes to plus or minus infinity. This behaviour is also due to the momentum contribution of the tomogram.

2.4. Morse Potential

Our last example is the phenomenological molecular potential given by the Morse potential. The Morse potential, which reads [34,35]

$$V\left(x\right)=D(e^{-2\beta x}-2e^{-\beta x}),$$

(29)

where D is the depth of the potential, and $\beta$ is associated to the range of the potential. The bound solutions of this potential are given by

$$\psi \left(y\right)=N_v^j{e}^{-y/2}{y}^{j-v}{L}_v^{2(j-v)}\left(y\right),N_v^j=\sqrt{{\displaystyle \frac{2\beta (j-v)v!}{\Gamma (2j-v+1)}}},y=(2j+1)e^{-\beta x},$$

(30)

where $v<j$ is an nonnegative integer and j is a positive real number; both numbers are related to the energy, depth, and range of the potential as follows:

$$2j+1=\sqrt{{\displaystyle \frac{8mD}{{\hslash }^2{\beta }^2}}},j-v=\sqrt{{\displaystyle \frac{-2mE}{{\hslash }^2{\beta }^2}}},$$

(31)

with m being the reduced mass of a molecule. The tomographic representation of the solutions of the Morse potential can be numerically found. As an example, we obtain the tomographic representation of the Morse potential solutions with $j=5$ and $v=1,2,3,4$.

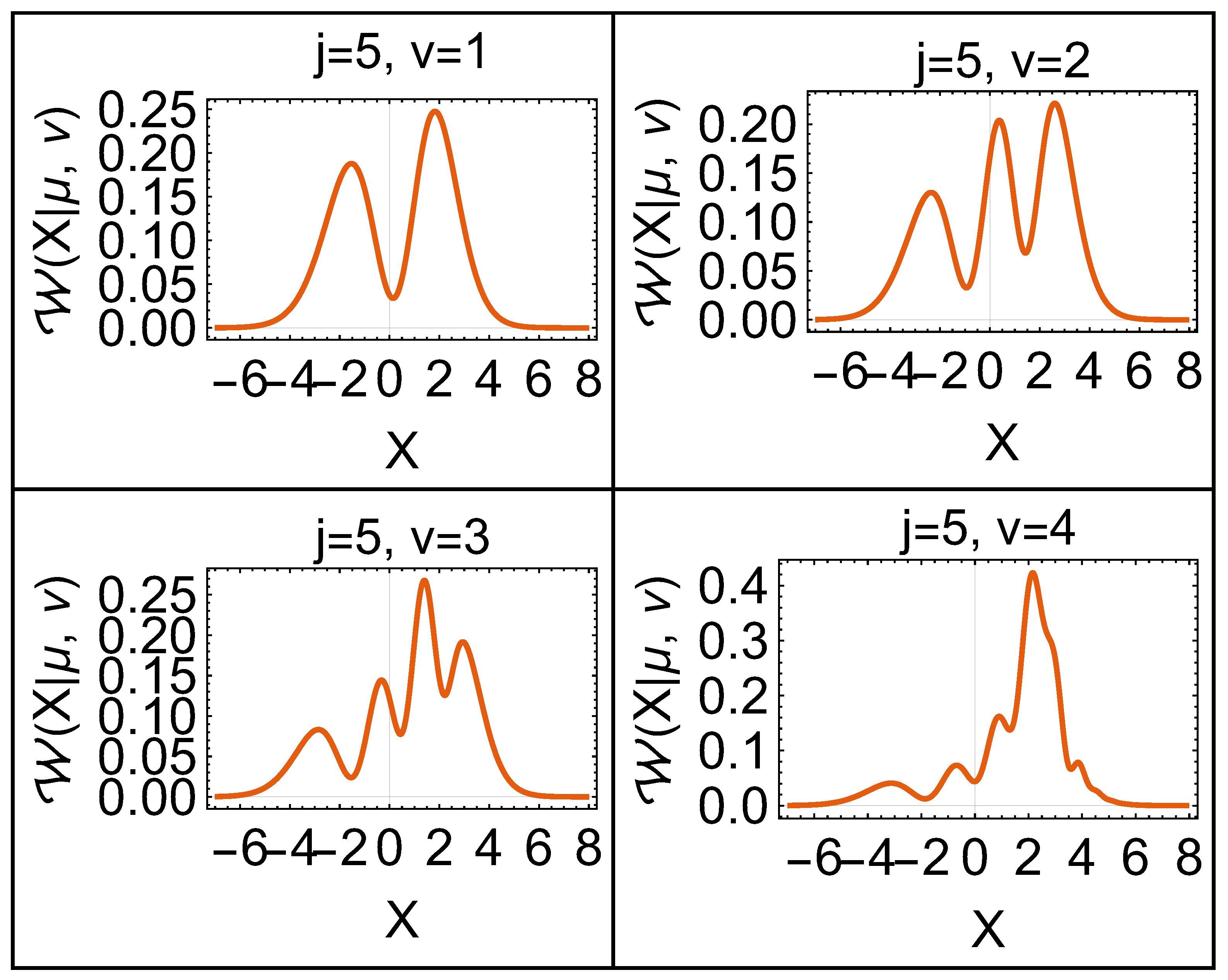
In Figure 5, the numerical solutions for the tomographic representations of four eigenfunctions at $j=5$ are shown. One can observe the complexity of the tomographic representation for the states. This complexity is bigger as the parameter v increases. We point out that the maximum of the tomographic probability distribution is located around the potential minimum, which coincides with the position probability distribution.

3. Separability Criteria for Asymmetric Real States

The tomographic representation of quantum mechanics is useful to obtain information on the system, using probabilities. At the same time, other probability distributions for a quantum system give different information on its behavior. In this section, we study the momentum probability representation and its relation to the separability properties of specific bipartite systems.

Let us consider an arbitrary n-partite wave function in the position representation

$$\psi (x_1,x_2,\dots ,x_n,t)=\psi (\overrightarrow{x},t)=\mathcal{N}\sum _{m=1}^N{c}_m\left(t\right){\varphi }_{l_m^{\left(1\right)}}\left(x_1\right){\varphi }_{l_m^{\left(2\right)}}\left(x_2\right)\cdots {\varphi }_{l_m^{\left(n\right)}}\left(x_n\right),$$

(32)

where the integers $l_m^{\left(i\right)}$; $i=1,2,\dots ,n$ characterize a particular state, $\mathcal{N}$ is a normalization constant, and the set of states $\left\{{\varphi }_n\left(x\right)\right\}$ form an orthogonal basis of functions. It is known, that this state together with its conjugate must satisfy the probability conservation equation,

$$\begin{array}{c}\hfill {\displaystyle \frac{d\rho (\overrightarrow{x},t)}{dt}}+\nabla ·\overrightarrow{j}=0,\rho (\overrightarrow{x},t)=\psi (\overrightarrow{x},t){\psi }^{*}(\overrightarrow{x},t),\\ \hfill \overrightarrow{j}={\displaystyle \frac{i\hslash }{2m}}(\psi (\overrightarrow{x},t)\nabla {\psi }^{*}(\overrightarrow{x},t)-{\psi }^{*}(\overrightarrow{x},t)\nabla \psi (\overrightarrow{x},t)),\end{array}$$

(33)

where we can express the gradient for a system of unidimensional particles as $\nabla =\left({\displaystyle \frac{\partial }{\partial x_1}},{\displaystyle \frac{\partial }{\partial x_2}},\cdots ,{\displaystyle \frac{\partial }{\partial x_n}}\right)$. This probability conservation implies that, in the case of stationary states, the divergence of the probability current is equal to zero,

$$\nabla ·\overrightarrow{j}=0.$$

(34)

In particular, this stationary probability conservation equation can be satisfied for quantum systems, where the probability current is equal to zero,

$$\overrightarrow{j}=0.$$

(35)

For this type of systems, one can prove the following theorem for the total momentum probability distribution $\rho \left(\overrightarrow{p}\right)=\tilde{\psi }\left(\overrightarrow{p}\right){\tilde{\psi }}^{*}\left(\overrightarrow{p}\right)$ and reduced momentum probability distributions ${\displaystyle \rho \left(p_k\right)=\int \tilde{\psi }\left(\overrightarrow{p}\right){\tilde{\psi }}^{*}\left(\overrightarrow{p}\right)\prod _{l\ne k}^{n}d{p}_l}$.

Theorem 1

For a stationary system, with $\overrightarrow{j}=0$ and depicted by an asymmetric wave function $\psi \left(\overrightarrow{x}\right)$, with momentum representation written as

$${\displaystyle \tilde{\psi }\left(\overrightarrow{p}\right)=\frac{1}{{\left(\sqrt{2\pi \hslash }\right)}^n}\int \psi \left(\overrightarrow{x}\right)exp\left(-i\sum _{l=1}^n{p}_l{x}_l/\hslash \right)\prod _{k=1}^{n}d{x}_k,}$$

in a momentum domain $(-p_M,p_M)$, the total momentum probability distribution $\rho \left(\overrightarrow{p}\right)=\tilde{\psi }\left(\overrightarrow{p}\right){\tilde{\psi }}^{*}\left(\overrightarrow{p}\right)$ and the reduced momentum probability distributions ${\displaystyle \rho \left(p_k\right)=\int \tilde{\psi }\left(\overrightarrow{p}\right){\tilde{\psi }}^{*}\left(\overrightarrow{p}\right)\prod _{l\ne k}^{n}d{p}_l}$ are even functions of the momentum variables. That is, $\rho (-\overrightarrow{p})=\rho \left(\overrightarrow{p}\right)$ and $\rho (-p_k)=\rho \left(p_k\right)$, $k=1,\dots ,n$.

Proof

To demonstrate the property for a unidimensional system, one first integrate Eq. (35) in the position x, that is,

$$\int jdx=0,\mathrm{with}j={\displaystyle \frac{i\hslash }{2m}}\left(\psi \left(x\right){\displaystyle \frac{d{\psi }^{*}\left(x\right)}{dx}}-{\psi }^{*}\left(x\right){\displaystyle \frac{d\psi \left(x\right)}{dx}}\right),$$

(36)

where j can be rewritten with the help of the Dirac notation, and the momentum operator properties $\widehat{p}|x\rangle =i\hslash {\displaystyle \frac{d}{dx}}|x\rangle$ and $\langle x|\widehat{p}=-i\hslash {\displaystyle \frac{d}{dx}}\langle x|$, namely,

$$\begin{array}{ccc}\hfill \int jdx& =& {\displaystyle \frac{i\hslash }{2m}}\int dx\left(\langle x|\psi \rangle {\displaystyle \frac{d}{dx}}\langle \psi |x\rangle -\langle \psi |x\rangle {\displaystyle \frac{d}{dx}}\langle x|\psi \rangle \right)\hfill \\ & =& {\displaystyle \frac{1}{2m}}\int dx\left(\langle \psi |\widehat{p}|x\rangle \langle x|\psi \rangle +\langle \psi |x\rangle \langle x|\widehat{p}|\psi \rangle \right),\hfill \end{array}$$

(37)

which, along with the completeness condition ${\displaystyle \int |x\rangle \langle x|dx=\widehat{I}}$, allow us to write the integral of the probability current

$$\int jdx={\displaystyle \frac{\langle \widehat{p}\rangle }{m}}=0,$$

(38)

since the mean value of the momentum operator can be written in integral form, using the momentum probability distribution $\rho \left(p\right)=\tilde{\psi }\left(p\right){\tilde{\psi }}^{*}\left(p\right)$, as

$$\langle \widehat{p}\rangle ={\int }_{-L}^{L}p\rho \left(p\right)dp=0,$$

(39)

where p is an antisymmetric function; then, $\rho \left(p\right)$ must be a symmetric function. This shows the theorem for a unimodal and unidimensional system.

In the n-partite, multidimensional case, one can prove this theorem for each component of $\overrightarrow{j}$, which reduces to the unidimensional case □.

In particular, any asymmetric real wave function $\overrightarrow{j}=0$ satisfies the previous theorem, and thereof this aspect can be written as the following corollary.

Corollary 1

Any asymmetric real wave function in the position domain has an even probability distribution in the momentum domain and even reduced momentum probability distributions.

This property can be extended for any real density matrix since, in general, any real $\widehat{\rho }$ can be constructed by a convex sum of products of real wave functions as follows:

$$〈\overrightarrow{x}\left|\widehat{\rho }\right|{\overrightarrow{x}}^{\prime }〉=\sum _{m=1}^N{\mathcal{P}}_m{\psi }_m\left(\overrightarrow{x}\right){\psi }_m\left({\overrightarrow{x}}^{\prime }\right),\mathrm{with}\sum _{m=1}^N{\mathcal{P}}_m=1,$$

(40)

where $\psi \left(\overrightarrow{x}\right)$ is a real function. Then, the density matrix of Eq. (40) in the momentum representation reads

$$\langle \overrightarrow{p}|\widehat{\rho }|{\overrightarrow{p}}^{\prime }\rangle =\sum _{m=1}^N{\mathcal{P}}_m{\tilde{\psi }}_m\left(\overrightarrow{p}\right){\tilde{\psi }}_m^{*}\left({\overrightarrow{p}}^{\prime }\right),{\tilde{\psi }}_m\left(\overrightarrow{p}\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{n/2}}}{\int }_{-\infty }^{\infty }{e}^{-i{\sum }_{j=1}^n{p}_j{x}_j}\psi \left(\overrightarrow{x}\right)d{x}_1\cdots d{x}_n,$$

(41)

with every superposed momentum probability distribution ${\rho }_m\left(\overrightarrow{p}\right)={\tilde{\psi }}_m\left(\overrightarrow{p}\right){\tilde{\psi }}_m^{*}\left(\overrightarrow{p}\right)$ being even functions of the momentum, as given by theorem 1. Then the probability distribution

$$\langle \overrightarrow{p}|\widehat{\rho }|\overrightarrow{p}\rangle =\sum _{m=1}^N{\mathcal{P}}_k{\rho }_m\left(\overrightarrow{p}\right)$$

(42)

is a convex sum of even functions, which is also an even function. These arguments can be summarized in the following corollary.

Corollary 2

Any asymmetric (a state with at least one asymmetrical reduced probability distribution $\rho \left(x_i\right)$) real density matrix: $\langle \overrightarrow{x}\left|\widehat{\rho }\right|{\overrightarrow{x}}^{\prime }\rangle$, has an even momentum probability distribution $\langle \overrightarrow{p}\left|\widehat{\rho }\right|\overrightarrow{p}\rangle$ and even reduced momentum probability densities ${\displaystyle \rho \left(p_k\right)={\int }_{-L}^L\langle \overrightarrow{p}|\widehat{\rho }|\overrightarrow{p}\rangle \prod _{l\ne k}d{p}_l}$.

Stressing the importance of this corollary for our study, we give a more detailed proof in Appendix A.

Then, the theorem and corollaries above can be used to examine the entanglement of a bipartite system, which can be described by an asymmetric real density matrix. The idea behind this is to explore the symmetries in the momentum space of an asymmetric density matrix under the partial inversion of one of its momentum variables, either $p_1\to -p_1$ or $p_2\to -p_2$. This property can be given as the following theorem.

Theorem 2

A necessary condition of separability for a bipartite asymmetric real density matrix is if the probability distribution of the system $\langle \overrightarrow{p}\left|\widehat{\rho }\right|\overrightarrow{p}\rangle$ is symmetric under both partial momentum inversions $p_1\to -p_1$ and $p_2\to -p_2$. In other words, $\rho (-p_1,p_2)=\rho (p_1,-p_2)=\rho (p_1,p_2)$.

Proof

Any real asymmetrical bipartite separable density matrix can be written as a convex sum

$$\langle x_1,x_2|\widehat{\rho }|x_1^{\prime },x_2^{\prime }\rangle =\sum _{k=1}^N{\mathcal{P}}_k\langle x_1|{\widehat{\rho }}_{1k}|x_1^{\prime }\rangle \langle x_2|{\widehat{\rho }}_{2k}|x_2^{\prime }\rangle ,\mathrm{with}\sum _{k=1}^N{\mathcal{P}}_k=1,$$

(43)

where $\langle x_1|{\widehat{\rho }}_{1k}|x_1^{\prime }\rangle$ and $\langle x_2\left|{\widehat{\rho }}_{2k}\right|x_2^{\prime }\rangle$ are real and define at least one asymmetrical reduced position probability distribution; thus, using the results of corollary 2, the reduced momentum probability distributions $\rho \left(p_1\right)=\langle p_1|{\widehat{\rho }}_{1k}|p_1\rangle$ and $\rho \left(p_2\right)=\langle p_2|{\widehat{\rho }}_{2k}|p_2\rangle$ are even functions. In other words, the transformations

$$\langle p_1,p_2|\widehat{\rho }|p_1^{\prime },p_2^{\prime }\rangle =\langle -p_1,-p_2|\widehat{\rho }|-p_1^{\prime },-p_2^{\prime }\rangle =\langle -p_1,p_2|\widehat{\rho }|-p_1^{\prime },p_2^{\prime }\rangle =\langle p_1,-p_2|\widehat{\rho }|p_1^{\prime },-p_2^{\prime }\rangle$$

(44)

map density matrices into density matrices.

On the other hand, to demonstrate that, if a real asymmetrical bipartite density matrix does not obey the Peres–Horodecki criterion [36,37,38] for separability, then the bipartite momentum probability distribution $\rho (p_1,p_2)$ may not be symmetrical on at least one partial momentum inversion (either $p_1\to -p_1$ or $p_2\to -p_2$), we can first take into account a general entangled state, using the harmonic oscillator basis ${\varphi }_n\left(x\right)$ (without loss of generality),

$$\langle x_1,x_2|\widehat{\rho }|x_1^{\prime },x_2^{\prime }\rangle =\sum _{n,n^{\prime },m,m^{\prime }=0}^{\infty }{c}_{n,m,n^{\prime },m^{\prime }}{\varphi }_n\left(x_1\right){\varphi }_m\left(x_2\right){\varphi }_{n^{\prime }}\left(x_1^{\prime }\right){\varphi }_{m^{\prime }}\left(x_2^{\prime }\right).$$

(45)

This leads us to the following bipartite momentum probability distribution:

$$\rho (p_1,p_2)=\langle p_1,p_2|\widehat{\rho }|p_1,p_2\rangle =\sum _{n,n^{\prime },m,m^{\prime }=0}^{\infty }{c}_{n,m,n^{\prime },m^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right),$$

(46)

where the momentum eigenfunctions of the harmonic oscillator are

$${\tilde{\varphi }}_n\left(p\right)={\displaystyle \frac{{(-i)}^n}{{\pi }^{1/4}\sqrt{2^{n}n!}}}{e}^{-p^2/2}{H}_n\left(p\right),$$

(47)

and they have the same symmetry properties as the position eigenfunctions: ${\tilde{\varphi }}_n(-p)={(-1)}^n{\tilde{\varphi }}_n\left(p\right)$. The Hermitian condition of Eq. (45) implies $c_{n,m,n^{\prime },m^{\prime }}=c_{n^{\prime },m^{\prime },n,m}$, and the normalization condition is represented by ${\sum }_{n,m=0}^{\infty }{c}_{n,m,n,m}=1$. The nonseparability of the system can be summarized, using the Peres–Horodecki criteria: the partial transpose density matrices $\langle x_1^{\prime },x_2\left|\widehat{\rho }\right|x_1,x_2^{\prime }\rangle$ and $\langle x_1,x_2^{\prime }\left|\widehat{\rho }\right|x_1^{\prime },x_2\rangle$ may not represent a well-defined quantum system when the system is non-separable.

Given these properties, the symmetry under the partial inversions $p_1\to -p_1$ and $p_2\to -p_2$ of the bipartite momentum probability can be directly obtained from Eq. (46) as follows:

$$\begin{array}{c}\hfill \rho (-p_1,p_2)=\sum _{n,n^{\prime },m,m^{\prime }=0}^{\infty }{c}_{n,m,n^{\prime },m^{\prime }}{(-1)}^{n+n^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right),\\ \hfill \rho (p_1,-p_2)=\sum _{n,n^{\prime },m,m^{\prime }=0}^{\infty }{c}_{n,m,n^{\prime },m^{\prime }}{(-1)}^{m+m^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right),\end{array}$$

(48)

which may be equal to the original probability distribution $\rho (p_1,p_2)$, if both

$$\begin{array}{c}\hfill c_{n,m,n^{\prime },m^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right)=c_{n,m,n^{\prime },m^{\prime }}{(-1)}^{n+n^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right)\\ \hfill =c_{n,m,n^{\prime },m^{\prime }}{(-1)}^{m+m^{\prime }}{\tilde{\varphi }}_n\left(p_1\right){\tilde{\varphi }}_m\left(p_2\right){\tilde{\varphi }}_{n^{\prime }}^{*}\left(p_1\right){\tilde{\varphi }}_{m^{\prime }}^{*}\left(p_2\right);\end{array}$$

(49)

this may be satisfied, if the pairs $n,n^{\prime }$ and $m,m^{\prime }$ are both even–even and/or odd–odd numbers always (the system has symmetrical position probability distributions) or when, for given the correspondence ${\tilde{\varphi }}_n^{*}\left(p\right)={(-1)}^n{\tilde{\varphi }}_n\left(p\right)$, one has

$$c_{n,m,n^{\prime },m^{\prime }}=c_{n^{\prime },m,n,m^{\prime }}=c_{n,m^{\prime },n^{\prime },m},$$

(50)

which means that the partial transpose operations $\langle x_1,x_2^{\prime }\left|\widehat{\rho }\right|x_1^{\prime },x_2\rangle$ and $\langle x_1^{\prime },x_2\left|\widehat{\rho }\right|x_1,x_2^{\prime }\rangle$ are bona-fide density matrices and, thus, the system is separable (for more details; see Appendix B), contradicting our initial suppositions of asymmetry and non-separability. So we conclude that $\rho (p_1,p_2)=\rho (-p_1,p_2)=\rho (p_1,-p_2)$ is hold for a real density matrix, only when the system is separable or when it has a defined symmetry for both subsystems ($\rho \left(x_1\right)=\rho (-x_1)$ and $\rho \left(x_2\right)=\rho (-x_2)$) □.

The necessary separability condition given in theorem 2 is also a sufficient criterion in the cases, where the Peres–Horodecki criterion is a sufficient condition for separability. These cases include both conditions – when the sums of the parameters $n,n^{\prime }$ have two contributions and $m,m^{\prime }$ have two or three elements.

This separability criterion may allow us to detect bipartite entanglement, directly using the momentum probability distribution of the system and, thus, may be more convenient when working with continuous variable systems. On the other hand, this criteria may have implications in the probabilistic representation given by the tomogram. As we have discussed, the tomogram contains information on both the position and momentum probability distributions.

3.1. Example

For a better understanding of our results, we present an specific example of our separability criteria. Let us suppose a two-mode harmonic oscillator state of the form

$$\widehat{\rho }={\displaystyle \frac{1}{3}}|0,0\rangle \langle 0,0|+{\displaystyle \frac{1}{3}}|0,1\rangle \langle 0,1|+{\displaystyle \frac{1}{6}}\left(\right|0,1\rangle \langle 0,0|+|0,0\rangle \langle 0,1\left|\right)+{\displaystyle \frac{1}{3}}|1,1\rangle \langle 1,1|,$$

(51)

which is not a factorizable state but may be separable. One can obtain the reduced density matrices

$${\widehat{\rho }}^{\left(1\right)}={\displaystyle \frac{2}{3}}|0\rangle \langle 0|+{\displaystyle \frac{1}{3}}|1\rangle \langle 1|,{\widehat{\rho }}^{\left(2\right)}={\displaystyle \frac{1}{3}}|0\rangle \langle 0|+{\displaystyle \frac{2}{3}}|1\rangle \langle 1|+{\displaystyle \frac{1}{6}}\left(\right|0\rangle \langle 1|+|1\rangle \langle 0\left|\right),$$

(52)

these define a symmetric probability function for mode 1 and an asymmetrical probability function for mode 2, in the position representation. In other words, this density matrix is real and asymmetric as established by theorem 2.

The momentum probability distribution of the system is then given by the function

$$\langle p_1,p_2|\widehat{\rho }|p_1,p_2\rangle ={\displaystyle \frac{e^{-p_1^2-p_2^2}}{3\pi }}\left(1+2p_2^2+4p_1^2{p}_2^2\right),$$

(53)

being a symmetric function of both $p_1$ and $p_2$. From this result and theorem 2, one can conclude that the system is separable. This can be corroborated as the system can be expressed as the following convex sum of product states

$$\widehat{\rho }={\displaystyle \frac{1}{2}}|0\rangle \langle 0|\otimes |{\psi }_{+}\rangle \langle {\psi }_{+}|+{\displaystyle \frac{1}{3}}|1\rangle \langle 1|\otimes |1\rangle \langle 1|+{\displaystyle \frac{1}{6}}|0\rangle \langle 0|\otimes |{\psi }_{-}\rangle \langle {\psi }_{-}|,$$

(54)

with the states $|{\psi }_{\pm }\rangle =\left(\right|0\rangle \pm |1\rangle )/\sqrt{2}$. Similarly to this example, more complicated states can be taken into account and their separability information may be obtained by examining the symmetry of the momentum probability distribution.