Methodology for Modeling Coupled Rigid Multibody Systems Using Unitary Quaternions: The Case of Planar RRR and Spatial PRRS Parallel Robots

1. Introduction

The kinematic analysis of parallel kinematic machines is a challenging field since such machines are complex multi-body systems involving at least one pair of closed kinematic loops [1]. There are important differences between serial and parallel configuration robots, for example, the latter due to their robust structure, higher load capacity, versatility and excellent positioning accuracy [2].

In fact, in industrial automation, parallel manipulators have been considered an alternative to traditional automation to achieve a high load capacity, intelligent dynamic performance, and precise positioning that provide higher quality and more economical processes [3]. The main drawbacks of parallel robots are their small workspace and the singularities that can appear within the latter [2].

Parallel robots are currently used in various applications such as machining operations [4], additive manufacturing for construction [5], and dimensional metrology [6]. This type of robot is also used for medical operations [7] and in rehabilitation [8], as well as in flight simulators [9] and in telescope mechanisms [10], among others.

For the kinematic modeling of parallel robots, there are several mathematical methods and tools; the following is a summary. Homogeneous matrices and Denavit-Hartenberg parameters are regularly used for the kinematic modeling of this type of robot [11,12]. Also, geometrical methods have been used to study the planar motion of parallel-type robots [13,14] and their singularities [15]. Screw theory is also used in the modeling of parallel robots [16,17]. Complex number algebra [18] and quaternions [19,20] are used to model robot rotations in the plane and in space, respectively. Other versions of quaternions, such as dual representations, are also applied to the modeling of parallel robots [21,22].

While each mathematical tool and modeling method used to study parallel robots has its advantages and disadvantages, quaternions stand out due to their compact notation and ease of composition, and they are more efficient than matrix methods, involving fewer algebraic operations and, hence less computational storage. In fact, the performance of dual quaternions has been shown to improve by 30-40% in forwarding kinematics over conventional homogeneous transformation matrices [23]. These and other important features of quaternions and their representations make them ideal for modeling parallel robots. Recently, a PUMA-type robot has been modeled with the algebra of quaternions [24]. In this work, the systematization of the quaternions developed in 1990 at INRIA France [25,26] was applied. The results showed that it was possible to model the rotations of the links of an open chain robot clearly and systematically, performing all the operations in the vector space of quaternions avoiding the use of trigonometric relations during modeling. The PUMA robot was modeled using sequences of rotations and the numerical solution of the mathematical model associated with the inverse kinematics was obtained with the Newton-Raphson method.

In other works, quaternions have been applied to the analysis and synthesis of parallel robots, for example, in [27] the kinematic synthesis problem of a planar parallel robot of the RPR type was modeled using planar quaternions. The generated model allowed to achieve any desired configuration and the definition of the problem in the space of planar quaternions resulted in a definition of the work space of the parallel manipulator as the intersection of quadratic equations. In another study, the modes of operation and transition configurations of the parallel cylindrical mechanism 1-RPU-2-UPU were analyzed [28]. In that study, a reconfiguration analysis of a parallel manipulator was performed and the constraint equations were modeled using Euler parameter quaternion. Liu et al. [29] proposed an analytical algorithm using unitary quaternions to model the direct kinematics of a 6-UPS parallel robot with an additional displacement sensor mounted at the top and bottom platform centers ((6+1)-UPS). Birlescu et al [30] proposed a mathematical method to redefine motion parameterizations based on the joint space representation of parallel robots. The mathematical models were developed using dual quaternions, and the main feature of the model was that, instead of directly studying the motion of the moving platform, the joint space of the mechanism was analyzed by eliminating the study parameters. Finally, Liu et al. [31] analyzed the modes of operation and corresponding motion characteristics of low-mobility parallel mechanisms using unitary dual quaternions.

On the other hand, many mathematical models related to robot motions and mechanisms consider the unitary norm of quaternions which implies that the systems of equations are nonlinear. To solve this type of problem, the Newton-Raphson method is commonly used [24]. Quasi-Newton methods and the Davidon-Fletcher-Powell (DFP) algorithm have also been used to solve mathematical models of robots and mechanisms. For example, in [32] the DFP algorithm was applied to determine the numerical solution and optimization of parasitic motions of a 3 DOF parallel robot. There are several variants of the quasi-Newton methods and in all of them the idea is to consider the Hessian matrix in the quadratic model. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) method is a variant of the DFP method and was used by Kashyap and Parhi (Kumar; Dayal) [33] to solve a path planning problem for a humanoid robot. In turn, Xie et al. [34], used the BFGS algorithm, the Newton-Raphson method and the Levenberg-Marquardt algorithm to compute the inverse kinematic problem for a 7 DOF open-chain robot.

On the other hand, the PRRS type and the RRR planar robot stand out from the existing set of parallel spatial and planar robots. The PRRS space robot has been studied in [35] where its design was developed using structural synthesis modeling and degrees of freedom analysis. On the other hand, the RRR planar robot, due to its simple configuration, has been used to test different kinematic and dynamic modeling [36,37]. In other works, this robot was used to develop artificial intelligence tests [38,39] and to test different control models [40,41], as well as for the study and analysis of singularities [42,43].

This paper describes and applies a novel methodology using unitary quaternions for the study of the motions of parallel PRRS and RRR type robots. This methodological proposal is a continuation of the modeling method described in [24] and aims to extend the applications of the quaternion systematization developed by Reyes [25,26] to other types of robots, in this case, to the study of parallel robots. With the mathematical models generated for each robot analyzed, inverse kinematic problems were formulated. These problems were solved using the formal calculation platform Mathematica V12. The novelties of this work with respect to the results presented in [24], are: 1) for the modeling of the robots under study two configurations are not considered, 2) the mathematical models generated are non-square and non-linear and 3) the solution method used was BFGS optimization method [44,45,46]. Although there are already several methodologies that take quaternions into account as the basis for modeling robot motions [24,47,48,49,50,51,52], the method proposed in this paper is general and can be applied to model parallel robots in the plane and in space.

2. Materials and Methods

In this section a summary of the theoretical framework of Quaternion algebra and the methodology to systematize rotations using unitary quaternions is presented. In addition, modeling of RRR and PRRS robots of parallel configuration is developed. The inverse kinematic problem is formulated for both robots and the BFGS optimization method with which the generated mathematical models were solved is described.

2.1. Preliminaries of the Algebra of Quaternions

A systematic way of constructing the algebra of quaternions with a modern linear algebra focus is presented in [24,25,26]. Let the set $ℛ$⁴, on which the binary operations are defined ⊕:$ℛ$⁴×$ℛ$⁴®$ℛ$⁴ and ∗: $ℛ$⁴× $ℛ$⁴®$ℛ$⁴ be expressed:

i) (a,b,c,d) ⊕ (α,β,γ,δ) = (a+α, b+β , c+γ , d+δ)    (1)

ii) (a,b,c,d) ∗ (α,β,γ,δ) = (aα − bβ − cγ − dδ, aβ + bα + cδ − dγ, aγ − bδ + cα + dβ, aδ + bγ-cβ + dα ), ∀ (a,b,c,d), (α,β,γ,δ) ∈ $ℛ$⁴

The pairs ($ℛ$⁴,⊕) and ($ℛ$⁴,∗) form a commutative additive group and a non-commutative multiplicative group, respectively. The triple ($ℛ$⁴,⊕,∗) forms a non-commutative field. This is:

The operation ∗:$ℛ$⁴×$ℛ$⁴®$ℛ$⁴ is associative, since:

i)

p∗(q∗s) = (p∗q)∗s; ∀ p, q, s∈$ℛ$⁴        (2)

ii)

The element 1 = (1,0,0,0) ∈ $ℛ$⁴ is such that: 1∗p=p∗1=p, ∀p∈$ℛ$⁴. This element is known as the neutral element of the multiplication in $ℛ$⁴.

iii)

iii) ∀p∈$ℛ$⁴, p ≠ (0,0,0,0); p’∈$ℛ$⁴ such that p∗p’ = 1. The element p’ is called the multiplicative inverse of the quaternion p.

iv)

iv) The operation ∗:$ℛ$⁴×$ℛ$⁴®$ℛ$⁴ is not commutative. This is:

v)

p∗q ≠ q∗p

vi)

The following distributive properties are satisfied:

a) (p⊕q)∗s = p∗s ⊕ q∗s          (3)

b) p∗(q⊕s) = p∗q ⊕ p∗s, ∀p, q, s∈$ℛ$⁴

On the other hand, the operation ∙:$ℛ$×$ℛ$⁴®$ℛ$⁴ is defined by:

α∙(a,b,c,d) = (αa,αb,αc,αd), ∀(a,b,c,d)∈$ℛ$⁴, α∈$ℛ$         (4)

It is a scalar product on $ℛ$⁴, so the term ($ℛ$⁴,⊕,∙) is a real vector space. The transformation <∙,∙>:$ℛ$⁴× $ℛ$⁴®$ℛ$, is defined by:

$<\mathbf{p},\mathbf{q}\ge \sum _{\mathrm{i}=0}^3{\mathrm{p}}_{\mathrm{i}}{\mathrm{q}}_{\mathrm{i}}\in$          (5)

It is an inner product in $ℛ$⁴ and, therefore, the structure Q=($ℛ$⁴,⊕,∗,∙,<∙,∙>) is a real vector space with inner product, and the norm associated with this inner product is the following:

||p|| = <p,p>^1/2 = (p₀²+p₁²+p₂² +p₃²) ^1/2         (6)

For which the structure Q=($ℛ$⁴,⊕,∗,∙, |∙|) is a normed space which will be called the vector space of quaternions, and its elements will be called quaternions [25].

It is possible to represent a quaternion as the sum of a real quaternion and a vector quaternion. Let the following subsets be:

Q_r = {(a,0,0,0) : a∈$ℛ$}⊂Q,          (7)

Q_v = {(0,b,c,d) : b,c,d∈$ℛ$}⊂Q

The transformations are defined by:

T_r(a,0,0,0) = a      ∀(a,0,0,0)∈Q_r         (8)

T_v(0,b,c,d) = (b,c,d)      ∀(0,b,c,d)∈Q_v

are isomorphic, and therefore, if p=(a,b,c,d)∈Q, then:

p = ${\mathbf{T}}_{\mathbf{r}}^{-1}$(a)

${\mathbf{T}}_{\mathbf{v}}^{-1}$(b, c, d)          (9)

In a similar way to the algebra of complex numbers, a conjugate quaternion can be defined as follows:

$\stackrel{\mathrm{-}}{\mathrm{p}}=\left({\mathrm{p}}_0,-{\mathrm{p}}_1,-{\mathrm{p}}_2,-{\mathrm{p}}_3\right)$          (10)

given p=(p₀, p₁, p₂, p₃) and q=(q₀, q₁, q₂, q₃) ∈Q, then:

1)

$\stackrel{\mathbf{-}}{\mathbf{p}\oplus \mathbf{q}}=\stackrel{\mathrm{-}}{\mathbf{p}}\oplus \stackrel{\mathrm{-}}{\mathbf{q}}$          (11)

2)

$\stackrel{\mathbf{-}}{\mathbf{p}*\mathbf{q}}=\stackrel{\mathbf{-}}{\mathbf{q}}*\stackrel{\mathbf{-}}{\mathbf{p}}$

3)

$\mathbf{p}*\stackrel{\mathrm{-}}{\mathbf{p}}=\stackrel{\mathrm{-}}{\mathbf{p}}*\mathbf{p}\in {\mathbf{Q}}_{\mathbf{r}}$

2.2. Parametric Representation of Rotations of a Rigid Body

Let ρ(p,•):Q→Q, p∈Q be a linear transformation defined by:

$\mathsf{\rho }\left(\mathbf{p},\mathbf{q}\right)=\mathbf{p}*\mathbf{q}*{\mathbf{p}}^{-1}={\displaystyle \frac{1}{{‖\mathbf{p}‖}^2}}·\left(\mathbf{p}*\mathbf{q}*\stackrel{\mathrm{-}}{\mathrm{p}}\right),\forall \mathbf{p},\mathbf{q}\in \mathbf{Q}$    (12)

This function is a rotation that preserves the inner product, the norm, and the angle [25]. The transformation ρ(p,∙):Q→Q, is linear, orthogonal and ρ(p, q)∈Q_v, by all q∈Q_v. Let θ∈[0, nπ], n∈$ℛ$⁺, w∈Q_v, ||w||=1; then, the quaternion p∈Q, with p₀∈$ℛ$−{0} and p_v = ± sinθw, is such that, ρ(p, w)=w, where p₀ satisfies the equation:

4 p₀⁴ − 4 p₀² ||p||²cosθ − ||p||⁴sin²θ = 0      (13)

The quaternion p represents a rotation of angle θ∈[0, nπ], with axis w∈Q_v, giving:

p₀ = ||p|| cos(θ/2), p_v = ± ||p||sin(θ/2)w      (14)

In general, the norm of p can be arbitrary. Unit quaternions will be used in this article; that is, ||p||=1, so expression (14) reduces to:

p₀ = cos(θ/2), p_v = ± sin(θ/2)w      (15)

2.3. Kinematic Modeling of Coupled Bodies

This section presents the methodology for modeling the rotations of coupled rigid multi bodies using the algebra of quaternions [25], to later be applied in the analysis of the movement of RRR parallel planar and PRRS spatial robots. The modeling process involves a representation of a rigid body to determine the position of a point on it with respect to an inertial reference system. To achieve a systematic representation of the rotations, it is necessary to define functions that allow transforming vectors defined in $ℛ$³ to the Q space and vice versa.

2.3.1. Isomorphism of the Vectors of $ℛ$³ to the Vector Space Q

It is possible to define a function T_v: Q_v→$ℛ$³, between the subspace of the vector quaternion Q_v and the vector space $ℛ$³, according to expressions (8). This is:

T_v(0,b,c,d) = (b,c,d); ∀(0,b,c,d) ∈Q_v

Subsequently, the transformations described by expressions (8) are isomorphic; then there is an inverse transformation ${\mathbf{T}}_{\mathbf{v}}^{-1}$: $ℛ$³→Q_v, such that:

${\mathbf{T}}_{\mathbf{v}}^{-1}$(b,c,d) = (0,b,c,d); ∀(b,c,d) ∈$ℛ$³         (16)

Therefore, any vector of $ℛ$³ can be considered an element of the vector space of quaternions [25]. Thus, by applying the proposed isomorphism of expression (16) to the canonical basis in $ℛ$³ defined by:

B= {(1,0,0), (0,1,0), (0,0,1)}        (17)

the following is obtained:

e₁ = ${\mathbf{T}}_{\mathbf{v}}^{-1}$(1,0,0) = (0,1,0,0)         (18)

e₂ = ${\mathbf{T}}_{\mathbf{v}}^{-1}$(0,1,0) = (0,0,1,0)

e₃ = ${\mathbf{T}}_{\mathbf{v}}^{-1}$(0,0,1) = (0,0,0,1)

Here, {e_j }∈$ℛ$⁴ and j=0,1,2,3, are vectors of the canonical base of $ℛ$⁴, which is completed with the vector e₀=(1,0,0,0). It is important to highlight that the previous isomorphism allows us to work with the elements of $ℛ$³ using the algebraic properties of the space of the quaternions Q.

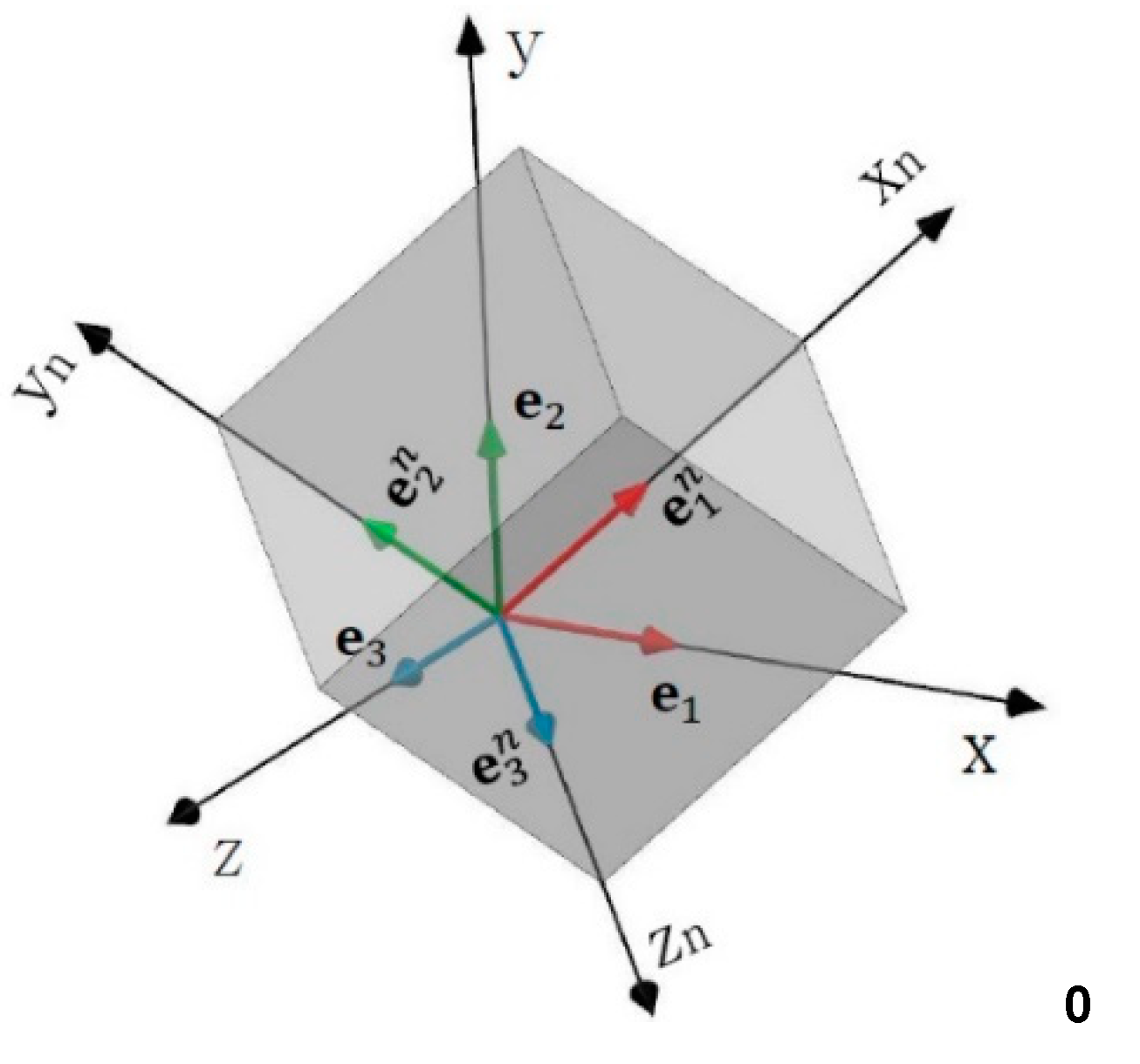
2.3.2. Rotation of a Cartesian Frame of Reference

This section presents the procedure to apply a rigid rotation with the algebra of quaternions. The linear transformation ρ(p,•):Q→Q, with p=(p₀,p₁,p₂,p₃) fixed, described in expression (12) is a rotation [24,25]. The components of rotation are described by expressions (15), where θ∈[0, nπ] is the angle of rotation and w=(w₁,w₂,w₃), w∈Q_v, is the axis of rotation. When considering quaternions of unitary norm, the expression (12) takes the following form:

$\mathsf{\rho }\left(\mathbf{p},\mathbf{q}\right)=\mathbf{p}*\mathbf{q}*\stackrel{\mathrm{-}}{\mathrm{p}}$         (19)

Expression (19) is very useful in kinematics applications when one reference system has to be associated with another, relating it by means of rotations of the base that forms each of these systems. To characterize a rotation between bases, an inertial base e_j∈$ℛ$³ is established, for j=1,2,3, and a local base e_jⁿ∈$ℛ$³, attached to a rigid body and rotating with it. The orientation of the body is defined by the orientation of the local base e_jⁿ.

We also establish the bases e_j ∈$ℛ$⁴ and e_jⁿ ∈$ℛ$⁴ which are associated with the bases e_j∈$ℛ$³ and e_jⁿ ∈$ℛ$³ which will allow us to perform operations in the vector space of quaternions. These bases are related to each other by the transformations e_j = T_v(e_j) and e_jⁿ = T_v(e_jⁿ). To determine the relationships between these bases, unit vectors e₁, e₂, e₃ in Figure 1, can be seen directed along the coordinate axes x, y, z, respectively. We also have unit vectors e₁ⁿ, e₂ⁿ, e₃ⁿ, directed along the coordinate axes x_n, y_n, z_n, attached to the rigid body. At the beginning of the movement, both bases e_j and e_jⁿ coincide.

For any rotational movement of the body shown in Figure 1, there is a general quaternion p = (p₀, p₁, p₂, p₃) which defines the final orientation of the body and is expressed as follows:

${\underset{\_}{\mathbf{e}}}_{\mathbf{j}}^{\mathbf{n}}=\mathit{\rho }\left(\mathrm{p},{\underset{\_}{\mathbf{e}}}_{\mathbf{j}}\right)=\mathrm{p}*{\underset{\_}{\mathbf{e}}}_{\mathbf{j}}*\stackrel{\mathrm{-}}{\mathrm{p}}$          (20)

For the case where the orientation of a rigid body in three-dimensional space is defined by three rotations in the axes x, y, z, (although they can be defined in other axes) [53], expression (20) must be put in terms of the composition of three rotating quaternions p = p₁*p₂*p₃, where p₁ = (p₁₀, p₁₁, 0, 0), p₂ = (p₂₀, 0, p₂₂, 0), and p₃ = (p₃₀, 0, 0, p₃₃). The order of composition of the quaternions is explained in Appendix A.

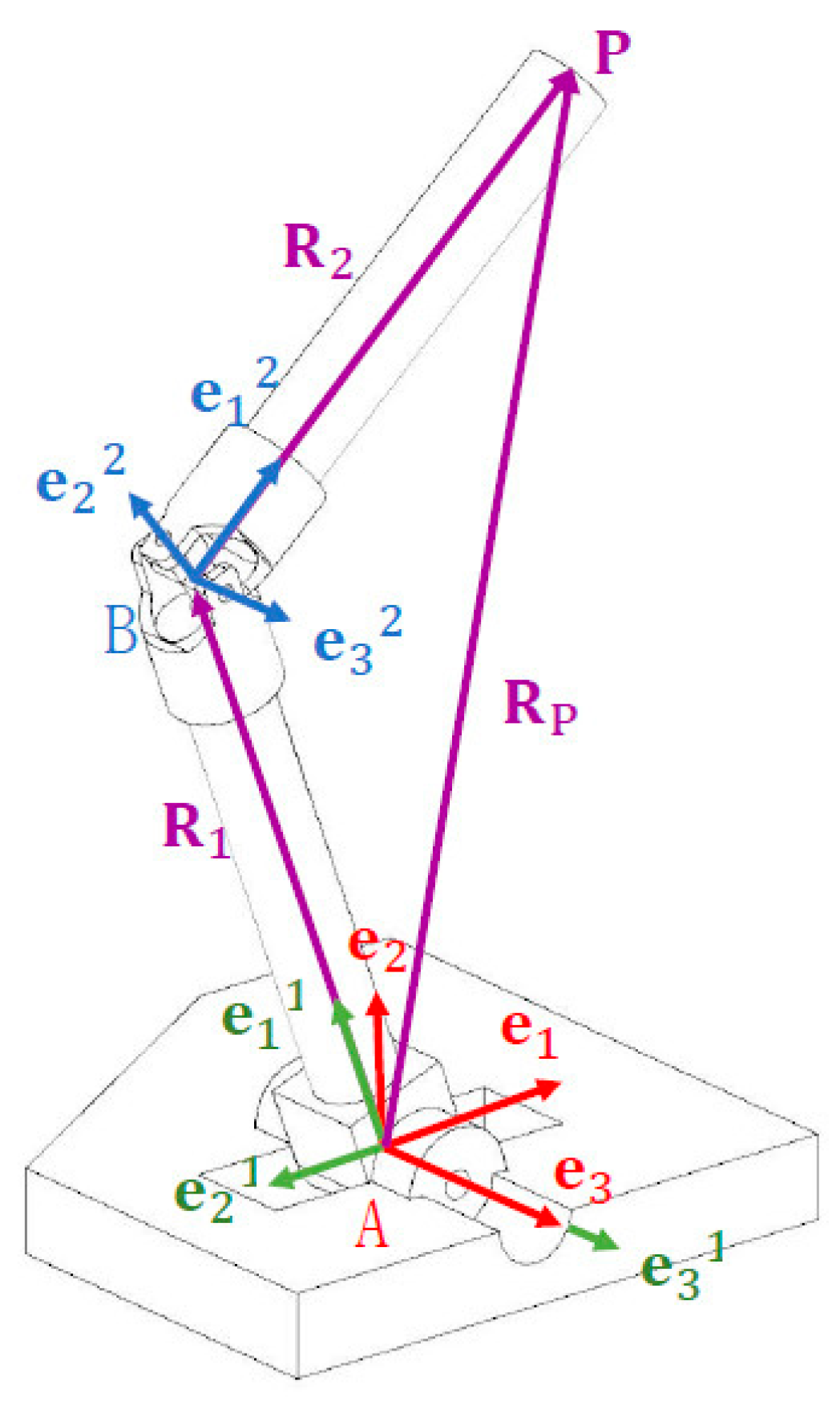
2.3.3. Configuration of Coupled Bodies

The objective of this section is to determine the relationships between the bases associated with coupled bodies. According to Figure 2, the links of a kinematic chain are represented by the vectors R₁, R₂∈$ℛ$³. The link R₁ is joined to the base by means of a rotational joint at point A. Link R₂ is joined to R₁ by means of a universal joint at point B. This allows modeling a general movement of the articulated links which can then be applied to model mechanisms. To start the modeling process, a global reference system is first defined e_j and local reference systems e_jⁿ, j=1,2,3 over the links. The position vector R_P and the vectors R₁, R₂ associated with the links are represented in $ℛ$⁴ as follows:

R_P = (0,x,y,z)           (21)

R₁ = r₁ e₁¹

R₂ = r₂ e₁²

Here, R₁, R₂, R_P ∈$ℛ$⁴, and r₁, r₂∈$ℛ$⁺ are the length of the links.

The modeling process is as follows:

The first step consists in determining the coordinates of the point "p" by means of the vector R_P and considering vectors R₁ and R₂. The vector R_P defines the position of the final end of the kinematic chain with respect to the global base e_j. This vector can be written as follows:

R_P = R₁ ⊕ R₂ = r₁ e₁¹ ⊕ r₂ e₁²           (22)

The second step consists in transforming the elements of the bases e₁¹ and e₁² to the canonical base e_j to obtain the vector R_P referenced to the global base. The cases of spatial and planar motion will be considered.

1. In the case of spatial movement, this is modeled through the composition of relative movements, and the bases are defined as follows:

e₁¹ = ρ(p₁, e₁)           (23)

e₁² = ρ(q,e₁)

where,

q = p₁*p₂*p₃           (24)

and where:

p₁ = (p₁₀, 0, 0, p₁₃)           (25)

p₂ = (p₂₀, 0, 0, p₂₃)

p₃ = (p₃₀, 0, p₃₂, 0)

2. For the case of planar movement, p₂=0, p₁ and p₃ have a rotation axis in the z axis. This movement can be modeled by the composition of relative movements or also by mean absolute movements. For relative motion, the bases are defined as:

e₁¹ = ρ(p₁, e₁)           (26)

e₁² = ρ(q,e₁)

Here,

q = p₁*p₃           (27)

where:

p₁ = (p₁₀, 0, 0, p₁₃)           (28)

p₃ = (p₃₀, 0, 0, p₃₃)

For absolute motion, the bases are defined as follows:

e₁¹ = ρ(p₁, e₁)           (29)

e₁² = ρ(p₃,e₁)

The last step consists in obtaining a general expression of equation (22) and this is achieved by substituting, for the case of spatial movement, equations (23) in equation (22). This is:

R_P = r₁ ρ(p₁, e₁) ⊕ r₂ ρ(q,e₁)           (30)

=${\mathrm{r}}_1\left({\mathrm{p}}_1*{\underset{\_}{\mathbf{e}}}_1*{\overline{\mathbf{p}}}_1\right){\mathrm{r}}_2\left({\mathrm{p}}_1*{\mathrm{p}}_2*{\mathrm{p}}_3*{\underset{\_}{\mathbf{e}}}_1*\overline{{\mathrm{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3}\right)$

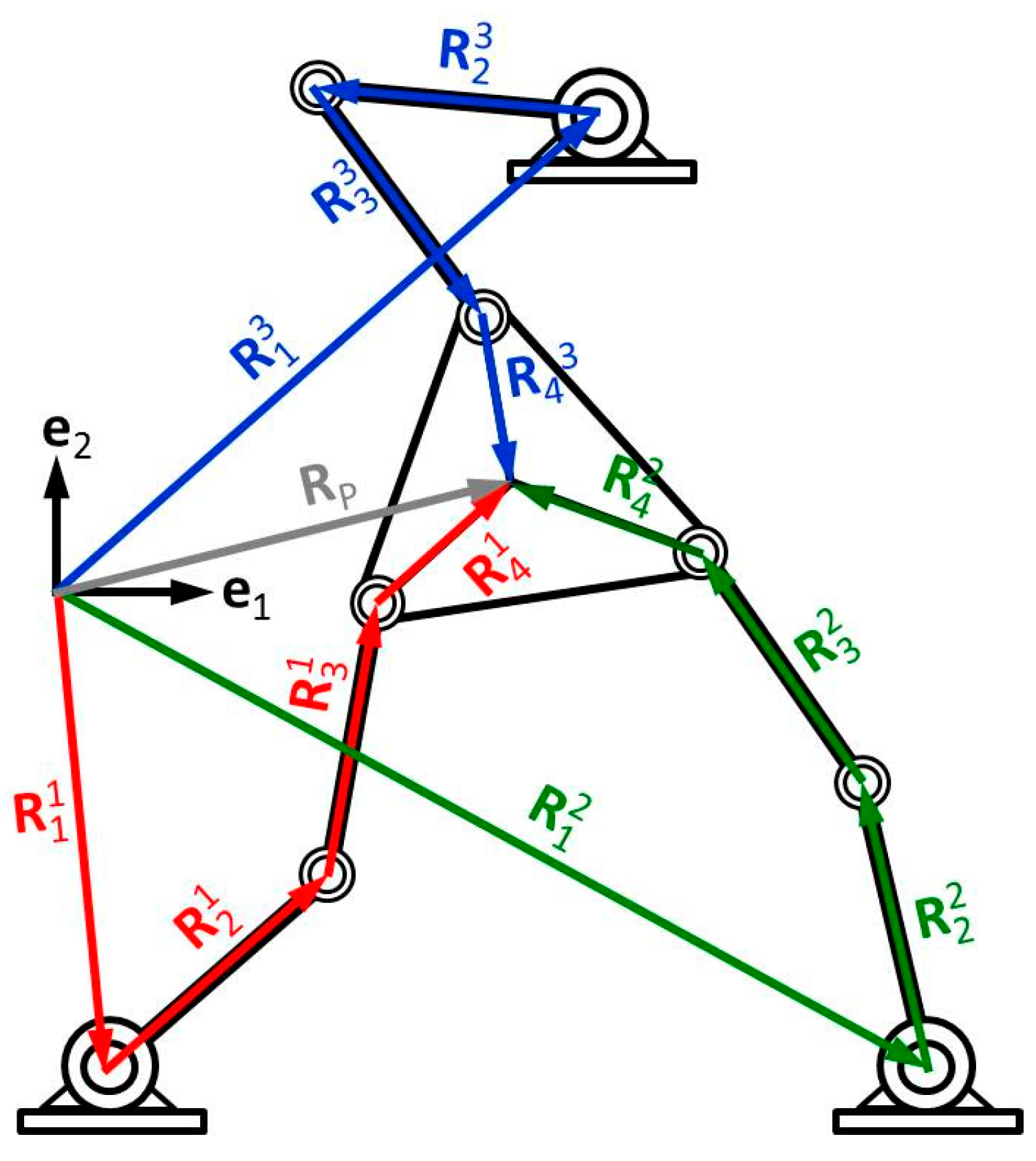
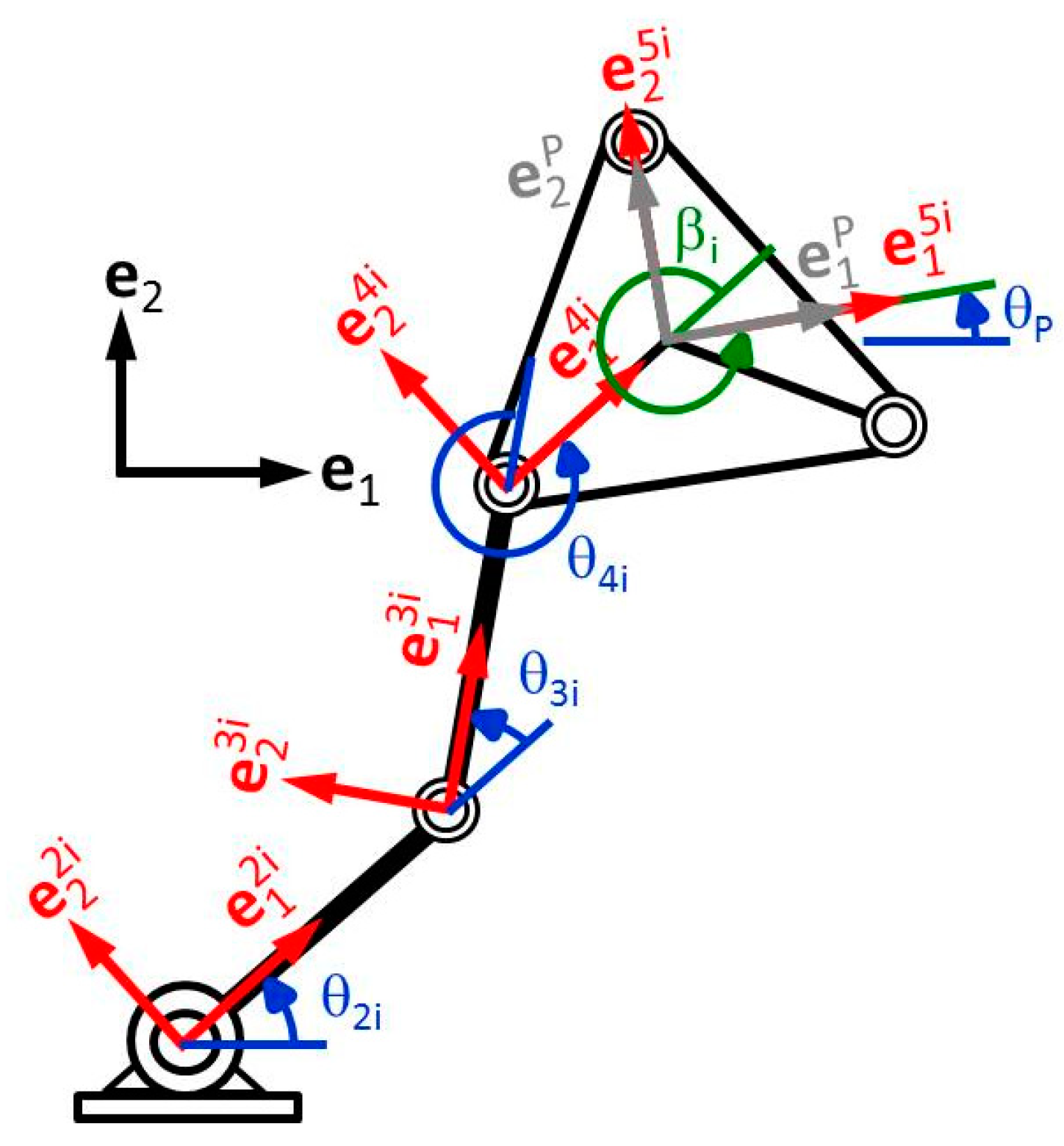
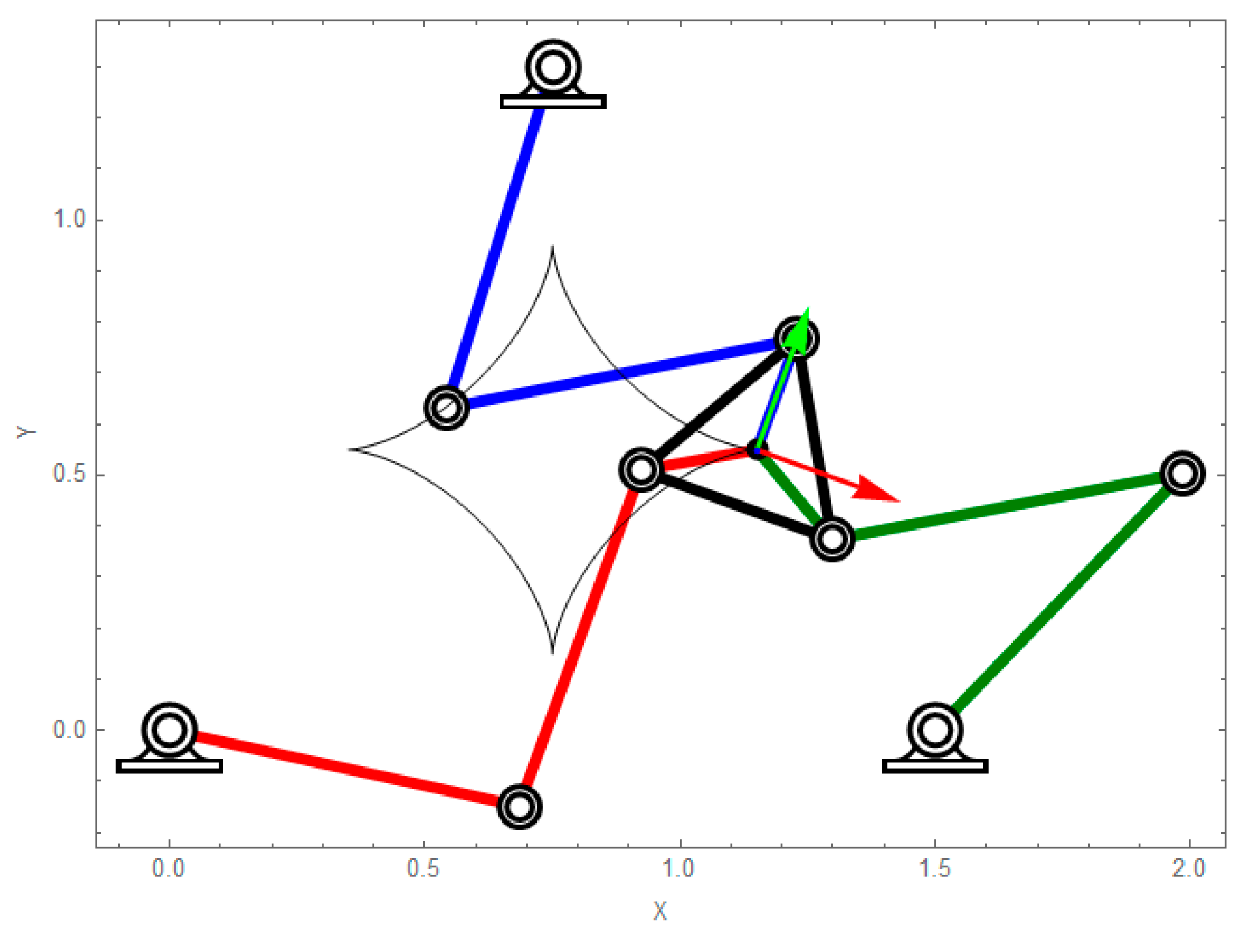
2.4. Modeling of a RRR Planar Parallel Robot

This section presents the modeling of a RRR planar robot using the results of the previous sections. The formal definition of a parallel robot is as follows: A parallel robot is made up of an end-effector with n degrees of freedom, and of a fixed base, linked together by at least two independent kinematic chains. Motion is originated by n single actuators [54].

This definition is important because it has implications for robot modeling, which consists of building a mathematical model through which it is possible to formulate the inverse kinematic problem associated with a said robot, which is shown in Figure 3. The degrees of freedom of the kinematic chain shown in Figure 3 are obtained using the following expression [55]:

DOF = 3(L −1) − 2J₁ – J₂           (31)

Here, L is the number of links, J₁ is the number of full joints, and J₂ the number of semijoints. Therefore, for L=8, J₁=9, and J₂=0, the degrees of freedom of the studied mechanism is DOF =3.

The robot shown in Figure 3 consists of a mobile platform that moves freely along the work plane and six links, three of which are connected to three actuators which provide movement, and three coupling links.

The objective of the modeling is to pose the inverse kinematic problem associated with the robot configuration shown in Figure 3. This problem is formulated as follows:

"Given the coordinates of the centroid of the mobile platform and its angle with respect to the x-axis, find the angles of the driving and driven links that make up the robot."

To start the modeling, it is necessary to consider the definition of a parallel robot to build the equations that govern the inverse kinematic problem, decoupling each chain that composes it, and to study each separately. The parallel robot shown in Figure 3 consists of three independent kinematic chains. Each chain has an associated motor, drive link, driven link, and moving platform. The modeling process for the planar case and for each kinematic chain is as follows:

1) Locate a coordinate system (x, y) and the fixed inertial base.

2) Select a kinematic chain.

3) Associate vectors to each link of the selected kinematic chain.

4) Associate mobile bases for each rotation movement when going through the chain (Figure 4).

5) Construct the equation of position that locates the centroid of the platform with the origin (x, y).

6) Model the base rotations using expression (19).

7) Represent the position equation from step 5 in terms of quaternions.

8) Repeat the process for each of the remaining kinematic chains.

9) Formulate the inverse kinematic problem.

Figure 4. Inertial base and mobile bases.

Figure 4. Inertial base and mobile bases.

Figure 4 shows the inertial base and the moving bases associated with each link. Figure 5 shows the rotation angles of each link and of the mobile platform.

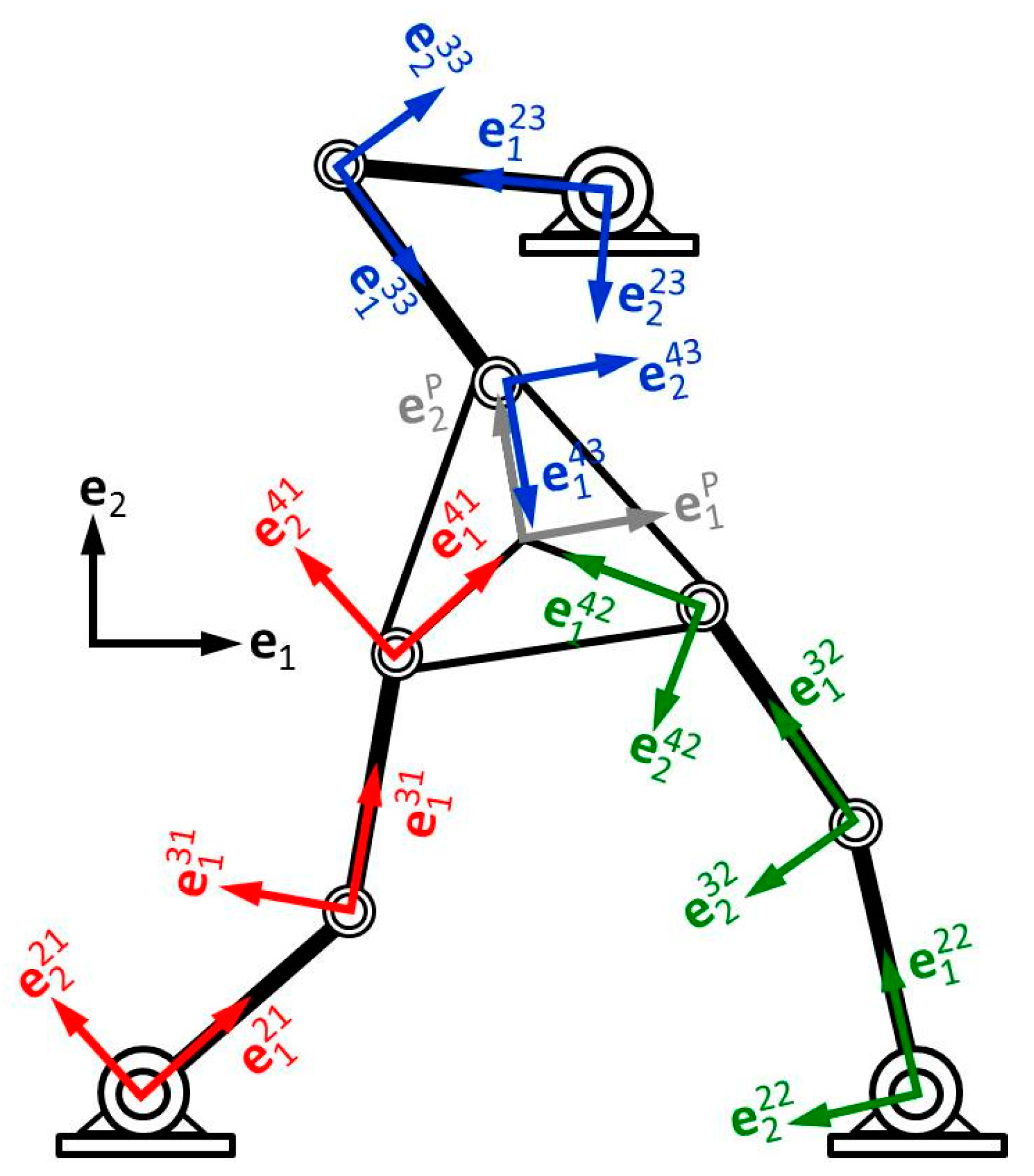
2.4.1. Loop Equations

In this section, the loop equations related to each kinematic chain associated with the robot under study are generated. Each link is represented by the vectors R₂ⁱ, R₃ⁱ, R₄ⁱ∈$ℛ$³ on which the mobile bases e_j²ⁱ, e_j³ⁱ and e_j⁴ⁱ are defined. Therefore, the position vector R_P∈$ℛ$³ that locates the platform centroid from the origin of the coordinates can be expressed in terms of the vector sum in $ℛ$⁴ for the case of the kinematic chains that make up the robot in the following way:

R₁ⁱ ⊕ R₂ⁱ ⊕ R₃ⁱ ⊕ R₄ⁱ = R_P           (32)

Furthermore, by considering unitary quaternions to represent the rotations of each link that make up each chain, unitary norm equations are generated. This is:

||p_2i||² = 1           (33)

||p_3i||² = 1

||p_4i||² = 1

Each vector associated with the links can be represented in terms of its length and in the direction of a unitary vector, according to expressions (21), as follows:

R₁ⁱ = (0, x_i, y_i, 0)           (34)

R₂ⁱ = r₂ⁱ e₁²ⁱ

R₃ⁱ = r₃ⁱ e₁³ⁱ

R₄ⁱ = r₄ⁱ e₁⁴ⁱ

R_P = (0, x_P, y_P, 0)

where i=1,2,3, in addition to r₂ⁱ, r₃ⁱ and r₄ⁱ are the lengths of the links. Each mobile base represents a rotation of the inertial base e_j. Such rotations can be expressed in terms of relative quaternions. This is:

e₁²ⁱ = ρ(q_2i, e₁);    q_2i = p_2i          (35)

e₁³ⁱ = ρ(q_3i,e₁);    q_3i = p_2i*p_3i

e₁⁴ⁱ = ρ(q_4i, e₁);    q_4i = p_2i*p_3i*p_4i

e_j⁵ⁱ = ρ(q_5i, e_j);   q_5i = p_2i*p_3i*p_4i*p_5i

e_j^P = ρ(q_P, e_j);    q_P = p_P

or, in terms of absolute quaternions:

e₁²ⁱ = ρ(p_2i, e₁)           (36)

e₁³ⁱ = ρ(p_3i,e₁)

e₁⁴ⁱ = ρ(p_4i, e₁)

e₁⁵ⁱ = ρ(s_5i, e₁);    s_5i = p_4i*p_5i

where:

p_2i = (p_20i, 0, 0, p_23i)           (37)

p_3i = (p_30i, 0, 0, p_33i)

p_4i = (p_40i, 0, 0, p_43i)

p_5i = (c(β_i/2), 0, 0, s(β_i/2))

p_P = (c(θ_P/2), 0, 0, s(θ_P/2))

The quaternions p_2i, p_3i, and p_4i, are associated with the angles θ_2i, θ_3i, and θ_4i. In addition, the quaternions p_2i, p_3i, and p_4i, allow the rotations of the first, second and third link of each kinematic chain to be carried out.

2.4.2. Platform Orientation Equation

The mobile platform of the robot under study can be oriented in each movement. The orientation equation is obtained by considering the following equality:

e_j⁵ⁱ = e_j^P           (38)

For the case of relative quaternions, we have:

ρ(q_5i, e_j) = ρ(q_P, e_j)           (39)

if and only if:

q_5i = q_P           (40)

Finally,

p_2i*p_3i*p_4i*p_5i = p_P           (41)

2.4.3. Formulation of the Inverse Kinematic Problem of the RRR Planar Parallel Robot

In this section, a problem of fundamental importance for rigid body kinematics is formulated: the inverse problem, which is associated with the configuration of the planar parallel robot shown in Figure 3. The formulation of said problem is as follows:

“Once the coordinates of the position vector R_P and the angleθ_P are known, which respectively define the position of the origin and the orientation of the base e_j^P on the mobile platform, determine the angles (θ_2i,θ_3i,θ_4i) of the chains kinematics associated with the quaternions p_2i, p_3i, p_4i, such that equations (32), (33) and (41) are satisfied.”

The formulation of the inverse problem of the RRR robot modeled with unitary quaternions generates a system of 21 nonlinear equations with 18 unknowns of the algebraic type.

For each string, equation (32) generates two algebraic equations in x and y, equations (33) represent three unitary norm equations, and expression (41) generates two other algebraic equations, so adding them together, 21 equations are obtained. Similarly, for each chain, there are six unknowns, which are the components of the quaternions p_2i, p_3i, and p_4i; that is (p_2i0, p_2i3, p_3i0, p_3i3, p_4i0, p_4i3) and, therefore, there are 18 unknowns.

Once the quaternions p_2i, p_3i, and p_4i, have been calculated, the associated angles (θ_2i, θ_3i, θ_4i) can be determined using the following relationships:

θ_2i = 2 tan^-1(p_2i3/p_2i0)           (42)

θ_3i = 2 tan^-1(p_3i3/ p_3i0)

θ_4i = 2 tan^-1(p_4i3/ p_4i0)

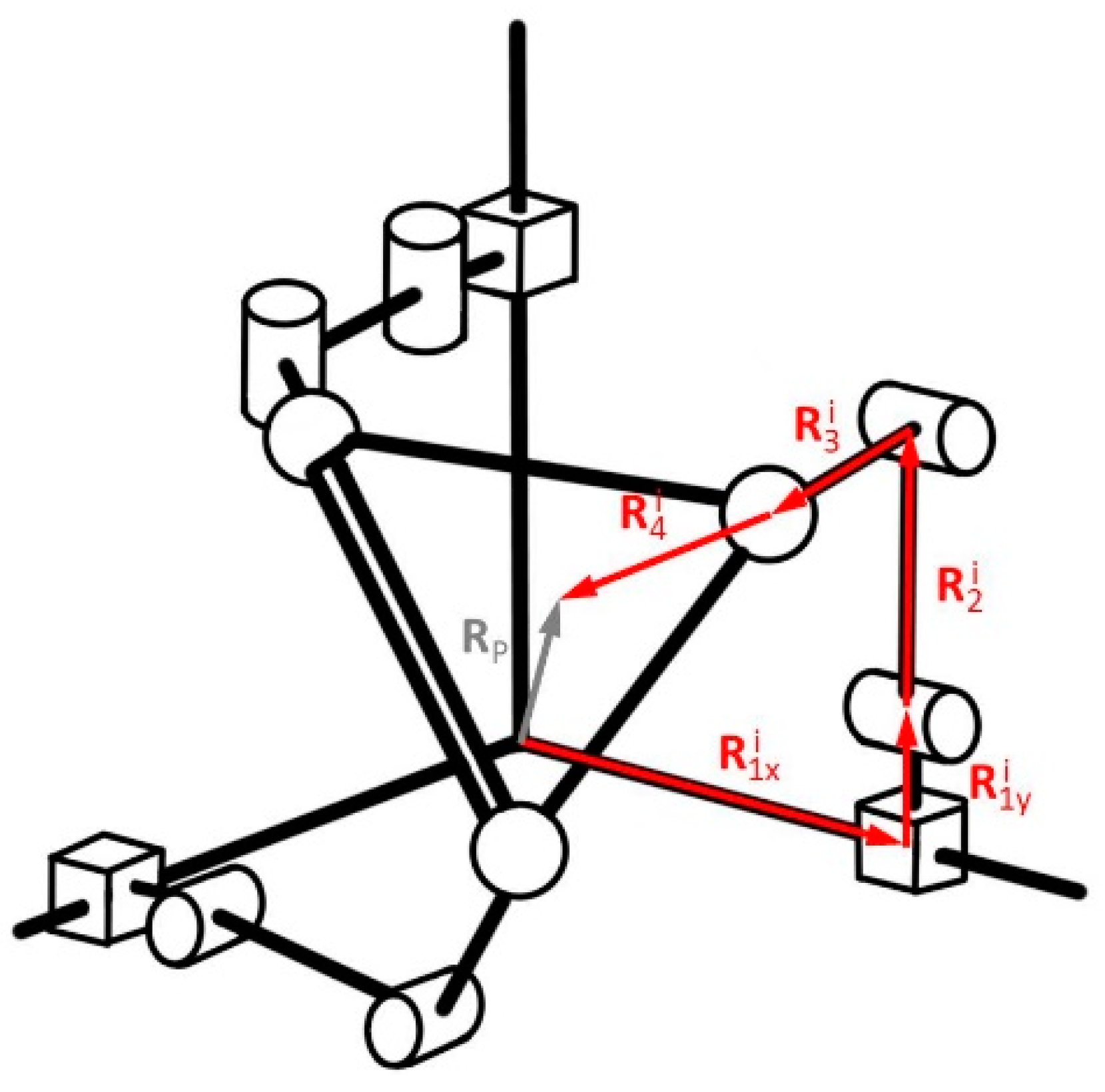
2.5. Modeling of a PRRS Spatial Parallel Robot

The objective in this section is to apply the unitary quaternion modeling methodology described in section 2.3.3 to study the motions of a PRRS-type spatial parallel robot [35]; that is, the robot has prismatic (P), rotational (R) and spherical (S) joints, like the one shown in Figure 6. Said robot consists of three independent kinematic chains and a mobile platform. The links that connect the robot with the bed or ground of the system have associated prismatic joints (P) that move along the axes of a Cartesian system. Each chain has two links that are articulated by means of rotational joints (R) and finally the connection of the links with the mobile platform is by means of a spherical joint (Figure 6).

The objective of the study is to determine a mathematical model that allows formulating the inverse kinematic problem associated with the configuration of the robot.

2.5.1. Loop Equations

According to Figure 6, to locate the coordinates of point "P" located at the centroid of the mobile platform from the origin of coordinates of the entire system, the closed-loop equations must be formulated. These expressions are obtained by means of the following vector equation:

R_1xⁱ ⊕ R_1yⁱ ⊕ R₂ⁱ ⊕ R₃ⁱ ⊕ R₄ⁱ = R_P           (43)

When considering unitary quaternions to model the rotations of the links with R- and S-type connections that make up each chain, unitary norm equations are generated. This is:

||p_4i||² = 1           (44)

||p_5i||² = 1

||p_6i||² = 1

||p_7i||² = 1

||p_8i||² = 1

The vectors associated with the links that make up the robot can be put in the function of the local bases which are shown in Figure 7. That is

R_1xⁱ = xⁱ e₁¹ⁱ           (45)

R_1yⁱ = yⁱ e₂¹ⁱ

R₂ⁱ = r₂ⁱ e₂²ⁱ

R₃ⁱ = r₃ⁱ e₂³ⁱ

R₄ⁱ = r₄ⁱ e₁⁴ⁱ

R_P = (0, x_P, y_P, z_P)

The mobile bases (see Figure 7) associated with the links can be written in terms of unitary quaternions and in terms of the canonical basis as follows:

e_j¹ⁱ = ρ(q_1i, e₁);     q_1i = p_1i*p_2i*p_3i           (46)

e₂²ⁱ = ρ(q_2i, e₁);     q_2i = q_1i*p_4i

e₂³ⁱ = ρ(q_3i,e₁);     q_3i = q_2i*p_5i

e₁⁴ⁱ = ρ(q_4i, e₁);     q_4i = q_3i*p_6i*p_7i*p_8i

e_j⁵ⁱ = ρ(q_5i, e_j);    q_5i = q_4i*p_9i

e_j^P = ρ(q_P, e_j)    q_P = p_ψ*p_θ*p_φ

The configurations of each quaternion in terms of the angles of rotation are (see Figure 8):

p_1i = (c(β_1i/2), 0, s(β_1i/2), 0)           (47)

p_2i = (c(β_2i/2), 0, 0, s(β_2i/2))

p_3i = (c(β_3i/2), s(β_3i/2), 0, 0)

p_4i = (p_40i, p_41i, 0, 0)

p_5i = (p_50i, p_51i, 0, 0)

p_6i = (p_60i, 0, 0, p_63i)

p_7i = (p_70i, 0, p_72i, 0)

p_8i = (p_80i, 0, 0, p_83i)

p_5i = (c(β_5i/2), 0, 0, s(β_5i/2))

p_ψ = (c(ψ/2), 0, 0, s(ψ/2))

p_θ = (c(θ/2), 0, s(θ/2), 0)

p_φ = (c(φ/2), 0, 0, s(φ/2))

Figure 7. Inertial and mobile bases.

Figure 7. Inertial and mobile bases.

Figure 7 shows the inertial base and the moving bases associated with each link. Figure 8 shows the rotation angles of each link and of the mobile platform.

Figure 8. Angles of the bases.

Figure 8. Angles of the bases.

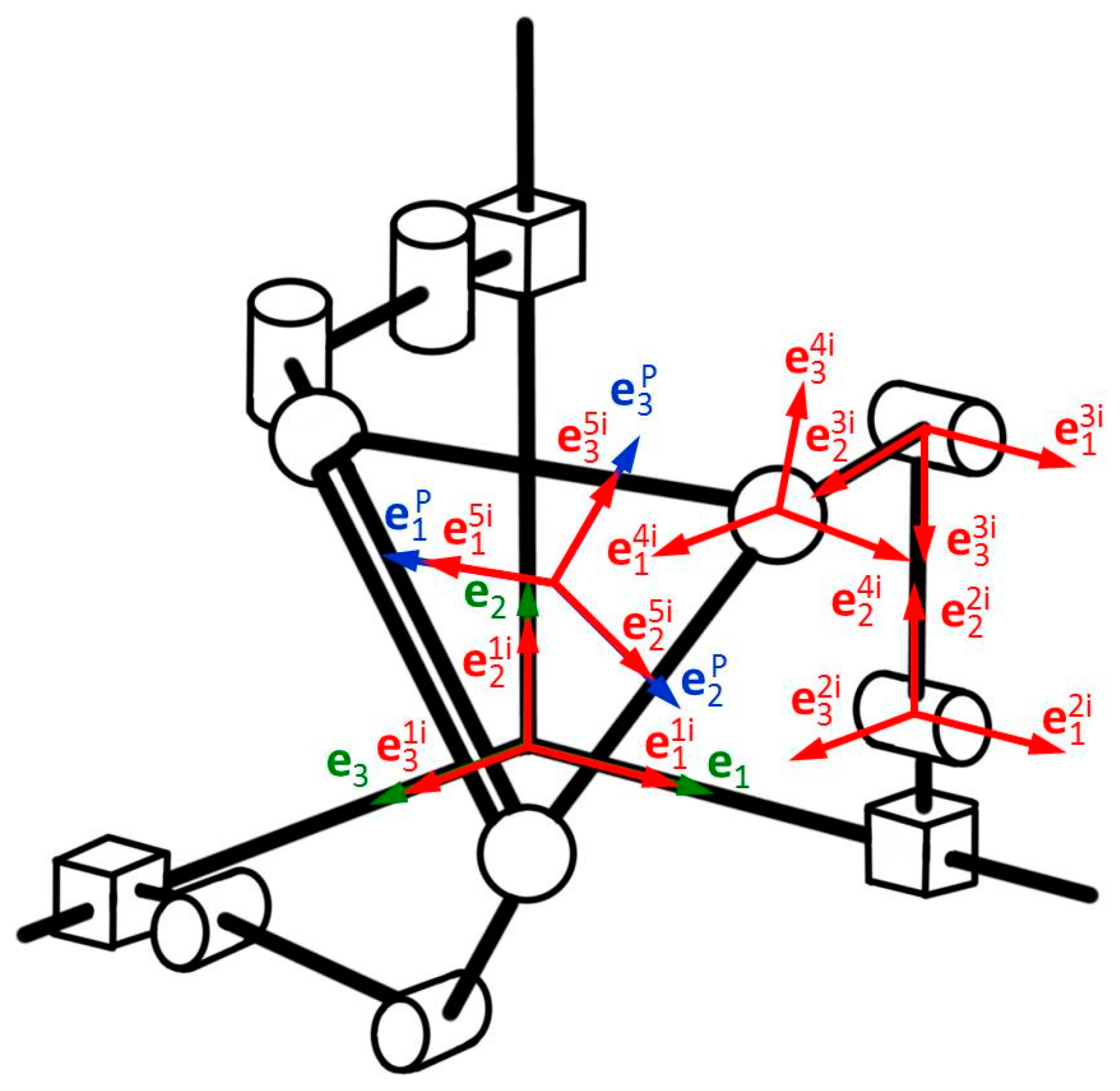
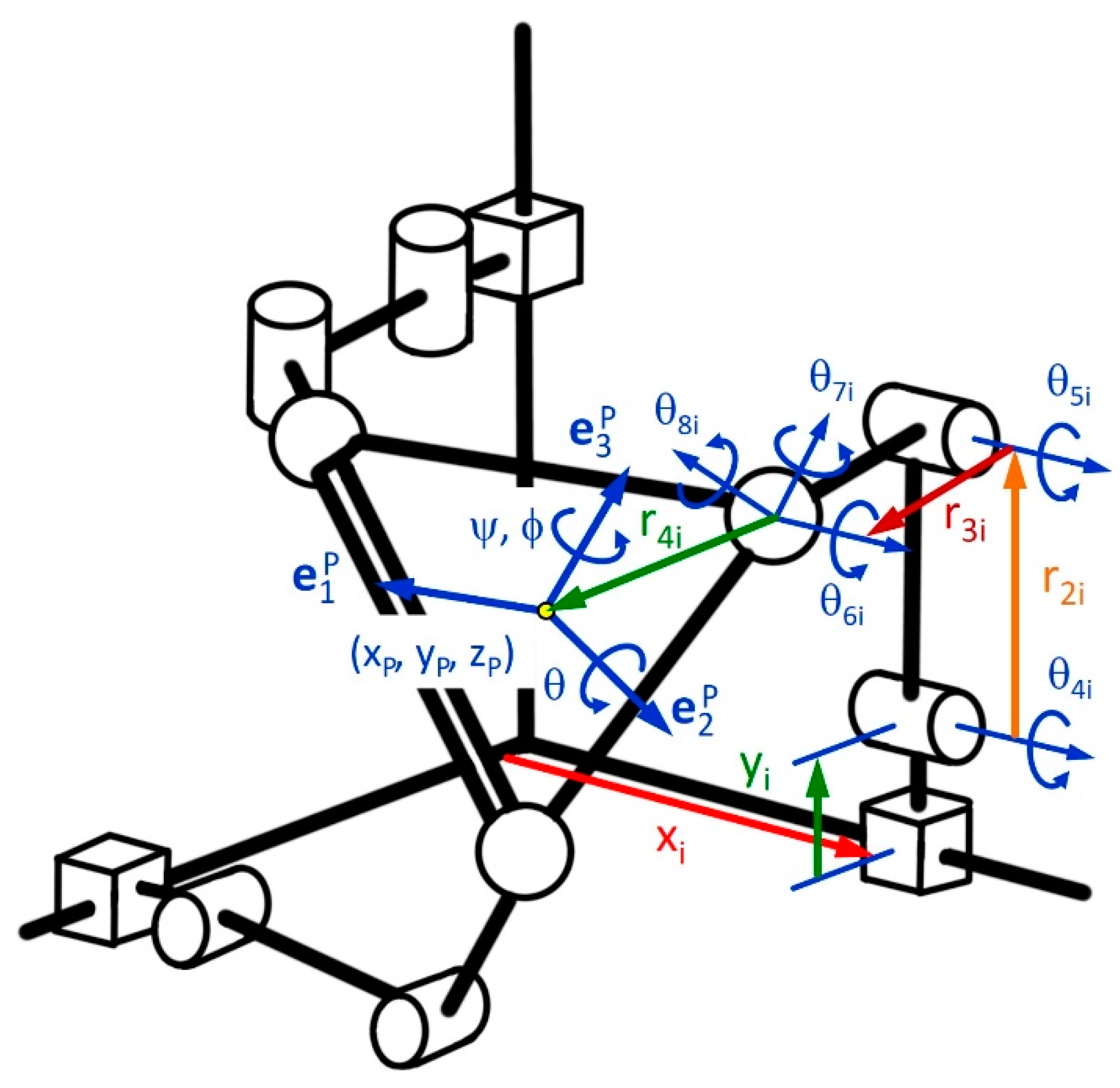
2.5.2. Equation of Platform Orientation

To complete the modeling of the robot under study, it is necessary to build the equations that allow defining the orientation of the mobile platform. This equation is obtained by considering the following equality:

e_j⁵ⁱ = e_j^P           (48)

Being

ρ(q_5i, e_j) = ρ(q_P, e_j)        (49)

and,

q_5i = q_P        (50)

then

p_1i*p_2i*p_3i*p_4i*p_5i*p_6i*p_7i*p_8i*p_9i = p_ψ*p_θ*p_φ        (51)

2.5.3. Formulation of the PRRS-Type Inverse Problem

In this section, the inverse kinematic problem associated with the configuration of the PRRS robot shown in Figure 6 is formulated. This formulation is as follows:

“Known the coordinates of the point “p” (R_P) located in the centroid of the mobile platform, and the anglesψ,θ,φ, which respectively define the position of the origin and the orientation of the base e_j^P in the mobile platform, determine the magnitude xi and the angles (θ_4i,θ_5i,θ_6i,θ_7i,θ_8i) of the kinematic chains associated with the quaternions p_4i, p_5i, p_5i, p_6i, p_7i, p_8i,, such that equations (43 ), (44) and (51), be satisfied.

The formulation of the inverse problem of the PRRS robot modeled with unitary quaternions generates a system of 36 nonlinear equations with 33 unknowns of the algebraic type.

For each string, equation (43) generates three algebraic equations in x, y, z, equations (44) represent five unitary norm equations, and expression (51) generates another four algebraic equations, so when added together 36 equations are obtained. In the same way for each chain, there are 11 unknowns, which are the components of the quaternions p_4i, p_5i, p_5i, p_6i, p_7i y p_8i, that is (p_40i, p_41i, p_50i, p_51i, p_60i, p_63i, p_70i, p_72i, p_80i, p_83i) and the displacement xⁱ of the prismatic joint.

Once the quaternions p_4i, p_5i, p_5i, p_6i, p_7i y p_8i are calculated, the associated angles (θ_4i, θ_5i, θ_6i, θ_7i, θ_8i) can be determined by means of the following relations:

θ_4i = 2 tan^-1(p_41i/p_4i0)        (52)

θ_5i = 2 tan^-1(p_51i/p_50i)

θ_6i = 2 tan^-1(p_63i/p_60i)

θ_7i = 2 tan^-1(p_72i/p_70i)

θ_8i = 2 tan^-1(p_83i/p_80i)

2.6. Numerical Experimentation

In this section, the numerical experimentation for the solution of the inverse kinematic problems of both robots is presented. To solve the nonlinear and non-square systems of equations derived from the inverse problem statements, the BFGS nonlinear programming algorithm [46] was used.

The Davidon-Fletcher-Powell (DFP) method is a quasi-Newton method and is used to find the unconstrained minimum of a differentiable function “f” of several variables, and consists of generating successive approximations of the inverse of the Hessian of the function under study. The DFP method has been and remains a widely used gradient technique. The method tends to be robust; that is, it typically tends to perform well on a wide variety of practical problems and was first proposed by Davidon [56] and later reformulated by Fletcher and Powell [57]. A variant or improvement of the DFP is the BFGS algorithm [33,34], which is currently considered the most efficient of all Quasi-Newton update formulas, and is a computational iterative technique used to solve nonlinear optimization problems by using the first derivative and the Hessian matrix of the objective function [58]. The DFP update formula is bastantly effective, but it is outperformed by the BFGS formula [33,59]. In this paper we propose the objective functions associated with the position kinematics of each robot studied and use the BFGS algorithm which is automated in the Mathematica V12 formal computation library [46].

3. Results

This section presents the results obtained by solving the mathematical models of the robots studied in this work. An objective function and a trajectory are proposed for each analysis.

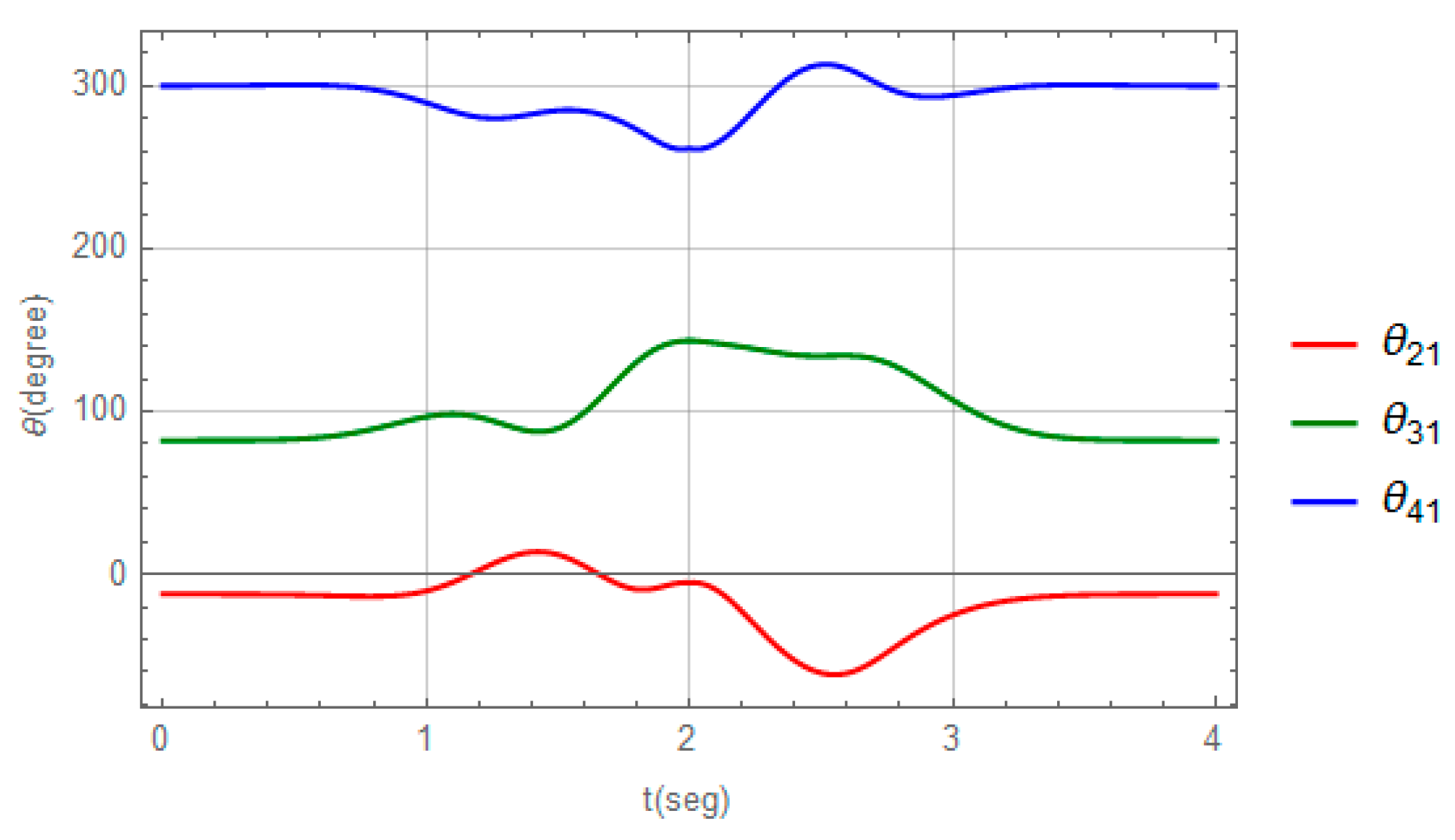
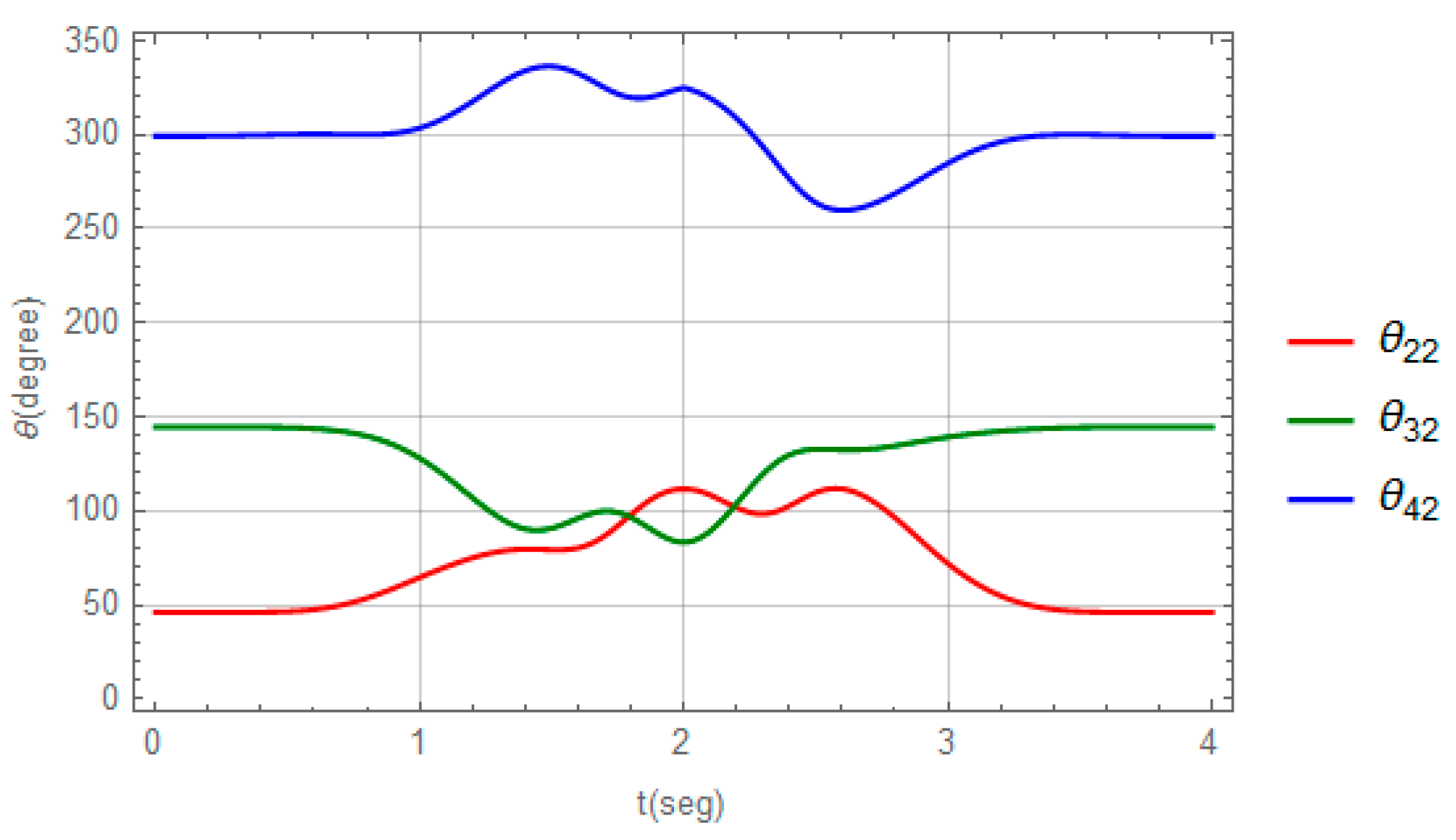
3.1. Numerical Model and Solution for the RRR Parallel Robot

The inverse problem of the RRR planar parallel robot generated a system of 21 nonlinear equations with 18 polynomial unknowns. To use the BFGS algorithm in the solution of the inverse problem related to the RRR-type robot, the following objective function was proposed:

$F=\sum _{i=1}^3\left(\sum _{j=2}^3{({\underset{\_}{\mathrm{R}}}_1^i\oplus {\underset{\_}{\mathrm{R}}}_2^i\oplus {\underset{\_}{\mathrm{R}}}_3^i\oplus {\underset{\_}{\mathrm{R}}}_4^i-{\underset{\_}{\mathrm{R}}}_{\mathrm{P}})}_{ij}^2+\sum _{k=2}^4{({‖{\mathbf{p}}_{ki}‖}^2-1)}_{ik}^2+\sum _{l=1}^4{({\mathbf{p}}_{2i}*{\mathbf{p}}_{3i}*{\mathbf{p}}_{4i}*{\mathbf{p}}_{5i}-{\mathbf{p}}_{\mathrm{P}})}_{il}^2\right)$      (53)

Here, i = kinematic chain, j; l = component of the vector; k = quaternion.

To solve the model the following trajectory was considered to 0 ≤ t ≤ 4 seconds

s = 2π(10(t/4)³ − 15(t/4)⁴ + 6(t/4)⁵)        (54)

x_P = 0.75 + 0.4 cos(s)³

y_P = 0.55 + 0.4 sin(s)³

The following intervals are defined for platform orientation:

If 0 ≤ t < 2, then θ_P = s/6 − π/9

If 2 ≤ t ≤ 4, then θ_P = (2π − s)/6 − π/9

The initial configuration of the robot and the graph of the geometric place of the trajectory is shown in Figure 9.

Figure 10, Figure 11 and Figure 12 show the graphics of the angular displacements associated with each kinematic chain that integrate the robot:

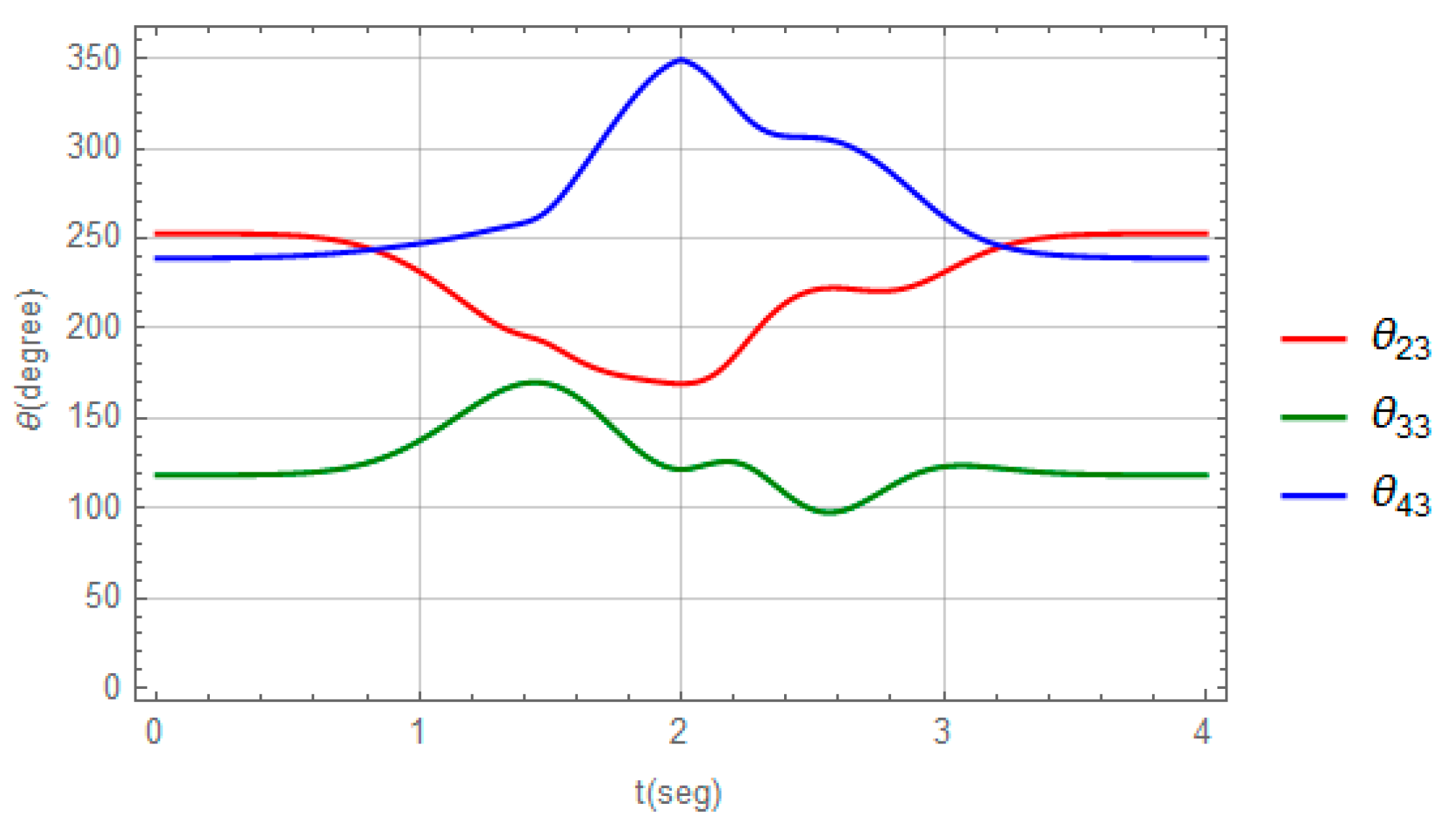
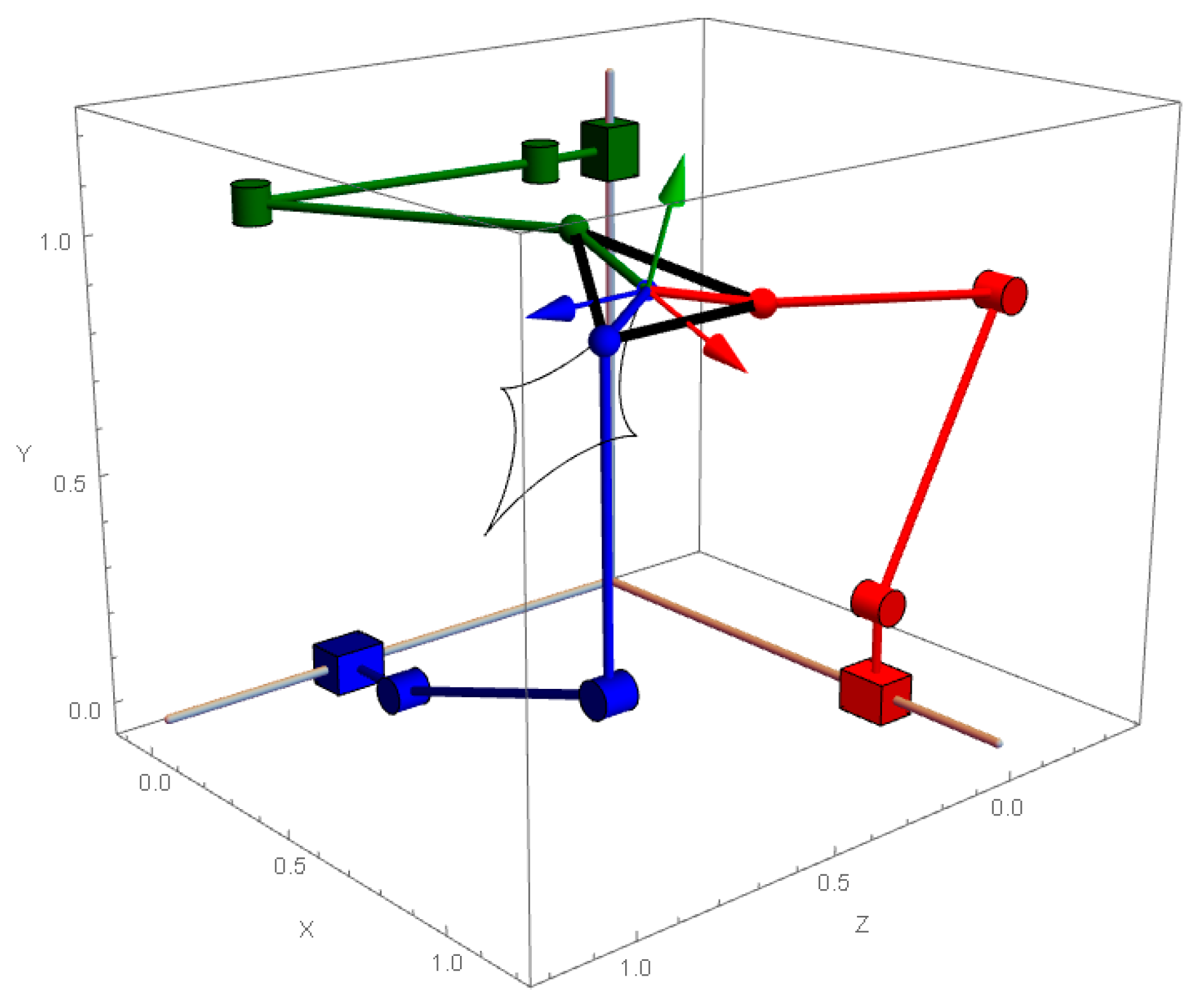
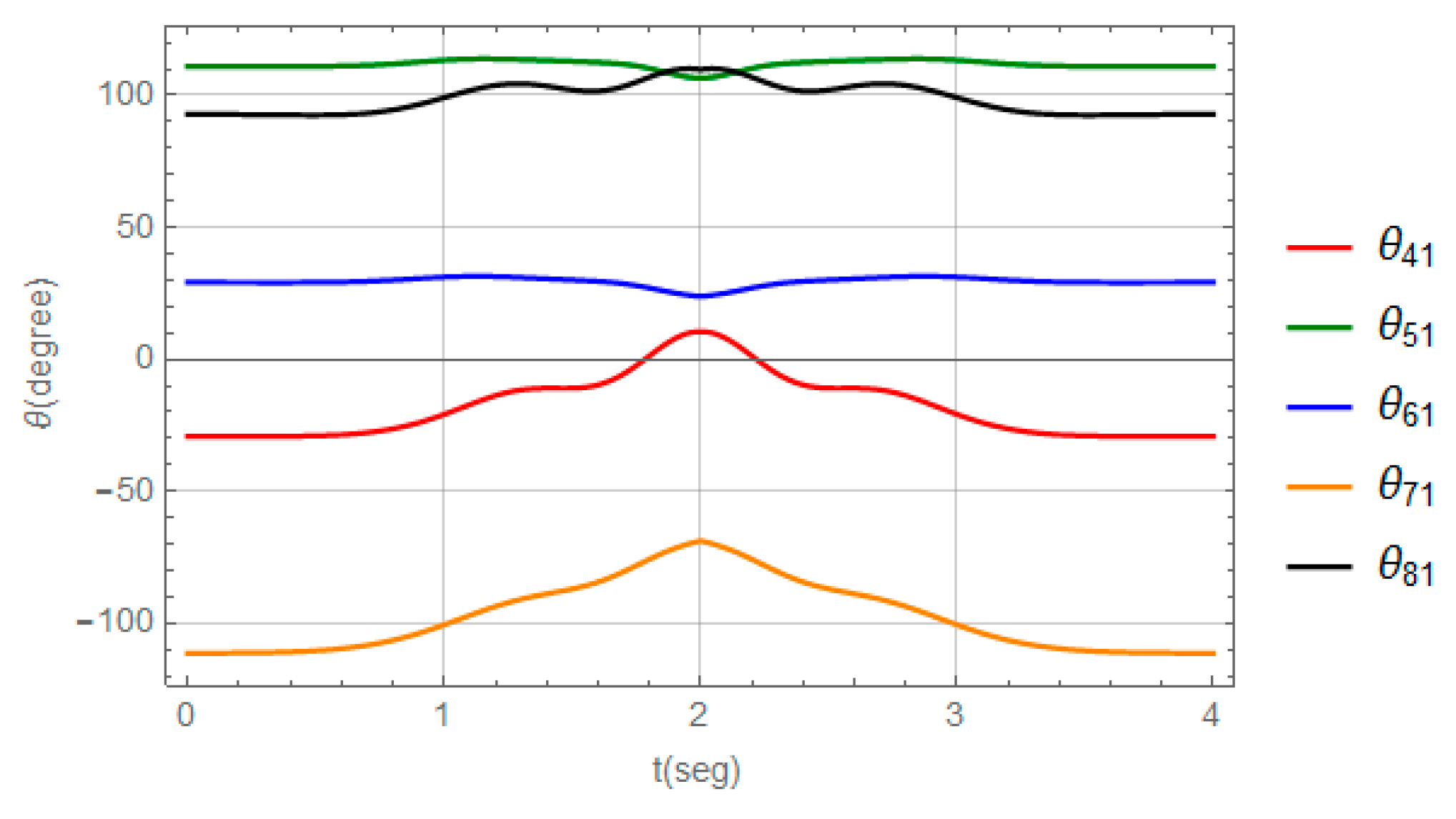
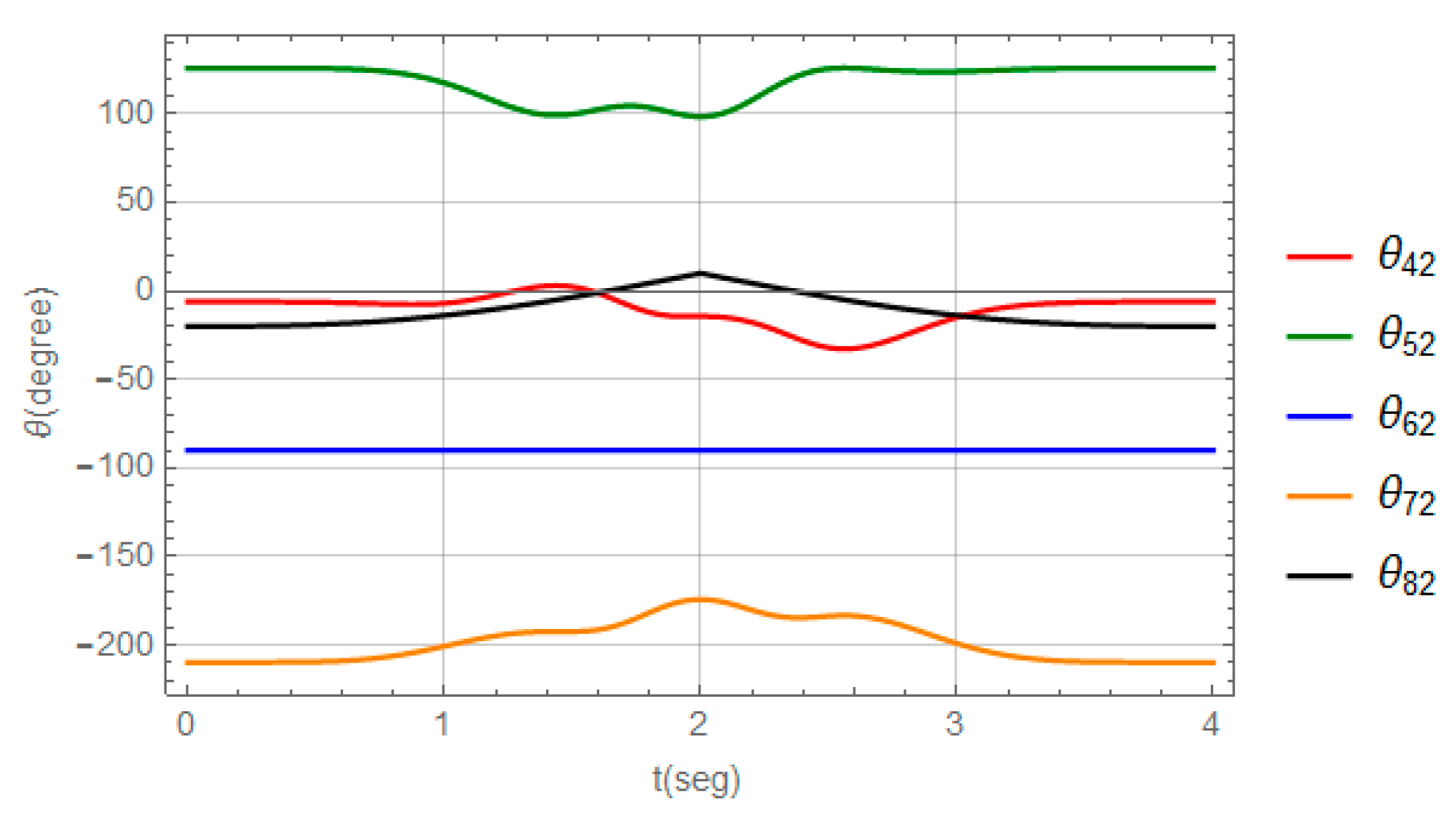
3.2. Numerical Model and Solution for the PRRS Parallel Robot

The mathematical model related to the PRRS robot has a configuration of 36 nonlinear equations and 33 unknowns for each kinematic chain. To use the BFGS algorithm in the solution of the inverse problem related to the PRR-type robot, the following objective function was proposed:

$F=\sum _{i=1}^3\left(\sum _{j=2}^4{\left({\underset{\_}{\mathbf{R}}}_{1\mathrm{x}}^i\oplus {\underset{\_}{\mathbf{R}}}_{1\mathrm{y}}^i\oplus {\underset{\_}{\mathbf{R}}}_2^i\oplus {\underset{\_}{\mathbf{R}}}_3^i\oplus {\underset{\_}{\mathbf{R}}}_4^i-{\underset{\_}{\mathbf{R}}}_{\mathrm{P}}\right)}_{ij}^2+\sum _{k=4}^8{\left({‖{\mathbf{p}}_{ki}‖}^2-1\right)}_{ik}^2+\sum _{l=1}^4{({\mathbf{p}}_{1i}*{\mathbf{p}}_{2i}*{\mathbf{p}}_{3i}*{\mathbf{p}}_{4i}*{\mathbf{p}}_{5i}*{\mathbf{p}}_{6i}*{\mathbf{p}}_{7i}*{\mathbf{p}}_{8i}*{\mathbf{p}}_{9i}-{\mathbf{p}}_{\Psi }*{\mathbf{p}}_{\theta }*{\mathbf{p}}_{\Phi })}_{il}^2\right)$        (55)

where i = kinematic chain, j; l = component of the vector; k = quaternion.

Similarly, the following trajectory is proposed for the PRRS space robot by 0 ≤ t ≤ 4 seconds:

s = 2π(10(t/4)³ − 15(t/4)⁴ + 6(t/4)⁵)

x_P = 0.75 + 0.2 sin(s)³

y_P = 0.75 + 0.2 cos(s)³

z_P = 0.75 − 0.2 cos(s)³

The following intervals are defined for platform orientation:

If 0 ≤ t < 2 then ψ = s/6 − π/9

If 2 ≤ t ≤ 4 then ψ = (2π − s)/6 − π/9

θ = 0

φ = 0

The initial configuration of the robot and the graph of the geometric place of the trajectory are shown in Figure 13.

Figure 14, Figure 15 and Figure 16 show the graphs of the calculated angular displacements and Figure 17 shows the displacements on the Cartesian axes:

4. Discussion

The methodology presented in this article made it possible to generate the inverse kinematic models of the RRR and PRRS parallel robots in a systematic manner, so that this methodology can be applied to various configurations and types of parallel kinematic chains. The methodological proposal took into consideration the systematization of the quaternion algebra developed by Reyes [25] and applied by Jiménez et al. [24]. The kinematic modeling of the position was a function of the unknown parameters of the quaternions. The binary operations defined by the expressions (1) and the linear transformation described by equation (12), allowed to establish the kinematic modeling in a vectorial way by means of loop equations and platform orientation equations as a multiplication of quaternions representing relative spins in x, y, and z axes. The kinematic modeling developed with the method proposed in this work does not require matrix representations, nor does it take into account in its development the trigonometric functions defined between the parameters of the quaternions given by equation (15), which produces highly nonlinear polynomial equations, which were solved numerically to obtain the parameters or components of the quaternions. On the other hand, the movements of the moving platform of the PRRS robot example were represented by 3 quaternions associated to the 3 DOFs required for its orientation, although a general quaternion can also be used as was the case presented in [28] and [29].

It should be noted that the mathematical models associated with the inverse kinematic problems of each robot were solved by applying the Broyden-Fletcher-Goldfarb-Shanno method [46], which is automated in Mathematica V12 software. With the obtained solutions it was possible to plot the robot movements (see Figure 9 and Figure 17). Two trajectories were taken into account in order to solve the inverse kinematic problem of each robot and thus generate, from a given function, the calculation of the rotations, as well as the linear displacements (for the case of the PRRS robot), related to the RRR type flat robot and the PRRS space robot.

A methodology similar to that of the present work was proposed by Jiménez et al [24]. It is possible to find four important differences between the methodology proposed in this paper and the modeling method developed by Jiménez et al. [24]: the first difference is presented in the study of the movements, since in [24] sequences of rotations were used and the axes of rotation of each rotation were updated in the modeling of the movements of an anthropomorphic RRR robot, while in the modeling of parallel robots developed in this article it was not required to update the axes of rotations, since this process is performed by multiplying quaternions when representing relative spins, resulting in a reduction of operations. The second difference is in the modeling of the robot configurations, since in [24] the initial and final positions of the robot were considered for the construction of the model, while to develop the models of the parallel robots of the present study only the initial position was required, thus simplifying the modeling of the kinematics. The third difference is presented in the configuration of the mathematical models, since in the work developed by Jiménez et al. [24], systems of square equations were formed (same number of equations and unknowns), while the modeling proposed in this article generated systems of non-linear non-square equations, due to the fact that the equation representing the platform orientation is constituted by a multiplication of quaternions that generates four-element vectors and produces extra equations. The advantage of having the orientation equation is that it allows to calculate the angles at all joints. The fourth difference is in the numerical method used, since in [24] having a square system of equations and unknowns, the Newton-Raphson method was used to obtain the numerical solution of the kinematics of a 3 DOF PUMA robot, and in the present study the Broyden-Fletcher-Goldfarb-Shanno quasi-Newton method was applied to solve the rectangular systems of equations of each robot studied.

5. Conclusions

In this article, a methodology to model rigid multibody in the plane and in space using unit quaternions was presented. The methodology was used to model the movements of two parallel robots. The main conclusions are summarized in the following points:

• The methodology proposed in this work and the application of unitary quaternions in the modeling process made it possible to build in a systematic and functional way the mathematical models that define the inverse kinematic problem of a flat RRR-type robot and a PRRS-type space robot.
• The mathematical models generated by the application of the methodology to each robot had the following characteristics: 1) the inverse kinematic problem associated with the RRR robot moving in the plane generated a system of 21 nonlinear equations with 18 unknowns of the polynomial type, and 2) the inverse kinematic problem associated with the PRRS robot moving in space generated a system of 36 nonlinear equations with 33 unknowns of the polynomial type for each kinematic chain.
• To solve the mathematical models generated from the inverse kinematic problem approach in both robots, two linear and angular trajectories were used, and the Broyden-Fletcher-Goldfarb-Shanno numerical method was used to calculate the parameters of the quaternions that define the rotations and displacements of each joint. The BFGS optimization method was used due to the high number of equations and unknowns related to the mathematical models of both robots and the advantage offered by formal calculation packages such as Mathematica V12 that has such method programmed.
• The systematization of unitary quaternions developed by Reyes [25] and applied by Jiménez et al. [24] in the modeling of a PUMA robot, has allowed the construction of kinematic models of parallel robots using the binary operations of addition and multiplication between quaternions. Thus, it was possible to model open and closed kinematic chains in a systematic way, which increases the scope of the theory developed by [25].

The methodology presented in this paper can be extended to the complete kinematic study of parallel robots by incorporating the velocity, acceleration and higher derivative models, and with them, it will be possible to model the dynamics of parallel robots. Likewise, it will be possible to study the direct kinematic problem and mechanism synthesis problems using and improving the methodology.

Appendix A.1

Since the orientation of a rigid body in three-dimensional space is completely defined by three rotations [53], it is possible to define this orientation by the composition of three rotation unitary quaternions. For this purpose, the following considerations are described:

1)

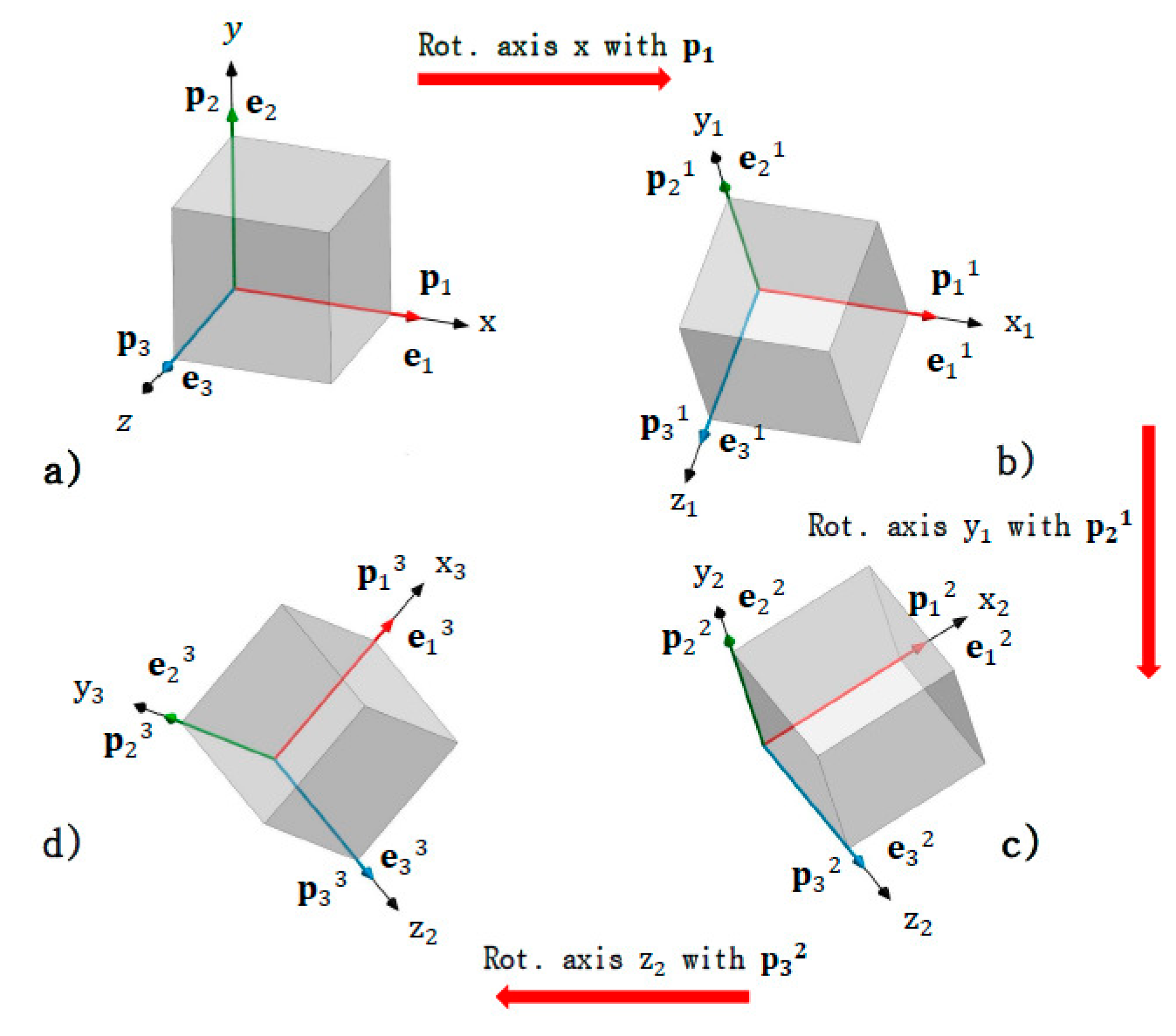
Quaternions p₁, p₂, p₃, are associated to the axes x, y, z, respectively, which will rotate with the body as shown in Figure A.a.

2)

The rotation in the x-axis is produced using the quaternion p₁. The e_j¹ basis elements and the quaternions experience the rotation shown in Figure A.b.

3)

Subsequently, the rotation in the y1 axis is produced using the quaternion p21 (previously rotated). The ej2 basis elements and the quaternions undergo the rotation shown in the Figure. A.c.

4)

Finally, the rotation in the z2 axis is produced using the quaternion p32 (previously rotated). The ej3 basis elements and the quaternions undergo the rotation shown in Figure A.d.

Figure A. Composition of rotations.

Figure A. Composition of rotations.

The different orientations of the elements of the bases e_j¹, e_j², e_j³, and the quaternions p₂¹, p₃², will be defined analytically by means of the rotation function ρ. Then we have the following proposition:

Proposition. The orientation in space of a local basis e_jⁿ attached to a rigid body undergoing three rotations about an inertial basis e_j, is expressed as follows:

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^{\mathrm{n}}=\rho \left(\mathrm{q},{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}\right)={\displaystyle \frac{1}{{‖\mathrm{q}‖}^2}}\mathrm{q}{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}\stackrel{\mathrm{-}}{\mathrm{q}}$             (A1)

Such that e_jⁿ = T_v(e_jⁿ) and q = p₁*p₂*p₃, for p₁ = (p₁₀, p₁₁, 0, 0), p₂ = (p₂₀, 0, p₂₂, 0) and p₃ = (p₃₀, 0, 0, p₃₃) quaternions with axis of rotation in x, y, z, respectively.

Demonstration:

Given the quaternions p₁ = (p₁₀, p₁₁, 0, 0), p₂ = (p₂₀, 0, p₂₂, 0), p₃ = (p₃₀, 0, 0, p₃₃), with turning axes on x, y, z, respectively, rotation of the base occurs e_j¹, and of the quaternions p_j¹ (Figure A.b), on x-axis by p₁. This is:

e_j¹ = ρ(p₁, e_j)             (A2)

p_j¹ = ρ(p₁, p_j)             (A3)

Equation (A3) establishes the current position of the rotation quaternions. The rotation of the base e_j² and of the quaternions p_j² (Figure A.c) occurs on the y1 axis through p₂¹, which is represented as follows:

e_j² = ρ(p₂¹, e_j¹)             (A4)

p_j² = ρ(p₂¹, p_j¹)             (A5)

The rotation of the base e_j³ and of the quaternions p_j³ (Figure A.d) is produced in the z₂ axis by p₃². This is:

e_j³ = ρ(p₃², e_j²)             (A6)

p_j³ = ρ(p₃², p_j²)             (A7)

In addition, the following properties are satisfied:

$\stackrel{\mathrm{-}}{\mathrm{p}*\mathrm{q}}=\stackrel{\mathrm{-}}{\mathrm{q}}*\stackrel{\mathrm{-}}{\mathrm{p}}$             (A8)

$\mathrm{p}*\stackrel{\mathrm{-}}{\mathrm{p}}=\stackrel{\mathrm{-}}{\mathrm{p}}*\mathrm{p}=1=\left(\mathrm{1,0},\mathrm{0,0}\right)$             (A9)

By substituting equations (A2), (A3) in equation (A4) and using equation (A9), the following equality is obtained:

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^2={\displaystyle \frac{1}{{‖{\mathbf{p}}_2^1‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_1‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$             (A10)

By substituting equation (A3) in equation (A5) and obtaining its conjugate, the following expressions are generated:

${\mathbf{p}}_3^2={\displaystyle \frac{1}{{‖{\mathbf{p}}_2^1‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_1‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$             (A11)

${\overline{\mathbf{p}}}_3^2={\displaystyle \frac{1}{{‖{\mathbf{p}}_2^1‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_1‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*\overline{{\mathbf{p}}_3}*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$             (A12)

By substituting equations (A10), (A11) and (A12) in the expression (A6) and using the properties (A9), we have:

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^3={\displaystyle \frac{1}{{‖{\mathbf{p}}_3^2‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_2^1‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_1‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3*{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}*\overline{{\mathbf{p}}_3}*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$             (A13)

From the orthogonality property <ρ(p,q),ρ(p,r)> =<q,r> we have [25]:

${‖{\mathbf{p}}_3^2‖}^2=<{\mathbf{p}}_3^2,{\mathbf{p}}_3^2>{=‖{\mathbf{p}}_3‖}^2$             (A14)

${‖{\mathbf{p}}_2^1‖}^2=<{\mathbf{p}}_2^1,{\mathbf{p}}_2^1>{=‖{\mathbf{p}}_2‖}^2$             (A15)

In addition, the following equality is fulfilled:

${‖{\mathbf{p}}_1‖}^2{‖{\mathbf{p}}_2‖}^2{‖{\mathbf{p}}_3‖}^2={‖{\mathbf{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3‖}^2$             (A16)

Substituting equations (A14), (A15) and (A16) in expression (A13) the following expression is generated:

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^3={\displaystyle \frac{1}{{‖{\mathbf{p}}_1‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_2‖}^2}}{\displaystyle \frac{1}{{‖{\mathbf{p}}_3‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3*{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}*\overline{{\mathbf{p}}_3}*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$             (A17)

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^3={\displaystyle \frac{1}{{‖{\mathbf{p}}_1\mathit{*}{\mathbf{p}}_2\mathit{*}{\mathbf{p}}_3‖}^2}}\left({\mathbf{p}}_1*{\mathbf{p}}_2*{\mathbf{p}}_3*{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}*\overline{{\mathbf{p}}_3}*\overline{{\mathbf{p}}_2}*\overline{{\mathbf{p}}_1}\right)$

Finally, by renaming e_j³ by e_jⁿ, equation (A17) can be written as follows:

${\underset{\_}{\mathbf{e}}}_{\mathrm{j}}^{\mathrm{n}}=\rho \left(\mathrm{q},{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}\right)={\displaystyle \frac{1}{{‖\mathrm{q}‖}^2}}\mathrm{q}*{\underset{\_}{\mathbf{e}}}_{\mathrm{j}}*\stackrel{\mathrm{-}}{\mathrm{q}}$             (A18)

where q = p₁*p₂*p₃, which is what was wanted.