Linearized Expressions of 3D Rotational Motion

1. Introduction

Rotational motion [1] in the three-dimensional physical world is regarding to the circular movement of an object around a fixed axis [2]. It is a basic concept and commonly used in physics, computer graphics, computer vision, robotics, aerospace, and other scientific fields [3,4,5,6]. More specifically, in many practical applications, rotational motion is not only an important way of constructing the motion of the target system [7,8,9] but also an important state parameter to be estimated [10,11,12]. However, rotation motion is typically formulated as a non-linear and non-convex process [11,12,13]. It not only makes some linear algorithms, such as Kalman filter [14,15], impossible to directly apply [16], but also makes solving the related problem more sophisticated and difficult [13,17].

In this paper, a new perspective is proposed that the rotation motion can be linearized without dropping any constraints and increasing any singularities. It is particularly worth pointing out that there are no special and advanced techniques, such as Lie groups and Lie algebras [18,19], for the methods used in this paper. Only some basic knowledge of linear algebra [20,21,22] is required to understand the ideas presented in this paper.

The structure of this paper is as follows: it first reviews rotational motion in the second section, then presents the linearized expression for rotation in the third section. The fourth and fifth sections discuss two special cases,i.e., $\tau =0$ and $\tau ={\displaystyle \frac{1}{2}}\pi$, providing in-depth analysis.

2. Rotation Motion

Mathematically, given a point $\mathit{x}\in {\mathbb{R}}^3$, if it is rotated about a fixed unit vector $\mathbf{r}\in {\mathbb{S}}^2$ through the origin and the rotated angle is $\theta$, then the rotation motion can be formulated by multiplication of a matrix and a vector,

$$\mathbf{R}\mathit{x}\to \mathit{y}$$

(1)

where $\mathit{y}\in {\mathbb{R}}^3$ is the rotated point by $\mathit{x}$ and $\mathbf{R}$ is a $3\times 3$ rotation matrix. There are some properties regarding the rotation motion [23],

• Shape and Size: Rotation does not alter the shape or size of the object. More Specifically,
  • $\parallel \mathbf{R}\mathit{x}\parallel =\parallel \mathbf{R}\parallel ·\parallel \mathit{x}\parallel =\parallel \mathit{x}\parallel$. It means the length of the point $\mathit{x}$ will not be changed by rotation motion. Without loss of generality, the rotation motion in this paper is studied with unit norm vectors, i.e., $\mathit{x}\in {\mathbb{S}}^2$ on the unit sphere surface, which represents a unit direction vector in the 3D physical world.
  • $\angle \left(\mathbf{R}{\mathit{x}}_1,\mathbf{R}{\mathit{x}}_2\right)=\angle \left({\mathit{x}}_1,{\mathit{x}}_2\right)$ where ${\mathit{x}}_1,{\mathit{x}}_2\in {\mathbb{S}}^2$ are any two unit vectors. It means the angle (structure) of the object is unchanged.
• Axis of Rotation: Rotational motion occurs around a fixed axis. Given a vector $\mathit{x}\in {\mathbb{S}}^2$, if $\mathbf{R}\mathit{x}=\mathit{x}$, it means the after the rotation $\mathbf{R}$, the vector direction $\mathit{x}$ remains unchanged, and the vector $\mathit{x}$ must be parallel to the rotation axis $\mathbf{r}$, which is from Euler’s rotation theorem and screw theory [24,25,26,27]. In addition,

  $$\mathbf{R}\mathit{x}=\mathit{x}\Rightarrow \left(\mathbf{R}-{\mathbf{I}}_{3\times 3}\right)\mathit{x}=0$$

  (2)

  where ${\mathbf{I}}_{3\times 3}$ is the 3 × 3 identity matrix. Algebraically, Eq.(2) means the rotation axis direction $\mathbf{r}$ lies in the null space of $\mathbf{R}-{\mathbf{I}}_{3\times 3}$. Alternatively, let $\mathbf{R}\mathit{x}=\lambda \mathit{x}$, then the rotation axis direction $\mathbf{r}$ is an eigenvector of $\mathbf{R}$ corresponding to the eigenvalue $\lambda =1$.

At first glance, the rotation motion is a linear process, which might be misled by the matrix representation Eq.(1). Unfortunately, $\mathbf{R}$ is not a regular matrix in ${\mathbb{R}}^{3\times 3}$. A rotation only has three degrees of freedom, since it can be determined by a rotation axis $\mathbf{r}\in {\mathbb{S}}^2$ and a rotation angle $\theta \in [0,\pi ]$. Formally, $\mathbf{R}\in \mathbb{SO}\left(3\right)$, and a rotation can be represented by a matrix and non-linear constraints,

$$\mathbf{R}=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right],s.t.{\mathbf{R}}^T\mathbf{R}={\mathbf{I}}_{3\times 3},det\left(\mathbf{R}\right)=+1$$

(3)

According to the famous Rodrigues’ rotation formula [28,29], given the rotation axis $\mathbf{r}={\left[\begin{array}{ccc}{r}_1& r_2& r_3\end{array}\right]}^T\in {\mathbb{S}}^2$ and rotation angle $\theta$, the matrix can be constructed by

$$\mathbf{R}=exp\left(\theta {\left[\mathbf{r}\right]}_{\times }\right)={\mathbf{I}}_{3\times 3}+sin\left(\theta \right){\left[\mathbf{r}\right]}_{\times }+\left(1-cos\left(\theta \right)\right){\left[\mathbf{r}\right]}_{\times }^2,{\left[\mathbf{r}\right]}_{\times }=\left[\begin{array}{ccc}0& -r_3& r_2\\ r_3& 0& -r_1\\ -r_2& r_1& 0\end{array}\right]$$

(4)

Moreover, a rotation matrix can be represented by a quaternion vector with unit length [30,31], such that $\mathit{q}={\left[\begin{array}{cccc}{q}_0& q_1& q_2& q_3\end{array}\right]}^T\in {\mathbb{S}}^3$. Specifically,

$$\mathbf{R}=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2\left(q_1{q}_2-q_0{q}_3\right)& 2\left(q_1{q}_3+q_0{q}_2\right)\\ 2\left(q_1{q}_2+q_0{q}_3\right)& q_0^2-q_1^2+q_2^2-q_3^2& 2\left(q_2{q}_3-q_0{q}_1\right)\\ 2\left(q_1{q}_3-q_0{q}_2\right)& 2\left(q_2{q}_3+q_0{q}_1\right)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]$$

(5)

It is worth noting that many different forms of parameter representation can represent the same rotation, and each form of representation has its appropriate application scenario [32,33,34,35]. For example, since a rotation can be determined by a fixed rotation axis $\mathbf{r}\in {\mathbb{S}}^2$ and a rotation angle $\theta \in \left[0,\pi \right]$, then the rotation can be represented by axis–angle representation $\theta ·\mathbf{r}$ [36], which geometrically is a point in a 3D ball of radius $\pi$ [29] and has been widely used in pose estimation problems [29,37,38]. Nonetheless, throughout most of this paper, quaternions are used to represent rotations [30,31] and thus to illustrate the proposed linearization theory.

3. Linear Expressions for Rotation Motion

Given $\mathit{a}=\left[\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right]\in {\mathbb{S}}^2$ and a rotation $\mathbf{R}\in \mathbb{SO}\left(3\right)$, the rotation motion can be formulated as

$$\mathbf{R}\mathit{a}=\mathit{b}\iff \angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=0\iff {\mathit{b}}^T\mathbf{R}\mathit{a}=1$$

(6)

where $\mathit{b}=\left[\begin{array}{ccc}{b}_1& b_2& b_3\end{array}\right]\in {\mathbb{S}}^2$ is rotated by $\mathit{a}$. This formulation is actually a special case of the general rotational motion. Generally, given $\mathit{a},\mathit{b}\in {\mathbb{S}}^2$ and $\mathbf{R}\in \mathbb{SO}\left(3\right)$ whose quaternion expression is $\mathit{q}\in {\mathbb{S}}^3$, consider an arbitrary angle $\tau \in [-\pi ,\pi ]$, there is

$$\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau \iff {\mathit{b}}^T\mathbf{R}\mathit{a}=cos\left(\tau \right)\iff {\mathit{q}}^T\mathbf{M}\mathit{q}=cos\left(\tau \right)$$

(7)

Here $\mathbf{M}$ is constructed by $\mathit{a}$ and $\mathit{b}$ [30,40]. Specifically,

$$\mathbf{M}={\left[\begin{array}{cccc}\hfill 0& -a_1& -a_2\hfill & -a_3\\ \hfill a_1& 0& a_3\hfill & -a_2\\ \hfill a_2& -a_3& 0\hfill & a_1\\ \hfill a_3& a_2& -a_1\hfill & 0\end{array}\right]}^T\left[\begin{array}{cccc}\hfill 0& -b_1& -b_2\hfill & -b_3\\ \hfill b_1& 0& -b_3\hfill & b_2\\ \hfill b_2& b_3& 0\hfill & -b_1\\ \hfill b_3& -b_2& b_1\hfill & 0\end{array}\right]$$

(8)

When $\tau =0$, Eq.(7) degenerates back to Eq.(6).

It is worth noting that there are two facts concerning $\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau$,

For the first point, it is understandable. For the second point, observe $\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau \Rightarrow \angle \left({\mathbf{R}}^{\prime }\left(\theta \right)\mathbf{R}\mathit{a},\mathit{b}\right)=\tau$, where ${\mathbf{R}}^{\prime }\left(\theta \right)$ is a rotation whose rotation axis is $\mathbf{R}\mathit{a}$ and rotation angle is $\theta$; $\theta$ is an arbitrary angle. It means if $\mathbf{R}$ satisfy $\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau$, then there are an infinite number of rotations ${\mathbf{R}}^{\prime }\left(\theta \right)\mathbf{R}$ that also satisfy the given rotation motion. Therefore, given a rotation constraint $\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau$, all rotations that satisfy the given rotation motion should be in some special regions in $\mathbb{SO}\left(3\right)$.

By conducting eigendecomposition of the real symmetric matrix $\mathbf{M}=\mathit{u}\mathsf{\Lambda }{\mathit{u}}^T$ [22,41], where and $\mathit{u}=\left[\begin{array}{cccc}{\mathit{u}}_0& {\mathit{u}}_1& {\mathit{u}}_2& {\mathit{u}}_3\end{array}\right]\in {\mathbb{R}}^{4\times 4}$ is an orthogonal matrix $\mathit{u}{\mathit{u}}^T={\mathbf{I}}_{4\times 4}$. Observe

$$det\left(\mathbf{M}-\lambda {\mathbf{I}}_{4\times 4}\right)=0\Rightarrow {\left({\lambda }^2-1\right)}^2=0$$

(9)

Therefore, the eigenvalue matrix of $\mathbf{M}$ is

$$\mathsf{\Lambda }=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right]$$

(10)

Accordingly, ${\mathit{q}}^T\mathit{u}\mathsf{\Lambda }{\mathit{u}}^T\mathit{q}=cos\left(\tau \right)$.

Let $\mathit{p}={\left[p_0,p_1,p_2,p_3\right]}^T={\mathit{u}}^T\mathit{q}$, then $\mathit{q}=\mathit{u}\mathit{p}=p_0{\mathit{u}}_0+p_1{\mathit{u}}_1+p_2{\mathit{u}}_2+p_3{\mathit{u}}_3$. Observe

$$\left\{\begin{array}{cc}\hfill {\mathit{p}}^T\mathit{p}={\mathit{q}}^T\mathit{u}{\mathit{u}}^T\mathit{q}=p_0^2+p_1^2+p_2^2+p_3^2& =1\hfill \\ \hfill {\mathit{q}}^T\mathit{u}\mathsf{\Lambda }{\mathit{u}}^T\mathit{q}={\mathit{p}}^T\mathsf{\Lambda }\mathit{p}=p_0^2+p_1^2-p_2^2-p_3^2& =cos\left(\tau \right)\hfill \end{array}\right.\Rightarrow \left\{\begin{array}{c}\hfill p_0^2+p_1^2={\displaystyle \frac{1}{2}}\left(1+cos\left(\tau \right)\right)\\ \hfill p_2^2+p_3^2={\displaystyle \frac{1}{2}}\left(1-cos\left(\tau \right)\right)\end{array}\right.$$

(11)

Therefore, it can be formulated

$$\left\{\begin{array}{cc}\hfill p_0={\displaystyle \frac{\sqrt{2\left(1+cos\left(\tau \right)\right)}}{2}}cos\left(\varphi \right),& p_1={\displaystyle \frac{\sqrt{2\left(1+cos\left(\tau \right)\right)}}{2}}sin\left(\varphi \right)\hfill \\ \hfill p_2={\displaystyle \frac{\sqrt{2\left(1-cos\left(\tau \right)\right)}}{2}}cos\left(\psi \right),& p_3={\displaystyle \frac{\sqrt{2\left(1-cos\left(\tau \right)\right)}}{2}}sin\left(\psi \right)\hfill \end{array}\right.$$

(12)

As a consequence, the possible rotation $\mathit{q}$ can be reformulated linearly

$$\begin{array}{cc}\hfill \mathit{q}=& p_0{\mathit{u}}_0+p_1{\mathit{u}}_1+p_2{\mathit{u}}_2+p_3{\mathit{u}}_3\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill =& {\displaystyle \frac{\sqrt{2\left(1+cos\left(\tau \right)\right)}}{2}}\left(cos\left(\varphi \right){\mathit{u}}_0+sin\left(\varphi \right){\mathit{u}}_1\right)+{\displaystyle \frac{\sqrt{2\left(1-cos\left(\tau \right)\right)}}{2}}\left(cos\left(\psi \right){\mathit{u}}_2+sin\left(\psi \right){\mathit{u}}_3\right)\hfill \end{array}$$

(14)

where $\varphi ,\psi \in [-\pi ,\pi ]$. This result clearly shows that the rotational motion can be expressed in linear forms.

Geometrically, if $\angle \left(\mathbf{R}\mathit{a},\mathit{b}\right)=\tau$, then all possible rotation $\mathit{q}$ that satisfy the constraint will be in a two-dimensional torus in ${\mathbb{S}}^3$. For better understanding, some special cases can be visualized, i.e., $\tau =\{0,{\displaystyle \frac{\pi }{9}},{\displaystyle \frac{3\pi }{9}},{\displaystyle \frac{6\pi }{9}},{\displaystyle \frac{8\pi }{9}}\}$ via stereographic projection [42,43], as in Figure 1.

It is worth noting that when $\tau =\{0,\pi \}$, i.e., $\mathbf{R}\mathit{a}=\pm \mathit{b}$, the torus in ${\mathbb{S}}^3$ is degenerated into a one-dimensional circle, more specifically, a great circle [44,45,46] in ${\mathbb{S}}^3$. Formally,

$$\begin{array}{cccc}\hfill & \left(a\right):\mathrm{when}\tau =0\hfill & \hfill \Rightarrow & \mathit{q}=cos\left(\varphi \right){\mathit{u}}_0+sin\left(\varphi \right){\mathit{u}}_1\hfill \\ \hfill & \left(b\right):\mathrm{when}\tau =\pi \hfill & \hfill \Rightarrow & \mathit{q}=cos\left(\psi \right){\mathit{u}}_2+sin\left(\psi \right){\mathit{u}}_3\hfill \end{array}$$

(15)

In addition, when $\tau ={\displaystyle \frac{\pi }{2}}$, the torus is becoming to the Clifford torus in ${\mathbb{S}}^3$ [47,48], since it has the equal diameters in cross directions. Specifically,

$$\mathit{q}={\displaystyle \frac{\sqrt{2}}{2}}\left(cos\left(\varphi \right){\mathit{u}}_0+sin\left(\varphi \right){\mathit{u}}_1\right)+{\displaystyle \frac{\sqrt{2}}{2}}\left(cos\left(\psi \right){\mathit{u}}_2+sin\left(\psi \right){\mathit{u}}_3\right)$$

(16)

4. Special Case I: Great Circle in ${\mathbb{S}}^3$

If $\tau =0$, which means $\mathbf{R}\mathit{a}=\mathit{b}$, it is one of the most common cases in practical applications [33,37]. Then according to Eq. (15) all rotations that satisfy $\mathbf{R}\mathit{a}=\mathit{b}$ should be in

$$\mathit{q}=cos\left(\varphi \right){\mathit{u}}_0+sin\left(\varphi \right){\mathit{u}}_1$$

(17)

where ${\mathit{u}}_0$ and ${\mathit{u}}_{\mathbf{1}}$ are the basis vectors in ${\mathbb{S}}^3$, and they depend on $\mathbf{M}$, i.e., $\mathit{a}$ and $\mathit{b}$. Geometrically speaking, $\mathit{q}$ is a unit vector in ${\mathbb{R}}^4$, which is a linear combination of the two vectors ${\mathit{u}}_0$ and ${\mathit{u}}_1$. In addition, ${\mathit{q}}^T\mathit{q}=1$, which means $\mathit{q}$ is on the surface of the unit quaternion sphere. Therefore, the region where all possible rotations satisfy a specific rotation motion is a great circle in ${\mathbb{S}}^3$ [44].

Figure 2. The illustration of great circles in ${\mathbb{S}}^3$; for better visualization, they is imitatively drawn in ${\mathbb{R}}^3$. (a) Given $\mathbf{R}\mathit{a}=\mathit{b}$, all possible solution of the to-be-solved rotation will be in a circle-shape region on ${\mathbb{S}}^3$ (b) Given two rotation motion, there are two circles on the surface, and the intersections of the circles are the solutions that meet both rotation motions. Note that the intersections are symmetrical on the surface, and they are corresponding to the same rotation matrix. (c) Given more rotation motions, there are more circles. The intersections of the circles should be the rotation solution meet all given rotation motions.

Figure 2. The illustration of great circles in ${\mathbb{S}}^3$; for better visualization, they is imitatively drawn in ${\mathbb{R}}^3$. (a) Given $\mathbf{R}\mathit{a}=\mathit{b}$, all possible solution of the to-be-solved rotation will be in a circle-shape region on ${\mathbb{S}}^3$ (b) Given two rotation motion, there are two circles on the surface, and the intersections of the circles are the solutions that meet both rotation motions. Note that the intersections are symmetrical on the surface, and they are corresponding to the same rotation matrix. (c) Given more rotation motions, there are more circles. The intersections of the circles should be the rotation solution meet all given rotation motions.

In order to determine a unique rotation, two independent constraints are required. Specifically, given two pair of inputs $\mathbf{R}{\mathit{a}}_1={\mathit{b}}_1$ and $\mathbf{R}{\mathit{a}}_2={\mathit{b}}_2$, two circles can be calculated according to Eq.(17), which is however not easy.

$$\left\{\begin{array}{c}\hfill \mathit{q}=cos\left({\varphi }_1\right){\mathit{u}}_{1,0}+sin\left({\varphi }_1\right){\mathit{u}}_{1,1}\\ \hfill \mathit{q}=cos\left({\varphi }_2\right){\mathit{u}}_{2,0}+sin\left({\varphi }_2\right){\mathit{u}}_{2,1}\end{array}\right.\Rightarrow ?$$

(18)

In fact, it does not need to be that complicated. Since ${\mathit{u}}^T\mathit{u}={\mathbf{I}}_{4\times 4}$, there will be

$$\left\{\begin{array}{c}\hfill \left(cos\left(\varphi \right){\mathit{u}}_0^T+sin\left(\varphi \right){\mathit{u}}_1^T\right){\mathit{u}}_2=0\\ \hfill \left(cos\left(\varphi \right){\mathit{u}}_0^T+sin\left(\varphi \right){\mathit{u}}_1^T\right){\mathit{u}}_3=0\end{array}\right.\Rightarrow \left\{\begin{array}{c}\hfill {\mathit{q}}^T{\mathit{u}}_2=0\\ \hfill {\mathit{q}}^T{\mathit{u}}_3=0\end{array}\right.$$

(19)

Consequently, given $\mathbf{R}\mathit{a}=\mathit{b}$, there will be $\left[\begin{array}{c}{\mathit{u}}_2^T,{\mathit{u}}_3^T\end{array}\right]\mathit{q}=0$, where ${\mathit{u}}_2$ and ${\mathit{u}}_3$ are constructed by $\mathit{a}$ and $\mathit{b}$. Given $\{{\mathit{a}}_1,{\mathit{b}}_1\}$ and $\{{\mathit{a}}_2,{\mathit{b}}_2\}$, there will be

$$\left\{\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathit{u}}_{1,2}^T& {\mathit{u}}_{1,3}^T\end{array}\right]\mathit{q}=\mathbf{0}\\ \hfill \left[\begin{array}{cc}{\mathit{u}}_{2,2}^T& {\mathit{u}}_{2,3}^T\end{array}\right]\mathit{q}=\mathbf{0}\end{array}\right.\Rightarrow \left[\begin{array}{cccc}{\mathit{u}}_{1,2}^T& {\mathit{u}}_{1,3}^T& {\mathit{u}}_{2,2}^T& {\mathit{u}}_{2,3}^T\end{array}\right]\mathit{q}=\mathbf{0}\stackrel{def}{⟺}{\mathit{k}}_{4\times 4}\mathit{q}=\mathbf{0}$$

(20)

Similarly, given N inputs, ${\{{\mathit{a}}_i,{\mathit{b}}_i\}}_{i=1}^N$, there will be

$$\left\{\begin{array}{cc}\hfill \mathbf{R}{\mathit{a}}_1& ={\mathit{b}}_1\hfill \\ \hfill \mathbf{R}{\mathit{a}}_2& ={\mathit{b}}_2\hfill \\ \hfill & \cdots \hfill \\ \hfill \mathbf{R}{\mathit{a}}_N& ={\mathit{b}}_N\hfill \end{array}\right.\Rightarrow \left\{\begin{array}{cc}\hfill \left[\begin{array}{cc}{\mathit{u}}_{1,2}^T& {\mathit{u}}_{1,3}^T\end{array}\right]\mathit{q}& =\mathbf{0}\hfill \\ \hfill \left[\begin{array}{cc}{\mathit{u}}_{2,2}^T& {\mathit{u}}_{2,3}^T\end{array}\right]\mathit{q}& =\mathbf{0}\hfill \\ \hfill & \cdots \hfill \\ \hfill \left[\begin{array}{cc}{\mathit{u}}_{N,2}^T& {\mathit{u}}_{N,3}^T\end{array}\right]\mathit{q}& =\mathbf{0}\hfill \end{array}\right.\stackrel{def}{⟺}{\mathit{k}}_{2N\times 4}\mathit{q}=\mathbf{0}$$

(21)

Up until this point, the rotation motion can be surprisingly linearly solved.

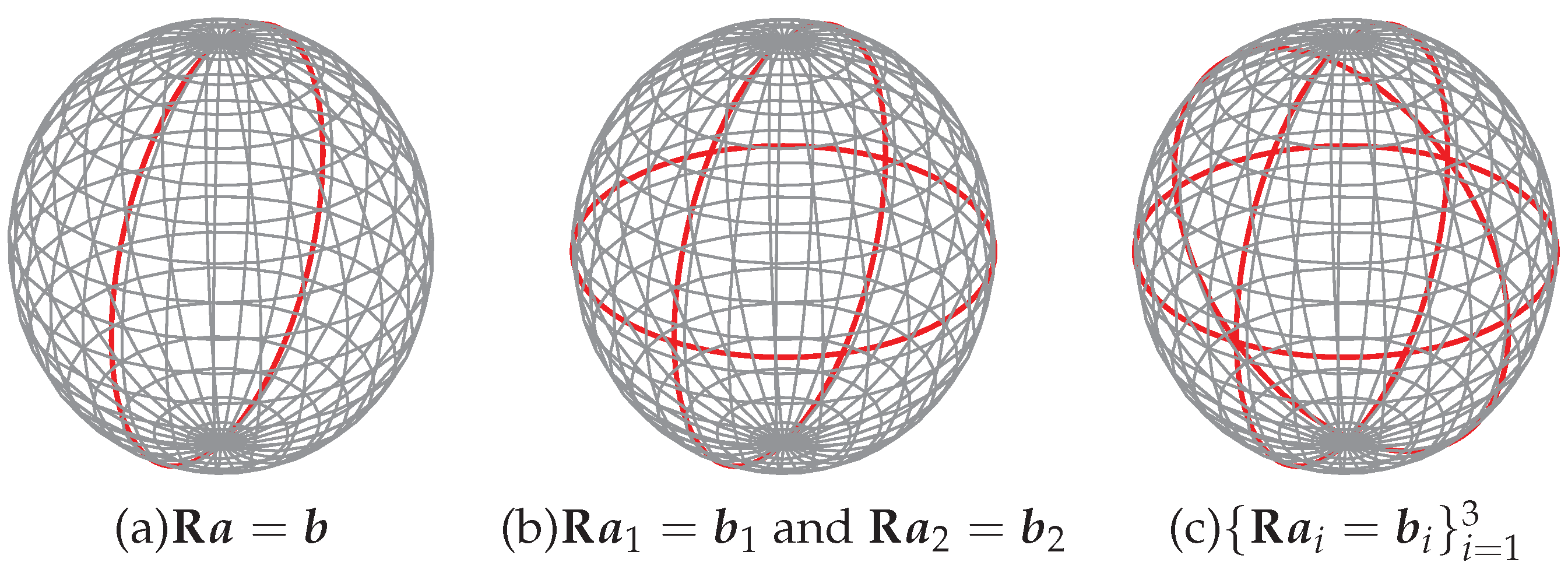
4.1. Eigenvector of $\mathbf{M}$

It is worth noting that the linear expression of rotation motion is closely related to $\mathit{u}=\left[\begin{array}{cccc}{\mathit{u}}_0& {\mathit{u}}_1& {\mathit{u}}_2& {\mathit{u}}_3\end{array}\right]$. Due to $\mathbf{M}\mathit{u}=\mathit{u}\mathsf{\Lambda }$, there will be

$$\mathbf{M}{\mathit{u}}_0=1·{\mathit{u}}_0;\mathbf{M}{\mathit{u}}_1=1·{\mathit{u}}_1;\mathbf{M}{\mathit{u}}_2=-1·{\mathit{u}}_2;\mathbf{M}{\mathit{u}}_3=-1·{\mathit{u}}_3$$

(22)

It is easy to confirm [49,50],

$$\begin{array}{cc}\hfill \mathbf{M}\left[\begin{array}{cc}0& -{\left(\mathit{a}-\mathit{b}\right)}^T\\ -\left(\mathit{a}-\mathit{b}\right)& {\left[\mathit{a}+\mathit{b}\right]}_{\times }^T\end{array}\right]=& -1·\left[\begin{array}{cc}0& -{\left(\mathit{a}-\mathit{b}\right)}^T\\ -\left(\mathit{a}-\mathit{b}\right)& {\left[\mathit{a}+\mathit{b}\right]}_{\times }^T\end{array}\right]\stackrel{def}{=}-1·{\mathsf{\Omega }}^{-}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \mathbf{M}\left[\begin{array}{cc}0& -{\left(\mathit{a}+\mathit{b}\right)}^T\\ -\left(\mathit{a}+\mathit{b}\right)& {\left[\mathit{a}-\mathit{b}\right]}_{\times }^T\end{array}\right]=& +1·\left[\begin{array}{cc}0& -{\left(\mathit{a}+\mathit{b}\right)}^T\\ -\left(\mathit{a}+\mathit{b}\right)& {\left[\mathit{a}-\mathit{b}\right]}_{\times }^T\end{array}\right]\stackrel{def}{=}+1·{\mathsf{\Omega }}^{+}\hfill \end{array}$$

(24)

Therefore, any row of ${\mathsf{\Omega }}^{-}$ can be the eigenvector of $\mathbf{M}$ with eigenvalue $-1$. Similarly, any row of ${\mathsf{\Omega }}^{+}$ can be the eigenvector of $\mathbf{M}$ with eigenvalue 1.

Accordingly, there will be

• any row of ${\mathsf{\Omega }}^{-}$ is a linear combination of ${\mathit{u}}_0$ and ${\mathit{u}}_1$.
• any row of ${\mathsf{\Omega }}^{+}$ is a linear combination of ${\mathit{u}}_2$ and ${\mathit{u}}_3$.

Consequently, $\mathrm{rank}\left({\mathsf{\Omega }}^{-}\right)=\mathrm{rank}\left({\mathsf{\Omega }}^{+}\right)=2$; ${\mathsf{\Omega }}^{-}$ and ${\mathsf{\Omega }}^{+}$ are not necessarily orthogonal matrices. Nonetheless, there is still ${\mathsf{\Omega }}^{-}\mathit{q}=\mathbf{0}$, more specifically,

$$\begin{array}{c}\hfill {\mathsf{\Omega }}^{-}\mathit{q}=\mathbf{0}\iff \left[\begin{array}{cc}0& {\left(\mathit{a}-\mathit{b}\right)}^T\\ -\left(\mathit{a}-\mathit{b}\right)& {\left[\mathit{a}+\mathit{b}\right]}_{\times }\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\mathbf{0}\end{array}$$

(25)

$$\begin{array}{c}\hfill \iff \left[\begin{array}{cccc}0& a_1-b_1& a_2-b_2& a_3-b_3\\ -\left(a_1-b_1\right)& 0& -\left(a_3+b_3\right)& a_2+b_2\\ -\left(a_2-b_2\right)& a_3+b_3& 0& -\left(a_1+b_1\right)\\ -\left(a_3-b_3\right)& -\left(a_2+b_2\right)& a_1+b_1& 0\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]=\mathbf{0}\end{array}$$

(26)

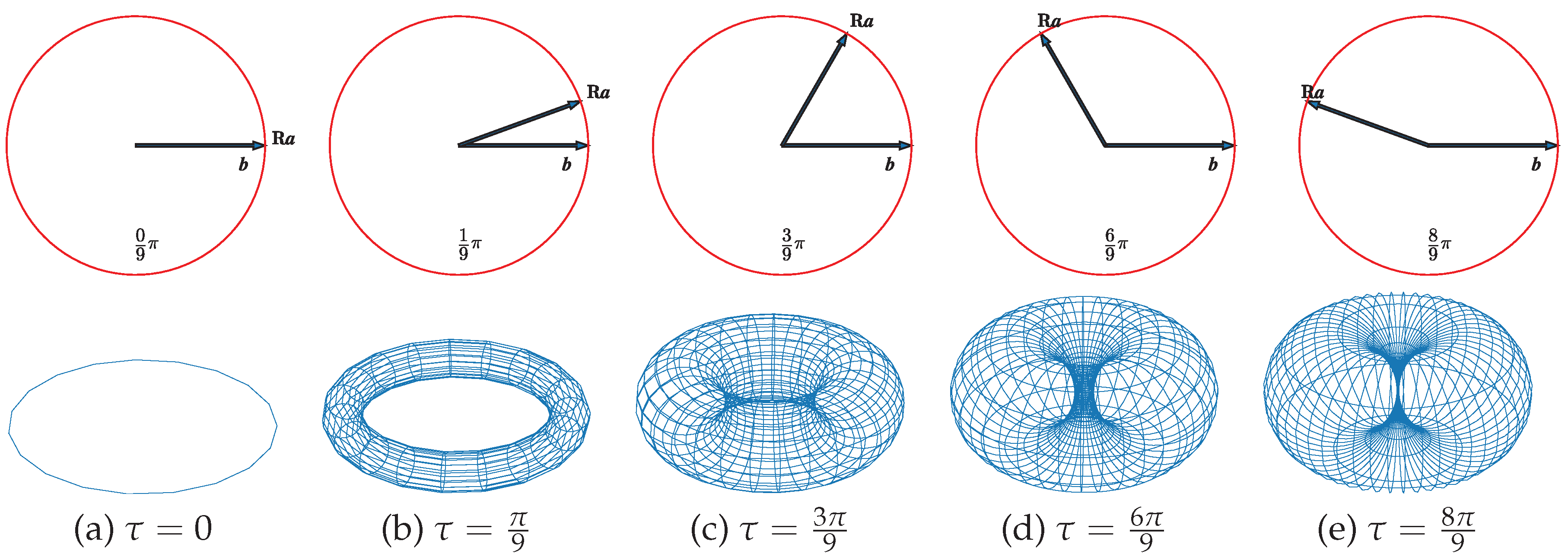
5. Special Case II: Clifford Torus in ${\mathbb{S}}^3$

In the previous description, we provide a general derivation for the connection between rotation constraint, i.e., ${\mathit{b}}^T\mathbf{R}\mathit{a}=0$ and Clifford torus. Here we show an alternative way to obtain a Clifford torus from rotation constraint.

Given a rotation constraint ${\mathit{b}}^T\mathbf{R}\mathit{a}=0$, the possible rotation $\mathbf{R}$ can be (see Figure 3)

$$\mathbf{R}\left(\alpha ,\beta \right)={\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0,\alpha ,\beta \in \left[-\pi ,\pi \right]$$

(27)

where ${\mathit{v}}_2=\mathit{b}$, ${\mathit{v}}_1^T{\mathit{v}}_1=1$ and ${\mathit{v}}_1^T{\mathit{v}}_2=0$; ${\mathbf{R}}_0$ is a rotation that rotates $\mathit{a}$ to ${\mathit{v}}_1$; ${\mathbf{R}}_{v_1}\left(\alpha \right)=exp\left(\alpha {\left[{\mathit{v}}_1\right]}_{\times }\right)$ and ${\mathbf{R}}_{v_2}\left(\beta \right)=exp\left(\beta {\left[{\mathit{v}}_2\right]}_{\times }\right)$ are rotations around directions ${\mathit{b}}_1$ and $\mathit{b}$, respectively. The rotation motion can be as follows,

$${\mathit{v}}_1={\mathbf{R}}_0\mathit{a},⟶{\mathit{v}}_1={\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0\mathit{a},⟶{\mathit{b}}^T\left({\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0\mathit{a}\right)=0$$

(28)

To use quaternion to represent rotation [30]

$$\begin{array}{cc}\hfill {\mathbf{R}}_{v_2}\left(\beta \right):=& {\mathit{q}}_{v_2}\left(\beta \right)={\left[\begin{array}{cc}cos\left({\displaystyle \frac{\beta }{2}}\right)& {\mathit{v}}_2^{T}sin\left({\displaystyle \frac{\beta }{2}}\right)\end{array}\right]}^T\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\mathbf{R}}_{v_1}\left(\alpha \right):=& {\mathit{q}}_{v_1}\left(\alpha \right)={\left[\begin{array}{cc}cos\left({\displaystyle \frac{\alpha }{2}}\right)& {\mathit{v}}_1^{T}sin\left({\displaystyle \frac{\alpha }{2}}\right)\end{array}\right]}^T\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\mathbf{R}}_0:=& {\left[\begin{array}{cc}{q}_0& {\mathit{q}}_{123}^T\end{array}\right]}^T\hfill \end{array}$$

(31)

The formula for the multiplication of two quaternions is [30]

$$(r_1,\overrightarrow{v_1})(r_2,\overrightarrow{v_2})=(r_1{r}_2-\overrightarrow{v_1}\overrightarrow{v_2},r_1\overrightarrow{v_2}+r_2\overrightarrow{v_1}+\overrightarrow{v_1}\times \overrightarrow{v_2})$$

(32)

Define ${\mathit{v}}_3={\mathit{v}}_1\times {\mathit{v}}_2$, then

$$\begin{array}{c}{\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right):=\hfill \\ {\left[\begin{array}{cc}cos\left({\displaystyle \frac{\beta }{2}}\right)cos\left({\displaystyle \frac{\alpha }{2}}\right)& {\mathit{v}}_2^{T}sin\left({\displaystyle \frac{\beta }{2}}\right)cos\left({\displaystyle \frac{\alpha }{2}}\right)+{\mathit{v}}_1^{T}sin\left({\displaystyle \frac{\alpha }{2}}\right)cos\left({\displaystyle \frac{\beta }{2}}\right)-{\mathit{v}}_3^{T}sin\left({\displaystyle \frac{\beta }{2}}\right)sin\left({\displaystyle \frac{\alpha }{2}}\right)\end{array}\right]}^T\hfill \end{array}$$

(33)

In addition, let $w_1={\displaystyle \frac{1}{2}}(\alpha -\beta )$ and $w_2={\displaystyle \frac{1}{2}}(\alpha +\beta )$,

$$\begin{array}{cc}\hfill cos\left({\displaystyle \frac{\beta }{2}}\right)cos\left({\displaystyle \frac{\alpha }{2}}\right)=& {\displaystyle \frac{1}{2}}\left(cos\left({\displaystyle \frac{\alpha -\beta }{2}}\right)+cos\left({\displaystyle \frac{\alpha +\beta }{2}}\right)\right)={\displaystyle \frac{1}{2}}\left(cos\left(w_1\right)+cos\left(w_2\right)\right)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill sin\left({\displaystyle \frac{\beta }{2}}\right)cos\left({\displaystyle \frac{\alpha }{2}}\right)=& {\displaystyle \frac{1}{2}}\left(sin\left({\displaystyle \frac{\alpha +\beta }{2}}\right)-sin\left({\displaystyle \frac{\alpha -\beta }{2}}\right)\right)={\displaystyle \frac{1}{2}}\left(sin\left(w_2\right)-sin\left(w_1\right)\right)\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill sin\left({\displaystyle \frac{\alpha }{2}}\right)cos\left({\displaystyle \frac{\beta }{2}}\right)=& {\displaystyle \frac{1}{2}}\left(sin\left({\displaystyle \frac{\alpha +\beta }{2}}\right)+sin\left({\displaystyle \frac{\alpha -\beta }{2}}\right)\right)={\displaystyle \frac{1}{2}}\left(sin\left(w_2\right)+sin\left(w_1\right)\right)\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill sin\left({\displaystyle \frac{\beta }{2}}\right)sin\left({\displaystyle \frac{\alpha }{2}}\right)=& {\displaystyle \frac{1}{2}}\left(cos\left({\displaystyle \frac{\alpha -\beta }{2}}\right)-cos\left({\displaystyle \frac{\alpha +\beta }{2}}\right)\right)={\displaystyle \frac{1}{2}}\left(cos\left(w_1\right)-cos\left(w_2\right)\right)\hfill \end{array}$$

(37)

Then,

$$\begin{array}{c}{\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right):=\hfill \\ {\displaystyle \frac{1}{2}}{\left[\begin{array}{cc}cos\left(w_1\right)+cos\left(w_2\right)& sin\left(w_1\right)\left({\mathit{v}}_1^T-{\mathit{v}}_2^T\right)-cos\left(w_1\right){\mathit{v}}_3^T+sin\left(w_2\right)\left({\mathit{v}}_1^T+{\mathit{v}}_2^T\right)+cos\left(w_2\right){\mathit{v}}_3^T\end{array}\right]}^T\hfill \end{array}$$

(38)

Therefore,

$$\begin{array}{cc}\hfill & \mathbf{R}\left(\alpha ,\beta \right)={\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & :={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathit{k}}_0& {\mathit{k}}_1& {\mathit{k}}_2& {\mathit{k}}_3\end{array}\right]\left[\begin{array}{c}cos\left(w_1\right)\\ sin\left(w_1\right)\\ cos\left(w_2\right)\\ sin\left(w_2\right)\end{array}\right],w_1={\displaystyle \frac{1}{2}}(\alpha -\beta ),\mathrm{and},w_2={\displaystyle \frac{1}{2}}(\alpha +\beta )\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill =& {\displaystyle \frac{1}{2}}\left({\mathit{k}}_{0}cos\left(w_1\right)+{\mathit{k}}_{1}sin\left(w_1\right)+{\mathit{k}}_{2}cos\left(w_2\right)+{\mathit{k}}_{3}sin\left(w_2\right)\right)\hfill \end{array}$$

(41)

where

$$\begin{array}{cc}\hfill {\mathit{k}}_0=\left[\begin{array}{c}{q}_0+{\mathit{v}}_3^T{\mathit{q}}_{123}\\ {\mathit{q}}_{123}-q_0{\mathit{v}}_3-{\mathit{v}}_3\times {\mathit{q}}_{123}\end{array}\right]& {\mathit{k}}_1=\left[\begin{array}{c}-{\left({\mathit{v}}_1-{\mathit{v}}_2\right)}^T{\mathit{q}}_{123}\\ q_0\left({\mathit{v}}_1-{\mathit{v}}_2\right)+\left({\mathit{v}}_1-{\mathit{v}}_2\right)\times {\mathit{q}}_{123}\end{array}\right]\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill {\mathit{k}}_2=\left[\begin{array}{c}{q}_0-{\mathit{v}}_3^T{\mathit{q}}_{123}\\ {\mathit{q}}_{123}+q_0{\mathit{v}}_3+{\mathit{v}}_3\times {\mathit{q}}_{123}\end{array}\right]& {\mathit{k}}_3=\left[\begin{array}{c}-{\left({\mathit{v}}_1+{\mathit{v}}_2\right)}^T{\mathit{q}}_{123}\\ q_0\left({\mathit{v}}_1+{\mathit{v}}_2\right)+\left({\mathit{v}}_1+{\mathit{v}}_2\right)\times {\mathit{q}}_{123}\end{array}\right]\hfill \end{array}$$

(43)

It is easy to verify

$${\left[\begin{array}{cccc}{\mathit{k}}_0& {\mathit{k}}_1& {\mathit{k}}_2& {\mathit{k}}_3\end{array}\right]}^T\left[\begin{array}{cccc}{\mathit{k}}_0& {\mathit{k}}_1& {\mathit{k}}_2& {\mathit{k}}_3\end{array}\right]=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 2& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 2\end{array}\right]$$

(44)

Geometrically, Eq. (39) describes a Clifford torus [51] in ${\mathbb{S}}^3$.

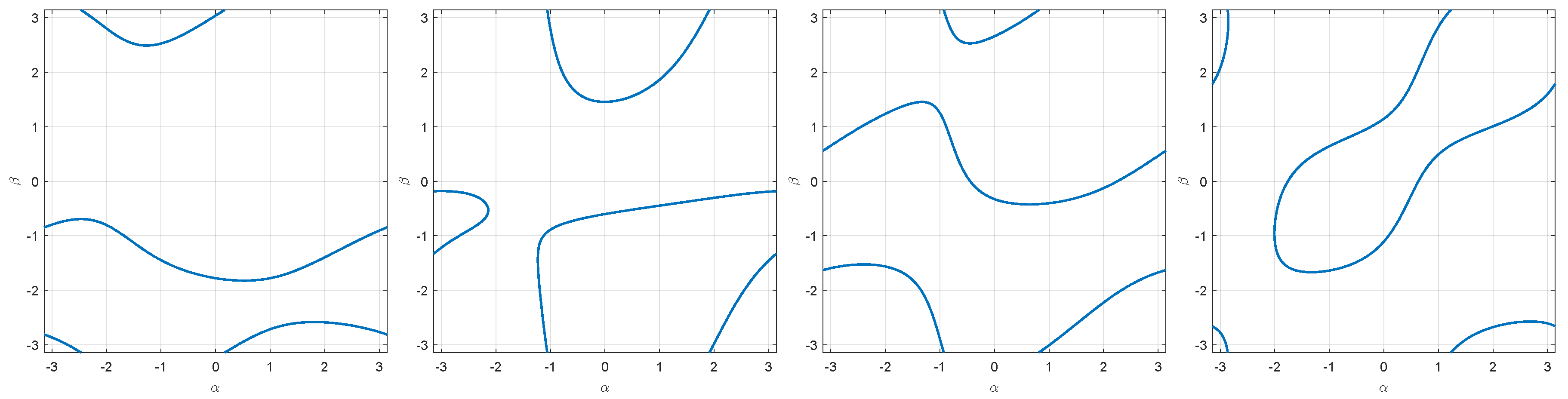
5.1. Intersections of Two Different Clifford Tori

Given two rotation constraints ${\mathit{b}}_1^T\mathbf{R}{\mathit{a}}_1=0$ and ${\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2=0$, the possible rotation can be considered in the intersections of two Clifford tori (see Figure 4). Here, a solution to solve the intersection line is presented. Specifically,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\mathit{b}}_1^T\mathbf{R}{\mathit{a}}_1=0\\ \hfill {\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2=0\end{array}\right.\Rightarrow \left\{\begin{array}{cc}\hfill \mathbf{R}\left(\alpha ,\beta \right)& ={\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0\hfill \\ \hfill {\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2& =0\hfill \end{array}\right.\Rightarrow {\mathit{b}}_2^T{\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_2=0\end{array}$$

(45)

where ${\mathit{v}}_2={\mathit{b}}_1$ and ${\mathit{v}}_1\in {\mathbb{S}}^2$ is an arbitrary vector and satisfies ${\mathit{v}}_1^T{\mathit{v}}_2=0$; ${\mathbf{R}}_0$ is a specific arbitrary rotation that can rotate $\mathit{a}$ to ${\mathit{v}}_1$; ${\mathbf{R}}_{v_1}\left(\alpha \right)=exp\left(\alpha {\left[{\mathit{v}}_1\right]}_{\times }\right)$ and ${\mathbf{R}}_{v_2}\left(\beta \right)=exp\left(\beta {\left[{\mathit{v}}_2\right]}_{\times }\right)$.

According to Rodrigues’ rotation formula [3], we have

$$\begin{array}{c}\hfill {\mathbf{R}}_{v1}\left(\alpha \right)=exp\left(\alpha {\left[{\mathit{v}}_1\right]}_{\times }\right)=\mathbf{I}+sin\left(\alpha \right){\left[{\mathit{v}}_1\right]}_{\times }+\left(1-cos\left(\alpha \right)\right){\left[{\mathit{v}}_1\right]}_{\times }^2\end{array}$$

(46)

$$\begin{array}{c}\hfill {\mathbf{R}}_{v2}\left(\beta \right)=exp\left(\beta {\left[{\mathit{v}}_2\right]}_{\times }\right)=\mathbf{I}+sin\left(\beta \right){\left[{\mathit{v}}_2\right]}_{\times }+\left(1-cos\left(\beta \right)\right){\left[{\mathit{v}}_2\right]}_{\times }^2\end{array}$$

(47)

Therefore,

$$\begin{array}{c}\hfill {\mathit{b}}_2^T\left(\mathbf{I}+sin\left(\beta \right){\left[{\mathit{v}}_2\right]}_{\times }+\left(1-cos\left(\beta \right)\right){\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(\mathbf{I}+sin\left(\alpha \right){\left[{\mathit{v}}_1\right]}_{\times }+\left(1-cos\left(\alpha \right)\right){\left[{\mathit{v}}_1\right]}_{\times }^2\right){\mathbf{R}}_0{\mathit{a}}_2=0\end{array}$$

(48)

Clearly, Eq.(48) shows a one-dimensional curve constructed by $\alpha$ and $\beta$ (see Figure 5).

Specifically, given a $\alpha \in [-\pi ,\pi ]$, $\beta$ would be computed by Eq. (48). Intuitively, one should solve the following equation

$$sin\left(\beta \right)A+cos\left(\beta \right)B+C=0$$

(49)

where $A={\mathit{b}}_2^T{\left[{\mathit{v}}_2\right]}_{\times }{\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_2$, $B=-{\mathit{b}}_2^T{\left[{\mathit{v}}_2\right]}_{\times }^2{\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_2$ and $C={\mathit{b}}_2^T{\mathit{v}}_2{\mathit{v}}_2^T{\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_2$. According to the tangent half-angle formula, when $\beta \ne \pm \pi$,

$$\begin{array}{c}{\displaystyle \frac{2tan\left(\frac{\beta }{2}\right)}{1+{tan}^2\left(\frac{\beta }{2}\right)}}A+{\displaystyle \frac{1-{tan}^2\left(\frac{\beta }{2}\right)}{1+{tan}^2\left(\frac{\beta }{2}\right)}}B+C=0\hfill \\ \hfill \stackrel{y\triangleq tan\left({\displaystyle \frac{\beta }{2}}\right)}{\to }2Ay+(1-y^2)B+(1+y^2)C=0\Rightarrow (C-B)y^2+2Ay+B+C=0\end{array}$$

(50)

Accordingly, $\beta$ can be computed and rotation $\mathbf{R}\left(\alpha ,\beta \right)$ can be computed as well. Formally,

$$f:\alpha \in [\pi ,\pi ]\stackrel{\beta \mathrm{by}\mathrm{Eq}.()}{\to }\mathbf{R}\left(\alpha ,\beta \right)$$

(51)

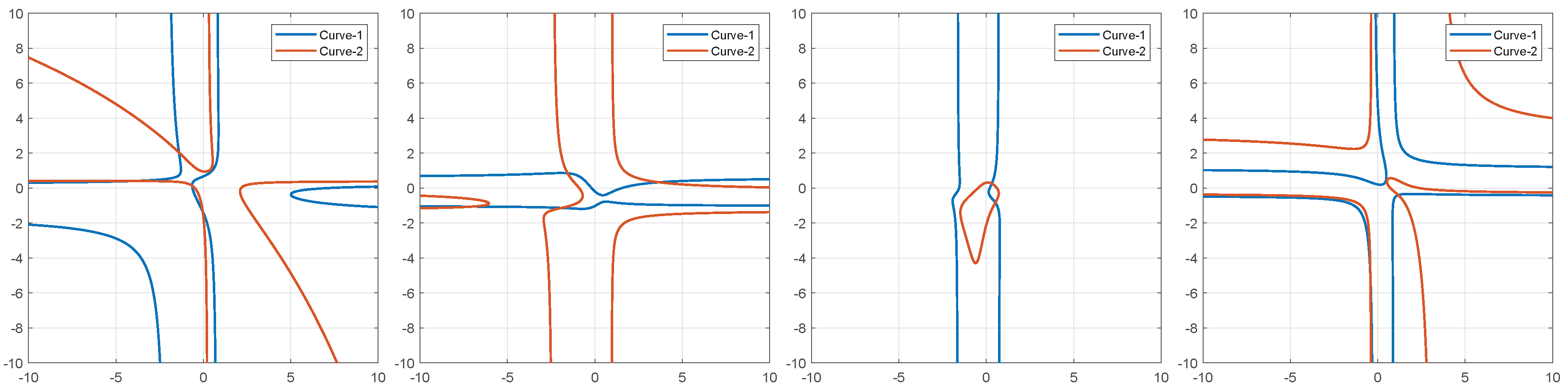
5.2. Intersections of Three Different Clifford Tori

Given three rotation constraints ${\mathit{b}}_1^T\mathbf{R}{\mathit{a}}_1=0$, ${\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2=0$ and ${\mathit{b}}_3^T\mathbf{R}{\mathit{a}}_3=0$, the possible rotation can be considered in the intersections of three Clifford tori. Note that it belongs to the famous E3Q3 problem [52], and there are many solutions have been proposed to solve it [53,54,55,56,57]. Here this paper provides a more straight linear way. Specifically,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\mathit{b}}_1^T\mathbf{R}{\mathit{a}}_1=0\\ \hfill {\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2=0\\ \hfill {\mathit{b}}_3^T\mathbf{R}{\mathit{a}}_3=0\end{array}\right.\Rightarrow \left\{\begin{array}{cc}\hfill \mathbf{R}\left(\alpha ,\beta \right)& ={\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0\hfill \\ \hfill {\mathit{b}}_2^T\mathbf{R}{\mathit{a}}_2& =0\hfill \\ \hfill {\mathit{b}}_3^T\mathbf{R}{\mathit{a}}_3& =0\hfill \end{array}\right.\Rightarrow \left\{\begin{array}{c}\hfill {\mathit{b}}_2^T{\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_2=0\\ \hfill {\mathit{b}}_3^T{\mathbf{R}}_{v_2}\left(\beta \right){\mathbf{R}}_{v_1}\left(\alpha \right){\mathbf{R}}_0{\mathit{a}}_3=0\end{array}\right.\end{array}$$

(52)

Therefore,

$$\begin{array}{c}\hfill {\mathit{b}}_2^T\left(\mathbf{I}+sin\left(\beta \right){\left[{\mathit{v}}_2\right]}_{\times }+\left(1-cos\left(\beta \right)\right){\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(\mathbf{I}+sin\left(\alpha \right){\left[{\mathit{v}}_1\right]}_{\times }+\left(1-cos\left(\alpha \right)\right){\left[{\mathit{v}}_1\right]}_{\times }^2\right){\mathbf{R}}_0{\mathit{a}}_2=0\end{array}$$

(53)

$$\begin{array}{c}\hfill {\mathit{b}}_3^T\left(\mathbf{I}+sin\left(\beta \right){\left[{\mathit{v}}_2\right]}_{\times }+\left(1-cos\left(\beta \right)\right){\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(\mathbf{I}+sin\left(\alpha \right){\left[{\mathit{v}}_1\right]}_{\times }+\left(1-cos\left(\alpha \right)\right){\left[{\mathit{v}}_1\right]}_{\times }^2\right){\mathbf{R}}_0{\mathit{a}}_3=0\end{array}$$

(54)

There are two unknown variables $\alpha$ and $\beta$ for two constraints, and the intersections can be computed. According to tangent half-angle formula (a.k.a. Weierstrass substitution formulas),

$$\begin{array}{c}\hfill sin\left(\alpha \right)={\displaystyle \frac{2tan\left(\frac{\alpha }{2}\right)}{1+{tan}^2\left(\frac{\alpha }{2}\right)}},cos\left(\alpha \right)={\displaystyle \frac{1-{tan}^2\left(\frac{\alpha }{2}\right)}{1+{tan}^2\left(\frac{\alpha }{2}\right)}},\end{array}$$

(55)

$$\begin{array}{c}\hfill sin\left(\beta \right)={\displaystyle \frac{2tan\left(\frac{\beta }{2}\right)}{1+{tan}^2\left(\frac{\beta }{2}\right)}},cos\left(\beta \right)={\displaystyle \frac{1-{tan}^2\left(\frac{\beta }{2}\right)}{1+{tan}^2\left(\frac{\beta }{2}\right)}}\end{array}$$

(56)

Let $x=tan\left({\displaystyle \frac{\alpha }{2}}\right)$, and $y=tan\left({\displaystyle \frac{\beta }{2}}\right)$, and when $\alpha \ne \pm \pi$, $\beta \ne \pm \pi$,

$$\begin{array}{c}\hfill {\mathit{b}}_2^T\left((1+y^2)\mathbf{I}+2y{\left[{\mathit{v}}_2\right]}_{\times }+2y^2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left((1+x^2)\mathbf{I}+2x{\left[{\mathit{v}}_1\right]}_{\times }+2x^2{\left[{\mathit{v}}_1\right]}_{\times }^2\right){\mathbf{R}}_0{\mathit{a}}_2=0\end{array}$$

(57)

$$\begin{array}{c}\hfill {\mathit{b}}_3^T\left((1+y^2)\mathbf{I}+2y{\left[{\mathit{v}}_2\right]}_{\times }+2y^2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left((1+x^2)\mathbf{I}+2x{\left[{\mathit{v}}_1\right]}_{\times }+2x^2{\left[{\mathit{v}}_1\right]}_{\times }^2\right){\mathbf{R}}_0{\mathit{a}}_3=0\end{array}$$

(58)

The system of equations can be reformulated as

$$\mathcal{F}(x,y)=\left[\begin{array}{ccc}{y}^2& y& 1\end{array}\right]\mathbf{A}\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=0,\mathcal{G}(x,y)=\left[\begin{array}{ccc}{y}^2& y& 1\end{array}\right]\mathbf{B}\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=0$$

(59)

where $\mathbf{A}$ and $\mathbf{B}\in {\mathbb{R}}^{3\times 3}$, Specifically,

$$\begin{array}{c}\begin{array}{c}\mathbf{A}=\left[\begin{array}{ccc}{A}_{1,1}& A_{1,2}& A_{1,3}\\ A_{2,1}& A_{2,2}& A_{2,3}\\ A_{3,1}& A_{3,2}& A_{3,3}\end{array}\right]=\hfill \end{array}\hfill \\ {\mathit{b}}_2^T\ast \left[\begin{array}{ccc}\begin{array}{c}\hfill \left[l\right]\left(\mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(\mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2\right)\end{array}& \left(\mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(2{\left[{\mathit{v}}_1\right]}_{\times }\right)& \mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\\ \left(2{\left[{\mathit{v}}_2\right]}_{\times }\right)\left(\mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2\right)& \left(2{\left[{\mathit{v}}_2\right]}_{\times }\right)\left(2{\left[{\mathit{v}}_1\right]}_{\times }\right)& 2{\left[{\mathit{v}}_2\right]}_{\times }\\ \mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2& 2{\left[{\mathit{v}}_1\right]}_{\times }& \mathbf{I}\end{array}\right]\ast {\mathbf{R}}_0{\mathit{a}}_2\hfill \end{array}$$

(60)

$$\begin{array}{c}\begin{array}{c}\mathbf{B}=\left[\begin{array}{ccc}{B}_{1,1}& B_{1,2}& B_{1,3}\\ B_{2,1}& B_{2,2}& B_{2,3}\\ B_{3,1}& B_{3,2}& B_{3,3}\end{array}\right]=\hfill \end{array}\hfill \\ {\mathit{b}}_3^T\ast \left[\begin{array}{ccc}\begin{array}{c}\hfill \left[l\right]\left(\mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(\mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2\right)\end{array}& \left(\mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\right)\left(2{\left[{\mathit{v}}_1\right]}_{\times }\right)& \mathbf{I}+2{\left[{\mathit{v}}_2\right]}_{\times }^2\\ \left(2{\left[{\mathit{v}}_2\right]}_{\times }\right)\left(\mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2\right)& \left(2{\left[{\mathit{v}}_2\right]}_{\times }\right)\left(2{\left[{\mathit{v}}_1\right]}_{\times }\right)& 2{\left[{\mathit{v}}_2\right]}_{\times }\\ \mathbf{I}+2{\left[{\mathit{v}}_1\right]}_{\times }^2& 2{\left[{\mathit{v}}_1\right]}_{\times }& \mathbf{I}\end{array}\right]\ast {\mathbf{R}}_0{\mathit{a}}_3\hfill \end{array}$$

(61)

and * is to calculate the matrix item by item. Geometrically, if only considering real solutions, it describes the intersections of two cures computed by observations in $z=0$ plane (see Figure 6).

Algebraically, it is a polynomial system containing two equations in two variables, which can be generally solved by resultant-based method [58,59]. We donate

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}{y}^2& y& 1\end{array}\right]\mathbf{A}\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=\mathcal{A}\left(y\right)\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=0,\left[\begin{array}{ccc}{y}^2& y& 1\end{array}\right]\mathbf{B}\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=\mathcal{B}\left(y\right)\left[\begin{array}{c}{x}^2\\ x\\ 1\end{array}\right]=0\end{array}$$

(62)

Both sides of the equations are multiplied by x,

$$\mathcal{A}\left(y\right)\left[\begin{array}{c}{x}^3\\ x^2\\ x\end{array}\right]=0,\mathcal{B}\left(y\right)\left[\begin{array}{c}{x}^3\\ x^2\\ x\end{array}\right]=0$$

(63)

By stacking equations,

$$\left[\begin{array}{cc}0& \mathcal{A}\left(y\right)\\ 0& \mathcal{B}\left(y\right)\\ \mathcal{A}\left(y\right)& 0\\ \mathcal{B}\left(y\right)& 0\end{array}\right]\left[\begin{array}{c}{x}^3\\ x^2\\ x\\ 1\end{array}\right]=\mathcal{H}\left(y\right)\left[\begin{array}{c}{x}^3\\ x^2\\ x\\ 1\end{array}\right]=0$$

(64)

To solve y, it is to solve $\left|\begin{array}{c}\mathcal{H}\left(y\right)\end{array}\right|=0$. This determinant is also known as a hidden-variable resultant in computer vision filed [60,61], and it is an univariate polynomial with degree 8 of the hidden variable y.

$$\begin{array}{c}\hfill \left|\begin{array}{c}\mathcal{H}\left(y\right)\end{array}\right|=a_8{y}^8+a_7{y}^7+a_6{y}^6+a_5{y}^5+a_4{y}^4+a_3{y}^3+a_2{y}^2+a_{1}y+a_0=0\end{array}$$

(65)

In fact, the problem is not very complex, one can directly calculate the explicit expression of each term for the resultant-based method using symbolic math. Practically, one can obtain explicit coefficients ${\left\{a_i\right\}}_{i=0}^8$ by the function resultant in Matlab 1 or the function sympy.polys.polytools.resultant in SymPy2, and this paper will not list all details to avoid long-and-tedious expressions for readability. Nonetheless, the solution of y can be directly computed by solving roots of a univariate polynomial [62,63]. After solving y, it is easy to calculate x.

5.2.1. Linear Solution to Solve Intersections of Three Different Clifford Tori

Alternatively, Eq. (64) can be rewritten as a quadratic eigenvalue problem, i.e., $\left({\lambda }^2{\mathbf{H}}_2+\lambda {\mathbf{H}}_1+{\mathbf{H}}_0\right)\mathit{v}=0$ [60,61,64].

$$\mathcal{H}\left(y\right)\left[\begin{array}{c}{x}^3\\ x^2\\ x\\ 1\end{array}\right]=0\Rightarrow \left(y^2{\mathbf{H}}_2+y{\mathbf{H}}_1+{\mathbf{H}}_0\right)\left[\begin{array}{c}{x}^3\\ x^2\\ x\\ 1\end{array}\right]=0$$

(66)

where ${\mathbf{H}}_0$, ${\mathbf{H}}_1$ and ${\mathbf{H}}_2\in {\mathbb{R}}^{4\times 4}$. Specifically,

${\mathbf{H}}_2=\left[\begin{array}{cccc}0& A_{1,1}& A_{1,2}& A_{1,3}\\ 0& B_{1,1}& B_{1,2}& B_{1,3}\\ A_{1,1}& A_{1,2}& A_{1,3}& 0\\ B_{1,1}& B_{1,2}& B_{1,3}& 0\end{array}\right]$	${\mathbf{H}}_1=\left[\begin{array}{cccc}0& A_{2,1}& A_{2,2}& A_{2,3}\\ 0& B_{2,1}& B_{2,2}& B_{2,3}\\ A_{2,1}& A_{2,2}& A_{2,3}& 0\\ B_{2,1}& B_{2,2}& B_{2,3}& 0\end{array}\right]$
${\mathbf{H}}_0=\left[\begin{array}{cccc}0& A_{3,1}& A_{3,2}& A_{3,3}\\ 0& B_{3,1}& B_{3,2}& B_{3,3}\\ A_{3,1}& A_{3,2}& A_{3,3}& 0\\ B_{3,1}& B_{3,2}& B_{3,3}& 0\end{array}\right]$

Notably, there is no x and y in ${\mathbf{H}}_2$, ${\mathbf{H}}_1$ and ${\mathbf{H}}_0$. Accordingly, it is easy to solve the system of polynomial equations by linear way [64].

Specifically, the to-be-solved eigenvector of this problem is $\mathit{v}={\left[\begin{array}{cccc}{x}^3& x^2& x& 1\end{array}\right]}^T$ and corresponding eigenvalue is $\lambda =y$. Furthermore, the quadratic eigenvalue problem can be transformed into a generalized eigenvalue problem, i.e., $\mathit{a}x=\lambda \mathit{b}x$ [65], which has been extensively studied [61,65,66,67]. Specifically,

$$\left({\lambda }^2{\mathbf{H}}_2+\lambda {\mathbf{H}}_1+{\mathbf{H}}_0\right)\mathit{v}=0\Rightarrow \left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\\ -{\mathbf{H}}_0& -{\mathbf{H}}_1\end{array}\right]\left[\begin{array}{c}\mathit{v}\\ \lambda \mathit{v}\end{array}\right]=\lambda \left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& {\mathbf{H}}_2\end{array}\right]\left[\begin{array}{c}\mathit{v}\\ \lambda \mathit{v}\end{array}\right]$$

(67)

Therefore, there will be 8 eigenvalues of this linear problem. The easiest way to solve this problem is using the Matlab function built-in polyeig3. SciPy also provides a function scipy.linalg.eig4 to solve generalized eigenvalue problems.