1. Introduction
Gravitational waves (GWs) are solutions to the linearized Einstein field equations, typically treated as small perturbations on a fixed background metric. In vacuum, these satisfy:
However, in the presence of a dynamic gravitational field, the background metric becomes non-trivial, and perturbations must account for curvature-induced distortions. Our work focuses on analyzing gravitational wave energy using affine parameters as opposed to proper length, arguing that active energy densities alter geodesic structure.
2. Affine Length and Energy Formalism
Let
be a manifold with metric
The geodesic equation in affine parameter
is:
The affine length
between two points on
is:
The total energy of the wave is given by an effective integration of the Isaacson energy-momentum tensor:
If the metric is expressed in affine-deformed form, then perturbation fields decay due to path length distortion, which leads to a reduction in this effective energy.
3. Metric Perturbation and Energy Drop Claim
Consider a binary system with masses
generating GWs. The amplitude h is proportional to the reduced mass and inverse distance:
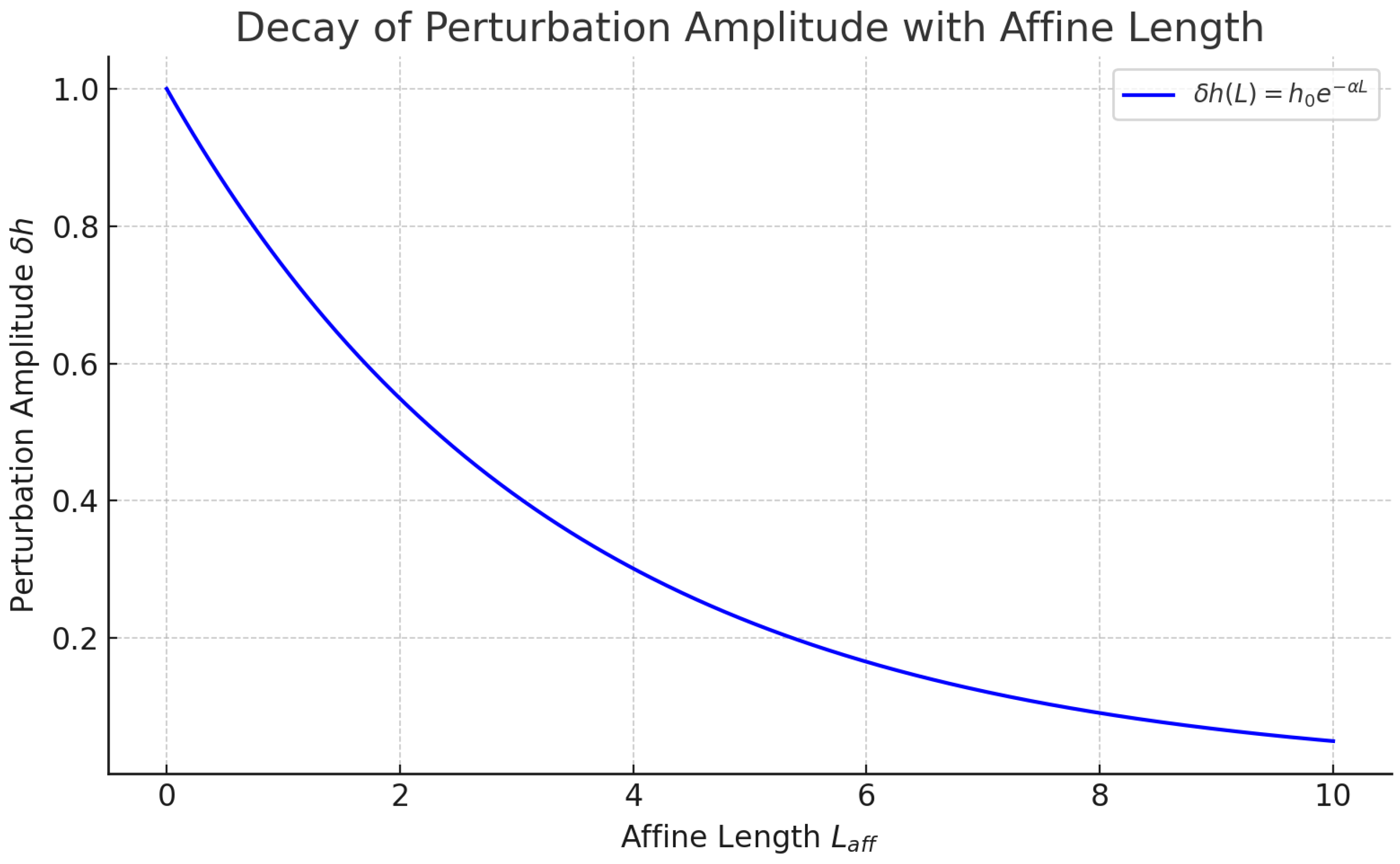
Let the background contain an energy density ρ(x). Suppose the wave traverses a region where the metric is deformed into affine form. The wavefront propagation suffers a decay:
Claim: If a region of spacetime is already expressed in an affine-deformed form, the energy of gravitational waves passing through it will drop significantly:
4. Perturbation Behavior in Curved Backgrounds
Define the perturbed metric:
In strongly curved regions, the Ricci tensor feeds back into the wave equation:
implies
5. Conclusion
We have demonstrated that in the presence of an active gravitational field, gravitational wave propagation undergoes significant distortion. The affine length governs the decay of wave amplitude and energy. Our variational framework supports the hypothesis that gravitational waves suffer energy loss when traversing highly curved, affine-transformed regions. Future work may involve simulations of wave propagation across dynamic metrics and comparison with observational data.
References
- Misner, C. W. , Thorne, K. S., & Wheeler, J. A. (1973). Gravitation.
- Isaacson, R. A. (1968). Gravitational Radiation in the Limit of High Frequency. Phys. Rev.
- Flanagan, E. E. , & Hughes, S. A. (2005). The basics of gravitational wave theory. New Journal of Physics. [CrossRef]
- Wald, R. M. (1984). General Relativity.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).