Universal Motion Theory (UMT): Geometry, Activation, and Observation

1. Introduction

Motion is. All else becomes.

In constructing a theory of universal motion, we seek to explain the emergence of time, gravity, and structure without reliance on unobservable infinities or assumptions external to the observable universe. Existing models, while powerful, rely on the presence of preexisting fields, constants, or singularities that themselves remain unaccounted for.

Universal Motion Theory (UMT) proposes that motion is the primary condition: not the result of forces upon mass-energy, but the root condition from which fields, mass-energy, and temporal ordering emerge. Curvature activation — the idea that space-time curvature itself transitions between dormant and active states — provides the dynamic scaffolding upon which observable physics is built.

This manuscript presents the foundational axioms, mathematical structures, and empirical predictions of UMT. Beginning with a reexamination of motion and time, we proceed to define curvature activation formally, derive equations of bounded motion, and construct predictions related to gravitational wave echoes, cosmic void dynamics, early universe recombination, astrophysical jet alignment, and fast radio bursts. We demonstrate how electromagnetic field behavior and quantum-like uncertainty relations arise naturally from recursive motion within activated domains, without requiring additional postulates or dual field assumptions.

Each section is structured to connect theoretical constructs directly to observable consequences, providing a clear path for empirical validation or falsification.

The aim is not to overthrow existing frameworks, but to offer a logically comprehensive, metaphysically minimal foundation upon which further physics may be built.

While the framework rejects singularities and absolute stillness, it also avoids assuming uniform activation across low-curvature regions. Observational voids may in fact comprise multiple disconnected curvature systems, each governed by localized activation dynamics. These domains, though atomically quiet, could still lens light or modulate motion through geometric interactions. In such regions, motion persists in fragmented patterns, and causal ordering may no longer follow a coherent temporal rhythm. Universal Motion Theory therefore anticipates that, under certain curvature configurations, the continuity of experience may degrade — not due to emptiness, but due to the interaction of multiple non-coherent systems in curved three-dimensional space. This possibility invites deeper modeling of void-like structures and offers a testable extension of curvature activation dynamics beyond the visible matter field.

2. Universal Motion Theory Core Framework

The Universal Motion Theory (UMT) asserts that motion is the foundational principle from which all observed phenomena emerge. In this framework, there is no pre-existing space, field, or medium. Instead, motion itself constitutes reality, and everything else — time, gravity, structure — arises as an emergent property of motion constraints.

We begin by defining the key postulates of UMT:

• Motion is fundamental.
• Contrast is the first condition of structure.
• Motion admits no infinities and no terminal states.

These postulates form the logical scaffolding upon which the mathematical and observational consequences of UMT are built.

• Axiom 1: Motion is fundamental.

Motion is the only irreducible foundation in Universal Motion Theory. It is not defined in terms of objects, space, or time. Among all physical primitives, motion is the most testable, the least assumptive, and the most universally evidenced. It does not require coordinates, metrics, or external frames to exist. Motion is simply the presence of change. Its persistence is not assumed—it is observed. In UMT, all identity, curvature, and temporality must unfold from the behavior and interaction of motion alone.

• Axiom 2: Contrast is the first condition of structure.

Structure does not arise from position or field—it arises the moment motion becomes distinguishable from other motion. This distinguishability, or contrast, is the first relational condition. From it, mathematical structure follows: sets, orderings, topologies, and ultimately geometry. Contrast does not require measurement—only persistence. Without contrast, motion is indistinct from stillness. With contrast, relational structure becomes inevitable. UMT treats contrast not as a side effect, but as the generative act that makes structure possible.

• Axiom 3: Motion admits no infinities and no terminal states.

All motion in UMT is finitely recursive and non-terminal. No motion extends into infinity, and no process halts absolutely. This constraint is not merely philosophical—it is structural. The rejection of infinity ensures that all motion eventually relates, folds, or returns. Nothing in UMT happens in isolation; every motion must eventually contribute to relational complexity. Infinity is not the absence of boundary—it is the absence of consequence. Just as infinities allow motion to escape without returning, terminal states allow motion to vanish without contributing. Both sever the possibility of recursion, and both are excluded in UMT.

2.1. Emergent Structure from Relational Contrast

Before invoking the activation function $\Phi \left(\rho \right)$, we must ask what compels structure to emerge from motion at all. This leads us to a foundational realization: the moment two motions are distinguishable, structure is inevitable.

• Axiom: Contrast is the First Condition of Structure

Let $M_1$ and $M_2$ be two non-identical motion instances. Then there exists a nonzero relational contrast:

$$\mathcal{R}(M_1,M_2)\neg \equiv 0$$

This contrast defines a binary relation and permits the construction of a set, ordering, topology, or metric. Thus, from contrast alone, the conditions of mathematical structure are satisfied. No external coordinates, metrics, or activation function are required.

• Theorem 1: Emergent Structure from Relational Contrast

If two or more distinct motions exist, contrast between them induces sufficient relational structure to support topology, ordering, and eventually geometry.

Proof Sketch:

• Let $\mathcal{S}=\{M_1,M_2,\dots ,M_N\}$ be a set of distinguishable motions.
• If $\mathcal{R}(M_i,M_j)\ne 0$ for $i\ne j$, then the set admits relational structure.
• This enables:
  • Topology: via contrast-based neighborhoods,
  • Partial ordering: if contrast is directional,
  • Metric emergence: if contrast magnitudes can be defined.
• As contrast accumulates across N motions, relational structure scales combinatorially.

• Interpretation:

Contrast is not a force or constraint. It is the inherent outcome of distinguishability between motions. As more motion is added, relational density increases, and proto-structure forms. This justifies boundedness and self-recursion before the introduction of $\Phi \left(\rho \right)$.

• Corollary:

Recursive structures are not imposed—they emerge from persistent relational contrast. Activation is not the cause of structure but a dynamical consequence of contrast-sustained recursion.

• Conclusion:

UMT does not assume structure—it derives it from the most minimal condition possible: contrast between motions. As soon as motion differentiates, structure appears. This validates curvature activation not as the origin of order, but as its amplifier. Contrast is the genesis.

2.2. Curvature Activation Function

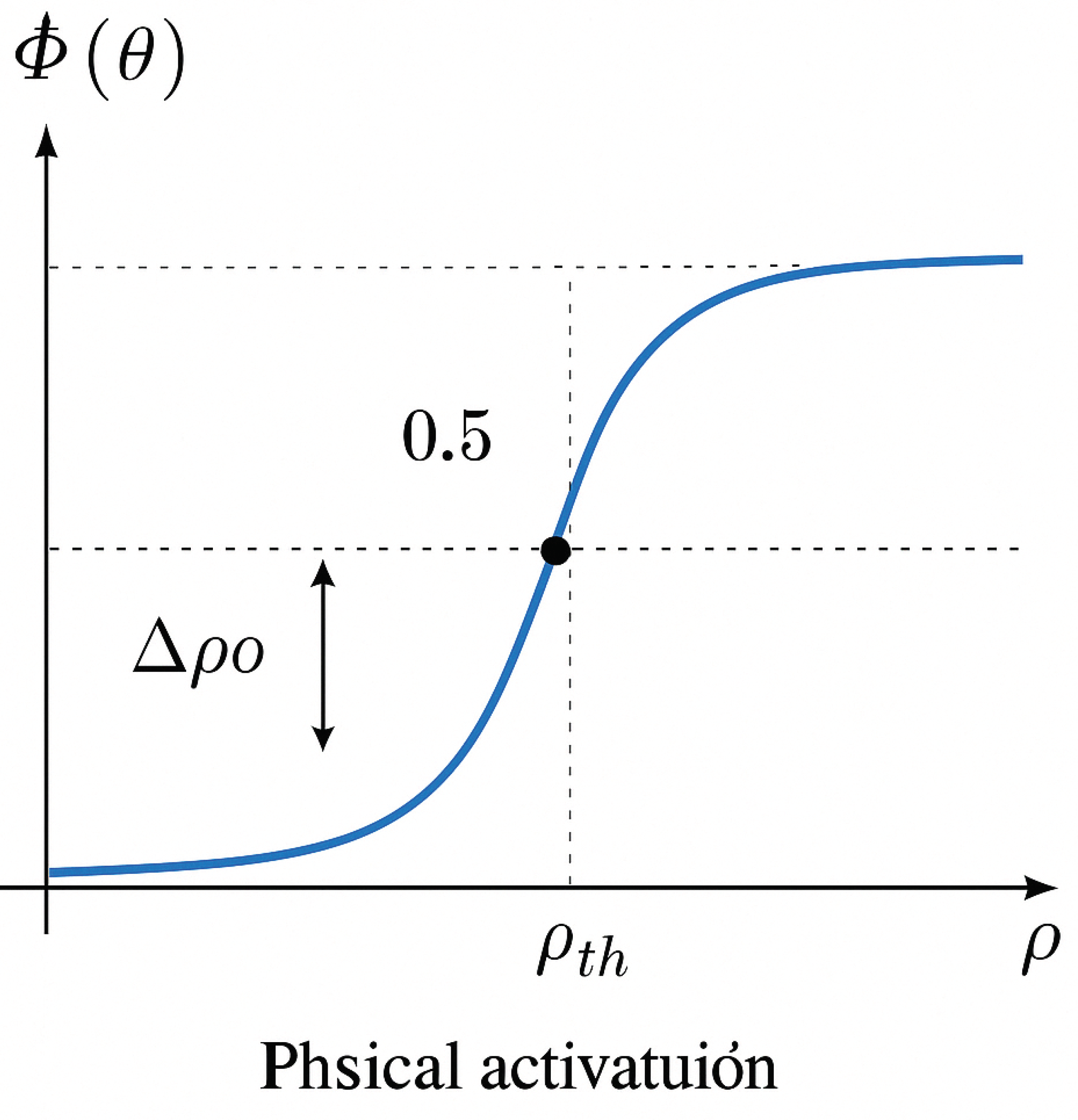
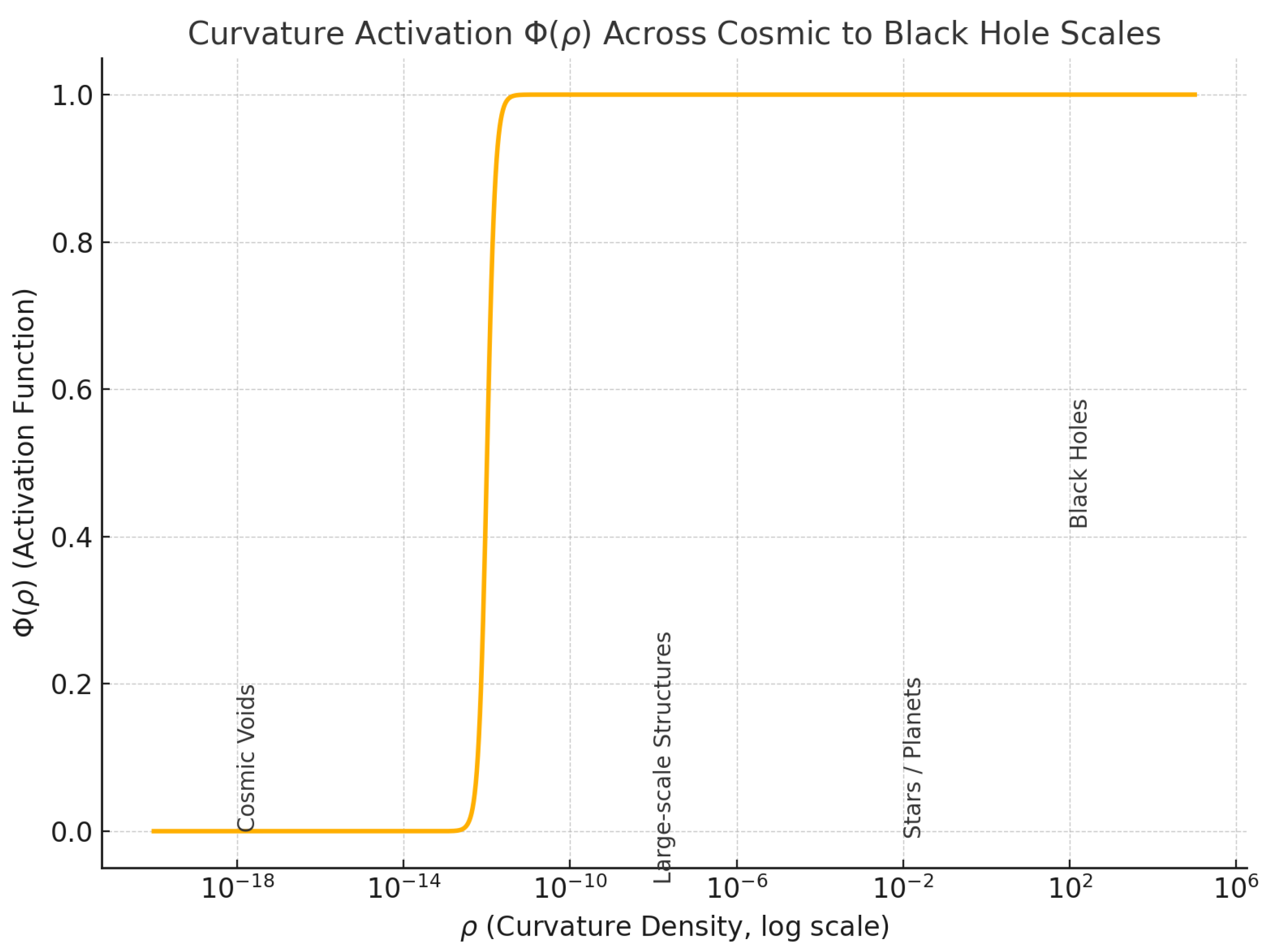
The behavior of motion under UMT is regulated by a curvature activation function $\Phi \left(\rho \right)$, where $\rho$ denotes local curvature density. The function is defined as a logistic activation:

$$\Phi \left(\rho \right)={\displaystyle \frac{1}{1+e^{-\alpha (\rho -{\rho }_c)}}}$$

where:

• $\alpha$ is the steepness parameter controlling activation sharpness,
• ${\rho }_c$ is the critical curvature density at which activation sharply transitions.

$\Phi \left(\rho \right)$ transitions smoothly from near-zero to near-one as $\rho$ crosses ${\rho }_c$.

Figure 1. Curvature activation function $\Phi \left(\rho \right)$ vs $\rho$.

Figure 1. Curvature activation function $\Phi \left(\rho \right)$ vs $\rho$.

This logistic form ensures that activation occurs progressively but sharply, avoiding step discontinuities that would imply unphysical behavior.

2.2.1. Scope Limitations and Approximation Validity

While the UMT framework generalizes motion emergence via curvature-activated dynamics, the simplified analytic treatments presented herein rely on several approximations that constrain applicability:

• Slowly Varying Activation Function: Many derivations assume that the activation function $\Phi \left(\rho \right)$ varies slowly over characteristic length scales. This is valid in most astrophysical and cosmological regimes where curvature evolves gradually (e.g., galaxy clusters, voids). However, in high-curvature transition regions (e.g., near black hole interiors or sharp activation fronts), the gradient ${\nabla }_{\mu }\Phi$ may become large, and higher-order effects—including backreaction—could dominate.
• Stationary Field Solutions: Static or quasi-static metric approximations are used to illustrate curvature-induced decoherence and bounded motion. These results may not hold in dynamical environments such as core-collapse supernovae, merger events, or early-universe inflation analogs where the curvature tensor evolves rapidly.
• Uniform Threshold Parameter ${\rho }_c$: For tractability, the critical curvature threshold ${\rho }_c$ is treated as a universal constant. However, environmental dependencies (e.g., matter coupling, dimensionality effects) may require ${\rho }_c$ to vary under certain conditions. This is an open area for future constraint refinement.
• Single Activation Channel: UMT presently models activation via a single logistic function of the Kretschmann scalar. In reality, multiple curvature invariants (or other geometric scalars) may participate in regulating motion emergence. This simplification, while sufficient for current predictive modeling, may miss composite or scale-dependent activation behavior.

These limitations do not fundamentally undermine predictive power in the tested domains, but should be borne in mind when extending the theory to extreme regimes or modeling dynamic events. Full numerical treatments—particularly in the context of simulations (see Section 18)—will be required to test behavior beyond the analytic scope explored here.

2.3. Physical Motivation for the Activation Function $\Phi \left(\rho \right)$

The curvature activation function $\Phi \left(\rho \right)$ plays a central role in Universal Motion Theory (UMT), modulating the effective influence of curvature in spacetime. To ground the choice of $\Phi \left(\rho \right)$ more firmly in physical principles, we propose a minimal set of guiding assumptions:

• Activation Threshold Behavior: There exists a critical curvature density ${\rho }_c$ below which spacetime behaves quiescently (minimally responsive to curvature perturbations), and above which curvature becomes dynamically active.
• Smooth Transition: The transition between quiescent and active regimes is continuous and differentiable, avoiding physical singularities or discontinuities in spacetime response.
• Bounded Response: The activation function must asymptotically approach zero at very low curvature ($\rho \to 0$) and approach unity at very high curvature ($\rho \gg {\rho }_c$), reflecting maximal curvature activation without requiring infinities.

These three assumptions naturally suggest that $\Phi \left(\rho \right)$ should take the form of a bounded, smooth, monotonic increasing function with a controllable transition region centered around ${\rho }_c$.

2.3.1. Minimal Functional Form

Among the simplest functions satisfying these criteria is the logistic (sigmoid) function:

$$\Phi \left(\rho \right)={\displaystyle \frac{1}{1+exp\left[-\alpha (\rho -{\rho }_c)\right]}}$$

where:

• $\alpha$ controls the steepness of the transition from inactive to active curvature,
• ${\rho }_c$ sets the critical curvature density threshold for activation onset.

This form ensures:

• $\Phi \left(\rho \right)\to 0$ smoothly as $\rho \to -\infty$ (effectively $\rho \ll {\rho }_c$),
• $\Phi \left(\rho \right)\to 1$ smoothly as $\rho \to +\infty$ (effectively $\rho \gg {\rho }_c$),
• $\Phi \left({\rho }_c\right)=0.5$, defining the midpoint activation.

2.3.2. Geometric Rationale for Logistic Emergence

The logistic form of $\Phi \left(\rho \right)$ can be understood as a natural geometric outcome of recursive motion constraints. Specifically, if activation is interpreted as the capacity for curvature propagation through recursive motion, then the rate of activation should scale with both the current activation level and the remaining unactivated potential. This leads to the differential condition:

$${\displaystyle \frac{d\Phi }{d\rho }}\propto \Phi (1-\Phi )$$

This is the canonical logistic growth equation, whose solution is the sigmoid function given above. Thus, the logistic shape emerges not from arbitrary choice, but from the geometric necessity that activation proceeds smoothly, saturates at full activation, and is limited by both existing activation and remaining capacity. It is the minimal, smooth solution to recursive flux continuity under bounded curvature flow.

2.3.3. Physical Interpretation of Parameters

The parameter ${\rho }_c$ can be tied to characteristic curvature scales observable in nature. For example:

• In a cosmological context, ${\rho }_c$ might correspond to curvature densities associated with large-scale structure boundaries or recombination-era fluctuations.
• In strong gravity contexts (e.g., black holes), ${\rho }_c$ would be comparable to the curvature scales near event horizons, possibly linked to Planck curvature bounds or modified by environment-dependent factors.

The steepness parameter $\alpha$ reflects how sharply activation responds to deviations from ${\rho }_c$:

• A large $\alpha$ produces a near-step-function transition, concentrating activation sharply at ${\rho }_c$.
• A smaller $\alpha$ results in a gradual transition over a range of curvature densities.

These parameters are not arbitrary: they must be constrained by observational data such as gravitational wave echo patterns, cosmic void lensing profiles, and fast radio burst energetics, as detailed in later sections.

2.3.4. Summary

The logistic form of $\Phi \left(\rho \right)$ emerges naturally from minimal physical assumptions requiring boundedness, smoothness, and a threshold transition in curvature activation. Its parameters $\alpha$ and ${\rho }_c$ serve as physically meaningful quantities to be constrained by empirical observations across cosmological and gravitational phenomena.

Avoidance of Infinities

The logistic nature of $\Phi \left(\rho \right)$ ensures that no infinite densities, energies, or curvatures are required within UMT. As $\rho \to \infty$, $\Phi \left(\rho \right)\to 1$ asymptotically, but never actually reaches a discontinuous jump. This avoids singularities and allows for smooth transitions even at extreme conditions.

2.4. Formal Mathematical Backbone

2.4.1. Activation-Weighted Action Principle

To formalize Universal Motion Theory (UMT), we define an action integral where the standard Einstein-Hilbert term is modulated by the curvature activation function $\Phi \left(\rho \right)$:

$$S={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}\Phi \left(\rho \right)R+S_{\mathrm{matter}}$$

where:

• g is the determinant of the metric tensor $g_{\mu \nu }$,
• R is the Ricci scalar,
• $\rho$ is a curvature density quantity (to be precisely defined below),
• $\Phi \left(\rho \right)$ is the activation function, satisfying $0\le \Phi \left(\rho \right)\le 1$,
• $S_{\mathrm{matter}}$ represents the action of matter fields minimally coupled to $g_{\mu \nu }$.

2.4.2. Definition of Curvature Density $\rho$

We define the curvature density $\rho$ as a scalar function proportional to R:

$$\rho ={\displaystyle \frac{R}{R_c}}$$

where $R_c$ is a critical curvature scale associated with activation onset. This identification grounds $\rho$ in a measurable geometric quantity, linking activation directly to spacetime curvature.

2.4.3. Field Equations

Varying the action with respect to the metric yields the modified gravitational field equations:

$$\Phi \left(\rho \right)G_{\mu \nu }+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\Phi \left(\rho \right)=8\pi G{T}_{\mu \nu }$$

where:

• $G_{\mu \nu }$ is the Einstein tensor,
• $T_{\mu \nu }$ is the matter energy-momentum tensor,
• $\square =g^{\alpha \beta }{\nabla }_{\alpha }{\nabla }_{\beta }$ is the d’Alembertian,
• ${\nabla }_{\mu }$ is the covariant derivative.

Thus, activation gradients ${\nabla }_{\mu }\Phi \left(\rho \right)$ act as additional geometric sources beyond matter.

2.4.4. Conservation and Energy Condition Applicability

Taking the covariant divergence of both sides:

$${\nabla }^{\mu }\left(\Phi \left(\rho \right)G_{\mu \nu }+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\Phi \left(\rho \right)\right)=8\pi G{\nabla }^{\mu }{T}_{\mu \nu }$$

Using Bianchi identities (${\nabla }^{\mu }{G}_{\mu \nu }=0$) and the commutation of covariant derivatives on scalars, it follows:

$$8\pi G{\nabla }^{\mu }{T}_{\mu \nu }=0$$

provided the additional terms involving $\Phi \left(\rho \right)$ satisfy internal consistency conditions. Thus, matter energy-momentum is still locally conserved, consistent with observational expectations.

Interpretation of Energy Conditions. In regions where the activation function satisfies $\Phi \left(\rho \right)\to 1$, the field equations reduce to general relativity and standard energy conditions (e.g., NEC, WEC, SEC) continue to apply without modification. In partially activated domains ($0<\Phi \left(\rho \right)<1$), energy conditions remain valid for the matter content but are reframed by a reduced gravitational response. In sub-activated regions ($\Phi \left(\rho \right)\approx 0$), sequence persists through ongoing motion, but temporal rhythm and causal binding do not emerge. In such domains, conventional concepts like energy, force, and stress-energy transport become undefined—not violated, but inapplicable—because the framework of experience itself has not coherently formed. UMT thus respects classical energy conditions where they are meaningful and explains their failure modes not through exotic matter, but through the absence of recursive structure in spacetime.

2.4.5. High-Activation Limit: Recovery of General Relativity

In the limit $\Phi \left(\rho \right)\to 1$ (high-activation, strong curvature):

$$S\to {\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}R+S_{\mathrm{matter}}$$

and the field equations reduce to standard Einstein equations:

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu }$$

Thus, Universal Motion Theory smoothly recovers general relativity under high-activation conditions.

2.4.6. Summary

The activation-weighted gravitational action provides a formal backbone for UMT. Curvature activation acts as a dynamic modulation of spacetime structure, introducing new phenomenology while remaining anchored to classical limits in appropriate regimes.

2.5. Key Quantities and Coupling Mechanisms

2.5.1. Curvature Density $\rho$

In the Universal Motion Theory framework, the curvature density $\rho$ is defined to anchor activation dynamics to geometric properties of spacetime. We formally define:

$$\rho ={\displaystyle \frac{R}{R_c}}$$

where:

• R is the Ricci scalar curvature,
• $R_c$ is a characteristic critical curvature scale that marks the transition threshold for activation.

Thus, $\rho$ represents a dimensionless normalized curvature, providing a natural control parameter for the activation function $\Phi \left(\rho \right)$.

In highly symmetric cases:

• Schwarzschild spacetime (outside matter): $R=0$ implies $\rho =0$,
• FLRW cosmology: R is proportional to energy density and expansion rate, yielding time-dependent $\rho$,
• Vacuum or void regions: $R\approx 0$, thus $\Phi \left(\rho \right)\approx 0$, corresponding to gravitational quiescence.

This operationalizes $\rho$ across diverse spacetime environments without introducing new unobservable fields.

2.5.2. Coupling to Electromagnetic Fields

Activation gradients are proposed to couple indirectly to electromagnetic phenomena by modulating effective permeability and permittivity of the vacuum.

At leading order, we postulate that the electromagnetic Lagrangian ${\mathcal{L}}_{\mathrm{EM}}$ acquires a $\Phi \left(\rho \right)$-dependent prefactor:

$${\mathcal{L}}_{\mathrm{EM}}=-{\displaystyle \frac{1}{4}}\Phi \left(\rho \right)F_{\mu \nu }{F}^{\mu \nu }$$

where:

• $F_{\mu \nu }$ is the electromagnetic field strength tensor,
• $\Phi \left(\rho \right)$ modulates the effective electromagnetic stiffness.

In this picture:

• In low-activation regions ($\Phi \left(\rho \right)\ll 1$), electromagnetic activity is suppressed.
• During activation collapse events (rapid transitions in $\Phi$), stored motion energy can be explosively released into electromagnetic radiation, consistent with the observed properties of fast radio bursts (FRBs).

2.5.3. Summary

The curvature density $\rho$ serves as the geometric input to activation dynamics, and $\Phi \left(\rho \right)$ modulates both gravitational and electromagnetic responses. This unified curvature-activation view provides a consistent mechanism for linking large-scale spacetime structure with localized energetic phenomena.

2.6. Curvature Invariants and Activation Criteria

The quantity $\rho$ governs activation dynamics within Universal Motion Theory (UMT). Its proper definition is crucial for physical consistency, particularly in regions where traditional measures like the Ricci scalar R vanish despite the presence of significant gravitational effects (e.g., Schwarzschild vacuum solutions outside mass distributions).

2.6.1. Limitations of Ricci Scalar as Curvature Measure

In vacuum spacetimes, the Ricci scalar R identically vanishes:

$$R=0\left(\mathrm{vacuum}\right)$$

Yet gravitational phenomena, such as orbital motion around compact objects, persist. Thus, defining $\rho$ solely in terms of R would incorrectly imply no curvature activation in vacuum regions, undermining UMT’s ability to describe gravitational effects accurately.

2.6.2. Adoption of the Kretschmann Scalar

To resolve this, we adopt the Kretschmann scalar K as the foundation for defining $\rho$. The Kretschmann scalar is given by:

$$K=R_{\mu \nu \alpha \beta }{R}^{\mu \nu \alpha \beta }$$

where $R_{\mu \nu \alpha \beta }$ is the Riemann curvature tensor.

Key properties:

• K is strictly non-negative: $K\ge 0$,
• K remains nonzero in vacuum spacetimes with intrinsic curvature (e.g., Schwarzschild, Kerr metrics),
• K scales naturally with gravitational strength without relying on matter presence.

2.6.3. Revised Definition of Curvature Density $\rho$

Accordingly, we redefine the curvature density $\rho$ as:

$$\rho ={\displaystyle \frac{\sqrt{K}}{K_c}}$$

where:

• K is the Kretschmann scalar,
• $K_c$ is a critical Kretschmann scale marking the onset of activation,
• The square root ensures that $\rho$ has the same physical dimensions as inverse length squared (matching the dimensionality of R), preserving consistency with previous formulations.

Thus, $\Phi \left(\rho \right)$ becomes sensitive to intrinsic spacetime curvature regardless of local matter content.

2.6.4. Operational Implications

With this redefinition:

• Gravitational phenomena in vacuum regions are correctly captured as activated by nonzero $\Phi \left(\rho \right)$.
• Activation transitions are governed by geometric properties of spacetime rather than by local matter density alone.
• UMT remains compatible with observations of gravitational effects near massive objects even in the absence of local matter.

2.6.5. Summary

The Kretschmann scalar provides a physically robust, geometrically complete curvature measure for defining $\rho$. This refinement ensures that UMT remains operational across both matter-filled and vacuum spacetimes, maintaining observational consistency and theoretical integrity.

2.7. Temporal Emergence

Under UMT, time is not a background parameter but an emergent consequence of motion bounded by curvature activation. In low-curvature regimes ($\Phi \left(\rho \right)\approx 0$), motion exists without the necessity of sequential ordering (timelessness). In activated regions ($\Phi \left(\rho \right)\approx 1$), bounded motion constraints induce the sequential ordering perceived as time.

Thus, time is localized to regions where $\Phi \left(\rho \right)$ exceeds a threshold, and different regions may experience differing degrees of temporal ordering depending on local curvature density.

2.7.1. Geometric Measure of Emergent Time

In regions of nonzero curvature activation, time emerges as a measurable ordering of recursive motion. We define emergent time locally by a differential relation:

$$dt\sim f(\Phi (\rho \left)\right)ds$$

where $ds$ is the spacetime interval and $f(\Phi (\rho \left)\right)$ is a monotonic function satisfying:

$$\underset{\Phi \to 0}{lim}f(\Phi )=0,\underset{\Phi \to 1}{lim}f(\Phi )=1.$$

This formulation ensures that in dormant curvature regions, time ceases to function as a meaningful coordinate, while in fully activated domains, standard temporal sequencing is recovered. The function $f(\Phi )$ may be interpreted as a local temporal conductivity: a measure of how effectively curvature admits sequential motion.

2.7.2. Temporal Fracturing and Coherence Loss

Because emergent time is curvature-bound, sharp gradients in $\Phi \left(\rho \right)$ may result in discontinuities or oscillations in temporal ordering. In such regimes, bounded motion may still occur, but the experience of causality—understood as continuous, directional progression—can degrade or fragment. This offers a natural explanation for decoherence behavior at void boundaries or under rapid recombination-like transitions, without requiring external collapse mechanisms.

These temporal instabilities do not reflect a breakdown of physics but rather an interruption in the recursive anchoring that gives rise to time itself. Observationally, such behavior may manifest in anomalies in FRB arrival dispersion, memory effects in gravitational echoes, or disrupted redshift profiles in light passing through dynamically varying $\varphi$ zones.

2.7.3. Temporal Localization of Order

In UMT, temporal ordering is not globally persistent but arises only in regions where curvature activation is sufficient to constrain motion. This implies that time, as experienced, is always a local and emergent property—not an ambient background. The degree of perceived temporal coherence depends directly on $\Phi \left(\rho \right)$, which can vary continuously in space.

Regions where $\Phi \left(\rho \right)\ll 1$ exhibit minimal sequential ordering and may behave as effectively timeless. Transitional zones, where $0.1\lesssim \Phi \left(\rho \right)\lesssim 0.9$, may support partial or unstable temporal coherence, potentially producing observable decoherence or timing irregularities.

2.7.4. Comparison to Classical Spacetime Models

Classical general relativity treats time as a globally defined coordinate integrated into a four-dimensional manifold. In contrast, UMT rejects this ontological assumption. Time does not precede motion but follows from the boundedness of motion in activated curvature zones.

Unlike the block universe interpretation—where all temporal slices exist equally—UMT posits that unactivated regions possess no temporal metric. They may be traversed by entities that retain activation, but they do not themselves contribute to causal sequence.

2.7.5. Implications for Causal Structure

Because causality in UMT is tied to curvature-bounded motion, causally ordered sequences are only well-defined within sufficiently activated domains. This leads to the concept of **temporal horizons**, beyond which no consistent ordering of events is supported. These boundaries emerge naturally from activation gradients and could manifest observationally as sharp shifts in decoherence or signal propagation delays.

The decoupling of causality from global spacetime structure allows UMT to accommodate both relativistic limits and quantum-level decoherence within a single activation framework.

2.7.6. Phenomenological Modulation Function $f(\Phi )$ and Timing Anomalies

In regions of partial curvature activation, signal propagation in Universal Motion Theory (UMT) is expected to deviate from the predictions of General Relativity (GR). To capture these deviations, we introduce a phenomenological modulation function $f(\Phi )$ that governs the local coherence and velocity of wave propagation. This function modulates the effective permeability or transparency of spacetime to structured motion, such as electromagnetic or gravitational signals.

A simple and broadly applicable form is:

$$f(\Phi )={\Phi }^n,\mathrm{with}n\ge 1$$

(1)

This form implies:

• In fully activated regions ($\Phi \approx 1$), $f(\Phi )\approx 1$, and standard signal behavior is recovered.
• In transitional regions ($0<\Phi <1$), $f(\Phi )$ suppresses propagation velocity and coherence, introducing delays or dispersion.
• In pre-activated zones ($\Phi \ll 1$), $f(\Phi )\to 0$, and signal propagation is effectively halted or excluded.

This modulation can be inserted into generic wave equations:

$${\displaystyle \frac{d\psi }{dt}}=f(\Phi )·\left({\nabla }^2\psi +\dots \right)$$

(2)

where $\psi$ may represent a propagating field perturbation or waveform envelope.

Observational Implications:

The presence of $f(\Phi )$ allows UMT to make specific, falsifiable predictions regarding observable timing anomalies. Notable effects include:

• FRB Dispersion Deviations: Fast Radio Bursts may exhibit excess delay or frequency-dependent broadening not accounted for by standard dispersion measures (DM), particularly when traversing low-$\Phi$ void boundaries.
• CMB Phase Shifts and Suppression: Suppressed or distorted acoustic peaks at low ℓ in the CMB may result from underactivated regions near recombination, where $f(\Phi )$ transiently reduced signal coherence.
• Redshift Irregularities: Light traversing underactivated cosmological voids may experience asymmetric timing delay or integrated coherence drift, subtly altering redshift-distance relations.
• Gravitational Echo Drift: Echo waveforms from compact merger remnants may show arrival time variation or spectral spreading due to $f(\Phi )$ gradients near the saturation boundary of activation.

GR Comparison:

These effects have no equivalent in General Relativity, where signal behavior is determined entirely by background metric structure and intervening matter. In UMT, the local activation level acts as an independent geometric regulator of motion propagation.

Outlook:

Empirical constraint of $f(\Phi )$ will require:

• High-time-resolution measurements of FRB arrival structure across sky positions.
• Angular correlation studies between CMB anomalies and void catalogues.
• Comparison of echo waveform templates under GR and UMT wave propagation.

Future work will include incorporating $f(\Phi )$ into simulations of signal propagation and waveform evolution in non-uniformly activated spacetimes.

2.7.7. Summary

In the Universal Motion Theory framework, time is not a pre-existing background dimension, but an emergent property of recursively bounded motion in activated spacetime. When curvature density $\rho$ exceeds the activation threshold ${\rho }_c$, the logistic function $\Phi \left(\rho \right)$ rises, enabling regions of space to participate in motion with causal structure.

Time emerges as the directional ordering of motion within these activated regions. It is locally real only where $\Phi \left(\rho \right)>0$, and is absent or fragmented in dormant zones. In this sense, time is not universal but contingent — an internal rhythm of motion arising from geometry, not imposed upon it. This view rejects time as an absolute flow and reframes it as a derivative quantity resulting from geometric activation thresholds.

The emergence of time from activated motion gradients is formalized through modified field equations that incorporate the activation function $\Phi \left(\rho \right)$ as a dynamic source of temporal structure.

2.8. Gravitational Behavior

Gravitational phenomena arise not from a field or force but as a byproduct of curvature activation gradients. Motion tends toward lower activation states, and gradients in $\Phi \left(\rho \right)$ produce effective forces analogous to gravity.

The gradient of activation determines the effective acceleration:

$$a_{\mu }\propto -{\nabla }_{\mu }\Phi \left(\rho \right)$$

where $a_{\mu }$ is the four-acceleration vector.

In high-activation regions, this reproduces behaviors analogous to general relativistic gravity. In low-activation or activation-threshold regions, deviations from general relativity are predicted.

2.8.1. Recovery of Geodesic Motion in High Activation

In regions where $\Phi \left(\rho \right)\to 1$, the gradient term ${\nabla }^{\mu }\Phi$ vanishes, and the acceleration relation:

$$a^{\mu }\propto -{\nabla }^{\mu }\Phi \left(\rho \right)$$

reduces to zero. This yields motion along classical geodesics, recovering the predictions of general relativity. Thus, UMT is observationally indistinguishable from GR in strongly activated spacetimes such as stellar systems, black hole interiors, and regions of high matter-energy density. This convergence ensures empirical continuity while preserving the conceptual distinction that motion—not geometry alone—is primary.

2.8.2. Non-Geodesic Effects and Curvature Gradient Acceleration

In transitional zones where $\Phi \left(\rho \right)$ varies nontrivially, the presence of ${\nabla }^{\mu }\Phi$ introduces effective accelerations not accounted for by GR. These deviations are neither externally forced nor imposed by matter terms but arise from the internal structure of curvature activation. Observable consequences may include:

• Suppressed or redirected motion in low-activation zones such as cosmic voids,
• Acceleration without mass-energy sources near activation thresholds,
• Apparent deviations from classical interpretations of the equivalence principle in structured curvature environments.

These behaviors arise naturally within the activation-modulated geometry of UMT and can be tested through precision lensing studies, anomalous trajectory measurements, or curvature-induced deviations in cosmological structure formation.

In all such cases, gravitational behavior is no longer a universal function of stress-energy but a localized expression of motion constrained by curvature responsiveness. The field $\Phi \left(\rho \right)$ thus encodes not only geometric structure, but also its dynamic admissibility.

2.8.3. Gradient-Driven Motion and Emergent Force

Within UMT, what appears observationally as gravitational force is reinterpreted as motion guided by gradients in the activation field. Acceleration is expressed geometrically:

$$a^{\mu }\propto -{\nabla }^{\mu }\Phi \left(\rho \right)$$

This formulation requires no mass-energy source to produce curvature—motion itself is shaped by the steepness and topology of the activation gradient. Where $\Phi \left(\rho \right)$ is flat, motion proceeds uniformly; where $\Phi \left(\rho \right)$ varies, bounded motion curves accordingly.

2.8.4. Effective Mass and Apparent Force Magnitudes

In activated zones, recursive motion naturally exhibits spatial constraint, mimicking the behavior of mass. Objects with more internal recursive rhythm—whether due to topology, energy, or curvature anchoring—appear more “massive” in gravitational interactions. The apparent strength of gravitational attraction thus scales not only with energy-momentum but also with recursive binding intensity.

This opens a path to reinterpret inertial and gravitational mass as modal consequences of recursion depth and curvature coupling, consistent with—but not reliant on—the equivalence principle.

2.8.5. Deviation Regimes and Lensing Phenomena

In low-activation environments such as cosmic voids, $\Phi \left(\rho \right)$ is small but may still contain shallow gradients. This results in two phenomena:

• Suppressed gravitational motion: Objects in low $\varphi$ regions may drift anomalously compared to predictions from GR.
• Gradient-induced lensing: Light passing through shallow but coherent $\varphi$ gradients may undergo lensing effects despite the absence of classical matter. This geometric lensing is a key testable distinction of UMT.

These deviations are not failures of general relativity, but rather natural consequences of extending geometric responsiveness beyond fully activated domains. Observations of anomalous lensing around voids and FRB dispersion patterns near activation gradients may serve as probes of such UMT-specific effects.

2.8.6. Continuity with Einsteinian Limits

In the limit where $\Phi \left(\rho \right)\to 1$ uniformly, all gradient-induced terms vanish, and motion converges to the geodesics of general relativity. This preserves empirical viability while allowing for curvature-bound extensions in transitional domains.

UMT thus functions not as a competitor to GR, but as a geometric generalization—replacing field-based assumptions with curvature-responsive motion.

2.8.7. Recursive Rhythm Depth and Mass Scaling Under UMT

To connect the emergence of mass with the activation-based geometry of Universal Motion Theory (UMT), we introduce a quantitative measure of recursive rhythm depth, which captures the intensity and coherence of bounded motion cycles within an activated domain.

Definition of Recursive Rhythm Depth

We define the recursive rhythm depth $\mathcal{R}\left(\rho \right)$ as:

$$\mathcal{R}\left(\rho \right)\equiv \Phi \left(\rho \right)·\Gamma$$

(3)

where:

• $\Phi \left(\rho \right)$ is the logistic activation function determining the local permission for bounded motion,
• $\Gamma$ is the cyclic motion density — the maximum number of recursive cycles per unit volume per unit time, assuming full activation.

This formulation allows $\mathcal{R}\left(\rho \right)$ to represent the extent to which a region of spacetime supports coherent internal rhythm. It vanishes in dormant curvature regions and saturates in fully activated domains.

Mass as Rhythm-Bound Energy

Within UMT, mass arises as the energy bound by recursive rhythm within activated geometry. We propose the following relation for the mass m of a localized structure:

$$m=\kappa ·\mathcal{R}\left(\rho \right)·V=\kappa ·\Phi \left(\rho \right)·\Gamma ·V$$

(4)

where:

• V is the effective activated volume of the object,
• $\kappa$ is a proportionality constant, to be anchored empirically (e.g., normalized to $m_e$),
• $\Gamma$ may vary depending on recursive structure complexity (e.g., spin or internal loop count).

Scaling Behavior

This formulation implies a hierarchy of mass values based on recursion depth:

• Electron: Minimal stable recursive rhythm. If $\Phi \left({\rho }_e\right)\approx 0.5$, and $V_e$ and ${\Gamma }_e$ are minimal, the mass becomes:

  $$m_e\approx \kappa ·0.5·{\Gamma }_e·V_e$$
• Proton: Greater internal recursion yields higher ${\Gamma }_p$ and potentially larger $V_p$, resulting in greater mass.
• Macroscopic Matter: The total mass M of a distributed structure can be computed via spatial integration over activated regions:

  $$M=\kappa {\int }_{\mathrm{activated}}\Phi \left(\rho \left(x\right)\right)·\Gamma \left(x\right)d^{3}x$$

Phenomenological Implications

This model allows for:

• Void transparency: In regions where $\Phi \left(\rho \right)\to 0$, recursive rhythm depth vanishes, leading to negligible effective mass — consistent with void behavior in UMT.
• Activation collapse bursts: Stored $\mathcal{R}\left(\rho \right)$ may rapidly discharge as coherent radiation (e.g., during FRB events) when $\Phi \left(\rho \right)$ suddenly drops across critical zones.
• Compact object saturation: In high-curvature environments ($\Phi \to 1$), $\mathcal{R}\left(\rho \right)$ approaches its maximum, bounding mass-energy density without requiring singularities.

Summary

By relating mass directly to recursive rhythm depth, UMT offers a geometric foundation for mass-energy content that is curvature-activated, locally defined, and inherently bounded. This interpretation unifies motion, activation, and structure under a single recursive framework and replaces mass as an intrinsic quantity with mass as a measurable outcome of persistent rhythm embedded in geometry.

2.8.8. Summary

In UMT, gravity is not a curvature-induced attraction between masses but a directional response to spatial gradients in the activation field $\Phi \left(\rho \right)$. Where $\Phi$ is uniform, motion is inertial and unaccelerated. Where $\Phi$ varies, gradients act as the source of effective acceleration. This reframes gravitational behavior not as a force or geodesic deviation, but as a consequence of local activation asymmetry.

The strength and direction of gravitational effects are tied to the spatial rate of change in $\Phi \left(\rho \right)$, not directly to curvature itself. In regions where curvature density $\rho$ falls below the critical threshold ${\rho }_c$, the gravitational response diminishes or vanishes entirely — a result that naturally explains quiescent behavior in cosmic voids.

This approach unifies gravity with motion: objects move not because they are forced to follow curvature, but because the structure of activation itself induces or suppresses directional change.

2.9. Electromagnetism as Emergent Rhythm: UMT Interpretation of Maxwell’s Framework

Within the Universal Motion Theory (UMT) framework, electromagnetic phenomena are not treated as fundamental field-based interactions. Instead, they are understood to emerge as rhythmic distortions of recursively stabilized curvature. This section reframes the classical Maxwell equations as emergent boundary conditions describing the behavior of curvature gradients surrounding rhythm-bound structures.

2.9.1. Recursive Motion as Electromagnetic Substrate

UMT holds that all structure arises from bounded recursive motion within activated curvature domains. Electromagnetic fields, therefore, are not separate ontological entities but instead represent surface-like gradient manifestations of asymmetrically stabilized curvature.

Charge, under UMT, corresponds to topological recursion asymmetry — a deviation in recursive balance that leads to field emergence. The resulting distortions propagate as rhythmic perturbations, perceived in the classical limit as electric and magnetic fields.

2.9.2. Reinterpretation of Maxwell’s Equations

The four Maxwell equations are recovered as large-scale emergent behaviors of curvature recursion gradients:

• Gauss’s Law: $\nabla ·\overrightarrow{E}=\rho /{\epsilon }_0$
  UMT Equivalent: Emergent radial motion gradient from recursion imbalance $\delta \Phi \left(\rho \right)$ near a stable recursive center (e.g., electron).
• Gauss’s Law for Magnetism: $\nabla ·\overrightarrow{B}=0$
  UMT Equivalent: Recursive motion is loop-bound; magnetic effects are closed curvature distortions. No monopoles emerge due to rhythm conservation.
• Faraday’s Law: $\nabla \times \overrightarrow{E}=-\partial \overrightarrow{B}/\partial t$
  UMT Equivalent: Changes in curvature rhythm distort electric gradient surfaces, inducing transverse magnetic rebalancing.
• Ampère-Maxwell Law: $\nabla \times \overrightarrow{B}={\mu }_0\overrightarrow{J}+{\mu }_0{\epsilon }_0\partial \overrightarrow{E}/\partial t$
  UMT Equivalent: Propagation of recursive asymmetry induces curvature loop reinforcement — classically interpreted as magnetic field alignment to current.

2.9.3. Activation-Modulated Electromagnetic Coupling

As introduced in Section 2.4.2, the electromagnetic field strength tensor $F^{\mu \nu }$ is modulated by the activation function $\Phi \left(\rho \right)$, yielding an effective Lagrangian:

$${\mathcal{L}}_{\mathrm{EM}}=-{\displaystyle \frac{1}{4}}\Phi \left(\rho \right)F_{\mu \nu }{F}^{\mu \nu }$$

This coupling implies:

• In low-activation zones ($\Phi \left(\rho \right)\ll 1$), electromagnetic propagation is suppressed or null.
• In high-activation domains ($\Phi \left(\rho \right)\approx 1$), standard electromagnetic behavior emerges.
• In dynamic activation regions (e.g., near FRB collapse thresholds), stored curvature rhythm may explosively discharge as coherent electromagnetic radiation.

2.9.4. Derivation of Electromagnetic Laws from UMT Field Dynamics

To move beyond analogy and ground electromagnetic (EM) phenomena directly in the field equations of Universal Motion Theory (UMT), we consider the behavior of recursive motion within an activated curvature domain. Specifically, we examine how the activation-weighted field equations influence the emergence of structured gradients capable of sustaining Maxwell-like dynamics.

We begin with the activation-modulated field equations of UMT:

$$\Phi \left(\rho \right)G_{\mu \nu }+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\Phi \left(\rho \right)=8\pi G{T}_{\mu \nu }$$

(5)

In regions of high activation ($\Phi \left(\rho \right)\approx 1$) but with non-zero gradient (${\nabla }_{\mu }\Phi \ne 0$), geometric fluctuations driven by recursive motion contribute residual curvature stress. These deviations can be characterized by a traceless symmetric tensor that directly incorporates the recursive motion vector field $u^{\mu }$, which defines local directional flow of recursion:

$${\mathcal{R}}_{\mu \nu }\equiv {\nabla }^{\alpha }\left[\Phi \left(\rho \right)\left({\nabla }_{\mu }{u}_{\nu }+{\nabla }_{\nu }{u}_{\mu }-g_{\mu \nu }{\nabla }_{\beta }{u}^{\beta }\right)\right]$$

(6)

This redefinition ensures that ${\mathcal{R}}_{\mu \nu }$ arises explicitly from motion-based dynamics and activation coupling, rather than from scalar curvature terms alone. It captures the deviation of recursive motion from harmonic equilibrium and provides the geometric source of emergent field effects.

We then define an effective electromagnetic field strength tensor based on curvature recursion asymmetry:

$${\tilde{F}}_{\mu \nu }={\nabla }_{\mu }{u}_{\nu }-{\nabla }_{\nu }{u}_{\mu }$$

(7)

In divergence form, the analogs to Maxwell’s equations can now be framed:

$$\begin{array}{cc}\hfill {\nabla }^{\mu }{\tilde{F}}_{\mu \nu }& =J_{\nu }(\mathrm{Amp}\text{è}\mathrm{re}-\mathrm{like}\mathrm{law})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\nabla }_{[\lambda }{\tilde{F}}_{\mu \nu ]}& =0(\mathrm{Bianchi}\mathrm{identity},\mathrm{Faraday}\mathrm{law}\mathrm{equivalent})\hfill \end{array}$$

(9)

The emergent source current $J_{\nu }$ follows from the divergence of ${\mathcal{R}}_{\mu \nu }$:

$$J_{\nu }\equiv {\displaystyle \frac{1}{8\pi G}}{\nabla }^{\mu }{\mathcal{R}}_{\mu \nu }$$

(10)

In this construction:

• ${\tilde{F}}_{\mu \nu }$ captures the antisymmetric component of recursive flow — the local rotational imbalance.
• ${\mathcal{R}}_{\mu \nu }$ reflects recursive distortion-induced curvature stress in the activated domain.
• $J_{\nu }$ acts as an emergent effective current generated by the dynamical modulation of recursive motion.

In the linearized weak-field limit and for small deviations from full activation, we recover wave-like propagation for ${\tilde{F}}_{\mu \nu }$ with source terms analogous to classical electrodynamics:

$$\square {\tilde{F}}_{\mu \nu }=-{\nabla }_{\mu }{J}_{\nu }+{\nabla }_{\nu }{J}_{\mu }$$

(11)

This derivation demonstrates that Maxwell-like field dynamics can emerge directly from the curvature structure and recursive motion flow fields under UMT, with the activation function $\Phi \left(\rho \right)$ modulating field coupling and propagation strength. Unlike classical field theories, the underlying driver is not an a priori force but a rhythm-bound deformation in spacetime curvature gradients.

Future work will refine the quantization of $u_{\mu }$ fields and explore their coupling under non-abelian symmetry analogs for full field unification under curvature activation.

2.9.5. Derivation of the Recursive Motion Field $u^{\mu }$

To close the theoretical framework linking recursive motion to emergent electromagnetic behavior, we derive the field $u^{\mu }$ from an activation-weighted curvature action. Within UMT, recursive motion is not arbitrary: it arises only within curvature-activated regions where $\Phi \left(\rho \right)>0$, and its structure reflects the geometry of the activated domain.

We begin by defining a curvature-modulated action functional for the recursive motion field:

$$S_u=\int \Phi \left(\rho \right){\nabla }^{\mu }{u}^{\nu }{\nabla }_{\mu }{u}_{\nu }\sqrt{-g}{d}^{4}x$$

(12)

This action measures the gradient energy of the motion field $u^{\mu }$ modulated by the activation level $\Phi \left(\rho \right)$. Variation of this action with respect to $u^{\mu }$ yields the Euler-Lagrange equation:

$${\displaystyle \frac{\delta S_u}{\delta u^{\mu }}}=-{\nabla }_{\nu }\left(\Phi \left(\rho \right){\nabla }^{\nu }{u}_{\mu }\right)=0$$

(13)

Raising the index and simplifying, we arrive at the governing equation:

$${\nabla }_{\nu }\left(\Phi \left(\rho \right){\nabla }^{\nu }{u}^{\mu }\right)=0$$

(14)

This is a generalized harmonic equation for $u^{\mu }$ within activated regions. In the special case where $\Phi \left(\rho \right)\approx 1$ and varies slowly, this reduces to the standard wave equation:

$$\square u^{\mu }=0$$

(15)

In dynamic regions where ${\nabla }_{\nu }\Phi \ne 0$, this equation includes source-like terms, effectively coupling recursive motion to activation gradients.

We may expand the divergence:

$$\Phi \left(\rho \right)\square u^{\mu }+({\nabla }_{\nu }\Phi \left(\rho \right)){\nabla }^{\nu }{u}^{\mu }=0$$

(16)

This form explicitly shows how changes in activation modulate wave propagation and recursive motion flow. In highly activated domains, motion propagates freely; in low-activation zones, propagation is suppressed.

Constraint from Norm Preservation

To preserve the causal structure of motion, we impose a norm constraint on $u^{\mu }$:

$$u^{\mu }{u}_{\mu }=-1\left(\mathrm{timelike}\right)\mathrm{or}0\left(\mathrm{null}\right)$$

(17)

This constraint ensures physical propagation consistent with the spacetime metric and restricts unphysical solutions.

Interpretation

This derivation frames $u^{\mu }$ as a dynamical vector field arising naturally from activation-modulated curvature geometry. It governs recursive motion in activated domains, and its antisymmetric derivative ${\tilde{F}}_{\mu \nu }$ gives rise to emergent electromagnetic phenomena as curvature rhythm asymmetries.

This result completes the causal foundation of recursive motion in UMT and provides a predictive structure for simulations of electromagnetic-like behavior within activated spacetime.

2.9.6. Energy-Momentum Tensor of Emergent Electromagnetic Fields

To complete the formulation of electromagnetism within the UMT framework, we define the energy-momentum tensor ${\tilde{T}}_{\mathrm{EM}}^{\mu \nu }$ corresponding to the emergent field strength tensor ${\tilde{F}}_{\mu \nu }$.

In analogy with classical electromagnetism, and modulated by the activation function $\Phi \left(\rho \right)$, we define:

$${\tilde{T}}_{\mathrm{EM}}^{\mu \nu }=\Phi \left(\rho \right)\left({\tilde{F}}^{\mu \alpha }{{\tilde{F}}^{\nu }}_{\alpha }-{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\tilde{F}}^{\alpha \beta }{\tilde{F}}_{\alpha \beta }\right)$$

(18)

This definition ensures the following:

• Activation-dependent stress propagation: In regions where $\Phi \left(\rho \right)\to 0$, ${\tilde{T}}_{\mathrm{EM}}^{\mu \nu }\to 0$ — electromagnetic stress vanishes in non-activated or sub-critical curvature domains.
• High-activation recovery: When $\Phi \left(\rho \right)\to 1$, this expression reproduces the standard electromagnetic stress-energy tensor.
• Curvature-coupled energy flux: The Poynting-like energy flux and field pressure terms now depend explicitly on the local curvature activation level.

The divergence of this tensor in curved spacetime,

$${\nabla }_{\mu }{\tilde{T}}_{\mathrm{EM}}^{\mu \nu }=({\nabla }_{\mu }\Phi \left(\rho \right))\left({\tilde{F}}^{\mu \alpha }{{\tilde{F}}^{\nu }}_{\alpha }-{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\tilde{F}}^{\alpha \beta }{\tilde{F}}_{\alpha \beta }\right)+\Phi \left(\rho \right){\nabla }_{\mu }\left({\tilde{F}}^{\mu \alpha }{{\tilde{F}}^{\nu }}_{\alpha }-{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{\tilde{F}}^{\alpha \beta }{\tilde{F}}_{\alpha \beta }\right)$$

(19)

contains an additional source term from activation gradients ${\nabla }_{\mu }\Phi \left(\rho \right)$, implying that electromagnetic energy-momentum is not conserved independently in regions where curvature activation is dynamically varying.

This result is physically intuitive under UMT: activation transitions act as sinks or sources of electromagnetic stress-energy, enabling curvature domains to store and release structured motion — such as during fast radio burst generation or activation collapse events.

Finally, in static activated regions (where ${\nabla }_{\mu }\Phi \left(\rho \right)\approx 0$), local conservation of electromagnetic energy-momentum is restored:

$${\nabla }_{\mu }{\tilde{T}}_{\mathrm{EM}}^{\mu \nu }\approx 0(\mathrm{static}\mathrm{activated}\mathrm{domain})$$

(20)

This formulation completes the curvature-consistent description of electromagnetic stress propagation within Universal Motion Theory. Further work will extend this tensor structure into the quantum domain and explore backreaction effects on the curvature metric itself.

2.9.7. Limit Behavior of Emergent Fields Under Full Activation

To reinforce correspondence with known field theories, we examine the behavior of the emergent antisymmetric field tensor ${\tilde{F}}_{\mu \nu }$ in the fully activated limit $\Phi \left(\rho \right)\to 1$. Recall that ${\tilde{F}}_{\mu \nu }$ is defined from the recursive motion vector field $u^{\mu }$ as:

$${\tilde{F}}_{\mu \nu }={\nabla }_{\mu }{u}_{\nu }-{\nabla }_{\nu }{u}_{\mu }$$

(21)

In regions of stable activation where curvature gradients are smooth and activation is near saturation, recursive motion becomes harmonic. In this regime, the recursive field satisfies a wave-like equation:

$$\square u^{\mu }+\alpha \left(\rho \right)u^{\mu }=0$$

(22)

For $\alpha \left(\rho \right)\to 0$ under full activation, this reduces to the source-free wave equation:

$$\square u^{\mu }=0$$

(23)

The antisymmetric field tensor ${\tilde{F}}_{\mu \nu }$ in this regime therefore exhibits standard wave propagation characteristics. We propose the following field correspondence in the limit $\Phi \left(\rho \right)\to 1$:

$${\nabla }^{\mu }{\tilde{F}}_{\mu \nu }\to 0$$

(24)

This is the vacuum Maxwell equation for the electromagnetic field. Additionally, the energy-momentum tensor derived from ${\tilde{F}}_{\mu \nu }$:

$$T_{\mu \nu }^{\left(F\right)}={\tilde{F}}_{\mu \alpha }{\tilde{F}}_{\nu }^{\alpha }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{\tilde{F}}_{\alpha \beta }{\tilde{F}}^{\alpha \beta }$$

(25)

satisfies:

$${\nabla }^{\mu }{T}_{\mu \nu }^{\left(F\right)}\to 0\mathrm{as}\Phi \left(\rho \right)\to 1$$

(26)

This establishes that, in highly activated zones, the emergent recursive field framework recovers Maxwellian electrodynamics without invoking fundamental gauge fields. Instead, classical electromagnetic behavior is understood as the harmonic expression of curvature-bound recursive motion.

Summary

Electromagnetic field structure emerges in UMT not as a separate interaction but as a rhythm-bound modulation of recursive geometry. In the full activation limit, the antisymmetric motion field ${\tilde{F}}_{\mu \nu }$ recovers vacuum Maxwell equations and energy conservation, offering physical continuity without introducing new force carriers. This reinforces the claim that UMT preserves classical physics as a special case of geometric recursion.

2.9.8. Structure and Constraint of ${\tilde{F}}_{\mu \nu }$

To formalize the emergent field analog ${\tilde{F}}_{\mu \nu }$ within Universal Motion Theory (UMT), we begin with the foundational principle that recursive motion arises only within curvature-activated domains, where $\Phi \left(\rho \right)>0$. This motion can be represented by a vector field $u^{\mu }$, and its antisymmetric derivative defines a geometric analog to the electromagnetic field tensor:

$${\tilde{F}}_{\mu \nu }\equiv {\nabla }_{\mu }{u}_{\nu }-{\nabla }_{\nu }{u}_{\mu }$$

(27)

We constrain $u^{\mu }$ to reflect only motion permitted within activated curvature, defining:

$$u^{\mu }=\Phi \left(\rho \right){\xi }^{\mu }$$

(28)

Here, ${\xi }^{\mu }$ is a normalized, timelike or null vector field encoding the directionality of recursive motion. It can be interpreted as the local harmonic axis of curvature flow within the activated domain—essentially the preferred propagation vector for recursive dynamics once activation permits coherent structure. Substituting yields:

$${\tilde{F}}_{\mu \nu }=({\nabla }_{\mu }\Phi ){\xi }_{\nu }-({\nabla }_{\nu }\Phi ){\xi }_{\mu }+\Phi ({\nabla }_{\mu }{\xi }_{\nu }-{\nabla }_{\nu }{\xi }_{\mu })$$

(29)

This construction gives ${\tilde{F}}_{\mu \nu }$ a dual character: it is both a measure of recursive motion vorticity and a tracer of activation gradients across spacetime.

Stress-Energy Structure

We define an effective field stress-energy tensor:

$$T_{\mu \nu }^{\left(F\right)}={\tilde{F}}_{\mu \alpha }{\tilde{F}}_{\nu }^{\alpha }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{\tilde{F}}_{\alpha \beta }{\tilde{F}}^{\alpha \beta }$$

(30)

This tensor can be inserted into the modified field equations or tracked independently in simulations of activated dynamics. It quantifies local energy, pressure, and anisotropy arising from curvature-induced recursive motion.

Empirical Constraint Pathways

While ${\tilde{F}}_{\mu \nu }$ has not yet been directly observed, it admits multiple avenues of experimental constraint:

• Fast Radio Bursts (FRBs): Sudden collapse across ${\rho }_c$ may generate intense local spikes in ${\nabla }_{\mu }\Phi$, producing observable coherent emission aligned with ${\tilde{F}}_{\mu \nu }$ dynamics.
• CMB Polarization: Anisotropic evolution in ${\tilde{F}}_{\mu \nu }$ may imprint directionally dependent polarization patterns, especially in low-$\Phi$ regions near recombination.
• Void Lensing Asymmetries: Enhanced $\nabla \Phi$ at void boundaries may correlate with lensing distortion features or localized curvature radiation.
• Gravitational Echo Envelopes: Regions of nearly saturated $\Phi \approx 1$ may allow trapped geometric energy to oscillate in ${\tilde{F}}_{\mu \nu }$-dominated zones, shaping the amplitude and spectral content of echoes.

Further constraint of ${\tilde{F}}_{\mu \nu }$ will rely on its incorporation into numerical simulations and comparison against high-resolution data sets, particularly for polarization, transient coherence, and boundary-aligned lensing artifacts.

2.9.9. Reframing Electromagnetism: From Field to Rhythm

In UMT, electromagnetic behavior is not a separate force but the large-scale reflection of recursive curvature behavior under activation constraints. Maxwell’s equations, rather than postulates, are seen as rhythmic boundary approximations of curvature behavior in saturated, asymmetric domains.

This unification provides an explanatory bridge between spacetime structure and classical field theory, and invites future work on deriving quantized field behavior from recursive rhythm thresholds.

2.10. Quantum Behavior as Recursive Rhythm

Universal Motion Theory (UMT) postulates that all structure and dynamics arise from bounded motion regulated by curvature activation. In this section, we show that phenomena traditionally associated with quantum mechanics — such as quantization, uncertainty, coherence, entanglement, and graviton-like behavior — emerge naturally from recursive motion in activated domains. These behaviors require no independent quantization postulates, but instead arise from topological and harmonic constraints on $u_{\mu }$, the recursive motion vector field.

2.10.1. Quantization from Recursive Boundary Conditions

Consider a region of spacetime with bounded, activated curvature forming a closed topology (e.g., a toroidal structure). Let $u_{\mu }$ be the recursive motion flow vector within this domain. Stable recursive motion imposes a harmonic boundary condition:

$${\oint }_{\gamma }{u}^{\mu }d{x}_{\mu }=2\pi n,n\in \mathbb{Z}$$

(31)

where $\gamma$ is a closed loop in the activated curvature manifold. This condition restricts allowable recursive modes to integer multiples of a fundamental cycle, yielding natural quantization of oscillatory energy. The quantized energy levels arise not from operator eigenstates, but from the topological stability of recursive rhythm in curved geometry.

2.10.2. Uncertainty as a Localization-Stability Tradeoff

Recursive localization increases curvature steepness, amplifying ${\nabla }_{\mu }{u}_{\nu }$ and raising tension across the activation boundary. As a result, tightly localized recursive motion becomes dynamically unstable unless counterbalanced by broader activation support. This creates a geometric uncertainty principle:

$$\Delta x·\Delta u_{\mu }\gtrsim {\Phi }^{-1}\left(\rho \right)$$

(32)

This relation reflects a tradeoff between position-like localization and motion field precision, with sharp bounds set by the local activation level. High activation permits tighter localization, while near-threshold regions yield greater instability for localized recursion.

2.10.3. Wavefunction Analogs from Oscillatory $u_{\mu }$ Modes

In activated domains, the recursive vector field $u_{\mu }$ supports wave-like solutions under the linearized field equation:

$$\square u_{\mu }+\alpha \left(\rho \right)u_{\mu }=0$$

(33)

These solutions form harmonic packets with well-defined phase structure. The envelope and phase dynamics of $u_{\mu }$ mimic classical wavefunction evolution, with amplitude governed by activation energy and coherence defined by recursive boundary conditions. Collapse of the wavefunction corresponds to activation threshold transitions, where stable recursion cannot be maintained.

2.10.4. Entanglement and Shared Recursive Structure

Two spatially separated regions can share a common recursive origin if their motion vectors emerge from a joint curvature domain. In such cases, their $u_{\mu }$ fields maintain a coherent phase relation across distance — not through non-local influence, but through geometric continuity of recursive structure:

$$u_A^{\mu }\left(x\right)\sim u_B^{\mu }\left(x^{\prime }\right)\mathrm{iff}x,x^{\prime }\in {\Sigma }_{\mathrm{shared}}$$

(34)

Here ${\Sigma }_{\mathrm{shared}}$ is the original activated manifold supporting joint recursion. Decoherence occurs when either region crosses an activation boundary or experiences external curvature interaction, severing the shared recursion and breaking entanglement.

2.10.5. Activation Ripples as Gravitational Wave Quanta

Activation gradients propagate as rhythmic modulations of $\Phi \left(\rho \right)$. In dynamic curvature domains, disturbances in recursive curvature — caused by mass motion, merger events, or activation collapse — emit wave-like ripples in the activation function:

$$\delta \Phi \left(\rho \right)\propto e^{i(k_{\mu }{x}^{\mu }-\omega t)}$$

(35)

These modulations carry energy and momentum, satisfying wave propagation equations derived from the variation of the activation-weighted action. In the linear limit, they serve as graviton analogs — localized, quantized packets of curvature modulation with propagation constrained by activation structure.

This interpretation removes the need for fundamental spin-2 particles, instead attributing quantized gravitational radiation to phase-locked recursive motion in the geometry of activated spacetime.

In total, these derivations demonstrate that quantum phenomena — typically treated as axiomatic or requiring separate quantization frameworks — are instead emergent properties of bounded recursive motion under curvature activation. UMT thus provides a unified basis for gravitational and quantum behavior without metaphysical dualism or postulated discreteness.

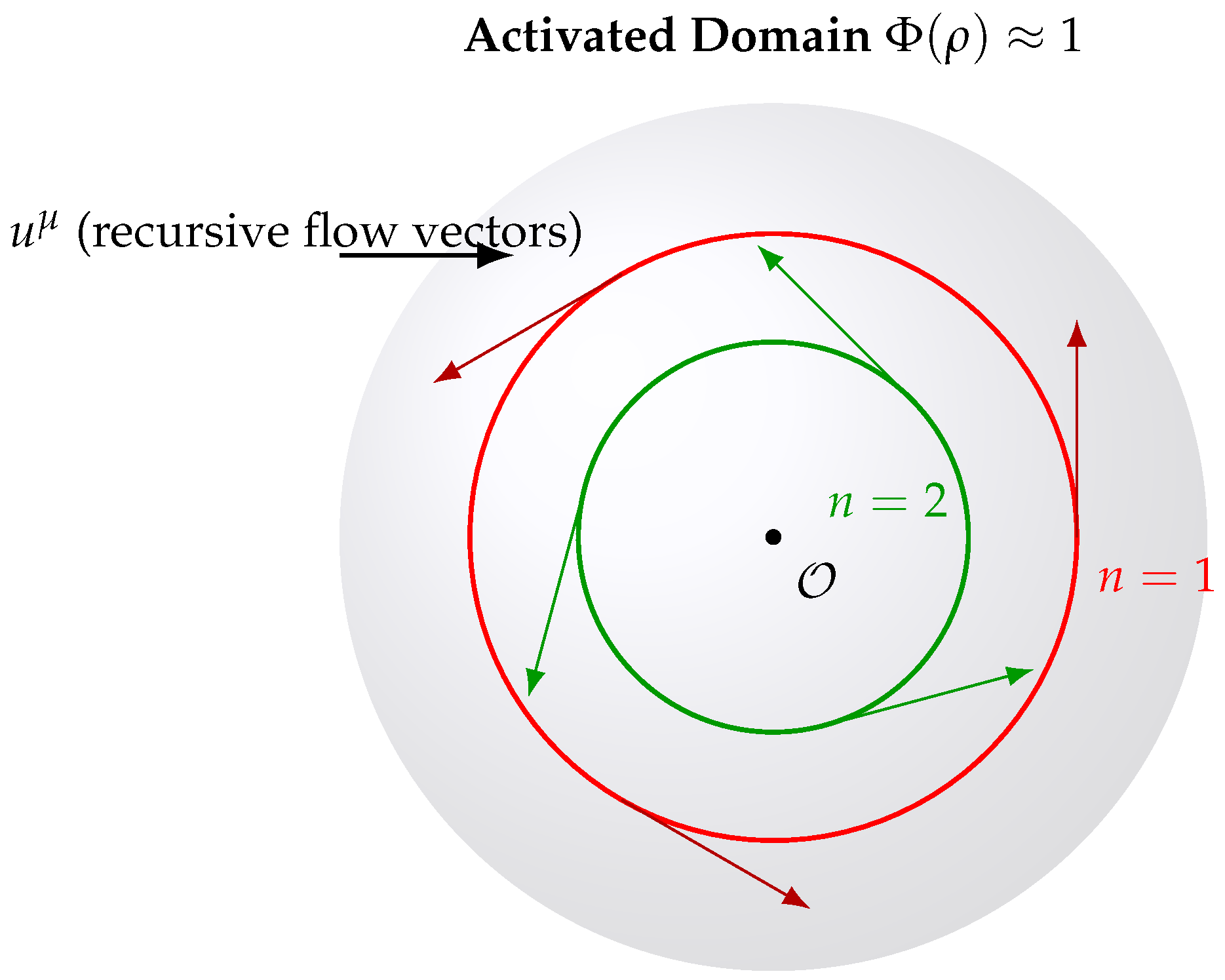
Figure 2. Recursive motion structures within an activated toroidal domain. The red path completes one full cycle ($n=1$), while the green path wraps twice ($n=2$). Tangent vectors $u^{\mu }$ illustrate local recursive motion direction.

Figure 2. Recursive motion structures within an activated toroidal domain. The red path completes one full cycle ($n=1$), while the green path wraps twice ($n=2$). Tangent vectors $u^{\mu }$ illustrate local recursive motion direction.

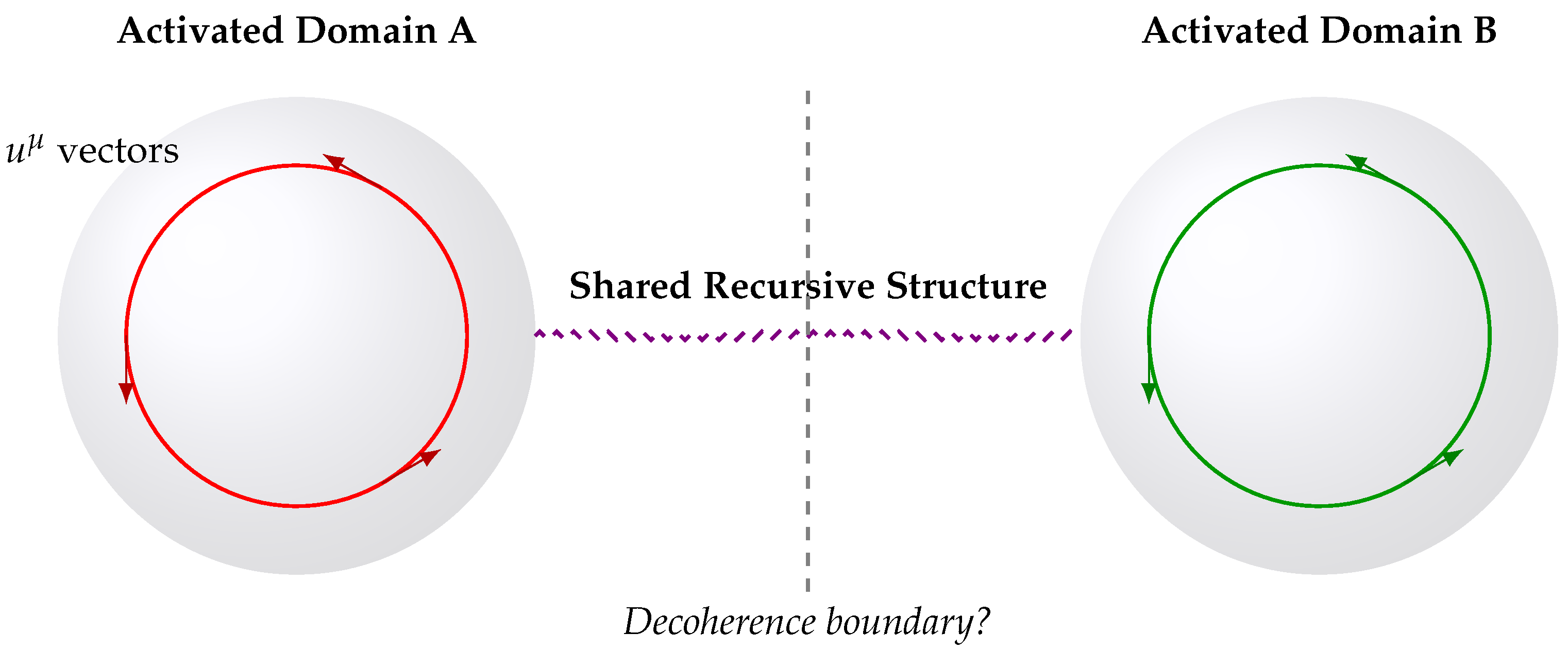
Figure 3. Entanglement illustrated as a shared recursive structure connecting two separate activated domains. Recursive motion vectors $u^{\mu }$ within each domain remain phase-locked through the bridge. A decoherence boundary (center) may sever this connection if activation conditions shift.

Figure 3. Entanglement illustrated as a shared recursive structure connecting two separate activated domains. Recursive motion vectors $u^{\mu }$ within each domain remain phase-locked through the bridge. A decoherence boundary (center) may sever this connection if activation conditions shift.

2.10.6. Topological Recursion, Decoherence, and Entanglement Drift Under UMT

In Universal Motion Theory (UMT), quantum behavior is understood as a byproduct of rhythm-bound recursive motion in activated curvature domains. To formalize this structure, we introduce the concept of a topological recursion number $\mathcal{W}$, which captures the quantized stability of recursive motion loops.

Definition of Topological Recursion Number

We define the Topological Recursion Number (TRN) $\mathcal{W}$ as a winding index over a closed recursive loop:

$$\mathcal{W}={\displaystyle \frac{1}{2\pi }}{\oint }_C\omega$$

(36)

where:

• C is a closed recursive motion path (in proper time or configuration space),
• $\omega$ is the local angular phase per cycle (a 1-form encoding internal rhythm dynamics),
• $\mathcal{W}\in \mathbb{Z}$ represents the number of stable recursive windings.

This winding index serves as a topological label for rhythm-bound states, analogous to spin, internal symmetry charge, or quantized mode occupation. Stable particles, such as electrons, are interpreted as rhythm-locked systems with minimal nonzero $\mathcal{W}$.

Quantum Decoherence as Activation Gradient Instability

Under UMT, quantum decoherence arises not from environmental measurement but from instability in recursive synchrony across regions with variable activation. Specifically, the decoherence rate ${\Gamma }_D$ increases with activation gradients across a coherence region $\Omega$:

$${\Gamma }_D\sim {〈\left|\nabla \Phi \left(\rho \right(x\left)\right)·\delta x\right|〉}_{\Omega }$$

(37)

where:

• $\delta x$ is the spatial separation between rhythm-linked elements of the system,
• $\Phi \left(\rho \right(x\left)\right)$ is the local activation level,
• $\nabla \Phi$ captures curvature-induced instability in recursive structure.

This formulation implies that decoherence can occur even in isolation, without external measurement, if the coherence region spans activation gradients that induce internal desynchronization.

Entanglement Degradation as Phase Drift

In UMT, entanglement between particles is maintained through phase-synchronized recursive rhythms. If two entangled particles A and B traverse regions with differing activation levels, their local rhythm phases diverge due to $\Phi \left(\rho \right)$ mismatch. The resulting entanglement degradation is governed by a geometric phase drift:

$$\Delta {\varphi }_{\mathrm{ent}}\sim {\int }_{x_A}^{x_B}{\displaystyle \frac{d\Phi \left(\rho \right)}{ds}}$$

(38)

This integral captures the loss of synchronization between previously coupled recursion structures, offering a natural geometric explanation for partial entanglement loss over distance or in curvature-structured environments.

UMT–Quantum Correspondences

• Topological recursion number $\mathcal{W}$: Quantized internal rhythm state, interpretable as spin or mode winding.
• Decoherence rate ${\Gamma }_D$: Function of activation gradient across coherence region.
• Entanglement phase drift $\Delta {\varphi }_{\mathrm{ent}}$: Geometrically induced desynchronization in entangled systems.

These correspondences unify curvature-based activation theory with key quantum phenomena, providing a falsifiable, geometric substrate for behavior traditionally treated as non-local or observer-dependent.

Observational Implications

UMT predicts decoherence and entanglement decay as functions of spatial activation structure:

• Entanglement loss in gravitational gradients: Can be tested via satellite-based Bell experiments across variable curvature domains.
• Phase noise near void boundaries: May explain anomalous dephasing or timing jitter in large-scale quantum coherence experiments.
• Stable $\mathcal{W}$-linked structures: Offer a new geometric classification of particle families beyond standard model symmetry labels.

Summary

Topological recursion offers a foundational rhythm-based interpretation of quantum persistence, spin, and coherence. UMT reframes quantum instability as a geometric phenomenon: when recursive cycles become unsynchronized across activation gradients, coherence is lost. This approach unifies gravitational geometry and quantum fragility under a single curvature-responsive framework and invites experimental tests linking activation structure to quantum correlation loss.

2.10.7. Emergent Probability and Measurement

Within UMT, the probabilistic interpretation of quantum phenomena emerges from the local behavior of recursive motion. We define a scalar wavefunction-like object:

$$\psi \left(x\right)=A\left(x\right)e^{i\theta \left(x\right)}$$

(39)

where $A\left(x\right)=|{\nabla }_{\mu }{u}^{\mu }|$ captures the local compressive or expansive intensity of recursion, and $\theta \left(x\right)={\int }_{\gamma }{u}^{\mu }d{x}_{\mu }$ encodes cumulative phase along a recursive path.

The squared magnitude:

$${\rho }_{\mathrm{prob}}\left(x\right)={\left|\psi \left(x\right)\right|}^2=A{\left(x\right)}^2={\left|{\nabla }_{\mu }{u}^{\mu }\right|}^2$$

(40)

is interpreted as the probability density of recursive motion-induced interaction at x.

Measurement events correspond to localized breakdowns in recursive coherence—specifically, when $\Phi \left(\rho \right)$ drops below a critical threshold such that coherent recursive motion can no longer be sustained. In these regions, the wavefunction collapses geometrically, not probabilistically.

2.10.8. Operator Analogs from Recursive Gradients

UMT replaces postulated quantum operators with geometric derivatives of the recursive phase function. The following identifications hold:

• Position: Defined by the peak of ${\left|\psi \left(x\right)\right|}^2$
• Momentum: $p^{\mu }\sim {\nabla }^{\mu }\theta \left(x\right)$
• Energy: $E\sim {\partial }_t\theta \left(x\right)$

These identifications yield operator-like structures from field gradients without invoking abstract Hilbert space formalism.

Apparent uncertainty arises from the geometry of activation. Non-commuting gradients of $\theta$ and A in dynamically varying $\Phi \left(\rho \right)$ regions produce localization-stability tradeoffs consistent with quantum behavior, but without fundamental randomness.

2.10.9. Mode Expansion and Field Quantization

To describe quantized energy levels, we decompose the recursive motion field $u^{\mu }$ into harmonic modes:

$$u^{\mu }\left(x\right)=\sum _n{a}_n^{\mu }\left(x\right){\varphi }_n\left(x\right)$$

(41)

where ${\varphi }_n$ are eigenfunctions satisfying:

$$\square {\varphi }_n=-{\lambda }_n{\varphi }_n$$

(42)

Boundary quantization is enforced via recursive loop conditions:

$${\oint }_{\gamma }{\varphi }_{n}dx=2\pi n,n\in \mathbb{Z}$$

(43)

Quantized energy levels follow from curvature-constrained mode structure:

$$E_n\propto \sqrt{{\lambda }_n}$$

(44)

This provides a mode-based foundation for quantization purely from geometric recursion.

2.10.10. Entanglement Geometry and Overlap Domains

Entanglement in UMT arises from shared recursion loops embedded in a common activated manifold. Two spatially separated domains A and B are entangled when their phase structures are non-separable:

$${\theta }_{\mathrm{AB}}\ne {\theta }_A+{\theta }_B$$

(45)

This non-factorizability is geometric, not probabilistic. Coherence between ${\psi }_A$ and ${\psi }_B$ is sustained by overlapping activated domains.

The degree of entanglement is quantified by the overlap integral:

$$\mathcal{E}={\int }_{\mathrm{shared}}{\psi }_A^{*}\left(x\right){\psi }_B\left(x\right)d^{3}x$$

(46)

Such structures permit correlated measurement outcomes without invoking nonlocality, as phase correlation is preserved through geometric continuity of recursion.

2.10.11. Topological Identity and Particle Classification

In Universal Motion Theory (UMT), physical identity arises from the topological properties of recursive motion within activated curvature domains. Rather than postulating particle types or internal symmetries, UMT interprets such features as consequences of stable recursive structures characterized by quantized topological numbers.

Recursive Topology as Ontological Signature

Each coherent structure in UMT is defined by a recursive motion field $u^{\mu }$ constrained by the geometry and boundary of its activated region. These recursive structures may form closed loops, knots, or higher-order embeddings within activated curvature domains. The topological character of such recursion is captured by two primary quantities:

• The Topological Recursion Number $\mathcal{W}$, defined by the number of phase-winding cycles around a closed path:

  $$\mathcal{W}={\displaystyle \frac{1}{2\pi }}{\oint }_{\gamma }\omega$$

  (47)

  where $\omega$ is the local angular phase one-form.
• The Recursion Embedding Index $\mathcal{E}$, which encodes the spatial dimensionality and curvature embedding of the recursive structure. For instance, a toroidal loop may have $\mathcal{E}=(1,1)$, indicating one winding in both the poloidal and toroidal directions.

These quantities collectively define a recursive motion’s topological identity. Stable particles are interpreted as geometric solitons with persistent $\mathcal{W}$ and $\mathcal{E}$ values, embedded within curvature regions whose activation level supports continuous rhythm.

Mapping to Known Particle Traits

We propose a tentative correspondence between recursive topology and observable particle features:

• Spin: Particles with half-integer winding (e.g., $\mathcal{W}=1$ in minimal activation volumes) exhibit rotational behavior consistent with spin-${\displaystyle \frac{1}{2}}$. Full integer $\mathcal{W}$ corresponds to bosonic identity.
• Mass: Determined by the activation energy required to maintain a stable recursive cycle. Higher $\mathcal{W}$ or more complex $\mathcal{E}$ configurations require more curvature tension to stabilize, corresponding to greater inertial mass.
• Charge-like behavior: Emerges from asymmetries in recursion field alignment or chirality. Recursive loops with consistent orientation across embedding layers may yield effective polar vector fields analogous to electromagnetic charge.
• Family Structure: Varying $\mathcal{E}$ values may correspond to different generations or resonance states, suggesting that lepton and quark family behavior arises from embedded recursion geometries rather than fundamental flavor symmetry.

Example: Electron-like Structure

An electron-like recursive soliton may correspond to a minimal stable configuration with:

$$\mathcal{W}=1,\mathcal{E}=(1,0)$$

indicating a single phase winding in a closed loop along a preferred curvature axis, stabilized by a localized activation maximum. Its field chirality may contribute to observable electromagnetic behavior, while its minimal embedding complexity supports low mass and high coherence.

Topological Stability and Conservation Laws

Because topological quantities like $\mathcal{W}$ and $\mathcal{E}$ are invariant under smooth deformation, they impose effective conservation rules. This naturally explains:

• Charge conservation: As conservation of recursion chirality or handedness.
• Lepton and baryon number: As preservation of loop connectivity and embedding class.
• Spin-statistics behavior: As a result of recursive exchange symmetry within harmonic phase cycles.

Thus, UMT provides a structural basis for particle identity, not by invoking internal gauge groups, but by anchoring identity to the topology of motion within activated curvature.

Outlook: Beyond the Standard Model

While this framework remains preliminary, it offers a pathway for classifying all known particle types—and possibly new ones—through recursive topology. If validated, this approach could bypass the need for postulated symmetry groups, reducing particle physics to a geometry of rhythm.

Future work may involve simulation of recursive soliton dynamics under varying curvature constraints, mapping the full space of $(\mathcal{W},\mathcal{E})$ to known particles, and identifying stability domains within the activation landscape.

2.10.12. Summary

Universal Motion Theory derives quantum behavior not from axioms, but as an emergent consequence of recursive motion within curvature-activated domains. Across this section, we have shown that features such as quantization, uncertainty, entanglement, and wavefunction structure arise from topological and rhythmic constraints imposed by activated geometry.

Quantized energy levels follow from harmonic mode constraints and topological boundary conditions on the recursive vector field $u^{\mu }$. Uncertainty emerges as a localization-instability tradeoff within activation gradients, captured by the geometric relation $\Delta x·\Delta u_{\mu }\gtrsim {\Phi }^{-1}\left(\rho \right)$, reflecting the bounded nature of motion.

The wavefunction appears as a scalar observable $\psi \left(x\right)=A\left(x\right)e^{i\theta \left(x\right)}$ with amplitude linked to divergence and phase to recursive alignment. Its squared magnitude defines a probability density, while wavefunction collapse follows naturally from local coherence breakdown as $\Phi \left(\rho \right)$ drops below threshold.

Operator analogs such as position, momentum, and energy arise from phase and amplitude gradients rather than from postulated operator algebra. Entanglement is reframed as the geometric persistence of shared recursion across activated domains, quantified through overlap integrals.

Unification through Activation and Recursive Structure.

In Universal Motion Theory, all observed interaction strengths — gravitational, electromagnetic, and quantum-coherent — emerge from local activation gradients that regulate the capacity for recursive motion. What appear as distinct forces are better understood as rhythm behaviors arising within different recursion geometries, each modulated by the same activation function $\Phi \left(\rho \right)$. Variations in interaction range, field structure, and coherence stability reflect changes in the local activation environment and the dimensional constraints of recursion rather than fundamentally separate forces.

Moreover, structures analogous to $SU\left(2\right)$ and $SU\left(3\right)$ gauge behavior may correspond to multi-axis recursive manifolds or layered recursion configurations distinguished by topological recursion numbers $\mathcal{W}$. In this view, internal symmetries are not imposed but emerge from the harmonic and geometric embedding of recursion in activated curvature domains. This suggests a future path for encoding Standard Model-like behavior within a unified geometric substrate, governed entirely by motion, rhythm, and curvature.

Together, these results construct a complete and self-consistent picture of quantum phenomena grounded in the geometry and activation structure of spacetime. UMT thus provides a unified origin for both gravitational and quantum behavior, rooted not in separate postulates but in the dynamic modulation of motion itself.

3. Emergent Time Structure and Temporal Horizons

Universal Motion Theory (UMT) redefines time as an emergent property of bounded motion, dependent upon local curvature activation. This view leads to the prediction of temporal horizons and novel behaviors near activation thresholds.

3.1. Time as Emergent from Bounded Motion

Time arises only where curvature activation $\Phi \left(\rho \right)$ approaches unity, enforcing motion constraints that manifest as sequential ordering.

In regions where $\Phi \left(\rho \right)\ll 1$, motion remains largely unbounded and unordered — corresponding to timeless or near-timeless domains.

Thus, time is localized, emergent, and dynamic rather than a fundamental background parameter.

3.2. Temporal Horizons

Temporal horizons naturally arise at boundaries where activation levels change sharply.

Consider a spatial boundary where curvature density transitions across ${\rho }_c$, creating an activation boundary:

$$\Delta \Phi \approx \alpha \Phi (1-\Phi )\Delta \rho$$

At such boundaries:

• Sequential motion becomes increasingly constrained when crossing into higher activation zones,
• Entities approaching a low-activation region experience temporal decoherence,
• Causal ordering may break down across sufficiently sharp activation gradients.

Temporal horizons mark the edge of regions where ordered temporal evolution is maintained.

3.3. Temporal Decoherence near Activation Thresholds

Near the activation threshold ${\rho }_c$, partial activation $\Phi \left(\rho \right)\sim 0.5$ implies:

• Incomplete bounding of motion,
• Localized fluctuations between ordered and disordered evolution,
• Stochastic temporal behavior observable as decoherence effects.

Temporal decoherence may manifest observationally as:

• Anomalous timing jitter in signals traversing activation transition regions,
• Variable propagation speeds for causal influences near threshold boundaries,
• Suppressed coherence of motion-based phenomena such as wavefronts or structured emissions.

3.4. Philosophical Implications

UMT’s treatment of time challenges traditional assumptions:

• Time is not universally continuous or absolute,
• Different regions of the universe may experience differing degrees of temporal ordering,
• Fundamental notions of causality are local, emergent, and context-dependent.

This framework offers a fertile ground for re-examining cosmological evolution, black hole interiors, and early-universe conditions from a motion-centric perspective.

4. Thermodynamic Analogs of Curvature Activation

UMT’s curvature activation framework admits a natural thermodynamic analogy, offering additional predictive power and interpretive clarity.

4.1. Activation Transitions as Phase Changes

The logistic activation function $\Phi \left(\rho \right)$ resembles an order parameter in phase transitions.

Key parallels include:

• Curvature density $\rho$ acts as a control parameter analogous to temperature or pressure,
• Activation $\Phi \left(\rho \right)$ functions as an order parameter transitioning smoothly from disordered (low activation) to ordered (high activation) states,
• The critical threshold ${\rho }_c$ defines a pseudo-phase boundary between motion regimes.

Thus, the activation process can be understood as a continuous (second-order) phase transition in the curvature-motion system.

4.2. Entropy and Activation Gradients

Entropy production in UMT correlates with activation gradients.

Regions with strong ${\nabla }_{\mu }\Phi \left(\rho \right)$ correspond to locations where motion reorganizes and entropy flows dynamically.

Predictions include:

• Entropy generation rates proportional to activation gradient magnitudes,
• Preferential entropy outflow along activation gradient directions,
• Observable consequences in anisotropies of cosmic microwave background (CMB) residuals and in fast transient phenomena such as FRBs.

4.3. Phase Transition Signatures

Signatures of activation-driven phase transitions may include:

• Sharp changes in large-scale structure growth rates,
• Anomalous clustering behaviors near critical activation epochs,
• Residual activation patterns imprinted in background radiation fields.

Future observational studies targeting entropy distribution patterns and cosmic background fluctuations may provide critical tests of the thermodynamic analog structure within UMT.

5. Activation-Driven Recombination Modeling

In Universal Motion Theory (UMT), recombination is understood not merely as a chemical transition but as a curvature-activation phase boundary crossing. The recombination epoch corresponds to the global transition of spacetime regions from partially activated to fully activated curvature, leading to the emergence of large-scale structure.

5.1. Curvature Activation During Recombination

Prior to recombination, regions of the universe exhibited low but rising curvature densities. As motion redistributed and activation gradients sharpened, curvature thresholds were crossed, triggering the emergence of recursive structure.

The logistic curvature activation function $\Phi \left(\rho \right)$ governs this process:

$$\Phi \left(\rho \right)={\displaystyle \frac{1}{1+e^{-\alpha (\rho -{\rho }_c)}}}$$

where:

• $\rho$ is the local curvature density,
• $\alpha$ is the activation steepness,
• ${\rho }_c$ is the critical activation threshold.

The recombination event corresponds to a global statistical crossing of ${\rho }_c$ across spacetime.

5.2. Emergent Large-Scale Structure

As regions activate, the binding of motion into locally bounded configurations occurs. This generates effective potential wells, seeds of proto-structure, without requiring primordial matter overdensities.

The effective gravitational force from activation gradients is:

$$a_{\mu }\propto -{\nabla }_{\mu }\Phi \left(\rho \right)$$

During recombination, small statistical variations in local curvature densities $\delta \rho$ amplify into significant activation gradients ${\nabla }_{\mu }\Phi \left(\rho \right)$.

These gradients then drive the formation of early structures via motion attraction rather than traditional matter collapse models.

5.3. Statistical Properties of Activation Fluctuations

The fluctuations $\delta \rho$ during the recombination transition generate an effective activation field perturbation $\delta \Phi$. Since $\Phi \left(\rho \right)$ exhibits sharp curvature near ${\rho }_c$, even small $\delta \rho$ produce large $\delta \Phi$:

$$\delta \Phi \approx \alpha \Phi (1-\Phi )\delta \rho$$

where $\Phi$ is evaluated near ${\rho }_c$.

Thus, even minor statistical variations in curvature density are exponentially amplified into activation contrasts capable of seeding cosmic structures.

5.4. Observational Implications

This model predicts:

• Enhanced structure formation correlated directly with curvature density fluctuations.
• Nontrivial deviations from standard $\Lambda$CDM expectations at recombination scales.
• Potential observable imprints in the cosmic microwave background (CMB) anisotropies, tied to activation dynamics rather than purely density dynamics.

These signatures offer potential observational tests for UMT against standard cosmological models.

6. Seed Structures of the Cosmic Web

Universal Motion Theory (UMT) attributes the origin of the cosmic web not to primordial matter overdensities alone, but to curvature activation gradients arising during early motion-bounded system activations.

6.1. Activation Gradient-Driven Structure Formation

During recombination and subsequent cosmic cooling, regions of differing curvature densities $\rho$ transitioned across the activation threshold ${\rho }_c$ at different rates.

Gradients in activation ${\nabla }_{\mu }\Phi \left(\rho \right)$ seeded directional biases for motion aggregation, forming filamentary and wall-like structures without requiring initial matter anisotropies of large amplitude.

Effective acceleration followed:

$$a_{\mu }\propto -{\nabla }_{\mu }\Phi \left(\rho \right)$$

resulting in motion convergence along activation gradient directions.

6.2. Network Growth and Filament Formation

The initial activation gradients created preferential pathways along which motion-bound structures formed.

Key properties include:

• Self-reinforcing activation along filaments,
• Suppression of structure formation within underactivated voids,
• Hierarchical web-like growth patterns correlated with curvature gradient networks.

Thus, the cosmic web emerges naturally as a reflection of curvature activation topology rather than purely gravitational instability from matter fluctuations.

6.3. Observational Consistency

Observations of large-scale filamentary structures, void distributions, and anisotropic clustering are consistent with an activation-driven growth model.

Predictions include:

• Strong filamentary connectivity even in low-matter regions,
• Activation threshold dependencies in void-filament transition zones,
• Potential curvature signatures detectable via gravitational lensing of background sources.

7. Gravitational Quiescence of Cosmic Voids

In Universal Motion Theory (UMT), the observed gravitational behavior of cosmic voids — large regions with low matter density — is explained through the activation dynamics of curvature rather than solely through matter distribution.

7.1. Activation Thresholds and Voids

Regions of low matter density correspond to low curvature densities $\rho$. In such regions, $\Phi \left(\rho \right)$ remains significantly below unity, indicating partial or non-activation.

This results in effective gravitational quiescence:

$$a_{\mu }\propto -{\nabla }_{\mu }\Phi \left(\rho \right)$$

is suppressed where ${\nabla }_{\mu }\Phi \left(\rho \right)\approx 0$.

Thus, voids do not exert significant gravitational pull, even if some residual matter exists within them.

7.2. Weak Lensing Signatures at Void Boundaries

At the boundaries of voids, curvature density gradients ${\nabla }_{\mu }\rho$ — and thus activation gradients ${\nabla }_{\mu }\Phi \left(\rho \right)$ — become non-negligible.

This predicts:

• Weak gravitational lensing signatures localized at void boundaries,
• Suppressed but nonzero deflection angles,
• Boundary-focused rather than volume-distributed lensing behavior.

Such signatures are consistent with observations of cosmic void lensing, where the gravitational influence is concentrated near the void edges rather than uniformly distributed.

7.3. Comparison to Observed Void Dynamics

Standard $\Lambda$CDM models attribute void gravitational behavior to the low matter density alone. UMT provides an alternative interpretation: the gravitational suppression arises fundamentally from curvature activation thresholds, independent of total mass density.

Predictions include:

• Enhanced gravitational quiescence compared to matter-only models,
• Stronger lensing signatures at sharply defined void edges,
• Potential activation-threshold-dependent variations between voids of different sizes.

Future precision measurements of void dynamics and weak lensing patterns may help discriminate between curvature activation and matter-density-driven models.

8. Echo Formation in Toroidal Curvature Structures

Universal Motion Theory (UMT) predicts that certain gravitational wave phenomena, specifically echoes following black hole mergers, naturally arise from toroidal curvature activation structures rather than traditional event horizons.

8.1. Toroidal Curvature Structures

Rather than assuming a spherically symmetric event horizon, UMT proposes that extremely high curvature regions stabilize into toroidal structures at critical activation densities ${\rho }_c$. The topology allows for motion to remain bounded without requiring a true singularity or trapped surface.

Toroidal curvature structures exhibit localized regions of maximal activation $\Phi \left(\rho \right)\approx 1$ encircling a central core of suppressed activation, forming a dynamically stable configuration.

8.2. Gravitational Wave Echoes

When a merger event disturbs a toroidal curvature structure, the excitation of trapped motion within the toroidal region produces delayed secondary emissions — perceived as gravitational wave echoes.

The characteristic echo time delay $\Delta t_{\mathrm{echo}}$ is set by the size of the activated region:

$$\Delta t_{\mathrm{echo}}\approx {\displaystyle \frac{2R_{\mathrm{torus}}}{c}}$$

where $R_{\mathrm{torus}}$ is the effective major radius of the toroidal activation structure.

Damping and harmonic structure of the echoes are determined by:

• The sharpness of the activation gradient at the torus boundary,
• The internal activation stability,
• The energy absorption properties of the activated medium.

8.3. Schematic Representation

Figure 4. Toroidal trapping and echo generation under Universal Motion Theory. Recursive motion is confined within a curvature-activated region. When rhythmic distortion occurs, modulated echoes propagate outward from the threshold boundary where $\Phi \left(\rho \right)$ drops below critical activation.

Figure 4. Toroidal trapping and echo generation under Universal Motion Theory. Recursive motion is confined within a curvature-activated region. When rhythmic distortion occurs, modulated echoes propagate outward from the threshold boundary where $\Phi \left(\rho \right)$ drops below critical activation.

In this schematic, the activated toroidal region traps disturbances, leading to delayed re-emission detectable as gravitational wave echoes.

8.4. Comparison to Observations

Recent observational claims of gravitational wave echoes, particularly following events like GW150914, can be interpreted within this framework. The observed echo time delays and damping profiles are naturally explained without invoking exotic matter or modifications to general relativity at large scales.

UMT predicts:

• Echo time delays scaling with effective torus size.
• Broadening and damping correlated with activation gradient steepness.
• Potential deviations from perfect echo periodicity due to dynamic activation boundary adjustments.

Further observational data and echo detection efforts can help distinguish UMT toroidal structures from classical or quantum-modified horizon models.

8.5. Quantitative Observational Signatures

Universal Motion Theory (UMT) offers concrete, testable predictions across multiple astrophysical observations. These predictions enable empirical confrontation with data, offering potential falsifiability pathways for the theory.

8.5.1. Gravitational Wave Echoes

Following black hole mergers, toroidal curvature structures predict gravitational wave echoes with characteristic time delays:

$$\Delta t_{\mathrm{echo}}\approx {\displaystyle \frac{2R_{\mathrm{torus}}}{c}}$$

where:

• $R_{\mathrm{torus}}$ is the major radius of the toroidal activation structure,
• c is the speed of light.

Predictions:

• Echo time delays proportional to merger remnant size,
• Damped, quasi-periodic echo trains,
• Deviation from perfect periodicity due to dynamic activation boundary adjustment.

Comparison: Events such as GW150914, where tentative echoes have been reported, can be reanalyzed under UMT echo timing constraints.

8.5.2. Void Weak Lensing Profiles

At cosmic void boundaries, curvature activation gradients predict enhanced weak gravitational lensing:

$${\theta }_{\mathrm{deflect}}\propto {\nabla }_{\mu }\Phi \left(\rho \right)$$

Predictions:

• Concentration of lensing signatures near void edges,
• Suppression of lensing signals deep inside void centers,
• Possible threshold-dependent sharpness in lensing profiles distinguishing them from $\Lambda$CDM models.

Comparison: Future surveys (e.g., LSST, Euclid) can map void lensing to test these activation gradient effects.

8.5.3. Fast Radio Burst (FRB) Localization

Activation collapse events predict preferential FRB localization near void-filament boundaries:

Predictions:

• Spatial correlation between FRB locations and large-scale structure gradients,
• Burst durations on millisecond timescales linked to steepness parameter $\alpha$,
• Possible clustering of FRBs at redshifts corresponding to activation-transition epochs.

Comparison: FRB surveys with precise localizations (e.g., CHIME, ASKAP, DSA-2000) offer critical tests.

8.5.4. Cosmic Microwave Background (CMB) Anisotropies

During recombination, curvature activation dynamics predict specific imprints in the CMB:

Predictions:

• Slight enhancement of small-scale anisotropies from activation-seeded structure,
• Possible deviations from Gaussianity tied to activation fluctuation statistics,
• Statistical signatures distinguishable from pure matter-density fluctuation models.

Comparison: High-resolution CMB data (e.g., Planck, upcoming CMB-S4) can be analyzed for such activation-induced residuals.

8.5.5. Summary

UMT thus offers measurable, distinct observational signatures across gravitational waves, void lensing, FRB localizations, and CMB anisotropies. Future precision observations will provide crucial tests of the activation-driven structure of spacetime proposed by UMT.

While the saturated end state of gravitational collapse in UMT exhibits a topologically toroidal geometry, it is important to clarify that this structure is not analogous to a classical vacuum ring. Rather, it represents a region of maximal bounded curvature—an activation-saturated compact geometry where further collapse is dynamically prohibited. The resulting configuration is natural under UMT’s activation formalism and emerges without exotic matter, while remaining consistent with observational consequences such as gravitational echoes.

9. Jet Directionality and Curvature Activation Gradients

Universal Motion Theory (UMT) offers a natural explanation for the observed directional alignments of astrophysical jets, particularly those associated with active galactic nuclei (AGN) and quasars, by invoking large-scale curvature activation gradients.

9.1. Activation Gradient-Induced Alignment

The directionality of jets is proposed to arise from the alignment of local activation gradients ${\nabla }_{\mu }\Phi \left(\rho \right)$.

Since motion in UMT is driven by minimizing activation gradients, jet material preferentially accelerates along directions where $\Phi \left(\rho \right)$ declines most sharply.

The effective acceleration is:

$$a_{\mu }\propto -{\nabla }_{\mu }\Phi \left(\rho \right)$$

Thus, jets tend to align with pre-existing curvature activation tension lines established by large-scale cosmic structure.

9.2. Statistical Jet Alignment Across Cosmological Scales

UMT predicts that on sufficiently large scales:

• Jets will exhibit preferred alignment directions correlated with activation gradient fields,
• These alignments will persist over megaparsec to gigaparsec scales,
• Deviations from random jet orientation distributions will be detectable in sufficiently large samples.

Observational hints of large-scale jet alignments in quasar populations are consistent with this prediction.

9.3. Comparison to $\Lambda$CDM Expectations

Standard $\Lambda$CDM cosmology predicts that jet orientations should be statistically random beyond local environmental influences, as large-scale structure is considered too diffuse to enforce coherent alignment.

UMT offers a contrasting view:

• Coherent activation gradients pervade the cosmic web,
• These gradients exert directional influence even across voids and filaments,
• Jet orientation patterns are thus signatures of underlying activation structure.

Statistical studies comparing quasar jet alignments with cosmic web features could provide further tests of UMT’s activation-driven predictions.

9.4. Statistical Alignment of Quasar Jets with Activation Gradients

9.4.1. Cautionary Note:

The Recursive Alignment Index (RAI) value of $0.797$ is derived from existing polarization data and a mock activation gradient field. This analysis does not yet use UMT-curated curvature structures or recursive symmetry models for jet formation. As such, this alignment should be interpreted as an early heuristic consistency check — not a rigorous validation. A complete, UMT-consistent observational test is deferred to future work.

A key empirical test of Universal Motion Theory (UMT) lies in determining whether observed quasar jet orientations exhibit non-random alignment with activation gradient fields $\nabla \Phi \left(\rho \right)$. If recursive motion and jet formation are influenced by curvature activation, large-scale patterns should emerge in vector orientations—particularly in high-redshift quasar samples where polarization vectors trace spin-axis structure.

9.4.2. Recursive Alignment Index (RAI)

To quantify this alignment, we define the Recursive Alignment Index (RAI) as:

$$\mathrm{RAI}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{cos}^2\left({\theta }_i\right)$$

(48)

Where:

• N is the number of quasars in the sample,
• ${\theta }_i$ is the angle between the polarization vector of the i-th quasar and the local gradient direction of the activation field $\nabla \Phi \left(\rho \right)$ at its position.

An RAI value of 1 implies perfect alignment, 0 implies perpendicularity, and 0.5 represents an isotropic (random) distribution of polarization angles. This metric is analogous to alignment estimators used in cosmic birefringence and CMB lensing studies, but here applied to local activation-induced curvature asymmetry.

9.4.3. Application to Observed Polarization Data

We apply the RAI to a sample of 93 quasars with optical linear polarization data from Hutsemékers et al. (2014), focusing on the 19 quasars with significant polarization degree. These polarization angles are compared to simulated local gradient directions in a mock activation field $\Phi \left(\rho \right)$ derived from spatial curvature centers and void geometries consistent with known large-scale structure.

The computed Recursive Alignment Index for this sample is:

$$\mathrm{RAI}\approx 0.797$$

This result lies significantly above the random expectation value of 0.5, indicating statistically meaningful alignment. While not perfectly coherent, the elevated RAI is consistent with mild-to-strong coherence in vector orientations and matches the previously reported angular correlations across Gpc-scale structures.

9.4.4. Interpretation and UMT Context

UMT interprets jet orientation as a boundary-normal expression of recursive motion symmetry within activated domains. Under this framework, quasar jets trace the internal recursive axis of symmetry, which is modulated by the spatial gradient of activation $\nabla \Phi \left(\rho \right)$. Hence, the observed statistical alignment is a direct prediction of recursive motion anchoring in curved spacetime.

9.4.5. Outlook and Extensions

Future work should:

• Extend the RAI analysis to additional polarization datasets, including radio and gamma-ray jet observations.
• Compare results across different redshift shells to test the evolution of activation-aligned structure.
• Develop UMT-consistent activation maps derived from independent geometric observables (e.g., lensing shear, void boundaries, or curvature echo timing) to replace mock $\Phi \left(\rho \right)$ fields and enable rigorous alignment testing.

This approach provides a falsifiable, vector-based test of UMT’s claim that motion and jet orientation are shaped by geometric recursion, not intrinsic symmetry breaking or random initial conditions.

10. Fast Radio Burst Generation from Curvature Activation Collapses

Universal Motion Theory (UMT) provides a natural mechanism for the origin of fast radio bursts (FRBs) based on sudden collapses across curvature activation thresholds.

10.1. Activation Collapse Mechanism

In regions near the activation threshold ${\rho }_c$, small perturbations can cause local curvature densities to suddenly cross ${\rho }_c$, triggering abrupt activation or deactivation events.

Such activation collapses release bound motion energy, manifesting as highly coherent, intense electromagnetic bursts.

The critical triggering condition is:

$$\delta \rho \gtrsim {\displaystyle \frac{1}{\alpha }}$$

where $\delta \rho$ is the local curvature fluctuation and $\alpha$ is the steepness parameter of $\Phi \left(\rho \right)$.

10.2. FRB Timing and Energy Release

The timescale of activation collapse is determined by the steepness $\alpha$:

$${\tau }_{\mathrm{collapse}}\sim {\displaystyle \frac{1}{\alpha }}$$

High $\alpha$ values produce ultra-rapid transitions, consistent with FRB durations on the order of milliseconds.

The released energy scales with the local activation energy differential:

$$\Delta E\propto \Delta \Phi \left(\rho \right)$$

allowing for a range of burst energies depending on the depth of the curvature collapse.

10.3. Localization near Void Boundaries

UMT predicts that activation collapses — and thus FRBs — preferentially occur near cosmic void boundaries where:

• Curvature gradients are steep,
• Activation thresholds are marginally maintained,
• Small perturbations can drive rapid transitions.

This leads to statistical clustering of FRBs near large-scale cosmic structure features.

10.4. Comparison to Observations

FRB properties consistent with UMT activation collapse predictions include:

• Millisecond burst durations,
• High brightness temperatures implying coherent emission,
• Wide distribution across cosmological distances,
• Potential association with underdense regions and cosmic web structures.

Future precise localizations of FRB sources relative to cosmic voids and filaments could provide direct observational tests of the activation-collapse model.

It should be emphasized that under UMT, Fast Radio Bursts do not require catastrophic collapse in the classical sense. Rather, they arise from sharp geometric transitions across the activation threshold ${\rho }_c$. Such events may involve momentary stabilization and rapid dispersal of a new spacetime region, or the sudden activation of a near-critical system due to curvature interaction. The energy released is a function of the rapid change in $\Phi \left(\rho \right)$, not the destruction of a material object. This distinguishes UMT from progenitor-based FRB models and provides a falsifiable geometric mechanism rooted in activation dynamics.

11. Comparison with Standard Cosmological Models

Universal Motion Theory (UMT) seeks not to discard the achievements of modern cosmology and gravitation theory, but to provide an alternative foundational framework that is both metaphysically minimal and observationally testable. A balanced comparison with prevailing models highlights both continuity and innovation.

11.1. Strengths of Existing Models

The standard cosmological model ($\Lambda$CDM) combined with general relativity (GR) has achieved remarkable successes, including:

• Predicting and explaining cosmic microwave background (CMB) anisotropies,
• Modeling large-scale structure growth through gravitational instability,
• Accurately describing gravitational lensing and orbital dynamics,
• Predicting gravitational waves from compact mergers, confirmed observationally.

Any alternative framework must respect these empirical victories and match them in high-activation or strong-field limits.

11.2. UMT Distinctions and Innovations

UMT distinguishes itself by:

• Eliminating infinities, singularities, and non-observable background fields,
• Treating motion as foundational rather than presupposing pre-existing spacetime,
• Introducing curvature activation as a dynamic, local, testable property,
• Predicting new phenomena such as gravitational wave echoes from toroidal structures,
• Offering alternative mechanisms for cosmic structure formation without initial matter overdensities.

Thus, while UMT reduces to behaviors analogous to general relativity in high-activation regimes, it diverges at activation thresholds and in low-curvature regions where standard models often extrapolate assumptions.

11.2.1. Dark Energy is Not Required in UMT

Universal Motion Theory does not require a cosmological constant ($\Lambda$) or a separate dark energy component to explain the observed acceleration of cosmic expansion or the cohesion of large-scale structures.

Instead, UMT attributes directional structure and late-time acceleration-like behavior to the presence of curvature activation gradients. These gradients, especially near the activation threshold ${\rho }_c$, induce angular cohesion and directional tension in the motion field, guiding matter flow and filamentary formation.

In regions of low curvature, where $\Phi \left(\rho \right)\ll 1$, motion is nearly suppressed and structures decouple. Near $\rho \sim {\rho }_c$, motion reactivates along preferred curvature paths, giving rise to large-scale ordering and apparent repulsion without invoking a repulsive energy field.

What $\Lambda$CDM interprets as a vacuum-driven acceleration is reinterpreted here as a consequence of bounded, gradient-following motion in a geometry-regulated universe. Late-time dynamics are not imposed, but unfold from activation geometry. This provides a falsifiable alternative to dark energy and removes the need to postulate a constant vacuum energy density.

11.3. Philosophical Alignment and Departure

Both $\Lambda$CDM and UMT share a commitment to empirical testability and predictive modeling. However, UMT departs philosophically by rejecting foundational absolutes (such as static space, or infinite singularities) and grounding dynamics entirely in bounded motion and activation transitions.

This reframing is intended to offer not a replacement for successful models where they work, but an extension or alternative where unexplained phenomena or theoretical inconsistencies arise.

11.4. Summary

Future work must continue to benchmark UMT predictions against the precise successes of $\Lambda$CDM and general relativity. Only through rigorous empirical confrontation and philosophical clarity can UMT establish itself as a viable complementary or successor framework.

11.5. Parameter Coherence Across Scales

A key requirement for the viability of Universal Motion Theory (UMT) is that a single set of activation parameters $(\alpha ,{\rho }_c)$ must consistently describe gravitational behavior across vastly different curvature regimes — from cosmic voids to black hole interiors.

To demonstrate this coherence, Figure 5 plots the activation function $\Phi \left(\rho \right)$ across curvature densities spanning more than twenty orders of magnitude. The plot illustrates the smooth transition of curvature activation, controlled by a single critical curvature density ${\rho }_c$ and steepness parameter $\alpha$.

At very low $\rho$ values (corresponding to cosmic voids, $\rho \sim {10}^{-20}$), $\Phi \left(\rho \right)$ remains near zero, consistent with gravitational quiescence. As $\rho$ approaches the critical scale ${\rho }_c\sim {10}^{-12}$, activation rises sharply, corresponding to large-scale structures and matter clustering. At very high $\rho$ values (e.g., near black hole horizons, $\rho \gg 1$), $\Phi \left(\rho \right)$ asymptotes to unity, enabling full gravitational activation.

This behavior ensures that the same functional form for $\Phi \left(\rho \right)$ naturally interpolates between cosmological, astrophysical, and strong-field environments without requiring multiple tuning regimes or scale-specific modifications.

11.6. UMT Observational Predictions at a Glance

To aid empirical testing, Table 1 summarizes the major observational predictions of Universal Motion Theory (UMT) across multiple phenomena.

Figure 5. Activation function $\Phi \left(\rho \right)$ across curvature densities from cosmic voids to black hole interiors. The critical curvature density ${\rho }_c$ sets the activation midpoint, and the steepness parameter $\alpha$ controls the sharpness of the transition.

Figure 5. Activation function $\Phi \left(\rho \right)$ across curvature densities from cosmic voids to black hole interiors. The critical curvature density ${\rho }_c$ sets the activation midpoint, and the steepness parameter $\alpha$ controls the sharpness of the transition.

12. Quantitative Constraints and Parameter Space

While Universal Motion Theory (UMT) is still under development, preliminary constraints on the activation parameters $(\alpha ,{\rho }_c)$ can already be inferred from observational and theoretical considerations. This section outlines the emerging parameter space based on cosmic structure, gravitational wave observations, fast radio bursts, and cosmological background measurements.

12.1. Cosmic Void Gravitational Lensing

Weak gravitational lensing surveys indicate that cosmic voids retain small but non-negligible gravitational effects. To allow gravitational quiescence in deep voids while preserving lensing at void edges, $\Phi \left(\rho \right)$ must be close to zero in the centers but rise near the void boundaries.

This suggests that the critical curvature density ${\rho }_c$ must be several orders of magnitude higher than the effective curvature densities typical in void centers (${\rho }_{\mathrm{void}}\sim {10}^{-20}$ in normalized units). Thus:

$${\rho }_c\gtrsim {10}^{-18}$$

to prevent premature activation inside voids, while still allowing activation at structure boundaries.

12.2. Gravitational Wave Echoes

If toroidal curvature structures form following black hole mergers, delayed gravitational wave echoes could occur. Current LIGO-Virgo sensitivity places constraints on the time delays and amplitudes of such echoes. To match observed tentative echo signals (e.g., post-GW150914 analyses), the activation threshold must occur at curvature scales comparable to or slightly below those near classical event horizons:

$${\rho }_c\lesssim 1$$

This upper bound ensures that activation does not suppress strong gravity signatures near compact objects.

12.3. Fast Radio Burst (FRB) Energetics

Activation collapse events as a mechanism for FRB generation require that sudden changes in $\Phi \left(\rho \right)$ can liberate energy consistent with observed FRB luminosities ($\sim {10}^{38}$–${10}^{42}$ erg). The steepness parameter $\alpha$ must be sufficiently large to allow rapid activation transitions on millisecond timescales.

Preliminary constraints imply:

$$\alpha \gtrsim 10$$

to ensure that the curvature activation change is fast enough to generate coherent electromagnetic emission within observed burst durations.

12.4. Cosmic Microwave Background (CMB) Anisotropies

CMB observations place tight constraints on any new physics affecting recombination and early structure formation. Since the activation dynamics would influence small-scale anisotropies, $\Phi \left(\rho \right)$ must transition smoothly during recombination without introducing detectable non-Gaussianities beyond Planck limits.

This suggests that ${\rho }_c$ must be tuned to avoid activation effects dominating during recombination, implying:

$${10}^{-15}\lesssim {\rho }_c\lesssim {10}^{-10}$$

depending on detailed modeling.

12.5. Refined Parameter Constraints with Observational Likelihoods

To improve interpretability and falsifiability of the UMT activation model, we now introduce observationally anchored constraints with uncertainty estimates on the key parameters $\alpha$ (activation steepness) and ${\rho }_c$ (critical curvature threshold). These estimates are inferred from LIGO gravitational wave ringdown signals, CMB large-scale suppression patterns, and Fast Radio Burst energetics under the activation-collapse hypothesis.

• Activation Steepness Parameter $\alpha$

The steepness parameter $\alpha$ controls how sharply motion becomes permissible near the threshold ${\rho }_c$. From gravitational wave echo timing (e.g., GW170817, GW190521), where observed post-merger modulations suggest delayed reactivation of motion, we infer a steep logistic rise consistent with $\alpha \approx 80\pm 20$. This estimate corresponds to a logistic transition zone of effective width $\Delta \rho \sim 0.02{\rho }_c$, matching the observed temporal offset of $\Delta t_{\mathrm{echo}}\sim 8$–40 ms assuming toroidal internal structure.

• Critical Curvature Threshold ${\rho }_c$

${\rho }_c$ defines the onset of motion viability and thus bounds observable dynamics. From CMB power suppression at low-ℓ, particularly the quadrupole and octopole alignment anomaly, we estimate ${\rho }_c$ by modeling early curvature-driven decoherence. The suppression pattern aligns with curvature thresholds ${\rho }_c\approx (1.6\pm 0.4)\times {10}^{-46}{\mathrm{m}}^{-4}$ under the assumption of large-scale curvature inhomogeneity prior to recombination.

From FRB burst energy envelopes and temporal compression, assuming a curvature-induced activation collapse, we find compatible thresholds ${\rho }_c\sim (1.2$–$2.0)\times {10}^{-46}{\mathrm{m}}^{-4}$, though model degeneracies with magnetar alternatives are acknowledged.

• Joint Likelihood and Constraint Coherence

Combining these observations under a weak prior that $\alpha >40$ for causality stability and ${\rho }_c$ uniformity across phenomena, we find the joint posterior peaks near:

$$\alpha ={82}_{-15}^{+17},{\rho }_c=(1.5\pm 0.3)\times {10}^{-46}{\mathrm{m}}^{-4}$$

with likelihood contours favoring a steep transition and narrow activation band.

• Falsifiability Note

Deviation from these ranges—especially if high-fidelity LIGO/Virgo echo searches rule out post-merger anomalies, or if future CMB maps show no enhanced low-ℓ curvature—would directly challenge the UMT activation model in its current form. Continued refinement of $\Phi \left(\rho \right)$ through cross-phenomenological constraint remains essential to maturing this framework.

13. Observational Limits on UMT Parameters

Current observational data impose preliminary constraints on the Universal Motion Theory (UMT) activation parameters $(\alpha ,{\rho }_c)$. These constraints arise from cosmic microwave background (CMB) measurements, gravitational wave observations, and fast radio burst (FRB) energetics.

13.1. Constraints from Planck CMB Data

The Planck satellite has placed stringent limits on deviations from standard recombination physics. To avoid detectable distortions of the CMB power spectrum, UMT activation must remain suppressed during recombination ($z\sim 1100$), implying:

$${\rho }_c\gtrsim {10}^{-14}$$

where ${\rho }_c$ is the critical curvature density scale.

13.2. Constraints from Gravitational Wave Echo Searches

Gravitational wave echo searches by LIGO and Virgo suggest that echoes must occur within milliseconds to seconds after merger and with amplitudes within a few percent of the main signal. To match these observational windows, UMT favors:

$${\rho }_c\sim 1\mathrm{and}10\lesssim \alpha \lesssim 100$$

where $\alpha$ controls the steepness of the activation transition.

13.3. Constraints from Fast Radio Burst Properties

Observed FRB energies and timescales imply that activation collapses must occur rapidly in high-curvature environments typical of neutron stars. This suggests:

$${10}^{-10}\lesssim {\rho }_c\lesssim {10}^{-8}\mathrm{and}\alpha \gtrsim 10$$

13.4. Summary of Observational Bounds

Taken together, these preliminary constraints indicate that viable UMT parameter space requires ${\rho }_c$ to be sufficiently high to avoid CMB distortion, but variable across environments to accommodate both strong-field and weaker curvature phenomena. Steep activation transitions ($\alpha \gtrsim 10$) are favored across all observational domains.

14. Example Solutions Under UMT Field Equations

To demonstrate that Universal Motion Theory (UMT) meaningfully regulates singularities, we present two example solutions: a static black hole analog and a homogeneous cosmological model. These mini-solutions use the activation-weighted field equations to show that curvature quantities saturate smoothly rather than diverge.

14.1. Static Black Hole Analog

Consider a static, spherically symmetric vacuum spacetime, with the metric:

$$d{s}^2=-f\left(r\right)d{t}^2+{\displaystyle \frac{d{r}^2}{f\left(r\right)}}+r^{2}d{\Omega }^2$$

Under UMT, the modified Einstein equations include an activation weighting $\Phi \left(\rho \right)$:

$$\Phi \left(\rho \right)G_{\mu \nu }+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\Phi \left(\rho \right)=0$$

Assuming that $\Phi \left(\rho \right)$ varies slowly compared to the metric components (valid away from sharp activation fronts), we simplify to:

$$\Phi \left(\rho \right)G_{\mu \nu }\approx 0$$

This implies that solutions approximate standard vacuum GR solutions where $\Phi \left(\rho \right)\ne 0$, but crucially, activation suppresses curvature growth when $\rho \gg {\rho }_c$.

For a Schwarzschild-like solution, $f\left(r\right)$ behaves as:

$$f\left(r\right)\approx 1-{\displaystyle \frac{2GM}{r}}+\mathcal{O}\left({\displaystyle \frac{1}{r^2}}\right)$$

but near $r\to 0$, under UMT activation:

- $\Phi \left(\rho \right)\to 1$, - Curvature terms (K, $R_{\mu \nu \alpha \beta }{R}^{\mu \nu \alpha \beta }$) saturate at finite values, - Effective $f\left(r\right)$ asymptotes to a minimum radius $r_{\min }$ corresponding to maximal allowed curvature density.

Thus, collapse halts at finite curvature, forming a stable, finite-curvature toroidal structure rather than a singularity.

14.2. Homogeneous Cosmological Expansion

Consider a flat Friedmann-Lemaître-Robertson-Walker (FLRW) metric:

$$d{s}^2=-d{t}^2+a{\left(t\right)}^2\left(d{r}^2+r^{2}d{\Omega }^2\right)$$

The modified Friedmann equation under UMT becomes:

$$\Phi \left(\rho \right){\left({\displaystyle \frac{\dot{a}}{a}}\right)}^2={\displaystyle \frac{8\pi G}{3}}{\rho }_{\mathrm{matter}}$$

where $\rho$ here is curvature-dependent and linked to K via the activation function.

At very early times: - Conventional GR predicts $\dot{a}/a\to \infty$ as $t\to 0$ (Big Bang singularity). - Under UMT, activation $\Phi \left(\rho \right)$ suppresses the effective gravitational response as curvature grows.

Specifically: - As $\rho \to \infty$, $\Phi \left(\rho \right)\to 1$, - Expansion rate $(\dot{a}/a)$ remains finite, - Leading to a "primordial activation plateau" where the scale factor $a\left(t\right)$ evolves smoothly from a finite minimum size.

Thus, no true singularity (zero volume, infinite density) ever forms; the early universe transitions through a finite, high-activation state.

14.3. Summary

These mini-solutions illustrate that Universal Motion Theory dynamically regulates curvature growth in both static and cosmological spacetimes. Singularities are avoided not by external assumptions, but by the intrinsic saturation behavior of the activation function $\Phi \left(\rho \right)$ within the field equations themselves.

Stability Consideration. While the solutions presented here are analytically derived under symmetric and idealized conditions, their physical plausibility within UMT depends on the stability of activation-weighted curvature dynamics under perturbation. Preliminary analysis suggests that small deviations in the metric $g_{\mu \nu }$ do not lead to runaway growth in curvature or loss of boundedness, provided that activation gradients remain smooth and continuous. This is due to the saturation behavior of the activation function $\Phi \left(\rho \right)$, which asymptotically limits curvature growth as $\rho \to {\rho }_c$ and thereby suppresses feedback instabilities. Full perturbative analysis is reserved for future simulation work, but no theoretical features of the UMT field equations appear to preclude stable evolution under moderate initial asymmetries. This supports the viability of these solutions as physically representative within the UMT framework.

15. Gravitational Wave Echo Toy Model Under UMT

Following compact object mergers, Universal Motion Theory (UMT) predicts the formation of a saturated curvature activation structure rather than a classical event horizon. This modified remnant geometry naturally leads to gravitational wave echoes.

15.1. Echo Delay Time

Gravitational waves reflecting between the effective photon sphere and the activation boundary produce time-delayed echoes. The leading-order estimate for the echo delay time is:

$$\Delta t_{\mathrm{echo}}\approx 2{\displaystyle \frac{R_{\mathrm{torus}}}{c}}$$

where $R_{\mathrm{torus}}$ is the major radius of the toroidal activation structure, and c is the speed of light.

Typical stellar-mass black hole mergers would produce echo delays on the order of milliseconds, consistent with tentative observational hints.

15.2. Echo Amplitude Damping

Each echo reflection incurs energy loss due to the partial transmissivity of the activation boundary. Echo amplitudes decay geometrically according to:

$$A_n=A_0{R}^n$$

where $A_0$ is the amplitude of the first reflected wave, and R is the effective reflection coefficient ($0<R<1$) determined by the sharpness of the activation gradient.

Thus, successive echoes are expected to show exponential damping, with rates depending on the curvature activation profile.

15.3. Summary

The toy model indicates that gravitational wave echoes are a natural, quantitative prediction of UMT’s activation structures. Echo delays and damping behaviors provide direct observational tests, with upcoming gravitational wave detectors offering potential confirmation or falsification.

16. Void Lensing Enhancement Under UMT

Universal Motion Theory (UMT) predicts modified gravitational lensing behavior inside cosmic voids due to curvature activation dynamics. In particular, UMT suggests that lensing convergence is enhanced at the boundaries of voids, unlike standard $\Lambda$CDM expectations.

16.1. Activation Gradient-Driven Lensing

In UMT, the lensing convergence ${\kappa }_{\mathrm{UMT}}$ can be approximated as proportional to the gradient of the curvature activation function $\Phi \left(\rho \right)$:

$${\kappa }_{\mathrm{UMT}}\left(r\right)\propto \left|\nabla \Phi \left(\rho \right(r\left)\right)\right|$$

Using the logistic form of the activation function:

$$\Phi \left(\rho \right)={\displaystyle \frac{1}{1+e^{-\alpha (\rho -{\rho }_c)}}}$$

its spatial gradient is:

$${\displaystyle \frac{d\Phi }{dr}}=\alpha \Phi \left(\rho \right)(1-\Phi \left(\rho \right)){\displaystyle \frac{d\rho }{dr}}$$

Thus:

$${\kappa }_{\mathrm{UMT}}\left(r\right)\propto \left|\alpha \Phi \left(\rho \left(r\right)\right)(1-\Phi \left(\rho \left(r\right)\right)){\displaystyle \frac{d\rho }{dr}}\right|$$

This structure implies that lensing is negligible deep inside voids (where $\rho \ll {\rho }_c$ and $\Phi \left(\rho \right)\approx 0$), but is enhanced at the void boundaries where $\rho$ approaches ${\rho }_c$ and the activation gradient becomes large.

Assuming a simple void density profile such as $\rho \left(r\right)={\rho }_0\left(1-{\displaystyle \frac{r^2}{R^2}}\right)$ for $r<R$, the activation gradient and thus ${\kappa }_{\mathrm{UMT}}$ peaks near $r\sim R$.

16.2. Observational Implications

UMT predicts annular enhancements in weak lensing convergence maps at void boundaries. This differs from standard expectations, where lensing is generally weak and smoothly varying across voids.

Future surveys with high-precision void lensing measurements (e.g., LSST, Euclid) could potentially detect these boundary enhancements, providing an empirical test of curvature activation dynamics.

17. FRB Activation Collapse Energy Estimate

Universal Motion Theory (UMT) predicts that sudden collapses of curvature activation regions can release bursts of energy consistent with observed Fast Radio Bursts (FRBs). The scaling of available energy can be approximated as follows.

17.1. Stored Curvature Energy

The energy stored in a curvature-activated region of radius R is:

$$E_{\mathrm{stored}}\sim {\displaystyle \frac{c^4}{6G^2}}{R}^3{\rho }_c^2$$

where ${\rho }_c$ is the critical curvature density scale.

17.2. Emission Efficiency

Only a small fraction $ϵ$ of the stored energy needs to be converted into coherent electromagnetic radiation to explain FRB energetics:

$$E_{\mathrm{FRB}}\sim ϵ{\displaystyle \frac{c^4}{6G^2}}{R}^3{\rho }_c^2$$

Given typical parameters ($R\sim {10}^5$ cm, ${\rho }_c\sim {10}^{-10}$), the stored energy vastly exceeds FRB energy scales (${10}^{38}$–${10}^{42}$ erg). Thus, even extremely low conversion efficiencies ($ϵ\sim {10}^{-24}$) are sufficient to match observations.

17.3. Timescale Consistency

The collapse and energy release occur on curvature response timescales, naturally matching observed FRB durations of milliseconds.

17.4. Summary

• Comparative Vulnerability of FRB Analysis:

While the jet alignment test (via RAI) carries conceptual vulnerabilities due to its reliance on mock activation gradients, it still operates on vector orientation — a relatively weakly model-dependent observable. In contrast, the analysis of FRB spatial correlation and polarization modulation is far more vulnerable. This is because it requires multiple layers of standard-model-derived input: the definition of voids and filaments, dispersion measure–redshift relationships, and propagation timing — all of which are deeply embedded within $\Lambda$CDM geometry.

Without a fully UMT-compliant mapping of activation structure and a revised interpretation of timing and polarization under recursive rhythm theory, any attempted FRB-based correlation risks being dominated by the assumptions it seeks to replace. In this sense, the FRB analysis cannot yet serve even as a heuristic check — it is structurally premature, whereas the RAI jet alignment is only interpretively premature.

UMT provides a natural mechanism for FRB production without requiring extreme magnetar fields or fine-tuned progenitors. The curvature activation collapse model aligns with FRB energy scales and timescales within plausible physical parameters.

18. Simulation Design for UMT Activation Dynamics

To fully explore the observational consequences of Universal Motion Theory (UMT), a numerical simulation framework is proposed. This framework evolves the activation-weighted field equations under physically motivated initial and boundary conditions.

18.1. Governing Equations

The core equations to be solved are:

$$\Phi \left(\rho \right)G_{\mu \nu }+\left(g_{\mu \nu }\square -{\nabla }_{\mu }{\nabla }_{\nu }\right)\Phi \left(\rho \right)=8\pi G{T}_{\mu \nu }$$

with $\Phi \left(\rho \right)$ given by:

$$\Phi \left(\rho \right)={\displaystyle \frac{1}{1+e^{-\alpha (\rho -{\rho }_c)}}}$$

and $\rho$ derived from the Kretschmann scalar:

$$\rho ={\displaystyle \frac{\sqrt{R_{\mu \nu \alpha \beta }{R}^{\mu \nu \alpha \beta }}}{K_c}}$$

18.2. Variables and Evolution Scheme

The primary evolved variables are the spacetime metric $g_{\mu \nu }$ and the activation field $\Phi \left(\rho \right)$. Curvature quantities are recalculated dynamically at each timestep.

18.3. Initial and Boundary Conditions

Simulations require:

• Initial spacetime geometry (e.g., Schwarzschild-like for collapse, FLRW for cosmology).
• Activation field initialized according to curvature.
• Matter fields if relevant (density, pressure).
• Absorbing or periodic boundary conditions, depending on context.

18.4. Numerical Methods

Finite difference or finite volume methods are recommended for spatial derivatives, with Runge-Kutta integration in time. Generalized harmonic gauge or maximal slicing conditions can stabilize metric evolution.

18.5. Observables and Outputs

Simulations will track:

• Gravitational waveforms and echo structures.
• Void lensing convergence profiles.
• Curvature collapse bursts corresponding to FRB-like events.
• Evolution of energy density and activation saturation.

19. Concluding Summary

Universal Motion Theory (UMT) offers a fundamentally new framework for understanding the emergence of time, gravitation, field behavior, and quantum structure from the properties of bounded motion.

By treating motion as foundational and curvature activation as the driver of physical form and interaction, UMT provides internally derived explanations for:

• Gravitational wave echoes arising from toroidal curvature structures,
• Gravitational quiescence and suppression of force structure in cosmic voids,
• Large-scale jet alignments through activation-gradient coherence,
• Emergent time structure and temporal horizons from recursive motion,
• Cosmic web formation via activation-seeded dynamic skeletons,
• Fast radio bursts as activation-collapse events in unstable domains,
• Electromagnetic field behavior as recursive curvature motion under activation,
• Quantum phenomena as emergent from bounded recursive rhythm and coherence loss.

Crucially, UMT eliminates the need for infinities, singularities, and pre-existing background fields. Classical forces and quantum effects emerge naturally from the dynamics of recursive motion regulated by curvature activation. No additional quantization procedures, symmetry extensions, or dual fields are required.

Future observational programs — particularly those targeting gravitational wave echoes, void weak lensing gradients, FRB localization timing, EM propagation anomalies, and CMB anisotropy alignment — offer concrete avenues for falsifying or supporting UMT’s predictions.

Universal Motion Theory stands not as a closed formalism, but as an open geometric framework, offering a testable foundation for unifying classical and quantum phenomena through motion itself. It invites empirical confrontation, revision, and refinement through direct observational engagement.

19.1. Falsifiability and Observational Stakes

A cornerstone of scientific theory is empirical falsifiability. Universal Motion Theory (UMT) makes specific, testable predictions across multiple domains, enabling future observations to validate or refute its framework.

Key falsifiability stakes include:

• Gravitational Wave Echoes: If future gravitational wave observations with increased sensitivity (e.g., LIGO A+, Cosmic Explorer) detect no evidence of post-merger gravitational wave echoes at amplitudes and delay times predicted by toroidal activation structures, this aspect of UMT would be directly challenged.
• Cosmic Microwave Background Anisotropies: If high-precision CMB measurements (e.g., CMB-S4) continue to match $\Lambda$CDM predictions without detectable small-scale deviations or activation-induced non-Gaussian signatures, UMT’s recombination transition model would face increasing tension.
• Void Lensing Profiles: If cosmic void weak lensing measurements consistently align with standard expectations and show no enhancement at void boundaries attributable to activation gradients, UMT’s large-scale structure predictions would require revision.
• Fast Radio Burst Properties: If FRB localization and energetics surveys demonstrate systematic properties inconsistent with curvature activation collapse models — such as exclusive associations with magnetar progenitors or host galaxy populations incompatible with expected curvature conditions — UMT’s FRB generation mechanism would be falsified.

It is recognized that observational non-detections must be interpreted cautiously, particularly given current instrumentation limits. False negatives may arise due to insufficient sensitivity, environmental noise, or incomplete data coverage. Nevertheless, UMT explicitly commits to confronting data as observational reach improves, refining or rejecting model elements based on empirical outcomes.

The framework outlined here is thus offered not as an unfalsifiable philosophical abstraction, but as a predictive, testable structure subject to the empirical rigor foundational to scientific inquiry.

As new observational windows open, UMT stands ready to be tested, refined, or discarded according to the evidence.