1. Introduction
Einstein's general relativity predicted gravitational waves, which have since been experimentally confirmed. These waves manifest as perturbations in spacetime geometry, described by linearized metrics of the form:
where Represents the gravitational field perturbation. While the wave characteristics themselves have been extensively studied, this paper focuses on the interaction between gravitational waves and background gravitational fields, particularly examining energy relationships through the lens of affine geometry.
The fundamental strain-perturbation relationship can be expressed as:
This relationship provides crucial insight into the spatial deformation characteristics of gravitational waves and serves as a foundation for our subsequent analysis. More detailed basic information about the gravitational waves is given in [
2].
2. Theoretical Framework
2.1. Energy-Distance Relationships
In vacuum spacetime, gravitational wave perturbations follow the relationship:
where l represents the manifold length and t denotes time. This relationship becomes particularly interesting when examining wave propagation through regions of varying energy density.
2.2. Metric Perturbation Analysis
In regions of high energy density, gravitational wave behavior demonstrates unique characteristics. The presence of active gravitational fields transforms proper lengths into affine lengths, modifying the standard vacuum relationships. This transformation leads to:
Here, represents gravitational wave energy and Denotes the energy density along the wave's path.
2.3. Affine Length Considerations
The presence of active gravitational fields necessitates consideration of affine geometry in length measurements. This affects both wave propagation and energy distribution, leading to our primary theoretical claim:
Theorem: Gravitational waves traversing regions of affine geometry experience significant energy attenuation.
3. Mathematical Framework as an Argument for Theorem
For a spacetime region defined by vectors
and
, the perturbation relationship becomes:
This expression approaches zero as (where Is large), demonstrating energy attenuation in affine regions.
4. Conclusions
This study establishes a clear relationship between gravitational wave energy and background gravitational field strength. Our analysis demonstrates that energy density variations in space significantly influence gravitational wave propagation, particularly through the mechanism of metric distortion. The findings suggest that affine geometry plays a crucial role in gravitational wave energy attenuation, opening new avenues for understanding gravitational wave behavior in complex gravitational environments.
Future research directions might include quantitative analysis of energy attenuation rates in specific gravitational field configurations and investigation of potential observational signatures of this effect.
Author's Statements
There is no conflict of interest on this issue.
There is no commercial funding received.
Appendix A
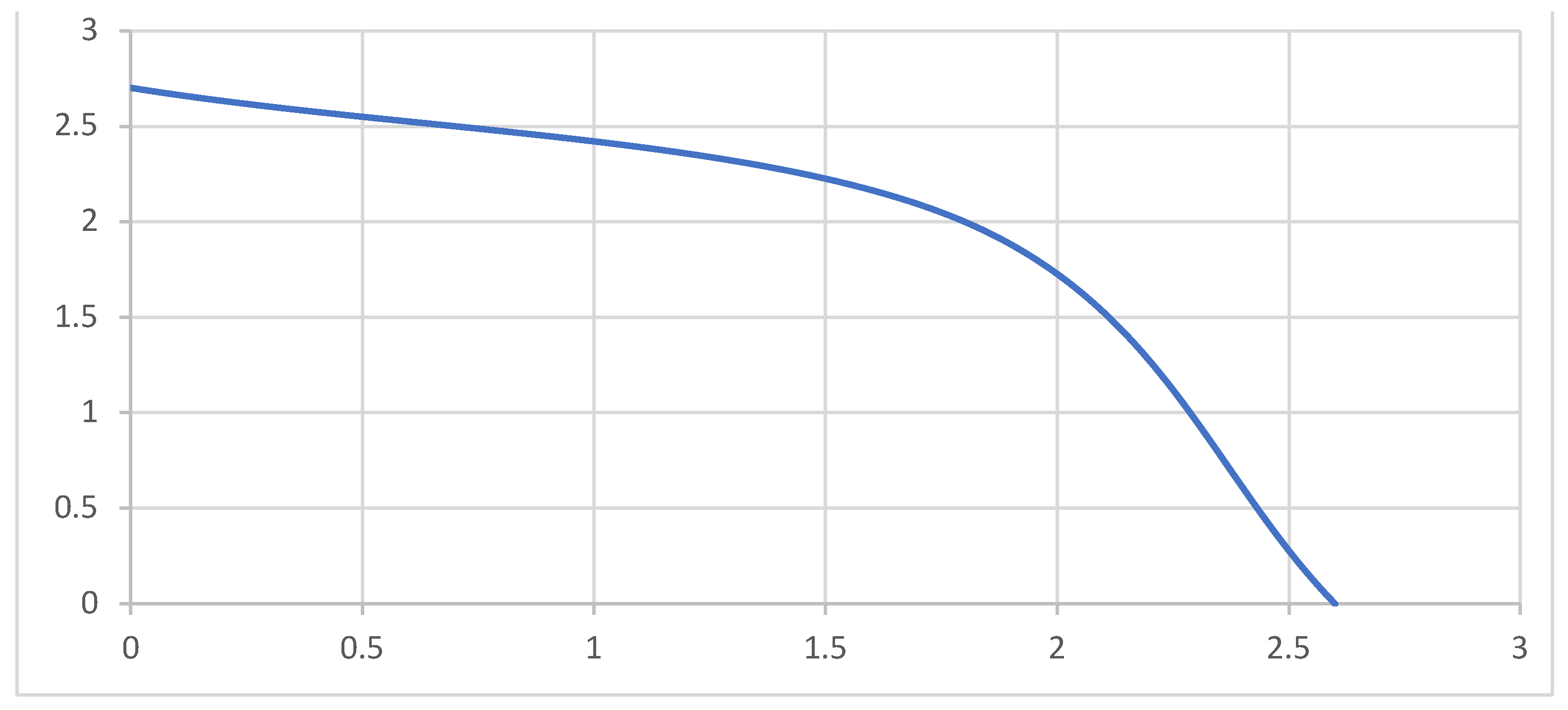
Figure A1.
Graph 1*:- With perturbation.
Figure A1.
Graph 1*:- With perturbation.
References
- A. Einstein, N. Rosen, On gravitational waves, Journal of the Franklin Institute, Volume 223, Issue 1 (1937). [CrossRef]
- The basics of gravitational wave theory by Eanna E Flanagan and Scott A Hughes. New Journal of Physics 7 (2005). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).