Submitted:
26 July 2024
Posted:
26 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Method
2.1. Premise of Analysis: The Speed of Light Invariance Hypothesis
2.2. Compatibility of New Kinetic energy Formulae with Newton’s kinetic energy equation at Low Velocities
3. Disscussion
3.1. Yuyunrui Factor
3.2. Analysis of the Unidirectional Time Scaling Factor in Three Dimensions at Light Speed
3.3. visualization of the scaling and time dilation effect for six categories
- Category I:
- Category II: , we select
- Category III: , we choose
- Category IV: , we select
- Category V: , we choose
- Category VI: , we select
4. Conclusions
References
- Newton, I. Philosophiae naturalis principia mathematica; Vol. 1, G. Brookman, 1833.
- Einstein, A. On the electrodynamics of moving bodies 1905.
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In Collected Papers: Volume V; Springer, 1937; pp. 172–197.
- Pauli, W. Theory of relativity; Courier Corporation, 2013.
- Ives, H.E.; Stilwell, G.R. An experimental study of the rate of a moving atomic clock. JOSA 1938, 28, 215–226. [Google Scholar] [CrossRef]
- Eddington, S.A.S. The nature of the physical world; University of Michigan Press, 1968.
- Bailey, J.; Borer, K.; Combley, F.; Drumm, H.; Krienen, F.; Lange, F.; Picasso, E.; Von Ruden, W.; Farley, F.; Field, J.; et al. Measurements of relativistic time dilatation for positive and negative muons in a circular orbit. Nature 1977, 268, 301–305. [Google Scholar] [CrossRef]
- Shankland, R.S. Michelson-morley experiment. American Journal of Physics 1964, 32, 16–35. [Google Scholar] [CrossRef]
- Michelson, A.A.; Morley, E.W. On the relative motion of the Earth and the luminiferous ether. American journal of science 1887, 3, 333–345. [Google Scholar] [CrossRef]
- Essen, L.; Parry, J.V. An atomic standard of frequency and time interval: a caesium resonator. Nature 1955, 176, 280–282. [Google Scholar] [CrossRef]
- Ramsey, N.F. History of atomic clocks. Journal of research of the National Bureau of Standards 1983, 88, 301. [Google Scholar] [CrossRef] [PubMed]
- Tymms, V. Newtonian mechanics for undergraduates; World Scientific Publishing Company, 2015.
- Weinberg, S. The quantum theory of fields; Vol. 2, Cambridge university press, 1995.
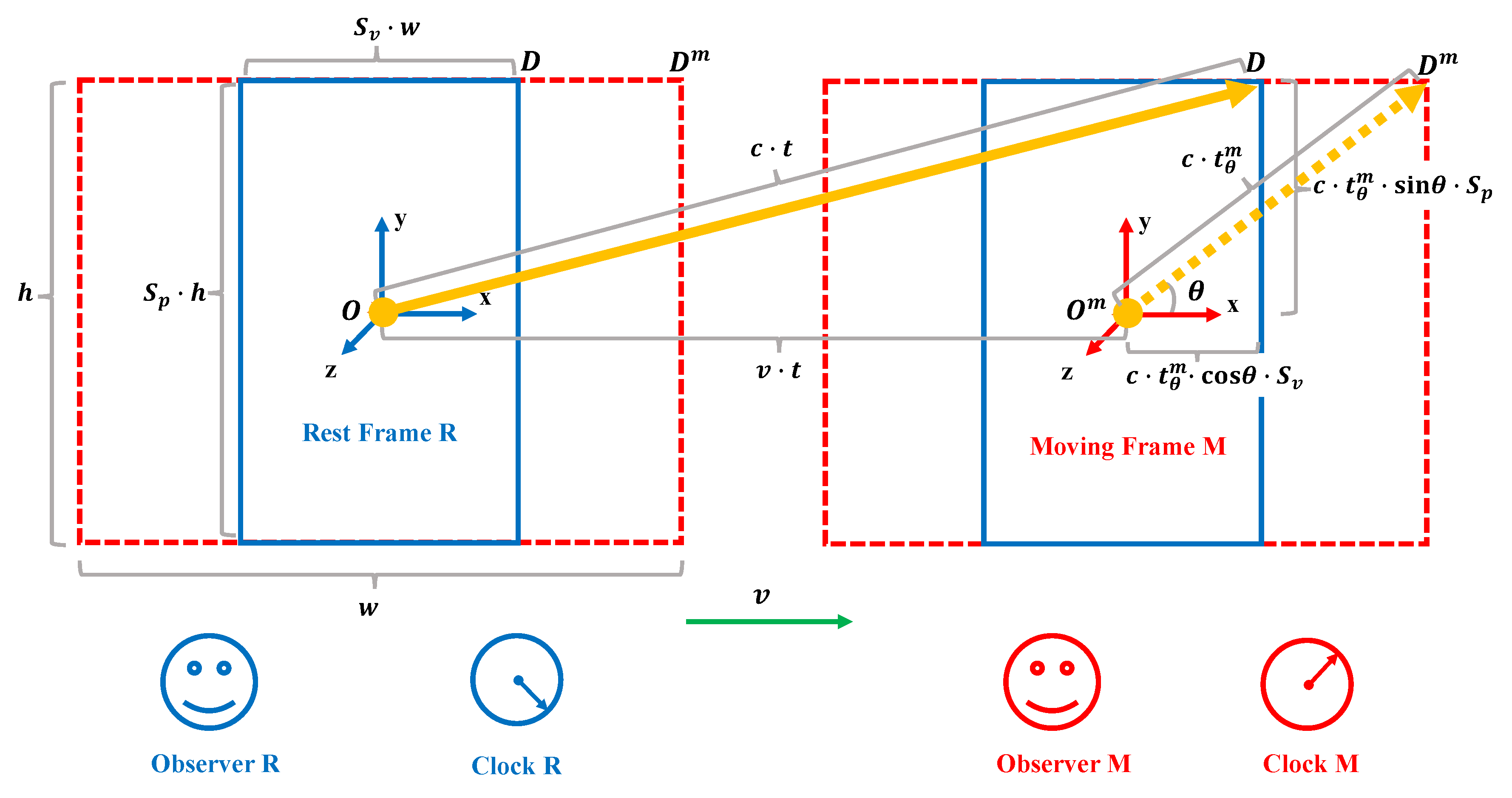
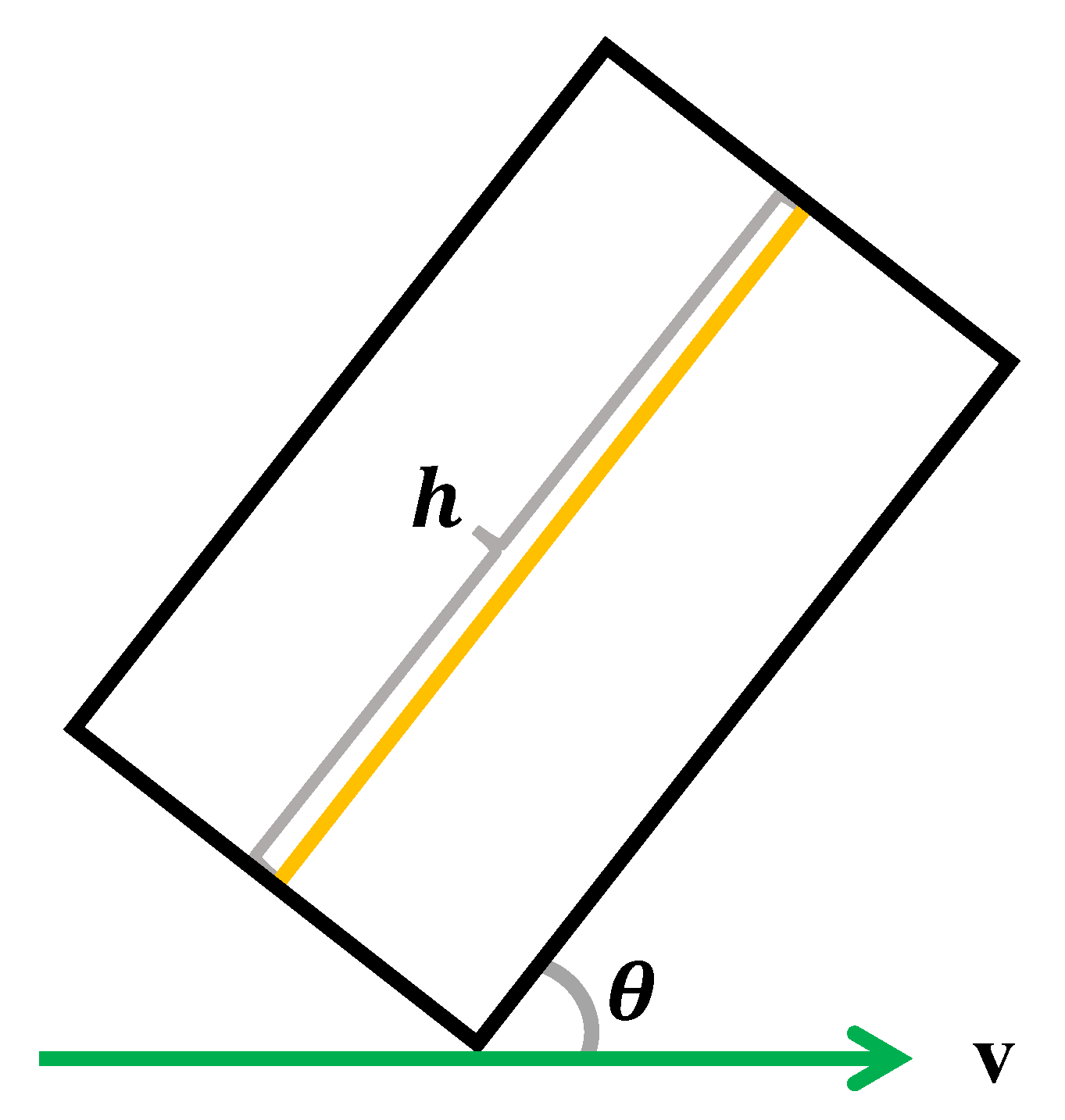

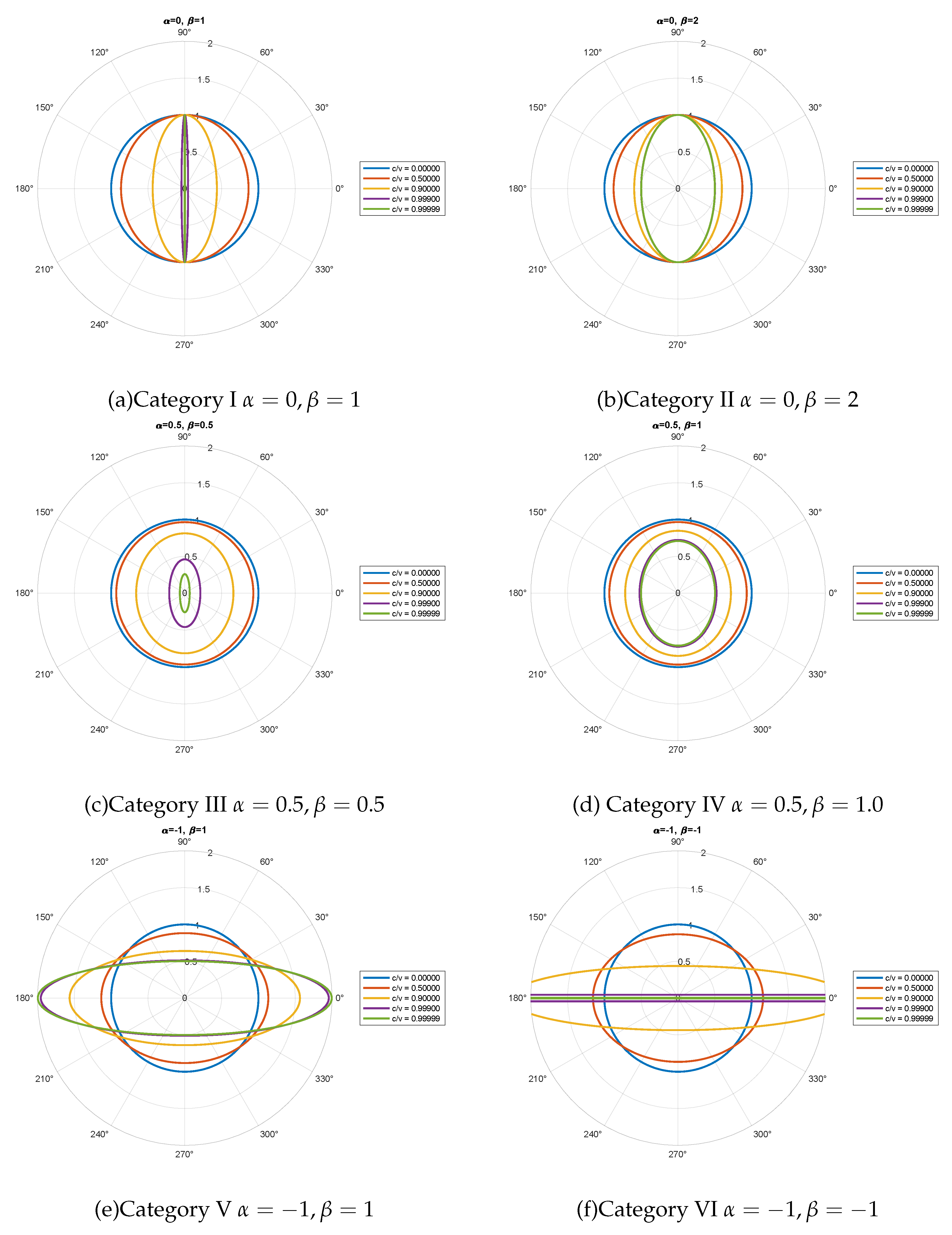
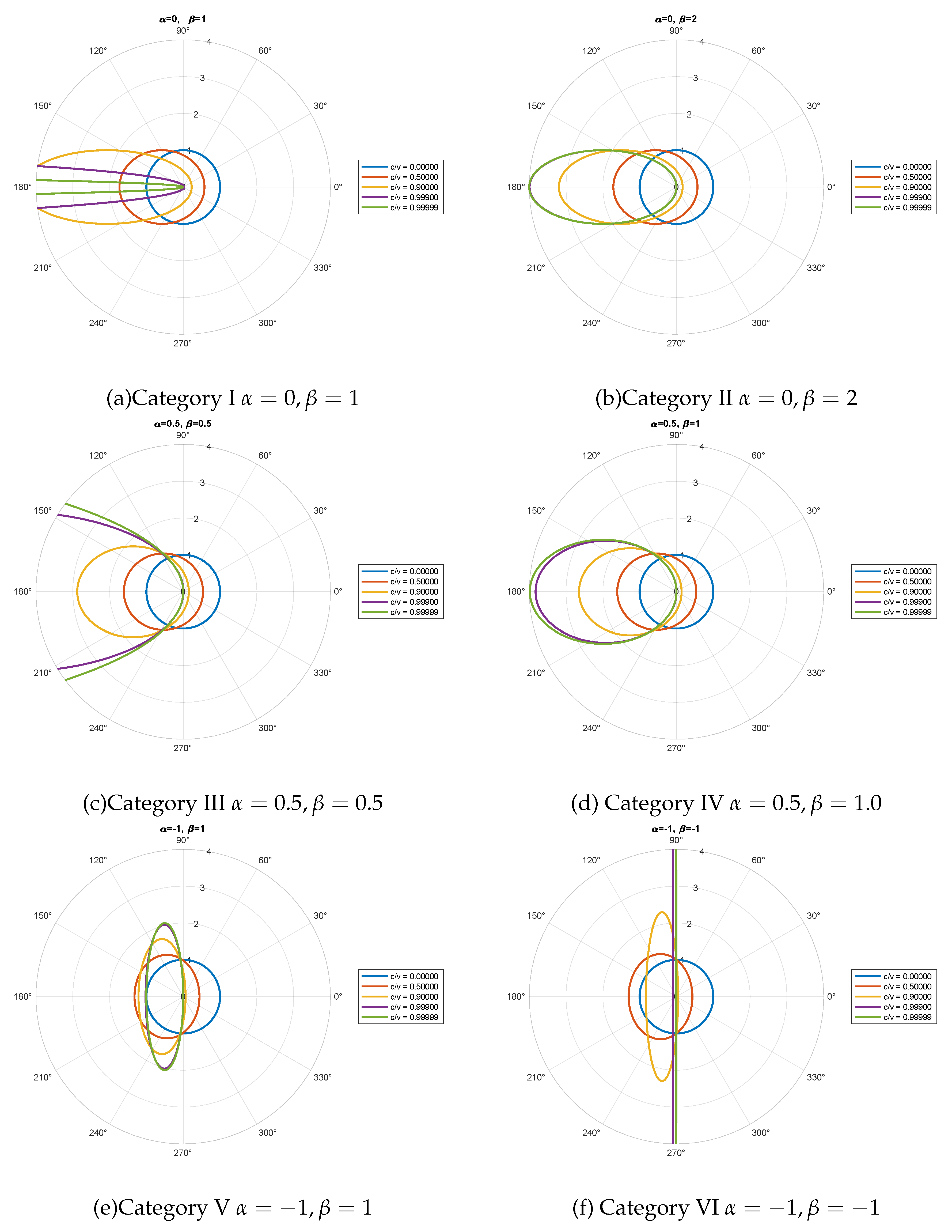
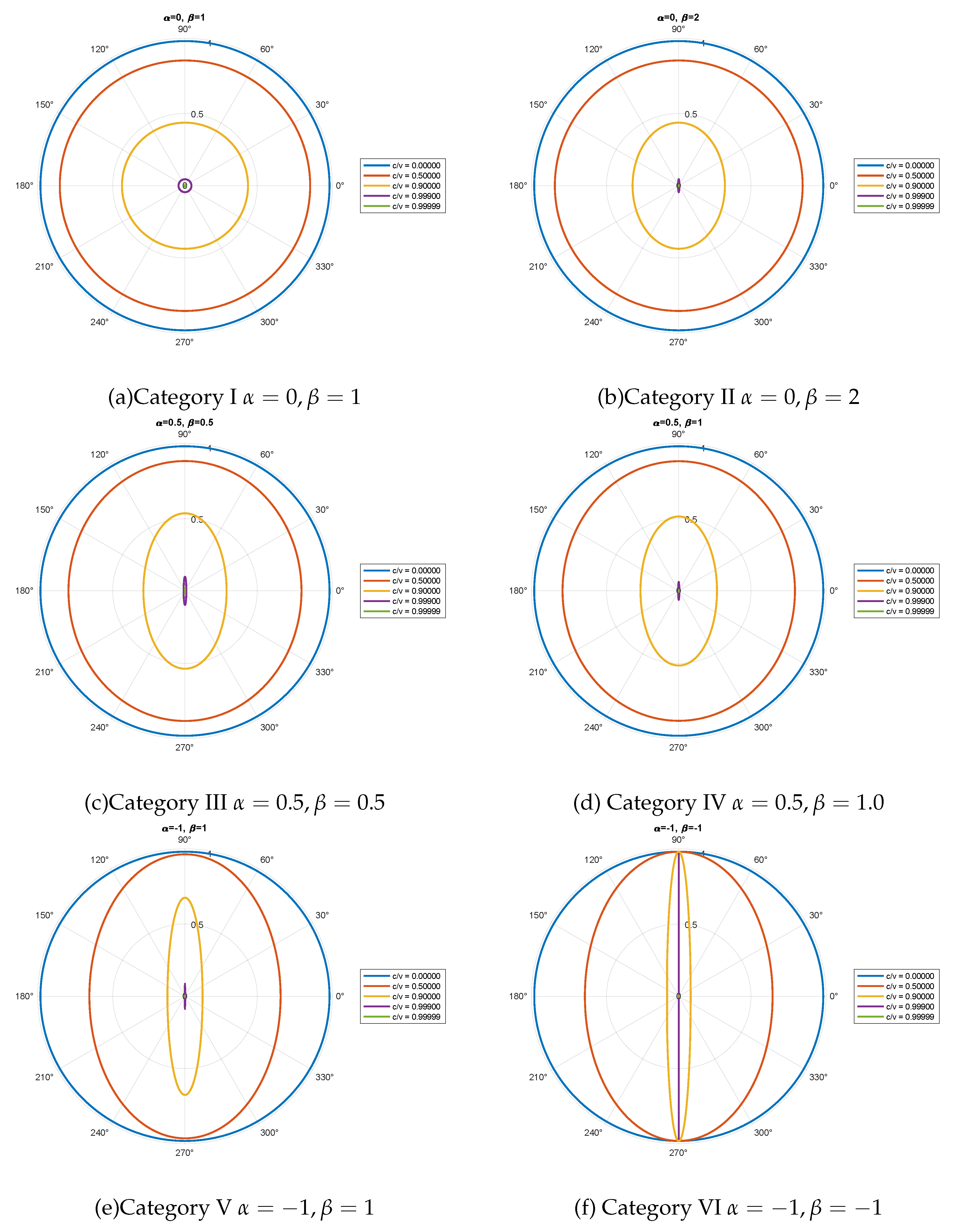
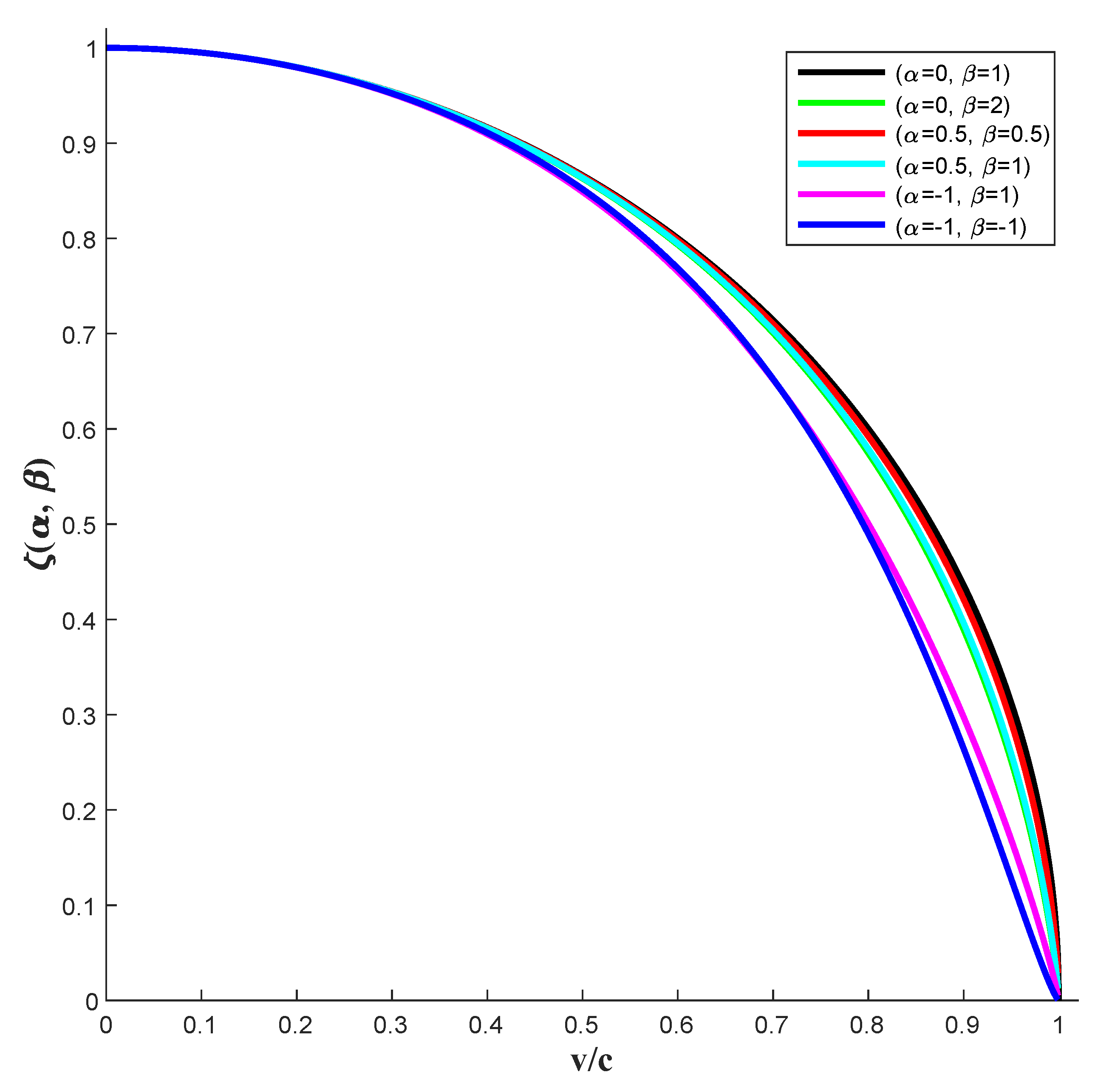
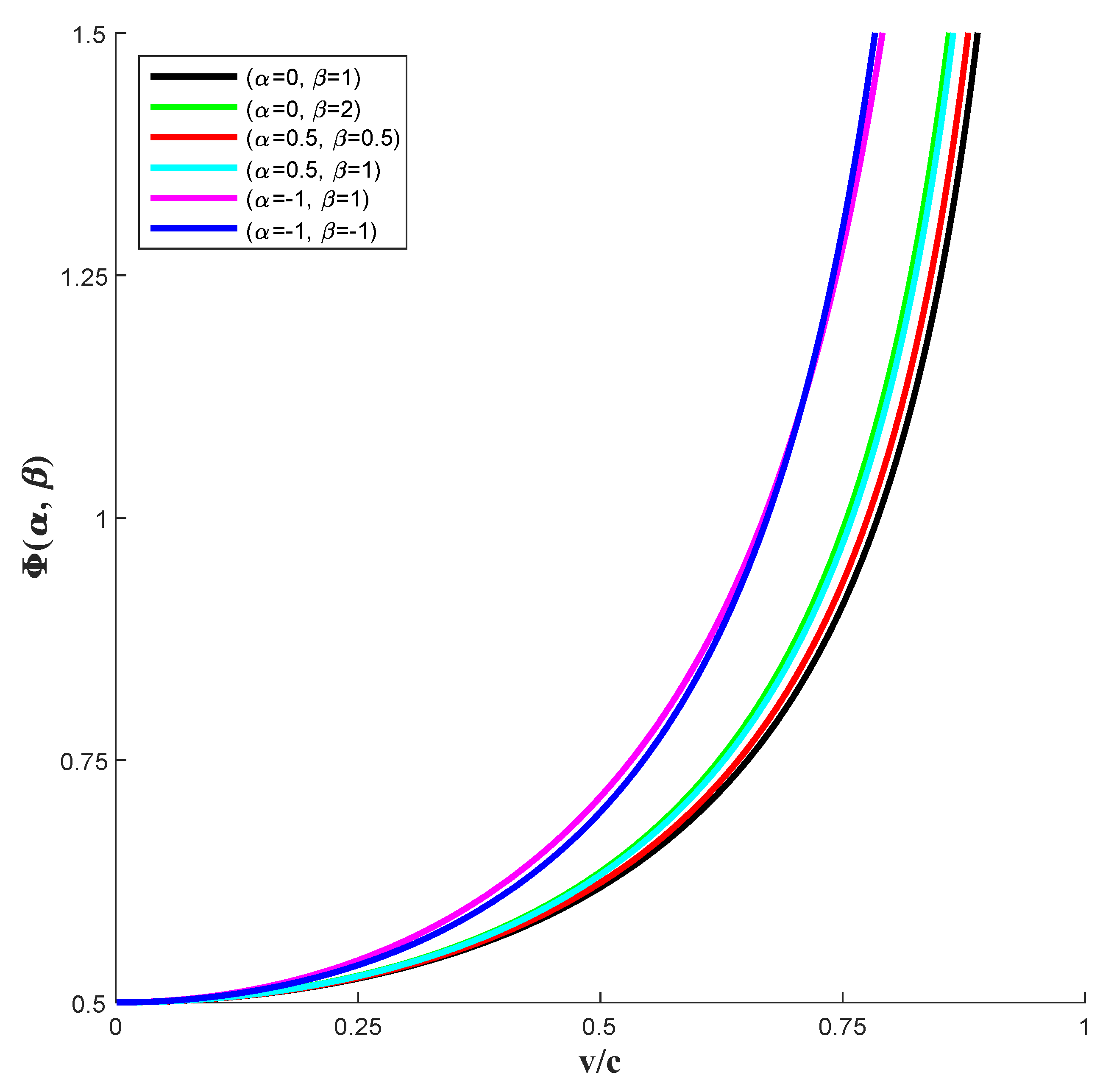
| Category | Expression | Description |
|---|---|---|
| I: = 1 | Dimensions in the direction of velocity contract as the object moves, reducing to zero as v approaches c, while dimensions perpendicular to the direction of velocity remain unchanged. | |
| II: > 1 | Dimensions in the direction of velocity contract and reduce to as v approaches c, while dimensions perpendicular to the direction of velocity remain unchanged. | |
| III: = 12+ 1 | Dimensions in both the direction of velocity and perpendicular to it reduce during motion, reaching zero as v approaches c. | |
| IV: > 12+ 1 | given by formula (17), | Dimensions in both the direction of velocity and perpendicular to it reduce, reaching and respectively as v approaches c. |
| V: > 0 | given by formula (17), | Dimensions increase in the direction of velocity and decrease perpendicular to the direction of velocity, reaching and respectively as v approaches c. |
| VI: < 0 | given by formula (17), | Dimensions increase in the direction of velocity, expanding to infinity as v approaches c, while dimensions perpendicular to the direction of velocity decrease to zero. |
| Category | Expression | Description |
|---|---|---|
| I: = 1 | when when | If the angle between the direction of the object’s motion and the spaceship’s motion is in the range , the time spent traveling unidirectionally in this direction appears to the observer in the rest frame as completely stationary. However, at an angle of , the time appears non-stationary. |
| II: > 1 | when when | When the angle is in the range , the time traveling unidirectionally appears completely stationary to the observer in the rest frame. For angles , the time appears non-stationary, increasing with the angle and reaching its fastest at . |
| III: = 12+ 1 | when when | For angles , the unidirectional travel time appears stationary to the rest frame observer. When , the travel time is non-stationary and increases with the angle, reaching its maximum at . |
| IV: > 12+ 1 | when when | For angles , the unidirectional travel time appears stationary to the observer in the rest frame. When , the travel time becomes non-stationary and speeds up with the angle, reaching its peak at . |
| V: > 0 | when when | When the angle is in the range , the unidirectional travel time appears stationary to the rest frame observer. For angles , the passage of time first speeds up and then slows down. |
| VI: < 0 | when when | If the angle is not equal to , the unidirectional travel time appears stationary to the rest frame observer. At an angle of , the travel time appears non-stationary. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




