Isothermic Patches and Property-Preserving Transformations in Gridshell Design

1. Introduction

The need for sustainable design has driven architectural geometry to explore geometric methods for creating and constructing doubly curved shapes, focusing on making them buildable by identifying those with fabrication advantages. This paper investigates the design and fabrication of gridshells based on IS using a pre-rationalization approach, with a focus on the wide variation of surface types and transformations that preserve the key geometric properties. By definition IS admit CC-patches, which are characterized by several geometric properties. To start, since they are in particular OC-patches (orthogonal conjugate), they give rise to (almost) planar mesh faces and orthogonal intersection of the network curves. Additionally, their conformal property introduces the square-like proportionality of sub-divisions.

These geometric properties of CC-patches offer numerous constructive advantages, as highlighted below in Figure 1. Hence, allowing for an efficient material usage, simplified fabrication processes, and enhanced structural stability. An important example of these advantages, is the straight unfolding of the lateral faces of Edge-Offset blocks, constructed from a discrete isothermic Minimal Surface mesh, cf. Section 2.5.3. Moreover, symmetry and periodicity found in certain CC-patches on Minimal Surfaces, allow us to construct global surfaces from fundamental patches and thus, allowing for a modular construction. This multiple CC-patch configuration is preserved by transformations giving rise to a wide variety of non-symmetric global surfaces designs, all having perfectly matching patches. Therefore, allowing for more complex topologies, something that is valuable in large scale (grid)shells design.

Section 2 introduces the geometric construction of CC-patches, focusing on six surface types; Quadrics (Quad), Cyclides (Cyc), Revolution (Rev), Minimal (MS), Constant Mean Curvature (CMC) and General (Gen) surfaces. Each type is explored in detail, with particular emphasis on the various methods used to generate it, including reparameterization and transformations preserving the CC-patch property (some of them not the type). These include Möbius, Christoffel, Goursat, and BDR transformations. While the IS are a well-established topic in (discrete) differential geometry, their application in architectural design remains somewhat challenging due to their non-trivial methods of generation. Thus, to bridge this gap, this paper provides explicit parameterizations of CC-patches of the six IS types. In doing so, facilitates the use of IS in architectural practice, allowing them to be incorporated into parametric design workflows. The paper then transitions into the practical design explorations of CC-patches.

Section 3 focuses on the design application of the CC-patches of the six types along with their associated transformations, within a pre-rationalization approach. This section emphasizes how the choice of certain initial functions, together with varying their input parameters, influences the shapes of the surfaces. Thus, showcasing the flexibility and adaptability of our approach. Of all the types, the Gen-type in particular, naturally offers the greatest design freedom. This is because it allows for any transformation to be applied to any of the other surface types, preserving only the CC-patch property while allowing the surface type to change. This characteristic is particularly valuable for adaptive designs, as it enables the structure to better address architectural needs. Finally, a prototype is presented to illustrate the architectural potential of the presented parametric design workflow of CC-patches, including the design of the structural elements that benefit from the fabrication advantages shown in the Figure 1.

2. Geometry

In this section we will use the references [1] and [2].

2.1. Isothermic Patches (CC-Patch)

To begin let us give the precise definitions of CC-patches, to this end let us start be recalling the following notions. In this paper, × and $〈·,·〉$ denote the vector and scalar products on ${\mathbb{R}}^3$ and $|·|$ denotes the associated norm. A surface patch is always given by a smooth immersion $X(u,v)$ defined on some domain in ${\mathbb{R}}^2$ with values in ${\mathbb{R}}^3$. The normal field defines a smooth immersion $N(u,v)$ with values in the unit sphere ${\mathbb{S}}^2$, called the spherical image (or Gauss map) of the surface. The partial derivatives $X_u,X_v$ allow us to define the coefficients $E,F,G$ and $e,f,g$ of the first and second fundamental forms of X. Similarly, the $N_u,N_v$ allow us to define the coefficient of the first fundamental form of N. The Gaussian and Mean curvatures are denoted by $\mathcal{K}$ and $\mathcal{H}$ respectively. In particular, if $\mathcal{K}$ is constant then X parameterizes a constant Gaussian curvature (CGC) surface and if $\mathcal{H}$ is constant then X parameterizes a constant mean curvature (CMC) surface. Finally, if $\mathcal{H}$ is identically zero then X parameterizes a Minimal Surface (MS). A principal patch is Orthogonal-Conjugate (OC-patch) (i.e., $F=f=0$) while an Isothermic Surface (IS) patch is Conformal-Conjugate (CC-patch) that is:

$$\left\{\begin{array}{cc}\left(\mathrm{Conformal}\right)\hfill & F=0,E=G\hfill \\ \left(\mathrm{Conjugate}\right)\hfill & f=0\hfill \end{array}\right.$$

(1)

with $\Lambda =E=G$ its conformal factor. There are few known examples of IS, that is, surfaces admitting CC-patches, namely: Quadrics (Quad), Cyclides (Cyc), Revolution (Rev), MS and CMC surfaces [2]. In this paper we will focus on six types:

$$\mathrm{Quad},\mathrm{Cyc},\mathrm{Rev},\mathrm{MS},\mathrm{CMC},\mathrm{Gen}.$$

This Gen-type is referring to general arbitrary surfaces admitting CC-patches. Hence, it contains the (Quad, Cyc, Rev, MS, CMC) types but not necessarily limited to them. More precisely, the Gen-type can contain an IS which is none of the mentioned types. This can typically happen after applying a transform to one of the known types, preserving the CC-patch property but not the type of the surface.

2.2. Quad-Type

The first IS type we consider is the Quad-type.

2.2.1. Quad-Type from Reparameterization

Recall that Ellipsoids (Ell), Hyperboloids of one sheet (H1s) and Hyperboloids of two sheets (H2s) can be parameterized by principal patches $Q(r,s)$:

$${\displaystyle \left(\begin{array}{c}\sqrt{\frac{(a-q_o)(a-r)(a-s)}{(a-b)(a-c)}}\\ \sqrt{\frac{(b-q_o)(b-r)(b-s)}{(b-c)(b-a)}}\\ \sqrt{\frac{(c-q_o)(c-r)(c-s)}{(c-a)(c-b)}}\end{array}\right),\left\{\begin{array}{c}{\displaystyle q_o<c<s<b<r<a}\mathrm{Ell}\hfill \\ {\displaystyle s<c<q_o<b<r<a}\mathrm{H}1\mathrm{s}\hfill \\ {\displaystyle s<c<r<b<q_o<a}\mathrm{H}2\mathrm{s}.\hfill \end{array}\right.}$$

(2)

The idea now is to reparameterize the $r,s$-curves so that the obtained new patch is not only principal but also conformal. We have the following.

Lemma 2.1.

The patch $Z(R,S)=Q\left(r\right(R),s(S\left)\right)$ where $(r,s)$ are inverse functions of

$${\displaystyle R\left(r\right)={\int }_{r_0}^r\left(\sqrt{q\left(\underline{r}\right)}\right)d\underline{r},S\left(s\right)={\int }_{s_0}^s\left(\sqrt{-q\left(\underline{s}\right)}\right)d\underline{s}}$$

(3)

where ${\displaystyle q\left(t\right)=\frac{t-q_o}{4(a-t)(b-t)(c-t)}}$ is a CC-patch.

Proof. 

By applying the inverse function rule, we obtain the functions $r\left(R\right)$ and $s\left(S\right)$ so that:

$${\displaystyle \left\{\begin{array}{cc}{Z}_R=\dot{r}{Q}_r\hfill & \mathrm{thus}{E}_Z=\frac{1}{q\left(r\right)}(r-s)q\left(r\right)=(r-s)\hfill \\ Z_S=\dot{s}{Q}_s\hfill & \mathrm{thus}{G}_Z=\frac{-1}{q\left(s\right)}(r-s)(-q\left(s\right))=(r-s).\hfill \end{array}\right.}$$

It then follows that $E_Z=G_Z=(r\left(R\right)-s\left(S\right))$. Finally, recall that reparameterization (3) preserves principal curves hence $F_Z=0$ and $f_Z=0$. □

Figure 2. Quad-type from reparameterization.

Figure 2. Quad-type from reparameterization.

2.3. Cyc-Type

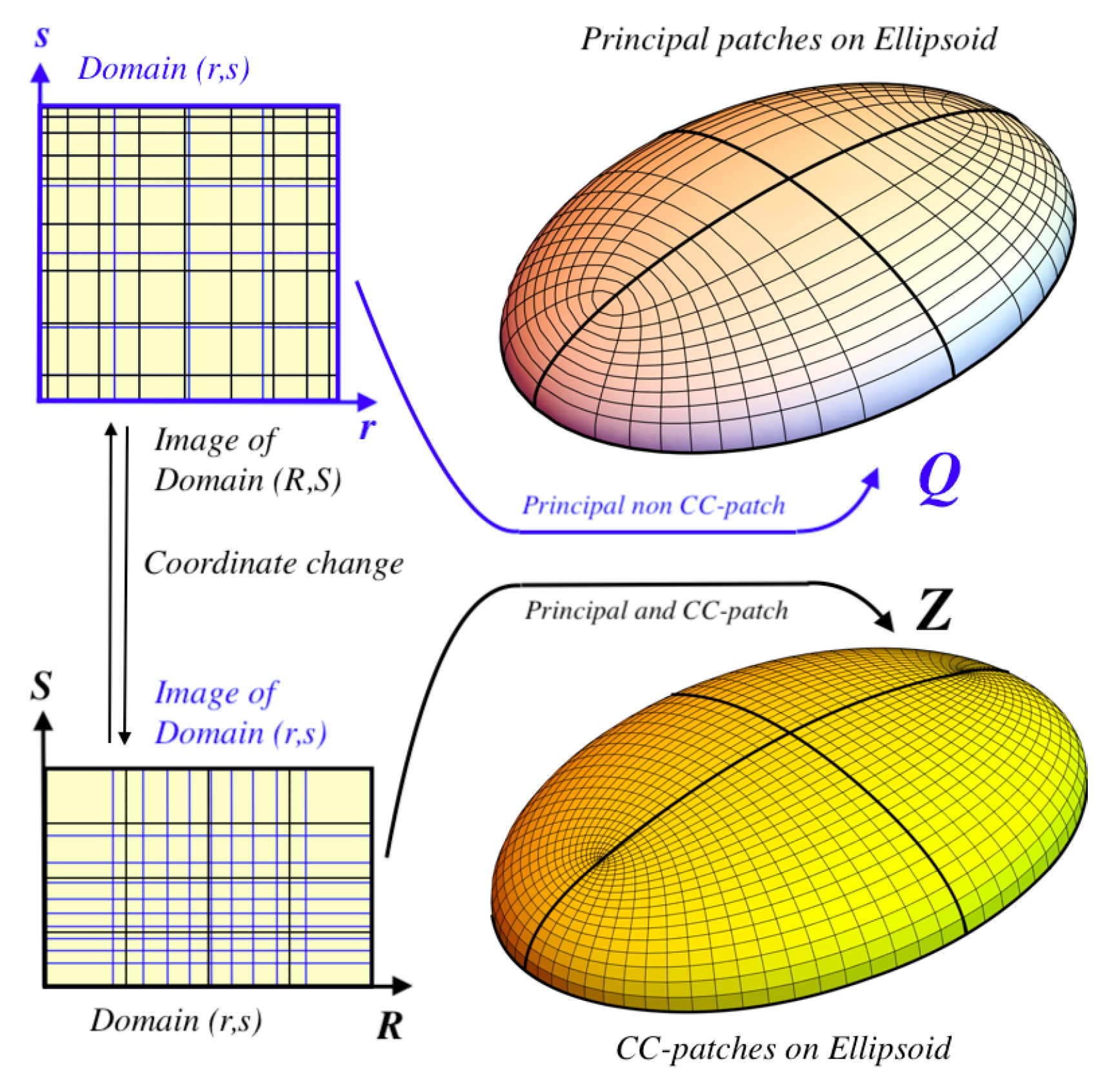
The second IS type we consider is the Cyc-type.

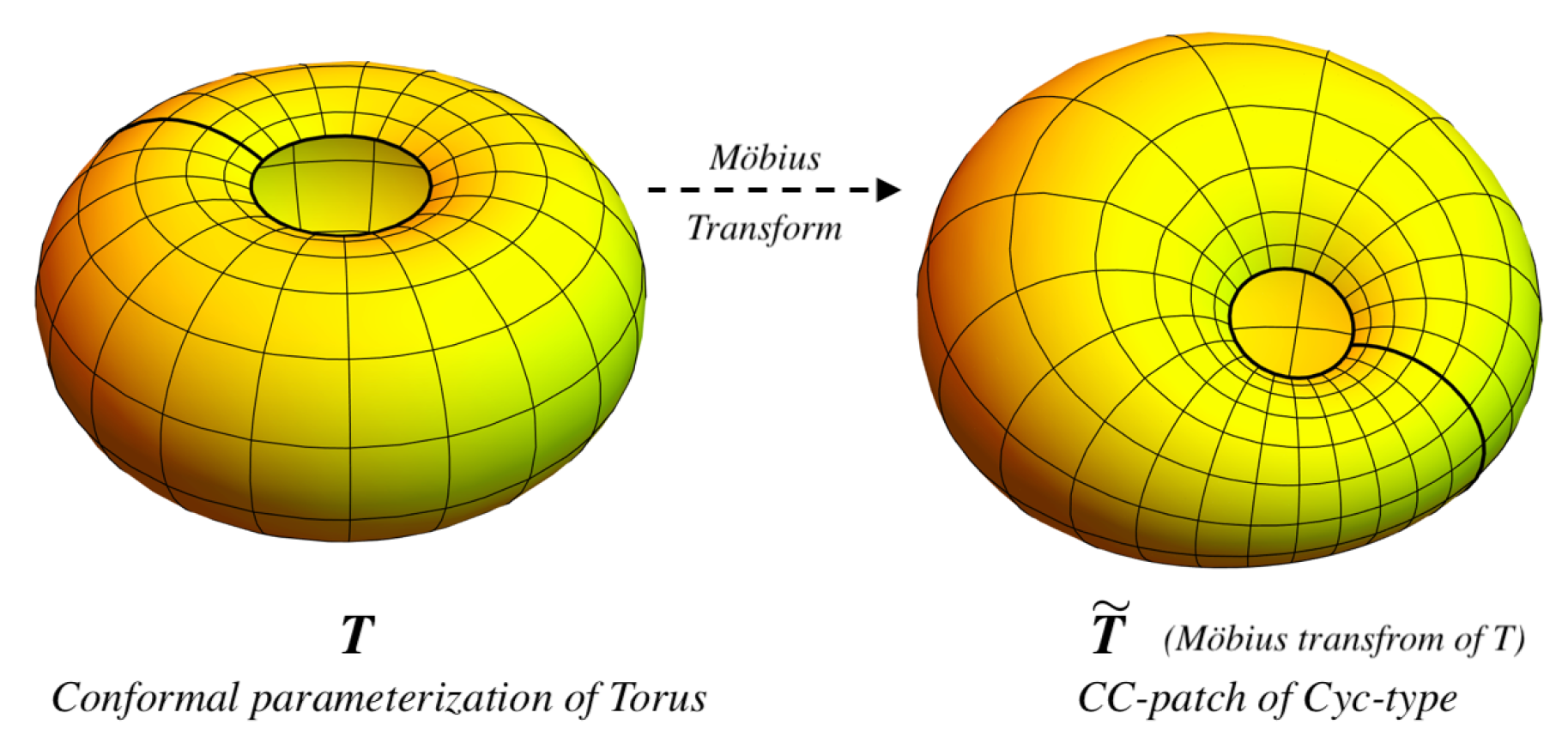
2.3.1. Cyc-Type from Möbius Transform

Recall that a Möbius transform sends circles to circles and preserves the CC-patch property [3]. Hence, consider a CC-patch $T(u,v)$ on the Torus:

$${\displaystyle \left(\frac{acos\frac{u}{a}}{\sqrt{a^2+1}-cosv},\frac{asin\frac{u}{a}}{\sqrt{a^2+1}-cosv},\frac{sinv}{\sqrt{a^2+1}-cosv}\right)}$$

(4)

then applying a Möbius transform (cf. (27)₁) yields a CC-patch of Cyc-type, as seen in Figure 3.

2.4. Rev-Type

The third IS type we consider is the Rev-type.

2.4.1. Rev-type from Reparameterization

Every revolution surface admits principal (not necessarily CC) patches defined by profile functions $\varphi ,\phi$:

$${\displaystyle \left\{\begin{array}{cc}\hfill & A(u,v)=(ucosv,usinv,\varphi (u\left)\right)\hfill \\ \hfill & B(u,v)=\left(\phi \right(u)cosv,\phi (u)sinv,u).\hfill \end{array}\right.}$$

(5)

A first approach is to find the profiles $\varphi ,\phi$ satisfying the ordinary differential equations (ODE) arising from setting $E=G$ in both cases, that is:

$${\displaystyle \varphi =\frac{u\sqrt{u^2-1}}{2}-\mathrm{arctanh}\left(\frac{\sqrt{u^2-1}}{u-1}\right),\phi =cosh\left(u\right).}$$

(6)

Similar to Lemma (2.1), a second approach is to reparametrize the patch B (same for A) and we have:

Lemma 2.2.

The patch $Z(U,V)=B\left(u\right(U),v(V\left)\right)$ is a CC-patch, where $(u,v)$ are inverse functions of

$${\displaystyle U\left(u\right)=\int \left(\frac{\sqrt{\dot{\phi }{\left(\underline{u}\right)}^2+1}}{\phi \left(\underline{u}\right)}\right)d\underline{u},V\left(v\right)=v.}$$

(7)

2.4.2. Rev-Type from Christoffel Transform

The second way to generate CC-patches X of Rev-type is obtained as Christoffel transforms (duals) of CC-patches R of Rev-type. Let now R be given by:

$${\displaystyle R(u,v)=\left(r\right(u)cosv,r(u)sinv,h(u\left)\right)}$$

(8)

which is the general form, containing the Forms (5) as special cases. We then have the following:

Proposition 2.3

(Definition). Consider the patch X defined by the differential system:

$${\displaystyle X_u=-\frac{R_u}{{\Lambda }_R},X_v=\frac{R_v}{{\Lambda }_R}.}$$

(9)

This patch is a CC-patch of Rev-type referred to as the Christoffel dual of the CC-patch R and given by:

$${\displaystyle X=\left(\frac{1}{r}cosv,\frac{1}{r}sinv,\int \frac{-\dot{h}}{r^2}\right).}$$

(10)

Proof. 

The fact that X is again is CC-patch is because Christoffel transform preserves the CC-patch property [2,4]. For the second point, note that:

$${\displaystyle \left\{\begin{array}{c}{X}_u=\left(\frac{-\dot{r}}{{\Lambda }_R}cosv,\frac{-\dot{r}}{{\Lambda }_R}sinv,\frac{-\dot{h}}{{\Lambda }_R}\right)\hfill \\ X_v=\left(\frac{-r}{{\Lambda }_R}sinv,\frac{r}{{\Lambda }_R}cosv,0\right)\hfill \end{array}\right.}$$

where ${\Lambda }_R=E_R=G_R=r^2$ is the conformal factor of R which insures the integrability condition $X_{uv}=X_{vu}$ of the system. Finally, by integration we obtain the CC-patch X of the Form (10). □

Figure 4. Rev-type from Christoffel transform.

Figure 4. Rev-type from Christoffel transform.

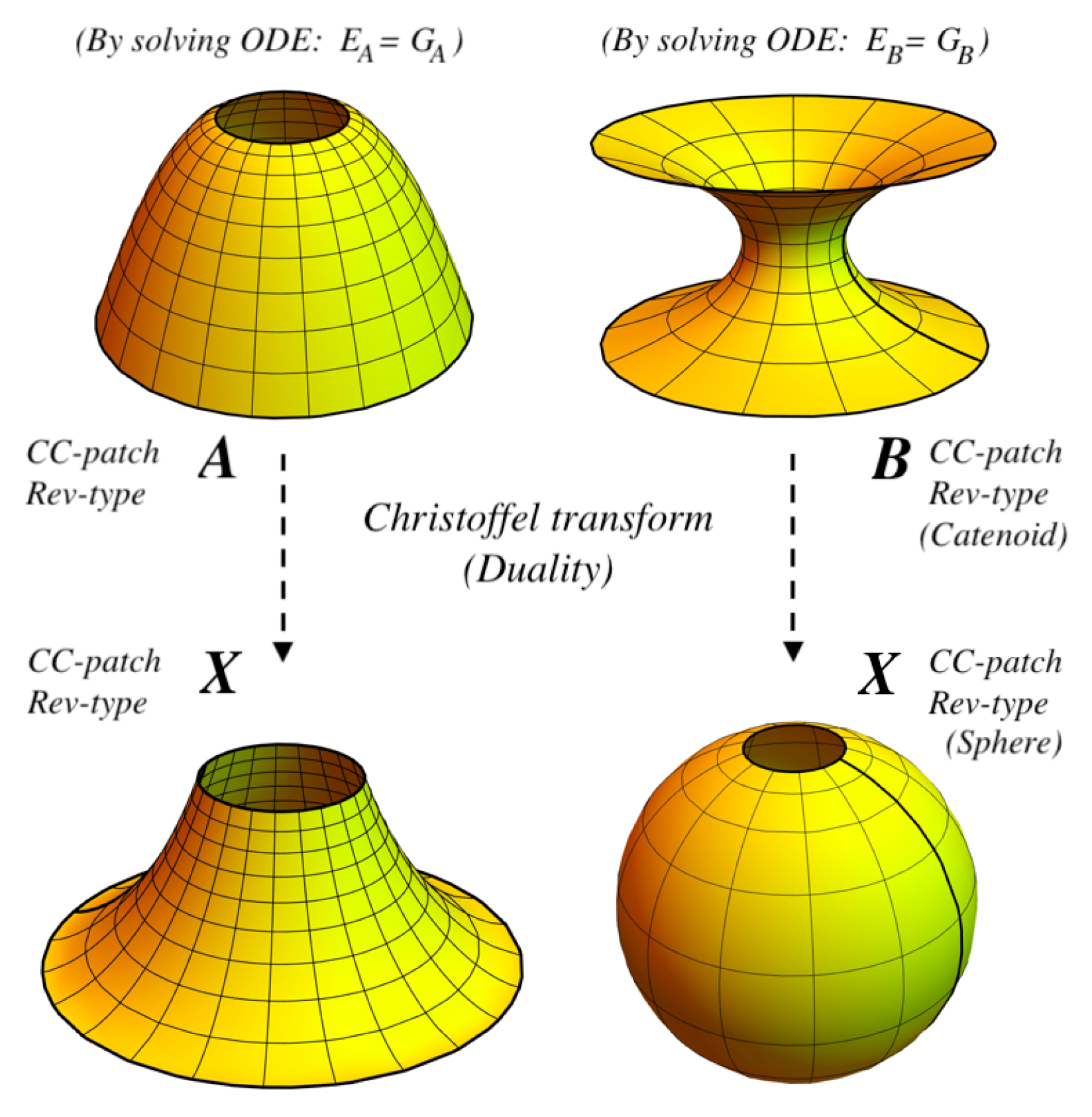
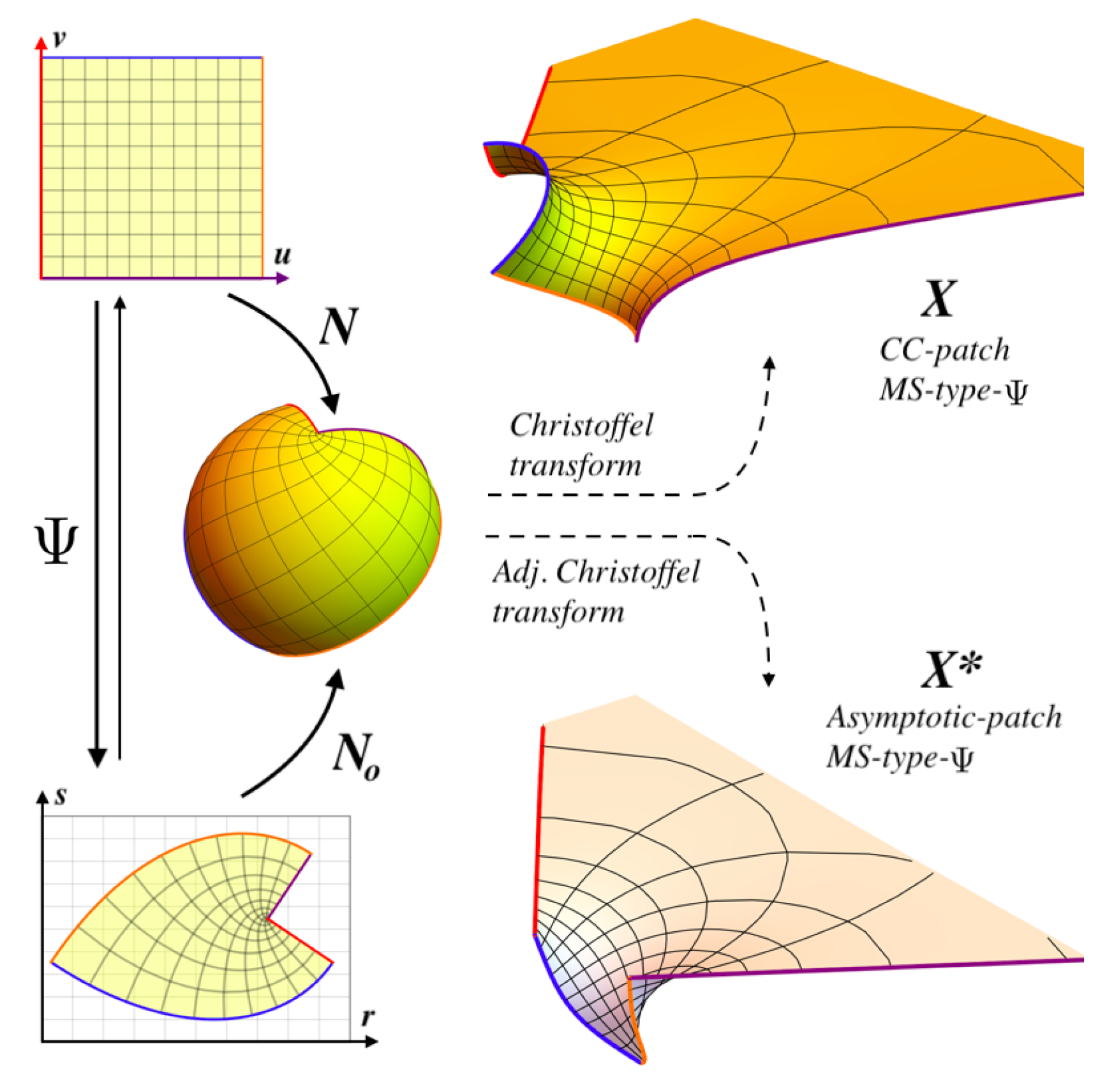
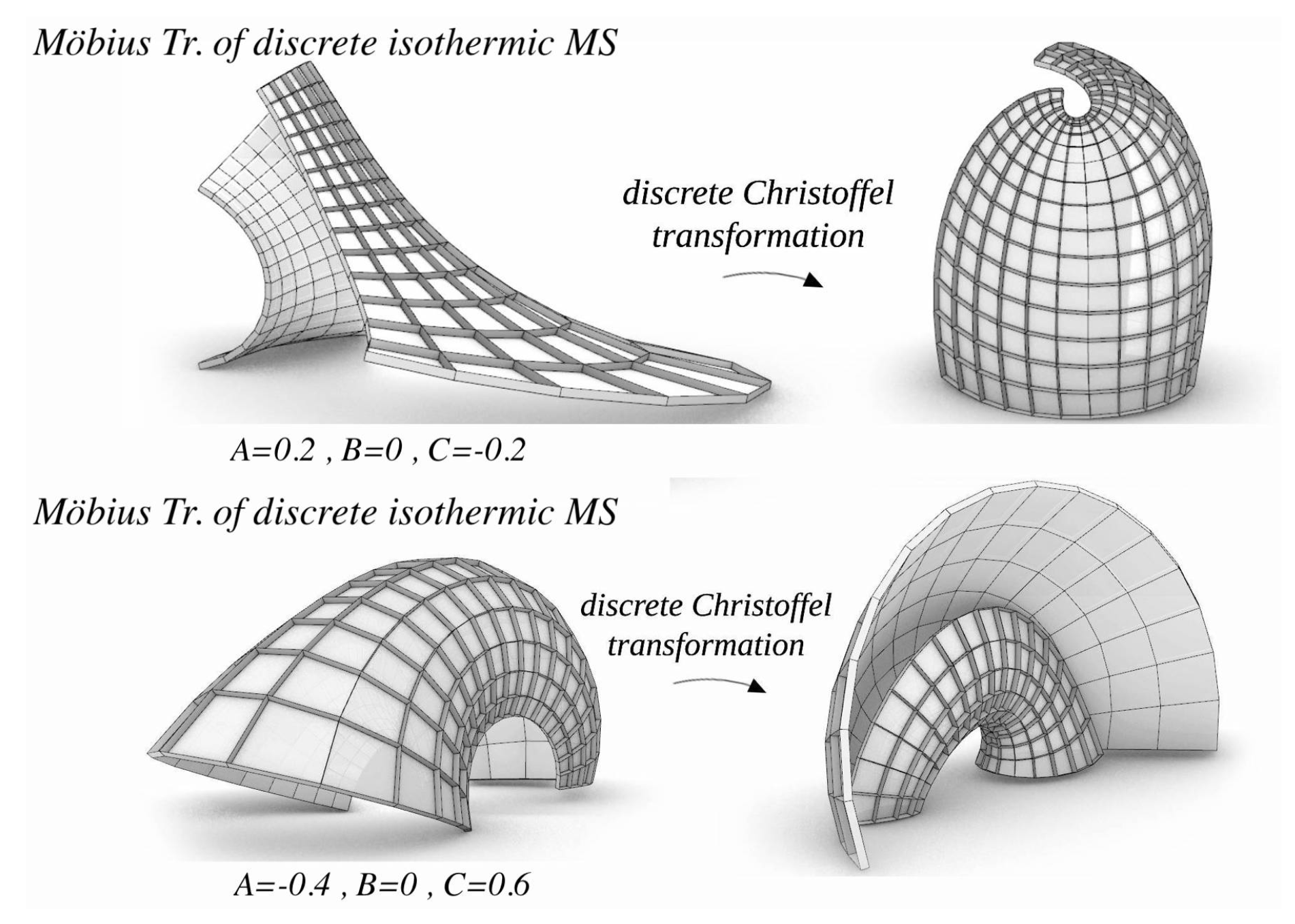
2.5. MS-Type

The third IS type we will consider is the MS-type. This type is generated it as a transform of certain IS.

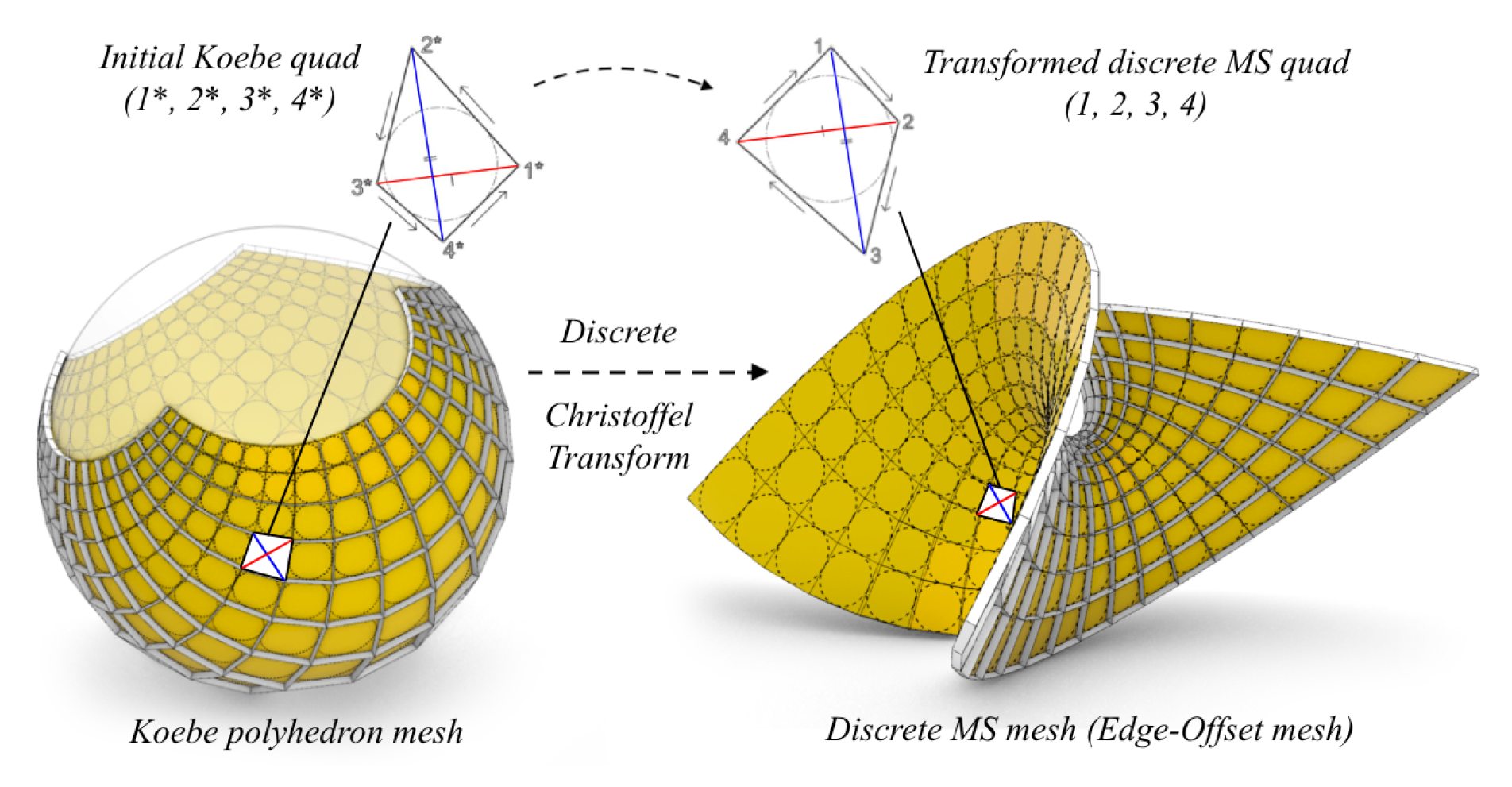
2.5.1. MS-Type from Christoffel Transform

The first way to generate CC-patches X of MS-type is obtained as Christoffel transforms (duals) of CC-patches N on the unit sphere ${\mathbb{S}}^2$. Note that any orthogonal patch ($F_N=0$) on ${\mathbb{S}}^2$ is necessarily conjugate, hence a conformal patch on ${\mathbb{S}}^2$ is thus a CC-patch. Let N be such a CC-patch on the unit spherical, with conformal factor ${\Lambda }_N=E_N=G_N$. We then have the following result due to [1,4]:

Proposition 2.4

(Definition). Consider the patch X defined by the differential system:

$$X_u=-{\displaystyle \frac{N_u}{{\Lambda }_N}},X_v={\displaystyle \frac{N_v}{{\Lambda }_N}}.$$

(11)

This patch is a CC-patch of MS-type referred to as the Christoffel dual of the CC-patch N.

Hence, to generate different CC-patches of MS-type we will use different spherical CC-patches, by taking N as the composition $N=N_o\circ \Psi$, where $N_o$ is the inverse of the stereographic projection and $\Psi$ a holomorphic map defined on some domain $\mathcal{U}$ in the plane, as seen in Figure 5. The obtained CC-patch X is referred to as of MS-type associated to the holomorphic function $\Psi$, for more detail on this construction, the reader is directed to [5].

2.5.2. MS-Type from Goursat Transform

The second method to generate CC-patches of MS-type is obtained as Goursat transforms of initial CC-patches of MS-type. To define the Goursat transform, we observe that differential System (11) comes with an adjoint system, defining the MS conformal patch $X^{*}$ adjoint to the MS CC-patch X. More precisely, we have the following result due to [1]:

Proposition 2.5

(Definition). Consider the patch $X^{*}$ defined by the differential system:

$$X_u^{*}=-{\displaystyle \frac{N_v}{{\Lambda }_N}},X_v^{*}=-{\displaystyle \frac{N_u}{{\Lambda }_N}}.$$

(12)

This patch is a conformal asymptotic MS-patch referred to as the adjoint of the CC-patch X, moreover, they are related by the Cauchy-Riemann equations:

$$X_u^{*}=-X_v,X_v^{*}=X_u.$$

(13)

Let $X=(x,y,z)$, $X^{*}=(x^{*},y^{*},z^{*})$ then, we have:

Proposition 2.6

(Definition). Consider the one-parameter family of patches $\widehat{X}\left(t\right)$ defined by:

$${\displaystyle \left(\left(\frac{1+t^2}{2t}\right)x+\left(\frac{1-t^2}{2t}\right)y^{*},\left(\frac{1+t^2}{2t}\right)y-\left(\frac{1-t^2}{2t}\right)x^{*},z\right).}$$

(14)

For all t (non-zero), this patch is a CC-patch of MS-type referred to as the Goursat transform $\widehat{X}$ of X.

Proof. 

The Goursat transform (14) preserves the MS property and principal curves ($F_{\widehat{X}}=f_{\widehat{X}}=0$) [6,7]. Moreover, the iso-speed property ($E_{\widehat{X}}=G_{\widehat{X}}=0$) is shown directly using the CR Relations (13). □

Figure 6. MS-type from Goursat transform.

Figure 6. MS-type from Goursat transform.

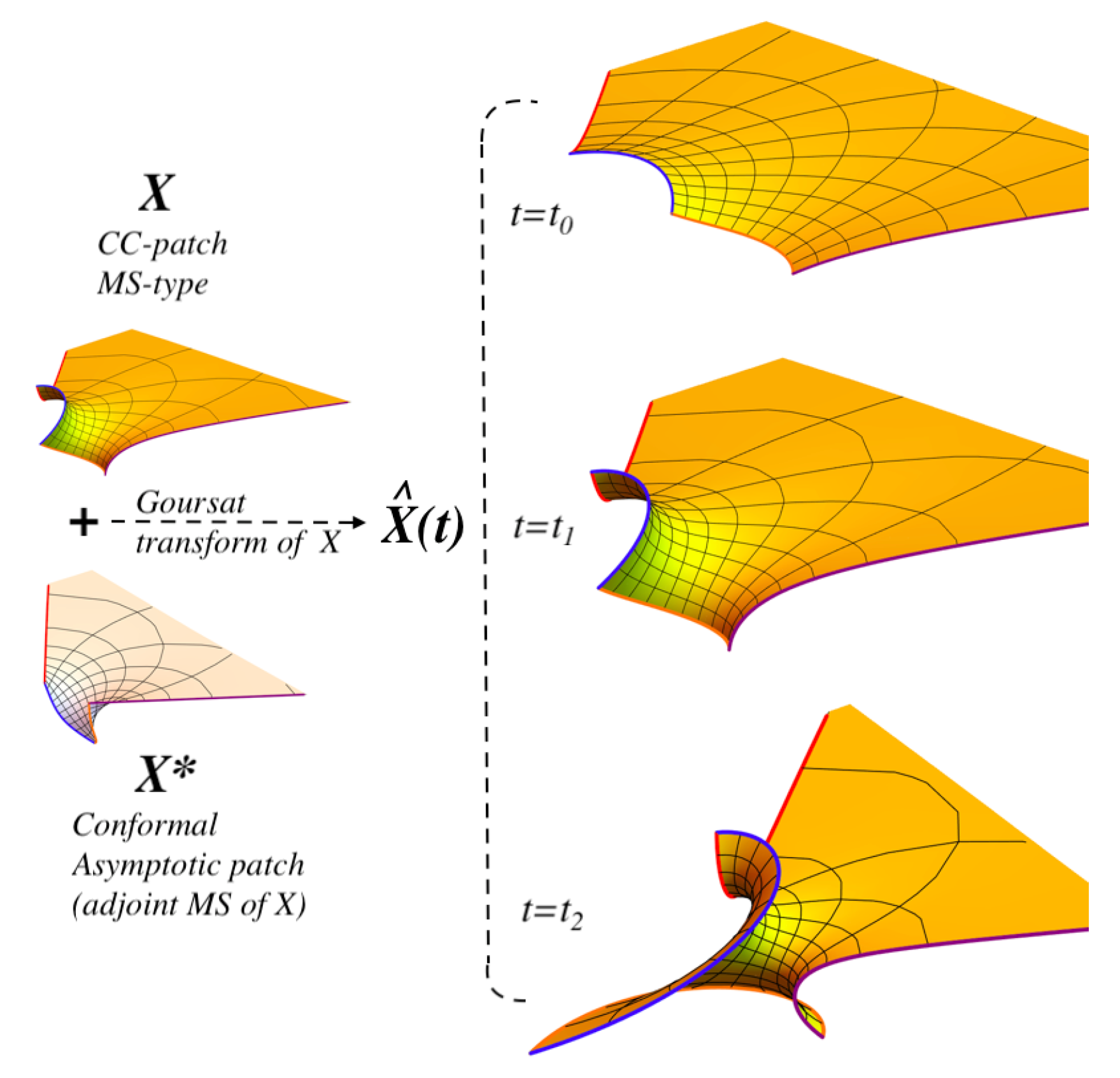
2.5.3. MS-Type Special Properties

There are few extra properties special to CC-patches of MS-type, associated to fabrication advantages.

• Symmetry and periodicity: This property arises from Schwarz symmetry principal for MS, cf. [7]. In particular, CC-patches of MS-type can admit (principal) planar parameter curves whose planes are normal to the surface, thus reflection symmetry planes. Similarly, CC-patches of MS-type can admit periodic behavior, hence translation symmetry along one or more directions, for details cf. [5,8]. These two properties allow the (global) MS to be constructed (tiled) from a single fundamental CC-patch through reflections and translations, as seen in Figure 1.

• Conformal spherical image: This property is special among IS. In fact, up to discarding umbilical (spherical or planar) patches, this property is unique to MS, more precisely, by a result in [1], we have:

Theorem 2.7.

Let X be a (non-umbilical) CC-patch, then its N is conformal if and only if X is MS-type.

Figure 7. Almost Koebe polyhedra from N.

Figure 7. Almost Koebe polyhedra from N.

Now, such a CC-patch X can be seen as a smooth analogue of a mesh admitting an Edge-Offset (EO). This is because its conformal Gauss map N can be seen as the limit of refinement a Koebe polyhedron. This is a mesh with planar faces whose edges touch the unit sphere tangentially at the contact points of orthogonal circle packings [9,10]. Now recalling that $N_o$ (inverse of stereographic projection) sends circles to circles, it then follows that for the Möbius map $\Psi \left(T\right)=(aT+b)/(cT+d)$, we have that $N=N_o\circ \Psi$ will send circles to circles. Hence, giving us a proper Koebe polyhedron, thus allowing us to use the discrete analogue of the Christoffel transform in (11), to obtain a discrete MS mesh [11].

This process transforms the polygons by reversing the order of points, making opposite diagonals parallel while keeping the edges but with reversed direction, as illustrated in Figure 8.

• Block sides unfolding straight: Let B be blocks arising from the discrete MS EO mesh. It is clear that the top and bottom faces of B are parallel, moreover, its lateral sides unfold to straight, cf. Figure 9. This is because the negative curvature makes the face-offsets blocks (red) overlap in one direction and gape in the other. Since, the EO vector (blue) lies in tetrahedron defined by the face normals (yellow), the lateral sides of B will alternate in and out of the face-offset block with constant angle $\theta$. This results in them unfolding to straight, as seen in Figure 9.

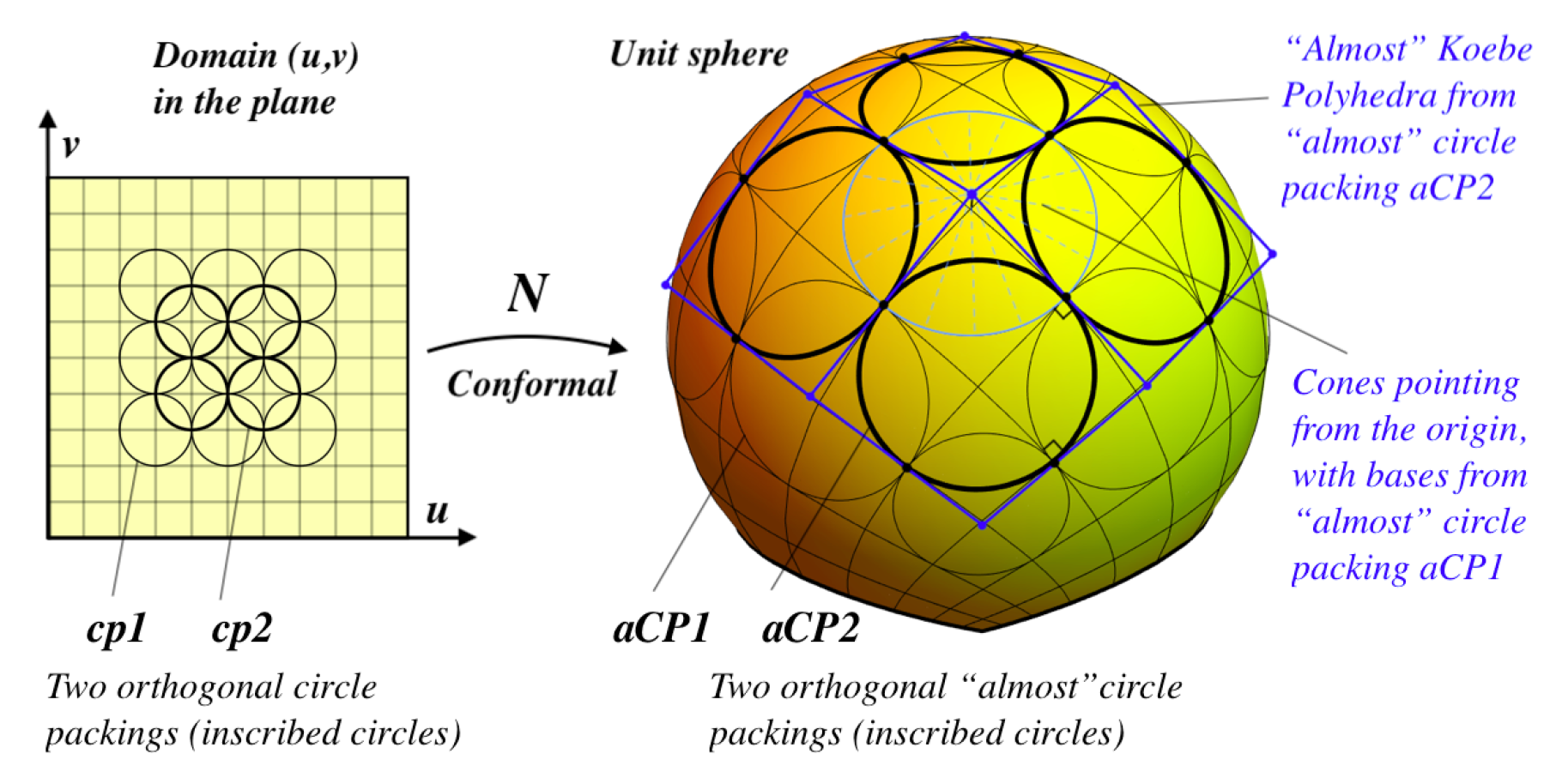
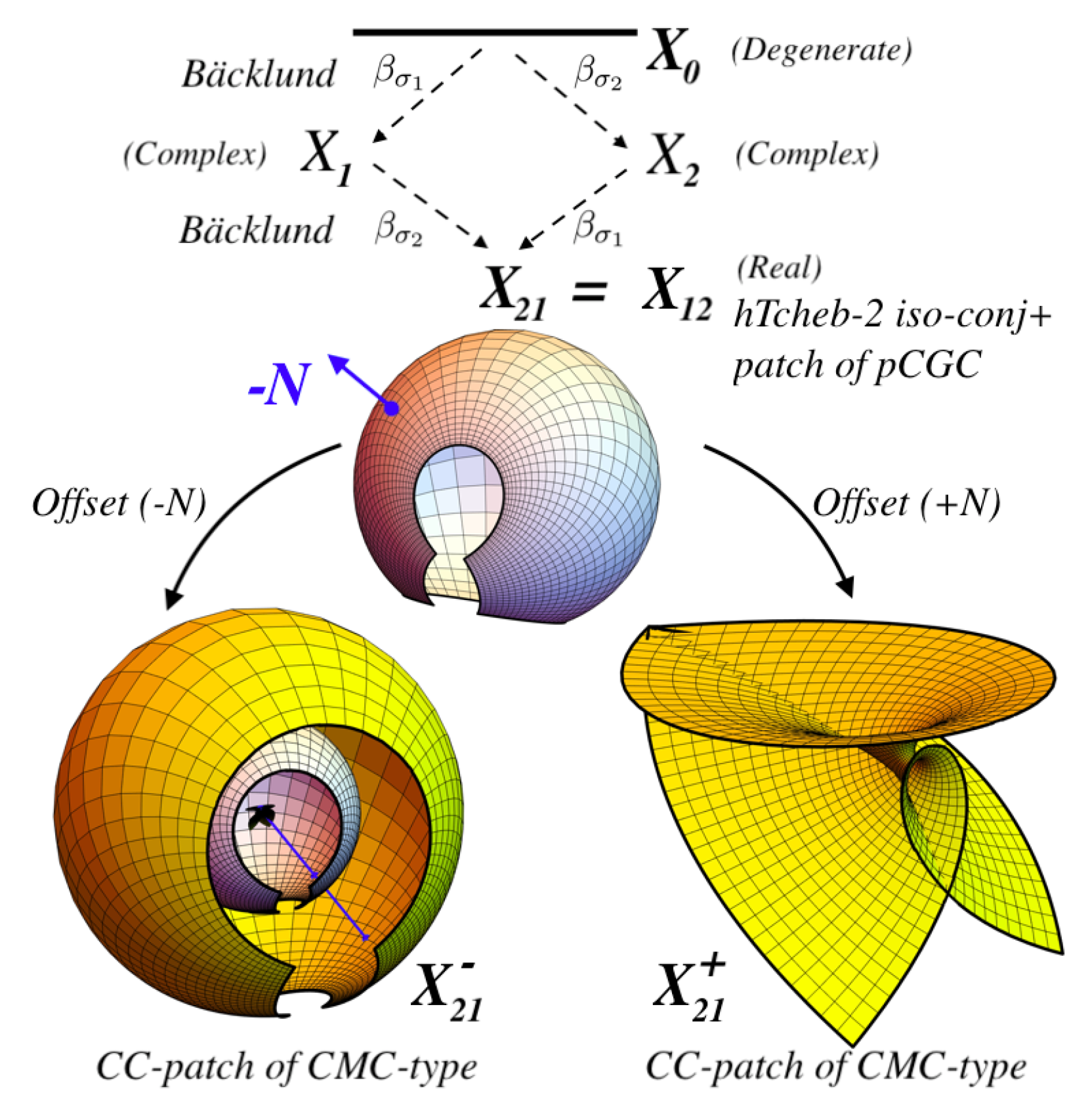
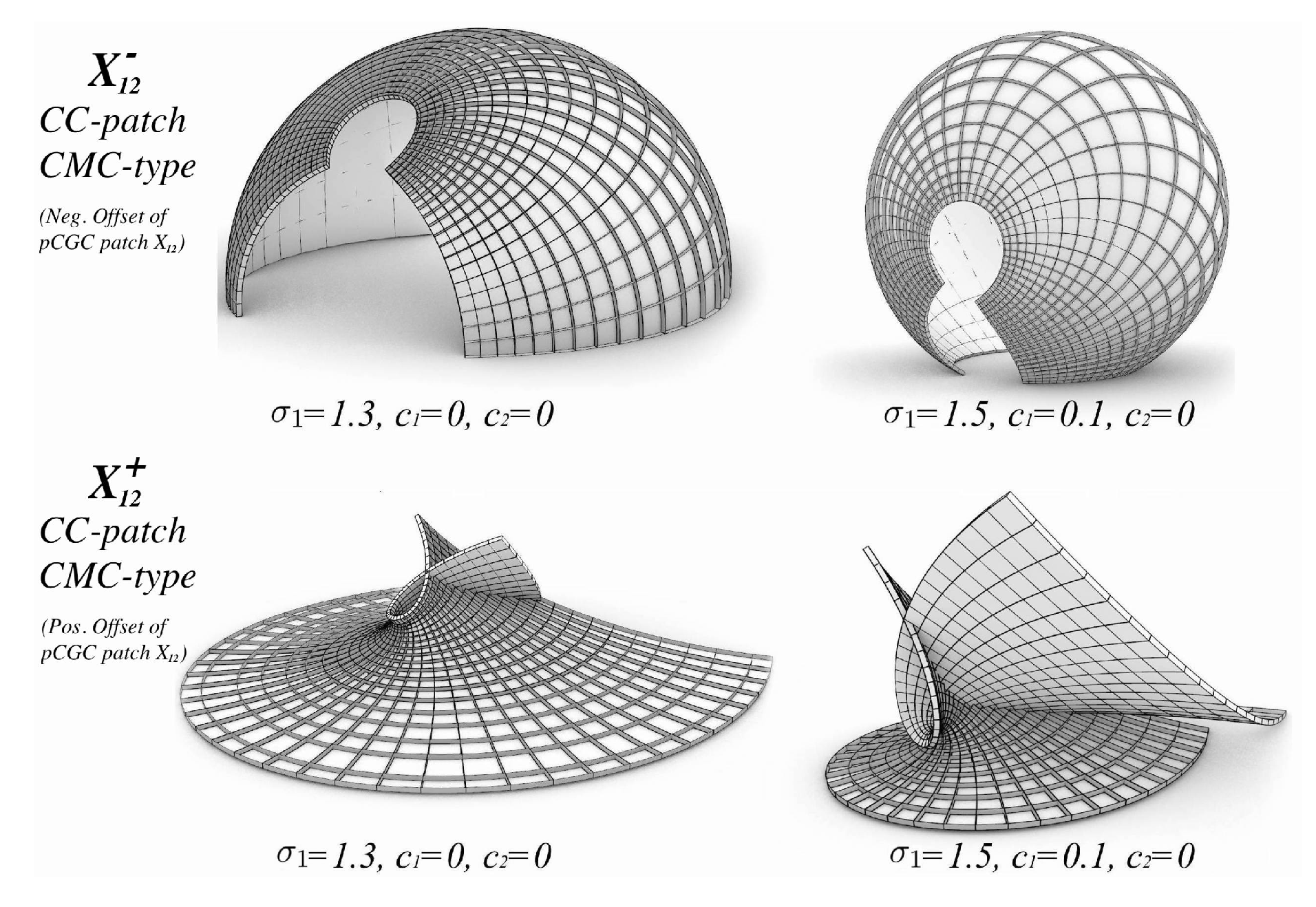
2.6. CMC-Type

The third IS type we will consider is the CMC-type, generated by Bäcklund transform of pCGC patches.

2.6.1. Connection pCGC - CMC Patches

To begin, we will first recall the classical result due to Bonnet [1,12]. This states that, given a pCGC patch X with $\mathcal{K}=1/{\rho }^2$ and normal N then its offsets:

$$X^{\pm }=X\pm \rho N\mathrm{for}\mathrm{some}\rho >0$$

(15)

are CMC patches (not necessarily CC-patches) with ${\mathcal{H}}^{\pm }=\mp 1/2\rho$, as seen in Figure 10. However, for these $X^{\pm }$ to be CC-patches, we need the following:

Theorem 2.8.

A surface of pCGC $\mathcal{K}=1/{\rho }^2$ admits a hTcheb-2 iso-conj⁺ patch X, that is:

$${\displaystyle \left\{\begin{array}{c}F=0,E={\rho }^2{cosh}^2\theta ,G={\rho }^2{sinh}^2\theta \hfill \\ f=0,e=g=\pm \rho cosh\theta sinh\theta \hfill \end{array}\right.}$$

(16)

with angle θ satisfying the Sinh-Gordon equation:

$${\displaystyle {\theta }_{uu}+{\theta }_{vv}=sinh\theta cosh\theta .}$$

(17)

Moreover, the CMC offsets $X^{\pm }$ given by (15) of such a CGC patch X, are CC-patches, that is:

$${\displaystyle \left\{\begin{array}{c}{F}^{\pm }=0,E^{\pm }=G^{\pm }={\rho }^2{\mathsf{e}}^{\mp 2\theta }\hfill \\ f^{\pm }=0,e^{\pm }=\pm \rho {\mathsf{e}}^{\mp \theta }sinh\theta ,g^{\pm }=\pm \rho {\mathsf{e}}^{\mp \theta }cosh\theta .\hfill \end{array}\right.}$$

(18)

Proof. 

For the first point, from Codazzi equation of a principal patch with pCGC $\mathcal{K}=k_1{k}_2=1/{\rho }^2$, we can show that $E(1-{\rho }^2{k}_1^2)$ and $G(1-{\rho }^2{k}_2^2)$ are functions of only u and only v respectively. Up to reparameterizing the u and v, we choose $\theta$ so that:

$${\displaystyle {\rho }^2{k}_1^2=\frac{E-{\rho }^2}{E}={tanh}^2\theta ,{\rho }^2{k}_2^2=\frac{G+{\rho }^2}{G}={coth}^2\theta .}$$

The resulting patch X has fundamental Forms (16). For the second point, using the relation between the fundamental forms of X and its normal N (cf. [1]), we can express the latter in terms of $\theta$. Then plug these in the relations between the fundamental forms of X and its offsets $X^{\pm }$ (cf. [1]) to show:

$${\displaystyle \left\{\begin{array}{c}{F}^{\pm }=0,f^{\pm }=0\hfill \\ E^{\pm }={\rho }^2{(cosh\theta \mp sinh\theta )}^2,G^{\pm }={\rho }^2{(sinh\theta \mp cosh\theta )}^2\hfill \\ e^{\pm }=\pm \rho (cosh\theta \mp sinh\theta ),g^{\pm }=\pm \rho (sinh\theta \mp cosh\theta ).\hfill \end{array}\right.}$$

Finally, the Expressions (18) are by recalling:

$${\displaystyle sinh\theta =\frac{{\mathsf{e}}^{\theta }-{\mathsf{e}}^{-\theta }}{2},cosh\theta =\frac{{\mathsf{e}}^{\theta }+{\mathsf{e}}^{-\theta }}{2}}$$

□

2.6.2. CMC-Type from Bäcklund tr. of pCGC

Let us without loss of generality take the $\rho =1$. Similar to nCGC case [2,13], a Bäcklund transform with inclination ${\sigma }_1$ of a pCGC pair $(X_0,{\theta }_0)$ satisfying (16),(17) is again a pCGC pair denoted by ${\displaystyle (X_1,{\theta }_1)=({\beta }_{{\sigma }_1}\left(X_0\right),{\beta }_{{\sigma }_1}\left({\theta }_0\right))}$ characterized by having $(X_1-X_0)$ tangent to both patches, with constant length and the normals having a constant angle. More precisely, $X_1$ is given by:

$${\displaystyle X_1=X_0+\left(\frac{\mathrm{csch}{\sigma }_{1}cosh{\theta }_1}{cosh{\theta }_0}\right)X_{0,u}+i\left(\frac{\mathrm{csch}{\sigma }_{1}sinh{\theta }_1}{sinh{\theta }_0}\right)X_{0,v}}$$

(19)

with angle ${\theta }_1$ obtained from the system:

$${\displaystyle \left\{\begin{array}{c}{\theta }_{1,u}+i{\theta }_{0,v}=sinh{\sigma }_{1}sinh{\theta }_{1}cosh{\theta }_0+cosh{\sigma }_{1}cosh{\theta }_{1}sinh{\theta }_0\hfill \\ i{\theta }_{1,v}+{\theta }_{0,u}=-sinh{\sigma }_{1}cosh{\theta }_{1}sinh{\theta }_0-cosh{\sigma }_{1}sinh{\theta }_{1}cosh{\theta }_0.\hfill \end{array}\right.}$$

(20)

For the patches to be real, a second Bäcklund transform with ${\sigma }_2=i\pi -{\sigma }_1$ is applied [14,15]. That is, a pCGC pair ${\displaystyle (X_{21},{\theta }_{21})=({\beta }_{{\sigma }_2}{\beta }_{{\sigma }_1}\left(X_0\right),{\beta }_{{\sigma }_2}{\beta }_{{\sigma }_1}\left({\theta }_0\right))}$ where, the patch $X_{21}$ is given by:

$${\displaystyle X_{21}=X_1+\left(\frac{\mathrm{csch}{\sigma }_{2}cosh{\theta }_{21}}{cosh{\theta }_1}\right)X_{1,u}+i\left(\frac{\mathrm{csch}{\sigma }_{2}sinh{\theta }_{21}}{sinh{\theta }_1}\right)X_{1,v}}$$

(21)

with ${\theta }_{21}$ obtained from the permutability condition:

$${\displaystyle {\theta }_{21}={\theta }_0+2\mathrm{arctanh}\left[\left(\frac{cosh\left(\frac{{\sigma }_1-{\sigma }_2}{2}\right)}{sinh\left(\frac{{\sigma }_1-{\sigma }_2}{2}\right)}\right)tanh\left(\frac{{\theta }_1-{\theta }_2}{2}\right)\right].}$$

(22)

which insures ${\beta }_{{\sigma }_2}{\beta }_{{\sigma }_1}={\beta }_{\sigma 1}{\beta }_{{\sigma }_2}$. In particular, we take $X_0=(u,0,0)$ with ${\theta }_0=0$ to obtain $X_{21}$, then take its offsets $X_{21}^{\pm }$, as seen in Figure 10.

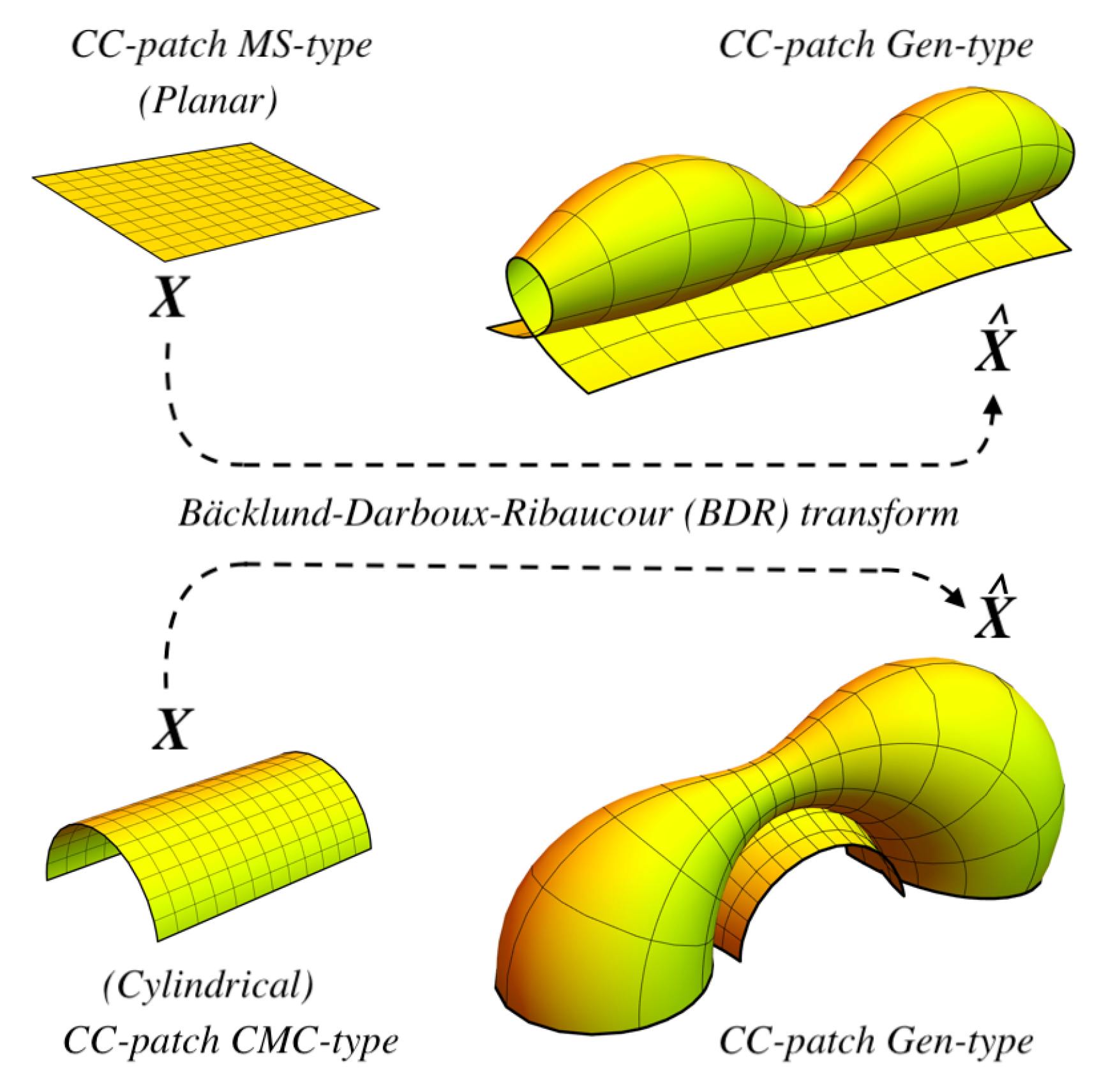
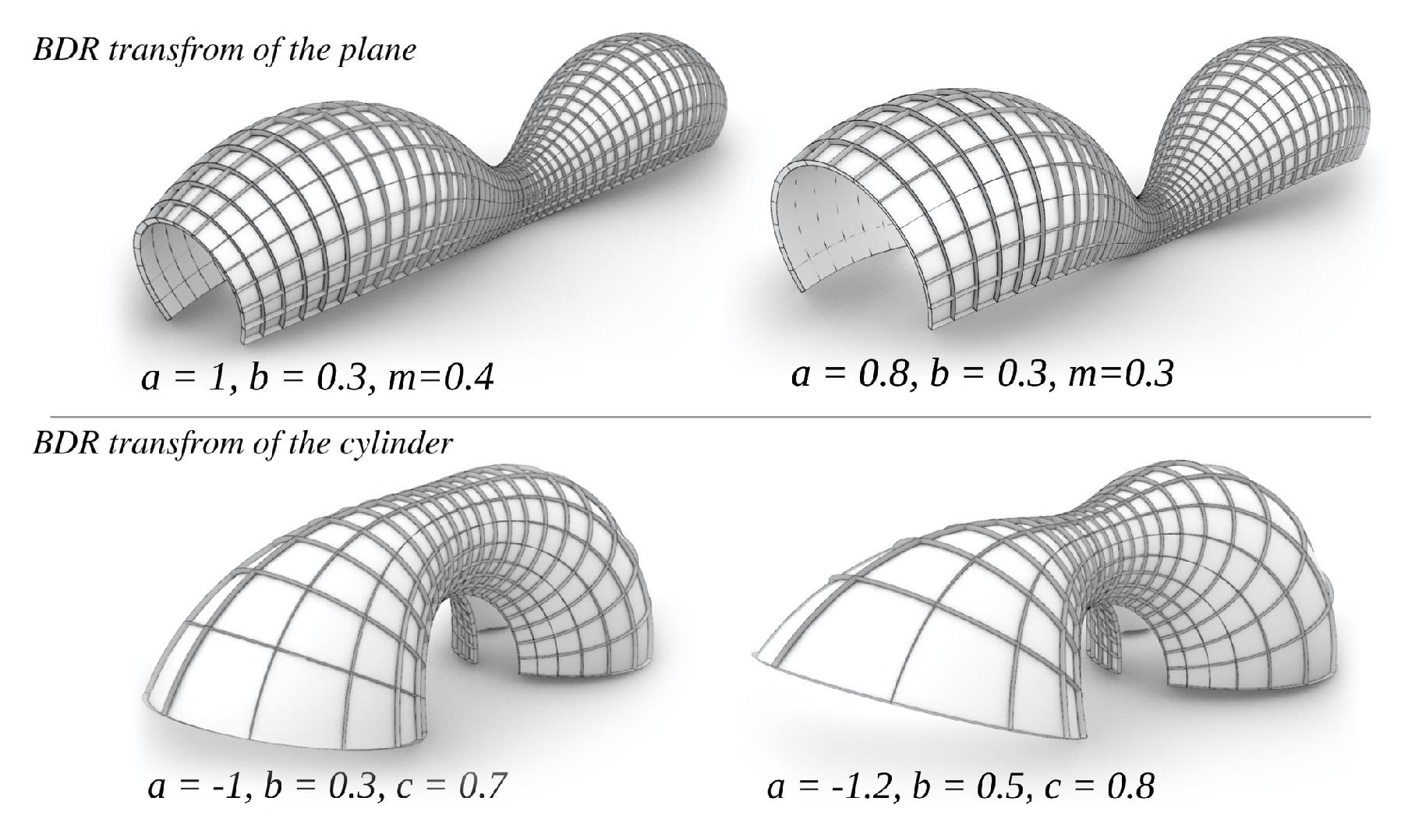
2.7. Gen-Type

The final IS type we consider is Gen-type, which we generate using transforms applied to previous types.

2.7.1. Gen-Type from BDR Transform

This Bäcklund-Darboux-Ribaucour (BDR) transform is a special form of the general Ribaucour transform (preserving OC-patches) to preserve CC-patches. More precisely, we recall that an OC-pair $(X,\theta )$ is given by solutions to:

$${\displaystyle \left\{\begin{array}{c}\left(\mathrm{Patch}\right)X_{uv}={(log\mathsf{H})}_v{X}_u+{(log\mathsf{K})}_u{X}_v\hfill \\ \left(\mathrm{Function}\right){\theta }_{uv}={(log\mathsf{H})}_v{\theta }_u+{(log\mathsf{K})}_u{\theta }_v\hfill \end{array}\right.}$$

(23)

with the coefficients $\mathsf{H}=\sqrt{E}$ and $\mathsf{K}=\sqrt{G}$. Next, we define the orthonormal frame $(\mathsf{U},\mathsf{V},N)$ with its scalar companion $(\mathsf{u},\mathsf{v},\eta )$ given by:

$${\displaystyle \left\{\begin{array}{c}\mathsf{U}=X_u/\mathsf{H},\mathsf{V}=X_v/\mathsf{K},N=\mathsf{U}\times \mathsf{V}\hfill \\ \mathsf{u}={\theta }_u/\mathsf{H},\mathsf{v}={\theta }_v/\mathsf{K}\mathrm{with}\eta \mathrm{given}\mathrm{by}\text{:}{\eta }_u={\mathsf{H}}^o\mathsf{u},{\eta }_v={\mathsf{K}}^o\mathsf{v}\hfill \end{array}\right.}$$

with coefficients ${\mathsf{H}}^o=-e/\sqrt{E}$ and $\mathsf{K}=-g/\sqrt{G}$. Then, a Ribaucour transform $\widehat{X}$ of X is given by:

$${\displaystyle \widehat{X}=X-\left(\frac{\theta }{{\theta }^{\prime }}\right)X^{\prime }\mathrm{with}\left\{\begin{array}{c}{X}^{\prime }=\mathsf{u}\mathsf{U}+\mathsf{v}\mathsf{V}+\eta N\hfill \\ {\theta }^{\prime }=({\mathsf{u}}^2+{\mathsf{v}}^2+{\eta }^2)/2.\hfill \end{array}\right.}$$

(24)

This patch $\widehat{X}$ is an OC-patch satisfying (23) with coefficients $\widehat{\mathsf{H}},\widehat{\mathsf{K}}$ (cf. [2,16]). Next, we will pass from the Ribaucour to the BDR transform. For that let us, first assume that the OC-patch X is a CC-patch with conformal factor ${\mathsf{H}}^2={\mathsf{K}}^2={\mathsf{e}}^{2\mu }$. Furthermore, we require that ${\widehat{\mathsf{H}}}^2={\widehat{\mathsf{K}}}^2$ which turns ${\displaystyle \frac{\theta }{{\theta }^{\prime }}}$ into ${\displaystyle \frac{1}{m{\theta }^{*}}}$ where m is a constant and ${\theta }^{*}$ is as shown in System (26). We thus obtain the result due to [2]:

Proposition 2.9

(Definition). The BDR transform $\widehat{X}$ of a CC-patch X (of any type) is given by:

$${\displaystyle \left\{\begin{array}{c}\widehat{X}=X-\left(\frac{1}{m{\theta }^{*}}\right)(\mathsf{u}\mathsf{U}+\mathsf{v}\mathsf{V}+\eta N)\hfill \\ \mathrm{with}\mathrm{admissible}\mathrm{cond}.({\mathsf{u}}^2+{\mathsf{v}}^2+{\eta }^2)=2m\theta {\theta }^{*}\hfill \end{array}\right.}$$

(25)

where the functions $(\mathsf{u},\mathsf{v},\eta ,\theta ,{\theta }^{*})$ satisfy:

$${\displaystyle \left\{\begin{array}{c}{\mathsf{u}}_u=-{\mu }_v\mathsf{v}-{\mathsf{H}}^o\eta +m{\mathsf{e}}^{-\mu }\theta +m{\mathsf{e}}^{\mu }{\theta }^{*},{\mathsf{v}}_u={\mu }_v\mathsf{u}\hfill \\ {\mathsf{v}}_v=-{\mu }_u\mathsf{u}-{\mathsf{K}}^o\eta -m{\mathsf{e}}^{-\mu }\theta +m{\mathsf{e}}^{\mu }{\theta }^{*},{\mathsf{u}}_v={\mu }_u\mathsf{v}\hfill \\ {\eta }_u={\mathsf{H}}^o\mathsf{u},{\theta }_u={\mathsf{e}}^{\mu }\mathsf{u},{\theta }_u^{*}={\mathsf{e}}^{-\mu }\mathsf{u}\hfill \\ {\eta }_v={\mathsf{K}}^o\mathsf{v},{\theta }_v={\mathsf{e}}^{\mu }\mathsf{v},{\theta }_v^{*}=-{\mathsf{e}}^{-\mu }\mathsf{v}.\hfill \end{array}\right.}$$

(26)

This patch $\widehat{X}$ is a CC-patch of Gen-type.

In particular, we take X once planar CC-patch (MS-type) and once cylinderical CC-patch (CMC-type), resulting in CC-patch of Gen-type, as in Figure 11.

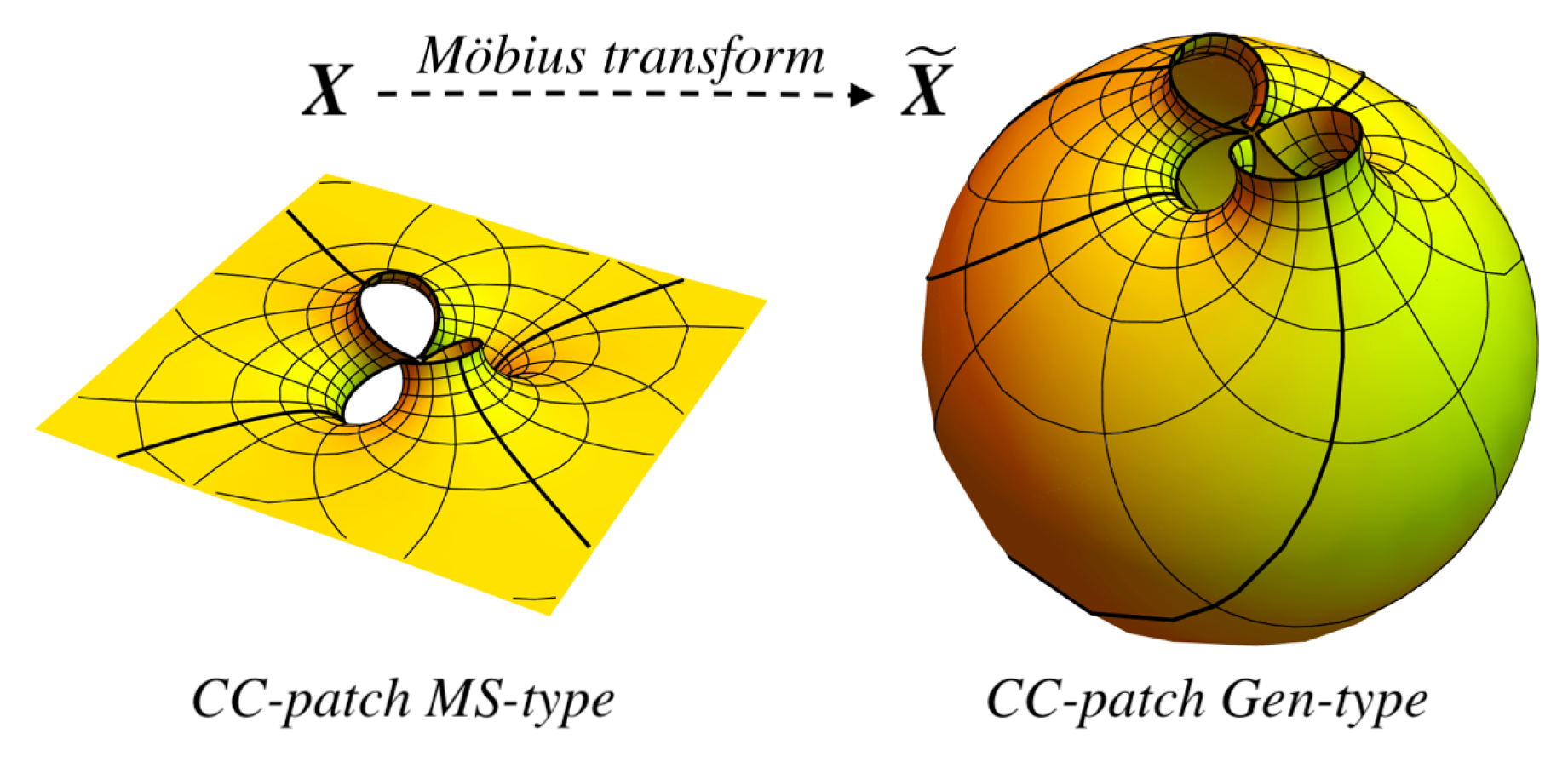
2.7.2. Gen-Type from Möbius Transform

The final way we are going to generate CC-patches of Gen-type is using Möbius transform as well as from Christoffel transform. These two transforms preserve the CC-patch property [3], but not the type (except for the Rev-type preserved by Christoffel). There follows that we have the following result:

Lemma 2.10.

Let X be a CC-patch (of any type) and let $\tilde{X}$ be its transform given by either one of:

$$\left\{\begin{array}{cc}\left(\mathrm{M}\text{ö}\mathrm{bius}\right)\hfill & \tilde{X}=o+kA\left({\displaystyle \frac{X-p}{{|X-p|}^n}}\right)\hfill \\ \left(\mathrm{Christoffel}\right)\hfill & {\tilde{X}}_u=-{\displaystyle \frac{X_u}{{\Lambda }_X}},{\tilde{X}}_v={\displaystyle \frac{X_v}{{\Lambda }_X}}\hfill \end{array}\right.$$

(27)

where $o,p\in {\mathbb{R}}^3$, $n=0,2$, $\lambda \in \mathbb{R}$ and $A\in \mathrm{O}(3,\mathbb{R})$. Then, $\tilde{X}$ is a CC-patch of Gen-type.

Thus, we have large design freedom cf. Figure 12.

3. Design Explorations

In this section we will provide concrete examples of the CC-patches types, based on the geometric theory, providing explicit parameterizations with input parameters for design experimentation, available via Python code for Grasshopper on GitHub [17]. A space of design variants is thus constituted by these generated patches. Note that, the definition of most of these patches already involve transforms and upon applying further (different) transforms, we create even more complex-shaped CC-patches.

3.1. Design with Quad, Rev and Cyc-Types

• Quad-type from parameters $(q_o,a,b,c)$: Varying these parameter respecting Relations (2) gives different quadric types (Ell, H1s, H2s) and deformations.

• Rev-type from profile map $\phi \left(u\right)=a+b{u}^2$: The first design variation comes from choosing the profile function indicated. Next, further design variations are then obtained by varying the parameters a and b. More precisely, varying a adjusts the middle section, while varying b changes the boundary’s inclination, as seen in Figure 13.

• Cyc-type from parameters $(A,B,C)$: We start by the conformal patch X on the Torus (4) and apply (iterations of) the Möbius transform (27)₁, namely

$${\displaystyle X⟼{\left|X\right|}^2\frac{X-{\left|X\right|}^2(A,B,C)}{{|X-|X|}^2{(A,B,C)|}^2}.}$$

(28)

It follows that different design variants of Cyc-type arise by varying $A,B,C$, as seen in Figure 13.

3.2. Design with MS-Type

• From holomorphic map $\Psi \left(T\right)=(a+ib)T^3$: As indicated in the geometry section, we constructed CC-patches of MS-type by selecting holomorphic functions. In this particular example, we use the holomorphic function $\Psi$ indicated, allowing design variation by changing the parameters a and b. Moreover, by applying the Goursat transform (14) with its parameter t, we can give further shape deformations. Finally, we apply reflection symmetry to a fundamental patch to construct a global surface

Figure 14. MS-type variation from $a,b$ and t.

Figure 14. MS-type variation from $a,b$ and t.

• From holomorphic map $\Psi \left(T\right)=asin(bT+c)$: In this second example, we use the holomorphic function indicated. Once again by varying the parameters $a,b$ and c we generate design variations and by applying Goursat transform (14), we can use its parameter t to generate further shape deformations. Furthermore, similar to the previous example, we have reflection symmetry that allows us to construct a global surface from a fundamental patch. In contrast to the previous example, in here we have translation symmetry (periodicity), as seen in Figure 15.

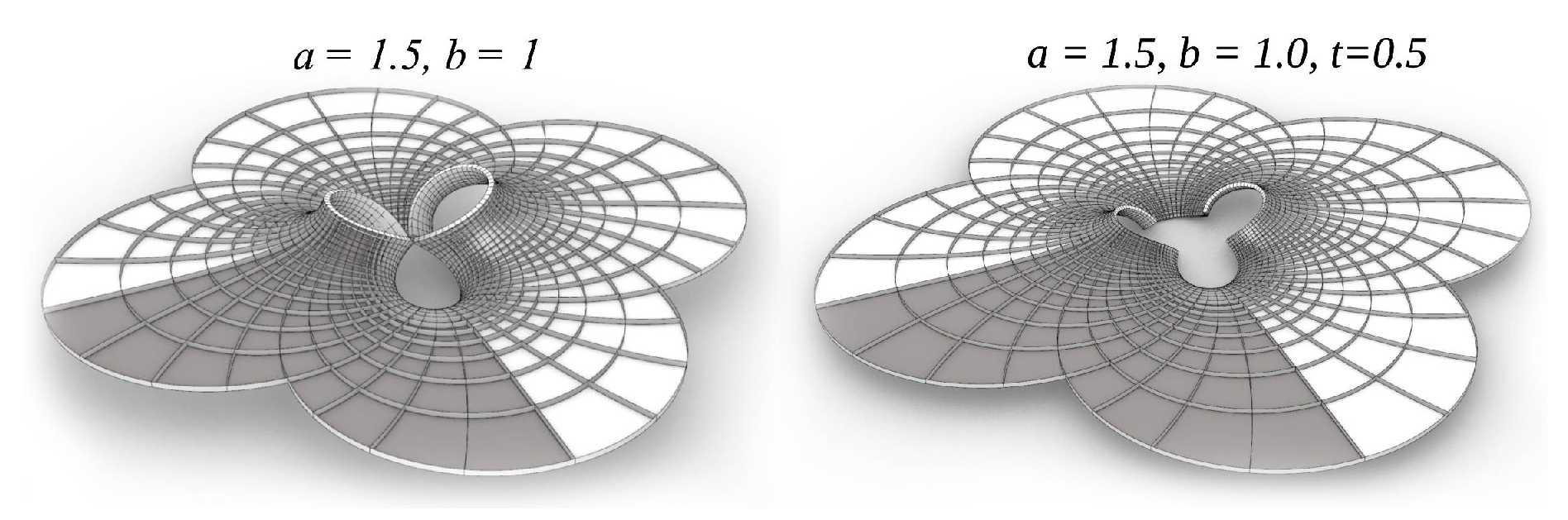
3.3. Design with CMC-Type

Variations in the CMC-type (offsets $X_{12}^{\pm }$ of $X_{12}$ the pCGC patch (15)) arise by varying Bäcklund inclination parameter ${\sigma }_1$ and parameters $c_1,c_2$ emerging as integration constants to the solutions ${\theta }_1,{\theta }_2$ of (20). In particular, changes in ${\sigma }_1$ can extend and curve the surfaces, while $c_1,c_2$ translate the domain, thus can generate asymmetric shapes, as seen in Figure 16.

3.4. Design with Gen-Type

Design with Gen-type somewhat offers the most freedom among the types, as it contain all of them, and all other CC-patches in general. As explained in the geometry section, any of types can be sent to the Gen-type by applying transforms only preserving the CC-patch property. To help the reader navigate these connections between types, we introduce below, the possible design flows. Notably, showing the effect of the different transforms applied to the different CC-patch types leading them to either remain in their initial types or to jump into the Gen-type. These design flows help keeping track of the applied transforms.

Figure 17. Design flows of types and transforms.

Figure 17. Design flows of types and transforms.

• From Möbius transform of MS-type: Starting from the discrete MS mesh constructed from Koebe polyhedron and applying the Möbius transform (28), we get a (non-minimal) discrete isothermic mesh cf. [3]. Finally, we apply (discrete) Christoffel transform cf. Figure 8, to obtain further deformed shapes. This is done to two Möbius transforms (defined by parameters $(A,B,C)$) of the discrete MS, cf. Figure 18.

• From BDR transform of plane and cylinder: The initial CC-patches to which the BDR transform is applied, are the plane $(u,v,0)$ and the cylinder $(cosv,sinv,u)$. Next, solving System (26) to obtain the functions $(\mathsf{u},\mathsf{v},\eta ,\theta ,{\theta }^{*})$. For the plane, we have parameters $a,b$ emerging as constant of integration and m from admissiblity Condition (26)₂. For the cylinder, we have $a,b,c$ emerging as constant of integration and $m=(-c^2+c\sqrt{16a^2-16b^2+c^2})/4c^2$. Design variations are obtained by varying these parameters, as seen in Figure 19.

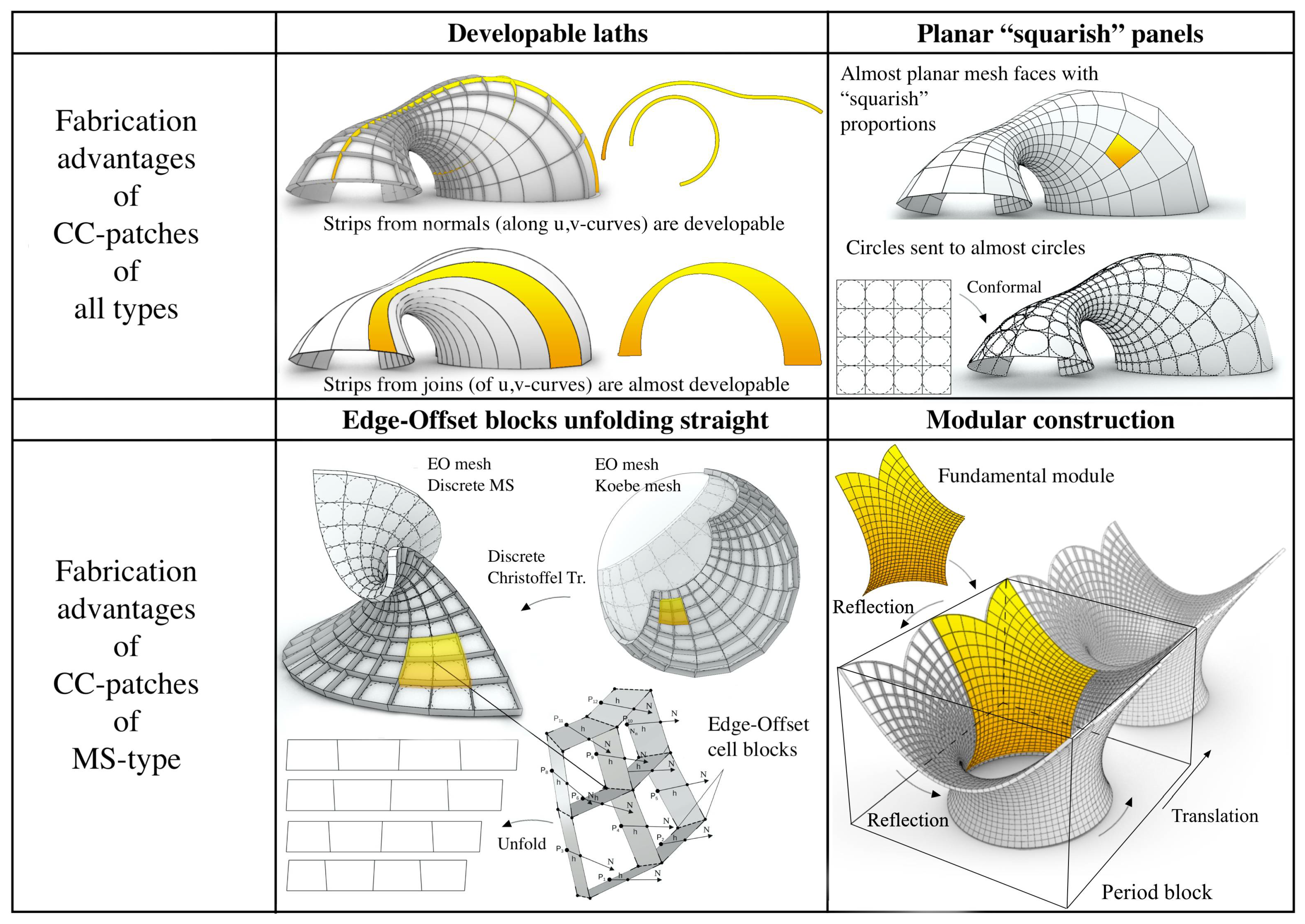
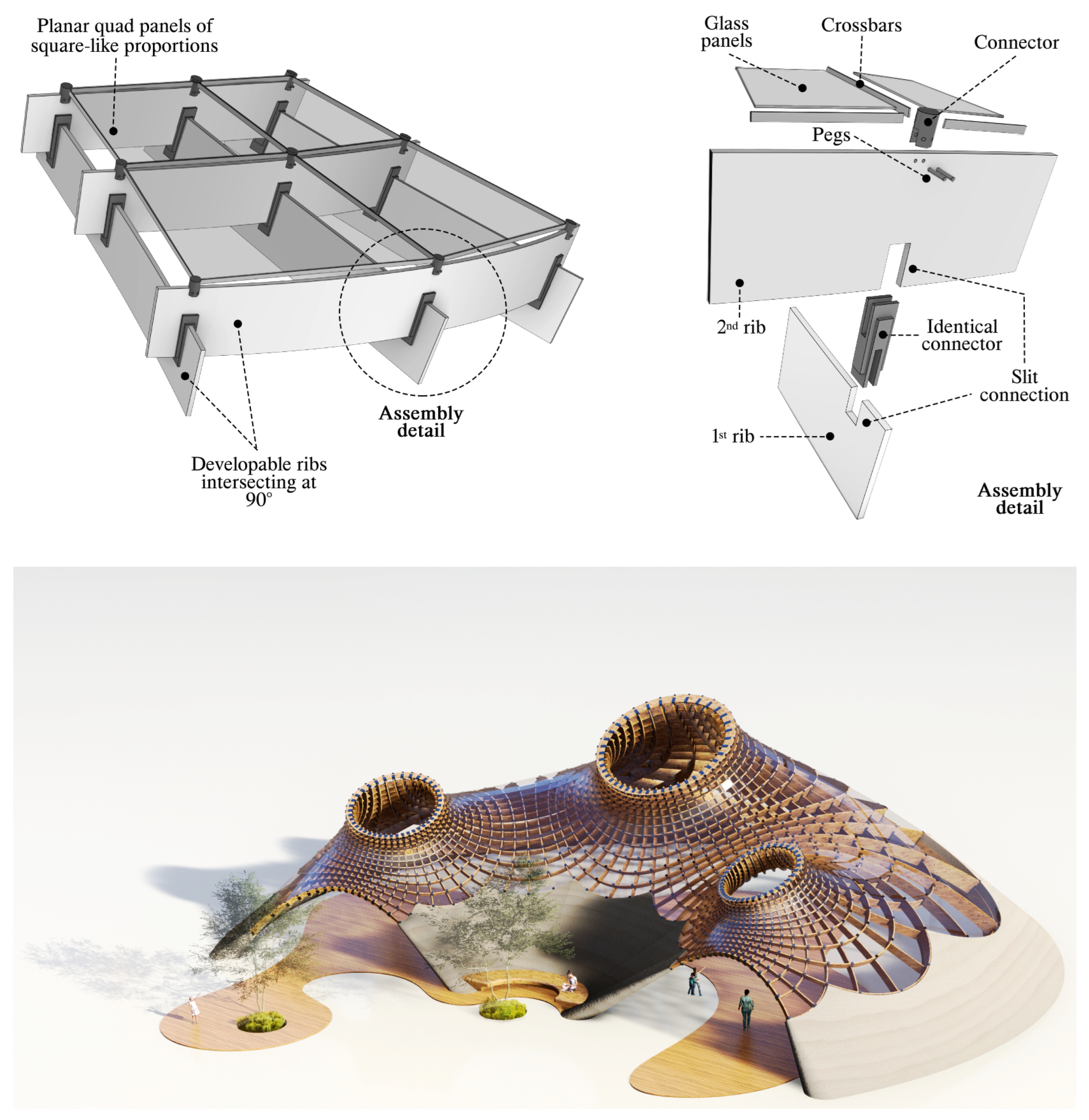
4. Prototyping

In the Figure 20, we see a demonstrator of multi-layer structure based on CC-patches of Gen-type obtained by applying a Möbius transform to the MS-type from the function $\Psi \left(T\right)=asin(bT+c)$. The global form leverages the symmetry and periodicity of the CC-patch of MS-type and demonstrates the preserved multiple-patches configuration.

On a local level, the fabrication advantages highlighted in Figure 1 are evident. The developability of the ribs and the orthogonality of their intersections simplify assembly and allow for a unique connector across the structure. Planar quadrilateral panels with square-like proportions are installed over the ribs, successfully cladding of the structure.

5. Conclusions

This research introduces a framework for designing gridshells with Isothermic Surfaces (IS), combining geometric principles and parametric tools to help in expanding the ever growing field of architectural geometry. It provides a method for creating complex yet, fabrication-efficient structures, through presenting the well-known types of IS by explicit CC-patches and preserving transforms (Christoffel, Bäcklund-Darboux-Ribaucour (BDR) and Möbius). The tools presented demonstrate the versatility of designing using CC-patches by employing intuitive input parameters, while addressing pre-rationalization challenges. These tools streamline fabrication while improving material efficiency, stability, and aesthetics, through trying to generalize modular low-tech construction to non-standard shaped (grid)shells. The parametric design flows enable tailored architectural forms compatible with prefabrication technologies. The straight unfolding of lateral faces of edge-offset blocks, seen in the discrete MS mesh, emphasizes sustainable, cost-efficient construction. While, their symmetry and periodicity enable modular, complex topologies and multiple-patch configuration, important for intricate designs, as shown in the prototype. In conclusion, this work connects theoretical concepts in geometry to practical applications in architecture, hopefully establishing CC-patches as a viable tool for architectural design.