Heterodyne Light Source Using Two Tandem Acousto-Optic Modulators Under Bragg Diffraction Conditions

1. Introduction

Heterodyne light sources commonly used in research include Zeeman lasers [1,2], Mach–Zehnder architectures [3,4], and electro-optic modulator (EOM) architecture [5]. Among these, the Zeeman laser functions as a self-contained heterodyne light source, offering a high beat frequency but at a high cost. The heterodyne light source based on the Mach–Zehnder architecture consists of two acousto-optic modulators (AOM); however, as it lacks a common-path architecture, it is susceptible to environmental disturbances. Additionally, the 0th-order light is not used, so the utilization rate of the laser is low. The heterodyne light source based on the EOM architecture requires full-wave voltage modulation, which causes a temperature rise in the electro-optic crystal, potentially leading to phase errors due to the high voltage.

Recently, Chiu et al. [6] proposed a heterodyne light source using two AOMs connected in series. While this setup is simple to implement, the diffraction efficiency remains suboptimal because the modulators are not operated under Bragg-diffraction conditions. In order to address these shortcomings, we propose an optimized configuration with two AOMs connected in series, both operating under Bragg-diffraction conditions. Through fine-tuning of the mirror and the two AOMs to ensure that the two orthogonally polarized light beams coincide, the heterodyne interference signal is substantially enhanced and the utilization rate of the laser approaches 90%.

2. Materials and Methods

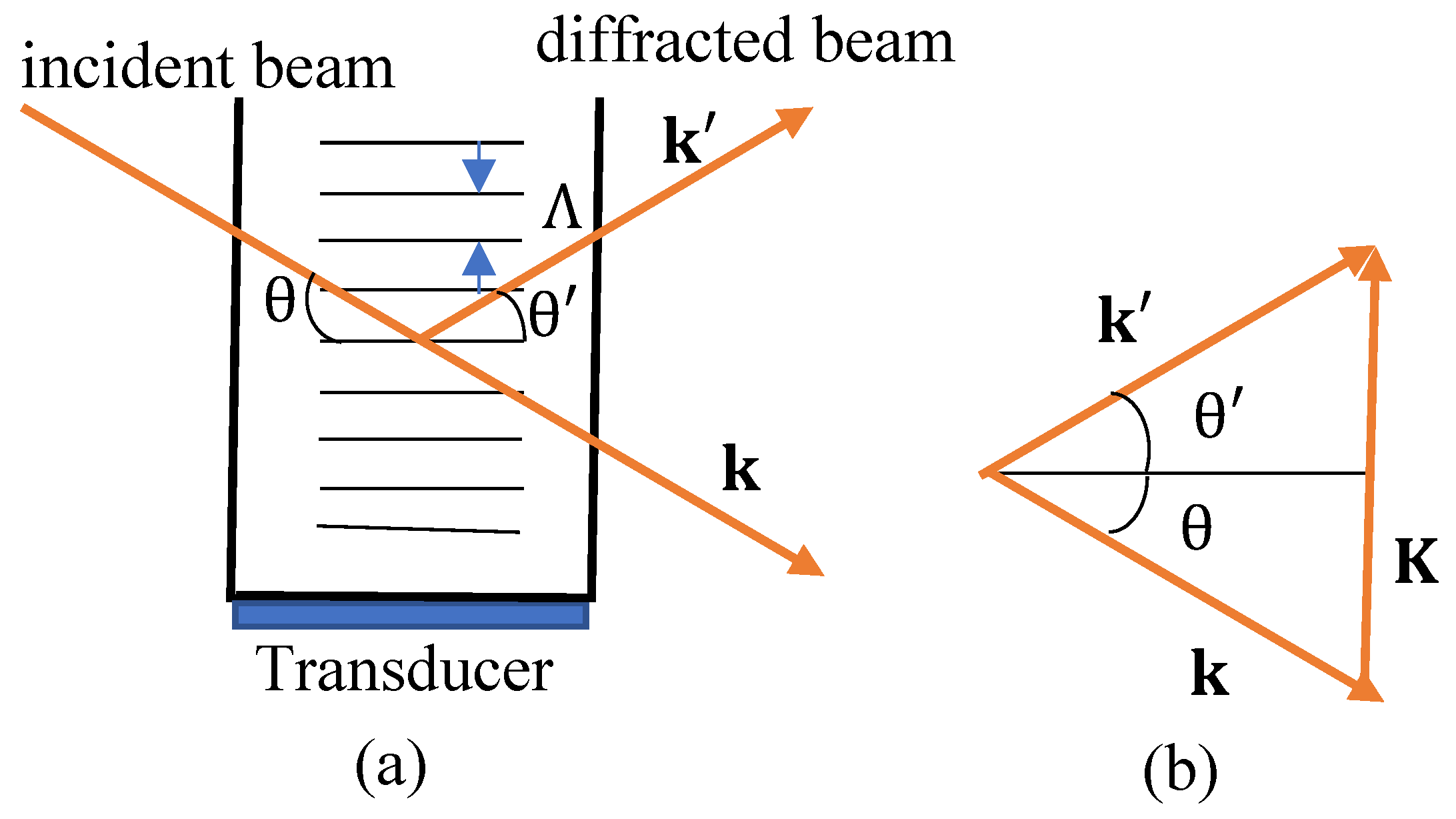
In the acousto-optic modulator (AOM) shown in Figure 1a, the Bragg diffraction conditions are derived from the triangle in Figure 1b and are expressed as [7]:

$${\mathbf{k}}^{\prime }=\mathbf{k}+\mathbf{K}$$

(1)

then $\mathrm{K}={\mathrm{k}}^{\prime }\mathrm{s}\mathrm{i}\mathrm{n}{\mathsf{\theta }}^{\prime }+\mathrm{k}\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\theta }.$ If $\mathsf{\theta }\prime \approx \mathsf{\theta }$ and ${\mathrm{k}}^{\prime }\approx \mathrm{k}={\displaystyle \frac{2\pi }{\lambda }}$, then $\mathrm{K}={\displaystyle \frac{2\pi }{\mathsf{\Lambda }}}=2\mathrm{k}\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\theta }$ and:

$$\mathsf{\Lambda }={\displaystyle \frac{\lambda }{2sin\theta }}={\displaystyle \frac{v_s}{f_s}}$$

(2)

where $\mathbf{K}$, $\mathbf{k}\prime$, and $\mathbf{k}$ are the wave vectors of the sound wave, diffracted beam, and incident beam, respectively, while $\mathsf{\theta }$ and $\mathsf{\theta }\prime$ are the incident and diffracted angles, respectively. Here, $v_s$ is the sound velocity, $f_s$ is the frequency of the sound wave or the modulation frequency, $\mathsf{\Lambda }$ is the wavelength of sound, and $\mathsf{\lambda }$ is the wavelength of the beam in the medium. If the frequency of the incident beam is ${f=f}_0$, then the Doppler effect causes the frequency of the diffracted beam to be $f^{\prime }=f_0-f_s$, where the beam is the +1st-order beam. Equation (2) represents the Bragg condition.

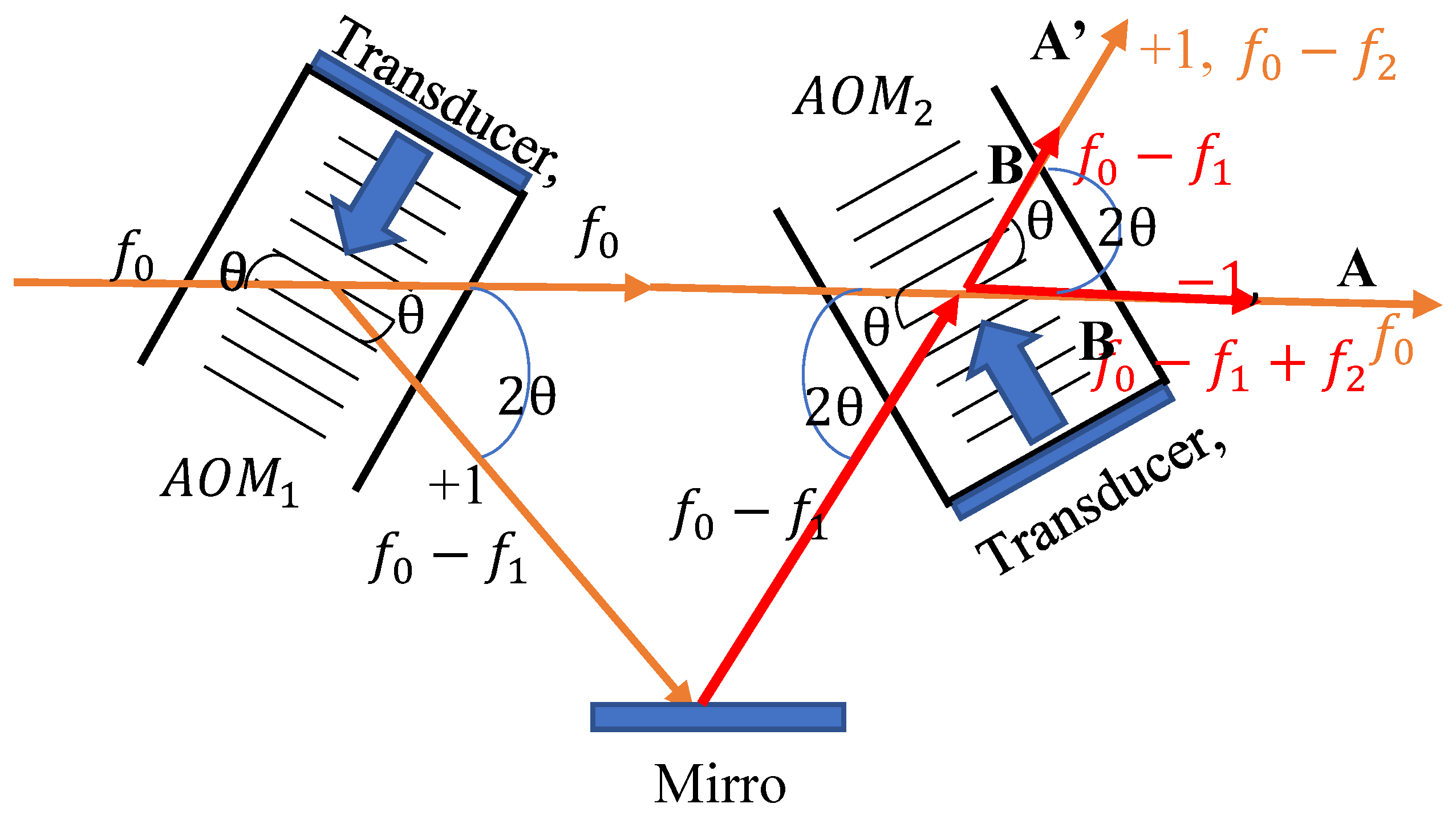
The basic optical setup of the heterodyne light source is shown in Figure 2 to further illustrate the principle of the coincidence of the two beams produced by the two AOMs connected in series. Here the modulation frequencies of AOM₁ and AOM₂ are $f_1$ and $f_2$, respectively. Under Bragg diffraction conditions, if the optical frequency of the laser light is $f_0$, then the optical frequency of the 0th-order beam from AOM₁ is unchanged at $f_0$, while the optical frequency of the +1st-order beam is $f_0-f_1.$ The angle between these two beams is 2θ. The 0th-order beam from AOM₁ is incident on the second AOM (AOM₂). The optical frequency of the direct beam remains unchanged at $f_0,$ which is denoted as beam A, while the optical frequency of the +1st-order beam is $f_0-f_2$ and is denoted as beam A′. The angle between these two beams is 2θ. In addition, the diffracted light with a frequency of $f_0-f_1$ is reflected into AOM₂ after passing through mirror M. The direct light frequency remains $f_0-f_1$, denoted as beam B, and its −1st-order beam has a frequency of $f_0-f_1+f_2$, denoted as beam B′. By fine-tuning the angle of mirror M so that the angle of incidence is θ (that is, the angle between the 0th-order beams is 2θ), the two sets of beams can coincide. One set consists of beam A′ coincident with beam B, while the other set consists of beam A coincident with beam B′. The frequency difference between the two beams in both sets is$f=\left|f_2-f_1\right|$.

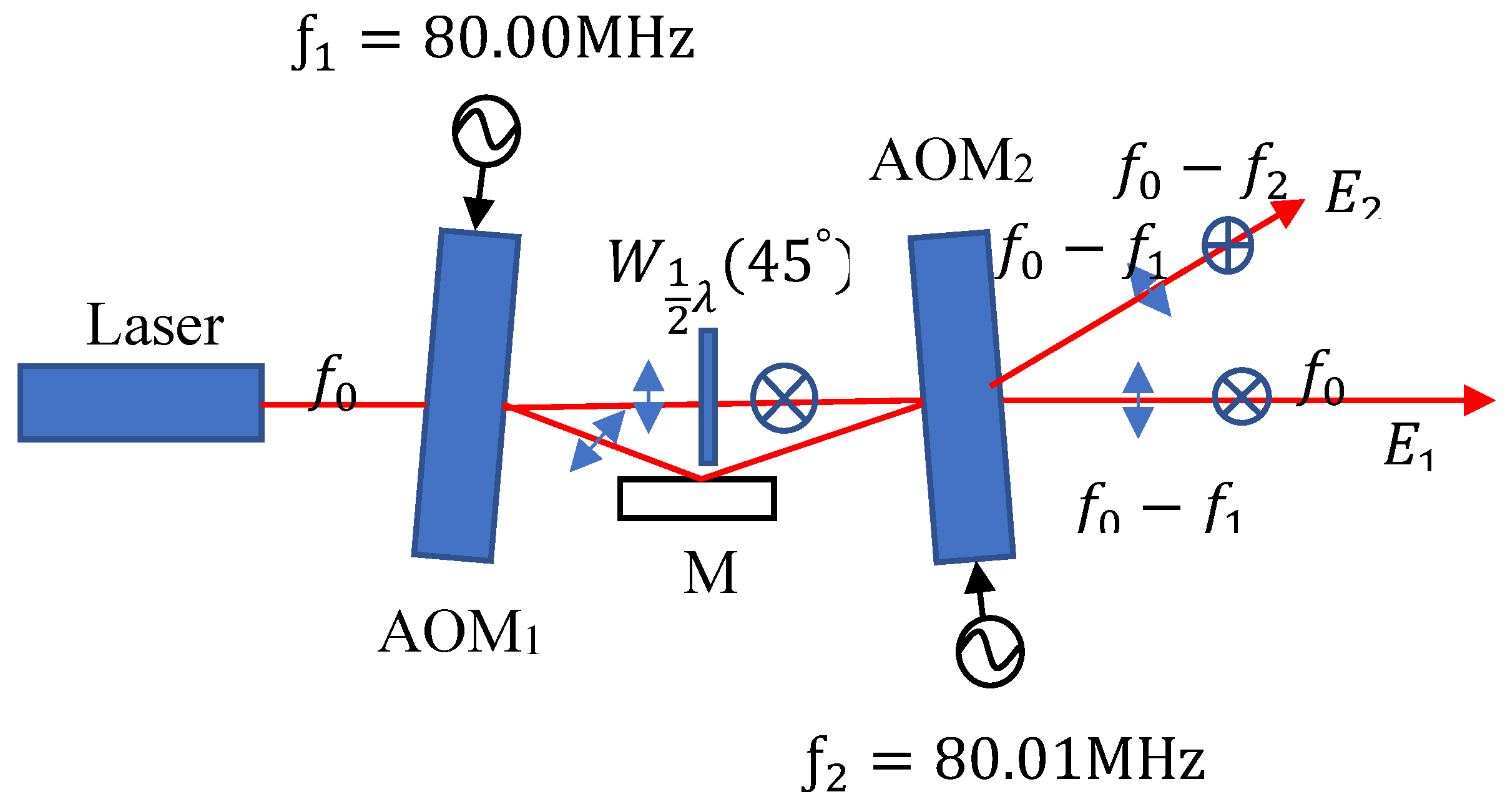
As illustrated in Figure 3, the proposed heterodyne light source consists of a laser, two AOMs (AOM₁, AOM₂), a mirror (M), and a half-wave plate ($W_{\lambda /2}(45°)$) positioned at an azimuth angle of 45°.

The acoustic waves of the two AOMs propagate in opposite directions. In this configuration, the laser operates at a frequency of $f_0$, and the modulation frequencies of AOM₁ and AOM₂ are set to $f_1$ (80.00 MHz) and $f_2$ (80.01 MHz), respectively. Fine-tuning the AOMs enables them to operate under Bragg-diffraction conditions, the diffraction efficiency of the ±1st-order light reaches approximately 44%, while the 0th-order light achieves approximately 51% efficiency. When the 0th-order light from AOM₁, which is p-polarized, passes through the half-wave plate$W_{\lambda /2}(45°)$, the outgoing light becomes s-polarized, making its polarization perpendicular to that of the +1st-order light. The +1st-order light from AOM₁, after being reflected by mirror M, is directed into AOM2. Upon passing through AOM2, the frequencies of the 0th- and −1st-order light beams become $f_0-f_1$ and $f_0-f_1+f_2$, respectively. In addition, after the 0th-order light of AOM1 passes through AOM2, the frequencies of the 0th- and +1st-order lights from AOM2 are $f_0$ and $f_0-f_2$, respectively, as illustrated in Figure 3. By adjusting the angle of mirror M relative to the AOMs, the 0th-order p-polarized light ($f_0-f_1$) coincides with the +1st-order s-polarized light ($f_0-f_2$), while the −1st-order p-polarized light ($f_0-f_1+f_2$) coincides with the 0th-order s-polarized light ($f_0$). The Jones vectors of the electric field intensities $E_1$ and $E_2$ can be expressed as:

$$E_1=\left[\begin{array}{c}{A}_{x1}{e}^{j2\pi \left(f_0-f_1+f_2\right)t}\\ A_{y1}{e}^{j2\pi f_{0}t}\end{array}\right],$$

(3)

And

$$E_2=\left[\begin{array}{c}{A}_{x2}{e}^{j2\pi \left(f_0-f_1\right)t}\\ A_{y2}{e}^{j2\pi (f_0-f_{2}t}\end{array}\right],$$

(4)

respectively, where $A_{x1}$ and $A_{y1}$ are the amplitudes of the electric field $E_1$ in the x and y directions, and $A_{x2}$ and $A_{y2}$ are the amplitudes of the electric field $E_2$in the x and y directions, respectively. Once the two orthogonally polarized light beams coincide, two sets of heterodyne light sources are formed, with a frequency difference of $f=\left|f_2-f_1\right|=$ 10 kHz.

3. Results

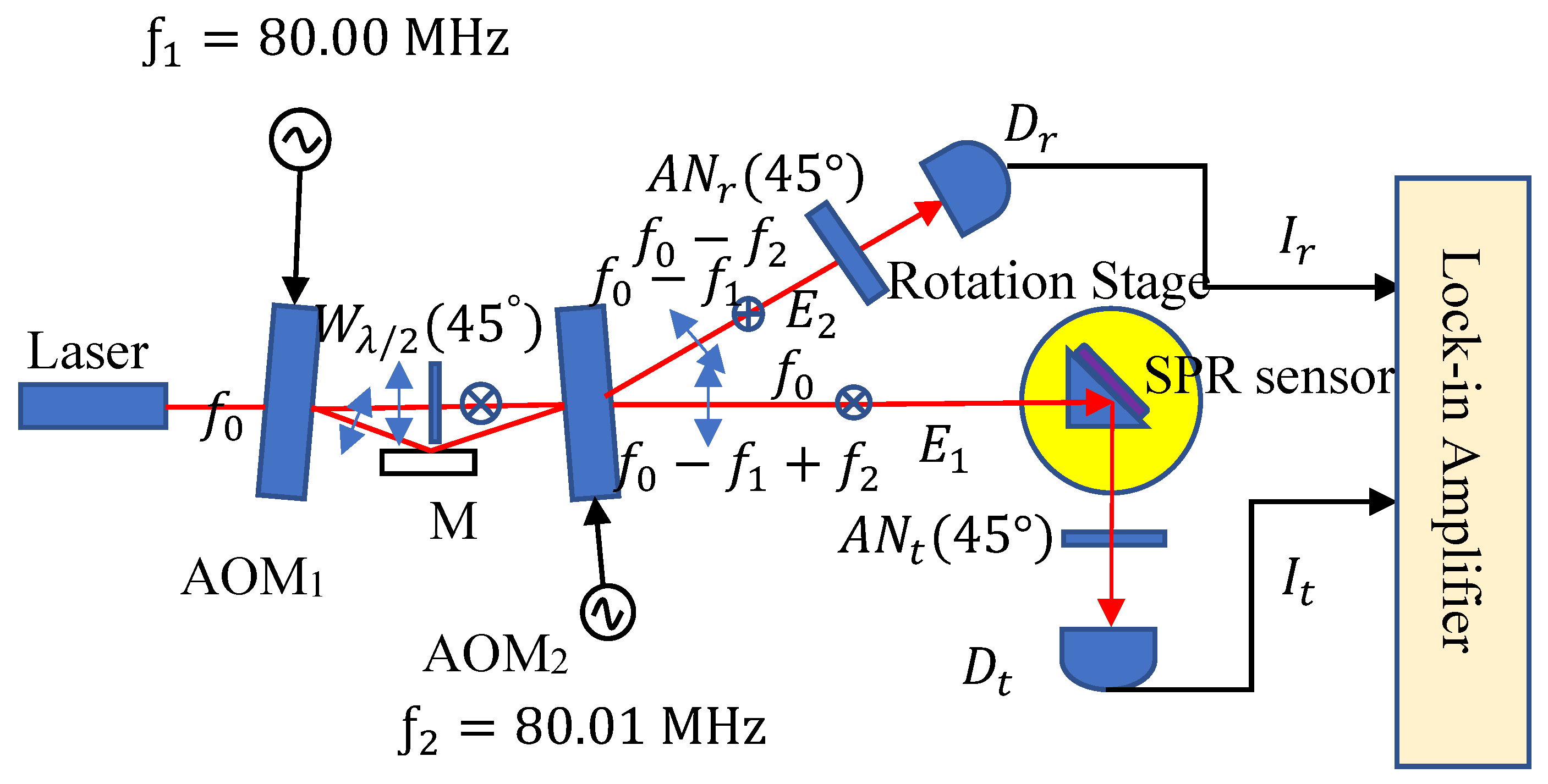
In order to demonstrate the feasibility of the proposed heterodyne light-source architecture, we use common-path heterodyne interferometry to measure the thickness of the gold film of a known surface plasmon resonance (SPR) sensor. The experimental architecture is illustrated in Figure 4.

We use an analyzer with a transmission axis set at a 45° angle to allow the orthogonal polarized light beams to interfere. The resulting interference signal was detected by a photodetector. The reference signal detected by $D_r$ is expressed as

$$I_r=I_{r0}\left(1+V_{r}cos\left(2\pi ft\right)\right)$$

(5)

and the test signal detected by $D_t$ can be expressed as:

$$I_t=I_{t0}\left(1+V_{t}cos\left(2\pi ft+\varphi \right)\right),$$

(6)

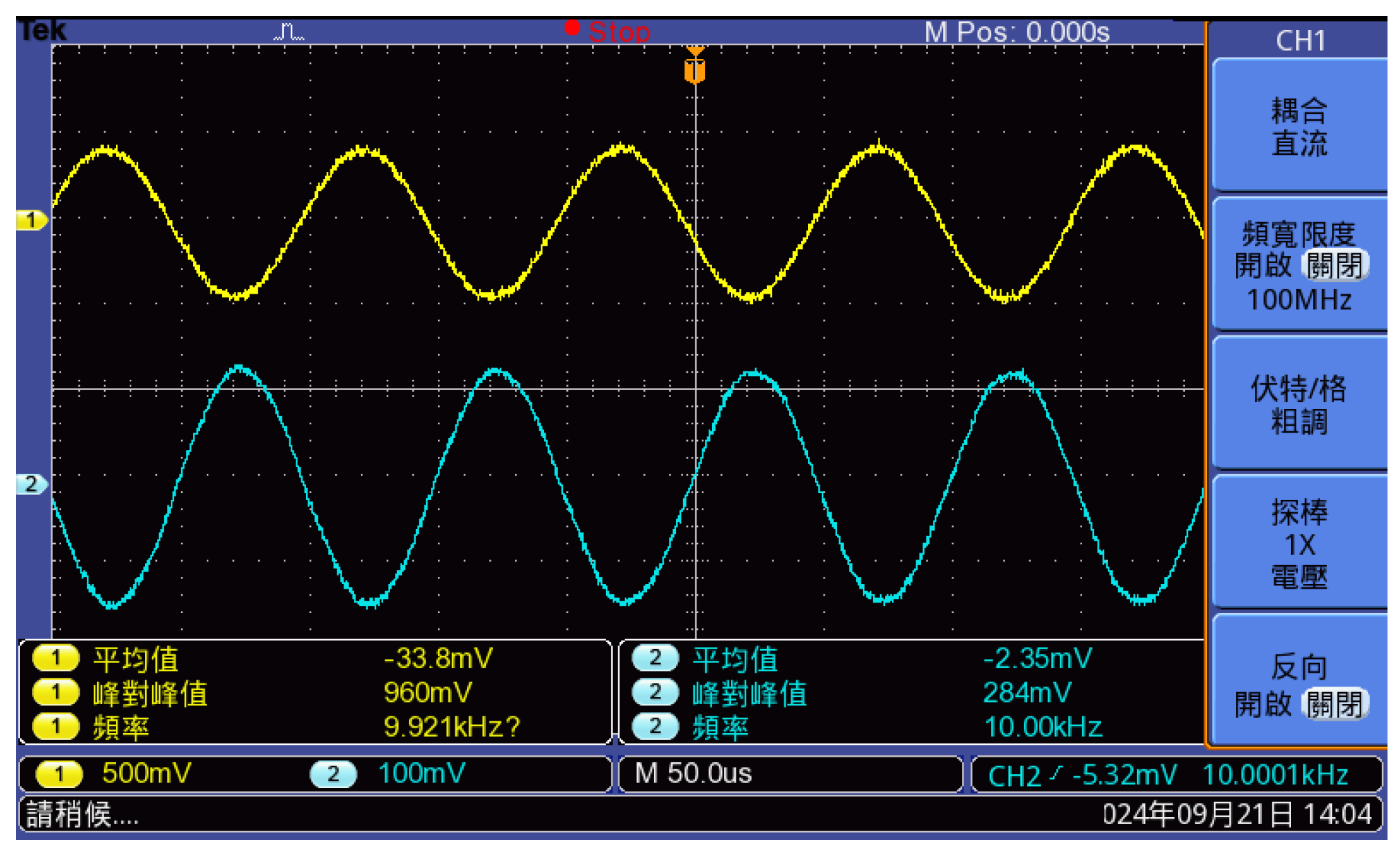
where $I_{r0}$ and $I_{t0}$ are the average intensities, $V_r$ and $V_t$ are the visibilities, and $\varphi$ is the phase-shift difference of the SPR sensor. The interference signals were recorded using an oscilloscope, as shown in Figure 5. According to the principle of the SPR sensor, the phase shift difference ϕ can be expressed as:

$$\mathsf{\varphi }={\delta }_p-{\delta }_s,$$

(7)

where ${\delta }_p$ and ${\delta }_s$ are the phase shifts of the p- and s-polarized light beams after passing through the SPR sensor.

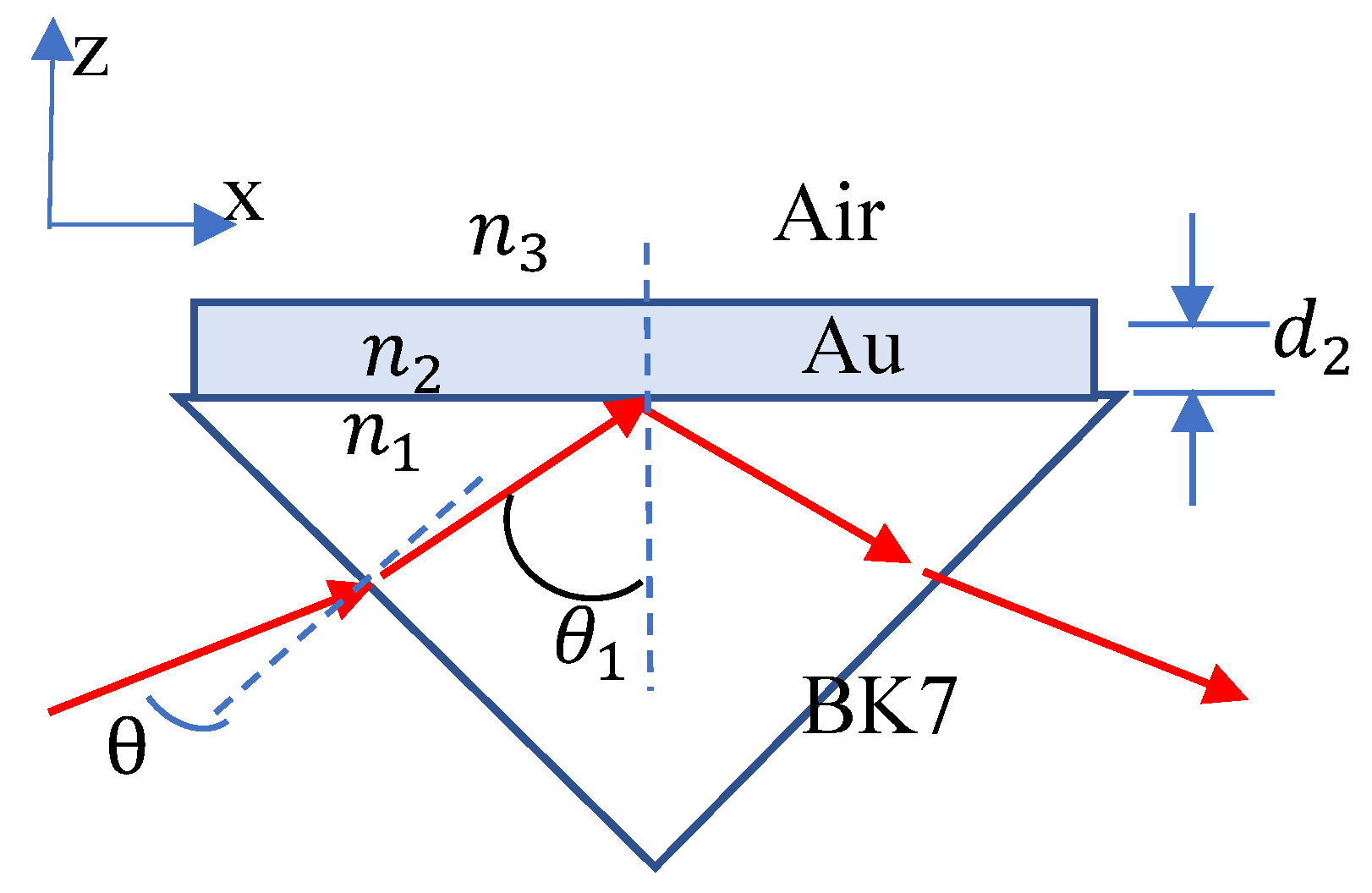
As illustrated in Figure 6, the refractive indices of the prism (BK7), Au, and air are denoted by $n_1,n_{2,}$, and $n_3$, respectively.

The total reflection coefficient of the p- or s-polarized light can be expressed as [8]:

$$r_{123}^t={\displaystyle \frac{r_{12}^t+r_{23}^t{e}^{i2k_{z2}{d}_2}}{1+r_{12}^t{r}_{23}^t{e}^{i{2k}_{z2}{d}_2}}}=\left|r_{123}^t\right|\mathrm{\angle }{\delta }_t,t=pors,$$

(8)

where $d_2$ is the thickness of Au and:

$$k_{z2}{d}_2=k_0{n}_2{d}_{2}cos{\theta }_2={\displaystyle \raisebox{1ex}{$2\pi d_2$}\!\left/ \!\raisebox{-1ex}{${\lambda }_0$}\right.}{\left(n_2^2-n_1^2{sin}^2{\theta }_1\right)}^{1/2}$$

(9)

where $n_2$ and $n_1$ are the refractive indices of Au and the prism, respectively; ${\theta }_2$ and ${\theta }_1$ are the angles of the light beams at the Au–prism interface; $r_{ij}^t={\displaystyle \frac{E_i^t-E_j^t}{E_i^t+E_j^t}},(t=sorp)$ is the reflection coefficient at the boundary between mediums $i$and j, where $E_{i\left(j\right)}^p={\displaystyle \raisebox{1ex}{${n_{i\left(j\right)}}^2$}\!\left/ \!\raisebox{-1ex}{$k_{zi\left(j\right)}$}\right.}$; $E_{i\left(j\right)}^s=k_{zi\left(j\right)}$; and $i,j=1,2,3.$ For a laser wavelength of 632.8 nm, the refractive indices of the BK7 prism, Au, and air are 1.51509, ${\left(-12+1.26i\right)}^{1/2}$, and 1.0003, respectively. Substituting these values into Equations (7)–(9) yields the total reflection coefficient and the phase shift difference $\mathsf{\varphi }$. The resonance angle is near at $43.5°$ for the boundary between Au and Bk7 and surface plasmon resonance conditions must be met

$$k_{sp}=\sqrt{{\displaystyle \frac{{\epsilon }_1{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2}}}{k}_0$$

(10)

where ${\mathsf{\epsilon }}_2$ and ${\epsilon }_1$ are the relative permittivity of Au and the Bk7 prism, respectively and $k_0$ is the wavenumber in vacuum.

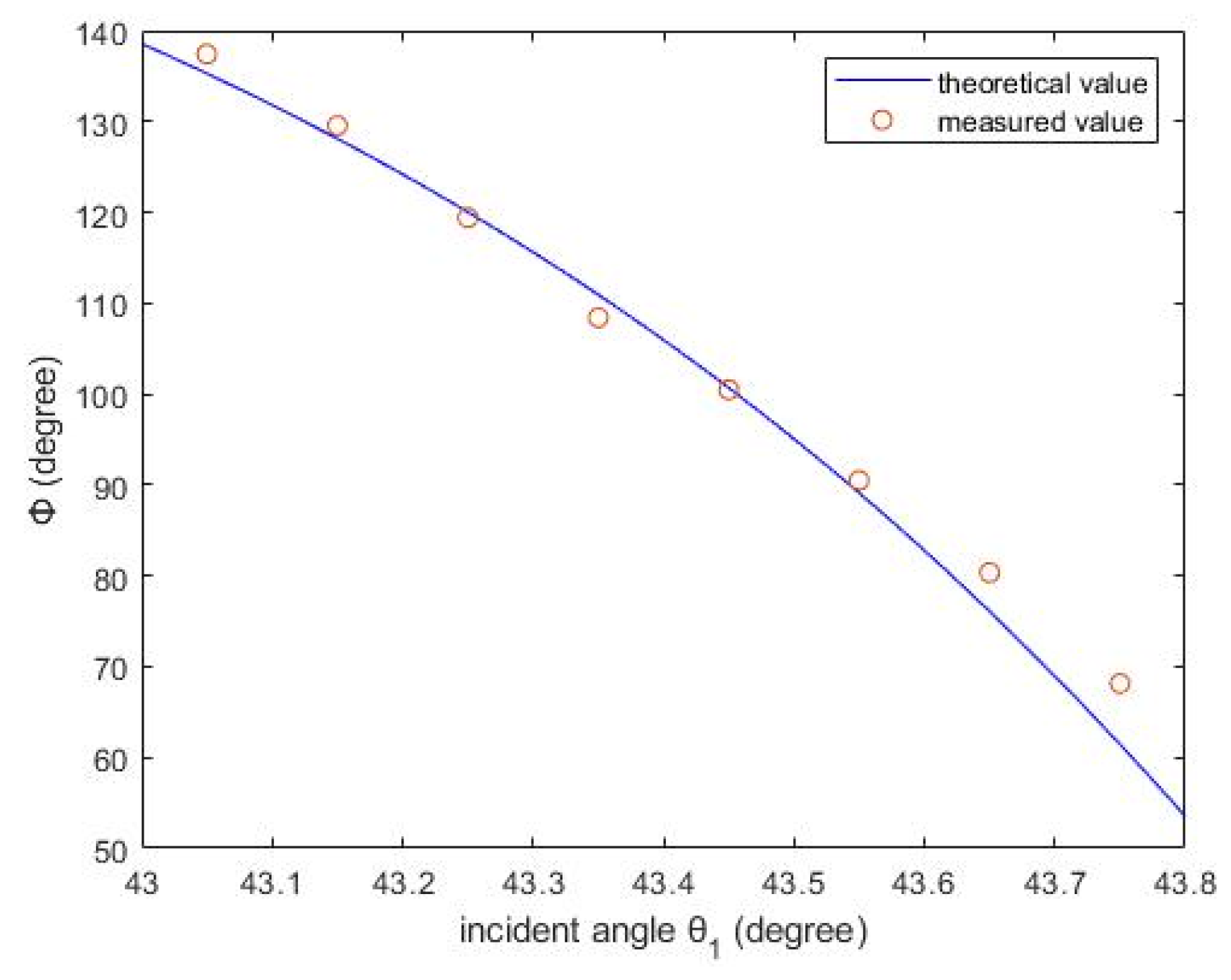
By rotating the SPR sensor counterclockwise near the resonance angle (from $43°$ to $48°$), the phase-shift difference $\mathsf{\varphi }$ and the angle of incidence ${\theta }_1$ were recorded. The experimental data, denoted by red circles, are shown in Figure 7, alongside simulation results (solid line) generated using MATLAB. The optimal gold-film thickness obtained from the experiment was 35 nm, which is in good agreement with the actual gold-film thickness of the SPR sensor.

4. Discussion

These experiments confirm the feasibility of the proposed heterodyne light source as a reliable component for a common-path heterodyne interferometer. The phase resolution determined by stander deviation test was 0.04° as shown in Figure 8. From Table 1, the phase resolution of our structure is better than that of the Mach-Zehnder AOM structure and EOM architecture in our experiments. Although it is not better than Zeeman laser. But because of the low price, it still has its value. Under Bragg-diffraction conditions, the interference contrast could exceed 0.7 and the utilization rate of the light source was approximately 90%.

5. Conclusions

This heterodyne light-source architecture, featuring dual AOMs in tandem under Bragg-diffraction conditions, addresses the limitations of the Mach–Zehnder architecture regarding light-source utilization, as well as the low diffraction efficiency of previous dual-AOM architectures [6]. It offers ease of assembly and reduces the need for components such as beamsplitters, polarized beamsplitters, and an additional mirror, while only requiring the addition of a half-wave plate. This makes it a highly efficient and practical solution.