D-Entropy: A New Approach to the Dynamics and Evolution of Systems

1. Introduction

Motion and fundamental interactions are integral properties of matter. Evolution, however, should also be considered one of these properties. Although evolution encompasses motion and interactions, it is not limited to these aspects; it also involves the processes of birth, development, and decay of complex systems. While there are well-developed theories for studying the dynamics and interactions of material objects, the same cannot be said for evolution. As I. Prigogine stated, today we have a physics that describes “what exists,” but there is no “physics of becoming”—or, as we will refer to it, evolutionary physics [1].

In evolutionary physics, the primary task is to describe the processes of emergence, development, and decay of systems within the framework of fundamental physical laws. In other words, the scope of evolutionary physics is defined by the problems that can be addressed using these laws. One of its main objectives is the study of the Universe, which cannot be fully understood without accounting for the evolutionary processes associated with the motion of objects in inhomogeneous external force fields.

There are several challenges on the way to creating the physics of evolution [2,3]. The principal obstacles–without overcoming which its development is impossible—are that modern physics is highly fragmented, whereas a unified approach is required to describe evolution. Moreover, these fragments are insufficiently interconnected. Today, physics can be broadly divided into two main areas.

In the first area, we include disciplines focused on studying the dynamics and interactions of material objects, all based on the fundamental laws of physics. The dynamics of bodies is primarily studied using Newton’s laws, often without accounting for the role of their internal structures in motion [4,5,6]. The formalisms in this field are typically constructed for systems under the assumption of holonomic constraints, a condition that precludes the study of dissipative processes—processes essential for the emergence of attractors and, consequently, evolution [7].

The nature of matter is primarily studied through quantum mechanics [8]. In many respects, quantum mechanics also relies on the principles of classical mechanics. Both quantum and classical mechanics are linear and do not account for dissipative processes. Moreover, quantum mechanics encounters issues related to the principle of causality [9,10,11,12]. In the first section, kinetic energy and momentum serve as the main parameters.

The second section addresses the behavior of the internal state of bodies in response to changes in external conditions. In this context, relatively large, stationary, closed systems are typically used as models of bodies, representing statistical ensembles of equilibrium subsystems. As examples of such subsystems, sets of potentially interacting material points (MP) may be considered. We refer to these subsystems as structured bodies (SB).

Studies of the internal states of bodies are conducted within the frameworks of thermodynamics, statistical physics, and kinetics, relying on empirical and probabilistic laws [13,14]. One qualitatively new characteristic of these internal states—absent in the first section—is entropy. In thermodynamics, entropy represents the portion of energy required to maintain a particular state of the system, while internal energy corresponds to the total energy of the system’s constituents moving relative to its center of inertia (CI). The justification for entropy is grounded in statistical laws; for stationary systems, it is defined as the logarithm of the statistical weights of the macroscopic states of the subsystems of a statistical ensemble [13]. Thus, the primary parameters characterizing the internal states of bodies are internal energy and entropy.

As we can see, physics can be divided into two sections. The first section focuses on the dynamic characteristics of bodies without considering the influence of their internal structure, while the second section examines the behavior of the internal states of bodies independently of their dynamics. This division arises from the distinct research methods employed in each area. To describe a body’s dynamics, the equations and formalisms of classical mechanics are used. However, when studying the structure of bodies—where the number of independent variables is determined by the enormous number of atoms in a system—a complete description based solely on classical mechanics is practically impossible [13]. This limitation led to the development of statistical physics, which enables the study of internal states using the laws of statistics. The feasibility of independently describing a body’s dynamics and its internal states stems from the linear nature of physical laws, whereas the relationship between a body’s dynamics and its internal states is inherently nonlinear.

Evolution processes are determined by both the dynamics of bodies and the changes in their internal states. Therefore, the study of evolution must integrate these two domains. Given the requirement for the unity of physics and adherence to the principle of causality, this integration must be based on the fundamental laws of physics. In other words, the statistical methods used for the micro-description of systems should derive from deterministic physical laws. However, before these domains can be successfully combined, it is necessary to resolve the contradictions between them, which stem from the limitations inherent in their respective theories [2].

The primary contradiction lies in the reversibility of classical mechanics versus the irreversibility of thermodynamic processes. In classical mechanics, reversibility arises from the assumption of holonomic constraints in its formalisms [4,5,6,15], a condition that precludes the description of dissipative processes. To address this contradiction, attempts have been made to develop a dynamic interpretation of entropy. For instance, one approach involved utilizing positive Lyapunov exponents, which characterize the degree of mixing in systems [7]. However, this mechanism for irreversibility requires the presence of arbitrarily small external fluctuations—thus, statistical regularities are invoked regardless.

The limitations of the second section primarily arise from the requirement that systems remain near equilibrium and from the neglect of the role that a system’s dynamics play in altering its internal state. Furthermore, a major obstacle to unification is the inconsistency between the statistical methods and the deterministic approaches used to describe systems. Together, these limitations prevent the study of evolution solely within the framework of conventional physical laws.

Here, we consider a relatively new approach to overcoming these challenges, which opens up the possibility of constructing a physics of evolution. This approach is based on accounting for the role of the internal structure of bodies in their dynamics [16]. Such an accounting has been successfully implemented through the equation of motion for (SB). This equation is derived from the invariance of the total energy of an SB, thereby eliminating the need for the holonomicity condition and the assumption of potential collective forces [17]. It takes into account not only the work done by external forces in producing motion, as in classical mechanics, but also the work that changes the internal state of the SB.

To quantify the transformation of kinetic energy into internal energy, we introduce the concept of D-entropy. Defined in terms of the system’s dynamic parameters, D-entropy is expressed as the ratio of the change in internal energy to its total value [16]. In this way, D-entropy characterizes evolutionary processes and provides a means to unify the two sections of physics.

Below, we will discuss the essence of D-entropy, its role in physics, and its relationship to existing concepts of entropy. To this end, we will briefly review works addressing the challenges associated with entropy in physics. We will demonstrate how the equation of motion for SB is derived—taking into account the interplay between the dynamics of bodies and their internal states—and examine how D-entropy emerges from this equation, resolving certain issues present in traditional thermodynamic definitions of entropy.

It has been 160 years since Clausius introduced the concept of entropy, which quantifies the portion of the work done by external forces on a gas that is converted into heat. He established that entropy can only increase [9].

In his attempts to construct an atomic theory of gases based on classical mechanics, Boltzmann laid the foundation for statistical physics by defining the macrostates of a system probabilistically in terms of its microstates. Boltzmann’s statistical mechanics not only provided a justification for thermodynamics but also served as compelling evidence for the atomic nature of matter [18]. He proposed a statistical definition of entropy [13].

To date, numerous definitions of entropy have been proposed for systems near equilibrium [19]. The most influential definitions are those by Gibbs and Boltzmann [20]. Gibbs entropy is defined for a macroscopic classical system in terms of a probability distribution function over the phase space of an ensemble. In contrast, Boltzmann entropy is based on the quantization of microstates in phase space and is defined for an individual system [13]. Most authors agree that Boltzmann’s definition is the most general [21].

Entropy possesses the same fundamental generality in physics as concepts such as energy, momentum, and angular momentum [22]. Yet, despite its widespread use across various scientific disciplines, there is still no consensus on the true physical essence of entropy [23]. Some argue that the statistical concept of entropy lacks a sufficiently clear definition that reflects its inherent physical nature [24], and there are even claims that entropy is not a physical quantity at all [19]. This controversy is often attributed to the incompatibility between the probabilistic laws of statistical physics, which underpin the definition of entropy, and the deterministic laws of physics. According to some, despite numerous attempts to explain its physical meaning, “its physical meaning remains shrouded in the deepest of mysteries” [25]. There are also works suggesting that entropy is nothing more than a mathematical invention, illogically employed to explain the physics of collective phenomena [26]. Furthermore, some studies conclude that the second law of thermodynamics cannot be derived statistically from first principles [27,28]. These conclusions are supported by the observation that statistical explanations of the second law violate the principle of causality, which is essential for constructing a consistent physical theory [29].

Additional analyses of quantum systems have led to the assertion that the arrow of time is a fundamental feature intrinsic to the evolution of systems, both large and small [30]. During the early development of quantum mechanics, it was proposed that randomness is a fundamental aspect of the theory—a view supported by Bohr and Born [31,32]. Einstein, however, famously objected, arguing that “God does not play dice” and that the observed randomness merely reflects the incompleteness of quantum mechanics [9,10]. Many issues remain concerning the foundations of statistical mechanics, its connection to thermodynamics, and the very concept of entropy. Some works even suggest that, in order to resolve the problems of defining entropy and explaining irreversibility, these phenomena should be incorporated directly into the laws of microscopic physics [49]. Much of the ongoing debate surrounding entropy stems from disagreements over the various definitions and proposed applications of the concept [33,34].

The greatest difficulties arise when attempting to apply the concept of entropy to nonequilibrium systems, which include nearly all complex natural objects. Although some progress has been made in extending the concept of entropy to systems slightly removed from equilibrium [35], this work is crucial for developing a physics of evolution, since evolutionary processes are inherently nonlinear and occur exclusively in nonequilibrium systems. A comprehensive overview of these studies can be obtained from reviews on the development of nonequilibrium thermodynamics, where approaches based on statistical theory, information theory, kinetic theory, and numerical modeling are discussed [36]. Notably, debates often center on Einstein’s relation [37], which is known to be violated in nonequilibrium systems [38].

Furthermore, attempts have been made to introduce the concept of evolutionary entropy for living organisms, defining it as a statistical measure that quantifies the number and diversity of metabolic cycles within a population of replicating organisms [39]. In such work, the Fundamental Theorem of Evolution is derived to describe the direction of energy transformation in biological populations. It is claimed that in open systems, “evolutionary entropy increases when the energy source is rare and diverse, and decreases when the energy source is abundant and solitary.”

In summary, this review suggests that the principal challenges in understanding the physical essence of entropy stem from its statistical interpretation. Existing expressions for entropy fail to account for the dependence of changes in internal energy on the motion and interactions of bodies. Moreover, the incompatibility between the probabilistic laws that underpin thermodynamics and the deterministic laws of physics further exacerbates the contradictions between different branches of physics [32]. This underscores the importance of seeking an expression for entropy in terms of the dynamic parameters of bodies, grounded in the fundamental laws of physics [7].

2. D—Entropy of Nonequilibrium Systems

2.1. Equation of Motion for Structured Bodies

The evolution of bodies, as determined by their dynamics, can be understood through a complete description of the motion of their individual elements, since each element contributes both to the kinetic energy and to the internal energy of the system [13]. To account for the interplay between these contributions, it is necessary to derive an equation that governs the change in the internal energy of a SB while considering the influence of its motion.

To obtain such an equation, one must rely on physical principles characteristic of moving systems. These principles include:

1) Physical Equivalence: The same physical laws apply to both the system and its environment.

2) Duality of Symmetry: The dynamics of a structured body are governed not only by the symmetries of space, as in classical mechanics, but also by the intrinsic symmetries of the system itself.

3) Nonlinear Interrelation: Evolution is determined by the nonlinear relationship between the system’s dynamics and changes in its internal state, a relationship influenced by both macroscopic dynamic parameters of the SB and the microscopic parameters governing the movements of its constituent elements [17].

Using these principles, an equation of motion for the structured body was derived. This equation follows from the condition of invariance of the total energy, defined as the sum of the SB’s kinetic energy and its internal energy. It accounts for the fact that the work performed by external forces contributes both to changes in the kinetic energy of the SB and to alterations in its internal energy. In other words, neither the kinetic energy of the MP nor the internal energy remains invariant during evolution, underscoring the impossibility of studying evolution within the framework of only one of the two traditional sections of physics [16]. Next, we explain how the equation of motion for a structured body (SB) was derived.

The equations of motion for SB in classical mechanics are derived from a set of formalisms originally constructed based on Newton’s equations of motion for material points (MP). These formalisms assume that the constraints are holonomic and that all collective forces are conservative [4,5]. However, these assumptions preclude the description of evolution because they do not account for dissipative processes. Consequently, it became necessary to derive an equation of motion for SB that eliminates these restrictions.

This was achieved by formulating the equation of motion for SB from the condition of conservation of its total energy—expressed as the sum of its kinetic energy and internal energy. In contrast to SB, the total energy of a material point, which lacks internal structure, coincides with its kinetic energy. Newton’s equation of motion for MP can be derived by differentiating their kinetic energy with respect to time [5]. According to this equation, the acceleration of an MP is proportional to the external force acting on it, with the work of external forces being entirely devoted to accelerating the MP.

Owing to the additive nature of energy, the equation of motion for an SB can likewise be derived from the invariance of its total energy. In practice, it was necessary to represent the total energy of an SB as the sum of its internal energy and its kinetic energy [16]. The kinetic energy is determined by the motion of the SB’s CI, its mass, and the speed and potential energy of the CI in an external field. In contrast, the internal energy is defined by the velocities of the material points relative to the CI and by the energy associated with their mutual interactions. The analytical form of the SB’s kinetic energy follows from the symmetries of space and time, while the expression for its internal energy is dictated by the intrinsic symmetries of the SB [17].

According to the resulting equation of motion for an SB, the acceleration is proportional to the net force acting on its CI. However, unlike in the case of a material point, the work done by external forces on an SB contributes not only to its translational motion but also to changes in its internal energy. This distinction highlights a significant difference between the formulations of the laws of motion for MPs and SBs.

The representation of the total energy as the sum of the internal energy of SB and the energy of its motion is carried out in independent micro- and macrovariables. Microvariables determine the internal dynamics of the elements of SB. Macrovariables determine the movement of the SB CI in space. The dual representation of the total energy made it possible to take into account the transition of the energy of motion into the internal energy of SB [16]. Differentiating the total energy with respect to time, represented through micro- and macrovariables as the sum of the energy of motion and internal energy, under the condition of its invariance, after simple transformations we obtain the equation of motion of SB [17]:

$$M_N{\dot{V}}_N=-F_N^0-{\mu }^d{V}_N,$$

(1)

where:

$$F_N^0={\displaystyle {\sum }_{i=1}^N{F}_i^0},$$

where is the external force acting on the i-th MP;

$${\mu }^d={\dot{E}}_N^{\mathrm{int}}/{(V_N^{max})}^2;$$

where is the interaction force i and j MP;

$$F_{ij}^0=F_i^0-F_j^0$$

$${\dot{E}}_N^{\mathrm{int}}={\displaystyle {\sum }_{i=1}^{N-1}{\displaystyle {\sum }_{j=i+1}^N{v}_{ij}}}(m{\dot{v}}_{ij}+F_{ij}^0+N{F}_{ij})$$

$$V_N^{max}=-{\dot{E}}_N^{\mathrm{int}}/F_N^0$$

Equation (1), unlike the equation of motion of a body obtained within the framework of the formalisms of classical mechanics, takes into account the relationship between the energy of motion of a body and its internal energy. In its righthand side, the first term defines the external potential forces that change the velocity of the CI of SB. The second term is bilinear. It depends on micro- and macrovariables and defines the relationship between the energy of motion and the internal energy. This term is non-zero only when the condition holds: that is, when the field of external forces is non-uniform. It characterizes the evolution of SB, caused by the relationship between its energy of motion and its internal energy. Its mathematical essence is determined by the fact that due to the motion of SB in a non-uniform external field of forces, a change in its state occurs as a result of the coupling of vectors from the symmetry groups of space and SB. The first term in the right-hand side is zero when the work of the external forces is completely spent on changing the internal energy of SB. If the second term in the right-hand side is zero, then the work of the external forces is completely spent on the motion of SB. That is, equation (1) satisfies the correspondence principle. Based on the properties of a vector field in space, we will show that equation (1) uniquely characterizes the dynamics of systems. According to the Helmholtz theorem [40], any vector field, if it is unique, continuous and vanishes at infinity, can be represented as the sum of the gradient of a scalar function and the curl of a vector , whose divergence is zero. Then the expression for the force vector can be represented as follows [40]:

$$F=gradU(x,y,z)+rotB(x,y,z),divB(x,y,z)=0$$

(2)

Equation (2) reflects the fact that for an MP moving in an external force field, there is a change in the modulus and direction of the velocity. The change in the mod-ulus of the MP velocity vector is associated with the force that is determined by the gradient of the scalar potential U. The change in the direction of the MP velocity vector is determined by the vector potential B. That is, the MP participates in two independent motions: in translational motion with acceleration determined by the potential -force and rotational motion caused by the force orthogonal to the MP velocity vector. The classical equation of MP motion takes into account only the scalar potential.

The right side of the equation of motion of SB should also be the sum of the gradient and rotor components of the forces. Indeed, unlike MP, SB has internal energy. Therefore, the first term of equation (1), which determines the change in the modulus of the velocity of SB, is equal to the sum of the gradient in the scalar potential, acting on the MP. The second term is the resulting curl of the vector potential of forces. It determines the changes in the directions of the velocity vectors of the MP.

Thus, due to the fact that equation (1) is obtained from the total energy SB, presented as the sum of internal energy and the energy of motion, it uniquely determines the behavior of the velocity vector SB in space. Obviously, to uniquely determine the evolution of SB, equation (1) should be supplemented with the equations of motion of all elements of the system. Although such a solution is very difficult to implement, equation (1) itself allows us to understand the laws of evolution.

2.2. The Nature of Irreversibility and Bifurcations

Since classical mechanics excludes irreversibility, its explanation was initially based on probabilistic laws [7]. The basis of such an explanation is the exponential instability of Hamiltonian systems according to Lyapunov and the hypothesis of the existence of random external fluctuations. That is, this mechanism has a probabilistic nature and cannot be used to construct the physics of evolution. Below we will consider the deterministic mechanism of irreversibility that follows from equation (1). We will show that, according to equation (1), the establishment of equilibrium in SB ensembles is due to the transition of the energy of relative SB movements into their internal energy. We will do this based on the mechanism of formation of the flow of internal energies of the SB ensemble [41].

Let $E^{tr}$ be the energy of relative motions of SB. According to equation (1), part of this energy $\Delta E^{tr}$ is converted into its internal energy, where $\Delta E^{tr}$ is determined by the bilinear term of the second order of smallness of equation (1). This can be written as follows: $\Delta E^{tr}\sim {\chi }^2$, where $\chi$ is a small parameter, for example, the perturbation of the internal energy. First, consider the case $\Delta E^{tr}/E^{\mathrm{int}}$ <<1, when the violation of the equilibrium of SB can be neglected. In this case, the quantity $\Delta E^{tr}$ is equivalent to the increment of the thermal energy of SB. Irreversibility takes place here, since, by virtue of the law of conservation of momentum, the reverse transformation of the thermal energy of SB into the energy of its motion is impossible.

Let us consider the second case, when the interaction forces SB or their gradients are large enough. In this case, SB will not be in equilibrium, and they can be represented as a set of equilibrium subsystems moving relative to each other. Then, to change the internal energy of the subsystems as a result of their interactions, we can write: $\Delta E^{tr}=\Delta E_{ins}^{tr}+\Delta E^h$, where $\Delta E_{ins}^{tr}$ is the energy of relative motions and $\Delta E^h$ is the increment of the internal energies of the subsystems. That is, $\Delta E_{ins}^{tr}<\Delta E^h$. But energy $\Delta E^h$ cannot be converted into the energy of motion of the subsystems. Therefore, we will proceed from the fact that only $\Delta E_{ins}^{tr}$. Let us denote the reverse flow of internal energy as SB as $\Delta E_{ret}^{tr}$. According to equation (1), the value $\Delta E_{ret}^{tr}$ is determined by a bilinear function of micro- and macrovariables of the second order of smallness. And since, $\Delta E^{tr}~{\chi }^2$ we obtain that $\Delta E_{ret}^{tr}~{\chi }^4$. Consequently, the balance of energies of subsystems is determined by the condition:

$$H=\Delta E_{dec}^{tr}=\alpha {\chi }^2-\beta {\chi }^4$$

(3)

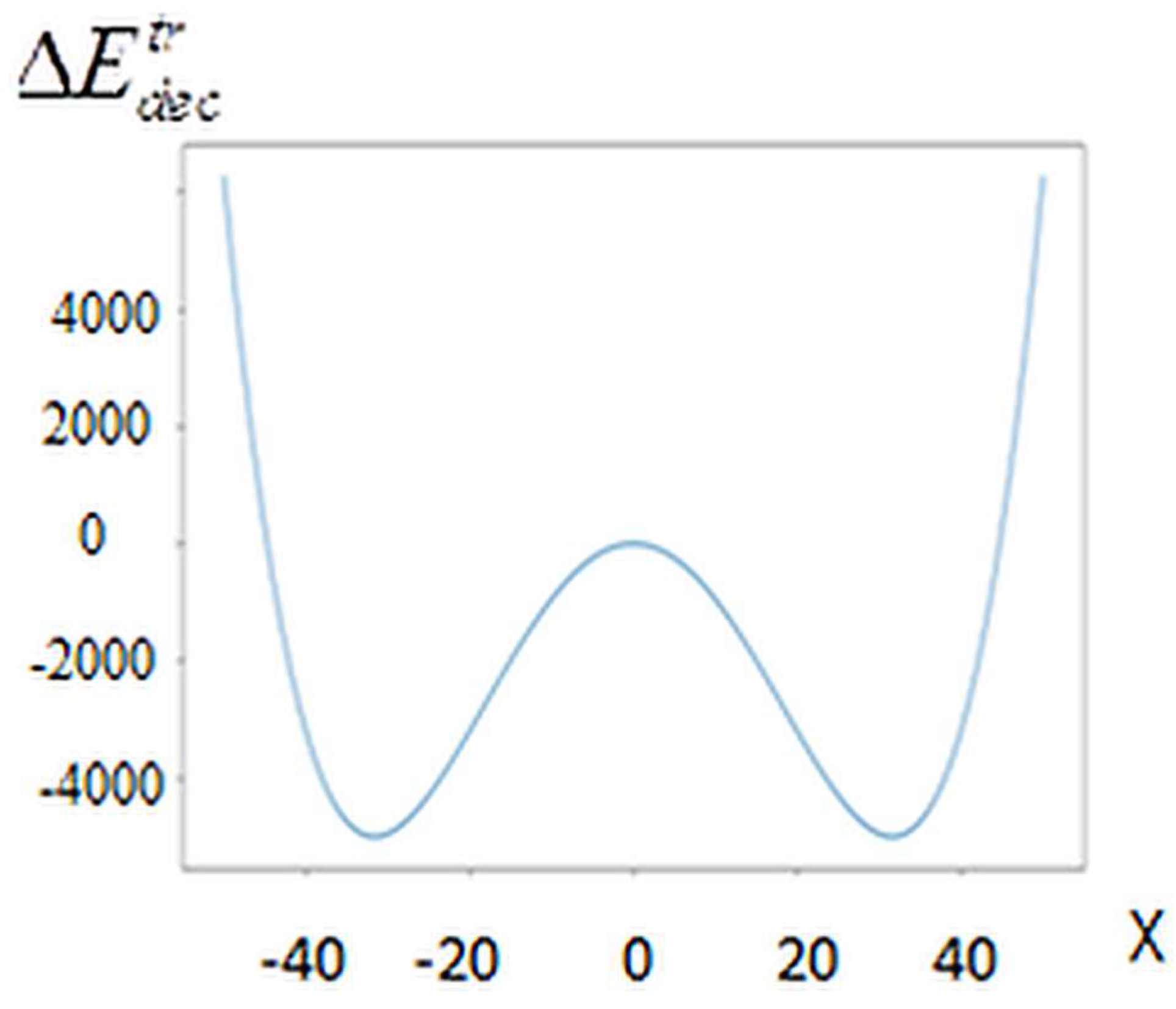
Here are $\alpha ,\beta$ the constants defined by equation (1). That is, the increase in internal energy SB $H=\Delta E_{dec}^{tr}>0$. Figure 1 shows the graph $\Delta E_{dec}^{tr}$. For values: $\left|\chi \right|\prec {\chi }_0$, where $\pm {\chi }_0$ are the roots of equation (8) irreversibility takes place. For SB with N > >1 we have $\Delta E_{dec}^{tr}>0$. For the systems to be stationary, the equality must be satisfied: $\Delta E_{dec}^{tr}=0$. Thus, according to the equation of motion (1), irreversibility conditioned by positive flow of energy of the system’s motion into its internal energy.

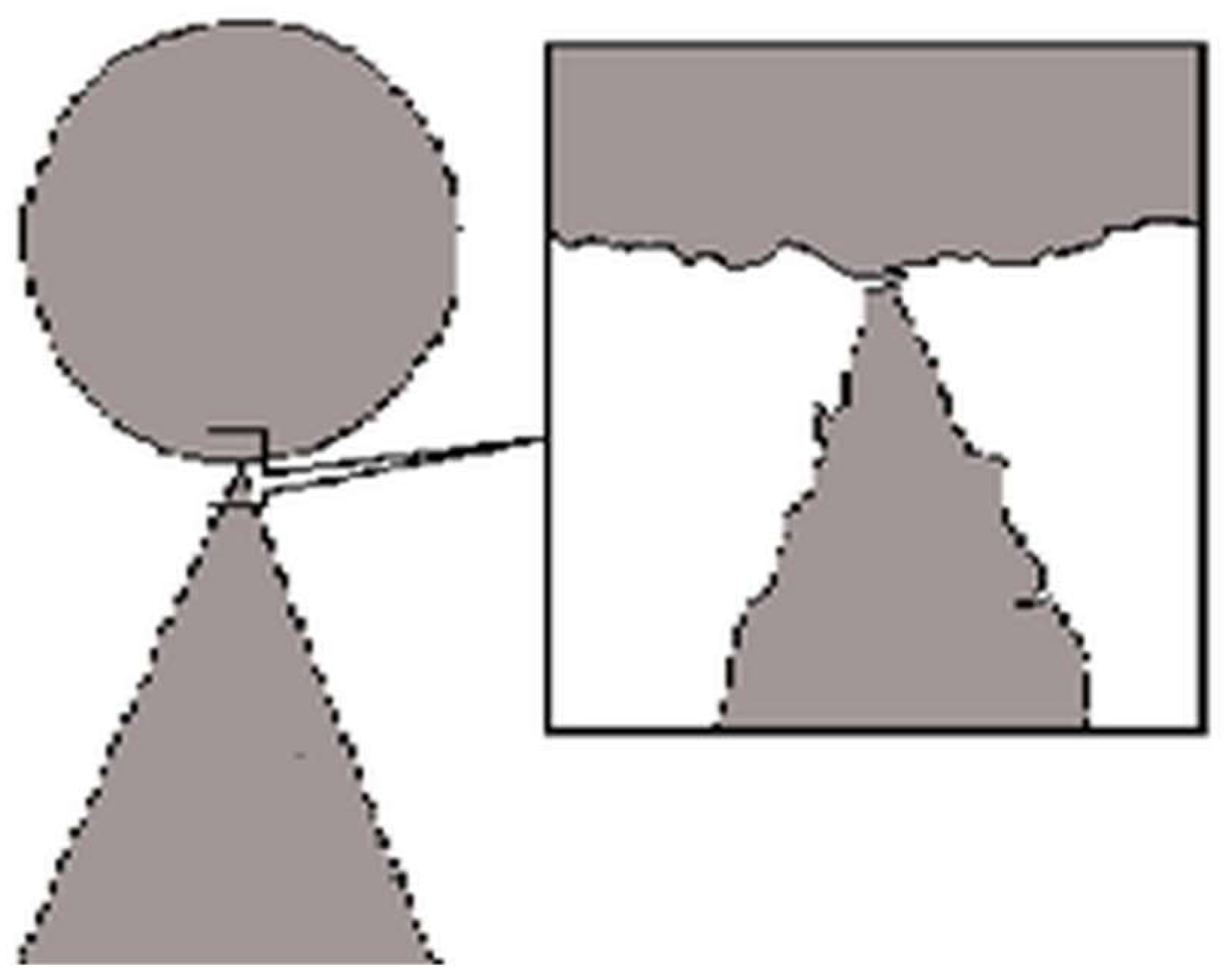
An example demonstrating microscopic natures of irreversibility, is bifurcation (Figure 2).

The dynamics at the bifurcation point are determined by the movements of the system elements (the sphere and the hill). In the micro description, the symmetries of the sphere and the hill are not absolute or “pure”, as is defined mathematically in the macro description. This can be considered as the domain of existence or admissibility of the corresponding type of symmetry. In this case, this domain of existence of symmetries is determined by the micro variables when the admissibility of the macro description is violated (see Figure 2). Therefore, here we have an example of the need to use a micro description due to the violation of the validity of the macro description at the bifurcation point [42]. Thus, within the framework of the micro description, bifurcation is a deterministic process. In accordance with the described mechanism, the “ideality of symmetries” is an approximation. It will be violated during the interaction between the hierarchical levels of infinitely divisible matter, up to its field state [16]. The physical essence of bifurcation is that in it the macrodynamics of the body depends on microdynamics its elements. Such a mechanism of symmetry breaking corresponds to the principle of causality. If symmetry breaking were random in nature and not a consequence of limitations of description methods, then constructing an evolutionary picture of the world within the framework of the laws of physics would be impossible.

2.3. The Nature of D-Entropy

The processes of heat absorption for bodies at rest are characterized by entropy [13,14]. However, the example of the growth of the entropy of a body when it rolls down an inclined surface with friction due to gravity demonstrates the need to take into account the dependence of entropy on the relative velocity of the interacting systems. To eliminate this shortcoming, it is necessary to have a concept of entropy for moving bodies in a non-uniform field of forces. This concept of entropy is introduced based on equation (1). We will call it D-entropy and define it as the ratio of the increment of internal energy to its total value due to the energy of motion [43].

$$\Delta S_N^d=\Delta E_N^{\mathrm{int}}/E_N^{\mathrm{int}}$$

(4)

where $\Delta S_N^d$ is the D-entropy, which determines the transformation of the energy of motion into internal energy. The prefix “D” means that the entropy is determined in a deterministic manner. The D-entropy can also be written as follows:

$$\Delta S^d~\Delta E_{dec}^{tr}/E_{\mathrm{int}}$$

(5)

Let us emphasize that in the general case, D-entropy may also contain a share of work that is associated with the expansion of the body under external pressure. However, this work can be identified based on the laws of thermodynamics. Thus, D-entropy, firstly, is determined by the transformation of the energy of motion into internal energy; secondly, it is determined; thirdly, for a sufficiently large system, it obeys the second law of thermodynamics. And, most importantly, it determines evolution. According to equation (1), using D-entropy, the work of external forces can be written as follows:

$$dA=-F_N^{0}dR-E_N^{\mathrm{int}}\Delta S_N^d$$

(6)

Let us explain equation (6) using the example of a body rolling with friction on an inclined surface. The first term in (6) determines the work of gravity to move the body. The second term determines the change in internal energy. It coincides with the change in thermodynamic potential [9]:

$$dU=TdS-PdV$$

(7)

It should be borne in mind that $dU$ it does not take into account the work of external forces caused by the body’s motion. That is, D-entropy through dynamic parameters determines the total work of external forces that goes to change the internal state of a moving system. This is the physical essence of the concept of D-entropy and its important difference from the thermodynamic concept of entropy.

Equation (7) is applicable only to equilibrium systems. However, if external forces are significant, then the equilibrium is violated. In this case, the system is an ensemble of SBs moving relative to each other. The change in the entropy of each SB is due to the absorption of the energies of their relative movements. A clear example of such a mechanism is the interaction of galaxies in the Universe. Since the pressure there can be considered zero, then in the equilibrium approximation in the right-hand side of Equation (7) only the first term will remain, which in this case coincides with Equation (4).

For non-stationary external forces, the internal energy will change even without the body’s motion. In this case, in the absence of pressure, the D-entropy coincides with the thermodynamic potential. Thus, the measure of change in internal energy is associated with the D-entropy. It follows that with the invariance of the total energy; the state of systems is determined by changes in the energy of motion and the D-entropy. Consequently, the evolution of systems is determined by two physical factors. These are the energy of motion and the D-entropy. The energy of motion determines the dynamic properties of bodies and is a measure of “Order”. The D-entropy characterizes the change in the measure of “Chaos” of the motion of elements of bodies due to the energy of “Order” [44]. In this case, the measure of “Chaos “and the measure of “Order “change under the condition of conservation of the total energy of the system.

Internal energy is determined by the chaotic motion of the body’s elements, for example, thermal. For an equilibrium system consisting of a sufficiently large number of elements, the sum of the MP impulses in any selected subsystem is zero. The complete equilibrium of the system corresponds to the state of maximum “Chaos” with maximum D-entropy. In general, D-entropy characterizes evolution, since it determines the change in the internal macrostate of the system through the set of microstates of its elements. This is what determines the physical meaning of D-entropy.

Numerical calculations have shown that when a sufficiently small system moves in non-uniform fields of external forces, its internal energy can either increase or decrease. That is, D –entropy for small systems can be negative. But already at N₁ >100, the internal energy only increases. That is: $\Delta S_{100}^d>0$. At N₂ >10³, the value of the internal energy increment reaches an asymptotic value, which determines the range of applicability of the thermodynamic description of the system [45]. Of course, these numbers depend on the parameters of the problem. That is, the occurrence of irreversibility is different for each substance and for different conditions. But in any case, it occurs according to equation (2) with a sufficient number of particles in the system. D-entropy eliminates the contradictions between classical mechanics and thermodynamics.

Thus, equation (1) allows us to introduce a concept that corresponds to thermodynamic entropy. This opens up the possibility of unifying sections of physics.

2.4. D-Entropy for Open Nonequilibrium Dynamic Systems

The evolution of natural objects is determined by dissipative processes. They occur during the interaction of bodies with the external environment as a result of the exchange of energy, momentum and matter with it. Therefore, to describe evolutionary processes, it is necessary to take into account openness. Dissipation is possible only due to the structure of bodies. This means that if the world has evolved, then matter is infinitely divisible and represents an infinite hierarchy of systems. That is, any arbitrarily small isolated part of a body is a system. From the condition of infinite divisibility of matter, it follows that it is impossible for bodies with zero internal energy to exist. Thus, if bodies have all these properties and have arisen as a result of evolution, then they belong to open non-equilibrium dynamic systems (ONDS), and matter represents an infinite hierarchy of ONDS [8,10,36].

In the simplest case, the ONDS is SB. Let us call this the first step of the ONDS hierarchical ladder. The second step of the ONDS is the statistical ensemble composed of SB moving relative to each other. This approximation of the mother model corresponds to the ONDS model used in statistical physics [8]. Let us consider how D-entropy is determined for such a system.

Each SB of a nonequilibrium system moves in a non-uniform field of forces created by all other SB and external forces. The total energy of a closed ensemble of SB is invariant, and the change in D—entropy is determined by the sum of the entropy increments of each SB due to their energies of relative motion. The D-entropy of such an ensemble has the form [17]:

$$\Delta S_N^d=\Delta E_N^{\mathrm{int}}/E_N^{\mathrm{int}}={\displaystyle {\sum }_{L=1}^a\left\{N_L{\displaystyle {\sum }_{k=1}^{N_L}[{\displaystyle \int {\displaystyle {\sum }_s{F}_{ks}^L{v}_{k}dt]}/E_L}}\right\}}$$

(8)

$E_L$-internal energy L—subsystems; $F_{ks}^L$-the force acting on— $k$ particles of the subsystem from particles of other subsystems; $s$-is an external particle in relation to $L$-subsystem, interacting with its $k$-particles; $v_k$-the velocity i -th particle; $N_L$ – the number of particles in $L$-subsystems; $L$ = 1,2,3…; a—the number of subsystems in a nonequilibrium system.

Calculations of the dependence of fluctuations of internal energy on the $\Delta S_N^d$ number of MP in systems moving in inhomogeneous fields, performed on the basis of the equation of motion (1), showed that it obeys the law [45]:

$$\delta E^{tr}\sim 1/\sqrt{N}$$

(9)

The same law is known in statistical physics [13]. This means that condition (9) is determined by deterministic laws of physics. This result indicates that the scope of application of statistical laws can be determined on the basis of the laws of physics.

The entropy for the second stage ONDS can be obtained either using equation (1) or using the distribution function $f_p=f_p(r,p,t)$, which follows from the extended Liouville equation [46]:

$$d{f}_p/dt=\partial f_p/\partial t+{\displaystyle {\sum }_{i=1}^N\{v_i(\partial f_p/\partial r_i)+{\dot{p}}_i(\partial f_p/\partial p_i)\}}=-f_p\sigma$$

(10)

Here $i=1,2,3\dots N$ is the number SB, $F_i^p$ are the forces acting on the i -th SB, $p_i$-SB impulse $\sigma ={\displaystyle {\sum }_{i=1}^N\partial F_i^p/\partial p_i}$.

Equation (10) is obtained using equation (1). It differs from the canonical Liouville equation in that the phase volume SB, determined by its energy of motion, is not conserved. According to equation (1), the magnitude of the change in the distribution function is proportional to the gradients of the forces. For a closed nonequilibrium ensemble, the value $\sigma$ decreases with decreasing energy of relative motions SB due to its transformation into the internal energy SB. The contribution to the change in the function $f_p=f_p(r,p,t)$ only non-potential forces contribute. The solution to equation (10) is as follows:

$$f_p=f_p^o\exp {\displaystyle \int \sigma }dt$$

(11)

Community $f_p=f_p(r,p,t)$ is that this function is obtained taking into account the work of dissipative forces. That is, this function also follows from the equation of motion (1).

Using the distribution function (10), we can obtain the entropy for systems close to equilibrium: $S^B=-{\displaystyle \int (f_p\ln f_p)dpdq}$ [8]. From equation (10) it follows that if $\sigma =0$, then we have: $d{S}^B/dt=0$. Consequently, $S^B$ has a maximum when the SB ensembles have no relative velocities.

According to the principle of dualism of symmetry, the energy at all hierarchical levels of matter is equal to the sum of the energy of motion, which is a measure of “Order”, and the internal energy, which is a measure of “Chaos”. Therefore, the change in D –entropy at each hierarchical level consists of increments of the energies of “Order” and the energies of “Chaos” of this level as a result of the impact on it from the external hierarchical level. That is, these increments are carried out due to the energy of external hierarchical levels. Let us consider the relationship between the energy of motion and D-entropy for the hierarchical levels of ONDS.

2.5. The Relationship Between the Energy of Motion and D-Entropy of Hierarchical Links of Matter

We will proceed from the condition that any nonequilibrium ONDS can be represented by a set of subsystems moving relative to each other. The justification for this statement can be found in statistical physics [13,14]. Let external forces begin to act on the ONDS at a certain moment. In the general case, this will lead to a change in the energy of motion and internal energies of the ONDS elements at the first hierarchical level of the ONDS. If the external forces are large enough and the characteristic scales of their inhomogeneities are small enough, then a change in the energy of motion of the first level will lead to a change in the energy of the second hierarchical level of the ONDS, and so on. Thus, we obtain:

$$\Delta E^0=\Delta E_1^m+\Delta E_1^{\mathrm{in}};\Delta E_1=\Delta E_2^m+\Delta E_2^{\mathrm{in}};\Delta E_{N-1}=\Delta E_N^m+\Delta E_N^{\mathrm{in}};\Delta E_N^{\mathrm{in}}=\Delta E_N^m$$

(12)

$$\Delta S_i^d=\Delta E_i^{\mathrm{in}}/E_i^{\mathrm{in}}$$

(13)

Here $\Delta E_0$ is the work of external energy, i = 1,2,3… N, m is the index that determines the energy of motion, in is the index corresponding to the internal energy. That is, the energies of the corresponding hierarchical levels of the ONDS consist of the sum of the energies of the movement of elements and their internal energies of a given level.

Equations (12, 13) represent chains of increments of the energy of motion and D -entropy of the subsystems of each hierarchical level due to the energy of motion of the external level. We will call this the principle of relativity of energy and D -entropy for the steps of the hierarchical ladder of the ONDS. From these equations it follows that for the ONDS the inequality always holds: $S_0^d\succ {\displaystyle {\sum }_i^N{S}_i^d}$, where $S_0^d$ is the D-entropy of the system that has reached the equilibrium state. That is, there is a decrease in the energy of motion of the elements of a given level due to its transformation into their internal energy, which is equivalent to dissipation -$\Delta E_i^{dis}$. As a result, the change in the energy of motion at each level of the ONDS hierarchy can be represented as follows:

$$\delta E_i^m=\Delta E_i^m-\Delta E_i^{dis}$$

(14)

Since nonequilibrium systems are characterized by dissipative processes, the ability of such a system to be in a stationary state is ensured by the work of external forces, compensating for dissipative processes at hierarchical levels of matter. The amount of energy required to compensate for the energy of motion lost as a result of dissipation at a given level, let’s call D- negentropy:

$$\Delta W_i^{ND}=\Delta E_i^{dis}/\Delta E_i^{in}$$

(15)

If the value of D- negentropy at each hierarchical level of the ONDS compensates for dissipation, then this will ensure the stationarity of the ONDS state, determined by the condition:

$$\delta E_i^m=\Delta E_i^m-\Delta E_i^{dis}+\Delta W_i^{ND}=0$$

(3)

That is, due to $\Delta W_i^{ND}$, the ONDS can be in a stationary nonequilibrium state. The following conclusion follows: for nonequilibrium systems placed in a non-uniform external field, their entropy evolves not to an equilibrium state, but to a corresponding stationary nonequilibrium state determined by the external field of forces. This scenario for establishing stationary ONDS does not take into account all factors. For example, in the case of a solar radiation flux to the Earth, the external impact on the atmosphere with a sufficient spectrum width of this flux can directly affect several of its hierarchical levels. In fact, this mechanism determines the emergence of life. It consists of a decrease in the entropy of the system due to an increase in the entropy of the non-uniform field of external forces [50,51].

When a stationary nonequilibrium state of the system is established, the positive influx of energy and entropy is compensated by Planck radiation. But in any case, the nature of the external influence is subject to the principle of relativity of the energy of motion and D -entropy, and the stationarity of the ONDS is ensured by condition (16). It follows from this principle that the Boltzmann entropy, determined by the logarithm of the number of microstates, does not uniquely determine the state of a nonequilibrium system that has the energy of relative motion of subsystems.

According to equation (1), the influence of level “m” on level “m -1” is determined by the second order of smallness, but then its influence on level “m -2” will be of the fourth degree of smallness. Therefore, to describe evolution with sufficient accuracy, one can use the equation of motion (1) for each two adjacent hierarchical levels of matter. That is, there is no need to construct a complete equation of motion for all hierarchical levels, which significantly simplifies the task of describing the evolution of matter.

Important note. The infinite divisibility of matter means that the work of external forces, although decreasing exponentially with the growth of the level number, can go to change the state of all hierarchical levels, up to the field state of matter. This allows us to propose a corresponding scenario of irreversibility, due to the fact that the process of excitation of all hierarchical levels will require infinite time, which is equivalent to accepting the condition of inelastic collisions of the elements of the level [48]. The question arises, can such a scenario explain irreversibility? But the principle of Occam’s razor allows us to choose a simpler mechanism of irreversibility, considered above. Although this scenario also requires study.

The physical meaning of D-entropy implies the essence of the probabilistic definition of entropy and the scope of its limitations. This allows us to take a more optimistic view of John von Neumann’s statement: “...nobody knows what entropy is...” [47].

The fact that D-entropy characterizes the evolution of interacting bodies makes it indispensable for describing the evolution of matter, especially for an expanding Universe, when the role of the relative motions of objects in changing their internal states cannot be neglected.

3. Discussion

In this work, a new concept was introduced — D-entropy, which allows one to describe evolutionary processes in systems moving in non-uniform fields of external forces. Unlike classical entropy, based on statistical methods and applicable only to equilibrium systems, D-entropy deterministically describes changes in internal energy caused by the system’s motion. This approach allows one to combine the dynamic and thermodynamic aspects of evolution, which is a significant step toward creating a unified physics of evolution.

Classical entropy is defined as a measure of the disorder of a system and is used to analyze stationary states. However, its application to moving systems and systems in nonequilibrium is problematic. D-entropy, on the contrary, characterizes the transformation of the energy of motion into internal energy, which is especially important for moving systems in non-uniform fields. This allows us to overcome the limitations of classical thermodynamics and describe processes that do not fit into the framework of the equilibrium approach.

The main difference of D-entropy is its dependence on dynamic parameters, which makes it applicable to a wide class of systems, from macroscopic to microscopic. Numerical calculations have shown that for sufficiently small systems, D-entropy can take negative values, which reflects the possibility of reducing the internal energy of the system due to external factors. With an increase in the number of particles in the system, D-entropy becomes positive, which corresponds to the second law of thermodynamics.

One of the most significant features of the proposed approach is the explanation of the irreversibility of processes. In classical mechanics, reversibility is due to the use of holonomic conditions for constraints and the exclusion of dissipative processes. In our study, it was shown that irreversibility arises due to the transition of the energy of motion into the internal energy of the system, which is described by the bilinear term in the equation of motion SB. This approach allows us to explain the mechanisms of establishing equilibrium in the system based on deterministic laws, and not only statistical assumptions.

The bifurcations considered in this paper also provide insight into the microscopic nature of irreversibility. It is shown that when considering the motion of system elements at the level of microstates, bifurcation is a deterministic process caused by the relationship between macrodynamics and microdynamics. This contradicts classical ideas about the randomness of bifurcations and emphasizes the need to take into account microstructural features when describing the evolution of systems.

The introduction of D-entropy has eliminated the contradictions between mechanics and thermodynamics that existed due to differences in the description of dynamic and internal states of systems. This unification is important for the construction of the physics of evolution, where the processes of development, emergence and decay of systems should be described within the framework of a single theory. The possibility of determining entropy through the dynamic parameters of bodies opens up new ways to study complex nonequilibrium systems, such as the expanding Universe, where the interaction of objects and their evolution cannot be described only by the thermodynamic approach.

Despite the successful introduction of D-entropy, some limitations should be noted. In particular, the application of the proposed approach requires taking into account the structural features of the system, which complicates its use for systems with an unknown or complex structure. In addition, numerical calculations show that determining the areas of applicability of D-entropy for specific systems requires further research, especially in the context of quantum mechanics and systems far from equilibrium.

Future research should be aimed at developing methods for quantitative description of D-entropy in complex natural systems, such as the Earth’s atmosphere or galaxies. In addition, it is important to study the influence of D-entropy on the evolution of open systems, where the exchange of energy and matter with the external environment plays an important role.

4. Conclusions

A solution to the problem of obtaining an analytical expression for the entropy of moving bodies is proposed. This expression follows from the equation of motion of a system of potentially interacting material points moving in a non-uniform field of external forces. The peculiarity of such an equation is that it takes into account the role of the system structure in its dynamics. The equation of motion follows from the condition of invariance of the total energy. Because the total energy was represented by the sum of the energy of motion and the internal energy, the equation determines both the work of external forces that goes both to the motion of the system and the work that changes the internal energy of the system. The value characterizing the change in internal energy was called D-entropy. It is defined as the ratio of the change in the internal energy of the system to its total value. That is, D-entropy characterizes dissipative evolutionary processes in moving systems. D-entropy for large systems is always positive, which corresponds to the second law of thermodynamics. D-entropy allows one to determine the criteria characterizing the applicability range of statistical definitions of entropy. Its advantage is its applicability to moving large and small systems, for which statistical definitions of entropy are unsuitable. The equation of motion and the expression for D-entropy remove the contradictions between the mechanics of bodies and their thermodynamics, which opened up the possibility of constructing the physics of evolution, the task of which includes describing the processes of emergence, development and decay of systems within the framework of the laws of physics.

Thus, the introduction of D-entropy into the physics of evolution is an important step towards the creation of a unified theory describing both dynamic processes and changes in the internal state of systems. This approach eliminates existing contradictions and allows description of evolutionary processes in both classical mechanics and thermodynamics. This opens up new opportunities for re-search in the field of evolutionary physics.