Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Seismic Activation Modeling with Statistical Physics

Submitted:

08 May 2025

Posted:

09 May 2025

Read the latest preprint version here

Abstract
Starting from fault dynamic equations, it is explained how real time evolution of a seismic activation region's elastic parameters preceding a major earthquake can be modeled in terms of statistical physics. Initial evidence for model validity is provided by deriving previously reported deviation of seismic activation earthquake occurence statistics from Gutenberg-Richter statistics in time intervals preceding a major earthquake.
Keywords: 
seismic activation
;  
fault dynamics
;  
statistical physics
;  
signal processing
Subject: 
Physical Sciences  -   Applied Physics

Introduction

An increase in the number of intermediate sized earthquakes ( M > 3.5 ) in a seismic region preceding the occurrence of an earthquake with magnitude M > 6 , referred to as seismic activation, has been documented by various researchers [7]. For example, seismic activation was observed in a geographic region spanning 21 ∘ N − 26 ∘ N × 119 ∘ E − 123 ∘ E for a period of time between 1991 and 1999 preceding the magnitude 7.6 Chi-Chi earthquake [11]. Figure 1 shows a schematic plot of the cumulative distribution of earthquakes of different magnitudes in a seismic activation region in two different time intervals of equal duration preceding occurrence of a major ( 7 < M < 8 ) earthquake at time τ = τ 0 . In this figure, τ is a real time parameter, and τ 0 is the characteristic time of major earthquake recurrence assuming an earthquake of similar magnitude occurred in the same region at τ = 0 [20,29]. Importantly, the cumulative distribution of earthquakes in a time interval of fixed width increasingly deviates away from a Gutenberg-Richter linear log-magnitude plot as the end of the time interval approaches τ 0 .
As a means of predicting the time τ = τ 0 at which a major earthquake preceded by seismic activation occurs, it has been hypothesized that the average seismic moment 〈 M 〉 τ of earthquakes occuring in intervals of time ( τ , τ + Δ τ ) preceding a major earthquake obeys an inverse power of remaining time to failure law:
〈 M 〉 τ ∝ 1 ( τ 0 − τ ) γ 1
and that the cumulative Benioff strain C ( τ ) , defined as:
C ( τ ) = ∑ i = 1 n ( τ ) M 0 , i 1 / 2 ,
where M 0 , i is the seismic moment of the i t h earthquake in the region starting from a time τ = 0 preceding the major earthquake, and n ( τ ) is the number of earthquakes occurring in the region up to time τ , satisfies [27]:
C ( τ ) = a − b ( τ 0 − τ ) γ 2 , γ 2 = 1 − γ 1 / 2 .
The exponent selection of 1 / 2 in equation (2) is not necessary to derive formula (3) with a different arithmetic relation between γ 1 and γ 2 , but appears to have been selected by previous researchers based on resulting predictions of major earthquake occurrence time when formula (3) is fit to real seismic data, which suggest a typical value of γ 2 is 0.3 [7,28]. Notably, the validity of the accelerating seismic moment release hypothesis (1) has been questioned by some researchers who claim normal foreshock and aftershock can account for seismic measurements without moment acceleration [15,31].
A model of seismic activation based on fault damage mechanics (FDM) has been used to derive equation (3) with a value γ 2 = 1 / 3 [4]. In this derivation, the occurrence of seismic activation earthquakes progressively decreases the average shear modulus of fault material in the seismic region where subsequent seismic activation earthquakes occur, and the result γ 2 = 1 / 3 is obtained using a Boltzman kinetic type description of the rupture nucleation process in which ruptured faults of different lengths at different positional locations grow and join together [26].
In addition to the FDM model of seismic activation, an empirical statistical physics model of seismic activation known as the Critical Point (CP) model has been put forth to derive equation (3) with a value γ 2 = 1 / 4 [20]. In this derivation, the inverse power of remaining time to failure law:
〈 M 〉 τ ∝ 1 ( τ 0 − τ ) 3 / 2
is asserted based on identifying the mean rupture length L ( τ ) of earthquakes occuring at time τ with the correlation length of a statistical physical system described by Ginzburg-Landau mean field theory with a τ -dependent temperature parameter, whereby:
L ( τ ) ∝ 1 ( τ 0 − τ ) 1 / 2 ,
and relation (4) follows from the scaling relation 〈 M 〉 τ ∝ L ( τ ) 3 which holds when the fault material shear modulus is constant [21].
Importantly, previous work on the CP model has not explained why it is physically reasonable to describe seismic activation earthquake occurrence statistics with thermal equilibrium statistical physics formalism [24]. Therefore, the first objective of this article is to clarify how the FDM and CP models of seismic activation can be in correspondence with each other. The second objective of the article is to use this correspondence to advance rigorous testing of seismic activation model predictions against seismic measurements, and in the event of positive experimental verification, advance earthquake prediction technology.
Motivating the presented correspondence between FDM and CP seismic activation models is previous work suggesting that the real time evolution of the elastic model of a seismic activation region, expressed in terms of a finite element method stiffness matrix, can in certain cases be described with statistical physics renormalization group flow equations [2,13]. This theoretical work may have computational utility to seismic activation modeling if dimensional reduction of statistical physics models at critical points can be used to systematize dimensional reduction of seismic activation region stiffness matrices in windows of time preceding a major earthquake.
The outline of the article is as follows. Section 2 explains how fault rupture dynamics can be described in terms of soliton equations, and how these soliton equations can be used to characterize critical points of statistical physics models whose mean field values at criticality correspond to unstable seismic displacements. Section 3 further claims that seismic activation earthquake occurrence statistics are expressible in terms of the Yang-Lee zero distribution of a statistical physics model partition function, and uses this claim to account for deviation of occurrence statistics from Gutenberg-Richter statistics before a major earthquake. Section 4 concludes by commenting on how validity of statistical physics modeling of seismic activation can be tested against seismic measurements.

Materials and Methods

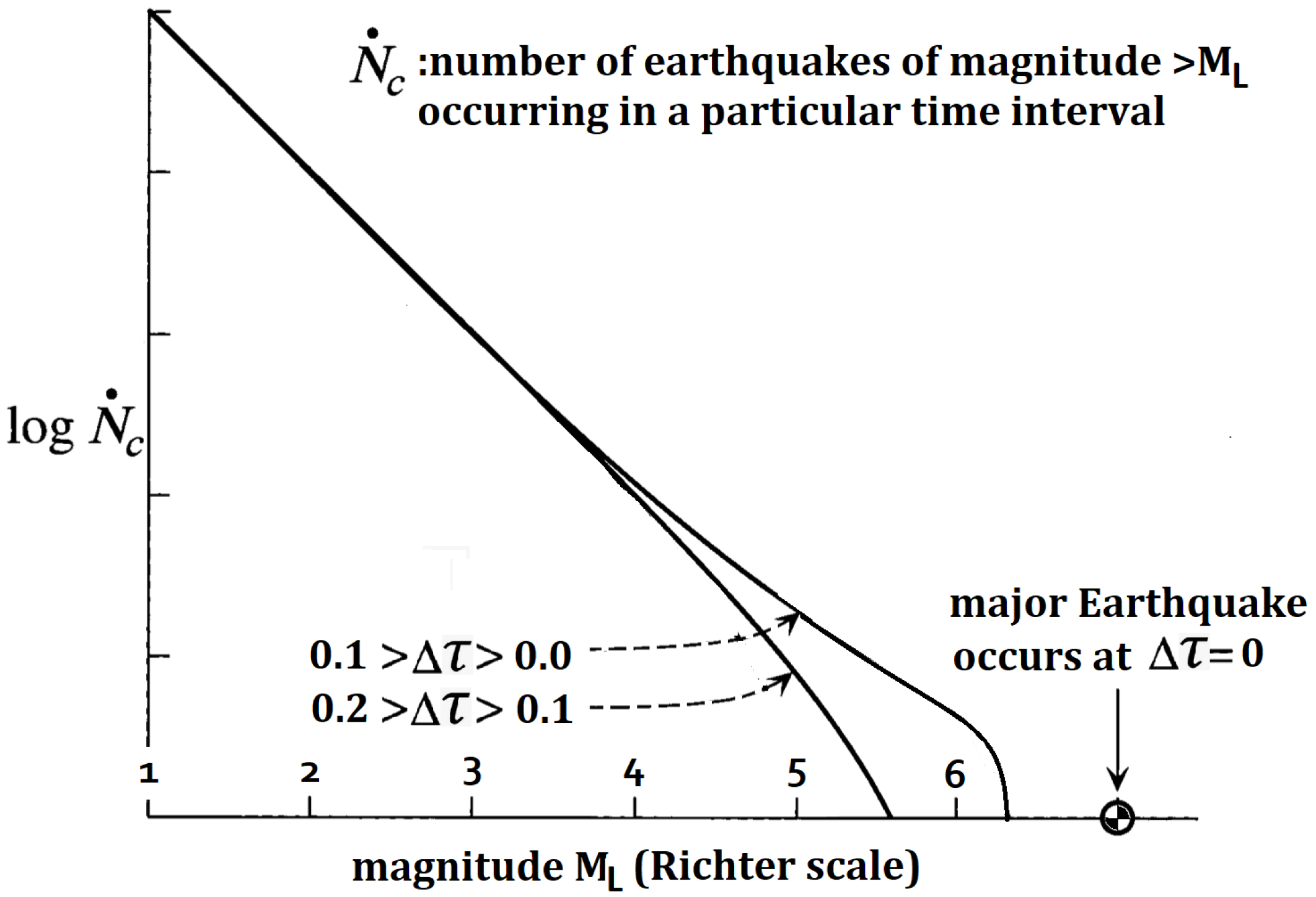
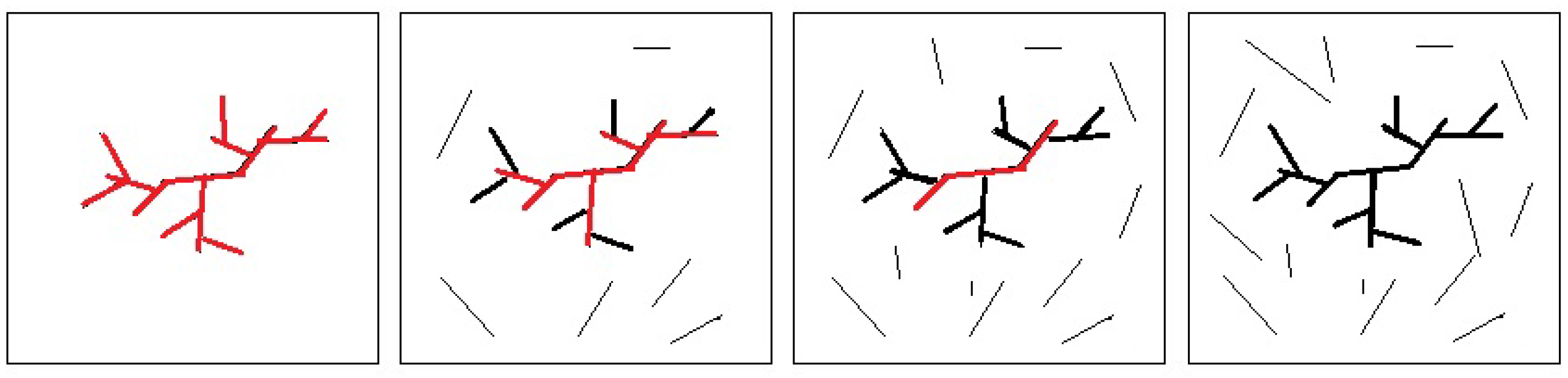
Seismic Activation Fault Dynamics

Figure 2 shows a 2D schematic of earthquake occurrence in a seismic activation region [18]. In this figure, the activation region is shown at 4 different times up to and including the moment after a major earthquake has occurred. At each time, black lines indicate fault ruptures associated with earthquakes that have occurred, and red lines indicate faults where stress is accumulating prior to earthquake occurrence. Qualitatively, the picture suggests the occurrence of successively larger earthquakes, associated with successively longer rupture lengths, leads to increased strain along the major earthquake fault as seismic activation proceeds. From an FDM point of view, this increased strain occurs with a reduction in the average shear modulus of material in the vicinity of the fault, until fault rupture occurs at time τ = τ 0 , when fault material is marginally stable with respect to material displacement perturbation [10].
Quantitatively, this picture of seismic activation leading to rupture along a major earthquake fault is supported by modeling of earthquake fault dynamics in 1+1 spacetime dimensions, whereby the differential equation:
A ∂ τ 2 U ( τ , z ) − B ∂ z 2 U ( τ , z ) + C ∂ τ U ( τ , z ) = − sin ( U ( τ , z ) / D ) .
has been used to model both creep along a major earthquake fault and rupture propagation, depending on whether or not frictional forces dominate the fault dynamics and shear stress evolution along the fault is more appropriately described with a reaction diffusion equation or a solitary wave equation [9]. In this equation, τ is real time, z coordinates a direction of creep or slip along an earthquake fault, U ( τ , z ) is the local displacement of elastic material across the earthquake fault, A ∂ τ 2 U ( τ , z ) is the local inertial force acting on the fault material, B ∂ z 2 U ( τ , z ) is the local elastic restoring force acting on the fault material, and C ∂ τ U ( τ , z ) and sin ( U ( τ , z ) / D ) are local frictional forces acting on the fault material attributed to contact of the material with tectonic plates on either side of the fault. For C = 0 , an (anti-kink) soliton solution to equation can be interpreted as propagation of earthquake fault rupture [30].
To generalize this description of fault creep and rupture in 1 spatial dimension to 3 spatial dimensions, first note that if the seismic activation region resides in an elastic half space H , then real time evolution of the elastic displacement of material in the region is specified by a path γ ( τ ) in the Lie group G = D i f f ( H ) [1]. For τ < τ 0 , this path specifies a gradual deformation of the activation region’s quasi-elastostatic equilibrium configuration in which strain energy is minimized, whereby a displacement u → of the region’s equilibrium configuration at tme τ increases the strain energy of the region by:
Δ E = 1 2 u → T K ( τ ) u → ,
for K ( τ ) equal to a positive definite stiffness matrix of the region at time τ . At τ = τ 0 , this stiffness matrix has at least one zero eigenvalue corresponding to a marginally stable seismic displacement u → 0 that describes the major earthquake faulting mechanism. For τ > τ 0 , when the path γ ( τ ) specifies fault rupture propagation, the equation of motion of the tangent vector γ ′ ( t ) , pulled back to the Lie algebra g of vector fields on H by left (or right) translation, is a soliton equation describing parallel transport of the initial unstable seismic displacement u → 0 .

Seismic Activation Region Finite Element Model

In finite element method terms, the Lie algebra g is approximated by the vector space of nodal displacements associated with a mesh of H . More specifically, suppose a major earthquake hypocenter resides in a 3D elastic half space H in such a way that the elastic parameters of the half space are constant outside a hemisphere of diamater L 0 centered at the earthquake epicenter. Then, if each fracture within the region is defined as a thin low elastic impedance layer, a Dirichlet-to-Neumann map is defined at the hemisphere boundary, and a finite element mesh accounting for fracture and boundary geometry is defined, the elastic model of the region at time τ can be written as a frequency dependent stiffness matrix K ( ω ; τ ) with dimension equal to the number of finite element nodes [5,25]. Similarly, using the density of the activation region, a time dependent lumped mass matrix M ( τ ) can be written with dimension equal to the number of finite element nodes. Together, the stiffness and mass matrices define a nonlinear eigenvalue problem:
K ( ω ; τ ) − ω 2 M ( τ ) u → = 0 ,
at each time τ , whose non-zero solution vectors u → specify nodal displacements associated with elastic resonant frequencies ω of the activation region.

Statistical Physics Mean Field Theory

To introduce the relevance of statistical physics to modeling real time evolution of the seismic activation region elastic model, suppose that in a window of time preceding τ = τ 0 , K ( ω , τ ) is independent of ω , and W ( τ ) = K ( τ ) M ( τ ) − 1 has ( τ -dependent) real eigenvalues λ i associated with orthonormal eigenvectors u → i . In this event, writing:
u → = ∑ c i u → i ,
it follows that:
u → T W ( τ ) u → = ∑ λ i ( τ ) c i 2 ,
and assuming each λ i ( τ ) > 0 for τ < τ 0 , the onset of instability of the seismic activation region at τ = τ 0 coincides with vanishing λ 1 ( τ 0 ) = 0 of at least one of the eigenvalues.
Now suppose that a statistical physics mean field theory is defined in such a way that its Landau free energy is given by expression (10) plus higher order terms in mean field values c i [Goldenfeld]. Also suppose that the temperature of the system is determined by the parameter τ in such a way that the sign change of λ 1 ( τ ) at τ = τ 0 corresponds to ordering of the statistical physics system with a non-zero value of c 1 for τ > τ 0 . With these suppositions, the stiffness matrix K ( ω , τ ) M ( τ ) − 1 is a matrix coefficient of a statistical field theory with a critical point at τ = τ 0 , and the order parameter fields of this theory have a classical physics interpretation as magnitudes of activation region nodal displacement from mechanical equilibrium. Moreover, if the statistical physics model is defined so that a discontinuous gap in the coefficient λ 1 ( τ ) occurs at τ = τ 0 , as known to occur for the 2D XY model, the mean field condition c 1 2 ∝ − λ 1 ( τ ) implies the quantity − λ 1 ( τ 0 + ) is proportional to the rupture length of the major earthquake.

Results

To relate the discussion in the previous chapter to seismic activation earthquake occurrence statistics, now suppose the negative eigenvalues of the stiffness matrix K ( τ ) M ( τ ) − 1 are the Yang-Lee zeroes of the statistical physics model partition function [Bena et al.]. With this supposition, Yang-Lee zero statistics should describe the cumulative distribution of seismic activation earthquakes with rupture length − λ , a prediction that is now verified to the extent that it accounts for the deviation of seismic activation earthquake occurrence statistics from Gutenberg-Richter statistics.
In the time interval ( τ , τ + Δ τ ) , let ω be the corner frequency of an activation earthquake with rupture length − λ , where λ is an eigenvalue of the stiffness matrix that changes sign during the time interval. Then, assuming the earthquake occurs within the time interval with probability proportional to ω d τ , and ρ ( ω ) is the density of corner frequencies in the interval ( ω , ω + d ω ) associated with activation earthquakes occurring in the time interval, the number of earthquakes with corner frequency less than or equal to ω occurring during the time interval is:
N ˙ c d τ = ∫ ω c ( τ ) ω ω ¯ ρ ( ω ¯ ) d τ d ω ¯ ,
where ω c ( τ ) is the corner frequency of the largest activation earthquake occurring up until time τ .
To specify the mathematical form of the integral in equation (11), recall that the Gutenberg-Richter law implies the total number of earthquakes of Richter magnitude in the interval ( M R , M R + d M R ) occurring in the seismic activation region in the time interval ( τ , τ + d τ ) is proportional to:
10 − b M R d M R d τ ,
which according to the relation between Richter magnitude and seismic moment:
M R = log 10 ( M s ) − 9 / 1.5 ,
and scaling relation M s ∝ ω − 3 , satisfies:
10 − b M R d M R d τ ∝ M s − 1 − b / 1.5 d M s d τ ∝ ω 2 b − 1 d ω d τ .
Therefore, assuming the Gutenberg-Richter law is valid, it follows that:
ρ ( ω ) ∝ ω 2 b − 2 .
To account for modification of the Gutenberg-Richter law in time intervals preceding a major earthquake, now assume that for corner frequencies ω satisfying:
ω ≈ ω c ( τ 0 ) ≡ ω 0 ,
with ω 0 equal to the corner frequency of the largest seismic activation earthquake preceding the major earthquake at time τ = τ 0 , the quantity ρ ( ω ) is determined by a distribution of the eigenvalues λ satisfying:
∫ ω 0 ω ρ ( ω ¯ ) d ω ¯ ∝ ( ω − ω 0 ) β 0 , 1 > β 0 > 0 .
With this assumption, equation (11), modified to account for occurrence of an earthquake at corner frequency ω 0 , implies:
N ˙ c = 1 + ∫ ω 0 ω ω ¯ ρ ( ω ¯ ) d ω ¯ ≈ 1 + c ( ω − ω 0 ) β 0 .
Consequently:
log 10 N ˙ c ≈ log 10 1 + c ( ω − ω 0 ) β 0 ,
when plotted against Richter magnitude M R ∝ − 2 log 10 ω for β 0 < 1 , can have either of the cumulative distribution curve shapes shown in Figure 1 for different time intervals, depending on the value of β 0 .
In passing, it is also noted that in accordance with previous statistical physics models of seismic activation, the identification β 0 = β ( τ 0 ) , where β ( τ ) is a parameter in a τ -dependent statistical physics model such as the 2D XY model, is logical. From this point of view, the parameters of the statistical physics models, including β ( τ ) , are related by renormalization group flow, and an increase in the value of β ( τ ) as τ → τ 0 accounts for increasing steepness of the cumulative distribution curve shown in Figure 1.

Discussion

Previous research has identified predicting the time of occurrence of major earthquakes as a possible application of statistical physics models of seismic activation, but this application has not yet been realized [7]. In more recent times, the earthquake early warning algorithm Virtual Seismologist has been developed which can in principle use previous earthquake occurrence statistics as input to improve warning accuracy, and the artificial intelligence algorithm QuakeGPT has been developed for predicting the occurrence of major earthquakes using seismic event records created with stochastic simulator training data [6,12,22]. Therefore, a practical applied science goal for the statistical physics model presented in this article appears to be improving statistical characterization of earthquake precursors for use in earthquake warning and/or forecasting technologies, acknowledging that preliminary tests of the model’s validity against real seismic data must be passed before achieving this application objective can be considered a realistic possibility.
From a geophysical testing point of view, if it is true that renormalization of a 2D sine-Gordon model describes real time evolution of the elastic model of a seismic activation region and, as a result, a nonlinear dynamical system of finite phase space dimension characterizes the elastic model during nucleation of shear stress in a seismic region preceding a major earthquake, a geophysical signal processing technique known as singular spectrum analysis should apply to determine this phase space dimension [8]. Specifically, it is suggested that measurements of relative changes in seismic surface wave and/or body wave velocity be performed between pairs of seismic stations in a seismic region over a duration of time during which seismic activation is known to have occurred, and used as input to a time domain multichannel singular spectrum analysis algorithm [19]. The number of channels of this algorithm would equate to the number of station pairs, and the number of singular values output by the algorithm in different time windows preceding occurrence of a major earthquake should categorize the region’s elastic model if the statistical physics model of seismic activation is correct in principle. With reference to previous geophysical application of singular spectrum analysis, performed in the frequency domain, the signal processing algorithm suggested here is different in that it should be carried out in the time domain τ rather than the frequency domain [23].
In conclusion, work towards improving current earthquake early warning systems can proceed in two directions. Firstly, as an initial check on whether or not the statistical physics modelling approach presented here could be of practical utility, work can be done to determine whether or not observed changes of the Earth’s elastic velocity model preceding major earthquakes can be processed to extract an integer identifiable as the phase space dimension of a nonlinear dynamical system. Secondly, work can be done to elaborate upon the statistical physics mathematical model of seismic activation presented in this article to determine other tests of its scientific validity and potential for practical application.

Author Contributions

Not applicable.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Acknowledgments

Thanks to my family for their support throughout completion of this research. Thanks to Dr. Girish Nivarti, Dr. Evans Boney, and Professor Richard Froese for their willingness to entertain communication regarding the content of the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Arnold VI. Mathematical methods of classical mechanics. Springer Science and Business Media.
  2. Balog I, Carpentier D, Fedorenko AA. Disorder-driven quantum transition in relativistic semimetals: functional renormalization via the porous medium equation. Physical review letters. 2018 121(16):166402. [CrossRef]
  3. Bena I, Droz M, Lipowski A. Statistical mechanics of equilibrium and nonequilibrium phase transitions: the Yang–Lee formalism. International Journal of Modern Physics B. 2005 Nov 20;19(29):4269-329. [CrossRef]
  4. Ben-Zion Y, Lyakhovsky V (2002) Accelerated seismic release and related aspects of seismicity patterns on earthquake faults. Earthquake processes: Physical modelling, numerical simulation and data analysis Part II :2385–2412.
  5. Bindel DS. Structured and parameter-dependent eigensolvers for simulation-based design of resonant MEMS (Doctoral dissertation, University of California, Berkeley). 2006.
  6. Böse M, Andrews J, Hartog R, Felizardo C. Performance and next-generation development of the finite-fault rupture detector (FinDer) within the United States West Coast ShakeAlert warning system. Bulletin of the Seismological Society of America. 2023 Apr 1;113(2):648–63.
  7. Bowman D, Ouillon G, Sammis C, Sornette A, Sornette D (1998) An observational test of the critical earthquake concept. Journal of Geophysical Research: Solid Earth 103(B10):24359–24372. [CrossRef]
  8. Broomhead D S, King G P (1986) Extracting qualitative dynamics from experimental data. Physica D: Nonlinear Phenomena 20(2-3):217–236.
  9. Bykov V G (2001) Solitary waves on a crustal fault. Volcanology and Seismology 22(6):651–661.
  10. Carlson J M, Langer J S, Shaw B E (1994) Dynamics of earthquake faults. Reviews of Modern Physics 66(2):657. [CrossRef]
  11. Chen CC. Accelerating seismicity of moderate-size earthquakes before the 1999 Chi-Chi, Taiwan, earthquake: Testing time-prediction of the self-organizing spinodal model of earthquakes. Geophysical Journal International. 2003 155(1):F1-5. [CrossRef]
  12. Cua G., Heaton T. (2007) The Virtual Seismologist (VS) method: A Bayesian approach to earthquake early warning. In Earthquake Early Warning Systems , ed. Gasparini P, Manfredi G, and Zschau J, 97–132. Berlin and Heidelberg: Springer.
  13. Friedan DH (1980) Nonlinear models in 2+ϵ dimensions. Phys. Rev. Lett. 45, 1057.
  14. Goldenfeld. Goldenfeld N. Lectures on phase transitions and the renormalization group. CRC Press; 2018.
  15. Hardebeck JL, Felzer KR, Michael AJ (2008) Improved tests reveal that the accelerating moment release hypothesis is statistically insignificant, J. Geophys. Res., 113. [CrossRef]
  16. Kasman A (2023). Glimpses of soliton theory: the algebra and geometry of nonlinear PDEs. American Mathematical Society.
  17. Khan BA, Chatterjee S, Sekh GA, Talukdar B (2020) Integrable systems: From the inverse spectral transform to zero curvature condition. arXiv preprint arXiv:2012.03456.
  18. Lei Q, Sornette D (2022) Anderson localization and reentrant delocalization of tensorial elastic waves in two-dimensional fractured media. Europhys. Letters 136(3): 1–7. [CrossRef]
  19. Merrill RJ, Bostock MG, Peacock SM, Chapman DS (2023) Optimal multichannel stretch factors for estimating changes in seismic velocity: Application to the 2012 Mw 7.8 Haida Gwaii earthquake. Bulletin of the Seismological Society of America 113(3):1077–1090. [CrossRef]
  20. Rundle JB, Klein W, Turcotte DL, Malamud BD (200undle JB, Klein W, Turcotte DL, Malamud BD (2001) Precursory seismic activation and critical-point phenomena. Microscopic and Macroscopic Simulation: Towards Predictive Modelling of the Earthquake Process 2165–21821) Precursory seismic activation and critical-point phenomena.
  21. Rundle JB, Turcotte DL, Shcherbakov R, Klein W, Sammis C (2003) Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Reviews of Geophysics 41(4). [CrossRef]
  22. Rundle JB, Fox G, Donnellan A, Ludwig IG (2024) Nowcasting Earthquakes with QuakeGPT: Methods and First Results. arXiv e-prints. 2024 Jun:arXiv-2406.
  23. Sacchi M (2009) FX singular spectrum analysis. Cspg Cseg Cwls Convention 392–395.
  24. Saleur H, Sammis C, Sornette D (1996) Renormalization group theory of earthquakes. Nonlinear Processes in Geophysics 3(2):102–109. [CrossRef]
  25. Schoenberg M. Elastic wave behavior across linear slip interfaces. The Journal of the Acoustical Society of America 68(5):1516-21.
  26. Tzanis A, Vallianatos F (2003) Distributed power-law seismicity changes and crustal deformation in the SW Hellenic ARC. Natural Hazards and Earth System Sciences 3(3/4):179–195. [CrossRef]
  27. Tzanis A, Vallianatos F, Makropoulos K (2000) Seismic and electrical precursors to the 17-1-1983, M7 Kefallinia earthquake, Greece: Signatures of a SOC system. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy 25(3):281–7. [CrossRef]
  28. Vallianatos F, Chatzopoulos G (2018) A complexity view into the physics of the accelerating seismic release hypothesis: Theoretical principles. Entropy 20(10):754. [CrossRef]
  29. Vallianatos F, Sammonds P (2004) Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 590:52–8. [CrossRef]
  30. Wu ZL, Chen YT. Solitary wave in a Burridge-Knopoff model with slip-dependent friction as a clue to understanding the mechanism of the self-healing slip pulse in an earthquake rupture process. Nonlinear Processes in Geophysics. 1998 Sep 30;5(3):121-5. [CrossRef]
  31. Zhou S, Johnston S, Robinson R, Vere-Jones D (2006),Tests of the precursory accelerating moment release model using a synthetic seismicity model for Wellington, New Zealand, J. Geophys. Res., 111. [CrossRef]
Preprints 158849 g001
Figure 1. Plot of the cumulative distribution of earthquakes of different magnitudes in a seismic zone in two different time intervals of equal width preceding occurrence of a major earthquake at Δ τ = τ 0 − τ = 0 [20,29].
Figure 1. Plot of the cumulative distribution of earthquakes of different magnitudes in a seismic zone in two different time intervals of equal width preceding occurrence of a major earthquake at Δ τ = τ 0 − τ = 0 [20,29].
Preprints 158849 g001
Preprints 158849 g002
Figure 2. Schematic illustration of seismic activation in a 2D geometry at four different times τ in which each black line represents an earthquake fault rupture that has already occured, and the red lines represent earthquake faults along which shear stress is increasing prior to rupture [18].
Figure 2. Schematic illustration of seismic activation in a 2D geometry at four different times τ in which each black line represents an earthquake fault rupture that has already occured, and the red lines represent earthquake faults along which shear stress is increasing prior to rupture [18].
Preprints 158849 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated