Physics-Informed Risk Analysis Of Anthropogenic Seismicity

1. Introduction

Anthropogenic activities induce seismicity, adding to the complexities geophysicists face in understanding the physical processes causing earthquakes.In the case of seismicity caused by carbon capture and storage (CCS), such quakes can threaten the integrity of seals, undermining costly CCS operations. Deformation of Earth’s crust, which translates into earthquakes, involves many-body problems, leading to the emergence of a complex system. 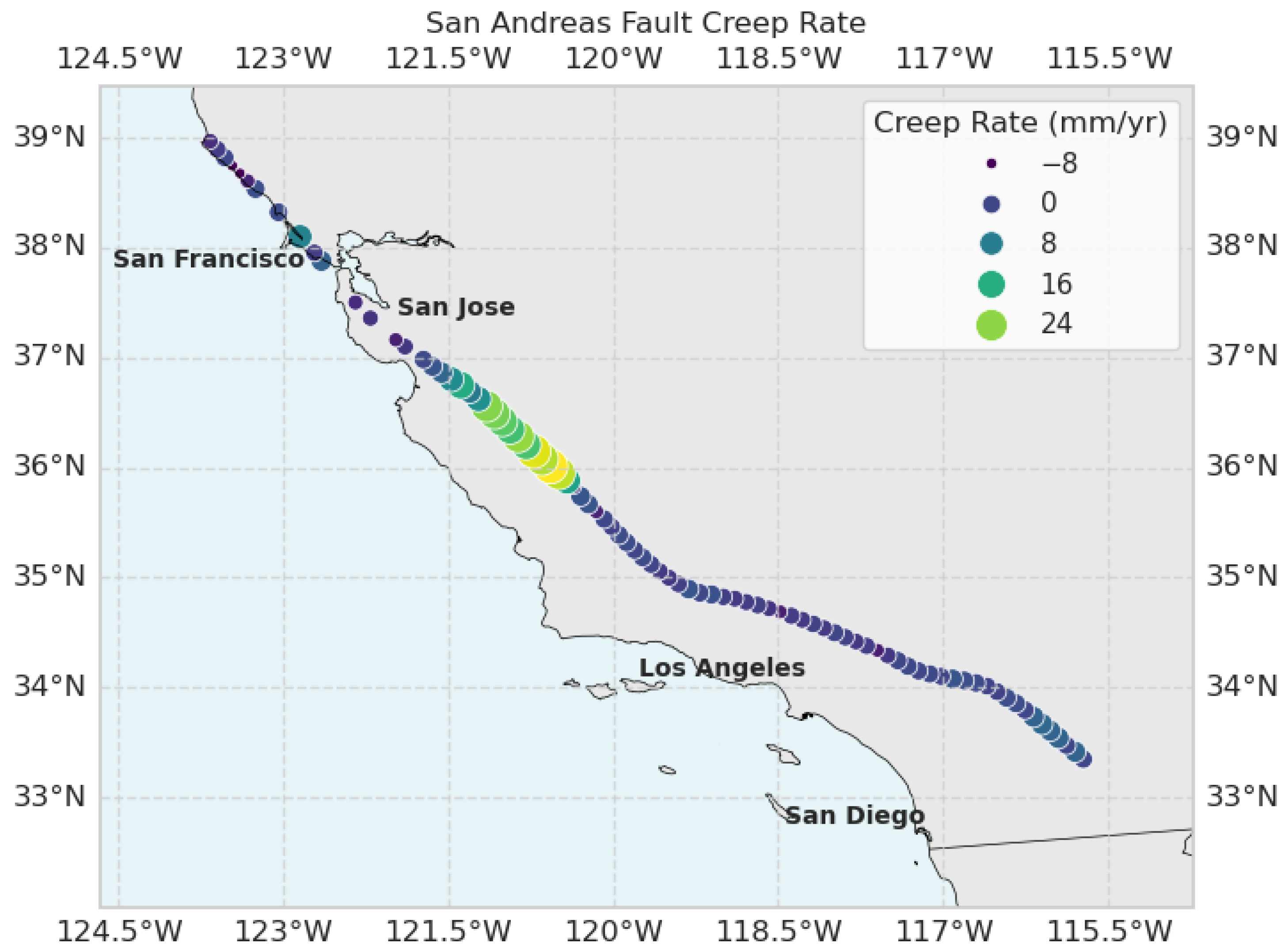As an alternative approach to earthquake mechanics, Turcotte and Malamud have proposed that the tools of complexity rooted in statistical physics are capable of describing faults as a self-organizing complex system [1]. 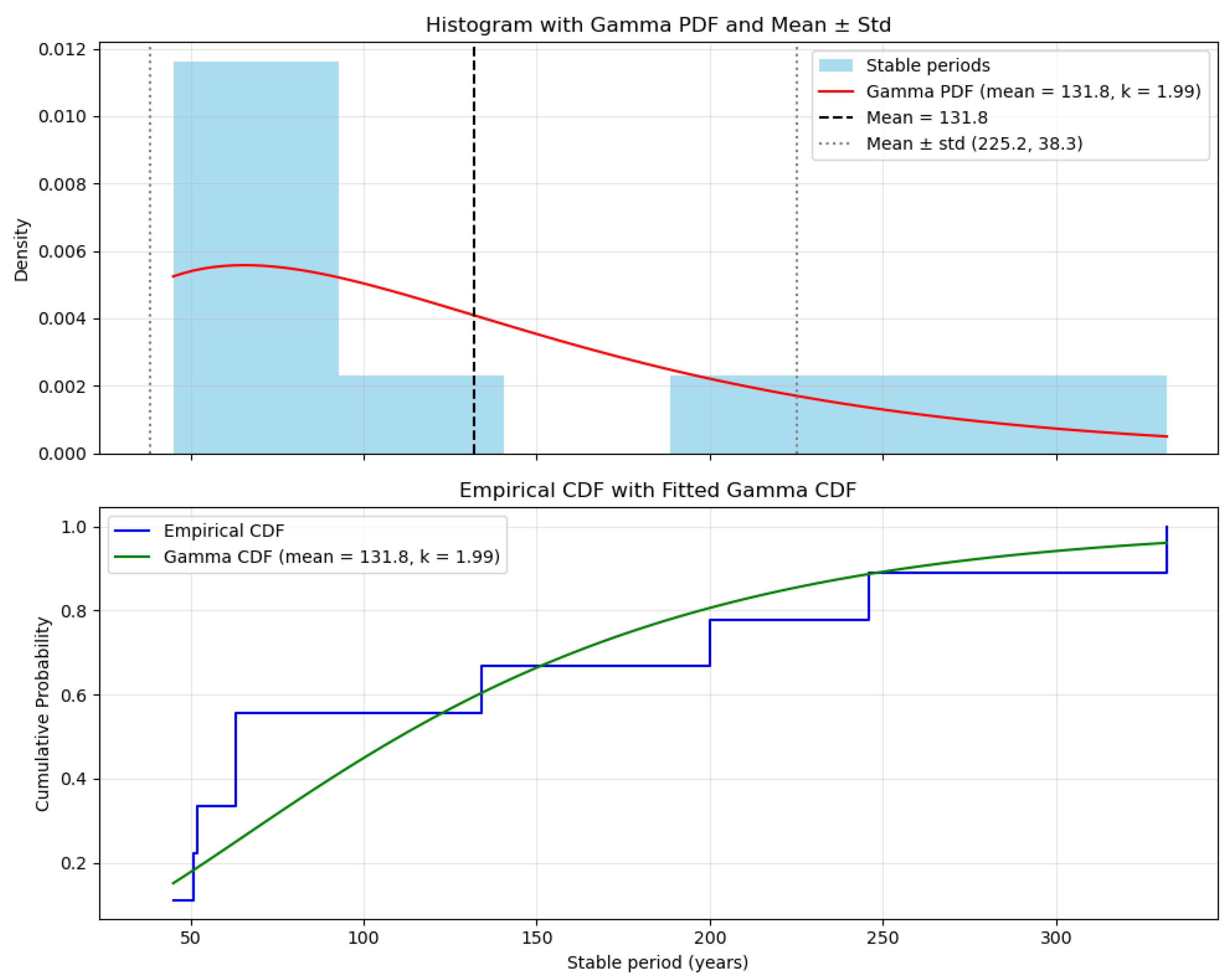The San Andreas Fault (SAF) is an example of such a complex system in seismology, extending approximately 750 miles across central California (Figure 1). Radiocarbon dating methods performed on this fault reveal the history of at least 10 episodes of large earthquakes on average every 132 years, ranging from the year 671 to January 9 1857 (with an estimated magnitude of 8.25) [2]. The PDF, the empirical fit, and the CDF for these events are plotted and shown in Figure 2.

The absence of large earthquake episodes since 1857 is explained by the theory that fault-zone materials do not heal after deformation and lack the strength needed for more destructive movements [4]. Analyzing tectonic fault behavior is a central problem in geophysics and seismology [5,6,7]. Probabilistic hazard assessments require data assimilation and careful geophysical data analysis, extending beyond complexity tools alone. Modern computational approaches, such as Markov Chain Monte Carlo (MCMC) and Bayesian inference, rooted in statistical physics, are used in this study to analyze fault behaviors under external factors like hydrologic loads and anthropogenic activities (e.g., wastewater disposal and CO₂-induced seismicity), which are known to trigger earthquakes [8], to guide better policy recommendations.

1.1. The Carbonate-Silicate Cycle

1.1.1. Earth

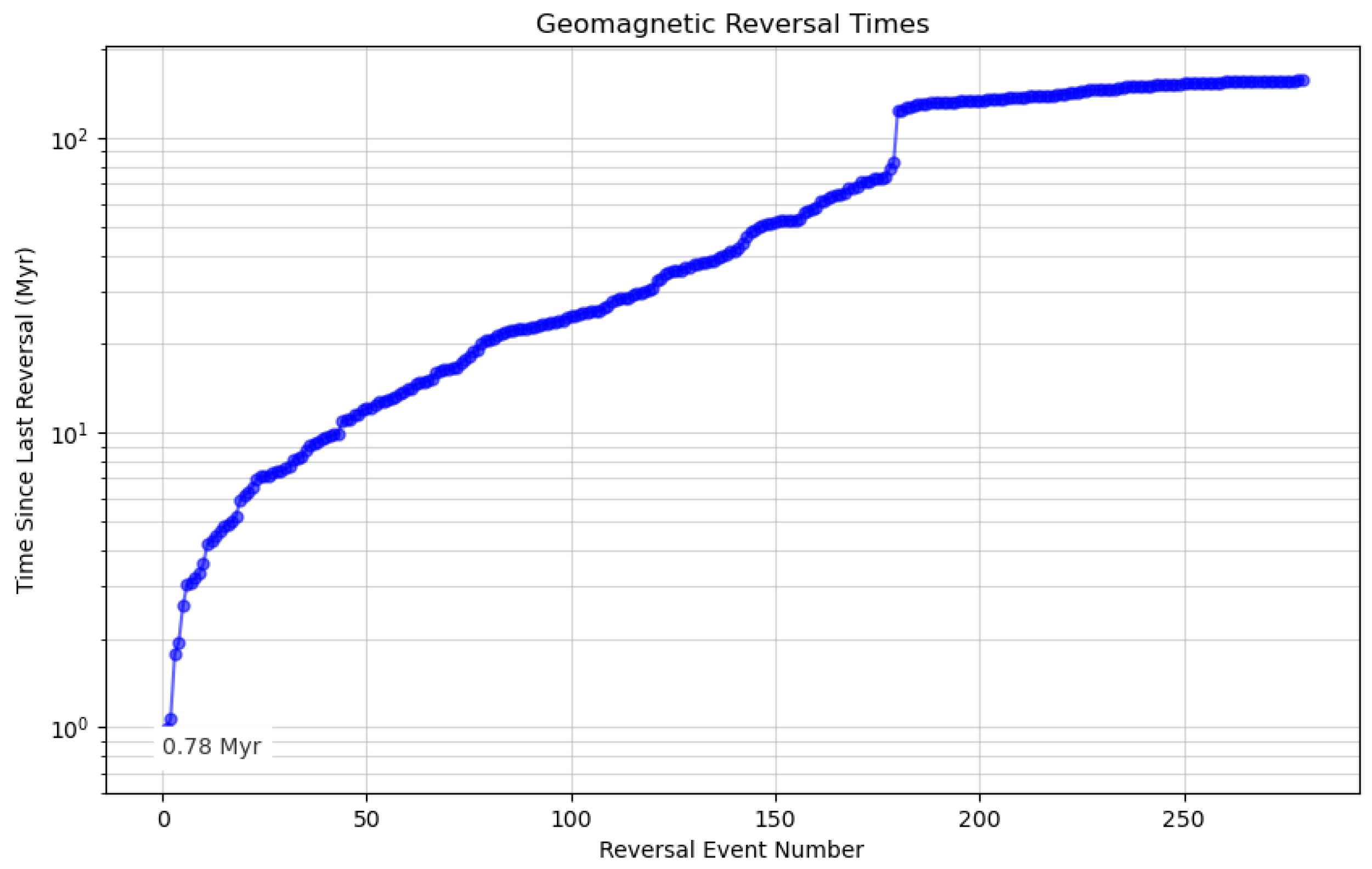
Walker et al. (1981) argued that atmospheric CO₂ levels on Earth are controlled by the carbonate–silicate geochemical cycle over geological timescales (Gyr) [9]. Silicate weathering also impacts the Earth’s climate and carbon cycle [10], which is a key process for removing anthropogenic fossil fuel emissions over the next 10–100 kyr without human intervention [11,12,13,14]. The Earth has been through numerous extreme events. From Geomagnetic reversals to super-volcanic eruptions. These events are rare, but have shaped Earth’s history profoundly. As an example, a geomagnetic reversal timeline is plotted in Figure 3.

1.1.2. Mars

On Mars, the carbonate-silicate cycle is less understood due to limited experimental verification, which requires space missions for exploration (e.g., NASA’s Mariner 9 and Viking Missions). Nevertheless, the carbonate-silicate cycle, driven by an (H₂, CO₂) greenhouse gas, is proposed as the primary mechanism for Mars’ warming, with cycles lasting up to 10 Myr, followed by extended glaciation periods [15].

2. Bayesian Fault Analysis: SAF

Markov chain Monte Carlo (MCMC) has been widely used in Earth and Environmental sciences [16,17,18,19] and even in Cosmology and Materials Science [20,21,22]. Liu et al. [23] demonstrated that Bayesian inference can be applied to inverse modeling of contaminants, air quality, and source retrieval. For example, after the Soviet Union’s Cosmos-954 satellite crashed in Canada on January 24, 1978, enriched uranium levels in rain samples from Fayetteville, Arkansas, rose significantly [24].

This author will use Bayesian Inference and MCMC to determine fault parameters from geophysical data, given a geophysical model, improving our understanding of fault mechanisms which lead to seismicity (for instance to study the relative motion of the American and Pacific plates across the SAF system, as shown in Figure 1). The model is validated against collected data, and the corresponding root mean square errors (RMSEs) are calculated.

2.1. The Inverse Problem: Why MCMC?

An inverse problem in science is the process (or processes) of calculating from a set of observations the causal factor(s) that produce(s) those observations [25].

$$d={[d_1,d_2,d_3,...,d_N]}^T$$

(1)

$$M={[M_1,M_2,M_3,...,M_N]}^T$$

(2)

That is to arrive at model parameters (The M Matrix), given data (The d Matrix). The complexity of this task increases with the model complexity and uncertainty. Meaning regular fitting methods would fail to produce satisfactory model parameters. Also, simple fittings do not use prior knowledge 1 whereas MCMC as a tool in Bayesian Inference updates beliefs about model parameters based on data [25,26].

Unlike frequentist approaches, which treat errors as measurement flaws, the Bayesian approach views errors as a feature, aligning with the philosophy behind data assimilation applications.

2.2. Single Fault Model

The velocity function describing fault slip is given by [27]:

$$v\left(x\right)={\displaystyle \frac{v_0}{\pi }}{tan}^{-1}\left({\displaystyle \frac{x-x_0}{D}}\right),$$

(3)

Where $v_0$ is the fault slip rate, D is the locking depth,$x_0$ is the fault location, and x is the spatial coordinate.

The validity of this model when applied to the SAF, will be examined using Bayesian Inference and will be compared to the values reported in the literature. Smaller earthquakes are explained by the theory that fault-zone materials do not heal after deformation, lacking the strength for more destructive movements [4].

2.3. Data

The creep rate GPS and InSAR data [3] is plotted and shown in Figure 4 and Figure 1. The creep rate data, shown in Figure 4 and Figure 1, are analyzed further in Figure 5.

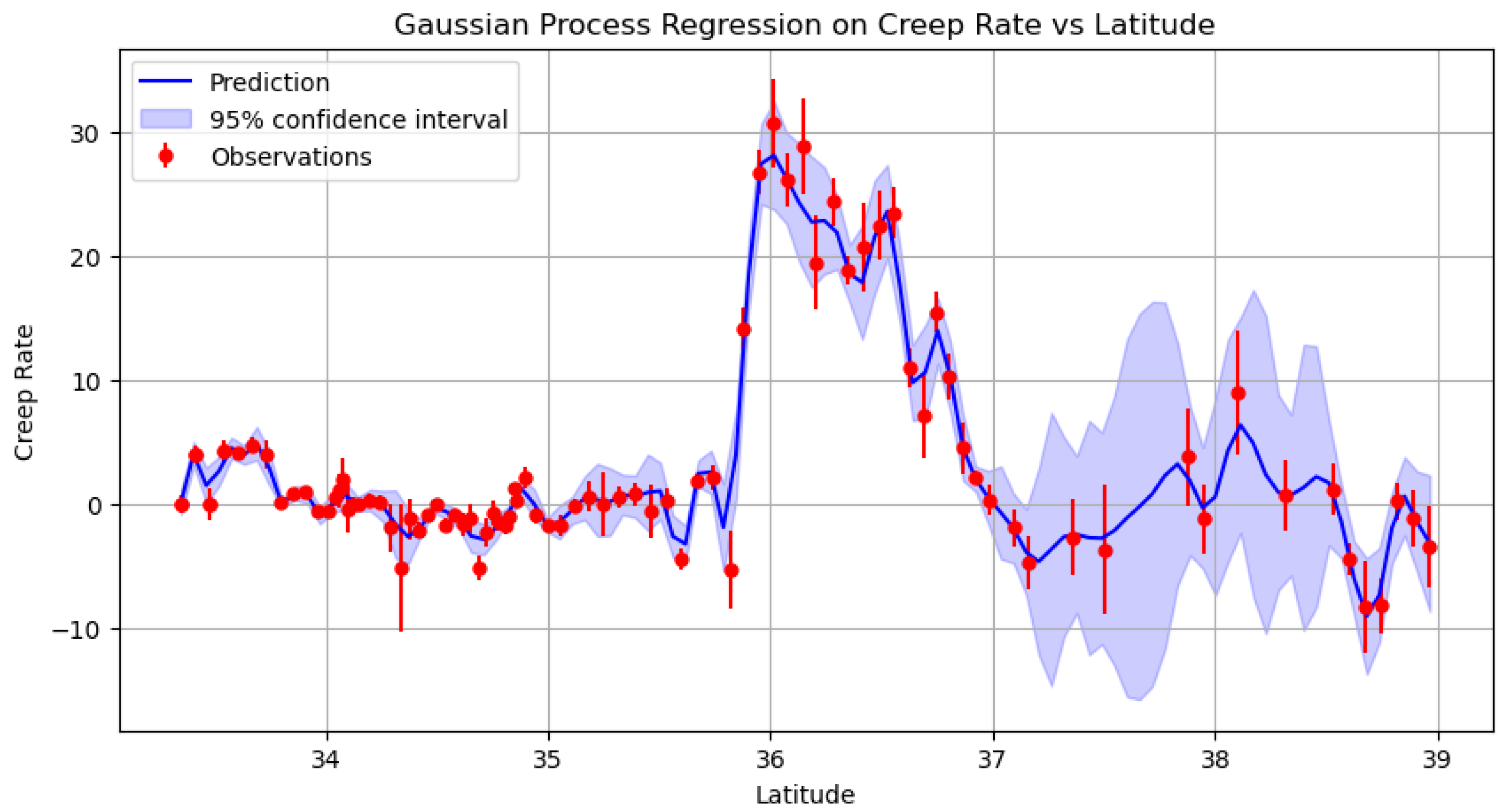
2.4. Gaussian Processes: GPs

A Gaussian Processes-based model was fitted to the creep rate data (Figure 6).

2.5. Line Of Sight Velocities (LOS)

The Line Of Sight (LOS) velocity data [28] is assumed to have a variance of 1.

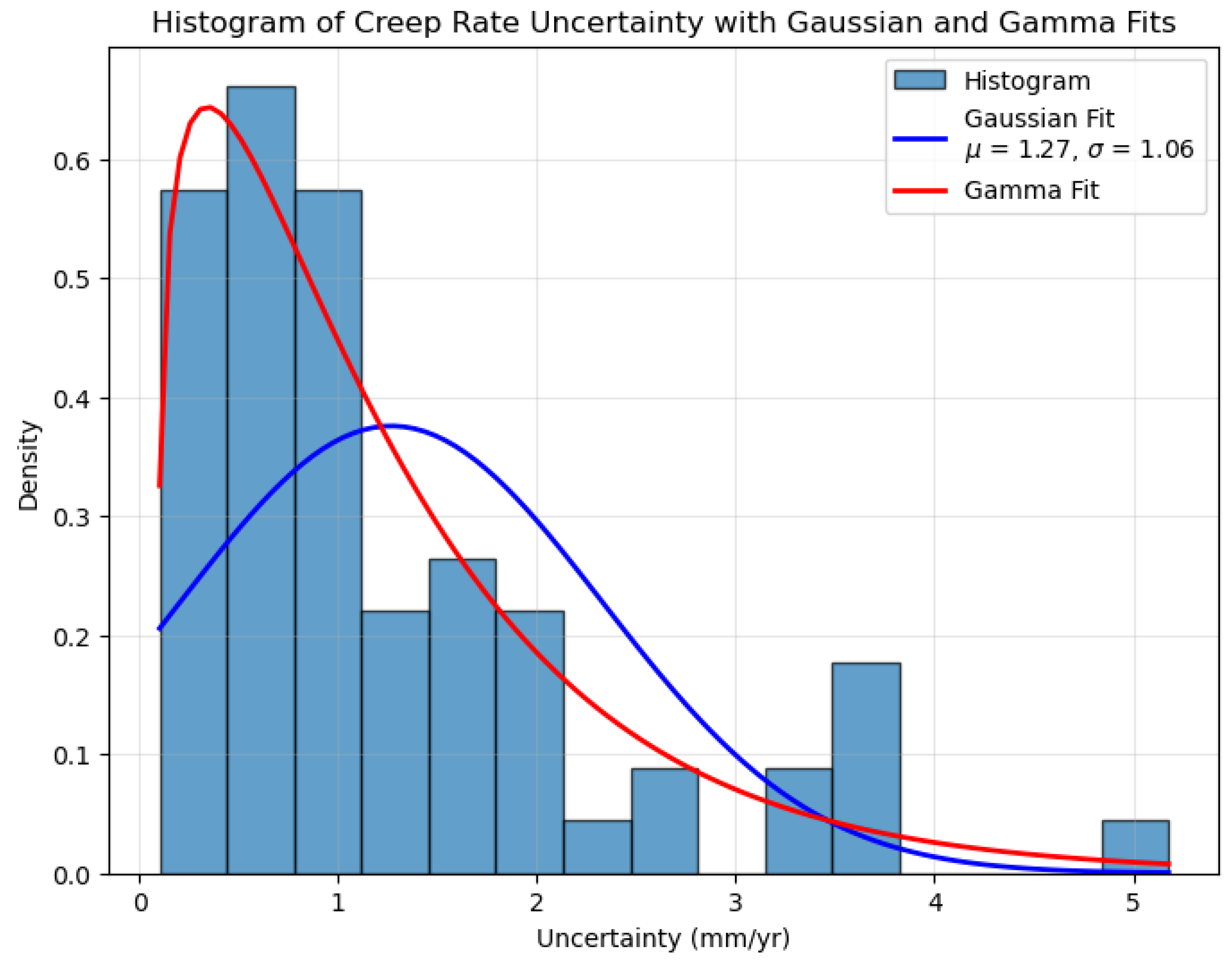
Creep rate uncertainty as suggested in [3] is 1.2 ± 1 (mm/year). The distribution of this uncertainty in measurement of the creep rate is shown in Figure 7. The data is loaded from a file (available in the GitHub repository for this project), assuming a two column structure separated by commas. First column is assumed to be the x(positions) and the second is the velocities $v\left(x\right)$. We also assume that the observational errors follow a Normal distribution, $y_j=v\left(x_j\right)+{ϵ}_j$, where ${ϵ}_j\sim N(0,{\sigma }^2)$ and $\sigma =1$, with respect to the model equation in Equation 3.

Figure 7. Creep rate uncertainty distribution for the SAF based on high-resolution GPS and InSAR data from Ref. [3]. A Gaussian fit yields a mean of 1.27 mm/year, but heavy tails suggest a Gamma fit may be more appropriate, with a representative value of $0.9\pm 0.4$ mm/year.

Figure 7. Creep rate uncertainty distribution for the SAF based on high-resolution GPS and InSAR data from Ref. [3]. A Gaussian fit yields a mean of 1.27 mm/year, but heavy tails suggest a Gamma fit may be more appropriate, with a representative value of $0.9\pm 0.4$ mm/year.

2.6. Two-Fault

The volocities are additive (superposition of two single-faults).

2.7. Defining Log-Likelihood and Log-Prior

We want to know how well the model fits the data.

For Gaussian errors, the likelihood, as described in [26,29], is:

$$p\left(y_j\right|\theta )=\prod _{j=1}^{N_j}{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}exp\left(-{\displaystyle \frac{{(y_j-v(x_j,\theta ))}^2}{2{\sigma }^2}}\right).$$

(4)

When taking the Log-Likelihhood, the product becomes a sum. Given $\sigma =1$, it simplifies to

$$logp\left(y_j\right|\theta )=A(-{\displaystyle \frac{1}{2}}\sum {(y_j-v\left(x_j\right))}^2)$$

(5)

Where A is a constant throughout the MCMC process.

2.8. Bayesian Context

In Bayesian Context, the Posterior distribution of the parameters given the data $p\left(\theta \right|y)$ , which is our goal, is given as:

$$p\left(\theta \right|y)={\displaystyle \frac{p\left(y\right|\theta \left)p\right(\theta )}{p\left(y\right)}}$$

(6)

$p\left(y\right|\theta )$ is the likelihood (How probable the observed data is under specific parameter values). $p\left(\theta \right)$ is our initial beliefs about the parameters. $p\left(y\right)$ is the Evidence, which is a normalizing constant, which can be ignored in MCMC since we are sampling ratios. So in order to find the posterior, we need to compute the likelihood, which determines how well a given set of parameters $\theta$ explains the data y.

2.9. Log-Prior, Single Fault

We have a uniform prior, where $p\left(\theta \right)$ is a constant if within bounds, and if not, zero. So log prior would be 0 if valid and $-\infty$ if not. The purpose of this is to constrain parameter ranges. For instance, $v_0$ and D both range between 0 and 80 while $x_0$ ranges from -50 to 50.

2.10. Random Walk Metropolis Sampler : Markov Chain Monte Carlo (MCMC)

$$p\left(\theta \right|y)\propto p(y\left|\theta \right)p\left(\theta \right)$$

(7)

This algorithm implements the Metropolis-Hastings MCMC algorithm. Starting at an initial guess, we propose a new point ${\theta }^{\prime }=\theta +S·N(0,1)$ with S being the step scale. We then compute the log-posterior by taking the log of eq. 7, we arrive at:

$$logp\left(\theta \right|y)\propto logp(y\left|\theta \right)+logp\left(\theta \right)$$

(8)

The outputs are chain of samples, log-posterior values and acceptance rate.

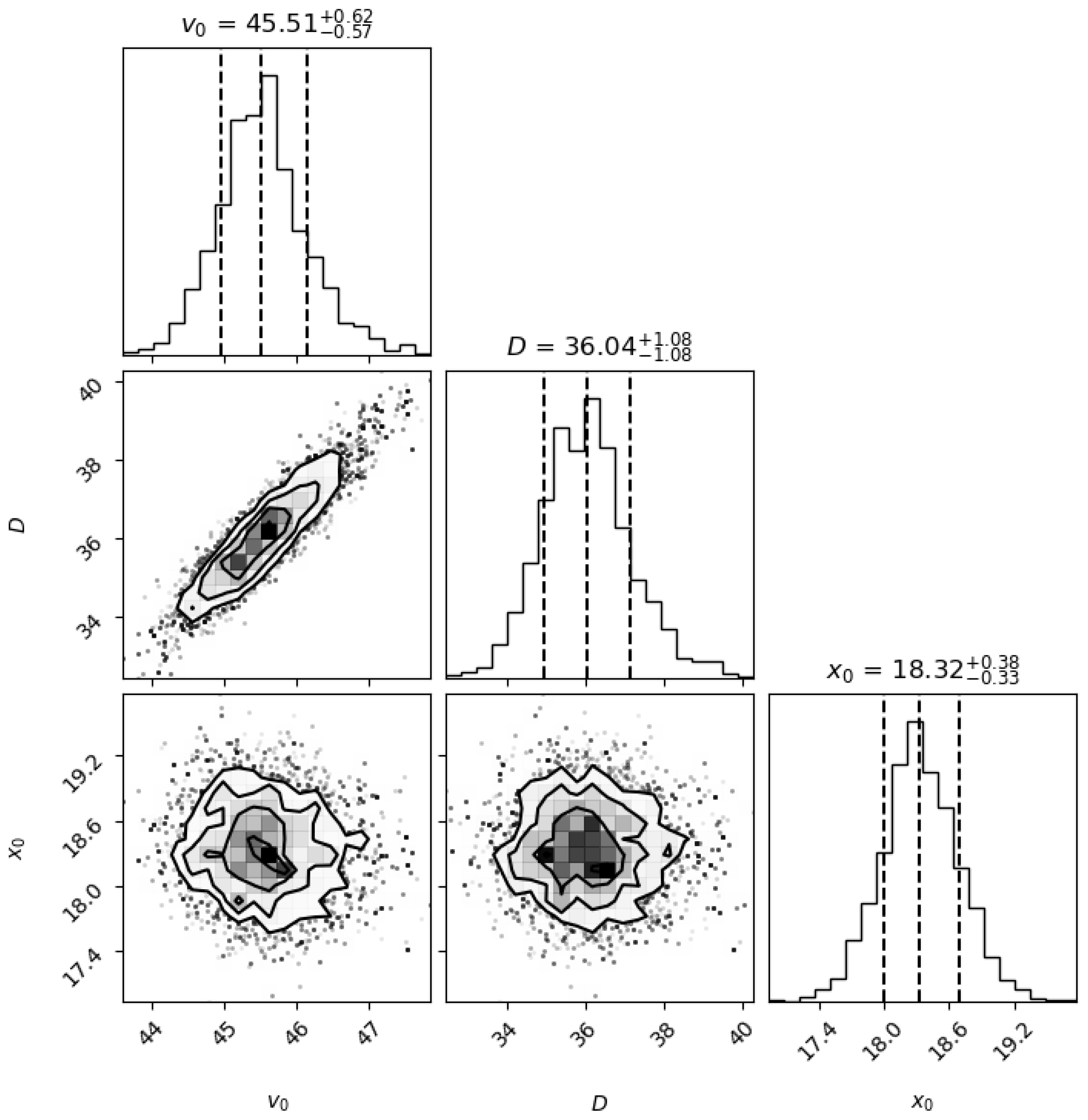
2.11. Applying MCMC: Single Fault Model Analysis

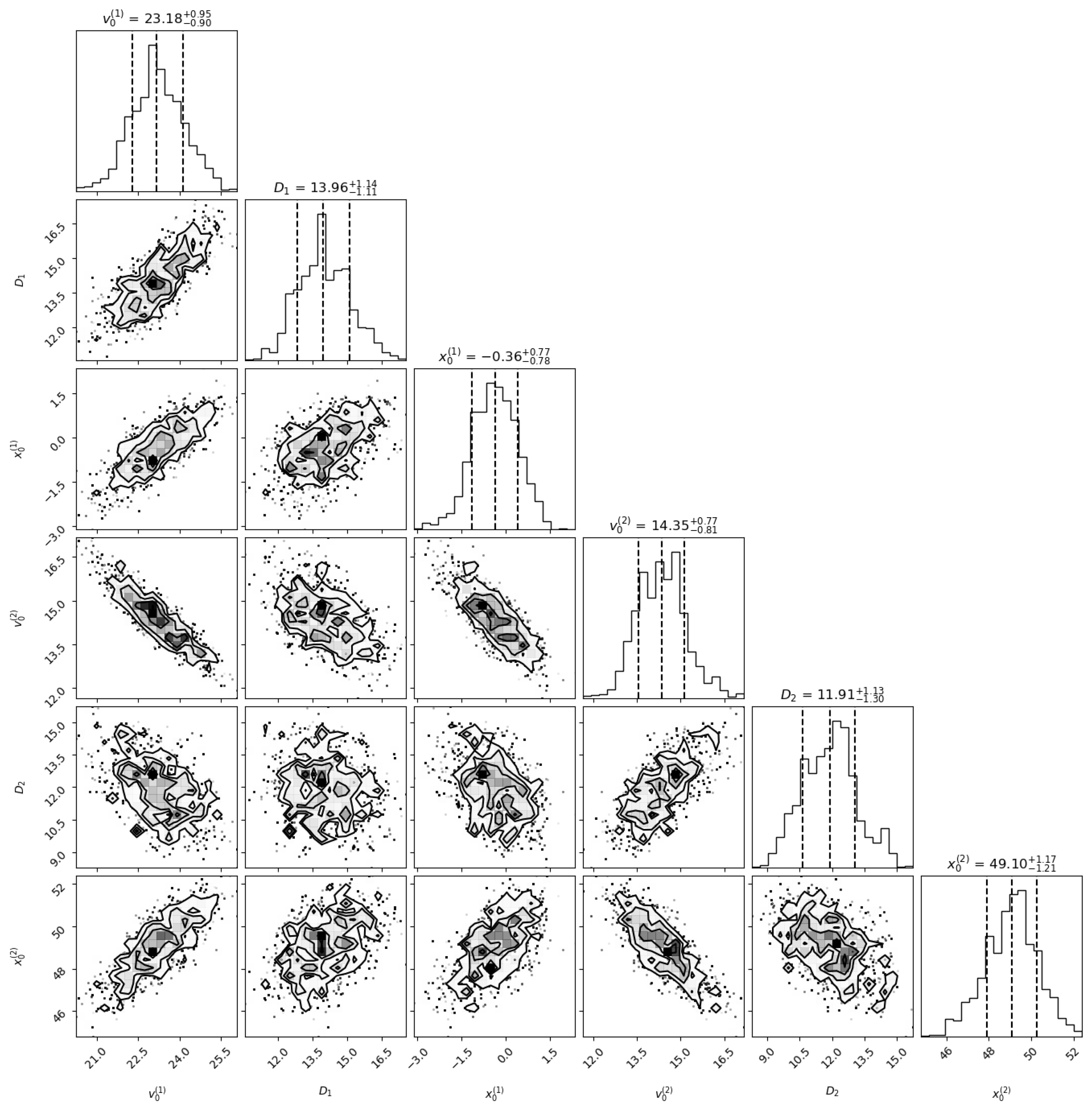
The mean and STD of $v_0$, D, $x_0$ are our posterior stats. The posterior distribution and correlations are plotted in Figure 8.

The MCMC model run over 30,000 samples burn-in of 5,000, step size 1.0:

2.12. Posterior Samples VS Data

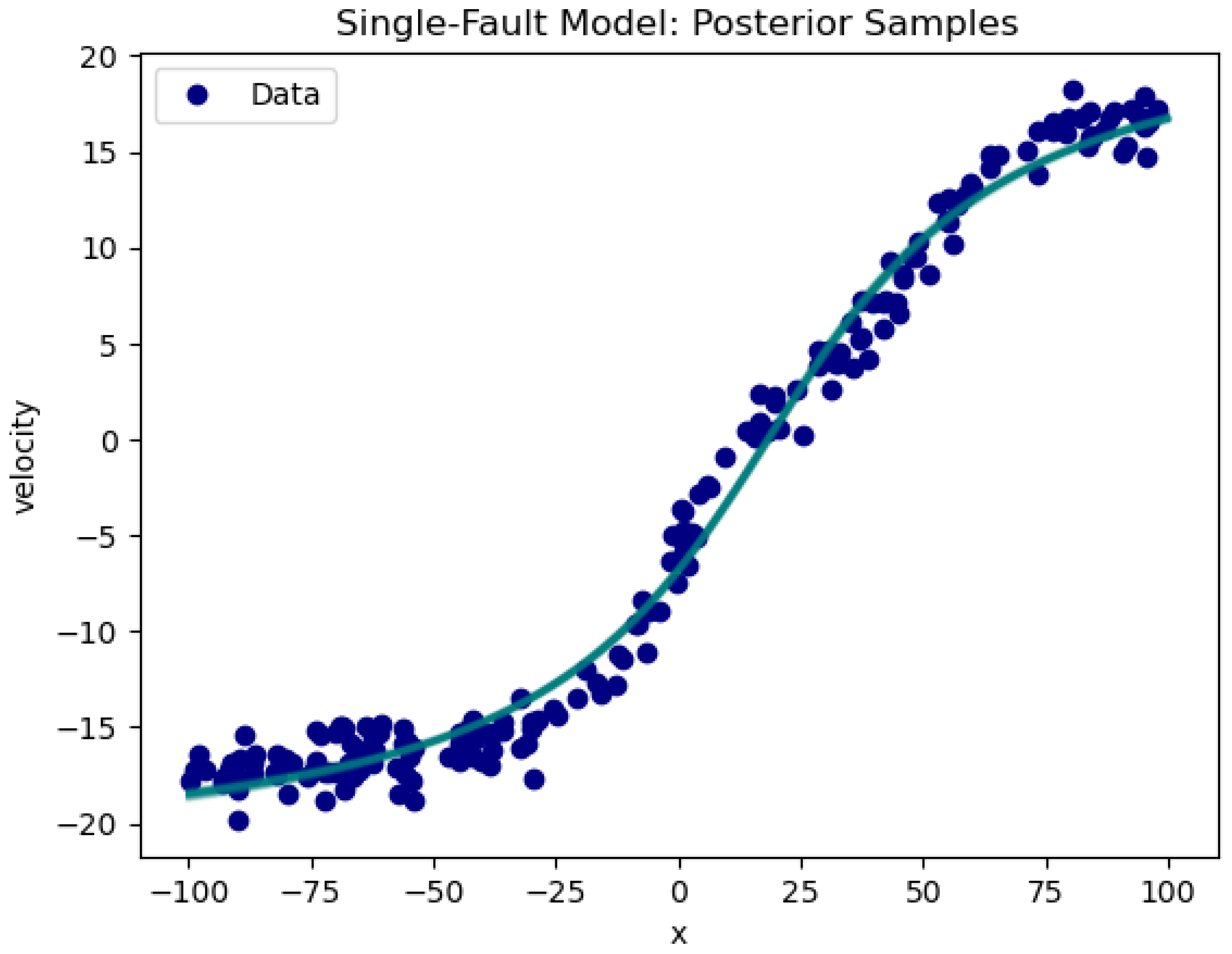
Plot of the posterior samples vs Data is shown in Figure 11.

2.13. RMSE and the Two-Fault Model

The RMSE is defined as

$${\mathrm{RMSE}}_i={\left({\displaystyle \frac{1}{N_s}}\sum _{j=1}^{N_y}{\left({\displaystyle \frac{y_j-\widehat{v}(x_j,{\theta }_i)}{{\sigma }_j}}\right)}^2\right)}^{1/2}$$

(9)

where $y_i$ are the $N_y$ observations of the velocity, ${\sigma }_j$ are the standard deviations of the model errors and $\widehat{v}(x_j,{\theta }_i)$ is the velocity at location $x_j$, using parameters ${\theta }_i$. The RMSE for single-fault model is approximately $1.4$. This is not disastrous, but not ideal either. To improve this, we consider a modified version of this model, namely "Two-Fault" model and see if we can arrive at a better RMSE.

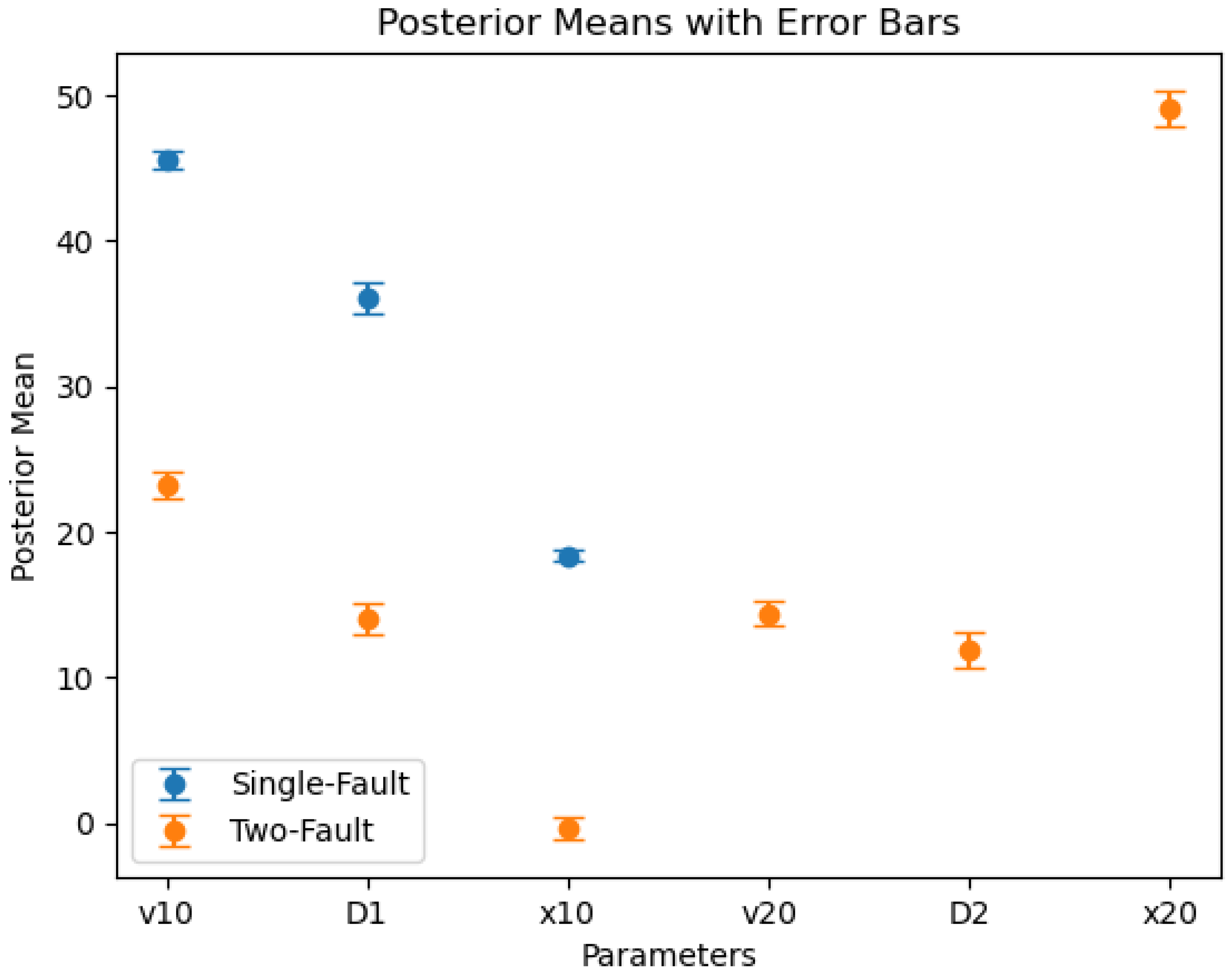
Single Fault Model Parameters are displayed in Table 1.

2.14. The Two-Fault Model

In this model, instead of one fault, we consider two faults. We start by two-fault velocity, generalizing equation 3. , arriving at

$$v={\displaystyle \frac{v_{10}}{\pi }}arctan\left({\displaystyle \frac{x-x_{01}}{D_1}}\right)+{\displaystyle \frac{v_{02}}{\pi }}arctan\left({\displaystyle \frac{x-x_{02}}{D_2}}\right)$$

(10)

The MCMC analysis is similar to that of single-fault model. The Two Fault Model Parameters are calculated and shown in Table 2.

Figure 9. Triangle corner plot of two-fault model Parameters, obtained using the two-fault velocity model. The velocities are in (mm/year), Depth and x are in (km).

Figure 9. Triangle corner plot of two-fault model Parameters, obtained using the two-fault velocity model. The velocities are in (mm/year), Depth and x are in (km).

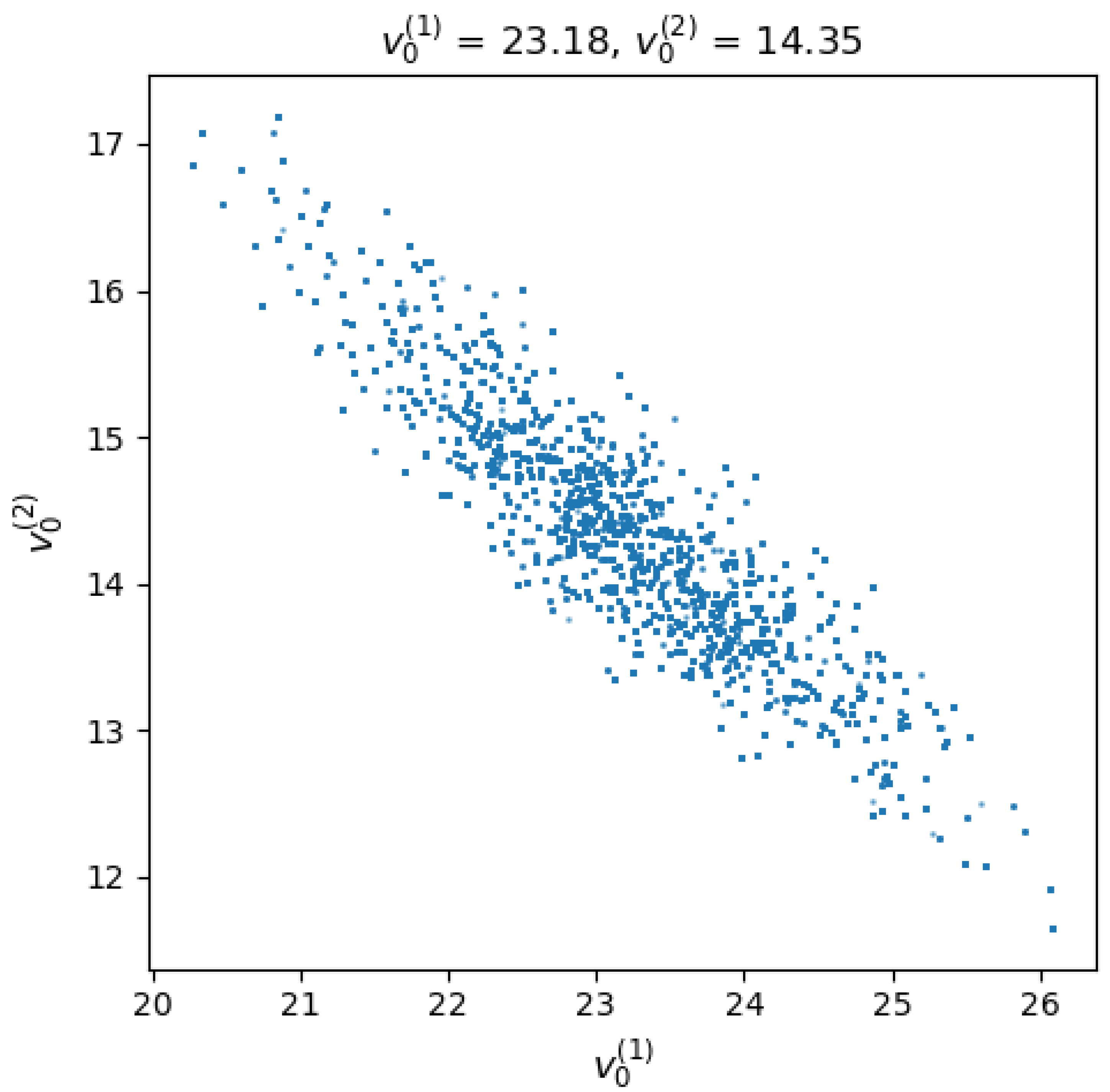
It is noteworthy that there is a negative correlation between the two velocities $v_0^1$ and $v_0^2$ and these are exclusively shown in Figure 10.

For model validation, posterior samples are directly compared to experimental data. The error bars are not graphically displayed since they are relatively small and the points in Figure 11 overlap in representing the data and the corresponding uncertainty.

Figure 11. Posterior Samples VS Experimental Data for the geophysical single-fault model. The model fits well, but it is not ideal, given a relatively large RMSE of 1.4.

Figure 11. Posterior Samples VS Experimental Data for the geophysical single-fault model. The model fits well, but it is not ideal, given a relatively large RMSE of 1.4.

Although not very far from 1, the value of 1.4 for the RMSE is not ideal. Particularly around the origin (see Figure 11), the deviation of data from model become more obvious.

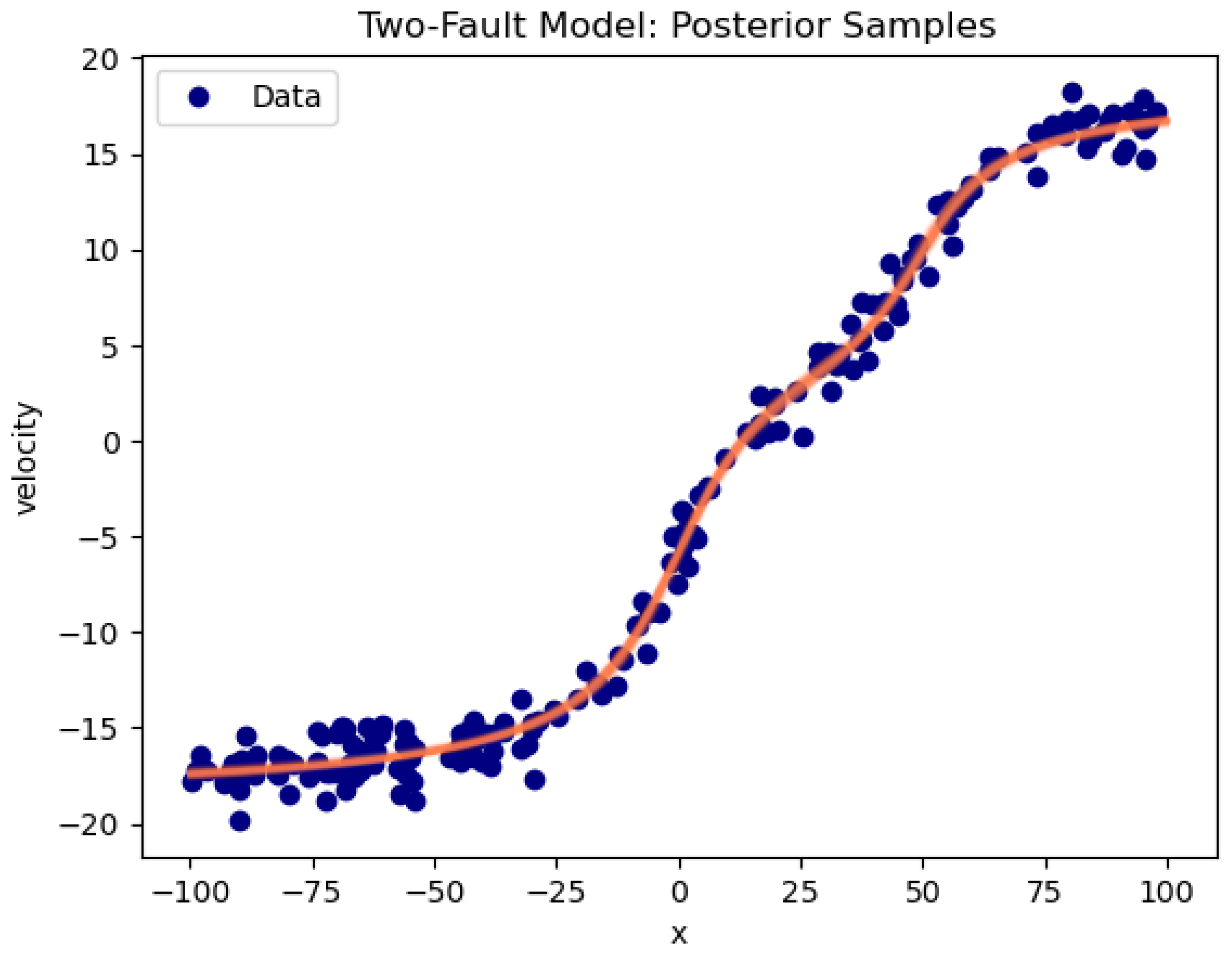
Figure 12. Two Fault Model Posterior VS Experimental Data. The RMSE is ≈ 1. The model fits data within expected uncertainty.

Figure 12. Two Fault Model Posterior VS Experimental Data. The RMSE is ≈ 1. The model fits data within expected uncertainty.

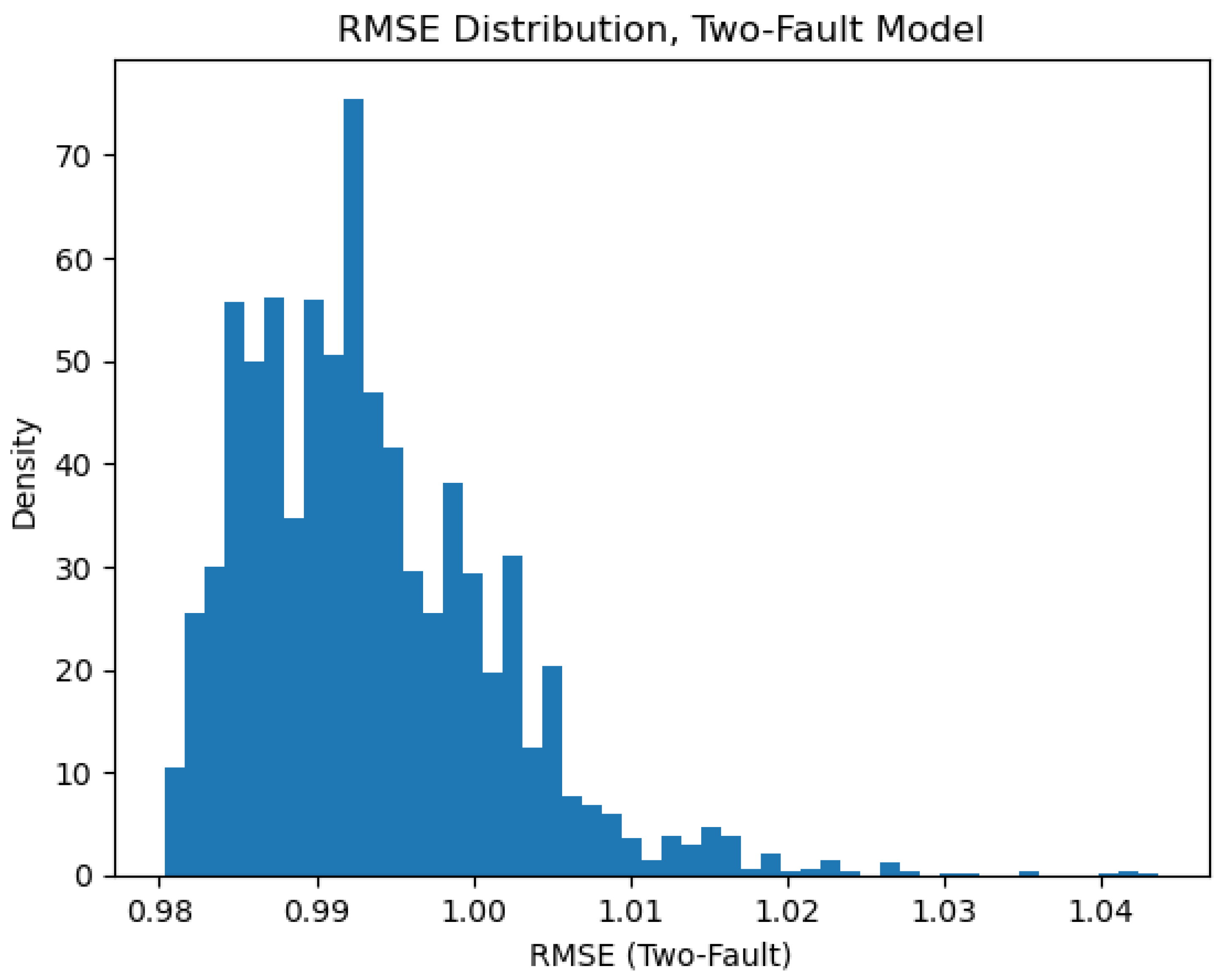
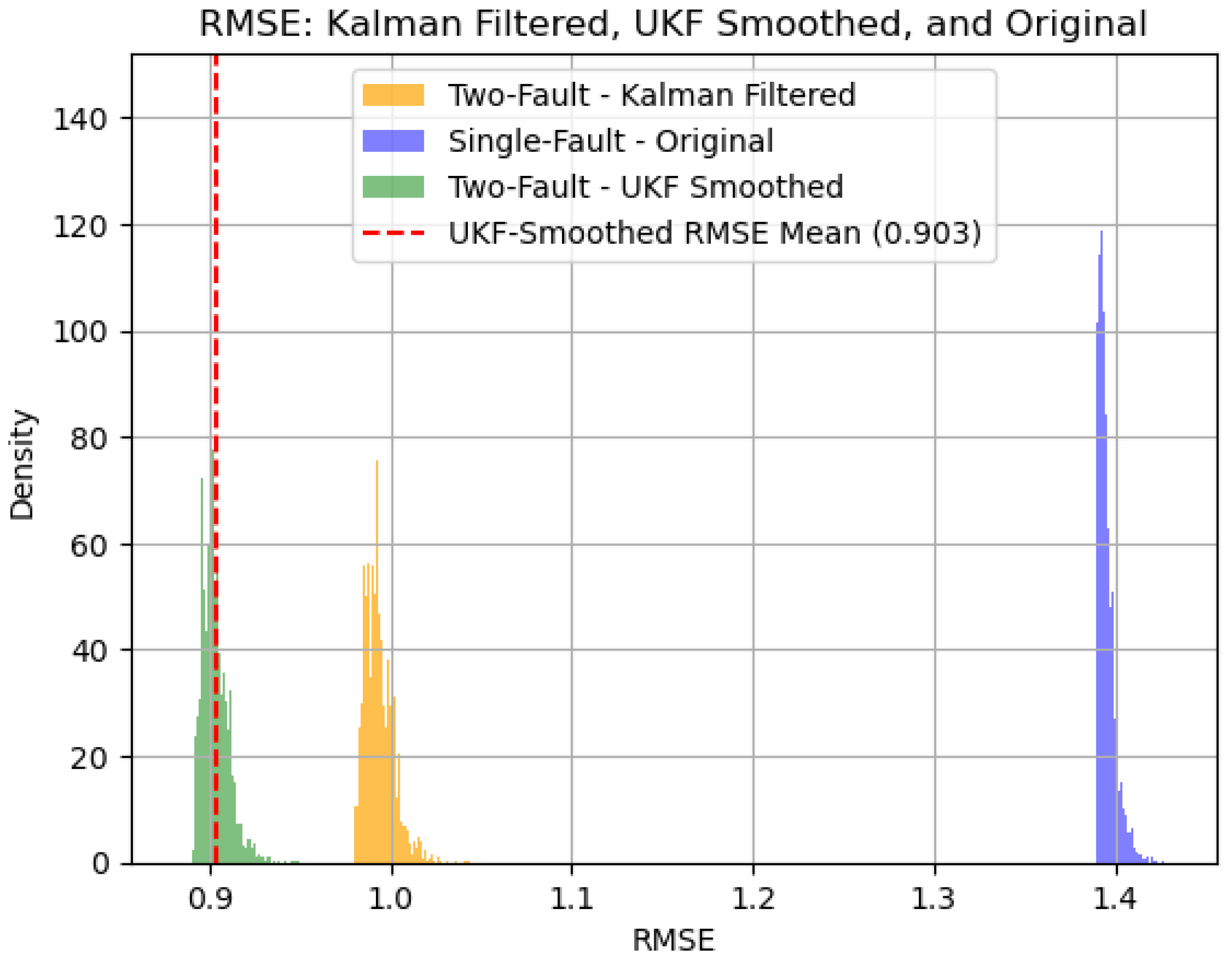
Figure 13. Two-Fault Model RMSE distribution, which is centered around value of 1. This is expected, given the background noise of around 1 mm/year.

Figure 13. Two-Fault Model RMSE distribution, which is centered around value of 1. This is expected, given the background noise of around 1 mm/year.

Heavy tails in the RMSE usually hint at unexpected noise, systemic error or even model inadequacy.

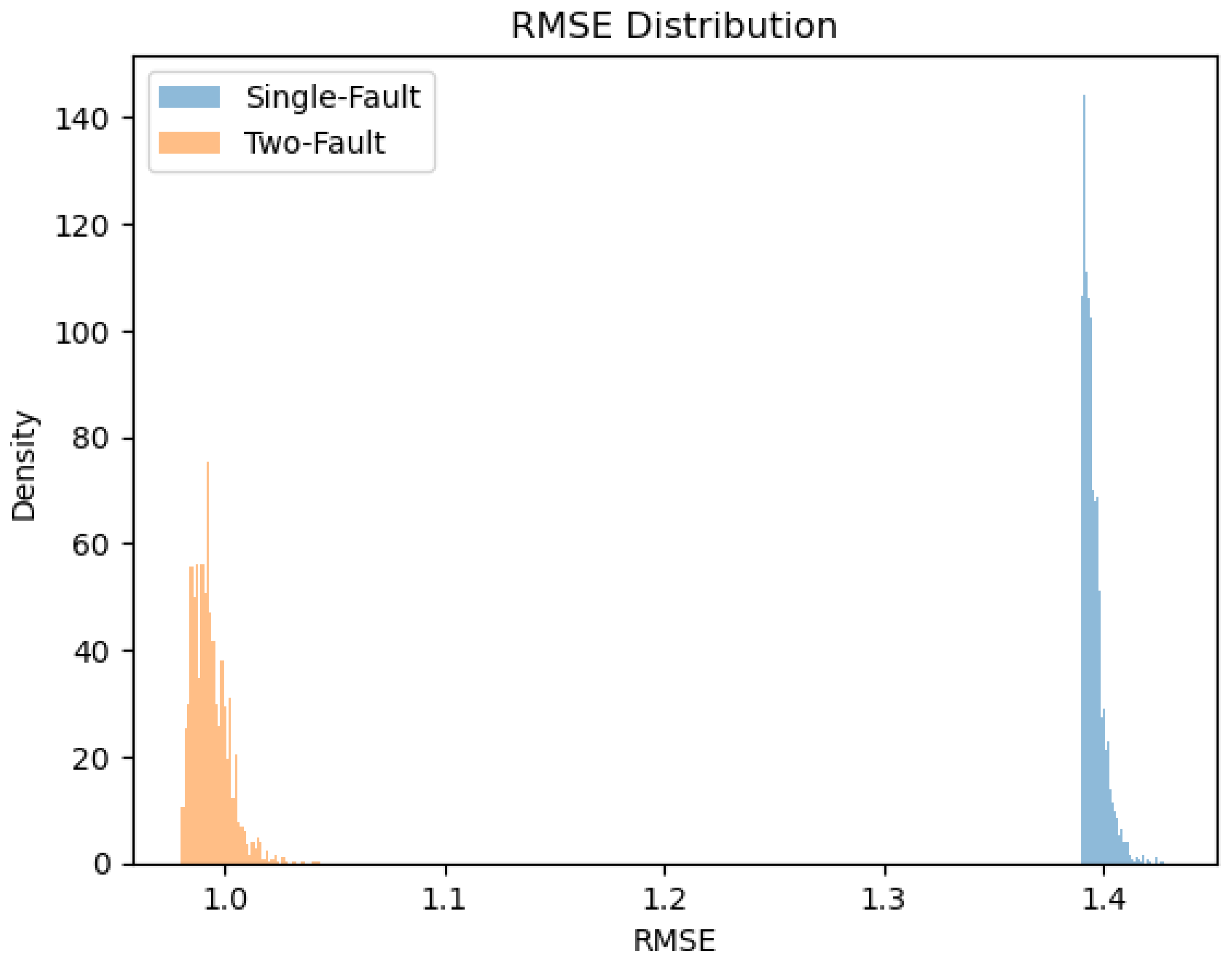
Figure 14. Two Fault Model RMSE distribution ≈ 1 (Left) VS Single Fault RMSE ≈ 1.4 (Right). This RMSE compares closely to the background noise level, further strengthening the two-fault hypothesis.

Figure 14. Two Fault Model RMSE distribution ≈ 1 (Left) VS Single Fault RMSE ≈ 1.4 (Right). This RMSE compares closely to the background noise level, further strengthening the two-fault hypothesis.

2.15. Fault Analysis: Discussion

Markov Chain Monte Carlo is a powerful method for Data Analysis. In this study, it was used as a tool in Inverse Problem, fitting model parameters to data. This geophysical model elegantly fit to data of 200 points. Using a single-fault model, the parameters were obtained, however with a RMSE of 1.4, which was not ideal. Therefore a Two-fault model was examined, arriving at a RMSE of 1. Given the expected variance as seen in figure (7), this RMSE is in a good agreement with the data. The ration of this RMSE to the STD is given in eq. 11.

$${\displaystyle \frac{RMSE}{\sigma }}\approx 1.1\pm 0.5$$

(11)

These parameters and their error bars are plotted and presented in Figure 15.

The RMSE is already improved to the level of background noise and this can be easily seen comparing Figure 7 and Figure 14.

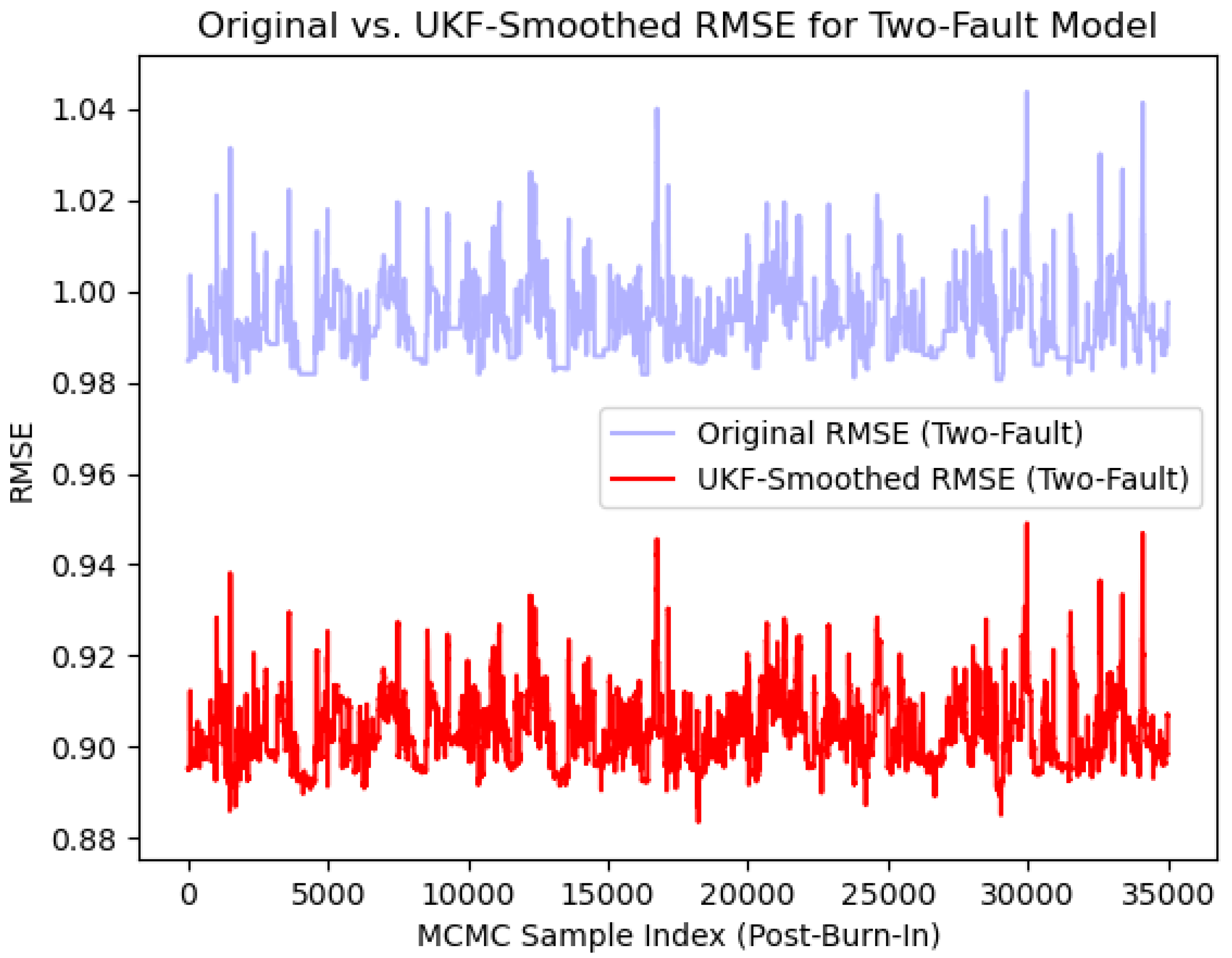
Having achieved a reasonable RMSE, one can further explore ways to reduce RMSE, given a predictive model. One can use Kalman Gain to smooth such data:

$$K=P_{n,n-1}{H}^T{(H{P}_{n,n-1}{H}^T+R_n)}^{-1}$$

(12)

Here, $K_n$ is the Kalman Gain itself, $P_{n,n-1}$ is the prior estimate cov. matrix of the current state, H is the observation matrix and $R_n$ is the measurement noise cov. matrix. The non-linear Kalman Filter (Unscented Kalman Filter)is used for systems with non-linearity.

This method, applied to the two-fault model, reduces the RMSE even further (RMSE ≈ 0.9). A comparison is shown in Figure 16.

and all RMSE distributions have been plotted in Figure 17.

This suggests that the SAF does not act in isolation and is influenced by other fault systems such as San Jacinto fault (SJF) in southern California, which can contribute to the velocity field. The $v_0^{\left(2\right)}=$ (14 ± 1) is consistent with the the SJF velocity rate of (11 ± 4) mm/yr reported by Rockwell et al. [30].

3. Anthropogenic Seismicity

Under load, soil deforms gradually at a variable rate, a phenomenon known as consolidation, mathematically formulated by Biot in 1940 [31]. Hill et. al.[32] argue that stress perturbations in the order of 0.5 MPa are sufficient to trigger seismicity. These perturbations are dominated by pore pressure changes. They furthermore correlated the past 6 major earthquake events on the SAF with high-stands of the ancient Lake Cahuilla, which its remnant is known today as the Salton Sea (shown in Figure 18). Using Finite Element Methods (FEM) to arrive at such correlations, their model seems to be applicable to other regions where hydrologic loading is associated with seismicity, anthropogenic or not.

3.1. Seismic Risk Threshold

Higher pressures of fluid introductions are usually carried out over shorter periods of time and lower pressures are carried out over a larger period of time. In other words, there is a tradeoff. When examined as a complex system, this resembles a path which constraints the system’s evolution in which soil consolidation undergoes dissipation.

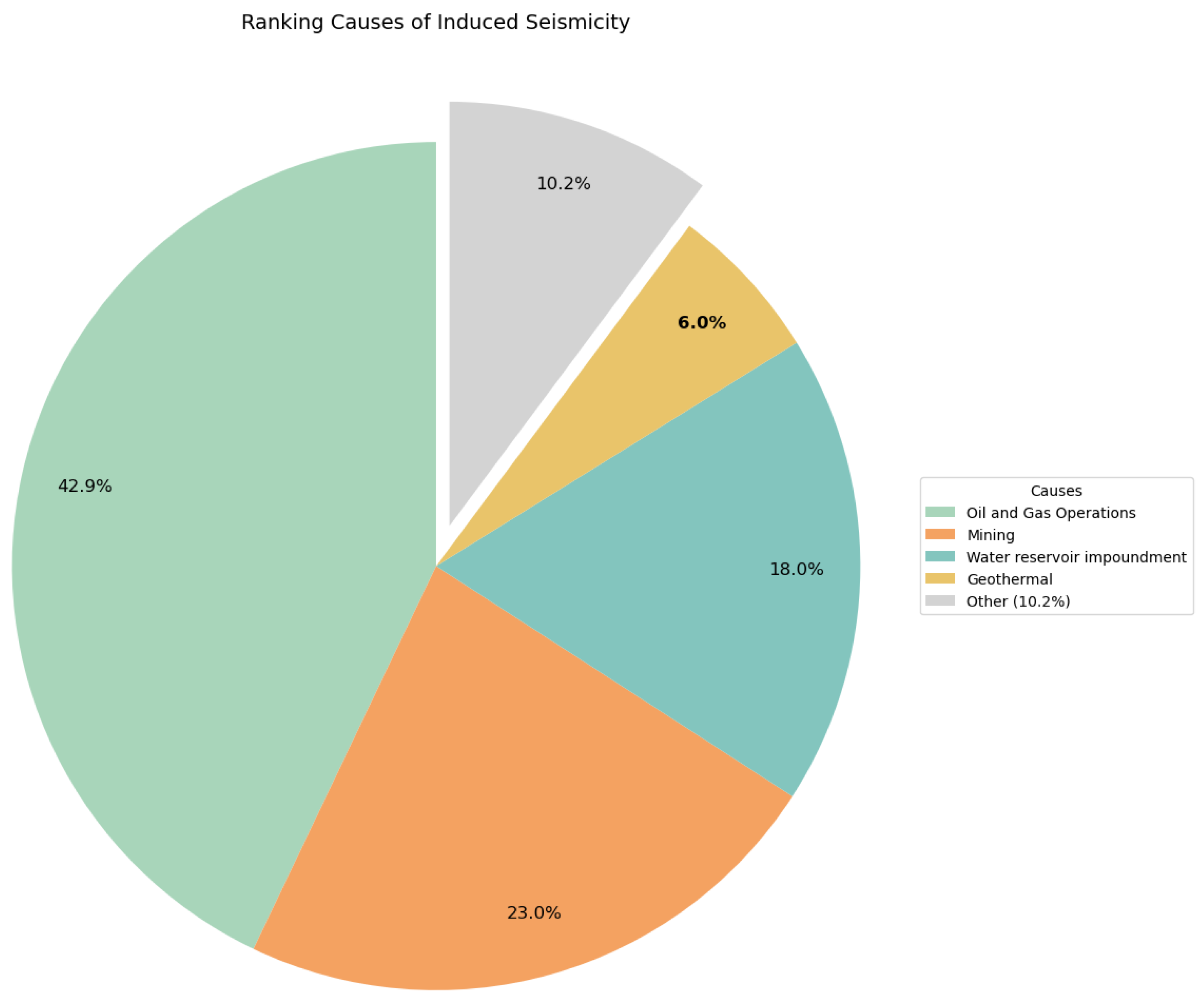
A breakdown of these operations and their corresponding share of caused anthropogenic seismicity can be found in Figure 19.

3.2. Oil and Gas Operations

The probability of reservoir-seismicity to be widespread and deeper for a large reservoir is higher than that of a small one [34]. Oil and gas extraction and fluid injections have caused elevated seismicity in Texas, likely due to pore pressure changes [35].

It is noteworthy that the Los Angeles Oil Field produces about 3.5 barrels of oil per day and also faster than 1 $mm/year$ LOS movement on the fault [36]. The state of California is phasing out Oil Drilling operations by 2045 citing climate change as the reason for this decision [37].

3.3. CCS & Wastewater

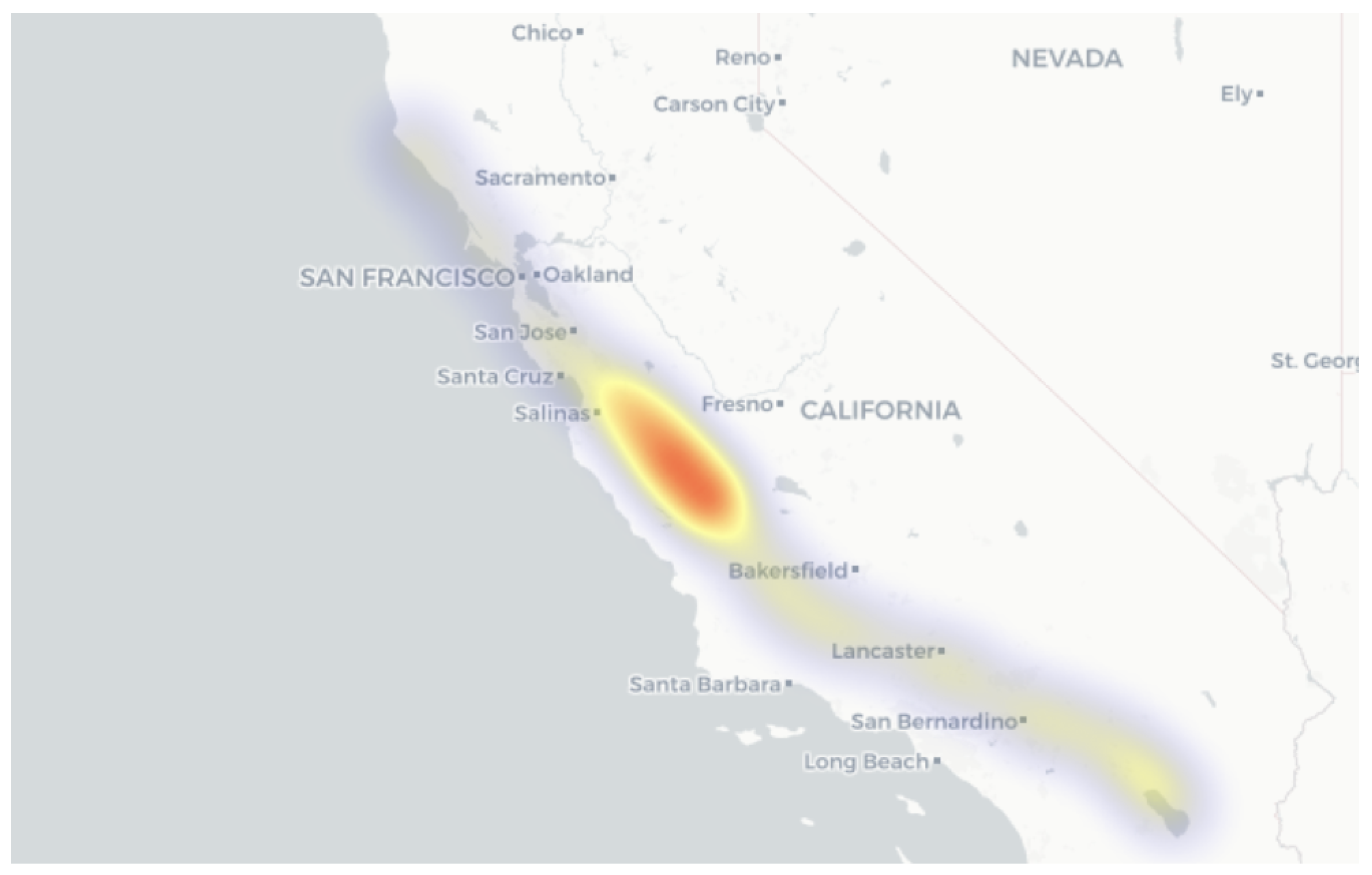
CO₂ injection stimulates plate tectonics due to mechanical pressure exerted by the injected fluids. In the past few years, as part of broader mitigation efforts, $C{O}_2$ has been injected into the earth. It is postulated that the injected $C{O}_2$ stays underground for decades. The pressure excreted by this gas can however threaten the integrity of the seals at injection sites. This requires further analysis on the operations as well as more simulations which could shed light on anthropogenic seismicity caused by geological injections. Zoback et. al. 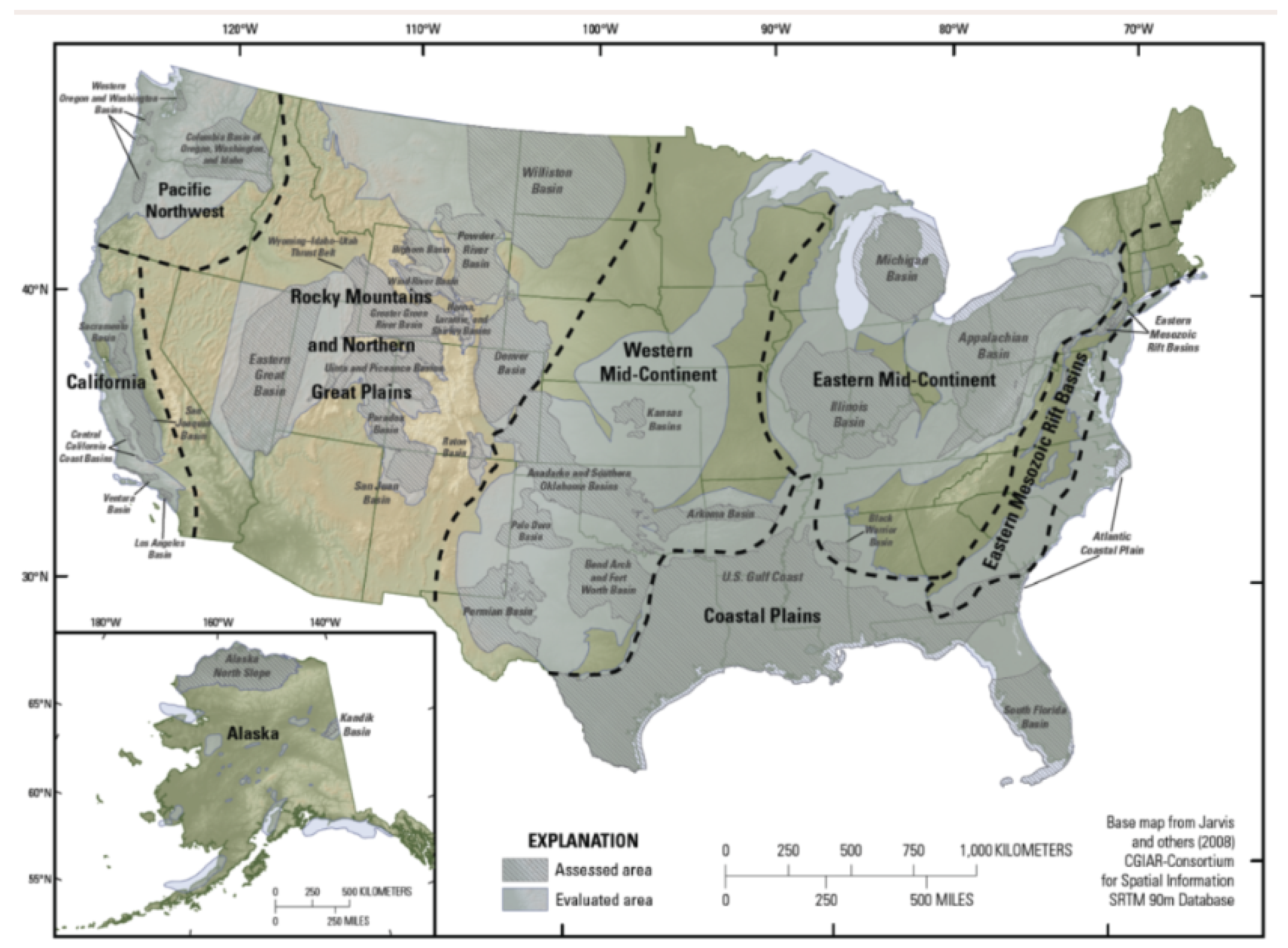argue that in order to reduce the risk of seismicity from such operations, the $\Delta p$ (pressure), as shown in my uncertainty relationship (??), should be limited. Increasing pressure can also trigger an earthquake and as a result, threaten the integrity of the CCS seals. A map of areas in the United States with active or potential CCS operations is shown in Figure 20.

3.4. Geothermal: The Brawley seismic zone (BSZ)

The Brawley seismic zone encompasses Salton Sea and the surronding area and is home to Geothermal operations, most notably the Imperial Valley Geothermal Project. It has a $\sim 3000$ MW of geothermal capacity. It also provides a high level of battery-grade lithium for electric vehicles (currently at ∼ 75,000 tons) [39]. Despite the strategic advantages, it has also introduced background level seismicity to the region, particularly at the North Brawley Geothermal Field (NBGF) and at the Salton Sea Geothermal Field (SSGF) [40]. .

3.5. Policy Error: The 1906 San Francisco Earthquake

In 1905, the Colorado River flooded the Salton Sink due to a failed irrigation project, forming the Salton Sea. In 1906, San Francisco experienced a magnitude 7.9 earthquake, leaving over 3,000 casualties. Supported by paleo-seismic data, major SAF earthquakes are shown to be modulated by ancient lake-fillings [32].

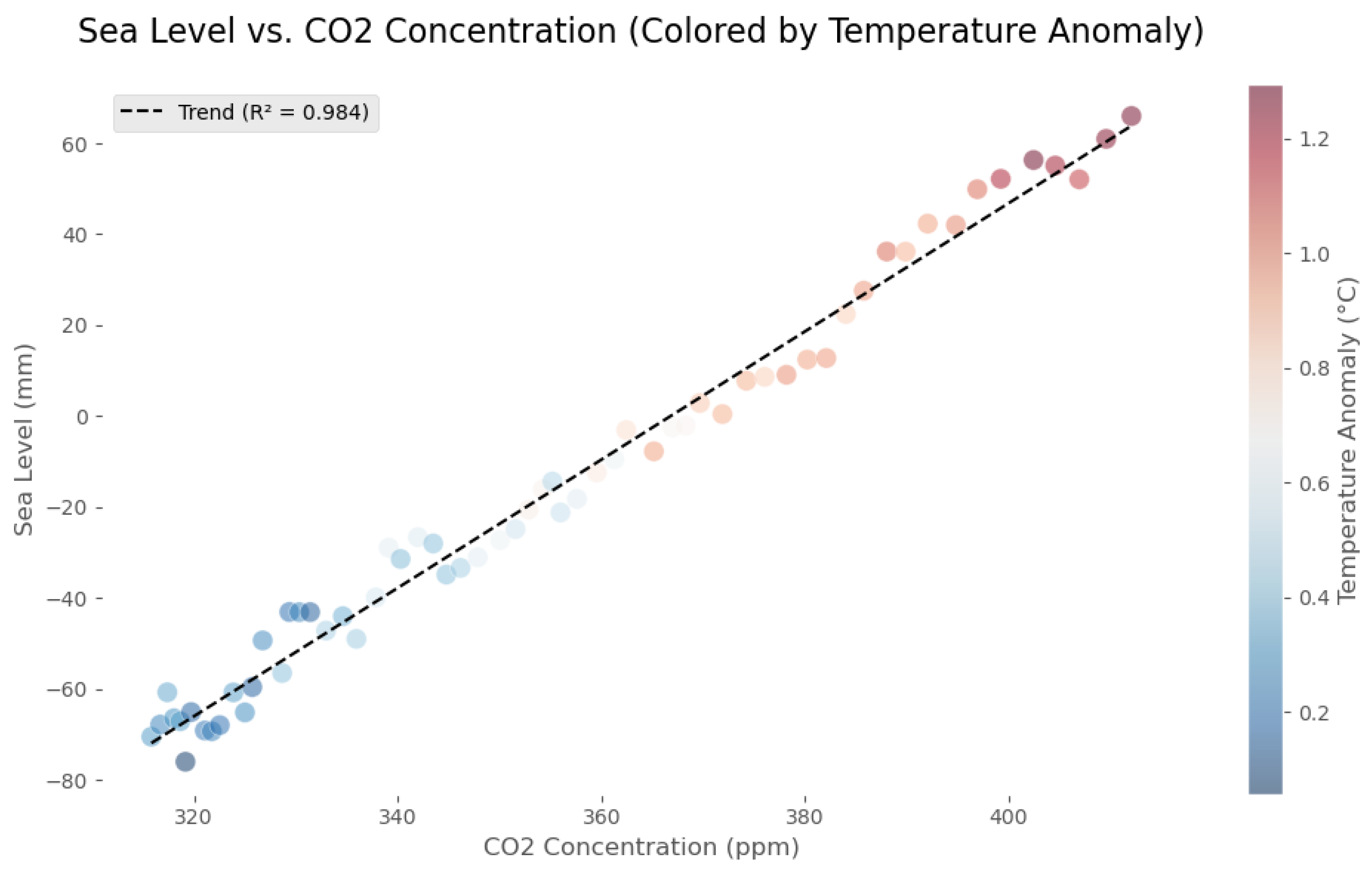
4. Sea Level Rise

Sea level rise (SLR), estimated at $1.75\pm 0.55$ mm/year globally [41], increases water loads, inducing pressure changes that can trigger seismicity. Figure 21 illustrates the correlation between rising CO₂ levels, sea level, and temperature anomalies from 1959 to 2020, highlighting the SLR [42,43,44].

The mechanism can be explained by the pore pressure $p(\mathbf{x},t)$ in a poroelastic medium, induced by hydrologic loads from sea level rise, satisfies the following diffusion equation derived from Biot’s theory of poroelasticity, which is a diffusion PDE:

$${\displaystyle \frac{\partial p}{\partial t}}=M\kappa {\nabla }^{2}p-\alpha M{\displaystyle \frac{\partial {\epsilon }_v}{\partial t}}$$

(13)

This equation basically shows the relationship between pressure change as well as temporal and spatial diffusion. p is the fluid pressure, M is the Biot modulus, $\kappa ={\displaystyle \frac{k}{\eta }}$ is the Hydraulic conductivity, with k being permeability and $\eta$ the fluid viscosity. $\alpha$ is the Biot-Willis coefficient, ${ϵ}_v=\nabla .u$ is the Volumetric strain where u is the solid displacement vector. ${\nabla }^2$ is the Laplacian operator.

4.1. Relation to Seismicity

The pore pressure p alters the effective stress on faults, following Terzaghi’s principle:

$${\sigma }_{\mathrm{eff}}=\sigma -p,$$

(14)

where ${\sigma }_{\mathrm{eff}}$ is the effective normal stress. An increase in p reduces ${\sigma }_{\mathrm{eff}}$, which may trigger fault failure under the Coulomb failure criterion:

$${\tau }_c\propto \mu {\sigma }_{\mathrm{eff}},$$

(15)

where ${\tau }_c$ is Critical shear stress, $\mu$ is Friction coefficient.

For SLR, the slow loading rate ($1.75\mathrm{mm}/\mathrm{year}$) induces small $\Delta p$ over large $\Delta t$, resembling low-pressure, long-timescale processes (e.g., CO₂ injection in CCS). The product $\Delta p\Delta t\ge \overline{R}$ indicates that cumulative pore pressure changes can still meet or exceed $\overline{R}$, potentially triggering seismicity in critically stressed fault systems.

4.2. Seismicity Triggering

The pore pressure p from Equation (13) reduces the effective normal stress on faults, following Terzaghi’s principle:

$${\sigma }_{\mathrm{eff}}=\sigma -p,$$

(16)

where ${\sigma }_{\mathrm{eff}}$ is the effective stress. A decrease in ${\sigma }_{\mathrm{eff}}$ brings faults closer to failure under the Coulomb criterion:

$${\tau }_c=\mu {\sigma }_{\mathrm{eff}}+C,$$

(17)

where ${\tau }_c$ is the critical shear stress, $\mu$ is the friction coefficient, and C is cohesion.

5. Online Forecasting Models

Broccardo et al. [46] developed a Bayesian model based on a nonhomogeneous Poisson process (NHPP) to forecast induced seismicity. A successful decision-making criterion emerging from such model, would benefit the communities. Such forecasting models can also be used in other areas of anthropogenic activities known to cause seismicity.

The probability of observing $n_h$ seismic events in the time window $[t,t+h]$, given the observed data $D\left(t\right)$ up to time (t), $P(N_h\left(t\right)=n_h\mid D\left(t\right))$, or simply $\Xi$, is:

$$\begin{array}{c}\hfill \Xi =\\ \hfill & {\int }_{\theta }[{\displaystyle \frac{{\left({\int }_t^{t+h}\lambda (t^{\prime }\mid \theta )d{t}^{\prime }\right)}^{n_h}}{n_h!}}\hfill \\ \hfill & exp\left(-{\int }_t^{t+h}\lambda (t^{\prime }\mid \theta )d{t}^{\prime }\right)]\hfill \\ \hfill & f_{\theta }^{\prime \prime }(\theta \mid D\left(t\right))d\theta \hfill \end{array}$$

(18)

$\Xi$ represents the predictive probability of observing $n_h$ seismic events in a future time window $[t,t+h]$, given observed data $D\left(t\right)$ . Here, $N_h\left(t\right)$ is the number of events in the time window of interest, $\lambda (t^{\prime }\mid \theta )$ is the time dependent seismicity rate which depends on model parameters $\theta$ and ${\int }_t^{t+h}\lambda (t^{\prime }\mid \theta )d{t}^{\prime }$ is the expectation value of the number of events in that interval. The first term is the Poisson probability of observing $n_h$ events, given the rate.

The posterior distribution $f_{\theta }^{\prime \prime }(\theta \mid D\left(t\right))$ updates the knowledge about $\theta$, using $D\left(t\right)$, and the integral over $\theta$ takes into account the uncertainties by averaging.

6. Discussions & Policy Recommendations

Bayesian Inference certainly helps us better understand anthropogenic risks. Modern analysis tools such as the MCMC are therefore certainly useful in shedding light on contemporary problems in Earth Science and particularly inverse problems in geophysics.

Bayesian inference cannot compensate for missing data or poorly designed experiments. No data analysis tool can generate information absent from the data. That said, Bayesian inference could be used to better arrange for experimental setups to hunt for information that otherwise could not be captured [47]. This approach can even further improve geophysics experiments which could contribute to the understanding of Earth and planetary processes and anthropogenic risk factors in seismicity. Given the complexity of the issue of induced seismicity, effective data assimilation and analysis as well as up to date analysis tools and technologies are required to minimize the impact of activities which would cause anthropogenic seismicity. Several guidelines, such as the ETH Zürich “Good-Practice Guide for Managing Induced Seismicity in Deep Geothermal Energy Projects in Switzerland” [48], exist. These should be updated to incorporate new physics-informed methods discussed herein.