Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Seismic Activation Modeling with Statistical Physics

Submitted:

01 May 2025

Posted:

06 May 2025

Read the latest preprint version here

Abstract
Using a finite element modeling approach, it is explained how real time evolution of a seismic activation region's elastic parameters, described with a frequency dependent stiffness matrix, can be modeled in terms of statistical physics. Postulating the relevant statistical physics model is a 2D sine-Gordon model, previously reported deviation of seismic activation earthquake occurence statistics from Gutenberg-Richter statistics in time intervals preceding a major earthquake is derived.
Keywords: 
seismic activation
;  
fault dynamics
;  
statistical physics
;  
signal processing
Subject: 
Physical Sciences  -   Applied Physics

Introduction

An increase in the number of intermediate sized earthquakes (M > 3.5) in a seismic region preceding the occurrence of an earthquake with magnitude M > 6, referred to as seismic activation, has been documented by various researchers [Bowman et al.(1998)]. For example, seismic activation was observed in a geographic region spanning 21◦N−26°N × 119°E − 123°E for a period of time between 1991 and 1999 preceding the magnitude 7.6 Chi-Chi earthquake [Chen(2003)]. 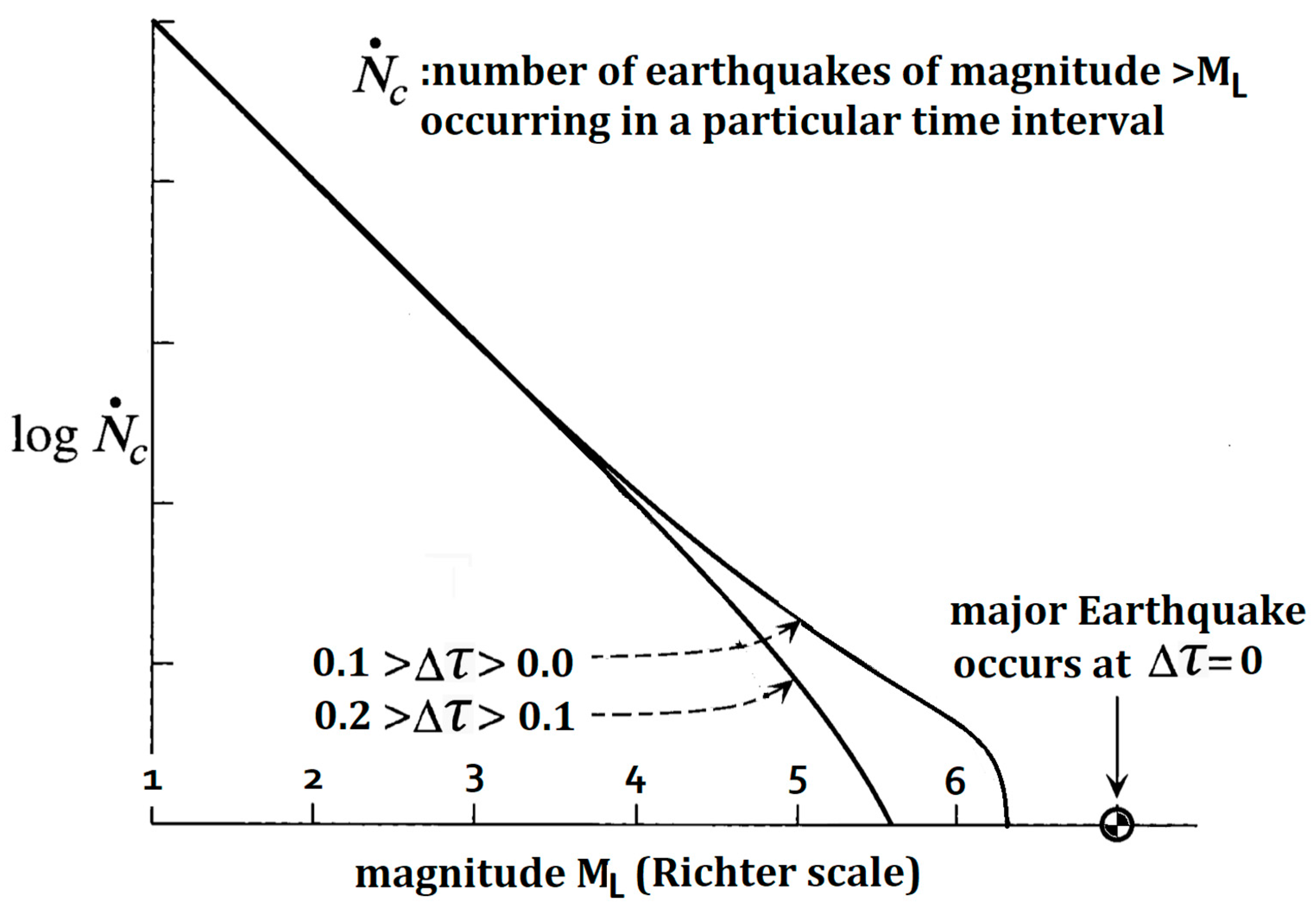Figure 1 shows a schematic plot of the cumulative distribution of earthquakes of different magnitudes in a seismic activation region in two different time intervals of equal duration preceding occurrence of a major (7 < M < 8) earthquake at time τ = τ 0 . In this figure, τ is a real time parameter, and τ 0 is the characteristic time of major earthquake recurrence assuming an earthquake of similar magnitude occurred in the same region at τ = 0 [Rundle et al.(2001), Vallianatos and Sammnds(2004)]. Importantly, the cumulative distribution of earthquakes in a time interval of fixed width increasingly deviates away from a Gutenberg Richter linear log-magnitude plot as the end of the time interval approaches τ 0 .
As a means of predicting the time τ = τ 0 at which a major earthquake preceded by seismic activation occurs, it has been hypothesized that the average seismic moment 〈 M 〉 τ of earthquakes occuring in intervals of time ( τ , τ + Δ τ ) preceding a major earthquake obeys an inverse power of remaining time to failure law:
〈 M 〉 τ ∝   1 ( τ 0 − τ ) γ 1 ,
and that the cumulative Benioff strain C ( τ ) , defined as:
C ( τ ) = ∑ i = 1 n ( τ ) M 0 , i 1 / 2 ,
where M 0 , i is the seismic moment of the i t h earthquake in the region starting from a time τ = 0 preceding the major earthquake, and n ( τ ) is the number of earthquakes occurring in the region up to time τ , satisfies [Tzanis et al.(2000)]:
C ( τ ) = a − b ( τ 0 − τ ) γ 2 ,   γ 2 = 1 − γ 1 / 2 .
The exponent selection of 1/2 in equation (2) is not necessary to derive formula (3) with a different arithmetic relation between γ 1 and γ 2 , but appears to have been selected by previous researchers based on resulting predictions of major earthquake occurrence time when formula (3) is fit to real seismic data, which suggest a typical value of γ 2 is 0.3 [Vallianatos and Chatzopoulos(2018),Bowman et al.(1998)].
Notably, the validity of the accelerating seismic moment release hypothesis (1) has been questioned by some researchers who claim normal foreshock and aftershock can account for seismic measurements without moment acceleration [Zhoul et al.(2006), Hardebeck et al.(2008)].
A model of seismic activation based on fault damage mechanics (FDM) has been used to derive equation (3) with a value γ 2 = 1 / 3 [Ben-Zion and Lyakhovsky(2002)]. In this derivation, the occurrence of seismic activation earthquakes progressively decreases the average shear modulus of fault material in the seismic region where subsequent seismic activation earthquakes occur, and the result γ 2 = 1 / 3 is obtained using a Boltzman kinetic type description of the rupture nucleation process in which ruptured faults of different lengths at different positional locations grow and join together [Tzanis and Vallianatos(2003)].
In addition to the FDM model of seismic activation, an empirical statistical physics model of seismic activation known as the Critical Point (CP) model has been put forth to derive equation (3) with a value γ 2 = 1 / 4 [Rundle et al.(2001)]. In this derivation, the inverse power of remaining time to failure law:
〈 M 〉 τ ∝   1 ( τ 0 − τ ) 3 / 2 ,
is asserted based on identifying the mean rupture length L ( τ ) of earthquakes occuring at time τ with the correlation length of a statistical physical system described by Ginzburg-Landau mean field theory with a τ -dependent temperature parameter, whereby:
L ( τ ) ∝   1 ( τ 0 − τ ) 1 / 2 ,
and relation (4) follows from the scaling relation 〈 M 〉 τ ∝ L ( τ ) 3 which holds when the fault material shear modulus is constant [Rundle et al.(2003)]. Importantly, previous work on the CP model has not explained why it is physically reasonable to describe seismic activation earthquake occurrence statistics with thermal equilibrium statistical physics formalism [Newman et al.(1995)]. Therefore, the first objective of this article is to clarify how the FDM and CP models of seismic activation can be in correspondence with each other. The second objective of the article is to use this correspondence to advance rigorous testing of seismic activation model predictions against seismic measurements, and in the event of positive experimental verification, advance earthquake prediction technology.
Central to the presented correspondence between FDM and CP seismic activation models is the idea that the elastic model of the activation region, expressed in terms of spatially and frequency dependent material density and Lame parameters ( ρ ( x , y , z , ω ) , λ ( x , y , z , ω ) , μ ( x , y , z , ω ) ) (isotropic), depends on the real time parameter τ , and the classical field equations describing this τ -dependence are identifiable with statistical physics renormalization group flow equations [Friedan(1980)]. This identification has computational utility to seismic activation modeling because dimensional reduction of statistical physics models at critical points systematizes dimensional reduction of activation region stiffness matrices in windows of time preceding a major earthquake.
The outline of the article is as follows. Section 2 explains how finite element stiffness and mass matrices of an activation region can be defined, and how real time evolution of these can be modeled with statistical physics. Section 3 explains how the 2D sine-Gordon model quantifies seismic activation earthquake occurrence statistics, and accounts for deviation of these statistics from Gutenberg-Richter statistics before a major earthquake. Section 4 concludes by commenting on how statistical physics modeling can be used to characterize rupture nucleation in the seismic activation region from seismic measurements.

Methods

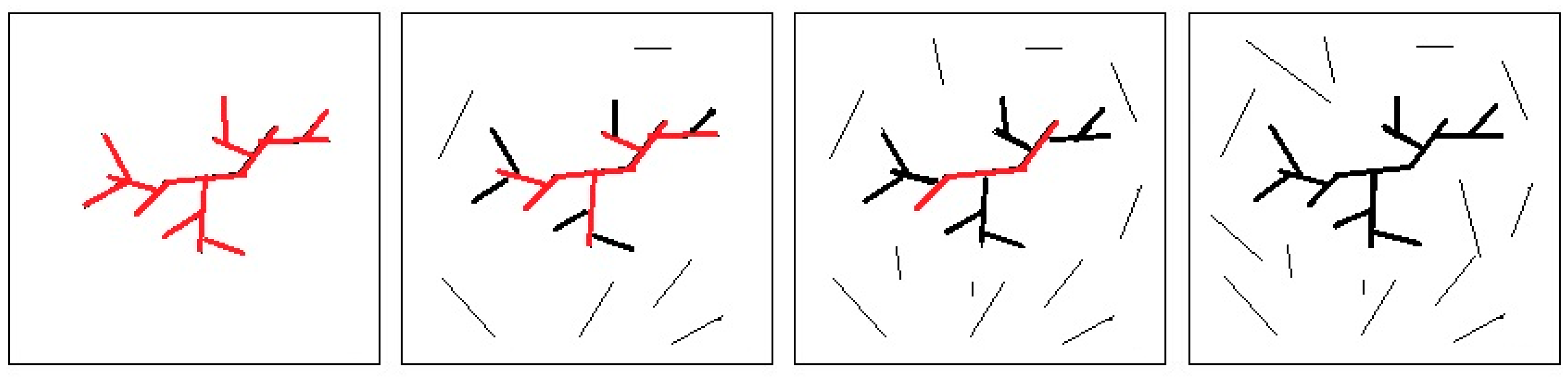
Seismic Activation Fault Dynamics. Figure 2 shows a 2D schematic of earthquake occurrence in a seismic activation region [Lei and Sornette(2022)]. In this figure, the activation region is shown at 4 different times up to and including the moment after a major earthquake has occurred. At each time, black lines indicate fault ruptures associated with earthquakes that have occurred, and red lines indicate faults where stress is accumulating prior to earthquake occurrence. Qualitatively, the pictures suggests the occurrence of successively larger earthquakes, associated with successively longer rupture lengths, leads to increased accumulation of stress along the major earthquake fault as seismic activation proceeds.
Quantitatively, this picture of seismic activation leading to rupture along a major earthquake fault is supported by modeling of earthquake fault dynamics in 1+1 spacetime dimensions, whereby the differential equation:
A ∂ τ 2 U ( τ , z ) − B ∂ z 2 ( τ , z ) + C ∂ τ ( τ , z ) = − sin ( U ( τ , z ) / D ) ,
has been used to model both creep along a major earthquake fault and rupture propagation, depending on whether or not frictional forces dominate the fault dynamics and shear stress evolution along the fault is more appropriately described with a reaction-diffusion equation or a solitary wave equation [Bykov(2001)]. In this equation, τ is real time, z coordinates a direction of creep or slip along an earthquake fault, U ( τ , z ) is the local displacement of elastic material across the earthquake fault, A ∂ τ 2 U ( τ , z ) is the local inertial force acting on the fault material, B ∂ z 2 ( τ , z ) is the local elastic restoring force acting on the fault material, and C ∂ τ ( τ , z ) and sin ( U ( τ , z ) / D ) are local frictional forces acting on the fault material attributed to contact of the material with tectonic plates on either side of the fault. For C = 0, an (anti-kink) soliton solution to equation can be interpreted as propagation of earthquake fault rupture [Wu and Chen(1998)].
Seismic Activation Region Finite Element Model. To model real time evolution of the activation region elastic model in which a nonuniform spatial dependence of elastic parameters and random configuration of fractures is anticipated, the finite element method can be used. To this end, suppose a major earthquake hypocenter resides in a 3D elastic half space in such a way that the elastic parameters of the half space are constant outside a hemisphere of diamater L 0 centered at the earthquake epicenter. Then, if each fracture within the region is defined as a thin low elastic impedance layer, a Dirichlet-to-Neumann map is defined at the hemisphere boundary, and a finite element mesh accounting for fracture and boundary geometry is defined, the elastic model of the region at time τ can be written as a frequency dependent stiffness matrix K ( ω , τ ) with dimension equal to the number of finite element nodes [Schoenberg(1980),Bindel(2006)]. Similarly, using the density of the activation region, a time dependent lumped mass matrix M ( τ ) can be written with dimension equal to the number of finite element nodes. Together, the stiffness and mass matrices define a nonlinear eigenvalue problem:
( K ( ω , τ ) − ω 2 M ( τ ) ) u ⇀ = 0 ,
at each time τ , whose non-zero solution vectors u ⇀ specify elastic resonant frequencies ω of the activation region that quantify the region’s elastic model and fracture pattern.
Resonant Frequency Statistics. For a deterministic time evolution of the activation region’s elastic model, the region’s set of elastic resonant frequencies also evolves deterministically. For example, in 1 spatial dimension, the 1D elastic wave equation:
∂ t 2 Ψ ( t , z ) − B ∂ z 2 Ψ ( t , z ) + V ( z ) Ψ ( t , z ) = 0 ,
in which the function V ( z ) defines non-zero variation of the elastic wave velocity on a compact interval, determines the eigenvalue problem:
− B ∂ z 2 Ψ ^ ( z ) + V ( z ) Ψ ^ ( z ) = ω 2 Ψ ^ ( z ) ,
where:
Ψ ( t , z ) = e i ω t Ψ ^ ( z ) ,
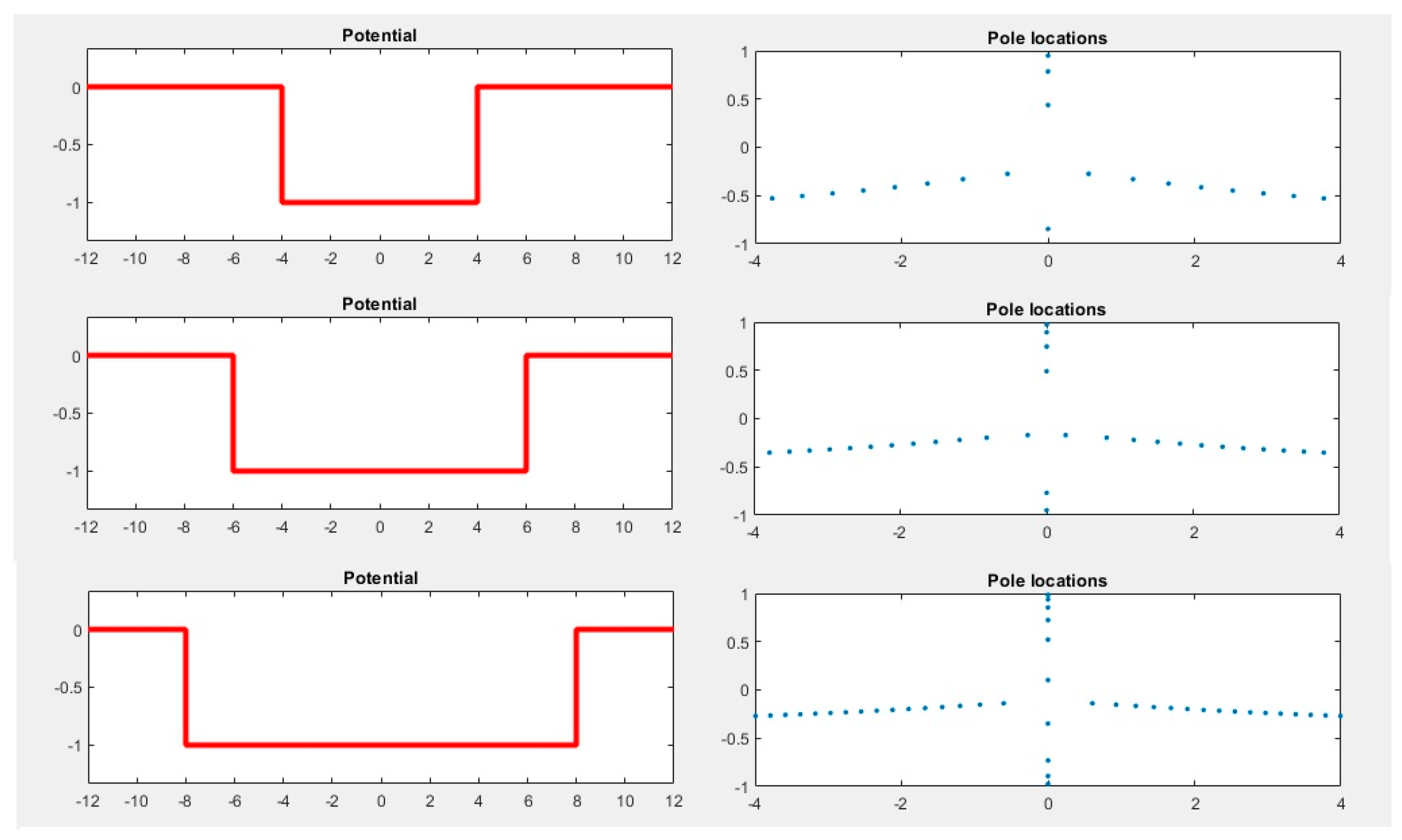
with infinitely many resonant state eigenfunctions with oscillatory decay and finitely many bound state eigenfunctionsΨ¯ j(z) with exponential growth/decay. Figure 3 shows a plot of resonant and bound state frequency locations for three different square well potentials − V ( z ) / B of increasing width and fixed height, an example of deterministic correspondence between elastic model and resonant frequency set.
A special case of deterministic correspondence between elastic model and resonant frequency set is an activation region elastic model varying with τ in such a way that the region’s resonant frequency set is τ invariant. This condition, known as isospectrality, is known to hold for elastic models in 1+1 spacetime dimensions whose real time evolution is governed by a soliton equation such as the KdV equation [Kasman(2023)]. Therefore, for the purpose of modeling real time evolution of an activation region’s elastic model preceding a major earthquake, it is now hypothesized that isospectrality of non-linear eigenvalue problem (7) occurs at the time τ = τ 0 of major earthquake occurrence, in that a solitary wave equation describing propagation of a rupture along the major earthquake fault governs evolution of the activation region’s elastic model. By interpreting the solitary wave equation as a classical field equation, this hypothesis permits rupture front propagation at time τ = τ 0 to be described by renormalization group flow equations of a statistical physics model at a critical point, in keeping with original formulations of the CP model [Friedan(1980), Saleur et al.(1996)].
For τ < τ 0 , a deterministic view of the activation region’s elastic model and corresponding resonant frequency set { ω j } imply the resonant frequency set is discontinuously updated with occurrence of each seismic activation earthquake changing the fault rupture pattern. For this reason, rather than describing the resonant frequency set deterministically, it is now put forth that the matrix K ( ω ; τ ) M ( τ ) − 1 belongs to a τ -dependent ensemble of random matrices, whereby its eigenvalues, the elastic resonant frequencies of the activation region, are distributed as the eigenvalues of a random matrix. From this point of view, it is postulated that 2D Coulomb gas statistics describe the distribution of resonant frequencies at each time τ < τ 0 , and the sine-Gordon mean field theory of the 2D Coulomb gas satisfies renormalization group flow equations characterizing real time evolution of the distribution of matrices K ( ω ; τ ) M ( τ ) − 1 , with deterministic evolution of the activation region elastic model at time τ = τ 0 .

Results

To relate the discussion in the previous chapter to seismic activation earthquake occurrence statistics, it is now hypothesized that before its occurrence, each seismic activation earthquake can be identified with an elastic scattering resonant frequency ω of the activation region for which Re   ω = 0 and Im   ω ∝ ω c , where ω c is the corner frequency of the earthquake [Carlson and Langer(1989)]. Evidence for this hypothesis is presented in this chapter by showing how it accounts for the deviation of seismic activation earthquake occurrence statistics from Gutenberg-Richter statistics.
Suppose that in the time interval ( τ ,   τ + Δ   τ ) , an elastic resonant frequency ω with R e   ω = 0 identifies a seismic activation earthquake occurring with probability proportional to | ω | d τ . Then, if ρ ( | ω | ) is the density of elastic resonant frequencies with magnitude in the interval ( | ω | , | ω | + d | ω | ) , the number of earthquakes with corner frequency less than or equal to | ω | occurring during the time interval is:
N ˙ c d τ = ∫ ω c ( τ ) | ω | r ρ ( r ) d τ d r   .
To specify the mathematical form of the integral in equation (14), recall that the Gutenberg-Richter law implies the total number of earthquakes of Richter magnitude in the interval   ( M R , M R + d M R ) occurring in the seismic activation region in the time interval ( τ ,   τ + Δ   τ ) is proportional to:
10 − bM R d M R d τ ,
which according to the relation between Richter magnitude and seismic moment:
M R = ( log 10 M s − 9 ) / 1.5 ,
satisfies:
10 − bM R d M R d τ ∝ M s − 1 − b / 1.5 d M s d τ ∝ | ω | 2 b − 1 d | ω | d τ .
Therefore, assuming the Gutenberg-Richter law is valid, it follows that:
ρ ( | ω | )   ∝ | ω | 2 b − 2 .
To account for modification to the Gutenberg-Richter law in time intervals preceding a major earthquake using statistical physics, it is now conjectured that for elastic resonant frequencies:
| ω | ≈ ω c ( τ 0 ) ≡ ω 0 ,
with ω 0 equal to the lowest corner frequency of a seismic activation earthquake preceding the major earthquake at time τ =   τ 0 , the quantity ρ ( | ω | ) describes the density of a 2D Coulomb gas in the vicinity of a test charge located at | ω | =   ω 0 [Goldenfeld]:
ρ ( | ω | )   ∝   ( | ω | − ω 0 ) β 0 ,   β 0 < 0 ,
With this conjecture, equation (11), modified to account for occurrence of an earthquake at corner frequency ω 0 , implies:
N ˙ c = ∫ ω 0 | ω | r ( r − ω 0 ) β 0 d r ,
which in turn implies the quantity:
log 10 N ˙ c   ≈ log 10 ( 1 + c ( | ω | − ω 0 ) 1 + β 0 ) ,
when plotted against Richter magnitude M R   ∝ − 2 log 10 | ω | for β 0 > − 1 , can have either of the cumulative distribution curve shapes shown in Figure 1 for different time intervals, depending on the value of β 0 .
Having conjectured 2D Coulomb gas statistical physics are relevant to accounting for deviation of earthquake occurrence statistics from Gutenberg-Richter statistics during seismic activation, it is now further conjectured, in accordance with previous statistical physics models of seismic activation, that β 0 = β ( τ 0 ) , where β ( τ ) is a parameter in a τ-dependent 2D sine-Gordon statistical physics model whose parameters at different values of τ are related by renormalization group flow [Carpentier(1999), Balog et al. (2018)]. 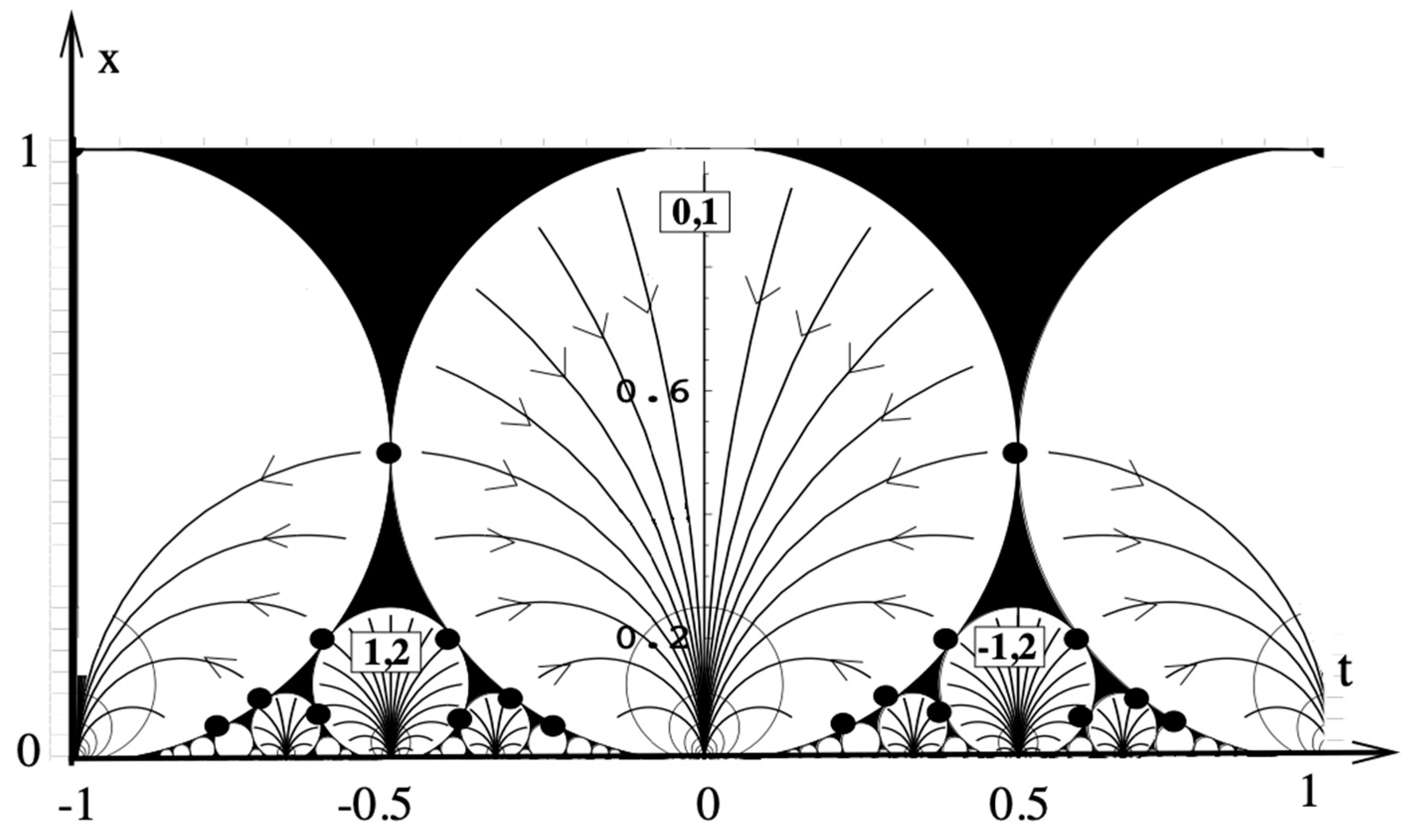With this additional conjecture, an increase in the value of β ( τ ) as τ   →   τ 0 accounts for increasing steepness of the cumulative distribution curve shown in Figure 1. A phase diagram of a 2D sine-Gordon model with a renormalization group flow indicated by arrows is shown in Figure 4. In this diagram, different vaues of the flow coordinate ‘t’ equate to β ( τ ) at different values of τ in such a way that β ( τ 0 ) is the horizontal coordinate of a point of tangency between two of the Ford circles. It is noted that this phase diagram corresponds to the k = 1 description of a more general 2D sine Gordon statistical physics model defined by a field theory with 4 k fields [Zabrodin(2010),Dubrovin and Yang(2020),Varchenko(1990)].

Conclusions

Previous research has identified predicting the time of occurrence of major earthquakes as a possible application of statistical physics models of seismic activation, but this application has not yet been realized [Bowman et al.(1998)]. In more recent times, the earthquake early warning algorithm Virtual Seismologist has been developed which can in principle use previous earthquake occurrence statistics as input to improve warning accuracy, and the artificial intelligence algorithm QuakeGPT has been developed for predicting the occurrence of major earthquakes using seismic event records created with stochastic simulator training data [Bose et al.(2023),Rundle et al.(2024),Cua and Heaton(2007)]. Therefore, a practical applied science goal for the statistical physics model presented in this article appears to be improving statistical characterization of earthquake precursors for use in earthquake warning and/or forecasting technologies, acknowledging that preliminary tests of the model’s validity against real seismic data must be passed before achieving this application objective can be considered a realistic possibility.
From a geophysical testing point of view, if it is true that renormalization of a 2D sine-Gordon model describes the real time evolution of activation region elastic models, and as a result, a nonlinear dynamical system of finite phase space dimension characterizes elastic model evolution before a major earthquake, a geophysical signal processing technique known as singular spectrum analysis should apply to determine this phase space dimension [Broomhead and King(1986)]. More specifically, it is suggested that measurements of relative changes in seismic surface wave and/or body wave velocity be performed be tween pairs of seismic stations in a seismic region over a duration of time during which seismic activation is known to have occurred, and used as input to a time domain multichannel singular spectrum analysis algorithm [Merrill et al.(2023)]. The number of channels of this algorithm would equate to the number of station pairs, and the number of singular values output by the algorithm in different time windows preceding occurrence of a major earthquake should characterize the elastic model during rupture nucleation if the statistical physics modeling approach is correct in principle. With reference to previous geophysical application of singular spectrum analysis, performed in the frequency domain, the signal processing algorithm suggested here is different in that it should be carried out in the time domain τ rather than the frequency domain [Sacchi(2009)].
In conclusion, work towards improving current earthquake early warning systems can proceed in two directions. Firstly, as an initial check on whether or not the statistical physics modelling approach presented here could be of practical utility, work can be done to determine whether or not observed changes of the Earth’s elastic velocity model preceding major earthquakes can be processed to extract an integer identifiable as the phase space dimension of a nonlinear dynamical system. Secondly, workcan be done to elaborate upon the statistical physics mathematical model of seismic activation presented in this article to determine other tests of its scientific validity and potential for practical application.

Acknowledgments and Funding

Thanks to my family for their support throughout completion of this research. Thanks to Dr. Girish Nivarti, Dr. Evans Boney, and Professor Richard Froese for their willingness to entertain discussions about the content of the article. The author declares they have no conflicts of interest.

References

  1. Akemann G, Mielke A, P äβler (2021) Spacing distribution in the 2D Coulomb gas: Surmise and symmetry classes of non-Hermitian random matrices at non-integer β.
  2. Aki K, 1967. Scaling law of seismic spectrum, J. geophys. Res., 72, 1217–1231. [CrossRef]
  3. Balog I, Carpentier D, Fedorenko AA. Disorder-driven quantum transition in relativistic semimetals: functional renormalization via the porous medium equation. Physical review letters. 2018 121(16):166402. [CrossRef]
  4. Ben-Zion Y, Lyakhovsky V (2002) Accelerated seismic release and related aspects of seismicity patterns on earthquake faults. Earthquake processes: Physical modelling, numerical simulation and data analysis Part II :2385–2412.
  5. Bindel DS. Structured and parameter-dependent eigensolvers for simulation-based design of resonant MEMS (Doctoral dissertation, University of California, Berkeley). 2006.
  6. B öse M, Andrews J, Hartog R, Felizardo C. Performance and next-generation development of the finite-fault rupture detector (FinDer) within the United States West Coast ShakeAlert warning system. Bulletin of the Seismological Society of America. 2023 Apr 1;113(2):648–63. [CrossRef]
  7. Bowman D, Ouillon G, Sammis C, Sornette A, Sornette D (1998) An observational test of the critical earthquake concept. Journal of Geophysical Research: Solid Earth 103(B10):24359–24372.
  8. Broomhead D S, King G P (1986) Extracting qualitative dynamics from experimental data. Physica D: Nonlinear Phenomena 20(2-3):217–236.
  9. Bykov V G (2001) Solitary waves on a crustal fault. Volcanology and Seismology 22(6):651–661.
  10. Carlson JM, Langer JS. Properties of earthquakes generated by fault dynamics. Physical Review Letters. 62(22):2632. [CrossRef]
  11. Carpentier D (1999) Renormalization of modular invariant Coulomb gas and sine Gordon theories, and the quantum Hall flow diagram. Journal of Physics A: Mathematical and General 32(21):3865.
  12. Chen CC. Accelerating seismicity of moderate-size earthquakes before the 1999 Chi-Chi. [CrossRef]
  13. Taiwan, earthquake: Testing time-prediction of the self-organizing spinodal model of earthquakes. Geophysical Journal International. 2003 155(1):F1-5.
  14. Cua G., Heaton T. (2007) The Virtual Seismologist (VS) method: A Bayesian approach to earthquake early warning. In Earthquake Early Warning Systems, ed. Gasparini P, Manfredi G, and Zschau J, 97–132. Berlin and Heidelberg: Springer.
  15. Dubrovin B, Yang D (2020) Matrix resolvent and the discrete KdV hierarchy. Communications in Mathematical Physics 377:1823–1852.
  16. Dyatlov S, Zworski M (2019) Mathematical theory of scattering resonances, volume 200. American Mathematical Soc.
  17. Dyson FJ. Fredholm determinants and inverse scattering problems. Communications in Mathematical Physics 47(2):171-83. [CrossRef]
  18. Dyson FJ, Mehta ML (1963) Statistical theory of the energy levels of complex systems. iv. Journal of Mathematical Physics 4(5):701–712.
  19. Friedan DH (1980) Nonlinear models in 2+ε dimensions. Phys. Rev. Lett. 45, 1057.
  20. Goldenfeld N. Lectures on phase transitions and the renormalization group. CRC Press; 2018.
  21. Hardebeck JL, Felzer KR, Michael AJ (2008) Improved tests reveal that the accelerating moment release hypothesis is statistically insignificant, J. Geophys. Res., 113.
  22. Hofstetter E, Schreiber M (1993) Statistical properties of the eigenvalue spectrum of the three-dimensional Anderson Hamiltonian. Physical Review B 48(23):16979.
  23. Ito R, Kaneko Y (2023). Physical Mechanism for a Temporal Decrease of the Gutenberg-Richter b-Value Prior to a Large Earthquake. Journal of Geophysical Research: Solid Earth 128(12):e2023JB02741312.
  24. Kasman A (2023). Glimpses of soliton theory: the algebra and geometry of nonlinear PDEs. American Mathematical Society.
  25. Khan BA, Chatterjee S, Sekh GA, Talukdar B (2020) Integrable systems: From the inverse spectral transform to zero curvature condition. arXiv preprint arXiv:2012.03456.
  26. Lei Q, Sornette D (2022) Anderson localization and reentrant delocalization of tensorial elastic waves in two-dimensional fractured media. Europhys. Letters 136(3): 1–7.
  27. Markos P (2006) Numerical analysis of the Anderson localization. arXiv preprint cond mat/0609580.
  28. Merrill RJ, Bostock MG, Peacock SM, Chapman DS (2023) Optimal multichannel stretch factors for estimating changes in seismic velocity: Application to the 2012 Mw 7.8 Haida Gwaii earthquake. Bulletin of the Seismological Society of America 113(3):1077–1090.
  29. Newman WI, Turcotte DL, Gabrielov AM (1995) Log-periodic behavior of a hierarchical failure model with applications to precursory seismic activation. Physical Review E 52(5):4827. [CrossRef]
  30. Rundle JB, Klein W, Turcotte DL, Malamud BD (2001) Precursory seismic activation and critical-point phenomena. Microscopic and Macroscopic Simulation: Towards Predictive Modelling of the Earthquake Process 2165–2182.
  31. Rundle JB, Turcotte DL, Shcherbakov R, Klein W, Sammis C (2003) Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Reviews of Geophysics 41(4). [CrossRef]
  32. Rundle JB, Fox G, Donnellan A, Ludwig IG (2024) Nowcasting Earthquakes with QuakeGPT: Methods and First Results. arXiv e-prints. 2024 Jun:arXiv-2406.
  33. Sacchi M (2009) FX singular spectrum analysis. Cspg Cseg Cwls Convention 392–395.
  34. Saleur H, Sammis C, Sornette D (1996) Renormalization group theory of earthquakes. Nonlinear Processes in Geophysics 3(2):102–109.
  35. Schoenberg M. Elastic wave behavior across linear slip interfaces. The Journal of the Acoustical Society of America 68(5):1516-21.
  36. Soerensen M, Schneider T (1991) Level-spacing statistics for the Anderson model in one and two dimensions. Physik B Condensed Matter 82(1):115–119.
  37. Sornette D (1989) Acoustic waves in random media: II Coherent effects and strong disorder regime, Acustica 67(4):251–265.
  38. Tzanis A, Vallianatos F (2003) Distributed power-law seismicity changes and crustal deformation in the SW Hellenic ARC. Natural Hazards and Earth System Sciences 3(3/4):179–195.
  39. Tzanis A, Vallianatos F, Makropoulos K (2000) Seismic and electrical precursors to the 17-1-1983, M7 Kefallinia earthquake, Greece: Signatures of a SOC system. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy 25(3):281–7.
  40. Vallianatos F, Chatzopoulos G (2018) A complexity view into the physics of the accelerating seismic release hypothesis: Theoretical principles. Entropy 20(10):754. [CrossRef]
  41. Vallianatos F, Sammonds P (2004) Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 590:52–8. [CrossRef]
  42. Varchenko A (1990) Multidimensional hypergeometric functions in conformal field theory, algebraic K-theory, algebraic geometry. In Proceedings of the International Congress of Mathematicians 1:281–300.
  43. Wu RS, Aki K (1985) Scattering characteristics of elastic waves by an elastic heterogeneity. Geophysics 50(4):582–95.
  44. Wu ZL, Chen YT. Solitary wave in a Burridge-Knopoff model with slip-dependent friction as a clue to understanding the mechanism of the self-healing slip pulse in an earthquake rupture process. Nonlinear Processes in Geophysics. 1998 Sep 30;5(3):121-5. [CrossRef]
  45. Zabolotskaya EA, Ilinskii YA, Hay TA, Hamilton MF. Green’s functions for a volume source in an elastic half-space. The Journal of the Acoustical Society of America 131(3):1831– 42.
  46. Zabrodin A (2010) Canonical and grand canonical partition functions of Dyson gases as tau functions of integrable hierarchies and their fermionic realization. Complex Analysis and Operator Theory 4:497–514. [CrossRef]
  47. Zhou S, Johnston S, Robinson R, Vere-Jones D (2006),Tests of the precursory accelerating moment release model using a synthetic seismicity model for Wellington, New Zealand, J. Geophys. Res., 111. [CrossRef]
Preprints 158100 g001
Figure 1. Plot of the cumulative distribution of earthquakes of different magnitudes in a seismic zone in two different time intervals of equal width preceding occurrence of a major earthquake at Δ τ = τ 0 − τ = 0 [Rundle et al.(2001), Vallianatos and Sammnds(2004)].
Figure 1. Plot of the cumulative distribution of earthquakes of different magnitudes in a seismic zone in two different time intervals of equal width preceding occurrence of a major earthquake at Δ τ = τ 0 − τ = 0 [Rundle et al.(2001), Vallianatos and Sammnds(2004)].
Preprints 158100 g001
Preprints 158100 g002
Figure 2. Schematic illustration of seismic activation in a 2D geometry at four different times τ in which each black line represents an earthquake fault rupture that has already occurred, and the red lines represent earthquake faults along which shear stress is increasing prior to rupure [Lei and Sornette(2022)].
Figure 2. Schematic illustration of seismic activation in a 2D geometry at four different times τ in which each black line represents an earthquake fault rupture that has already occurred, and the red lines represent earthquake faults along which shear stress is increasing prior to rupure [Lei and Sornette(2022)].
Preprints 158100 g002
Preprints 158100 g003
Figure 3. Plot of resonant frequency and bound state frequency locations for 3 square well potentials of increasing width.
Figure 3. Plot of resonant frequency and bound state frequency locations for 3 square well potentials of increasing width.
Preprints 158100 g003
Preprints 158100 g004
Figure 4. Phase diagram of 2D sine-Gordon statistical physics model with renormalization group flow indicated by arrows and KT critical points identified by circle tangencies [Carpentier(1999)].
Figure 4. Phase diagram of 2D sine-Gordon statistical physics model with renormalization group flow indicated by arrows and KT critical points identified by circle tangencies [Carpentier(1999)].
Preprints 158100 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated