Connection between Variations of the Probability Distribution of the Recurrence Time and Phases of the Seismic Activity

1. Introduction

The time between two successive earthquakes referred to as recurrence or waiting or interevent time is one of the most studied quantities describing the seismic activity; it plays an important role in seismic hazard assessment being the main component of some stochastic processes - such as renewal processes, Markov processes - which model the temporal evolution of seismic phenomenon. Several probability distributions have been proposed in the literature to model the recurrence time $\tau$, including the gamma, Weibull, lognormal, and exponential distributions; but the most remarkable result was that the shape of this distribution appeared to be universal when the times were suitably scaled by some critical indices such as the Gutenberg-Richter b value, the exponent $\alpha$ of the Omori law and the fractal dimension $d_f$ of the set of earthquake epicenters [1]. In other words the distribution $F\left(\tau \right)$ would be independent of the spatial scale and of the magnitude threshold of the observations, which expresses a hierarchical organization in time, space, and magnitude. Further studies found that scaling by the average rate $\lambda$ of seismic activity - number of earthquakes per unit time - was sufficient to get approximately the same distribution in many different seismic regions [2]. A similar behavior was also obtained by Corral by fitting the density function given by:

$$f\left(\tau \right)=\frac{C\delta }{a\Gamma (\gamma /\delta )}{\left(\frac{\tau }{a}\right)}^{\gamma -1}{e}^{-{(\tau /a)}^{\delta }}\gamma ,\delta ,a>0$$

(1)

to some regional data sets [3], where C is the normalizing constant, a is a scale parameter, and $\gamma$ and $\delta$ control the shape for small and large $\tau$ respectively. This scaling function shows a power-law behavior for short times, and an exponential decrease for long times.

By simulations of the ETAS model with varying rate $\mu$ of independent events, which can be considered as a proxy for regional size, Touati et al. [4] have shown that the interevent time distribution is generally bimodal, and is best described as a mixture of two distribution: a gamma distribution for short waiting times between correlated events which belong to the same aftershock sequence, and an exponential distribution for longer waiting times between uncorrelated events. Completely general forms for the interevent time distribution can be obtained by resorting to a Bayesian nonparametric estimation method and considering the unknown distribution as a random measure [5].

Properties such as fractal structures and long-range correlations present in the earthquake activity have led to adopt theoretical tools of non-extensive statistical physics in the analysis of the statistical properties of some quantities describing the seismic activity in the space-time-magnitude domain. This approach is based on a generalization of the classic Boltzmann-Gibbs entropy proposed by Tsallis in 1988 [6]; by maximizing the non-extensive Tsallis entropy a probability distribution, denoted as q-exponential distribution, was obtained which has been later successfully applied to investigate the distribution of various seismic quantities such as magnitude ([7] and references therein), fault length [8], spatial distribution of epicenters [9], and interevent time [10]. To improve the fit of the gamma distribution by exploiting the results obtained through the q-exponential distribution, Michas et al. [11] used the q-generalized gamma distribution borrowed from Queirós [12], which behaves as a power-law function both at short and large interevent times so as to provide a best fit when the seismicity is correlated at all timescales.

Generally the aforementioned studies aim at obtaining the best probability distribution for sets of interevent times which cover a large period where the occurrences may involve a complex summation of triggered and/or independent events in different time scales. On the contrary, in this work we wonder whether the probability distribution changes over time and whether these variations can be associated with different phases of the seismic process. To do that, we consider data from time windows with the same number of observations which shift at each new event; we compare the performance of some distributions chosen among the most studied ones by evaluating their posterior marginal likelihood in the Bayesian framework. We apply this procedure to two data sets related to the severe seismic sequences that hit central Italy in the last decades. The best probability distribution, that is the distribution which outperforms significantly the others, varies over time; in particular, we highlight that these changes characterize specific periods in the temporal evolution of seismic activity and therefore could be used for forecasting purposes.

2. Probability Distributions

Let us consider the sequence of $(N+1)$ seismic events that occurred at times $\left\{t_0,t_1,\dots ,t_N\right\}$, and let $\mathcal{T}={\left\{{\tau }_i\right\}}_{i=1}^N$ be the set of the interevent times $\tau$ between successive events defined as ${\tau }_i=t_i-t_{i-1}$, $i=1,2,\dots ,N$. We assume that all the events have magnitude larger than or equal to the threshold $M_c$ which guarantees a sufficient degree of completeness for the data set. We present the main properties of the most studied probability distributions of the intervent time random variable.

Exponential distribution 

The simplest probability distribution for the interevent time is the exponential distribution with density function given by:

$$f_1\left(\tau \right)=\lambda e^{-\lambda \tau }.$$

(2)

It describes the time between events in a homogeneous Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; hence the exponential distribution states uncorrelated behavior. Its key property is that it is memoryless, that is the probability that the waiting time $\tau$ for an event exceeds a value $(t+s)$, conditioned on the fact that the time t has already passed, is equal to the original probability of exceeding s:

$$Prob(\tau >t+s|\tau >t)=Prob(\tau >s)=e^{-\lambda s}.$$

(3)

Consequently the exponential distribution is the only continuous probability distribution that has constant hazard rate equal to $\lambda$. According to Bayesian inference the conjugate prior for the exponential distribution is the gamma distribution; hence we consider the parameter $\lambda$ as a gamma-distributed random variable with hyperparameters $a_0$, $b_0$ so that its posterior distribution is still a gamma distribution with parameters $(a_0+N)$ and $(b_0+{\sum }_{i=1}^N{\tau }_i)$.

Gamma distribution 

The gamma probability density function is given by:

$$f_2\left(\tau \right)=\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}{\tau }^{\alpha -1}{e}^{-\beta \tau }$$

(4)

where $\alpha$ is the shape parameter and $\beta$ the scale parameter, both positive. In particular, the gamma distribution models the sum of exponentially distributed random variables; that is, if we consider a sequence of events such that each interevent time follows the exponential distribution with parameter $\beta$, then the waiting time of the n-th event is a gamma-distributed random variable with integer shape ${\displaystyle \alpha =n}$. In general the extensive use of the Gamma distribution is due to its ability to model the intertime between triggered aftershocks through its short-term scale power-law factor and the long-term scale Poissonian background activity through the exponential factor. Regarding parameter inference, since there is only the conjugate prior distribution of the scale parameter, we prefer to estimate the posterior distribution of both parameters through the Metropolis-Hastings algorithm, a stochastic simulation method of the class of Markov chain Monte Carlo (MCMC) methods. This algorithm generates a Markov chain that converges to the target distribution - in our case the posterior distribution - using a proposal density for generating new candidate values and a method for rejecting some of the proposed values [13]. In this way, we obtain not only the parameter estimates, typically as their posterior means (average of the sampled, possibly thinned, values), but also a measure of their uncertainty, as expressed through the simulated posterior distribution of each parameter.

Q-exponential distribution 

Nonlinear dynamical systems that exibit fractal structures and long-range correlations are successfully studied in the framework of non-extensive statistical physics. The presence of the same properties also in seismicity [11] suggests to analyze the temporal behavior of the seismic activity through the q-exponential distribution obtained by maximizing the non-additive Tsallis entropy under suitable constraints [6]:

$$f_3\left(\tau \right)=\frac{1}{\gamma }{\left(1-\frac{(1-q)}{(2-q)}\frac{\tau }{\gamma }\right)}^{{\displaystyle 1/(1-q)}},1<q<2$$

(5)

where q is called the entropic index and $\gamma$ is the generalized expectation value, that is, the mean with respect to the escort probability distribution ([14]):

$$f_q\left(x\right)=\frac{f^q\left(x\right)}{{\displaystyle {\int }_0^{+\infty }{f}^q\left(x\right)dx}}.$$

(6)

For large $\tau$, the q-exponential density function (5) goes to zero as a power ${\displaystyle {\tau }^{-1/(q-1)}}$, and it is also always bounded below by the exponential density function; hence it is a fat-tailed distribution and, in particular, a heavy-tailed distribution being:

$$\underset{\tau \to +\infty }{lim}{e}^{t\tau }{\overline{F}}_3\left(\tau \right)=\underset{\tau \to +\infty }{lim}{e}^{t\tau }{\left(1+\frac{q-1}{2-q}\frac{\tau }{\gamma }\right)}^{-(2-q)/(q-1)}=+\infty \forall \tau >0$$

(7)

where ${\overline{F}}_3\left(\tau \right)=1-F_3\left(\tau \right)$.

Since conjugate priors of the q and $\gamma$ parameters with respect to the q-exponential function are missing, we again resort to Markov chain Monte Carlo methods to sample from the posterior probability distributions of the parameters after reparameterizing as follows: $\theta =(2-q)/(q-1)$ with $\theta \in (0,+\infty )$.

Q-generalized gamma distribution 

Substituting the exponential term in (4) with the q-exponential function defined as

$${exp}_q\left(x\right)={[1+(1-q\left)x\right]}^{1/(1-q)}$$

borrowed from the nonextensive statistical mechanics, one obtains the so-called q-generalized gamma density function which is characterized by two power-law regimes indicating clustering effects at all time scales and both short- and long-term memory in the seismogenic process. This distribution was proposed for the first time in financial framework by Queirós [12]; it is based on local fluctuations of the $\omega$ mean value of the Gamma distributed $\tau$ variable under study. Hence, scaling the variable by its mean value we have the conditional density function:

$$f(\tau \mid \omega )=\frac{{\phi }^{\phi }}{\omega \Gamma \left(\phi \right)}{\left(\frac{\tau }{\omega }\right)}^{\phi -1}exp\left[-\frac{\phi }{\omega }\tau \right]$$

(8)

where $E\left(\tau \right)=\omega$. Let us assume that $\omega$ varies over time and follows the inverse gamma distribution:

$$g\left(\omega \right)=\frac{{\left(\frac{\phi }{\lambda }\right)}^{\delta }}{\Gamma \left(\delta \right)}{\omega }^{-\delta -1}exp\left[-\frac{\phi }{\omega \lambda }\right].$$

(9)

Integrating the joint density $f(\tau \mid \omega )g\left(\omega \right)$ with respect to $\omega$, we get the marginal density function:

$$h\left(\tau \right)=\frac{\lambda \Gamma (\phi +\delta )}{\Gamma \left(\phi \right)\Gamma \left(\delta \right)}{\left(\lambda \tau \right)}^{\phi -1}{(1+\lambda \tau )}^{-\phi -\delta }$$

(10)

and carrying out the changes of variables

$$\lambda =\frac{\rho -1}{\xi },\delta =\frac{1}{\rho -1}-\phi ,\alpha =\phi -1$$

(11)

we have the q-generalized gamma probability density function

$$f_4\left(\tau \right)=\frac{{(\rho -1)}^{\phi }\Gamma \left(\frac{1}{\rho -1}\right)}{\xi \Gamma \left(\frac{1}{\rho -1}-\phi \right)\Gamma \left(\phi \right)}{\left(\frac{\tau }{\xi }\right)}^{\phi -1}{\left[1+\frac{\rho -1}{\xi }\tau \right]}^{1/(1-\rho )}.$$

(12)

In the limit $\rho \to 1$, it recovers the ordinary gamma distribution. Finally, as in the case of the q-exponential distribution (5), we reparametrize as follows: $\eta =\frac{(2-\rho )}{(\rho -1)}$, to simplify parameter estimation through MCMC methods.

3. Inferencial Issues

We briefly give the basic concepts on the Bayesian approach we have followed in estimation and comparison of the four models. Let us assume that the data $\tau =({\tau }_1,{\tau }_2,\dots ,{\tau }_N)$ are realizations of a random variable $\mathcal{T}$ whose density function belongs to the parametric family $\mathcal{F}=\left\{f\right(\tau ;\psi ):\psi \in \Psi \}$. Contrary to the frequentist setting the parameter $\psi$ is considered as a random variable and its prior distribution $p_0\left(\psi \right)$ collects our initial beliefs about the phenomenon under study. Through the Bayes’ theorem the information provided by data and expressed by the likelihood $\mathcal{L}\left(f\left(\tau \right|\psi )\right)={\prod }_{i=1}^{N}f({\tau }_i;\psi )$ is combined with that in the prior distribution into the posterior distribution:

$$p\left(\psi \right|\tau )=\frac{p_0\left(\psi \right)\mathcal{L}\left(f\left(\tau \right|\psi )\right)}{{\int }_{\Psi }{p}_0\left(\psi \right)\mathcal{L}\left(f\left(\tau \right|\psi )\right)d\psi }.$$

(13)

From this distribution we get not only the parameter estimate, typically as the posterior mean $E_p\left(\psi \right)$, but also indications on its accuracy through statistical summaries such as the posterior mean or the quartiles. The computational difficulties due to the evaluation of the integral in(13) which often, and also in our case, is multi-dimensional, can be solved by resorting to the application of Markov chain Monte Carlo (MCMC) methods which produce a sequence of random samples from the posterior distribution (13) through which the distribution can be approximated [15]. In particular we apply the Metropolis-Hastings (MH) algorithm which consists of the following steps: a) generate an initial value ${\psi }_0$ from its prior distribution $p_0\left(\psi \right)$ and set $i=0$, b) for each iteration i generate a next candidate sample $\tilde{\psi }$ from an arbitrary probability density $q(\psi \mid {\psi }_i)$, referred to as proposal or jumping density, c) calculate the acceptance probability

$${\alpha }_i=min\left({\displaystyle 1,\frac{\mathcal{L}\left(f(\tau \mid \tilde{\psi })\right)p_0\left(\tilde{\psi }\right)q({\psi }_i\mid \tilde{\psi })}{\mathcal{L}\left(f(\tau \mid {\psi }_i)\right)p_0\left({\psi }_i\right)q(\tilde{\psi }\mid {\psi }_i)}}\right),$$

and accept $\tilde{\psi }$ as ${\psi }_{i+1}$ with probability ${\alpha }_i$, or set ${\psi }_{i+1}={\psi }_i$ with probability $(1-{\alpha }_i)$.

The initial values of the chain may be highly dependent on the starting value; for this we will neglect the first k samples and use the sequence ${\left\{{\psi }_i\right\}}_{i=k+1}^{M+k}$, for large enough values of k and M, to estimate the posterior distribution $p(\psi \mid \tau )$ and to approximate the posterior marginal log-likelihood:

$$log\mathcal{L}\left(f\left(\tau \right)\right)={\int }_{\Psi }log\mathcal{L}\left(f(\tau \mid \psi )\right)p(\psi \mid \tau )d\psi \approx 1/M\sum _{j=k+1}^{M+k}log\mathcal{L}\left(f(\tau \mid {\psi }_j)\right)$$

(14)

that enables us to verify how well the fitted model $f(·)$ is able to describe the observed data. In general, given two statistical models $f_j(·|\varphi )$ and $f_k(·|\eta )$ we can compare them by the difference of their posterior marginal log-likelihoods ${\Delta }_{jk}=log\mathcal{L}\left(f_j\left(\tau \right)\right)-log\mathcal{L}\left(f_k\left(\tau \right)\right)$, and then, similar to the Bayes factor, we establish the degree of evidence in favor of the first model according to the value $\mathcal{K}$ of the Jeffreys scale ([16,17]).

Considering our four probability models in detail, we note that only the $\lambda$ parameter of the exponential distribution has the gamma distribution as conjugate prior. For each of the parameters of the other models we choose a lognormal distribution both as prior and as proposal distribution in the Metropolis-Hastings algorithm. Let us consider, for instance, the parameter $\theta$ of the q-exponential distribution; we express our initial beliefs about it by specifying its prior distribution $\mathrm{Lognormal}({mean}_{\theta },{var}_{\theta })$ where $mean$ and $var$ indicate the mean and variance of the random variable $\theta$ and not the mean and variance of its logarithm, as in the common representation of the lognormal distribution. Moreover, regarding the generation of the Markov chain converging to the posterior distribution of $\theta$, at the $(i+1)$-th iteration, we adopt $\mathrm{Lognormal}({\theta }_i,{({\theta }_i/{\kappa }_1)}^2)$ as proposal distribution of the next candidate value, where ${\theta }_i$ is the current value of the Markov chain and the value of ${\kappa }_1$ is calibrated through pilot runs, so that the acceptance rate of the MH algorithm is about 25% to 40%. The same for the other parameters.

4. Case Studies

To evaluate the performance of the four probability distributions of the interevent time presented in Section 2 we examine two sequences of earthquakes related to two strong seismic crises that occurred in central Italy in the last decades: the L’Aquila ($M_{w}6.1$) earthquake in 2009 and the Amatrice ($M_{w}6$) - Norcia ($M_{w}6.5$) earthquakes in 2016. These earthquakes have been associated with two composite seismogenic sources of the Database of Individual Seismogenic Sources (DISS, version 3.2.1) [18] that can have the potential for earthquakes of up to $M_{max}6.5$. Both the data sequences analyzed in this study are drawn from the Italian National Institute of Geophysics and Volcanology (Istituto Nazionale di Geofisica e Vulcanologia; INGV) web services: Italian Seismological Instrumental and Parametric Database (ISIDe) working group (2016), version 1.0, accessible at http://cnt.rm.ingv.it/en/iside [19], in which the size of the events is expressed in different units of magnitude, as local magnitude $M_L$, duration magnitude $M_D$, and moment magnitude $M_w$. We have therefore applied the orthogonal regression relationships: $M_w=1.066M_L-0.164$ and $M_w=1.718M_D-1.897$ [20] to convert $M_L$ and $M_D$ to $M_w$ so as to construct homogenous data sets. The spatial extension of the areas under examination is established by taking into account the empirical relationship between magnitude and rupture length $RL$ - ${log}_{10}\left(RL\right)=-3.22+0.69M_{max}$ - by Wells and Coppersmith [21].

For each of the two sequences we calculate the time between pairs of successive earthquakes so as to obtain a set of N observed interevent times; then we consider time windows that consist of $n=100$ observations and that shift at each new event through the seismic sequence under examination. In this way we obtain $(N-n+1)$ datasets on which to evaluate the fitting of the probability distributions listed in Section 2 and to investigate whether the best distribution is unique or varies over time with the change of the seismic phases.

4.1. L’Aquila Sequence

On April 6, 2009 (01:13:40 UTC), a $M_{w}6.1$ shock was recorded with epicenter at latitude 42.342, longitude 13.380 near L’Aquila, the capital of the Abruzzo region in central Italy. Consistently with the criteria set out above we choose the rectangular area centered on the epicenter, of latitude size (41.8, 43.0) degrees and longitude size (12.8, 13.8) degrees as study area, and we analyze the temporal period from April 7, 2005 to the end of July 2009 taking $m_0=2$ as the magnitude threshold in order to guarantee the completeness of the data set with the exception of, at most, a few hours after the main shock when temporary partial incompleteness can be observed due to the well-known difficulty in recording all of the events at the beginning of the aftershock sequence, and especially those of low magnitude [22]. The main shock was preceded by a $M_{w}4$ foreshock on March 30, 2009 [23], and was followed by an aftershock sequence which lasted more than a year, the strongest of which of $M_{w}5.4$ occurred on April 7, 2009 [24].

Overall we have 2725 events, that is $N=2724$ interevent times through which we construct $m=2625$ temporal windows, each of 100 consecutive observations, shifting at each new event. To observe how the temporal distribution changes we fit the four probability models (Section 2) to the data set associated with each time window, and then compare the pairwise differences of their posterior marginal log-likelihoods with the value $\mathcal{K}=2.3026$ of the Jeffreys scale that indicates strong evidence in favor of the first model. In the case of the exponential probability density: $f_1\left(\tau \right)=\lambda exp\left\{-\lambda \tau \right\}$, we adopt the conjugate Gamma(2,1) distribution as prior distribution of the $\lambda$ parameter so that the expected seismic rate is about 2 (time in days). For the other three probability models under examination Table 1 reports the parameters of the prior distributions and the $\kappa$ coefficients used in the proposal distributions of the MH algorithm to obtain suitable acceptance rates.

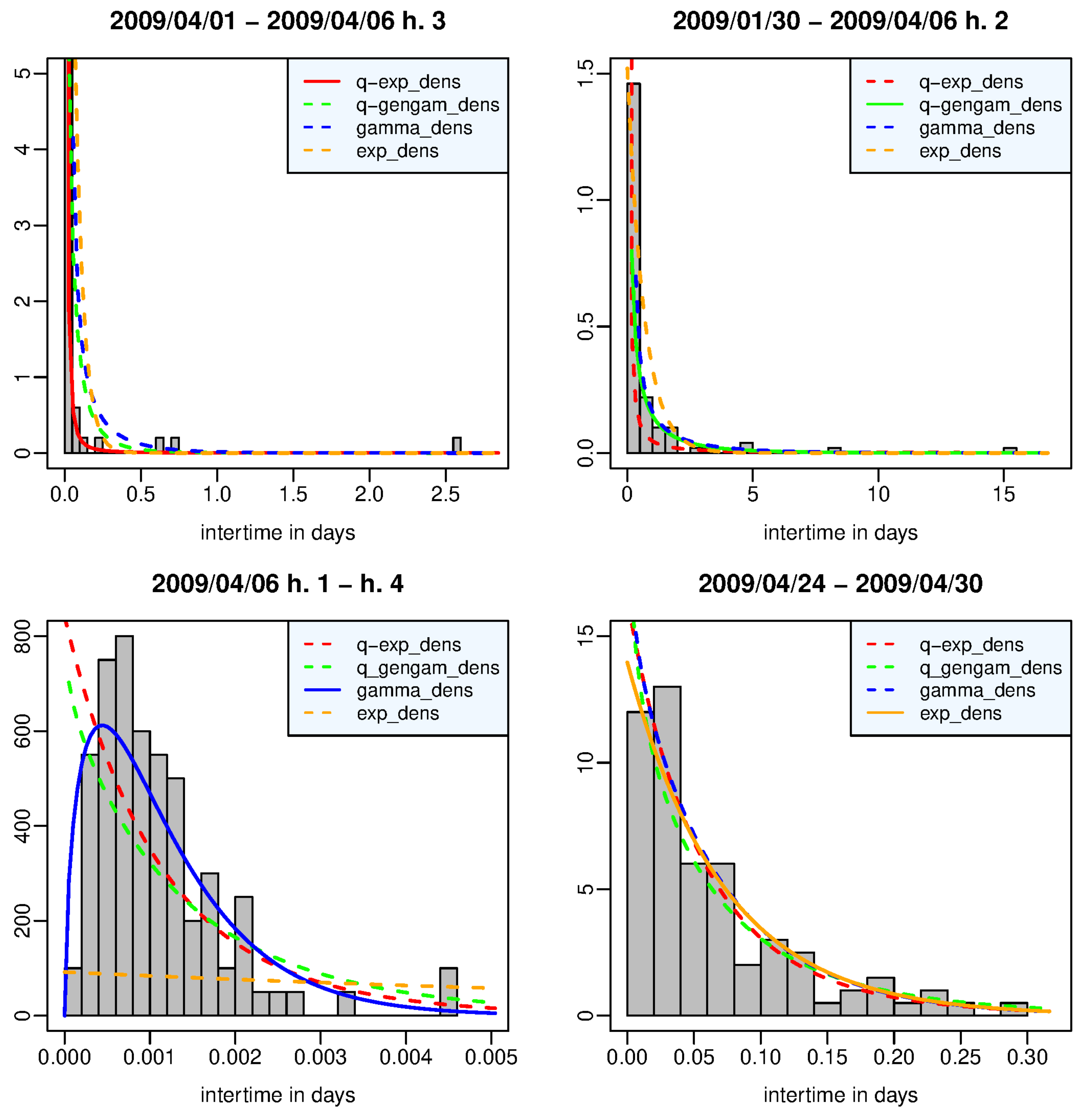
Figure 1 shows the estimated density functions and the histogram of the interevent times belonging to the time window in which each density function, represented by a solid line, provides respectively the best fit to the data; in particular, a) the window in the left top panel refers to the events that occurred from April 1, 2009 up to two hours after the main shock, 90% of which are aftershocks; the q-exponential density function has both its largest posterior marginal likelihood and the maximum difference from the second best density function (q-generalized gamma); b) right top panel: the window contains the events from January 30, 2009 to 1 hour after the main shock; the q-generalized gamma density function is the best model but it is worth no more than a mere mention for the evidence shown by its fit to the data with respect to the second best density (gamma); c) left bottom panel: the window is all made up of aftershocks that occurred in the first three hours after the main shock; the gamma density function is the best model and it has decisive strength of the evidence against the second best model (q-exponential); d) right bottom panel: the window covers the period from April 24 to April 30, 2009; there is no more than a barely worth mentioning evidence in favor of the exponential density against the q-exponential and gamma density functions. We note that the heavy-tailed q-exponential distribution describes best the data set with the mass most concentrated on the left and skewned to the right, whereas the gamma density fits well the unimodal histogram associated with the aftershock set immediately following the main shock. The relative lack of very short interevent times is probably related to the temporary incompleteness of the catalog in that period.

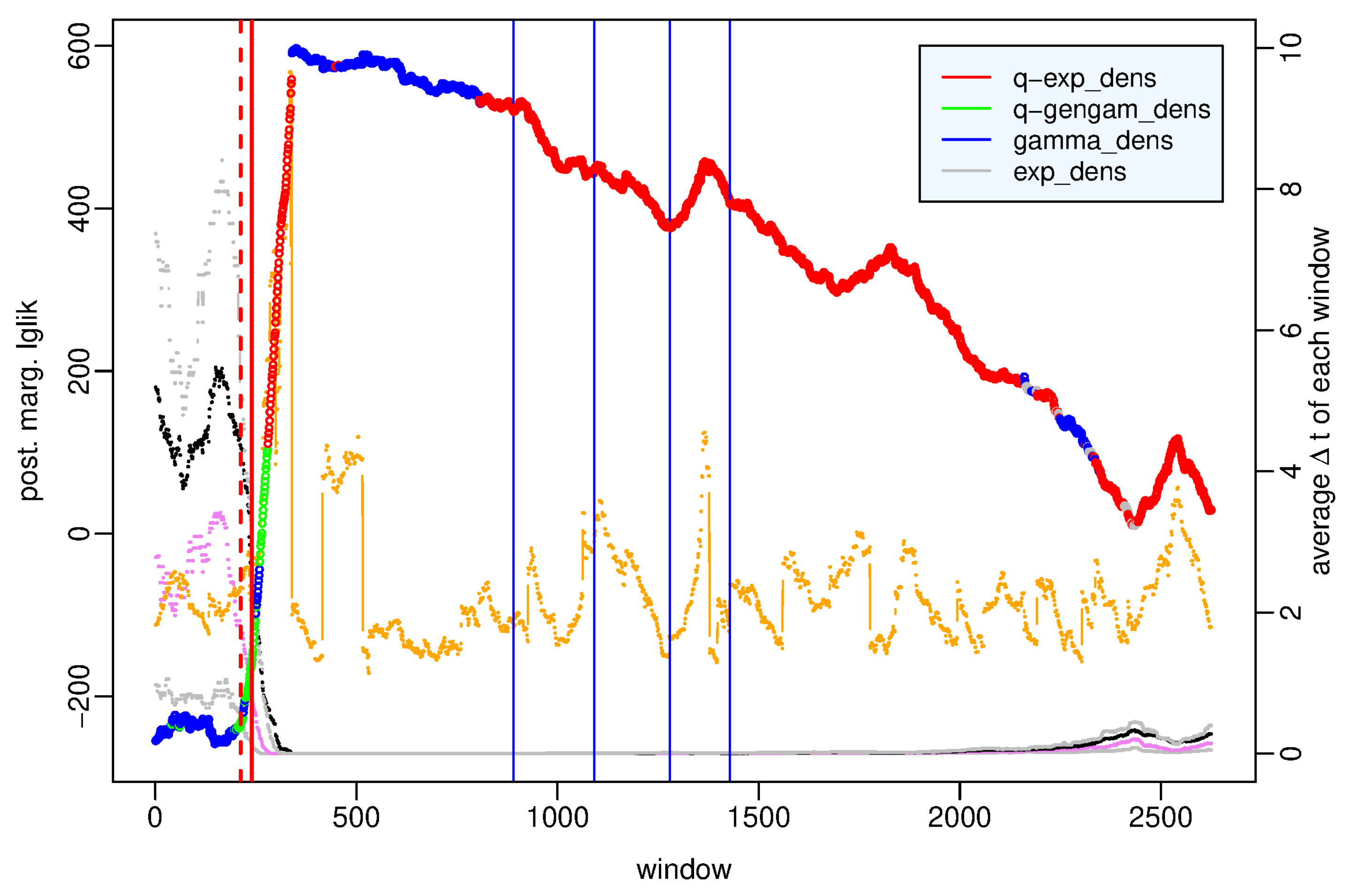
Figure 2 shows the largest value among the posterior marginal likelihoods of the four probability models at each time window; different colors highlight how the probability distribution that fits best the observations varies over time. To understand the motivations of these changes we analyze the characteristics of each data set by showing some of their statistical summaries such as first and third quartiles, median, mean and skewness. We remind that skewness is a measure of the asymmetry of the probability distribution. When it is positive, as in our cases, the right tail is longer and the mean is larger than the median; more precisely, the larger the skewness is, the more left-leaning the distribution is, that is, the more the observed intertimes are concentrated around short values; viceversa smaller skewness corresponds to more homogeneously distributed data in which the median is closer to (to the left of) the mean.

The time windows are divided as follows: in 1745 (66%) the q-exponential distribution represents the best model, in 68 (2.6%) the q-generalized gamma distribution, in 760 (29%) the gamma distribution, and in 52 (2%) the exponential distribution. We point out that the strength of the evidence in favor of the best distribution with respect to the second best model is strong just in about half of the time windows; in particular, as for the q-exponential and the gamma distribution in 828 and 334 windows respectively, concentrated in the hours after the main shock, whereas as for the q-generalized gamma and the exponential distribution in no window. Moreover we note that the difference among all of the four models is not particularly significant in 143 (∼ 5%, approximately from the 2300-th to 2450-th window) time windows mainly concentrated between May and June 2009; we address this issue in more detail in the Supplementary Material. For brevity we will say hereinafter that the models are interchangeable when the difference between their posterior marginal log-likelihoods does not exceed the threshold $\mathcal{K}=2.3026$.

We examine the characteristic features of each probability model; the q-exponential distribution shows very strong evidence with respect to the other distributions (the q-generalized gamma is the second best model) in the time windows over the main shock, that is, which include some pre-main shock event and some aftershock and during the aftershock sequence, in particular from the end of June. The gamma distribution exceeds the other distributions on the day of the main shock - April 6, 2009 - and is the second best model early in the aftershock sequence, often interchangeable with the best q-exponential model. Substantially the exponential distribution outperforms the other distributions with slight evidence only in a few time windows in May-June 2009.

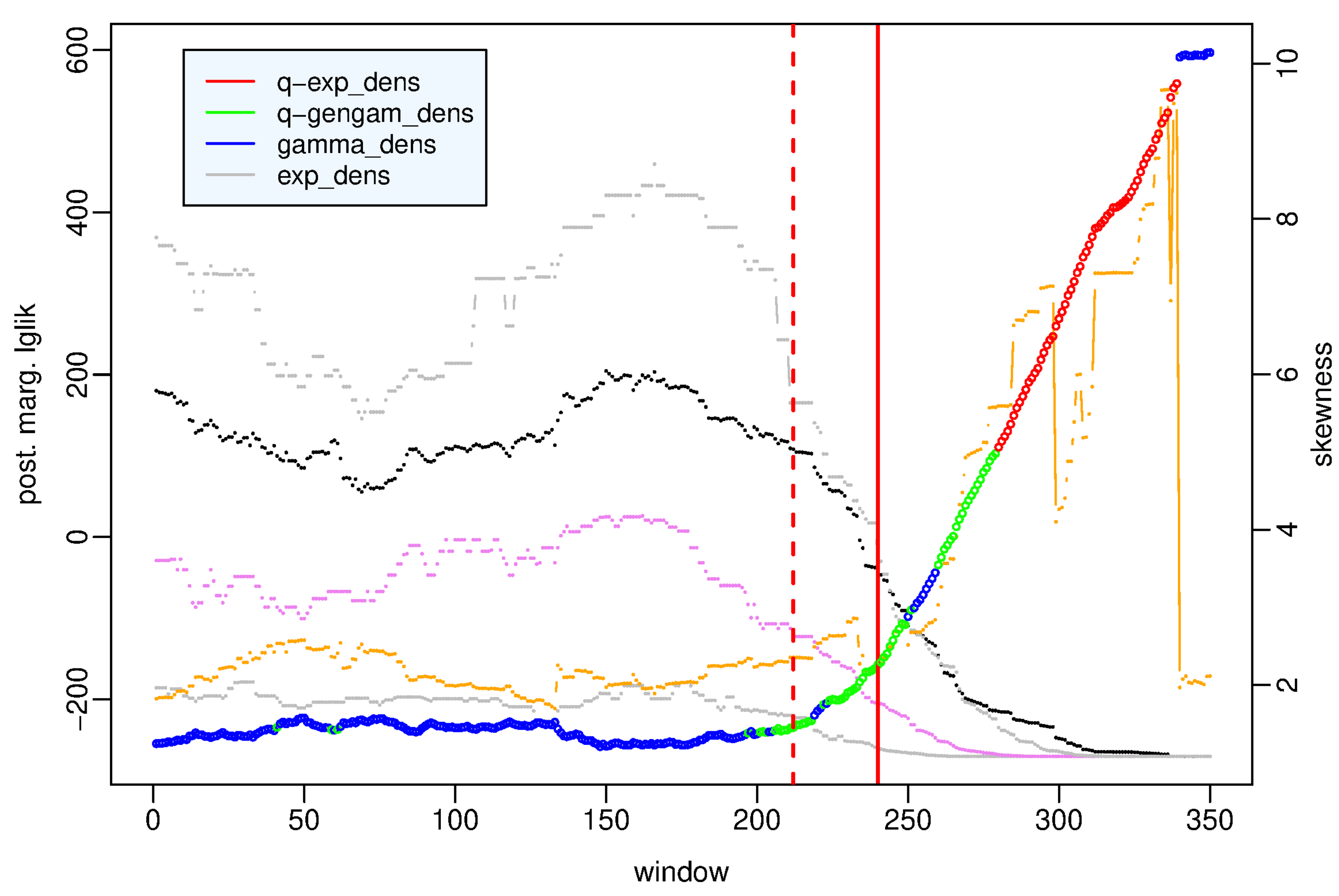
To better understand what happens before the main shock, in Figure 3 we zoom on the first 350 time windows covering the period from 2005/04/07 to 2009/04/06 h. 4. The q-generalized gamma distribution is the best model in the period from March 12, 2009 to April 6, 2009, a hour after the main shock; that is, the period that we can denote as preparatory phase in the seismic crisis because it includes the foreshock occurred on March 30, 2009 and denoted by a red dotted line in Figure 3. In this period the q-generalized gamma distribution is interchangeable with the gamma distribution but exceeds with strong evidence the other distributions. The role exchanges in the preceding period of background activity between April 2005 and March 2009, in which the gamma distribution is the best model, interchangeable with the q-generalized gamma distribution and exceeding with strong evidence the other distributions (see the Supplementary Material).

As for the statistical summaries we note that the preparatory phase is characterized by a constant decrease in the mean and in the median of the data sets approximately from the beginning of 2009, while overall the skewness increases up to April 2, 2009 and then decreases. This means that the interevent times get shorter between January and March 2009; obviously the minimum values of the mean and median are observed during the aftershock sequence.

4.2. Amatrice-Norcia Sequence

In 2016-2017 the junction area of the three regions Lazio. Marche, and Umbria in central Italy was hit by a complex sequence of destructive seismic events; on August 24, 2016 (01:36:32 UTC, latitude 42.698, longitude 13.234), an earthquake of $M_{w}6$ shook the city of Amatrice and caused about 300 fatalities. This shock, initially considered the main shock, later proved to be the foreshock of the $M_{w}6.5$ strongest shock that struck the city of Norcia on October 30, 2016 (06:40:17 UTC, latitude 42.830, longitude 13.109). The aftershock sequence lasted roughly up to July 2017 [24] and recorded four $M_{w}5+$ earthquakes on January 18, 2017. We consider 5062 events ($N=5061$ interevent times) which fall in the rectangular area of latitude size (42.3, 43.2) degrees and longitude size (12.7, 13.5) degrees and which span the temporal period from January 2014 to June 2018 taking $m_0=2.5$ as the magnitude threshold in order to guarantee the completeness of the data set apart the first hours following the main shock on October 30, 2016.

We investigate the behavior of the four probability distributions, given in Section 2, in $m=4962$ data sets, each of which obtained by shifting at each new event a time window constituted of 100 consecutive waiting times. First we evaluate the posterior marginal log-likelihood of each distribution in every time window by applying the MH algorithm to estimate the posterior distribution of the model parameters; Table 1 shows the parameters of the prior distributions and the $\kappa$ coefficients used in the proposal distributions of the MH algorithm to obtain suitable acceptance rates. Comparing the pairwise differences between the four posterior marginal log-likelihoods with the value $\mathcal{K}=2.3026$ of the Jeffreys scale we obtain the probability distribution with the best performance in each time window and the strength of its evidence with respect to the other distributions.

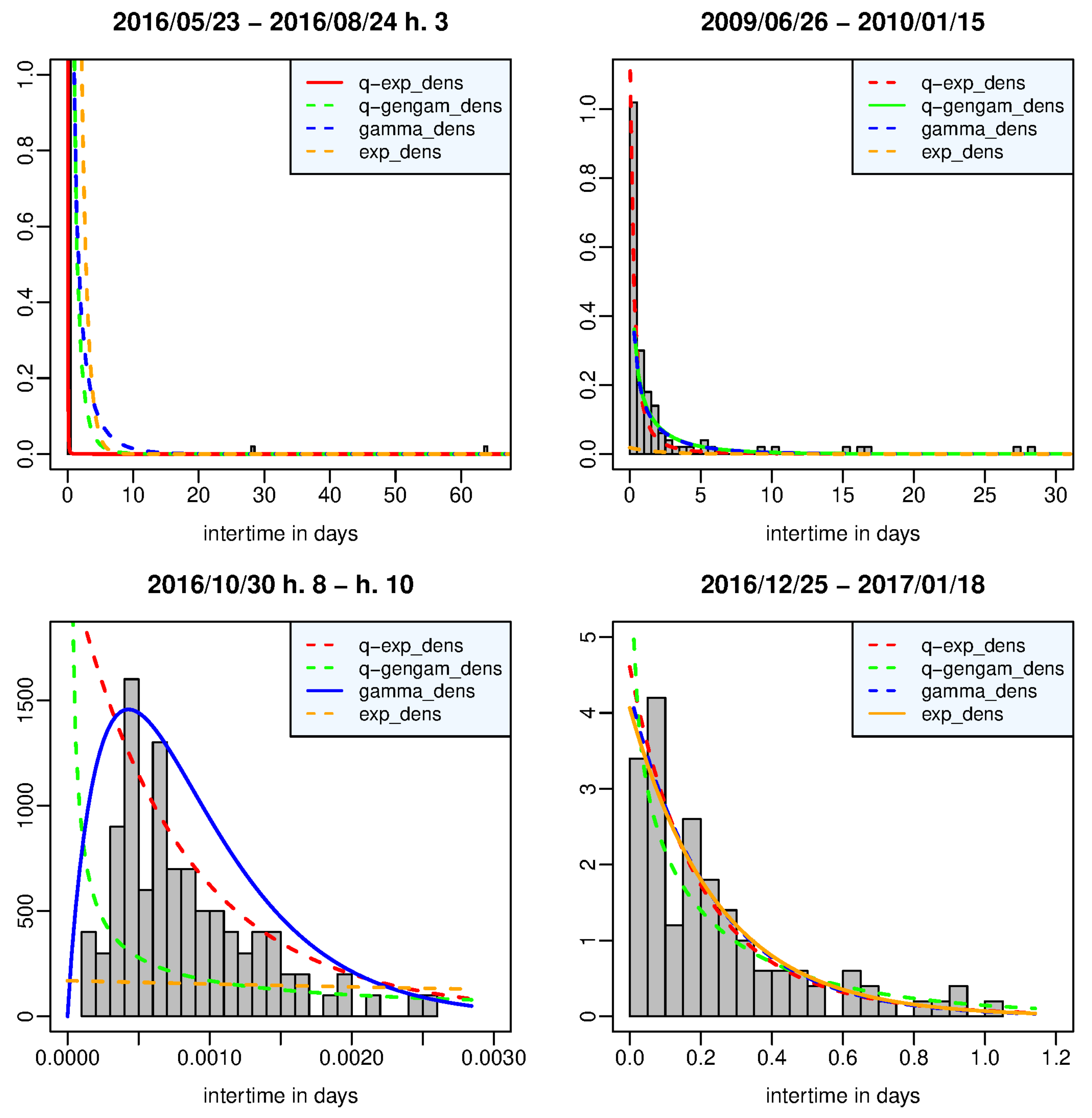
Figure 4 shows the estimated density functions and the histogram of the interevent times belonging to the time window in which each density function, represented by a solid line, provides respectively the best fit to the data, that is, it has its largest posterior marginal likelihood and the maximum difference from the likelihood of the second best density function. In particular, a) the left top panel refers to the time window which includes the first 98 aftershocks covering the two hours following the Amatrice shock which was preceded by two waiting times of approximately 28 and 63 days; the data set is therefore very right-skewned with long right tail, it is best described by the q-exponential density function which outperforms the other distributions with decisive evidence; b) right top panel: the q-generalized gamma distribution is the best model in the time window from June 26, 2009 to January 15, 2010 which includes the final part of the L’Aquila aftershock sequence; c) left bottom panel: the time window includes the aftershocks that occurred between h. 8 and h. 10 of the occurrence day of the Norcia main shock (October 30, 2016, 06:40:17 UTC); the gamma density function shows a decisive strength of evidence against the other probability distributions by adapting very well to the unimodal histogram of the interevent times which are probably missing the shorter ones due to the temporary incompleteness of the catalog after the strongest event; d) right bottom panel: the exponential distribution is interchangeable with the gamma and q-exponential distribution in the time window from December 25, 2016 to January 18, 2017 when the first of the four $M_{w}5+$ events occurs at Capitignano.

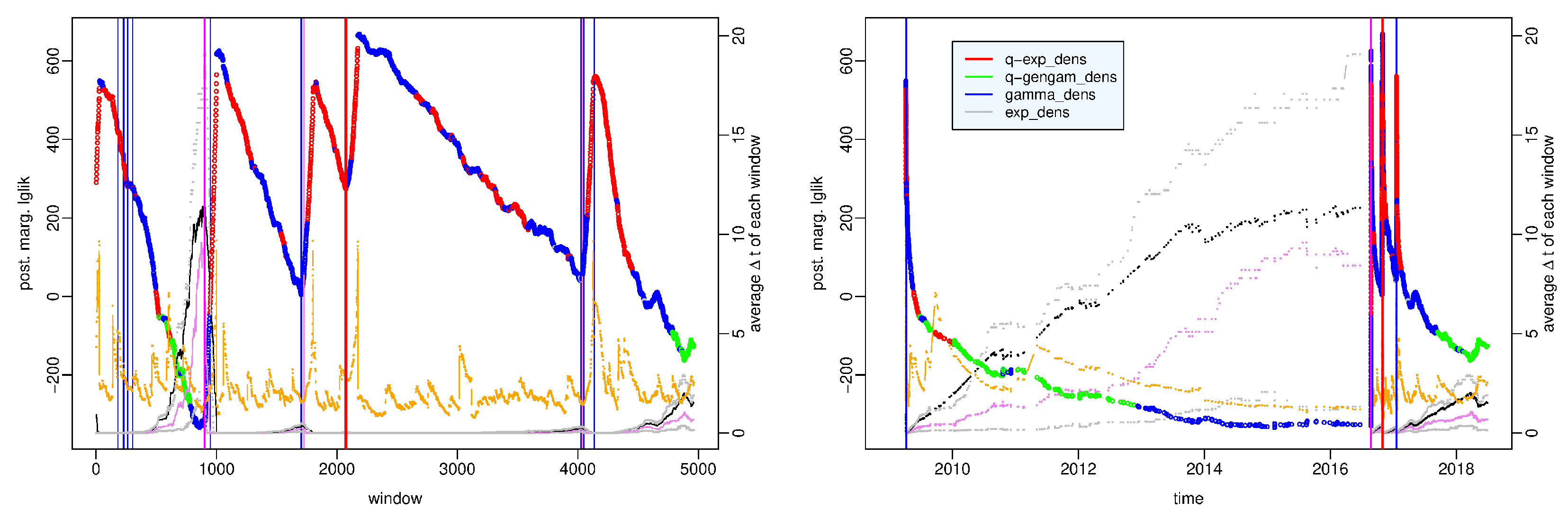
Figure 5 shows the value of the largest posterior marginal log-likelihood in each time window and the different colors indicate to which probability model this value corresponds; the x axis represents the window number in the left panel and the time in the right panel. First and third quartiles, median, mean and skewness of each data set are shown to highlight how the distribution of the observations changes over time. The time windows are divided as follows: in 1825 (36.8%) the q-exponential distribution represents the best model, in 360 (7.3%) the q-generalized gamma distribution, in 2748 (55.4%) the gamma distribution, and in 29 (0.6%) the exponential distribution. The strength of the evidence in favor of the best distribution with respect to the second best model is strong or decisive just in about a third of the time windows, in which the outperforming distribution is especially q-exponential or gamma; in particular, as for the q-exponential, the q-generalized gamma and the gamma distribution in 613, 12 and 1025 windows respectively, essentially concentrated in the hours after the strongest shocks, whereas as for the exponential distribution in no window. The Supplementary Material provides a detailed visualisation of the time windows in which the strength of evidence in favor of a probability model is particularly significant and those in which it is not.

Let’s take a more thorough look at the behavior of the various distributions. The q-exponential distribution is significantly the best model essentially in the first hours following the strongest earthquakes: from h. 5 to h. 8 of the day of occurrence of the L’Aquila earthquake (2009/04/06), from h. 2 to h. 3 of the day of occurrence of the Amatrice earthquake (2016/08/24), in the time windows including the first aftershocks of the Norcia earthquake (2016/10/30), and in the days of occurrence of the $M_{w}5+$ shocks on January 18 and 19, 2017; in the other time windows in which it has the largest log-likelihood, always during the aftershock sequences, it is interchangeable with the gamma distribution (see the Supplementary Material). The q-generalized gamma distribution characterizes the periods from January 2010 to November 2012 and from September 2017 to the end of our study; the difference from the other distributions has strong evidence only in January 2010, while in the other time windows the q-generalized gamma density is interchangeable with the gamma density (see the Supplementary Material).

The gamma distribution has the largest value of the posterior marginal log-likelihood in most of the time windows - in almost half of them with strong or decisive evidence - and precisely in those that cover both part of the aftershock sequences (in particular the windows including the first forty aftershocks following the Amatrice shock and the first hours after the Norcia main shock) and the quiescence period from December 2012 to August 2016; in some of the first ones the gamma model is interchangeable with the q-exponential model, while in the second ones it is interchangeable with the q-generalized gamma model (see the Supplementary Material).

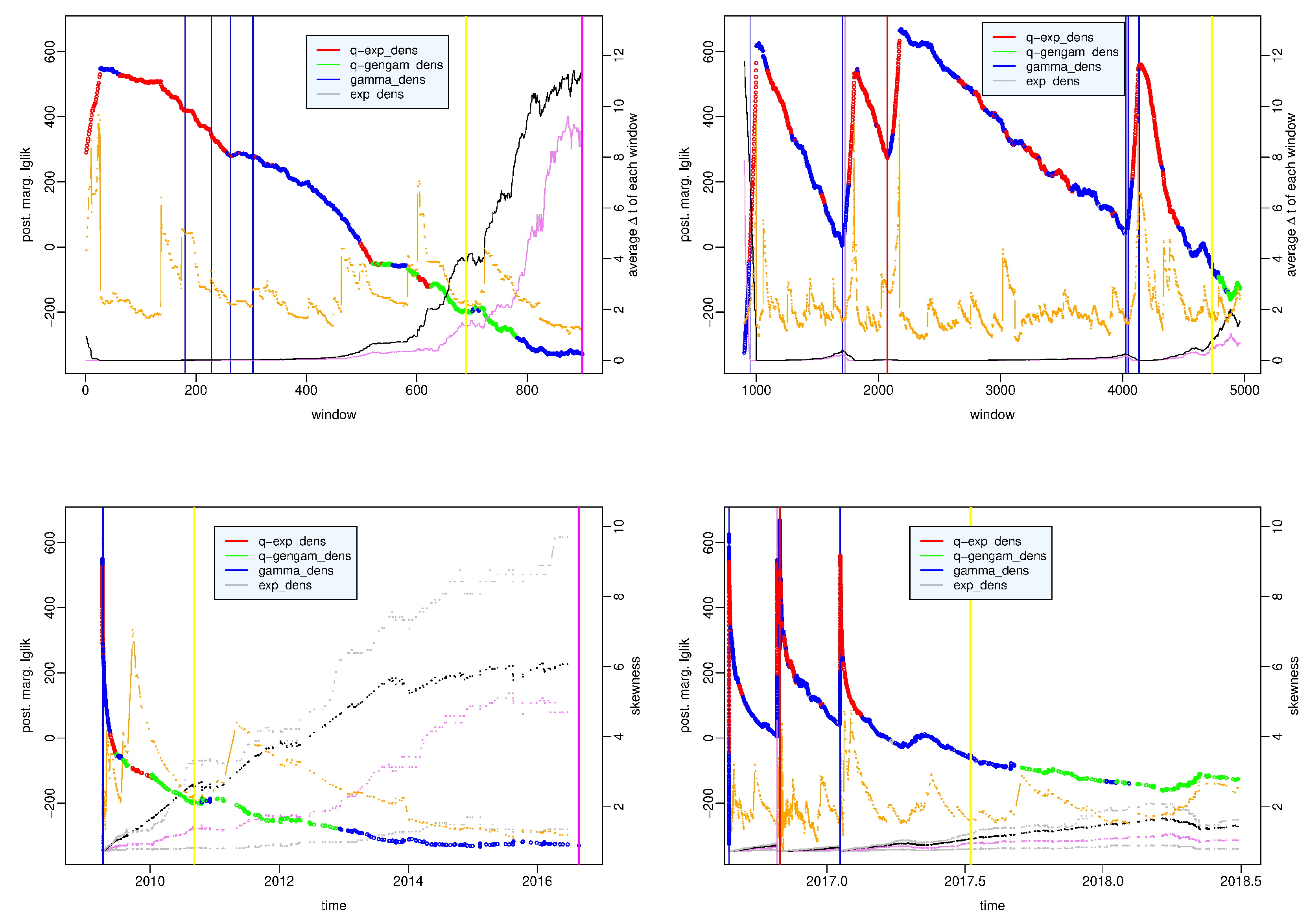
In Figure 6 we distiguish the results obtained before the start of the Amatrice-Norcia seismic crisis (left panels) from those produced by the sequence of earthquakes following the Amatrice shock (right panels); the value of the largest posterior marginal log-likelihood is plotted versus the number of the time window in the top panels and versus time in the bottom panels. We note that the average interevent time and the likelihood are inversely correlated, i.e. the more the observed recurrence times are concentrated in short times, the greater the likelihood, or in other words the likelihood decreases as the seismic activity decreases. Furthermore, the gamma distribution is the best model in correspondence with the minimum values of likelihood: local minima before the shocks of greater magnitude and the absolute minimum reached on February 11, 2015. The years leading up to the onset of the Amatrice-Norcia seismic crisis are characterized by decreasing values of the log-likelihood and by the gamma distribution as the best model but with barely noteworthy evidence with respect to the q-generalized gamma distribution which is the second best model; vice versa the q-generalized gamma distribution is the best model and it is interchangeable with the gamma distribution in the years between the end of the L’Aquila aftershock sequence and the beginnig of 2013. Since 2009 the average interevent time has a constantly increasing trend which becomes almost flat starting from 2015 at the same time as the value of the median approaches that of the average.

5. Discussion

We have investigated the probability distributions of the time between two successive earthquakes with the aim of finding out if there are links between seismic phases and variations of the probabilistic model that best fits the data in those phases. To this end, we have examined two seismic crises that hit central Italy and are related to the L’Aquila earthquake in 2009 and the Amatrice-Norcia shocks in 2016. Their retrospective analysis has shown that the first crisis had a foreshock of $M_{w}4$ on March 30, 2009, while the second had one so strong - $M_{w}6$ - that it was initially mistaken for the main shock. Overall the Amatrice-Norcia sequence turned out more complex with greater release of energy. As for the relationships between seismic phases and variations of the best probability distribution of the recurrence time the two events share some features:

• most of the probability densities estimated in the various time windows have decreasing shape as an inverse power law;
• the time windows with many very short interevent times - like those in the aftershock sequences - are associated with great likelihood, while the data sets which are less concentrated around short times, typical of the quiescence period, have smaller likelihood;
• the q-exponential distribution outperforms the other distributions in the initial part of the aftershock sequence and it becomes interchangeable with the gamma distribution;
• the q-generalized gamma distribution is associated with time intervals following aftershock sequences such as, for example, the years from 2010 to 2012 following the aftershock sequence of L’Aquila earthquake and from September 2017 after the $M_{w}5+$ Capitignano shocks; in these periods it slightly exceeds the gamma distribution; only in the case of the L’Aquila earthquake it characterizes the initial phase of the activation between the fore- and the main shock;
• the gamma distribution is interchangeable with the q-generalized gamma distribution in the periods of low seismic activity and with the q-exponential distribution in part of the aftershock sequences.

Similar results have also been found in other studies in which the phases of a seismic cycle have been related to changes of the probability distribution of the magnitude [25] and of the spatial location of the epicenters [9].

Another remark can be done on the value of the log-likelihood in the case of the Amatrice-Norcia crisis. As we expect it decreases during the aftershock sequences, however we note that it becomes even negative just over two months after the Capitignano $M_{w}5+$ earthquakes while it remains high when the same time has elapsed after the Amatrice and Norcia shocks. This could suggest that we should expect further energy releases after the Amatrice and Norcia events.

6. Conclusion

If repeating the same analyses on different cases and in different seismotectonic contexts the connection between changes in the probability distributions and seismic phases were confirmed, it could be hypothesized that these observations have the value of precursors of the activation level in a seismic region. The existence of the seismic precursors is still a widely open problem; but, already in 1999 Evison claimed that “despite the difficulties confronting experimentation in this field, there is growing empirical evidence that precursors exist.” [26]. Just as it is true that the most informative way to convey an earthquake prediction, including the uncertainties, is by means of probability distributions in the space-time-magnitude domain [27], it could be the same probability distributions that play the role of precursors.

We conclude by adopting Evison’s statement [26]: “Prediction is ubiquitous in science as a test of understanding: to the extent that a phenomenon is understood, it can be predicted, and vice-versa. If earthquakes were unpredictable, seismogenesis would be a closed book, research would be futile, and the earthquake would remain, in the words of Alexander McKay [28] “a visitation and a mistery”.