Submitted:
09 February 2025
Posted:
10 February 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Methods
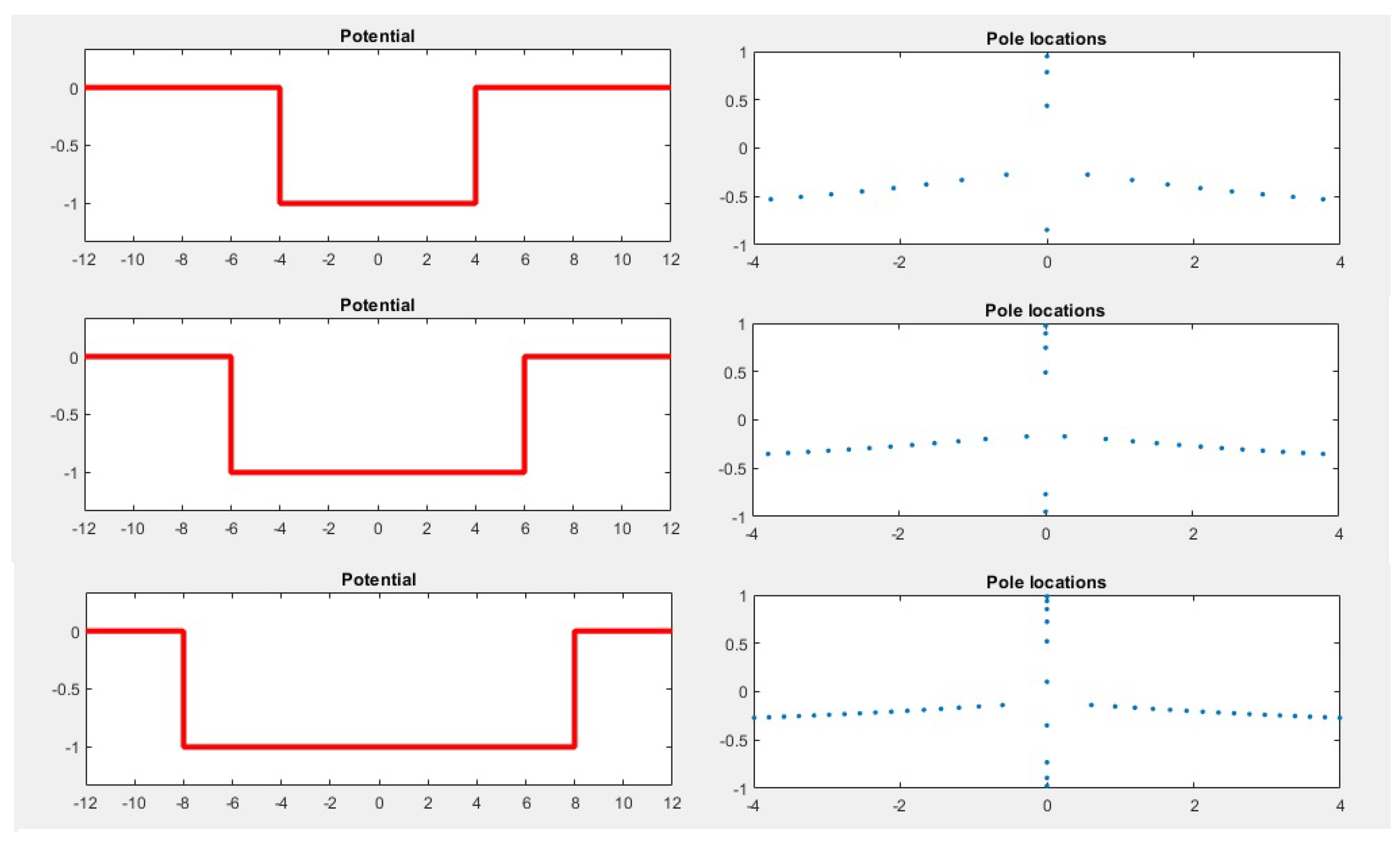
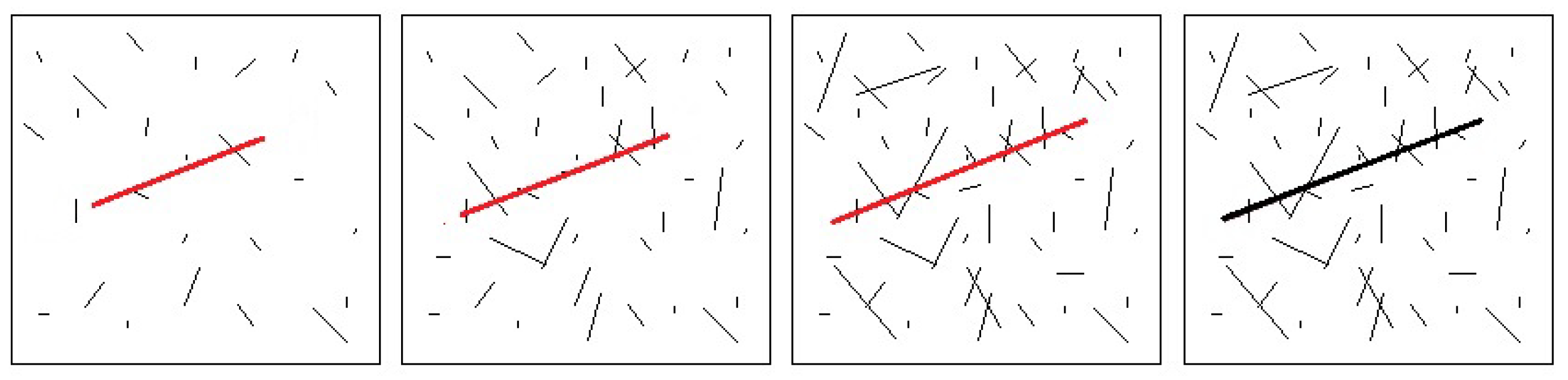
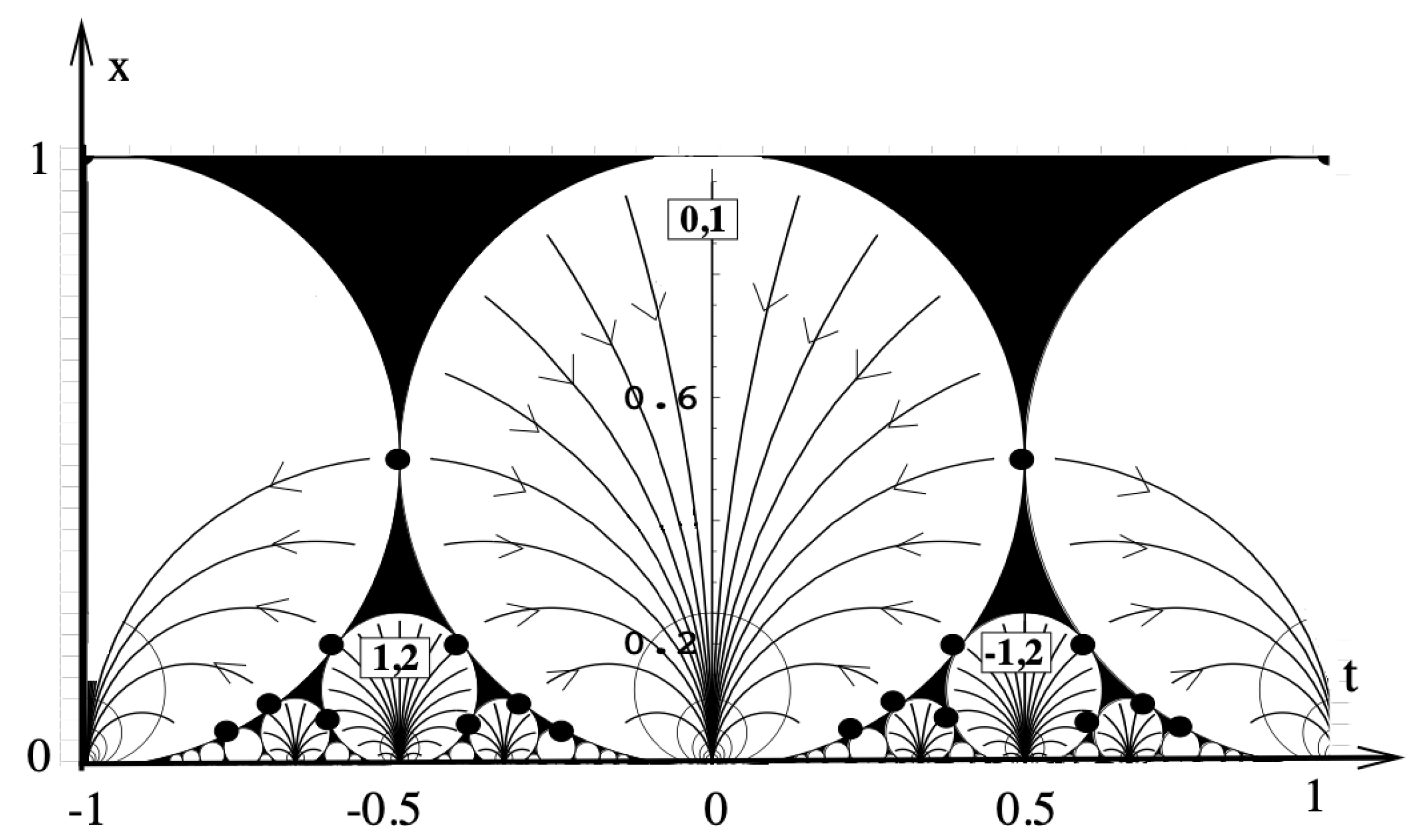
2.1. 1D Fault Dynamics Inverse Scattering Theory
2.2. 3D Fault Dynamics to Statistical Physics
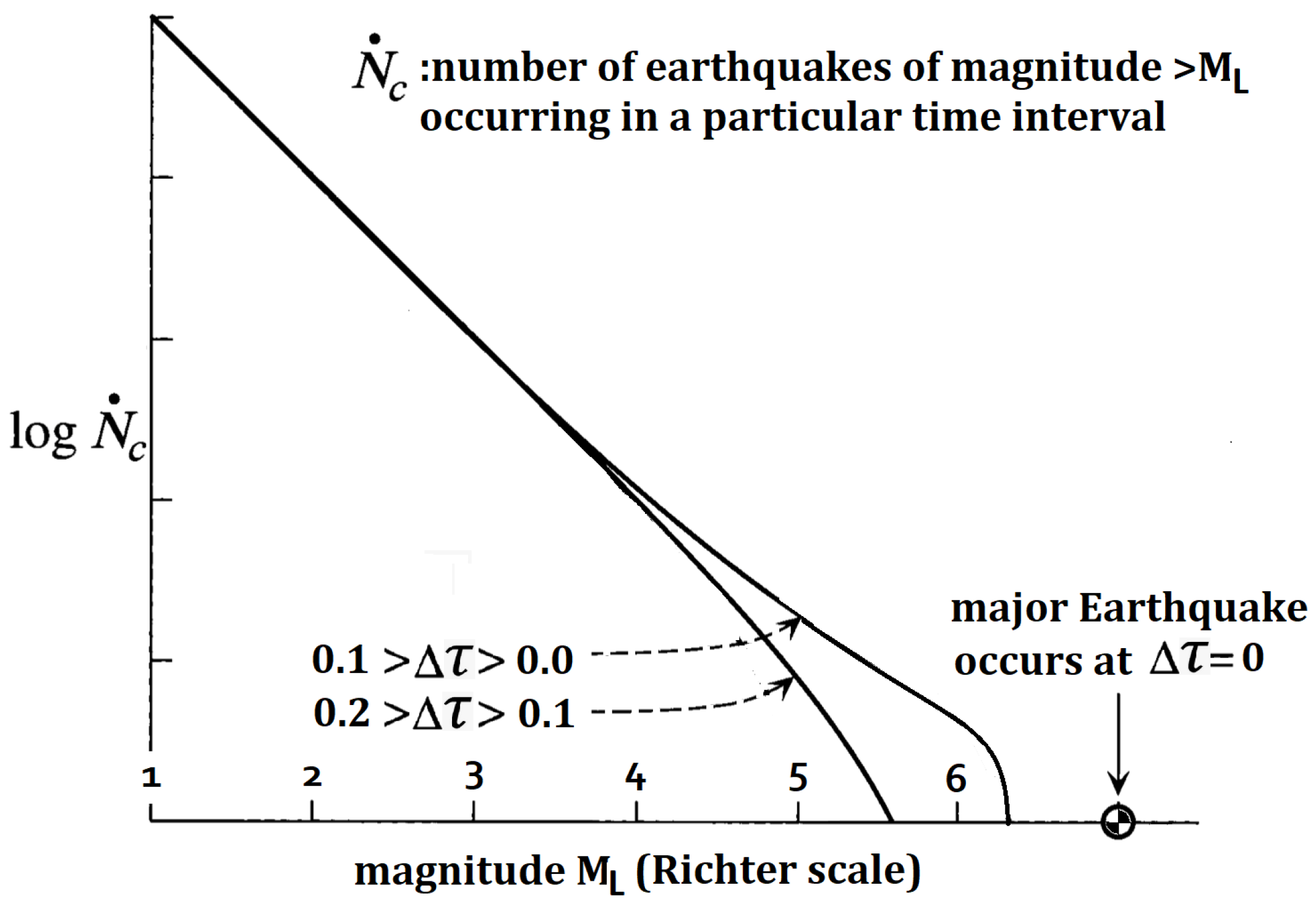
3. Results
4. Discussion
Acknowledgments
References
- Akemann G, Mielke A, Pβler (2021) Spacing distribution in the 2D Coulomb gas: Surmise and symmetry classes of non-Hermitian random matrices at non-integer β.
- Aki K, 1967. Scaling law of seismic spectrum, J. geophys. Res., 72, 1217–1231. [CrossRef]
- Aktosun T, Demontis F, F Van der Mee C. Exact solutions to the sine-Gordon equation. Journal of Mathematical Physics. 51(12). [CrossRef]
- Balog I, Carpentier D, Fedorenko AA. Disorder-driven quantum transition in relativistic semimetals: functional renormalization via the porous medium equation. Physical review letters. 2018 121(16):166402. [CrossRef] [PubMed]
- Ben-Zion Y, Lyakhovsky V (2002) Accelerated seismic release and related aspects of seismicity patterns on earthquake faults. Earthquake processes: Physical modelling, numerical simulation and data analysis Part II :2385–2412.
- Bindel DS. Structured and parameter-dependent eigensolvers for simulation-based design of resonant MEMS (Doctoral dissertation, University of California, Berkeley).
- Bindel D, Zworski M. Symmetry of bound and antibound states in the semiclassical limit. Letters in Mathematical Physics. 2007 Aug;81:107–17. [CrossRef]
- Böse M, Andrews J, Hartog R, Felizardo C. Performance and next-generation development of the finite-fault rupture detector (FinDer) within the United States West Coast ShakeAlert warning system. Bulletin of the Seismological Society of America. 2023 Apr 1;113(2):648–63. [CrossRef]
- Bowman D, Ouillon G, Sammis C, Sornette A, Sornette D (1998) An observational test of the critical earthquake concept. Journal of Geophysical Research: Solid Earth 103(B10):24359–24372. [CrossRef]
- Broomhead D S, King G P (1986) Extracting qualitative dynamics from experimental data. Physica D: Nonlinear Phenomena 20(2-3):217–236. [CrossRef]
- Bykov V G (2001) Solitary waves on a crustal fault. Volcanology and Seismology 22(6):651–661.
- Carlson J M, Langer J S, Shaw B E (1994) Dynamics of earthquake faults. Reviews of Modern Physics 66(2):657. [CrossRef]
- Carpentier D (1999) Renormalization of modular invariant Coulomb gas and sine-Gordon theories, and the quantum Hall flow diagram. Journal of Physics A: Mathematical and General 32(21):3865. [CrossRef]
- Chen CC. Accelerating seismicity of moderate-size earthquakes before the 1999 Chi-Chi, Taiwan, earthquake: Testing time-prediction of the self-organizing spinodal model of earthquakes. Geophysical Journal International. 2003 155(1):F1-5. [CrossRef]
- Dubrovin B, Yang D (2020) Matrix resolvent and the discrete KdV hierarchy. Communications in Mathematical Physics 377:1823–1852. [CrossRef]
- Dyatlov S, Zworski M (2019) Mathematical theory of scattering resonances, volume 200. American Mathematical Soc.
- Dyson FJ. Fredholm determinants and inverse scattering problems. Communications in Mathematical Physics 47(2):171-83. [CrossRef]
- Dyson FJ, Mehta ML (1963) Statistical theory of the energy levels of complex systems. iv. Journal of Mathematical Physics 4(5):701–712. [CrossRef]
- Goldenfeld N. Lectures on phase transitions and the renormalization group. CRC Press; 2018.
- Hofstetter E, Schreiber M (1993) Statistical properties of the eigenvalue spectrum of the three-dimensional Anderson Hamiltonian. Physical Review B 48(23):16979. [CrossRef]
- Ito R, Kaneko Y (2023). Physical Mechanism for a Temporal Decrease of the Gutenberg-Richter b-Value Prior to a Large Earthquake. Journal of Geophysical Research: Solid Earth 128(12):e2023JB027413. [CrossRef]
- John S. Localization of light. Physics Today. 1991 May 1;44(5):32–40. [CrossRef]
- Khan BA, Chatterjee S, Sekh GA, Talukdar B (2020) Integrable systems: From the inverse spectral transform to zero curvature condition. arXiv preprint arXiv:2012.03456.
- Lei Q, Sornette D (2022) Anderson localization and reentrant delocalization of tensorial elastic waves in two-dimensional fractured media. Europhys. Letters 136(3): 1–7.
- Markos P (2006) Numerical analysis of the Anderson localization. arXiv preprint cond-mat/0609580.
- Merrill RJ, Bostock MG, Peacock SM, Chapman DS (2023) Optimal multichannel stretch factors for estimating changes in seismic velocity: Application to the 2012 Mw 7.8 Haida Gwaii earthquake. Bulletin of the Seismological Society of America 113(3):1077–1090. [CrossRef]
- Newman WI, Turcotte DL, Gabrielov AM (1995) Log-periodic behavior of a hierarchical failure model with applications to precursory seismic activation. Physical Review E 52(5):4827. [CrossRef] [PubMed]
- Rundle JB, Klein W, Turcotte DL, Malamud BD (2001) Precursory seismic activation and critical-point phenomena. Microscopic and Macroscopic Simulation: Towards Predictive Modelling of the Earthquake Process 2165–2182.
- Rundle JB, Turcotte DL, Shcherbakov R, Klein W, Sammis C (2003) Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Reviews of Geophysics 41(4). [CrossRef]
- Rundle JB, Fox G, Donnellan A, Ludwig IG (2024) Nowcasting Earthquakes with QuakeGPT: Methods and First Results. arXiv e-prints. 2024 Jun:arXiv-2406.
- Sacchi M (2009) FX singular spectrum analysis. Cspg Cseg Cwls Convention 392–395.
- Saleur H, Sammis C, Sornette D (1996) Renormalization group theory of earthquakes. Nonlinear Processes in Geophysics 3(2):102–109. [CrossRef]
- Soerensen M, Schneider T (1991) Level-spacing statistics for the Anderson model in one and two dimensions. Physik B Condensed Matter 82(1):115–119. [CrossRef]
- Sornette D (1989) Acoustic waves in random media: II Coherent effects and strong disorder regime, Acustica 67(4):251–265.
- Tzanis A, Vallianatos F (2003) Distributed power-law seismicity changes and crustal deformation in the SW Hellenic ARC. Natural Hazards and Earth System Sciences 3(3/4):179–195. [CrossRef]
- Tzanis A, Vallianatos F, Makropoulos K (2000) Seismic and electrical precursors to the 17-1-1983, M7 Kefallinia earthquake, Greece: Signatures of a SOC system. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy 25(3):281–7. [CrossRef]
- Vallianatos F, Chatzopoulos G (2018) A complexity view into the physics of the accelerating seismic release hypothesis: Theoretical principles. Entropy 20(10):754. [CrossRef] [PubMed]
- Vallianatos F, Sammonds P (2004) Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 590:52–8. [CrossRef]
- Varchenko A (1990) Multidimensional hypergeometric functions in conformal field theory, algebraic K-theory, algebraic geometry. In Proceedings of the International Congress of Mathematicians 1:281–300.
- Wu RS, Aki K (1985) Scattering characteristics of elastic waves by an elastic heterogeneity. Geophysics 50(4):582–95. [CrossRef]
- Wu RS, Aki K (1988) Multiple scattering and energy transfer of seismic waves—Separation of scattering effect from intrinsic attenuation II. Application of the theory to Hindu Kush region. Scattering and Attenuations of Seismic Waves, Part I:49–80.
- Zabolotskaya EA, Ilinskii YA, Hay TA, Hamilton MF. Green’s functions for a volume source in an elastic half-space. The Journal of the Acoustical Society of America 131(3):1831–42. [CrossRef] [PubMed]
- Zabrodin A (2010) Canonical and grand canonical partition functions of Dyson gases as tau-functions of integrable hierarchies and their fermionic realization. Complex Analysis and Operator Theory 4:497–514. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



