Submitted:
05 February 2025
Posted:
06 February 2025
You are already at the latest version
Abstract
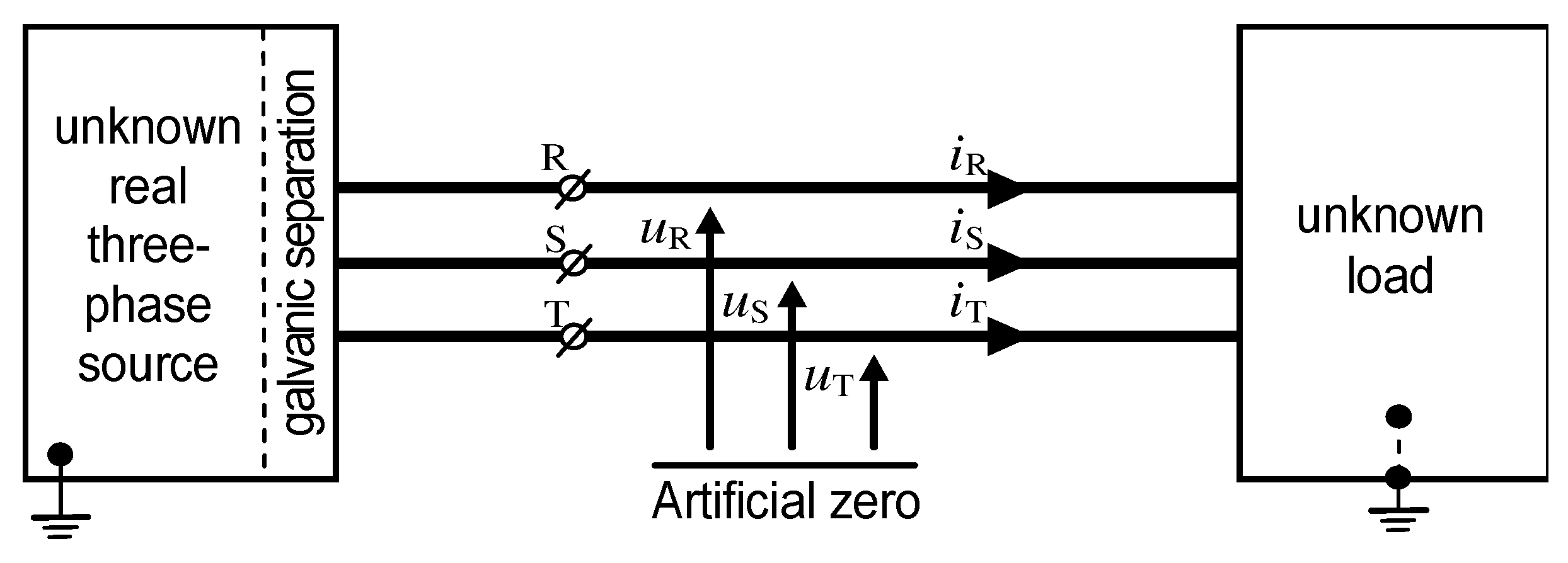
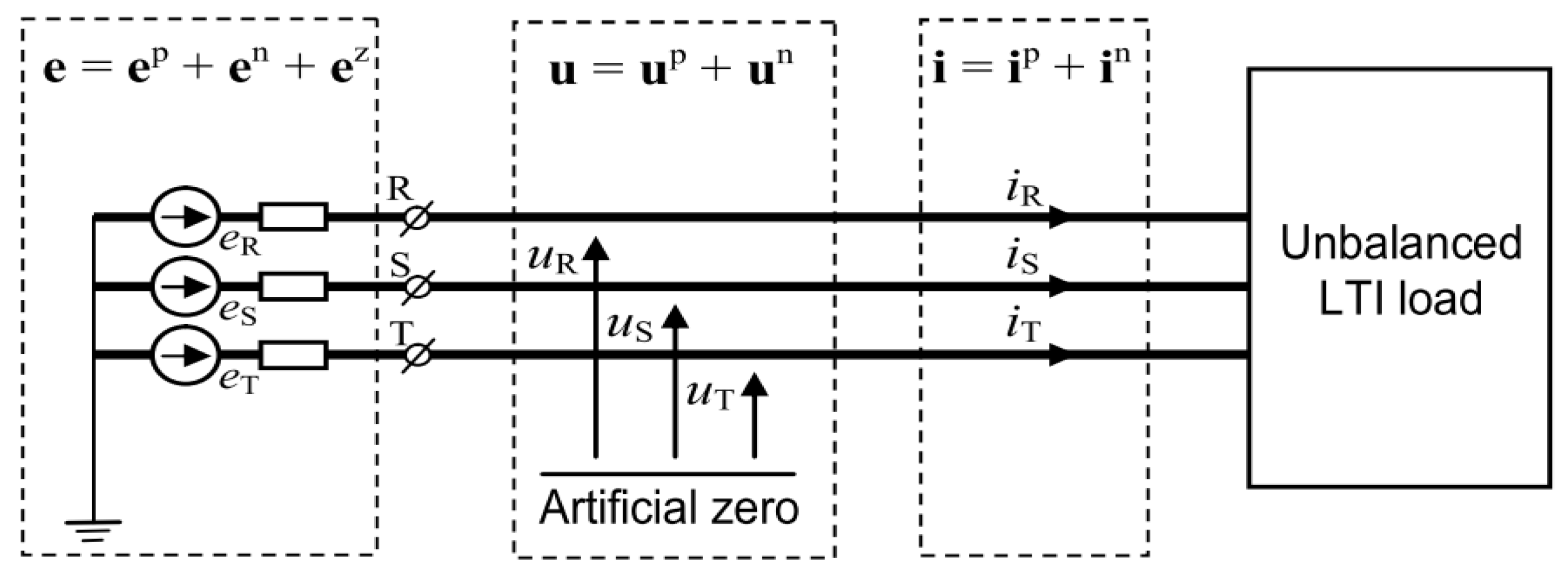
Asymmetry in the supply voltage in three-phase circuits disrupts the flow of currents. This worsens the efficiency of the distribution system and increases the problems in determining the mathematical model of the energy system. Among many power theories, the most accurate is the Currents' Physical Components (CPC) power theory, which tries to justify the physical essence of each component. Such knowledge can be used to improve efficiency and reduce transmission losses in the power system. The article discusses the method of mathematical decomposition of current components in the case of a three-wire line connecting an asymmetric power source with of linear time-invariant (LTI) loads. Special cases where irregularities appear in the results of calculations according to the CPC theory has been discussed. The method is illustrated with a numerical examples.
Keywords:
1. Introduction
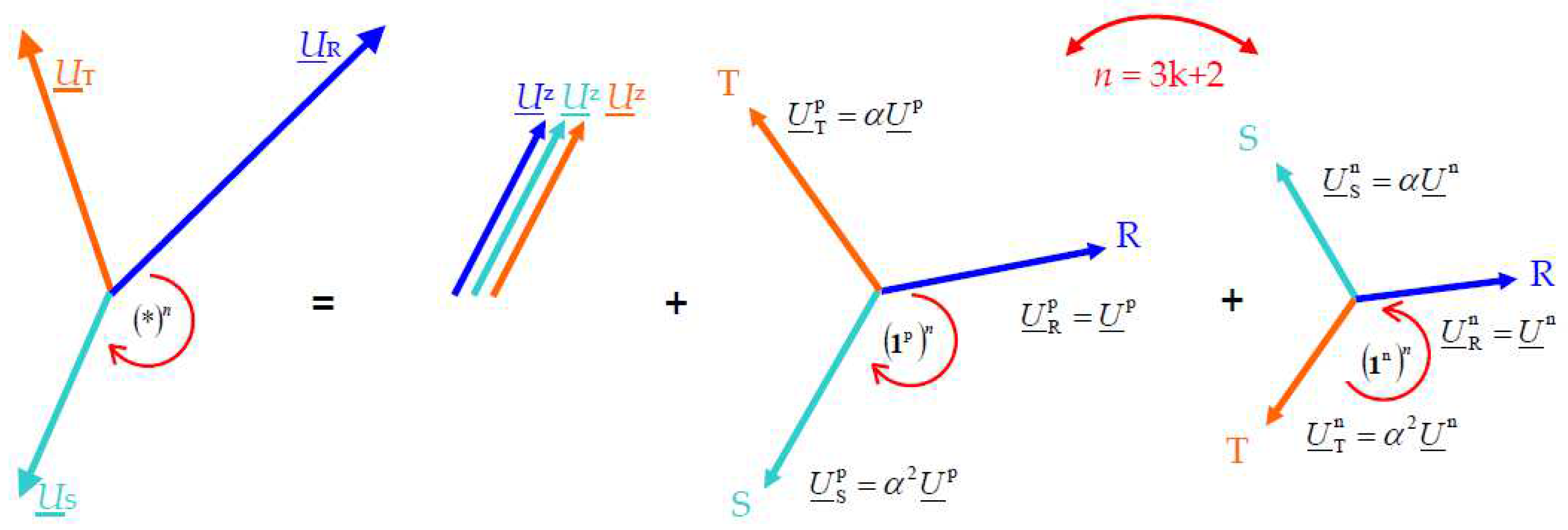
2. Shift of Vectors by 90°
3. Pitfalls in Determining the rms value of Voltage
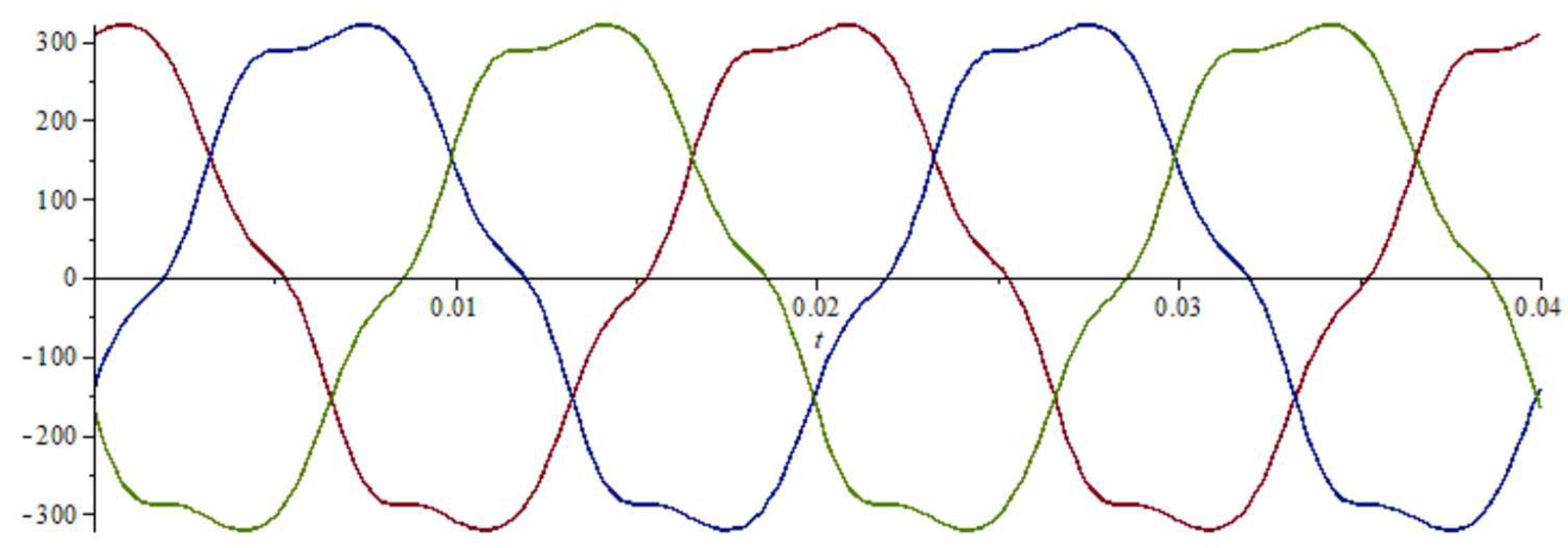
4. Notes on the Three-Phase Current Components in Time-Domain
4.1. Definition of Instantaneous Values of Three-Phase Symmetrical Voltage for Multiple Harmonics
4.2. Using of Symmetrical Components in the Case of Many Harmonics
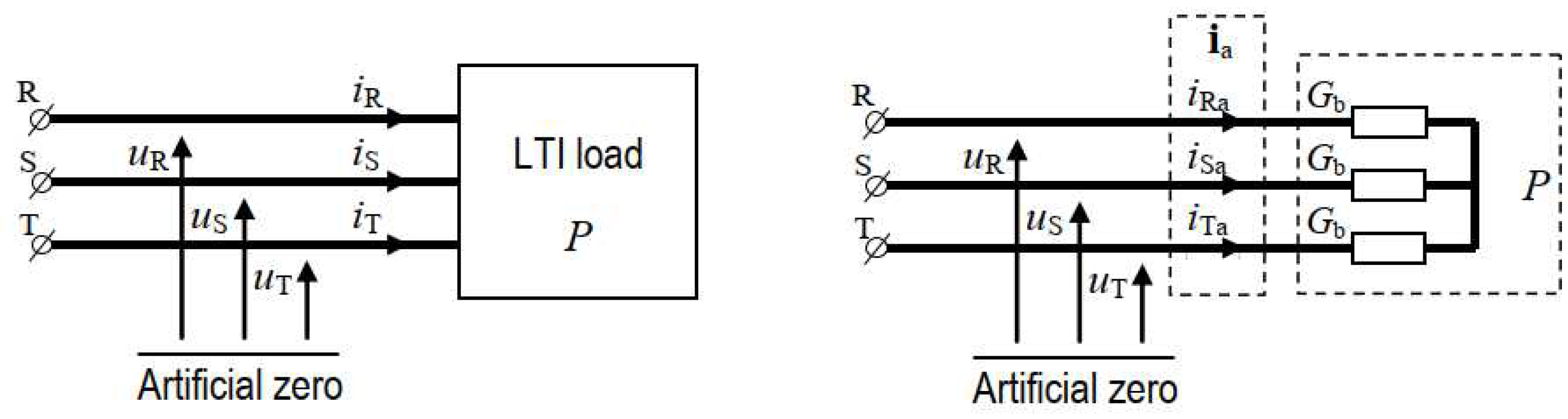
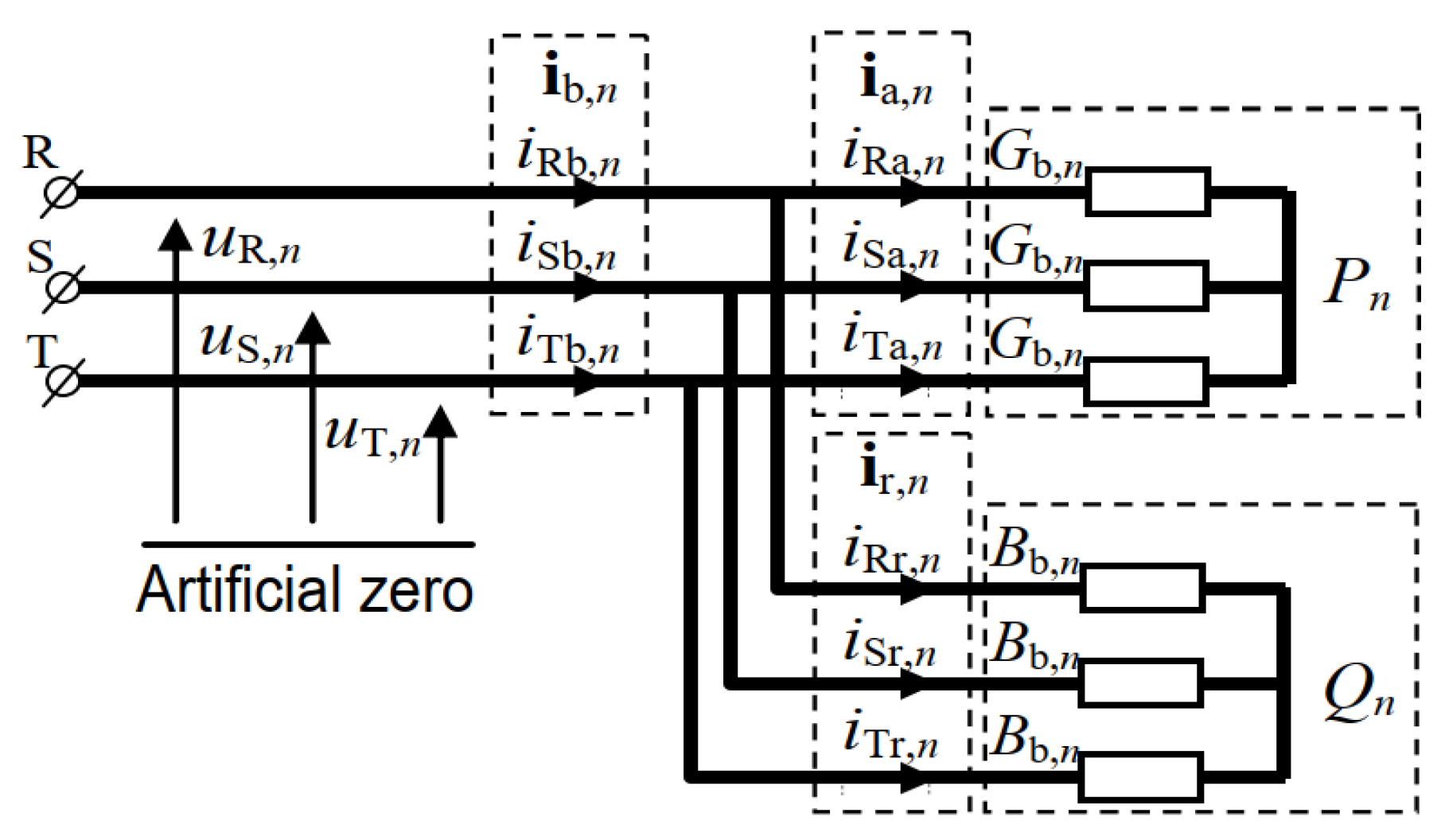
5. Revised CPC Theory Definitions
6. Conclusions
- The 90° shift of vectors discussed in point 2 is important in the case of time-domain notation and comparing calculation results with oscilloscope measurements. To deal with this problem, one can use the relationship (4), or each of the determined numerical values in the time domain can be shifted by a constant angle of -90°.
- The problem shown in point 3 concerns a special case when harmonics appear that do not participate in the transmission of the energy. An example is a situation when the load has a series capacitance, which, as is known, does not carry a DC component. In such a situation, it remains to use formula (8) only for those harmonics that are related to energetic interactions.
- The method of notation of three-phase waveforms, discussed in point 4, revealed the need to change the definition of symmetrical components (17) when the instantaneous values are described by periodic non-sinusoidal functions. Determining the symmetric components using multiplied three-phase unit vectors (19) improves the mathematical notation. This observation revealed the need to improve the development of algorithms determining the unbalanced components and parameters of reactive compensators. These issues should be considered in further research.
Symbols
| 1 | three phase symmetrical unit vector |
| a, b | Fourier series coefficients |
| α | rotation vector |
| Bb | balanced susceptance, S |
| C | capacitance, F |
| e | electromotive force, emf, V |
| φ | phase shift |
| Gb | balanced resistive load of conductance, S |
| Ge | equivalent conductance, S |
| i | vector of instantaneous currents in a three-phase system, A |
| I | vector of complex currents in a three-phase system, A |
| iR, iS, iT | instantaneous values of line currents, A |
| ia | active component of the current—three-phase vector, A |
| ir | reactive component of the current—three-phase vector, A |
| is | scattered component of the current—three-phase vector, A |
| iu | unbalanced component of the current—three-phase vector, A |
| N | set of harmonics |
| P | active power, W |
| Q | reactive power, var |
| R | resistance, Ω |
| sL | phase shift |
| t | time, s |
| T | the repetition period of the instantaneous value, rad/s |
| u | vector of instantaneous voltages in a three-phase system, V |
| U | vector of complex voltages in a three-phase system, V |
| uR, uS, uT | instantaneous voltage values relative to the virtual star point, V |
| ω1 | basic pulsation, rad/s |
| X | reactance, Ω |
| Yb | balanced admittance, S |
| Yd | voltage asymmetry dependent admittance, S |
| Ye | equivalent admittance, S |
| Yu | unbalanced admittance, S |
Subscripts, Superscripts
| R,S,T,N | phase and neutral wires |
| n | harmonic number |
| L | phase number, L = {R,S,T} |
| p, n, z | positive, negative, zero sequence |
Acronyms
| CPC | Currents’ Physical Components |
| crms | complex root mean square |
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zajkowski, K. Reactive power compensation in a three-phase power supply system in an electric vehicle charging station. Journal of Mechanical and Energy Engineering 2018, 2, 75–84. [Google Scholar] [CrossRef]
- Gubarevych O, et al. Research and assessment of the reliability of railway transport systems with induction motors. Energies 2023, 16, 6888. [Google Scholar] [CrossRef]
- Duer S, et al. Examination of multivalent diagnoses developed by a diagnostic program with an artificial neural network for devices in the electric hybrid power supply system House on Water. Energies 2021, 14, 2153. [Google Scholar] [CrossRef]
- Rosinski A, et al. Safety Analysis for the Operation Process of Electronic Systems Used Within the Mobile Critical Infrastructure in the Case of Strong Electromagnetic Pulse Impact. Theory and Applications of Dependable Computer Systems. DepCoS-RELCOMEX 2020. Advances in Intelligent Systems and Computing, vol 1173. Springer, Cham. [CrossRef]
- Zajkowski, K. An innovative hybrid insulation switch to enable/ disable electrical loads without overvoltages. E3S Web of Conf. 2017, 19, 01033. [Google Scholar] [CrossRef]
- Suproniuk, M. , Pas J. Analysis of electrical energy consumption in a public utility buildings. Przegląd Elektrotechniczny 2019, 95. [Google Scholar] [CrossRef]
- Duer S, Zajkowski K. Taking decisions in the expert intelligent system to support maintenance of a technical object on the basis information from an artificial neural network. Neural Computing and Appl. 2013, 23, 2185–2197. [Google Scholar] [CrossRef]
- Duer S, et al. Reliability Testing of Wind Farm Devices Based on the Mean-time Between Failures (MTBF). Energies 2023, 16, 1659. [CrossRef]
- Czarnecki LS, Bhattarai PD. A Method of Calculating LC Parameters of Balancing Compensators for AC Arc Furnaces. IEEE Trans. on Power Deliv. 2017, 32, 688–695. [Google Scholar] [CrossRef]
- Czarnecki LS, Bhattarai PD. Reactive Compensation of LTI Loads in Three-Wire Systems at Asymmetrical Voltage. Przegląd Elektrotechniczny 2015, 91, 7–11. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Reactive and unbalanced currents compensation in three-phase circuits under nonsinusoidal conditions. IEEE Trans 1989, IM-38, 754–459. [Google Scholar] [CrossRef]
- Czarnecki, L.S. , Almousa M., Adaptive balancing by reactive compensators of three-phase linear loads supplied by nonsinusoidal voltage from four-wire lines. Am. J. Electr. Power Energy Syst 2021, 10, 32–42. [Google Scholar] [CrossRef]
- Ginn, H. Chen G. Switching compensator control strategy based on CPC power theory, International School on Nonsinusoidal Currents and Compensation, Łagów, 2008.
- Czarnecki, L.S. , Hsu S.M. Thyristor controlled susceptances for balancing compensators operated under nonsinusoidal conditions. IEE Proc.-Electr. Power Appl 1994, 14. [Google Scholar]
- Zajkowski, K. , Rusica I., The method of calculating LC parameters of balancing compensators in a three-phase four-wire circuit for an unbalanced linear receiver. IOP Conf. Series: Materials Science and Engineering 2019, 564, 012134. [Google Scholar] [CrossRef]
- Zajkowski, K. Two-stage reactive compensation in a three-phase four-wire systems at nonsinusoidal periodic waveforms. Electric Power Systems Research 2020, 184, 106296. [Google Scholar] [CrossRef]
- Marcu, M. Popescu F.G., Niculescu T., Pana L., Handra A.D. Simulation of power active filter using instantaneous reactive power theory, 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), pp. 581-585, Bucharest.
- Haugan, T.S. Tedeschi E. Active power filtering under non-ideal voltage conditions using the conservative power theory, IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, 2015.
- Rosa, R.B. , Vahedi H., Godoy R.B., Pinto J.O.P., Al-Haddad K. Conservative Power Theory Used in NPC-Based Shunt Active Power Filter to Eliminate Electric Metro System Harmonics, 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, 2015.
- Zhu, L. , et al., Research on shunt active power filter based on the improved instantaneous reactive power theory, 2015 Sixth International Conference on Intelligent Control and Information Processing (ICICIP), pp. 459-464, Wuhan.
- Abdullah, A. , Biswal G.R., Roy A.K. Modeling and control of hybrid power filter using p-q theory, 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi.
- Busarello, T.D.C. , Pomilio J.A., Simões M.G. Passive Filter Aided by Shunt Compensators Based on the Conservative Power Theory. IEEE Transactions on Industry Applications 2016, 52, 3340–3347. [Google Scholar] [CrossRef]
- Hanzelka, Z. , Mondzik A. Different LC power filter topologies—effectiveness of reducing voltage distortion. Renewable Energy and Power Quality Journal 2016, 14. [Google Scholar]
- Lada, M.Y. , Mohamad S.S., Gani J.A.M., Nawawi M.R.M., Kim G.C. Reduction of harmonic using single phase shunt active power filter based on instantaneous power theory for cascaded multilevel inverter, 2016 IEEE International Conference on Power and Energy (PECon), Melaka.
- Mboving CSA., Hanzelka Z. Hybrid Power Active Filter - Effectiveness of Passive Filter on the Reduction of Voltage and Current Distortion. Electric Power Quality and Supply Reliability 2016.
- Tobola, A. Mikołajuk K. Multiobjective Optimization Approach to the Active Power Filter Control, Proc.of 17th International Conference Computational Problems Of Electrical Engineering (CPEE), 2016.
- Moghaddam, F.K. Farhangi S. Improvement of the stand-alone DFIG performance feeding nonlinear and unbalanced loads using active and reactive power theory, 2015 IEEE Conference on Energy Conversion (CENCON), pp. 128-133, Johor Baru.
- Zajkowski K, Rusica I, Palkova Z. The use of CPC theory for energy description of two nonlinear receivers. MATEC Web Conf. 2018, 178, 09008. [Google Scholar] [CrossRef]
- Zajkowski, K. , Duer S., Paś J., Pokorádi L. Cooperation of a Non-Linear Receiver with a Three-Phase Power Grid. Energies 2023, 16, 1418. [Google Scholar] [CrossRef]
- Zajkowski, K. The method of solutions of equations with coefficients that contain measurement errors, using artificial neural network. Neural Computing and Appl. 2014, 24, 431–439. [Google Scholar] [CrossRef]
- IEEE Trial use standard for the measurement of electric power quantities under sinusoidal, nonsinusoidal, balanced and unbalanced conditions. IEEE 1459-2000.
- IEEE standard definitions for the measurement of electric power quantities under sinusoidal, nonsinusoidal, balanced and unbalanced conditions. IEEE 1459-2010.
- Czarnecki, LS. Orthogonal Decomposition of the Currents in a 3-Phase Nonilnear Asymmetrical Circuit with a Nonsinusoidal Voltage Source. IEEE Trans. on Instr. and Measur. 1988, 37, 30–34. [Google Scholar] [CrossRef]
- Czarnecki, LS. Currents’ Physical Components (CPC) concept: a fundamental of Power Theory. Przegląd Elektrotechniczny 2008, 84, 28–37. [Google Scholar] [CrossRef]
- Czarnecki LS, Haley PM. Unbalanced Power in Four-Wire Systems and Its Reactive Compensation. IEEE Trans. on Power Deliv 2015, 30. [CrossRef]
- Czarnecki LS, Bhattarai PD. CPC−Βased Reactive Compensation of Linear Loads Supplied with Asymmetrical Non-sinusoidal Voltage. Annals University of Craiova 2019, 42, 1–9. [Google Scholar]
- Currents’ Physical Components (CPC) in systems with semi-periodic voltages and currents, International School on Nonsinusoidal Currents and Compensation (ISNCC)<italic>, </italic> Łagów.
- Czarnecki, L.S. Almousa M., Conversion of fixed-parameters compensator in four-wire system with nonsinusoidal voltage into adaptive compensator. Przegląd Elektrotechniczny 2021, 97. [Google Scholar]
- Czarnecki, L.S. , Almousa M. Adaptive Compensation of Reactive, Unbalanced and DC Currents of AC Arc Furnaces. Przegląd Elektrotechniczny 2023, 99. [Google Scholar]
- Jeltsema, D. Woude J. Currents’ Physical Components (CPC) in the time-domain: Single-phase systems, European Control Conference (ECC), Strasbourg, 2014.
- Martell, F. Izaguirre A., Macías M. CPC power theory for analysis of Arc Furnaces, International School on Nonsinusoidal Currents and Compensation (ISNCC), Łagów, 2015.
- Weixing Li, Rahmani B., Liu G. Expansion of Current Physical Components (CPC) to Three-Phase Four-Wire Systems under Non-Ideal Waveforms by the AUPQS. IEEE Conf 2016.
- Borges, A.M. , Alves S., Currents’ physical components (CPC): Case studies in single phase systems. IEEE Conf. 2018. [Google Scholar]
- Zajkowski K, Rusica I. Comparison of electric powers measured with digital devices relative to powers associated with distinctive physical phenomena. IOP Conf. Series: Materials Science and Engineering 2019, 564, 012133. [Google Scholar] [CrossRef]
- Zajkowski, K. Settlement of reactive power compensation in the light of white certificates. E3S Web of Conf. 2017, 19, 01037. [Google Scholar] [CrossRef]
- Zajkowski K, Smyczek J. Simulation of overvoltages for switching off lagging load from mains. 2nd International Industrial Simulation Conference 2004, p. 278-281, EUROSIS, 2004.
- Duer S, et al. Designing of an effective structure of system for the maintenance of a technical object with the using information from an artificial neural network. Neural Computing and Appl. 2013, 23, 913–925. [Google Scholar] [CrossRef]
- Duer S, et al. Analyses of the method development of decisions in an expert system with the use of information from an artificial neural network. MATEC Web Conf. 2018, 178, 07002. [Google Scholar] [CrossRef]
- Duer S, et al. Training of an artificial neural network in the diagnostic system of a technical object. Neural Computing and Appl. 2013, 22, 1581–1590. [Google Scholar] [CrossRef]
- Bhattarai PD, Czarnecki LS. Currents’ Physical Components (CPC) of the Supply Current of Unbalanced LTI Loads at Asymmetrical and Nonsinusoidal Voltage. Przegląd Elektrotechniczny 2017, 93, 30–35. [Google Scholar] [CrossRef]
- Fryze S, Active, reactive and apparent power in circuits with nonsinusoidal voltages and currents. Przegląd Elektrotechniczny 1931, 1932, 7, p. 193–203, 8, p 225.
- Zajkowski K, Duer S. Decomposition of the Voltages in a Three-Phase Asymmetrical Circuit with a Non-Sinusoidal Voltage Source. Energies 2023, 16, 7616. [Google Scholar] [CrossRef]
- Czarnecki LS, Haley PM. Power Properties of Four-Wire Systems at Nonsinusoidal Supply Voltage. IEEE Trans. on Power Deliv. 2016, 31, 513–521. [Google Scholar] [CrossRef]
- Czarnecki, LS. Why the Power Theory has a Limited Contribution to Studies on the Supply and Loading Quality?. 18th Int. Conf. on Harmonics and Quality of Power (ICHQP), 2018. [CrossRef]
- Czarnecki, LS. Degradation of the Energy Transfer Effectiveness Described in Terms of Currents’ Physical Components (CPC)-based Power Theory. Int. Symp. on Computer Science and Intelligent Controls (ISCSIC) 2017, 39–48. [Google Scholar] [CrossRef]
- Calamero N, et al. Defining the Unique Signatures of Loads Using the Currents’ Physical Components Theory and Z-Transform. IEEE Trans. on Industrial Informatics 2015, 11, 155–165. [Google Scholar] [CrossRef]
- Mikulovic J, Sekava T, Skrbio B. Currents’ physical component (CPC) power theory for three-phase four-wire systems. Mediterranean Conference on Power Generation Transmission Distribution and Energy Conversion (MedPower) 2016, 1–7. [CrossRef]
- Grasso F, et al. Improvement of Power Flow Analysis based on Currents’ Physical Component (CPC) Theory. IEEE Int. Symp. on Circuits and Systems (ISCAS) 2018. [CrossRef]
- Samet H, Ghanbari T, Ghaisari J. Maximum performance of electric arc furnace by optimal setting of the series reactor and transformer taps using a nonlinear model. IEEE Trans. on Power Deliv. 2015, 30, 764–772. [Google Scholar] [CrossRef]
- Bielecki S, Skoczkowski T. An enhanced concept of Q-power management. Energy 2018, 162, 335–353. [Google Scholar] [CrossRef]
- Czarnecki, L.S. oups T.N., Working and Reflected Active Powers of Three-Phase Loads, 12th International School on Nonsinusoidal Currents and Compensation (ISNCC), Łagów, 2015.
- Izaguirre, A.R. Macias M.E., Martell F., Accurate CPC Power Analysis under Extreme EAF’s Distortion Conditions. 12th International School on Nonsinusoidal Currents and Compensation (ISNCC) Łagów, 2015.
- Busarello, T.D.C. Péres A., Mortezaei A., Simões M.G., Application of the current decomposition of the Conservative Power Theory in Distributed Energy Resources, 12th IEEE International Conference on Industry Applications (INDUSCON), Curitiba, 2016.
- Busarello, T.D.C. , Mortezaei A., Péres A., Simões M.G. Application of the Conservative Power Theory Current Decomposition in a Load Power-Sharing Strategy Among Distributed Energy Resources. IEEE Transactions on Industry Applications 2018, 54. [Google Scholar] [CrossRef]
- Siergiejczyk, M. , Pas J., Rosinski A. Modeling of Process of Maintenance of Transport Systems Telematics with Regard to Electromagnetic Interferences. Tools Of Transport Telematics 2015, 531, 99–107. [Google Scholar]
- Paś, J. , Rosiński A., Wisnios M., Stawowy M. Assessing the Operation System of Fire Alarm Systems for Detection Line and Circuit Devices with Various Damage Intensities. Energies 2022, 15, 3066. [Google Scholar] [CrossRef]
- Popescu, M. Bitoleanu A., Suru V. Currents’ physical components theory implementation in shunt active power filtering for unbalanced loads. International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC), Zielona Góra.
- Wisnios, M. , Pas J. The assessment of exploitation process of power for access control system. E3S Web of Conferences 2017, 19, 01034. [Google Scholar] [CrossRef]
- Busarello, T.D.C. Simões M.G. Power quality enhancement by means of shunt compensators based on the conservative power theory, Clemson University Power Systems Conference (PSC), Clemson, SC, 2015.
- Haugan, T.S. Tedeschi E. Reactive and harmonic compensation using the conservative power theory, Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, 2015.
- Janabi, A. Wang B. Hybrid matrix converter based on instantaneous reactive power theory, IECON 2015 - 41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, 2015.
- Javadi, A. Hamadi A., Al-Haddad K. Three-phase power quality device tor weak Systems based on SRF and p-q theory controller, IECON 2015 - 41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, 2015.
- Kong, X. Yuan Y., Huang H., Wang Y. Overview of the instantaneous reactive power theory in three-phase systems, 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), pp. 2331-2336, Changsha, 2015.
- Abbasi, M. Tousi B. Novel controllers based on instantaneous p-q power theory for transformerless SSSC and STATCOM, 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), Milan.
- Hanzelka, Z. Blueprint for the combinatorial strategy in transactive energy-based control mechanism by using energy flexibility platform and interface, CIRED - Open Access Proceedings Journal, 2017.
- Mortezaei, A. Simões M., Savaghebi M., Guerrero J., Durra A.A. Cooperative control of multi-master-slave islanded microgrid with power quality enhancement based on conservative power theory, 2017 IEEE Power & Energy Society General Meeting, Chicago.
- Oruganti, V.S.R. V, Bubshait A.S., Dhanikonda V.S.S.S., Simões M.G. Real-time control of hybrid active power filter using conservative power theory in industrial power system. IET Power Electronics 2017, 10, 196–207. [Google Scholar] [CrossRef]
- Salim, C. Five-level series active power filter performances based on modified instantaneous reactive power theory for harmonic voltage disturbances compensation, 2017 5th International Conference on Electrical Engineering - Boumerdes (ICEE-B), Boumerdes.
- Savant, V. Kadrolkar A., Gupte S. Bidirectional tie-line inverter based on instantaneous reactive power theory for microgrid applications, 2017 Second International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore.
- Taher, S.A. Alaee M.H., Dehghani A.Z., Model predictive control of PV-based shunt active power filter in single phase low voltage grid using conservative power theory, 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad.
- Tobała, A. Mikołajuk K. Reference Signal Detection for Voltage Harmonic Damping in Three-Phase Systems, Proc.of 18th Int.Conf.on Computational Problems Of Electrical Engineering (CPEE), 2017.
- Alaee, M.H. Taher S.A., Dehghani A.Z. Improved performance of single-phase shunt active power filter by using conservative power theory and model predictive control, 2018 9th Annual Power Electronics, Drives Systems and Technologies Conference (PEDSTC), Tehran.
- Harirchi, F. , Simoes M.G. Enhanced Instantaneous Power Theory Decomposition for Power Quality Smart Converter Applications. IEEE Trans. on Power Electron. 2018. [Google Scholar] [CrossRef]
- Kumar, H. Patra J., Yadav A., Pal N., Power quality assessment and improvement of 3-phase 3-wire non-linear system using instantaneous power theory based DSTATCOM, 4th International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, 2018.
- Souza, W.A. Liberado E.V., da Silva L.C.P., Paredes H.K.M., Marafão F.P. Load analyser using conservative power theory, International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC), Zielona Góra.
- Busarello, T.D.C. Pomilio J.A. Synergistic operation of distributed compensators based on the conservative power theory, IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference, 2015 (COBEP/SPEC), Fortaleza.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




