Kruskal-Szekeres Equivalent Coordinates for the FRW Metric

1. Introduction

The structure of the flat FRW metric can be shown to be quite similar to the structure of the interior Schwarzschild metric. When expressing the Schwarzschild metric in Kruskal-Szekeres coordinates, physicists have found that the Schwarzschild metric is actually describing multiple symmetric regions.

In this paper, we wish to determine if the flat FRW metric is also describing more than one spacetime. This is done by transforming the coordinates of the flat FRW metric into Kruskal-Szekeres equivalent coordinates. If this can be achieved, then it can be proven that the flat FRW spacetime in fact has two branches instead of one and those branches would be CPT symmetric mirrors of each other.

2. Transforming the Coordinates of the FRW Spacetime

The flat FRW metric is typically given in the following form:

$$d{\tau }^2=d{t}^{\prime 2}-a{\left(t^{\prime }\right)}^{2}d{r}^2-a{\left(t^{\prime }\right)}^{2}d{\mathsf{\Omega }}^2$$

(1)

In this paper, we will be focused on the $dt$ and $dr$ terms in the metric. We show the time coordinate as $t^{\prime }$ in Equation (1) because we will begin by changing the time coordinate so that we have the inverse of the scale factor multiplying the temporal term. Therefore, we define:

$$\begin{array}{c}\hfill d{t}^{\prime }={\displaystyle \frac{1}{a\left(t^{\prime }\right)}}dt\end{array}$$

(2)

And from this we see that:

$$\begin{array}{c}\hfill t=\int a\left(t^{\prime }\right)d{t}^{\prime }\end{array}$$

(3)

Since we have t as a function of $t^{\prime }$, we are able to express the scale factor a as a function of t instead of $t^{\prime }$ and rewrite the flat FRW metric as (without the angular term):

$$d{\tau }^2={\displaystyle \frac{1}{a{\left(t\right)}^2}}d{t}^2-a{\left(t\right)}^{2}d{r}^2$$

(4)

Contrast this with the interior Schwarzschild metric given below:

$$d{\tau }^2={\displaystyle \frac{1}{\frac{u}{r}-1}}d{r}^2-\left({\displaystyle \frac{u}{r}}-1\right)d{t}^2$$

(5)

Now it is important to keep in mind that in the interior Schwarzschild metric, r is the timelike coordinate and t is the spacelike coordinate, which is opposite to the FRW coordinate labels.

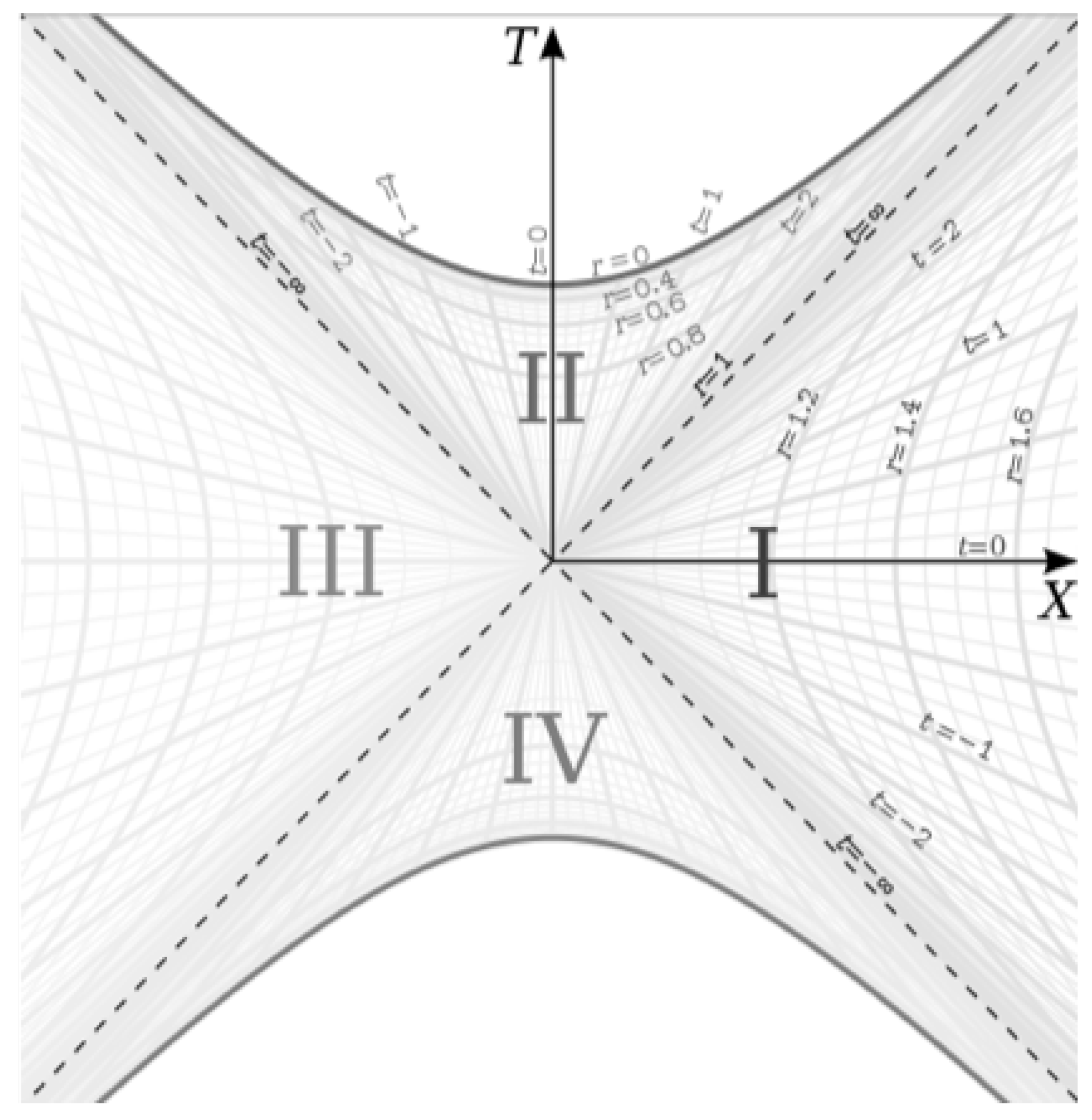
Comparing Equations (4) and (5), we see that (when ignoring the angular terms), they have the same form with a time-dependent scale factor multiplying the spacelike coordinate and the inverse of the scale factor multiplying the timelike coordinate. This is interesting because the Schwarzschild metric, when expressed in Kruskal-Szekeres coordinates, is shown to have two ’branches’ in its geometry. In Schwarzschild coordinates, the Schwarzschild metric has an exterior solution and an interior solution. In Kruskal-Szekeres coordinates, we get an additional exterior region and an additional interior region, as can be seen in the Kruskal-Szekeres coordinate chart below [1]:

So the metric in Schwarzschild coordinates gives regions I and II in Figure 1 and when converting to Kruskal-Szekeres coordinates, we get the additional regions III and IV. Since the metrics have such similar structures, we’d like to see if we can get an additional branch for the flat FRW metric by doing a similar coordinate transformation for that metric.

We will define the new coordinates for the FRW metric as follows:

$$\begin{array}{c}\hfill T=f\left(t\right)cosh\left({\displaystyle \frac{r}{\mu }}\right)\\ \hfill X=f\left(t\right)sinh\left({\displaystyle \frac{r}{\mu }}\right)\end{array}$$

(6)

Where $\mu$ is a constant with units of time. Our goal is to find the function $f\left(t\right)$ for the FRW metric. If we take the differentials of T and X we get:

$$\begin{array}{c}\hfill dT=\dot{f}\left(t\right)cosh\left({\displaystyle \frac{r}{\mu }}\right)dt+{\displaystyle \frac{f\left(t\right)}{\mu }}sinh\left({\displaystyle \frac{r}{\mu }}\right)dr\\ \hfill dX=\dot{f}\left(t\right)sinh\left({\displaystyle \frac{r}{\mu }}\right)dt+{\displaystyle \frac{f\left(t\right)}{\mu }}cosh\left({\displaystyle \frac{r}{\mu }}\right)dr\end{array}$$

(7)

Where $\dot{f}\left(t\right)$ is ${\displaystyle \frac{df}{dt}}$. Next, we find $d{T}^2-d{X}^2$:

$$\begin{array}{c}\hfill d{T}^2-d{X}^2=\dot{f}{\left(t\right)}^{2}d{t}^2-{\left({\displaystyle \frac{f\left(t\right)}{\mu }}\right)}^{2}d{r}^2\end{array}$$

(8)

Next, we assume the metric in these coordinates will have the form:

$$\begin{array}{c}\hfill d{\tau }^2=g{\left(t\right)}^2\left[d{T}^2-d{X}^2\right]\end{array}$$

(9)

Comparing Equations (8) and (9) with Equation (4), we can derive the constraints we need to determine $f\left(t\right)$ and $g\left(t\right)$. First, we recognize that:

$$\begin{array}{cc}\hfill g\left(t\right)\dot{f}\left(t\right)& ={\displaystyle \frac{1}{a\left(t\right)}}\hfill \\ \hfill \dot{f}\left(t\right)& ={\displaystyle \frac{1}{g\left(t\right)a\left(t\right)}}\hfill \end{array}$$

(10)

And,

$$\begin{array}{cc}\hfill g\left(t\right){\displaystyle \frac{f\left(t\right)}{\mu }}& =a\left(t\right)\hfill \\ \hfill g\left(t\right)& ={\displaystyle \frac{a\left(t\right)\mu }{f\left(t\right)}}\hfill \end{array}$$

(11)

If we substitute Equation (11) into Equation (10), we get the following differential equation for $f\left(t\right)$:

$$\begin{array}{c}\hfill \dot{f}\left(t\right)={\displaystyle \frac{1}{\mu }}{\displaystyle \frac{f\left(t\right)}{a{\left(t\right)}^2}}\end{array}$$

(12)

Equation (12) is a differential equation that allows us to solve for $f\left(t\right)$ given $a\left(t\right)$.

Let us first consider the matter-dominated FRW Spacetime. In $t^{\prime }$ coordinates, we know that $a\left(t^{\prime }\right)\propto {\left(t^{\prime }\right)}^{{\displaystyle \frac{2}{3}}}$. We can make this an equality with the $\mu$ constant such that $a\left(t^{\prime }\right)={\left({\displaystyle \frac{t^{\prime }}{\mu }}\right)}^{{\displaystyle \frac{2}{3}}}$. We can integrate this to get t as a function of $t^{\prime }$ per Equation (3). The integration gives us:

$$\begin{array}{cc}\hfill {\displaystyle \frac{t}{\mu }}& ={\displaystyle \frac{3}{5}}{\left({\displaystyle \frac{t^{\prime }}{\mu }}\right)}^{{\displaystyle \frac{5}{3}}}\hfill \\ \hfill {\displaystyle \frac{t^{\prime }}{\mu }}& ={\left({\displaystyle \frac{5}{3}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{3}{5}}}\hfill \end{array}$$

(13)

With this, we can get the scale factor as a function of t:

$$\begin{array}{c}\hfill a\left(t\right)={\left({\displaystyle \frac{5}{3}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{2}{5}}}\end{array}$$

(14)

Plugging Equation (14) into Equation (12), we can solve for the function $f\left(t\right)$:

$$\begin{array}{c}\hfill f\left(t\right)=e^{3{\left({\displaystyle \frac{5}{3}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{1}{5}}}}\end{array}$$

(15)

We can repeat the same procedure for the radiation dominated case where $a\left(t^{\prime }\right)\propto {\left(t^{\prime }\right)}^{{\displaystyle \frac{1}{2}}}$ and therefore $a\left(t^{\prime }\right)={\left({\displaystyle \frac{t^{\prime }}{\mu }}\right)}^{{\displaystyle \frac{1}{2}}}$. In this case, ${\displaystyle \frac{t^{\prime }}{\mu }}={\left({\displaystyle \frac{3}{2}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{2}{3}}}$. Solving for a we get:

$$\begin{array}{c}\hfill a\left(t\right)={\left({\displaystyle \frac{3}{2}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{1}{3}}}\end{array}$$

(16)

And the solution for $f\left(t\right)$ with the radiation dominated scale factor is:

$$\begin{array}{c}\hfill f\left(t\right)=e^{2{\left({\displaystyle \frac{3}{2}}{\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{1}{3}}}}\end{array}$$

(17)

And $g\left(t\right)$ can be found for each case using Equation (11).

We can give the general formulas for $a\left(t\right)$ and $f\left(t\right)$ for scale factors of the form $a\left(t^{\prime }\right)={\left({\displaystyle \frac{t^{\prime }}{\mu }}\right)}^{\beta }$:

$$\begin{array}{c}\hfill a\left(t\right)={\left((\beta +1){\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{\beta }{\beta +1}}}\end{array}$$

(18)

$$\begin{array}{c}\hfill f\left(t\right)=e^{{\displaystyle \frac{1}{1-\beta }}{\left((\beta +1){\displaystyle \frac{t}{\mu }}\right)}^{{\displaystyle \frac{1-\beta }{1+\beta }}}}=e^{{\displaystyle \frac{1}{1-\beta }}a{\left(t\right)}^{{\displaystyle \frac{1-\beta }{\beta }}}}\end{array}$$

(19)

And the full metric in these coordinates is given by:

$$\begin{array}{c}\hfill d{\tau }^2=a{\left(t\right)}^2\left({\displaystyle \frac{{\mu }^2}{f{\left(t\right)}^2}}\left[d{T}^2-d{X}^2\right]-r^{2}d{\mathsf{\Omega }}^2\right)\end{array}$$

(20)

So we have successfully found Kruskal-Szekeres equivalent coordinates for the FRW metric. The coordinate chart can be constructed from:

$$\begin{array}{c}\hfill T^2-X^2=f{\left(t\right)}^2\end{array}$$

(21)

Something interesting to note here is that for both the matter dominated and radiation dominated cases, when $t=0$, $f\left(t\right)=1$. This means that the singularity of the FRW metric in these coordinates is at $T=1$ (when $X=0$), which is also where the Schwarzschild singularity resides. Furthermore, if we again consider the $X=0$ case, as t goes to infinity in the FRW spacetime, $f\left(t\right)$ and therefore T also go to infinity.

In Figure 1 we see that the spacetime of the interior Schwarzschild metric (regions II and IV) ends at $T=\pm 1$ (for $X=0$). Keep in mind that for the FRW metric, the hyperbolas on the diagram for $T>1$ (not shown) are constant time t coordinates and the hyperbolic angles are constant space r coordinates, opposite to the labeling for the Schwarzschild metric.

So what we see is that the FRW spacetime fills the missing part of this coordinate chart. The FRW metric occupies all the space on the coordinate chart not covered by the Schwarzschild metric, and the hyperbolas representing the Schwarzschild and FRW singularities are coincident, indicating that they are perhaps two sides of the same singularity.

3. The Antiverse

We have shown that with a coordinate transformation, the FRW spacetime can be mapped onto the Kruskal-Szekeres coordinate chart. This fact has very important consequences because just like the interior Schwarzschild metric exists in both regions II and IV, the FRW metric also resides in both quadrants. This fact implies that if the FRW spacetime is indeed the spacetime of our Universe, then there exists an Antiverse on the other side of the Big Bang. In region II, time moves toward the future when going upward on the diagram. In region IV, time moves toward the future when going down the diagram, so it is as though the Universe and Antiverse are moving in opposite directions of time. Left and right are also swapped when going from the Universe to Antiverse. We know this because in region II, the negative hyperbolic angles are on the left and the positive ones are on the right. In region IV, the opposite is true.

We can further conjecture that since the Anitverse moves in the opposite direction of time compared to the Universe, it is likely made of mostly anti-matter as opposed to our Universe which is mostly matter. This would mean that the pair of Universes are CPT symmetric. They are perfect mirrors of each other, and this quality may explain the absence of antimatter after the Big Bang in our Universe. At creation, two CPT symmetric Universes were created. So the reason we don’t see the missing anti-matter in our Universe is because it is contained in the mirror Antiverse on the other side of the Big Bang.

4. Conclusions

The coordinates of the FRW metric were transformed into Kruskal-Szekeres equivalent coordinates. Doing this revealed that the FRW metric fills the empty regions on the Kruskal-Szekeres coordinate chart beyond the Schwarzschild singularity.

On the Kruskal-Szekeres coordinate chart, the hyperbolas representing the Schwarzschild and FRW singularities are coincident, implying that the singularities may be connected in some way.

By expressing the FRW metric in Kruskal-Szekeres equivalent coordinates, we see that just as with the Schwarzschild metric, the FRW metric actually describes two CPT symmetric spacetimes. This implies the existence of a mirror Anitverse in which the anti-matter that seems to be missing from our Universe after creation may reside.