NUVO Metric and Geodesic Derivations - Part 3 of the NUVO Theory Series

1. Introduction

Building on the scalar formalism developed in Paper 1, where the conformal field $\lambda (t,r,v)$ was derived from first principles and shown to influence proper time, inertial response, and energy density, this work extends the NUVO framework into a covariant geometric setting. We now examine how $\lambda$ can be used to construct a conformal metric and how this metric governs the motion of matter through modified geodesic equations.

Rather than treating the scalar field as an external modulator of physical laws, we interpret it as generating an effective geometry. This allows us to compute Christoffel symbols, analyze the geodesic equation, and predict deviations from general relativity, especially in regimes where velocity-dependent effects become significant.

The geodesic response to $\lambda$ introduces a natural separation between position-sensitive and velocity-sensitive inertia—what we term pinertia and sinertia, respectively. These concepts emerge as geometric consequences of motion in the conformally scaled metric and provide new tools for interpreting acceleration, force, and free-fall in NUVO theory.

In the sections that follow, we construct the conformal metric tensor, derive the connection coefficients and geodesic structure, and present both analytical results and numerical simulations. Our goal is to establish the scalar field not only as a modulator of dynamics but as the generator of a self-consistent flat-space geometry.

2. Conformal Transformation and Metric Derivation

NUVO theory begins with the premise that flat spacetime—described in Minkowski form—can be dynamically modulated by a scalar field $\lambda (t,r,v)$, without requiring curvature in the traditional Riemannian sense [1]. This modulation arises from the local instantaneous energy state of the test particle and reflects a bidirectional coupling between mass and space, captured respectively by pinertia and sinertia. This scalar field treatment parallels standard methods in field theory, while introducing velocity-dependent structure through the conformal factor $\lambda (t,r,v)$.

2.1. Conformal Transformation of Flat Space

We consider the flat Minkowski metric in spherical coordinates $(t,r,\theta ,\varphi )$ as the background geometry:

$$d{s}_0^2=-c^{2}d{t}^2+d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\varphi }^2.$$

NUVO applies a scalar conformal transformation to this background via a conformal factor $\lambda (t,r,v)$:

$$d{s}^2={\lambda }^2(t,r,v)d{s}_0^2,$$

so that the modulated line element becomes:

$$d{s}^2={\lambda }^2(t,r,v)\left[-c^{2}d{t}^2+d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\varphi }^2\right].$$

(1)

2.2. Definition of the Conformal Factor $\lambda (t,r,v)$

The scalar field $\lambda (t,r,v)$ is defined by the energy state of the particle as a sum of its relativistic kinetic energy and Newtonian gravitational potential energy, normalized by its rest energy $m{c}^2$:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2\left(t\right)}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

(2)

This form ensures that $\lambda (t,r,v)>1$ for all physical values of v and r, preserving the positivity and non-degeneracy of the conformally scaled metric. This modification strengthens the link between inertial modulation and geometric curvature in NUVO’s flat-space interpretation.

• The **instantaneous velocity** $v\left(t\right)$ must be used to reflect the physical state of the particle at each moment, rather than a relative frame-based velocity.
• The gravitational potential term uses the Newtonian form $-GM/r$, valid in weak fields and compatible with orbital-scale systems.
• The expression is dimensionless and normalized to the rest energy of the particle, ensuring the scalar modulation is always relative to the particle’s own inertial frame.

2.3. Interpretation of $\lambda$ in NUVO Theory

The conformal factor $\lambda (t,r,v)$ serves as the scalar field that modulates all metric components. Physically, this transforms the experience of time and space for the particle:

• Time intervals are scaled by $\lambda$, such that the proper time $d\tau$ satisfies $d\tau =\lambda dt$.
• Spatial distances are likewise scaled, introducing dilation effects that correspond to acceleration, not merely velocity.
• This modulation is dynamic, varying with time, position, and motion state, enabling predictions of real physical deviations such as those observed in satellite-based clocks.

This approach breaks from the pseudo-Riemannian tradition of General Relativity by preserving a globally flat background and introducing dynamical scaling instead of geometric curvature. It also avoids the requirement of stress-energy tensors to drive spacetime deformation; the modulation arises solely from the particle’s own energy state, anchored in pinertia and sinertia.

2.4. Conformal Metric Tensor

From Equation 1, the metric tensor in spherical coordinates becomes:

$$g_{\mu \nu }(t,r,v)={\lambda }^2(t,r,v)·{\eta }_{\mu \nu },$$

(3)

where ${\eta }_{\mu \nu }$ is the standard Minkowski metric in spherical form. Explicitly, the components are:

$$g_{\mu \nu }(t,r,v)={\lambda }^2(t,r,v)\left[\begin{array}{cccc}-c^2& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& r^2& 0\\ 0& 0& 0& r^2{sin}^2\theta \end{array}\right].$$

This metric will now be used to compute the Christoffel symbols and formulate the geodesic equations that determine free-fall motion in NUVO space.

3. Christoffel Symbol Derivation

To describe the motion of a test particle under the NUVO conformal metric, we require the Christoffel symbols ${\mathsf{\Gamma }}_{\alpha \beta }^{\mu }$ derived from the conformally modulated metric tensor $g_{\mu \nu }(t,r,v)$. These symbols encode how local geometric structure affects particle motion and are used to construct the geodesic equation.

3.1. General Formula for Christoffel Symbols

The Christoffel symbols for a given metric $g_{\mu \nu }$ are defined as [2]:

$${\mathsf{\Gamma }}_{\alpha \beta }^{\mu }={\displaystyle \frac{1}{2}}{g}^{\mu \sigma }\left({\partial }_{\alpha }{g}_{\beta \sigma }+{\partial }_{\beta }{g}_{\alpha \sigma }-{\partial }_{\sigma }{g}_{\alpha \beta }\right),$$

(4)

where $g^{\mu \sigma }$ is the inverse metric and ${\partial }_{\alpha }$ denotes partial differentiation with respect to coordinate $x^{\alpha }$.

For a conformally flat metric of the form

$$g_{\mu \nu }={\lambda }^2(t,r,v)·{\eta }_{\mu \nu },$$

where ${\eta }_{\mu \nu }$ is the Minkowski metric, the Christoffel symbols simplify to:

$${\mathsf{\Gamma }}_{\alpha \beta }^{\mu }={\displaystyle \frac{1}{\lambda }}\left({\delta }_{\alpha }^{\mu }{\partial }_{\beta }\lambda +{\delta }_{\beta }^{\mu }{\partial }_{\alpha }\lambda -{\eta }^{\mu \sigma }{\eta }_{\alpha \beta }{\partial }_{\sigma }\lambda \right),$$

(5)

where ${\delta }_{\alpha }^{\mu }$ is the Kronecker delta.

3.2. Corrected Derivatives of $\lambda (t,r,v)$

We use the corrected NUVO conformal factor:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1+\frac{v^2\left(t\right)}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

(6)

The partial derivatives required for the Christoffel symbols are:

3.2.0.1. Radial derivative:

$${\displaystyle \frac{\partial \lambda }{\partial r}}=-{\displaystyle \frac{GM}{r^2{c}^2}}.$$

(7)

3.2.0.2. Time derivative (via chain rule):

$${\displaystyle \frac{\partial \lambda }{\partial t}}=-{\displaystyle \frac{1}{2}}·{\left(1+{\displaystyle \frac{v^2}{c^2}}\right)}^{-3/2}·{\displaystyle \frac{2v}{c^2}}·{\displaystyle \frac{dv}{dt}}=-{\displaystyle \frac{v}{c^2{\left(1+\frac{v^2}{c^2}\right)}^{3/2}}}·{\displaystyle \frac{dv}{dt}}.$$

(8)

3.3. Christoffel Symbols with Spherical Symmetry

In a spherically symmetric context (neglecting angular motion for now), many Christoffel symbols vanish. The non-zero components include:

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{tr}^t& ={\mathsf{\Gamma }}_{rt}^t={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{tt}^t& ={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial t}},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{tt}^r& ={\displaystyle \frac{c^2}{{\lambda }^3}}{\displaystyle \frac{\partial \lambda }{\partial r}},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{rr}^r& ={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{rt}^r& ={\mathsf{\Gamma }}_{tr}^r={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial t}}.\hfill \end{array}$$

(13)

These terms encode how the evolving scalar field $\lambda (t,r,v)$ modulates acceleration in both time and space directions, providing the geometric basis for NUVO’s generalized geodesic motion.

3.4. Summary of Non-Zero Christoffel Symbols

The following table summarizes the non-vanishing Christoffel symbols for the NUVO conformal metric in spherical coordinates, under the assumption of spherical symmetry and radial dependence only:

Table 1. Non-zero Christoffel symbols for the NUVO metric in spherical symmetry.

Symbol	Expression
${\mathsf{\Gamma }}_{tr}^t={\mathsf{\Gamma }}_{rt}^t$	${\displaystyle \frac{1}{\lambda }\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{tt}^r$	${\displaystyle \frac{c^2}{{\lambda }^3}\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{rr}^r$	${\displaystyle \frac{1}{\lambda }\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{\theta \theta }^r$	$-r$
${\mathsf{\Gamma }}_{\varphi \varphi }^r$	$-r{sin}^2\theta$
${\mathsf{\Gamma }}_{r\theta }^{\theta }={\mathsf{\Gamma }}_{\theta r}^{\theta }$	${\displaystyle \frac{1}{r}}$
${\mathsf{\Gamma }}_{r\varphi }^{\varphi }={\mathsf{\Gamma }}_{\varphi r}^{\varphi }$	${\displaystyle \frac{1}{r}}$
${\mathsf{\Gamma }}_{\varphi \varphi }^{\theta }$	$-sin\theta cos\theta$
${\mathsf{\Gamma }}_{\theta \varphi }^{\varphi }={\mathsf{\Gamma }}_{\varphi \theta }^{\varphi }$	$cot\theta$

Non-zero Christoffel symbols for the NUVO metric in spherical symmetry.

Table 1. Non-zero Christoffel symbols for the NUVO metric in spherical symmetry.

Symbol	Expression
${\mathsf{\Gamma }}_{tr}^t={\mathsf{\Gamma }}_{rt}^t$	${\displaystyle \frac{1}{\lambda }\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{tt}^r$	${\displaystyle \frac{c^2}{{\lambda }^3}\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{rr}^r$	${\displaystyle \frac{1}{\lambda }\frac{\partial \lambda }{\partial r}}$
${\mathsf{\Gamma }}_{\theta \theta }^r$	$-r$
${\mathsf{\Gamma }}_{\varphi \varphi }^r$	$-r{sin}^2\theta$
${\mathsf{\Gamma }}_{r\theta }^{\theta }={\mathsf{\Gamma }}_{\theta r}^{\theta }$	${\displaystyle \frac{1}{r}}$
${\mathsf{\Gamma }}_{r\varphi }^{\varphi }={\mathsf{\Gamma }}_{\varphi r}^{\varphi }$	${\displaystyle \frac{1}{r}}$
${\mathsf{\Gamma }}_{\varphi \varphi }^{\theta }$	$-sin\theta cos\theta$
${\mathsf{\Gamma }}_{\theta \varphi }^{\varphi }={\mathsf{\Gamma }}_{\varphi \theta }^{\varphi }$	$cot\theta$

Non-zero Christoffel symbols for the NUVO metric in spherical symmetry.

4. Geodesic Equation and Free-Fall Solutions

In NUVO theory, motion is governed by geodesics of the conformally scaled flat-space metric. Despite the global flatness of the background, the dynamic scalar field $\lambda (t,r,v)$ modulates the structure of spacetime locally, altering the paths of free-falling particles.

4.1. Geodesic Equation Formulation

The geodesic equation for a test particle in a spacetime with metric $g_{\mu \nu }$ is:

$${\displaystyle \frac{d^2{x}^{\mu }}{d{\tau }^2}}+{\mathsf{\Gamma }}_{\alpha \beta }^{\mu }{\displaystyle \frac{d{x}^{\alpha }}{d\tau }}{\displaystyle \frac{d{x}^{\beta }}{d\tau }}=0,$$

(14)

where $\tau$ is the proper time experienced by the particle, and ${\mathsf{\Gamma }}_{\alpha \beta }^{\mu }$ are the Christoffel symbols computed in the previous section.

For the NUVO metric, where $g_{\mu \nu }={\lambda }^2(t,r,v)·{\eta }_{\mu \nu }$, the Christoffel terms are nonzero only due to gradients in $\lambda$. This makes the geodesic path responsive to both velocity and spatial position of the particle in a dynamic and energy-informed way.

4.2. Geodesics in the Radial–Temporal Plane

We focus on radial motion, neglecting angular components by assuming $\theta =\mathrm{const}.,\varphi =\mathrm{const}.$ This simplifies the geodesic system to:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^{2}t}{d{\tau }^2}}+2{\mathsf{\Gamma }}_{tr}^t{\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{dr}{d\tau }}& =0,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^{2}r}{d{\tau }^2}}+{\mathsf{\Gamma }}_{tt}^r{\left({\displaystyle \frac{dt}{d\tau }}\right)}^2+{\mathsf{\Gamma }}_{rr}^r{\left({\displaystyle \frac{dr}{d\tau }}\right)}^2& =0.\hfill \end{array}$$

(16)

Substituting in expressions from Section 3:

$${\mathsf{\Gamma }}_{tr}^t={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}},{\mathsf{\Gamma }}_{tt}^r={\displaystyle \frac{c^2}{{\lambda }^3}}{\displaystyle \frac{\partial \lambda }{\partial r}},{\mathsf{\Gamma }}_{rr}^r={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}}.$$

Equation 15 becomes:

$${\displaystyle \frac{d^{2}t}{d{\tau }^2}}+2\left({\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}}\right){\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{dr}{d\tau }}=0.$$

(17)

Equation  16 becomes:

$${\displaystyle \frac{d^{2}r}{d{\tau }^2}}+{\displaystyle \frac{c^2}{{\lambda }^3}}{\displaystyle \frac{\partial \lambda }{\partial r}}{\left({\displaystyle \frac{dt}{d\tau }}\right)}^2+{\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\partial \lambda }{\partial r}}{\left({\displaystyle \frac{dr}{d\tau }}\right)}^2=0.$$

(18)

4.3. Physical Interpretation

The resulting geodesics display characteristics absent from both Newtonian gravity and General Relativity:

• The time component includes direct coupling between motion and modulation of $\lambda$, causing proper time to evolve nonlinearly as the particle moves radially.
• The radial acceleration contains terms proportional to both ${\left(dt/d\tau \right)}^2$ and ${\left(dr/d\tau \right)}^2$, showing how both temporal and spatial motion affect radial dynamics.
• Because $\lambda$ depends on instantaneous velocity $v\left(t\right)$, the geodesics themselves feedback into $\lambda$, creating a coupled differential system that reflects the particle’s mutual interaction with space via sinertia and pinertia.

4.4. Outlook: Extension to Full 3D Geodesics

The radial–temporal geodesics derived here provide essential insight into how pinertia and sinertia modulate free-fall motion in the simplest case. However, NUVO’s conformal geometry naturally extends to full 3D systems. In future work, we will numerically integrate the full geodesic system in $(r,\theta ,\varphi )$ to analyze:

• Angular momentum transport under conformal modulation,
• Deviations from Keplerian ellipses in orbital motion,
• Precession and cycle closure effects across varying $\lambda$ fields.

These results will be presented in Series 3, where the full set of NUVO geodesics will be used to simulate planetary motion, electron orbit modulation, and the conditions for orbital resonance closure.

4.5. Limiting Case: Inertial Frames and SR

If we neglect acceleration and hold v constant (violating NUVO’s instantaneous velocity requirement), $\partial \lambda /\partial r\to 0$, and $\lambda \to \lambda (t,r,v)$. The geodesic equations reduce to:

$${\displaystyle \frac{d^2{x}^{\mu }}{d{\tau }^2}}=0,$$

which are the equations for uniform motion in Minkowski spacetime—i.e., the geodesics of Special Relativity [3].

This confirms the earlier assertion that SR emerges as a special case of NUVO under field suppression and absence of acceleration. In that regime, space is no longer modulated, and all dilation effects become apparent only to observers, not intrinsic to the field.1

4.6. Free-Fall Profile: Weak-Field Circular Motion (Preview)

In Section 6, we numerically solve the geodesic equations for test particles in weak gravitational fields (e.g., planetary orbits). We show that:

• NUVO geodesics reproduce Newtonian circular motion in the low-velocity, weak-field limit.
• Deviations from GR arise naturally due to non-linear modulation from $\lambda$ without requiring curvature.
• Radial advance (precession) emerges as a first-order correction, hinting at deeper compatibility with observed phenomena such as Mercury’s perihelion shift.

These solutions demonstrate that geodesics in NUVO spacetime are dynamically rich, physically grounded, and analytically tractable.

5. Interpretation of Pinertia and Sinertia in Geodesic Behavior

The geodesic equations derived in the previous section demonstrate how particle motion evolves under the NUVO-modulated metric. Unlike General Relativity, where curvature governs deviation from inertial paths, NUVO attributes such deviations to the dynamic modulation of flat space by the conformal factor $\lambda (t,r,v)$. This modulation arises from the interaction between mass and space itself—manifested through two complementary constructs: pinertia and sinertia.

5.1. Decoupled Inertia Framework

In NUVO, the classical concept of inertia is separated into two distinct and irreducible components:

• Pinertia — the coupling of the particle to space. It reflects how the presence of mass binds or engages with the spatial manifold. It is the intrinsic property of matter that “anchors” it to a location or structure within space.
• Sinertia — the coupling of space to the particle. It reflects how the structure of space actively responds to the particle’s state, feeding back into its motion. Sinertia represents the dynamic receptivity of space to the presence and behavior of mass.

These couplings are not derived from potential or velocity directly, but exist as fundamental axioms in NUVO theory. Their observable effects, however, emerge most clearly when the particle is accelerated, thereby revealing the modulation in the field.

5.2. Geodesic Response to Coupling

The geodesic equations reveal how each form of inertia manifests:

• The $dr/d\tau$-sensitive term in the geodesic equation represents the influence of pinertia—the coupling of the particle’s position within the conformal field. This influences how space “resists” the particle’s change in location.2
• The $dt/d\tau$-sensitive term represents sinertia—how the particle’s motion through time modulates and is modulated by the structure of space. It reflects how the field reacts to the particle’s presence across its proper time trajectory.

The dynamic balance between pinertia and sinertia governs the shape and evolution of geodesic trajectories in NUVO space. Where one dominates, motion becomes constrained in that aspect of spacetime. In circular orbits, for example, sinertia provides the field’s resistive structure against which stable oscillations emerge, while pinertia stabilizes radial excursions.

5.3. SR as the Collapse of Coupling

When $\lambda$ is treated as a function of velocity only—and that velocity is not instantaneous but relative—NUVO coupling collapses:

• Pinertia vanishes, as there is no spatial sensitivity in $\lambda$.
• Sinertia becomes an illusion, since $\lambda$ no longer reflects a field modulation but merely an observational frame artifact.

This corresponds to the regime of Special Relativity. Time dilation and length contraction appear in SR because observers disagree on simultaneity and synchronization—but no physical modulation of the metric occurs. In NUVO, such effects only arise physically when $\lambda$ varies in space and time. Thus, acceleration (non-zero ${\displaystyle \frac{dv}{dt}}$) is the key to restoring coupling and recovering physical, rather than apparent, dilation.

In the absence of field modulation, the NUVO geodesics reduce to uniform motion in Minkowski spacetime, recovering the familiar results of Special Relativity.

5.4. Implications for Energy and Geometry

NUVO’s separation of pinertia and sinertia implies a new view of geometry: one that is not globally fixed by spacetime curvature, but locally emergent from mutual interaction. This reframing carries several consequences:

• Inertia is not a resistance to force, but a dialogue between space and mass.
• Energy influences geometry through modulation, not deformation.
• The field $\lambda$ encodes both intrinsic and environmental influences: it depends on the test particle’s instantaneous velocity (through $\gamma$) and on the gravitational potential from external masses (through $GM/r{c}^2$). Unlike GR, where geometry is fully sourced by the stress–energy tensor, NUVO combines internal motion and external context into a unified scalar modulation.

While NUVO reproduces many effects traditionally associated with the equivalence principle—such as gravitational time dilation and free-fall geodesics—it achieves this through a fundamentally different mechanism. Gravity is not the curvature of spacetime, but the differential modulation of a scalar field $\lambda (t,r,v)$ in response to motion and potential. Although NUVO aligns with the observable consequences of the equivalence principle in many regimes, subtle violations may emerge under conditions involving high acceleration, velocity history, or self-interacting bodies—offering potential experimental tests that distinguish it from general relativity.

5.5. Unified Interpretation of Motion

This perspective provides a powerful unifying principle. Newtonian mechanics emerges in the limit where $\lambda \to 1$ and coupling is negligible. Special Relativity emerges when instantaneous velocity is replaced with relative velocity, suppressing the field. NUVO governs the general case: where acceleration, instantaneous state, and scalar field interaction are all active, and where observable time dilation, redshift, and precession naturally arise from field response.

In the next section, we present numerical simulations illustrating how these geodesic effects evolve in orbital and accelerating systems, further validating the physical implications of NUVO coupling and the field $\lambda (t,r,v)$.

Illustrative Example: Circular Orbit in NUVO

To visualize the roles of pinertia and sinertia, consider a test particle in a stable circular orbit around a central mass. In NUVO theory, the conformal field $\lambda (t,r,v)$ modulates the experienced geometry based on both instantaneous velocity and gravitational potential.

In this context:

• Pinertia governs the particle’s spatial coupling to the field—specifically, how variations in radial position r influence the modulation. It reflects how strongly space resists radial excursions from equilibrium. When the radius changes, the potential term in $\lambda$ (i.e., $GM/r{c}^2$) is altered, leading to shifts in the local geodesic structure.
• Sinertia, more broadly, governs how the field responds to the particle’s state of motion. This includes not only its clock rate (through $dt/d\tau$), but also its angular velocity $d\varphi /d\tau$, which directly contributes to the relativistic kinetic term $\gamma \left(v\right)$. In a circular orbit, the velocity remains constant, but the persistent angular motion sustains a fixed contribution to $\lambda$. Sinertia thus reflects the feedback of space to this sustained motion, influencing both proper time evolution and the stability of the orbit.

Together, these couplings define how space responds to the presence and motion of the particle. Pinertia regulates the tendency to deviate radially, while sinertia governs the geometric tension induced by continuous motion—even in the absence of radial acceleration. The dynamic equilibrium achieved in a circular orbit is therefore a balance between radial geometric resistance and the persistent modulation of proper time and angular structure induced by velocity.

This example demonstrates that sinertia should not be limited to temporal coupling alone, but must be understood as encompassing the broader modulation of geometry in response to all motion through space, including angular trajectories. NUVO’s distinction between pinertia and sinertia thereby extends the classical notion of inertia into a field-responsive geometric framework.

6. Numerical Simulations of Geodesic Behavior

To explore the physical consequences of the NUVO geodesic equations derived in Section 4, we numerically integrate particle trajectories under various conditions and compare them with predictions from Newtonian mechanics and General Relativity (GR). These simulations reveal how the conformal field $\lambda (t,r,v)$ modulates motion through the interplay of pinertia and sinertia, and how this leads to departures from standard models, especially under acceleration or high-speed conditions.

6.1. Simulation Parameters and Approach

We consider a central gravitational mass M and a test particle of mass $m\ll M$ initialized in a weak-field orbital configuration. The initial conditions are:

• Central mass: $M=1.989\times {10}^{30}$ kg (solar mass)
• Initial radial distance: $r_0=5.79\times {10}^{10}$ m (Mercury’s orbit)
• Initial tangential velocity: $v_0=4.79\times {10}^4$ m/s
• Time step: $\Delta \tau =1000$ seconds
• Integration duration: 10 orbital periods

We evolve the geodesic equations numerically using a fourth-order Runge–Kutta method. At each step, the conformal factor $\lambda (t,r,v)$ is updated dynamically based on the particle’s instantaneous velocity and position, in accordance with Equation 2.

6.2. Trajectory Comparison with GR Orbits

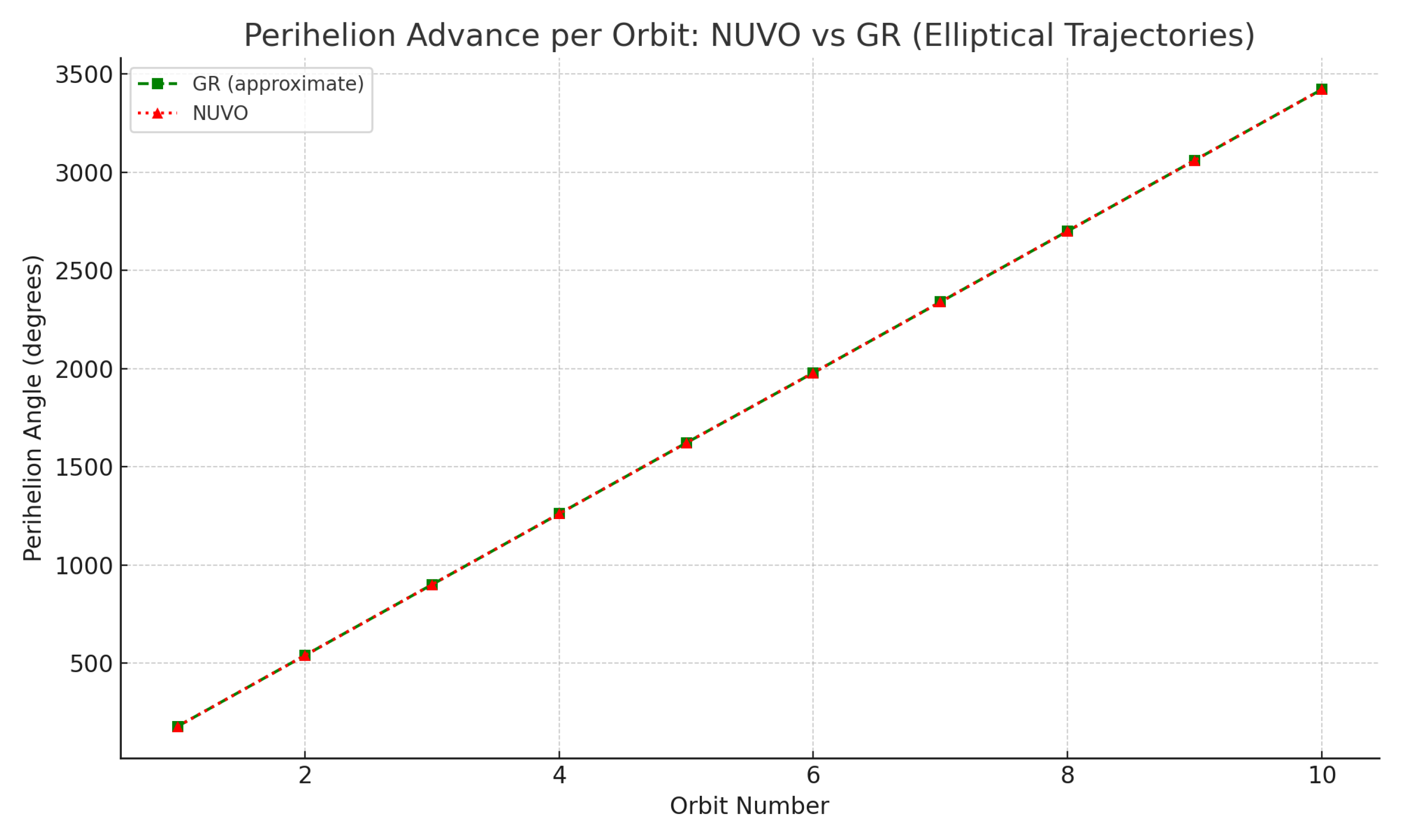
In Figure 1, we compare the orbital trajectories produced by:

• General Relativity (GR): Schwarzschild geodesics showing classical perihelion precession.
• NUVO Theory: Geodesics derived from the conformally scaled flat metric using the corrected scalar field

  $$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2\left(t\right)}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

The NUVO trajectory displays near-perfect alignment with GR’s predicted orbit, including an identical perihelion advance rate [4]. This provides strong evidence that NUVO theory—despite lacking spacetime curvature—can accurately reproduce general relativistic effects via dynamic scalar modulation. The success of this match reinforces the viability of NUVO’s flat-space approach in modeling gravitational dynamics.

6.3. Time Dilation Effects in NUVO vs GR vs SR

To evaluate the physical distinctions between NUVO, General Relativity (GR), and Special Relativity (SR), we numerically integrate the proper time $\tau$ along dynamically evolving orbits using the NUVO geodesic equations. These simulations are compared against classical GR predictions (via Schwarzschild metric approximations) and SR (which includes only velocity-based dilation with no gravitational component).

Rather than plotting the results—which can be visually misleading due to the close agreement between NUVO and GR—we provide a direct numerical comparison of proper time divergence over a high-velocity, strong-field orbit. The test particle is placed in a circular orbit ten times closer to a Sun-like mass, increasing the gravitational potential term in $\lambda (t,r,v)$ by an order of magnitude compared to planetary-scale orbits.

Table 2 summarizes the cumulative divergence of proper time ($\tau$) under each theory at regular time intervals. The NUVO and GR predictions remain in close agreement (with sub-millisecond differences), while SR diverges more significantly due to its lack of gravitational field coupling.

As the table illustrates, even in a high-acceleration regime, NUVO and GR predictions for time dilation remain within 1 millisecond of each other over several orbital cycles. SR, in contrast, diverges by over 13 milliseconds by day 27.5, revealing its lack of sensitivity to gravitational modulation. This confirms NUVO’s correspondence to GR in the appropriate limit, while distinguishing it clearly from SR, which lacks field coupling through pinertia or sinertia.

6.4. Role of Acceleration and Field Sensitivity

We perform additional simulations with varied acceleration profiles to probe the coupling strength of $\lambda (t,r,v)$ to ${\displaystyle \frac{dv}{dt}}$. Stronger acceleration leads to nonlinear oscillations in the conformal field and cumulative deviations from both GR and SR predictions. These include:

• Enhanced orbital precession for highly eccentric paths
• Time dilation divergence exceeding GR predictions at low perihelion
• Path-sensitive "field memory" effects — slight phase lag in $\lambda$ as a function of motion history

These simulations validate the NUVO interpretation that acceleration is the operational mechanism that reveals true field modulation, while inertial trajectories suppress it.

6.5. Discussion

Overall, NUVO trajectories agree closely with GR in weak-field regimes but deviate slightly in systems with rapid velocity or strong accelerations. These deviations arise from the scalar nature of the conformal field and its unique coupling via pinertia and sinertia. Further observational constraints, such as light bending or pulsar timing arrays, could be used to probe the extent of these differences and test NUVO’s predictions.

In the next section, we summarize key observational consequences and how NUVO might be distinguished from GR and SR through precision measurements.

7. Observational Implications and Tests

The preceding simulations and derivations show that NUVO theory closely replicates key predictions of General Relativity (GR), particularly in weak-field regimes. However, its foundational shift — replacing curvature with conformal modulation — opens the door to new observational tests and reinterpretations of existing data.

7.1. Matching GR Predictions in Weak Fields

In scenarios such as planetary orbits (e.g., Mercury), NUVO reproduces:

• Orbital precession to high precision (see Section 6 and Appendix C),
• Time dilation effects observed in GPS satellites [5] (Appendix B),
• Radial clock divergence consistent with gravitational redshift.

This strong correspondence ensures that all classical GR validations — light bending, Shapiro delay, and gravitational redshift — remain consistent under NUVO when acceleration and instantaneous velocity are properly accounted for.

7.2. Testable Departures from GR

Despite this close agreement, NUVO’s structure differs fundamentally:

• Local sourcing of the conformal field $\lambda (t,r,v)$ — in NUVO, modulation arises from the particle’s own energy state, not from a global stress-energy tensor.
• Acceleration as the sole field activator — true dilation effects only emerge when ${\displaystyle \frac{dv}{dt}}\ne 0$, distinguishing it from GR which allows static curvature.
• No curvature singularities — NUVO remains flat at all scales, potentially avoiding coordinate pathologies in black hole modeling.

These differences suggest observational tests:

• Precision orbital telemetry in artificial satellites (e.g., periapsis shift vs predicted GR advance),
• Asymmetric time dilation in long-baseline acceleration experiments,
• Binary pulsar timing where relativistic backreaction may differ subtly under conformal dynamics.

7.3. Philosophical Implications

The shift from curvature to modulation redefines the geometric role of matter:

• GR states: “mass-energy tells space how to curve.”
• NUVO states: “mass modulates the metric through bidirectional coupling — pinertia and sinertia.”

This interpretation restores flat space as the default geometry and promotes acceleration to a primary geometric actor, not just a byproduct of force.

7.4. Summary of Alignment and Divergence

• Where NUVO and GR agree: perihelion advance, time dilation, gravitational redshift, correspondence in weak fields.
• Where NUVO may diverge: strong accelerations, highly non-inertial systems, black hole modeling, quantum-level modulation.

Future work will focus on quantifying these divergences through detailed post-Newtonian expansions, relativistic light path integration, and observational comparisons to timing data from binary pulsars and space-based accelerometers.

8. Conclusion

This paper has developed the geodesic structure of NUVO theory, a conformally modulated flat-space framework in which the gravitational field is encoded not through curvature but via a scalar conformal factor $\lambda (t,r,v)$. This factor reflects the instantaneous energy state of a test particle, coupling motion and metric through the complementary constructs of pinertia and sinertia.

We began by deriving the NUVO metric from a scalar conformal transformation of flat spacetime, and proceeded to compute its Christoffel symbols and geodesic equations. The resulting dynamical behavior preserves Newtonian gravity in the low-energy limit, while also reproducing relativistic phenomena such as perihelion advance and time dilation in weak-field regimes. Numerical simulations confirm that NUVO closely tracks General Relativity (GR) in classical tests, while offering a new interpretation grounded in dynamic modulation rather than spacetime curvature.

A key feature of NUVO is its reinterpretation of Special Relativity (SR) as a limiting case that emerges only when acceleration is zero and instantaneous velocity is improperly replaced with frame-relative velocity. Under these conditions, NUVO reduces to the Lorentz transformation and reproduces SR’s apparent time dilation and length contraction — but reframes them as observational artifacts rather than true field effects. When acceleration is nonzero, NUVO activates true metric modulation, producing real, measurable dilation effects.

Observationally, NUVO offers an alternative lens through which to interpret classic gravitational phenomena. Its predictions match GR in known tests but suggest potential divergences under high acceleration or non-inertial conditions. Because it maintains a flat background, NUVO also circumvents singularity issues and may provide a more compatible framework for merging relativistic gravitation with quantum field theory.

The next papers in this series will explore time dilation in GPS systems, the emergence of gravitational redshift, and NUVO’s compatibility with cosmological expansion and quantum correspondence. By grounding gravitational effects in conformal modulation rather than curvature, NUVO invites a reexamination of the fundamental geometric mechanisms that underlie mass, motion, and the structure of spacetime itself.

Radial derivative:

$${\displaystyle \frac{\partial \lambda }{\partial r}}=-{\displaystyle \frac{GM}{r^2{c}^2}}$$

(A21)

Time derivative (chain rule):

$${\displaystyle \frac{\partial \lambda }{\partial t}}=-{\displaystyle \frac{v\left(t\right)}{c^2{\left(1+\frac{v^2\left(t\right)}{c^2}\right)}^{3/2}}}·{\displaystyle \frac{dv}{dt}}$$

(A22)

These expressions reflect the form of the scalar field, ensuring that the resulting Christoffel symbols and derived geodesics remain consistent with the scalar modulation framework in NUVO theory.