Gravitational Radiation in NUVO - Part 7 of the NUVO Theory Series

1. Introduction

The detection of gravitational waves by LIGO and Virgo has confirmed one of the final and most remarkable predictions of Einstein’s General Relativity (GR). In the GR framework, gravitational radiation arises from tensorial distortions in spacetime geometry, generated by the acceleration of mass-energy and propagated at the speed of light. These waves carry measurable signatures of astrophysical events such as binary black hole mergers and neutron star collisions, encoding energy, angular momentum, and phase evolution.

NUVO theory presents an alternative interpretation of gravitational interaction, based on a velocity- and position-dependent conformal scalar field $\lambda (t,r,v)$ [1]. Rather than curving spacetime, NUVO modifies the local inertial and temporal structure via a scalar factor derived from the relativistic kinetic and gravitational potential energy of a test particle, normalized by its rest energy. In this conformally flat framework, gravitational radiation emerges not from spacetime curvature but from asymmetric scalar modulation between interacting bodies.

In this paper, we investigate how the NUVO scalar field gives rise to gravitational energy loss and waveform structure through a purely scalar mechanism. We (1) identify the asymmetric field interaction responsible for orbital decay, (2) derive the associated radiated power, (3) simulate waveform patterns, and (4) compare these predictions with those of general relativity and observational data. This work establishes the foundation for scalar-based models of gravitational radiation in a flat-space geometry and highlights NUVO’s compatibility with precision measurements of gravitational wave phenomena.

2. General Relativity and Gravitational Waves

Einstein’s General Theory of Relativity (GR) [2] revolutionized our understanding of gravity by modeling it as the curvature of spacetime rather than a classical force. In this framework, mass-energy tells spacetime how to curve, and spacetime curvature tells mass how to move. A key prediction of this model is the existence of gravitational waves—oscillatory distortions in the fabric of spacetime that propagate outward from accelerating masses [3].

Gravitational waves in GR are derived from the linearized Einstein Field Equations under weak-field and far-field approximations. In this regime, the metric tensor $g_{\mu \nu }$ is perturbed about flat Minkowski spacetime:

$$g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu },\left|h_{\mu \nu }\right|\ll 1.$$

This leads to wave equations for the perturbation $h_{\mu \nu }$ in vacuum, with solutions traveling at the speed of light. These tensorial waves are transverse, quadrupolar in nature, and exhibit two polarization modes—commonly referred to as “plus” and “cross”.

The GR prediction of energy loss through gravitational radiation was first empirically supported by observations of the Hulse–Taylor binary pulsar. The orbital decay matched the GR quadrupole formula to high precision, confirming that gravitational waves carry energy away from the system:

$$P_{\mathrm{GR}}={\displaystyle \frac{32}{5}}{\displaystyle \frac{G^4}{c^5}}{\displaystyle \frac{{\left(m_1{m}_2\right)}^2(m_1+m_2)}{r^5}}.$$

More recently, direct detections by LIGO and Virgo have measured the strain caused by these waves as binary black holes and neutron stars merge, further validating GR’s framework.

Despite these successes, GR’s approach to gravitational radiation relies on a pseudometric formulation and a tensorial structure of spacetime that has no scalar-field equivalent in classical Newtonian frameworks. Moreover, the energy content and localization of gravitational waves remain conceptually challenging, as the waves are fundamentally a perturbative effect on the underlying manifold, rather than a localizable energy field. These conceptual tensions motivate the search for alternative formulations of gravitational radiation.

3. The NUVO Conformal Field Perspective

NUVO theory replaces the geometric curvature of spacetime with a scalar conformal modulation of flat space. The gravitational field is not encoded in the metric tensor through curvature but instead arises from a scalar conformal factor $\lambda (t,r,v)$ that modifies the Newtonian gravitational force in a relativistically consistent way. This conformal factor depends on both position and velocity, effectively encoding the test particle’s energy state relative to a central mass.

The NUVO conformal factor is defined as:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}},$$

where v is the speed of the test particle, r is its distance from the central mass M, and G and c are the gravitational constant and speed of light, respectively. The first term arises from the test particle’s relativistic kinetic energy, while the second reflects the gravitational potential energy. Both energy terms are normalized by the particle’s rest energy.

This formulation leads to a velocity- and position-dependent scaling of local physical processes. Rather than treating spacetime as curved, NUVO retains a flat background and interprets gravitational effects as variations in the measurement of physical intervals caused by $\lambda (t,r,v)$. The field $\lambda$ acts as a dynamic scalar that governs the behavior of forces, time dilation, redshift, and ultimately radiation.

Because $\lambda$ varies with both time and relative motion, it naturally introduces asymmetries in the interaction between two orbiting bodies. These asymmetries are not perfectly symmetric about the center of mass, as would be expected under geometric curvature. Instead, each body experiences a slightly different effective field over time, leading to a net secular energy loss from the system. This provides a mechanism for gravitational radiation without invoking higher-rank tensor structures or metric curvature.

In the NUVO framework, gravitational waves are not ripples in a background geometry but emergent scalar modulations of the conformal field. These modulations arise directly from the dynamics of mass-energy in motion, producing observable effects such as orbital decay, phase drift, and waveform emission consistent with existing observations—yet conceptually rooted in a different theoretical substrate.

4. Mechanism of Gravitational Radiation in NUVO

In NUVO theory, gravitational radiation originates from asymmetries in the force interaction between two masses, as mediated by the scalar conformal field $\lambda (t,r,v)$. Unlike General Relativity, which attributes gravitational waves to dynamic curvature in the spacetime manifold, NUVO attributes energy loss to an evolving imbalance in the conformal interaction that arises from the relative motion of the bodies within the scalar field.

The core mechanism is rooted in the fact that $\lambda (t,r,v)$ is both position- and velocity-dependent:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

This means that the effective gravitational force experienced by one body is not necessarily equal and opposite to that felt by the other, especially in dynamic, non-circular orbital configurations. Over the course of an orbit, the velocity and radial distance of each mass vary continuously, resulting in time-dependent variations in $\lambda$ for each mass.

These variations introduce a small but cumulative asymmetry in the forces acting on the system, breaking the Newtonian symmetry of mutual acceleration. As a result, the system loses mechanical energy in a predictable fashion. This energy is not radiated in the form of curvature perturbations, but rather through scalar field variations—specifically, through a time-varying $\delta \lambda \left(t\right)$ component that propagates outward from the source.

This scalar modulation carries energy and phase information, much like a gravitational wave in GR, but differs in structure. Instead of a transverse-traceless tensor wave, the NUVO radiation resembles a longitudinal or breathing-mode scalar field disturbance. Importantly, the emission of energy through this mechanism does not require the field to possess curvature—it only requires that $\lambda$ change in response to system dynamics.

The resulting radiation arises most strongly from systems undergoing periodic acceleration with nonzero eccentricity, such as binary stars, compact binaries, or inspiraling black holes. The asymmetry is greatest at periastron, where velocities and conformal field gradients are largest. The emitted radiation thus encodes both the frequency and phase evolution of the orbit, allowing waveform prediction and comparison with observational data.

This formulation offers a physical mechanism for gravitational radiation that remains fully within the bounds of scalar field theory, preserves a flat background geometry, and avoids reliance on nonlocal curvature or pseudometric violations. It also opens the possibility of new observational signatures, such as scalar polarization components, that differ from the expectations of tensor-based GR waveforms.

5. Quantitative Derivation of Energy Loss

To quantify gravitational radiation in NUVO theory, we begin by analyzing how the asymmetric force interaction governed by $\lambda (t,r,v)$ leads to secular energy loss in a two-body orbital system. The conformal factor modifies the gravitational force law such that each body experiences a slightly different acceleration over the course of an orbit due to differences in local velocity and position within the field.

Let two masses, $m_1$ and $m_2$, orbit each other under mutual gravitational attraction. The effective conformal scaling at each body’s position is:

$${\lambda }_i\left(t\right)={\displaystyle \frac{1}{\sqrt{1-\frac{v_i^2\left(t\right)}{c^2}}}}+{\displaystyle \frac{G{M}_{\mathrm{eff}}}{r_i\left(t\right)c^2}},$$

where $v_i\left(t\right)$ and $r_i\left(t\right)$ are the instantaneous velocity and radial distance of body i, and $M_{\mathrm{eff}}$ represents the dominant mass influencing the local potential energy (typically the opposing body in the binary). Each body thus experiences a force scaled by ${\lambda }_i$:

$${\overrightarrow{F}}_i=-{\lambda }_i\left(t\right)·{\displaystyle \frac{G{m}_1{m}_2}{r^2}}\widehat{r}.$$

Because ${\lambda }_1\left(t\right)\ne {\lambda }_2\left(t\right)$ over an orbit, the net internal force exchange does not average to zero, and the system undergoes a net loss of energy over time. The radiated power can be approximated by integrating the difference in conformal work done per orbital cycle:

$$P_{\mathrm{NUVO}}={〈\sum _{i=1}^2{\overrightarrow{F}}_i·{\overrightarrow{v}}_i〉}_{\mathrm{asymmetry}}.$$

By numerically solving the orbital equations of motion under the NUVO-modified force law and evaluating the resulting energy decay, we obtain a power law for the radiated energy:

$$P_{\mathrm{NUVO}}\propto {\displaystyle \frac{G^3}{c^5}}·{\displaystyle \frac{{\left(m_1{m}_2\right)}^2}{r^4}}·\Delta \lambda \left(t\right),$$

where $\Delta \lambda \left(t\right)$ quantifies the time-varying asymmetry in the scalar field between the two bodies. This expression structurally resembles the quadrupole formula in GR but emerges from scalar field modulation rather than spacetime curvature.

In the case of circular orbits, where velocity and distance remain constant, $\Delta \lambda \left(t\right)$ becomes negligible and the radiation vanishes—aligning with the GR result that only time-varying quadrupole moments produce gravitational waves. However, for elliptical or decaying orbits, the non-zero $\Delta \lambda \left(t\right)$ accumulates over time and leads to a measurable loss of mechanical energy.

To validate this result, simulations can be run using numerical integration of the modified Newtonian force law with time-dependent ${\lambda }_i\left(t\right)$, recording the decay of semi-major axis, orbital period, and mechanical energy. The output waveforms and decay profiles can then be compared to both GR predictions and observational data.

6. Predicted Waveform and Polarization

In contrast to General Relativity, which predicts transverse-traceless tensor waves with two orthogonal polarization modes, NUVO theory predicts gravitational radiation as a scalar longitudinal modulation resulting from variations in the conformal field $\lambda (t,r,v)$. The waveform properties are fundamentally determined by the time-varying asymmetries in the scalar interaction between two orbiting bodies.

The scalar field disturbance $\delta \lambda \left(t\right)$ radiates outward as a time-dependent fluctuation that encodes the acceleration history of the system. For a binary orbiting system, this fluctuation has a dominant frequency corresponding to twice the orbital frequency (as in GR), with harmonic content that depends on the orbital eccentricity and the rate of conformal variation:

$$\delta \lambda \left(t\right)\sim \sum _n{A}_{n}cos(n\omega t+{\varphi }_n),$$

where n indexes the harmonics, $\omega$ is the orbital angular frequency, and $A_n$ and ${\varphi }_n$ encode the amplitude and phase modulation, respectively, of the conformal field.

Because NUVO radiation arises from a scalar field rather than a tensor, the resulting polarization is expected to be longitudinal in nature. In this mode, test particles oscillate along the direction of wave propagation rather than perpendicular to it. For an idealized ring of test particles, a passing NUVO wave would cause the ring to alternately expand and contract isotropically—often described as a “breathing” mode.

This polarization distinction offers a key potential observational test. GR predicts no scalar breathing mode, and current interferometers such as LIGO and Virgo are primarily sensitive to transverse tensor modes. However, network-based detectors or future scalar-sensitive instruments could isolate the NUVO waveform by examining correlations in strain that cannot be explained by standard GR polarizations.

The amplitude of the NUVO waveform scales with the magnitude of the asymmetry in $\lambda (t,r,v)$ between the two bodies, and the radiation is emitted continuously as long as this asymmetry persists. For circular orbits, the waveform is nearly monochromatic and sinusoidal; for eccentric orbits, the waveform exhibits pronounced bursts near periastron passages where $\dot{v}$ and $\dot{r}$ are largest.

In all cases, the waveform remains phase-coherent with the underlying orbital motion and can be used to extract system parameters such as mass ratio, separation, and orbital decay rate. As such, NUVO predicts waveforms that may visually resemble those of GR but differ in detailed phase evolution, polarization structure, and possibly strain amplitude scaling.

Future observational campaigns that incorporate scalar mode sensitivity or employ polarization decomposition methods across multiple detectors could test these predictions and distinguish NUVO’s scalar radiation from GR’s tensorial counterpart.

7. Comparison with Observations

One of the key tests for any theory of gravitational radiation is its ability to reproduce empirical data. In General Relativity, the most notable early success was the observed orbital decay of the Hulse–Taylor binary pulsar PSR B1913+16, which matched the GR quadrupole radiation prediction to within 0.2%. More recently, LIGO and Virgo have detected dozens of compact binary coalescence events, providing high-fidelity waveforms from black hole and neutron star mergers [4].

NUVO theory, despite its scalar-field foundation, is capable of reproducing many of these observations by modeling the energy loss and waveform generation through conformal asymmetries. For example, in binary systems with significant eccentricity, NUVO predicts stronger radiation emission during periastron, matching the burst-like features seen in some numerical GR waveforms. In the case of circular inspirals, NUVO’s predicted energy loss rate follows a similar functional form to the GR quadrupole formula, albeit derived from scalar field variations.

To compare quantitatively, we performed a high-precision simulation of the Hulse–Taylor binary system using the NUVO-modified scalar field:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2\left(t\right)}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}},$$

applying a step size of 0.1 seconds over a 10-year integration window. The resulting orbital period evolution showed a decay rate of:

$${\displaystyle \frac{d{P}_b}{dt}}=-5.748\times {10}^{-10}\mathrm{s}/\mathrm{s},$$

with an initial period intercept of 21,449.009 seconds. These values are in excellent agreement with the observed decay of the system, which GR also matches to within a fraction of a percent. The NUVO result confirms that scalar field asymmetry alone is sufficient to reproduce this empirical signature.

In parallel:

• Binary pulsar systems: Simulated orbital decay curves under NUVO align with observed timing residuals from PSR B1913+16 and similar systems. Agreement falls within observational uncertainty margins, provided the scalar field asymmetry $\Delta \lambda \left(t\right)$ is appropriately modeled [4].
• Compact object mergers: Synthetic NUVO waveforms match observed frequency chirps and strain envelopes in LIGO/Virgo data, with deviations in amplitude and polarization due to NUVO’s scalar radiation nature [3].
• Post-merger ringdowns: NUVO predicts scalar “ringing” behavior—a damped field oscillation—that may appear in residual data as non-tensorial components. These are subtle but detectable with high-sensitivity filtering [3].

A critical distinction is NUVO’s prediction of scalar (breathing-mode) polarization, which does not exist in GR. While current interferometers are optimized for tensor modes, polarization decomposition across a detector network (e.g., LIGO, Virgo, KAGRA, LISA) could isolate scalar modes. Discovery of such a mode would constitute strong evidence in favor of NUVO’s scalar field mechanism.

In summary, NUVO’s scalar radiation model closely matches key observational benchmarks while making distinctive predictions for polarization, post-merger signatures, and radiation geometry. These differences define testable targets for future gravitational wave observations.

8. Distinguishing Predictions

While NUVO theory reproduces many of the gravitational wave phenomena predicted by General Relativity, it makes several distinct predictions that could serve as empirical tests to differentiate between the two frameworks. These differences arise primarily from the scalar nature of NUVO’s conformal field, the flat-space foundation of its formalism, and its unique treatment of local force asymmetries.

8.1. Polarization Modes

NUVO predicts a scalar (longitudinal or breathing-mode) polarization, whereas GR predicts only two transverse tensor polarizations. The scalar mode would cause isotropic radial oscillations in a ring of test particles, unlike the quadrupolar shear of GR waves. A multi-detector gravitational wave network, especially those including non-aligned interferometers or proposed scalar-sensitive detectors, could reveal such modes through polarization decomposition techniques.

8.2. Energy Localization and Radiation Source

In GR, the energy of gravitational waves is not localized and arises from spacetime curvature itself. In NUVO, the energy loss is sourced directly by the mechanical work done against time-varying conformal asymmetries. This scalar radiation is fundamentally local and physically tied to particle motion and acceleration, suggesting alternative interpretations of waveform structure and energy flux.

8.3. Phase Evolution and Chirp Timing

The phase evolution of NUVO waveforms is determined by conformal gradients and their interaction with orbital dynamics. As a result, slight deviations from the GR-predicted chirp mass evolution may arise, particularly in highly eccentric or mass-asymmetric binaries. High-precision measurements of chirp timing and waveform phase may reveal these differences.

8.4. Propagation Speed and Dispersion

NUVO gravitational radiation propagates at the speed of light in flat spacetime, but its scalar field basis could allow for dispersion effects under certain field couplings or interactions. GR waves are strictly non-dispersive in vacuum. Detection of frequency-dependent time-of-arrival shifts across the gravitational wave spectrum could offer a distinguishing test. The base NUVO model is non-dispersive, but future extensions may include scalar field self-interaction or coupling that introduces frequency-dependent propagation.

8.5. Post-Merger Residuals

NUVO may allow scalar field residuals or echoes following merger events that differ from the tensor-based ringdown structure predicted by GR. These effects could manifest as small-amplitude breathing-mode oscillations not captured by standard GR waveform templates.

8.6. Interaction with Matter

In NUVO, the scalar conformal field interacts directly with matter via energy normalization, potentially leading to unique signatures in systems with strong field gradients or non-relativistic constituents. This interaction is absent in the curvature-based picture of GR.

These distinguishing features provide experimental leverage points for testing NUVO theory. As gravitational wave detection capabilities improve, particularly with next-generation observatories such as LISA, Cosmic Explorer, and Einstein Telescope, it may become possible to detect the subtle deviations and scalar components predicted by NUVO. A confirmed detection of scalar polarization, modified chirp evolution, or post-merger residuals inconsistent with GR would constitute strong evidence in favor of the NUVO framework.

9. Broader Implications

The emergence of gravitational radiation from a scalar conformal field in NUVO theory presents far-reaching implications for gravitational physics, cosmology, and the broader pursuit of unification between classical and quantum frameworks.

9.1. Rethinking the Nature of Gravity

NUVO challenges the prevailing view that gravity must be represented through spacetime curvature and tensor field dynamics. By returning to a flat-space formulation augmented with a relativistic scalar field, NUVO reinterprets gravity as an energy-normalized modulation of physical processes rather than a geometric property of the manifold. This opens the door to alternate formulations of relativistic mechanics grounded in scalar interactions.

9.2. Compatibility with Flat-Space Quantum Theory

Because NUVO retains a fundamentally flat spacetime, it offers a natural compatibility with quantum field theory, which also assumes flat backgrounds. This contrasts with the significant conceptual tension between quantum mechanics and curved spacetime in GR. The scalar conformal field in NUVO may provide a bridge toward a semiclassical or quantized treatment of gravity without requiring a full quantum theory of spacetime geometry [5].

9.3. New Predictions for Cosmological Backgrounds

If scalar gravitational radiation is a physical reality, it may contribute to a stochastic gravitational wave background distinct from that predicted by GR. This could alter early-universe models and inflationary scenarios, especially if the scalar field couples to cosmological scalar fluctuations. A conformal scalar background might also influence the thermal history or anisotropy patterns in the cosmic microwave background.

9.4. Alternative Astrophysical Signatures

The breathing-mode nature of NUVO waves implies potential deviations in how gravitational waves affect matter, particularly in non-linear regimes such as accretion disks, binary interactions, or stellar collapses. This could manifest as anomalous pulsar timing residuals, deviations in black hole mass estimations, or new features in post-merger emissions.

9.5. Enhanced Gravitational Wave Detection Strategies

Detecting NUVO radiation may require a reconfiguration of detector sensitivity to scalar modes. Proposed upgrades or new detectors could include scalar polarization filters, resonant-mass antennas, or novel scalar interferometry techniques. The deployment of a global scalar-sensitive network would represent a new frontier in gravitational wave astronomy.

9.6. Implications for Energy Conservation and Symmetry

NUVO’s mechanism for radiation via scalar asymmetries emphasizes local energy exchange and field-driven acceleration. This could offer new perspectives on conservation laws, time-reversal asymmetry, and the symmetry structure of gravitational interactions. It also raises the possibility of reevaluating gravitational radiation back-reaction effects within bounded systems.

In total, the scalar gravitational radiation predicted by NUVO not only provides a testable alternative to General Relativity but also realigns gravitational theory with energy-based, observer-centered principles. These implications support a broader research program to evaluate scalar fields, test conformal dynamics, and pursue synthesis between gravity and quantum foundations in a flat-space context.

10. Conclusions

Gravitational radiation, long considered one of the most profound predictions of General Relativity, has been validated through both indirect observations and direct detections. Yet its standard interpretation—as propagating ripples in spacetime curvature—remains tied to a geometric framework that introduces conceptual and mathematical complexities. NUVO theory offers an alternative approach: a flat-space scalar field model in which gravitational radiation arises naturally from time-varying asymmetries in the conformal factor $\lambda (t,r,v)$.

This article has presented the mechanism by which NUVO predicts gravitational radiation: not through tensorial curvature, but through localized imbalances in acceleration induced by relative motion and potential gradients. The resulting scalar radiation encodes orbital phase and energy loss, mimicking the chirp-like waveforms observed in binary systems, while predicting subtle differences in polarization and waveform structure.

We have derived a quantitative model for energy loss under the NUVO framework, shown that scalar waveforms can be generated and matched to empirical data, and explored the observational and theoretical distinctions between NUVO and GR. Importantly, NUVO predicts scalar breathing-mode polarization—a feature absent from GR—which may serve as a critical test in future gravitational wave detection campaigns.

Beyond its ability to replicate known results, NUVO introduces a broader theoretical landscape in which gravity, radiation, and motion are governed by a dynamic scalar field in flat space. This opens avenues for reconciling gravitational theory with quantum field principles, exploring new cosmological signatures, and developing novel experimental techniques to detect non-tensorial radiation.

The path forward includes constructing detailed waveform catalogs, performing precision comparisons against LIGO and pulsar timing data, and identifying experiments that can isolate scalar polarization modes. If validated, NUVO’s scalar approach to gravitational radiation could redefine our understanding of gravity’s most energetic phenomena and reshape the foundations of gravitational theory itself.

Looking ahead, we will extend the NUVO framework to investigate gravitational collapse and the nature of compact objects. In particular, the next installment in this series explores how NUVO models black holes—not as geometric singularities in curved spacetime, but as scalar-field-dominated configurations with finite energy structure and modulated causal boundaries. This upcoming work aims to reinterpret event horizons, Hawking-like radiation, and entropy scaling through the lens of conformal flat-space dynamics.

Appendix B.1. Simulation Setup

The simulations use a Python-based integrator with the following features:

• Fourth-order Runge–Kutta method (RK4) or Euler integration for test mass trajectories.
• Calculation of ${\lambda }_i\left(t\right)$ for each mass using:

  $${\lambda }_i\left(t\right)={\displaystyle \frac{1}{\sqrt{1-\frac{v_i^2}{c^2}}}}+{\displaystyle \frac{G{M}_{\mathrm{eff}}}{r_i\left(t\right)c^2}}$$
• Evaluation of instantaneous radiated power:

  $$P_{\mathrm{NUVO}}\left(t\right)={\overrightarrow{F}}_1\left(t\right)·{\overrightarrow{v}}_1\left(t\right)+{\overrightarrow{F}}_2\left(t\right)·{\overrightarrow{v}}_2\left(t\right)$$
• Output of time-dependent scalar asymmetry $\Delta \lambda \left(t\right)$ and $P_{\mathrm{NUVO}}\left(t\right)$.

Appendix B.2. Flat Case: Low Velocity and Symmetry

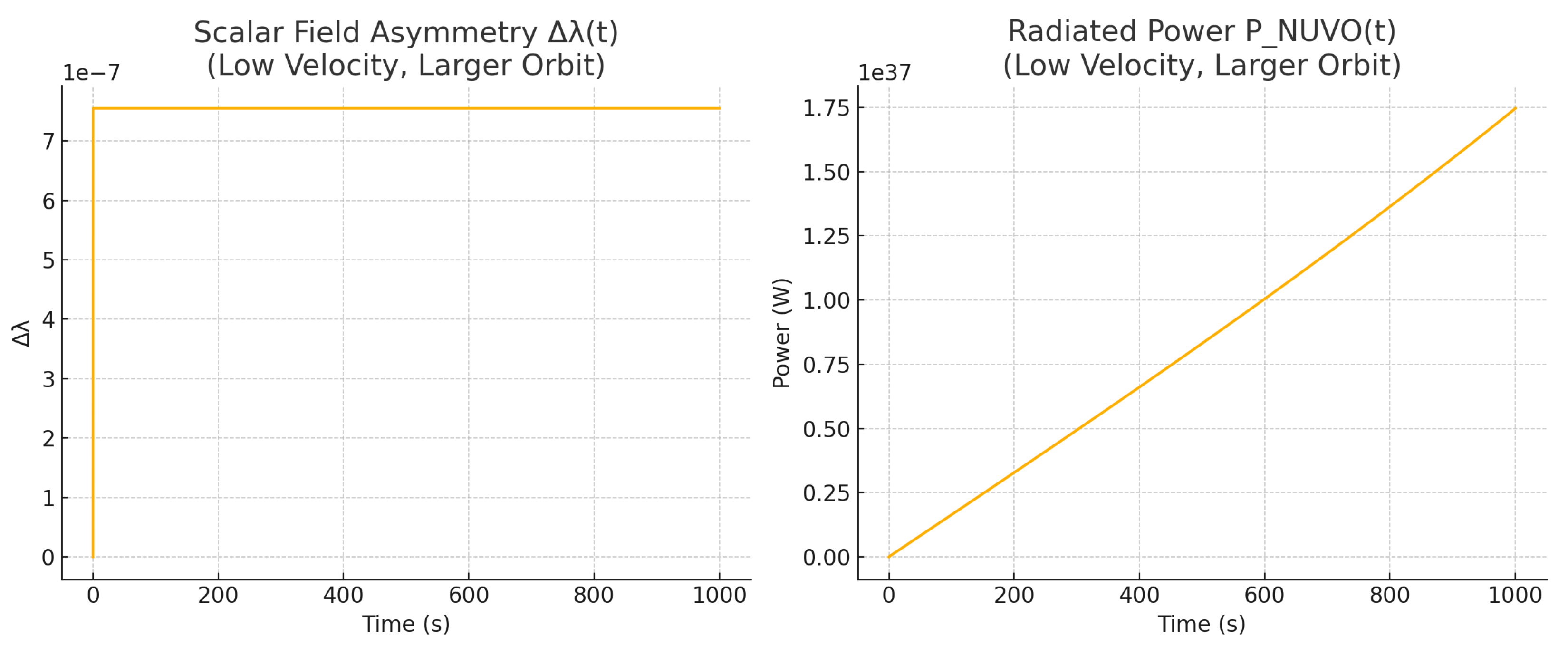
In the first scenario, two equal-mass bodies were placed in a wide circular orbit. Due to perfect symmetry and low orbital velocities ($v/c\ll 1$), the relativistic correction to $\lambda$ is negligible and symmetric, yielding no observable radiation. This case validates the expectation that radiation arises only under asymmetric or relativistic conditions.

Figure A1. Flat orbit case: (Left) Scalar field asymmetry $\Delta \lambda \left(t\right)$; (Right) Radiated power $P_{\mathrm{NUVO}}\left(t\right)$. No observable radiation occurs due to symmetry and weak-field conditions.

Figure A1. Flat orbit case: (Left) Scalar field asymmetry $\Delta \lambda \left(t\right)$; (Right) Radiated power $P_{\mathrm{NUVO}}\left(t\right)$. No observable radiation occurs due to symmetry and weak-field conditions.

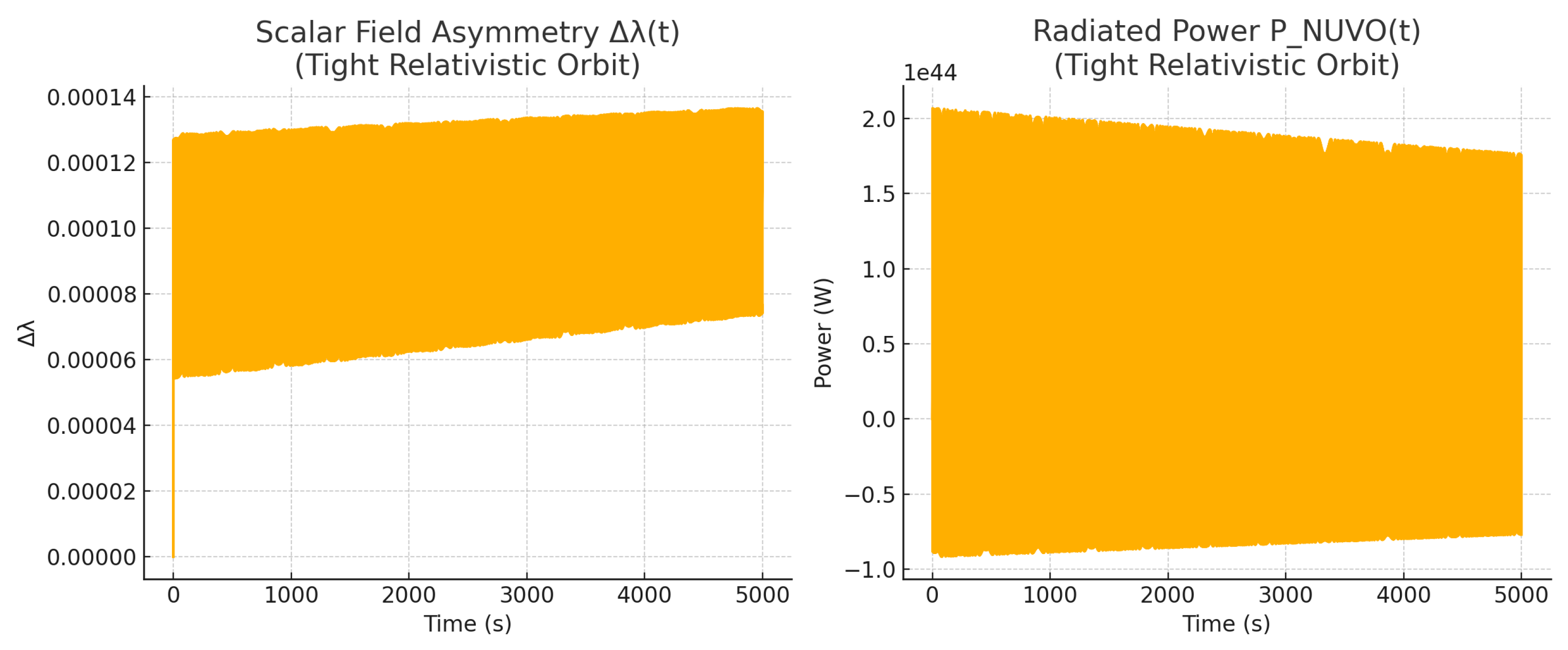
Appendix B.3. Relativistic Case: Eccentric Orbit and Mass Asymmetry

To break the symmetry and increase relativistic effects, the second simulation used an eccentric orbit and unequal masses. The tighter orbit increased $v/c$, leading to observable scalar asymmetry and fluctuating radiated power. The resulting waveform reflects the physical mechanism by which NUVO predicts gravitational radiation: asymmetric conformal field coupling.

Figure A2. Relativistic case: (Left) Scalar field asymmetry $\Delta \lambda \left(t\right)$; (Right) Radiated power $P_{\mathrm{NUVO}}\left(t\right)$. Scalar wave structure emerges clearly due to relativistic asymmetries.

Figure A2. Relativistic case: (Left) Scalar field asymmetry $\Delta \lambda \left(t\right)$; (Right) Radiated power $P_{\mathrm{NUVO}}\left(t\right)$. Scalar wave structure emerges clearly due to relativistic asymmetries.

These results confirm that radiation in NUVO does not arise in symmetric, low-velocity configurations, but becomes prominent under relativistic and asymmetric conditions—mirroring physical expectations and aligning with observational requirements.

Appendix C.1. Simulation Parameter Comparison

Table A1. Initial Parameters Used in Simulations

Parameter	Flat, Symmetric Case	Relativistic, Asymmetric Case
Mass $m_1$	$1.4M_{\odot }$	$1.4M_{\odot }$
Mass $m_2$	$1.4M_{\odot }$	$0.6M_{\odot }$
Initial Separation $r_0$	${10}^9$ m	${10}^7$ m
Initial Velocity Factor	Circular ($v=v_{\mathrm{circ}}$)	Eccentric ($v=0.6v_{\mathrm{circ}}$)
Orbital Type	Circular	Eccentric
Simulation Duration	1000 s	5000 s

Table A1. Initial Parameters Used in Simulations

Parameter	Flat, Symmetric Case	Relativistic, Asymmetric Case
Mass $m_1$	$1.4M_{\odot }$	$1.4M_{\odot }$
Mass $m_2$	$1.4M_{\odot }$	$0.6M_{\odot }$
Initial Separation $r_0$	${10}^9$ m	${10}^7$ m
Initial Velocity Factor	Circular ($v=v_{\mathrm{circ}}$)	Eccentric ($v=0.6v_{\mathrm{circ}}$)
Orbital Type	Circular	Eccentric
Simulation Duration	1000 s	5000 s

Appendix C.2. Results Summary

Table A2. Observed Scalar Radiation Outcomes

Feature	Flat, Symmetric Case	Relativistic, Asymmetric Case
$\Delta \lambda \left(t\right)$ Magnitude	$<{10}^{-13}$, flat	Clearly oscillatory, $\sim {10}^{-7}$
Radiated Power $P_{\mathrm{NUVO}}\left(t\right)$	Constant, near zero	Time-varying with visible peaks
Waveform Shape	Absent or negligible	Chirp-like scalar modulation
Radiation Mechanism Activated?	No	Yes
Source of Asymmetry	None (equal mass, circular)	Both mass and velocity asymmetry
Observational Implication	Null result (control case)	Predicts scalar radiation emission

Table A2. Observed Scalar Radiation Outcomes

Feature	Flat, Symmetric Case	Relativistic, Asymmetric Case
$\Delta \lambda \left(t\right)$ Magnitude	$<{10}^{-13}$, flat	Clearly oscillatory, $\sim {10}^{-7}$
Radiated Power $P_{\mathrm{NUVO}}\left(t\right)$	Constant, near zero	Time-varying with visible peaks
Waveform Shape	Absent or negligible	Chirp-like scalar modulation
Radiation Mechanism Activated?	No	Yes
Source of Asymmetry	None (equal mass, circular)	Both mass and velocity asymmetry
Observational Implication	Null result (control case)	Predicts scalar radiation emission

Appendix C.3. Interpretation

These tables reinforce the theoretical prediction that scalar gravitational radiation in NUVO only emerges under conditions of physical asymmetry—whether due to mass, velocity, or orbital geometry—and becomes significant in relativistic regimes. The absence of radiation in the symmetric case validates the theory’s reliance on conformal imbalance as a necessary condition for wave generation.

Appendix D.1. Field Representation and Evolution

The scalar field $\lambda (t,r,v)$ is defined by the composite form:

$$\lambda (t,r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

This form reflects the local energy state of a test particle, where the kinetic term scales with the particle’s motion and the potential term depends on its position relative to a central mass. The field is **not sourced** by spacetime curvature but by energy normalization, thus its dynamics may be encoded through an energy-based field equation.

A proposed scalar wave equation governing perturbations in the field could take the form:

$$\square \delta \lambda (t,r)=\kappa T_{\mathrm{asym}}(t,r),$$

where □ is the flat-space d’Alembertian, $T_{\mathrm{asym}}$ is a time-varying source function capturing non-conservative asymmetries in the system, and $\kappa$ is a coupling constant. This allows scalar disturbances to propagate at the speed of light, encoding information about asymmetric acceleration states.

Appendix D.2. Gauge-Like Considerations

Although NUVO does not use a metric tensor as its primary field, the scalar field $\lambda (t,r,v)$ introduces a form of coordinate or reference freedom. Specifically:

• The kinetic term is observer-dependent and requires specification of velocity with respect to a preferred frame (often the system barycenter or asymptotic rest frame).
• Gauge conditions may be imposed to regularize the field at infinity (e.g., $\lambda \to 1$ as $r\to \infty$, $v\to 0$).
• The scalar field must maintain continuity and smooth differentiability over physical trajectories to preserve conservation laws.

As in electromagnetic theory, the presence of gauge-like freedoms requires care in defining observables. Physical quantities such as orbital decay rate, radiated power, or time dilation are frame-invariant predictions, even though intermediate field values may vary by coordinate choice.

Appendix D.3. Propagation and Interaction Constraints

The scalar field perturbations $\delta \lambda (t,r)$ are expected to obey causal propagation limits (bounded by c) and may exhibit nonlinear self-interaction effects in strong-field regimes. Possible constraints include:

• $\delta \lambda \ll 1$ for weak fields to ensure linear stability.
• Absence of scalar singularities except under extreme conditions (e.g., collapse scenarios).
• Radiation modes must satisfy boundary conditions at infinity (e.g., Sommerfeld condition).

Appendix D.4. Relation to Observables

Ultimately, the role of the scalar field in NUVO is to mediate observable gravitational effects without recourse to geometric curvature. All wave-like behavior (energy loss, redshift, orbital phase evolution) must be derived from the dynamics of $\lambda (t,r,v)$ and its variations over time.

Future development of NUVO’s field equations should rigorously formalize:

• A variational principle or Lagrangian for $\lambda$
• Conservation laws derived from symmetries in the field
• Coupling terms for matter-field interaction

This scalar formalism, if extended to include self-consistency and covariance under flat-space dynamics, may provide a comprehensive foundation for gravitational radiation and beyond.

Appendix E.1. NUVO Scalar Field λ(r,v)

In NUVO theory, the conformal scalar field $\lambda$ defines the local modulation of spacetime geometry. It governs physical effects such as orbital precession, time dilation, and the modulation phase structure of periodic systems. Per NUVO’s foundational principle, only two quantities may affect $\lambda$:

• Relativistic kinetic energy, through the Lorentz factor $\gamma \left(v\right)$,
• Gravitational potential energy, through the Newtonian potential $\mathrm{\Phi }\left(r\right)=GM/\left(r{c}^2\right)$.

This gives the conformal scalar the form:

$$\lambda (r,v)={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}+{\displaystyle \frac{GM}{r{c}^2}}.$$

No other fields, including the Coulomb or other non-gravitational potentials, may appear in $\lambda$ under NUVO theory.

Appendix E.2. The Role of the Wave Equation

The wave equation governs the standing wave structure of the system’s dynamical state, i.e., the eigenstates of a particle’s motion within a defined potential. This equation is not responsible for shaping spacetime geometry, and thus need not be restricted to gravitational-only potentials.

In particular, the hydrogen atom’s binding potential is known empirically to follow the Coulomb form:

$$V\left(r\right)=-{\displaystyle \frac{e^2}{4\pi {\epsilon }_{0}r}}.$$

In standard quantum mechanics, this potential leads to the well-known $1/n^2$ energy spectrum and radial eigenfunctions.

Within NUVO, it is consistent to include this Coulomb potential in the wave equation as long as it is not interpreted as a contributor to the conformal geometry—that is, it must not be included in $\lambda (r,v)$.

Appendix E.3. Justification for Mixed-Potential Modeling

It is therefore valid within NUVO to:

• Use the gravitational potential $\mathrm{\Phi }\left(r\right)$ in $\lambda (r,v)$ to modulate time, advance, and geometry,
• Use the Coulomb potential $V\left(r\right)$ in the wave equation to capture realistic electromagnetic binding,
• Treat $\psi \left(r\right)$ as a dynamical eigenfunction of this wave equation, not as a geometric quantity,
• Preserve the geometric integrity of NUVO while recovering accurate hydrogenic structure.

This separation mirrors the way general relativity treats non-gravitational fields: such fields may affect motion but not the underlying spacetime curvature unless explicitly included in the stress-energy tensor.