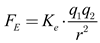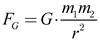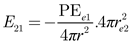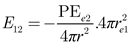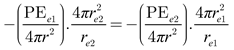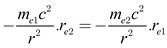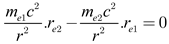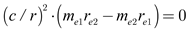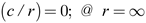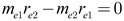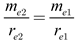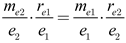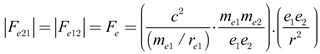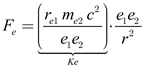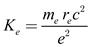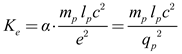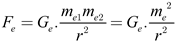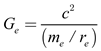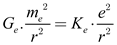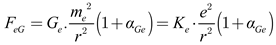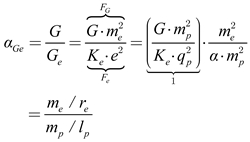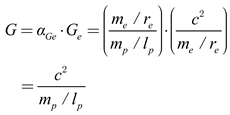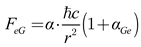A New Theoretical Framework for Unification: The Surprising Link Between Newton’s Gravity and Coulomb’s Law

1. Introduction

The fundamental forces of nature—gravity and electromagnetism (EM)—govern the structure and behavior of the universe on both cosmic and atomic scales. Despite their stark differences in strength and range, Newton’s law of gravitation and Coulomb’s law of electrostatics share striking structural similarities. Both forces follow inverse-square laws, where their effects diminish proportionally to the square of the distance between interacting bodies [1,2]. This similarity has fueled enduring curiosity about whether these forces are interconnected or governed by deeper, unified principles [3,4,5,6]. Understanding the relationship between Newtonian gravity and Coulomb’s law is crucial for advancing our knowledge of these forces, particularly as they manifest across vastly different scales—from galaxies to subatomic particles.

Newton’s law of gravitation describes the attractive force between two masses, playing a central role in shaping the large-scale structure and dynamics of the universe. It explains phenomena such as galaxy formation, stellar behavior, and the evolution of cosmic systems. However, at atomic and subatomic scales, gravity’s influence on particles with negligible mass, such as electrons and protons, is minimal, as it is vastly overpowered by the electromagnetic force [7]. Coulomb’s law, on the other hand, describes the force between electric charges, which can either attract or repel depending on their polarity. Electromagnetic interactions govern atomic structure, chemical bonding, and virtually all processes involving charged particles.

The interplay between electromagnetism and gravity lies at the foundation of physics and is essential for understanding the universe’s mechanics. The Standard Model of particle physics successfully describes the electromagnetic force alongside the strong and weak nuclear forces. However, incorporating gravity into this framework remains a long-standing challenge due to its unique characteristics. This challenge has driven extensive efforts to unify these forces, particularly through the pursuit of a quantum theory of gravity. Could there be a hidden symmetry or principle connecting Newtonian gravity and Coulomb’s law? Despite their differences, could these forces represent distinct manifestations of the same fundamental interaction? Newton described force in terms of mass, while Coulomb expressed it in terms of charge.

In this paper, we propose that Newton’s gravitational force and Coulomb’s electrostatic force are expressions of a single underlying interaction, applied to different properties—mass and charge, respectively. To support this hypothesis, we derive a unified equation in Section 2, demonstrating that Newton’s and Coulomb’s laws share a common mathematical structure. This derivation suggests that, while these forces are typically considered distinct because of the properties they act upon, they may represent different manifestations of a single fundamental force.

Exploring this potential unification holds profound implications for both classical and quantum mechanics. Gravity governs celestial motion and structure on macroscopic scales, while electromagnetism facilitates the existence and interactions of matter on quantum scales [8,9,10]. Together, these forces form the foundation of physical phenomena across all scales of nature. In Section 3, we analyze this unification by introducing a key parameter—the electron-gravitational coupling constant—that links these forces. Finally, in Section 4, we summarize the implications of this perspective and outline potential directions for future research.

2. Coulomb’s Law Versus Newton’s Gravity

2.1. The Similarity Between Coulomb’s and Newton’s Equations

Coulomb’s law is a fundamental electrostatic principle, that describes the force between charged particles. It lays the foundation for understanding interactions between attractive or repulsive charges. This law is crucial not only for classical physics but also in fields such as electromagnetism, chemistry, and materials science. Coulomb’s law expresses the force F_E between two charges q₁ and q₂ as [11]:

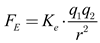(1)

where K_e is Coulomb’s constant, approximately 8.99×10⁹ N⋅m²/C², q_1, and q₂ are the magnitudes of the charges in Coulombs, and r is the distance between the charges in meters. This equation shows the inverse-square law dependency in Coulomb’s law. Interestingly, it is similar to Newton’s law of gravity [12]:

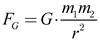(2)

where F_G is the magnitude of Newton’s gravitational force, G is the gravitational constant, approximately 6.674×10⁻¹¹ m³/kg⋅s², m₁, and m₂ are the masses of the objects in kilograms, and r is the distance between them in meters. Comparing equations (1) and (2) reveals a similar pattern and the inverse-square relationship. If we can understand the underlying mechanism of attraction, we may also gain insight into the nature of gravity in the classical and quantum world.

2.2. Deriving Coulomb’s Law

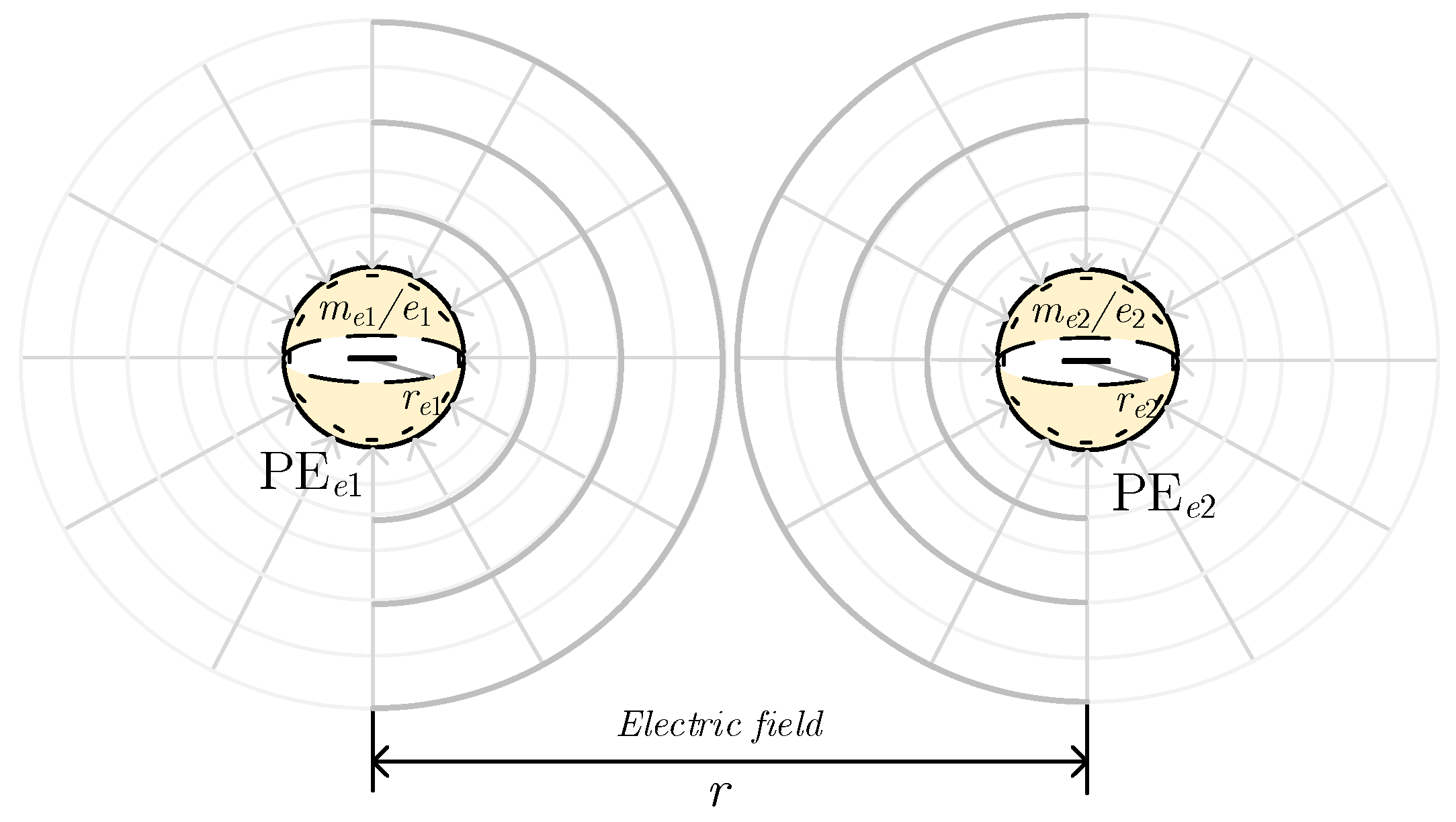
The interaction between the electron charges is illustrated in Figure 1. Assume that electrons e₁ and e₂ are separated by a distance r, with no other forces or energy acting upon them. We consider the energy intensity exerted by electron e₁ on electron e₂ (E₂₁) and by electron e₂ on electron e₁ (E₁₂), which can be represented as:

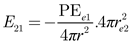	(3.1)
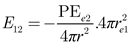	(3.2)

where PE_e1, PE_e2, r_e1, and r_e2 represent the potential energy and classical radius of electrons e₁ and e₂, respectively. The negative sign indicates an opposite direction. At equilibrium, the repulsive forces satisfy the condition:

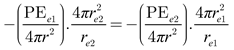(4)

The potential energy of an electron can be expressed as m_e·c², c is the speed of light, approximately 3×10⁸ m/s. By substituting this into equation (4), we find

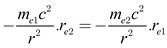(5)

and rearrange the equations as follows:

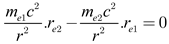	(6.1)
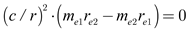	(6.2)

From equation (6.2), we find that the values that satisfy the equation are

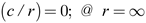	(7.1)
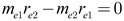	(7.2)

Thus, the relationship between electron mass and radius at equilibrium is:

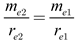(8)

From equation (8), it can be rearranged in terms of the mass-to-charge ratio of electrons expressed as:

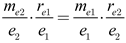(9)

By substituting equation (9) into equation (5), we obtain the repulsive force between electrons:

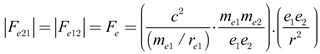(10)

Rearranging equation (10) into the form of Coulomb’s law yields

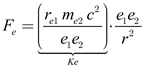(11)

From equation (11), we find that it is equivalent to Coulomb’s law as given in equation (1), where Coulomb’s constant K_e is given by [13]

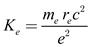(12)

where m_e1 = m_e2 = m_e, r_e1 = r_e2 = r_e, and e₁ = e₂ = e. Upon revisiting equations (12), we find that m_er_e = α·m_pl_p [14]. Hence, we can show the Coulomb’s constant in the terms of

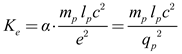(13)

where m_p and l_p represent Planck’s mass and length, with values 2.176×10⁻⁸ kg and 1.616×10⁻³⁵ meters, respectively. α is the fine-structure constant and q_p is Planck’s charge, with values 0.00729 and 1.875×10⁻¹⁸ C, respectively. Substituting these values into equation (13) yields 8.99×10⁹ N⋅m²/C², matching the empirical value of 1/4πε₀, where the permittivity of free space (ε₀) is valued at 8.85×10⁻¹² C²/N·m².

3. The Unified Electro-Gravity Force

In this section, we derive a unified equation that integrates Newtonian gravity and Coulomb forces into a single framework, referred to as the unified electro-gravity model [15,16,17,18]. This model unifies two seemingly distinct forces—gravitational and electrostatic—into a cohesive theory, providing deeper insights into their interplay. This integration is crucial for describing interactions at both microscopic and cosmic scales. Disparities in force magnitudes highlight the importance of key coupling constants, such as the electron-gravitational coupling constant.

We begin with equation (10), carefully analyzing it to reformulate the repulsive force. This force can be expressed as an interaction between the masses of electrons, as shown:

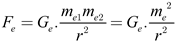(14)

Here, G_e is the electron-gravitational constant, representing the coefficient of the gravitational force between electron masses. It is determined using:

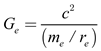(15)

By substituting the electron’s mass and radius into equation (15), we find that G_e = 2.789×10³² m³/kg⋅s². Notably, equation (14) has a form strikingly similar to Newton’s gravitational equation, as shown in equation (2). However, the coefficients of the gravitational force differ. Upon careful consideration of equations (11) and (14), we find that both equations yield the same value, which can be compared as follows:

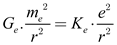(16)

Using equations (16) and (2), we then combine the Coulomb attraction and the Newtonian gravitational force acting on electrons to derive the electro-gravity force (F_eG), expressed as:

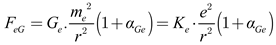(17)

Here, α_Ge represents the electron-gravitational coupling constant, defined as the ratio G/G_e. This dimensionless constant has a value of 2.4×10⁻⁴³, which corresponds to the ratio of the gravitational force to the electrostatic force between electrons [19], expressed as:

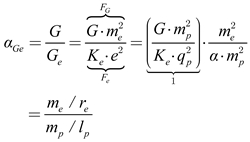(18)

By carefully considering equations (15) and (18), we can demonstrate that the universal gravitational constant is related as expressed in the following equation:

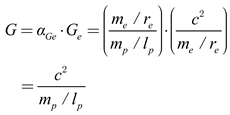(19)

This equation indicates that gravitational interaction propagates at the speed of light, consistent with the prediction of the general theory of relativity. In 2015, the existence of gravitational waves was first confirmed through the groundbreaking detection by LIGO (Laser Interferometer Gravitational-Wave Observatory) [20].

From equation (17), we can rearrange the expression for K_e based on the relationship of the fine-structure constant, as described in equation (13). Consequently, the electro-gravity force (F_eG) can be expressed in terms of Planck’s constant, as shown in the equation:

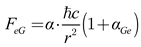(20)

where ℏ is the reduced Planck constant, defined as h/2π, where h is Planck’s constant (≈6.626×10⁻³⁴ J⋅s). Notably, this equation demonstrates that the gravitational force can be unified with the electromagnetic force through the electron-gravitational coupling constant. However, α_Ge specifically represents the relative weakness of gravity compared to electromagnetism in this unified framework, which is negligible.

Table 1 summarizes the values of fundamental physical constants. Notably, these constants are related to Planck’s constant, implying that all of them are interconnected through the fine-structure constant, a key parameter in quantum electrodynamics that quantifies the strength of electromagnetic interaction. In addition to unifying gravity with electromagnetic force, this also integrates gravity with quantum mechanics.

4. Conclusions

This paper investigates the striking structural parallels between Newton’s law of gravitation and Coulomb’s law of electrostatics, proposing a unified framework that identifies these forces as distinct manifestations of a single, underlying interaction. By deriving a shared mathematical structure, we demonstrate that both laws adhere to an inverse-square dependence, emphasizing their fundamental similarities despite acting on different properties: mass and charge. The unified electro-gravity framework introduces a novel perspective by revealing the electron-gravitational coupling constant (α_Ge), a dimensionless parameter that bridges these forces. While gravity’s influence is negligible at atomic scales compared to electromagnetism, this unification highlights a profound connection across vastly different scales, from the subatomic to the cosmic.

Beyond its immediate implications, this framework opens a promising avenue for addressing a major challenge in modern physics: formulating a theory of quantum gravity. By integrating electromagnetism and gravity, the electro-gravity framework lays a foundational basis for exploring the quantum nature of spacetime. The dimensional consistency and coupling constants identified here could serve as critical tools for bridging the macroscopic predictions of the general theory of relativity with the microscopic dynamics of quantum mechanics. This study underscores the importance of discovering symmetries and constants that unify fundamental forces. Future research, including empirical validations and extensions into quantum field theory, may unveil deeper connections between this unified model and the principles governing quantum gravity. Such advances could ultimately lead to a more comprehensive understanding of the universe’s fundamental laws.