1. Introduction
Computer-aided chemical process simulation has been an important tool not just in chemical engineering education, but also in commercial platform for the design and analysis of industrial systems that process bulk chemicals, specialty chemicals, pharmaceuticals and many more [
1,
2]. Among several software packages, the AspenPlus®, which is part of Aspen Tech’s suite of software packages [3-5], has been the state-of-the-art due to its wide array of functional capabilities (e.g., property analysis, rigorous models, process flowsheeting, API for external software such as Fortran and Python, etc.), and extensive database of chemical and physical properties [3,6-10]. Amid being the most advanced chemical process modeling software, this software has its inherent limitations [
11]. One such limitations is that it still requires users to perform manual iterative optimization of certain designs that can sometimes result in extended periods spent on iterations by the user, or to sub-optimal final design [
12]. These challenges can be exacerbated when dealing with a high-dimensional space of design parameters being explored [
11,
12]. Addressing these challenges and establishing solutions can significantly make the design process via this software tool (and other similar software packages) to be more efficient. This work aimed to demonstrate the use of reinforcement learning (RL), specifically the soft actor-critic (SAC) algorithm [
13,
14], to improve the design optimization task for the internals of multistage distillation column (
Figure 1).
1.1. The Challenge: Distillation Column Internals Design
The specification of column internals in a multistage distillation column significantly dictates the hydraulics involved in the interactions of vapor and liquid streams through the various stages inside the column (
Figure 1). This consequently creates a feedback loop in the usual design process – the hydraulics in the column become metrics of the goodness of the column internals design specifications [
15]. In this study, the hydraulics parameter called percent (%) approach to flooding, which is denoted here using the notation
, is used to measure the goodness of distillation column internals design. This parameter
is not the only metric of good column design [
2,
15], but it is a significant indicator [
16]. The numerous nonlinear relations and models involved in computing the column internal parameters that produce allowable values of
make this design task very difficult to automate using traditional programming techniques. Even the AspenPlus® software does not currently have a built-in automated optimization function for this task [
3,
10]. Hence, this current study demonstrates SAC RL approach to provide this valuable automation. For a seamless integration between the distillation column internal parameters, and the SAC RL model, this study uses the RadFrac module available in AspenPlus®. The RadFrac module is the most rigorous model in AspenPlus® fitting to be used in column internals design because of the stage-by-stage vapor-liquid calculations, hydraulics analysis, and its support for trayed and packed column designs [
17,
18]. A Python module called ‘pywin32’ [
19] serves as API to read data from and to send data to AspenPlus®.
1.1. The Solution: SAC algorithm-based Design Optimization
This work evaluates the capability of SAC to automatically learn the best design parameter settings in the RadFrac column. SAC is an algorithm that optimizes a stochastic policy in an off-policy manner, which implements the combined capabilities of stochastic policy optimization and deep deterministic policy gradient (DDPG) approaches [
13,
14,
20]. Because of the blend of stochastic and deterministic capabilities, the prediction of AC model for the next action steps are well within the bounds of the defined action space [
13,
14]. This is a feature that can be fitting to implement in distillation column design because the column parameters are allowed to be sampled only from a finite range of values due to limitations of fluid dynamics, vapor-liquid equilibrium, energy balance and other constraints imposed by natural law.
Note that a DDPG model was also evaluated during the preliminary works for this project and the DDPG model predictions failed to stay within the bounds of the action variables (column internal design parameters) resulting in input value errors of column design parameters when implemented in the AspenPlus® model file. This prompted the researchers to eliminate DDPG and focus only on SAC as the RL to evaluate for column design optimization in this work.
2. Methodology
2.1 Environment: Multi-stage Distillation Column as RadFrac in AspenPlus
A model of a tray-type multi-stage distillation for the separation of ethanol (C2H5OH) and water (H2O) was chosen because this binary chemical system is commonly used in many design analysis tasks in chemical engineering. Nonetheless, the methodology of this study should naturally be applied to other chemical systems undergoing distillation in a trayed column. The well-established AspenPlus software was chosen as the modeling platform for the tray-type column using its RadFrac module. Please refer to the accompanying AspenPlus file (.apw and .bkp) for all other details of the model used (see Data Availability section).
The details of the binary mixture to be separated via distillation are based on literature materials [
2,
15] and are as follows. A mixture of ethanol-water must be distilled in a sieve tray-type distillation column. The feed contains 35% ethanol and 65% water, and the distillate product stream must contain at least 80% ethanol. The feed is flowing at 20,000 kmol/hr, is a saturated liquid, and is coming to the column at pressure of 1 bar. The distillate rate must be at 104 kmol/hr and the external reflux ratio must be 2.5. After some preliminary graphical method of estimating the number of stages (using McCabe-Thiele method) [
2,
15,
21], it was determined that the total number of stages must be 20 and the feed tray must be on stage 10. The column must have a total condenser, and a partial reboiler. The task is to design a sieve tray type multistage distillation column (see
Figure 2) using the RadFrac module in AspenPlus®.
To simplify the modeling in AspenPlus® and the implementation of SAC RL, the feed tray was assigned to the TOP section of the column. So, the TOP section covers the Stage 1 to Stage 10 while the BOT section covers the Stage 11 to Stage 20.
2.2 Distillation Column Flooding
The state variable for this study is the column flooding measured as % approach to flooding (denoted here as
), which is one of the main performance metrics for sizing of distillation column internals [
16]. Flooding is the excessive accumulation of liquid in the column resulting in poor equilibrium contact between the vapor and liquid streams. The % approach to flooding must be minimized and a typical range of % approach to flooding is 65% to 90% according to Wankat [
15] while Jones and Mellborn [
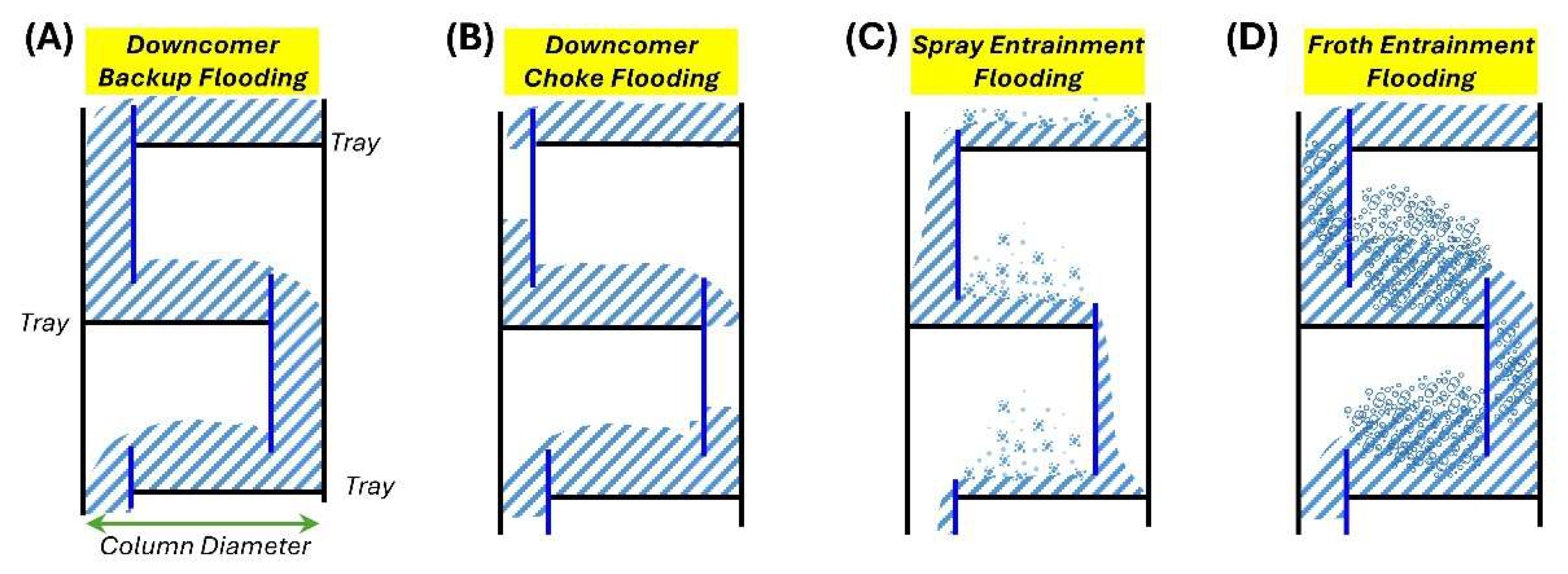
22] suggests a 75% approach to flooding is a good value for various chemical systems. There are four main mechanisms of flooding as shown in
Figure 3. Downcomer backup flooding (
Figure 3A) occurs when the liquid is backed-up into the downcomer due to tray pressure drop, which is usually caused by short tray spacing [
16,
22]. Downcomer choke flooding (
Figure 3B) occurs when the entrance to the downcomer is too narrow resulting in build-up of excesses friction losses for the liquid to overcome [
16]. Spray entrainment flooding (
Figure 3C) occurs when there is a relatively low amount of liquid on the tray because of relatively short weir height and narrow downcomer clearance [
16]. Froth entrainment flooding (
Figure 3D) occurs when significant height of froth reaches the tray above resulting to compromise of the stream concentrations, and this can be a significant effect of settings in the tray spacing, sieve hole diameter, and fraction of the tray allocated for vapor-liquid exchange [
15,
16].
2.3 Notation
We now present notations to formally define the various components of the task in relation to the established notations in RL. The RL problem at hand is a policy search in a Markov Decision Process (MDP) involving the tuple
. The state space
is a continuous space consists of the following column internal design parameters (
Figure 1 and 2): top section (TOP) % approach to flooding, and bottom section (BOT) % approach to flooding. Note that the state % approach to flooding can be greater than 100% according to distillation column design principles, so
. The action space
is a continuous space consists of the following column internal design parameters (
Figure 1 and 2): tray spacing, weir height, downcomer clearance, weir side length, and hole diameter. The action space is bounded by the allowable values of column design parameters in the AspenPlus software, and the actual values also scale with the units (i.e., ft, cm, or mm; kg or lb; etc.) they are assigned in the software by the user as explained above. The state transition probability
represents the probability density of the next state
given the current state
and action
. The environment (i.e., column internal design) emits a reward
from each transition (i.e., process simulation). Note that this current study also evaluated how various forms of the reward system
may affect the SAC performance.
Table 1 summarizes the variables for the action space and state space with their corresponding description according to the actual settings of the AspebPlus® model used in the study. Also refer to
Figure 2 for visualization of the action variables defined in
Table 1. The action space
is multidimensional consists of
(
Table 1). The state space
is two-dimensional consists of
and
(
Table 1). Note that each section of the column, i.e., TOP and BOT, were represented in the action and state spaces even though the design parameters between the sections were similar.
2.4 SAC RL
We present in this section the key equations of the SAC RL algorithm, but the reader should consult the original works [
13,
14,
20] that established this algorithm if more details are needed. Training a SAC model involves learning policy
by solving the following problem:
where
trade-off coefficient for the entropy
term, and
discount factor in the value function [
20]. SAC concurrently learns the policy
, and two Q-functions
and
. The
is the actor network and the
is the critic network.
The smoothing constant,
, is a hyperparameter that controls updating the weighs in of the target networks for the actor
and critic
networks based on the prior derivation and implementations by Lillicrap, Hunt [
23]. In notation:
; and
.
The fourth hyperparameter to be evaluated is the ‘replay buffer length’, which originates from using replay buffer as a solution to extract more information from the history sequential data for RL training [
23]. Replay buffer is a component of the computation of the target Q-functions
and
presented above. The replay buffer is a finite sized (replay buffer length) memory data. The buffer is created by sapling transitions from the environment according to according to the exploration policy and the tuple
is stored in the replay buffer. As more tuple entries are added the buffer becomes filled and when the buffer length is reached, the oldest samples are discarded while maintaining the buffer length. At each timestep the actor and critic are updated by sampling a minibatch uniformly from the buffer.
2.5 Implementation: OpenAI Gymnasium, PyTorch
To eliminate the need to create our custom RL environment, we used the prebuilt RL module called “Gymnasium” by OpenAI [
24,
25]. This module implements the necessary algorithms and functions to define variable spaces and efficient action space-sampling mechanisms to ensure that RL models are exposed to a wide variety of scenarios resulting to improved learning performance [
24,
26].
2.5.1 Action variables
Since all action variables in
are continuous, these were defined using the ‘Gymnasium.Box()’ function, which is designed to handle tensor of continuous variables. The lower and upper bounds of these action variables were required arguments in the ‘Gymnasium.Box()’ functions. Hence the Python code line for defining the action space consists of
was: ‘self.action_space= gymnasium.spaces.Box(low=np.array([30,1,10,5,0.1,30,1,10,5,0.1]),high=np.array([150,7,150,15,1,150,7,150,15,1]),shape=(10,),dtype=np.float32)’ based on the actual values in
Table 1.
2.5.2 State Variables
Defining the state space was very similar to how the action space was defined. Hence the code line defining the state space consists of
and
was: self.observation_space = gymnasium.spaces.Box(low=np.array([0,0]),high=np.array([300,300]),shape=(2,),dtype=np.float32)’ based on the definitions in
Table 1.
2.5.3 Reward Scheme
The reward schemes studied are summarized in
Table 2. Reward is based on the flooding level
of each column section and the scheme for awarding the reward values. Previous works have demonstrated that reward scheme can significantly affect the performance of RL algorithms [27-30]. The unique aspect of the reward schemes adopted for this study is the separate computation of reward for each column section
, and then aggregating these by summation (weighted and unweighted) into a single reward value
(
Table 2). Scheme 1 and Scheme 2 are built on a model that computes the penalty for deviating from the target state by taking difference of the target state value(s) and the current value of the state [
30]. Scheme 3 and Scheme 4 are based on the concept of dividing the state values according to ranges and assigning the highest score on the target range while assigning decreasing reward score was the binning range moves away from the target range. Scheme 5 is built on top of a binary reward system; hence, it represents a binary scheme. The coding of these reward schemes were done in the environment definition via Python scripting.
2.5.4 Hardware Setup
The computer specifications are the following. Unit: Dell Precision 7670 Mobile Workstation; CPU: Intel Core i7-12850HX, 25MB Cache, 24 Threads, 16 Core, 2.1GHz-4.8GHz; Memory: 64GB DDR5; GPU: NVIDIA GeForce RTX 3080Ti with 16GB GDDR6. All computational work done were implemented in this laptop computer running the AspenTech version 12 software suite containing the AspenPlus®, and Anaconda Navigator version 2.5 software [
31] containing Python version 3.10 and all the necessary Python packages such as PyTorch (CUDA-enabled), Gymnasium by OpenAI, and the pywin32 package [
19] that interfaces with Windows to access the AspenPlus® file. Note that even though this study used a GPU-enabled computer to accelerate PyTorch computations, a CPU-only implementation of PyTorch can still accomplish the computations but at slower computation speeds. Nonetheless, the computations in this work do not require specialized computer hardware beyond a typical hardware requirement for running the AspenPlus® software.
2.5.4 Code and Documentation of the Work Done
The necessary codes used in this work have been organized and stored in an online repository via GitHub as detailed in the Data Availability section. There are two main code files: (1) a Python class file that defines all functions used to read data from (output data) and write data to (input data) AspenPlus® via Python, and (2) Jupyter Notebook files that document the implementation of the SAC RL.
2.6 SAC RL Runs
Since RL training is very sensitive to randomization of the initial weight in the deep neural networks in the actor and in the critic components of the SAC model, a set of ten runs was implemented for each learning setting. Each run has a unique random number generator (RNG) index value used for all PyTorch computations, which consequently fixed the random number used in initializing the weights of the neural networks. The ten unique RNG indices can be seen in the accompanying Jupyter Notebook files in the project online repository (see Data Availability section). This deliberate randomization using known RNG indices accomplishes two crucial tasks: (1) testing the robustness if SACR RL models, and (2) allowing for the repeatability of the randomized runs and results.
All runs were set to a maximum of 500 iterations per SAC learning run, where each iteration consists of one cycle of SAC model reading the current state and reward values of the environment (column model in AspenPlus®), SAC model making prediction for the next actions, and sending the predicted actions to the environment for simulation (to get the next state and reward for next cycle). Even though the traditional fields implementing RL (e.g., computer science, robotics, etc.) would usually set maximum iterations up to the range of millions [
13], distillation column design iteration becomes impractical if the maximum iterations become very high, so our setting of a maximum of 500 iterations per SAC learning run was based on practical basis. The data collected from each run as discussed above would not require extensive downstream processing as these data by themselves are sufficient to evaluate the performance of SAC RL.
Furthermore, each run started with an untrained SAC RL model. This design of the study aimed to demonstrate that even an untrained SAC RL model can learn to optimize within a reasonable length of time (max of 500 iterations).
2.7 Data Collection and Analysis
There were numerous data that could be collected in this study because the nature of the environment is highly data-intensive inherent in computer-based design of distillation columns in AspenPlus®, and because the SAC RL training is data-intensive. This prompted the research team to focus collecting only on key data that would enable evaluation of the performance of SAC RL in column internals design. The data for following variables were saved and used for discussion: levels of the action variables, levels of the state variables, levels of the reward variables, and runtime per iteration. The saving of these data sets were coded in the run codes to eliminate user errors and streamline the analysis.
3. Results and Discussion
The results are presented in the following order: Section 3.1 covers the results to demonstrate the feasibility of using SAC RL for distillation column design; section 3.2 covers he results to show the effect of reward scheme on the performance of SAC RL; section 3.3 covers the results to show the effect of column diameter on the performance of SAC; and section 3.4 covers the results to show the effect of SAC hyperparameters setting on its performance.
3.1 Feasibility of Using SAC RL for Distillation Column Internals Design
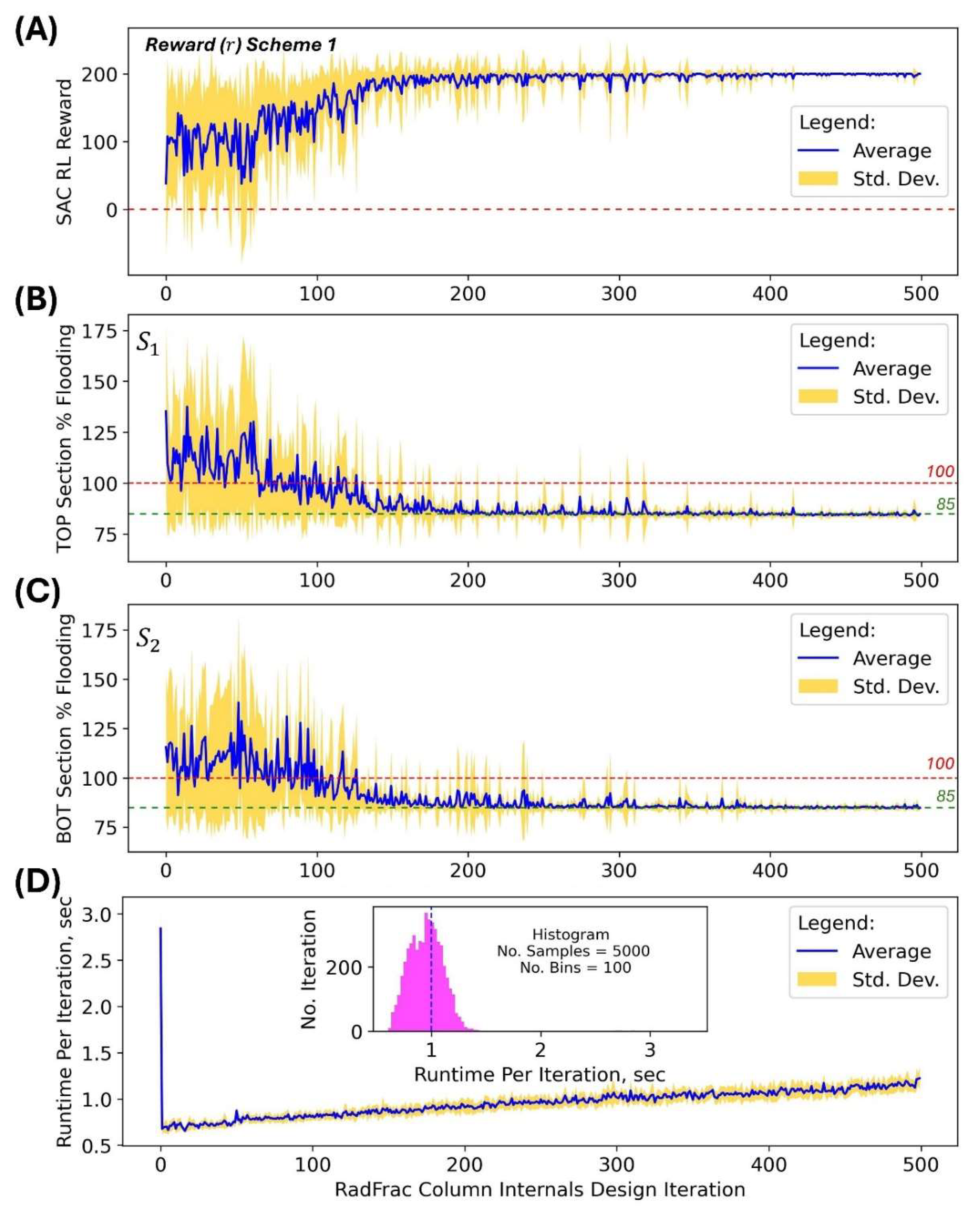
The first question that must be answered is “Does SAC RL work as automation method in optimizing distillation column internals design?” The answer is yes, it works. The evidence for this claim can be seen in
Figure 4 and
Figure 5, which were the results when SAC RL was implemented on the column with fixed uniform (in both TOP and BOT sections) diameter of 6-feet. Using the reward Scheme 1, the SAC model learned how to optimize the column design as the training progressed and converging to predicting column designs that maximize the reward (max of 200) as seen in
Figure 4A, and selecting actions (column design parameter levels) that resulted to % flooding within the target range of 80-90% (
Table 2 Scheme 1) as seen in
Figure 4B and 4C. Initially, the SAC model does not have any optimal policy in determining the best next actions because the deep neural network in the critic and actor components were randomly initialized. This is evident in the very large standard deviation of the reward values and state variable values at the beginning of the training (
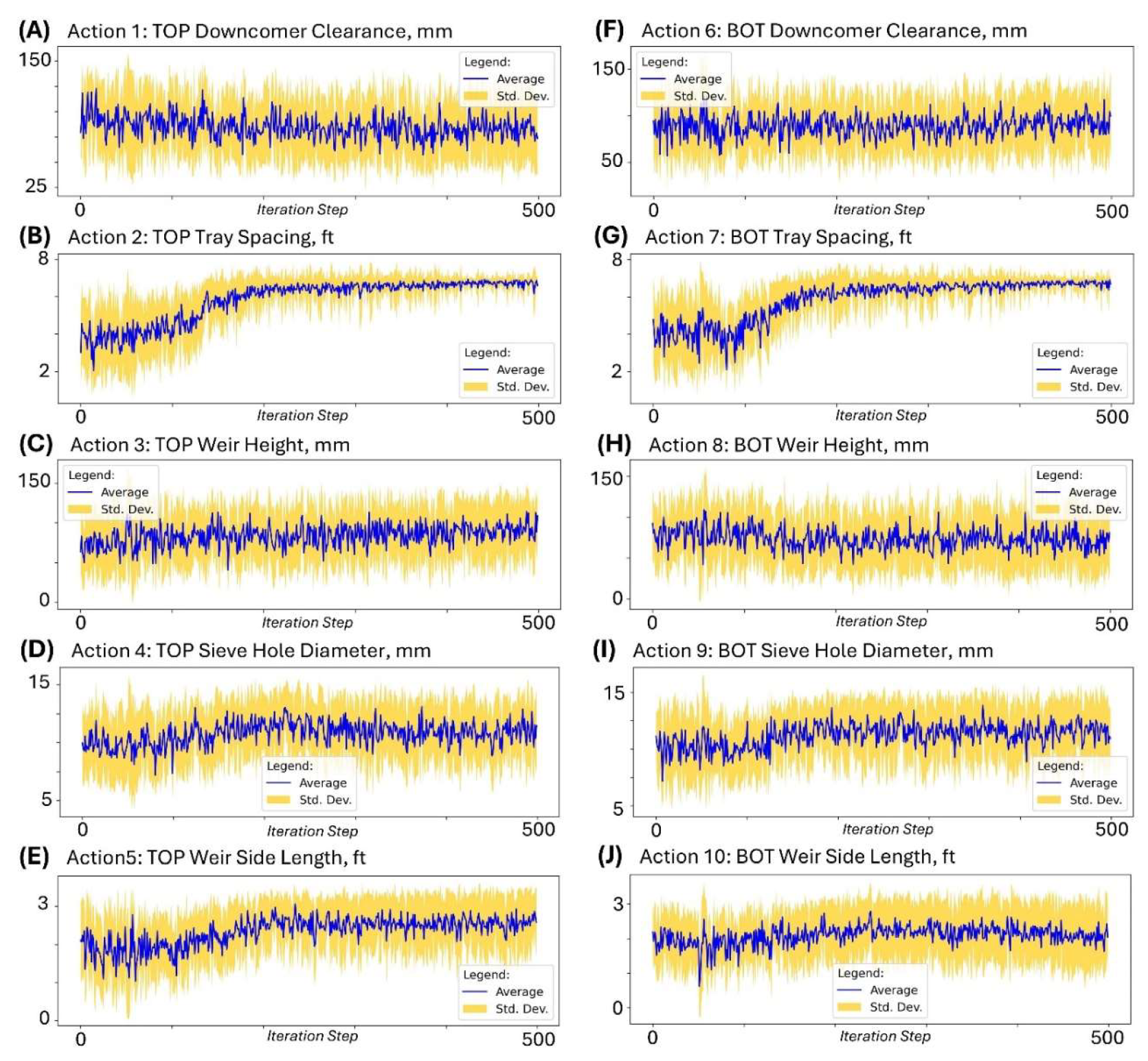
Figure 4A, 4B, and 4C). However, as the cycle of training-prediction-implementation steps progresses, the model learns the best actions that result to high rewards and the bad actions that results to low rewards, and eventually converges to optimal policies (actor and critic) that favor prediction of actions (
Figure 5) that result in favorable
values resulting to highest rewards (
Figure 4). This trend of convergence is very evident in the last 100 iterations, i.e., 400-500 iteration steps accompanied by smaller (narrower) standard deviation of reward and state variable values (
Figure 4).
Another crucial aspect of the design task is the duration of the SAC RL automated optimization because chemical process design can be time sensitive [
3]. The summary of runtime (in seconds) as shown in
Figure 4D indicates that the average time per design iteration by the SAC model is 1 second (on the laptop computer used in this study – see section 2.5.4 Hardware Setup for details on the computer). This means that a single run with a maximum of 500 iterations (
Figure 4) takes only around 10 minutes, which may be significantly lower than the time it takes to manually iterate the design.
With the numerous iterations that resulted in
values within the target range [80%, 90%) as shown in
Figure 4B and 4C, the SAC-based optimization essentially exhaustively discovered numerous ways on how the column internal parameters can be set while achieving target design specification, i.e.,
. The action space trends shown in
Figure 5 show the corresponding column design parameters for these design iterations that meet design specification.
3.4 Effect of SAC Hyperparameters on Performance
Inherent in training RL models is the tuning of hyperparameters in order to further refine the models. This section covers the results in evaluating the effect of four hyperparameters:
,
,
, and reply buffer length. Of the numerous hyperparameters, these four have direct effects on SAC RL because of their roles in the fundamental equations of SAC.
Table 4 summarizes the flooding results for the top section (TOP) of the column set at fixed diameter of 6 feet. Even though data were also collected for the bottom-section (BOT) of the column, space limitations in the manuscript prompted reducing the presented data to half; hence,
Table 4 shows data for TOP section.
The effect of hyperparameter
can be seen by first comparing the results between Setting 10 and 11, between Setting 7 and 8 (
Table 4). The general trend is that a lower
value of 0.1 will produce higher fractions of runs that fall within the target condition
compared when
is set higher at 0.5. However, when comparing between Setting 8 and 9, it can be seen that
has lower fraction
compared to
. This means that there is an optimal value for
in the range 0.1 to 0.5, and this value may be close to 0.2. Since the value of
is a measure of the fraction of entropy contribution in the loss function (see Equation 1), this observed trend means that the term in the loss function for maximizing entropy should not be zero but it should also be not very large part of the loss function. This is just a fitting observation because this entropy term is a unique feature of the SAC in comparison to other RL algorithms implementing actor-critic networks [
13,
32].
The effect of hyperparameter
can be seen by first comparing results between Setting 3 and 10, and between Setting 4 and 12 (
Table 4). Both pairs show that lower value of
results to higher fraction
. If there is any optimum value somewhere, these data pairs cannot support such possibility – perhaps a more extensive scan of the hyperparameter space can discover an optimum but this is beyond the scope of this study. Since hyperparameter
represents the smoothing coefficient for the target Q-functions, setting its value to zero may not be a good idea because this number controls the update of the Q-function deep neural network weights.
The effect of hyperparameter
can be seen by first comparing results between Setting 1 and 2, between Setting 4 and 5, and between Setting 12 and 13 (
Table 4). It can be seen in these pairs that the trends for fraction
do not follow a clear consistent trend. It is possible that there are confounding effects in the SAC RL training that cannot be easily isolated to be sole effect of
. Therefore, there is no conclusive trend for the effect this hyperparameter based on data.
The effect of hyperparameter ‘replay buffer length’ can be seen by first comparing results between Setting 2 and 4, between Setting 6 and 13, and between Setting 8 and 11 (
Table 4). It can be seen in these pairs that the trends for fraction
do not follow a clear consistent trend. Similar to hyperparameter
, it is possible that there are confounding effects in the SAC RL training that cannot be easily isolated to be sole effect of ‘replay buffer length’. Therefore, there is no conclusive trend for the effect this hyperparameter based on data.
4. Conclusions
This study focused on developing an automated method using soft actor-critic (SAC) reinforcement leaning for optimizing the design of distillation column, and this aim was achieved as supported by the results. The integration of SAC RL into AspenPlus® model optimization was achieved by using Python codes written to allow a cyclic interaction between the distillation column model AspenPlus® and the SAC model in PyTorch. The specific chemical system used as case study is a binary mixture of ethanol-water, and the RadFrac module in AspenPlus® was used to enable rigorous column internal design. The results clearly support the following findings: (1) SAC RL works as automation approach for the design of distillation column internals, (2) the reward scheme in the SAC model significantly affects SAC performance, (3) column diameter is a significant constraint in achieving column internals design specification in flooding, and (4) SAC hyperparameters have varying effect on SAC performance.
This study also demonstrated that an untrained SAC RL model can quickly learn how to optimize the design of a distillation column. This has significant implications for possible future implementation of the technique as integral part of computer-based chemical process modeling, e.g., if this technique becomes part of AspenPlus® software (and other similar computer packages). That is, there is no need to install a pre-trained SAC RL model into a computer-based chemical process simulation package that would utilize this technique.
Author Contributions
Conceptualization, D.L.B.F., H.B., R.W., C.B., and A.P.M.; methodology, D.L.B.F. and H.B.; software, D.L.B.F. and H.B.; formal analysis, DLBF, A.P.M., M.A.B., and M.E.Z.; investigation, D.L.B.F., H.B., R.W., and C.B.; resources, M.A.B. and M.E.Z.; data curation, D.L.B.F. and H.B.; writing, D.L.B.F., H.B., and A.P.M.; project administration, D.L.B.F.; funding acquisition, D.L.B.F. and M.E.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by two grants: (1) LURA Grant by the Louisiana Space Grant Consortium (LaSPACE) with subaward number PO-0000277305 under primary NASA grant number 80NSSC20M0110, and (2) LaSSO Grant by the Louisiana Space Grant Consortium (LaSPACE) and Louisiana Sea Grant (LSG) with subaward number PO-0000277330 under primary NASA grant number 80NSSC20M0110.
Data Availability Statement
All Python codes, Jupyter Notebook files, AspenPlus® model files, sample raw data in spreadsheet, and sample graphics used in the paper are archived online in the project GitHub repository [
33]:
https://github.com/dhanfort/aspenRL.git. This is an open-access repository under MIT License. The reader is encouraged to contact the corresponding author if there is a need for more information beyond the open-access materials.
Acknowledgments
We acknowledge the support of the staff of the Energy Institute of Louisiana (EIL): Sheila Holmes and Bill Holmes. EIL facilities have been instrumental in completing this work.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Seidel T, Biegler LT. Distillation column optimization: A formal method using stage-to stage computations and distributed streams. Chemical Engineering Science. 2025 2025/02/05/;302:120875.
- Seader JD, Henley EJ, Roper DK. Separation Process Principles: With Applications Using Process Simulators. 4th ed. New York: Wiley 2016.
- Al-Malah KIM. Aspen Plus: Chemical Engineering Applications. 2nd ed.: Wiley; 2022.
- Haydary, J. Chemical Process Design and Simulation: Aspen Plus and Aspen Hysys Applications. Wiley; 2019.
- AspenTech. AspenPlus: AspenTech; 2024 [cited v12]. Available from: https://www.aspentech.com/en.
- Bao J, Gao B, Wu X, et al. Simulation of industrial catalytic-distillation process for production of methyl tert-butyl ether by developing user’s model on Aspen plus platform. Chemical Engineering Journal. 2002 2002/12/28/;90(3):253-266.
- Kamkeng ADN, Wang M. Technical analysis of the modified Fischer-Tropsch synthesis process for direct CO2 conversion into gasoline fuel: Performance improvement via ex-situ water removal. Chemical Engineering Journal. 2023 2023/04/15/;462:142048.
- Syauqi A, Kim H, Lim H. Optimizing olefin purification: An artificial intelligence-based process-conscious PI controller tuning for double dividing wall column distillation. Chemical Engineering Journal. 2024 2024/11/15/;500:156645.
- Byun M, Lee H, Choe C, et al. Machine learning based predictive model for methanol steam reforming with technical, environmental, and economic perspectives. Chemical Engineering Journal. 2021 2021/12/15/;426:131639.
- Schefflan, R. Teach Yourself the Basics of Aspen Plus. 2nd ed.: Wiley; 2016.
- Agarwal RK, Shao Y. Process Simulations and Techno-Economic Analysis with Aspen Plus. In: Agarwal RK, Shao Y, editors. Modeling and Simulation of Fluidized Bed Reactors for Chemical Looping Combustion. Cham: Springer International Publishing; 2024. p. 17-73.
- Chen Q, editor The Application of Process Simulation Software of Aspen Plus Chemical Engineering in the Design of Distillation Column. Cyber Security Intelligence and Analytics; 2020 2020//; Cham: Springer International Publishing.
- Haarnoja T, Zhou A, Abbeel P, et al. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv e-prints. 2018. arXiv:1801.01290.
- Haarnoja T, Zhou A, Hartikainen K, et al. Soft Actor-Critic Algorithms and Applications. ArXiv. 2018;abs/1812.05905.
- Wankat, P. Separation Process Engineering - Includes Mass Transfer Analysis. 3rd ed. New York: Prentice Hall; 2012. (Wankat P, editor.).
- Kister, H. Distillation Design. Boston: McGraw-Hill; 1992.
- Taqvi SA, Tufa LD, Muhadizir S. Optimization and Dynamics of Distillation Column Using Aspen Plus®. Procedia Engineering. 2016 2016/01/01/;148:978-984.
- Tapia JFD. Chapter 16 - Basics of process simulation with Aspen Plus∗. In: Foo DCY, editor. Chemical Engineering Process Simulation (Second Edition): Elsevier; 2023. p. 343-360.
- Hammond, M. pywin32: PyPi; 2024 [cited 2025 Jan. 9]. Available from: https://pypi.org/project/pywin32/.
- OpenAI. Soft Actor-Critic: OpenAI; 2025 [cited 2025 Jan. 9]. Available from: https://spinningup.openai.com/en/latest/algorithms/sac.html.
- McCabe WL, Thiele EW. Graphical Design of Fractionating Columns. Industrial & Engineering Chemistry. 1925 1925/06/01;17(6):605-611.
- Jones E, Mellborn M. Fractionating column economics. Chemical Engineering Progress (CEP). 1982:52-55.
- Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. arXiv e-prints. 2015. arXiv:1509.02971.
- Towers M, Kwiatkowski A, Terry J, et al. Gymnasium: A Standard Interface for Reinforcement Learning Environments. arXiv e-prints. 2024. arXiv:2407.17032.
- Brockman G, Cheung V, Pettersson L, et al. OpenAI Gym. ArXiv. 2016;abs/1606.01540.
- Zhang X, Mao W, Mowlavi S, et al. Controlgym: Large-Scale Control Environments for Benchmarking Reinforcement Learning Algorithms. arXiv e-prints. 2023. arXiv:2311.18736.
- Nath A, Oveisi A, Pal AK, et al. Exploring reward shaping in discrete and continuous action spaces: A deep reinforcement learning study on Turtlebot3. PAMM. 2024 2024/10/01;24(3):e202400169.
- Viswanadhapalli JK, Elumalai VK, S S, et al. Deep reinforcement learning with reward shaping for tracking control and vibration suppression of flexible link manipulator. Applied Soft Computing. 2024 2024/02/01/;152:110756.
- Veviurko G, Böhmer W, de Weerdt M. To the Max: Reinventing Reward in Reinforcement Learning. arXiv e-prints. 2024. arXiv:2402.01361.
- Dayal A, Cenkeramaddi LR, Jha A. Reward criteria impact on the performance of reinforcement learning agent for autonomous navigation. Applied Soft Computing. 2022 2022/09/01/;126:109241.
- Anaconda. Anaconda: The Operating System for AI: Anaconda; 2025. Available from: https://www.anaconda.com/.
- Liu J, Guo Q, Zhang J, et al. Perspectives on Soft Actor–Critic (SAC)-Aided Operational Control Strategies for Modern Power Systems with Growing Stochastics and Dynamics. Applied Sciences. 2025 [cited. [CrossRef]
- Fortela DLB. aspenRL: Enhanced AspenPlus-based Multi-stage Distillation Design Using SAC Reinforcement Learning: GitHub; 2025 [cited 2025 Jan. 19]. Available from: https://github.com/dhanfort/aspenRL.
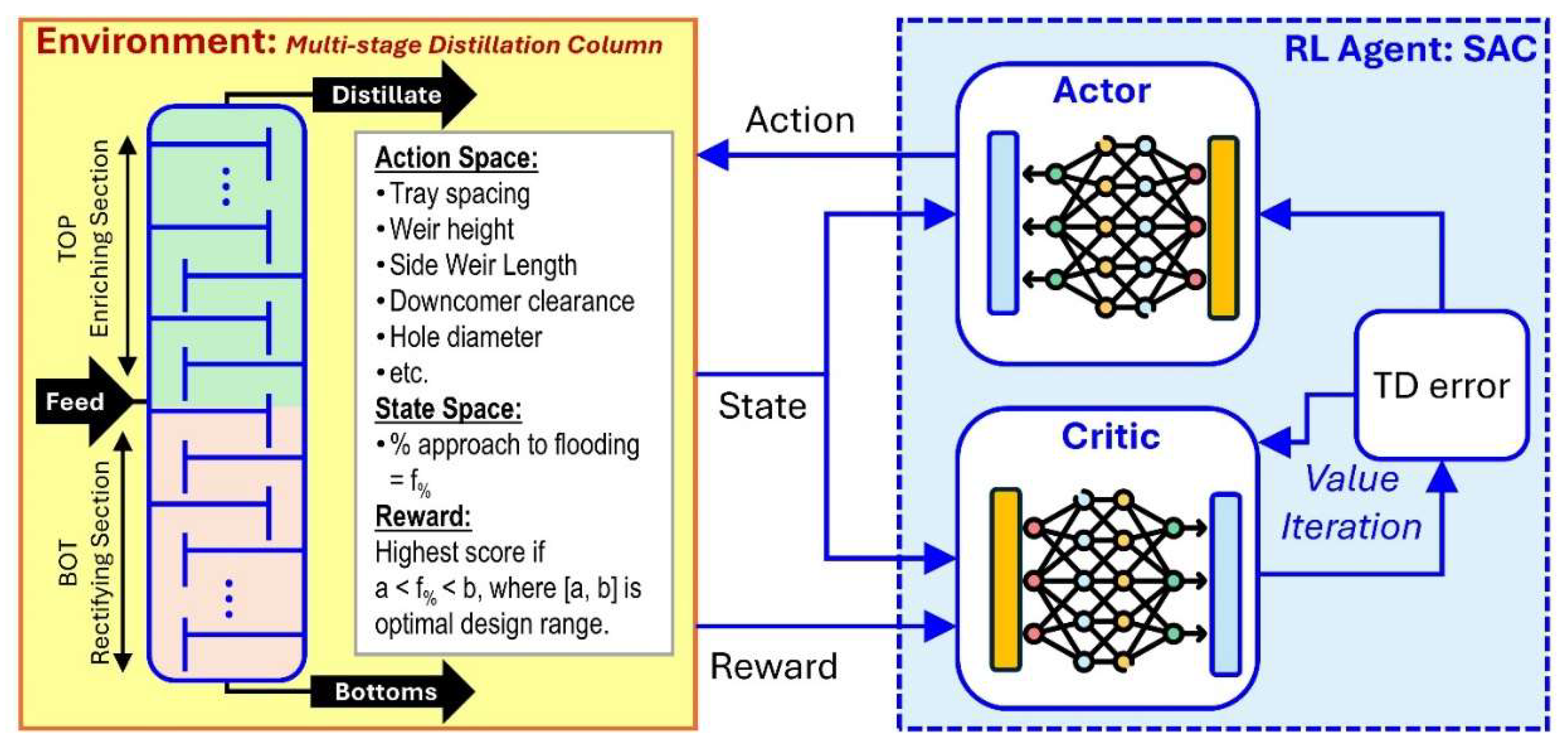
Figure 1.
Schematic of the implementation of soft actor-critic (SAC) RL algorithm in the optimization of column internals design in multi-stage distillation column.
Figure 1.
Schematic of the implementation of soft actor-critic (SAC) RL algorithm in the optimization of column internals design in multi-stage distillation column.
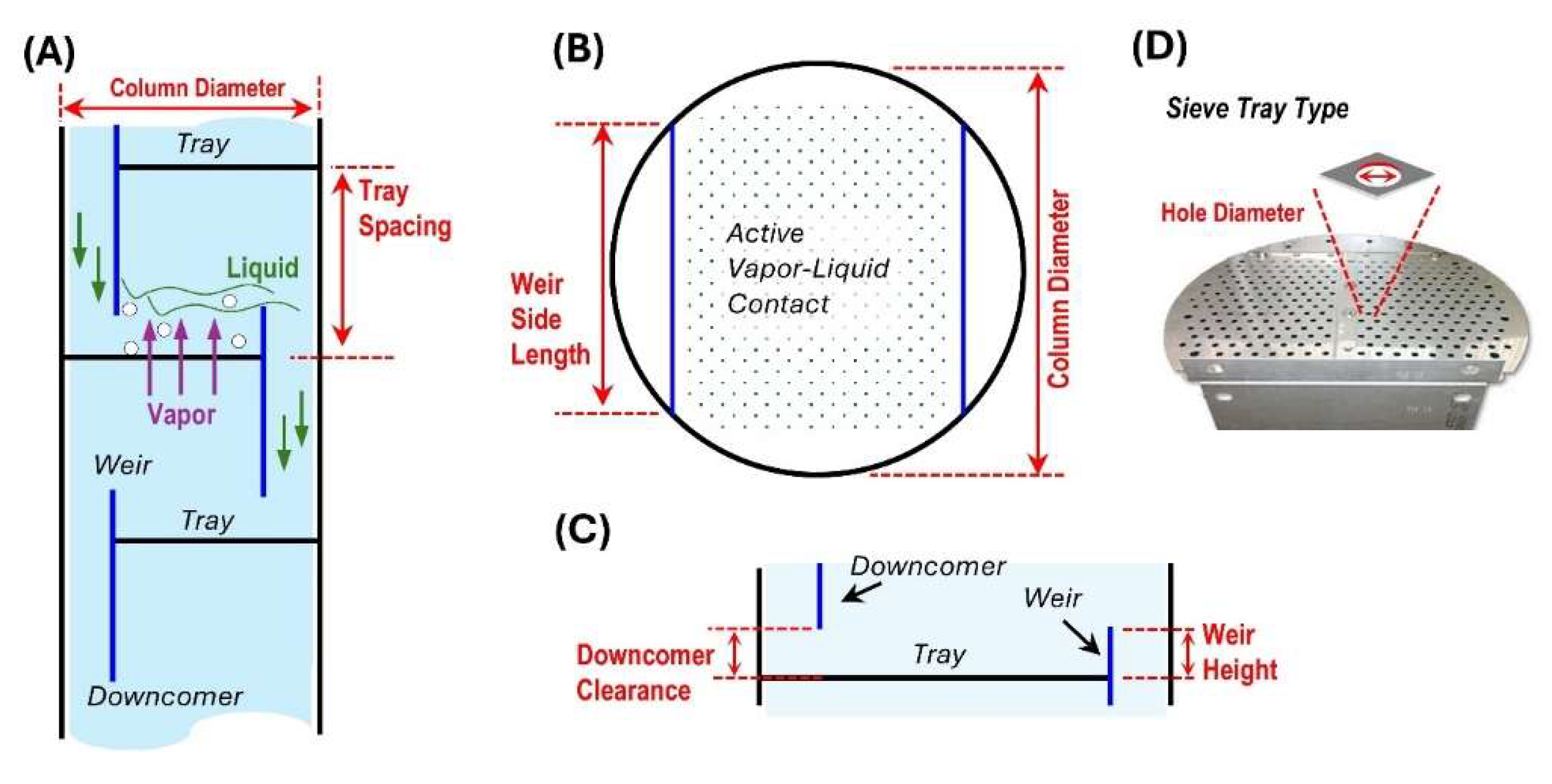
Figure 2.
Distillation column internals design parameters studied for the application of SAC. (A) cross-section view of a vertical section of the column indicating the parameters column diameter and tray spacing, (B) top-view on a tray indicating the parameters weir side length and column diameter, (C) view indicating the parameters downcomer clearance and weir height, and (D) view of a sieve tray indicating parameter hole diameter.
Figure 2.
Distillation column internals design parameters studied for the application of SAC. (A) cross-section view of a vertical section of the column indicating the parameters column diameter and tray spacing, (B) top-view on a tray indicating the parameters weir side length and column diameter, (C) view indicating the parameters downcomer clearance and weir height, and (D) view of a sieve tray indicating parameter hole diameter.
Figure 3.
Distillation tray flooding mechanisms. (A) downcomer backup flooding, (B) downcomer choke flooding, (C) spray entrainment flooding, and (D) froth entrainment flooding.
Figure 3.
Distillation tray flooding mechanisms. (A) downcomer backup flooding, (B) downcomer choke flooding, (C) spray entrainment flooding, and (D) froth entrainment flooding.
Figure 4.
Performance of implementing SAC RL to optimize distillation column internals design by using the reward Scheme 1 for a maximum of 500 iterations. The distillation column diameter was fixed at 6 feet. Ten runs were implemented with each run having its unique RNG index. The following SAC RL model settings were used:
,
,
, and
. (A) SAC RL reward value, (B) column TOP section % flooding level, (C) column BOT section % flooding level; and (D) runtime in seconds per SAC RL iteration. The associated actions (column internal design levels) predicted by the SAC RL model are shown in the next figure (
Figure 5).
Figure 4.
Performance of implementing SAC RL to optimize distillation column internals design by using the reward Scheme 1 for a maximum of 500 iterations. The distillation column diameter was fixed at 6 feet. Ten runs were implemented with each run having its unique RNG index. The following SAC RL model settings were used:
,
,
, and
. (A) SAC RL reward value, (B) column TOP section % flooding level, (C) column BOT section % flooding level; and (D) runtime in seconds per SAC RL iteration. The associated actions (column internal design levels) predicted by the SAC RL model are shown in the next figure (
Figure 5).
Figure 5.
Actions (column internal design levels) predicted by the SAC RL model as it learns the best policies to optimize the reward. Ten runs were implemented with each run having its unique RNG index. The following SAC RL model settings were used: , , , and . (A) Action 1 () = TOP Downcomer clearance, (B) Action 2 () = TOP Tray spacing, (C) Action 3 () = TOP Weir height, (D) Action 4 () = TOP Sieve hole diameter, (E) Action 5 () = TOP Weir side length, (F) Action 6 () = BOT Downcomer clearance, (G) Action 7 () = BOT Tray spacing, (H) Action 8 () = BOT Weir height, (I) Action 9 () = BOT Sieve hole diameter, and (J) Action 10 () = BOT Weir side length.
Figure 5.
Actions (column internal design levels) predicted by the SAC RL model as it learns the best policies to optimize the reward. Ten runs were implemented with each run having its unique RNG index. The following SAC RL model settings were used: , , , and . (A) Action 1 () = TOP Downcomer clearance, (B) Action 2 () = TOP Tray spacing, (C) Action 3 () = TOP Weir height, (D) Action 4 () = TOP Sieve hole diameter, (E) Action 5 () = TOP Weir side length, (F) Action 6 () = BOT Downcomer clearance, (G) Action 7 () = BOT Tray spacing, (H) Action 8 () = BOT Weir height, (I) Action 9 () = BOT Sieve hole diameter, and (J) Action 10 () = BOT Weir side length.
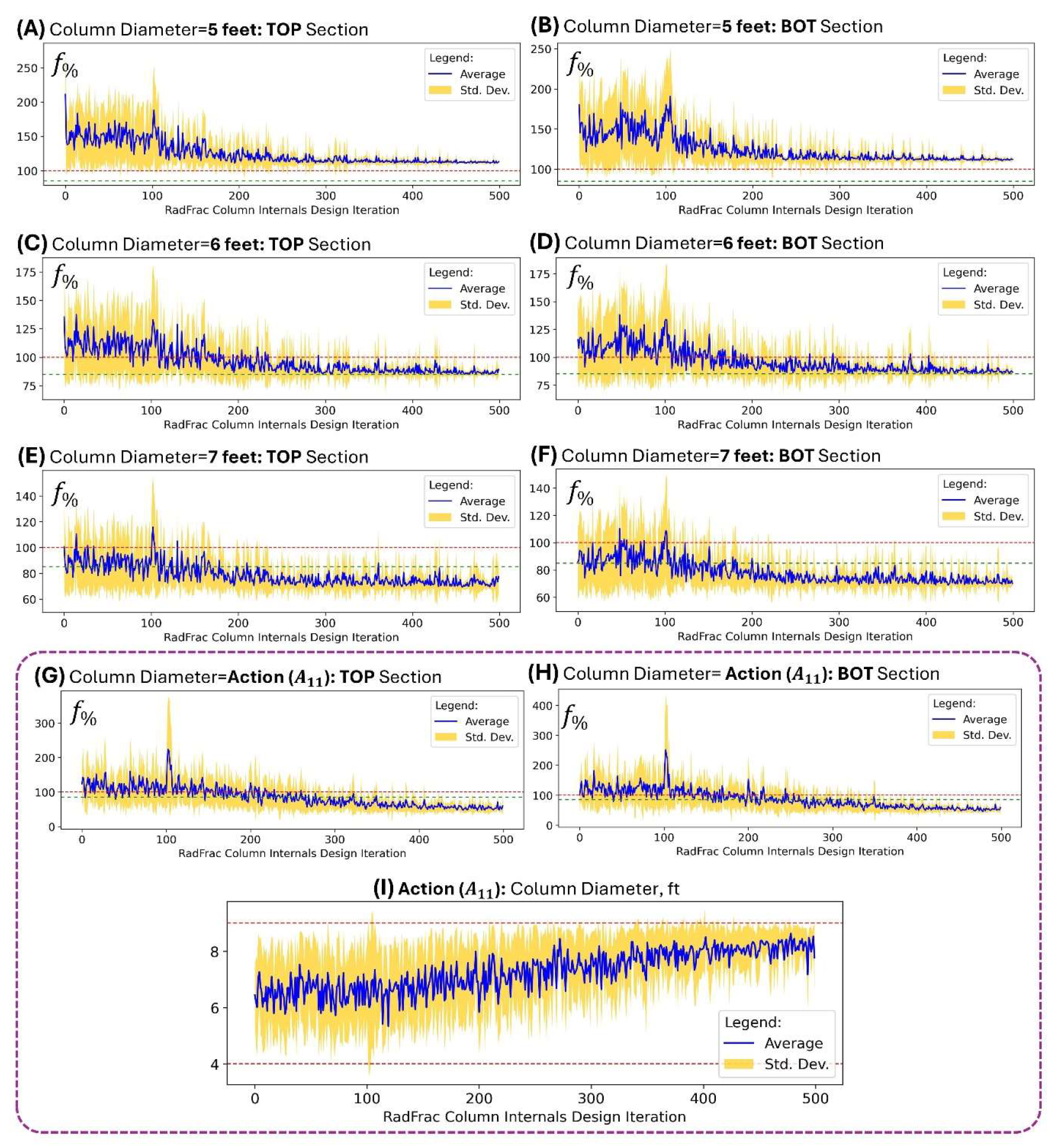
Figure 6.
Flooding results when SAC RL was implemented at varied column diameter levels. (A) TOP at 5 ft diameter, (B) BOT at 5 ft diameter, (C) TOP at 6 ft diameter, (D) BOT at 6 ft diameter, (E) TOP at 7 ft diameter, and (F) BOT at 7 ft diameter. When column diameter is in action space as of SAC RL: (G) TOP flooding, (H) BOT flooding, and (I) column diameter predictions by SAC RL.
Figure 6.
Flooding results when SAC RL was implemented at varied column diameter levels. (A) TOP at 5 ft diameter, (B) BOT at 5 ft diameter, (C) TOP at 6 ft diameter, (D) BOT at 6 ft diameter, (E) TOP at 7 ft diameter, and (F) BOT at 7 ft diameter. When column diameter is in action space as of SAC RL: (G) TOP flooding, (H) BOT flooding, and (I) column diameter predictions by SAC RL.
Table 1.
Summary of action and state variables used in the study.
Table 1.
Summary of action and state variables used in the study.
| Action/State Variable |
Description |
|
) = TOP Downcomer clearance |
Distance between the bottom edge of the downcomer and the tray below; Value range: [30, 150]; Units: mm |
|
) = TOP Tray spacing |
Distance between two consecutive trays; Value range: [1, 7]; Units: ft |
|
) = TOP Weir height |
Height of a tray outlet weir, which regulates the amount of liquid build-up on the plate surface; Value range: [10, 150]; Units: mm |
|
) = TOP Sieve hole diameter |
Diameter of the holes on the sieve tray; Value range: [5, 15]; Units: mm |
|
) = TOP Weir side length |
Length of the tray outlet weir; Value range: [0.1, 1]; Units: ft |
|
) = BOT Downcomer clearance |
Distance between the bottom edge of the downcomer and the tray below; Value range: [30, 150]; Units: mm |
|
) = BOT Tray spacing |
Distance between two consecutive trays; Value range: [1, 7]; Units: ft |
|
) = BOT Weir height |
Height of a tray outlet weir, which regulates the amount of liquid build-up on the plate surface; Value range: [10, 150]; Units: mm |
|
) = BOT Sieve hole diameter |
Diameter of the holes on the sieve tray; Value range: [5, 15]; Units: mm |
|
) = BOT Weir side length |
Length of the tray outlet weir; Value range: [0.1, 1]; Units: ft |
|
) = Column diameter** |
Diameter of the column; Value range: [4, 9]; Units: ft |
|
|
; Units: % |
|
|
; Units: % |
Table 2.
Summary of reward schemes used in this study.
Table 2.
Summary of reward schemes used in this study.
| Reward Model |
Definition |
|
Scheme 1
|
where is the reward in section of the column. For each :
where or
|
|
Scheme 2
|
where is the reward in section of the column. For each :
where
|
|
Scheme 3
|
Reward is based on the intervals of with highest score for the target interval .
where is the reward in section of the column. For each :
if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if |
|
Scheme 4
|
Reward is similar to Scheme 3 but with reward values lower by a factor of 10.
where is the reward in section of the column. For each :
if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if ; if |
|
Scheme 5
|
where is the reward in section of the column. For each :
|
Table 3.
Summary of fractions of column design iterations that are below cut-off values for % flooding values . The last 100 iteration steps of each of the 10 runs was used, i.e., 1000 samples per reward model. The following SAC RL model settings were used: , , , and . Column diameter was fixed at 6 feet.
Table 3.
Summary of fractions of column design iterations that are below cut-off values for % flooding values . The last 100 iteration steps of each of the 10 runs was used, i.e., 1000 samples per reward model. The following SAC RL model settings were used: , , , and . Column diameter was fixed at 6 feet.
| Reward Model |
Column Section |
|
|
|
|
|
|
|
Scheme 1
|
TOP |
88.5 |
8.7 |
0.955 |
0.826 |
0.251 |
0 |
| BOT |
88.8 |
8.6 |
0.945 |
0.796 |
0.216 |
0 |
|
Scheme 2
|
TOP |
87.9 |
7.1 |
0.963 |
0.837 |
0.293 |
0 |
| BOT |
88.2 |
6.1 |
0.974 |
0.835 |
0.146 |
0 |
|
Scheme 3
|
TOP |
87.7 |
6.0 |
0.971 |
0.841 |
0.29 |
0 |
| BOT |
88.0 |
5.6 |
0.976 |
0.823 |
0.214 |
0 |
|
Scheme 4
|
TOP |
93.8 |
14.6 |
0.851 |
0.587 |
0.111 |
0 |
| BOT |
94.0 |
14.6 |
0.845 |
0.57 |
0.102 |
0 |
|
Scheme 5
|
TOP |
101.9 |
21.8 |
0.686 |
0.371 |
0.067 |
0 |
| BOT |
102.4 |
22.0 |
0.686 |
0.359 |
0.052 |
0 |
Table 4.
Summary of fractions of column design iterations that are below the cut-off value for flooding values . The last 100 iteration steps of each of the 10 runs was used, i.e., 1000 samples per reward model. The runs implemented were for a column diameter = 6 feet and reward model Scheme 1.
Table 4.
Summary of fractions of column design iterations that are below the cut-off value for flooding values . The last 100 iteration steps of each of the 10 runs was used, i.e., 1000 samples per reward model. The runs implemented were for a column diameter = 6 feet and reward model Scheme 1.
| SAC Setting |
Hyperparameter |
Fraction of
|
Mean
|
Std. Dev.
|
|
|
|
Replay buffer length |
| 1 |
0.2 |
0.05 |
0.99 |
50 |
0.945 |
85.3 |
4.0 |
| 2 |
0.2 |
0.05 |
0.9 |
50 |
0.918 |
85.9 |
3.6 |
| 3 |
0.5 |
0.05 |
0.9 |
100 |
0.881 |
86.8 |
5.3 |
| 4 |
0.2 |
0.05 |
0.9 |
100 |
0.886 |
86.8 |
6.3 |
| 5 |
0.2 |
0.05 |
0.99 |
100 |
0.826 |
88.5 |
8.7 |
| 6 |
0.2 |
0.01 |
0.99 |
50 |
0.978 |
84.8 |
2.1 |
| 7 |
0.5 |
0.01 |
0.9 |
50 |
0.865 |
86.8 |
5.2 |
| 8 |
0.1 |
0.01 |
0.9 |
50 |
0.881 |
86.7 |
5.1 |
| 9 |
0.2 |
0.01 |
0.9 |
50 |
0.938 |
85.4 |
3.2 |
| 10 |
0.5 |
0.01 |
0.9 |
100 |
0.916 |
86.5 |
5.3 |
| 11 |
0.1 |
0.01 |
0.9 |
100 |
0.947 |
85.8 |
3.2 |
| 12 |
0.2 |
0.01 |
0.9 |
100 |
0.932 |
86.4 |
6.1 |
| 13 |
0.2 |
0.01 |
0.99 |
100 |
0.870 |
87.5 |
7.7 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).