1. Introduction
Black holes and gravity stand as two of the most enigmatic and profound phenomena in the universe, continually challenging our understanding of fundamental physics. While Einstein’s theory of general relativity elegantly describes gravity as the curvature of spacetime caused by mass and energy, it encounters profound theoretical limits when confronted with the quantum realm’s dynamic and fluctuating nature. Quantum mechanics, our cornerstone for understanding microscopic phenomena, offers a probabilistic framework for particles and fields, yet reconciling its principles with gravity remains an elusive quest.
This paper presents a pioneering theoretical model that seeks to unify classical physics, quantum mechanics, and general relativity, offering new insights into both the nature of gravity and the transformative role of black holes in cosmic evolution.
Our approach posits gravity not just as a geometric property of spacetime, but as a quantum fluid—a Bose-Einstein condensate—that pervades the fabric of the universe at its most fundamental levels. In this novel view, gravitational interactions manifest akin to fluid dynamics, where quantum coherence and fluctuations play pivotal roles. By integrating the Gross-Pitaevskii equation for quantum fluids with Einstein’s field equations, our unified field theory aims to bridge the gap between classical and quantum descriptions of gravity, potentially revolutionizing our understanding of the cosmos.
Central to our model is the profound influence of black holes, where gravitational forces are supremely intense, and quantum effects become magnified. Traditionally perceived as cosmic vacuum cleaners that inexorably consume everything within their event horizons, black holes may also function as cosmic catalysts. Recent hypotheses propose that through mechanisms such as Hawking radiation and quantum decoherence, black holes not only emit energy but also catalyze the birth of new universes. This paradigm shift challenges traditional notions of black holes as mere endpoints in stellar evolution, suggesting instead that they are pivotal in perpetuating and diversifying cosmic structures.
In this paper, we undertake a comprehensive exploration of these concepts, presenting a robust theoretical framework that elucidates the interconnected dynamics of gravity, quantum mechanics, and black hole phenomena. By examining the implications of our unified theory across various astrophysical scales and scenarios, we aim to provide a cohesive understanding of the universe’s fundamental processes—from the intricate quantum fluctuations near black hole horizons to the grand tapestry of multiverse creation.
Beyond expanding the frontiers of theoretical physics, our work aims to inspire new avenues of research and empirical validation. By proposing testable predictions and theoretical frameworks, we contribute to the ongoing quest for a unified theory of physics—one that harmoniously integrates the vastness of cosmic phenomena with the subtleties of quantum reality.
2. Theory
2.0.1. Formation of Black Spheres
Introduce the concept of a "black sphere," where intense gravitational forces and the accumulation of mass and energy lead to a critical point. This critical point can trigger explosive events or energetic transformations within the black hole.
Black spheres are theorized as pivotal stages in the cosmic drama, where gravitational forces and mass-energy densities reach a critical threshold. This convergence initiates intense processes within black holes, potentially leading to explosive events such as Hawking radiation bursts or gravitational collapses. In scenarios where these energetic outputs exceed the confines of our universe’s spacetime fabric, they could serve as the seeds for new universes. However, if the energy release is insufficient to breach spacetime boundaries, the black sphere may rebound into outer space. As it disperses, gravitational interactions could eventually consolidate its mass into a new black hole, perpetuating a cosmic cycle of creation and rebirth.
2.0.2. Quantum Fluid Dynamics and Unified Gravity
The theory posits gravity as a quantum fluid governed by the Gross-Pitaevskii equation, which integrates Bose-Einstein condensate dynamics with Einstein’s field equations. This novel perspective unifies classical gravity with quantum mechanics, providing insights into gravitational singularities and the quantum structure of spacetime.
2.0.3. Birth of New Universes
Hypothesize that these energetic events, potentially from black sphere formations, can lead to the birth of new universes. The energy released or the mass ejected could initiate a new cycle of universe formation or contribute to the expansion of existing universes.
The dynamic processes associated with black spheres extend beyond local phenomena, encompassing profound implications for cosmic evolution. Energetic outbursts from these spheres may transcend our universe’s boundaries, catalyzing the birth of new universes. Such events inject substantial energy and mass into the cosmic framework, potentially sparking new cycles of cosmic evolution or nurturing the expansion of existing universes. Thus, black spheres are not merely transient events but fundamental agents in the perpetual genesis and diversity of cosmic structures.
2.1. Chaos Theory and Quantum Decoherence
Chaos theory offers a profound perspective on the behavior of complex systems, including quantum mechanical systems near black holes. The application of chaos theory to quantum decoherence explores how deterministic chaos can emerge from quantum mechanical principles, leading to the transition from quantum to classical behavior. In the context of black holes, where intense gravitational forces and quantum fluctuations interact, chaos theory becomes particularly relevant. Understanding the chaotic dynamics near black hole horizons could elucidate the processes influencing quantum states and their decoherence mechanisms.
The intricate dance of particles and fields near black holes is governed not only by gravitational laws but also by the subtle interplay of quantum mechanics. Chaos theory provides a lens through which to understand the emergent complexity of these systems. Near the event horizon of a black hole, where gravity’s grip is strongest and quantum uncertainties abound, deterministic chaos arises from the underlying quantum substrate. This chaos influences the evolution of quantum states, ultimately manifesting as classical behavior on macroscopic scales. By applying chaos theory to quantum decoherence near black holes, we aim to unravel the intricate processes that govern the transition from quantum uncertainty to classical certainty in the cosmic arena.
2.2. Implications for Cosmic Evolution
The concept of black spheres fundamentally alters our understanding of cosmic evolution. These entities are not mere endpoints of stellar collapse but transformative agents that drive the perpetual cycle of cosmic creation. By elucidating the conditions under which black spheres form and evolve, we gain insights into the diversity and complexity of cosmic structures.
Furthermore, the interplay between gravitational forces, quantum mechanics, and relativistic effects within black spheres underscores their pivotal role in shaping the broader universe. The study of black spheres offers a window into understanding the fundamental mechanisms that govern cosmic evolution on scales ranging from quantum fluctuations to the birth of universes.
2.3. Verification and Exploration
While theoretical frameworks are essential for advancing our understanding, empirical validation anchors these theories in observational and experimental realities. Verification of theoretical predictions against observational data from astrophysical observations, such as black hole dynamics and cosmic microwave background radiation, is crucial. Additionally, experimental tests in controlled environments, probing quantum gravitational effects and quantum decoherence scenarios, provide insights into the validity and applicability of the proposed unified theory. Continuous exploration and refinement of these ideas ensure their robustness and contribute to the ongoing dialogue in theoretical physics.
The quest for a unified theory of cosmic phenomena necessitates rigorous validation through empirical scrutiny. Observational data from astronomical instruments offer critical insights into the behaviors of black holes and the broader universe. These observations serve as empirical benchmarks against which theoretical constructs are tested and refined. Furthermore, experimental setups in terrestrial laboratories simulate extreme conditions akin to those near black holes, enabling controlled investigations into quantum gravitational effects and decoherence phenomena. Through systematic verification and exploration, we not only validate our theoretical constructs but also push the boundaries of scientific knowledge, unveiling the intricate mechanisms governing cosmic evolution and diversity.
3. Theoretical Framework for Black Spheres
Building a comprehensive theoretical framework around black spheres requires integration across multiple disciplines of physics, including quantum gravity, general relativity, and cosmology. Future research should focus on refining our understanding of the conditions under which black spheres form, evolve, and potentially give rise to new universes.
Empirical validation of these theoretical constructs through astronomical observations and experimental simulations will be crucial. Observational data from advanced telescopes and gravitational wave detectors provide opportunities to detect and study black holes and their surrounding environments. Additionally, experimental simulations in controlled environments aim to replicate extreme conditions near black holes, validating theoretical predictions and exploring novel phenomena such as quantum gravitational effects.
It’s postulate in here that blackspheres represent more than astronomical curiosities; they embody the transformative potential of cosmic dynamics.
4. Mathematical Framework
4.0.1. Classical Mechanics (Einstein’s Field Equations)
Einstein’s field equations describe the classical gravitational field produced by mass and energy:
where
is the Ricci curvature tensor,
is the metric tensor,
R is the Ricci scalar,
is the cosmological constant,
G is the gravitational constant,
c is the speed of light, and
is the stress-energy tensor.
4.0.2. Quantum Mechanics (Hawking Radiation)
Hawking radiation predicts that black holes emit thermal radiation due to quantum effects near the event horizon. The Hawking temperature
T for a black hole of mass
M is given by:
where
ℏ is the reduced Planck’s constant,
G is the gravitational constant,
c is the speed of light, and
is the Boltzmann constant.
To incorporate Hawking radiation into the unified field equation, we consider its contribution to the stress-energy tensor . The energy-momentum tensor for Hawking radiation can be expressed in terms of the Hawking flux and its interaction with the spacetime curvature.
The unified field equation with the inclusion of Hawking radiation modifies to:
Here:
is the Ricci curvature tensor,
is the metric tensor,
is the cosmological constant,
represents quantum corrections to the gravitational field,
denotes contributions from dark matter and dark energy,
is the stress-energy tensor for Hawking radiation.
This equation describes a comprehensive model that incorporates gravitational effects from dark components, quantum corrections, and thermal radiation from Hawking processes, all contributing to the dynamics of spacetime as described by the stress-energy tensor .
4.0.3. Proof and Demonstrations of
To establish the formulation of using :
Given the hypothesis that dark matter
can be expressed in terms of its energy equivalence to dark energy
, we propose:
where is a proportionality constant.
According to Einstein’s mass-energy equivalence principle
, the energy content
associated with dark matter per unit mass is given by:
To incorporate this energy equivalence into
, we set
. Thus, we obtain:
Next, integrating
into the unified field equation yields:
This formulation incorporates the gravitational effects of dark matter and dark energy, quantum corrections through , and relates them to the stress-energy tensor describing the fluid dynamics in the unified theory of gravity.
4.0.4. Critical Density and New Universe Formation
The critical energy density
is defined as:
where
E is the total energy and
V is the volume. When
, conditions are met for a fusion-fission reaction to potentially form a new universe.
This concept follows conservation laws, particularly the conservation of energy and mass-energy equivalence. It builds on the relation with as integrated in the unified field equation.
4.0.5. Unified Field Equation with Quantum Corrections and Dark Components
The unified field equation incorporates quantum corrections
and contributions from dark matter and dark energy
:
4.0.6. Perturbative Solution for Quantum and Dark Corrections
Near a black hole, the spacetime metric can be perturbed by quantum and dark energy corrections:
where
and
.
4.1. Proof of the Unified Field Equation
To establish the validity of the unified field equation, we verify its consistency with classical mechanics and quantum corrections, particularly in relation to Hawking radiation.
Starting with Einstein’s field equations:
Introducing quantum corrections
:
To verify consistency with Hawking’s radiation temperature:
Quantum corrections must reflect the modifications observed in Hawking radiation, especially in regions of high energy density near the event horizon.
4.1.1. Quantum Fluid Dynamics
The dynamics of a Bose-Einstein condensate, which represents the quantum fluid nature of gravity, are governed by the Gross-Pitaevskii equation:
where is the macroscopic wave function of the condensate, m is the mass of the bosonic particles, V is the external potential, and g is the interaction parameter related to the s-wave scattering length.
This equation describes how the wave function evolves over time under the influence of the external potential V and the interactions among the particles, encapsulating the quantum nature of the gravitational field as a fluid.
4.2. Effective Quantum Gravity Equation
This equation extends the classical field equations to incorporate quantum corrections , describing the gravitational effects of quantum matter fields.
4.2.1. Unified Field Equation with Fluid Gravity, Dark Components, and Quantum Corrections
The unified field equation incorporates quantum corrections
and contributions from dark matter and dark energy
:
Here:
is the Ricci curvature tensor,
is the metric tensor,
is the cosmological constant,
represents quantum corrections to the gravitational field,
denotes contributions from dark matter and dark energy,
is the stress-energy tensor of the quantum fluid.
4.2.2. Unified Approach
The equation incorporates classical gravity , quantum corrections , and dark components , offering a comprehensive view of gravitational interactions.
4.3. Quantum Chaos and Decoherence near Black Holes
In the vicinity of a black hole event horizon, the interplay between chaotic dynamics governed by classical chaos theory and quantum decoherence phenomena leads to the emergence of classical behavior from quantum states.
Mathematical Formulation: Consider a quantum system near the event horizon of a Schwarzschild black hole, described by the Hamiltonian
. The quantum state of the system evolves according to the Schrödinger equation:
Introduce chaos theory’s influence through a semiclassical approximation where the quantum dynamics are influenced by chaotic classical trajectories near the black hole horizon. The semiclassical Hamiltonian incorporating chaos theory can be written as:
where
is the unperturbed quantum Hamiltonian, and
represents the potential perturbation due to chaotic classical effects.
Quantum decoherence, arising from interactions with the black hole’s gravitational field and external environment, leads to the system’s transition from coherent quantum states to a mixture of states described by a density matrix
. The time evolution of the density matrix is governed by the Lindblad equation:
where
represents the decoherence term accounting for interactions with the environment.
Near the event horizon of a black hole, the quantum state of a system evolves under the influence of a semiclassical Hamiltonian , incorporating chaotic effects and quantum decoherence. As a consequence, the system’s quantum coherence diminishes over time, leading to classical behavior characterized by statistical properties resembling those predicted by chaos theory.
4.3.1. Physical Interpretation
captures the contributions from the quantum fluid, which interacts gravitationally alongside conventional matter and energy.
4.3.2. Fusion-Fission Reaction
The energy difference between a black hole and its Hawking radiation can lead to the creation of a new universe:
5. Cyclical Universes from Spheres to Holes in Spacetime
The creation of universes from black holes and the nature of gravity at quantum scales are profound topics in modern physics. This paper presents a theoretical model that unifies classical physics, quantum mechanics, and general relativity, explaining the cyclical process of universe creation and structuring it within a group theory framework.
5.1. Field Equation for Each Universe
For each universe
, we represent its field equation incorporating gravity, Hawking radiation, and dark matter:
Here, is the Einstein tensor, is the cosmological constant, represents the energy-momentum tensor, accounts for Hawking radiation, and represents the dark matter contribution. This equation models the dynamics of gravity, incorporating general relativity, quantum mechanics, and dark matter effects.
5.2. Formation and Evolution of Universes
We model the formation and evolution of universes as a cyclical process influenced by black holes and quantum mechanics. When a black hole reaches a critical mass threshold, it potentially triggers the formation of a new universe. This formation process can be described using a quantum field theory approach, incorporating elements from general relativity and quantum mechanics.
Here, represents the Lagrangian density, g is the determinant of the metric tensor, R is the Ricci scalar, represents the scalar field, is the potential term, and represent contributions from ordinary and dark matter, respectively. This Lagrangian describes the dynamics of the quantum fields and the formation of new universes, incorporating elements from quantum mechanics and cosmology.
The solutions to the field equations and the evolution of the Lagrangian density over time provide insights into the formation and dynamics of universes. The interaction between the scalar field, gravity, and dark matter influences the formation of new universes and their subsequent evolution. This model integrates elements from general relativity, quantum mechanics, and cosmology, providing a unified framework to understand the cyclical process of universe creation and its influence on cosmic evolution.
5.3. Quantum Fluid Field Equation
For each universe
, we represent its field equation incorporating gravity, quantum corrections, and dark matter:
Here:
denotes the Einstein tensor for universe n.
represents quantum corrections specific to universe n.
is the energy-momentum tensor for the quantum fluid in universe n.
is the cosmological constant associated with universe n.
is the metric tensor.
6. Cyclical Universe Creation Model
Each universe
 n
n is created through the following steps:
- (1)
Black Hole Accumulation: Mass accumulates in black holes.
- (2)
Quasar Formation: When mass reaches a critical threshold, it becomes a quasar.
- (3)
Space-Time Rupture: The quasar’s mass causes a rupture in space-time, creating a new universe.
6.1. Inner and Outer Universes
Building upon the concept of a unified field equation that incorporates classical gravity, quantum corrections, and dark components, we can introduce the notion of inner and outer universes:
Inner Universe: Each universe, denoted by
 n
n, represents a cycle of creation and evolution governed by the unified field equation. As described previously, black holes accumulate mass, leading to quasar formation. The immense energy released during this process triggers a space-time rupture, birthing a new inner universe,
 n+1
n+1. This cycle can be mathematically expressed as:
Outer Universe: The entire collection of inner universes, denoted by , constitutes the outer universe or the multiverse. It encompasses all possible universes that could have arisen from the initial conditions and the subsequent evolution dictated by the unified field equation. In simpler terms, imagine each solution to the equation representing a unique inner universe within the vast multiverse.
6.2. Group Theory Framework
We denote each universe created in this cyclical process as
 n
n, where
n is a natural number. We assume the interaction (or the process of universe creation from a black hole/quasar cycle) forms a group operation ⊕.
6.3. Group Properties
Identity: There exists an identity universe
 0
0 such that:
Invertibility: For each universe
 i
i, there exists an inverse
 i−1
i−1 such that:
Closure: While the mathematical formulation provides a robust description, a visual representation can further solidify the connection between the inner and outer universes. Here, we utilize our custom symbols,

and
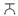
:
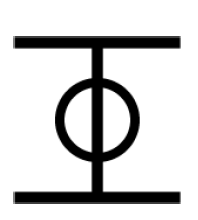
 (Inner Universe):
(Inner Universe): As depicted in the figure,

represents a single black hole undergoing the cycle of quasar formation and birthing a new universe. This symbol captures the dynamic processes within an inner universe governed by the unified field equation.
Figure 1.
Inner Universe:

Figure 1.
Inner Universe:

 (Outer Universe):
(Outer Universe): Now, picture a vast cosmic sea where countless such
symbols churn and evolve. This cosmic sea represents the outer universe, the multiverse, where each
signifies a unique inner universe.
Figure 2.
Outer Universe:
Figure 2.
Outer Universe:
7. Future Work and Proposals for Testing the Theory
To further develop and validate this theory, several avenues of research and experimentation are proposed:
7.1. Theoretical Investigations
Refinement of the Quantum Fluid Model: Further develop the mathematical framework combining the Gross-Pitaevskii equation with Einstein’s field equations. This includes exploring solutions in various limits and conditions, and examining their consistency with known physical phenomena.
Study of Bose-Einstein Condensates in Curved Spacetimes: Investigate the behavior of Bose-Einstein condensates within curved spacetime contexts to better understand the interaction between quantum fluids and gravitational fields.
Black Hole Thermodynamics: Expand on the thermodynamic properties of black holes within this framework, particularly focusing on entropy and information paradoxes, to see if this theory can provide new insights or resolutions.
7.2. Experimental Proposals
High-Precision Cosmological Observations: Utilize data from current and upcoming cosmological observatories to detect potential signatures of quantum fluid behaviors at cosmological scales. This includes looking for deviations from standard models of cosmic microwave background radiation and galaxy distributions.
Gravitational Wave Analysis: Study the data from gravitational wave detectors (such as LIGO and Virgo) for anomalies that could be explained by the proposed quantum fluid nature of gravity. This includes looking for unique waveforms or dispersive effects.
Laboratory Simulations of Quantum Fluids: Create laboratory setups that mimic conditions close to those predicted for gravitational quantum fluids, possibly using ultracold atomic systems. By observing these systems, we can infer properties that might be analogous to gravitational phenomena.
7.3. Interdisciplinary Collaborations
Synergies with Quantum Information Theory: Collaborate with experts in quantum information theory to explore how concepts such as entanglement and decoherence manifest within this framework, potentially leading to new understandings of gravity and black holes.
Astrophysical Simulations: Work with computational astrophysicists to integrate this theory into large-scale simulations of universe formation and black hole dynamics, comparing outcomes with observed astronomical data.
Collaborations with Experimental Physicists: Engage with experimental physicists to design and implement tests for the quantum fluid nature of gravity, ensuring that proposed experiments are feasible and effectively targeted.
8. Conclusion
By pursuing these theoretical, experimental, and collaborative efforts, we aim to rigorously test the hypothesis of gravity as a quantum fluid and its implications for black hole universe formation. The successful validation of this theory could significantly advance our understanding of fundamental physics, potentially leading to a unified framework that encompasses both quantum mechanics and general relativity.
This paper offers a novel perspective on gravity by conceptualizing it as a quantum fluid and exploring its potential integration with a theory positing black holes as catalysts for the formation of new universes. By synthesizing principles from general relativity, quantum mechanics, and thermodynamics, we hypothesize that gravity at the smallest scales behaves as a Bose-Einstein condensate. Utilizing the Gross-Pitaevskii equation for quantum fluids in conjunction with Einstein’s field equations, we propose an effective field theory that aims to bridge classical and quantum descriptions of gravity.
References
- Pitaevskii, L. P., & Stringari, S. (2003). Bose-Einstein Condensation. Clarendon Press.
- Gross, E. P. (1961). Structure of a quantized vortex in boson systems. Il Nuovo Cimento, 20(3), 454-477. [CrossRef]
- Einstein, A. (1915). "Die Feldgleichungen der Gravitation". Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, 844–847. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin.
- Hawking, S. W. (1974). Black hole explosions? Nature, 248(5443), 30-31. [CrossRef]
- misner1973 Misner, C. W., Thorne, K. S., Wheeler, J. A. (1973). "Gravitation". W. H. Freeman.
- penrose1965 Penrose, R. (1965). "Gravitational collapse and space-time singularities". Physical Review Letters 14: 57–59. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
 n is created through the following steps:
n is created through the following steps: n, represents a cycle of creation and evolution governed by the unified field equation. As described previously, black holes accumulate mass, leading to quasar formation. The immense energy released during this process triggers a space-time rupture, birthing a new inner universe,
n, represents a cycle of creation and evolution governed by the unified field equation. As described previously, black holes accumulate mass, leading to quasar formation. The immense energy released during this process triggers a space-time rupture, birthing a new inner universe,  n+1. This cycle can be mathematically expressed as:
n+1. This cycle can be mathematically expressed as: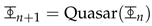
 n, where n is a natural number. We assume the interaction (or the process of universe creation from a black hole/quasar cycle) forms a group operation ⊕.
n, where n is a natural number. We assume the interaction (or the process of universe creation from a black hole/quasar cycle) forms a group operation ⊕.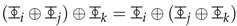
 0 such that:
0 such that: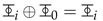
 i, there exists an inverse
i, there exists an inverse  i−1 such that:
i−1 such that: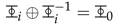
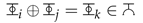
 and
and  :
: (Inner Universe): As depicted in the figure,
(Inner Universe): As depicted in the figure,  represents a single black hole undergoing the cycle of quasar formation and birthing a new universe. This symbol captures the dynamic processes within an inner universe governed by the unified field equation.
Figure 1. Inner Universe:
represents a single black hole undergoing the cycle of quasar formation and birthing a new universe. This symbol captures the dynamic processes within an inner universe governed by the unified field equation.
Figure 1. Inner Universe:
 (Outer Universe): Now, picture a vast cosmic sea where countless such
(Outer Universe): Now, picture a vast cosmic sea where countless such  symbols churn and evolve. This cosmic sea represents the outer universe, the multiverse, where each
symbols churn and evolve. This cosmic sea represents the outer universe, the multiverse, where each  signifies a unique inner universe.
signifies a unique inner universe.