The Integrated Structure of Language and Language Behavior with A Psychological Path

1. Introduction

Language ability is the most fundamental function of psychological life, bar none. I once took a course called Ancient Greek Philosophy, in which the creation of the Greek gods was discussed one by one. Among them, both Apollo and Hermes had some involvement with language, though it was not their main domain. I believe the ancient philosophers missed creating a dedicated god responsible solely for language. This may be because the creation of gods stems from awe of the unknown. However, the god of language is always with us, approachable and familiar, which diminishes people’s sense of reverence. In reality, language and linguistic behavior are the most mysterious entities in human life and in the universe. Though we think we know them well, they remain strangers to us, with their mysteries being among the hardest puzzles, incomparable even to the Millennium Problems of mathematics or the enigma of Einstein’s unified field theory.

It is often said that words reveal the person. Language affects the largest expanse of psychological phenomena in people, becoming the foundation upon which psychological life depends. Many things in the world arise from language. From household affairs to international relations, language can transform conflict into peace, but it can also cause misunderstandings, intensify contradictions, and lead to verbal battles. Human rationality comes from language; human emotions are influenced by language; human knowledge is accumulated through language; human cognition is passed down via language; human thought is filled with content through language; human information is transmitted by language; human communication is inspired by language; human interactions are executed through language. For individuals, "I speak, therefore I am"; for societies, without language, how could anything be shared? All of these layers are veiled, and the truth behind them is as elusive as the fog-shrouded peaks of Mount Lu. On one hand, language is omnipresent; on the other hand, linguistic behavior is richly diverse. How much do we truly understand about the interactions between language and linguistic behavior?

In short, language is a force, rippling through the psyche like a wave, a form of psychological vitality. Language is also a carrier of force, breaking into particles, with each particle coupling and interacting, forming the continuous cycle of psychological life. Language is a field, with fields interacting, revealing the ontological commitments of psychological reality. Language is an operator, acting upon mental intentions and revealing the contents of the mind’s cognition. Language is energy, sustaining psychological activities and reflecting the quality of mental life. Finally, language is a kind of metalogic, capable of generating self-referential statements, guiding psychological life towards reflection and introspection.

This paper’s discussion of language follows three intertwined threads. The first thread is the specific manifestations and new influences of Bourbaki structuralism in the analysis of language and linguistic behavior. The second thread is the modeling power and marvelous effects of theoretical physics in language and linguistic behavior. The third thread is the historical evolution and fresh interpretations of Wittgenstein’s philosophy of language. These three threads weave through one another, leading us to glimpse some previously undisclosed secrets of the linguistic world. Interestingly, Wittgenstein’s philosophical development can be embedded into the framework of gauge field theory. Gauge field theory distinctly separates the global and local levels. Early Wittgenstein focused on the global structure of language, while his later work shifted to local analyses of linguistic behavior. This remarkable convergence enhances our understanding of the period in which language plays a central role in psychological life.

Here is the structure of this paper. The entire text is divided into three parts:

The first part is titled: Early Wittgenstein’s Philosophy of Language, Equilibrium, and Global Structure. This section discusses the prescriptiveness, stability, and certainty of language, especially scientific language. Within the framework of early Wittgenstein’s philosophy of language, these properties were the pursuits and inquiries of his youth. In the framework of Newtonian mechanics, these properties are closely connected to the concept of equilibrium and can be characterized within that framework. Within the framework of gauge field theory, these properties are intricately linked to the global level and are modeled accordingly. We will discuss a fundamental special linguistic structure, namely the "dual-leg structure" composed of syntax and semantics. This dual-leg structure can serve as a tool for characterizing language across logical language [2], decision theoretic language [9], game theoretic language [6], quantum mechanics language [4], gauge field theory language [1], intrinsic dynamical geometrized language [14], and more. These topics will be introduced in Section 2, Section 3, Section 4, Section 5 and Section 6.

The second part is titled: Wittgenstein and Gödel: Disputes and Turning Points. The dual-leg structure of language is not just for posing and taking pictures but enables the running function of language. So, is this dual-leg structure sound, with both legs of equal length, or is one leg longer than the other? In logic, this is called metaproperties, or the overall properties of a system. The study of system metaproperties is called metalogic or metamathematics. The famous Gödel incompleteness theorem and Tarski indefinability theorem, also known as the twin theorems, reached the pinnacle of constructing a dual-leg structure [2], according to Bourbaki structuralism, and revealed the asymmetrical dual-leg structure that demonstrates the beauty of linguistic structure, like the Venus de Milo. In theoretical physics terms, the twin theorems represent the spontaneous symmetry-breaking mechanism of a language system at the global level. This is a metaproperty of linguistic structure. The debates between late Wittgenstein and Gödel foreshadowed Wittgenstein’s shift towards the localization of language systems and his focus on individual linguistic behavior, opening a new chapter in behaviorist linguistics. As a mental coordination of the dual-leg structure of syntax and semantics, this turn in Wittgenstein’s philosophy of language also paved the way for pragmatics and psycholinguistics [7]. This part will be discussed in Section 7, Section 8 and Section 9.

The third part is titled: Beyond Wittgenstein: Structure and Models. Language games are a representative concept in Wittgenstein’s philosophy of language [12], meaning that language communication can be viewed as language games. Wittgenstein even believed that language games themselves are language because language reflects forms of life. Language games and forms of life are mutually transformed through psychological games [13]. However, in his middle period, Wittgenstein found it difficult to define language games with a complete set of rules, which led him to become a leader of 20th-century skeptical philosophy. In his later period, Wittgenstein turned to the view that language games should follow rules and strove to find them [10]. The present author believes that Wittgenstein was a hero who didn’t quite complete his work, and this paper aims to offer some assistance.

The deep structure of language games is closely related to pragmatics, and their modeling exceeds the scope of this paper. This paper provides several modeling pathways for their surface structure. It discusses how, in an epistemological sense, Wittgenstein differs from the Platonic tradition. Language games vary by person, situation, and context, showing clear local characteristics in their structure. Because of this, they must follow causality and be limited in scope, which can be modeled by special relativity. Linguistic behavior is sensitive to sequence; the order in which things are said affects their impact. Even in rhetoric, there is sensitivity to sequence that word order affects meaning. This implies that the observation of linguistic behavior does not satisfy commutative relations but rather satisfies non-commutative relations. This is a condition for quantization and can be modeled by quantum mechanics. In fact, language games are themselves wave functions and are characterized by quantum field theory [4]. Linguistic behavior is socialized. In language world, individual language abilities vary, and linguistic advantage is a scarce resource. This means that language society is a competitive and unequal society. Standard educational tests are a typical example of this analysis. This level of analysis can be modeled by general relativity. The topics mentioned above will be discussed in Section 10 through 13. The paper concludes with a general discussion.

Part I: Early Wittgenstein’s Philosophy of Language: Equilibrium and Global Structure

1. The Dual-Leg Structure of Language

Human society cannot function without the service of language. Do you know that, in order to support this linguistic service, scientists, including linguists, psychologists, philosophers, cognitive scientists, and others, have long worked diligently on language maintenance? Early Wittgenstein, following the lead of logician Russell, engaged in such language maintenance, a discipline called the philosophy of language. From the distinction between syntax/grammar and semantics, we can abstract the concept of a dual-leg structure for language, which helps us understand why language exhibits stability and certainty. The balance of this dual-leg structure is akin to the concept of equilibrium in Newtonian mechanics. In a sense, the demand for the stability and certainty of language echoes the Newtonian scientific tradition, continuing in its vein. The characteristics of the Newtonian scientific tradition mentioned here generally refer to the direct observability of phenomena, the certainty of theories, and the stability of systems. Building bridges and railways, calculating ballistic trajectories, or even constructing tables and chairs all involve Newtonian mechanics. Newtonian mechanics satisfies most of our physical needs in daily life. Similarly, ordinary linguistic expressions can meet most of our everyday communicative needs. Whether chatting with others, speaking in meetings, buying goods at the supermarket, sending emails, discussing things on WeChat, writing a blog post, or even writing an exam essay, clear expression is required so that people can understand and comprehend. In the terminology of psycholinguistics, it means that linguistic behavior must be directly observable. If someone speaks or writes with lexical, syntactic, and grammatical confusion, lacking logic and clarity, they will be regarded as linguistically incompetent.

The stability of natural language relies on the stability of its syntactic and grammatical structure, while its certainty is reflected in the certainty of its semantics [10]. Clearly, the stability and certainty of natural language are based on the separation of its syntactic/grammatical structure from its semantics. This separation isn’t something granted; it represents a high stage of linguistic evolution. People often overlook how miraculous the formation of syntactic and grammatical structures is in the evolution of human language, akin to humans taking on divine work. Even more incredible is that humans also invented semantics, thereby determining the meaning of linguistic expressions—truly a masterpiece of ingenuity. This allowed humans to learn to stand and walk with just two linguistic legs in the mental world, freeing up the two mental hands to handle more complex tasks. Upright walking is a milestone in human evolution, as is the evolution of human language.

My doctoral advisor, the late Professor Martin D. S. Brain of the Department of Psychology at New York University, was an authoritative scholar in two fields: reasoning psychology and developmental psychology. In reasoning psychology, he built the theory of mental logic [3] and developed experimental methods. In developmental psychology, he became famous for his research on children’s language acquisition. The theory of mental logic posits that people reason using reasoning patterns based on linguistic abilities, automatically triggered during reading comprehension. Therefore, the theory of mental logic is also regarded as a syntactic reasoning theory.

Cognitive revolution pioneer Noam Chomsky first distinguished between linguistic competence and performance. Chomsky believed that humans possess an innate internal configuration for language acquisition, unique to the human species and the result of long-term evolution. A four-year-old child can freely communicate using language, not merely due to four years of language acquisition but due to this internal linguistic configuration. You cannot train any other species to acquire language because they lack the necessary internal configuration. So, how do children activate this internal configuration and exhibit linguistic performance? This was once a mystery. Professor Brain continuously observed his own children’s language development. He found that children, before formally learning conventional grammar, autonomously generate a child grammar in advance to facilitate language performance. This child grammar demonstrated the relative stability of children’s language, making communication possible—a finding that became Brain’s hallmark work.

My postdoctoral advisor, former Princeton University Professor of Psychology, Philip Johnson-Laird, proposed and developed the theory of mental models [5], asserting that people reason by constructing mental models. The construction of these mental models is based on the reasoner’s understanding of the meaning of premise sentences, which, in turn, is based on their perception of language. Another cognitive revolution pioneer, Professor George Miller, was also one of the founders of psycholinguistics. Miller and Johnson-Laird co-authored the magnum opus Language and Perception [8], which I believe was actually the prelude to the theory of mental models. I asked Professor Johnson-Laird about this more than 20 years ago, and he didn’t agree. Opinions of academic authorities should be regarded as references but not taken as gospel. For example, he also once said that there were no quantum events in the mental world—a view I obviously cannot endorse. Academic authorities have their strengths but also their limitations. At the same time, the formal representation of mental models bears comparability to logical semantics. Thus, the theory of mental models is regarded as a semantic reasoning theory. Together, the theories of mental logic and mental models provide syntactic stability and semantic certainty to reasoning psychology. Reasoning is the core capability of the mind and is also its representative linguistic performance. In experimental psychology, reasoning tasks are always linguistic tasks.

The stability and certainty brought about by the syntactic/grammatical structure and semantics of language—i.e., the so-called dual-leg structure of language—are even more evident in formal languages and scientific languages. I often tell my students that when learning a subject, the first step is to familiarize themselves with the language of the subject, then separate the syntactic/grammatical structure from the semantics, and finally comprehend the metaproperties that combine the two. In my courses, I analyze at least eight such scientific languages with dual-leg structures. The first involves logic, the second involves decision theory [2], the third involves game theory [6], the fourth involves metamathematics, the fifth involves quantum mechanical wave functions [4], the sixth involves gauge field theory [1], the seventh involves set theory [15], and the eighth involves the geometrization program of the Standard Model of particle physics [14].

In the kingdom of scientific languages, logic was the first discipline to use the dual-leg structure of language to stand upright and walk. Contemporary formal logic [5], also called standard or symbolic logic, is characterized by various formal systems. A logic system is a formal system with its own specially designed formal language. There are three basic levels for analyzing natural language in logical terms. The simplest is propositional logic, also known as propositional calculus. Another level is quantifier predicate logic, and yet another level is modal logic.

2. The Standard "Dual-Leg" Structure of Logic and Formal Language

2.1. Propositional Logic and the Truth-Value Semantics

Consider the following sentence: "If all the beads are red, then Tom plays games with some girls." At the level of propositional logic, a simple statement such as "all the beads are red" is treated as a whole, called a proposition, without delving into its internal syntactic structure. Words that logically connect sentences are called logical connectives or logical operators, including conjunction (and), disjunction (or), implication (if-then), equivalence (if and only if), and negation (not). Thus, in the vocabulary of propositional logic, there are countably infinite propositional variables, five logical connectives, and parentheses used as punctuation marks. With these symbolized words, an infinite number of finite symbol strings can be formed. To mechanically determine which symbol strings are grammatically proper formulas—both atomic and compound—and which are improper, ungrammatical formulas, we need a set of formation rules. Formation rules must, and can only, be inductively defined. Logic studies reasoning, and deductive reasoning proceeds from given premises step by step to derive conclusions. Each step in the reasoning process applies a rule of inference, known as a proof. As we can see, the formal syntax of propositional logic language consists of a vocabulary, formation rules, and inference rules.

So, what is the logical meaning of this set of propositional logic syntax? In logic, there is only one logical meaning: truth or falsity, known as truth-value. Only sentences that can be evaluated as true or false are considered propositions; this is called the propositional attitude. The semantics of propositional logic is called truth-value semantics. The propositional variables in a propositional logic system are called atomic formulas. Truth-value semantics defines how the truth-values of finite compound formulas of any complexity are derived from the truth-values of atomic formulas. Truth-value semantics is governed by a truth table. Specifically, a conjunction is true if and only if both conjuncts are true; a disjunction is false if and only if both disjuncts are false; a conditional is false if and only if the antecedent is true and the consequent is false; an equivalence is true if and only if the two components have the same truth-value; and, finally, a formula and its negation have opposite truth-values.

Do not underestimate this seemingly simple truth table—it has played a landmark role in the history of modern science. First, it was the first truly scientific semantics, separating and formalizing the theory of meaning. Second, it defined the logical meaning of the five logical connectives, which (and, or, if-then, if and only if, and not) represent the core expressive functions of natural language. It is hard to imagine how impaired natural language would be without these five connectives, or how chaotic communication would become if they were ambiguous. Furthermore, replacing truth with 1 and falsity with 0 transforms the truth table into Boolean algebra. Boolean algebra is the foundation of computer science and the prototype of "and-not gates" in circuit design, including integrated circuits.

In the discourse of logic, there are two central concepts. One is "proof," which is purely syntactic; the other is "validity," which is purely semantic. Some authors even argue that logic is the science of validity. Validity is defined by a conditional statement: if all the premises of an argument are true, then the conclusion must also be true. In other words, if a false premise is introduced in an argument, the reasoning remains valid regardless of whether the conclusion is true or false.

Thus, the dual-leg structure of a logical system consists of two standard components: formal syntax and formal semantics (also called a model). Standard logic has its logical standard, requiring that its syntactic structure and semantics be dually equivalent. This dual equivalence is established through the relationship between provability and validity. If all proofs are valid, we say the logical system is semantically sound. If all valid formulas or arguments are provable, we say the system is complete. Therefore, soundness and completeness describe the overall properties of a logical system, also known as metaproperties. They act like a two-way bridge connecting logical syntax with its semantics, even though the two are constructed independently. Propositional logic possesses both soundness and completeness.

2.2. Quantified Predicate Logic and the Value-Assignment Semantics

Building upon propositional logic, quantifier predicate logic delves into the internal structure of sentences. Consider again the previous example: "If all the beads are red, then Tom plays games with some girls." In this sentence, "are red" is expressed by a unary predicate (to be) paired with an adjective (red), representing a property. Additionally, "plays games" (more precisely, "plays") is a binary predicate, indicating a relationship between Tom and some children. The beads and children are individual variables, while Tom is an individual constant. "All" serves as a universal quantifier, and "some" is an existential quantifier. It is also important to note that in English, the sentence contains a definite article, "the," which often functions as a pronoun. By adding these components to the formal language’s vocabulary, along with appropriate formation and inference rules, we obtain the formal syntax of quantifier predicate logic.

The additional syntactic content here clearly surpasses the explanatory scope of propositional logic’s truth-value semantics. This necessitates the creation of a new semantics for predicate logic, known as valuation semantics, or a new model. To achieve this, we must first introduce a universal domain of individuals—essentially, the set of all things, including both real entities and any imaginable objects. Then, for each predicate, we specify a truth condition. For example, in the case of a unary predicate, its truth condition is a subset of the universal domain. A universal statement, such as "all things are red," is true if and only if its truth-condition set equals the universal domain. Similarly, an existential statement like "some things are red" is true if and only if its truth-condition set is non-empty, and so on. In 1930, Gödel proved that first-order predicate logic is complete—i.e., every valid formula is provable. Predicate logic is highly powerful and encompasses a significant portion of mathematical language.

2.3. Modal Logic and Possible World Semantics

In standard propositional and predicate logic, the focus is on declarative statements that do not include modal words (also called modal operators). Modal words encompass concepts such as: possibility, necessity, obligation, permission, duty, subjunctive mood, conditionals, tense, etc. These modal expressions enrich natural language, giving it flexibility, varied functionality, and the ability to express nuances appropriately, providing room for negotiation and adaptation. By introducing modal words into standard logic and establishing corresponding formation and inference rules, we create the syntactic structure of modal logic.

The semantics of modal logic is known as possible world semantics. For instance, the possible world semantics for modal propositional logic consists of a set of possible worlds and a binary accessibility relation defined over them. Depending on the specific axiomatization, this accessibility relation must satisfy particular properties, such as transitivity or reflexivity. For example, a necessary statement, "necessarily A," is true in a certain possible world if and only if statement A is true in all possible worlds accessible from that world. Conversely, a possible statement, "possibly A," is true in a certain possible world if and only if there exists at least one accessible world where statement A is true. This possible world semantics is also called Kripke semantics, named after Princeton logician Saul Kripke, who introduced the concept of accessibility relations and proved a form of completeness for modal logic.

In scientific languages, traditionally, there hasn’t been a clear distinction between syntactic and semantic structures. These scientific languages, akin to mermaids in water—elegant and mesmerizing—are often aesthetically appealing but distant and difficult to approach. How do we know that these mermaids don’t wish to evolve legs and walk on land, dancing with humanity? I can often sense the mermaid’s lament—the scientists, frolicking on land, have left her confined to her watery palace. Whether in the dim green lights of the deep sea or the shimmering blue rays of shallow waters, she gazes longingly, wondering where the human world is. Finally, a linguistic surgeon, armed with a scalpel, pioneered a method for constructing "legs" for scientific language.

My teaching experience shows that students grasp scientific language more easily when it is endowed with this dual-legged structure. Whenever I begin learning a new field, my first task is to familiarize myself with its language and identify its dual-legged structure and meta-properties. My progress in understanding certain areas in recent years, particularly while contemplating theoretical physics puzzles, has been greatly aided by this approach. This is a habit innate to logicians.

3. Decision Theory Syntax Structure and Its Utility Semantics

The classical axiomatized decision theory syntax is structured in three layers. The first layer consists of a set of choices or options. The second layer states that each choice can lead to a set of possible outcomes. The third layer indicates that each outcome is characterized by two and only two attributes: desire and feasibility. To formulate a decision theory problem, one must place the issue within this syntactic structure. Solving a decision theory problem involves establishing a total order preference relation over the set of choices, meaning that for any two choices, one must be preferred, and "non-preference" is not allowed. Preference is a syntactic concept. We can observe that the classical decision theory syntax’s vocabulary consists of five and only five concepts: choice, outcome, desire, feasibility, and preference. These are organized into a three-layer grammatical structure and resolution conditions. If any concept is missing, it does not form a classical decision problem. If there is an extra concept, it indicates that the decision problem has not been properly refined. So, what does classical decision theory mean, and how is a classical preference relation established? This is a semantic inquiry.

The classical decision theory syntax is constructed from the top down, while its semantics are defined from the bottom up. First, the decision-theoretic meaning of "desire" is reduced to a single value: money. No matter what the desire is, within the framework of decision theory, it must be converted into a monetary value. You may find this statement uncomfortable, perhaps feeling insulted—thinking, "Do you take me for a materialist? I love my country, which is priceless! I have my faith, which is unconditional!" This is understandable. However, people typically don’t say, "I decided to love my country," as love for one’s country is an ethical issue. Nor do people typically say, "I decided to believe in God," as that is a religious issue. Ethics and religion fall outside the boundaries of decision theory. This is the boundary of decision theory: a theory without boundaries is not scientific, and a science without clear boundaries is not a mature discipline.

The next concept is the feasibility of a possible outcome. If you want to buy a new car, or even to buy an entire car company, the feasibility of these two options is evidently different. The natural mathematical representation of feasibility is probability. However, in standard probability theory, a single independent event cannot have a probability assigned. Of course, psychology has theories about subjective probability, which assign a probability to isolated independent events, often referred to as likelihood, but this is not suitable for inclusion in standard decision theory. Note that a single choice can lead to several or even many possible outcomes, and decision-makers assign different weights to these potential outcomes based on their importance. This distribution of weights is called a strategy. To convert this strategy into a probability distribution, a mathematical normalization process is applied, ensuring that the sum of all probabilities equals 1. The reason is that all possible outcomes belong to the same choice, and if this choice is seen as the optimal preference, it becomes reality, and the probability of a real event is 1. With this normalized probability distribution, it becomes possible to assign a probability to each possible outcome. Thus, we can say that the decision-theoretic semantics of syntactic feasibility is its probability.

A possible outcome is characterized by its syntactic attributes of desire and feasibility. The decision-theoretic semantics of desire is monetary value, and the semantics of feasibility is probability. The product of these two values is called utility. Hence, the decision-theoretic semantics of a syntactic possible outcome is its utility. This is the origin of the name "utility semantics" in decision theory. This is the second layer, called the outcome layer. Moving one layer up brings us back to the choice layer. A single choice can produce several or many possible outcomes, each of which has its own utility. The sum of these utilities is called the mathematical expectation. Therefore, the decision-theoretic semantics of a syntactic choice is its mathematical expectation.

It should be emphasized that money is a number, probability is a number, and their product, utility, is also a number. Adding utilities still results in a number. Thus, utility semantics is also called numerical semantics. The meta-properties of the decision theory system require that its syntactic structure and utility semantics be precisely balanced—neither more nor less, but just right. This meta-property is expressed by the decision theory representation theorem: for any two choices, one is preferred over the other if and only if the mathematical expectation of the first choice is greater than that of the second. It is evident that requirements for such meta-properties are modeled on those found in standard logic. Why use numerical semantics to explain decision theory syntax? The reason is that we are not always clear on what the preference relation between two choices means and find it difficult to determine, but we do understand what it means for one number to be greater than another. Using the latter to explain the former is the function of semantics.

4. Game Theory Syntax Structure and Its Utility Semantics

In their classic work Theory of Games and Economic Behavior (1944), von Neumann and Morgenstern developed game theory, defining the concept of a game and clearly distinguishing between cooperative and non-cooperative games, thereby laying the foundation for game theory. However, modern game theory truly flourished under what is known as the Nash framework. Nash not only rigorously defined cooperative and non-cooperative games using mathematical language but also proved systemic meta-properties, such as the Nash solution and Nash equilibrium, establishing the basic framework for game theory research.

The syntactic structure of non-cooperative games is not complex, but conceptually, there is a challenge. First, assume there are $N$ players. Second, each player has a set of possible actions, denoted as $A_i$. This is similar to individual decision theory and poses no cognitive difficulty. Third, consider an $n$-tuple of possible actions $\left(a_1,\dots ,a_i,\dots ,a_n\right)$, where each player contributes an action from their own set of possible actions. This $n$-tuple is called a scenario. A game is the set of all possible situations, which is the Cartesian product of the action sets of all players, denoted as $X_1^n=\times A_i$. This is akin to a film, composed of individual frames. The essential difference from individual decision theory is that each player does not establish a preference relation over their own set of possible actions but must establish a preference relation over the set of all situations. This can cause cognitive discomfort for players because the mind is embodied in individuals, making it more natural in individual decision theory for decision-makers to establish preferences over their own action sets. Now, each player must establish preferences between any two situations, each involving the possible actions of all other players. This is the psychological reason behind the cognitive discomfort. Based on my teaching experience, once this cognitive discomfort is overcome, the language of game theory becomes more accessible.

The meta-property of non-cooperative games is the well-known Nash equilibrium, a purely syntactic property. A Nash equilibrium is a special situation, denoted $\left(a_i^{*},a_{-i}^{*}\right)$, that must hold to each player $i$. It satisfies the following condition:

$$a_i^{*}\succ a_{i}forall{a}_i\in A_{i}foreachplayeri.$$

The game-theoretic meaning of a situation is called utility. Similar to decision theory, utility is also a linear function of value and probability, so the semantics of non-cooperative games is called utility semantics. Note that, unlike in decision theory, assigning a value or probability to an individual action within a situation has no meaning. What matters is assigning a set of values and a normalized probability distribution to all actions within a situation simultaneously. Few people notice an interesting phenomenon: the "two-legged" structure of game theory also manifests in the distinction between the modes of expression of non-cooperative and cooperative games.

Cooperative games are characterized by a set of possible agreements. For example, in a two-person negotiation, the process of bargaining forms a price pair, denoted $\left(u,v\right)$, which represents a possible agreement. In theory, there can be many possible agreements. An important concept in cooperative games is the negotiable point, or more colloquially, the "turning point." Understandably, not all possible agreements are negotiable. If $u$ or else $v$ is too large—i.e., if the values of $u$ and $v$ are too disparate—one party may lose interest in negotiating. Therefore, there should be a turning point that defines the range of negotiable agreements. Within this range, there exists a special possible agreement called the Nash solution, which maximizes the product of the two values, making it greater than the corresponding products of other possible agreements within the negotiable range.

The above describes how standard game theory textbooks introduce non-cooperative and cooperative games. When teaching this content, I have noticed an interesting phenomenon. I observed that non-cooperative games are introduced syntactically, with components like the set of possible actions, the $n$-tuple of actions in a situation, and Nash equilibrium, all being syntactic elements. On the other hand, cooperative games are introduced semantically; concepts like possible agreements, value, and the Nash solution are semantic components. This distinctive "two-legged" structure, with one leg standing on the syntactic territory of non-cooperative games and the other on the semantic territory of cooperative games, allows the game theory framework to "stand upright." This phenomenon is ubiquitous in real life and even in international relations, with significant psychological implications. Imagine people in a conflict or fight threatening, "If you do this, I’ll do that." One country tells another, "If you continue doing this, I’ll sanction you." The other country retaliates, "If you sanction me, I’ll bomb a third country." This is the language of non-cooperative game theory. When one side starts naming prices and negotiating conditions, mentioning values, they begin signaling an intention to cooperate. Hence, the way textbooks introduce these concepts is not a coincidence or oversight but likely reflects the authors’ psychological understanding of the game theory framework.

5. Set Theory Generating Two-Legged Structure and Its Applications

Set theory is the universal language of contemporary mathematics. The Bourbaki group, representing structuralist mathematics, made significant contributions to this. Recently, the author has proposed a method for generating a two-legged structure directly from set theory. Consider a set $A$ and its power set $P\left(A\right)$, which is the set of all subsets of $A$. Let $a$ be an arbitrary element of $A$, denoted $a\in A$, where $\in$ represents the membership relation. Also, let $B$ be an arbitrary subset of $A$, denoted $B\subseteq A$, where $\subseteq$ represents the subset relation. Clearly, $B\in P\left(A\right)$. The definition of the power set is given by:

$$P\left(A\right)=\left\{B\right|B\subseteq A\},$$

meaning $B\in P\left(A\right)$ if and only if $B\subseteq A$. In terms of logic, $B\in P\left(A\right)$ is called the extension of $P\left(A\right)$, and $B\subseteq A$ is called the intension of $P\left(A\right)$. Thus, through the linguistic analysis of power sets, we have constructed the extension syntax and its intension semantics for set theory language, also known as "membership syntax" and "inclusion semantics," respectively denoted as syntax and semantics. This is a two-legged structure self-generated by the intrinsic structure of set theory language and hence has generality. The meta-property of this generated two-legged structure is self-evident, being both complete and coherent, as every member of the power set uniquely denotes a subset of the set. Professor Hongbin Wang of Texas A & M University once reminded me (personal communication) that, for a category, the set of all denotations is called the index set in category theory.

The two-legged structure of set theory is foundational and has strong descriptive power in empirical scientific statistics. In empirical science, the necessity and exclusivity of statistical language arise from the assumption of the unobservability of the population. What we can observe are randomly drawn samples. The relationship between samples and populations is an inclusion relation. The relationship between samples and the power set of the population is a membership relation. The latter represents the sample syntax of statistical language, while the former represents the semantics of the sample. In traditional empirical scientific methods, the statistical significance of experiments lies in using sample means to predict population means, and the two-legged structure of sample language precisely characterizes this systemic feature.

The idea of the set theoretic two-legged structure was inspired by Professor Hong Qian of the University of Washington (Seattle, personal communication). Briefly, in thermodynamic statistical methods, the assumption is that the data population is infinite. Individual events have no independent statistical meaning because individual independent events lack measure. However, a data sample is measurable, and thus, within the power set of the population, i.e., within the sample set, a measurable density function can be formed, and its probability distribution can be found. This two-legged structure is called the measure semantics of sample syntax.

6. Two-Legged Structure in Theoretical Physics

The previously introduced language structures with two legs are attached to formal or analytical sciences. This section will introduce three types of two-legged structures in the local languages of quantum physics. The first two are relatively well-established, and detailed discussions can be found elsewhere; here, the discussion will be brief. The third one is a topic still under research and may not be fully developed, so it requires a more extensive explanation.

6.1. The Two-Legged Structure of the Wave Function

Classical quantum mechanics has three equivalent formulations. The first is Heisenberg’s matrix mechanics, which uses non-commutative relations and the uncertainty principle as its primary language. The second is Schrödinger’s wave mechanics, which uses the Hamiltonian equation of the wave function as its primary language. The third formulation, considered the most general, is Dirac’s bra-ket notation, where "bra" denotes the left bracket and "ket" denotes the right bracket. Dirac famously stated: "The higher the disturbance in the measurement, the smaller the world we can observe." In this sense, quantum mechanics is a theory about microscopic observations. Dirac’s formalism captures this essence, denoted as $⟨\varphi \left|A_i\right)⟩$. For example, in standardized education testing, a student’s ability is a phenomenon difficult to observe directly, so an exam is given, with questions $A_i$ as stimuli and answers as responses. Thus, the variable $\psi$ becomes a function of the variable $A_i$, denoted as $\psi \left(A_i\right)$, which is the wave function. The Dirac notation $⟨\varphi \left|\psi \right(A_i)⟩$ represents the syntax of the wave function language.

The wave function has a probabilistic interpretation from the Copenhagen school. This is called amplitude semantics (also known as complex number semantics). Any two values of the wave function can be expressed as a complex number representing a possibility. The square of the modulus of this complex number is called the amplitude of the wave function, which is its probability. In Dirac’s words, "the square of the possibility is equal to the probability." This probabilistic interpretation highlights the meaning of the wave function, known as the amplitude semantics of the wave function. We see that the Dirac syntax of the wave function and the Copenhagen amplitude semantics together constitute the two-legged structure of the wave function language.

6.2. The Two-Legged Structure of Gauge Transformation Language

In the language of gauge field theory, the wave function is placed within a two-layer, two-level grid structure. The two layers refer to the global and local levels, and the two levels at each layer include gauge potentials and gauge fields. To derive the gauge fields from the gauge potentials, appropriate differential operators must be applied to the wave function. The wave function changes as the gauge potential transforms from one state to another, multiplied by a transformation factor $e^i$, i.e., $\psi \prime =e^i\psi$. Correspondingly, under the action of differential operators, the gauge fields also transform as $\partial \varphi \to e^i\varphi =e^i$.

At the global level, such transformations are called first-class gauge transformations, where the transformation factor $e^i$ is a constant. At the local level, the transformation factor becomes a function $e^i\left(x\right)$, and the corresponding gauge transformation is called a second-class gauge transformation. Combining these two types of gauge transformations forms the syntax structure and grammatical rules of gauge transformation language.

The significance of gauge transformations lies in the concept of gauge invariance. Gauge invariance means maintaining the uniqueness and conformal properties of the transformation factors. The conformal property requires that in gauge potential transformations, the transformation factor is prefixed to the wave function state, and thus in the corresponding gauge field transformation, the transformation factor must also be prefixed to the wave function’s derivative. The uniqueness property requires that no redundant terms should appear in gauge field transformations. These two requirements are straightforward at the global level in first-class gauge transformations since the transformation factor is a constant. However, at the local level in second-class gauge transformations, redundant terms can appear because the transformation factor is a function. To eliminate these redundant terms, covariant derivatives and gauge fields are introduced as semantic techniques. Therefore, the semantics of gauge transformations is called gauge invariance semantics. The syntax structure of gauge transformations and its gauge invariance semantics together constitute the two-legged structure of gauge transformation language.

A fundamental property of gauge transformations, known as the gauge principle, states that if first-class gauge transformations are not valid, then second-class gauge transformations cannot be valid either. In other words, although the former is simpler than the latter, the former is a necessary condition for the latter.

6.3. The Two-Legged Structure of Phase Language

The contemporary Standard Model of particle physics consists of several dynamical systems, including quantum electrodynamics, quantum chromodynamics, isospin dynamics, electroweak dynamics, and the Higgs mechanism, all described by the language of gauge field theory. Dynamical analysis is source analysis, where the sources are various charges, such as the electric charge carried by electrons and the color charge and fractional electric charge carried by quarks, among others. Particles’ charges are assigned internal spaces, and the number of possible charges generally corresponds to the dimension of the internal space. For example, an electron carries only electric charge, so its internal space is one-dimensional; conversely, quarks can carry three types of color charge, making their internal space three-dimensional. When a particle transitions from one state to another, its internal space undergoes rotation, and this rotation changes the phase, known as the dynamical phase. The rate of change in the phase, referred to as momentum, is the origin of the concept of spin. In quantum mechanics, spin is an intrinsic property of particles, with no equivalent in Newtonian mechanics, which does not assume internal space for particles.

In quantum field theory, particles are characterized by their wave functions, making phase language naturally the "mother tongue" of wave functions. As discussed in Section 6.2, in gauge field theory language, the wave function is placed within a given two-layer, two-level grid framework. Due to the action of differential operators, two types of gauge transformations are performed to ensure that the wave function remains invariant under these transformations. The purpose of invariance is to achieve gauge symmetry, which is described by symmetry groups. Symmetry groups are algebraic structures, so in this sense, the syntax structure of phase language is algebraic, referred to as the algebraic syntax of phase language.

To ensure the invariance of second-class gauge transformations, covariant derivatives and gauge fields must be introduced, expressed as follows:

$$\begin{gathered} D_{\mu }={\partial }_{\mu }+iq{A}_{\mu } \\ A{\prime }_{\mu }=A_{\mu }-{\displaystyle \frac{1}{q}}{\partial }_{\mu }{\theta }_{\mu } \end{gathered}$$

Here, we see that the covariant derivative includes the gauge field, and the difference in gauge fields between two states corresponds exactly to the differential of the dynamical phase function. In other words, the integral of the gauge field represents a phase known as the Berry phase. Yang and Mills refer to this as a non-integrable phase factor. If the dynamical phase of the wave function is the internal space phase, then the Berry phase is the external phase. In fiber bundle theory, the Berry phase represents the trajectory of a particle on the base manifold. In social science terms, the dynamical phase characterizes changes in individual mental activities and behaviors, while the Berry phase characterizes the impact one has in society. The Berry phase is a type of geometric phase. Gauge fields are used to balance changes in the dynamical phase, and the Berry phase along with Yang and Mills’ theory of non-integrable phase factors are important aspects of the geometric formulation in particle physics. Thus, the phase language’s two-legged structure consists of its algebraic syntax and its geometric semantics.

Part II. Wittgenstein and Gödel: Debate and Turning Point

There was debate between Wittgenstein and Gödel. In the framework of modern gauge theoretic structure, this controversy can be well-formulated as a unified account. In the following, we introduce Gödel’s incompleteness theorem, Tarski’s indefinability theorem, and Wittgenstein’s principles of incomplete rules of language game. Briefly speaking, these three topics cover the contents of three categories of linguistics: the syntax, the semantics, and pragmatics.

7. Gödel and The Realm of Language

In 1900, Hilbert presented 23 unsolved mathematical conjectures at the International Congress of Mathematicians, including the Riemann Hypothesis and the Continuum Hypothesis, collectively known as Hilbert’s Program. One of these puzzles concerned the logical foundations of the edifice of mathematics, specifically the question of consistency. In 1931, Austrian mathematician and logician Kurt Gödel provided a negative result, proving the incompleteness of first-order theories, now known as Gödel’s Incompleteness Theorem, or simply Gödel’s Theorem.

Gödel’s theorem has widespread applications. For example, the "Halting Problem" in computer science is a version of it. Gödel’s Incompleteness Theorem is one of the most well-known names in mathematical theorems and is widely discussed in various books. While the theorem is an intellectually rich and fascinating story, its content is simpler compared to other famous mathematical theorems and proofs. This section does not assume any prior knowledge. We will explore the profound ideas and exceptional wisdom contained in Gödel’s theorem and Tarski’s theorem through the introduction of their concepts, function construction, and proof techniques.

In this discussion, we will occasionally use a classical style, intentionally incorporating a certain literary touch to enhance cognitive engagement. The acquisition of knowledge involves more than just understanding—it also entails attention, memory, appreciation, and experience. Therefore, both teaching and learning must be appropriately paced. The Platonic tradition in epistemology emphasizes the three elements of truth, belief, and justification. Cognitive mechanics tells us that, for most learners, it is difficult to advance all three elements simultaneously; instead, they must proceed in a cyclical and iterative manner. Gödel’s and Tarski’s theorems are not only fascinating but also profound, making them valuable for personal intellectual development. Below are eight steps to understanding Gödel’s Incompleteness Theorem.

7.1. First-Order Theory

Discussing Gödel’s Incompleteness Theorem, it is not entirely accurate to say that no prior knowledge is needed. The one prerequisite is first-order logic. A logic system is a formal system, and mathematical logic is a formalization and logical treatment of mathematical language. For example, in mathematical language, we say, "For all $x$," which in formal logic is expressed as $\forall xA\left(x\right)$. The symbol $\forall$ is called a universal quantifier. $A\left(x\right)$ represents a predicate structure, where $A$ is a predicate and $x$ is an individual variable. When the quantifier is restricted to quantifying individual variables, the logic is first-order. When the quantifier is allowed to quantify predicates, the logic is second-order. Second-order logic is equivalent to set theory, and with the addition of the axiom of choice and the continuum hypothesis, it can account for the entire edifice of mathematics. Note that first-order logic is complete—this was proven by Gödel in 1930, known as Gödel’s Completeness Theorem. Thus, Gödel was first and foremost a logician. It is important to be careful not to confuse this result with Gödel’s 1931 Incompleteness Theorem.

Logic includes logical connectives such as conjunction, disjunction, implication, and negation, which are also called logical operators. In mathematics, there are mathematical operations such as addition and multiplication. Logical operators and mathematical operations differ fundamentally, as shown in the following simple comparison. First, consider logical operators. Disjunction, $P$ or not $P$, is a tautology, always true, and can be used to define the identity element 1 in Boolean algebra. Expressed formally, $P\vee \sim P=T\equiv 1$. For convenience, the equals sign here can denote either equality or equivalence. Conjunction, $P$ and not $P$, is a contradiction, always false, and can be used to define the identity element 0 in Boolean algebra. Formally, $P\wedge \sim P=F\equiv 0$. Now consider mathematical operations. Addition: $a+-a=0$. Multiplication: $a\times a^{-1}=1$. It is clear that disjunction and addition, conjunction and multiplication cannot be functionally interchanged, because the resulting identity elements differ. Furthermore, disjunction and multiplication, conjunction and addition cannot functionally replace each other. For example, true or $Q$ is still true, whereas 1 times $b$ equals $b$. Similarly, false and $Q$ is still false, whereas 0 plus $b$ equals $b$. The reason lies in the essential difference between the identity elements in logic and those in mathematics. This fundamental distinction separates logic and mathematics, creating a significant divide between them. In the fourth step discussed later, we will see how Gödel’s "arithmetization" bridges this divide, enabling smooth passage between them.

When two mathematical operations (addition and multiplication) are added to the first-order logic described earlier and formalized as a new formal system, it becomes what is known as "first-order theory." The prototypical example is Peano Arithmetic, an axiomatic system. Gödel’s Incompleteness Theorem characterizes two metamathematical properties of first-order theory, specifically its system properties. It is also worth noting that first-order theory is a very basic yet special level of mathematics, and Gödel’s Incompleteness Theorem shows that at this level, our axiomatization methods are limited. Looking downward, first-order logic does not require stronger axiomatization methods; looking upward, more complex number fields, such as the real or complex numbers, allow for richer axiomatization methods, whose completeness theorem was later proven by Tarski.

Additionally, it is helpful for the reader to distinguish between three domains of discourse, which will aid in navigating this section. One is ordinary naïve arithmetic, where for an $n$-ary relation, one can only speak in terms of whether it "holds." Another is the defined arithmetic structure, represented as a semantic model in first-order theory, where for an $n$-ary function or formula, one can only speak in terms of whether it is "true." The final domain is the syntactic formal system of first-order theory, denoted as $N$, where for a function or formula, one can only speak in terms of whether it is "provable." These three domains share a common origin in the natural numbers but are distinct from one another. The concept of expressibility used in Gödel’s theorem concerns the relationship between ordinary naïve arithmetic and the syntactic formal system of first-order theory. The concept of arithmetical definability used in Tarski’s theorem concerns the relationship between ordinary naïve arithmetic and the semantic model of first-order theory. Finally, Gödel’s and Tarski’s theorems themselves concern the relationship between the semantic model and the syntactic formal system of first-order theory.

7.2. Natural Numbers and Enumerers

The set of natural numbers is countably infinite: 0, 1, 2, 3, …, continuing indefinitely. This is well known, and in the literature, they are referred to as intuitive natural numbers. While number theorists regard natural numbers as familiar and fundamental, in other branches of mathematics, they are often seen as mere tools, akin to Cinderella serving others. Their primary role is to act as subscripts, superscripts, indices, explicit and implicit notations, as well as adhering to Einstein’s convention of upper and lower indices. In tensor transformations, due to the frequent appearance and manipulation of indices, natural numbers have often been a source of frustration for scholars. Although these "Cinderellas" seem content with their supporting roles, real and complex numbers may appear more glamorous, possessing a vast array of fields, continuous ecologies, rippling limits, and differentiability at every point. Nonetheless, one might argue that the variables moving across these fields still need to be countable, which ensures that natural numbers always have a place, however humble, to contribute their work as indices. It appears to be a situation of resigned acceptance.

However, Gödel had an extraordinary insight—he realized that natural numbers, far from being mere servants, were more akin to a hidden master, like the humble monk sweeping the floors in a Shaolin temple, secretly possessing great martial prowess. In subsections 7.4 and 7.5, Gödel’s method of arithmetization will be shown to encapsulate all proofs in a sweeping motion, and a self-referential statement will dramatically transform the very nature of formulas inside and outside the system. One is left speechless at the brilliance of this masterstroke.

In modern mathematics, natural numbers are no longer taken for granted—they must be defined and constructed. These constructed natural numbers are defined as ordinals. The construction process begins with the empty set $⌀$, from which subsequent numbers are inductively defined by a successor function. The empty set, containing no elements, is defined as the first ordinal, 0. The next ordinal is the set containing only the empty set, $\{⌀\}$, defined as the second ordinal, 1. Continuing this process, each subsequent ordinal is defined as a set containing all previously defined ordinals as its elements, denoted by $n$. This method of construction is called the successor function.

At first glance, the difference between intuitive natural numbers and ordinals seems to be nothing more than a redefinition of natural numbers using the language of set theory. One might dismiss this as a mere display of trivial skills, no more than elementary techniques. But Gödel, with his ability to discern the subtle from the imperceptible, was able to extract the concept of the expressibility from this foundation.

7.3. Expressibility

Expressibility establishes a connection between arithmetic relations and provability within first-order theories. In this context, an $n$-ary relation $R$ in arithmetic corresponds to an $n$-ary function $P$ in a first-order theory. To ask whether $n$ natural numbers satisfy the relation $R$ is equivalent to asking whether substituting the corresponding $n$ ordinals into the function $P$ results in a provable statement within the first-order theory $N$.

Expressibility conveys two essential propositions. First, if $R\left(a_1,\dots ,a_n\right)$ holds true, then $P\left({\mathit{a}}_1,\dots ,{\mathit{a}}_{\mathit{n}}\right)$ is provable in $N$. Second, if $R\left(a_1,\dots ,a_n\right)$ is false, then $\neg P\left({\mathit{a}}_1,\dots ,{\mathit{a}}_{\mathit{n}}\right)$ is provable in $N$, where $\neg$ denotes the negation operator.

In these two conditions of expressibility, the law of excluded middle is applied crosswise. Each proposition leads directly from one to the other, and the relationship between the two creates a sharp logical dichotomy, evoking a sense of the cold and unyielding nature of logical abstraction, where precision leaves little room for nuance. This may induce in the reader a powerful sense of logic’s conceptual reach, and of its unforgiving methods, eliciting feelings both of admiration and frustration. As Karl Popper’s philosophy of science teaches, any form of scientific abstraction comes with boundaries—what is gained in clarity often comes at the cost of something else. In mathematics, this is referred to as simplification: to establish two distinct dimensions, one must sacrifice certain entanglements, allowing the two to become orthogonal.

The second proposition of the expressibility, particularly, which forces a transition from the falsity of $R$ to the provability of $\neg P$ in $N$, is a strong condition that may even conflict with intuition. Whether examined through the lens of the competing mental logic theory or the mental models theory in the psychology of reasoning, this transition is handled differently by each. The expressibility represents a historical shift from naive arithmetic to syntactic formalization, embodying both the tragic grandeur of a Dunkirk-like retreat and the noble promise of humanity’s intellectual responsibility, reminiscent of the Normandy landing.

In the above discussion, we used the phrase "if the relation is true" as a semantic convenience for continuity. However, as we proceed to Tarski’s indefinability theorem, we will see the profound impact that the concept of "predicate truth" can have.

7.4. Gödel Numbering

This is the pinnacle of human intellect in the 20th century, the unrivaled summit of mathematical beauty. Comparable to Einstein’s principle of equivalence in general relativity, Gödel’s numbering method may be different in form but matches it in brilliance, excelling through its rigorous precision. No wonder Einstein once remarked that his daily walk to work at the Institute for Advanced Study in Princeton was merely an excuse to stroll with Gödel. Gödel’s numbering method can be explained in three steps.

Step 1: Each symbol can be mechanically assigned a unique odd number. In a formal system, such as first-order logic or first-order theory, the formal language may have infinitely many symbols, but they are always countable. Thus, it is always possible to arrange some mechanical procedure to assign each symbol a unique odd number, called the Gödel number of that symbol.

Step 2. Every formula is a finite sequence of symbols, and each formula can be mechanically assigned a unique composite number, its Gödel number. The generation of this Gödel number is profoundly sacred; with reverence, it is written as follows:

$$\begin{gathered} L=e_1{e}_2\dots e_n \\ g\left(L\right)=q_1^{g\left(e_1\right)}{q}_2^{g\left(e_2\right)}\dots q_n^{g\left(e_n\right)} \end{gathered}$$

On the left-hand side of the equation, $L$ represents the Gödel number of the formula. On the right-hand side is a product of $n$ exponents, where the base of the $n$-th exponent is the $n$-th prime number, and the exponent is the Gödel number of the $n$-th symbol in the formula $L$.

Step 3. Each proof is an ordered sequence of a finite set of formulas. Each proof can be mechanically assigned a unique composite number, its Gödel number. The generation of this Gödel number is even more sacred; with continued reverence, it is written as follows:

$$\begin{gathered} Bew\left(L\right)\equiv ⟨u_1,u_2,\dots ,u_m⟩ \\ g\left[Bew\left(L\right)\right)=q_1^{g\left(u_1\right)}{q}_2^{g\left(u_2\right)}\dots q_i^{g\left(u_i\right)}\dots q_m^{g\left(u_m\right)} \end{gathered}$$

On the left-hand side of the equation, $Bew\left(L\right)$ represents the Gödel number of a proof, which is also a composite number; $Bew$ is short for “proof” in German. On the right-hand side is another finite product of exponents, where the base of the $i$-th exponent is the $i$-th prime number, and the exponent is the Gödel number of the $i$-th formula $u_i$ in the proof sequence.

This is Gödel’s numbering method. Its magic lies in the reverse process: starting from the Gödel number of a proof, i.e., a composite number, using the uniqueness of prime factorization, one can recover the unique sequence of exponents that generated this Gödel number. Similarly, from the Gödel numbers of the formulas in the sequence, one can recover the sequences of symbols corresponding to each formula. Ultimately, this allows us to restore the sequence of formulas representing a proof. This enables a bidirectional conversion between a first-order theory and its arithmetic model.

7.5. Self-referential Sentences

One of the ingenious uses of Gödel’s numbering method is to generate self-referential sentences. Suppose $P\left(x\right)$ is a formula with only one free variable, and let its Gödel number be $n$. Substituting this Gödel number into $x$ gives a closed formula $P\left(n\right)$. The formula $P\left(n\right)$ is a self-referential sentence since it contains the Gödel number of its parent formula. If $P\left(n\right)$ is provable, it should have a proof, denoted as $Bew\left(P_n\right)$, which also has its own Gödel number.

We can now introduce a binary arithmetic relation $G\left(i,j\right)$, where $i$ is the Gödel number of a parent formula $P\left(x\right)$, which has one free variable, and $j$ is the Gödel number of the proof of its self-referential sentence $P_n$, i.e., $j=g\left[Bew\left(P_n\right)\right)$. As long as $i$ and $j$ satisfy the above conditions, $G\left(i,j\right)$ holds, and by the definition of expressibility, $\mathit{G}\left(\mathit{i},\mathit{j}\right)$ is provable in the so called first-order theory $N$.

This seems like constructive progress, quite positive. But who could have imagined that Gödel, while seemingly building in plain sight, was covertly undermining the foundations? By placing a negation operator in front of $G\left(i,j\right)$, the situation changes drastically, and offense turns to defense. The result is like turning one of the 23 pearls of wisdom on Hilbert’s chain backward, leaving us with endless philosophical reflection and ontological inquiry, like the broken beauty of the Venus de Milo. The formula Gödel ingeniously constructed says: For all $y$, $G\left(x,y\right)$ does not hold. Formally, it is written as:

$$\forall y\neg G\left(x,y\right)$$

Recalling the definition of the function $G$, this formula clearly tells us that no $y$ can be the Gödel number of any proof. Now, let the Gödel number of the formula $P\left(x\right)$ be $i$. This allows us to construct the self-referential sentence:

$$S=P_i=\forall y\neg G\left(\mathit{i},y\right)$$

This formula is the main character of Gödel’s theorem. It gracefully embodies both the self-reference of its parent formula $P\left(x\right)$ and the negation of the function $G\left(\mathit{i},y\right)$, without any sense of contradiction. The only thing it leaves ambiguous is whether it itself can be proven. Gödel’s incompleteness theorem and its proof are built around the question of proving the identity of this self-referential sentence $S$.

Gödel’s numbering method and the construction of self-referential sentences also evoke a deeper sense of aesthetics, blending the ancient mathematical traditions of East and West. Western mathematical culture, tracing back to Euclid’s Elements, emphasizes generalization and analysis. In contrast, ancient Eastern mathematical culture focused on examples—not ordinary examples, but exemplars of general principles, such as those found in China’s Nine Chapters on the Mathematical Art, or the works of (modern) India’s Ramanujan. The late logician Youding Shen once explained this principle to me. He had a Ph.D. student who worked on the history of ancient Chinese logic, and his dissertation was on this very subject. Shen also wrote a book on the logical thought of the Mohists. A mathematical proof becoming a Gödel number exemplifies this principle to the extreme.

7.6. Consistency and $\omega$-Consistency

After much groundwork and preparation, we are now nearing the main topic. We say that a formal system is syntactically consistent (also called simply consistent) if, for any given formula, either the formula is provable, or its negation is provable. This exhausts all possibilities and covers all cases. The proof of Gödel’s theorem also relies on an indispensable concept, namely, $\omega$-consistency. It states that, given any formula $P\left(x\right)$ with one free variable, if $P\left(n\right)$ is provable for every $n$, then $\neg \forall xP\left(x\right)$ is unprovable. There is a lemma that will be used later: $\omega$-consistency implies consistency.

7.7. Gödel’s Independence Theorem

Statement 1: If $N$ is consistent, then $S$ is unprovable. Using proof by contradiction, assume $S$ is provable, then there exists a proof $Bew\left(S\right)$, and the Gödel number $j$ of this proof satisfies $G\left(i,j\right)$. By expressibility, $G\left(i,j\right)$ is provable; however, by the construction of $S$, $\neg G\left(i,j\right)$ holds for all $y$, which is a contradiction. This contradiction disproves the assumption, so $S$ is unprovable.

Statement 2. If $N$ is $\omega$-consistent, then $\neg S$ is unprovable. Again, using proof by contradiction, assume $\neg S$ is provable. Then, by the lemma, $N$ is consistent, so the assumption leads to $S$ being unprovable. This means that no proof of $S$ exists, and therefore no Gödel number of such a proof exists. Consequently, for any $j$, the relation $G\left(i,j\right)$ does not hold. Conversely, for any $j$, the relation $\neg G\left(i,j\right)$ holds, which matches the formula $S=P_i=\forall y\neg G\left(i,y\right)$. Hence, by the definition of $\omega$-consistency, $S$ becomes provable. We previously deduced that $S$ is unprovable, but now we are claiming $S$ is provable. This contradiction disproves the assumption, proving that $\neg S$ is unprovable.

From the proofs of Statements 1 and 2, we conclude that the sentence $S$ is indeed neither provable nor refutable within the first-order theory $N$. We say that it is independent of the first-order theory. This result is known as Gödel’s Independence Theorem, or Gödel’s First Theorem. It is a general result; if one tries to add $S$ as an axiom to the first-order theory $N$, new independent sentences can continue to be constructed.

7.8. Gödel’s Incompleteness Theorem

Reflecting on this, the construction of the sentence $S$ asserts its own unprovability. We have now proven that $S$ is indeed unprovable, so $S$ is true. Hence, $S$ is true but unprovable, which implies that the first-order theory $N$ is incomplete. This is the famous Gödel’s Incompleteness Theorem. Finally, let us not forget to define completeness: A first-order theory $N$ is complete if, for any sentence $S$ in $N$, if $S$ is valid, then $S$ is provable.

Gödel’s Incompleteness Theorem, stemming from Hilbert’s grand project, ultimately reached an unforeseen conclusion. Earlier, for convenience, we mentioned the phrase “a relation is true” and also said, “$S$ is true.” But what does “true” really mean? This question belongs to the realm of philosophical inquiry known as the theory of truth. Next, we will discuss Tarski’s indefinability Theorem, which is a companion to Gödel’s Incompleteness Theorem.

8. Tarski: Levels of Language

According to contemporary formal science, a formal system—such as a logical system—consists of two standard components: its syntax and its semantics. This reflects the nature of formal languages. In the formal syntax of the system, the focus is on provability, while in its semantics, the focus is on truth values, which can only be true or false. This is a binary situation, hence the term propositional attitudes. The semantics of a first-order theory, also known as its model, is an arithmetic structure. Syntax and semantics should have equal status, meaning that there should be an if-and-only-if relationship between provability and validity. This is a requirement from metalogic regarding the overall properties of the system. Any provable formula should be valid, a property called soundness, and any valid formula should be provable, known as completeness. We desire that the syntax and semantics of a system are of equal strength. If syntax is stronger than semantics, this is known as under formalization or over-modeling; if syntax is weaker, this is called over formalization or under modeling. In decision theory, incompleteness is also referred to as corresponding irrationality, while unsoundness is known as reflective irrationality. Below are four steps to understanding Tarski’s theorem.

8.1. Arithmetic Definability

In Section 7.3, we introduced Gödel’s notion of expressibility, which establishes the connection between relations in naive arithmetic and provability in first-order syntactic theories. Tarski introduced the concept of arithmetic definability, which describes the relationship between relations in naive arithmetic and the semantics of first-order theories (i.e., the given arithmetic structure that serves as the model). It states that if an n-ary relation holds in naive arithmetic, then the corresponding function is declared true in the model of the first-order theory. Consequently, the relation $R$ is said to be arithmetically definable in the model.

Consider a formula $A\left(x\right)$ with one free variable, known as the base formula, whose Gödel number is $m$. Substituting $m$ for $x$ results in a new formula $B_m$, which is a closed expression (i.e., without free variables) and a self-referential statement of $A\left(x\right)$. We can further denote $n$ as the Gödel number of $B_m$. Strictly speaking, Tarski’s theorem, compared to Gödel’s theorem, presents a conceptual difficulty. Gödel’s theorem involves two Gödel numbers: one for the base formula and another for the proof of its self-referential statement, and these two tasks are easily distinguishable without cognitive hindrances. However, Tarski’s theorem also involves two Gödel numbers: one for the base formula and another for its self-referential statement. Conceptually, this is more tangled and demands greater cognitive effort to avoid memory blocks. I have observed this problem in my lectures. Therefore, for ease of distinction, we refer to the Gödel number of a base formula as the first-order Gödel number, while the Gödel number of the self-referential statement generated from the base formula and its Gödel number is called the second-order Gödel number.

By constructing second-order Gödel numbers, Tarski maximized the potential of Gödel’s numbering method. His motivation was to introduce a natural number relation denoted by $d\left(m,n\right)$, where $m$ is the first-order Gödel number of the base formula, and $n$ is the second-order Gödel number of its self-referential statement. Furthermore, from $d\left(m,n\right)$, one can arithmetically define a function $D\left(\mathit{m},\mathit{n}\right)$ in the first-order theory and its model, which can also be said to be arithmetically defined by the former. This effort demonstrates a dual self-reference and clearly serves future purposes. It is important to point out that $d\left(m,n\right)$ is a general binary relation that holds for any formula with one free variable, and thus $D\left(\mathit{m},\mathit{n}\right)$ is also a general binary predicate function.

Tarski was evidently influenced by Gödel’s work, as his use of Gödel’s numbering method attests. However, genius is genius. Gödel was a genius, a master of syntax, and Tarski was also a genius, a master of semantics. Both had a profound academic passion for the foundations of mathematical logic and the mission to communicate with the mysteries of the universe. They possessed the talent to cut through mountains and build bridges across rivers.

8.2. The Truth Predicate and Semantic Models

Truth, in mathematical logic, is essentially a semantic concept and only makes sense within models. One day, Tarski, the master of semantics, had a genius idea: what if one treated the propositional attitude "truth" syntactically? How would that feel? Hence, Tarski added a truth predicate $T$ to the formal language $N$ of the first-order theory. As a result, we obtain a hypothetical first-order theory with a truth predicate, denoted as $N^{+}=\left(N,T\right)$. This single flash of insight stirred great waves.

Notice that with the truth predicate $T$, one can construct sentences involving $T$. Simultaneously, one must extend the original model to accommodate these new truth-predicate sentences. The truth predicate is a unary predicate. In English, the verb “to be”, followed by an adjective or noun to express a property, such as “is red,” “is round,” or “is plastic.” In this way, creating a property like “is true” seems unproblematic.

For convenience, let us introduce three notations. First, let us denote the closed expression $B_m$ from Section 8.1 as $L$. Second, since we have now introduced a truth predicate into the syntax, there should logically be truth sentences in the model, denoted by $L_t$. Finally, this sentence $L_t$ should have a Gödel number, denoted as $L_g$. Thus, if $X$ is an arithmetic model of the truth predicate, the condition $L_g$ belongs to the extension of $X$ holds if and only if $L_t$ is interpreted as true under the intension of $X$. The model of the truth predicate is clearly and simply expressed by the definition of a set:

$$X=\left\{L_g\right|X\models L and L_t is preinterpreted as true under X\}.$$

Thus, the extension of $X$ is a set of Gödel numbers, and the intension of $X$ states that each of them corresponds to and only to the Gödel number of a formula interpreted as true in the model.

8.3. The Liar Paradox

It is often mistakenly believed that Gödel’s incompleteness theorem is a paradox, but it is not. Tarski’s theorem, however, is indeed a formalized version of the so-called "Liar Paradox." The Liar Paradox arises from the sentence: "This statement is false." Upon reflection, if this sentence is true, it implies that it is false; if it is false, it implies that it is true. This is what we call the Liar Paradox. Tarski ingeniously embedded the Liar Paradox within first-order theory by carefully constructing the following sentence: "For all $y$, if $D\left(x,y\right)$, then not $T\left(y\right)$." Formally, this can be written as:

$$A_x=\forall y[D\left(x,y\right)\to \neg T\left(y\right)).$$

This formula contains one free variable $x$, making it an open formula. This formula has a unique Gödel number, which we denote as $g_A=m$. By substituting $m$ for the free variable $x$, we obtain a closed formula $B\left(m\right)$, which is a self-referential statement of the form:

$$B_m=\forall y[D\left(m,y\right)\to \neg T\left(y\right)).$$

This formula is the centerpiece of Tarski’s theorem. It also has a unique Gödel number, denoted $g_{B\left(m\right)}=n$, which is a second-order Gödel number. Later, we will see how Tarski skillfully utilizes this formula in his proof.

8.4. Tarski’s Theorem

Tarski, full of enthusiasm, introduced the truth predicate into first-order theory—an act of extraordinary insight and courage. The result, however, was the discovery that no model could be found for this truth predicate. Some might claim that Tarski’s original intention was to produce a negative result, but this is generally a post hoc rationalization. Very few mathematicians set out with the express goal of proving a negative result. Gödel himself initially aimed to contribute to Hilbert’s program by providing a solid logical foundation for the rapidly advancing field of mathematics—a tragic yet heroic endeavor in the backdrop of mathematical beauty.

In brief, Tarski’s theorem states that within the framework of first-order theory, the truth predicate cannot have an arithmetic model. The proof proceeds by contradiction, which we will outline in three steps.

Step 1: Using proof by contradiction, we assume that there exists a model as defined earlier, $X=\left\{L_g\right|L_{t}istrueinX\}$.

Step 2: Since such a model $X$ exists, $L_t$ should be interpreted as true in $X$, meaning that $L_g$ belongs to $X$.

Step 3: Recall that $L_g$ is the Gödel number of $L_t$, and hence it is the second-order Gödel number of $B_m$. From the definition of $d\left(m,n\right)$ in Section 8.1, it follows that $d\left(m,L_g\right)$, and thus the function $D\left(m,L_g\right)$, is arithmetically definable. However, recalling the conditional structure of $B_m$, we can conclude $T\left(L_g\right)$, meaning that $L_t$ is not true in $X$, so $L_g$ does not belong to $X$.

The contradiction between steps 2 and 3 shows that the assumption in step 1 is false. In other words, the truth predicate cannot have an arithmetic model within the framework of first-order theory, meaning that the truth predicate is not arithmetically definable. This result is known as Tarski’s indefinability theorem.

Tarski later developed the theory of language levels. He concluded that the truth predicate for a given system is undefinable within that system itself. In other words, a truth-theoretic characterization for a given language level surpasses the descriptive capacity of that level, requiring the resources of a higher-level language. Gödel and Tarski’s twin theorems—the sword and the soul—are deeply intertwined. They are both majestic and breathtaking to read, yet elegant and seamless in their conclusions. Gödel, in his philosophy of mathematics, advocated for objective idealism, reflecting his ontological commitment to the realm of the mind.

9. Wittgenstein: Language Games

We can find many words of praise for Gödel and Tarski, but there is a special crown reserved for Wittgenstein—he is the hero of language studies. Wittgenstein studied under Russell, which gave him a background in logic. During the peak era of Gödel and Tarski, when studying various techniques of mathematical logic was the trend, Wittgenstein courageously turned his attention to studying everyday language and people’s daily linguistic interactions, a rare and commendable move. In my opinion, Wittgenstein was a pioneer of psycholinguistics and behaviorist linguistics.

Wittgenstein discovered that when people use everyday language to communicate, it is almost like they are engaging in a language game. As a professionally trained logician, he naturally had the academic impulse to define this language game. However, similar to the experiences of Gödel and Tarski, he further discovered that language games are nearly impossible to perfectly define. Games require a set of rules, but for language games, the rules seem to be both present and absent, both hidden and apparent, existent but incomplete. In Wittgenstein’s view, this was the very essence of language. He believed that there is no language independent of language games. This discovery can be called the principle of incompleteness of language game rules, an important insight in behaviorist linguistics.

The state of a language game varies depending on specific situations and differs across individuals. Hence, within the framework of the norm-field theory, language games belong to the local level. Gödel’s theorem and Tarski’s theorem are both general treatments of language and do not involve individual differences in language behavior, so they pertain to the global level. We know that logical theorems are created by logicians, making logicians the normative potential of logical theorems. Different logicians can prove the same logical theorem, which we call a "many-to-one" mapping. The strength of the norm field is the theorem that has been proven. On the local level, that is, in a language game, the interlocutor’s thoughts, linguistic ability, expression style, cognitive level, and subconscious impulses might all contribute to the normative potential. The actual linguistic behavior of the interlocutor is then the norm field strength. In this way, Gödel’s and Wittgenstein’s academic paths are placed within a unified four-box structure of gauge field theory. The gauge field theory was designed to study wave functions, and the incompleteness of language game rules suggests that language games are indeed a kind of wave function. This idea will be discussed in Section 12 of the third part of this article.

Wittgenstein believed that language is public and that there is no such thing as a private language. I think this is a limitation of his philosophy of language, possibly because his academic life mostly took place during the period when behaviorism was the dominant research paradigm. His close relationship with the Vienna Circle of logical positivism attests to this. He happened to miss the cognitive revolution that began in the mid-1950s. Had he been exposed to Chomsky’s theory of language acquisition or Fodor’s later arguments on the language of thought, he might have once again changed his views.

Wittgenstein’s discovery of the incompleteness of language game rules introduced a skeptical tone into his later philosophy of language. It is important to highlight a philosophical division here. We tend to believe that Gödel, within the framework of first-order theory, constructed his theorems and, in the process of formal linguistic techniques, created new linguistic structures such as self-referential statements. But Wittgenstein argued that assuming a language framework is meaningless. He thought that Gödel’s theorem was simply a language game that Gödel was playing, and the theorem itself represented the coherence of this first-order language game. Wittgenstein went so far as to argue that any attempt to formalize language is a mistake. In my view, this might be an overly extreme position. The question is: in the academic debate between Wittgenstein and Gödel, were they engaged in two separate language games, a unified game, or perhaps even three games simultaneously? Furthermore, does this involve two or three coherence standards? This question will be addressed in section 11 of this article. Moreover, this philosophical divide represents a structural epistemological division, which we will discuss in Section 10.

Wittgenstein’s students later edited and published his late notes, a short book titled On Certainty. This book mainly collects his arguments against Moore’s proof of the existence of an external world and his anti-skeptical positions. In his later thoughts, Wittgenstein proposed a type of anti-skeptical argument. He said that doubting everything is not really doubt. You can only doubt things you once believed. In this book, he introduced the concept of subjective certainty. This suggests that language games are not entirely without a foundation of certainty. This poses a challenge: can we find ways to structure and model language games? In the third part of this article, we will present three such paths: the special relativity path, the quantization path, and the general relativity path.

Part III: Beyond Wittgenstein: Structure and Models

10. Epistemological Structure

In the first part of this article, we explained the certainty and stability of language through the dual structures of various languages. In the second part, we explored how Gödel and Tarski pushed logical language to its limits, revealing the limitations of language, which may seem somewhat pessimistic. Just as people were busy seeking various philosophical excuses, Wittgenstein injected new vitality into language studies. He argued that logical language is merely an artificially constructed ideal language, while the uncertainty of everyday language is precisely what gives language its vitality. His principle of the unregulability of language games views the uncertainty of everyday language as an inherent and infinite charm. So, what is the functional difference between artificial ideal language and everyday language activity? This leads us to discuss the two epistemological paths: the “knowing path” and the “doing path.”

In epistemology, there is a Platonic tradition that states knowing a piece of knowledge, denoted as $P$, means satisfying three conditions simultaneously. First, $P$ is true. Second, you believe $P$. Third, you have appropriate justifications. If any of these conditions is not met, you cannot claim to know this piece of knowledge. Thus, there are only two modes for knowledge: knowing and not knowing. This knowing path, in an extended sense, is akin to Gödel’s logical path, investigating the provability of knowledge, or Tarski’s logical path, validating the truth or falsity of knowledge. If we consider language as a landmark, this can be termed the language path, which carries a dual-mode epistemological structure. The so-called propositional attitudes in logical language, either true or false, are a manifestation of this dual-mode structure.

In the same epistemological sense, Wittgenstein was concerned not with knowing but with doing, i.e., linguistic behavior or language as action. He proposed that language behavior, such as language games, carries three modes. Assuming that language games have rules, the possible modes of behavior are as follows: Mode 1 is following the rules, meaning actions are correct. Mode 2 is violating the rules, meaning actions are incorrect. Additionally, Mode 3 represents neither following nor violating the rules, implying that the actions are neither correct nor incorrect. For example, in a ball game, tossing the ball around randomly and making jokes may not be right or wrong. Similarly, if you go to the bathroom during an exam, it is unrelated to the correctness of answering questions, often termed as “going off-topic.” Going off-topic in language behavior is precisely where the vitality of language lies. How many new topics in the world and new discoveries in science are precisely due to going off-topic? This point can be illustrated by the content of this article.

Gödel’s incompleteness theorems arose from attempting to solve one of the problems posed in Hilbert’s mathematical program, namely the logical foundation’s coherence problem of the mathematical edifice. If Gödel had produced a positive result, it would correspond to Mode 1. However, Gödel’s results were unexpected, corresponding to Mode 2. For the language game of solving Hilbert’s problems, Wittgenstein’s language game theory, from many perspectives, could be seen as going off-topic. However, we should recognize that Wittgenstein’s language game theory itself corresponds to Mode 3. It is the identification of this third mode that allowed Wittgenstein to break away from the Platonic tradition and diverge from Gödel’s logical path. This third mode also infuses language games with vitality. This Wittgensteinian path emphasizes the classification of language behavior into three modes, taking language behavior as the essence of language, which can be termed the speech path, carrying a three-mode epistemological structure. Thus, we can clearly see that the epistemological difference between the language path and the speech path lies primarily in the number of modes they commit to, with one being a two-dimensional mode space and the other a three-dimensional mode space.

To go beyond Wittgenstein is not to discard his philosophy of language but to offer new insights within his conceptual framework. One of these insights is integrating his conceptual system with other systems, such as those in theoretical physics, which is termed modeling. Let us first understand a few concepts from Wittgenstein’s philosophy of language. The first concept is private language. Wittgenstein argued that there is no such thing as a private language, though this is controversial. In section 7 of this article, we introduced Gödel’s incompleteness theorems [16]. This theorem is well-documented, and many people know or have at least heard of it. This article aims to balance scientific rigor with readability, interspersing some narrative elements to ease the tension that readers might feel when encountering mathematical formulas. The article is written in public language, not as self-talk for oneself. Therefore, it does not engage in academic discussions about the existence of private language.

The second concept is language games. Wittgenstein’s focus was not on whether the discussion of Gödel’s theorem in this article is flawless or exciting. Instead, he was concerned with why you are discussing Gödel’s theorem in this article. Many articles discuss Gödel’s theorem; what differentiates the context in this article from others? Wittgenstein initially referred to this as the meaning of the term "Gödel’s theorem," later renaming it as language games. This is a highly descriptive concept with profound insight, offering a unique perspective. According to Wittgenstein, Gödel’s theorem represents the content and meaning of Gödel’s language game, reflecting a high standard of coherence.

The third concept is grammar. Wittgenstein’s concept of grammar has a specific meaning, not referring to the “order of things” or “logical arrangement of language expressions” as we commonly understand it, but to the overall set of rules, or the rule patterns that govern language games behind the scenes. It is manifested to us in an apparent way, but we cannot directly perceive it in language games. This is similar to the conceptual map in our minds; we cannot articulate why we use a particular concept, but we understand and use it well. For example, when we use concepts like time or space, we cannot precisely indicate where these concepts come from or what they mean, but we can use them effectively. Wittgenstein’s concept of grammar was mainly used in his mid-period philosophy and later transitioned to terms like "forms of life" or "world picture," which express similar ideas.

Next, focusing on language games and using theoretical physics as a modeling method, we will introduce three modeling paths: the special relativity path, the quantization path, and the general relativity path.

11. Special Relativity Structure

Note: In this section, any reference to "another article" refers to Yang, Y. (2022). Psychological Characteristics and Society [17].

11.1. Light Cones and Language Cones

In another article, we provided a detailed introduction to special relativity. Here, for the convenience of the reader, we will briefly review it. Special relativity is based on the principle of the constancy of the speed of light, introducing an invariant. Therefore, to apply the structure of special relativity to any other field, one must first introduce an invariant with light-like properties. In this context, the invariant with light-like properties we are introducing is the speed of language. Although Wittgenstein’s philosophy of language studies linguistic behavior, his works must be written in German and, to be globally influential, must be translated into other languages, such as English and Chinese, which are natural languages.

Linguistic behavior, whether in writing or speaking, has content, and at least its literal content is expressed through language. Even if there are implicit or implied meanings, they must be understood through literal expression or the original statement. Therefore, language has comprehensive coverage of content. Even if some content is difficult to express at the moment, natural language must be used to say something like "difficult to express in words." For example, in the novel Jane Eyre, there is a line: "I hold myself supremely blest - blest beyond what language can express." Such a splendid expression also needs to be conveyed through language. In set theory, axiomatic systems derived from either the universal set or the empty set are equivalent. Abstracting the comprehensive coverage of language content to the conceptualization of its potential contentlessness is a matter of course. In short, the light-like property of language in the world of linguistic behavior is because of its contentlessness, just as the speed of light is the fastest because of the masslessness of photons.

Since light travels at the fastest speed, it can be assumed to propagate in straight lines, scattering in all directions. Given a light source, its emission forms a cone-shaped scatter downward, called the lower cone; similarly, scattering upward also forms a cone, called the upper cone. The upper and lower cones together, with the apex at the light source, are known as the light cone. Any trajectory that passes through the lower cone, through the apex, and then through the upper cone is called a world line, reflecting the local causality of events. Having established the light-like property of language, we can correspondingly convert such a light cone into a language cone. Although the content is different, the structure remains analogous.

11.2. Language Games’ Standards and Cone forms

According to Wittgenstein, language games show that our linguistic activities are akin to games, and there is no language that exists apart from the activity of the game itself. In other words, we cannot assume a language and then use it to play language games. Instead, he believes that when we engage in linguistic activities, it is akin to engaging in other human activities, merely following rules within a game. Thus, the essence of language lies in linguistic activities, and language games are the basis and reason for language’s existence. Consequently, any attempt to formalize language and understand it through its form, according to Wittgenstein, is mistaken. Therefore, the previously mentioned language cone should be adapted to the concept of a language game cone, hereafter referred to as the game cone. The requirement for the game cone is to reflect people’s forms of life.

We propose (not Wittgenstein) that the game cone is a modification of the language cone. The difference is that while the language cone presupposes complete rules, the game cone should have incomplete rules, which is the geometric version of Wittgenstein’s principle of rule incompleteness. The reason for this will be explained in the next subsection. Wittgenstein had standards for language games, referred to as criteria of coherence. For convenience, in the evolution of Wittgenstein’s philosophy of language, the concept of language games evolved from the concept of meaning. Therefore, the game cone is also a meaning cone. How does a linguistic behavior move from a point to a cone? According to Wittgenstein, language games always carry a larger psychological game cone; events in the lower cone are psychological incentives for language games, while events in the upper cone are psychological consequences of language games.

In another article, we also introduced the concept of intervals in Minkowski space in detail. Here is its formula definition:

$${\left(S\right)}^2=C^2\Delta t^2-{\left(\Delta x\right)}^2-{\left(\Delta y\right)}^2-{\left(\Delta z\right)}^2$$

Given a game cone, events within the cone indicate that a linguistic behavior meets its coherence criteria, with a positive interval, referred to as a quasi-temporal event. That is, both correct and incorrect linguistic behaviors are within the cone. Events outside the cone indicate that a linguistic behavior does not meet its coherence criteria, with a negative interval, referred to as a quasi-empty event. Note that both the first and second modes of Wittgenstein’s linguistic behavior are within the cone, while the third mode is outside the cone. Events on the surface of the cone indicate that the linguistic behavior precisely meets the coherence criteria, with an interval equal to zero, referred to as a null event. Wittgenstein believed that language games are always concrete, and each language game has its distinct coherence criteria. With different standards, the events that can be included within the game cone vary, so the cone’s shape is not subject to fixed rules. The lower cone represents causal meaning, while the upper cone represents result meaning, and causality requires both to satisfy the same coherence criteria. A specific language game has different narrative causalities and should allow for varying strengths of coherence.

11.3. Proper Cones and Fitting Cones

In another context, we have introduced the concept of proper time (also known as clock time) in the theory of special relativity. Proper time is related to velocity; as the speed increases, the relative proper time decreases, showing an inverse relationship. Proper time is individualized and represents a typical local concept. In the definition of intervals, each term is divided by the proper time, resulting in what is called momentum. Accordingly, assuming that each player possesses an individualized intrinsic meaning, that is, the standard of intrinsic coherence within language games, this leads to the formation of an individualized intrinsic game cone.

Let us first discuss the single-player intrinsic game cone, and then move on to discuss multiple players with several intrinsic game cones. Language is a manifestation of the mind, and linguistic behavior is supported by mental stimulation. The mind is individualized, and the world of the mind is primarily registered individually, which is a common understanding in cognitive science. Writing articles, speaking, or giving lectures are all linguistic behaviors. From Wittgenstein's perspective, these naturally constitute single-player language games. Writing an article involves

considering structural layout, arrangement of sections for each level of meaning, etc. Writing is not just for oneself but also has public significance, taking into account its impact on the readership. These are aspects of larger psychological games. In other words, writing an article is engaging in a single-player language game. Here, the player has their unique considerations for the coherence of their language game. And this cannot be predicted in advance. Therefore, the shape of the single-player language game cone is not completely regular.

When people engage in discussions or exchanges through linguistic behavior, it forms a multi-player language game. Wittgenstein's philosophy of language assumes the existence of coherence in multi-player language games. I believe that the coherence of multi-player language games should be some function of the individual games of the participants. Correspondingly, the shape of the multi-player language game cone should be a fitting of the individual game cones of the participants. Why do we say that embedding a cone in a verbal game begins to structure it? We know that mathematical structures can be simple or complex, and the simpler the structure, the more fundamental it is. The simplest mathematical structure is

known as a metric structure. For example, in three-dimensional space, the concept of distance can be defined. It is obtained by summing up three square terms and then taking the square root. All three square-terms are positive. This is because the metric of three-dimensional space is (+,+,+), which is the most basic algebraic structure assigned to a set. In the theory of special relativity, the concept of the light cone is introduced through the concept of interval. Now, looking back at the four terms in the definition formula of the interval, you will find that its four-dimensional spaceti

looking back at the four terms in the definition formula of the interval, you will find that its four-dimensional spacetime metric becomes (+,-,-,-). This is the basic mathematical structure carried by the game cone. That is to say, under the psychological geometric structure of the language cone, there is an algebraic structure indicating how algebraic operations are performed between linguistic objects.

12. Quantum Structures

If we consider quantizing language, conceptually it presents difficulties. This difficulty essentially involves introducing a concept similar to language games. Directly quantizing language games seems as if quantum mechanics were custom-made for language games. Here, we will discuss three types of quantum structures: non-commutative relations, wave functions, and Dirac delta functions.

12.1. Non-commutative Relations

Finding a certain non-commutative relation in a phenomenon (simply put, meaning it does not satisfy the commutative property) signifies its quantization, formally known as canonical quantization. In mathematics, matrix multiplication does not satisfy the commutative property but satisfies non-commutative relations. Therefore, the initial form of quantum mechanics proposed by Heisenberg was also known as matrix mechanics. The order of two linguistic actions matters, as the result is clearly different and is sensitive to the order. For example, consider the well-known "20 Questions Game" to illustrate why this is the case.

The "20 Questions Game" is a two-player game. One player thinks of something, and the other player asks yes-or-no questions in sequence. For instance, if the object is an apple, the questions might be: "Is it used?" "Is it a living thing?" "Can it be eaten?" "Is it a vegetable?" "Is it a fruit?" It is evident that the order of questions affects how quickly the object is guessed. Therefore, the sequence of questions is sensitive to order and satisfies non-commutative relations. Such language games are common in everyday life. For example, when a child cries, an adult might ask, "Is the child hungry?" "Does the child need to use the toilet?" "Does the child want a toy?" Eventually, the adult discovers that the child simply wants to be held, seeking attention and security. The "20 Questions Game" has clear and specific coherence standards, making it a typical language game. In the sense of non-commutative relations, language games are quantized. Non-commutative relations represent an algebraic structure. In other words, language games carry an algebraic structure.

12.2. Wave Functions

Wave functions are fundamental concepts in quantum mechanics and quantum field theory, as introduced in Section 6.1. It can be argued that language games are well-characterized by wave functions. To illustrate this, consider standardized educational tests such as the SAT in the United States or the College Entry Exam in China. An exam can be seen as a language game, a common form of everyday activity with clear coherence standards. Especially, the reading comprehension section of these tests evaluates the examinees’ linguistic abilities. According to Wittgenstein, language is language games, and language games are language itself. Therefore, standardized educational tests are typical language games.

Regardless of the exam content, as long as the questions are presented in written form and responses are required in writing, it is referred to as a verbal task in experimental psychology. Verbal tasks assess various abilities, which may not necessarily be linguistic abilities per se; they can include reasoning ability, decision-making ability, understanding ability, or any other capabilities. These abilities are forms of life and each has its coherence standards. Thus, these verbal tasks are equivalent to language games. Such tasks come with implicit rules, which from a psychological perspective, differentiate reasoning tasks from decision-making tasks.

Why do exams exist? Because the examinees’ abilities are not directly observable. Let’s assume the ability of an examinee is denoted as $A$ and the exam is denoted as $b$. The exam questions are given, and the examinee provides answers. Thus, the examinee’s ability becomes a function of the exam, referred to as a wave function in physics. Quantum mechanics studies the dynamics of wave functions. Therefore, here the wave function represents a physical structure carried by language games. As discussed in Section 6.1, the meaning of a wave function is its amplitude; hence, the language game can also be referred to as an amplitude game. The amplitude of a wave function is the modulus squared of a complex number, so the language game also carries a mathematical complex number structure.

Generally speaking, staying close to Wittgenstein’s concepts, language games are the linguistic expressions of forms of life. This is equivalent to considering that the language game itself is the wave function of the form of life. Forms of life are not a priori but should be empirical. Thus, forms of life are not fixed; for example, no one can predict all possible forms of life in the metaverse. In physical terms, the observation of possible forms of life, especially future forms, has high interference. However, whenever a form of life that can be expressed appears, it is accompanied by a language game. Therefore, language games are functions of forms of life. Due to the high interference in observation, as Dirac put it, what we can observe or potentially experience is only the microscopic world. Thus, as a function of forms of life, language games can only be wave functions.

12.3. Dirac Delta Function

Assume that each question on an exam has a correct answer. This correct answer is referred to as the support point of the question. In the language of measure theory, a question compresses the examinee’s ability into a point, which can be visualized as a pendant on a necklace. According to von Neumann, quantum mechanical experiments are all “yes/no” experiments. Suppose there is an experimental apparatus and a particle detector. When the apparatus “thinks” it has excited a particle, if the particle is detected by the detector, it is said that the particle has entered the “yes gate.” If the particle is not detected, quantum physics asserts that the particle has entered the “no gate.” Newtonian physics, however, would say that the particle was never excited in the first place, and the apparatus cannot claim that anything has or has not happened. This illustrates the difference between the two types of physics. Such “yes/no” experiments are described by the Dirac delta function, which is expressed as follows:

$$\begin{gathered} \delta \left(x\right)=\{0,ifx\ne x_0\infty ,ifx=x_0) \\ {\int }_{-\infty }^{\infty }\delta \left(x\right)dx=1\left(\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}m\right) \end{gathered}$$

Here, $x_0$ is the support point. Note that the delta function is described by two formulas; the second formula is an integral expression, meaning that regardless of whether a particle was detected as having entered the “yes gate” or the “no gate,” ontologically, we must commit to the fact that the particle was indeed excited. Similarly, a student is acknowledged for having tried to answer a question, whether they got it right or wrong. In the context of Western philosophy, quantum mechanics adheres to the principle of presumption of innocence. We observe that in the integral formula above, the delta function becomes an integrand, known in measure theory as a test function. The test function requires the existence of at least one support point.

According to Wittgenstein, language games are always accompanied by a larger psychological game. This psychological game is the intermediate process through which forms of life are transformed into language games. It is hard to imagine whether a psychological life can continue without various support points, and if psychological life were to cease, there would be no psychological games to speak of. Thus, as a proposition, language games, or at least a large class of language games, carry the Dirac delta function structure, abbreviated as the Dirac structure. In other words, when language games are modeled by quantum mechanics or quantum field theory, they are endowed with the Dirac structure. Put differently, the Dirac structure is an inherent feature of language games.

13. Language Society and Efficiency

13.1. Linguistic Advantage and Curved Space

For now, let's temporarily step away from the concept of language games. That is to say, we are assuming here that we have not read Wittgenstein's philosophy of language and will directly discuss what we are accustomed to calling everyday language. From a psychological perspective, people's linguistic abilities vary significantly, with notable individual differences. We know that whether in daily life or in specific contexts, such as standardized educational tests, individual linguistic advantage is a scarce resource. In this sense, linguistic society is unequal. Geometrically speaking, linguistic society is not a flat space but an uneven, curved space. The mathematical background of general relativity is Riemannian geometry, which describes a curved space. Therefore, in physics, general relativity is known as the geometric program of physics. In this section, we will apply the principles of general relativity to model linguistic society. In our discussion, we will use some concepts from economics.

Since linguistic advantage is a scarce resource, there will be competition. This represents the tension within linguistic society. To quote Wittgenstein again, language games are always accompanied by larger psychological games. Linguistic advantage often serves as the root of psychological

superiority, while linguistic disadvantage frequently leads to psychological inferiority. Some say that linguistic advantage is the foundation of confidence; this is precisely what is meant. Therefore, language is an important indicator of psychological life. Given the competition for linguistic advantage, linguistic society naturally involves issues related to the efficient allocation of linguistic resources, which brings us to the concept of efficiency—what could be termed "linguistic economics." This is not an attempt to be overly mystical; consider the Chinese college entrance examination and standardized educational testing in the United States, and you will quickly feel the tension and sense of economy involved.

In welfare economics, there is an important theoretical cornerstone called Pareto efficiency. This means that the allocation of social welfare has reached a state where it is impossible to improve the welfare of one individual without simultaneously reducing the welfare of another. Such a state is referred to as Pareto efficiency or simply Pareto optimality. Pareto optimality is a fundamental concept in economics. It is clearly an ideal state in theory and difficult to achieve in reality; indeed, it has never been fully realized. However, in both natural and social sciences, modeling always implies some idealization of phenomena. It's like trying to identify an elephant by feeling its parts while blindfolded, aiming to find the trunk because once you touch the trunk, you can deduce that it belongs to an elephant and not to any other animal. Modeling also means characterization.

13.2. Linguistic Advantage and Curved Space

Let us momentarily set aside the concept of language games. That is, let us assume we have not read Wittgenstein’s philosophy of language and are discussing what we habitually call everyday language. From a psychological perspective, people’s linguistic abilities vary, and there are significant individual differences. We know that, whether in everyday life or in certain specific contexts such as standardized educational exams, individual linguistic advantages are a scarce resource. In this sense, the language society is unequal. Geometrically speaking, the language society is not a flat space but a curved space. The mathematical background of general relativity is Riemannian geometry, and Riemannian space is a type of curved space. Hence, in physics, general relativity is referred to as the geometric formulation of physics. In this section, we will apply general relativity to model the language society, using some concepts from economics.

Since linguistic advantage is a scarce resource, competition arises. This is the tension in the language society. Using Wittgenstein’s terminology, language games are always accompanied by a larger psychological game. Linguistic advantages often serve as the root of psychological advantages, while linguistic disadvantages are often the root of psychological disadvantages. It is said that linguistic advantage provides confidence, which is precisely the point. Thus, the period of linguistic development is an important indicator of psychological life. Given the competition for linguistic advantage, the language society naturally involves the issue of efficient allocation of linguistic resources, which involves the concept of efficiency, known as linguistic economics. This is not to be cryptic; consider the intense pressure you might feel during China’s College Entrain Examination or the SAT in the United States, and you will quickly grasp the economic sense.

In welfare economics, there is an important theoretical cornerstone known as Pareto efficiency. This means that the allocation of social welfare has reached a state where it is impossible to increase the welfare of one individual without simultaneously decreasing the welfare of others. This state is called Pareto efficiency, or Pareto optimality. Pareto optimality is a fundamental concept in economics. It is clearly an ideal state theoretically, difficult to achieve in reality, and has never been realized. However, in both natural and social sciences, modeling always implies some idealization of phenomena. It is a bit like blindfoldedly touching an elephant, aiming to touch the trunk, because once you touch the trunk, you can determine that it must be an elephant’s trunk rather than any other animal’s. Modeling also implies characterization.

13.3. The Gravitational Force of Language Society

Now, let us construct a Pareto state for the language society. Consider a purely language-based exam, such as the TOEFL in the US or the College Entry Exam in China. Assume that the exam assessment is dynamically balanced, meaning that the total score of all examinees is fixed. Thus, if the score of any one examinee is changed, it cannot be done without altering the score of one or more other examinees. This constitutes a Pareto welfare state because scores are equivalent to welfare. Then, if we connect each examinee’s score in any manner (clearly, the connection method is not unique), we obtain a curve known as the Pareto path. Each examinee, before or after the exam, will have expectations about their score or hopes for improvement. This intention is represented by the tangent vector at each point on the Pareto path. These tangent vectors generally point in different directions but have zero length, because this is a Pareto state where the scores of each examinee cannot change. Vectors of zero length are called isovectors. We say that all isovectors are approximately parallel, so the Pareto path is a geodesic, a shortest path in geometric terms. However, the expectations or intentions for improvement of the examinees differ from the scores indicated on the geodesic. This difference, to put it succinctly in Feynman’s terms, is curvature. In general relativity, Einstein stated that gravity is curvature. Thus, in the unequal language society, we introduce the concept of gravitational force, termed as language gravity.

In the term language game, “game” can also be read as competition. In Wittgenstein’s usage, language games have no notion of winning or losing, and do not imply strategic interactions. In Wittgenstein’s philosophy of language, language games are always accompanied by psychological games. From the previous analysis of language exams, we introduce a game mechanism into language games. There is no logical barrier to this, as Wittgenstein’s philosophy holds that language is public, not private. However, psychology is private. So, how can a game mechanism be embedded in psychological games? The following will explain that they are connected through normative transformations.

13.4. Gauge Transformations and Connections

To intuitively explain what gauge transformations are, we use the following diagram.

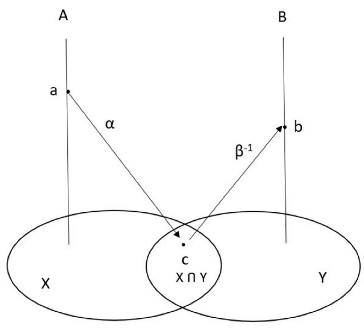
This diagram is situated within a framework called the base manifold (a concept from differential geometry). As shown in the figure, region $X$ represents the domain of language ability for individual $x$, and region $Y$ represents the domain for individual $y$. Testing these two individual domains separately does not have a gaming significance. The vertical lines $A$ and $B$ emerging from the domain $X$ represent the psychological normative potentials for individuals $x$ and $y$, respectively. Note that the potential points $a$ and $b$ are not directly comparable, as the potential lines $A$ and $B$ do not intersect and there is no mathematical operation between them.

To compare language abilities between individuals $x$ and $y$, one must conduct an examination within the intersection $C$ of the domains $X$ and $Y$. Let point $c$ represent an exam question. The mapping $\alpha$ maps potential point $a$ to the exam point $c$, and then maps it back to potential point $b$ through $\beta$, transforming potential point $a$ into potential point $b$. This transformation,

$g_{\alpha \beta }={\alpha \beta }^{-1}$, is called a gauge transformation.

The diagram and explanation above use the language of fiber bundles from differential geometry. The mathematics of General Relativity is Riemannian geometry. Riemannian space is a curved space where the Cartesian flat coordinate system has been lost. This requires establishing local frames on small neighborhoods and connections between these local frames. These details go beyond the scope of this paper. The key point is that when introducing competitive mechanisms in a language society and modeling it with General Relativity, a Riemannian space structure is embedded within the language society. This, of course, goes beyond the scope of Wittgenstein’s language philosophy.

14. General Discussions

In the introduction, we mentioned that this paper discusses language and linguistic behavior through three main threads. The first thread is the structuralism of the Bourbaki school. This paper introduces language, particularly the syntactic/semantic dual structure in scientific language, covering logic, decision theory, game theory, set theory, and gauge field theory. We have explored the fine formal structures and metamathematical structures created in Gödel’s and Tarski’s twin theorems. In examining language games, we introduced the concept of the language cone and the inherent cone structure of language games, non-commutative algebraic structures, the metric structure of algebraic spaces, wave functions and Dirac delta function structures, the local frame structures in Riemannian geometry, and the fiber bundle structure of gauge transformations. Of particular importance is the dual-layer, dual-level lattice structure of gauge field theory.

The second thread is the application of theoretical physics to the modeling of language and linguistic behavior. First, we identified the global nature of language and the local nature of linguistic behavior, thus establishing a unified gauge field theory model. Second, under the assumption of content-free language, we applied geometric conization to both language and linguistic behavior, leading to the development of a special relativity model for language and linguistic behavior. Third, we discovered the non-commutative relations in linguistic behavior, the wave function nature of language games, and the Dirac structure for public observations of linguistic behavior. On this basis, we introduced the quantum model of language and linguistic behavior. Fourth, we introduced the concept of language advantage as a scarce resource, noted the inequality in language societies, and thus applied a curvature treatment to the language society. By introducing competitive mechanisms and Pareto efficiency into language games, we defined the curvature and gravitational aspects of the curved language society. Consequently, incorporating local frames and connections from Riemannian geometry became essential. This forms the general relativity model for language societies.

The third thread is the evolution and development of Wittgenstein’s philosophy of language. First, we observed Wittgenstein’s early engagement with language, particularly his adherence to and training in formal language rules. Second, we noted Wittgenstein’s mid-period struggles and explorations, where he derived the principle of rule incompleteness in language games from Gödel’s incompleteness theorems. The distillation of linguistic behavior into the concept of language games was a stroke of genius. Next, we examined Wittgenstein’s later return to subjective determinacy and his pursuit and belief in the rule-governed nature of language games. Finally, between the concepts of language games and forms of life, he found an indispensable place for psychological games in his world schema. Thus, Wittgenstein carved out a path for the psychological approach to language and linguistic behavior.

A century ago, Hilbert’s ideal was to build a solid logical foundation for mathematics. More than half a century ago, Einstein’s ideal was to establish a unified field theory for the four fundamental forces of nature. The author’s ideal is to bridge the gap between social sciences and natural sciences, particularly mathematical physics, and to create a bridge between them for a better pursuit of knowledge. Through effort, this ideal is gradually being realized. The dynamic system of ideals and reality is the academic metaverse envisioned by the author.