Submitted:
18 December 2024
Posted:
20 December 2024
You are already at the latest version
Abstract
The development of urban areas has led to an increase use of subsoil for installing transportation networks. These systems usually comprise the construction of side-by-side twin running tunnels built sequentially and in close proximity. Different studies have demonstrated that under such conditions there is an interaction between tunnels, leading to greater settlements compared with those obtained if the tunnels were excavated separately. Supported by those findings, several analytical methods have been proposed to predict the settlements induced by the excavation of the second tunnel. This paper examines the applicability of these proposals across multiple case studies published in the literature by comparing the analytical predictions with the reported monitoring data of 57 sections. The results indicate that, regardless of the different soil conditions and geometrical characteristics of the tunnels, a Gaussian curve accurately describes the settlements in greenfield conditions and those induced by the second tunnel excavation, although with the curve becoming eccentric in this case. Despite some significant scatter observed, most methods predict the settlements induced by the second tunnel with reasonable accuracy, with Hunt’s method presenting the best fit metrics. The obtained findings confirm that existent methods can be a valid tool to predict at early stages of design the settlements induced by twin tunnelling, although contain limitations and pitfalls that are identified and discussed throughout the paper.
Keywords:
1. Introduction
2. Materials and Methods
2.1. Analytical Methods for Predicting Ground Movements Induced by Twin Tunnelling
2.2. Case Studies and Physical Model Tests
3. Results and Discussion
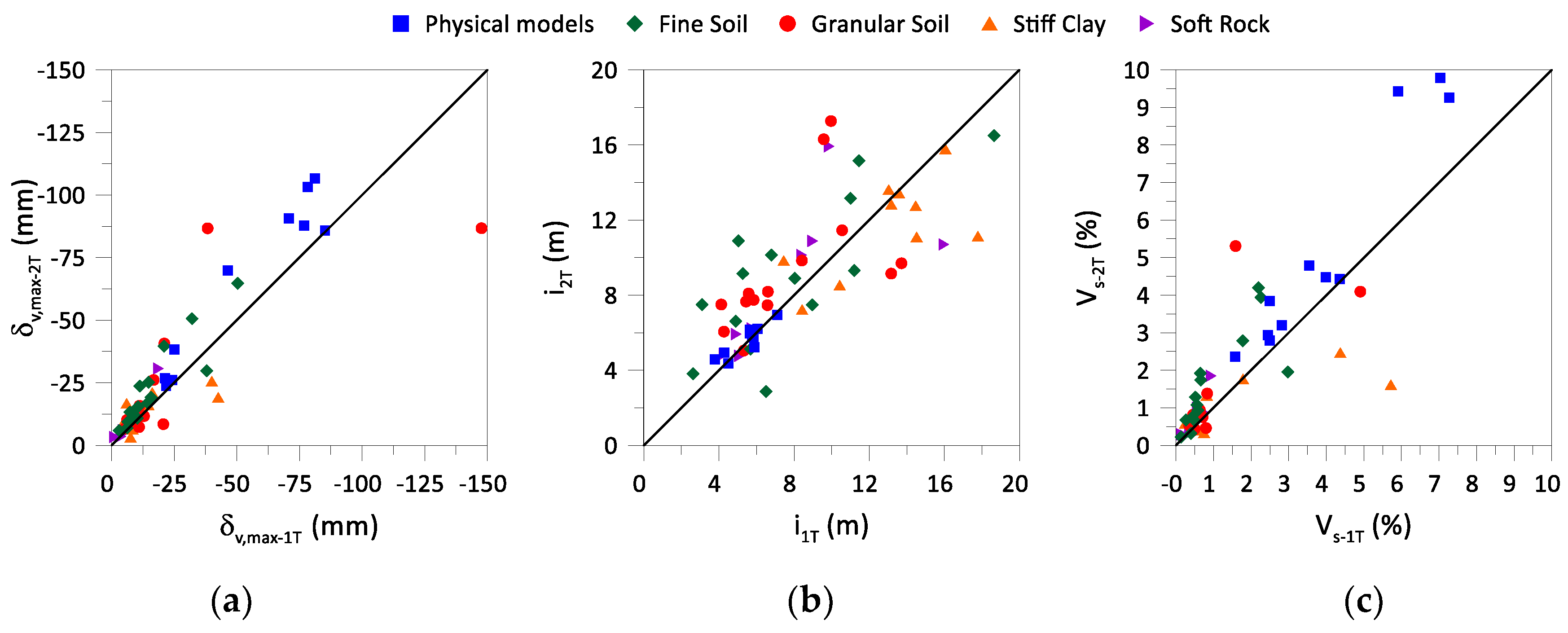
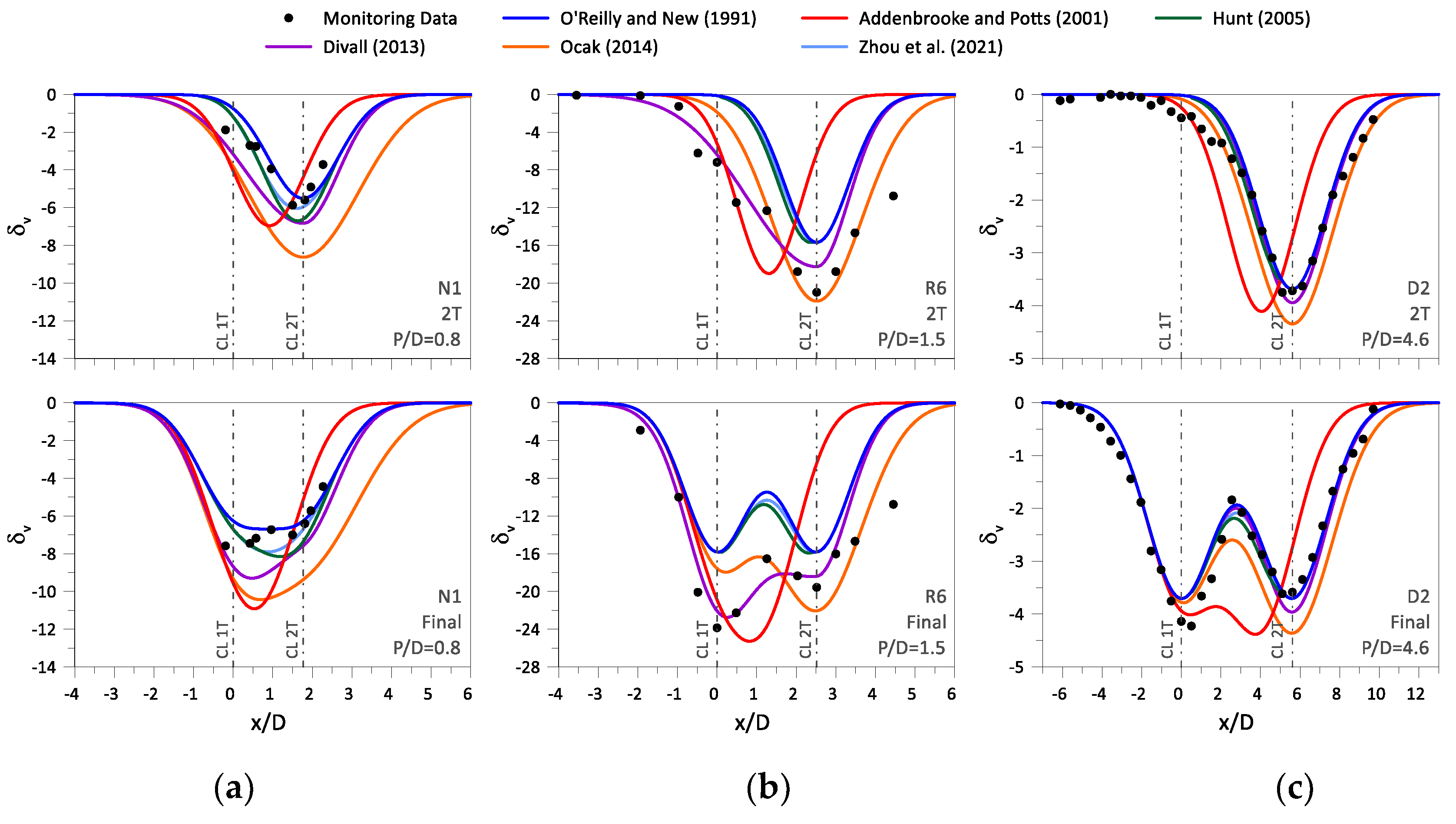
3.1. Adjustment of the Gaussian Curves to the Settlement Data
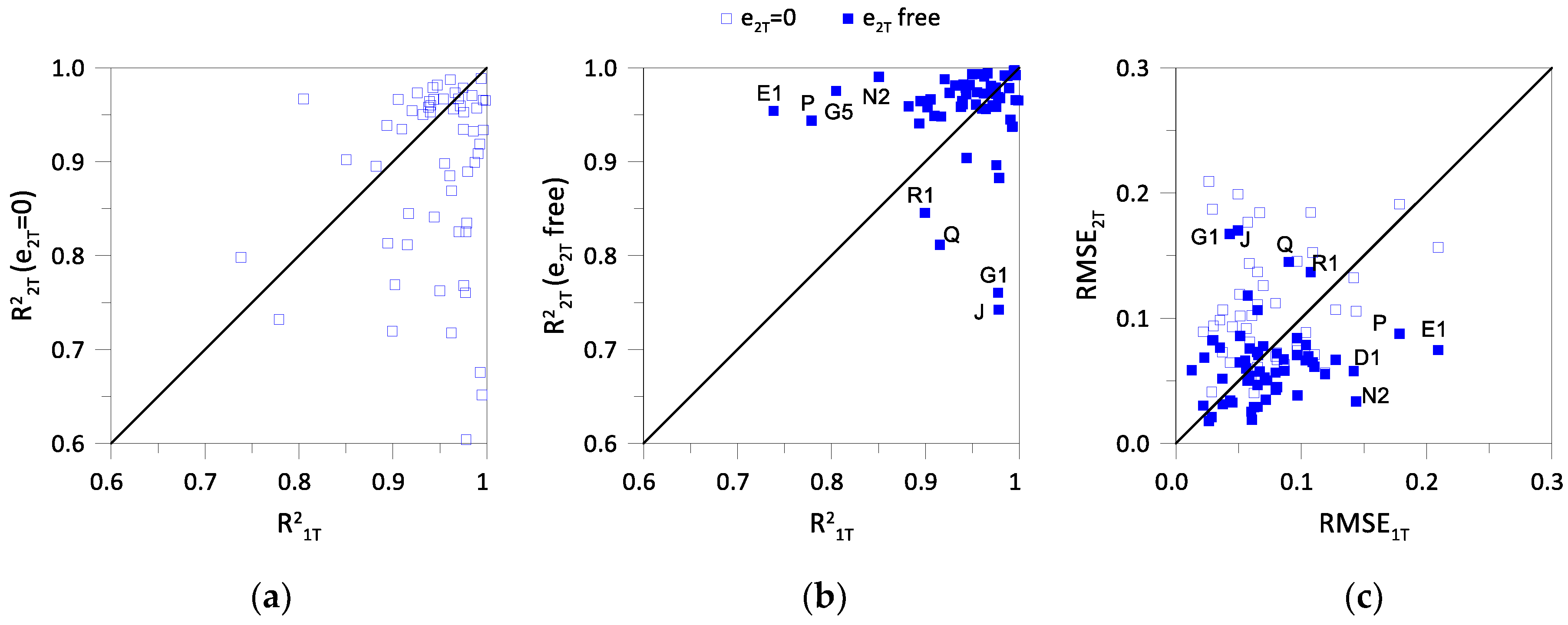
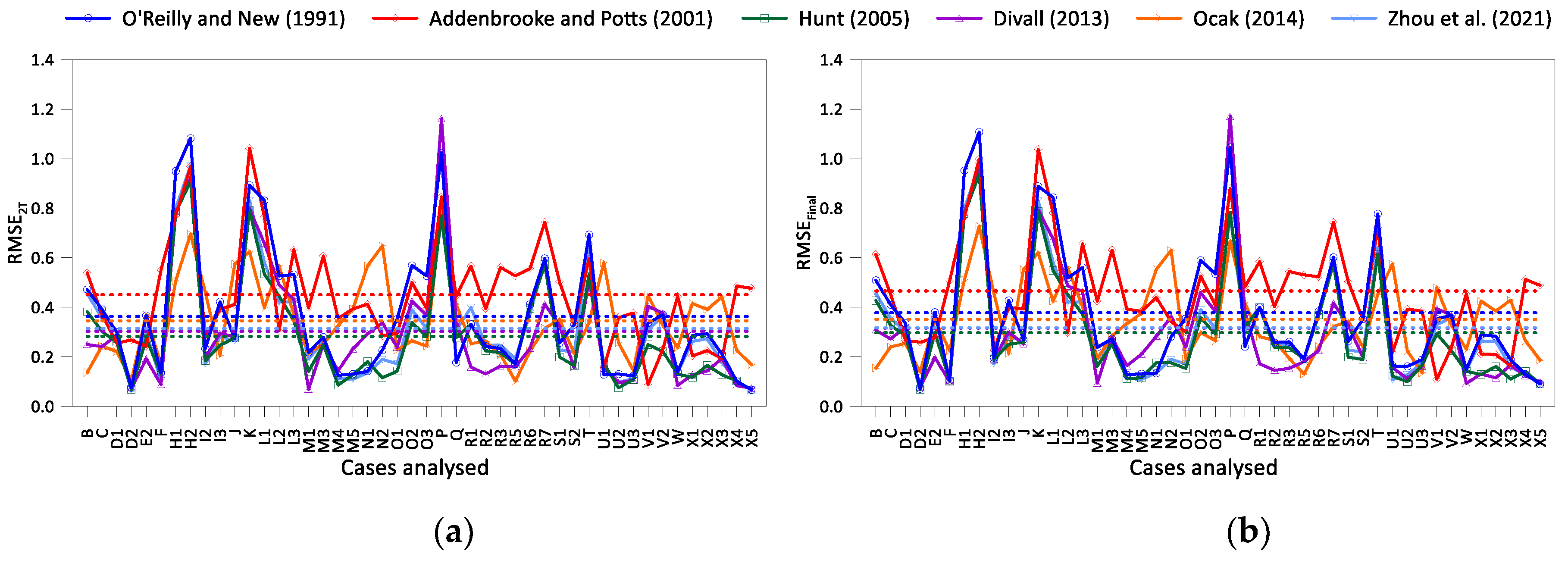
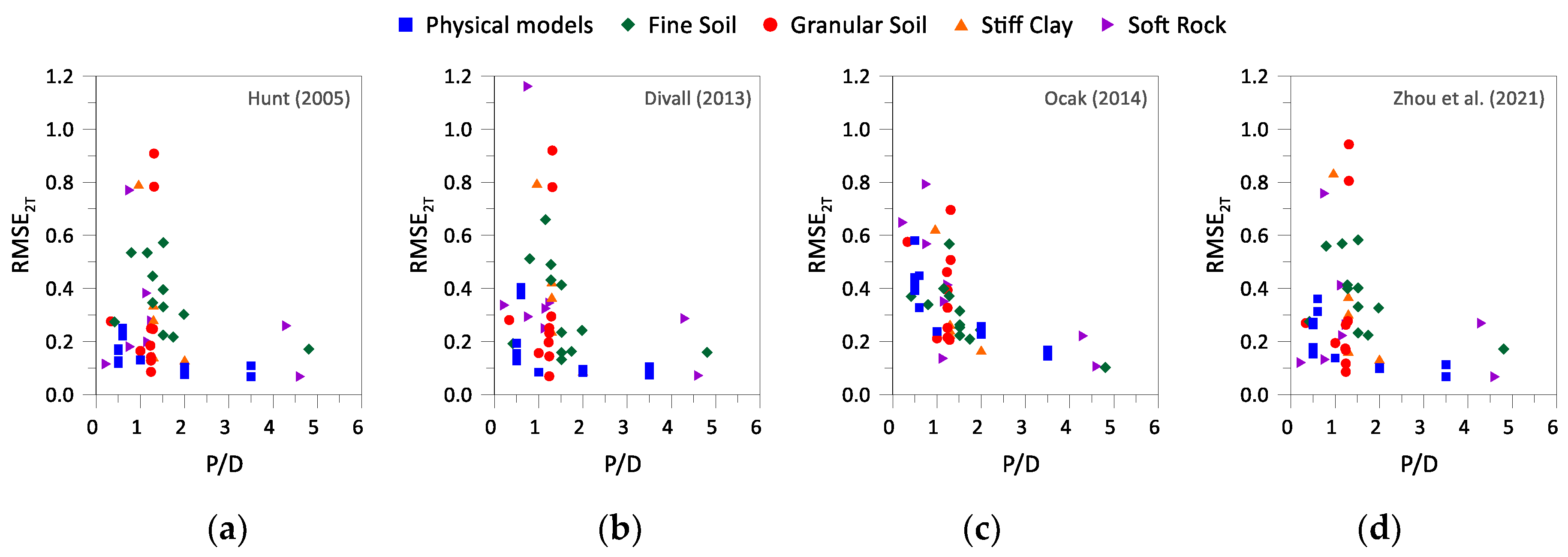
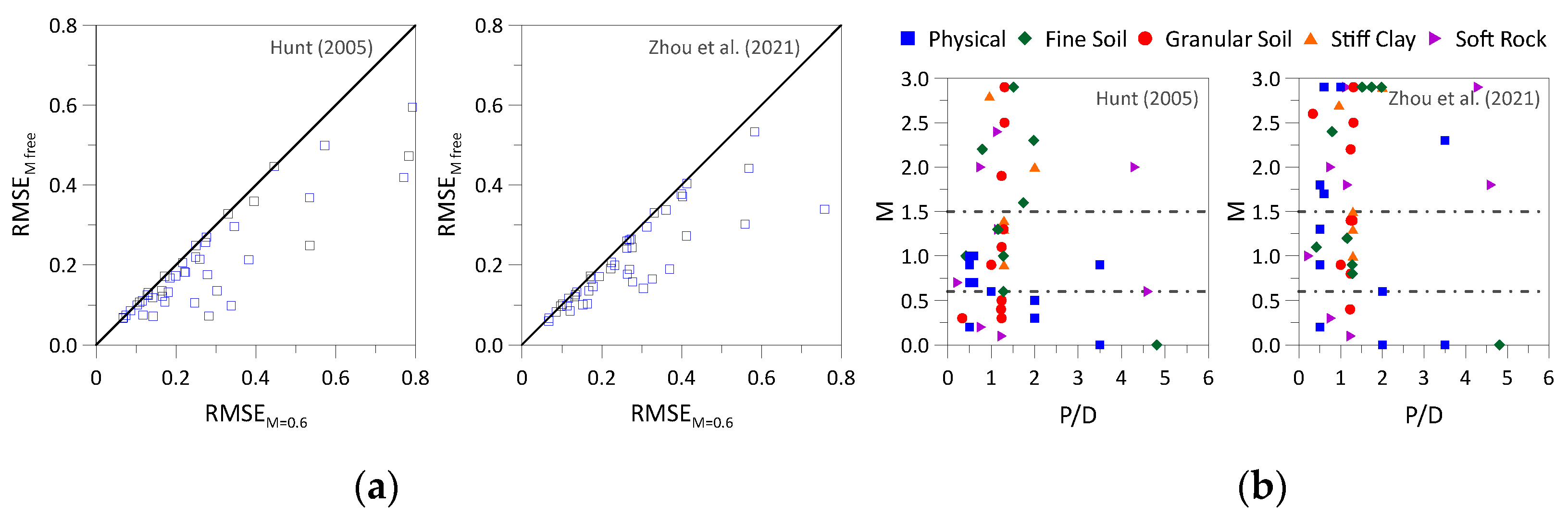
3.2. Assessment of the Analytical Methods
4. Conclusions
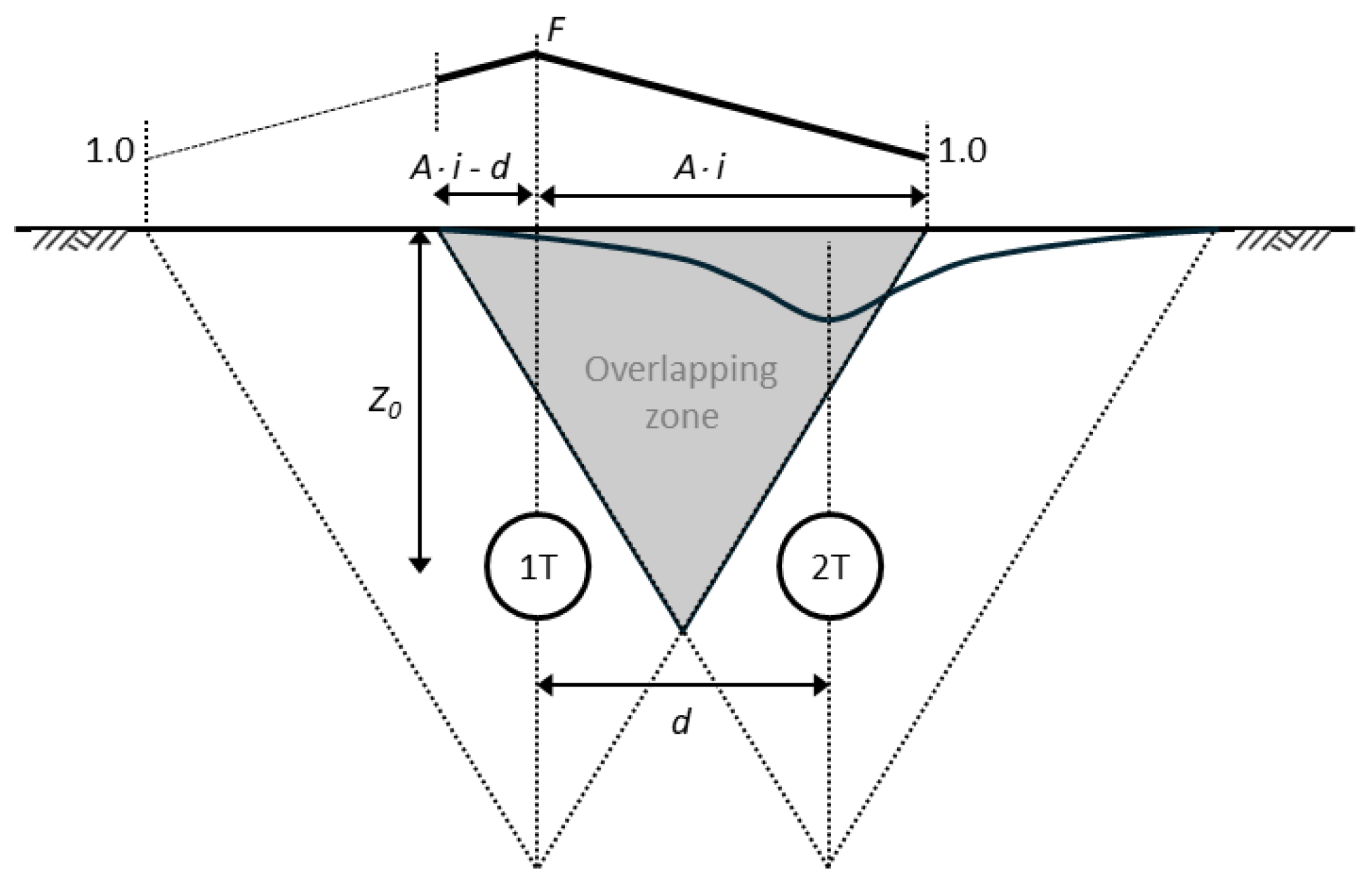
- All methods assume that the excavation of both the 1T and 2T induces a Gaussian settlement trough. With the exception of the O'Reilly and New [36] method, which does not account for tunnel interaction, all other methods predict that the 2T excavation induces higher settlements, with this increase being a function of the tunnels proximity;
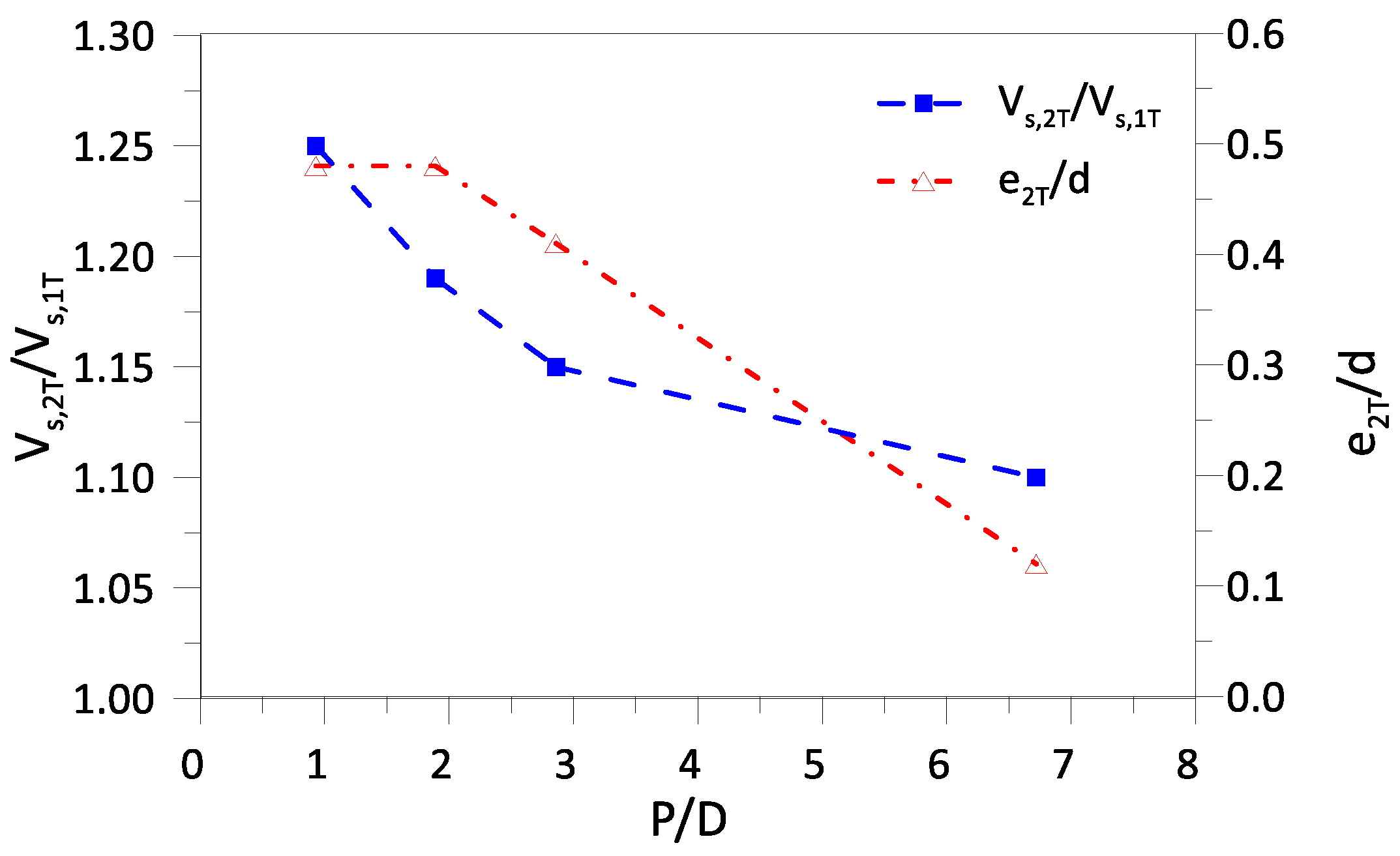
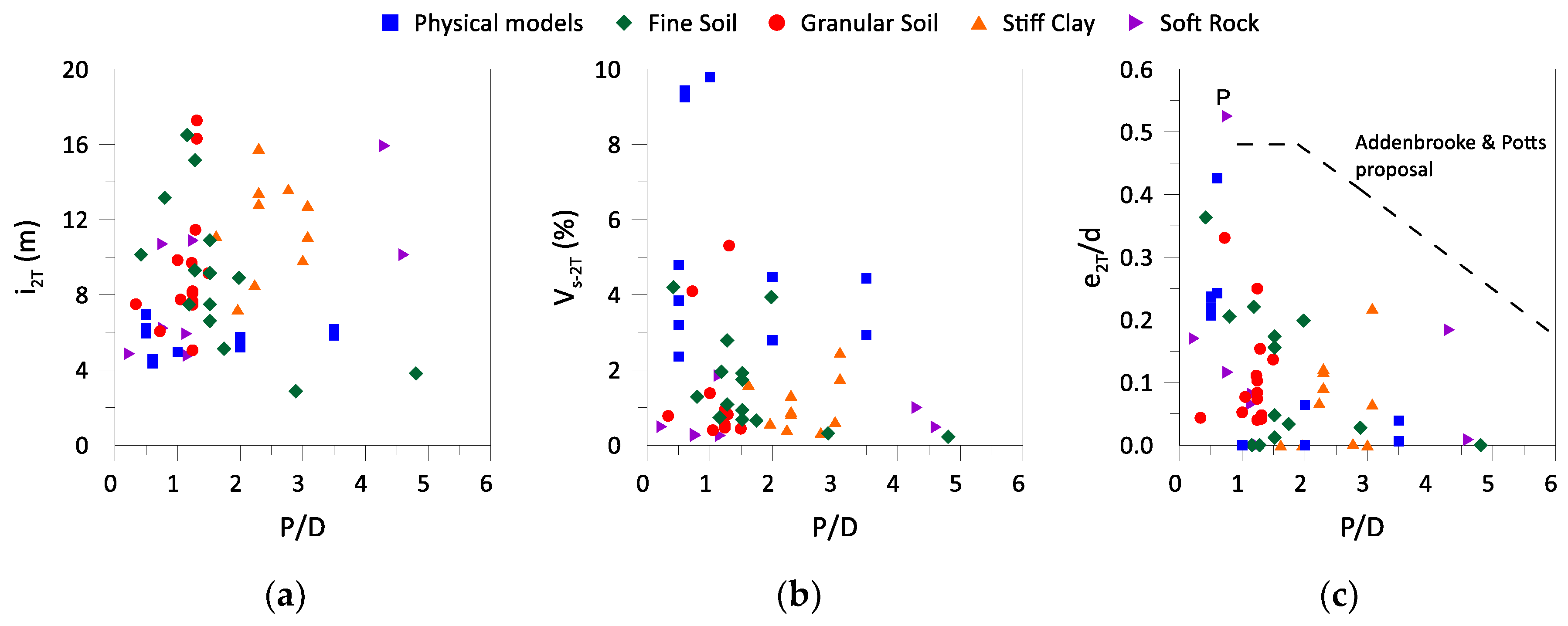
- The methods differ in how they account with the interaction effects: Addenbrooke and Potts [16] and Divall [43] suggest a correction for the volume loss (with an additional eccentricity correction in the case of the former); Hunt [39] and Zhou, et al. [38] propose the application of a corrective factor in the “overlapping zone” between both tunnels; and Ocak [37] suggests a correction factor applied to both the Gaussian parameters (maximum displacement and trough width);
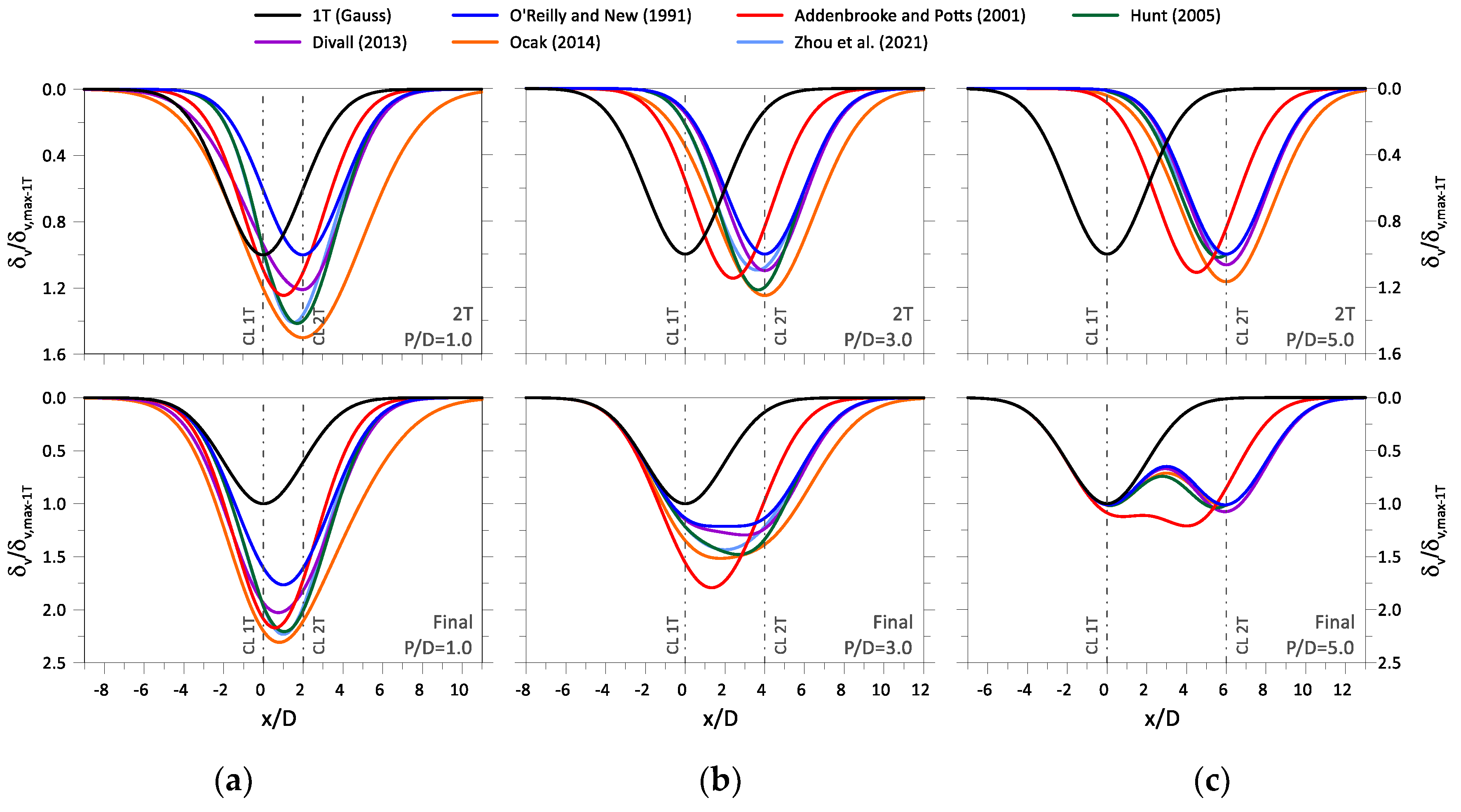
- The fitting of the monitoring data to the analyzed case studies confirmed that the settlements induced by the 1T are very adequately described by a Gaussian curve. However, for the settlements induced by the 2T a very good fit was only achieved if an eccentric Gaussian curve was considered. This confirms that the superposition method of two Gaussian curves is appropriate for predicting the settlements induced by twin tunnelling;
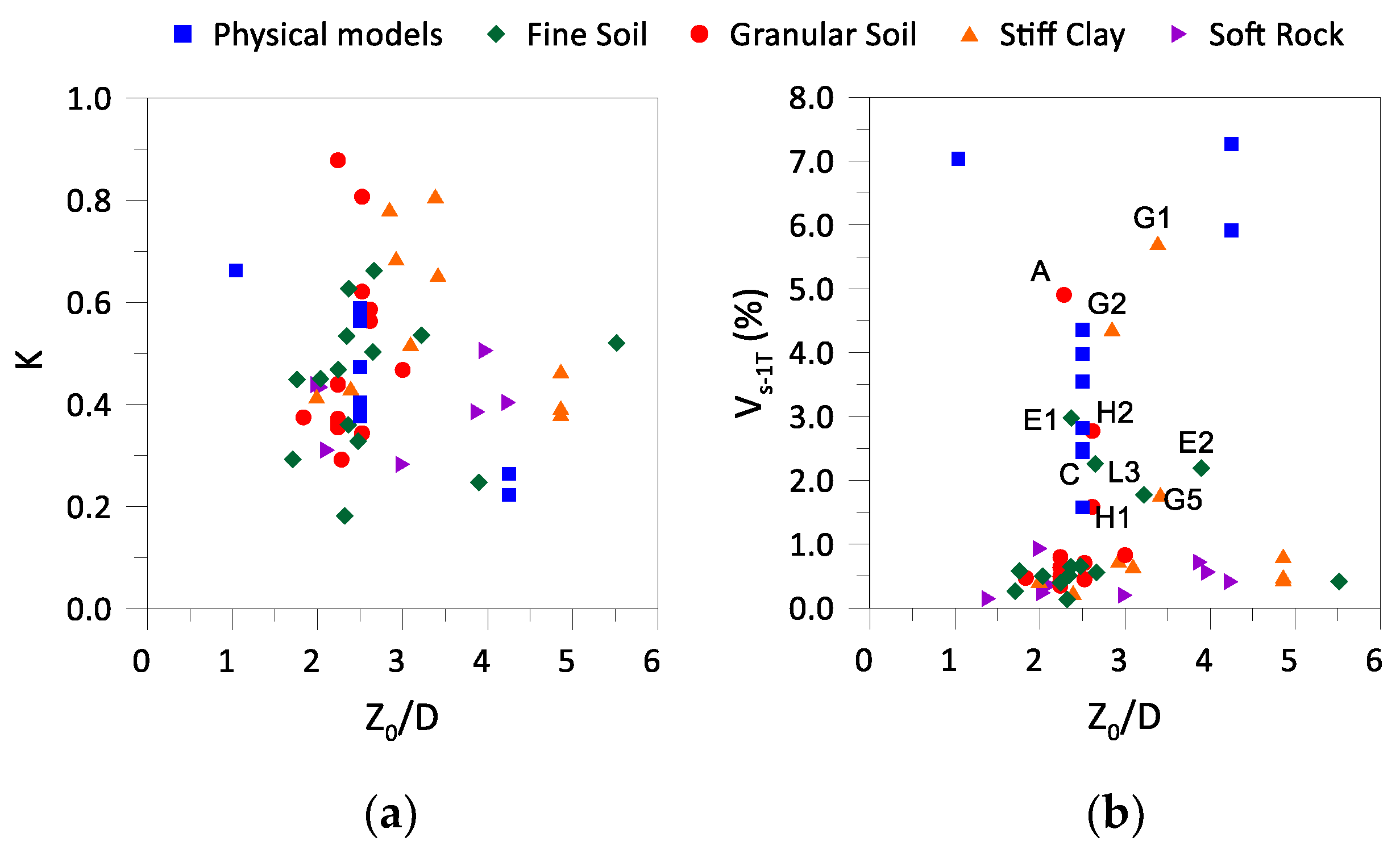
- Despite the very good fit the obtained Gaussian parameters exhibit significant scatter across all valid sections, and no clear trend was possible to establish in relation to either the soil type or the dimension of the pillar width;
- The application of the analytical methods to predict the monitoring data revealed that the Addenbrooke and Potts [16] proposal performs very poorly due to the application of the eccentricity correction, performing even worse than O'Reilly and New [36] method. The remaining methods predict the induced settlements of the 2T excavation with similar accuracy, with Hunt [39] proposal being slightly more reliable across all cases, and regardless of the soil type or the dimension of the pillar width;
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Code | Fitting of the 1T | K | Fitting of the 2T | e2T/d | Notes | ||||||||||
| (mm) | (m) | (%) | R2 | RMSE(mm) | e2T(m) | (mm) | (m) | (%) | R2 | RMSE(mm) | |||||
| A | -147.68 | 4.26 | 4.91 | 0.99 | 3.85 | 0.29 | -3.64 | -86.73 | 6.06 | 4.09 | 1.00 | 1.56 | 0.33 | 0.83 | (1) (15) |
| B | -18.63 | 4.92 | 0.93 | 0.93 | 1.48 | 0.44 | -0.79 | -30.69 | 5.93 | 1.85 | 0.98 | 1.31 | 0.07 | 1.99 | |
| C | -32.14 | 8.04 | 2.26 | 0.90 | 3.51 | 0.50 | -3.58 | -50.59 | 8.90 | 3.94 | 0.96 | 3.28 | 0.20 | 1.74 | |
| D1 | -4.30 | 9.86 | 0.56 | 0.89 | 0.61 | 0.51 | -4.79 | -4.72 | 15.93 | 1.00 | 0.96 | 0.27 | 0.18 | 1.77 | (3) |
| D2 | -3.69 | 8.40 | 0.41 | 0.97 | 0.21 | 0.40 | -0.24 | -3.56 | 10.13 | 0.48 | 0.98 | 0.18 | 0.01 | 1.16 | |
| E1 | -37.96 | 8.96 | 2.98 | 0.74 | 7.94 | 0.63 | -2.91 | -29.79 | 7.48 | 1.95 | 0.95 | 2.22 | 0.22 | 0.66 | (3) (15) |
| E2 | -50.39 | 6.80 | 2.19 | 0.97 | 2.94 | 0.25 | -3.63 | -64.73 | 10.13 | 4.20 | 0.98 | 3.47 | 0.36 | 1.92 | |
| F | -14.65 | 7.45 | 0.43 | 0.98 | 0.96 | 0.42 | 0.00 | -16.11 | 9.84 | 0.62 | 0.97 | 1.14 | 0.00 | 1.45 | (2) |
| G1 | -42.57 | 17.78 | 5.72 | 0.98 | 1.82 | 0.81 | 0.00 | -19.17 | 11.14 | 1.61 | 0.76 | 3.21 | 0.00 | 0.28 | (2) (5) (7)(15) |
| G2 | -39.99 | 14.47 | 4.37 | 0.92 | 3.86 | 0.78 | -4.37 | -25.63 | 12.76 | 2.47 | 0.95 | 2.16 | 0.22 | 0.56 | (8) (15) |
| G3 | -7.57 | 13.04 | 0.75 | 0.93 | 0.54 | 0.69 | -0.04 | -3.20 | 13.62 | 0.33 | 0.97 | 0.17 | 0.00 | 0.44 | (7) (15) |
| G4 | -8.37 | 10.43 | 0.66 | 0.97 | 0.50 | 0.52 | -0.98 | -6.36 | 8.53 | 0.41 | 0.99 | 0.16 | 0.07 | 0.62 | (8) (15) |
| G5 | -16.23 | 14.52 | 1.78 | 0.80 | 1.79 | 0.65 | -1.31 | -21.08 | 11.10 | 1.77 | 0.98 | 1.29 | 0.07 | 0.99 | (13) (15) |
| H1 | -21.06 | 9.96 | 1.58 | 0.89 | 2.50 | 0.59 | -0.63 | -40.67 | 17.27 | 5.31 | 0.94 | 2.25 | 0.04 | 3.35 | |
| H2 | -38.35 | 9.58 | 2.77 | 0.94 | 3.09 | 0.56 | -0.72 | -86.70 | 16.30 | 10.68 | 0.96 | 6.22 | 0.05 | 3.85 | (12) |
| I1 | -10.96 | 5.84 | 0.45 | 0.99 | 0.33 | 0.34 | -1.06 | -7.28 | 7.75 | 0.40 | 0.94 | 0.60 | 0.08 | 0.88 | (15) |
| I2 | -7.33 | 13.72 | 0.71 | 0.92 | 0.71 | 0.81 | -1.66 | -11.06 | 9.70 | 0.75 | 0.99 | 0.42 | 0.11 | 1.07 | |
| I3 | -6.13 | 10.56 | 0.45 | 1.00 | 0.13 | 0.62 | -2.37 | -10.13 | 11.46 | 0.82 | 0.99 | 0.31 | 0.15 | 1.79 | |
| J | -12.91 | 4.12 | 0.47 | 0.98 | 0.64 | 0.37 | -0.35 | -11.67 | 7.50 | 0.78 | 0.74 | 1.99 | 0.04 | 1.64 | (4) |
| K | -6.00 | 8.43 | 0.24 | 1.00 | 0.14 | 0.43 | 0.00 | -16.76 | 7.23 | 0.58 | 0.97 | 1.15 | 0.00 | 2.40 | (2) |
| L1 | -2.96 | 18.65 | 0.42 | 0.95 | 0.18 | 0.52 | 0.00 | -5.91 | 16.50 | 0.74 | 0.99 | 0.11 | 0.00 | 1.76 | (2) |
| L2 | -6.44 | 11.46 | 0.56 | 0.95 | 0.46 | 0.66 | 0.00 | -9.44 | 15.16 | 1.08 | 0.98 | 0.33 | 0.00 | 1.94 | (2) |
| L3 | -20.98 | 11.20 | 1.78 | 0.94 | 1.52 | 0.54 | 0.00 | -39.61 | 9.30 | 2.78 | 0.98 | 1.99 | 0.00 | 1.57 | (2) |
| M1 | -7.47 | 6.60 | 0.35 | 0.99 | 0.28 | 0.44 | -1.11 | -9.18 | 8.18 | 0.53 | 0.98 | 0.47 | 0.07 | 1.52 | |
| M2 | -20.65 | 5.44 | 0.80 | 0.99 | 0.60 | 0.36 | -3.75 | -8.46 | 7.66 | 0.46 | 0.94 | 0.69 | 0.25 | 0.58 | (9) (15) |
| M3 | -16.77 | 5.32 | 0.63 | 0.97 | 1.09 | 0.35 | -0.60 | -26.11 | 5.05 | 0.94 | 0.98 | 1.22 | 0.04 | 1.48 | |
| M4 | -8.78 | 6.58 | 0.41 | 0.98 | 0.49 | 0.44 | -1.54 | -9.24 | 7.47 | 0.49 | 0.97 | 0.55 | 0.10 | 1.19 | |
| M5 | -10.09 | 5.58 | 0.40 | 0.99 | 0.35 | 0.37 | -1.25 | -8.43 | 8.09 | 0.48 | 0.94 | 0.64 | 0.08 | 1.21 | |
| M6 | -5.28 | 13.17 | 0.49 | 0.96 | 0.34 | 0.88 | -2.28 | -6.69 | 9.15 | 0.44 | 0.99 | 0.19 | 0.14 | 0.88 | (11) (15) |
| N1 | -5.51 | 5.75 | 0.24 | 0.98 | 0.28 | 0.43 | -1.34 | -5.41 | 6.23 | 0.25 | 0.88 | 0.46 | 0.12 | 1.06 | |
| N2 | -11.13 | 4.27 | 0.36 | 0.85 | 1.60 | 0.31 | -1.36 | -13.35 | 4.86 | 0.49 | 0.99 | 0.45 | 0.17 | 1.36 | (5) |
| O1 | -8.03 | 16.05 | 0.82 | 0.96 | 0.50 | 0.47 | -1.50 | -13.27 | 15.79 | 1.33 | 0.99 | 0.39 | 0.09 | 1.62 | |
| O2 | -5.39 | 13.17 | 0.45 | 0.98 | 0.23 | 0.38 | -1.99 | -10.27 | 12.84 | 0.83 | 0.99 | 0.35 | 0.12 | 1.86 | |
| O3 | -5.74 | 13.58 | 0.49 | 0.99 | 0.16 | 0.39 | -1.91 | -10.50 | 13.44 | 0.89 | 1.00 | 0.22 | 0.12 | 1.81 | |
| P | -1.13 | 15.97 | 9.15 | 0.78 | 0.20 | 1.83 | -5.78 | -3.33 | 10.70 | 0.29 | 0.94 | 0.29 | 0.53 | 1.97 | (3) |
| Q | -9.03 | 8.99 | 0.72 | 0.92 | 0.81 | 0.39 | 0.00 | -9.15 | 10.89 | 0.88 | 0.81 | 1.33 | 0.00 | 1.23 | (2) (6) |
| R1 | -10.24 | 3.10 | 0.26 | 0.90 | 1.10 | 0.29 | -2.43 | -10.88 | 7.50 | 0.68 | 0.85 | 1.49 | 0.16 | 2.57 | (4) |
| R2 | -14.35 | 4.89 | 0.58 | 0.98 | 0.82 | 0.45 | -2.71 | -16.97 | 6.61 | 0.93 | 0.90 | 2.00 | 0.17 | 1.60 | |
| R3 | -10.56 | 5.68 | 0.50 | 0.94 | 1.02 | 0.45 | -0.57 | -15.37 | 5.13 | 0.65 | 0.96 | 1.09 | 0.03 | 1.32 | |
| R4 | -7.34 | 6.51 | 0.40 | 0.95 | 0.63 | 0.47 | -0.67 | -13.24 | 2.86 | 0.31 | 0.96 | 0.89 | 0.03 | 0.79 | (14) (15) |
| R5 | -6.19 | 2.62 | 0.13 | 0.91 | 0.64 | 0.18 | 0.00 | -6.95 | 3.81 | 0.22 | 0.97 | 0.46 | 0.00 | 1.63 | (2) |
| R6 | -15.69 | 5.04 | 0.66 | 0.94 | 1.66 | 0.33 | -0.19 | -19.19 | 10.90 | 1.74 | 0.96 | 1.33 | 0.01 | 2.65 | |
| R7 | -14.78 | 5.27 | 0.65 | 0.98 | 0.87 | 0.36 | -0.74 | -25.24 | 9.15 | 1.92 | 0.96 | 1.91 | 0.05 | 2.97 | |
| S1 | -4.43 | 5.09 | 0.20 | 0.94 | 0.29 | 0.28 | -1.06 | -6.03 | 4.77 | 0.25 | 0.90 | 0.64 | 0.08 | 1.27 | |
| S2 | -11.11 | 8.42 | 0.83 | 0.94 | 0.96 | 0.47 | -0.63 | -15.82 | 9.84 | 1.38 | 0.97 | 0.92 | 0.05 | 1.67 | |
| T | -11.27 | 11.00 | 0.51 | 0.95 | 0.89 | 0.53 | -3.24 | -23.69 | 13.16 | 1.28 | 0.97 | 1.34 | 0.21 | 2.51 | (10) |
| U1 | -24.17 | 5.85 | 2.82 | 0.88 | 3.08 | 0.58 | -1.42 | -26.18 | 6.12 | 3.19 | 0.96 | 1.75 | 0.24 | 1.13 | (16) |
| U2 | -21.23 | 5.88 | 2.49 | 0.94 | 1.71 | 0.59 | -0.77 | -26.81 | 5.21 | 2.79 | 0.98 | 1.20 | 0.06 | 1.12 | (16) |
| U3 | -21.74 | 5.64 | 2.45 | 0.91 | 2.25 | 0.56 | -0.70 | -23.84 | 6.17 | 2.93 | 0.95 | 1.87 | 0.04 | 1.20 | (16) |
| V1 | -81.15 | 4.49 | 7.27 | 0.96 | 5.42 | 0.26 | -2.73 | -106.56 | 4.36 | 9.26 | 0.97 | 6.13 | 0.43 | 1.27 | (16) |
| V2 | -78.30 | 3.79 | 5.92 | 0.99 | 2.92 | 0.22 | -1.55 | -103.18 | 4.58 | 9.43 | 0.99 | 3.22 | 0.24 | 1.59 | (16) |
| W | -200.03 | 4.29 | 7.04 | 1.00 | 2.50 | 0.66 | 0.00 | -241.69 | 4.94 | 9.79 | 0.97 | 14.12 | 0.00 | 1.39 | (2) (16) |
| X1 | -25.08 | 7.10 | 1.58 | 0.99 | 1.13 | 0.47 | -1.87 | -38.26 | 6.95 | 2.36 | 0.99 | 1.25 | 0.21 | 1.49 | (16) |
| X2 | -46.36 | 6.06 | 2.49 | 0.98 | 2.36 | 0.40 | -1.98 | -69.93 | 6.21 | 3.85 | 0.97 | 4.52 | 0.22 | 1.55 | (16) |
| X3 | -70.84 | 5.65 | 3.55 | 0.96 | 4.93 | 0.38 | -1.94 | -90.68 | 5.96 | 4.79 | 0.96 | 7.04 | 0.22 | 1.35 | (16) |
| X4 | -76.87 | 5.84 | 3.98 | 0.96 | 4.98 | 0.39 | 0.00 | -87.82 | 5.75 | 4.48 | 0.96 | 6.41 | 0.00 | 1.12 | (2) (16) |
| X5 | -85.20 | 5.77 | 4.36 | 0.97 | 4.70 | 0.38 | -0.16 | -85.83 | 5.83 | 4.43 | 0.96 | 5.64 | 0.01 | 1.02 | (2) (16) |
References
- Admiraal, H.; Cornaro, A. Why underground space should be included in urban planning policy – And how this will enhance an urban underground future. Tunnelling and Underground Space Technology 2016, 55, 214–220. [Google Scholar] [CrossRef]
- Bobylev, N. Underground space as an urban indicator: Measuring use of subsurface. Tunnelling and Underground Space Technology 2016, 55, 40–51. [Google Scholar] [CrossRef]
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunnelling and Underground Space Technology 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Divall, S.; Goodey, R.J. Twin-tunnelling-induced ground movements in clay. Proceedings of the Institution of Civil Engineers - Geotechnical Engineering 2015, 168, 247–256. [Google Scholar] [CrossRef]
- Islam, M.S.; Iskander, M. Twin tunnelling induced ground settlements: A review. Tunnelling and Underground Space Technology 2021, 110, 103614. [Google Scholar] [CrossRef]
- Burland, J.B.; Standing, J.R.; Jardine, F.M. Assessing the risk of damage due to tunneling - lessons from the Jubilee Line Extension, London. In Proceedings of the 14th South-East Asian Conference on Geotechnical Engineering, Hong Kong, 2001; pp. 17-44.
- Mair, R.J.; Taylor, R.N. Bored tunnelling in the urban environment. In Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering, State-of-the-art Report and Theme Lecture, Hamburg, 1997; pp. 2353-2385.
- Niu, G.; He, X.; Xu, H.; Dai, S. Tunnelling-induced ground surface settlement: A comprehensive review with particular attention to artificial intelligence technologies. Natural Hazards Research 2024, 4, 148–168. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavations and tunnelling in soft ground. In Proceedings of the 7th International conference on soil mechanics and foundations engineering, Mexico City, 1969; pp. 225-290.
- Cording, E.J.; Hansmire, W.H. Displacement around soft ground tunnels-General report. In Proceedings of the Proc. 5th Pan-American Conf. on Soil Mechanics and Foundation Engrg., Buenos Aires, 1975, 1975; pp. 571-632.
- Perez Saiz, R.; Garami, J.; Arcones, A.; Soriano, A. Experience gained through tunnel instrumentation. In Proceedings of the Proceedings of the Tenth International Conference on Soil Mechanics and Foundation Engineering, Stockholm., 1981.
- Fargnoli, V.; Boldini, D.; Amorosi, A. Twin tunnel excavation in coarse grained soils: Observations and numerical back-predictions under free field conditions and in presence of a surface structure. Tunnelling and Underground Space Technology 2015, 49, 454–469. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Describing Settlement Troughs over Twin Tunnels Using a Superposition Technique. Journal of Geotechnical and Geoenvironmental Engineering 2007, 133, 445–468. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Ranken, R.E. Interaction between two parallel tunnels. International Journal for Numerical and Analytical Methods in Geomechanics 1977, 1, 75–103. [Google Scholar] [CrossRef]
- Soliman, E.; Duddeck, H.; Ahrens, H. Two- and three-dimensional analysis of closely spaced double-tube tunnels. Tunnelling and Underground Space Technology 1993, 8, 13–18. [Google Scholar] [CrossRef]
- Addenbrooke, T.I.; Potts, D.M. Twin Tunnel Interaction: Surface and Subsurface Effects. International Journal of Geomechanics 2001, 1, 249–271. [Google Scholar] [CrossRef]
- Ng, C.W.; Lee, K.M.; Tang, D.K. Three-dimensional numerical investigations of new Austrian tunnelling method (NATM) twin tunnel interactions. Canadian Geotechnical Journal 2004, 41, 523–539. [Google Scholar] [CrossRef]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. Three-dimensional numerical simulation of a mechanized twin tunnels in soft ground. Tunnelling and Underground Space Technology 2014, 42, 40–51. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. 2D numerical investigations of twin tunnel interaction. Geomech Eng 2014, 6, 263–275. [Google Scholar] [CrossRef]
- Liu, H.Y.; Small, J.C.; Carter, J.P. Full 3D modelling for effects of tunnelling on existing support systems in the Sydney region. Tunnelling and Underground Space Technology 2008, 23, 399–420. [Google Scholar] [CrossRef]
- Nematollahi, M.; Dias, D. Three-dimensional numerical simulation of pile-twin tunnels interaction – Case of the Shiraz subway line. Tunnelling and Underground Space Technology 2019, 86, 75–88. [Google Scholar] [CrossRef]
- Chapman, D.N.; Rogers, C.D.F.; Hunt, D.V.L. Predicting the Settlements above Twin Tunnels Constructed in Soft Ground. In Proceedings of the 30th ITA-AITES world tunnel congess; 2002; p. 8. [Google Scholar]
- Pedro, A.M.G.; Cancela, T.; Almeida e Sousa, J.; Grazina, J. Deformations caused by the excavation of twin tunnels. In Proceedings of the 9th Int. Symp. on Geot. Aspects of Underground Const. in Soft Ground, Sao Paulo, Brazil, 2017; pp. 203-213.
- Miliziano, S.; Caponi, S.; Carlaccini, D.; de Lillis, A. Prediction of tunnelling-induced effects on a historic building in Rome. Tunnelling and Underground Space Technology 2022, 119, 104212. [Google Scholar] [CrossRef]
- Chapman, D.N.; Ahn, S.K.; Hunt, D.V. Investigating ground movements caused by the construction of multiple tunnels in soft ground using laboratory model tests. Canadian Geotechnical Journal 2007, 44, 631–643. [Google Scholar] [CrossRef]
- Divall, S.; Goodey, R.J.; Taylor, R.N. Ground movements generated by sequential twin-tunnelling in over-consolidated clay. In Proceedings of the 2nd European Conference on Physical Modelling in Geotechnics, Delft, Netherlands, 2012; p. 10.
- He, C.; Feng, K.; Fang, Y.; Jiang, Y.-c. Surface settlement caused by twin-parallel shield tunnelling in sandy cobble strata. Journal of Zhejiang University SCIENCE A 2012, 13, 858–869. [Google Scholar] [CrossRef]
- Zheng, G.; Tong, J.; Zhang, T.; Wang, R.; Fan, Q.; Sun, J.; Diao, Y. Experimental study on surface settlements induced by sequential excavation of two parallel tunnels in drained granular soil. Tunnelling and Underground Space Technology 2020, 98, 103347. [Google Scholar] [CrossRef]
- Vlachopoulos, N.; Vazaios, I.; Madjdabadi, B.M. Investigation into the influence of excavation of twin-bored tunnels within weak rock masses adjacent to slopes. Canadian Geotechnical Journal 2018, 55, 1533–1551. [Google Scholar] [CrossRef]
- Pedro, A.; Grazina, J.; Almeida e Sousa, J. Lining forces in tunnel interaction problems. Soils and Rocks 2022, 45, 1–12. [Google Scholar] [CrossRef]
- Shivaei, S.; Hataf, N.; Pirastehfar, K. 3D numerical investigation of the coupled interaction behavior between mechanized twin tunnels and groundwater – A case study: Shiraz metro line 2. Tunnelling and Underground Space Technology 2020, 103, 103458. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Kumar, J. Required Lining Pressure for the Stability of Twin Circular Tunnels in Soils. International Journal of Geomechanics 2018, 18, 04018069. [Google Scholar] [CrossRef]
- Yang, F.; Zheng, X.; Zhang, J.; Yang, J. Upper bound analysis of stability of dual circular tunnels subjected to surcharge loading in cohesive-frictional soils. Tunnelling and Underground Space Technology 2017, 61, 150–160. [Google Scholar] [CrossRef]
- Pedro, A.M.G.; Grazina, J.C.; Almeida e Sousa, J. Stress redistribution in the central pillar between twin tunnels. In Proceedings of the NUMGE18, Porto, Portugal, 2018; pp. 1309-1317.
- Zhang, T.; Taylor, R.N.; Divall, S.; Zheng, G.; Sun, J.; Stallebrass, S.E.; Goodey, R.J. Explanation for twin tunnelling-induced surface settlements by changes in soil stiffness on account of stress history. Tunnelling and Underground Space Technology 2019, 85, 160–169. [Google Scholar] [CrossRef]
- O'Reilly, M.P.; New, B.M. Settlements above tunnel in the United Kingdom - their magnitude and prediction. In Proceedings of the Conference Tunnelling ’82, London, 1982; pp. 173 -181.
- Ocak, I. A new approach for estimating the transverse surface settlement curve for twin tunnels in shallow and soft soils. Environmental Earth Sciences 2014, 72, 2357–2367. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, H.; Miao, L.; Gong, C. Predictive model for the surface settlement caused by the excavation of twin tunnels. Tunnelling and Underground Space Technology 2021, 114, 104014. [Google Scholar] [CrossRef]
- Hunt, D.V.L. Predicting the ground movements above twin tunnels constructed in London Clay. PhD thesis, University of Birmingham, Birmingham, 2005.
- Dong, C.; Lin, J.; Cao, G.; Cheng, H.; Shi, L.; Zhang, X. Analytical Study on Surface Settlement Troughs Induced by the Sequential Excavation of Adjacent and Parallel Tunnels in Layered Soils. Advances in Civil Engineering 2022, 2022, 2489711. [Google Scholar] [CrossRef]
- Mooney, M.; Grasmick, J.; Clemmensen, A.; Thompson, A.; Prantil, E.; Robinson, B. Ground deformation from multiple tunnel openings: analysis of Queens Bored Tunnels. Proc. North American Tunneling, Los Angeles, CA 2014.
- Pedro, A.M.G.; Grazina, J.C.D.; Sousa, J.A.e. Influence of the pillar width on the construction sequence of twin tunnels. In Proceedings of the NUMGE23 - 10th European Conference on Numerical Methods in Geotechnical Engineering, London, UK, 2023.
- Divall, S. Ground movements associated with twin-tunnel construction in clay. PhD thesis, City University London, London, 2013.
- Wan, M.S.P.; Standing, J.R.; Potts, D.M.; Burland, J.B. Measured short-term ground surface response to EPBM tunnelling in London Clay. Géotechnique 2017, 67, 420–445. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Hwang, R.N.; Lai, W.-J. Surface settlement during shield tunnelling at CH218 in Taipei. Canadian Geotechnical Journal 1998, 35, 159–168. [Google Scholar] [CrossRef]
- Withers, A.D. Chapter 37 - Surface displacements at three surface reference sites above twin tunnels through the Lambeth Group. In Building response to tunnelling; 2001; pp. 735-754.
- Wu, B.R.; Lee, C.J. Ground movements and collapse mechanisms induced by tunneling in clayey soil. International Journal of Physical Modelling in Geotechnics 2003, 3, 15–29. [Google Scholar] [CrossRef]
- Clayton, C.; Van Der Berg, J.; Thomas, A. Monitoring and displacements at Heathrow Express Terminal 4 station tunnels. Géotechnique 2006, 56, 323–334. [Google Scholar] [CrossRef]
- Mahmutoğlu, Y. Surface subsidence induced by twin subway tunnelling in soft ground conditions in Istanbul. Bulletin of Engineering Geology and the Environment 2011, 70, 115–131. [Google Scholar] [CrossRef]
- Bilotta, E.; Russo, G. Ground movements induced by tunnel boring in Naples. In Proceedings of the 2012 Proceedings of the 7th international symposium on geotechnical aspects of underground construction in soft ground, London, 2012.
- Standing, J.R.; Selemetas, D. Greenfield ground response to EPBM tunnelling in London Clay. Géotechnique 2013, 63, 989–1007. [Google Scholar] [CrossRef]
- Elwood, D.E.Y.; Martin, C.D. Ground response of closely spaced twin tunnels constructed in heavily overconsolidated soils. Tunnelling and Underground Space Technology 2016, 51, 226–237. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, C.; Liu, X.; Fan, Y.; Liang, N. Analysis of ground surface settlement induced by the construction of mechanized twin tunnels in soil-rock mass mixed ground. Tunnelling and Underground Space Technology 2021, 110, 103746. [Google Scholar] [CrossRef]
- Kannangara, K.K.P.M.; Ding, Z.; Zhou, W.-H. Surface settlements induced by twin tunneling in silty sand. Underground Space 2022, 7, 58–75. [Google Scholar] [CrossRef]
- Hu, Y.; Tang, H.; Xu, Y.; Lei, H.; Zeng, P.; Yao, K.; Dong, Y. Ground settlement and tunnel response due to twin-curved shield tunnelling in soft ground with small clear distance. Journal of Rock Mechanics and Geotechnical Engineering 2024, 16, 3122–3135. [Google Scholar] [CrossRef]
- Divall, S.; Goodey, R.J.; Stallebrass, S.E. Twin-tunnelling-induced changes to clay stiffness. Géotechnique 2017, 67, 906–913. [Google Scholar] [CrossRef]
- Chen, S.L.; Gui, M.W.; Yang, M.C. Applicability of the principle of superposition in estimating ground surface settlement of twin- and quadruple-tube tunnels. Tunnelling and Underground Space Technology 2012, 28, 135–149. [Google Scholar] [CrossRef]
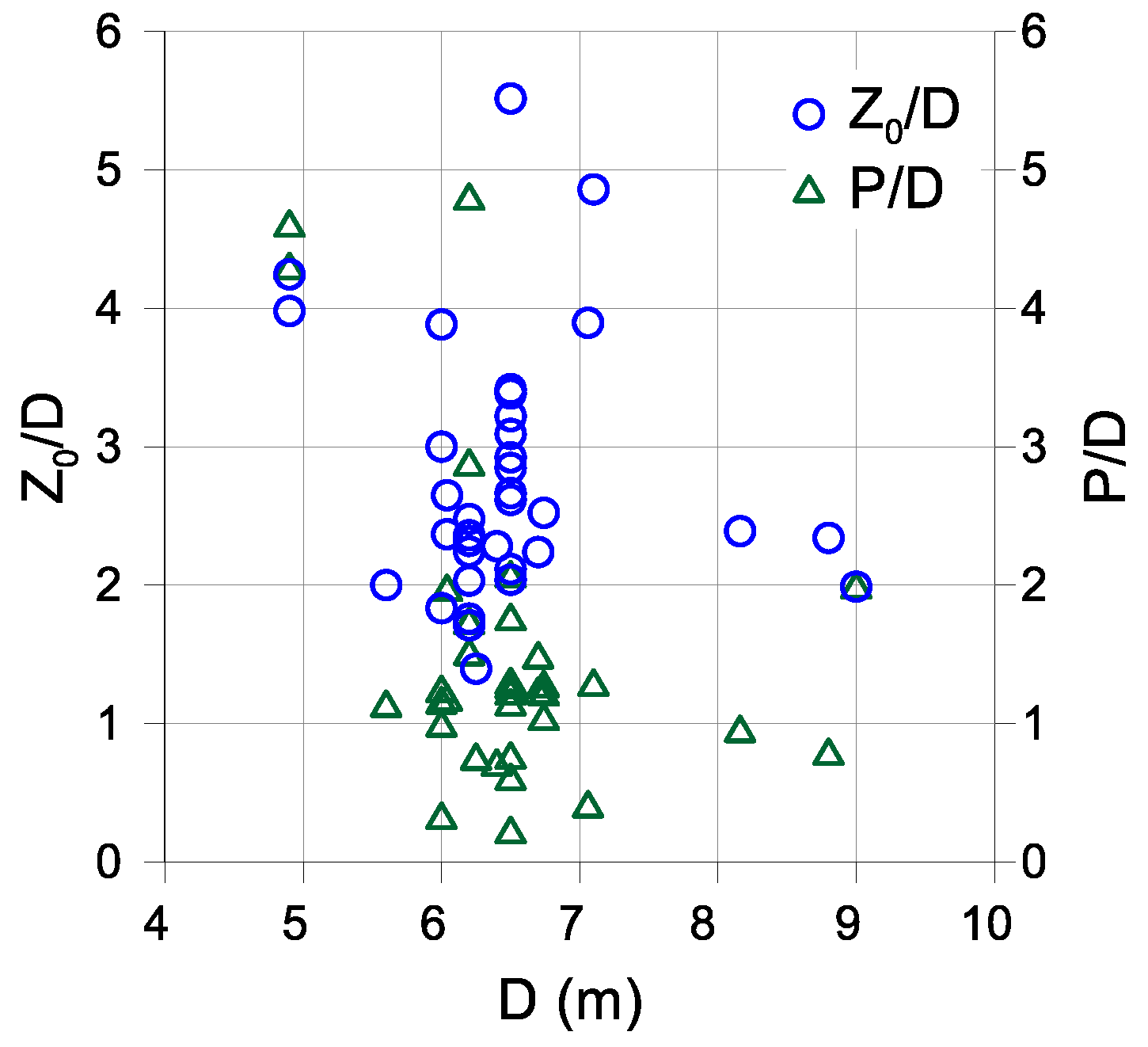
| Source | Project | Excavation method | Ground$$$conditions | Section | Code | D (m) | Z0 (m) | d (m) | P (m) |
|---|---|---|---|---|---|---|---|---|---|
| Cording and Hansmire [10] | Washington D. C. Metro | Shield$$$machine | Sand; gravel | C | A | 6.40 | 14.60 | 11.00 | 4.60 |
| Perez Saiz, et al. [11] | Caracas Metro | EPB | Soft rock | S-IV | B | 5.60 | 11.20 | 12.00 | 6.40 |
| Ou, et al. [45] | Taipei RTR | EPB | Silty sand/clay | CH218 A-A | C | 6.04 | 16.00 | 18.00 | 11.96 |
| Withers [46] | London Metro, Jubilee Line | EPB | Lambeth group | Old Jamaica R. | D1 | 4.90 | 19.50 | 26.00 | 21.10 |
| Southwark P. | D2 | 4.90 | 20.80 | 27.50 | 22.60 | ||||
| Wu and Lee [47] | Taipei RTR | EPB | Silty sand/clay | CN254 S2 | E1 | 6.04 | 14.30 | 13.20 | 7.16 |
| Japan Subway | Open shield | Clay | B-1 | E2 | 7.06 | 27.50 | 10.00 | 2.94 | |
| Clayton, et al. [48] | Heathrow E. T4 | Sequential | London Clay | MMS II | F | 9.00 | 17.90 | 27.00 | 18.00 |
| Suwansawat and Einstein [13] | Bangkok MRTA | EPB | Stiff clay | S-A 23-AR-001 | G1 | 6.50 | 22.00 | 10.50 | 4.00 |
| S-B 26-AR-001 | G2 | 6.50 | 18.50 | 20.00 | 13.50 | ||||
| S-C CS-8B | G3 | 6.50 | 19.00 | 18.00 | 11.50 | ||||
| S-C CS-8D | G4 | 6.50 | 20.10 | 14.50 | 8.00 | ||||
| S-D SS-5T-52e | G5 | 6.50 | 22.20 | 20.00 | 13.50 | ||||
| Mahmutoğlu [49] | Istanbul Subway | EPB | Dense sand | S-3a | H1 | 6.50 | 17.00 | 15.00 | 8.50 |
| S-3b | H2 | 6.50 | 17.00 | 15.00 | 8.50 | ||||
| Bilotta and Russo [50] | Naples Metro | EPB | Sand | S-1 | I1 | 6.74 | 17.00 | 13.80 | 7.06 |
| S-2 | I2 | 6.74 | 17.00 | 15.00 | 8.26 | ||||
| S-3 | I3 | 6.74 | 17.00 | 15.40 | 8.66 | ||||
| He, et al. [27] | Chengdu Metro | EPB | Sandy cobble | - | J | 6.00 | 11.00 | 8.00 | 2.00 |
| Standing and Selemetas [51] | Channel Tunnel Rail Link | EPB | London Clay | C250 | K | 8.16 | 19.50 | 16.00 | 7.84 |
| Ocak [37] | Istanbul Subway | EPB | Clay | S-4 | L1 | 6.50 | 35.85 | 14.00 | 7.50 |
| S-5 | L2 | 6.50 | 17.32 | 14.80 | 8.30 | ||||
| S-8 | L3 | 6.50 | 20.93 | 14.80 | 8.30 | ||||
| Fargnoli, et al. [12]l | Milan Metro | EPB | Gravelly-sand | S-2 | M1 | 6.70 | 15.00 | 15.00 | 8.30 |
| S-5 | M2 | 6.70 | 15.00 | 15.00 | 8.30 | ||||
| S-13 | M3 | 6.70 | 15.00 | 15.00 | 8.30 | ||||
| S-16 | M4 | 6.70 | 15.00 | 15.00 | 8.30 | ||||
| S-19 | M5 | 6.70 | 15.00 | 15.00 | 8.30 | ||||
| S-35 | M6 | 6.70 | 15.00 | 16.70 | 10.00 | ||||
| Elwood and Martin [52] | Edmonton Light Rail | Sequential | Glacial Till | S-C | N1 | 6.50 | 13.25 | 11.50 | 5.00 |
| S-E | N2 | 6.50 | 13.75 | 8.00 | 1.50 | ||||
| Wan, et al. [44] | Crossrail | EPB | London Clay | x-line | O1 | 7.10 | 34.50 | 16.30 | 9.20 |
| y-line | O2 | 7.10 | 34.50 | 16.30 | 9.20 | ||||
| Extensometer | O3 | 7.10 | 34.50 | 16.30 | 9.20 | ||||
| Zhong, et al. [53] | Chongqing Metro | EPB | Silty mudstone | Fengzhong R. | P | 6.25 | 8.73 | 11.00 | 4.75 |
| Zhou, et al. [38] | Changsha Metro | EPB | Arg. siltstone | - | Q | 6.00 | 23.30 | 13.50 | 7.50 |
| Kannangara, et al. [54] | Hangzhou Metro | EPB | Silty sand | DBC7 | R1 | 6.20 | 10.60 | 15.60 | 9.40 |
| DBC9 | R2 | 6.20 | 10.90 | 15.60 | 9.40 | ||||
| DBC11 | R3 | 6.20 | 12.60 | 17.00 | 10.80 | ||||
| DBC13 | R4 | 6.20 | 13.90 | 24.10 | 17.90 | ||||
| DBC15 | R5 | 6.20 | 14.38 | 36.00 | 29.80 | ||||
| DBC35 | R6 | 6.20 | 15.36 | 15.60 | 9.40 | ||||
| DBC36 | R7 | 6.20 | 14.63 | 15.60 | 9.40 | ||||
| Dong, et al. [40] | Changsha Metro | EPB | Arg. siltstone | Case 1 | S1 | 6.00 | 18.00 | 13.00 | 7.00 |
| Shenyang Utility | EPB | Gravelly sand | Case 2 | S2 | 6.00 | 18.00 | 12.00 | 6.00 | |
| Hu, et al. [55] | Tianjin Metro | EPB | Silty clay | S-A-A | T | 8.80 | 20.60 | 15.80 | 7.00 |
| Source | Physical model | Excavation method | Soil | Test | Code | D (m) | Z0 (m) | d (m) | P (m) |
|---|---|---|---|---|---|---|---|---|---|
| Divall, et al. [56] | Centrifuge (100g) | Support fluid | Speswhite kaolin clay | 1 | U1 | 4.00 | 10.00 | 6.00 | 2.00 |
| 2 | U2 | 4.00 | 10.00 | 12.00 | 8.00 | ||||
| 3 | U3 | 4.00 | 10.00 | 18.00 | 14.00 | ||||
| Chapman, et al. [25] | Small-scale (1/50) | Auger type cutter | Speswhite kaolin clay | A | V1 | 0.08 | 0.34 | 0.13 | 0.05 |
| B | V2 | 0.08 | 0.34 | 0.13 | 0.05 | ||||
| He, et al. [27] | Small-scale (1/12) | EPB prototype | Synthetic | S-2 | W | 0.52 | 0.54 | 1.04 | 0.52 |
| Zheng, et al. [28] | Small-scale (1/60) | Shrinking tunnel | Sand | T1 | X1 | 0.10 | 0.25 | 0.15 | 0.05 |
| T2 | X2 | 0.10 | 0.25 | 0.15 | 0.05 | ||||
| T3 | X3 | 0.10 | 0.25 | 0.15 | 0.05 | ||||
| T4 | X4 | 0.10 | 0.25 | 0.30 | 0.20 | ||||
| T5 | X5 | 0.10 | 0.25 | 0.45 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).