Submitted:
17 December 2024
Posted:
19 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Formalism: Structure Equations and Tidal Deformability
2.1. Hydrostatic Equilibrium
2.2. Gravito-Electric Tidal Love Numbers
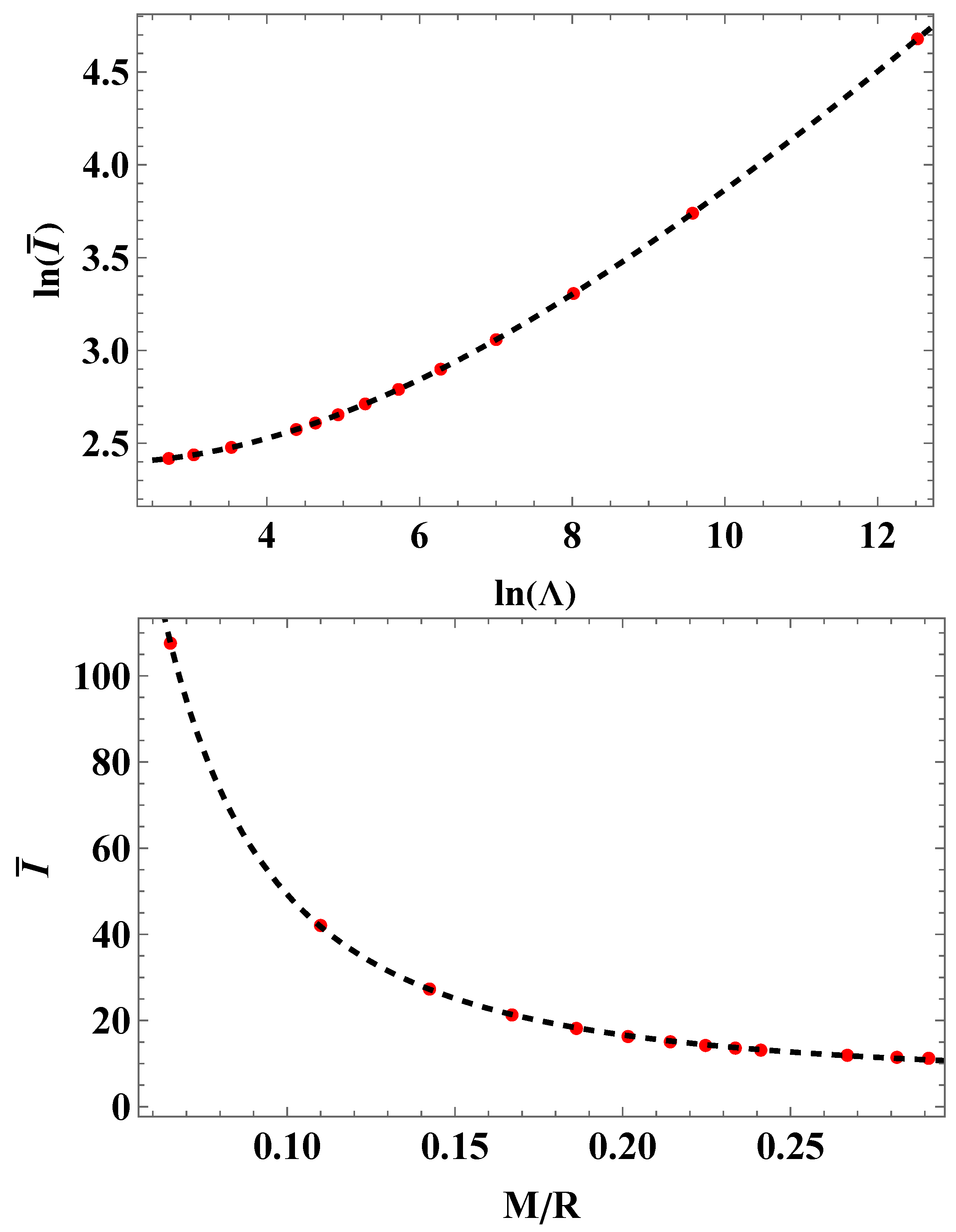
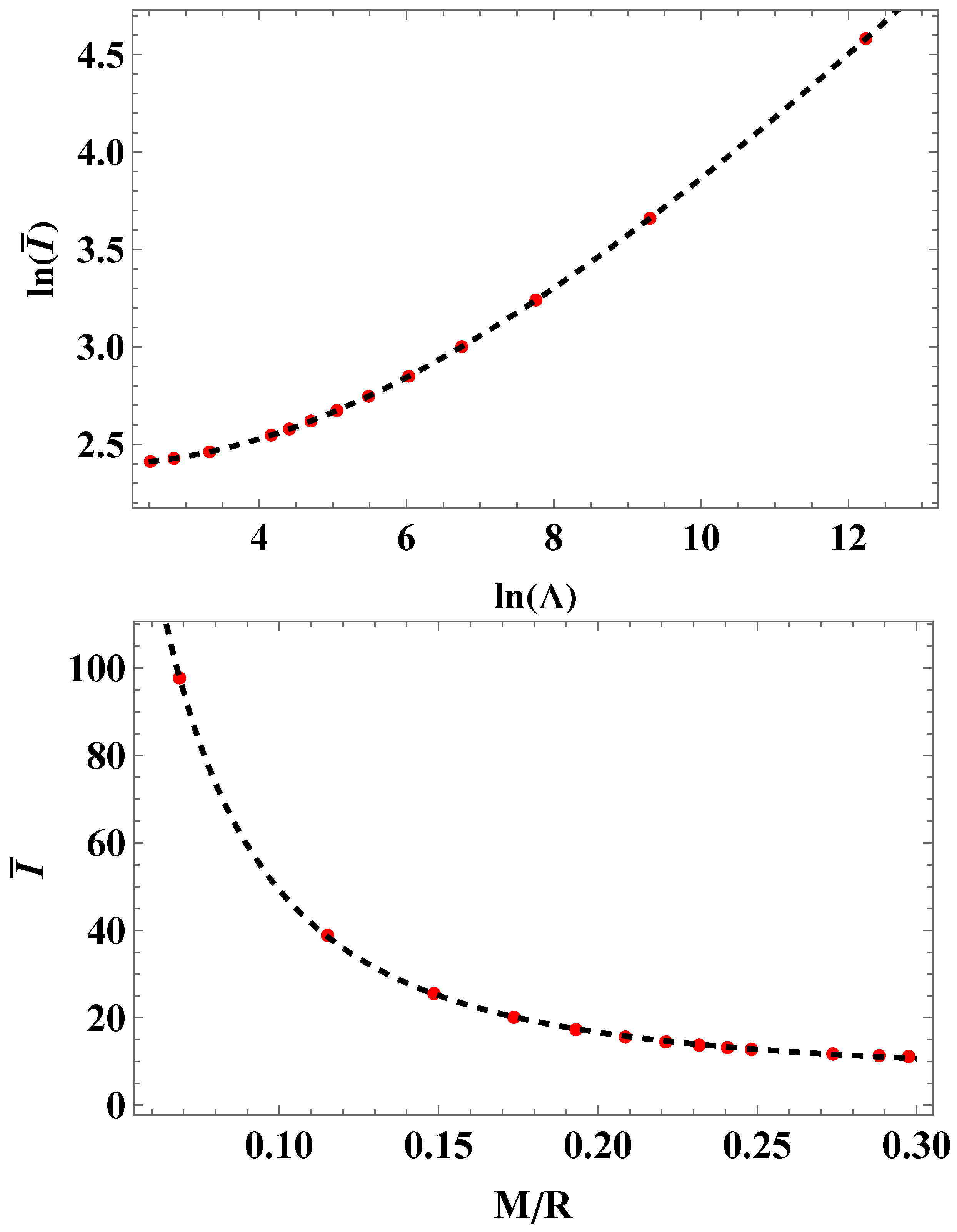
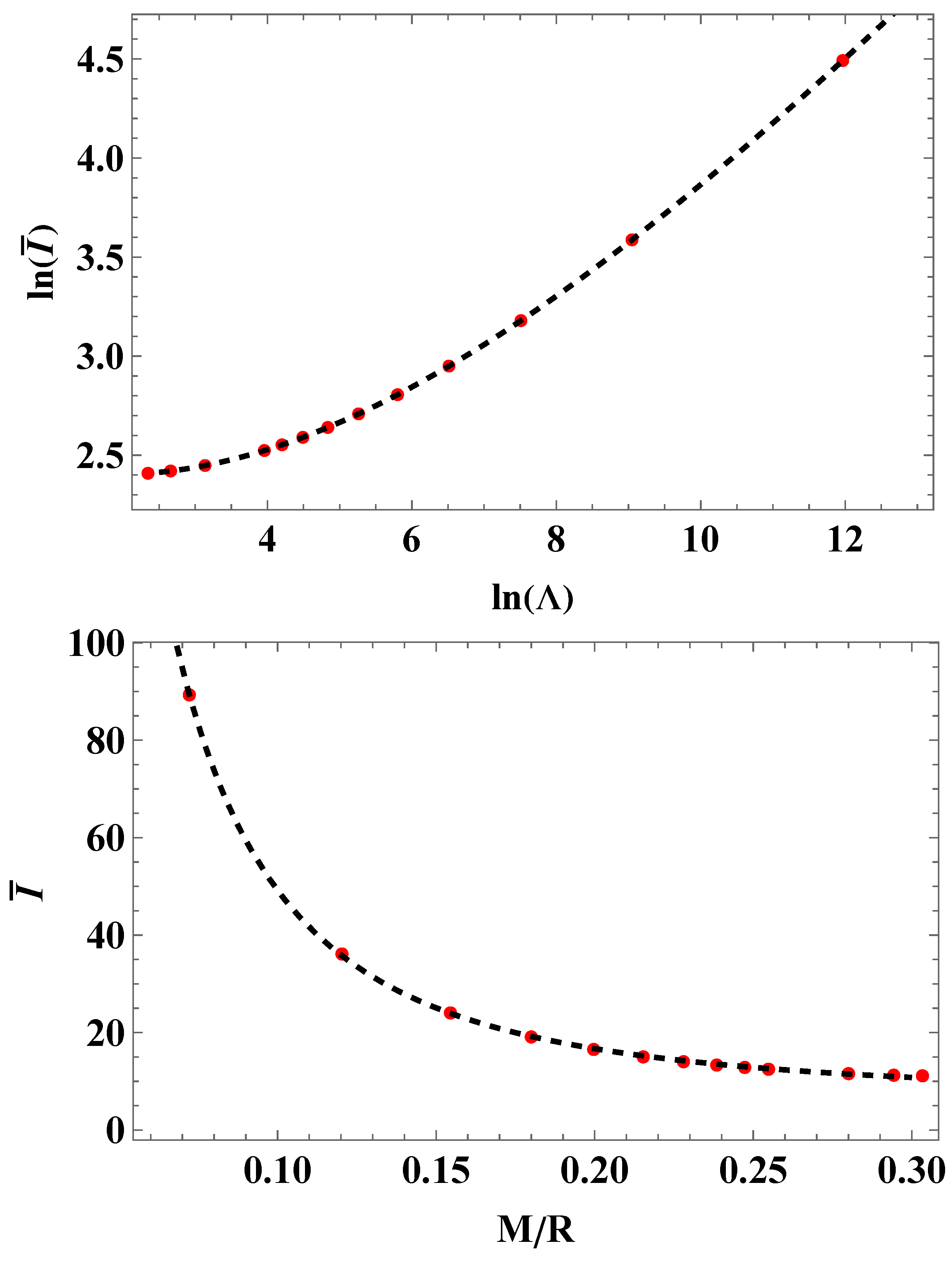
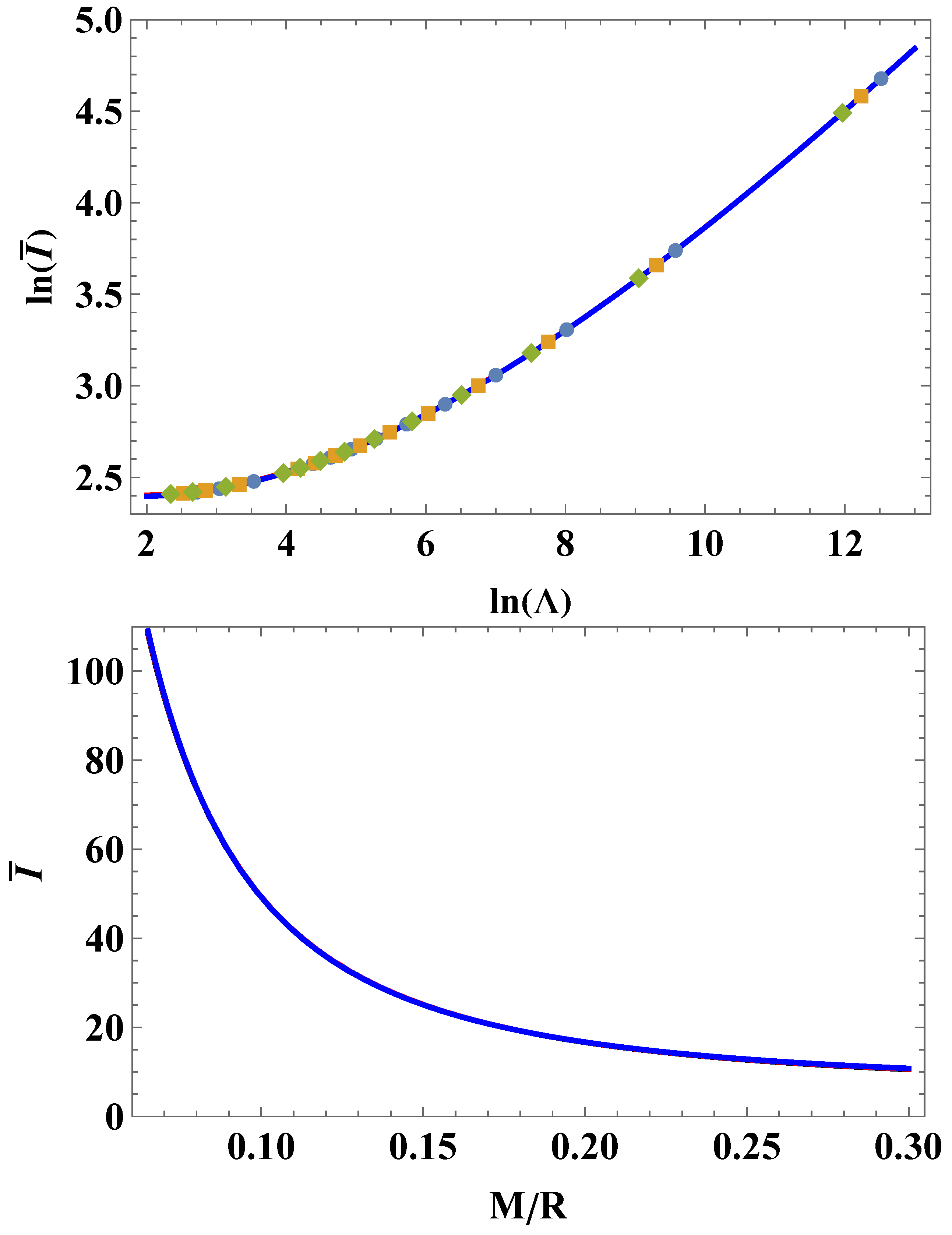
3. Numerical Analysis and Main Results
| Model | A | B |
| 1 | 0.23 × 0.001 km−2 | |
| 2 | 0.215 × 0.001 km−2 | |
| 3 | 0.2 × 0.001 km−2 |
| Coefficient | a | b | c | d | e |
| Model 1 | 2.506 | -0.124 | 0.037 | -0.0013 | |
| Model 2 | 2.515 | -0.128 | 0.038 | -0.0013 | |
| Model 3 | 2.522 | -0.131 | 0.038 | -0.0014 |
4. Discussion and Summary
References
- S. L. Shapiro and S. A. Teukolsky. Black holes, white dwarfs, and neutron stars: The physics of compact objects. [CrossRef]
- J. Schaffner-Bielich, Compact Star Physics, Cambridge University Press, 2020, ISBN 978-1-316-84835-7, 978-1- 107-18089-5.
- J. Chadwick, Nature 129, 312 (1932).
- J. Chadwick, Proc. Roy. Soc. Lond. A 136, no.830, 692-708 (1932).
- W. Baade and F. Zwicky, Phys. Rev. 46, no. 1934.
- A. Hewish, S. J. A. Hewish, S. J. Bell, J. D. H. Pilkington, P. F. Scott and R. A. Collins, Nature 217, 709-713 (1968). [CrossRef]
- S. Safi-Harb, J. Phys. Conf. Ser. 932, 012005 (2017) [arXiv:1712.06040 [astro-ph.HE]]. [CrossRef]
- J. M. Lattimer and M. Prakash, Science 304, 536-542 (2004) [arXiv:astro-ph/0405262 [astro-ph]]. [CrossRef]
- P. Haensel, J. L. Zdunik and R. Schaeffer, Astron. Astrophys. 160 (1986), 121-128.
- N. Itoh, Prog. Theor. Phys. 44 (1970), 291. [CrossRef]
- J. C. Collins and M. J. Perry, Phys. Rev. Lett. 34 (1975), 1353. [CrossRef]
- J. Madsen, Lect. Notes Phys. 516 (1999), 162-203 [arXiv:astro-ph/9809032 [astro-ph]]. [CrossRef]
- E. Witten, Phys. Rev. D 30, 272-285 (1984). [CrossRef]
- E. Farhi and R. L. Jaffe, Phys. Rev. D 30 (1984), 2379. [CrossRef]
- E. O. Ofek, P. B. Cameron, M. M. Kasliwal, A. Gal-Yam, A. Rau, S. R. Kulkarni, D. A. Frail, P. Chandra, S. B. Cenko and A. M. Soderberg, et al. Astrophys. J. Lett. 659 (2007), L13-L16 [arXiv:astro-ph/0612408 [astro-ph]]. [CrossRef]
- R. Ouyed, D. Leahy and P. Jaikumar, [arXiv:0911.5424 [astro-ph.HE]]. [CrossRef]
- J. A. Henderson and D. Page, Astrophys. Space Sci. 308 (2007), 513-517 [arXiv:astro-ph/0702234 [astro-ph]]. [CrossRef]
- A. Li, G. X. Peng and J. F. Lu, Res. Astron. Astrophys. 11 (2011), 482-490.
- A. Aziz, S. A. Aziz, S. Ray, F. Rahaman, M. Khlopov and B. K. Guha, Int. J. Mod. Phys. D 28 (2019) no. 1941; arXiv:1906.00063 [gr-qc]]. [Google Scholar] [CrossRef]
- F. Weber, Prog. Part. Nucl. Phys. 54 (2005), 193-288 [arXiv:astro-ph/0407155 [astro-ph]]. [CrossRef]
- N. Aghanim et al. [Planck], Astron. Astrophys. 641 (2020), A6 [erratum: Astron. Astrophys. 2021; arXiv:1807.06209 [astro-ph.CO]]. [CrossRef]
- A. G. Riess et al. [Supernova Search Team], Astron. J. 116 (1998), 1009-1038 [arXiv:astro-ph/9805201 [astro-ph]]. [CrossRef]
- S. Perlmutter et al. [Supernova Cosmology Project], Astrophys. J. 517 (1999), 565-586 [arXiv:astro-ph/9812133 [astro-ph]]. [CrossRef]
- W. L. Freedman and M. S. Turner, Rev. Mod. Phys. 75 (2003), 1433-1447 [arXiv:astro-ph/0308418 [astro-ph]]. [CrossRef]
- K. Newton Singh, A. K. Newton Singh, A. Ali, F. Rahaman and S. Nasri, Phys. Dark Univ. 1005; 29, arXiv:2005.00540 [gr-qc]]. [Google Scholar] [CrossRef]
- F. Tello-Ortiz, M. F. Tello-Ortiz, M. Malaver, Á. Rincón and Y. Gomez-Leyton, Eur. Phys. J. C 80, no. 2020; arXiv:2005.11038 [gr-qc]]. [Google Scholar] [CrossRef]
- G. Panotopoulos, Á. Rincón and I. Lopes, Eur. Phys. J. Plus 135, no. 2020; arXiv:2010.09373 [gr-qc]]. [CrossRef]
- G. Panotopoulos, Á. Rincón and I. Lopes, Phys. Dark Univ. 1008; 34, arXiv:2109.05619 [gr-qc]]. [CrossRef]
- B. Pourhassan and E. O. Kahya, Results Phys. 4 (2014), 101-102. [CrossRef]
- B. Pourhassan and E. O. Kahya, Adv. High Energy Phys. 2014; arXiv:1405.0667 [gr-qc]]. [CrossRef]
- A. Y. Kamenshchik, U. A. Y. Kamenshchik, U. Moschella and V. Pasquier, Phys. Lett. B 511, 265-268 (2001) [arXiv:gr-qc/0103004 [gr-qc]]. [CrossRef]
- M. C. Bento, O. M. C. Bento, O. Bertolami and A. A. Sen, Phys. Rev. D 66, 043507 (2002) [arXiv:gr-qc/0202064 [gr-qc]]. [CrossRef]
- A. E. H. Love, Proc. R. Soc. A 82, 73 (1909).
- A. E. H. Love, Some problems of geodynamics (Cornell University Library, Ithaca, USA, 1911).
- E. E. Flanagan and T. Hinderer, Phys. Rev. D 77, 021502(R) (2008); arXiv:0709.1915 [astro-ph]. [CrossRef]
- T. Hinderer, Astrophys. J. 677, 1216 (2008); arXiv:0711.2420 [astro-ph]. [CrossRef]
- T. Damour and A. Nagar, Phys. Rev. D 80, 084035 (2009); arXiv:10.48550/arXiv. [gr-qc]. [CrossRef]
- S. Postnikov, M. Prakash and J. M. Lattimer, Phys. Rev. D 82, 024016 (2010). arXiv:1004.5098 [astro-ph.SR]. [CrossRef]
- T. Binnington and E. Poisson, Phys. Rev. D 80, 084018 (2009). arXiv:0906.1366 [gr-qc]. [CrossRef]
- S. DeDeo and D. Psaltis, Phys. Rev. Lett. 90, 141101 (2003) [arXiv:astro-ph/0302095 [astro-ph]]. [CrossRef]
- K. Y. Ekşi, C. K. Y. Ek¸si, C. Güngör and M. M. Türko˘glu, Phys. Rev. D 89, no.6, 063003 (2014). arXiv:1402.0488 [astro-ph.HE]]. [CrossRef]
- M. Bejger and P. Haensel, Astron. Astrophys. 396, 917 (2002) [arXiv:astro-ph/0209151 [astro-ph]]. [CrossRef]
- J. M. Lattimer and B. F. Schutz, Astrophys. J. 629, 979-984 (2005) [arXiv:astro-ph/0411470 [astro-ph]]. [CrossRef]
- A. Maselli, G. Pappas, P. Pani, L. Gualtieri, S. Motta, V. Ferrari and L. Stella, Astrophys. J. 899, no.2, 139 (2020). arXiv:1905.05616 [astro-ph.HE]]. [CrossRef]
- I. Tews, J. Margueron and S. Reddy, Phys. Rev. C 98, no.4, 045804 (2018). arXiv:1804.02783 [nucl-th]]. [CrossRef]
- L. R. Weih, E. R. Most and L. Rezzolla, Astrophys. J. 881, no.1, 73 (2019). arXiv:1905.04900 [astro-ph.HE]]. [CrossRef]
- K. Yagi and N. Yunes, Science 341, 365-368 (2013). arXiv:1302.4499 [gr-qc]]. [CrossRef]
- K. Yagi and N. Yunes, Phys. Rev. D 88, no.2, 023009 (2013). arXiv:1303.1528 [gr-qc]]. [CrossRef]
- D. D. Doneva, S. S. D. D. Doneva, S. S. Yazadjiev, K. V. Staykov and K. D. Kokkotas, Phys. Rev. D 90, no.10, 104021 (2014). arXiv:1408.1641 [gr-qc]]. [CrossRef]
- T. K. Chan, Y. H. Sham, P. T. Leung and L. M. Lin, Phys. Rev. D 90, no.12, 124023 (2014). arXiv:1408.3789 [gr-qc]]. [CrossRef]
- C. Chirenti, G. H. de Souza and W. Kastaun, Phys. Rev. D 91, no.4, 044034 (2015). arXiv:1501.02970 [gr-qc]]. [CrossRef]
- K. Yagi and N. Yunes, Phys. Rev. D 91, no.12, 123008 (2015). arXiv:1503.02726 [gr-qc]]. [CrossRef]
- K. V. Staykov, D. D. Doneva and S. S. Yazadjiev, Phys. Rev. D 93, no.8, 084010 (2016). 0840; arXiv:1602.00504 [gr-qc]]. [CrossRef]
- D. D. Doneva and S. S. Yazadjiev, JCAP 11, 019 (2016). arXiv:1607.03299 [gr-qc]]. [CrossRef]
- D. D. Doneva and G. Pappas, Astrophys. Space Sci. Libr. 457, 737-806 (2018). [CrossRef]
- J. L. Blázquez-Salcedo and K. Eickhoff, Phys. Rev. D 97, no.10, 104002 (2018). arXiv:1803.01655. [CrossRef]
- J. B. Wei, A. Figura, G. F. Burgio, H. Chen and H. J. Schulze, J. Phys. G 46, no.3, 034001 (2019). arXiv:1809.04315. [CrossRef]
- D. Popchev, K. V. Staykov, D. D. Doneva and S. S. Yazadjiev, Eur. Phys. J. C 79, no.2, 178 (2019). arXiv:1812.00347. [CrossRef]
- G. Pappas, D. D. G. Pappas, D. D. Doneva, T. P. Sotiriou, S. S. Yazadjiev and K. D. Kokkotas, Phys. Rev. D 99, no.10, 104014 (2019). arXiv:1812.01117. [CrossRef]
- B. Kumar and P. Landry, Phys. Rev. D 99, no.12, 123026 (2019). arXiv:1902.04557. [CrossRef]
- G. Bozzola, P. L. Espino, C. D. Lewin and V. Paschalidis, Eur. Phys. J. A 55, no.9, 149 (2019). arXiv:1905.00028. [CrossRef]
- E. Benitez, J. Weller, V. Guedes, C. Chirenti and M. C. Miller, Phys. Rev. D 103, no.2, 023007 (2021). arXiv:2010.02619. [CrossRef]
- V. I. Danchev and D. D. Doneva, Phys. Rev. D 103, no.2, 024049 (2021). arXiv:2010.07392. [CrossRef]
- C. Adam, J. C. Mourelle, E. dos Santos Costa Filho, C. A. R. Herdeiro and A. Wereszczynski, Phys. Rev. D 110, no.8, 084017 (2024). [CrossRef]
- A. Einstein, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1915, 844-847 (1915).
- R. C. Tolman, Phys. Rev. 55, 364-373 (1939).
- J. R. Oppenheimer and G. M. Volkoff, Phys. Rev. 55, 374-381 (1939).
- K. Schwarzschild, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys. ) 1916, 189-196 (1916) [arXiv:physics/9905030 [physics]]. [CrossRef]
- T. Hinderer, B. D. T. Hinderer, B. D. Lackey, R. N. Lang and J. S. Read, Phys. Rev. D 81, 123016 (2010) . arXiv:0911.3535. [CrossRef]
- F. Iacovelli, M. Mancarella, C. Mondal, A. Puecher, T. Dietrich, F. Gulminelli, M. Maggiore and M. Oertel, Phys. Rev. D 108, no.12, 122006 (2023). arXiv:2308.12378. [CrossRef]
- G. A. Piovano, A. Maselli and P. Pani, Phys. Rev. D 107, no.2, 024021 (2023). arXiv:2207.07452. [CrossRef]
- G. Panotopoulos and I. Lopes, Int. J. Mod. Phys. D 27, no.09, 1850093 (2018). arXiv:1804.05023. [CrossRef]
- K. V. Staykov, D. D. Doneva, S. S. Yazadjiev and K. D. Kokkotas, JCAP 10, 006 (2014). arXiv:1407.2180. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




