Using General Relativity to Explain and Quantify Dark Energy

1. Introduction

1.1. Problem

Dark energy causes the masses in the universe to move apart. Based on the Wilkinson Microwave Anisotropy Probe (WMAP) at NASA [1], dark energy is estimated to be 71.35% of total energy. Dark energy theories are of different types, as described by Amendola [2], Misner [3] and Padmanabhan [4], including quintessence, modified gravity, and cosmic acceleration. The Lambda-CDM model uses only experimental data in the dark energy theory, providing the value of the cosmological constant Λ in Einstein’s field equation. Farnes [5] used a negative mass to explain the dark energy expansion. No current theory explains or numerically predicts dark energy.

1.2. Objectives

To explain and quantify dark energy just using the existing theory of general relativity [6,7,8,9,10]. The explanation of dark energy and its associated equations should logically follow from the principles of general relativity. The new explanation should be verified by predicting a percentage of dark energy close to the experimental value.

1.3. Summary of Method

When the two masses in Figure 1 travel together under the force of gravity, they gain kinetic energy. Mathematically, two masses are connected by elasticity with a force coming from Newton’s law $F={\displaystyle \frac{\mathrm{G}{m}_1,m_2}{x^2}}$. The potential energy, as in any spring, is stored in the elastic of space. If all objects in the universe collapse so they touch, all potential energy is converted into kinetic energy. A polar dark energy equation yields the amount of kinetic energy. The amount, when compared with total universe energy, is approximately 71%. Significantly, this suggests strongly that potential and dark energy are the same. The derivation of the dark energy equation in cartesian and polar coordinates is given in Section 2.

Newton’s law results in only a small amount of kinetic energy when all objects collapse. However, when all objects collapse to half their distance, the speed of light also halves because the dark energy stays constant while its 1D density doubles. This view is that of an outside observer who is not part of the collapse. The halving of the speed of light makes distances appear halved. Therefore, a distance x appears as $x/2$. If the ratio of the observed speed of light to the ambient speed of light is c”, then a distance x would now appear as $xc\mathrm{”}$. Substituting this for x in Newton’s law yields a more general Newtonian force law $F={\displaystyle \frac{\mathrm{G}{m}_1,m_2}{{(xc\mathrm{”}}^{)2}}}$, thus producing the inverse square law $F={\displaystyle \frac{\mathrm{G}{m}_1,m_2}{x^4}}$. This only applies in a collapsing universe and is responsible for the enormous energy release when all particles are enabled to collapse. This equation is confirmed by the two-mass theorem in Section 9.1.

The universe is built of dark matter, hydrogen, and helium. These atoms are built from electrons and quarks. The electrons are very small and light. However, quarks are heavy and have known upper radius. Therefore, the collapse assumes all quarks collapse into a compact lattice. Just take a quark Q. The dark energy KE is released by the collapse of all other quarks around quark Q. Assuming the mass-energy of a quark is EQ, the dark energy ratio is then given by $KE/(KE+EQ)$.

The kinetic energy generated when all mass collapses is described in the method Section 2.

1.4. Summary of Main Results

Section 9 proves the novel inverse fourth power equation $F={\displaystyle \frac{\mathrm{G}{m}_1,m_2}{x^4}}$, which calculates the massive inter-mass force when all masses move together in the same proportion.

Section 2 introduces a novel dark energy ratio equation which calculates the enormous kinetic energy released when all masses collapse together into a Gaussian lattice [11].

Section 2.2 introduces an accurate Cartesian dark energy equation which is impossibly slow in calculating the percentage ratio.

Section 2.3 introduces a polar dark energy equation which is concise and efficient.

Section 3 introduces results that predict a dark energy ratio of 71.5% compared with the experimental value of 71.35%.

2. Methods

2.1. General Dark Energy Ratio Equation

For the whole universe, the dark energy ratio is given by:

$${\mathit{E}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}}={\displaystyle \frac{{\mathit{E}}_{\mathit{s}}}{{\mathit{E}}_{\mathit{s}}+{\mathit{E}}_{\mathit{m}}}}$$

(2.1)

where $E_s$ is the total dark energy and $E_m$ is the total mass-energy of the universe. It is assumed that the dark energy related to dark matter energy is in the same proportion as dark energy relating to the baryonic particle energy.

The kinetic energy created by two masses moving from infinite to $x_{min}$ is introduced in Section 9 by Equation (9.10):

$$E={\displaystyle \frac{G{m}_1{m}_2}{{3x_{min}}^3}}$$

(2.2)

The distance between two masses $m_i,m_{\mathrm{j}}$ is $x_{i,j}$ which replaces $x_{min}$. Therefore, the kinetic energy $E_{i,j}$ created when $x_{i,j}$ moves apart is given by:

$$E_{i,j}={\displaystyle \frac{G{m}_i{m}_{\mathrm{j}}}{{3x_{i,j}}^3}}$$

(2.3)

The entire universe collapses to a compact Gaussian lattice [11]. The distance $x_{i,j}$ is their distance apart in this lattice. The total kinetic energy ${\mathit{E}}_{\mathit{s}}$ is given by summing the energy generated by all pairs of masses making this collapse:

$${\mathit{E}}_{\mathit{s}}={\sum }_{\mathit{i}}{\sum }_{\mathit{j}}{\displaystyle \frac{G{m}_i{m}_{\mathrm{j}}}{3{{\mathit{x}}_{\mathit{i},\mathit{j}}}^3}}$$

(2.4)

If $m_U$ is the mass of the universe, including dark matter, then the total mass-energy using Einstein’s equation is:

$${\mathit{E}}_{\mathit{m}}={\mathit{m}}_{\mathit{U}}{\mathit{c}}^2$$

(2.5)

The dark energy ratio is from Equation (2.1) with substitutions from Equations (2.4) and (2.5):

$${\mathit{E}}_{\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}}={\displaystyle \frac{{\mathit{E}}_{\mathit{s}}}{{\mathit{E}}_{\mathit{s}}+{\mathit{m}}_{\mathit{U}}{\mathit{c}}^2}}$$

(2.6)

The following sections provide a Cartesian solution that is slow but accurate and a polar solution that is fast but slightly less accurate.

2.2. Cartesian Solution to Dark Energy Ratio Equation

Instead of using the mass of the whole universe, it is only necessary to use a single quark Q and the dark energy between this quark Q and all the other quarks. The particles are maximally compressed when they touch in a Gaussian lattice [11] as depicted in Figure 2 and Figure 3. The total kinetic energy $E_{sq}$ originates from the collapse all other quarks onto only one quark Q.

Therefore, the dark energy ratio Equation (2.1) can be written as:

$$E_{ratio}={\displaystyle \frac{E_{sq}}{E_{sq}+E_{mq}}}$$

(2.7)

The kinetic energy $E_{sq}$ is derived and confirmed in Section 10 and yields Equation (10.1):

$$E_{Sq}={\displaystyle \frac{G{m_q}^2}{24{r_q}^3}}{\sum }_{i,j,k}{\displaystyle \frac{1}{{d_{i,j,k}}^3}}if(0>d_{i,j,k}<n_{max})$$

(2.8)

with $m_q$ replacing $m_p$ and $r_q$ replacing $r_p$

This is the kinetic energy generated when all quarks in a radius of $2r_q{n}_{max}$ collapse to touch each other, where:

$d_{i,j,k}$ is derived from Equations (10.2) to (10.5) between quarks in a lattice.

Layer $n_{max}$ is given by Equation (2.35) repeated below:

$$n_{max}=\sqrt[3]{{\displaystyle \frac{{3p}_{max}}{4\pi \surd 2}}}$$

(2.9)

The number of quarks $p_{max}$ in the universe’s mass $m_U$ is given by:

$$p_{max}={\displaystyle \frac{m_U}{m_Q}}$$

(2.10)

The mass of the quark is given by Equation (8.8).

NOTE: A Cartesian dark energy algorithm is given by restricting $i,j,k$ in Equation(2.8) to a maximum of $n_{max}$.

Finally, the dark energy ratio is given by Equation (2.7):

$$E_{ratio}={\displaystyle \frac{E_{sq}}{E_{sq}+E_{mq}}}$$

(2.11)

where $E_{sq}$ is the total dark energy given by Equations (2.7) and $E_{mq}$ is the energy in quark Q given by Einstein:

$$E_{mq}=m_q{c}^2$$

(2.12)

2.3. Polar Solution to Dark Energy Ratio Equation

2.3.1. Theorem Polar Dark Energy Equation

The Cartesian Equation (2.8) cannot be computed for all quarks in a reasonable time. However, using polar coordinates, a single compact Equation (2.37) repeated below is used:

$$E_s={\displaystyle \frac{G\prime \pi \surd 2{m_q}^2}{6{r_Q}^3}}(\ln (\sqrt[3]{{\displaystyle \frac{3m_U}{m_{q}4\pi \surd 2}}}),\mathrm{G}\text{’}={\displaystyle \frac{G{m_q}^2}{24{r_Q}^3}}$$

(2.13)

This equation uses continuous mass distributions rather than discrete in the Cartesian Equation (2.8).

2.3.2. Proof Polar Dark Energy Equation

The total dark energy from a mass pair is given in Equation (9.10):

$$E={\displaystyle \frac{G{m}_1{m}_2}{{3x_{min}}^3}}$$

(2.14)

This is the kinetic energy generated when two quarks move from ∝ to $x_{min}$ is given by:

$$E={\displaystyle \frac{G{m_q}^2}{{3x_{min}}^3}}$$

(2.15)

The radius of the quark Q is $r_Q.$ The other quarks are in layers of radius n, as depicted in Figure 4. Layers are defined as multiples of twice the radius of the quark. The distance between two quarks, $x_{min}$, is given by:

$$x_{min}=2n{r}_Q$$

(2.16)

When n=1, the quarks are in the first layer where they all touch the central quark Q; therefore, the value of $x_{min}$ is twice the radius 2$r_Q$. Substituting $x_{min}$ from Equation (2.16) into Equation (2.15) gives the kinetic energy generated for particles in layer n:

$$E_n={\displaystyle \frac{{{Gm}_q}^2}{3{(2n{r}_Q)}^3}}$$

(2.17)

$$\text{∴ }{E}_n={\displaystyle \frac{G{m_q}^2}{24n^3{r_Q}^3}}$$

(2.18)

$$\mathrm{LET}\mathrm{G}\text{’}={\displaystyle \frac{G{m_q}^2}{24{r_Q}^3}}$$

(2.19)

$$\text{∴ }{E}_n={\displaystyle \frac{G\mathrm{’}}{n^3}}$$

(2.20)

This kinetic energy is generated when a quark arrives from infinity to layer n, which is distance 2${nr}_Q$ from quark Q. If $n=1,$ then this is the dark energy released for quarks that touch quark Q. The total energy released by p particles in layer n is obtained by multiplying $E_n$ by the number of particles $p$ in layer n:

$$E=E_{n}p$$

(2.21)

Substituting for $E_n$ from Equation (2.20) yields:

$$E={\displaystyle \frac{G\mathrm{’}}{n^3}}p$$

(2.22)

The rate of change of dark energy, needed later, with the number of particles $p$ in a layer given by:

$$\text{∴ }\mathrm{d}E/dp={\displaystyle \frac{G\mathrm{’}}{n^3}}$$

(2.23)

The number of particles in each layer is approximated using the Gaussian lattice [11] as follows. In the gaussian lattice, the spheres are in steps of n = 1 in the x and, y planes. See Figure 2 and Figure 3. In the z direction, they are the height of a square pyramid. The steps of n are then $1/2$ apart. Consequently, in the z direction, there are √2 more quarks than in $xandy$ directions. As depicted in Figure 4, without this compression factor there would only be p particles in a sphere volume of layer radius $n$:

$$p={\displaystyle \frac{4}{3}}\pi n^3$$

(2.24)

However, because the z dimension contains √2 more particles per n step unit in the z direction, this formula becomes:

$$p={\displaystyle \frac{4}{3}}\pi \surd 2n^3$$

(2.25)

The rate of change particles $p$ wrt $n$ is then given by differentiation:

$$\text{∴ }{\displaystyle \frac{dp}{dn}}=4\pi \surd 2n^2$$

(2.26)

The rate of change of dark energy with n is ${\displaystyle \frac{dE}{dn}}$ and is given by:

$${\displaystyle \frac{dE}{dn}}={\displaystyle \frac{dE}{dP}}{\displaystyle \frac{dP}{dn}}$$

(2.27)

Substituting from (2.23) and (2.26) yields:

$${\displaystyle \frac{dE}{dn}}={\displaystyle \frac{G\mathrm{’}}{n^3}}4\pi \surd 2n^2$$

(2.28)

$$\text{∴ }{\displaystyle \frac{dE}{dn}}={\displaystyle \frac{\alpha G\mathrm{’}}{n}}$$

(2.29)

The total energy is then obtained by integrating the above term ${\displaystyle \frac{\mathrm{d}\mathrm{E}}{\mathrm{d}\mathrm{n}}}$ yields the total dark energy:

$$\text{∴ }E={\int }_{n=1}^{n_{max}}{\displaystyle \frac{\alpha G\mathrm{’}}{n}}dn$$

(2.30)

$$\text{∴ }E=4\pi \surd 2G\mathrm{’}\left[\ln n_{max}-\ln 1\right]$$

(2.31)

But $\ln 1$ is zero:

$$\text{∴ }E=4\pi \surd 2G\mathrm{’}\ln n_{max}$$

(2.32)

Using $E_s$ for E yields:

$$E_s(n_{max})=4\pi \surd 2G\mathrm{’}\ln n_{max},\mathrm{G}\text{’}={\displaystyle \frac{G{m_q}^2}{24{r_Q}^3}}$$

(2.33)

The value of $p_{max}$ is obtained by substituting $n=n_{max}$ in Equation (2.25):

$$\text{∴ }{p}_{max}={\displaystyle \frac{4\pi \surd 2}{3}}{n_{max}}^3$$

(2.34)

Rearranging yields:

$$n_{max}=\sqrt[3]{{\displaystyle \frac{{3p}_{max}}{4\pi \surd 2}}}$$

(2.35)

The number of quarks $p_{max}$ in the universe is given by dividing the mass of the universe $m_U$ by the mass of a quark $m_q$:

$$p_{max}={\displaystyle \frac{m_U}{m_q}}$$

(2.36)

Finally, substitute G’ from Equation (2.27), and $n_{max}$ from Equation (2.35), in Equation (2.33) yields the dark energy $E_s$:

$$E_s={\displaystyle \frac{G\prime \pi \surd 2{m_q}^2}{6{r_Q}^3}}(\ln (\sqrt[3]{{\displaystyle \frac{3m_U}{m_{q}4\pi \surd 2}}})$$

(2.37)

where $m_q$ is given by Equation (8.8).

QED

3. Dark Energy Percentage (%) Results

The dark energy ratio is given by Equation (2.7) repeated here:

$$E_{ratio}={\displaystyle \frac{E_{sq}}{E_{sq}+E_{mq}}}$$

The term $E_{sq}$ is given by Equations (2.37). The term $E_{mq}$ is given by Einstein as $m_Q{\mathrm{c}}^2$. The following data was used:

radius of quark, Zeus [12] $r_Q$ is 4.3E-19 metres,

mass of up quark [13] $m_{up}$ is 3.82E-30 Kgms.

mass of down quark [13] $m_{down}$ is 8.36E-30 Kgms.

mass of universe [14] $m_U$ is 1E+53 Kgms.

This equation estimates 71.50% dark energy compared with the total of all energy. This value is close to the experimental value from the NASA WMAP [12], which estimates dark energy at 71.35% (70.39 to 72.25).

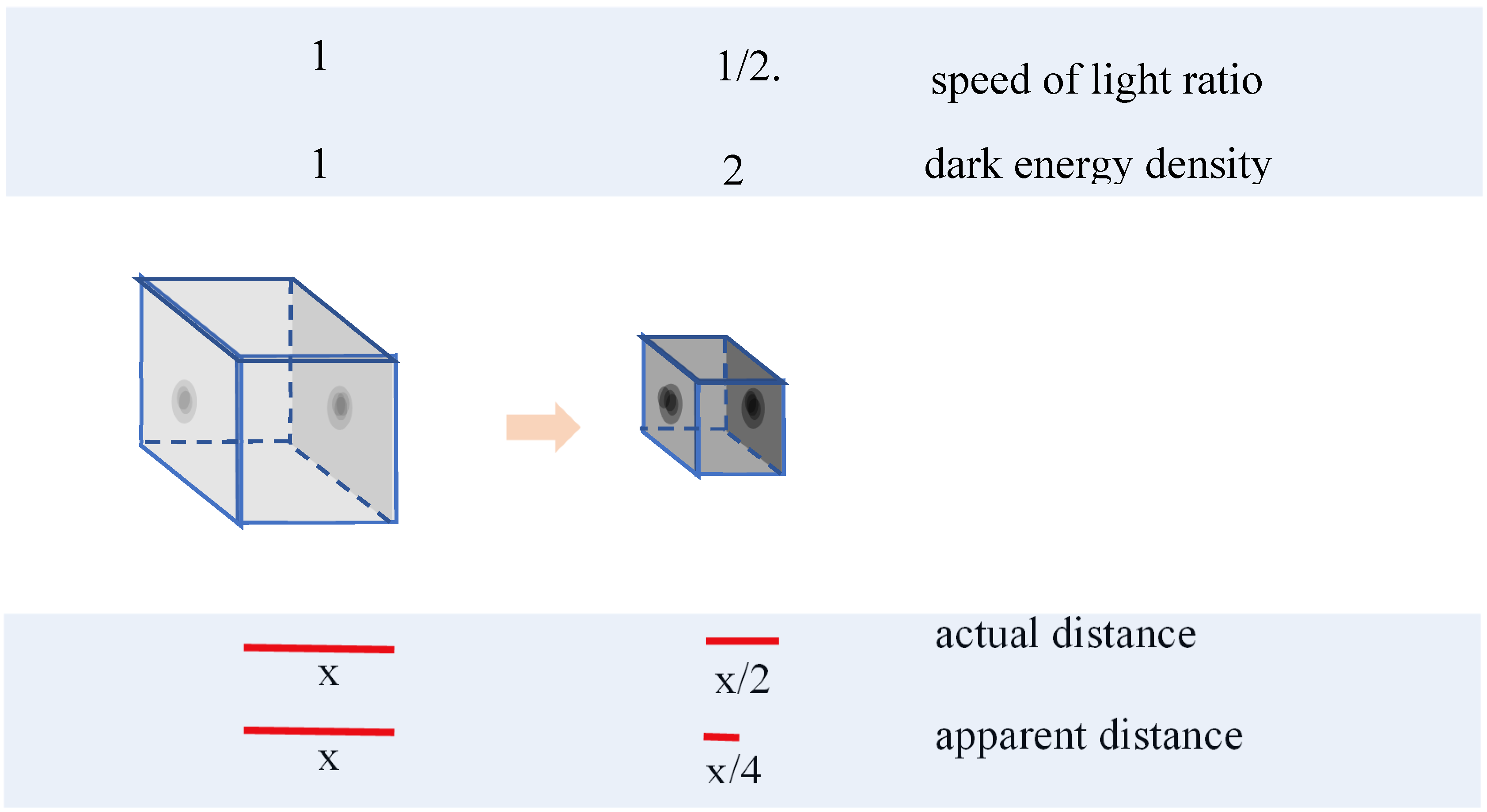
4. Discussion

4.1. Dark Energy Equation

The dark energy equation is solved using polar coordinates to sum the dark energy in layers around a single quark Q. It is only slightly more accurate to scan each quark in the Gaussian lattice [11] using the Cartesian equation. This scan was performed in an informal report for quarks in the nearest 200 layers [15] and gave essentially the same result.

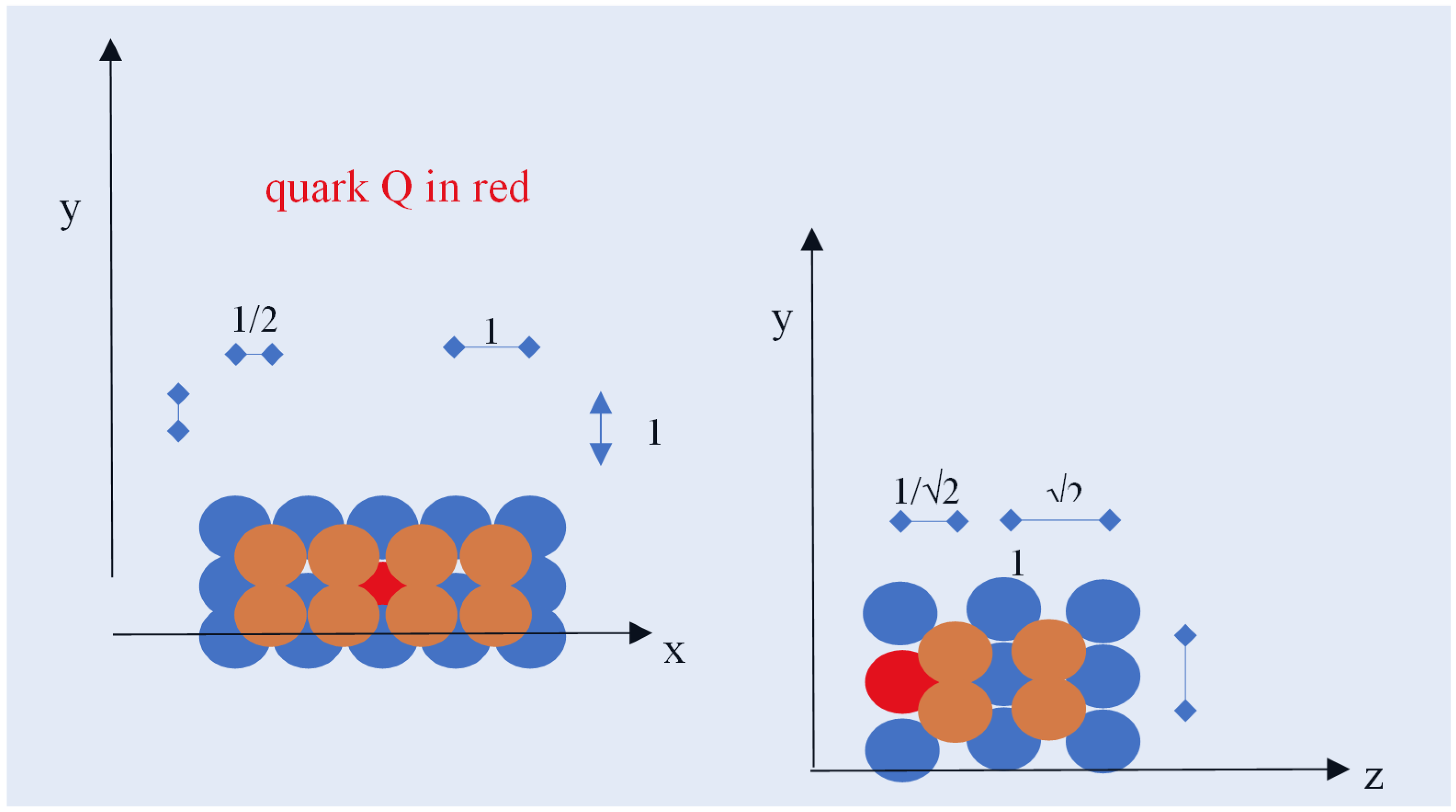
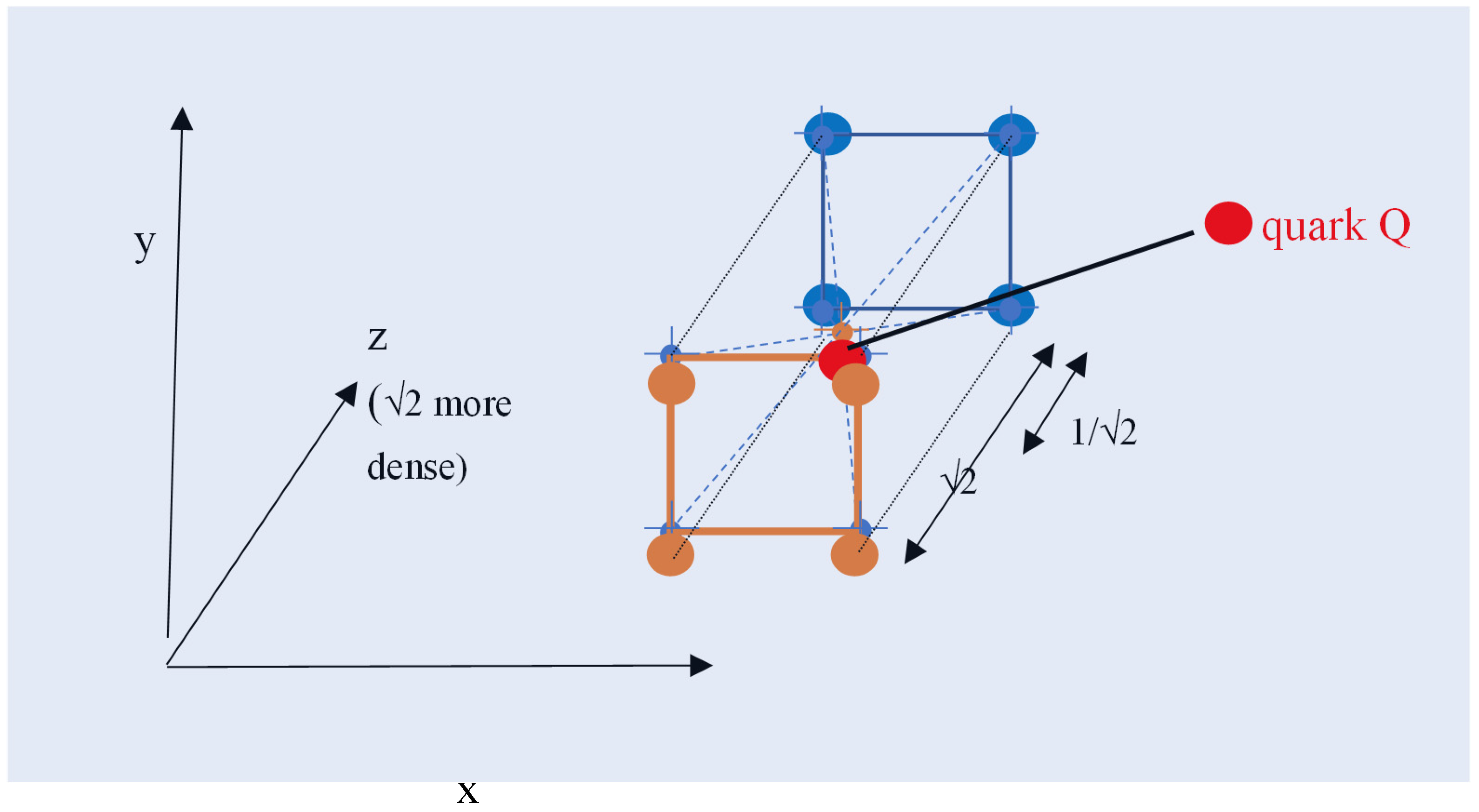
4.2. Radius of a Quark

The results reveal 71.5% dark energy, assuming the radius of a quark ${\mathit{r}}_{\mathit{Q}}$ is given by Zeus [12] which is the actual radius rather than the maximum radius. Using the experimental data of 71.50% backwards in the dark energy equation, the average quark radius is calculated as 4.3E-19 m, which is the experiment value.

4.3. Curvature of Space

Einstein’s field equations correctly give the curvature of space around each mass. Dark energy may introduce minor corrections to Einstein’s theory. For example, the density of dark energy between two masses may very slightly alter the curvature of space-time [15].

4.4. Rate of Expansion of Dark Energy

Radiation from stars creates dark energy because the photons lose kinetic energy which is converted into potential or dark energy [16]. The loss of kinetic energy changes the wavelength of the photons. Because all matter can eventually break down into radiation, the final state of the universe is probably just dark energy. The beginning of the universe is likely the reverse. Radiation going backwards in time removes dark energy. As radiation removes dark energy, it must return to a highly compressed form. It is thus consistent with the “Big Bang” theory.

4.5. Black Holes

5. Conclusion

A new equation is proposed for the amount of dark energy stored in the universe. This equation is derived using general relativity plus the assumption that potential and dark energy are the same. The most basic theorem provides an inverse fourth power law for the force between two masses when all masses move together based on a novel generalisation of Newton’s law to include the speed of light. The inverse 4th power equation depends on the Newtons law which is based on experiment.

The equation predicts the percentage of dark energy at 71.50%. The experimental results from the NASA WMAP study [12] indicate a range of 70.39% to 72.25%, which is sufficiently close to validate the new dark energy equation. Conversely, using experimental data of 71.50% in the dark energy equation yields an average quark radius of 4.3E-19 m, which is the experiment value.

Alternative theories explain dark energy by changing general relativity. An example is Farnes [5] who used a negative mass. This new approach makes no such changes.

6. Statements and Declarations

The author declares no conflicts of interest. This work was not supported by any external funding. E. Babb was the sole author of this study. The author has read and approved the final manuscript.

7. Appendices

The following sections contain the appendices giving important results used in the study.

8. Average Mass of a Quark

The elementary particle chosen was a quark. Quarks were used as the two masses because they are the heaviest elementary particles. There are many types of quarks, but the main ones are up and down quarks, which inhabit protons and neutrons in equal numbers. It is assumed that there is a single quark Q with an average of mass $m_Q$ of the up and down quarks. The other particle was the electron. This is lighter than a quark but much larger and thus contains much less dark energy. Therefore, it was not used in the calculations in this study.

The universe is composed of 73% hydrogen, 25% helium, and 2% something else [18]. The “something else” may be like hydrogen. The hydrogen atom has one proton, and so two up and one down quark with mass:

$$m_H=(2m_{up}+m_{down})$$

(8.1)

The helium atom has two protons and two neutrons and so has mass:

$$m_{HE}=2\left(2m_{up}+m_{down}\right)+2(m_{up}+{2m}_{down})$$

(8.2)

$$\text{∴ }{m}_{HE}=(6m_{up}+6m_{down})$$

(8.3)

Adding both together in a proportion of 75% to 25% yields:

$$m_{both}={3m}_H+m_{He}$$

(8.4)

$$m_{both}=3(2m_{up}+m_{down})+(6m_{up}+6m_{down})$$

(8.5)

$$\text{∴ }{m}_{both}=12m_{up}+9m_{down}$$

(8.6)

Thus, there are 12+9 quarks, yielding a total of 21 in the three hydrogen and one helium atoms. Therefore, the average quark has the mass:

$$m_Q=(12m_{up}+9m_{down})/21$$

(8.7)

$$\text{∴ }{\mathit{m}}_{\mathit{Q}}=4/7{\mathit{m}}_{\mathit{u}\mathit{p}}+3/7{\mathit{m}}_{\mathit{d}\mathit{o}\mathit{w}\mathit{n}}$$

(8.8)

The up quark [13] has a mass of approximately 2.3 MeV (3.82E-30 Kgms ), while the down quark [13] has a mass of approximately 4.8 MeV (8.36E-30 Kgms).

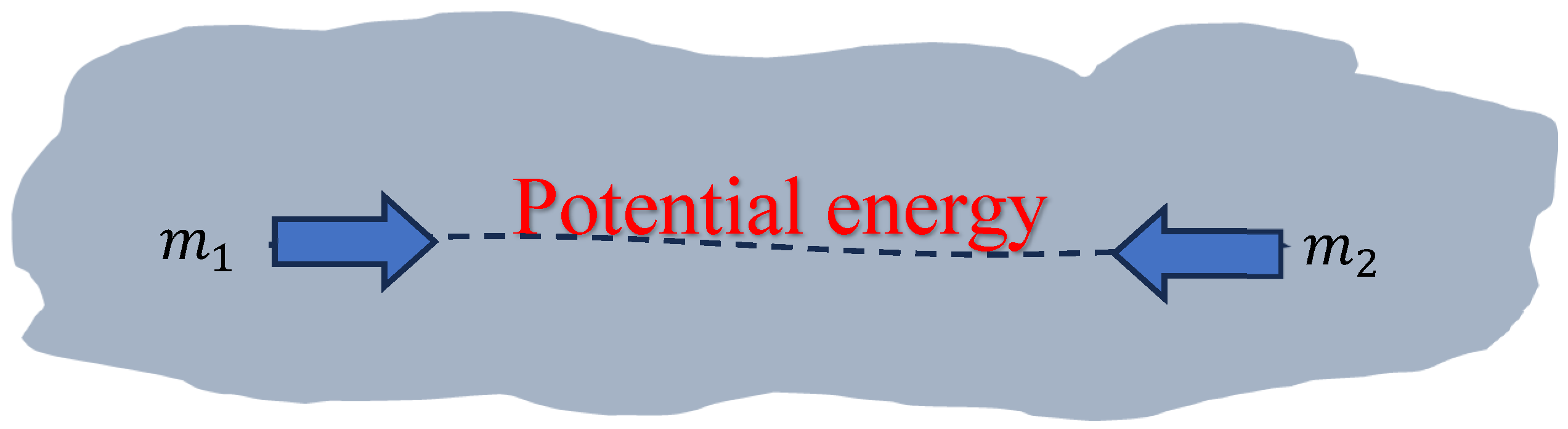
9. Two-Mass Theorems

The situation in which all the masses halve their distance apart is illustrated in Figure 5.

Suppose the side of a unit cube of space between masses is halved. The stored dark energy remains the same, and so its 1D density is doubled. Consequently, the speed of light is halved. An actual distance x is halved as shown. However, halving the distance also doubles the density to 2 and so the speed of light is halved. This means that the apparent or observed distance $x$ which was x/2 is further halved to x/4.

This effect occurs with objects under water. The lower speed of light in water makes objects appear less deep to the outside observer. If the speed of light in water is halved, the apparent depth is halved.

9.1. Theorem: Marginal Energy Two Masses

Space is elastic, obeys Newton’s gravity equation, and can store energy released as kinetic energy. The force or marginal change in dark energy for two masses $m_1$ and $m_2$ is given by the inverse fourth power from Equation (9.9):

$$F={\displaystyle \frac{\mathrm{G}{m}_1,m_2}{x^4}},F={\displaystyle \frac{dE}{dx}},$$

(9.1)

The term G has the same size but different dimensions to the standard G.

9.2. Proof: Marginal Energy Two Masses

The variable $c\mathrm{”}$ is the ratio of the speed of light, $c\mathrm{’}$ to $c$. The observer is always at c”=1, so everything shrinks relative to him. When the speed of light is c, the force between the two masses $m1,m2$ is given by the Newton’s inverse square law:

$${\mathrm{F}}_2(\mathrm{x})={\displaystyle \frac{G{\mathit{m}}_2{\mathit{m}}_2}{{\mathrm{x}}^2}}$$

(9.2)

However, when the speed of light ratio is less than 1, the dark energy density rises and the distance the observer sees is $x$ times the speed of light ratio $c\mathrm{”}$. This new value for x called $x_{obs}$ defined as.

$$x_{obs}=\mathrm{x}\mathrm{c}\mathrm{”}$$

(9.3)

The observed distance between $m_1{m}_2$ is now $x_{new}$ giving.

$${\mathrm{F}}_4(\mathrm{x})={\displaystyle \frac{dE}{dx}}={\displaystyle \frac{G{m}_1{m}_2}{{(x_{obs})}^2}}$$

(9.4)

Substituting $x_{obs}$ from equation (9.3) gives:

$${\mathbf{F}}_4(\mathbf{x})={\displaystyle \frac{\mathit{d}\mathit{E}}{\mathit{d}\mathit{x}}}={\displaystyle \frac{\mathit{G}{\mathit{m}}_1{\mathit{m}}_2}{{(\mathbf{x}\mathbf{c}\mathrm{”})}^2}}$$

(9.5)

This is a generalisation of Newton’s law, which includes dark energy density represented by c.” Calculating the total dark energy requires that the entire universe be shrink. Consequently, all masses move together in the same proportion. The drop in the speed of light ratio c,” and so rise in the density of dark energy, causes initial distances ${\mathrm{x}}_1$ to reduce by ratio c” giving:

$$\mathrm{c}\mathrm{”}={\displaystyle \frac{x}{{\mathrm{x}}_1}}$$

(9.6)

For example, if $c\mathrm{”}=1/2$ then the distance x becomes ${\mathrm{x}}_1/2$.

Substituting equation (9.6) in Equation (9.5) yields:

$${\mathrm{F}}_4(\mathrm{x})={\displaystyle \frac{dE}{dx}}={\displaystyle \frac{G{m}_2{m}_2}{{(\mathrm{x}x/{\mathrm{x}}_1)}^2}}$$

(9.7)

At c”=1 the force ${\mathrm{F}}_2(1)$ and ${\mathrm{F}}_4(1)$ must be the same. Therefore, the variable ${\mathrm{x}}_1=1$, yielding an extra term ${\mathrm{x}}_1=1$ below:

$${\mathrm{F}}_4(\mathrm{x})={\displaystyle \frac{dE}{dx}}={\displaystyle \frac{G{m}_2{m}_2}{{(\mathrm{x}x/{\mathrm{x}}_1)}^2}}\wedge {\mathrm{x}}_1=1$$

(9.8)

Removing ${\mathrm{x}}_1$ yields:

$${\mathbf{F}}_4(\mathbf{x})={\displaystyle \frac{\mathit{d}\mathit{E}}{\mathit{d}\mathit{x}}}={\displaystyle \frac{\mathit{G}{\mathit{m}}_1{\mathit{m}}_2}{{\mathbf{x}}^4}}$$

(9.9)

NOTE: The dimensions (but not the value) of G have now changed. However, it could be called ${\mathrm{G}}_4$ in the equation above if the reader wants it to have dimensions.

QED1

9.3. Theorem: Total Energy Released by Two Masses

The kinetic energy generated and 3D space-energy removed, when $m_1$ and $m_2$ move from ∞ to are $x_{min}$ apart, when all the masses in the universe move simultaneously, is given by Equation (9.14):

$$\mathit{E}={\displaystyle \frac{\mathit{G}{\mathit{m}}_1{\mathit{m}}_2}{{3{\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}}^3}}$$

(9.10)

9.4. Proof: Total Energy Released by Two Masses

The total energy is then obtained by integrating the force where F = ${\displaystyle \frac{dE}{dx}}$ for x = xmin to ${\mathit{x}}_{\mathit{o}\mathit{b}\mathit{s}}$:

$$E={\int }_{{\mathit{x}}_{\mathit{o}\mathit{b}\mathit{s}}}^{x_{min}}{\displaystyle \frac{dE}{dx}}dx$$

(9.11)

Substituting for ${\displaystyle \raisebox{1ex}{$\mathrm{d}\mathrm{E}$}\!\left/ \!\raisebox{-1ex}{$dx$}\right.}$ from Equation (9.10) yields:

$$\text{∴ }E={\left[-{\displaystyle \frac{G{m}_1{m}_2}{3x^3}}\right]}_{x_{obs}}^{x_{min}}$$

(9.12)

$$\text{∴ }E={\displaystyle \frac{G{m}_1{m}_2}{{3x_{min}}^3}}-{\displaystyle \frac{G{m}_1{m}_2}{{3x_{obs}}^3}}$$

(9.13)

However, assuming ${\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}$ << ${\mathit{x}}_{\mathit{o}\mathit{b}\mathit{s}}$, the second term is negligible and can be removed as follows:

$$\mathit{E}={\displaystyle \frac{\mathit{G}{\mathit{m}}_1{\mathit{m}}_2}{{3{\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}}^3}}$$

(9.14)

This is the kinetic energy generated when $m_1$ and $m_2$ (and all other masses) move from ∞ to $x_{min}$ apart.

QED2

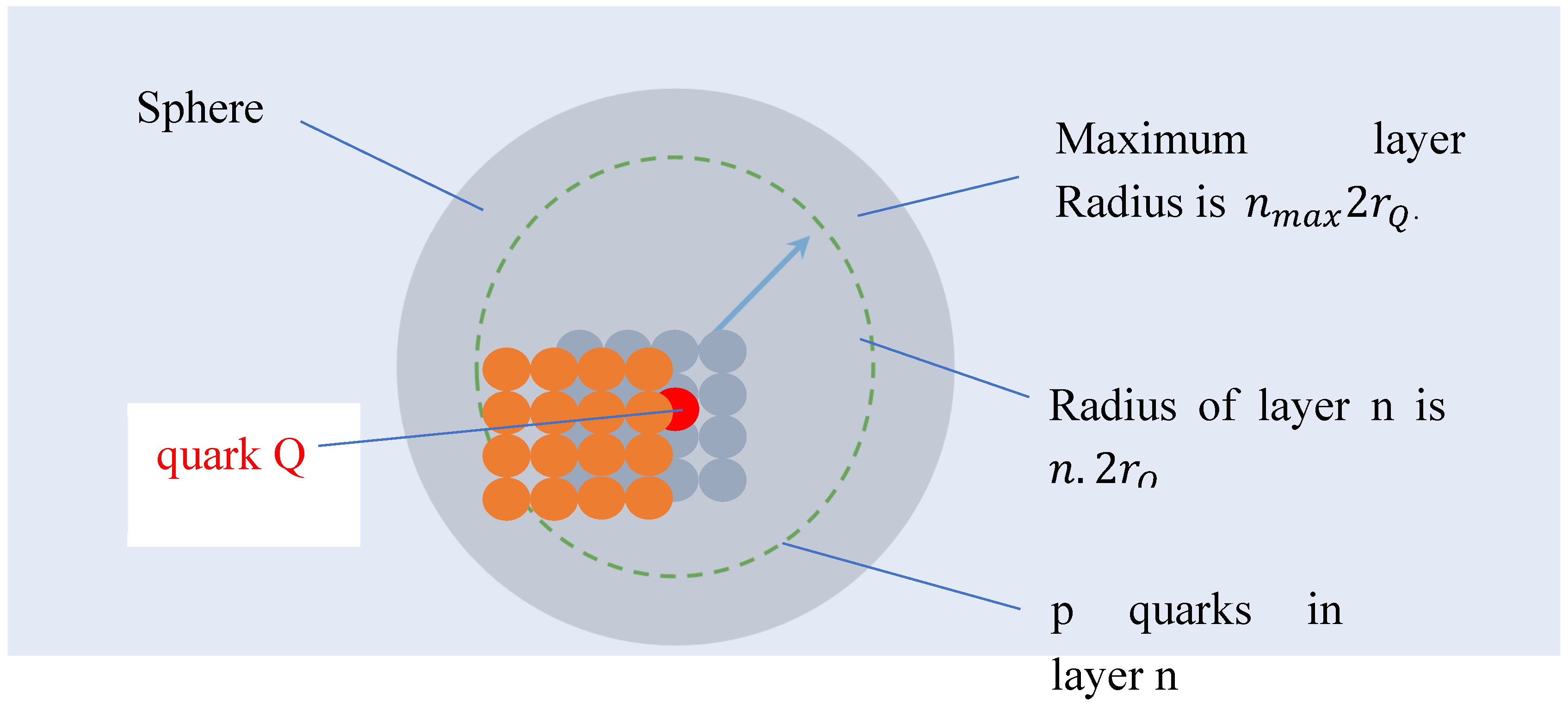
10. Theorem Dark Energy for n Masses

10.1. Theorem

When spherical particles of equal mass $m_p$ and radius $r_p$ fall together and surround particle P, they generate kinetic energy $E_{sp}$ and thus remove $E_{sp}$ of dark energy. They fall together into a lattice where the maximum distance between quarks is $n_{max}$

$$E_{Sp}={\displaystyle \frac{G{m_p}^2}{24{r_p}^3}}{\sum }_{i,j,k}{\displaystyle \frac{1}{{d_{i,j,k}}^3}}if(0>d_{i,j,k}<n_{max})$$

(10.1)

10.2. Proof

The particles are maximally compressed in a Gaussian lattice [11]. This is depicted in Figure 2 and Figure 3. The particles are indexed by <i,j,k> for the <x, y, z> directions. One unit of <i,j,k> is ${2r}_q$ metres. The target particle Q is at location 0,0,0. In the <x,y> plane the particles are just one unit apart. In the <z> plane they were 1$/\sqrt{2}$ units apart.

The lattice in Figure 2 and Figure 3 describes the position of each particle and, therefore, the associated dark energy. The blue particles in the lattice are just 1 unit or ${2r}_q$ metres apart. The orange quarks are arranged in the same way but are displaced left and vertically by 0.5 units. In the z direction, it was $1/\sqrt{2}$ above the blue layer. The distance $d_{i,j,k}$ of any quark at <x,y,z> from the particle Q at <0,0,0> is given by Pythagoras:

$$\mathrm{Distance}\mathrm{in}\mathrm{units}{d}_{i,j,k}=\sqrt{x^2+y^2+z^2}$$

(10.2)

$$ifeven\left(k\right)thenx=iandy=j$$

(10.3)

$$ifodd\left(k\right)thenx=i+{\displaystyle \frac{1}{2}}andy=j+1/2$$

(10.4)

$$z=k/\sqrt{2}$$

(10.5)

The total energy is found by summing the energy from every quark at <x,y,z> to the central quark Q at <0,0,0> using the two-mass Equation (9.14) repeated below:

$$\text{∴ }\mathit{E}={\displaystyle \frac{\mathit{G}{\mathit{m}}_1{\mathit{m}}_2}{{3{\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}}^3}}$$

(10.6)

Both masses ${\mathit{m}}_1{\mathit{m}}_2$ are $m_p$, so:

$$\text{∴ }\mathit{E}={\displaystyle \frac{G{m_p}^2}{{3{\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}}^3}}$$

(10.7)

Therefore, the total dark energy for $p_{max}$ particle pairs collapsing around particle Q is:

$$E_{Sq}={\sum }_i^{p_{max}}{\displaystyle \frac{G{m_p}^2}{{3{\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}}^3}}$$

(10.8)

The distance ${\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}$ is derived from distance $d_{i,j,k},$ defined in Equation (10.2);

$${\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}={2r}_q{d}_{i,j,k}\text{∧ }0>d_{i,j,k}<n_{max}$$

(10.9)

The constraint $0>d_{i,j,k}<n_{max}$ restricts the summation to particles outside particle Q and inside a sphere containing $p_{max}$ particles and $n_{max}$ layers in radius. Adding this to Equation (10.8) yields:

$$E_{Sq}={\sum }_{i,j,k}{\displaystyle \frac{G{m_q}^2}{3{({2r}_q{d}_{i,j,k})}^3}}if(0>d_{i,j,k}<n_{max})$$

(10.10)

$$\text{∴ }{E}_{Sq}={\sum }_{i,j,k}{\displaystyle \frac{{{Gm}_q}^2}{24{r_q}^3{d_{i,j,k}}^3}}if(0>d_{i,j,k}<n_{max})$$

(10.11)

$$\text{∴ }{\mathit{E}}_{\mathit{S}\mathit{q}}={\displaystyle \frac{\mathit{G}{{\mathit{m}}_{\mathit{q}}}^2}{24{{\mathit{r}}_{\mathit{q}}}^3}}{\sum }_{\mathit{i},\mathit{j},\mathit{k}}{\displaystyle \frac{1}{{{\mathit{d}}_{\mathit{i},\mathit{j},\mathit{k}}}^3}}\mathit{i}\mathit{f}(0>{\mathit{d}}_{\mathit{i},\mathit{j},\mathit{k}}<{\mathit{n}}_{\mathit{m}\mathit{a}\mathit{x}})$$

(10.12)

QED