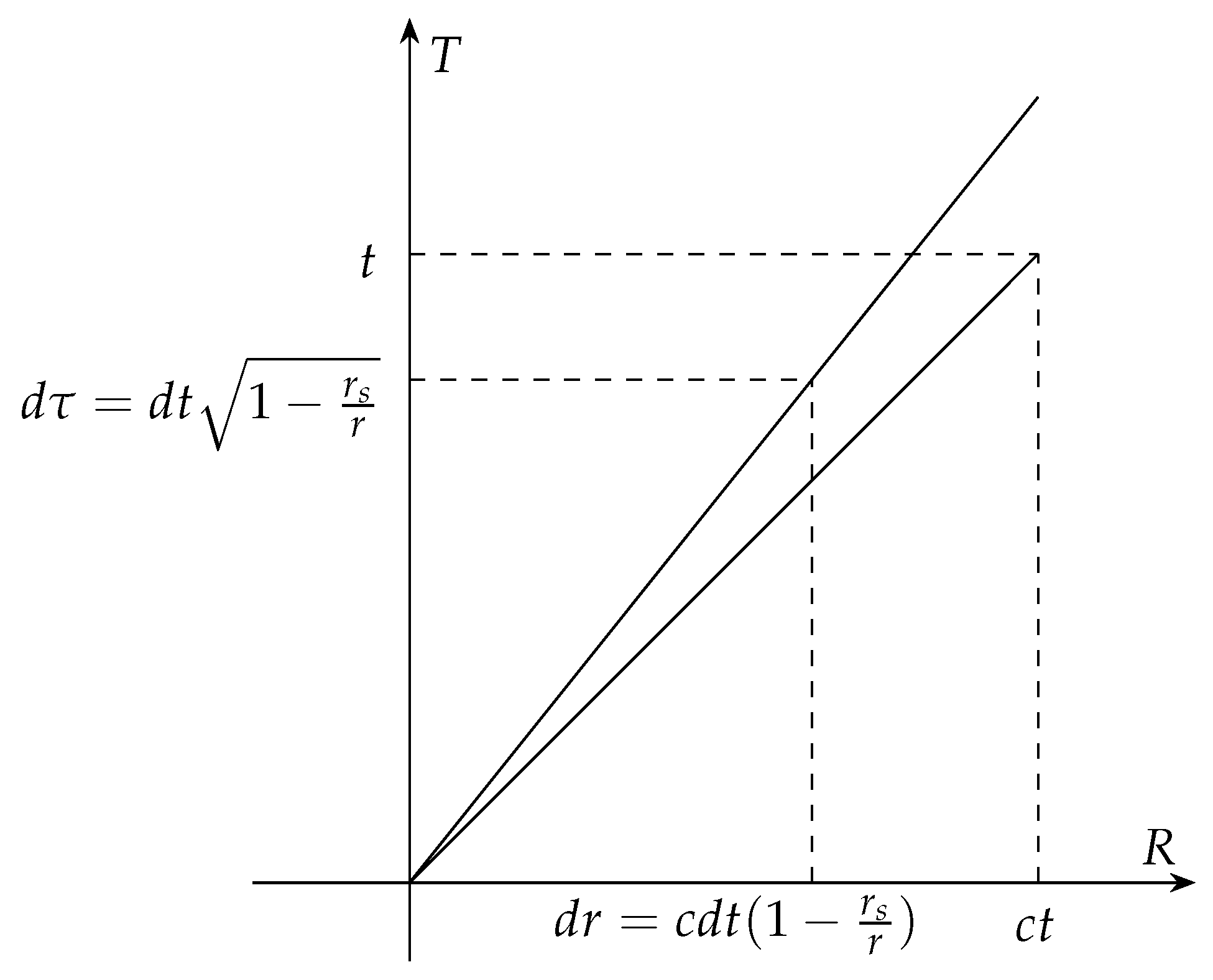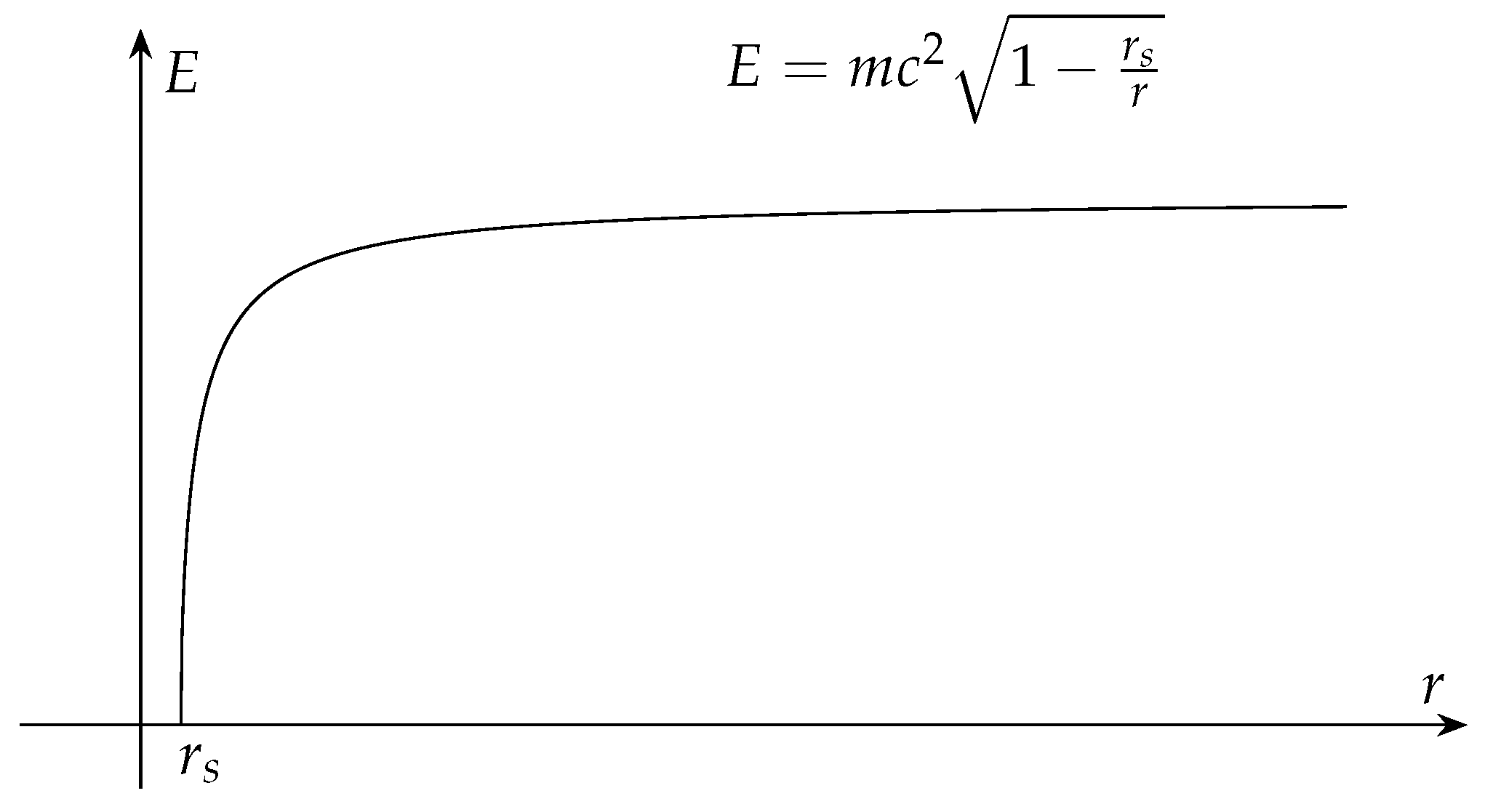Energy Transformation in Gravitational Fields: A New Perspective on Four-Velocity

1. Introduction

The four-velocity vector in special relativity is defined as:

$$U^{\mu }=\left(c{\displaystyle \frac{dt}{d\tau }},{\displaystyle \frac{dx}{d\tau }},{\displaystyle \frac{dy}{d\tau }},{\displaystyle \frac{dz}{d\tau }}\right)$$

(1)

The Schwarzschild solution for Einstein field equations is:

$$d{s}^2=-\left(1-{\displaystyle \frac{r_s}{r}}\right)c^{2}d{t}^2+{\left(1-{\displaystyle \frac{r_s}{r}}\right)}^{-1}d{r}^2+r^2\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right)$$

(2)

Where $r_s=2GM/c^2$ is the Schwarzschild radius. To generalize the four-velocity vector from Eq. (1) to Schwarzschild spacetime, we must consider every factor in both Eq. (1) and Eq. (2). To simplify the problem, we only consider stationary objects.

2. Metric Modification

For a stationary object, we only need to consider the $U^0$. Therefore, we attempt to modify the $dt/d\tau$. According to the Eq. (2), for a stationary object, $dr=0,d\theta =0,d\varphi =0$. Thus:

$$d{s}^2=-\left(1-{\displaystyle \frac{r_s}{r}}\right)c^{2}d{t}^2$$

(3)

For a time-like path $d{s}^2=-c^{2}d{\tau }^2$. Thus, we have:

$$d\tau =dt\sqrt{1-{\displaystyle \frac{r_s}{r}}}$$

(4)

Substituting Eq. (4) into Eq. (1), we obtain $U^0$ as:

$$U^0=c{\displaystyle \frac{dt}{d\tau }}={\displaystyle \frac{c}{\sqrt{1-\frac{r_s}{r}}}}$$

(5)

3. Consideration of the Significance of c in ${\mathit{U}}^{\mathbf{0}}$

According to Eq. (1), all the components of $U^{\mu }$ are defined by derivatives with respect to $d\tau$. Specifically, in $U^0$ the speed of light c is multiplied by the ration $dt/d\tau$. This implies we should use a speed of light that is also defined with respect to $d\tau$. Consequently, all the components of the four-velocity vector are expressed in a unified reference frame.

3.1. Incorporating the Effective Speed of Light into the Four-Velocity Vector

Let’s examine the effective speed of light in Eq. (2), under the conditions $d\tau =0,d\theta =0,d\psi =0$. For a time-like path $d{s}^2=-c^{2}d{\tau }^2$, we can derive the following:

$${\displaystyle \frac{dr}{dt}}=c\left(1-{\displaystyle \frac{r_s}{r}}\right)$$

(6)

Eq. (6) indicates that for a far-away observer in given time $dt$ the path length of light in Schwarzschild spacetime is not $cdt$, but rather $c(1-{\displaystyle \frac{r_s}{r}})dt$. On the other hand, according to Eq. (4) the proper time of stationary object in the same given time is $dt\sqrt{1-{\displaystyle \frac{r_s}{r}}}$. So, we can derive the effective speed of light as:

$$C_e={\displaystyle \frac{dr}{d\tau }}={\displaystyle \frac{c(1-\frac{r_s}{r})dt}{dt\sqrt{1-\frac{r_s}{r}}}}=c\sqrt{1-{\displaystyle \frac{r_s}{r}}}$$

(7)

As shown in Figure 1 The speed of light in flat spacetime is $c=ct/t$ which defines the worldline of light. The effective speed of light in Schwarzschild spacetime is slower then that in flat spacetime which defines the worldline of light in Schwarzschild spacetime.

By applying this metric modification to the speed of light c, denoted as $C_e$ in the Eq. (5), we obtain the new definition of $U^0$ in four-velocity vector in Schwarzschild spacetime as:

$$U^0={\displaystyle \frac{C_e}{\sqrt{1-\frac{r_s}{r}}}}={\displaystyle \frac{c\sqrt{1-\frac{r_s}{r}}}{\sqrt{1-\frac{r_s}{r}}}}=c$$

(8)

For a stationary object in Schwarzschild spacetime, we thus have $U^{\mu }$ as:

$$U^{\mu }=(c,0,0,0)$$

(9)

This means that from the perspective of a stationary object in Schwarzschild spacetime the rate of time flow is the same as it is in flat spacetime.

3.2. Momentum and Energy

According to the Eq. (9), the momentum of a stationary object can be calculated as:

$$P^{\mu }=\left(mc,0,0,0\right)$$

(10)

As we know in relativity, $P^0=E/C$. However, in the case of Schwarzschild spacetime, the effective speed of light is not c but $C_e$ in Eq.(7). Therefore, the energy of a stationary object is:

$$E=P^0*C_e=mc*c\sqrt{1-{\displaystyle \frac{r_s}{r}}}=m{c}^2\sqrt{1-{\displaystyle \frac{r_s}{r}}}$$

(11)

Eq. (11) indicates that the rest energy of a stationary object in Schwarzschild spacetime will decrease as it gets closer to the singularity as shown in Figure 2. According to the law of conservation of energy the lost rest energy is converted into kinetic energy during the process of free fall. That suggests a fundamental difference in energy transformation between an object continuously accelerating due to spacetime curvature in a gravitational field and an object continuously accelerating due to an external force in flat spacetime. The former does not gain energy but rather experiences a conversion of rest energy into kinetic energy under the specific spacetime structure. The latter, on the other hand, has its kinetic energy increased by the work done by other objects on it without losing its rest energy, resulting in an increase in total energy. Gravity is a manifestation of the geometry of spacetime rather than a force.

3.3. Gravitational Force Experienced by Objects

According to the analysis in Section 3.2, objects in Schwarzschild spacetime are not subject to any traditional forces but experience a transformation of energy forms under the influence of the spacetime geometric structure. To determine the force experienced by an object in Schwarzschild spacetime due to this energy transformation, we attempt to derive the force acting on the object using the kinetic energy formula. According to Eq. (11), the kinetic energy $E_k$ of an object in free fall in Schwarzschild spacetime is defined as the difference between the rest energy in flat spacetime and the rest energy in Schwarzschild spacetime.

$$E_K=m{c}^2\left(1-\sqrt{1-{\displaystyle \frac{r_s}{r}}}\right)$$

(12)

According to the definition of work, force is the derivative of kinetic energy with respect to distance.

$$F={\displaystyle \frac{d{E}_K}{dr}}=-{\displaystyle \frac{m{c}^2{r}_s}{r^2}}{\displaystyle \frac{1}{\sqrt{1-\frac{r_s}{r}}}}$$

(13)

This indicates a force opposite to the direction of r. Considering $r_s=2GM/c^2$ , we can get a more familiar equation for the force:

$$\left|F\right|={\displaystyle \frac{GMm}{r^2}}{\left(1-{\displaystyle \frac{r_s}{r}}\right)}^{-{\displaystyle \frac{1}{2}}}$$

(14)

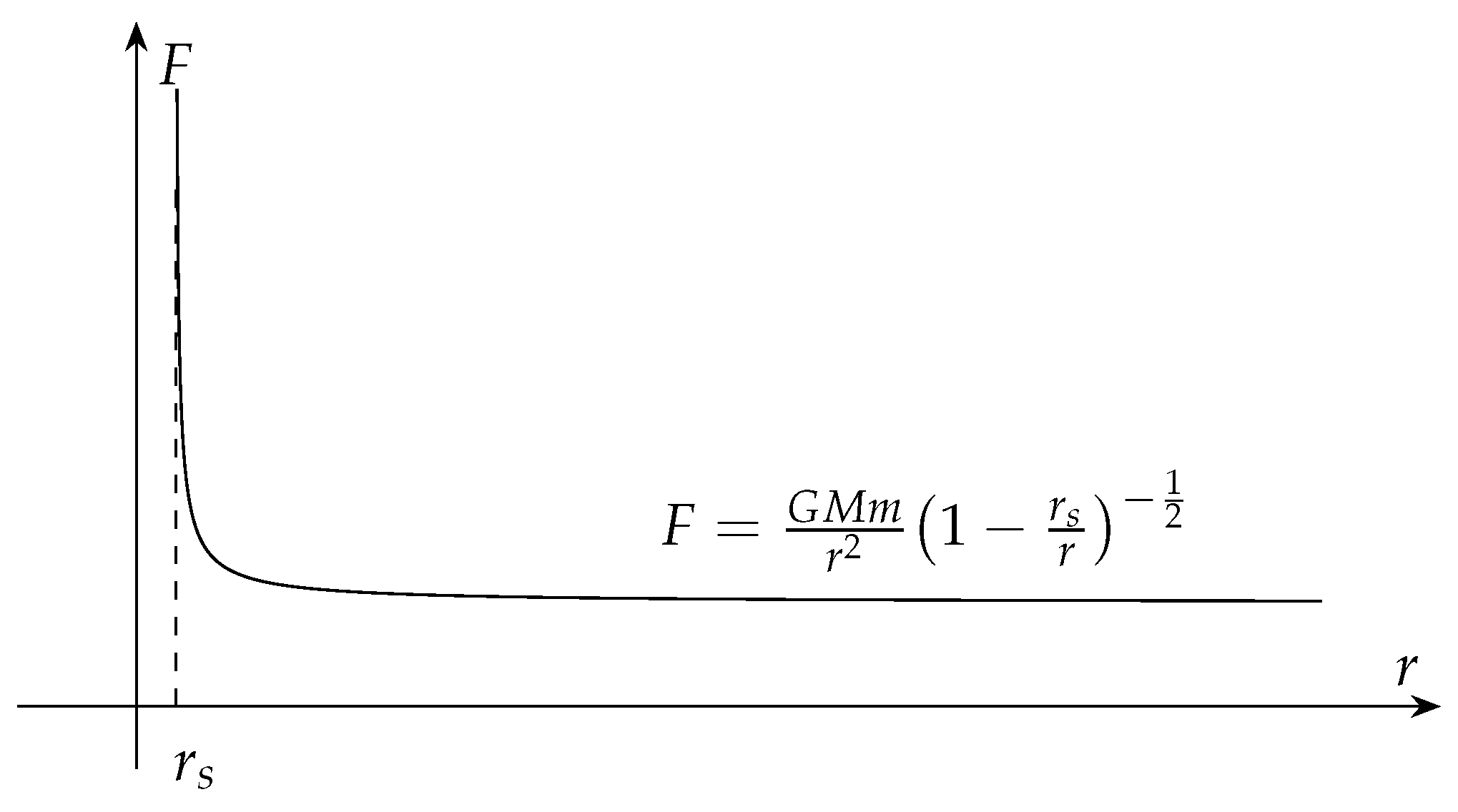
As shown in Figure 3, the force experienced by an object in Schwarzschild spacetime will increase as it approaches the singularity. On the other hand, as $r\to \infty$, Eq. (14) reduces to the Newton’s law for universal gravitation.

3.4. Gravitational Redshift

The energy of photons originates from the energy differences associated with electron transitions between various energy levels or orbits. In Schwarzschild spacetime, the reduction in the rest energy of objects results in a corresponding loss of energy in the emitted light. The redshift ratio is therefore expected to correspond to the ratio of the decrease in rest energy. Let $h{\nu }_1$ denote the energy of photons emitted by an object within Schwarzschild spacetime, and $h{\nu }_0$ represent the energy of photons emitted by the same object in a flat spacetime. The relationship between these energies can be expressed as:

$${\displaystyle \frac{h{\nu }_1}{h{\nu }_0}}={\displaystyle \frac{m{c}^2\sqrt{1-\frac{r_s}{r}}}{m{c}^2}}=\sqrt{1-{\displaystyle \frac{r_s}{r}}}$$

(15)

This equation demonstrates that the energy of the emitted photons in Schwarzschild spacetime is reduced by a factor of $\sqrt{1-{\displaystyle \frac{r_s}{r}}}$ compared to their energy in flat spacetime. Consequently, the frequency of the photons decreases, resulting in a gravitational redshift. This derivation aligns well with the traditional explanations of gravitational redshift, confirming that the observed redshift is a direct consequence of the gravitational time dilation described by the Schwarzschild metric [10].

3.5. Gravitational Lensing

In a gravitational field, the effective speed of light varies, and light propagating through Schwarzschild spacetime can be treated as if it were passing through a medium with a spatially varying refractive index. Consequently, when calculating the deflection of starlight, geometric optics methods can also be applied. The refractive index $n\left(r\right)$ of such a medium is defined as the ratio of the speed of light in a vacuum c to the effective speed of light in the medium $c_{\mathrm{eff}}\left(r\right)$:

$$n\left(r\right)={\displaystyle \frac{c}{c_{\mathrm{eff}}\left(r\right)}}={\displaystyle \frac{c}{c\left(1-\frac{r_s}{r}\right)}}={\displaystyle \frac{1}{1-\frac{r_s}{r}}}\approx 1+{\displaystyle \frac{r_s}{r}}$$

(16)

Please note that the $c_{\mathrm{eff}}\left(r\right)$ is derived from Eq. (6), which is the effective light speed with respect to $dt$. In this case we are calculating the lensing effect for the far-away observer. As per Equation (16), this expression aligns with the first-order approximation of equation [10] presented in reference [8]. So we can get the the total deflection angle of light caused by the solar gravitational field as:

$$\alpha ={\displaystyle \frac{2r_s}{b}}\approx 1.75arcseconds$$

(17)

Where the impact parameter b is the perpendicular distance between the asymptotic (unbent) path of the incoming light ray and the center of the Sun.

4. Results

In this paper, we explore the modifications necessary to extend the definition of the four-velocity vector from special to general relativity. We have derived a more plausible expression for the momentum and energy of stationary objects in Schwarzschild spacetime. This provides a clear explanation that gravitation is a manifestation of the geometry of spacetime rather than a traditional force, with gravitational potential energy reflecting the rest energy of objects. We have compared the results obtained using the concept of an effective speed of light with those derived from traditional general relativity for the problems of gravitational redshift and the deflection angle of starlight in the Sun’s gravitational field. The outcomes were found to be identical. This further demonstrates that introducing the effective speed of light is a valid and effective computational approach within the framework of general relativity. Our work contributes to a deeper understanding of the interplay between energy and gravity, paving the way for future explorations within the framework of general relativity.

5. Discussion

All calculations in this paper are based on the Schwarzschild solution of Einstein’s field equations. We have provided a new physical interpretation for the results of these calculations. This does not lead to any differences from the results of calculations of other studies that are also based on the Schwarzschild solution. However, the conclusion revealed in this paper regarding the decrease of rest energy of objects in a gravitational field may have implications for non-vacuum solutions of Einstein’s field equations, as it would affect $T_{00}$ . For example, this effect could manifest itself in the analysis of the energy-momentum tensor and spacetime metric for the interior of a rocky planet using Einstein’s field equations.

From the perspective of Quantum Field Theory (QFT), the observed decrease in an object’s rest energy within a gravitational field, characterized by the factor $\sqrt{1-r_s/r}$, can be interpreted as the spacetime metric reducing the energy required for quantum field excitations. Consequently, during free fall, the excess excitation energy is converted into the object’s kinetic energy. A similar transformation occurs with the object’s electromagnetic energy, highlighting how the spacetime geometry facilitates the conversion of internal energy forms into motion.