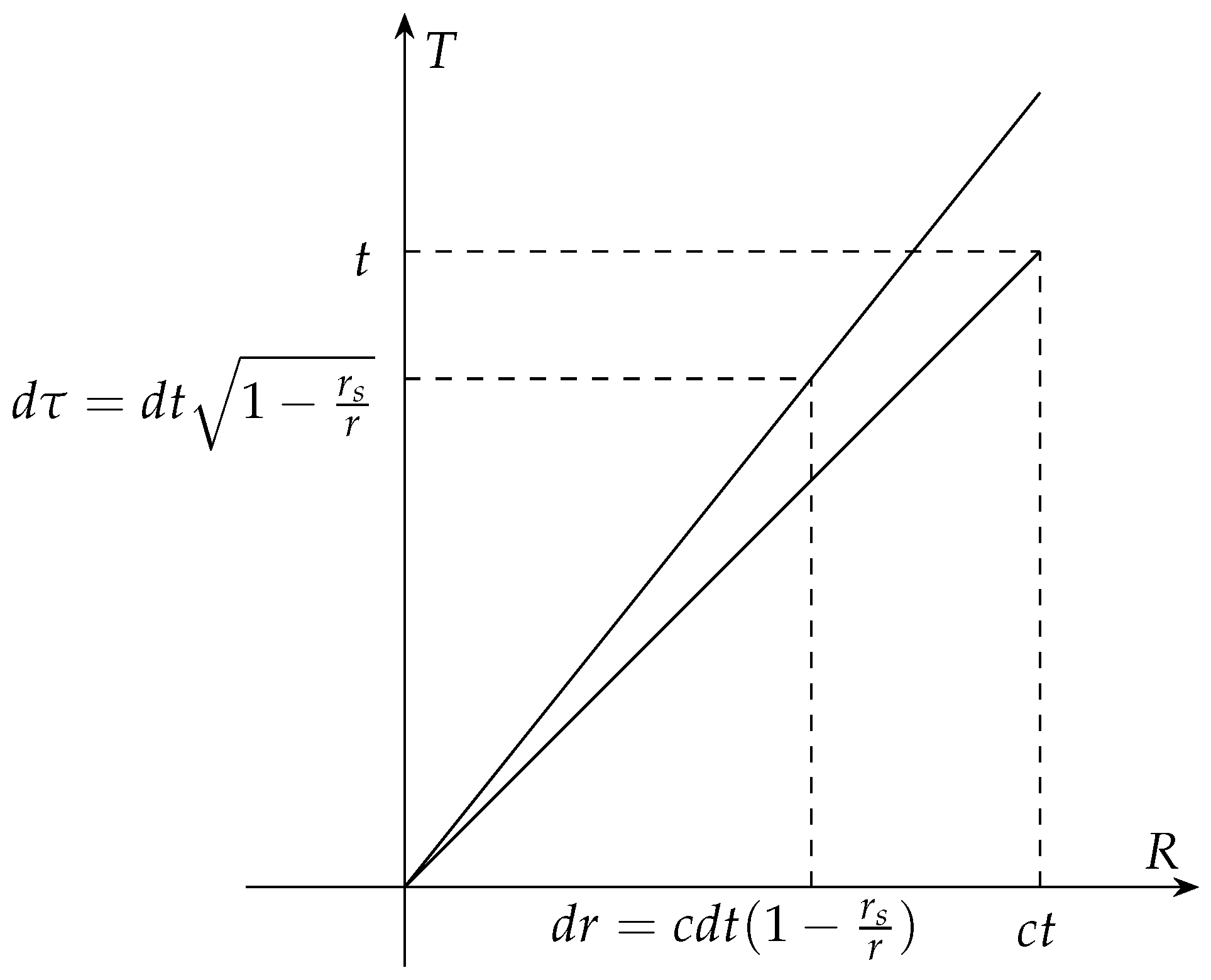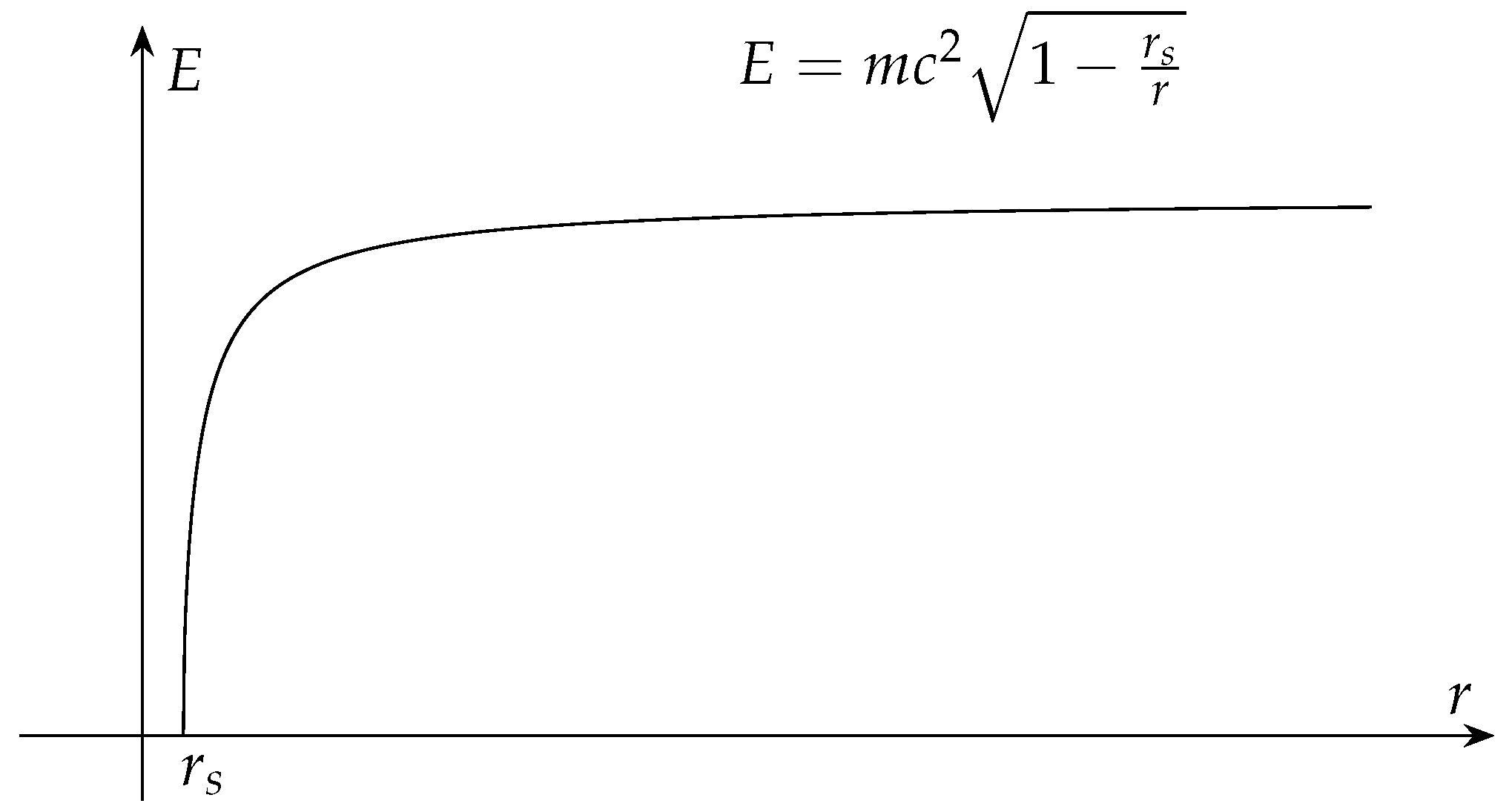1. Introduction
The four-velocity vector in special relativity is defined as [1], (p.10):
The Schwarzschild solution for Einstein field equations is [1, p.47]:
Where is the Schwarzschild radius. To generalize the four-velocity vector from Eq. (1) to Schwarzschild spacetime, we must consider every factor in both Eq. (1) and Eq. (2). To simplify the problem, we only consider stationary objects.
2. Metric Modification
For a stationary object, we only need to consider the
. Therefore, we attempt to modify the
. According to Eq. (2), for a stationary object,
. Thus:
For a time-like path
. Thus, we have [1, p.20]:
Substituting Eq. (4) into Eq. (1), we obtain
as:
Eq.(5), which could be derived from [2], (p.48, Eq.3.5), is commonly presented in traditional general relativity textbooks. It predicts an increase in rest energy within Schwarzschild spacetime, leading to the introduction of gravitational potential energy to explain energy transformations in gravitational fields. However, we will demonstrate that this interpretation is misleading because the consideration of the speed of light c has been neglected in both Eq. 5 and [2], (p. 48, Eq. 3.5).
3. Consideration of the Significance of c in
According to Eq. (1), all the components of are defined by derivatives with respect to . Specifically, in the speed of light c is multiplied by the ratio . This implies we should use a speed of light that is also defined with respect to . Consequently, all the components of the four-velocity vector are expressed in a unified reference frame.
3.1. Incorporating the Effective Speed of Light into the Four-Velocity Vector
Let’s examine the effective speed of light in Eq. (2), under the conditions
. For a time-like path
, we can derive the following:
Eq. (6) indicates that for a far-away observer in a given time
the path length of light in Schwarzschild spacetime is not
, but rather
. On the other hand, according to Eq. (4) the proper time of a stationary object in the same given time is
. So, we can derive the effective speed of light as:
As shown in
Figure 1 the speed of light in a flat spacetime is
, which defines the worldline of light. The effective speed of light in Schwarzschild spacetime is slower than that in flat spacetime, which defines the worldline of light in Schwarzschild spacetime.
Apply this metric modification to the speed of light c, denoted
in the Eq. (5), we obtain the new definition of
in the four-velocity vector in Schwarzschild spacetime as:
For a stationary object in Schwarzschild spacetime, we thus have
as:
This is the four-velocity vector of a stationary object in Schwarzschild spacetime, derived through rigorous mathematical analysis that accounts for the effective speed of light.
3.2. Momentum and Rest Energy
According to the Eq. (9), the momentum of a stationary object can be calculated as:
As we know in relativity
, but in case of Schwarzschild spacetime, the effective speed of light is not c but
in Eq.(7). Therefore, the rest energy of a stationary object in Schwarzschild spacetime is:
Eq. (11) indicates that the rest energy of a stationary object in Schwarzschild spacetime will decrease as it gets closer to the singularity, as shown in
Figure 2. According to the law of conservation of energy, the lost rest energy is converted into kinetic energy during the process of free fall. That suggests a fundamental difference in energy transformation between an object continuously accelerating due to an external force in flat spacetime and an object continuously accelerating due to spacetime curvature in a gravitational field. The former has its kinetic energy increased by the work done by other objects without losing rest energy. The latter, on the other hand, does not gain energy but rather experiences a conversion of rest energy into kinetic energy under a specific spacetime structure.
Why must an object’s rest energy decrease in a gravitational field? This can be understood by examining how the object’s electromagnetic energy changes within such a field. It is known that in a gravitational field, the electric field strength generated by a given amount of energy increases [2], (p. 121–123). To maintain a stable energy-state structure in Schwarzschild spacetime, this excess energy must be transformed into another form. A similar situation occurs with energies dominated by the other two fundamental forces to preserve the internal structure of the object within the gravitational field unchanged. This results in an energy gradient where the object’s rest energy in Schwarzschild spacetime decreases as r decreases. This energy gradient is the source of gravitation.
In the reverse process, an object is lifted in the gravitational field. By obtaining the work done by other objects, the lifted object gains energy and is able to establish a stable internal structure and energy level at a location farther away from the singularity.
3.3. Kinetic Energy and Gravitation
According to the analysis in
Section 3.2, objects in Schwarzschild spacetime are not subject to any traditional forces but experience a transformation of energy forms in special spacetime geometry. To determine the force experienced by an object in Schwarzschild spacetime due to this energy transformation, we attempt to derive the force acting on the object using the kinetic energy formula. According to Eq. (11), the kinetic energy
of an object in free fall in Schwarzschild spacetime is defined as the difference between the rest energy in flat spacetime and the rest energy in Schwarzschild spacetime.
According to the definition of work, force is the derivative of kinetic energy with respect to distance.
This indicates a force opposite to the direction of r. Considering
, we can get a more familiar equation for the force:
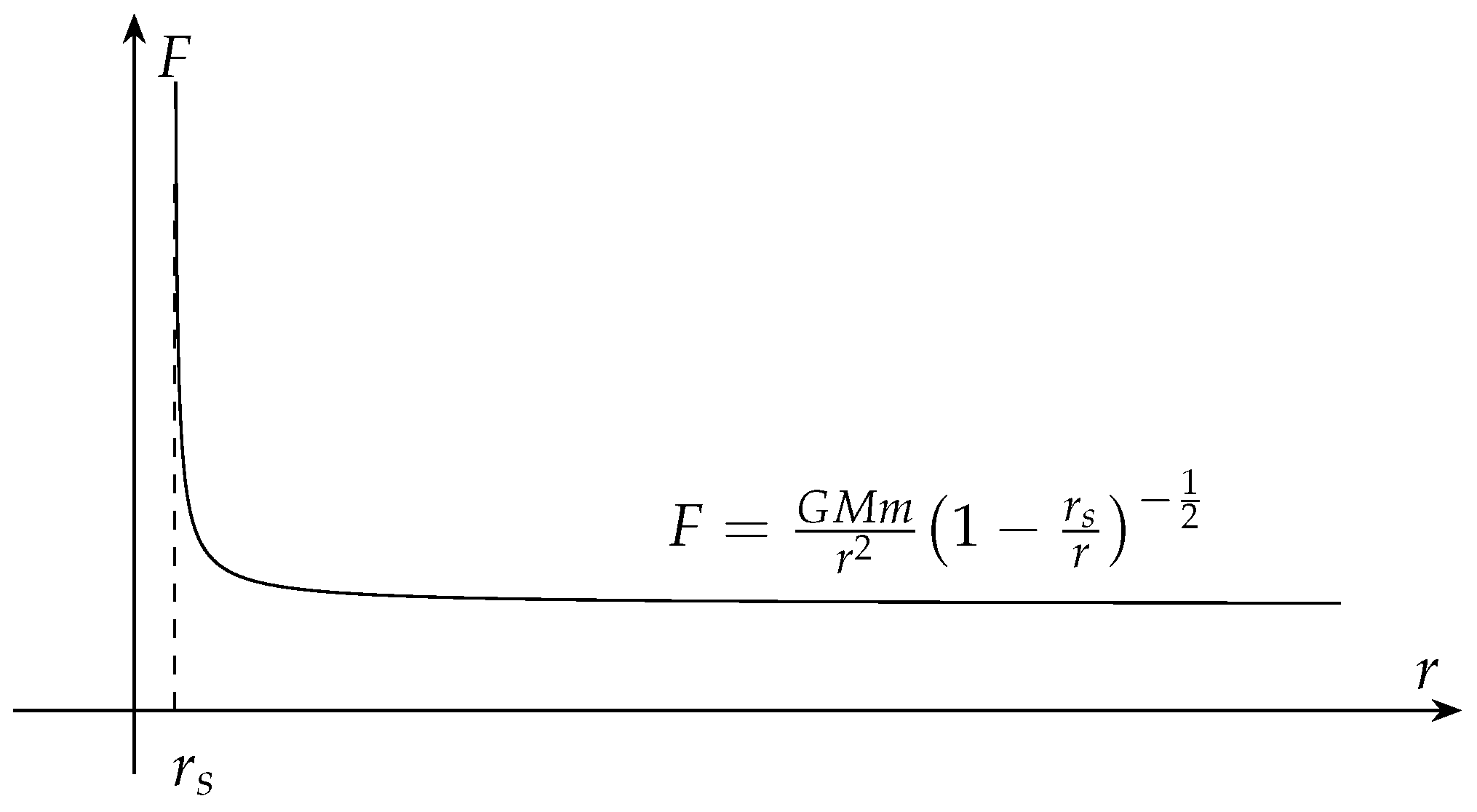
As shown in
Figure 3 the force experienced by an object in Schwarzschild spacetime will increase as it approaches the singularity. On the other hand, as
, Eq. (14) reduces to Newton’s law for universal gravitation.
4. Results
In this paper, we explore the modifications necessary to extend the definition of the four-velocity vector from special to general relativity. We have derived a more plausible expression for the momentum and energy of stationary objects in Schwarzschild spacetime. This result reveals that a free-falling object, continuously accelerating due to spacetime curvature in a gravitational field, experiences a conversion of rest energy into kinetic energy. Introducing the concept of gravitational potential energy is unnecessary. Instead, it is essential to incorporate the effective speed of light into the four-velocity vector. This approach necessitates re-examining all general relativity calculations that involve the speed of light. Our work contributes to a deeper understanding of the interplay between energy and gravitation, paving the way for future explorations within the framework of general relativity.
References
- Theodore Frankel,Gravitational Curvature: An Introduction to Einstein’s Theory,Courier Corporation, Jan 1, 2011.
- Bambi, C. Introduction to general relativity: a course for undergraduate students of physics. Springer; 2018 Jun 18.
- Ophir Flomenbom,The Gravity Field: In the Origin of Matter and Almost Everywhere Else, Reports in Advances of Physical Sciences, Vol. 8 (2024).
- Thibault Damour,Gilles Esposito,The Gravity Field: Testing gravity to second post-Newtonian order :a field-theory approach. Phys. Rev. D 1996, 53, 5541. [CrossRef] [PubMed]
- Tristan NeedHam, Visual Differential Geometry and Forms, Princeton University Press 2021.
- Steven Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, 1972.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).