Quantum Trans-Planckian Origin of the Universe and Multiverses

1. Introduction and Results

Most systems in the Universe have a "lifetime", they originate, decay, end (birth, grow, evolution, transformation...). We know approximately how systems in the universe begin or structurate: planets, stars, galaxies, clusters, superclusters,...

A black hole originates as the final state of a (massive enough ) star $M_{★}>M_{crit★}$, in fact the star transforms into a black hole. A black hole emit quantum mechanically and at the final evaporation stages when reaching the Planck mass scale (or a mass of the order of it), it transforms, e.g a phase transition occurs, into a quantum composite state which does decay into particles and radiation, as quantum heavy objects do, Refs. [1,2,3,4,5,7]. In turn, these quantum particles can collide themselves, desintegrate, or decay into another particle states ...In Nature, nothing is lost, all is transformed... [8]. A Scattering matrix or S operator could be then associated to the process, which is unitary and CPT invariant [1,12]

Let us physically formulate the question of how the Universe had started. (Or, more generally, how Multiverses started). By definition, the entire world is "Everything", (including, if any, the Multiverses). That is to say, the beginning was "Nothing", and had passed by a series of phase transitions, transforming eras, and evolutions, from Nothing or "Nothing(s)" to Something(s) and to Everything. The concept of entropy, gravitational entropy in particular, is well appropriated to describe "the arrow" of time and the cosmic gravitational history.

"Nothing" means Vacuum which, depending of its properties or state can have high activity and energy (quantum vacuum) or, on the contrary, be of very low energy, dilute and empty (classical vacuum), with the corresponding semi-classical or semi-quantum vacuum states. In fact, there are many and different vacuum states, e.g. vacua.

Our Universe today is mostly empty, filled by a very low energy (dark energy), e.g., a very dilute cosmological vacuum: This is a classical or semiclassical gravity vacuum, that is to say, our Universe today is not in a quantum gravity vacuum state, even if of course, a complete quantum theory of gravity must account for it too in its low energy limit.

The full quantum gravity domain is not reduced to be fixed to the Planck scale or to the neighborhoods of it, but it extends deeply in the highly quantum trans-Planckian domain:

$$E_{Planck}\le E<\infty ,0<L\le l_{Planck},0<t\le t_{Planck}$$

The era or state of "Nothing" from which the Universe could have started is a genuine quantum trans-Planckian era, which is the vacuum period before the Planck time, (the crossing scale), followed by the known inflation period which is a semiclassical (or semiquantum) gravity vacuum state, and followed by the different classical gravitational eras, radiation and matter dominated eras, until the today low energy vacuum phase (today dark energy).

The state of our Universe today is the most classical gravitational state: the most classical cosmological vacuum, the most diluted and empty, termed voids by the astronomical observations, with very low energy, (${10}^{-122}$ in Planck units) and very high gravitational entropy (${10}^{122}$, the highest physical magnitude in the Universe untill now). This is the classical or semiclassical dark energy de Sitter state of the Universe today.

The fact that the latest classical/semiclassical state of the Universe and the early quantum/semiclassical inflation state of the Universe are both de Sitter (or quasi-de Sitter) vacua states, is a manifestation of the classical-quantum (wave-particle, de Broglie) duality of Nature extended across and beyond the Planck scale to include gravity in the trilogy Refs [9,10,11].

In this paper we go forward in the physical understanding of the origins of the Universe and Multiverses with Planckian and trans-Planckian physics, classical-quantum gravity duality and quantum space-time in this context. We go forward in completing the Standard Model of the Universe back in time in the far past before inflation in agreement with observations.

The quantum trans-Planckian eras in the far past universe, determine the post-Planckian eras, e.g. inflation and the cosmological vacuum energy until today dark energy, namely the evolution from the quantum gravity very early phases to the semi-classical gravity and classical gravity phases, and the arrow of time as determined by the gravitational entropy.

The complete universe is composed of two main phases, the Planck scale being the transition scale between the two: (i) The quantum pre-Planckian or trans-Planckian phase $0<{10}^{-61}{t}_P\le t\le t_P$ which is a truly quantum gravity phase, and (ii) the semiclassical and mostly classical gravity post-Planckian universe $t_P\le t\le t_{today}={10}^{61}{t}_P$, $t_P$ being the Planck time. The pre-Planckian era could be tested indirectly through its post-Planckian observables, e.g. primordial graviton signals, inflation and the CMB observables until the today dark energy.

String theory entails multivacua or "multiverses", although it have serious problems to describe or reproduce our own universe, (except to introduce fine tunings or additional hypothesis or principles), and similarly in order to reproduce the observed/detected particle physics phenomenology described by the robustly tested Standard Model of Particle Physics.

The aim of a theory describing the origin of the Universe from "Nothing" could be :

"From the theory of Nothing to the theory of Everything".

In general, the Quantum trans-Planckian Vacuum is neccesarily of de Sitter type or Anti-de Sitter type nature, depending of the physical context involved, that is to say: (i) de Sitter vacuum (positive constant curvature) in the Universe and black hole interiors. (ii) Anti-de Sitter vacuum (negative constant curvature) for the particle physics vacuum. Vacuum dominance at the trans-Planckian era (eg the Universe arising from vacuum) implies that the Universe is a de Sitter or quasi de Sitter phase in its most earliest stage.

In Sections IV and V of this paper we describe the quantum de Sitter universe covering the different de Sitter regimes. The de Sitter vacuum is a simple and smooth constant curvature background without any physical singularity, it is maximally symmetric and can be described as a hyperboloid embedded in Minkowski space- time with one more spatial dimension.

We describe in Section V the de Sitter manifold with imaginary time, namely the complete (quantum) instanton: The classical gravity Gibbons-Hawking instanton, is cutted at the horizon: The classical de Sitter instanton is regular but not complete. The quantum trans-Planckian region which naturally does appear in quantum space-time allows to complete the classical de Sitter instanton. The quantum de Sitter instanton is thus both: regular and complete.

With these results we describe (in Section VI) the complete Partition function covering all (classical and quantum) gravity regimes, and the total gravity entropy, including the quantum gravity (trans-Planckian) entropy. This allows us to discuss the comparison between the Quantum Field Theory (point particle) entropy (without gravity), the gravitational entropy, and the quantum extended object (string) entropy. This is particularly enlighting here in terms of the ordered and non ordered partition number functions.

Our studies here and in Refs [9,10,11,12] show clearly that the vacuum energy everywhere in the universe is the remnant of the initial trans-Planckian vacuum energy: the known (post-Planckian) inflation era is the direct (and most diluted) continuation of this vacuum. And in turn, a remnant of this vacuum does yield the dark energy today: A Bose-Einstein condensate, with the axion (and a lightest neutrino) both in the meV = ${10}^{-3}$ eV mass scale, being the best candidate for dark energy, Ref. [13].

The Hubble constant is in fact a Hubble $H\left(t\right)$ rate, which value today is $H_0=H\left(t_0\right)$. Mainly in the early universe , such $H\left(t\right)$ is truly associated to a early $\Lambda \left(t\right)$ rate, which most classical remaining in the present Universe is the cosmological vacuum energy today $\Lambda \left(t_0\right)={\Lambda }_0$.

These results allow a clarification of dark energy as the vacuum cosmological energy or cosmological constant [9,10,11,12] : The huge difference between the observed low value of the cosmic classical vacuum energy $\Lambda$today and the theoretical evaluated value of the quantum particle physics vacuum ${\Lambda }_Q$, is correct and must be physically be like that, because the two values correspond to two huge different physical vacua states and eras. The low observed $\Lambda$ value today (${10}^{-122}$ in Planck units) corresponds to the classical, large and dilute (mostly empty) universe today, while the computed quantum value ${\Lambda }_Q$ corresponds to the quantum, small and highly dense energetic universe in its far remote (trans-Planckian) past, and this is consistent with its extremely high, trans-Planckian, value (${10}^{122}$ in Planck units), and both values are dual of each other in the precise sense of the classical-quantum gravity duality.

In this paper we analyze too the new quantum vacuum region inside the Planck scale hyperbolae which delimitate the quantum light cone in the de Sitter space-time. In Section IV we describe the global quantum de Sitter space-time structure; The quantum Penrose- de Siter diagramme.

Is important to mention that the gravitational length $L_G$ is the Universe size in the classical/semiclassical regime, while the quantum length (the Compton length) $L_Q=l_P^2/L_G$ is the Universe size in the quantum gravity regime. Similarly, for the Quantum mass $M_Q=m_P^2/M$, as well as for quantum surface gravity $K_Q={\kappa }_P^2/K_G$, and the other physical gravitational quantities or observables, (Temperature, Entropy, and other observables). That is the reason why we have defined complete or total$\left(QG\right)$ variables: $O_{QG}=O_{QG}(O_G,O_Q)$ which include both, the known gravity $\left(G\right)$ variables and the quantum $\left(Q\right)$ variables. The $QG$ variables reduce to each component (G or Q) in each of the corresponding sectors or regimes $G>>Q$ or $Q>>G$; they provide in particular the Planck scale for $Q=G$, and they do result invariant under the classical-quantum gravity duality through the Planck scale: $Q\leftrightarrow G^{-1}$.

The quantum space-time is totally regular. This is also true in the quantum Schwarschild-Kruskal space-time : the quantum hyperbolae $(T^2-X^2)=\pm \sqrt{2}$ which replace the classical singularity ${(T^2-X^2)}_{classical}(r=0)=\pm 1$, lie outside the allowed quantum levels ${(T^2-X^2)}_n=(2n+1),n=0,1,...$ and they are excluded by quantum physics: The singularity is removed out from the quantum space-time, Refs [1,3,10,12]. More results of this paper and remarks are summarized in the Conclusions Section VIII.

This paper is organized as follows: In Section II we describe the cosmic history extended back in time before inflation, thus covering its different gravity phases: classical, semiclassical and quantum-Planckian and transplanckian- phases and their properties, including the gravitational entropy and temperature. In Section III we discuss the different notions of vaccua and the origin of the universe and multiverses from "Nothing" which is truly trans-Planckian. In Section IV we describe the quantum de Sitter space-time structure with quantum space-time coordinates. In Section V we describe the complete, (eg with the quantum gravity phase included), imaginary time de Sitter instanton. Section VI we discuss the complete Partition Function and the complete quantum gravity de Sitter entropy. Section VII presents the expansion and contraction phases of the Universe and multiverses (bangs and crunchs) as a quantum gravity foam of borning and dying universes, quantum and decaying back holes, particles and / or strings and radiation. Section VIII presents our conclusions.

2. Cosmic Gravitational History. The New Earliest Trans-Planckian Era

The gravitational history of the universe before the Inflation era and the current picture can be extended by including the quantum precursor phase within the standard model of the universe in agreement with observations. Quantum physics adds a new quantum Planckian and trans-Planckian phase of the Universe from the Planck time $t_P$ until the extreme past ${10}^{-61}{t}_P$, which is an upper bound for the origin of the Universe, with energy $H_Q={10}^{61}{h}_P$, in a similar manner the present age of the Universe is a lower bound to the (unknown) future age.

The classical large dilute Universe today and the highly dense very early quantum trans-Planckian Universe are classical-quantum duals of each other in the precise meaning of the classical-quantum duality. This means the following: The classical Universe today $U_{\Lambda }$ is clearly characterized by the set of physical gravitational magnitudes or observables (age or size, mass, density, temperature, entropy) $\equiv (L_{\Lambda },M_{\Lambda },{\rho }_{\Lambda },T_{\Lambda },S_{\Lambda })$:

$$U_{\Lambda }=(L_{\Lambda },M_{\Lambda },{\rho }_{\Lambda },T_{\Lambda },S_{\Lambda })$$

(1)

The highly dense very early quantum Universe $U_Q$ is characterized by the corresponding set of quantum dual physical quantities $(L_Q,M_Q,{\rho }_Q,T_Q,S_Q)$ in the precise meaning of the classical-quantum duality:

$$U_Q=(L_Q,M_Q,{\rho }_Q,T_Q,S_Q)$$

(2)

$$U_Q={\displaystyle \frac{u_P^2}{U_{\Lambda }}},u_P=(l_P,m_P,{\rho }_P,t_P,s_P)$$

(3)

$u_P$ standing for the corresponding quantities at the fundamental constant Planck scale, the crossing scale between the two main (classical and quantum) gravity domains. The classical $U_{\Lambda }$ and quantum $U_Q$ Universe eras or regimes (classical/semiclassical eras of the known Universe and its quantum Planckian and trans-Planckian very early phases), satisfy Equations (1)-(3). The total Universe $U_{Q\Lambda }$ is composed by their classical/semiclassical and quantum phases:

$$U_{Q\Lambda }=\left(U_Q+U_{\Lambda }+u_P\right)$$

(4)

Subscript $\Lambda$ -or equivalently H for Hubble Lemaitre- stands for the classical magnitudes, Q stands for Quantum, and P for the fundamental Planck scale constant values.

The total or complete (classical plus quantum) physical quantities are invariant under the classical-quantum duality: $H\leftrightarrow Q$ (or $\Lambda \leftrightarrow Q$) as it must be: This means physically that: (i) what occurred in the quantum phase before $t_P$ determines through Equations (1)-(4) what occurred in the classical phase after $t_P$. And: (ii) what occurred in the quantum phase before the Planck time $t_P$ is the same observable which occurred after $t_P$ but in a different physical state in the precise meaning of Equations (1)-(4). That is to say: The quantum quantities in the phase before $t_P$, are the quantum precursors of the classical/semiclassical quantities after $t_P$.

As the wave-particle duality at the basis of quantum mechanics, the wave-particle-gravity duality is reflected in all cosmological eras and its associated quantites, temperatures and entropies.

Cosmological evolution goes from a quantum trans-Planckian vacuum energy phase to a semiclassical accelerated era (de Sitter inflation), then to the classical known eras until the present classical de Sitter phase.

The classical-quantum or wave-particle-gravity duality specifically manifests in this evolution, between the different gravity regimes, and could be view as a mapping between the asymptotic (in and out) early and late (today) states of the Universe characterized by the sets $U_Q$ and $U_{\Lambda }$ and thus as a Scattering-matrix (S-matrix in time) description: The most early quantum trans-Planckian state in the remote past being the "in-state", and the very late classical dilute state being the far future or today "out-state", Refs [9,10,11,12,13].

The quantum space-time structure consists of discrete levels of odd numbers Refs [10,12]

$$X_n^2=(2n+1),T_n^2=(2n+1)\left(inPlanckunits\right),n=0,1,2....$$

(5)

$$(X_n,T_n)andthe\mathit{mass}\mathit{levels}being\sqrt{(2n+1)}$$

(6)

The Planck scale $:(X,T)=1$ (in Planck units) is the fundamental level $(n=0)$ from which the levels $(X_n,T_n)$ go to the quantum post Planckian and semiclassical levels (low and intermediate n) levels, to the classical (large n) levels. Asymptotically, for very large n the space-time becomes continum.

While the Quantum trans-Planckian levels go as :

$${(X_n,T_n)}_Q=1/\sqrt{(2n+1)},$$

(7)

For very high n, the quantum ${(X_n,T_n)}_Q$ space-time levels are highly excited (deep in the trans-Planckian domain), and desexcite gradually till $n=0$. The total quantum levels cover all the range of scales from the smallest ones in the ${10}^{-61}{l}_P$ scales in the extreme past ${10}^{-61}{t}_P$ of the initial trans-Planckian phase to the largest cosmological scales and time ${10}^{61}{t}_P$ today, passing through the Planck scale $(l_P,t_P)$, thus covering the two principal phases: post and pre Planckian phases respectively.

3. Vacuum and Vacua. Universe and Multiverses

If the Universe started from Nothing, which is the possibility we consider here as the most natural to address the question of the origin of the Universe, the Vacuum state from which the Universe have started must be the most remote past vacuum state, the state with the lowest entropy, entropy being the appropriate concept for describe this quantum trans-Planckian (or quantum gravity) era. We consider this Quantum Gravity (QG) Vacuum of the origin as the more general initial "In" Vacuum, the "Absolute Nothing" or Total Vacuum

$$|{\Psi }_{TotalVacuum}\rangle ,$$

as a superposition of the various possible vacua, multivacua or "relative vacua":

$$|{\Psi }_{\left(vac1\right)}\rangle ,|{\Psi }_{\left(vac2\right)}\rangle ,....,|{\Psi }_{\left(vacn\right)}\rangle ,$$

with different amplitude probabilities: $A_1,...,A_n$, from which the different Universes, Multiverses, are created, in particular our Universe, namely:

$$|{\Psi }_{QGVacuum}\rangle =A_1|{\Psi }_{\left(vac1\right)}\rangle +A_2|{\Psi }_{\left(vac2\right)}\rangle +....+A_n|{\Psi }_{\left(vacn\right)}\rangle ,n=1,2,....$$

(8)

The origin initial state:

$${|\mathrm{In}\mathrm{Vacuum}\rangle }_{t=t_{in}}\equiv {|\mathrm{Nothing}\rangle }_{t=t_{min}}\equiv |{\Psi }_{QG-Vacuum}\rangle ,$$

is a state of quantum trans-Planckian nature, and therefore with high Planckian and trans-Planckian energy fluctuations, namely of "foam" nature, that is to say:

We consider this foam vacuum as an ensemble or "soup" of borning and "crushing" (or "dying") universes. The big crushing of the dying universes are Planckian and trans-Planckian events which are in turn borning events or big fluctuations (regular "big bangs") from which borning universes arise: These are all finite energy realisations, that is regular realisations of the "big bang(s)".

Notice that all these explosions, bangs, crushings do not reach any infinity energy nor infinity curvature, nor any other infinity magnitude. They are totally finite, without singularity. The classical - quantum gravity duality (namely, the wave - particle duality including gravity) precludes realisations of physical magnitudes having infinity values, Refs [1,9,10,11,12]. This is not a "principle" nor an "assumption" but the consequence of the "classical - quantum duality of Nature, which is universal, irrespective of the type of the fundamental interaction, number or type of dimensions, existence or not of compactifications, etc.

Moreover, and consistently, this framework strongly supports the idea that a Quantum Theory of Gravity must be a Finite Theory (which is more than a renormalizable theory), as we discussed too in Refs [1] and [14]. The idea of a renormalizable theory for quantum gravity does not apply at the conceptual level, and besides that, as is known, it does not work technically neither.

The finite quantum gravity scale explosions (regular big crushings and regular big bangs) in the most remote state, which is the "In state" ${|InVacuum\rangle }_{t=t_{in}}$ of the Universe could include too the final states of the black hole evaporations: At these last Planckian and trans-Planckian stages, black holes are quantum composite particles which necessarily decay as pure quantum particles states: This quantum decay is like the decay of a heavy particle or a soliton and is non-thermal.

The In Vacuum State ${|InVacuum\rangle }_{t=t_{in}}$, or Total Absolute Vacuum $|{\Psi }_{TotalVacuum}\rangle$, is the Trans-Planckian Vacuum State at the initial minimal time of the Universe $t_{in}$:

$$0<t_{in}<<t_{Planck}\equiv t_P$$

and with initial minimal Entropy $S_{in}$:

$$0<S_{in}<<S_{Planck}\equiv s_P$$

In the Universe evolution, $0<t\le t_{today}={10}^{61}{t}_P$ the classical-quantum gravity relations Eqs. (2)-(3) applied to our Universe fix the most remote past time or the minimal time, and the minimal Entropy of the Universe to be in the range:

$$0<t_{in}\le {10}^{-61}{t}_P:\mathrm{minimal}\mathrm{time}\mathrm{range}$$

(9)

$$0<S_{in}\le {10}^{-122}{s}_P:\mathrm{minimal}\mathrm{entropy}\mathrm{range}$$

(10)

The S-matrix as a Classical-Quantum Gravity Duality Transform:

The trans-Planckian (Quantum Gravity) phase is linked to the non trans-Planckian phases $t>t_P$, (Semiclassical Gravity and Classical Gravity phases), by a Quantum-Classical Duality transform across the Planck scale, the crossing scale, and conversely.

The Semiclassical Gravity phase is the usual (post-Planckian) Inflation era, followed by the known (radiation and matter dominated) stages untill the today era, which is the most classical gravitational state: This state have the biggest known size, largest time, maximal known Entropy (the biggest physical number ${10}^{122}$ in Planck units), and the minimal $\Lambda$ vacuum energy (${10}^{-122}$).

There is a classical- quantum duality transform among the different stages through the Universe evolution, which acts as a mapping or S- matrix transform between the asymptotic initial Vacuum state, namely $|InVacuum\rangle$, ("Nothing") at an initial time $t_{in}$, and the late Vacuum State $\left|LateVacuum\right(t)\rangle$, ("Everything") at the today era:

$$\left|LateVacuum\right(t)\rangle =S(t\left)\right|InVacuum\rangle$$

(11)

$$|\Lambda \left(t\right)\rangle =S\left(t\right)|\Lambda (t=t_{in})\rangle$$

(12)

The Evolution operator is like a Scattering matrix $S\left(t\right)$ in time, and must be unitary $S^{+}S=S{S}^{+}=1$. Or, in terms of the today time$t_0$:

$$|\Lambda \left(t\right)\rangle =S\left(t\right)S^{-1}\left(t_0\right)|\Lambda (t=t_0)\rangle$$

(13)

This $S-matrix$ evolution is a classical-quantum gravity duality mapping relating small quantum (trans-Planckian) scales to large classical scales, passing across the Planck scale (the crossing scale): After the Planck scale, the semi-classical (or semi-quantum) gravity scales and regimes do occur: as Inflation and those stages of classical gravity plus QFT particle physics, untill the present era (today dark energy).

A component of the Vacuum energy of the initial $|InVacuum\rangle$ state goes to the Vacuum (GUT energy) state of Inflation $|Inflation\rangle$, which dilutes afterwads into the remaining Vacuum energy of the today state (Dark Energy), namely $|{\Lambda }_{(t=t_0)}\rangle$, and we have the relation:

$$|\Lambda \left(t_{inflation}\right)\rangle =S\left(t_{inflation}\right)|{\Lambda }_{(t=t_{in})}\rangle$$

(14)

Thus,

$$|\Lambda \left(t\right)\rangle =S\left(t\right)S{\left(t_{inflation}\right)}^{-1}|\Lambda \left(t_{inflation}\right)\rangle ,$$

(15)

which implies in particular the today state: $\left|\Lambda \right(t_0)\rangle$ for $t=t_0$.

The dis-excitement of the states goes from the most highly excited quantum discrete Vacuum trans-Planckian levels ($n={10}^{122}$), to the Planck level ($n=0$) at the Planck time $t_P$, and as time increases (and n increases $n=1,2,....,{10}^{122}$) it goes into a continuum classical gravitational Vacuum today of very low energy: ${\Lambda }_{today}\equiv \Lambda \left(t_0\right)={10}^{-122}$ (in Planck units), today dark energy.

The cosmological Vacuum energy of the Universe today $\left|\Lambda \right(t_0)\rangle$ is well described self-consistently (with back reaction included) by Quantum Field Theory in a semiclassical expanding FRW universe, as a Bose-Einstein condensate, with the best candidate being an axion in the $meV={10}^{-3}eV$ mass scale and a lightest neutrino in the same ${10}^{-3}eV$ mass scale, Ref. [13].

Cosmological Vacuum Energy: We prefer the concept name cosmological vacuum energy (and not cosmological "constant") because:

The classical-quantum gravity duality Equations (2)- (3) and its quantum levels Equations (5), (6), (7) imply a varying vacuum energy, e.g a varying ${\Lambda }_n$ at each discrete level n in time, and yield support to it: $H_n$ varies and ${\Lambda }_n$ varies too, even if of course this variation is very mild. Inflation needs too such a vacuum $\Lambda$ variation in time. Moreover, what it is called Hubble constant is in fact a Hubble rate $H\left(t\right)$ which present value today $H\left(t_0\right)$ is the Hubble constant $H_0$. $\Lambda$ is precisely associated to H . It should be admitted too that what is called $\Lambda$ cosmological constant would be in fact a $\Lambda$ rate: $\Lambda \left(t\right)$ with $\Lambda \left(t_0\right)={\Lambda }_0$ its present value, as $H\left(t_0\right)=H_0$ is the present value of H.

We thus consider the S-matrix for the general universe evolution, from its origin trans-Planckian era $0<t\le t_P$ to its post-Planckian eras: (Inflation and late known eras), as a mapping or quantum - classical gravity duality transform from a state into another, from the initial to the final state. Quantum gravity implies a quantum discrete spectrum of levels for the gravitational physical magnitudes: mass, energy, size, time, entropy. Refs [1,3,10,12]. And such evolution imply inherently cosmic gravitational phase transitions:

Cosmic Gravitational Phase Transition: The passing from the quantum gravity discrete levels to the semiclassical gravity and the classical gravity continuum states can be considered as the effect of a gravitational phase transition into a semiclassical gravity spectrum and classical gravity continuum spectrum. And this phase transition could arise a graviton condensate state:

The remote past quantum trans-Planckian "soup" or "foam" is a gaz of borning (expanding) and dying (crushing) universes, each of them being of the de Sitter nature, which is the typical vacuum state, because among other properties, de Sitter state has Maximal Symmetry, it is a constant density vacuum , of constant curvature, totally regular, without any singularity, fully appropriate for a vacuum state, and having negative quantum pressure. We do correlate here with the Coleman statement (although in another, pure particle physics context, not in de Sitter context) Ref. [15]:

The Symmetries of the Vacuum are the Symmetries of Nature.

• The crushing dying universes would be the corresponding reverse time events of the borning and evolving universes. This ensemble of states can also include the latest states of black hole evaporation because they are of similar trans-Planckian de Sitter nature and then decaying (non thermally) in pure (non mixed) states as gravitons, particles and radiation. In such a self-gravitational gaz (whatever being their components: particles, black holes, and or strings), a typical phase transition towards a condensate, larger "single" state, does appear.
• Such gravitational phase transition is a common feature to several contexts: from Hagedorn and the Carlitz phase transition to the "long string" (Refs [16,17]), the
  de Vega - Sanchez self-gravitating bosonic phase transition (Refs [2,18,19,20,21]), the different types of black hole - string-particle phase transitions, (Refs [4,5,6,7]). Such a borning or emergent condensate state is a regular (without any singularity) constant curvature gravitational vacuum : the de Sitter vacuum.
• Such a gravitational phase transition with its vacuum condensate does occur at the two most separated asymptotic universe states or cosmic stages: the initial or most past remote quantum state $(0<t\le t_P)$ and the latest classical state, the today dark energy era, (besides of occurring under different physical conditions in other intermediate eras of the universe and its known astrophysical systems which are not the subject here). Both extreme cosmic states (initial and today stages) are precisely classical- quantum cosmological duals of each other in the precise meaning of the classical- quantum gravity duality Equations (2)-(3)., here classical- quantum cosmology duality.

The dynamical explicit descriptions of such gravitational phase transitions and the expressions for their corresponding complete physical magnitudes, is beyond the scope of this paper, but on the basis of all our previous results these gravitational phase transitions all have a square root branch point at the transition, eg in the temperature or its equivalent magnitude). For the case of only de Sitter universes, the expression would be of the type (leading order):

$$S_Q\left(H\right)={\displaystyle \frac{{\kappa }_B}{2}}log\sqrt{1-{\displaystyle \frac{T}{T_Q}}}$$

(16)

Let us recall that the Planck mass $m_{Planck}={10}^{-5}gr$ is the heaviest mass for a quantum elementary particle compatible with locality, (point particles with masses larger than $m_{Planck}$ have quantum sizes $L_Q$ - Compton lengths - smaller than their classical gravitational radius $L_G$). Quantum gravitational states are necessarily trans-Planckian, with masses larger than $m_{Planck}$, and being composite, eg having internal structure and discrete levels, Refs [1,12].

In the Euclidean (imaginary time) path integral of gravity Ref. [24], the Euclidean action provides the zero order term to the gravitational entropy S and the tunneling probability is

$$P=Aexp[-S]$$

(17)

with A the factor amplitude. Is not our aim here to discuss the well known several proposals or prescriptions for the wave function amplitude, but our aim is to include here the new component with which the trans-Planckian part of the gravitational action does complete this picture.

The total $Q\Lambda$ (classical and quantum) gravitational entropy $S_{Q\Lambda }$ derives from the general expression

$$S_{Q\Lambda }=(A_{Q\Lambda }/4l_P^2)k_B,$$

(18)

where the total area $A_{Q\Lambda }$ is precisely:

$$A_{Q\Lambda }=4\pi L_{Q\Lambda }^2=4\pi {(L_Q+L_{\Lambda })}^2=(A_Q+A_{\Lambda }+2a_P)$$

Recall that

$$L_Q=l_P^2/L_{\Lambda }\mathrm{and}{a}_P=4\pi l_P^2$$

As a consequence,

$$S_{Q\Lambda }=2s_P+S_{\Lambda }+S_Q=2s_P[1+{\displaystyle \frac{1}{2}}({10}^{+122}+{10}^{-122})]$$

(19)

$$s_P=\left({\kappa }_B{a}_P\right)/\left(4l_P^2\right)=\left(\pi {\kappa }_B\right)$$

$s_P$ being the Planck entropy.

The total $Q\Lambda$ gravitational entropy is the sum of its three gravitational components : classical gravity entropy (subscript $\Lambda$), quantum trans-planckian entropy (subcript Q) and Planck value entropy (subscript P) corresponding to the tree gravity regimes. The term $2s_P$ arises from the duality between the quantum and classical lengths $L_Q$ and $L_{\Lambda }$ across the Planck scale. The factor 2 reflects the complete (global) covering: The Planck scale being the bordering or crossing scale common to the two (classical and quantum) Q and $\Lambda$ domains.

Therefore, the total (complete) probality is:

$$P=exp[-(2s_P+S_{\Lambda }+S_Q)]=exp[-s_P(2+{10}^{+122}+{10}^{-122})]$$

(20)

The new results and implications of this expression in our context here are the following:

(i) The truly quantum gravity (trans-planckian) component of the gravitational entropy $S_Q={10}^{-122}$ dominates the tunneling probability P of the birth of the Universe from "Nothing", which is almost equal to 1. Therefore, this clearly shows that the transplanckian component is enterely consistent with (and does strongly support to) the "creation" of the Universe as a quantum process (tunneling) Ref. [22] from the Vacuum.

(ii) In the non- complete picture (without the trans-Planckian domain), the gravitational euclidean action is enterely classical or semiclassical, ie $S_{\Lambda }={10}^{+122}$, its value is huge, and the tunneling probability is extremely small, while in the complete picture here the value is the opposite.

(iii) The gravitational entropy $S_{\Lambda }$ of the present time large classical universe is a very large number, consistent with the fact that the universe today contains a very huge amount of information. Moreover, to reach such a huge size and entropy today ${10}^{+122}$, the universe in its very beginning state should have been in a hugely energetic quantum initial vacuum, consistently with its ${\Lambda }_Q={10}^{+122}$.

$S_{\Lambda }={10}^{+122}$ and ${\Lambda }_Q$ are the same numbers (in Planck units). As well as $S_Q={10}^{-122}$ and $\Lambda$ are the same numbers. $S_{\Lambda }$ and $S_Q$ are quantum gravity duals one of each other, as well as $\Lambda$ and ${\Lambda }_Q$.

(iv) The gravitational cosmic history can be described through its vacuum energy and their relevant physical properties: size, age, gravitational entropy and temperature, from the extreme past trans- Planckian phases, to the Planck scale and the post-Planckian phases:

trans-Planckian cosmic stages ⟶ Planck Scale ⟶ post-Planckian cosmic eras

(v) Post-Planckian phases go from Semiclassical gravity inflation, and the classical gravity phases until today most classical gravity phase (dark energy). The whole duration (of the trans-Planckian plus post-Planckians eras) is precisely: $t_{in}\le t\le {10}^{+61}{t}_P$, (being $t_P={10}^{-44}$ sec the Planck time), and $t_{in}$ is within the range $0<t_{in}\le {10}^{-61}{t}_P$, Eq. (9), as determined by the classical-quantum gravity relations Equations (2), (3) .

(vi) That is to say, each time component naturally dominates in each phase: classical time component ${10}^{+61}$ in the classical era, quantum Planck time $t_P$ in the quantum trans-Planckian era. The present time of the universe ${10}^{+61}{t}_P$, is a lower bound for the future (if any) age of the Universe, while its quantum dual ${10}^{-61}{t}_P$, is an upper bound for the most remote past $t_{in}$ at the origins of the Universe.

4. Quantum de Sitter Space-Time

De Sitter space-time can be described as a hyperboloid embedded in Minkowski space-time with one more spatial dimension. The classical and quantum lengths: $L_H$, $L_Q$ can be extended to the more complete length $L_{QH}$ which contains both: the Q and H lengths):

$$L_{QH}=(L_H+L_Q)=l_P({\displaystyle \frac{L_H}{l_P}}+{\displaystyle \frac{l_P}{L_H}})$$

(21)

and therefore for de Sitter space-time we have then :

$$X^2-T^2+X_j{X}^j+Z^2=L_{QH}^2=2l_P^2\left[1+{\displaystyle \frac{1}{2}}[{\left({\displaystyle \frac{L_H}{l_P}}\right)}^2+{\left({\displaystyle \frac{l_P}{L_H}}\right)}^2]\right]$$

(22)

with $j=2,3,...(D-2)$. Z is the extra coordinate for the embedding of de Sitter space-time in Minkowski space-time, and

$$L_H=c/H,L_Q=l_P^2/L_H=l_{P}H/c,$$

(23)

The gravitational and quantum dual masses $M_H$ and $M_Q$ associated to $L_H$ and $L_Q$ can be defined as well:

$$M_H=c^2{L}_H/G,M_Q=m_P^2/M_H=\hslash H/c^2$$

(24)

Equation (22) quantum generalize de Sitter space-time including the classical, semiclassical and quantum Planckian and trans-Planckian de Sitter regimes. It contains two non-zero lengths $(L_H,L_Q)$ or two relevant scales (H, $l_P$) enlarging the possibilities for the space-time phases: classical, semiclassical, quantum (trans-Planckian), Planckian, and Minkowski (flat) regimes. The total (classical and quantum) QH Hubble constant $H_{QH}$, curvature $R_{QH}$ and ${\Lambda }_{QH}$ from the $QH$ de Sitter length $L_{QH}$ are:

$$H_{QH}={\displaystyle \frac{c}{L_{QH}}},R_{QH}=H_{QH}^{2}D(D-1),{\Lambda }_{QH}={\displaystyle \frac{H_{QH}^2}{2}}(D-1)(D-2)$$

(25)

The $QH$ magnitudes are complete variables covering all gravity regimes and domains. The complete $QH$ de Sitter magnitudes $(L_{QH},H_{QH}$, $M_{QH})$, [and their constant Planck scale values $(l_P,h_P,m_P)$ only depending on $(c,\hslash ,G)]$, precisely characterize the classical, semiclassical, Planckian and quantum (super-Planckian) de Sitter regimes.

In Refs [12] we showed that de Sitter space-time can be described as an (inverted) harmonic oscillator. The $g_{00}$ component determined by the Einstein Equations for the de Sitter metric entails the harmonic oscillator potential, e.g.

$$d/dr\left(r{g}_{00}\right)=1-(8\pi {\rho }_0+\Lambda )r^2$$

Parametrization of the de Sitter hyperboloid in terms of the coordinates $(t,r,\theta ,\varphi )$:

$$T=H^{-1}{(1-H^2{r}^2)}^{1/2}sinh\left(Ht\right),X=H^{-1}{(1-H^2{r}^2)}^{1/2}cosh\left(Ht\right)$$

$$X_2=rcos\theta ,X_3=rsin\varphi cos\theta ,Z=rsin\varphi ,$$

yields:

$$d{s}^2=-(1-H^2{r}^2)d{t}^2+{(1-H^2{r}^2)}^{-1}d{r}^2+r^{2}d{\Omega }^2$$

and

$$X^2-T^2=H^{-2}(1-H^2{r}^2),$$

containing the (inverted) harmonic oscillator potential.

Inverted harmonic oscillator means that it has the minus sign in the potential or in the oscillator equations, that is to say, a imaginary frequency, the oscillator constant being precisely ${\kappa }_{oscill}=H^2$,

$$H\equiv \sqrt{\left(8\pi G\Lambda \right)/3}$$

(26)

The length of the oscillator is the Hubble radius and the Hubble constant is precisely the surface gravity of the universe (similar to the black hole surface gravity, the inverse of the its radius).

The de Sitter hyperboloid

$$X^2-T^2+X_j^2+Z^2=L_{QH}^2,j=2,3...,(D-2)$$

(27)

corresponds to a (inverted) harmonic oscillator $(X,P)$ embedded in a Minkowski space of $(D-2+2)=D$ spatial dimensions, ie a Minkowski space-time of $(D+1)$ space-time dimensions.

Quantum space-time can be described as a quantum oscillator with its quantum algebra. From the classical-quantum duality and quantum oscillator $(X,P)$ variables in global phase space, the space-time coordinates are promoted to quantum non-commuting operators. The relevant new and quantum light-cone structure refers to $(X,T)$, and not to the transverse spatial $X_j$ coordinates.

The quantum space-time coordinates $(X,T)$ can be considered quantum oscillator coordinates $(X,T=iP)$, including quantum space-time fluctuations and quantized levels.

The relevant quantum structure of the space-time arises from the relevant non-zero space-time commutator $[X,T]$, or non-zero quantum uncertainty $\Delta X\Delta T$ by considering quantum coordinates $(X,T)$. All other commutators are zero. The remaining transverse spatial coordinates $X_{\perp }$ have all their commutators zero. This is enough to capture the essential quantum light cone structure (as this is the case in the quantum black hole space-time too).

In terms of the phase-space representation $(x*,p*)$, $(X,P)$ are given by:

$$X=exp(\kappa x*)cos(\kappa p*),P=exp(\kappa x*)sin(\kappa p*)$$

(28)

$$(X^2+P^2)=exp(2\kappa x*)=2H_{osc},$$

(29)

$$(X^2-P^2)=exp(2\kappa x*)cos(2\kappa p*)=2H_{inv-osc}$$

(30)

with the star coordinate $x*$:

$$exp(Hx*)=H^{-1}\sqrt{1-H^2{r}^2}exp\left(Hr\right),Hr<1$$

(31)

being the Hubble constant $H=\kappa$ the dimensionless (in Planck units) gravity acceleration or surface gravity.

In terms of the quantum (non-commutative) star coordinates coordinates $(x*,t*)$ Equation (31) we have :

$$X=exp(\kappa x*)cosh(\kappa t*),T=exp(\kappa x*)sinh(\kappa t*)$$

(32)

$$(X^2-T^2)=exp(2\kappa x*)cosh\left(\kappa [x*,t*]\right)$$

(33)

$$(X^2+T^2)=exp(2\kappa x*)cosh(2\kappa t*)$$

(34)

$$[X,T]=exp(2\kappa x*)sinh\left(\kappa \right[x*,t*\left]\right)$$

(35)

where we used the usual exponential operator product:

$$exp\left(A\right)exp\left(B\right)=exp\left(B\right)exp\left(A\right)exp\left([A,B]\right)$$

New terms appear due to the quantum conmutators. At the classical level: $[X,T]=0,[x*,t*]=0$, the known classical de Sitter equations are recovered.

The equation for the quantum hyperbolic de Sitter "trajectories" is

$$(X^2-T^2)=\pm \sqrt{exp(4\kappa x*)+{[X,T]}^2}$$

(36)

$$=\pm \sqrt{{(1-H^2{r}^2)}^{2}exp\left(2Hr\right)+{[X,T]}^2}$$

(37)

The characteristic lines and what classically were the light-cone generating horizons

$X=\pm T$, (at $Hr=1$, or $x*=-\infty$), are now quantically:

$$X=\pm \sqrt{T^2+{[X,T]}^2}atHr=1:X\ne \pm T,\mathit{no}\mathit{horizons}$$

(38)

We see that $X\ne \pm T$ and the null horizons are quantum mechanically erased. In this respect, this is similar to the quantum Schwarzschild - Kruskal space-time structure Ref. [1], or to the quantum Rindler - Minkowski space-time Ref. [9], although the de Sitter manifold is totally regular, without curvature singularity already at the classical level.

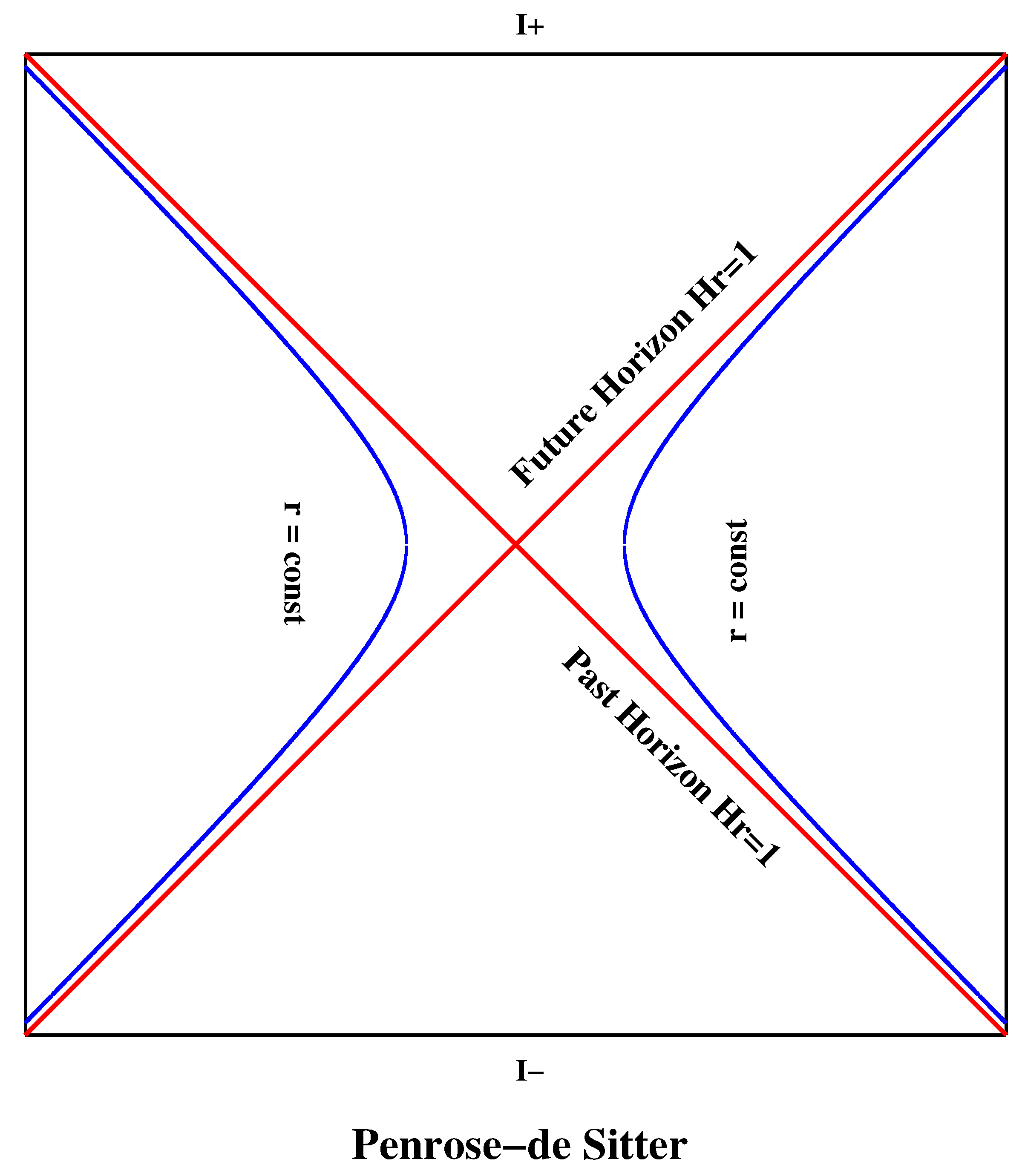
In Figure 1 we display the known Penrose diagram of the classical (non quantum) de Sitter space-time.

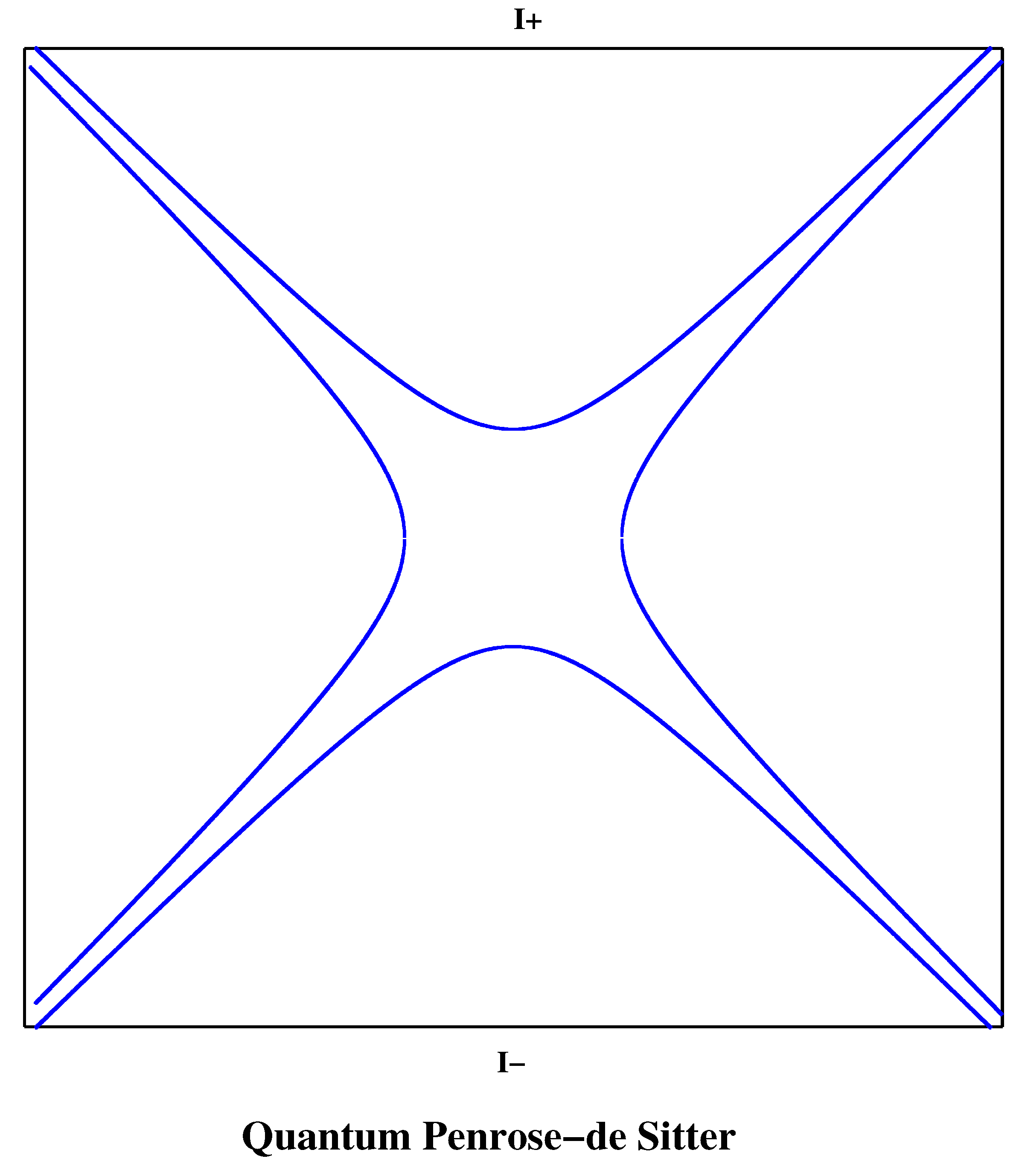
In Figure 2 we display the new Penrose diagram of the quantum de Sitter space-time.

We have seen in Refs [1,9] that in the complete analytic extension or global structure of the space-time underlies a classical-quantum duality structure: The external or visible region and its mirror copy are the classical or semiclassical gravitational domains while the internal region is fully quantum gravitational trans-Planckian domain. There does appear a duality symmetry between the two (left and right) space-time regions, and between the internal and external parts, as a classical - quantum duality with respect to the Planck scale (the crossing scale).

"External and internal" regions are meaning now with respect to the hyperbolae $X^2-T^2=\pm 1$, which correspond to the Planck scale (in Planck units). The internal region is enterely a finite (non-singular) quantum gravity (trans-Planckian) domain. The external region is the semiclassical and classical gravity domain. This applies too in Black holes of all types and whatever their masses, Ref. [1].

The quantum space-time description with non commutative coordinates $(X,T$), naturally provides discrete space - time levels $(X_n,T_n),n=0,1,2,...$ and discrete magnitudes, the Planck scale hyperbola $X^2-T^2=\pm 1$ corresponds to $n=0$, (the fundamental level).

A new quantum trans-Planckian vacuum region is present inside the Planck scale hyperbolae, which is absent classically, and in which interior: there are no future and past concepts, because the four space-time parts merge, Figure 1. The merging of the four space-time regions in the trans-Planckian light cone structure region is a quantum gravity consequence of quantum space-time.

5. Imaginary Time and the Complete Quantum Gravity de Sitter Instanton

As is known, in classical (non-quantum) space-time, taking imaginary time $T=i\mathcal{T}$, $t=i\tau$, transforms the hyperbolic space-time structure into circular structure: The characteristic lines $(X^2-T^2)=0$ collapse to $X=\pm \mathcal{T}=0$, and similarly in the cart $x=\pm \tau =0$. Therefore, the horizon $X=\pm T(Hr=1)$ collapses to the origin, and in the classical de Sitter instanton, (as well as in the black hole one), no horizon $Hr=1$, (and no singularity), does appear.

The euclidean (imaginary time) quantum instanton clearly shows the new trans-Planckian region because for $Hr=1$, $(X^2+{\mathcal{T}}^2)$ is not zero but have Planck length radius: The equation for the quantum instanton "trajectories" are

$$(X^2+{\mathcal{T}}^2)=\pm \sqrt{exp(4\kappa x*)-{[X,\mathcal{T}]}^2}$$

(39)

$$=\pm \sqrt{{(1-H^2{r}^2)}^{2}exp\left(2Hr\right)-{[X,\mathcal{T}]}^2}$$

(40)

What classically was the zero radius: $X=\pm \mathcal{T}=0atHr=1orx*=-\infty ,$

are now quantically:

$$X=\pm \sqrt{{\mathcal{T}}^2-{[X,\mathcal{T}]}^2}atHr=1:X\ne \pm \mathcal{T}=0,\mathit{no}\mathit{horizon}$$

(41)

We see that for the quantum de Sitter instanton, it is:

$$X\ne \pm \mathcal{T}\ne 0atHr=1.$$

The classical horizons corresponding to the origin $X=\pm \mathcal{T}=0$ in the euclidean signature space (instanton) are quantum mechanically replaced by the circle of Planck length radius:

$$(X^2+{\mathcal{T}}^2)={[X,\mathcal{T}]}^2=1.$$

That is to say, quantum theory consistently extends the instanton manifold: classically the instanton is "cutted" at the "horizon" $r=1/\left(2\kappa \right)$, while at the quantum level it extends beyond it: It contains the quantum region of Planck length radius $l_{Planck}$, which is neccesarily trans-Planckian and is absent at the classical level.

Figure 3. The new quantum gravity de Sitter instanton (imaginary time: $T=i\mathcal{T},t=i\tau$). The classical null horizons corresponding to the origin $X=\pm \mathcal{T}=0$ in the classical gravity (Gibbons-Hawking) instanton are extended at the quantum level to the Planck length circle of $(X^2+{\mathcal{T}}^2)=[X,\mathcal{T}]=1$, (in Planck units). The instanton manifold is consistently extended by the Quantum theory : The classical (non quantum) instanton is regular but is not complete because it is "cutted" at the null horizon $Hr=1$, while at the quantum level it is both: regular and complete: It is the known classical instanton for distances larger than the Planck length plus the new highly dense quantum region of Planck length radius, and of high finite curvature, which is absent classically. The difference between the four regions disappears in the euclidean manifold, (indicated here for "classical" memory). The imaginary time $\tau$ in the classical instanton is periodic with period $\beta =2L_G=1/\kappa$ : $1/\beta$ being the (Hawking) temperature. In the complete quantum gravity instanton, the imaginary time is periodic with complete$L_{QG}=(L_G+L_Q)$ including both quantum and classical magnitudes. The complete Temperature $T_{QG}$, Entropy $S_{QG}$ and density of states all include the truly quantum gravity (trans-Planckian) domain, described in Sections V and VI.

Figure 3. The new quantum gravity de Sitter instanton (imaginary time: $T=i\mathcal{T},t=i\tau$). The classical null horizons corresponding to the origin $X=\pm \mathcal{T}=0$ in the classical gravity (Gibbons-Hawking) instanton are extended at the quantum level to the Planck length circle of $(X^2+{\mathcal{T}}^2)=[X,\mathcal{T}]=1$, (in Planck units). The instanton manifold is consistently extended by the Quantum theory : The classical (non quantum) instanton is regular but is not complete because it is "cutted" at the null horizon $Hr=1$, while at the quantum level it is both: regular and complete: It is the known classical instanton for distances larger than the Planck length plus the new highly dense quantum region of Planck length radius, and of high finite curvature, which is absent classically. The difference between the four regions disappears in the euclidean manifold, (indicated here for "classical" memory). The imaginary time $\tau$ in the classical instanton is periodic with period $\beta =2L_G=1/\kappa$ : $1/\beta$ being the (Hawking) temperature. In the complete quantum gravity instanton, the imaginary time is periodic with complete$L_{QG}=(L_G+L_Q)$ including both quantum and classical magnitudes. The complete Temperature $T_{QG}$, Entropy $S_{QG}$ and density of states all include the truly quantum gravity (trans-Planckian) domain, described in Sections V and VI.

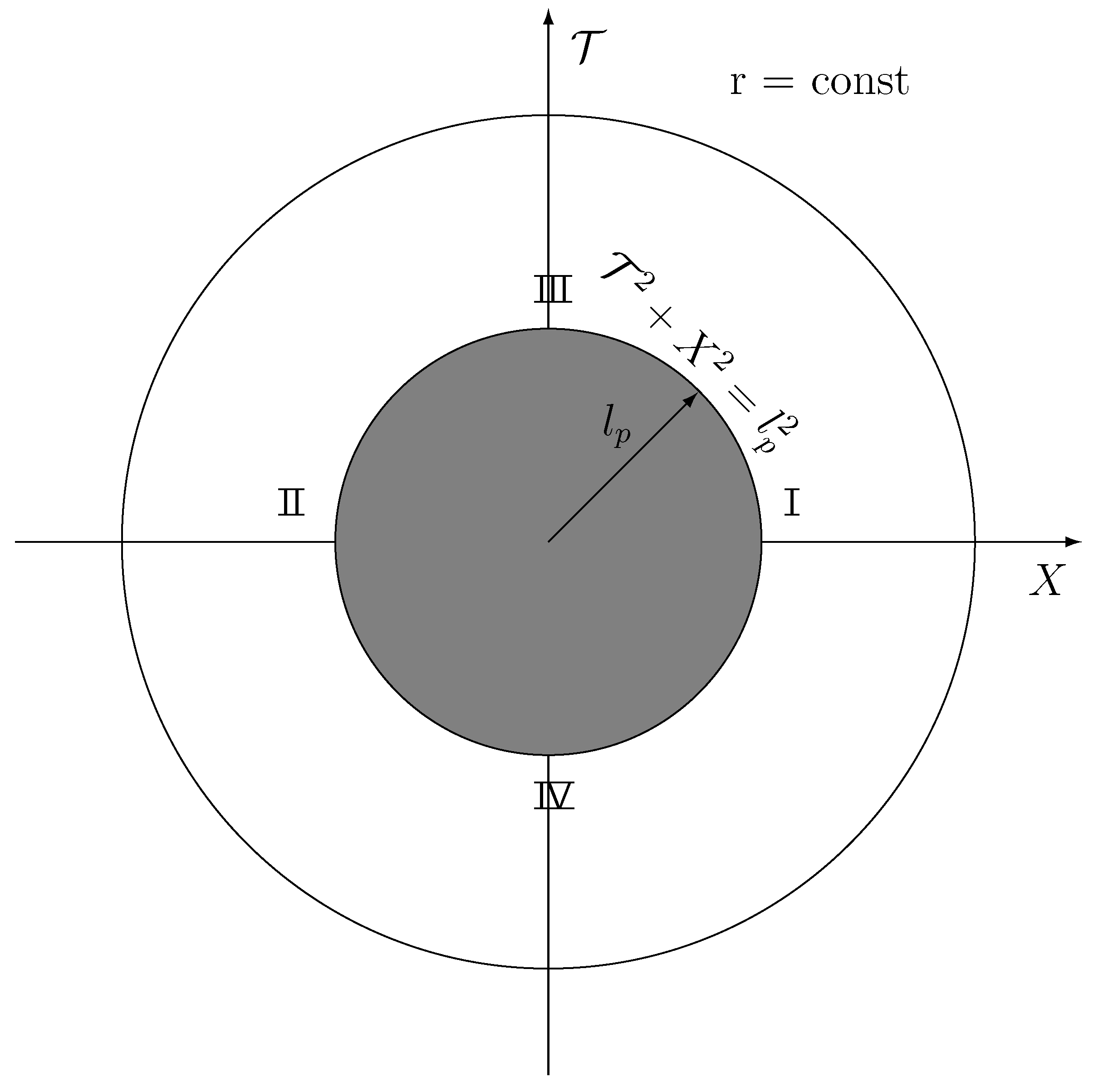
This means the following: The complete, quantum and regular imaginary time de Sitter space, (quantum gravitational instanton), is the usual classical/semiclassical instanton for radius larger than the Planck length plus a highly dense quantum domaine of Planck length radius, and of high finite curvature, which is the trans- Planckian initial stage of the universe, and which is absent classically.

The imaginary time $\tau$ in the classical instanton is periodic with period $\beta =1/\kappa$ :

$$0\le \tau \le \beta =1/\kappa$$

(42)

In the complete (quantum) instanton, the imaginary time is periodic as in Equation (42) but with the total $\kappa$ completed with the quantum trans-Planckian magnitudes:

The imaginary time $\tau$ in the classical instanton is periodic with period $\beta =2L_H=1/{\kappa }_H$

$$0\le \tau \le \beta =2L_H=1/{\kappa }_H,\left(\mathit{classically}\right)$$

(43)

$1/\beta$ being the intrinsic manifold semiclassical temperature: the Gibbons-Hawking de Sitter Temperature

$$T_Q=t_P\left({\displaystyle \frac{l_P}{2L_H}}\right)=t_P\left({\displaystyle \frac{H}{2h_P}}\right)=t_P\left({\displaystyle \frac{M_Q}{m_P}}\right)$$

(44)

$t_P=(m_P{c}^2/2\pi {\kappa }_B)$ being the Planck temperature.

In the complete or total quantum instanton, the imaginary time is periodic as in Equation (43) but with the complete $L_{QH}$ which includes the quantum Planckian and trans-Planckian magnitudes:

$$0\le \tau \le \beta =2L_{QH}=2(L_H+L_Q)=1/{\kappa }_{QH},$$

(45)

$${\kappa }_{QH}={\kappa }_P(l_P/L_{QH}),{\kappa }_Q={\kappa }_P^2/{\kappa }_H,{\kappa }_P=c^2/2l_P$$

(46)

$${\kappa }_{QH}={\displaystyle \frac{H}{[1+{(H/h_P)}^2]}}=H\sum _{n=0}^{\infty }{(-1)}^n{\left({\displaystyle \frac{H}{h_P}}\right)}^2$$

(47)

$$={\displaystyle \frac{H_Q}{[1+{(H_Q/h_P)}^2]}}$$

(48)

In the classical/semiclassical gravity domaine : ${\kappa }_H<<{\kappa }_P$, $(H<<h_P)$, it yields the usual Hubble constant or classical surface gravity ${\kappa }_H$ of the large universe stages, (eg massive $M_H)$ with masses $M_H>>m_P$.

In the quantum domaine of sizes and masses $L_H<l_P,H>h_P,M_H<m_P$: For ${\kappa }_Q<<{\kappa }_P$, it yields the quantum ${\kappa }_Q=(h_P/H){\kappa }_P=(M_H/m_P){\kappa }_P$. The corresponding complete temperature being :

$$T_{QH}=t_P{\kappa }_{QH}/\left(2\pi {\kappa }_P\right),T_Q=t_P^2/T_H=t_P(H/h_P)$$

(49)

$$T_{QH}={\displaystyle \frac{T_H}{[1+{(T_H/t_P)}^2]}}={\displaystyle \frac{T_Q}{[1+{(T_Q/t_P)}^2]}}$$

(50)

In the late (dark energy) de Sitter stage of large universe radius, (large mass $M_H$), it yields the Gibbons-Hawking de Sitter temperature $T_Q=(M_Q/m_P)t_P=(H/h_P)t_P$, which is a very low temperature in this stage $T_Q<<t_P$, as it must be.

For small radius and masses $(0<L_H\le l_P),(0<M_H<m_P)$, it yields the usual temperature $T_G<<t_P$, proportional to the mass $M_H$, and $T_Q>>t_P$, as it must be, in the quantum gravity early de Sitter phase (the remote past trans-planckian phase). This is also manifest in the de Sitter Partition function (described in Section VI below) and in the corresponding complete de Sitter entropy.

The Temperature is a measure of the length (in units of ${\kappa }_B$), $T_H=t_P(L_H/l_P),T_Q=t_P(L_Q/l_P)$, while the gravitational entropy is a measure of the area. In this respect, is interesting to notice that:

$$S_{QFT}=s_P{(L/l_P)}^3=>n$$

(51)

$$S_H=s_P{(L/l_P)}^2=s_P{(M/m_P)}^2=>{\left(\sqrt{n}\right)}^2$$

(52)

$$S_{string}=s_s(L/l_s)=s_s{(L/l_s)}^2=s_s(M/m_s)=>\sqrt{n}$$

(53)

$$S_Q=s_P{(l_P/L)}^2=s_P{(m_P/M)}^2=>1/{\left(\sqrt{n}\right)}^2$$

(54)

In quantum particle physics without gravity, that is Quantum Field Theory (QFT) the entropy is proportional to the volume (with a cut-off at the Planck scale $l_P$ because of the well known ultraviolet divergences of QFT.

In string theory, the string entropy $S_{string}$ is proportional to the length, being the string constant ${\alpha }^{\prime }$, (subscript s) playing the role of $c^2/G^2$ which is a tension.

In gravity theory, the gravitational entropy is proportional to the area, whatever be the classical/semiclassical gravity $S_H$ entropy or the quantum $S_Q$ gravity entropy. We understand thus clearly that the area (gravitational entropy) "interpolates" between the volume (non-gravitational entropy $S_{QFT})$ and the length (string entropy) $S_{string}$.

Thus, the many questions formulated along the years on the difference of the gravity (or black hole) entropy proportional to the surface and the usual QFT proportional to the volume, find in our Section here, a clear precise answer and a clarification on those questions. And the Section below on the Partitions functions provide strong support to these results, without invoking principles or hypothesis.

$S_H$ is, in particular the known Bekenstein-Hawking entropy which is the a classical/ semiclassical gravitational entropy, that is it is valid for $L>>l_P$ (or equivalently, $M_H>>m_P,{\kappa }_H<<{\kappa }_P,T_Q<<t_P$):

$$S_H=s_P(T_H/T_Q)=(M_H{c}^2/T_Q).$$

6. Partition Function and the Complete (Quantum Gravity) de Sitter Entropy

As is known, $(D+1)$ dimensional quantum field theory with imaginary periodic time

$(0\le \tau \le \beta )$ corresponds to a classical statistical mechanics or field theory with temperature $(1/\beta )$, which is used in the euclidean path integral of gravity Ref. [24],

$$\mathcal{Z}=Trexp(-\beta \mathcal{H}),$$

(55)

$\mathcal{H}$ being the euclidean Hamiltonian $\mathcal{H}$, the "evolution" generator in imaginary time, with the trace implaying periodic evolution $(0\le \tau \le \beta )$.

D-dimensional de Sitter space-time is the hyperboloid embedded in (D + 1) Minkowski space-time. The (D + 1) Minkowski imaginary time instanton with periodic time is the statistical mechanics theory in D-space dimensions. The (D -dimensional de Sitter instanton is the (D - 1) sphere embedded in a D-dimensional euclidean instanton.

The complete (including both classical and quantum) de Sitter radius and temperature are $L_{QH}$ and $T_{QH}$ and $T_{QH}$ as discussed in Section V above. The complete (whole range) discrete quantum levels are discussed in Section II, Equations (5), (6), (7). We recall that for the partitions or density of levels:

• The ordered or not ordered partitions, that is (counting or not counting the permutations), determines the states degeneracy: This is different depending on the nature of the quantum objects : point particles, composite or extended quantum objects.
• The ordered partitions $P_{ord}\left(n\right)$ grow exponentially with n , while the non ordered partitions of n,25] grow exponentially with $\sqrt{n}$.
• Point particles or quantum point oscillators belong to the ordered case, while quantum composite objects with internal structure, extended objects, strings, hadronic matter, are in the non-ordered case. Moreover, the $\sqrt{n}$ characterizes the mass spectra of composite or extended oscillating objects, while n is typical of the energy spectra of punctual objects.
• The existence or not of a limiting temperature in the corresponding ensembles is determined by a pure number combinatorial structure: that is to say, by whether permutations are or not included, eg by whether partitions are ordered or unordered, eg by whether the elements are point particles or quantum extended objects with internal composite structure as hadrons, strings or other higher dimensional objects.

The total gravitational entropy $S_{Q\Lambda }$ of the total or complete (classical and quantum) de Sitter euclidean manifold, is the sum of the classical, quantum and Planck scale entropies:

$$d_{Q\Lambda }=exp\left[S_{Q\Lambda }\right]$$

(56)

$$S_{Q\Lambda }=2[s_P+{\displaystyle \frac{1}{2}}(S_{\Lambda }+S_Q)],$$

(57)

$$S_{\Lambda }={\displaystyle \frac{{\kappa }_B}{4}}{\displaystyle \frac{A_{\Lambda }}{l_P^2}},S_Q={\displaystyle \frac{{\kappa }_B}{4}}{\displaystyle \frac{A_Q}{l_P^2}},s_P={\displaystyle \frac{{\kappa }_B}{4}}{\displaystyle \frac{a_P}{l_P^2}}=\pi {\kappa }_B,$$

(58)

$s_P$ is the Planck entropy, $A_{\Lambda }=4\pi L_{\Lambda }^2$, $A_Q=4\pi L_Q^2$ are the classical and quantum areas respectively (recall $L_Q=l_P^2/L_{\Lambda }$):

$$A_{\Lambda }=a_P{\left({\displaystyle \frac{L_{\Lambda }}{{\lambda }_P}}\right)}^2,A_Q=a_P{\left({\displaystyle \frac{{\lambda }_P}{L_{\Lambda }}}\right)}^2={\displaystyle \frac{a_P^2}{A_{\Lambda }}},a_P=4\pi l_P^2$$

(59)

$$S_{\Lambda }=s_P{\displaystyle \frac{{\rho }_Q}{{\rho }_P}}=s_P{\displaystyle \frac{{\lambda }_P}{\Lambda }}=s_P{10}^{+122}$$

(60)

$$S_Q=s_P{\displaystyle \frac{{\rho }_{\Lambda }}{{\rho }_P}}=s_P{\displaystyle \frac{\Lambda }{{\lambda }_P}}=s_P{10}^{-122}$$

(61)

$a_P$ being the Planck area, and ${\lambda }_P$ the $\Lambda$ Planck scale value : ${\lambda }_P=(3h_P^2/c^4)=3/\left(l_P^2{c}^2\right)$. The complete de Sitter entropy is then:

$$S_{Q\Lambda }=2s_P[1+{\displaystyle \frac{1}{2}}[{\displaystyle \frac{{\lambda }_P}{\Lambda }}+{\displaystyle \frac{\Lambda }{{\lambda }_P}}]]=2s_P[1+{\displaystyle \frac{1}{2}}[{\displaystyle \frac{h_P^2}{H^2}}+{\displaystyle \frac{H^2}{h_P^2}}]],$$

(62)

and consistently, the complete partition function is:

$${\mathcal{Z}}_{Q\Lambda }=exp\left[S_{Q\Lambda }\right]=z_P{\mathcal{Z}}_Q{\mathcal{Z}}_{\Lambda }$$

(63)

In the quantum trans-Planckian phase, which is the most early or precursor phase

$(t_{in}\le t\le t_P$), the total entropy $S_{QG}$ is dominated by the Planck entropy $s_P$, the quantum entropy $S_Q$ being extremely low: $S_Q={10}^{-122}$. The most remote past state $\left|In\right(t=t_{in}\rangle$ corresponds to the minimal time in the range $(0\le t_{in}\le {10}^{-61}{t}_P)$ and minimal entropy $S_{min}$ in the range $(0\le S_{in}\le {10}^{-122}{s}_P)$.

The total entropy $S_{QH}$ is high in the post-Planckian (eg semiclassical and classical) eras: $(t_P<t\le t_{today}={10}^{61}{t}_P)$ and dominated by the Gibbons- Hawking entropy $S_H$ which is a semiclassical gravity entropy, being maximal in the today phase: $S_H={10}^{122}$ (dark energy).

The discrete levels $n=0,1,2,....,$ cover all gravity regimes: from the quantum gravity (trans-Planckian and Planckian) phases to the post- Planckian universe (semiclassical and classical) gravity phases.

For $(0\le t\le t_P)$, ie in the pre-Planckian (trans-Planckian) phase,

the quantum trans-Plankian levels (Q denoting quantum) are:

$$H_{Qn}=\sqrt{(2n+1)},{\Lambda }_{Qn}=(2n+1),S_{Qn}=1/(2n+1),n=0,1,2,.....$$

(64)

For $(t_P<t\le t_{today}={10}^{61}{t}_P)$, ie in the post-Planckian universe,

the levels for the Hubble constant $H_n$, vacuum energy ${\Lambda }_n$, and gravitational (Gibbons-Hawking) entropy $S_n$ (in Planck units) are:

$$H_n=1/\sqrt{(2n+1)},{\Lambda }_n=1/(2n+1),S_n=(2n+1),n=0,1,2,.....$$

(65)

The corresponding associated masses are:

$$M_{Hn}=\sqrt{(2n+1)},M_{Qn}=1/\sqrt{(2n+1)}$$

(66)

and the scalar curvature levels in the respective stages are

$$R_n=1/(2n+1),R_{Qn}=(2n+1).$$

Therefore, the density of states in the classical/semiclassical gravity and quantum gravity stages are:

$$d_{\Lambda n}=exp(2n+1)=exp\left(M_{Hn}^2\right)=exp\left({\Lambda }_{Qn}\right)$$

(67)

$$d_{Qn}=exp[1/(2n+1\left)\right]=exp\left(M_{Qn}^2\right)=exp\left({\Lambda }_n\right)$$

(68)

$$d_{Q\Lambda n}=exp\left[\right(2n+1)+1/(2n+1\left)\right]=exp({\Lambda }_{Qn}+{\Lambda }_n)$$

(69)

• The complete $\left(Q\Lambda \right)$ density of states $d_{Q\Lambda n}$ contains both: the classical/semiclassical gravity density $d_{\Lambda n}$ with the known (Bekenstein-Hawking) entropy $S_{\Lambda n}$, and the quantum gravity density $d_{Qn}$ with the new trans-Planckian entropy $S_{Qn}$.
• In the initial quantum region, n diminishes from the most highly excited trans-Planckian levels, until $n=0$ and then increasing in the semiclassical and classical universe. The n-levels completely cover from the highest excited levels in the remote past of the universe until the lowest excited ones in the present era today, fully covering the twofold dual branches, classical and quantum, passing through the Planck $(n=0)$ level, the fundamental level, the crossing scale.
• As n increases, radius and mass of the Universe increase, $H_n$ and ${\Lambda }_n$ both decrease, $S_{Hn}$ increases and consistently the Universe classicalizes.
• The most remote past trans-Planckian level $t_{in}$ corresponds to the maximum trans-Planckian level $n_{max}$ with the most quantum values: maximum curvature $R_{Qmax}$, maximum vacuum ${\Lambda }_{Qmax}$ and minimum entropy $S_{Qmin}$:

  $${10}^{122}\le n_{max}<\infty ,{10}^{122}\le (R_{Qmax},{\Lambda }_{Qmax})<\infty ,$$

  (70)

  $$0<S_{Qmin}\le {10}^{-122}$$

  (71)
  n decreases crossing the Planck $(n=0)$ level:

  $$H_{Planck}=1={\Lambda }_{Planck}=S_{Planck},$$

  and then n enters the post-Planckian universe :

  $$n=1,2,...,n_{infl}={10}^{12},...,n_{cmb}={10}^{114},...,n_{reion}={10}^{118},...,n_{today}={10}^{122},...,n_{max}$$

  with the most classical values:

  $$H_{today}={10}^{-61},...,H_{min};{\Lambda }_{today}={10}^{-122},....,{\Lambda }_{min}$$

  $$S_{today}={10}^{122},....,S_{max}.$$

For n in the range:

$$nϵ[n_{max},0]:\mathrm{Quantum}\mathrm{Trans}-\mathrm{Planckian}\mathrm{Gravity}$$

the gravity spectrum is fully quantum and trans-Planckian.

For n in the range:

$$nϵ[0,n_{max}]:\mathrm{Semiclassical}\mathrm{and}\mathrm{Classical}\mathrm{Gravity}$$

the gravity spectrum is quantum for the low n which are highly excited quantum space-time levels with energies smaller than the Planck energy. The spectrum becames semiclassical for intermediate n, and classical for the high and very high n until reaching $n_{max}$, where

$${10}^{+122}\le n_{max}<\infty :\mathrm{Classical}\mathrm{Gravity}$$

$$n_{maxtoday}={10}^{+122}$$

$n_{max}$ is bounded because of the classical-quantum gravity duality, and corresponds to the highest excited trans-Planckian level, for example: the earliest level state in the early quantum gravity phase of the Universe, or the most central internal level in the constant curvature interior trans-Planckian core of the black hole.

On the other hand, $n_{max}$ corresponds to the lowest excited level of the post-Planckian Universe , eg. the most classical gravity and empty state of the Universe with maximal classical/semiclassical entropy, $S_{\Lambda }\mathit{today}={10}^{+122}$ which in this regime is the Gibbons - Hawking entropy, and vacuum energies in the $meV={10}^{-3}eV$ (today dark energy).

Consistently, in the Universe post-Planckian phase, the lowest excited level $n_{max}$ corresponds to the lowest energy and most classical gravity state eg, the most large size region with maximal Bekenstein-Hawking entropy.

7. Early and Last Stages of the Universe. Expansion and Contraction (Bangs and Crunchs)

Our results here and mainly the time, Hubble H and $\Lambda$ spectrum in Section VI not only have implications for the initial and late phases of the Universe but also for its future evolution and final phases.

$(X_n,T_n)$ are given in Planck (length and time) units. Eqs. (5) and (6) translate into the discrete levels for the Universe radius, Hubble constant and vacuum energy $\Lambda$

$$L_n=\sqrt{(2n+1)}=1/H_n,n=0,1,2,....$$

(72)

The Universe size , vacuum energy $\Lambda$, Hubble rate and their associated gravitational magnitudes : curvature and entropy have discrete levels from the most fundamental one $(n=0)$, going to the semiclassical stage (intermediate n), to the classical ones (large n) which yield a continumm classical space-time, radius and mass, as it must be. This is clearly seen from the global mass levels $M_{n\pm }$, (and similarly for the radius levels):

$$M_{n\pm }=[M_n\pm \sqrt{M_n^2-m_P^2}],$$

(73)

The whole spectrum is covered. The condition $M_n^2\ge m_P^2$ simply corresponds to the whole spectrum $n\ge 0$:

$$M_{n\pm }=m_P[\sqrt{2n+1}\pm \sqrt{2n}]$$

(74)

$$M_{(n=0)+}=M_{(n=0)-}=M_{Q(n=0)}=m_P,n=0:Planckmass$$

(75)

$$M_{n+}=m_P[2\sqrt{2n}-{\displaystyle \frac{1}{2\sqrt{2n}}}+O(1/n^{3/2})],branch(+):masses>m_P$$

(76)

$$M_{n-}={\displaystyle \frac{m_P}{2\sqrt{2n}}}+O(1/n^{3/2}),branch(-):masses<m_P$$

(77)

• Large n levels are semiclassical tending towards a classical continuum classical /semiclassical phase. Low n are quantum, the lowest mode ($n=0$) being the Planck scale. Two dual $(\pm )$ branches are present in the local variables ($\sqrt{2n+1}\pm \sqrt{2n}$) reflecting the duality of the large and small n behaviours and covering the whole spectrum: from the largest entropy and scales in branch $(+)$ to the quantum smallest entropy and scales in branch $(-)$ passing by the Planck entropy and length.
• The last stage of the universe of decreasing radius ("big crunch") and its quantum decay belong to the quantum mass branch (-) with Planck scale radius, mass and smaller until zero mass.
• The complete Universe magnitudes belong to the both branches (+) and (-): Branch (+) covers all macroscopic, classical universe phases as well as the semiclassical radius quantization $\sqrt{2n+1}$ until nearby the Planck lenght radius $(n=0)$.
• The microscopic quantum de Sitter universes (with masses near the Planck mass and smaller) ie originated from Planckian and trans-Planckian primordial fluctuations), or as a consequence of big crunchs, belong to the branch (-).
• The branches (+) and (-) cover respectively the early and late phases of the Universe. In its evolution from its remote past to today and the far future the universe goes from the branches (-) to (+), and would return to branch (-) (big crunch), and then again in a big expansion. Black holes in the process of their formation and evaporation do the opposite, going from the branches (+) to (-), decaying and then again passing from branch (+) to (-).
• There are no quantum objects at such heavy mass as the Planck mass which would remain stable. They naturally decay quantum mechanically in all particles, mainly gravitons and radiation. Therefore, the end of quantum trans-Planckian objects, the "remnant" states, are the last emitted particles, gravitons, and radiaton, and other elementary particles, but not totally stable heavy Planck mass quantum objects.

Finally, let us just point out that the whole process of the universe formation expansion and end by collapse and crunch can be considered in terms of a Scattering-matrix between the asymptotic states of such phases.

The Universe (U) formation through the quantum tunneling from the Vacuum can be described as a S-matrix evolution (${\mathcal{S}}_U$):

$$|{\Psi }_U\left(t\right)\rangle ={\mathcal{S}}_U\left(t\right)|{\Psi }_{Vacuum}(t=t_{in})\rangle$$

(78)

And in general:

$$|{\Psi }_U\left(t\right)\rangle ={\mathcal{S}}_U\left(t\right)|{\Psi }_{QU}\left(t_{in}\right)\rangle$$

(79)

It can be expressed in terms of the final Vacuum state at $t=t_{final}$ , in the final expansion phase that is to say, the future time at which the Universe reverses from expansion to contraction.

In addition, microscopic de Sitter states formed from the crunching universe phase can in turn decay, and end into a gaz of particles and radiation which eventually, under gravity and pressure conditions, forms again de Sitter states, stars and black holes. That is to say, the quantum initial gravitational Vacuum can be arised from the decay of the crunching Universe states (or at least a part of it):

$$|{\Psi }_{QU}\left(t_{in}\right)\rangle ={\mathcal{S}}_{QU}\left(t_{in}\right)|{\Psi }_{QU}\left(t_{final}\right)\rangle$$

(80)

Therefore,

$$|{\Psi }_U\left(t\right)\rangle ={\mathcal{S}}_U\left(t\right){\mathcal{S}}_{QU}{\left(t\right)}^{-1}|{\Psi }_{QU}\left(t\right)\rangle$$

(81)

This description applies too to black holes: The whole process of initial black hole formation from the end life of a star, quantum evaporation and full quantum gravity final decaying in pure (particle and radiation) states, can be described in similar terms and has, an analogous expression Ref. [1] :

$$|{\Psi }_{star}\left(t\right)\rangle ={\mathcal{S}}_{star}\left(t\right){\mathcal{S}}_{BH}{\left(t\right)}^{-1}|{\Psi }_{BH}\left(t\right)\rangle$$

(82)

These are relevant examples that gravitational unitarity does hold in a whole complete quantum process: the S-matrix in the whole process is unitary $S{S}^{+}=1=S^{+}S$ as it must be [8]: "In Nature nothing is lost, all is transformed ".

8. Conclusions

The Introduction and Sections of this paper include themselvels the novel results of this paper, and therefore we will not include all of them here. We summarize Conclusions and outlook below.

• We provide a description of gravitational Vaccua, the initial $|InVacuum\rangle$, ("Nothing"), and the late Vacuum State $\left|LateVacuum\right(t)\rangle$, ("Everything") today, and connected these two asymptotic states through an S - Matrix as a Classical-Quantum Dual Transform through the Planck scale, and which is unitary as it must be. The minimal or initial time is in the range $0<t_{in}\le {10}^{-61}{t}_P$, with the minimal entropy range $0<S_{in}\le {10}^{-122}$ ($t_P$, and $s_P$ being the Planck time and entropy). The late time being in the range $t_{today}={10}^{-61}{t}_P\le t_{late}\le t_{max}$ with the maximal entropy $S_{today}={10}^{122}\le S_{late}\le S_{max}$. This is accompassed with the discussion of the gravitationnal phase transitions in this context and the description of the early and last stages of the Universe as expansion and contraction phases (bangs and crunchs) The Initial Vacuum is thus a quantum gravitational foam of borning and dying (crushing) universes, quantum and decaying black holes, particles and or strings and radiation.
• For the origin of the Universe from Nothing we have very new results : The truly quantum gravity (trans-planckian) component of the gravitational entropy $S_Q={10}^{-122}$ dominates the tunneling probability P of the birth of the Universe from "Nothing", which is almost equal to 1. Therefore, this clearly shows that the transplanckian component is enterely consistent with (and does strongly support to) the "creation" of the Universe as a quantum process (tunneling) from the Vacuum.
• Notice that in the non- complete picture discussed until now in the litterature (without the trans-Planckian domain), the gravitational euclidean action is enterely classical or semiclassical, ie $S_{\Lambda }={10}^{+122}$, its value is huge, and the tunneling probability is extremely small, while in the complete picture here the value is the opposite.
• The global quantum structure of de Sitter space-time is found from quantum coordinates, and a consistent quantum picture of the de Sitter space-time does appear from the internal quantum and trans-Planckian, to the semiclassical and classical late regions until (today Universe), acompassed with their physical magnitudes and spectrum: size, mass, partition function, gravitational entropies and temperatures covering all mass range and gravity domains: quantum (trans-Planckian) gravity and semiclassical/classical gravity domains.
• Quantum space-time structure arises from the relevant non-zero commutator $[X,T]$. The quantum light-cone due to the quantum non-zero uncertainty $[X,T]$ allows the new quantum gravity region : this is a purely quantum vacuum or zero-point Planckian and trans-Planckian energy and constant curvature domain. This central quantum vacuum core is a de Sitter quantum trans-Planckian vacuum described through the relevant quantum non-commutative coordinates and the quantum hyperbolic structure.
• In the central quantum trans-Planckian core of the black hole, the levels extend from the Planck scale $(n=0)$ to the lengths smaller than the Planck scale, until the quantum highly excited trans-Planckian levels (very large n) which are those of smaller entropy $S_{Qn}=1/(2n+1)$ and higher vacuum density ${\Lambda }_{Qn}=(2n+1)$.
• There are no singularities of any kind here. The Planck scale is not just a useful system of units but its full physical meaning is being the onset of the quantum gravity scale; this scale precludes the extrapolations until zero time or length. de Sitter vacuum which is a smooth constant curvature vacuum without any curvature singularity. The small and a trans-Planckian vacuum have a high but bounded trans-Planckian constant curvature and therefore without singularity. No divergent no infinities arise here. This is a theory of finite magnitudes and numbers. This is also consistent with the fact that the number of Multiverses is finite and in agreement with Hawking last work [26].
• The quantum trans-Planckian region is present in all space-times as a consequence of the quantum global light cone structure. And all black holes, macroscopic and astrophysical one, have an interior central quantum trans-Planckian core without any $r=0$ singularity. In the imaginary time manifold (instanton), it appears too, and allows to complete the classical gravity Gibbons-Hawking instanton, which is cutted at the horizon: The classical de Sitter instanton is not complete. The de Sitter quantum instanton is complete. The quantum gravity partition function, temperature and entropy all clearly include the highly excited and dense trans-Planckian de Sitter region of radius $l_P$.
• The early quantum universe states from the trans-Planckian phase (regular "big bangs") reach the Planck mass smoothly into more and more massive decoherentized states (known expansion evolution phases including inflation). In the inverse process (regular "big crunchs"), the Universe states reach the Planck mass $m_P$ from the semiclassical or classical gravity "side" (as black holes do), and undergo a phase transition into pure (non mixed) quantum gravity states. They then decay in the way heavy particles, quantum strings, or Planck mass black holes do, into gravitons, other elementary particles and radiation.
• The results of this paper should open new research directions and new understanding whatever for quantum theory in its own right, and gravity , eg quantum gravitational signals, for e-LISA [32] for instance, after the success of LIGO [33,34], also for other observable cosmological effects [35,36,37,39], although the purpose of this paper is not to discuss them here.
• A Scattering-matrix between the asymptotic (in and out) different cosmological vaccua is described as a Dual Classical-Quantum mapping across the Planck scale. The most early quantum trans-Planckian Vacuum being the in-state, and the most late in the far future or today is the classical gravitational dilute Vacuum , the out- state, the dark energy today.
• The results of this paper provide further strong support to the feature described by this author in Ref. [1] that a complete quantum theory of gravity must be a finite theory, which is much more than a renormalizable theory, and a theory of pure numbers.
• The results of this paper on the cosmological initial and late Vaccua could help too for a better understanding or resolving of the present Hubble constant $H_0$ problem or other tensions, which are beyond the scope of this paper and we not discuss them here. In addition, a post-inflation early low vacuum energy (remnant of the inflationary vacuum) could not be excluded in principle, and if appropriately implemented, explain the $H_0$ problem too. Such vacuum energy rate accompasses a Hubble $H_0\left(t\right)$ rate, related to a early $\Lambda \left(t\right)$ rate, which most classical remaining in the present Universe is the cosmological vacuum energy $\Lambda \left(t_0\right)$, e.g ${\Lambda }_0$ today.