Entanglement Missed Detection of Two‐Mode Squeezed States Based on Inseparability Criterion

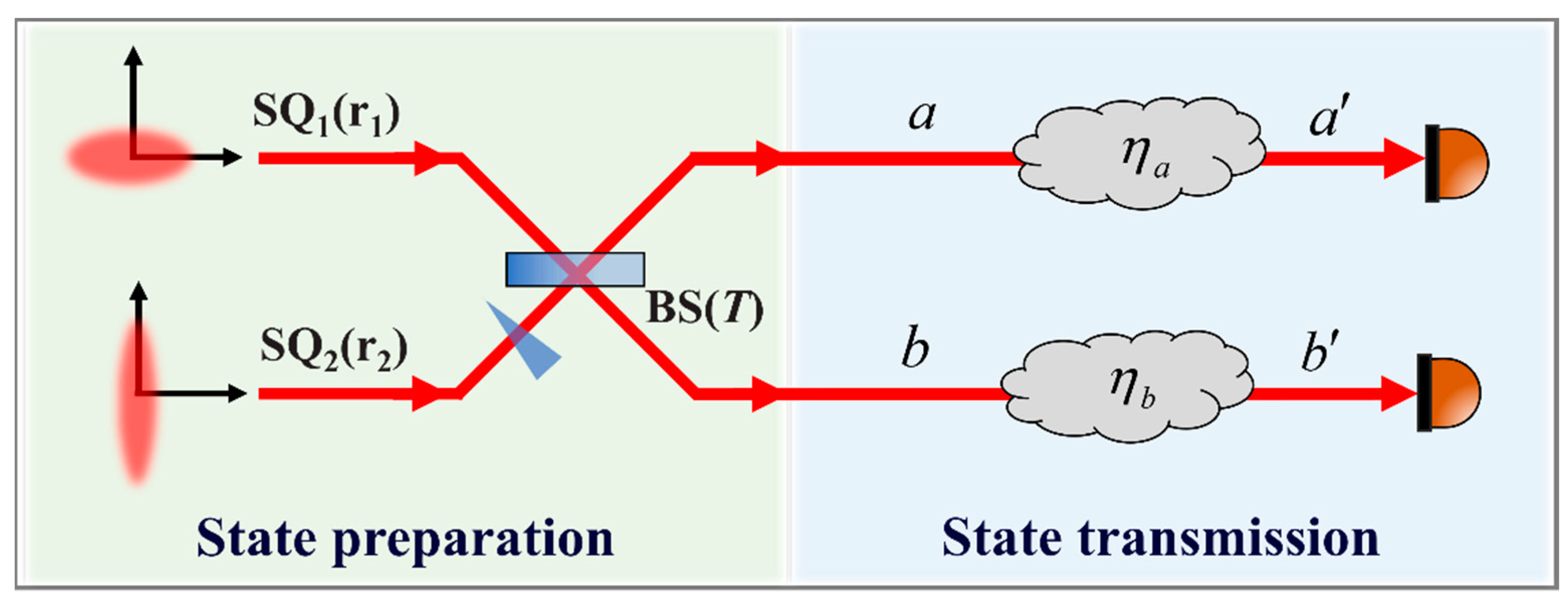
2. Theoretical Analysis

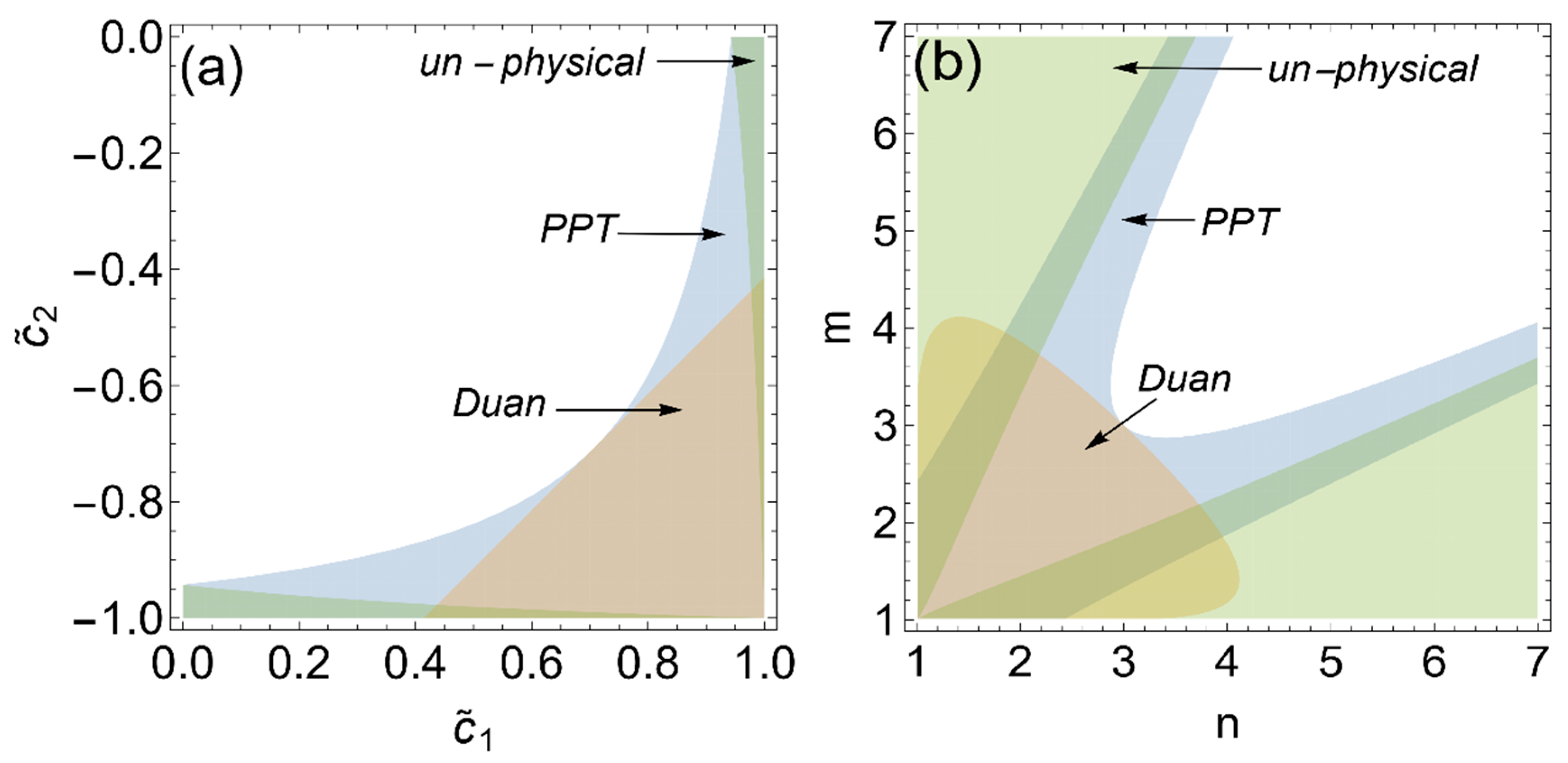
2.1. Asymmetry of Two-Mode Gaussian States

The two-mode squeezed state is a fundamental Gaussian quantum state in quantum optics, typically generated by a type-II nondegenerate optical parametric amplifier (NOPA) or by combining two independent single-mode squeezed fields using a 50/50 beam splitter. Mathematically, this state can be described by the symplectic eigenform of its covariance matrix, denoted as ${\mathit{\sigma }}_{ij}=〈\left(X_i{X}_j+X_j{X}_i\right)〉/2-〈X_i〉-〈X_j〉$, where $X\equiv \left(X_a^{+},X_a^{-},X_b^{+},X_b^{-}\right)$ represents the quadrature components of the field. The quadrature amplitude operator $X_i^{+}$​ and the quadrature phase operator $X_i^{-}$ are defined in terms of the annihilation operator $a_i$ and creation operator $a_i^{+}$ of the field as$X_i^{+}=a_i+a_i^{+}$ and $X_i^{-}=i\left(a_i^{+}-a_i\right)$，

$$\mathit{\sigma }=\left[\begin{array}{cc}A& \mathit{C}\\ {\mathit{C}}^{\mathit{T}}& \mathit{B}\end{array}\right]=\left[\begin{array}{cccc}n& 0& c_1& 0\\ 0& n& 0& c_2\\ c_1& 0& m& 0\\ 0& c_2& 0& m\end{array}\right]$$

(1)

where the submatrices$\mathit{A}$and $\mathit{B}$ correspond to the autocovariance matrices of the two subsystems, while the off-diagonal elements$\mathit{C}$represent the cross-covariance matrix between the two subsystems [39]. The relevant quantities$n$,$m$,$c_1$and$c_2$are determined by four local symplectic invariants:$\det \mathit{\sigma }=\left(nm-c_1^2\right)\left(nm-c_2^2\right)$, $\det \mathit{A}=n^2$, $\det \mathit{B}=m^2$and$\det \mathit{C}=c_1{c}_2$. Notably, the parameters are not arbitrary but must subject to specific physical constraints [22]:

$$\mathit{\sigma }+{\displaystyle \frac{i}{2}}\mathit{\omega }\oplus \mathit{\omega }\ge 0$$

(2)

where $\mathit{\omega }\equiv \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$．These constraints can be further elucidated as a function of the symplectic eigenvalues of the matrix elements, providing a deeper understanding of the state's properties,

$$\det \mathit{A}+\det \mathit{B}+2\det \mathit{C}\le 4\det \mathit{\sigma }+1$$

(3)

A state is termed symmetric when the covariance matrix satisfies$n=m$. For an ideal symmetric state, the parameters in the covariance matrix satisfy both $n=m$ and $c_1=-c_2$However, in practical applications, imperfections such as equipment noise and operational inefficiencies often result in asymmetry in two-mode squeezed states [40]. As illustrated in Figure 1, this asymmetry manifests primarily in two aspects: asymmetry in the orthogonal components of inter-mode correlations and asymmetry between the entangled modes. The former refers to the difference between the inter-mode covariance components $c_1$ and $c_2$. This asymmetry typically arises from inconsistencies in the degree of squeezing, squeezing direction, or phase differences between the two squeezed beams (SQ1 and SQ2) used to generate the two-mode squeezed state during the state preparation process [23]. Mode asymmetry, on the other hand, refers to the difference between the local covariance matrices $n$and $m$ of the two modes. This asymmetry is often a result of the state transmission and detection processes, commonly encountered in quantum information protocols involving asymmetric noise and loss channels, such as quantum illumination and one-sided device-independent quantum key distribution. Asymmetry can significantly impact the results of entanglement criteria, making it crucial to understand and analyze the effects in practical systems.

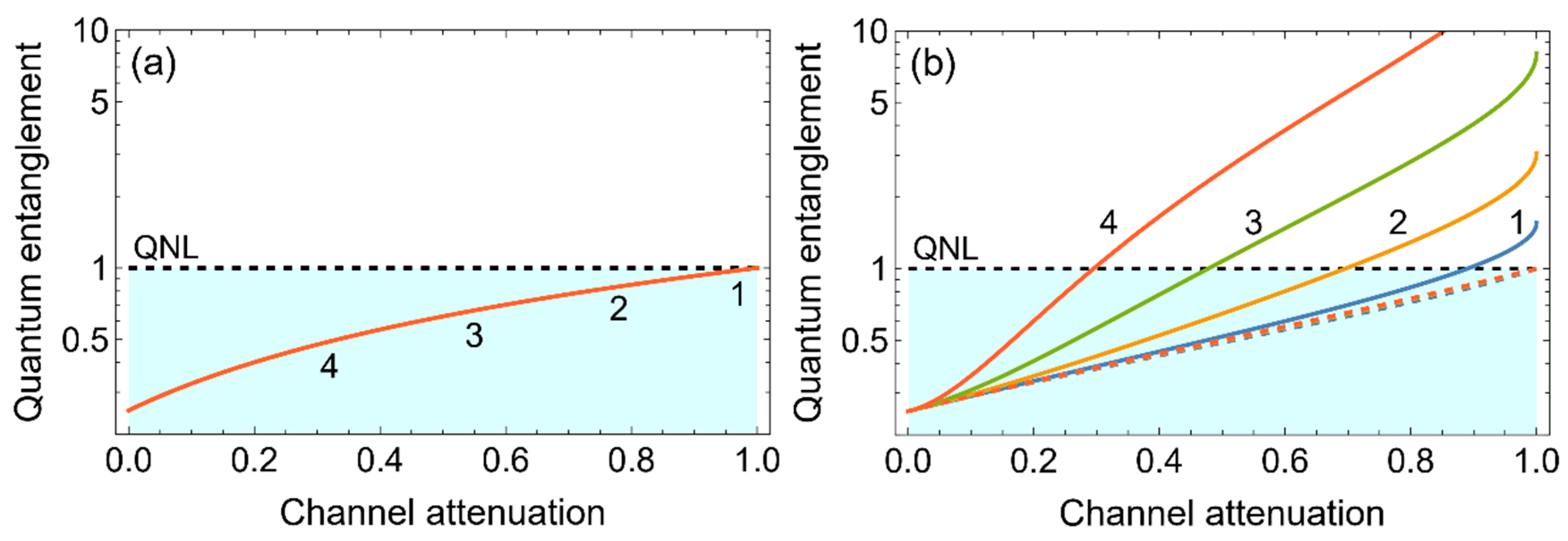
2.2. Missed Detection of Entanglement

The covariance matrix, as a vital representation of quantum state statistical information, provides a comprehensive statistical description of the correlation characteristics of two-mode squeezed states. However, it does not directly reveal the separability or entanglement of a state, nor does it quantify the degree of entanglement, necessitating the use of specific entanglement criteria. Inseparability criteria are widely employed in optical experiments, offering a straightforward and efficient tool for investigating the entanglement properties of continuous-variable quantum systems. The criteria typically equate separability with the positivity of the P-function. For states characterized by Gaussian noise distributions and symmetric correlations in conjugate quadrature components, the criteria can be linked to measurable correlations [6]. Specifically, for two-mode squeezed states, the inequality takes the form of:

$$En{t}_{Inse}={\Delta }^2{X}_{a\pm b}^{+}+{\Delta }^2{X}_{a\pm b}^{-}<1$$

(4)

where ${\Delta }^2{X}_{a\pm b}^{+}$represents the minimum value of the variance of the sum or difference of operators between beams $a$ and $b$, which has been normalized, i.e., ${\Delta }^2{X}_{a\pm b}^{+}=\min 〈{\left(\delta X_a^{+}\pm \delta X_b^{+}\right)}^2〉/4$. The elements of covariance matrix can be further utilized to calculate these variances:

$$En{t}_{Inse}={\displaystyle \frac{1}{4}}\left(\alpha +\beta \pm 2\gamma \right)<1$$

(5)

The value of $En{t}_{Inse}$directly reflects the strength of entanglement in the quantum state. The closer the value is to zero, the higher the degree of entanglement. It is important to note that the inseparability criterion is merely a sufficient condition for entanglement. Specifically, satisfying this inequality confirms the existence of entanglement. However, this criterion is not necessary —satisfying inequality (4) does not guarantee that the state is separable. The inseparability criterion fails to capture all entangled states, meaning certain entangled states may not satisfy this criterion, posing a risk of missed detections. This could result in misjudgments or errors in practical quantum information tasks, thereby adversely affecting the efficiency and accuracy of these tasks.

We aim to explore the potential risk of missing entangled states when applying the inseparability criterion to asymmetric two-mode squeezed states. To achieve this, we will compare the inseparability criterion with the PPT criterion, which is more reliable in detecting entanglement. The PPT criterion serves as a sufficient and necessary condition for two-mode squeezed states, determining the separability of a state by the positive definiteness of the partial transpose matrix of the two-mode Gaussian state. Specifically, the PPT criterion quantifies the entanglement properties by calculating the minimum symplectic eigenvalue of the covariance matrix,

$$En{t}_{PPT}=\sqrt{{\displaystyle \frac{\Gamma -\sqrt{{\Gamma }^2-4\det \mathit{\sigma }}}{2}}}<1$$

(6)

where $\Gamma =\det \mathit{A}+\det \mathit{B}-2\det \mathit{C}$. If the inequality holds, the two-mode Gaussian state is considered entangled, otherwise, it is separable. In Figure 2, we visually compare the inseparability and PPT criteria in defining the entanglement region under two scenarios: asymmetry in the intermodal correlation of orthogonal components and asymmetry in the entanglement modes. Specifically, Figure 2(a) shows the analysis of missed detections by the inseparability criterion in the case of asymmetry in the intermodal correlation orthogonal components, where we fix $n=m=3$ and analyze the evolution of the criterion by varying the values of ${\tilde{c}}_1$and ${\tilde{c}}_2$, with ${\tilde{c}}_i=c_i/c_{\max }$, where the state is maximally entangled when ${\tilde{c}}_i=1$; Figure 2(b) illustrates the analysis of missed detections by the inseparability criterion in the case of asymmetry in the entanglement modes, where we fix ${\tilde{c}}_1=-{\tilde{c}}_2=1/\sqrt{2}$ and vary the values of $n$ and $m$. In each subfigure, the orange region represents the entanglement range defined by the inseparability criterion, while the blue region shows the more comprehensive and rigorous entanglement definition given by the PPT criterion. The green region, a non-physical region, is defined by the constraints of Equation (3), reflecting the range of quantum states that are unattainable in actual physical systems. From the figures, it is evident that compared to the PPT criterion, the inseparability criterion covers a smaller region, entirely contained within the blue region defined by the PPT criterion. This indicates that the inseparability criterion fails to identify some entangled states recognized by the PPT criterion, highlighting the presence of missed entanglement detections. More specifically, in the case of ideal symmetric states (diagonally distributed from top left to bottom right in Figure 2(a) and anti-diagonally distributed from top right to bottom left in Figure 2(b)), the boundaries of the two criteria coincide, indicating that their judgments are equivalent: the inseparability criterion is both a sufficient and necessary condition for two-mode squeezed states. However, when this symmetry is broken, whether due to asymmetry in the intermodal correlation orthogonal components or asymmetry inherent in the entanglement modes—a significant divergence between the boundaries of the two criteria emerges, which deepens as asymmetry increases. This phenomenon reveals that under such circumstances, the inseparability criterion serves only as a sufficient condition, rather than a necessary, condition for determining whether a two-mode Gaussian state possesses entanglement properties. Consequently, when dealing with two-mode squeezed states with significant asymmetry, it may be necessary to apply the inseparability criterion more cautiously or consider using a more robust and rigorous criterion (such as the PPT criterion) that is less sensitive to asymmetry to ensure accurate entanglement detection.

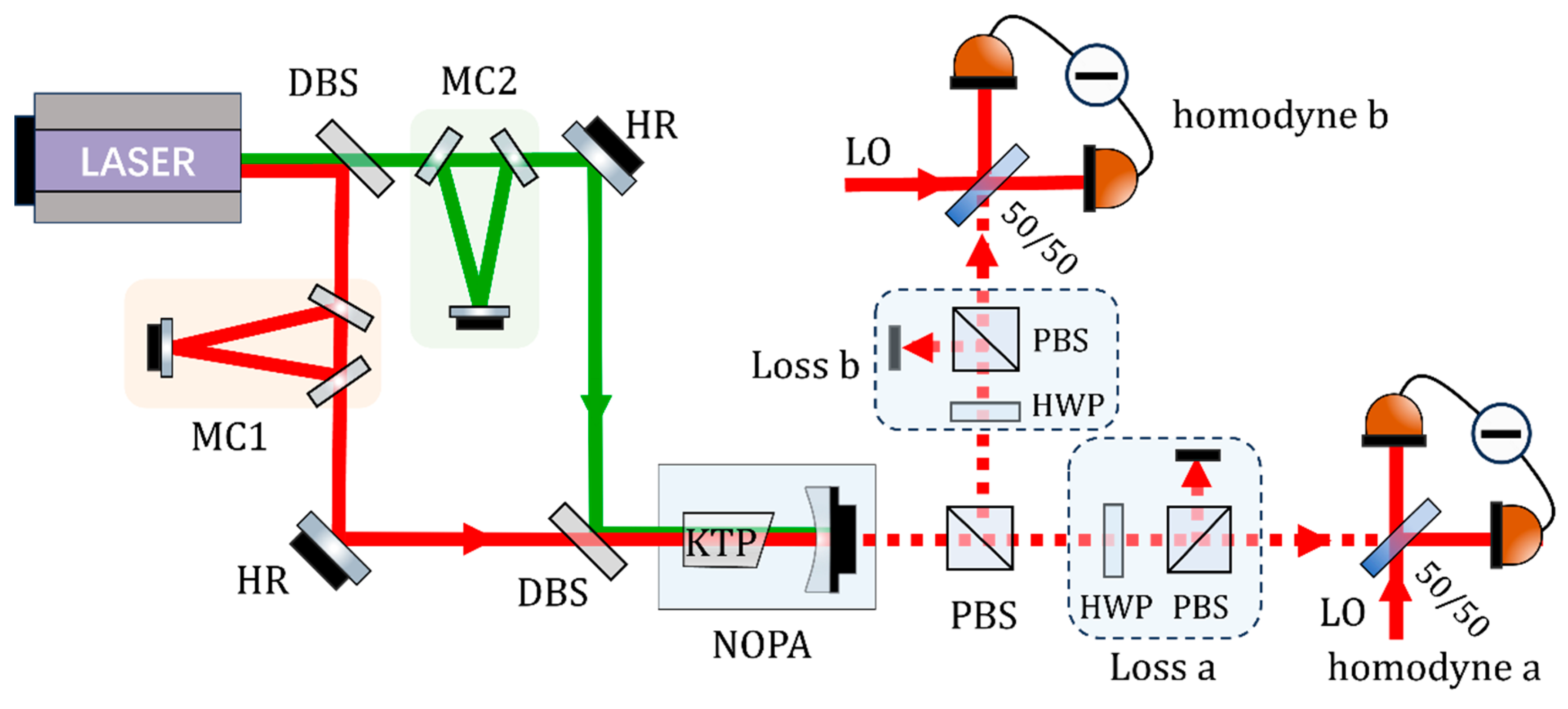
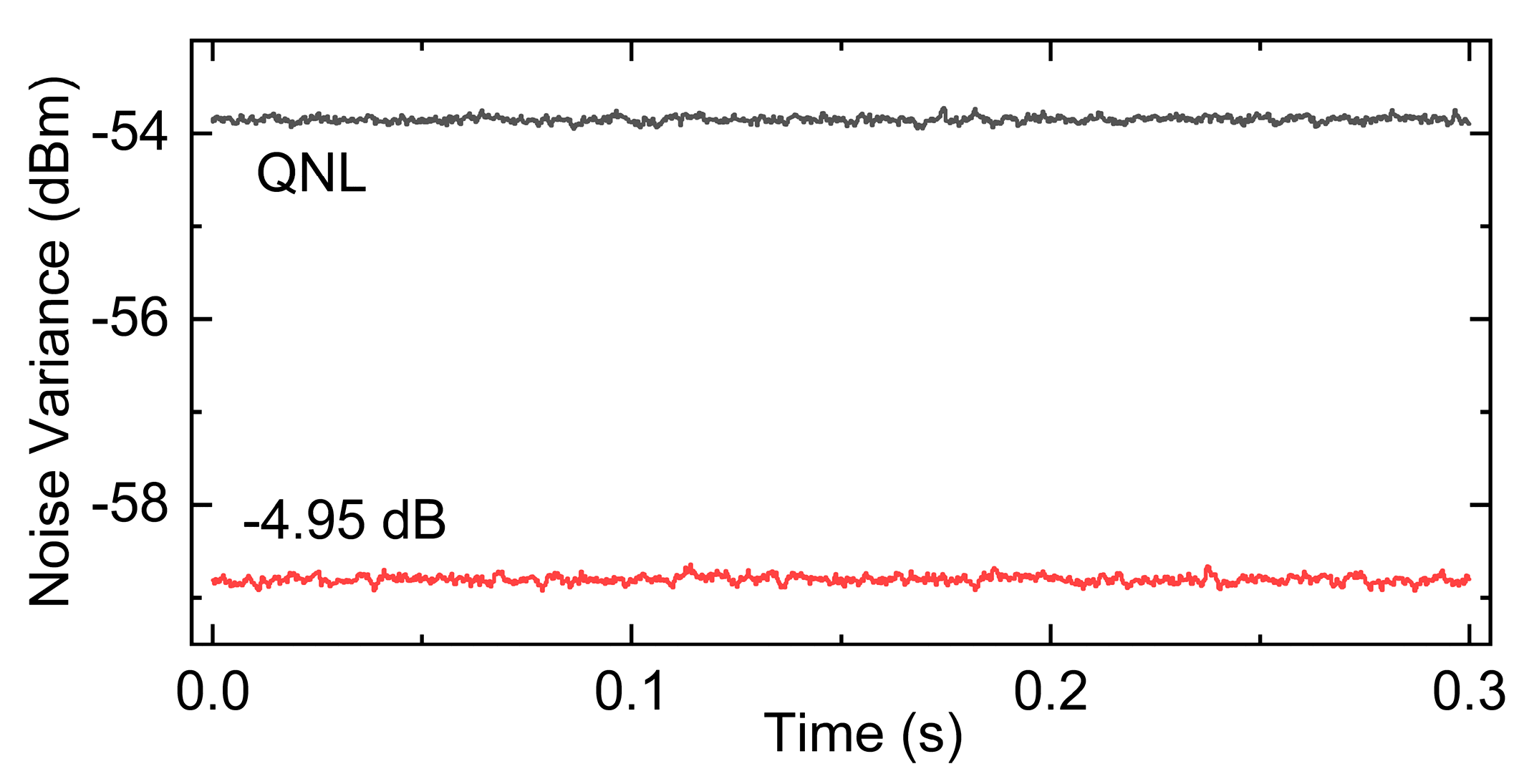
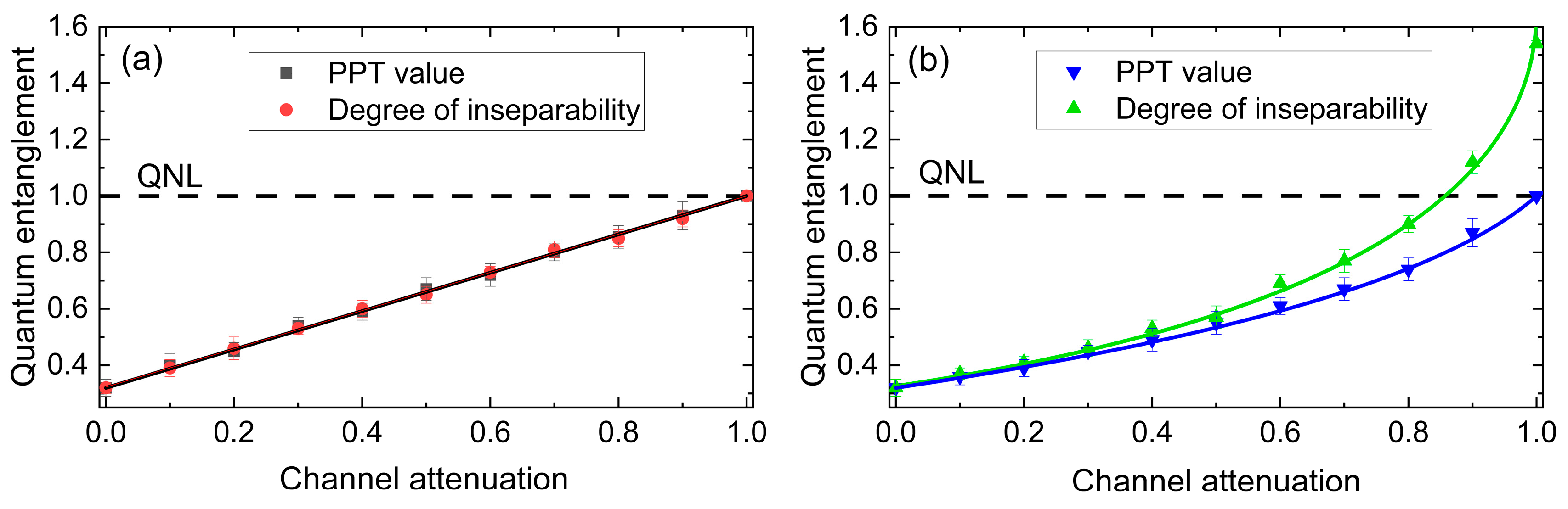
3. Experimental and Results

Our experimental validation was conducted through a NOPA system. Owing to the symmetry of the Hamiltonian, the state generated by NOPA is a fully symmetric state, implying that the elements of covariance matrix satisfy conditions, specifically $n=m$and $c_1=-c_2$. Figure 3 illustrates the experimental setup employed to generate the two-mode squeezed state. The NOPA comprises an α-cut type-II phase-matched KTiOPO4 (KTP) crystal (cut at 1°) and a plano-concave mirror. The system utilizes 1080 nm infrared light, noise-reduced by a three-mirror ring-cavity infrared mode cleaner (MC1), and 540 nm green light, noise-reduced by a green light mode cleaner (MC2), as the input and pump beams respectively. The NOPA cavity is operated below threshold, and when the relative phase between the pump and input beams is locked to the parametric deamplification state, the output port emits a two-mode squeezed state with orthogonal polarizations (signal field $a$and idler field$b$). This two-mode squeezed state exhibits anti-correlation in the quadrature amplitudes and positive correlation in the quadrature phases. In the experiment, the two sub-modes and of the two-mode squeezed state are separated using a polarizing beam splitter (PBS) and then directed to a balanced homodyne detection system for entanglement measurement. To achieve a lower pump threshold, the NOPA cavity is designed to be triply resonant for the pump, signal, and idler modes. This is experimentally realized by fine-tuning the phase-matching temperature and adjusting the transverse position of the crystal. During measurements, the system is operated at approximately 70% of the threshold power to avoid undesirable non-Gaussian effects. The experiment demonstrates a squeezing of -4.95 dB and an anti-squeezing of 6.53 dB at an analysis frequency of 2 MHz (see Figure 4). These measurements were obtained using a balanced homodyne detection system with a total detection efficiency of up to 85%. Complete measurements of the quadrature components allowed for the derivation of the covariance matrix, enabling a comparison between the PPT criterion and the inseparability criterion.

To introduce asymmetry in the entanglement, we strategically positioned independent beam splitters on the two entangled beams, prior to their arrival at the balanced homodyne detectors. This setup simulates propagation losses inherent quantum channels. These beam splitters were constructed using a half-wave plate and a polarizing beam splitter, enabling us to simulate channel attenuation ranging from 0% to 100% by adjusting the angle of the half-wave plate. The fields $a^{\prime }$ and $b^{\prime }$ preceding the balanced homodyne detectors can be mathematically expressed as $a^{\prime }=\sqrt{{\eta }_a}a+\sqrt{1-{\eta }_a}{a}_v$ and $b^{\prime }=\sqrt{{\eta }_b}b+\sqrt{1-{\eta }_b}{b}_v$, where $\sqrt{{\eta }_a}$ and $\sqrt{{\eta }_b}$ represent the channel transmission, and $a_v$ and $b_v$ are the vacuum fields introduced into the system due to the lossy channels. The two-mode Gaussian state ${\rho }_{a^{\prime }{b}^{\prime }}$, formed by the fields $a^{\prime }$ and $b^{\prime }$, can be effectively characterized by a covariance matrix:

$${\mathit{\sigma }}^{\prime }=\left[\begin{array}{cccc}{\eta }_{a}n+1-{\eta }_A& 0& \sqrt{{\eta }_a{\eta }_b}c& 0\\ 0& {\eta }_{a}n+1-{\eta }_a& 0& -\sqrt{{\eta }_a{\eta }_b}c\\ \sqrt{{\eta }_a{\eta }_b}c& 0& {\eta }_{b}n+1-{\eta }_b& 0\\ 0& -\sqrt{{\eta }_a{\eta }_b}c& 0& {\eta }_{b}n+1-{\eta }_b\end{array}\right]$$

(7)

For each attenuation, the inseparability value and PPT value are obtained by repeating the complete measurement process of the quadrature components. These entanglement criteria can be further formulated as functions of the channel attenuation, with the inseparability value,

$$\begin{array}{cc}\hfill En{t^{\prime }}_{Inse}& ={\Delta }^2{X}_{a^{\prime }\pm b^{\prime }}^{+}+{\Delta }^2{X}_{a^{\prime }\pm b^{\prime }}^{-}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left({\eta }_{a}n+{\eta }_{b}n+\left(1-{\eta }_a\right)+\left(1-{\eta }_b\right)+2\sqrt{{\eta }_a{\eta }_b}c\right)\hfill \end{array}$$

(8)

and PPT value,

$$En{t^{\prime }}_{PPT}=\sqrt{{\displaystyle \frac{{\Gamma }^{\prime }-\sqrt{{{\Gamma }^{\prime }}^2-4\det {\mathit{\sigma }}^{\prime }}}{2}}}$$

(9)

$${\Gamma }^{\prime }={\left({\eta }_{a}n+1-{\eta }_a\right)}^2+{\left({\eta }_{b}n+1-{\eta }_b\right)}^2+2{\eta }_a{\eta }_b{c}^2$$

(10)

$$\det {\mathit{\sigma }}^{\prime }={\left[\left({\eta }_{a}n+1-{\eta }_a\right)\left({\eta }_{b}n+1-{\eta }_b\right)-{\eta }_a{\eta }_b{c}^2\right]}^2$$

(11)

Figure 5 presents the experimental outcomes for entanglement detection utilizing the inseparability criterion. Panels (a) and (b) illustrate the scenarios of symmetric (${\eta }_a={\eta }_b=\eta$) and asymmetric channel attenuation (${\eta }_a=1$ and ${\eta }_b=\eta$), respectively. Value 1 represent the standard quantum noise limit (QNL), acquired by blocking the entangled light and allowing only the local light to enter the balanced homodyne detection system. The red dots and blue squares correspond to experimental measurements based on the inseparability and PPT criterion, respectively, with their respective theoretical fits depicted by matching colored curves. Data was collected at 10 distinct channel attenuation points, spaced at 0.1 intervals. At zero channel attenuation, the initial entanglement degree was -4.95 dB, accompanied by an anti-squeezing of 6.34 dB, indicative of a state purity of 0.73. In the case of symmetric losses, the results from both criterions coincide, revealing al linear decrease in entanglement with the increasing losses, remaining below 1 within a certain range of channel attenuation $\left[0,1\right)$. Conversely, under asymmetric losses, as the asymmetry intensifies, the inseparability criterion diverges from the PPT criterion. Notably, when the asymmetry exceeds 0.83, the inseparability value surpasses 1, signifying its inability to detect the entangled state. This underscores the intricacies of asymmetric losses in entanglement detection and emphasizes the significance of selecting an appropriate criterion. The close alignment between experimental measurements and theoretical predictions validates both the accuracy of our theoretical analysis and the reliability of the experimental procedure.

In practical experimental setups, the presence of cavity losses and noise effects inherent to optical oscillators necessitates the preparation and manipulation of mixed states rather than pure states. Consequently, these states fail to uphold the minimum uncertainty principle, i.e., ${\Delta }^2{X}_a^{+}·{\Delta }^2{X}_a^{-}={\Delta }^2{X}_b^{+}·{\Delta }^2{X}_b^{-}>1$, yielding a purity metric that falls short of the ideal unity value. To delve into the implications of input state purity on entanglement assessment criteria, we conducted an analysis as illustrated in Figure 6. By systematically varying the purity levels to 1.0, 0.40, 0.138, and 0.04, achieved by maintaining a constant squeezing parameter with $r_1=0.69$ and adjusting the anti-squeezing parameter to 0.69, 1.15, 1.7, and 2.3, respectively, we examined their influence. Figures (a) and (b) explicitly depict the effects of purity on entanglement criteria under symmetric and asymmetric loss conditions, respectively. Intriguingly, under symmetric losses, the inseparability criterion and the PPT criterion remain invariant to changes in the purity of the two-mode squeezed state, once the initial squeezing factor is established. Conversely, in the presence of asymmetric losses, the PPT criterion remains relatively immune, whereas the inseparability criterion becomes acutely sensitive to state purity. As purity diminishes, the violation of the inseparability criterion intensifies markedly, attributed to the heightened total uncertainty that may hinder the fulfillment of its criteria, ultimately hindering entanglement detection. Furthermore, an overemphasis on squeezing a single quadrature component can potentially lead to erroneous entanglement assessments.

4. Conclusions

This paper delves into the utilization of the inseparability criterion in assessing two-mode squeezed states, with a particular focus on analyzing the phenomenon of entanglement detection failures caused by entanglement asymmetry. To this end, we conducted a comparative analysis with the more stringent necessary and sufficient condition—PPT criterion, both theoretically and experimentally, investigating the instances where the inseparability criterion fails to detect entanglement. Experimentally, we employed a sub-threshold NOPA to generate two-mode squeezed states and introduced optical losses induce asymmetry in the entangled modes, thereby validating limitations of the inseparability criterion. Our results reveal that in the presence of symmetric entanglement, the inseparability criterion aligns with the PPT criterion, constituting a necessary and sufficient condition for two-mode Gaussian states. However, under asymmetry entanglement conditions, significant disparities emerge between the two criteria, with the inseparability criterion only serving as a sufficient condition. Consequently, exclusive reliance on the inseparability criterion may result in entanglement missed detection and erroneous entanglement assessments, with the misjudgment rate escalating alongside the intensification of entanglement asymmetry. Hence, when confronted with pronouncedly asymmetric two-mode squeezed states, a more prudent application of the inseparability criterion is warranted. This may involve adjusting the covariance matrix weights, incorporating compensation factors into the inseparability criterion calculation, or adopting stricter criteria to ensure accurate entanglement state determination. Additionally, exploring novel neural network-based methods for continuous-variable entanglement detection [42] offers promising avenues.

In conclusion, this study offers vital insights into the application and underlying principles of the inseparability criterion in quantum information tasks, while also highlighting its potential limitations. Future quantum information science research should prioritize the impact of asymmetric entanglement, continually refining entanglement detection and measurement methodologies. With ongoing research endeavors and technological advancements, we anticipate harnessing the extraordinary potential of quantum entanglement to propel the rapid evolution of quantum technologies.