Interplay of Spin Nernst Effect and Entanglement Negativity in Layered Ferrimagnets: A Study via Exact Diagonalization

1. Introduction

Quantum correlation in low-dimensional magnets is an important topic in recent years which connects quantum information theory and condensed matter physics [1,2,3]. In the context of quantum spin systems, quantum correlation refers to the entanglement and non-classical correlations that exist between quantum particles. In three-dimensional ferrimagnets or layered ferrimagnets, the interplay between topological phase transitions and quantum correlations give rise to a range of intriguing phenomena, where entanglement plays a crucial role in determining of ground state properties, and various other spin exotic phenomena observed in ferrimagnetic systems [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. On the other hand, the spin Nernst effect refers to the generation of an electric field perpendicular to both an applied temperature gradient and external field. It is an important phenomenon that occurs in materials with broken time-reversal symmetry, being a variant of the standard Nernst effect, where the generated electric field is proportional to the spin current rather than the charge current. In the framework of layered ferrimagnets, it may emerges in the system due to the interplay between temperature gradients, magnetic fields, and spin transport. In general, when a temperature gradient is applied through a ferrimagnet, it may induce a spin current perpendicular to the temperature gradient, resulting in a transverse voltage known as spin Nernst voltage. This effect is directly related to the magnon Hall effect and can provide insights into the spin dynamics of ferrimagnetic materials. To study quantum correlations and spin Nernst effect in a layered ferrimagnet, several theoretical models and computational techniques are employed such as spin wave theory, density matrix renormalization group, quantum Monte Carlo exact diagonalization. Being the predictions regarding quantum entanglement and spin Nernst effect depend on the specific model, Hamiltonian, and parameters used in the study. The goal is to explore these phenomena experimentally and theoretically to gain a deeper understanding of the behavior of quantum spins in magnetic materials. In the layered ferrimagnet, the influence of magnon bands on quantum correlation is an interesting aspect to explore. The Heisenberg model describes the system with anisotropic and isotropic interactions being a widely studied model for understanding of the behavior of layered ferrimagnets. In general, quantum correlations and entanglement in the Heisenberg model can be quantified using differents quantifiers as von Neumann entanglement entropy or entanglement spectrum. The von Neumann entropy provides information about the degree of entanglement between different regions of the spin system. The entanglement spectrum, on the other hand, gives insights into the energy levels associated with the entanglement.

The presence of anisotropic interactions introduces a characteristic anisotropy in the magnon dispersion which affects the entanglement dynamics, where the magnon bands determine the spectrum of magnons, which, in turn, affect the entanglement dynamics. The von Neumann entropy and spectrum may exhibit different behaviors depending on the specific features of the magnon bands, such as their bandwidth, dispersion relation, and anisotropy. For example, the presence of gapless magnon modes can lead to long-range entanglement and power-law scaling of the von Neumann entropy. On the other hand, the presence of a magnon gap can suppress entanglement and lead to short-range correlations. The study of magnon bands and their influence on entanglement in the ferromagnetic and antiferromagnetic Heisenberg model often involves theoretical approaches such as spin wave theory, bosonization techniques, or numerical methods like exact diagonalization, which provide insights into the entanglement properties and their connection to the magnon spectrum of the system. Thus, the understanding of the interplay of magnon bands and entanglement is crucial for unraveling of quantum nature of ferrimagnetic systems. Helping in characterizing of ground state properties, and exploring the emergence of novel phenomena in these systems [20].

The goal of this paper is to analyze the influence of variation of the spin Nernst coefficient with coupling parameters on entanglement negativity. The paper is organized as follows: in Section 2, we discuss about the three-dimensional layered ferrimagnet and theirs properties. In Section 3, we present our analytical and numerical, where we discuss the variation of the spin Nernst conductivity and the behavior of the entanglement negativity as a function of T. In the last Section 4, we present our conclusions.

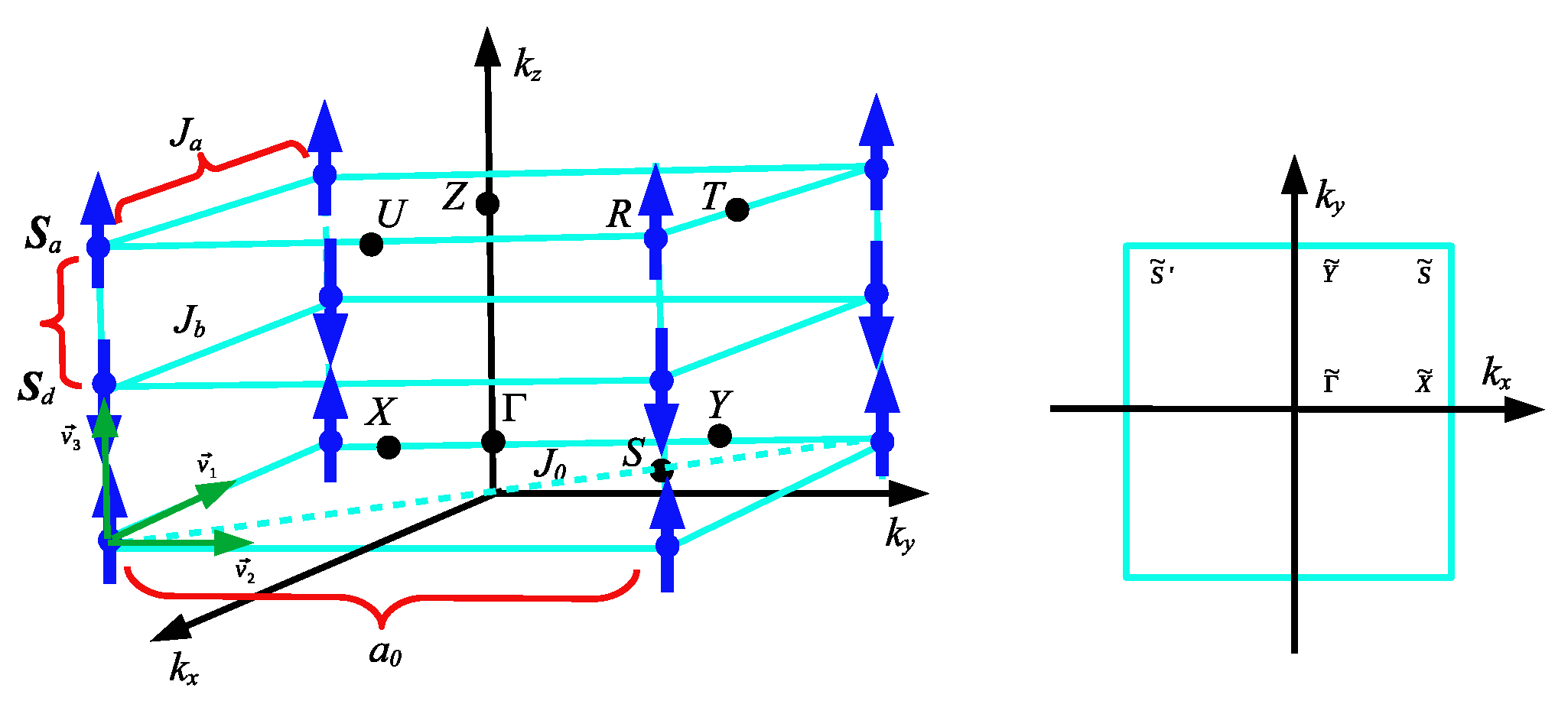
Figure 1. Lattice model for a layered ferrimagnet with ferromagnetic layers along z axis. $J_0$ is the inter-layer coupling, $J_a$ and $J_d$ indicate the exchange interactions between nearest-neighbors. The red arrows are the basis vectors, defined as ${\overrightarrow{v}}_1=(a_0,0,0)$. ${\overrightarrow{v}}_2=(0,a_0,0)$ and ${\overrightarrow{v}}_3=(0,0,2a_0)$, with $a_0$ being the in-plane lattice spacing.

Figure 1. Lattice model for a layered ferrimagnet with ferromagnetic layers along z axis. $J_0$ is the inter-layer coupling, $J_a$ and $J_d$ indicate the exchange interactions between nearest-neighbors. The red arrows are the basis vectors, defined as ${\overrightarrow{v}}_1=(a_0,0,0)$. ${\overrightarrow{v}}_2=(0,a_0,0)$ and ${\overrightarrow{v}}_3=(0,0,2a_0)$, with $a_0$ being the in-plane lattice spacing.

2. Model

General Hamiltonian for the layered ferrimagnet: For a layered ferrimagnet system with two types of ferromagnetic sublayers a and d sublattices stacked periodically, we consider the Hamiltonian with intralayer ferromagnetic exchange interactions for each sublattice; interlayer antiferromagnetic coupling between adjacent sublayers; magnetic anisotropy for each sublattice; external magnetic field applied to the system and dipole-dipole interaction as a perturbation to account for long-range dipolar effects. The model is composed by:

$$\begin{array}{c}\hfill {\mathcal{H}}_{intra}=-\sum _{\langle i,j\rangle \in a}{J}_a{\mathbf{S}}_i^a·{\mathbf{S}}_j^a-\sum _{\langle i,j\rangle \in d}{J}_d{\mathbf{S}}_i^d·{\mathbf{S}}_j^d.\end{array}$$

(1)

Antiferromagnetic interlayer exchange coupling between neighboring layers:

$$\begin{array}{c}\hfill {\mathcal{H}}_{inter}=-\sum _{\langle i,j\rangle }{J}_{inter}{\mathbf{S}}_i^a·{\mathbf{S}}_j^d.\end{array}$$

(2)

Magnetic anisotropy for each sublattice:

$$\begin{array}{c}\hfill {\mathcal{H}}_{anisotropy}=-\sum _{i\in a}{K}_a{\left({\mathbf{S}}_i^a\right)}^2-\sum _{i\in d}{K}_d{\left({\mathbf{S}}_i^d\right)}^2.\end{array}$$

(3)

External magnetic field:

$$\begin{array}{c}\hfill {\mathcal{H}}_{field}=-\sum _{i\in a}\mathbf{B}·{\mathbf{S}}_i^a-\sum _{i\in d}\mathbf{B}·{\mathbf{S}}_i^d.\end{array}$$

(4)

Dipole-dipole interaction (perturbative term):

$$\begin{array}{c}\hfill {\mathcal{H}}_{dipole}=\sum _{i,j}{\displaystyle \frac{{\mathbf{S}}_i·{\mathbf{S}}_j-3({\mathbf{S}}_i·{\widehat{\mathbf{r}}}_{ij})({\mathbf{S}}_j·{\widehat{\mathbf{r}}}_{ij})}{|{\mathbf{r}}_{ij}{|}^3}},\end{array}$$

(5)

where $\widehat{\mathbf{r}}$ is the unit vector between spins i and j and $|{\mathbf{r}}_{ij}|$ is the distance between them. $\mathbf{B}=\left(B_x,B_y,B_z\right)$ is the external magnetic field vector. Thus, the total Hamiltonian for the system is:

$$\begin{array}{c}\hfill \mathcal{H}={\mathcal{H}}_{intra}+{\mathcal{H}}_{inter}+{\mathcal{H}}_{anisotropy}+{\mathcal{H}}_{field}+{\mathcal{H}}_{dipole}.\end{array}$$

(6)

The model captures the interactions within and between the two sublattices as well as the influence of anisotropy, external fields and long-range dipolar effects.

3. Results

Entanglement is a quantum mechanical property that Schrödinger singled out as "the characteristic trait of quantum mechanics" and that has been many analyzed in connection with Bell’s inequality [25,26,27,28,29,30,31,32]. In general, a pure pair of quantum systems is called entangled whether it is unfactorable. It is a well known that the quantum information theory can be used together with condensed matter physics in characterizing of quantum phase transitions (QPT) that are characterized by the ground-state energy of quantum many-particle systems. The quantifying of quantum correlations in these many-body systems enhances the condensed matter physics and quantum information theory, being a measure of quantum correlation or entanglement in a system given by the entanglement negativity [30,33].

3.1. Negativity

The negativity is defined as the linear and partial transpose whose the trace norm is convex and monotone function however, not additive. Besides, it present a large deficiency i.e. a failure in satisfying the discriminant property, either that the entanglement $E\left(\rho \right)=0$ if and only if $\rho$ is separable [34]. The entanglement negativity [1,34,35] is given for a mixed state ${\rho }_{GE}$ by

$$\begin{array}{c}\hfill N\left(\rho \right)={\displaystyle \frac{\parallel {\rho }_A^T{\parallel }_1-1}{2}},\end{array}$$

(7)

where ${\rho }_A^T$ is the partial transpose of ${\rho }_{GE}$ with respect to the subsystem A, and ${\parallel ···\parallel }_1$ is the trace norm. The logarithmic negativity [36]

$$E_N\left(\rho \right)={log}_2{\parallel {\rho }_A^T\parallel }_1,$$

(8)

is used much often as a measure of thermal entanglement for disjoint intervals. Consequently, the negativity has been proven to be useful to detect topological order [37,38], where one makes ${\rho }_A={\rho }_{GE}$, we consider a bipartite lattice with $\mathcal{N}$ spins and in following we make $\mathcal{N}\to \infty$ in the partition, with the aim of the spin wave approach be valid to get the entanglement negativity as

$$\begin{array}{c}\hfill E_N={\displaystyle \frac{1}{k_{B}T}}\sum _{\nu }\sum _{\mathbf{k}}\left[{\mathsf{\Omega }}_{\nu }\left(\mathbf{k}\right)p\left({\mathsf{\Omega }}_{\nu }\left(\mathbf{k}\right)\right)+{log}_2(1+e^{-{\mathsf{\Omega }}_{\nu }\left(\mathbf{k}\right)/k_{B}T})\right],\end{array}$$

(9)

where the dispersion relation of magnons ${\mathsf{\Omega }}_{\nu }\left(\mathbf{k}\right)$ is given in Appendix and $p\left(x\right)={(e^{x/k_{B}T}-1)}^{-1}$ is the Bose-Einstein distribution.

3.2. Lanczos Algorithm and Exact Diagonalization

We get the entanglement negativity as a function of temperature for a finite lattice with $L=256$ sites using the Lanczos algorithm and exact diagonalization [39,40,41]. We perform a Python implementation using the Lanczos algorithm for approximate diagonalization, combined with the entanglement negativity calculation as a function of temperature for a 2D lattice with 256 sites. After constructing the Hamiltonian matrix for the system, we use the Lanczos algorithm to compute the low-lying eigenstates and eigenvalues. By calculating the reduced density matrix by tracing out part of the system (half the lattice), we compute the entanglement negativity from the partial transpose of the reduced density matrix. The number of Lanczos iterations (set to 100 here) determines how many eigenvalues and eigenvectors are approximated, which depends on how many low-energy states are important for the thermal ensemble. The Lanczos method is efficient for large systems and helps in approximating the eigenstates without requiring full diagonalization. We obtain $E_N\to 0$ at range of low temperature like obtained using the spin wave approach. This behavior is in accordance with the results obtained using basic linear algebra routines, where optimizations depending on the lattice size have given $E_N\to 0$ at range close to $T\sim 0$ as well. Since the results obtained by spin wave theory for higher temperature are only qualitative due to mean field approach used, the results obtained here are accurate at low-temperature limit.

In Figure 2, $E_N$ as a function of T using Lanczos Algorithm and Exact Diagonalization. We consider two different finite size lattice, $L=256$ sites above graphic and $L=1024$ below graphic. For all cases, we get a very small value for $E_N$ for all values of T, with $E_N$ tending to diverge at $T=0$ limit. The results obtained is convey of the results obtained using the spin wave approach where $E_N\to 0$ at $T=0$. However, we have that the results using the spin wave approach are valid in the continuum limit ($\mathcal{N}\to \infty$), where we consider a partition with $\mathcal{N}$ spins for which the local negativity is calculated and in following we make $\mathcal{N}\to \infty$ in the partition, with the aim the continuum theory be valid. The results obtained using exact diagonalization are valid for a finite lattice, considering a bipartite lattice of finite size L . Additionally, we have that the results of the spin wave theory are accurate at low temperature only, where the behavior given for higher temperatures is only qualitative.

3.3. Analysis by SWT Approach

In Appendix, we described the steps of diagonalization of the layered ferrimagnetic model with single-ion anisotropy K, and external field, using the spin wave theory (SWT). In Figure 3, we get the entanglement negativity $E_N$ as a function of T using the SWT approach, for $k_z=0$ and $k_z=\pi /2a_0$, that corresponds to the Brillouin zone edge in the z direction. We have ${\mathsf{\Omega }}^{\Vert (\perp )}=0.43{\mathsf{\Omega }}_{ex}^a$. As we have obtained a very small difference in the spin wave spectra with (without) dipole-dipole interaction as showed in Ref. [21], we must obtain a very small difference on entanglement negativity as well. Moreover, we get a small difference on behavior of $E_N$ on gap closing loop in $k_z=\pi /2a_0$ and $k_z=0$, where $E_N$ tends to zero at $T\to 0$ limit. In addition, we get that the small change in the curves of the entanglement negativity $E_N$ as a function of T, for different values $k_z=0$ and $k_z=\pi /2a_0$, in the gap closing loop and the system suffers a topological phase transition. We have a distribution of absolute values of the splitting between the two modes $\left(\right|{\mathsf{\Omega }}_1-{\mathsf{\Omega }}_2\left|\right)$ with ${\mathsf{\Omega }}_Z^{\Vert }=0.43{\mathsf{\Omega }}_{ex}^a$ in $k_z=\pi /2a_0$ and $k_z=0$. Furthermore, we get $E_N\left(\rho \right)$ tends to zero at $T\to 0$ as expected, in the range where quantum fluctuations in $T=0$ are large. Thus, the result indicates a small lost of quantum information at $T=0$ limit. The behavior at range of higher T is only qualitative due to limitations of the spin wave approach used. In general, the behavior of quantum correlations is determined by the behavior of the energy bands that depend on coupling parameters and which generates a large effect on quantum entanglement.

3.4. Magnon Nernst Effect

The magnon Hall effect refers to the generation of magnon currents transverse to the applied electric field. The magnons act in response to the external field, impacting in the magnon Hall conductivity, where the topological properties of magnon bands $\nu =\alpha ,\beta$ can be described by the Berry curvature $B^{\nu }\left(\mathbf{k}\right)$, that can give rise to anomalous Hall-like responses even in the absence of net magnetization. $B^{\alpha \left(\beta \right)}\left(\mathbf{k}\right)$ is defined as

$${\left(B^{\nu }\left(\mathbf{k}\right)\right)}_{ij}=\sum _{\mu \ne \nu }{\left({\sigma }_3\right)}_{\nu \mu }{\displaystyle \frac{2\mathrm{Im}\left[{\left(j_{i\mathbf{k}}^s\right)}_{\nu \mu }{\left({\sigma }_3\right)}_{\mu \mu }{\left({\nabla }_j{\mathcal{H}}_{\mathbf{k}}\right)}_{\mu \nu }\right]}{{[{\left({\sigma }_3\right)}_{\nu \nu }{\mathsf{\Omega }}_{\nu }\left(\mathbf{k}\right)-{\left({\sigma }_3\right)}_{\mu \mu }{\mathsf{\Omega }}_{\mu }\left(\mathbf{k}\right)]}^2}},$$

(10)

where $j_{j\mathbf{k}}^s={\displaystyle \frac{1}{4}}({\nabla }_j{\mathcal{H}}_{\mathbf{k}}{\sigma }_3{\mathbf{S}}^s+{\mathbf{S}}^s{\sigma }_3{\nabla }_j{\mathcal{H}}_{\mathbf{k}})$ is the polarized spin current and ${\sigma }_3=\mathrm{diag}(1,-1)\otimes {\mathbf{I}}_{N\times N}$ denoteing the bosonic commutator, where the bosonic Hamiltonian can be written as $\mathcal{H}={\mathbf{X}}^{†}\mathcal{H}\mathbf{X}$, where the basis $\mathbf{X}$ obeys the commutator relation $[\mathbf{X},{\mathbf{X}}^{†}]=g$. Moreover, it can be represented as $\mathbf{Y}=Q^{-1}\mathbf{X}$, where Q is a para-unitary matrix and $[\mathbf{Y},{\mathbf{Y}}^{†}]={\sigma }_3$.

The spin Nernst coefficient ${\alpha }_N^s$, is given by [42,43,44]

$$\begin{array}{c}\hfill {\alpha }_N^s={\displaystyle \frac{2k_{B}T}{V}}\sum _{\nu =\alpha ,\beta }\sum _{\mathbf{k}}{c}_1\left(p\left({\mathsf{\Omega }}_{\nu \mathbf{k}}\right)\right)B^{\nu }\left(\mathbf{k}\right),\end{array}$$

(11)

where V is the volume of the system and $c_1\left(x\right)=(1+x)ln(1+x)-xlnx$, being the integral of the Berry curvature is performed into the first Brillouin zone.

In Figure 4, we get the spin Nernst coefficient ${\alpha }_N^s$ as a function of T for $k_z=0$ and $k_z=\pi /2a_0$, which corresponds to the Brillouin zone edge in the z direction. We have ${\mathsf{\Omega }}^{\Vert (\perp )}=0.43{\mathsf{\Omega }}_{ex}^a$. We get that the very small variation of the curves of the spin Nernst coefficient ${\alpha }_N^s$ as a function of T for different values $k_z=0$ and $k_z=\pi /2a_0$ displayed in Figure 4, in the gap closing loop and where the system suffers a topological phase transition, generating a similar influence on the behavior of the curves of the entanglement negativity $E_N$ vs. T. In general, the spin Nernst effect introduces a non-equilibrium spin dynamics in the system, affecting the quantum correlations between spins, where depending on the strength of the spin-orbit coupling and the temperature gradient, the spin Nernst effect may influence the entanglement generation, propagation, or decay in the ferrimagnetic material. Thus, the interplay of spin Nernst effect, anisotropy, and quantum correlations may give rise to novel phenomena such as spin Hall effect described by the spin Nernst coefficient. The very small variation in the behavior of ${\alpha }_N^s$ with $k_z$ is showed in the inset of the Figure 4, indicating thus, a small effect of the different magnon bands induced by $k_z$ on ${\alpha }_N^s$. In Figure 5, we get ${\alpha }_N^s$ as a function of ${\mathsf{\Omega }}_{ex}^a$ for $T=0.1J$ held fixed, $k_z=\pi /2a_0$, $k_z=0$ and ${\mathsf{\Omega }}^{\Vert (\perp )}=0.43{\mathsf{\Omega }}_{ex}^a$. Since ${\mathsf{\Omega }}_{ex}^a$ depends on $J_0$ and biquadratic term $K_{a\left(b\right)}$, $J_0={\mathsf{\Omega }}_{ex}^a/2Z_{ab}{S}_{b\left(a\right)}$, $K_{a\left(b\right)}=0.45{\mathsf{\Omega }}_{an}^a/S_{a\left(b\right)}$, we obtain a dependence of ${\alpha }_N^s$ with $J_0$ and $K_{a\left(b\right)}$ in the same way. We get a small variation in the curves for different $k_z$ as showed in the inset of the Figure. The small variation obtained in the negativity and spin Nernst coefficient is a consequence of the small variation of the spin wave spectra with different intensities of external field along to the easy axis indicated by ${\mathsf{\Omega }}_Z^{\Vert }$.

4. Outlook

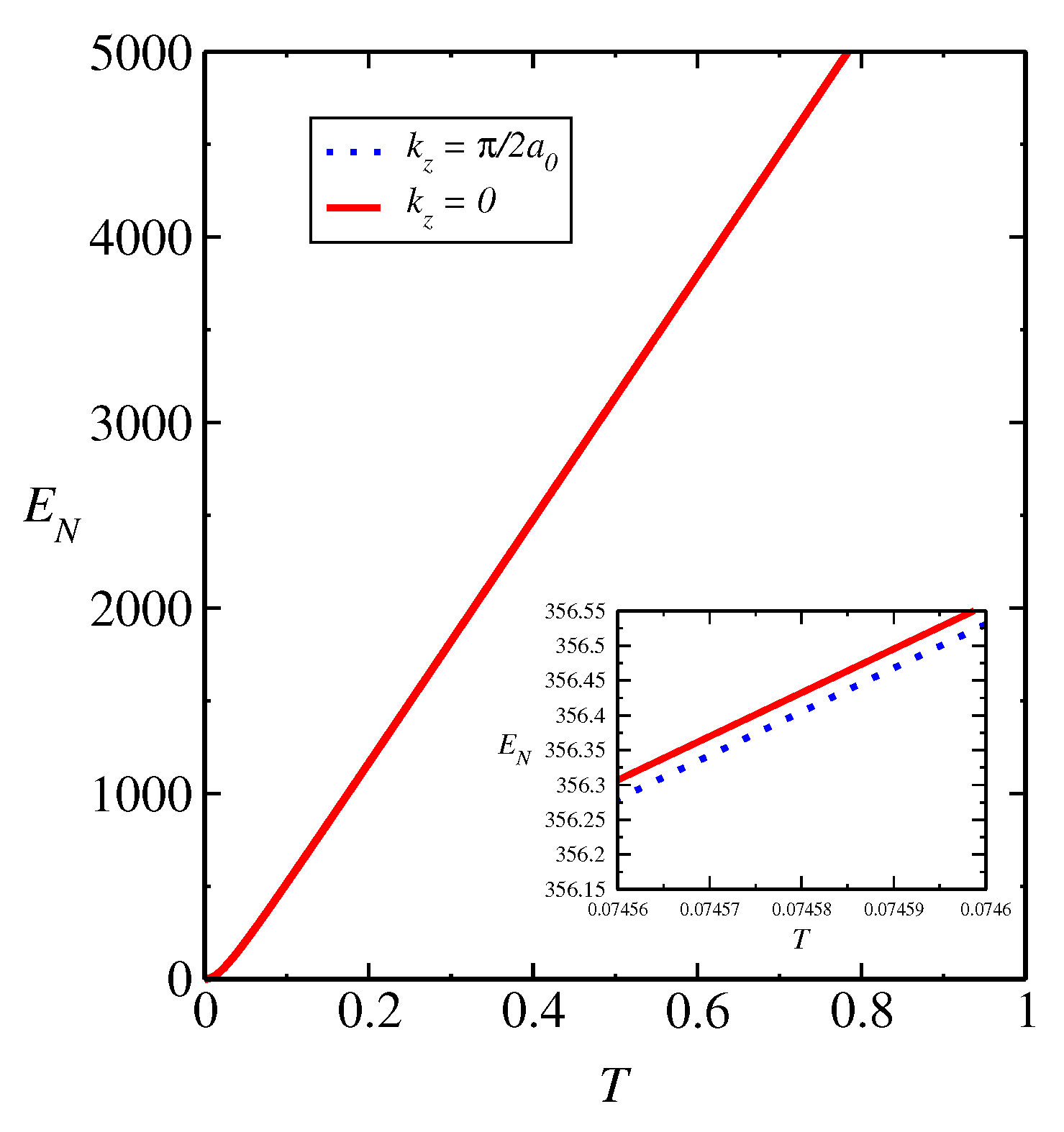
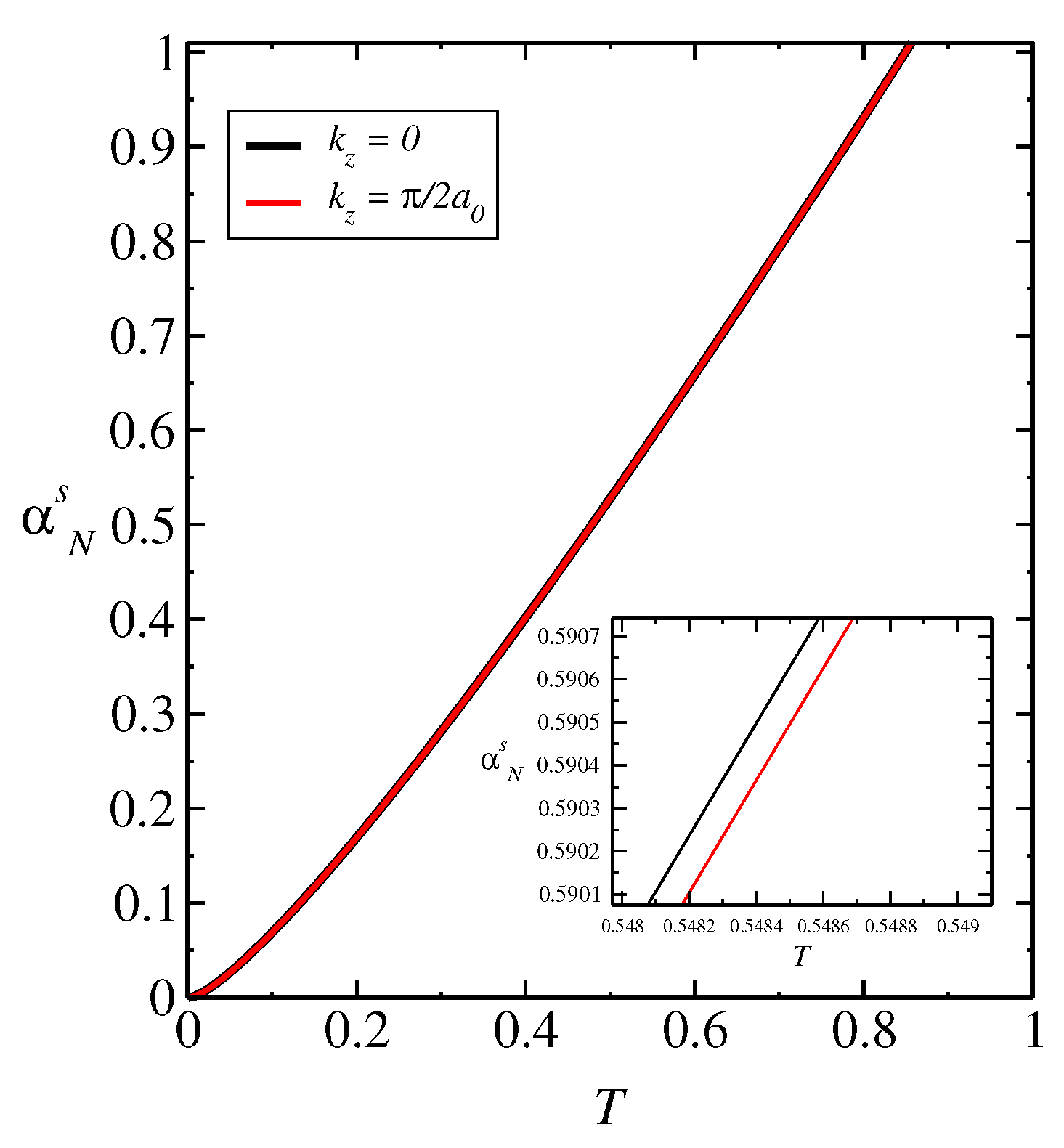
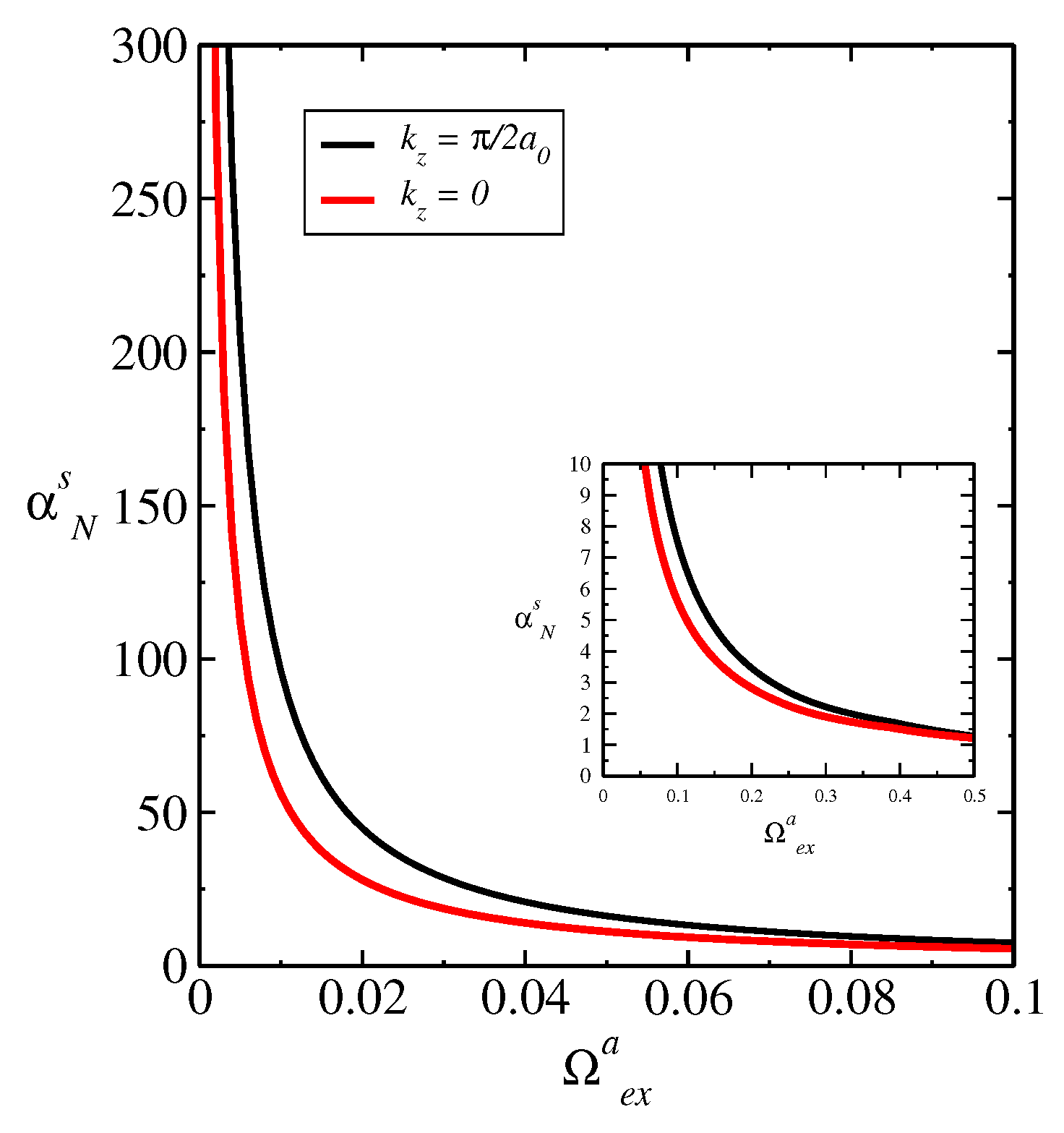
In brief, we analyzed the influence of dipole-dipole interaction on spin Nernst coefficient and quantum entanglement in a lattice model given by the layered ferrimagnet. The quantities reported well as the contribution to the Nernst coefficient of a given plane in k-space and entanglement negativity are experimentally relevant [1,36]. It’s worth noting that the specific details and predictions regarding quantum correlations and spin Nernst effect would depend on the specific model, Hamiltonian, and parameters used in the study. We got that the changes reported in the quantities analyzed are very small, where the contributions from the analyzed planes in k-space are relevant or dominant [21]. Moreover, we get that the small change in the curves of the spin Nernst coefficient ${\alpha }_N^s$ as a function of T, for different values $k_z=0$ and for $k_z=\pi /2a_0$, where the system suffers a topological phase transition, generating the same influence in the behavior of the curves of the entanglement negativity, $E_N$ vs. T. In a general way, the interplay of spin Nernst effect, entanglement negativity, and magnetism is a complex topic that requires further investigation and research. It is plausible that the spin Nernst effect influences the entanglement properties of the layered ferrimagnet by affecting the spin dynamics and correlations within the system. However, the specific details and quantitative aspects of this influence must depend on the particular characteristics of the material as well as its lattice structure and magnetic interactions.

Layered ferrimagnet with single-ion anisotropy K, external field with dipole-dipole interaction: The model is given by the Hamiltonian

$$\begin{array}{c}\hfill \mathcal{H}=\sum _{\langle \ell ,i,\ell ,j\rangle }{J}_{\ell }{\mathbf{S}}_{\ell ,i}·{\mathbf{S}}_{\ell ,j}+J_0\sum _{\langle \ell ,i,{\ell }^{\prime },i\rangle }{\mathbf{S}}_{\ell ,i}·{\mathbf{S}}_{{\ell }^{\prime },i}\\ \hfill +\sqrt{{\displaystyle \frac{2k}{{\mu }_0}}}\sum _{\ell ,i}{\mathbf{S}}_{\ell ,i}·\mathbf{B}-\sum _{\ell ,i}{K}_{\ell }{({\mathbf{S}}_{\ell ,i}·\widehat{\mathbf{k}})}^2\\ \hfill +k\sum _{\left(\ell ,i\right)\ne \left({\ell }^{\prime }j\right)}{\displaystyle \frac{{\mathbf{S}}_{\ell ,i}·{\mathbf{S}}_{{\ell }^{\prime },j}-3({\mathbf{S}}_{\ell ,i}·{\widehat{\mathbf{r}}}_{ij}^{\ell {\ell }^{\prime }})({\mathbf{S}}_{{\ell }^{\prime },j}·{\widehat{\mathbf{r}}}_{ij}^{\ell {\ell }^{\prime }})}{|{\mathbf{r}}_{ij}^{\ell {\ell }^{\prime }}{|}^3}},\end{array}$$

(A1)

where the unit vector $\widehat{\mathbf{k}}$ is in the direction of the easy axis, specified to z (x) for the in-plane (out-of-plane) magnetized geometry, $k={\mu }_0{\left(g{\mu }_B\right)}^2/2$ and ${\widehat{\mathbf{r}}}_{ij}$ is the unit vector pointed in the direction of the line joining of nearest-neighbors spins, and $r=|{\mathbf{r}}_{ij}|$ is the distance between them. Moreover, ${\mu }_0$ is the vacuum permeability constant, g is the Landé factor and ${\mu }_B$ is the Bohr magneton. The representation of the lattice considered is given in Figure 1. $K_{\ell }$ is the single-ion anisotropy and $J_{\ell }=J_a\left(J_d\right)$ are the ferrimagnetic intra-layer exchanges. The notation used ℓ and i in ${\mathbf{S}}_{\ell ,i}$ denote the layer and the site, respectively. Being $K_{\ell }=K_a\left(K_d\right)$ and $J_{\ell }=J_a\left(J_d\right)$ for the sublattice a (d). Moreover, $J_0$, $J_a$ and $J_d$ indicate the exchange constants between nearest-neighbors. The unit vector $\widehat{\mathbf{n}}$ is the direction of the easy axis, which is specified to x$\left(z\right)$ direction in-plane (out-of-plane).

HP transformation: We performed the Holstein-Primakoff (HP) transformation expanded up to first order, after performing a local rotation of the spin operators of the model above to the new operators ${\tilde{\mathbf{S}}}_{aj}^{+}$, ${\tilde{\mathbf{S}}}_{aj}^{-}$ and ${\tilde{S}}_{ja}^z$[21], so that the mean-field direction of the spins points along to the local z axis:

$$\begin{array}{c}\hfill {\tilde{\mathbf{S}}}_{aj}^{+}\approx \sqrt{2S}{a}_j,{\tilde{\mathbf{S}}}_{aj}^{-}\approx \sqrt{2S}{a}_j^{†},{\tilde{S}}_{ja}^z=S_a-a_j^{†}{a}_j,\end{array}$$

(A2)

where we obtain the magnon Hamiltonian in the form of creation and annihilation operators, $a_j^{†}\left(b_j^{†}\right)$ and $a_j\left(b_j\right)$, respectively.

Semimetal phase in collinear configuration: Whether the magnetic field is applied along to the easy axis with intensity below of the spin flop transition, we have a perpendicularly magnetized geometry, $\phi =0$. The ferrimagnetic state is in the collinear configuration with the spins aligning in the z direction, corresponding to ${\phi }_a={\phi }_d=\pi /2$. The addition of the dipole-dipole interaction opens an anti-crossing gap at the intersection regions of the $k_z$ plane within the Brillouin zone, while the bands display linear crossings at the Brillouin zone edge, reflecting in the role of dipole-dipole interaction as a source of magnon spin-orbit coupling [21,22] and nontrivial magnon band topology [23,24]. We consider the dipole-dipole interaction as a perturbation, considering its smaller magnitude compared to the other energy terms and projecting the magnon Hamiltonian into a reduced subspace with the basis consisting of the eigenstates of the Hamiltonian excluding the dipole-dipole interaction.

In the collinear configuration, we take the discrete Fourier transform of the bosons operators

$$\begin{array}{c}\hfill a_{\mathbf{k}}={\displaystyle \frac{1}{\sqrt{N}}}\sum _{\mathbf{k}}{a}_j{e}^{-i\mathbf{k}·{\mathbf{r}}_j};b_{\mathbf{k}}={\displaystyle \frac{1}{\sqrt{N}}}\sum _{\mathbf{k}}{b}_j{e}^{i\mathbf{k}·{\mathbf{r}}_j}\end{array}$$

(A3)

and the Bogoliubov transformation to get the dispersion relation of magnons [21]

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{\alpha \left(\beta \right)}\left(\mathbf{k}\right)=\sqrt{{\left({\displaystyle \frac{\mathcal{A}\left(\mathbf{k}\right)+\mathcal{B}\left(\mathbf{k}\right)}{2}}\right)}^2-{\left(\mathcal{C}\left(\mathbf{k}\right)\right)}^2}\pm {\displaystyle \frac{\left[\mathcal{A}\left(\mathbf{k}\right)-\mathcal{B}\left(\mathbf{k}\right)\right]}{2}},\end{array}$$

(A4)

where

$$\begin{array}{c}\hfill \mathcal{A}\left(\mathbf{k}\right)=-{\mathsf{\Omega }}_{ex}^{a}cos({\phi }_a+{\phi }_b)-{\mathsf{\Omega }}_{ex}^{aa}[1-{\gamma }^{aa}\left(\mathbf{k}\right)]\\ \hfill +{\displaystyle \frac{1}{2}}{\mathsf{\Omega }}_{an}^a(3{sin}^2{\phi }_a-1)-\left({\mathsf{\Omega }}_Z^{\Vert }sin{\phi }_a+{\mathsf{\Omega }}_Z^{\perp }cos{\phi }_a\right),\\ \hfill \mathcal{B}\left(\mathbf{k}\right)=-{\mathsf{\Omega }}_{ex}^{d}cos({\phi }_a+{\phi }_d)-{\mathsf{\Omega }}_{ex}^{dd}[1-{\gamma }^{dd}\left(\mathbf{k}\right)]\\ \hfill +{\displaystyle \frac{1}{2}}{\mathsf{\Omega }}_{an}^d(3{sin}^2{\phi }_d-1)+\left({\mathsf{\Omega }}_Z^{\Vert }sin{\phi }_d-{\mathsf{\Omega }}_Z^{\perp }cos{\phi }_d\right),\\ \hfill \mathcal{C}\left(\mathbf{k}\right)={\displaystyle \frac{{\mathsf{\Omega }}_{ex}^{ad}}{2}}[1-cos({\phi }_a+{\phi }_b)]{\gamma }^{ad}\left(\mathbf{k}\right),\end{array}$$

(A5)

and ${\mathsf{\Omega }}_{ex}^{a\left(d\right)}=2J_0{Z}_{ad}{S}_{d\left(a\right)}$, ${\mathsf{\Omega }}_{ex}^{ab}=2J_0{Z}_{ad}\sqrt{S_d{S}_a}$, ${\mathsf{\Omega }}_{ex}^{aa\left(dd\right)}=2J_{a\left(d\right)}{Z}_{aa\left(dd\right)}{S}_{a\left(d\right)}$, ${\mathsf{\Omega }}_{an}^{a\left(d\right)}=2K_{a\left(d\right)}{S}_{a\left(d\right)}$. Furthermore, we have ${\mathsf{\Omega }}_Z^{\Vert (\perp )}=g{\mu }_B{\mathbf{B}}_{\Vert (\perp )}$. ${\mathbf{B}}_{\Vert }\left({\mathbf{B}}_{\perp }\right)$ corresponding to external field component along to the easy axis. In addition, we have the form factors

$$\begin{array}{c}\hfill {\gamma }^{aa}\left(\mathbf{k}\right)={\gamma }^{dd}\left(\mathbf{k}\right)={\displaystyle \frac{1}{2}}\left[cos\left(k_x{a}_0\right)+cos\left(k_y{a}_0\right)\right],\\ \hfill {\gamma }^{ad}\left(\mathbf{k}\right)=cos\left(k_z{a}_0\right),k_z={\displaystyle \frac{\pi }{2a_0}},\end{array}$$

where $a_0$ the lattice spacing constant.