Dynamics of Neutron Transfer in the Reaction ³He+⁹Be

1. Introduction

Among stable weakly bound nuclei, the ⁹Be nucleus is of great interest. It has a Borromean structure in the ground state [1,2,3,4,5] and is typically represented as a system of two α-clusters and a neutron [6,7,8]. For instance, the (α+n+α) structure of the ⁹Be nucleus was considered in [9,10] using Feynman path integrals. Experimental works [7,11,12] on the cluster channels of the decay of the nucleus ⁹Ве are also in favor of the (α+n+α) structure. However, with some probability, the nucleus ⁹Ве can be in a state corresponding to a two-particle structure, as evidenced by the results of experimental works [13,14], where it was shown that the nucleus ⁹Ве can decay through the two-particle channels ⁹Ве→n+⁸Be or ⁹Ве→α+⁵Не. Because the ⁹Be nucleus is stable, it is much easier to be investigated compared to other Borromean nuclei.

Structural features of light nuclei are manifested in nucleon transfer reactions [15,16,17,18,19], for example, in the angular distributions of reaction products. The structure of the light nuclei d, ³He, and α is well known, and thus they are often employed to induce direct reactions, either as beams or as targets [15,16,17,18,19].

The process of the neutron transfer in a reaction with the ⁹Be nucleus is interesting due to the fact that the low binding energies of the neutron (1.666 MeV) and α-particle (2.462 MeV) should influence the dynamics and mechanism of the transfer. The interaction of deuterons and alpha particles with ⁹Be at an energy of 10-30 MeV/nucleon has been studied taking into account its cluster structure in [20,21]. The interaction potential for the colliding nuclei was constructed within the framework of the double folding model using a three-body wave function. Calculations with the double folding potential carried out within the optical model (OM) and Distorted Wave Born Approximation (DWBA) method provided good agreement between the theoretical cross sections and the experimental data.

In our previous works [16,17,18,19,20,21], we performed experimental and theoretical studies of the angular distributions of the products of nucleon and cluster transfer in the reactions d+⁹Be [17,20,21], ³He+⁹Be [16,18], and ⁶Li+⁹Be [19]. The obtained data were analyzed using the OM, the coupled reaction channel (CRC) method, and the DWBA method. The analysis of the experimental data showed the sensitivity of the cross sections to the potential parameters in the exit channels. In works of other authors [22,23,24], experimental data on the neutron transfer in the ⁹Be(³He, α)⁸Be reaction channel were also analyzed within the DWBA method.

This paper presents a study of the neutron transfer process in the ⁹Be(³He,α)⁸Be reaction channel. To describe the mechanism and dynamics this process, the data are analyzed using the DWBA method [25,26,27] and the time-dependent Schrödinger equation (TDSE) approach [28,29,30,31]. A direct comparison of the theoretical description of the neutron transfer process (in our case, in the d+⁹Be reaction) within the framework of the stationary (DWBA) and time-dependent approaches (TDSE) is the challenge that we intend to tackle in this work. Each approach has its own advantages and disadvantages, but if used together, they complement each other. For this purpose, in the TDSE calculations, we used the values of the potential parameters obtained in the DWBA calculations for the ³He+⁹Be entrance channel and for the initial neutron wave functions. The TDSE approach allows for both qualitative (reaction dynamics) and quantitative analysis of the neutron transfer process (probabilities of neutron transfer and neutron removal, reaction channel cross sections) [32,33,34].

The study of the dynamics and mechanisms of nuclear reactions with the ⁹Be nucleus is also important for applied research. For example, ⁹Be can be used as a structural material for the thermonuclear reactors [35,36], and the mechanisms of the ³He+⁹Be reaction must be taken into account when designing a reactor structure and modeling the processes of burning of a dense hot plasma with the d+³He combination of nuclei in a metal ⁹Be cylindrical liner [36]. ⁹Be can also be used as a target for neutron sources due to the large cross section of the ⁹Be(p,n) reaction [37,38].

2. Experiment

The experiment was performed on the U-120M cyclotron of the Nuclear Physics Institute, Řež, Czech Republic [39]. The ions of the ³He beam (30 MeV) were incident on a self-supporting ⁹Be foil target (2 mg/cm², 99%). Carbon and oxygen contaminations of the target were not observed in energy spectra. The average beam current was 10-20 nA [18,40].

To identify reaction products, energy loss ∆E and residual energy E_r were measured by four telescopes (∆E-E method). Each telescope consisted of three silicon-lithium detectors with thicknesses of 10 µm (∆E₁), 100 µm (∆E₂), and 3 mm (E_r) and was protected by a 5 mm thick Cu–Pb collimator and a circular hole of 3 mm diameter [18,40]. The energy resolution of the detectors was ∼ 150–200 keV (FWHM). The telescopes were located at a distance of ∼ 25 cm from the target and could be rotated around it in the angular range of θ_lab = 7–63° with a step of 1–2°.

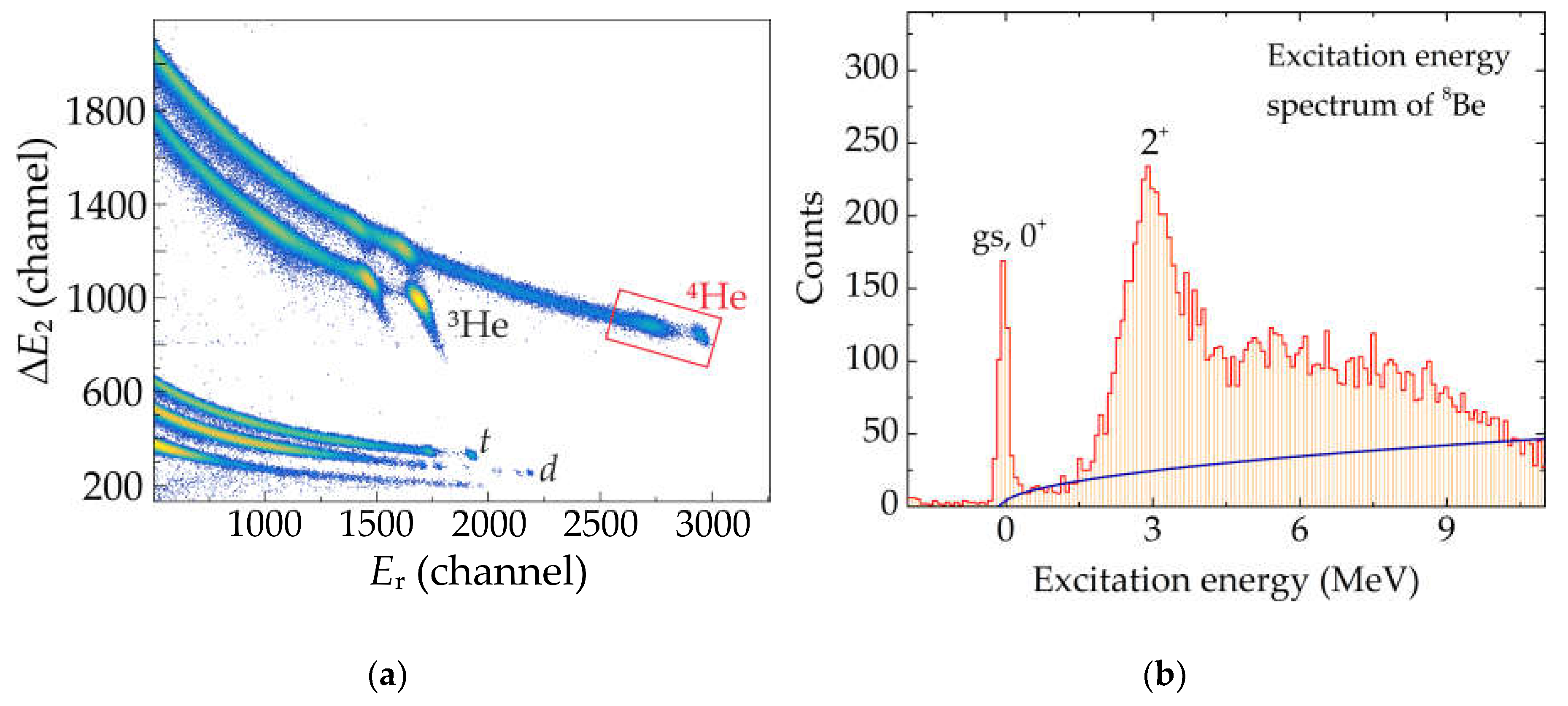
A typical example of a two-dimensional identification matrix obtained at an angle of θ_lab = 16° is shown in Figure 1a. It can be seen that A and Z of detected particles were unambiguously identified. The corresponding excitation energy spectrum of the ⁸Be nucleus, which is a complementary product to the detected ⁴He nucleus, is shown in Figure 1b. The first peak corresponds to the 0⁺ ground state of ⁸Be; the second peak is the 2⁺ excited state. Thus, these two peaks confirm the corresponding reaction channels with the neutron transfer from ⁹Be to ³He. Thus, the used technique allowed us to measure the energy of the products, identify reaction channels, and obtain their corresponding differential angular distributions.

The outlined region in the ΔE₂-E_r plot [Figure 1a] was used to obtain the excitation energy plot [Figure 1b]. It can be seen that the 0+ ground state of ⁸Be and the 2+ excited state are clearly separated. However, other reaction channels may contribute to the excitation energy plot in Figure 1b, in particular, breakup of ⁸Be, because it can undergo breakup with alpha particle emission. In the peak of the 0+ ground state, the contribution of the background is insignificant. In the peak of the 2+ excited state, the contribution of the background, mainly associated with the breakup process ⁸Be→⁴He+⁴He with the threshold energy of –0.0918 MeV, is less than 15%; the contribution from the breakup of ⁹Be is not present. To obtain the angular distributions presented in the next section, the background contribution was subtracted.

The following section presents the theoretical analysis of the experimental data on the reaction channels ⁹Be(³He,α)⁸Be_gs,3.03. Detailed information on other channels of the ³He+⁹Be reaction can be found in our previous papers [18,40].

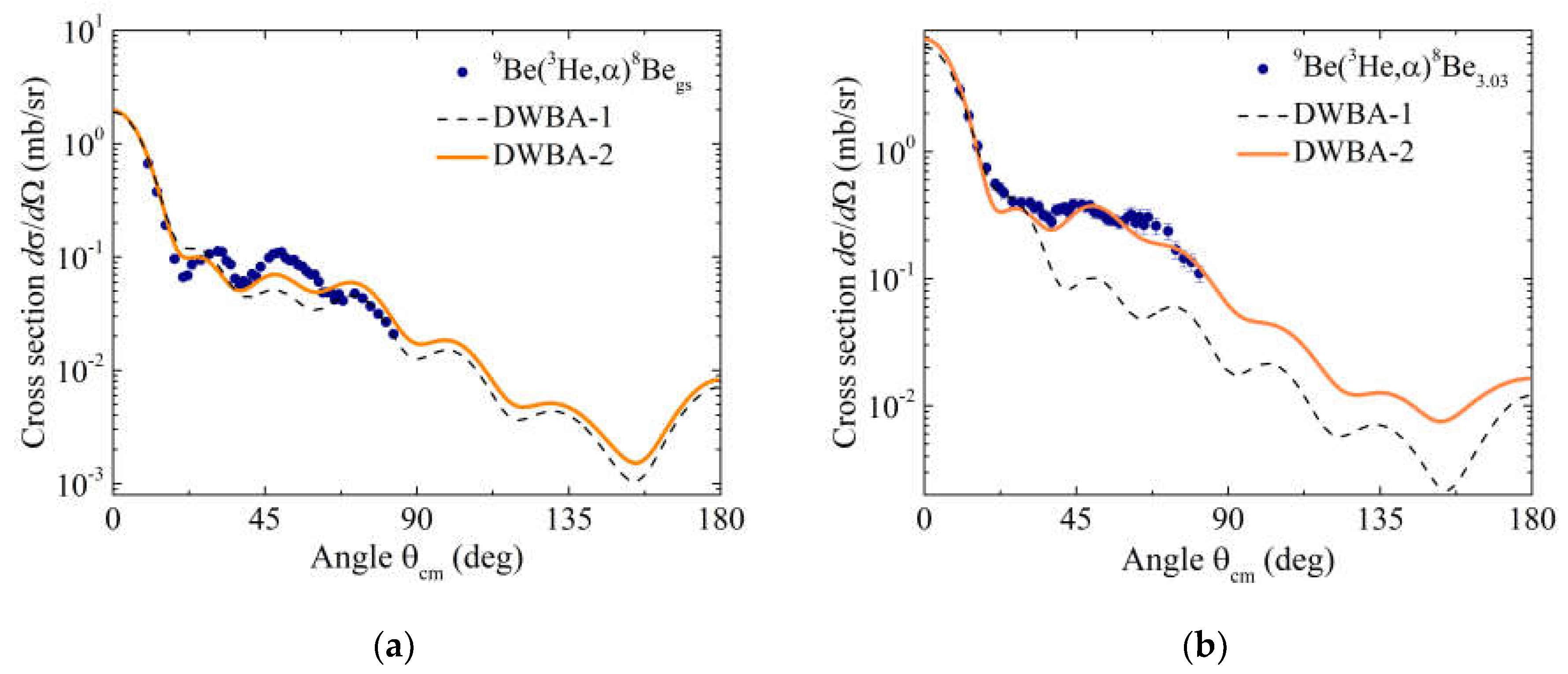
3. DWBA Calculations

Experimental differential cross sections for neutron transfer in ⁹Be(³He,α)⁸Be_gs,3.03 reaction channels are shown in Figure 2. To describe the experimental data, we used the prior formalism of the DWBA amplitude [25,26] and the FRESCO code [27]. For calculating the cross sections of neutron (n) transfer reaction A+b→a+B (A=a+n, B=b+n), the formalism of the DWBA method requires the potentials of the entrance and exit channels, the spectroscopic amplitudes S_x for the neutron in the systems A=a+n and B=b+n, and the potentials for calculating the neutron wave functions within the shell model.

The values of the spectroscopic amplitudes S_x = 0.791 for ⁹Be=⁸Be+n and S_x = –0.741 for ⁴He=³He+n were taken from our previous work [18]. The neutron wave functions were calculated within the shell model using the potential in the Woods-Saxon form with geometric parameters R = 1.25A^1/3 fm (radius) and a = 0.65 fm (diffuseness); the potential depths were adjusted to reproduce binding energies of a neutron.

As a starting point for searching for the optical potential U for the entrance and exit channels, we took the parameter sets from [18] (Table 1). These potential parameters have been successfully used to describe a large number of experimental data on the nucleon and cluster transfer channels in the ³He+⁹Be reaction. The potential U is defined as

$$U\left(r\right)=V_{\mathrm{C}}\left(r\right)-V_{\mathrm{V}}f(r;R_{\mathrm{V}},a_{\mathrm{V}})-i{V}_{\mathrm{W}}f(r;R_{\mathrm{W}},a_{\mathrm{W}}),$$

(1)

$$f(r;R_{\mathrm{V},\mathrm{W}},a_{\mathrm{V},\mathrm{W}})={\left[1+\exp \left({\displaystyle \frac{r-R_{\mathrm{V},\mathrm{W}}}{a_{\mathrm{V},\mathrm{W}}}}\right)\right]}^{-1},$$

(2)

$$R_{\mathrm{V},\mathrm{W}}=r_{\mathrm{V},\mathrm{W}}\left(A_{\mathrm{p}}^{1/3}+A_{\mathrm{t}}^{1/3}\right),$$

(3)

$$V_{\mathrm{C}}(r)=\left\{\begin{array}{c}{\displaystyle \frac{Z_{\mathrm{p}}{Z}_{\mathrm{t}}{e}^2}{2R_{\mathrm{C}}}}\left[3-{\left({\displaystyle \frac{r}{R_{\mathrm{C}}}}\right)}^2\right],r<R_{\mathrm{C}}\\ {\displaystyle \frac{Z_{\mathrm{p}}{Z}_{\mathrm{t}}{e}^2}{r}},r\ge R_{\mathrm{C}}\end{array}\right.,$$

(4)

$$R_{\mathrm{C}}=r_{\mathrm{C}}\left(A_{\mathrm{p}}^{1/3}+A_{\mathrm{t}}^{1/3}\right),$$

(5)

where V_C(r) is the Coulomb potential, Z_p and Z_t are the charges of the projectile and target, respectively; V_V,W are the depths of the real and imaginary parts of the potential, respectively; R_V,W, r_V,W, and a_V,W are their corresponding geometric parameters; A_p and A_t are the mass numbers of the projectile and target nuclei, respectively.

As can be seen from Figure 2, curves DWBA-1 calculated using the entrance and exit channel potentials with the parameters from [18] differ slightly from the experimental data for the ⁹Be(³He,α)⁸Be_gs reaction channel, but underestimate the data on the ⁹Be(³He,α)⁸Be_3.03 reaction channel in the angular range of 30–90°. Such a discrepancy between the DWBA calculations and the experimental data can be eliminated either by varying the values of the spectroscopic amplitudes or by reducing the depth V_W of the imaginary part of the exit channel potential [41,42]. We chose the second option, because the values of the spectroscopic amplitudes were obtained in [18] within the framework of the shell model calculations. Therefore, for better description of the experimental data, we reduced the depth V_W of the imaginary part of the exit channel potential (curves DWBA-2), i.e., V_W was obtained by fitting to the neutron transfer data. For the core-core potential (³He+⁸Be), we used the parameters of the entrance channel potential. The parameters of the optical potential (1) obtained for the entrance and exit channels are presented in Table 1.

The potential parameters for the exit channel α+⁸Be were obtained through a χ² minimization procedure based on the experimental data for the same reaction channel ³He(⁹Be,α)⁸Be with fixed spectroscopic amplitudes and potential parameters for the entrance channel, i.e., the elastic scattering channel ³He+⁹Be. It was found that the parameters of the fitted potential have unusually low values r_V = 0.252 fm and a_W = 0.34 fm; however, they are similar to those found for the α+⁸Be system in Ref. [43].

The discrepancy between the calculated differential cross sections and the experimental data for the ⁹Be(³He,α)⁸Be_gs reaction channel around the scattering angle of 55° in Figure 2a may be attributed to the following factors:

(i)

The ⁸Be and ⁹Be nuclei have a pronounced α-cluster structure which can be incorporated into three-body wave functions for better description of the data [2,3,4].

(ii)

Because of its α-cluster structure, the ⁹Be nucleus has a large deformation, while in this study it was treated as spherical for simplicity [44].

(iii)

It is possible that channel coupling effects are present, as observed in Refs [17,45]. Indeed, the waves with different neutron transfer configurations, originating from multiple channels (e.g., from the ground state and the first excited state), may either cancel each other out or amplify one another; their interference may be taken into account.

Accounting for these factors could lead to an improved theoretical description of the experimental data, but goes beyond the scope of this work.

To describe the dynamics of the ⁹Be(³He,α)⁸Be_gs reaction channel within the TDSE approach, we used the potential obtained for the ³He+⁹Be entrance channel (Table 1) and the shell model potentials from the DWBA calculations, which yielded curves DWBA-2 in Figure 2.

4. Formalism of the TDSE Approach

The theoretical approach is based on the numerical solution of the time-dependent Schrödinger equation [28,29,30,31]

$$\begin{array}{l}i\hslash {\displaystyle \frac{\partial }{\partial t}}\mathrm{\Psi }\left(\overrightarrow{r},t\right)=-{\displaystyle \frac{{\hslash }^2}{2m}}\mathrm{\Delta }\mathrm{\Psi }\left(\overrightarrow{r},t\right)+\\ +\left\{V_1\left(\left|\overrightarrow{r}-{\overrightarrow{r}}_1(t)\right|\right)+V_2\left(\left|\overrightarrow{r}-{\overrightarrow{r}}_2(t)\right|\right)+{\widehat{V}}_{LS}^{(1)}\left(\overrightarrow{r}-{\overrightarrow{r}}_1(t)\right)+{\widehat{V}}_{LS}^{(2)}\left(\overrightarrow{r}-{\overrightarrow{r}}_2(t)\right)\right\}\mathrm{\Psi }\left(\overrightarrow{r},t\right)\end{array},$$

(6)

where $\mathrm{\Psi }\left(\overrightarrow{r},t\right)$ is the wave function of the neutron with mass m; ${\overrightarrow{r}}_1(t),{\overrightarrow{r}}_2(t)$ are the centers of nuclei moving along classical trajectories; V₁, V₂ are the potentials of interaction of the neutron with the projectile and target nuclei; ${\widehat{V}}_{LS}^{(1)},{\widehat{V}}_{LS}^{(2)}$ are the potentials of spin-orbit interaction of the neutron with the cores.

As mentioned above, the neutron wave function at the initial moment of time was determined in the shell model with the parameters obtained in Section 3 and providing the energy of the single-particle level 1p_3/2 equal to the experimental value of the neutron separation energy (1.66 MeV) for the ⁹Be nucleus [46]. The shape of the ⁹Be nucleus was considered as spherical [28,29,30], because taking into account the deformation of ⁹Be [47] requires more complex calculations, which will be a subject of a separate theoretical work in the future. In addition, it should be noted that taking into account the deformation of weakly bound nuclei in the calculations within the TDSE approach does not have a strong effect on the resulting probabilities and cross sections of transfer reaction channels [28,29]. One of the reasons is that the wave functions calculated in the shell model for deformed and spherical nuclei have similar spatial extents due to the low binding energy of an outer neutron in such nuclei [48].

The wave function $\mathrm{\Psi }\left(\overrightarrow{r},t\right)$ of the neutron with the projection m_j of the total momentum at the initial moment of time can be written as

$${\tilde{\mathrm{\Psi }}}_{m_j}^{(0)}(\overrightarrow{r},t=0)=\left[\begin{array}{c}{\tilde{\mathrm{\psi }}}_{m_j}^{(0)}(\overrightarrow{r},t=0)\\ {\tilde{\phi }}_{m_j}^{(0)}(\overrightarrow{r},t=0)\end{array}\right]=\left[\begin{array}{c}{\mathrm{\psi }}_{m_j}^{(0)}\left\{\overrightarrow{r}-{\overrightarrow{r}}_2(t=0)\right\}\\ {\phi }_{m_j}^{(0)}\left\{\overrightarrow{r}-{\overrightarrow{r}}_2(t=0)\right\}\end{array}\right]\exp \left[i{\hslash }^{-1}m{\overrightarrow{v}}_2(t=0)\overrightarrow{r}\right],$$

(7)

where $\tilde{\mathrm{\Psi }}$ and $\tilde{\mathrm{\phi }}$ are the components of the spinor wave function for the spin projections 1/2 and –1/2, respectively; m is the mass of a neutron; ${\nu }_2(t)$ is the velocity of the target nucleus in the center of mass system [28,29,30]. Evolution of the probability density $\mathrm{\rho }(\overrightarrow{r},t)$ is calculated as

$$\mathrm{\rho }(\overrightarrow{r},t)={\displaystyle \frac{1}{\left(2j+1\right)}}{\displaystyle \sum _{-m_j}^{m_j}{\left|{\mathrm{\psi }}_{m_j}(\overrightarrow{r},t)\right|}^2+{\left|{\mathrm{\phi }}_{m_j}(\overrightarrow{r},t)\right|}^2}.$$

(8)

For the neutron from the single-particle level 1p_3/2 of the ⁹Be nucleus, the values of m_j are –3/2, –1/2, 1/2, and 3/2.

The probability of the neutron transfer is determined as

$$P_{\mathrm{tr}}(t)={\displaystyle \sum _k{\left|a_k(t)\right|}^2},$$

(9)

$$a_k(t)={\displaystyle \int \left[{\tilde{\mathrm{\psi }}}_k^{*}(\overrightarrow{r},t)\mathrm{\psi }(\overrightarrow{r},t)+{\tilde{\mathrm{\phi }}}_k^{*}(\overrightarrow{r},t)\mathrm{\phi }(\overrightarrow{r},t)\right]dV},$$

(10)

where $a_k(t)$ are the amplitudes of the probabilities of populating the unoccupied single-particle neutron levels [30]. The final probability of the neutron transfer is determined at time t, when the nuclei are already far away from each other, in our calculations, at distances more than 30 fm:

$${\overline{P}}_{\mathrm{tr}}=\underset{t\to \infty }{\lim }{P}_{\mathrm{tr}}(t).$$

(11)

The calculated probabilities ${\overline{P}}_{\mathrm{tr}}$ were approximated by the exponential function

$${\overline{P}}_{\mathrm{tr}}\left(R_{\min }\right)=\min \left\{\exp \left(a_0-b_0{R}_{\min }\right),1\right\}$$

(12)

with fitting parameters a₀ and b₀ [26].

The probability of the removal of the neutron is determined as

$$P_{\mathrm{rem}}(t)=1-{\left|c(t)\right|}^2,$$

(13)

$$с(t)={\displaystyle \frac{1}{\left(2j+1\right)}}{\displaystyle \sum _{-{m^{\prime }}_j}^{{m^{\prime }}_j}{\displaystyle \sum _{-m_j}^{m_j}{\displaystyle \int \left[{\tilde{\mathrm{\psi }}}_{{m^{\prime }}_j}^{(0)*}(\overrightarrow{r},t){\mathrm{\psi }}_{m_j}(\overrightarrow{r},t)+{\tilde{\mathrm{\phi }}}_{{m^{\prime }}_j}^{(0)*}(\overrightarrow{r},t){\mathrm{\phi }}_{m_j}(\overrightarrow{r},t)\right]dV}}},$$

(14)

where c(t) is the amplitude of the probability of conservation of the neutron in the initial state at time t [30]. Similar to the probability of the neutron transfer (11), the final probability of the neutron removal is determined at time t, when the nuclei are already far away from each other:

$${\overline{P}}_{\mathrm{rem}}=\underset{t\to \infty }{\lim }{P}_{\mathrm{rem}}(t).$$

(15)

The calculated probabilities ${\overline{P}}_{\mathrm{rem}}$ were approximated by the sum of two exponential functions:

$${\overline{P}}_{\mathrm{rem}}\left(R_{\min }\right)=\min \left\{\exp \left(a_1-b_1{R}_{\min }\right)+\exp \left(a_2-b_2{R}_{\min }\right),1\right\}$$

(16)

with fitting parameters a₁, b₁, a₂, b₂ [26].

The numerical solution of equation (4) was performed on a spatial grid of dimensions 96×60×105 fm³ (x×y×z) with the collision plane xOz and a grid step 0.3 fm [28,29,30]. We used the dimensionless time scale τ=t/t₀, where $t_0=m{x}_0^2/\hslash =1.57\cdot {10}^{-23}$ s, $x_0$=1 fm. The dimensionless time step was ∆τ = 0.1. The calculations were carried out using the heterogeneous computing cluster HybriLIT [49] of the Laboratory of Information Technologies, Joint Institute for Nuclear Research.

5. Results and Discussion

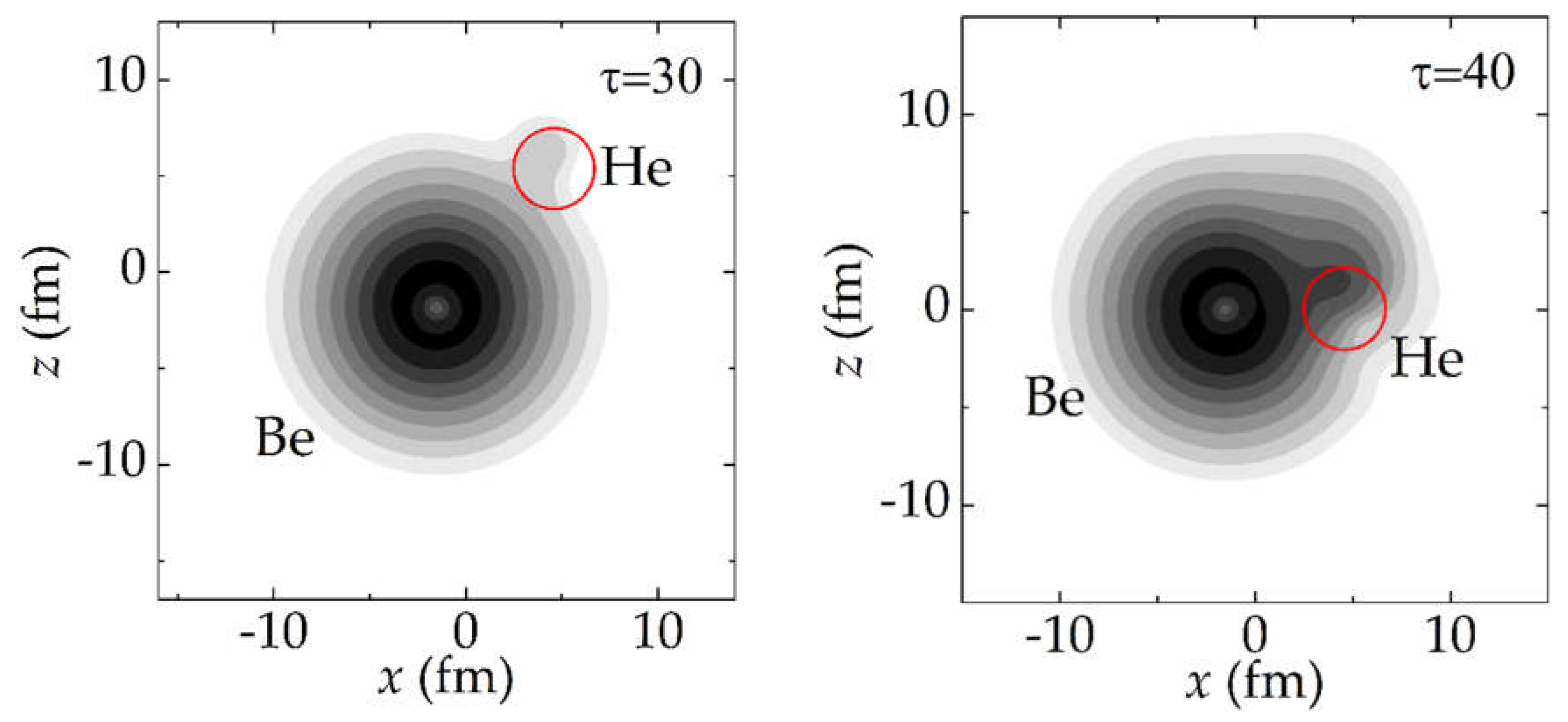
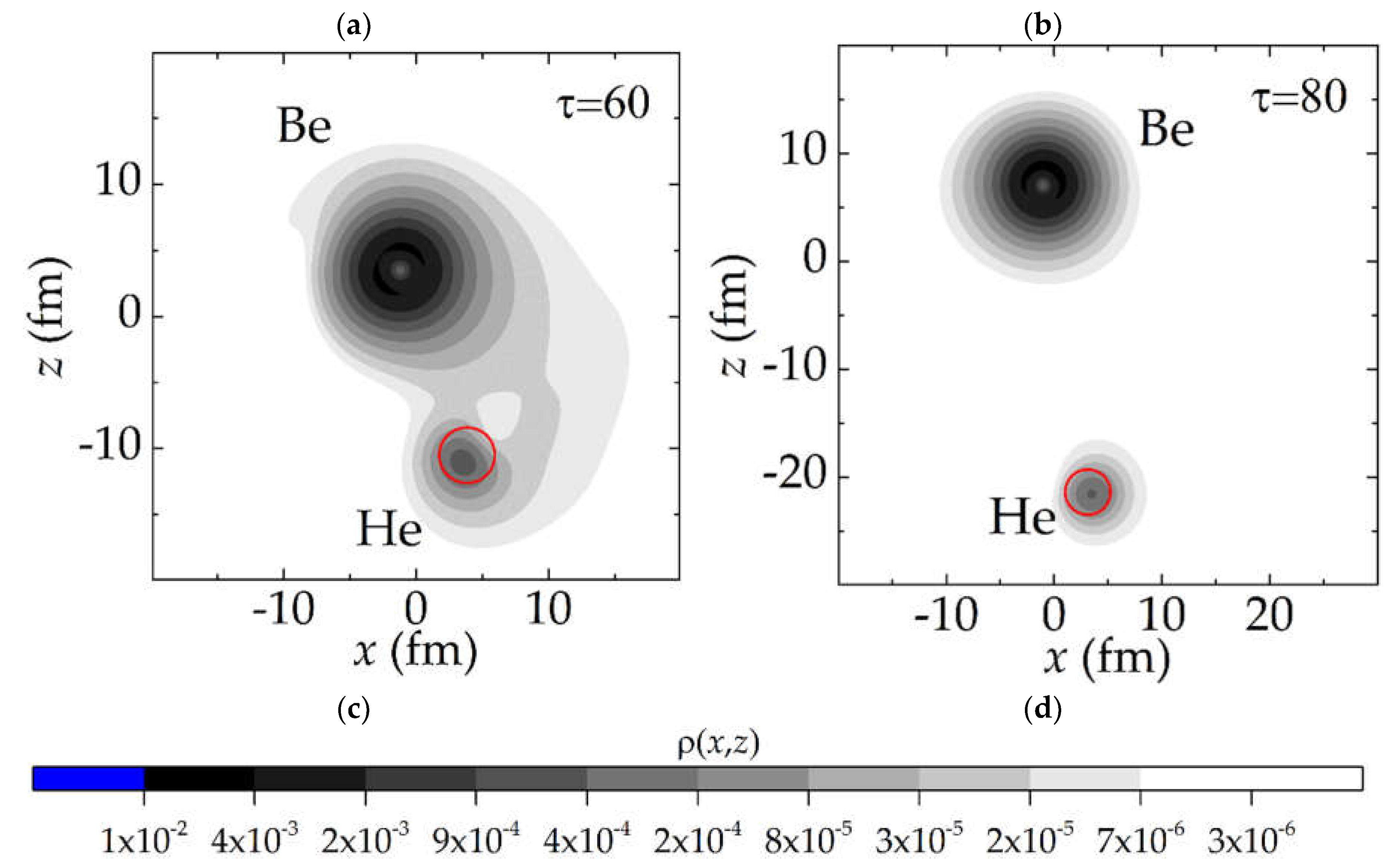
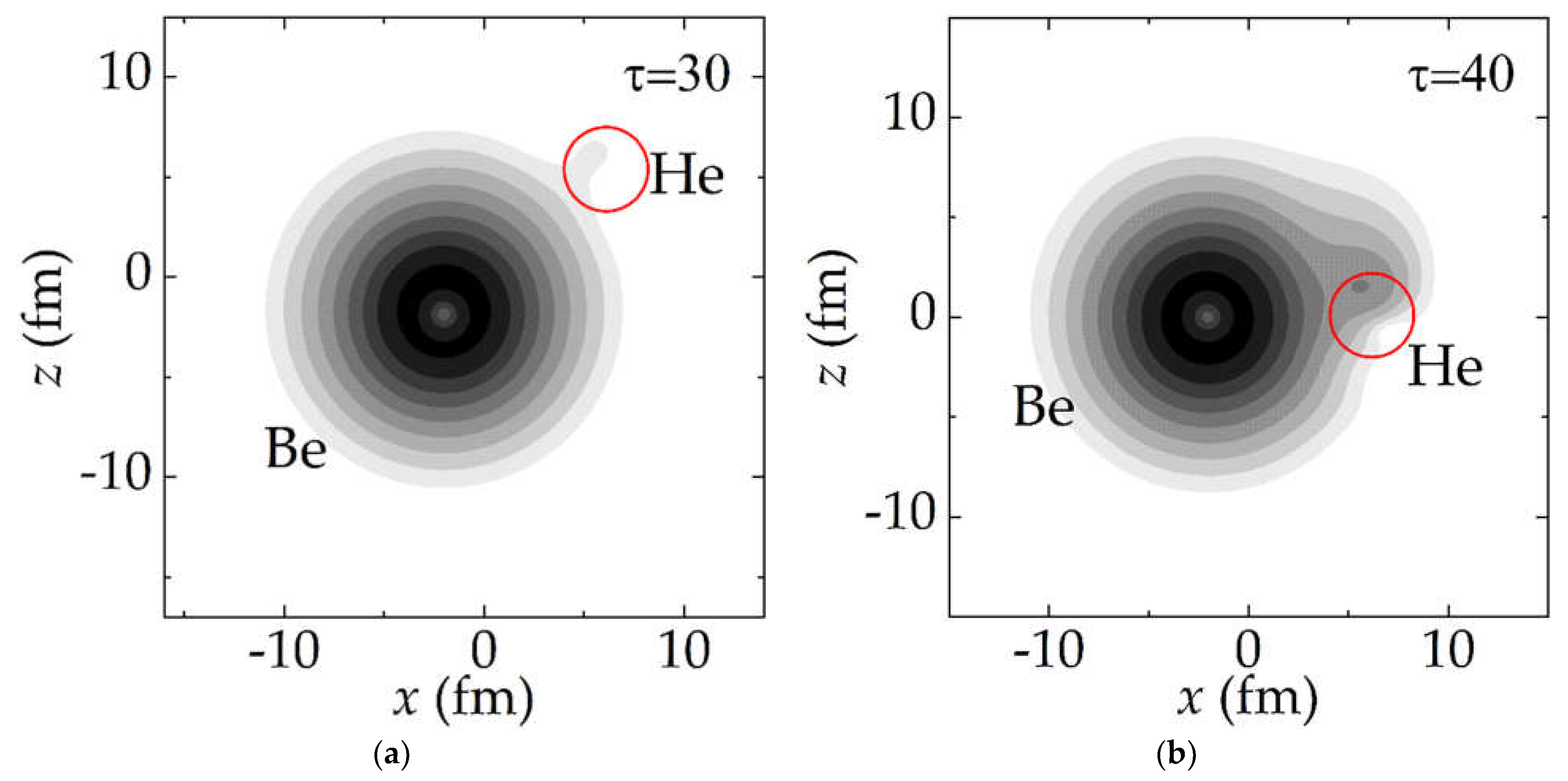
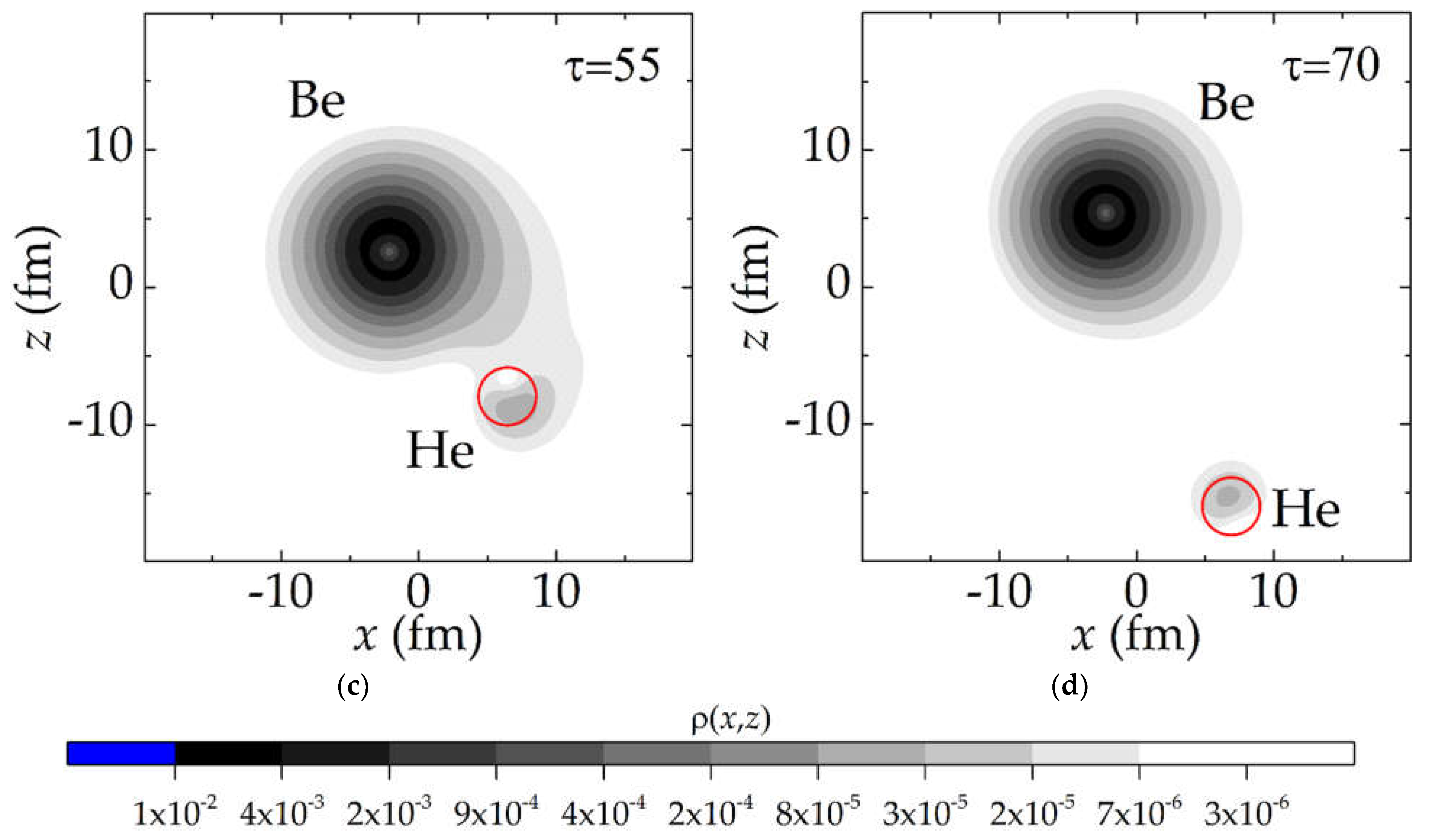
Evolution of the probability density (6) in dimensionless time τ for the neutron from the single-particle level 1p_3/2 of the ⁹Be nucleus during the collision of ³He+⁹Be at an energy of E_lab = 30 MeV (E_c.m. = 22.5 MeV) with the impact parameter b = 6 fm (the distance of the closest approach R_min = 6.12 fm) and b = 8 fm (R_min = 8.23 fm) is presented Figure 3 and Figure 4, respectively. The transition of the neutron probability density begins when the distance between the centers of the nuclei decreases to 9-10 fm [Figure 3a and Figure 4a]. As can be seen from Figure 3b and Figure 4b, the relative velocity of the nuclei is high enough that the flux of the neutron probability density lags behind the motion of the two nuclei and is shifted relative to the imaginary line connecting their centers. A more intense rearrangement of the probability density occurs at small distances between the projectile and target. As the distance between the nuclei increases, the neutron transfer is accompanied by the neutron transition to the continuum [Figure 3c and Figure 4c] [34]. In Figure 3c and Figure 4c, the neutron is emitted at a large angle to the direction of motion of the projectile nucleus, which indicates the manifestation of the so-called towing mode at energies above 5 MeV/nucleon [34,50,51].

According to the shell model, the ³He nucleus has only one single-particle level 1s_1/2 that can be occupied by the neutron transferred from the single-particle level 1p_3/2 of the ⁹Be nucleus. The spherically symmetric shape of the part of the neutron probability density transferred to the ³He projectile nucleus in Figure 3d and Figure 4d indicates the population of the state 1s_1/2 in ³He, which is consistent with the shell model.

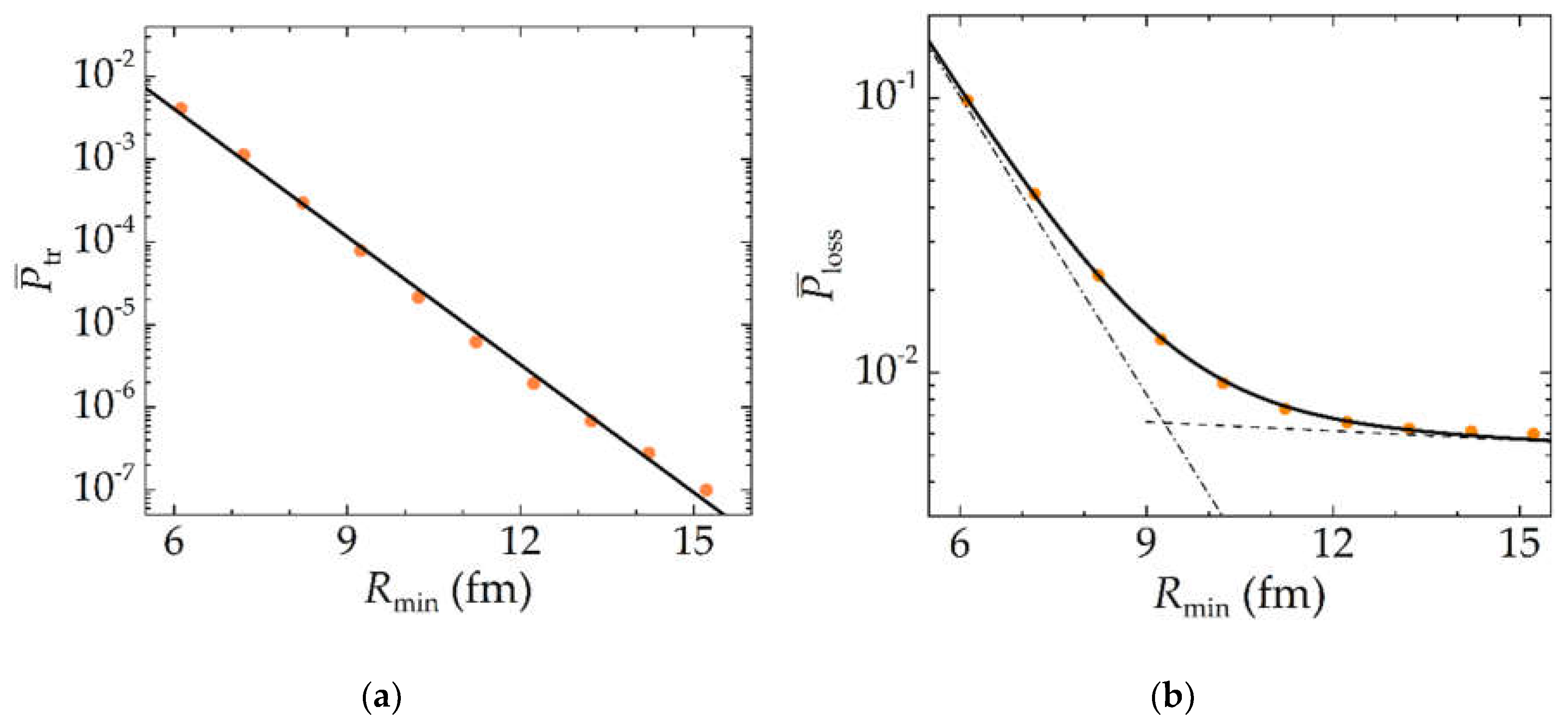
The obtained dependencies of the probability ${\overline{P}}_{\mathrm{tr}}$ (11,) (12) on the distance R_min of the closest approach of the centers of the nuclei are shown in Figure 5a; the values of the fitting parameters are a₀=0.696 and b₀=0.515 fm^-1.

The obtained dependencies of the probability ${\overline{P}}_{\mathrm{rem}}$ (15), (16) on the distance R_min of the closest approach of the centers of the nuclei are shown in Figure 5b; the values of the fitting parameters are a₁=1.178, b₁=0.362 fm^-1, a₂=–2.08, b₂=0.011 fm^-1. The first exponential function describes a rapid decrease of the probability ${\overline{P}}_{\mathrm{loss}}$ at the values of R_min, not greatly exceeding the Coulomb barrier radius, the second corresponds to a slow decrease at larger values and gives the main contribution at R_min more than 9 fm. The rapid decrease of the probability ${\overline{P}}_{\mathrm{loss}}$ is due to a sharp decrease of the probability of the neutron transfer ${\overline{P}}_{\mathrm{tr}}$ with the increasing impact parameter.

In the TDSE approach, the cross sections for the transfer and removal of the weakly bound neutron of the ⁹Be nucleus were calculated by integrating over the impact parameter b [29,31]

$${\sigma }_{\mathrm{tr}}=2\pi {\displaystyle \underset{b_{\min }}{\overset{\infty }{\int }}{\overline{P}}_{\mathrm{tr}}\left[R_{\min }\left(b\right)\right]bdb},$$

(17)

$${\sigma }_{\mathrm{rem}}=2\pi {\displaystyle \underset{b_{\min }}{\overset{\infty }{\int }}{\overline{P}}_{\mathrm{rem}}\left[R_{\min }\left(b\right)\right]bdb},$$

(18)

where b_min is the impact parameter corresponding to the trajectory, when the projectile is still captured by the target. In our calculations, we used b_min corresponding to the distance of the closest approach R_min = R_C + d, where R_C = 5.6 fm is the Coulomb barrier radius, d = 0.4 fm is the diffuse region, therefore R_min = 6 fm.

The comparison of the integrated cross sections σ_tr for the reaction channel ⁹Be(³He,α)⁸Be_gs obtained within the DWBA method (FRESCO code) and within the TDSE approach is presented in Table 2. It can be seen that the calculations in both models give close values. Taking into account that the differential cross sections obtained within the DWBA method are slightly below the experimental points in the region of angles around 55°, it can be concluded that the cross sections obtained within the TDSE approach are closer to the experimental data.

The integrated cross section σ_tr for the reaction channel ⁹Be(³He,α)⁸Be_3.03 obtained within the DWBA method is also presented in Table 2. The cross section value for this reaction channel is approximately twice as high as that for ⁹Be(³He,α)⁸Be_gs, which is consistent with the measured energy spectrum [Figure 1b], where the number of events for ⁸Be_3.03 is approximately twice as high as that for ⁸Be_gs.

Table 2 also includes the integrated cross section σ_rem for the removal of the weakly bound neutron of the ⁹Be nucleus obtained within the TDSE approach. According to (13), σ_rem = 315.690 mb includes the neutron transfer cross section σ_tr = 0.740 mb in the reaction channel ⁹Be(³He,α)⁸Be_gs and the cross section for the transition of the neutron into the continuum. It can be seen that the neutron transfer cross section σ_tr makes an insignificant contribution to the neutron removal cross section σ_rem.

6. Conclusions

The angular distributions for the neutron transfer channels ⁹Be(³He,α)⁸Be_gs,3.03 in the reaction of the ³He (30 MeV) ions with the ⁹Be target were measured. The experimental data were described by the DWBA method (FRESCO code). The results of the theoretical description are in agreement with the experimental data.

The parameters of the potentials for the ³He+⁹Be entrance channel and for the shell model obtained from the DWBA calculations were successfully used in the description of dynamics of the reaction channel ⁹Be(³He,α)⁸Be_gs within the TDSE approach. It has been shown that the neutron transfer process begins when the nuclei approach each other at a distance of 9-10 fm between the centers of the nuclei and the transfer process is accompanied by transition of the neutron to the continuum. In addition, the neutron can be emitted at a large angle to the direction of motion of the projectile nucleus, which indicates the manifestation of the towing mode.

The neutron transfer cross section does not make a significant contribution to the cross section for the removal of the weakly bound neutron of the ⁹Be nucleus. Calculations of the cross section for the reaction channel ⁹Be(³He,α)⁸Be_gs in the TDSE approach and DWBA method give close values.