Submitted:
19 March 2025
Posted:
21 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theory
2.1. Nuclear-Model Calculations
2.2. Ordinary Muon Capture (OMC)
2.3. Decay
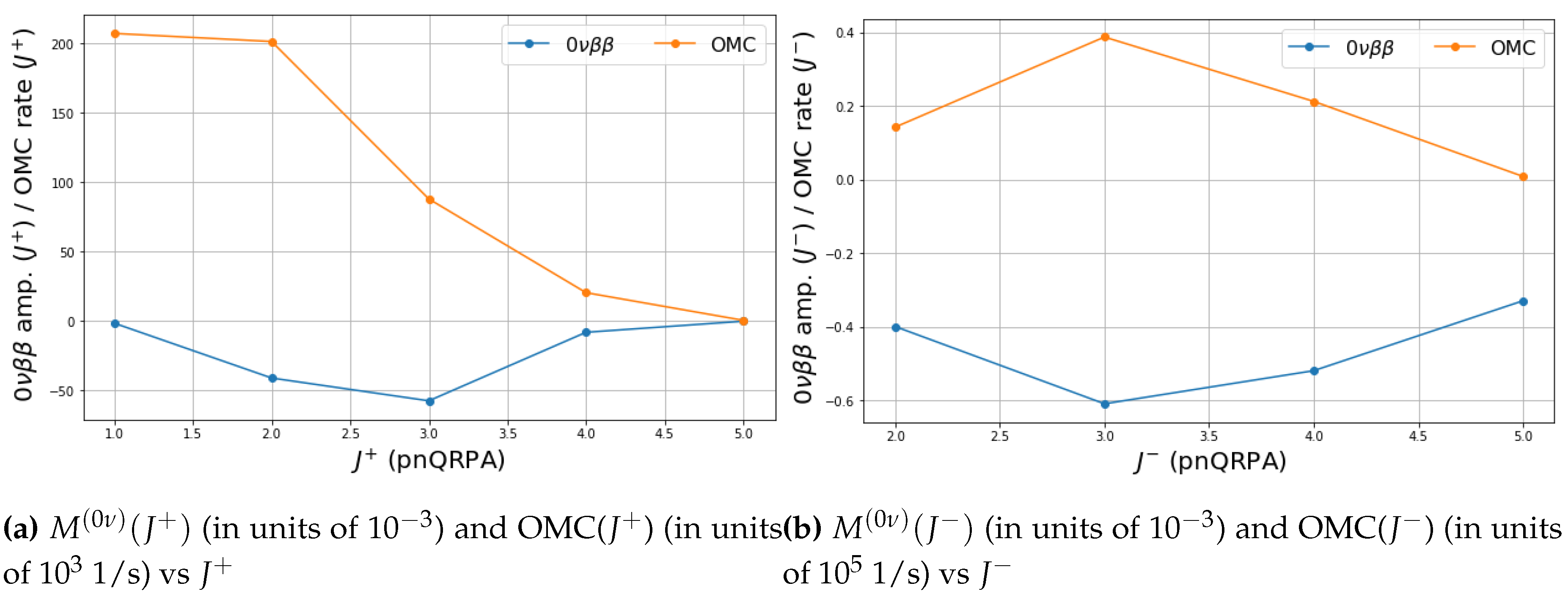
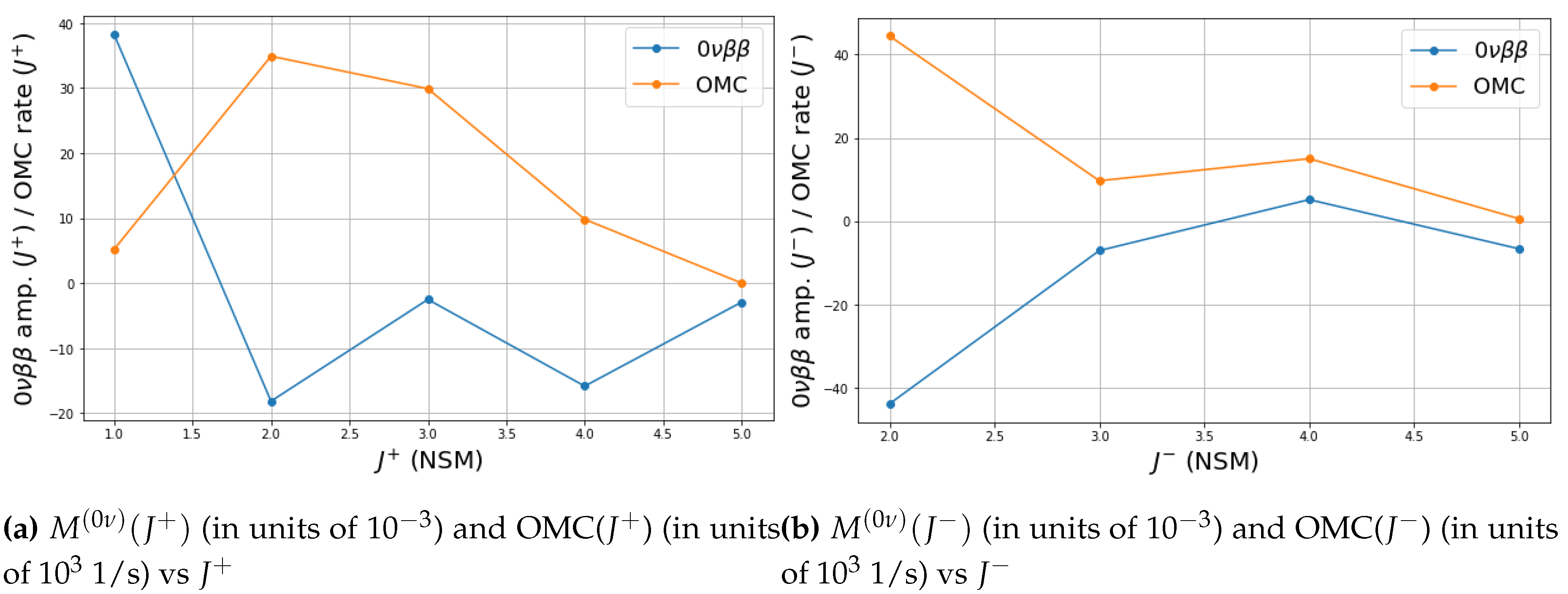
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agostini, M.; Benato, G.; Detwiler, J.A.; Menéndez, J.; Vissani, F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev. Mod. Phys. 2023, 95, 025002. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar]
- Engel, J.; Menéndez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Reports on Progress in Physics 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Physics Reports 1998, 300, 123–214. [Google Scholar] [CrossRef]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Physics Reports 2019, 797, 1. [Google Scholar]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar]
- Suhonen, J.T. Value of the Axial-Vector Coupling Strength in β and ββ Decays: A Review. Frontiers in Physics 2017, 5, 55. [Google Scholar]
- Suhonen, J.; Kostensalo, J. Double β Decay and the Axial Strength. Frontiers in Physics 2019, 7, 29. [Google Scholar]
- Measday, D. The nuclear physics of muon capture. Physics Reports 2001, 354, 243–409. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Ordinary muon capture as a probe of virtual transitions of ββ decay. Europhysics Letters 2002, 58, 666. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Microscopic study of muon-capture transitions in nuclei involved in double-beta-decay processes. Nuclear Physics A 2003, 713, 501–521. [Google Scholar] [CrossRef]
- Kortelainen, M.; Suhonen, J. Nuclear muon capture as a powerful probe of double-beta decays in light nuclei. Journal of Physics G: Nuclear and Particle Physics 2004, 30, 2003. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J.; Kotila, J. Comparative analysis of nuclear matrix elements of 0νβ+β+ decay and muon capture in 106Cd. Frontiers in Physics 2021, 9, 652536. [Google Scholar]
- Šimkovic, F.; Pantis, G.; Vergados, J.D.; Faessler, A. Additional nucleon current contributions to neutrinoless double β decay. Phys. Rev. C 1999, 60, 055502. [Google Scholar] [CrossRef]
- Kolbe, E.; Langanke, K.; Vogel, P. Muon capture, continuum random phase approximation, and in-medium renormalization of the axial-vector coupling constant. Phys. Rev. C 1994, 50, 2576–2581. [Google Scholar] [CrossRef]
- Johnson, B.L.; Gorringe, T.P.; Armstrong, D.S.; Bauer, J.; Hasinoff, M.D.; Kovash, M.A.; Measday, D.F.; Moftah, B.A.; Porter, R.; Wright, D.H. Observables in muon capture on 23Na and the effective weak couplings g˜a and g˜p. Phys. Rev. C 1996, 54, 2714–2731. [Google Scholar] [CrossRef]
- Gorringe, T.P.; Armstrong, D.S.; Arole, S.; Boleman, M.; Gete, E.; Kuzmin, V.; Moftah, B.A.; Sedlar, R.; Stocki, T.J.; Tetereva, T. Measurement of partial muon capture rates in 1s-0d shell nuclei. Phys. Rev. C 1999, 60, 055501. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Hjorth-Jensen, M. Shell-model effective operators for muon capture in 20Ne. Journal of Physics G: Nuclear and Particle Physics 1999, 25, L55. [Google Scholar] [CrossRef]
- Siiskonen, T.; Hjorth-Jensen, M.; Suhonen, J. Renormalization of the weak hadronic current in the nuclear medium. Phys. Rev. C 2001, 63, 055501. [Google Scholar] [CrossRef]
- Auerbach, N.; Brown, B.A. Weak interaction rates involving 12C, 14N, and 16O. Phys. Rev. C 2002, 65, 024322. [Google Scholar] [CrossRef]
- Gorringe, T.P.; Johnson, B.L.; Armstrong, D.S.; Bauer, J.; Kovash, M.A.; Hasinoff, M.D.; Measday, D.F.; Moftah, B.A.; Porter, R.; Wright, D.H. Hyperfine effect in μ- capture on 23Na and gp/ga. Phys. Rev. Lett. 1994, 72, 3472–3475. [Google Scholar] [CrossRef] [PubMed]
- Jonkmans, G.; Ahmad, S.; Armstrong, D.S.; Azuelos, G.; Bertl, W.; Blecher, M.; Chen, C.Q.; Depommier, P.; Doyle, B.C.; von Egidy, T.; et al. Radiative Muon Capture on Hydrogen and the Induced Pseudoscalar Coupling. Phys. Rev. Lett. 1996, 77, 4512–4515. [Google Scholar] [CrossRef] [PubMed]
- Gazit, D. Muon capture on 3He and the weak structure of the nucleon. Physics Letters B 2008, 666, 472–476. [Google Scholar] [CrossRef]
- Marcucci, L.E.; Kievsky, A.; Rosati, S.; Schiavilla, R.; Viviani, M. Chiral Effective Field Theory Predictions for Muon Capture on Deuteron and 3He. Phys. Rev. Lett. 2012, 108, 052502. [Google Scholar] [CrossRef]
- Brudanin, V.; Egorov, V.; Filipova, T.; Kachalkin, A.; Kovalenko, V.; Salamatin, A.; Shitov, Y.; Štekl, I.; Vassiliev, S.; Vorobel, V.; et al. Measurement of the induced pseudoscalar form factor in the capture of polarized muons by Si nuclei. Nuclear Physics A 1995, 587, 577–595. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Kuz’min, V.; Tetereva, T. Shell-model study of partial muon-capture rates in light nuclei. Nuclear Physics A 1998, 635, 446–469. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Kuz’min, V.; Tetereva, T. Shell-model study of partial muon-capture rates in light nuclei. Nuclear Physics A 1999, 651, 437–438. [Google Scholar] [CrossRef]
- Siiskonen, T.; Suhonen, J.; Hjorth-Jensen, M. Towards the solution of the CP/CA anomaly in shell-model calculations of muon capture. Phys. Rev. C 1999, 59, R1839–R1843. [Google Scholar] [CrossRef]
- Gorringe, T.; Fearing, H.W. Induced pseudoscalar coupling of the proton weak interaction. Rev. Mod. Phys. 2003, 76, 31–91. [Google Scholar] [CrossRef]
- Araujo, G.R. , Bajpai D., B.L.e.a. The Monument experiment: ordinary muon capture studies for 0νββ decay. Eur. Phys. J. C 2024, 84, 1188. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J. Comparative analysis of muon-capture and 0νββ-decay matrix elements. Phys. Rev. C 2020, 102, 024303. [Google Scholar] [CrossRef]
- Gimeno, P.; Jokiniemi, L.; Kotila, J.; Ramalho, M.; Suhonen, J. Ordinary Muon Capture on 136Ba: Comparative Study Using the Shell Model and pnQRPA. Universe 2023, 9. [Google Scholar] [CrossRef]
- Suhonen, J. From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory; Springer Berlin, Heidelberg, 2007.
- Jokiniemi, L.; Suhonen, J.; Ejiri, H.; Hashim, I. Pinning down the strength function for ordinary muon capture on 100Mo. Physics Letters B 2019, 794, 143–147. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J. Muon-capture strength functions in intermediate nuclei of 0νββ decays. Phys. Rev. C 2019, 100, 014619. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Miyagi, T.; Stroberg, S.R.; Holt, J.D.; Kotila, J.; Suhonen, J. Ab initio calculation of muon capture on 24Mg. Phys. Rev. C 2023, 107, 014327. [Google Scholar] [CrossRef]
- Hyvärinen, J.; Suhonen, J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys. Rev. C 2015, 91, 024613. [Google Scholar] [CrossRef]
| [keV] | |||||
| 0 | 0 | -0.18 | 0.040 | -0.14 | |
| 102 | 0 | -0.28 | 0.037 | -0.24 | |
| 120 | 0.20 | -0.13 | -0.034 | -0.46 | |
| 154 | 0.07 | -0.02 | -0.006 | -0.13 | |
| 193 | 0 | -1.61 | 0.021 | -1.59 | |
| 203 | 4.96 | -0.32 | -0.13 | -7.65 | |
| 264 | 0 | -51.6 | 16.3 | -35.2 | |
| 281 | 0 | -10.1 | 0.88 | -9.20 | |
| 338 | 0 | -9.46 | -3.27 | -12.7 | |
| 367 | 0.01 | -0.16 | -0.0041 | -0.22 | |
| 458 | 0.02 | -0.16 | -0.0060 | -0.25 | |
| 494 | -0.007 | -0.24 | -0.089 | -0.32 | |
| 515 | 0.03 | -0.11 | -0.050 | -0.21 | |
| 558 | 0 | -0.42 | 0.068 | -0.35 | |
| 561 | 5.29 | -24.5 | -8.22 | -40.4 | |
| 637 | 0.07 | -0.01 | -0.004 | -0.12 | |
| 695 | 0 | -0.24 | 0.084 | -0.16 | |
| 704 | 0 | -0.49 | 0.097 | -0.40 | |
| 926 | 0.23 | -0.02 | -0.008 | -0.36 |
| [keV] | |||||
| 0 | 0 | -4.355 | 1.411 | -2.944 | |
| 23 | 0 | -5.695 | 1.445 | -4.250 | |
| 39 | 1.230 | -0.153 | -0.058 | -1.633 | |
| 83 | 6.993 | -5.160 | -1.433 | -14.677 | |
| 181 | 0 | -2.269 | -0.555 | -2.824 | |
| 224 | 0.894 | -4.481 | -1.748 | -7.262 | |
| 244 | 0 | -1.647 | -0.059 | -1.706 | |
| 323 | 1.989 | -2.575 | -1.019 | -5.895 | |
| 498 | 2.582 | -3.525 | -1.578 | -8.088 | |
| 517 | 0 | 6.540 | -0.289 | 6.251 | |
| 522 | 0.723 | -2.483 | -1.048 | -4.366 | |
| 545 | 0.379 | -4.893 | -1.701 | -7.033 | |
| 545 | 0 | 33.820 | -1.602 | 32.218 | |
| 547 | 0 | 5.565 | 0.589 | 6.154 | |
| 615 | -1.426 | 2.804 | 0.780 | 5.232 | |
| 670 | 1.313 | -0.511 | -0.210 | -2.239 | |
| 752 | 0 | 6.066 | -0.064 | 6.003 | |
| 760 | 0 | -1.281 | 0.309 | -0.972 | |
| 803 | 0.290 | -0.889 | -0.251 | -1.475 | |
| 885 | 0.082 | -0.108 | -0.044 | -0.248 | |
| 1016 | 0 | -44.144 | 0.371 | -43.772 |
| qrpa-phen | sm-phen | |||
|---|---|---|---|---|
| () | OMC() | () | OMC() | |
| -0.14 | 0.50 | -2.944 | 0.0 | |
| -8.10 | 20.4 | -15.864 | 9.8 | |
| -57.4 | 87.8 | -2.529 | 29.9 | |
| -41.0 | 201.1 | -18.182 | 34.9 | |
| -1.59 | 206.9 | 38.221 | 5.2 | |
| -0.33 | 0.80 | -6.605 | 0.6 | |
| -0.52 | 21.2 | 5.182 | 15.0 | |
| -0.61 | 38.7 | -7.033 | 9.7 | |
| -0.40 | 14.2 | -43.772 | 44.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





