Closed Form Solution to the Hubble Tension Based on R_h = ct Cosmology for Generalized Cosmological Redshift Scaling of the Form: z = (R_h/R_t)x −1 Tested against the full Distance Ladder of Observed SN Ia Redshift

1. $R_h=ct$ Type Cosmological Models

The Haug and Tatum [1,2] cosmological model that we will discuss is unique in that it provides an exact mathematical relation between the CMB temperature, the Hubble constant and the cosmological red-shift. The Haug-Tatum cosmological model has developed over time in multiple stages. It is consistent with the $R_h=ct$ principle, which describes a universe expanding at the speed of light without accelerated expansion. There are several $R_h=ct$-type cosmological models, and these models are still actively discussed in recent literature, see for example [3,4,5,6]. Melia [7] has recently demonstrated that $R_h=ct$ cosmology seems more in line with recent observations from the James Webb Space Telescope than the $\Lambda$-CDM model. The question of which cosmological model best fits different observed properties of the universe will undoubtedly be an ongoing discussion in the years to come. This paper offers additional evidence in favor of $R_h=ct$ cosmology, as it seems that we with a closed-form mathematical solution can resolve the Hubble tension within such a cosmological model.

In 2015, Tatum et al. [8] heuristically presented the following formula for the Cosmic Microwave Background (CMB) temperature, which was later formally derived based on the Stefan-Boltzmann law [9,10] by Haug and Wojnow [11,12]:

$$T_{CMB,0}={\displaystyle \frac{\hslash c^3}{k_{b}8\pi G\sqrt{M_c{m}_p}}}={\displaystyle \frac{\hslash c}{k_{b}4\pi \sqrt{R_{H}2l_p}}}$$

(1)

where $k_b$ is the Boltzman constant and $m_p=\sqrt{{\displaystyle \frac{\hslash c}{G}}}$ is the Planck mass, $l_p=\sqrt{{\displaystyle \frac{G\hslash }{c^3}}}$ is the Planck length [13,14], and $R_h={\displaystyle \frac{c}{H_0}}$ is the Hubble radius and $M_c={\displaystyle \frac{c^3}{2G{H}_0}}$ is the mass (equivalent) of the critical Friedmann [15] universe. The Stefan-Boltzman law was developed basically for black bodies. The CMB temperature has been described as an almost perfect black body , see for example; Muller et al. [16] that states :

“Observations with the COBE satellite have demonstrated that the CMB corresponds to a nearly perfect black body characterized by a temperature $T_0$ at $z=0$, which is measured with very high accuracy, $T_0=2.72548\pm 0.00057k$."

Equation (1) has also recently been derived using a geometric mean approach, see [17]. Additionally, Haug and Tatum [1] have demonstrated that to be consistent with the observed relation $T_t=T_0(1+z)$, see [18,19,20], the predicted redshift seems like it must be given by:

$$z=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1$$

(2)

However, they also show that one can have the more common $z={\displaystyle \frac{R_h}{R_t}}-1$ scaling, but that this leads to $T_t=T_0{(1+z)}^{{\displaystyle \frac{1}{2}}}$, which does not seem to be supported by observational studies. However, we have to be careful here, as even in observational studies, there are often assumptions or hidden assumptions that one must carefully revisit before prematurely concluding one way or the other. In this paper, we will demonstrate that in a more general model with cosmological redshift scaling of the form:

$$z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$$

(3)

where x is what we can call the scaling factor. The x is decided by assumption based on observations and logic, for example if one decide the cosmological scaling should be $z={\displaystyle \frac{R_h}{R_t}}-1$ (a scaling used in multiple $R_h=ct$ models such as the Melia model) one simply set $x=1$ or if one want $z=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1$ scaling one set $x={\displaystyle \frac{1}{2}}$, but one can also set x to any other value and still one will by solving an equation we soon will look at get the one and the same value for $H_0$ that seems to solves the Hubble tension. Technically one could even make x time dependent $x\left(t\right)$.

It is important to be aware we only claim to solve the Hubble tension inside a class of $R_h=ct$ cosmological models this way and not at all inside the $\Lambda$-CDM model.

For example in the Melia $R_h=ct$ model has a cosmological redshift corresponding to $x=1$ in our suggested general redshift scaling formula. Melia has however no equation for the relation between the CMB temperature now and $H_0$. Haug and Tatum model B in [1] given above correspond then to $x={\displaystyle \frac{1}{2}}$, the Haug and Tatum model A [1] that has the same redshift scaling as the Melia model correspond to $x=1$, but this model is still different than the Melia model as we in this have a tight mathematical relation between CMB temperature and $H_0$ that Melia not have in his model.

For the general red-shift scaling equation (3) to be consistent with the CMB temperature formula derived from the Stefan-Boltzman law we get the following relation for the CMB temperature now and in past cosmoligcal epochs:

$$\begin{array}{c}\hfill z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1\end{array}$$

(4)

$$\begin{array}{c}\hfill z={\left({\displaystyle \frac{T_t^2}{T_0^2}}\right)}^x-1\end{array}$$

(5)

$$\begin{array}{c}\hfill {(z+1)}^{{\displaystyle \frac{1}{2x}}}={\displaystyle \frac{T_t}{T_0}}\end{array}$$

(6)

$$\begin{array}{c}\hfill T_t=T_0{(1+z)}^{{\displaystyle \frac{1}{2x}}}\end{array}$$

(7)

Observations seems to favor a $x\approx {\displaystyle \frac{1}{2}}$, even if the exact value of x not yet is experimentally fully settled. We will not in this paper conclude on the optimal scaling factor x, but leave it up to further research to find the optimal x. The important point in this paper is that the Hubble tension itself seems to be solved for any scaling factor x in the closed form solution we soon will present.

Haug and Tatum demonstrate that the predicted redshift in one of their two models models must satisfy:

$$z_{pre}=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1=\sqrt{{\displaystyle \frac{\frac{c}{H_0}}{{\left(\frac{\hslash c}{T_0(1+z_{obs,i})k_{b}4\pi }\right)}^2\frac{1}{2l_p}}}}-1.$$

(8)

be aware they do similar for $z_{pre}={\displaystyle \frac{R_h}{R_t}}-1$ red-shift scaling.

They then use a smart trial-and-error algorithm, such as the Newton-Raphson method or the bisection method, to find the value of $H_0$ that minimizes the sum of the prediction errors ${\sum }_{i=1}^n{\displaystyle \frac{z_{pre,i}-z_{obs,i}}{z_{obs,i}}}$. They demonstrate that this approach leads to a single $H_0$ value that perfectly matches the model with the full observed distance ladder, something that seems to solve the Hubble tension.

However, here we simply solve equation (8) for $H_0$, which yields:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}{\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}$$

(9)

In the case where the predicted redshift $z_{pre,i}$ is exactly equal to the observed redshift $z_{obs,i}$, we must have ${\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}=1$. Substituting ${\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}=1$ back into equation (12) gives:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}=T_0^2\mho$$

(10)

The last part, the Latin upsilon: $\mho ={\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}={\displaystyle \frac{k_b^{2}32{\pi }^2\sqrt{G}}{{\hslash }^{3/2}{c}^{5/2}}}$, is a composite constant made up of well-known constants (which we [21,23] have coined $\mho$). This is the same formula as given by [21], but here we have just demonstrated that this formula is strictly valid only when the predicted redshift exactly matches the observed redshift, or as we soon will see we can use equation (12) to match the full distance ladder of observed supernova redshifts by simply finding this one $H_0$ value directly from the current measured CMB temperature.

This means that we only need to know $T_0$ and this constant to closely match all observed cosmological redshifts. The reason we say “close to perfect" rather than "perfect" is due to small measurement errors in both the measured CMB temperature and in G, and that is the only uncertainty in this method. The Boltzmann constant, the speed of light, and the reduced Planck constant have no uncertainty, as they have been exactly defined since the 2019 NIST CODATA standard.

We can generalize this to any redshift scaling assumption $z_{pre}={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$ inside $R_h=ct$ cosmology as long as we assume the equation (1) that has been derived from the Stefan-Boltzman law is correct, we then get:

$$z_{pre}={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1={\left({\displaystyle \frac{\frac{c}{H_0}}{{\left(\frac{\hslash c}{T_0{(1+z_{obs,i})}^{\frac{1}{2x}}{k}_{b}4\pi }\right)}^2\frac{1}{2l_p}}}\right)}^x-1.$$

(11)

Solved for $H_0$ we get:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}{\displaystyle \frac{{(1+z_{obs,i})}^{\frac{1}{2x}}}{{(1+z_{pre,i})}^{\frac{1}{2x}}}}$$

(12)

when we have (or want) perfect prediction of redshift we must have $z_{pre,i}=z_{obs,i}$ and then we end up with ${\displaystyle \frac{{(1+z_{obs,i})}^{\frac{1}{2x}}}{{(1+z_{pre,i})}^{\frac{1}{2x}}}}=1$ and therefore we must have:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}$$

(13)

That is for any scaling factor x one get exactly the same $H_0$ dependent on only the CMB temperature measured now, the Boltzman constant, the Planck length, the speed of light and the Planck constant. The only variable is the CMB temperature that has been measured very precisely.

2. Distance, Hubble Constant and Redshift

If we solve the general redshift formula for $R_t$ we get:

$$\begin{array}{ccc}\hfill z& =& {\left({\displaystyle \frac{R_H}{R_t}}\right)}^x-1\hfill \\ \hfill R_t& =& {\displaystyle \frac{c}{H_0{(1+z)}^{\frac{1}{x}}}}.\hfill \end{array}$$

(14)

This means the predicted distance to the observed redshift must be:

$$\begin{array}{ccc}\hfill R_H-R_t& =& R_H-{\displaystyle \frac{c}{H_0{(1+z)}^{\frac{1}{x}}}}\hfill \\ \hfill R_H-R_t& =& {\displaystyle \frac{c}{H_0}}-{\displaystyle \frac{c}{H_0{(1+z)}^{\frac{1}{x}}}}\hfill \\ \hfill R_H-R_t& =& {\displaystyle \frac{c}{H_0}}\left(1-{\displaystyle \frac{1}{{(1+z)}^{\frac{1}{x}}}}\right)\hfill \end{array}$$

(15)

further if we solve this for $H_0$ we get:

$$H_0={\displaystyle \frac{c}{d}}\left(1-{\displaystyle \frac{1}{{(1+z)}^{\frac{1}{x}}}}\right)$$

(16)

Here $d=R_H-R_t$ will be the estimated distance to the object emitting the photons. For very low redshift we have $z\ll 1$ and we can use the first term of the Taylor expansion to get:

$$\begin{array}{ccc}\hfill d& \approx & {\displaystyle \frac{cz}{x{H}_0}}\hfill \end{array}$$

(17)

and now solved for z we get:

$$z\approx {\displaystyle \frac{xd{H}_0}{c}}$$

(18)

In the case $x=1$ this is identical to the standard $\Lambda$-CDM cosmological redshift prediction formula approximation when used for $z\ll 1$. Haug and Tatum looks at both the special case of $x=1$ where one get the standard distance formula when $z\ll 1$, in addition they looked at a model corresponding to $x={\displaystyle \frac{1}{2}}$ which give twice the predicted distance as $\Lambda$-CDM for low z, but here we will soon demonstrate one can use and x in the red-shift scaling and still solve the Hubble tension. What x to use is therefore dependent on other observations than predictions of the Hubble constant versus redshift. It is dependent on such things as finding what is the optimal $\beta$ in $T_t=T_0{(1+z)}^{(1-\beta )}=T_0{(1+z)}^{{\displaystyle \frac{1}{2x}}}$ versus observed data, see for example [22] that indicates $\beta$ should be close to 0. But again one must be very careful here and look closely into what any observational study has used as assumptions etc. to get to the results they have.

However, this is not the main focus of this paper. The primary discussion, as we will see in the next section, is that in the $R_h=ct$ cosmology model presented here, any choice of x can be used while still allowing us to match all observed SN Ia redshifts with a single $H_0$ value. Most values of x, and likely all except one, should be excluded based on other types of observations, such as the observed $T_t=T_0{(1+z)}^{(1-\beta )}$ scaling.

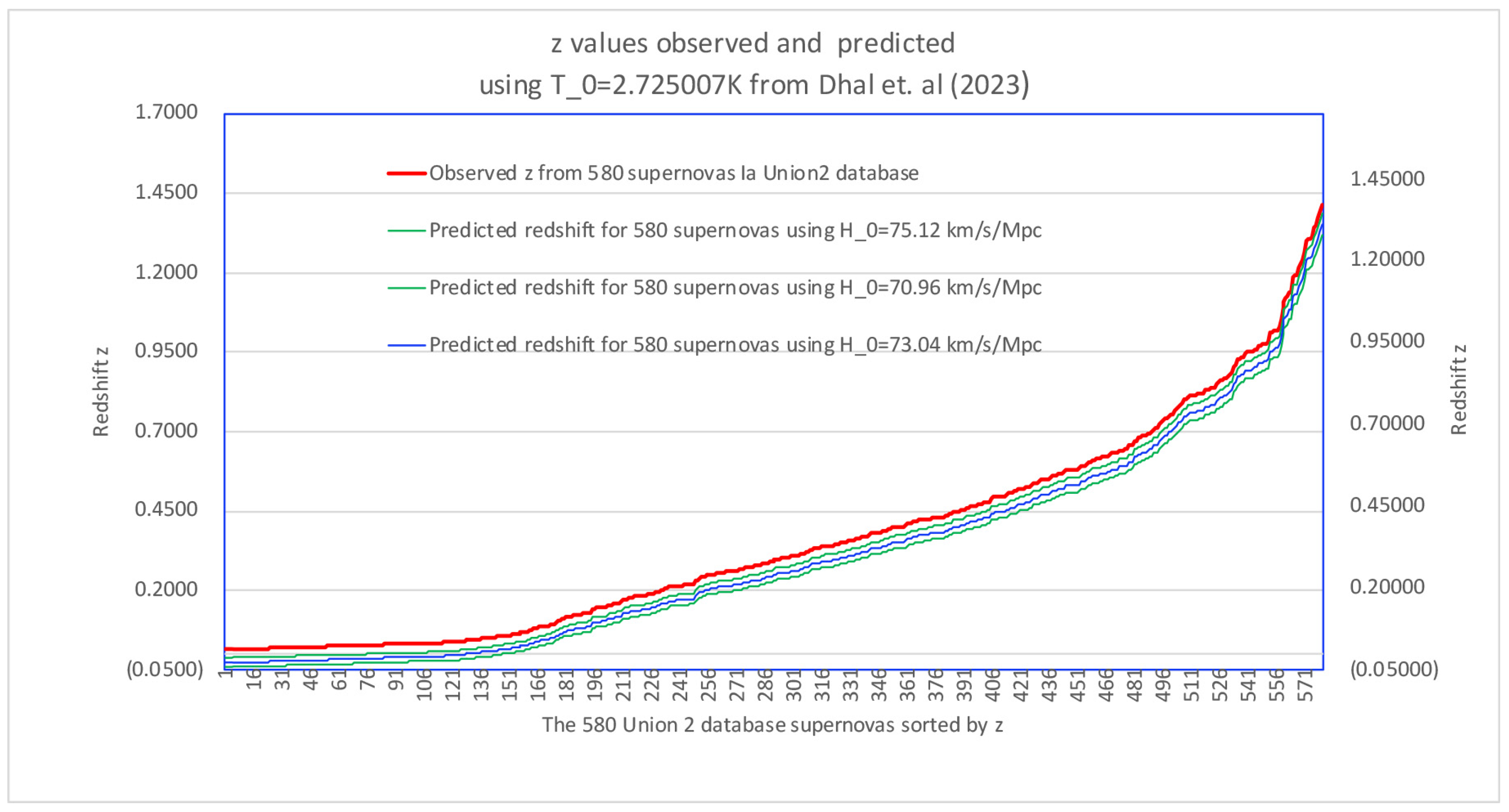
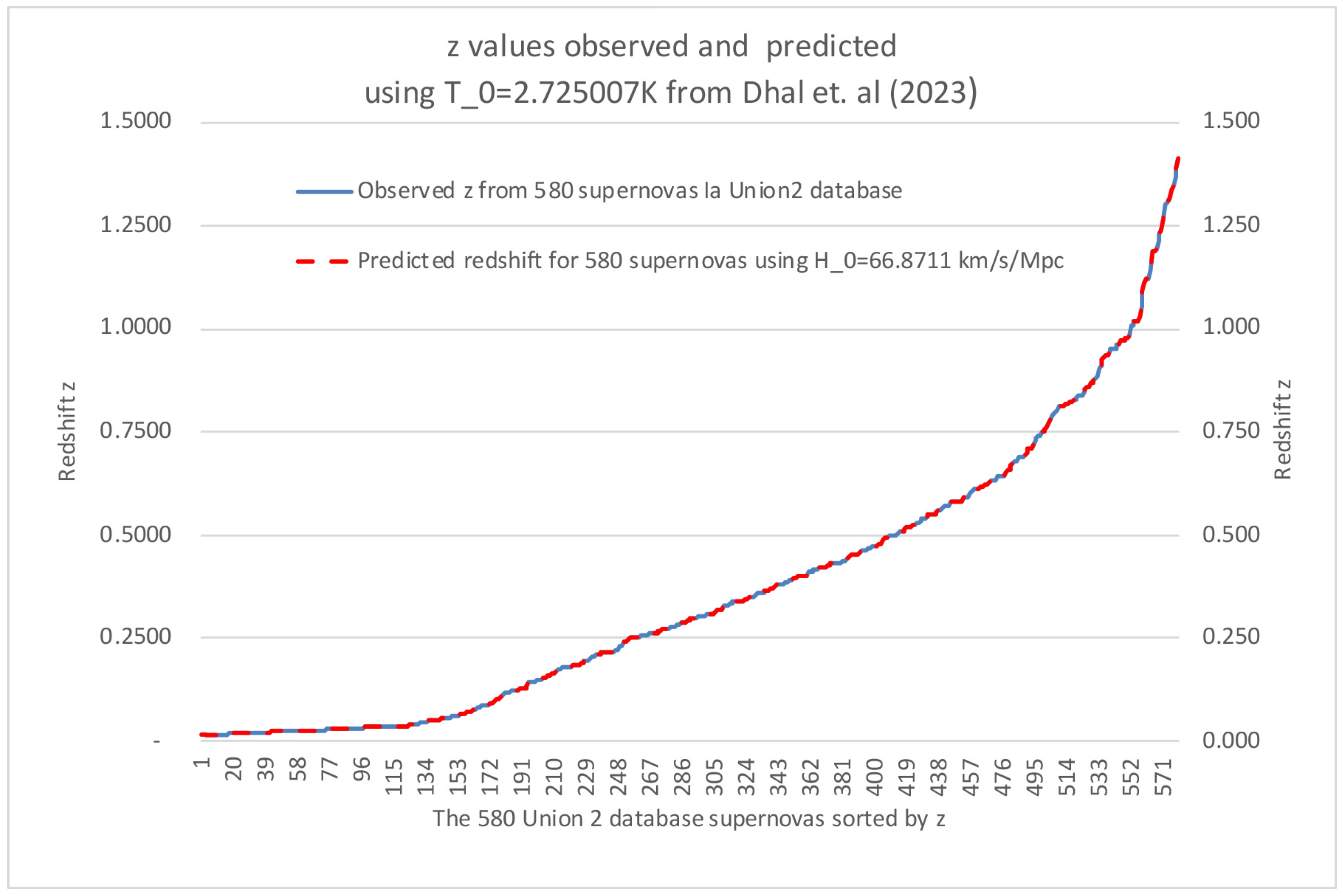
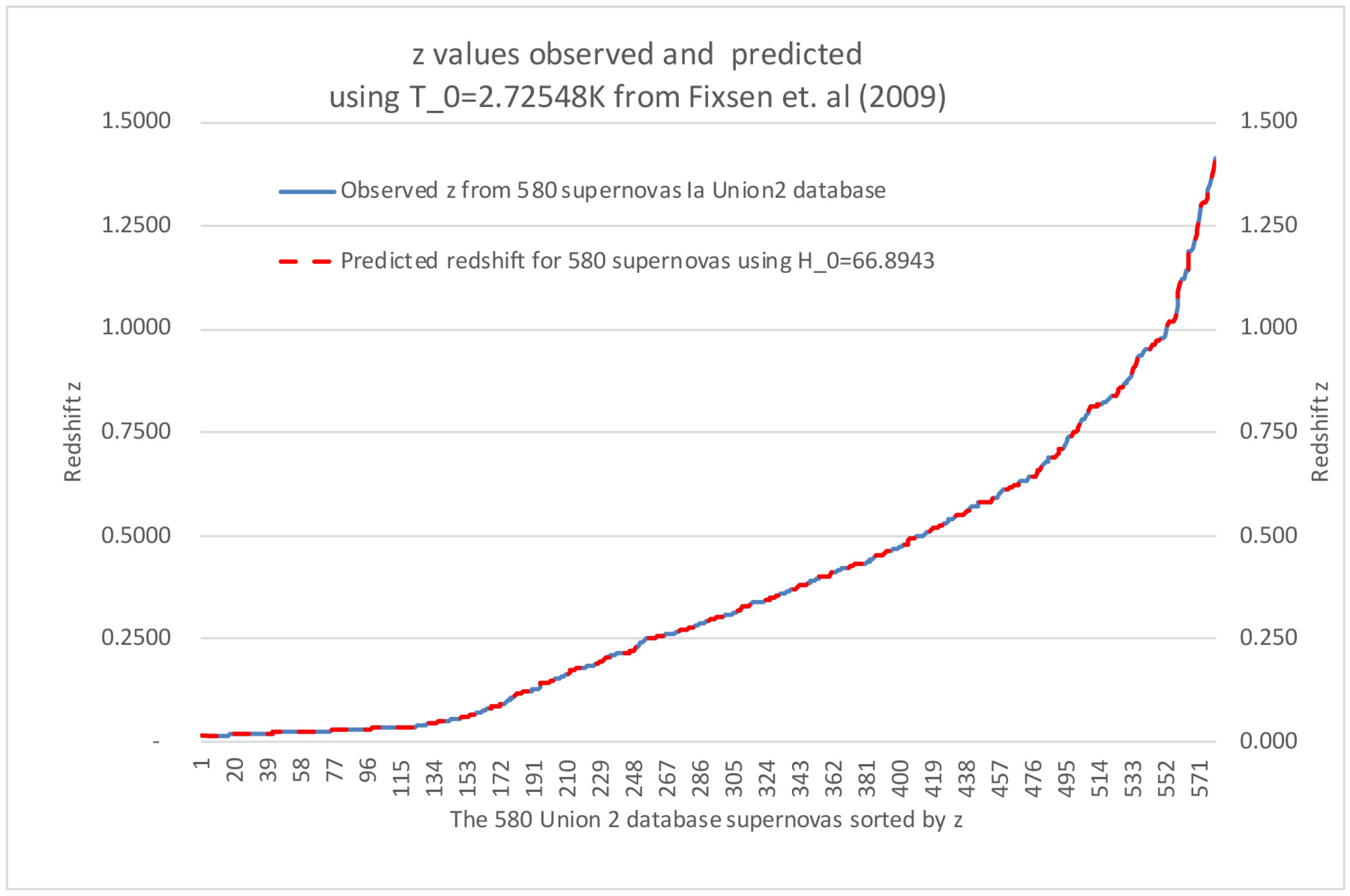
3. Predictions Relative to the Observations Using the Full Distance Ladder of the Union 2 Database

Here, we will see if our model can match all the observed cosmological redshifts by simply determining the $H_0$ constant from equation (13). However to demonstrate the superiority of equation (13), we will first instead use the predicted value for $H_0$ by for example Riess et al. [24] of $H_0=73.04\pm 1.04$ km/s/Mpc. We plot the Riess et al. value, accounting for 2 standard deviations (STD), and from this, we get Figure 1. The blue line represents the predicted redshift from $H_0=73.04$ km/s/Mpc, while the green lines represent the 2 STD confidence interval, i.e., $\pm 2\times 1.04$ km/s/Mpc. We can see that even the 95% confidence interval falls outside the observations, meaning that any $H_0$ value within this interval does not come close to matching the observed redshifts in our cosmological model.

Figure 2 demonstrates the results we get when we instead calculate $H_0$ based on equation (10) when using the Dhal et al [25] measured CMB value of $T_0=2.725007\pm 0.000024K$. According to our theory, this should provide a perfect match between the observed and predicted values, and as we can see, the observed and predicted values lie on top of each other. The confidence interval is now so narrow that even if we plotted it, it would appear to overlap with the observed values. The predicted $H_0=66.8712\pm km/s/Mpc$ when using this measured CMB temperature.

Figure 3 demonstrate the results we get when we calculate $H_0$ based on equation (13) when the measured CMB value of Fixsen [26]: $T_0=2.72548\pm 0.00057K$, this lead to a basically perfect match between predicted and observed SN Ia redshifts with a predicted $H_0=66.8943\pm 0.0287km/s/Mpc$

It is important to understand that the results in this section is independent on the value selected for the scaling factor x in $z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$ in our $R_h=ct$ cosmology.

4. The new Thermodynamic Friedmann Equation Consistent with the General Red-Shift Scaling $z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$

Haug and Tatum [27] have recently demonstrated that the critical Friedmann [15] equation:

$$H_0^2={\displaystyle \frac{8\pi G\rho }{3}}$$

(19)

can be rewritten in thermodynamical form:

$$T_0^4={\displaystyle \frac{{\hslash }^4{c}^{2}G\rho }{384k_b^4{\pi }^3{l}_p^2}}={\displaystyle \frac{{\hslash }^3{c}^5\rho }{384k_b^4{\pi }^3}}$$

(20)

Here we will generalize tis to

$$T_0^4={\displaystyle \frac{{\hslash }^3{c}^5\rho }{384k_b^4{\pi }^3}}{\displaystyle \frac{{(1+z_{obs,i})}^{\frac{1}{2x}}}{{(1+z_{pre,i})}^{\frac{1}{2x}}}}$$

(21)

and when $z_{pre,i}=z_{obs,i}$ this will simply to (20). We have simply replaced $H_0$ with $H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}{\displaystyle \frac{{(1+z_{obs,i})}^{\frac{1}{2x}}}{{(1+z_{pre,i})}^{\frac{1}{2x}}}}$. However when $z_{pre,i}=z_{obs,i}$ we end up getting equation (20) which demonstrate the thermodynamic form of the Haug and Tatum equation is very general and robust, it is valid for a wide range of redshift scaling choices (the choice off x) inside $R_h=ct$ cosmology.

From the sections above, it is clear that this thermodynamic Friedmann equation is valid and identical x scaling factors in $z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$, as they all lead to the exactly the same $H_0$.

More importantly, the thermodynamic Friedmann equation, when carefully studied in relation to our empirical and theoretical work, clearly seems to present a solution to the Hubble tension. However, further discussions and testing by many other researchers are needed before a consensus can be reached. We hope the research community is open-minded enough to carefully consider this possibility and not simply ignore it due to biases based on the current consensus model, where the Hubble tension has yet to be solved.

5. Conclusion

Haug and Tatum have outlined a way to solve the Hubble tension inside $R_h=ct$ cosmology based on new exact relations between the CMB temperature the Hubble constant and redshift, they however use a numerical search algorithm to do so and have only considered $z=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1$ and $z=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1$ cosmological redshift scaling. Even if their method is intuitive and powerful we here demonstrate one can simply solve one of their equations and further based on logic get to the one single $H_0$ value that make their model matching all observed SN Ia. In other words this leads to a closed form solution of the Hubble tension in side $R_h=ct$ cosmology. We get a $H_0=66.8712\pm 0.0019km/s/Mpc$ when relying on the very precise Dhal et al measured CMB value matching leading to matching all the observed SN Ia redshifts across the full distance ladder in the Union2 database. This is the same value Haug and Tatum got from their numerical search algorithm solution when solving the Hubble tension. It is basically the same solution, one is using numerical search algorithm while the later used closed form solution. The closed form solution is naturally more elegant as no numerical search rutine with many calculations are needed to find the $H_0$ that matches all the supernovas. Further the solution in this paper is generalized for $z={\left({\displaystyle \frac{R_h}{R_t}}\right)}^x-1$ cosmological scaling, while Haug and Tatum only have considered the case equivalent to $x=1$ and $x={\displaystyle \frac{1}{2}}$.

So it looks like we have a path to solving the Hubble tension in $R_h=ct$ cosmology, but this does not solve the Hubble tension inside $\Lambda$-CDM cosmology. Further investigation between $R_h=ct$ cosmology and $\Lambda$-CDM cosmology is therefore warranted.