Effective Models of QCD and Their Implications for Dark Matter Phenomenology

1. Introduction

The search for the constituents of dark matter has spanned several decades, invoking a broad spectrum of candidates across astrophysical, cosmological, and quantum mechanical frameworks. Among the most explored candidates are Weakly Interacting Massive Particles (WIMPs), axions, sterile neutrinos, and Massive Astrophysical Compact Halo Objects (MACHOs) [1,2,3]. WIMPs, with predicted interactions via the weak nuclear force and masses in the range of $10\mathrm{GeV}/c^2\le m_{\chi }\le 1000\mathrm{GeV}/c^2$, have garnered significant attention due to their compatibility with the thermal freeze-out mechanism in the early universe [1,4,5,6].

The evolution of the WIMP number density $n_{\chi }$ in the early universe is governed by the Boltzmann equation (see Figure 1):

$${\displaystyle \frac{d{n}_{\chi }}{dt}}+3H{n}_{\chi }=-\langle \sigma v\rangle \left(n_{\chi }^2-n_{\chi ,\mathrm{eq}}^2\right)$$

where $H={\displaystyle \frac{\dot{a}}{a}}$ is the Hubble parameter, $\langle \sigma v\rangle$ represents the thermally averaged WIMP annihilation cross-section, and $n_{\chi ,\mathrm{eq}}$ is the equilibrium number density. Defining the comoving number density $Y_{\chi }={\displaystyle \frac{n_{\chi }}{s}}$, where s is the entropy density, the equation simplifies to

$${\displaystyle \frac{d{Y}_{\chi }}{dx}}=-{\displaystyle \frac{\langle \sigma v\rangle s}{Hx}}\left(Y_{\chi }^2-Y_{\chi ,\mathrm{eq}}^2\right)$$

with $x={\displaystyle \frac{m_{\chi }}{T}}$, where $m_{\chi }$ is the mass of the WIMP and T is the temperature of the universe [7]. At high temperatures, when $x\ll 1$, the number density follows $n_{\chi }\sim n_{\chi ,\mathrm{eq}}\propto x^{-3/2}{e}^{-x}$. As the temperature drops and $x\sim 1$, annihilations cease, and $n_{\chi }$ freezes out at a value $Y_{\chi }\sim 1/x_f$, where $x_f\sim 20$ depending on $\langle \sigma v\rangle$ [5].

The relic density of WIMPs is obtained by integrating the Boltzmann equation from the freeze-out epoch to the present (see Figure 3):

$${\Omega }_{\chi }{h}^2={\displaystyle \frac{1.07\times {10}^9{\mathrm{GeV}}^{-1}}{g_{*}^{1/2}{M}_{\mathrm{Pl}}}}{\displaystyle \frac{x_f}{\langle \sigma v\rangle }}$$

where $g_{*}$ is the number of relativistic degrees of freedom at freeze-out, and $M_{\mathrm{Pl}}$ is the Planck mass. For weak-scale cross-sections $\langle \sigma v\rangle \sim 3\times {10}^{-26}{\mathrm{cm}}^3{\mathrm{s}}^{-1}$, this gives the observed dark matter abundance ${\Omega }_{\chi }{h}^2\approx 0.12$ [8].

Despite the theoretical elegance of WIMPs, experimental searches for direct detection remain inconclusive. Direct detection experiments aim to observe nuclear recoils induced by WIMP-nucleus scattering. The differential event rate for such a process is given by

$${\displaystyle \frac{dR}{d{E}_R}}={\displaystyle \frac{{\rho }_{\chi }}{m_{\chi }}}{\int }_{v_{\min }}^{v_{\max }}{d}^{3}vf\left(v\right)v{\displaystyle \frac{d\sigma }{d{E}_R}}$$

where ${\rho }_{\chi }\approx 0.3\mathrm{GeV}{\mathrm{cm}}^{-3}$ is the local dark matter density, $f\left(v\right)$ is the WIMP velocity distribution, and ${\displaystyle \frac{d\sigma }{d{E}_R}}$ is the differential cross-section for WIMP-nucleus scattering [9]. Stringent upper limits have been placed on the WIMP-nucleon cross-section, with LUX-ZEPLIN (LZ) setting exclusion limits down to $1.4\times {10}^{-47}{\mathrm{cm}}^2$ for a WIMP mass of $m_{\chi }\sim 30\mathrm{GeV}$ [10], while SuperCDMS explores the parameter space for lower-mass WIMPs [11].

Indirect detection strategies, such as searching for annihilation products like gamma rays or positrons, probe different regions of parameter space [12]. However, no conclusive evidence has emerged, and thus far, all WIMP search experiments have resulted in null detections, pushing the parameter space of WIMPs to increasingly constrained regimes. Additionally, anomalies such as the 130 GeV $\gamma$-ray feature in Fermi-LAT data have sparked significant debate but remain inconclusive [13].

Beyond conventional candidates, the early universe offers a fertile ground for exploring exotic configurations of dark matter. In particular, the quark-gluon plasma (QGP), formed during the quantum chromodynamics (QCD) phase transition at approximately $t\sim {10}^{-5}\mathrm{s}$ after the Big Bang, provides a unique framework for generating topological defects [14,15]. These defects arise from the non-trivial vacuum structure of QCD and can exhibit stability due to topological constraints [16,17,18,19,20,21].

Topological defects are categorized by their dimensionalities:

$${\pi }_n\left(\mathcal{M}\right)\ne 0\Rightarrow \left\{\begin{array}{cc}n=0\hfill & \left(\mathrm{monopoles}\right)\hfill \\ n=1\hfill & \left(\mathrm{strings}\right)\hfill \\ n=2\hfill & (\mathrm{domain}\mathrm{walls}),\hfill \end{array}\right.$$

where ${\pi }_n\left(\mathcal{M}\right)$ represents the n-th homotopy group of the vacuum manifold $\mathcal{M}$.

In the case of domain walls, their energy density per unit area $\sigma$ is given by:

$$\sigma ={\int }_{\mathcal{M}}{\left[{\displaystyle \frac{\partial \varphi }{\partial x}}\right]}^{2}dx,$$

where $\varphi \left(x\right)$ is the scalar field characterizing the defect. For flux tubes, the energy density is determined by the chromoelectric flux $E_a^i$:

$${\mathcal{E}}_{\mathrm{flux}}={\displaystyle \frac{1}{2}}{\int }_V\left(E_a^i{E}_a^i\right)d^{3}x.$$

Additionally, quark-gluon plasma bag models predict the formation of QGP nuggets, or "quark nuggets," stabilized by surface tension and quantum pressure [22]. Quark-gluon plasma bag models predict the formation of QGP nuggets. The stability condition for the quark nuggets has been explored in various studies, indicating that stable up-down quark matter (udQM) nuggets exist under specific conditions of symmetry energy and surface tension [23,24,25]. Moreover, the influence of magnetic properties on the stability of these nuggets has also been considered, suggesting that ferromagnetic behavior can enhance their stability [26]. Additionally, configurational entropy has been discussed as a factor in determining the stability of compact objects, including quark nuggets [27]. The stability condition for these nuggets can be expressed as:

$$E_{\mathrm{nugget}}\left(A\right)=a_1{A}^{1/3}-a_2{A}^{2/3}+a_{3}A+{\displaystyle \frac{\alpha }{A^{1/3}}},$$

where A is the baryon number, and $a_1,a_2,a_3,\alpha$ are constants determined by the QGP properties.

Recent studies also explore the gluonic Bose-Einstein condensate (Cosmic Gluonic Background, CGB) as a dark matter candidate, formed due to the QCD trace anomaly [28,29,30,31,32]. The energy density of the CGB, ${\rho }_{\mathrm{CGB}}$, is governed by the QCD vacuum expectation value:

$${\rho }_{\mathrm{CGB}}={\langle T_{\mu }^{\mu }\rangle }_{\mathrm{QCD}},$$

where $T_{\mu }^{\mu }$ is the trace of the QCD energy-momentum tensor.

This paper examines the hypothesis that topological defects formed during the QCD phase transition could constitute dark matter, with a focus on their dynamical stability, interactions with baryonic matter, and cosmological implications.

In particular, we examine the Skyrme model, a classical effective field theory that predicts topologically stable solitons, and explore their cosmological implications as analogs for dark matter. We extend this discussion to the Nambu-Jona-Lasinio model, focusing on the formation and dynamics of domain walls as potential dark matter candidates.

The effects of these defects on heavy quarkonium dissociation in an anisotropic QGP have been investigated, revealing significant shifts in dissociation energies [16,17,18,19,20,21,33]:

$$\Delta E_{\mathrm{diss}}={\displaystyle \frac{{\alpha }_s}{r}}-{\displaystyle \frac{\sigma r}{2}},$$

where ${\alpha }_s$ is the strong coupling constant, r is the quarkonium radius, and $\sigma$ is the string tension. These results suggest profound implications for the evolution of the early universe and the nature of dark matter.

2. Quark-Gluon Plasma in the Early Universe

Quark-gluon plasma (QGP) is a deconfined phase of quantum chromodynamics (QCD) matter, characterized by the liberation of quarks and gluons from their hadronic confines [14]. This state is hypothesized to have existed during the initial microseconds following the Big Bang, when the Universe’s temperature exceeded the QCD deconfinement scale, $T_c\sim 150$–$200\mathrm{MeV}$ [34,35]. The study of QGP not only deepens our understanding of the strong interaction but also serves as a window into the conditions of the early Universe [35,36,37,38,39].

Figure 4. Thermal History of the Universe. The figure depicts the transition epochs, including the QCD phase transition where quarks and gluons were deconfined in the early Universe.

Figure 4. Thermal History of the Universe. The figure depicts the transition epochs, including the QCD phase transition where quarks and gluons were deconfined in the early Universe.

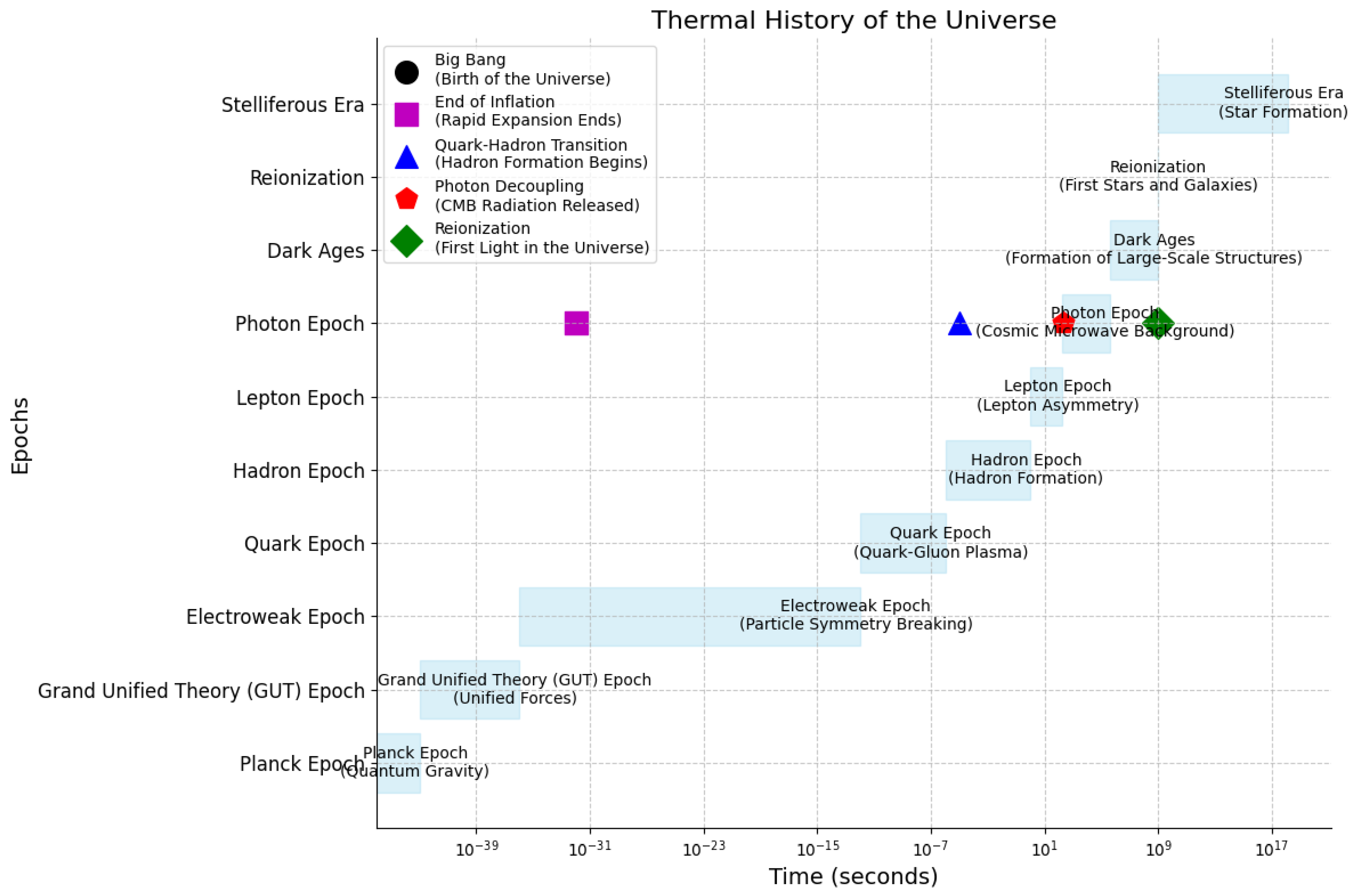
2.1. QCD Thermodynamics and QGP Formation

In QCD, the thermodynamic behavior of strongly interacting matter is encapsulated in the partition function:

$$\mathcal{Z}=\int \mathcal{D}A\mathcal{D}\overline{\psi }\mathcal{D}\psi e^{-S_{\mathrm{QCD}}[A,\overline{\psi },\psi ]},$$

(1)

where $S_{\mathrm{QCD}}$ is the Euclidean QCD action given by:

$$S_{\mathrm{QCD}}=\int d^{4}x\left[{\displaystyle \frac{1}{4}}{F}_{\mu \nu }^a{F}_a^{\mu \nu }+\overline{\psi }(i{\gamma }^{\mu }{D}_{\mu }-m)\psi \right].$$

(2)

Here, $F_{\mu \nu }^a$ is the gluon field tensor, $\psi$ represents the quark fields, and $D_{\mu }$ is the covariant derivative [34,40]. At temperatures $T\gg T_c$, the expectation value of the Polyakov loop $\langle L\left(\overrightarrow{x}\right)\rangle$ transitions from $\langle L\rangle =0$ (confined phase) to $\langle L\rangle \ne 0$ (deconfined phase), signaling QGP formation [41,42]. Modern studies using lattice QCD simulations provide precise insights into the equation of state and the nature of the phase transition [39,43,44,45,46].

2.2. Transport Properties of QGP

The QGP exhibits unique transport properties, characterized by a near-minimal shear viscosity to entropy density ratio:

$${\displaystyle \frac{\eta }{s}}\gtrsim {\displaystyle \frac{1}{4\pi }},$$

(3)

where $1/4\pi$ is the conjectured lower bound derived from the AdS/CFT correspondence [43,44,45,46,47,48]. The small value of $\eta /s$ implies a nearly perfect fluidity, which manifests in collective flow phenomena such as elliptic flow.

The energy density $ϵ\left(T\right)$ and pressure $p\left(T\right)$ of QGP are governed by the equation of state derived from lattice QCD:

$${\displaystyle \frac{ϵ-3p}{T^4}}={\displaystyle \frac{1}{T^4}}\left(T{\displaystyle \frac{\partial p}{\partial T}}-4p\right).$$

(4)

The rapid rise in $ϵ\left(T\right)$ near $T_c$ reflects the deconfinement transition and the liberation of partonic degrees of freedom [43,44,45,46,48,49].

2.3. Experimental Observables and Theoretical Models

Heavy-ion collision experiments probe the quark-gluon plasma (QGP) by creating a fireball of high-energy density. The space-time evolution of this fireball is modeled by relativistic hydrodynamics [50,51], governed by the equation:

$${\partial }_{\mu }{T}^{\mu \nu }=0,$$

(5)

where $T^{\mu \nu }$ is the energy-momentum tensor, expressed as:

$$T^{\mu \nu }=(ϵ+p)u^{\mu }{u}^{\nu }-p{g}^{\mu \nu }+{\pi }^{\mu \nu },$$

(6)

with $u^{\mu }$ as the fluid velocity and ${\pi }^{\mu \nu }$ representing the viscous stress tensor [52,53]. Elliptic flow, quantified by the Fourier coefficient $v_2$, serves as a key observable for the QGP [54,55]:

$$v_2={\displaystyle \frac{\int d\varphi cos\left(2\varphi \right)\frac{dN}{d\varphi }}{\int d\varphi \frac{dN}{d\varphi }}},$$

(7)

where $\varphi$ is the azimuthal angle of emitted particles.

2.4. Jet Quenching and Energy Loss Mechanisms

Jet quenching provides direct evidence for the dense medium created in heavy-ion collisions. The energy loss of a high-energy parton traversing the QGP is described by the Baier-Dokshitzer-Mueller-Peigné-Schiff (BDMPS) framework [56], which predicts that:

$$\Delta E\propto \widehat{q}{L}^2,$$

(8)

where $\widehat{q}$ is the jet transport coefficient, and L is the path length through the medium [57]. Suppression of high-transverse-momentum particles, quantified by the nuclear modification factor $R_{AA}$, serves as a hallmark of QGP [48]:

$$R_{AA}={\displaystyle \frac{d^2{N}^{\mathrm{AA}}/d{p}_{T}d\eta }{\langle N_{\mathrm{coll}}\rangle d^2{N}^{\mathrm{pp}}/d{p}_{T}d\eta }}.$$

(9)

Additionally, azimuthal anisotropy in particle emission, often quantified using the elliptic flow coefficient $v_2$, provides further insights into the properties of the QGP [54].

2.5. Cosmological Implications

The study of the quark-gluon plasma (QGP) offers profound insights into the thermodynamic evolution of the early Universe, particularly during the quantum chromodynamics (QCD) phase transition [58,59]. During this epoch, the speed of sound, $c_s$, in the primordial plasma is given by

$$c_s^2={\displaystyle \frac{\partial p}{\partial ϵ}},$$

(10)

where p is the pressure and $ϵ$ is the energy density of the plasma [60,61]. Significant changes in $c_s$ during the QCD phase transition affected the evolution of primordial density fluctuations, playing a crucial role in the formation of large-scale structures [61].

Moreover, the rapid cooling of the Universe could have resulted in the formation of topological defects, such as domain walls or cosmic strings, arising from symmetry-breaking processes [62,63]. These defects are hypothesized to contribute to dark matter candidates, such as axions or other relic particles, depending on the nature of the QCD phase transition [22,64].

The QGP also serves as a probe for extreme conditions of quantum chromodynamics, offering unique opportunities to connect the microphysics of heavy-ion collisions to macroscopic cosmological phenomena. Its study continues to challenge our understanding of fundamental physics and the interplay between particle physics and cosmology [37,65].

3. Topological Structures in QCD and Their Role in Dark Matter Physics

The hypothesis that Quantum Chromodynamics (QCD) may harbor topological structures, such as flux tubes, domain walls, or monopoles, presents an intriguing avenue for understanding the non-perturbative dynamics of the strong interaction. Furthermore, the potential connection between these structures and dark matter warrants a detailed exploration, provided the assertions are grounded in robust theoretical and mathematical frameworks. Here, we critically examine this hypothesis through the lens of gauge theory, lattice QCD, and effective field theory while addressing the fundamental issues raised in the literature [22,35,62,63,66,67,68,69,70,71,72,73,74,75,76,77].

3.1. Theoretical Foundations and Scale Symmetry Breaking

QCD, as a non-Abelian gauge theory described by the Lagrangian

$${\mathcal{L}}_{\mathrm{QCD}}=-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }^a{F}_a^{\mu \nu }+{\overline{\psi }}_f\left(i{\gamma }^{\mu }{D}_{\mu }-m_f\right){\psi }_f,$$

(11)

is classically scale-invariant, where $F_{\mu \nu }^a={\partial }_{\mu }{A}_{\nu }^a-{\partial }_{\nu }{A}_{\mu }^a+g{f}^{abc}{A}_{\mu }^b{A}_{\nu }^c$ is the gluon field strength tensor, $A_{\mu }^a$ represents the gauge fields, and ${\psi }_f$ denotes the quark fields of flavor f. Quantum corrections, however, introduce a scale through the renormalization group equation:

$$\mu {\displaystyle \frac{\mathrm{d}g}{\mathrm{d}\mu }}=\beta \left(g\right)=-{\beta }_0{g}^3-{\beta }_1{g}^5+\mathcal{O}\left(g^7\right),$$

(12)

where ${\beta }_0={\displaystyle \frac{11N_c-2N_f}{48{\pi }^2}}$ reflects the asymptotic freedom of QCD [66]. This scale-breaking effect, encapsulated in the QCD scale ${\Lambda }_{\mathrm{QCD}}$, raises the possibility of non-trivial vacuum structures, such as a quark-gluon condensate:

$$\langle 0\left|\overline{\psi }\psi \right|0\rangle \ne 0.$$

(13)

While these features suggest rich vacuum dynamics, the emergence of extended topological defects remains highly speculative [76].

3.2. Gauge-Invariant Formulation of Confinement and Flux Tubes

The confinement phenomenon in QCD, characterized by the linear growth of the potential between quarks,

$$V\left(r\right)=\sigma r+\mathcal{O}(1/r),$$

(14)

where $\sigma$ is the string tension, is often interpreted in terms of gluon flux tubes [69]. These flux tubes correspond to solutions of the Wilson loop operator:

$$W\left(C\right)=〈\mathrm{Tr}\mathcal{P}exp\left(ig{\oint }_C{A}_{\mu }^a{T}^a\mathrm{d}{x}^{\mu }\right)〉\propto e^{-\sigma A\left(C\right)},$$

(15)

where C is a closed loop, $\mathcal{P}$ denotes path ordering, and $A\left(C\right)$ is the minimal area spanned by C. However, these flux tubes are not independent topological objects; they exist solely as part of the quark confinement mechanism. The absence of gauge-invariant classical solutions for free-standing flux tubes challenges their identification as topological defects [68].

3.3. Low-Energy Effective Models and Solitonic Solutions

In contrast to QCD itself, several low-energy effective models, such as the Skyrme model [70], offer solitonic solutions with potential implications for dark matter. The Skyrme Lagrangian,

$${\mathcal{L}}_{\mathrm{Skyrme}}={\displaystyle \frac{f_{\pi }^2}{4}}\mathrm{Tr}\left({\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\right)+{\displaystyle \frac{1}{32e^2}}\mathrm{Tr}\left({\left[U^{†}{\partial }_{\mu }U,U^{†}{\partial }_{\nu }U\right]}^2\right),$$

(16)

admits soliton solutions, or Skyrmions, which carry topological charge:

$$Q={\displaystyle \frac{1}{24{\pi }^2}}\int {ϵ}^{ijk}\mathrm{Tr}\left(U^{†}{\partial }_{i}U{U}^{†}{\partial }_{j}U{U}^{†}{\partial }_{k}U\right){\mathrm{d}}^{3}x.$$

(17)

These structures, while mathematically well-defined, are derived from an effective theory and do not necessarily imply analogous structures in QCD itself [71].

3.4. Nambu–Jona-Lasinio Model and Dark Matter

The NJL model, developed to describe spontaneous chiral symmetry breaking in QCD [78,79], provides another framework for exploring dark matter candidates. The model is characterized by a four-fermion interaction:

$${\mathcal{L}}_{\mathrm{NJL}}=\overline{\psi }(i{\gamma }^{\mu }{\partial }_{\mu }-m)\psi +g\left({\left(\overline{\psi }\psi \right)}^2+{\left(\overline{\psi }i{\gamma }_5\tau \psi \right)}^2\right),$$

(18)

where $\psi$ is the quark field and g is a coupling constant. The spontaneous symmetry breaking in the NJL model gives rise to fermionic condensates, which could contribute to the formation of dark matter-like states, such as dark mesons or light baryons [77,80].

3.5. Chiral Perturbation Theory and Dark Matter Models

Chiral perturbation theory (ChPT) is the effective field theory of QCD that describes the dynamics of pions and other pseudo-Goldstone bosons. The Lagrangian of ChPT, at lowest order, is given by:

$${\mathcal{L}}_{\mathrm{ChPT}}={\displaystyle \frac{f_{\pi }^2}{4}}\mathrm{Tr}\left({\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\right)+\cdots ,$$

(19)

where $U\left(x\right)$ is the pion field and $f_{\pi }$ is the pion decay constant. ChPT provides a useful framework for describing low-energy QCD interactions, which are important for constructing models of dark matter that may interact via pseudo-scalar mediators [81,82].

The effective models of QCD, such as the Skyrme model, NJL model, and ChPT, provide a rich landscape for exploring the nature of dark matter. Their solitonic solutions, clustering behaviors, and potential gravitational signatures offer intriguing possibilities for dark matter analogs. Continued advancements in numerical simulations, coupled with observational probes like gravitational waves, will be key to verifying these models as viable candidates for dark matter.

3.6. Dark Matter Implications and Future Work

The role of topological structures in dark matter physics requires cautious interpretation. To draw meaningful connections, one must first identify physically realizable solutions within QCD or its extensions. Promising avenues include holographic QCD, where flux tubes emerge as string-like configurations in higher-dimensional spacetimes [72], and lattice studies of gluonic configurations under extreme conditions [73]. Ultimately, progress in this domain hinges on combining rigorous mathematical frameworks with state-of-the-art computational techniques [62,74,75].

Although the existence of topological defects in QCD remains unproven, the exploration of analogous structures in effective field theories and specialized contexts offers valuable insights. Future research must rigorously delineate between speculative analogies and physical phenomena, fostering a more robust understanding of the interplay between QCD, confinement, and dark matter.

4. Classical Solutions in Effective Models of QCD and Their Relevance to Dark Matter

Low-energy effective models of quantum chromodynamics (QCD), such as the Skyrme model [83], the Nambu–Jona-Lasinio (NJL) model [78,79], and chiral perturbation theory (ChPT) [81], offer valuable insights into non-perturbative phenomena. These models capture exotic dynamics like solitons, domain walls, and flux tubes, characterized by localized energy densities and remarkable stability properties. While initially developed to elucidate hadronic physics, their stability and interactions within the Standard Model (SM) provide intriguing parallels to dark matter (DM) candidates. Here, we explore the theoretical, computational, and astrophysical implications of these effective QCD models, focusing on their relevance for dark matter analogs.

4.1. Skyrme Model: Topological Solitons as Analogues of Dark Matter

The Skyrme model [83] represents one of the most studied field-theoretic frameworks for baryons, supporting topologically stable solitons termed Skyrmions. These solitons are characterized by a nontrivial topological charge, which stabilizes their structure and renders them analogous to dark matter: non-luminous, robust, and capable of clustering [84,85]. The model’s Lagrangian density is given by:

$${\mathcal{L}}_{\mathrm{Skyrme}}={\displaystyle \frac{f_{\pi }^2}{4}}\mathrm{Tr}\left({\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\right)+{\displaystyle \frac{1}{32e^2}}\mathrm{Tr}\left({[U^{†}{\partial }_{\mu }U,U^{†}{\partial }_{\nu }U]}^2\right),$$

(20)

where $U\left(x\right)\in \mathrm{SU}\left(2\right)$ is the pion field, $f_{\pi }$ is the pion decay constant, and e is a dimensionless coupling constant. The non-linear Euler-Lagrange equations derived from this Lagrangian yield stable field configurations corresponding to the Skyrmions. The Skyrme model’s potential to describe baryons as solitons was initially explored by Adkins, Nappi, and Witten [86], and it has since been expanded to include interactions with vector mesons [87].

4.1.1. Topological Charge and Stability

Skyrmions are stabilized by a topological charge B, which is typically identified with the baryon number. This topological charge is quantized, ensuring solitonic stability and an analogy with the long-lived nature of dark matter halos in astrophysics [85,88]. The topological charge is given by:

$$B={\displaystyle \frac{1}{24{\pi }^2}}{\int }_{{\mathbb{R}}^3}{ϵ}^{ijk}\mathrm{Tr}\left(\left(U^{†}{\partial }_{i}U\right)\left(U^{†}{\partial }_{j}U\right)\left(U^{†}{\partial }_{k}U\right)\right)d^{3}x,$$

(21)

which can be interpreted as a conserved quantity under suitable boundary conditions. The quantization of B leads to stable solitonic solutions, analogous to the stability of dark matter structures in the universe.

4.1.2. Energy Density and Compactness

Numerical simulations of the Skyrme model reveal that Skyrmions possess compact, localized energy configurations with a characteristic size given by:

$$R\sim {\displaystyle \frac{1}{f_{\pi }e}}.$$

(22)

These configurations exhibit the dense, non-luminous properties characteristic of dark matter [89,90]. The energy density is typically concentrated in a small region, reflecting the behavior of dark matter halos, which are observed to be diffuse yet dense at their cores.

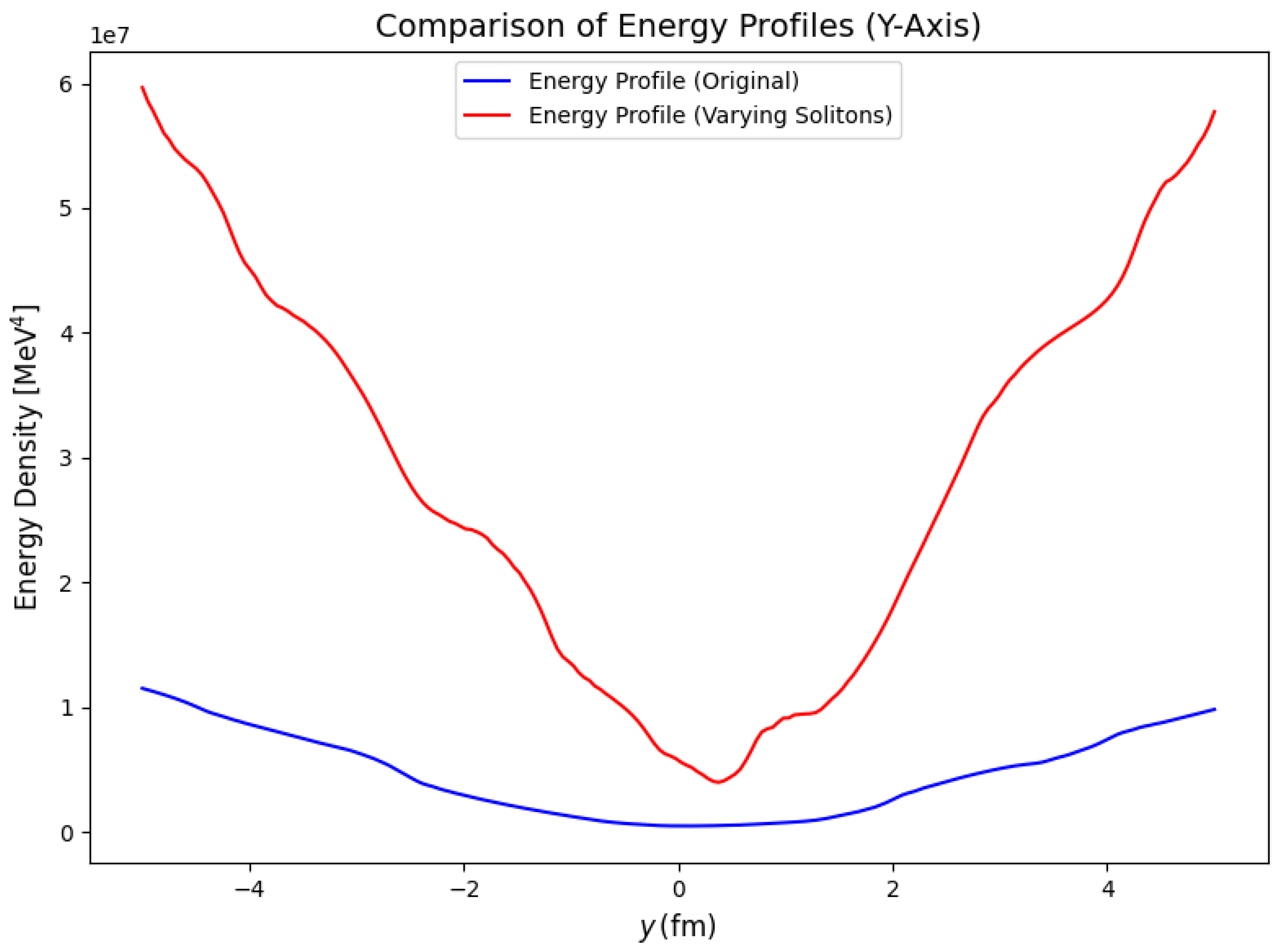
4.1.3. Skyrmion Clustering and Cosmological Implications

Skyrmions interact via a potential $V_{\mathrm{int}}$ that facilitates clustering, similar to the formation of dark matter halos. The interaction potential between two Skyrmions is modeled as:

$$V_{\mathrm{int}}\left(r\right)\sim -{\displaystyle \frac{c_1}{r^2}}+{\displaystyle \frac{c_2}{r^6}},r\gg R,$$

(23)

where the first term represents the attractive interaction at short distances, and the second term captures the repulsive behavior at large distances. These interactions lead to bound-state configurations, similar to the clustering of dark matter in cosmological simulations [88,91]. Multi-Skyrmion configurations can form lattice structures, mimicking the self-gravitating dynamics observed in dark matter simulations [85,91].

4.1.4. Extensions and Future Directions

The Skyrme model can be extended by introducing higher-order terms or coupling to vector mesons, enhancing its applicability to astrophysical scenarios [85,87]. Furthermore, embedding the Skyrme model in the AdS/CFT framework offers a promising route to understanding its behavior in the strong-coupling regime, potentially shedding light on the behavior of dark matter at higher energies [92]. Future research should focus on:

• The production mechanisms of Skyrmions in the early universe [77].
• Gravitational wave signatures from Skyrmion clusters, which could provide a new observational probe for dark matter [93].
• The reconciliation of Skyrmion masses with current dark matter constraints, as Skyrmion mass distributions are typically non-thermal [77].

Simulations incorporating Skyrmion dynamics with general relativity will play a critical role in addressing these questions, providing key insights into the potential role of Skyrmions as dark matter candidates [94].

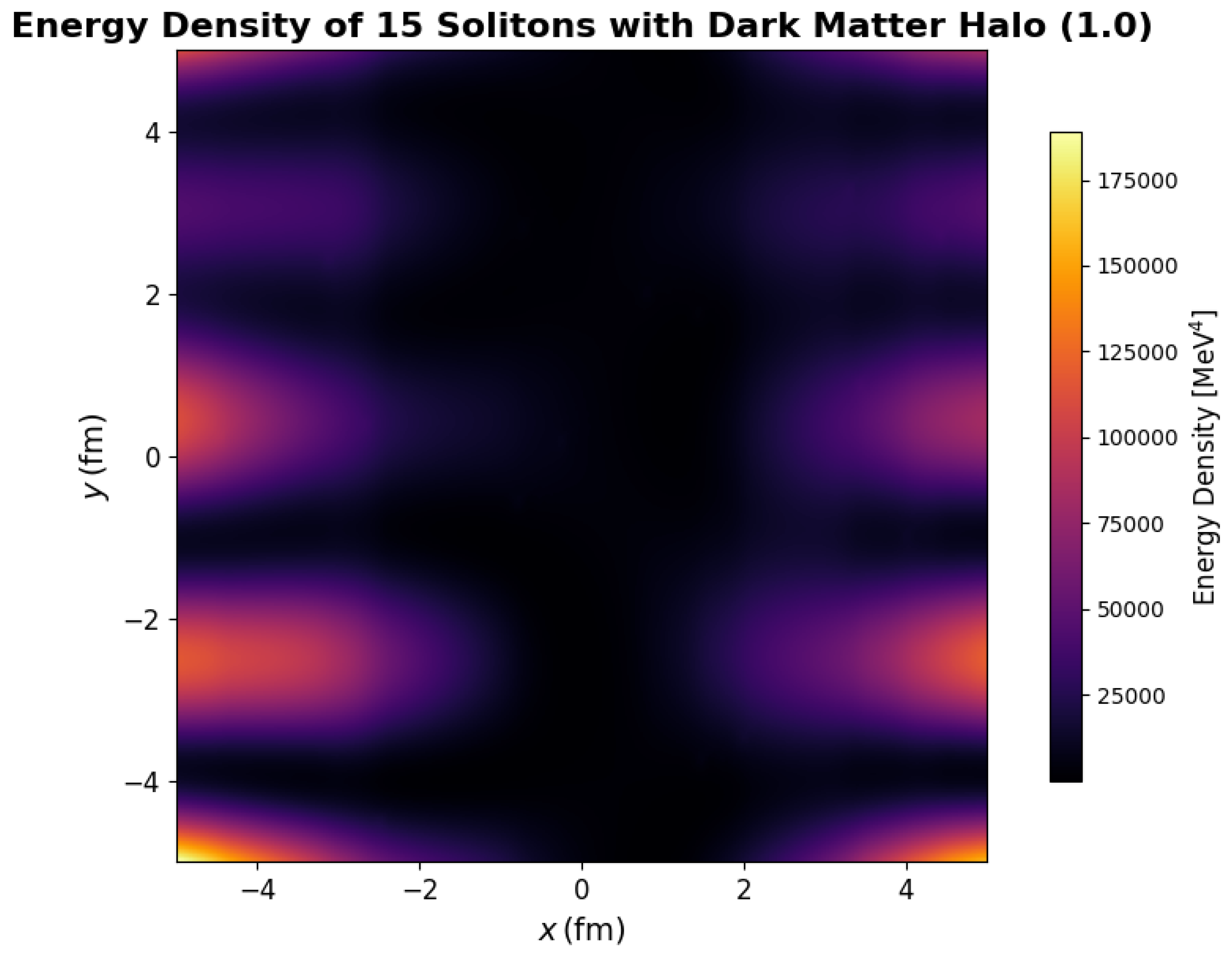
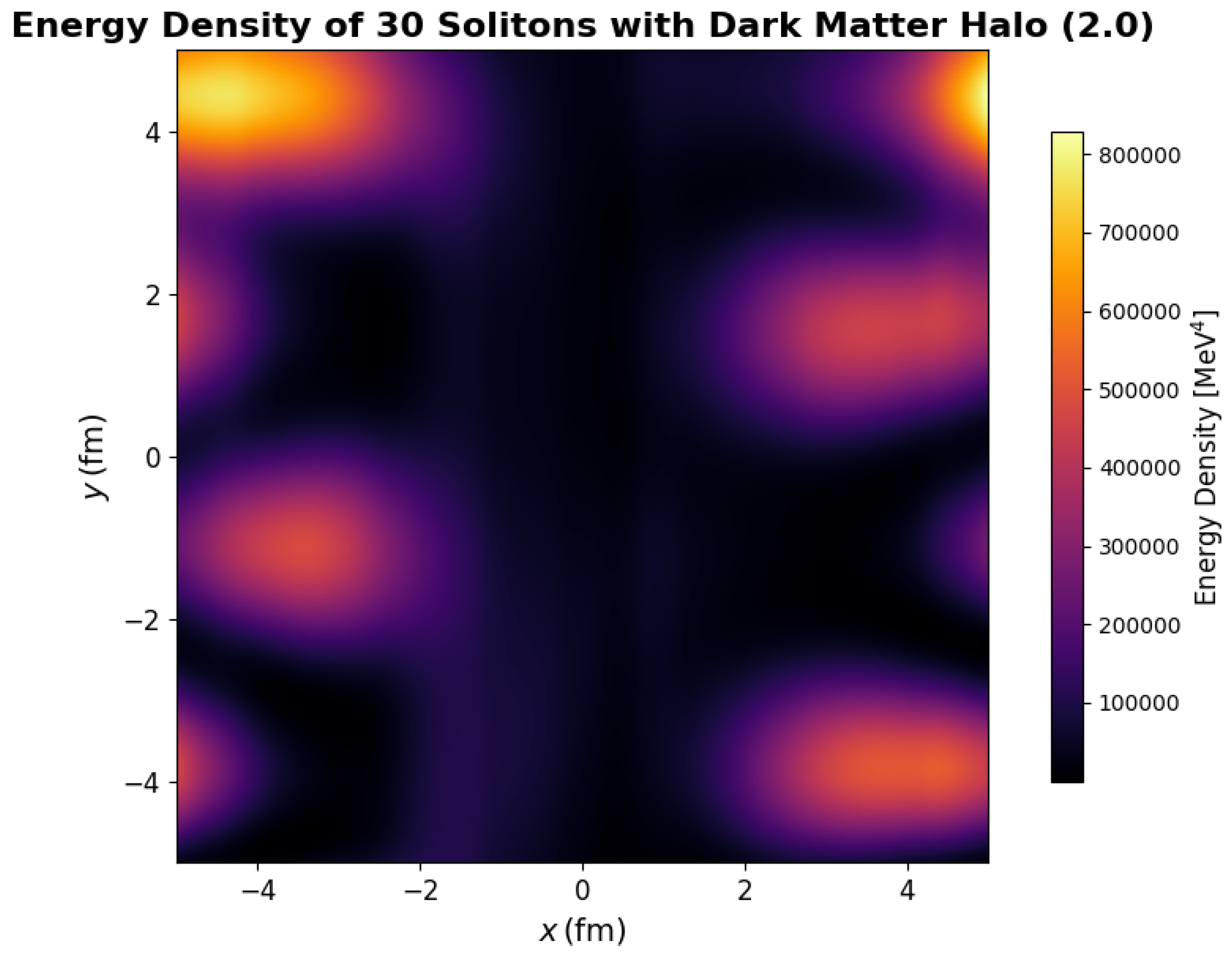
4.1.5. Simulating Skyrme Solitons and Dark Matter Halo Interactions

This section details the numerical simulation of Skyrme solitons interacting with a dark matter halo described by an NFW (Navarro-Frenk-White) profile [95]. The dynamics of the soliton field are computed by solving the coupled Skyrme and gravitational potential equations, employing a Runge-Kutta numerical integrator for time evolution.

The Skyrme field $U\left(x\right)$ is modeled using the hedgehog ansatz for the $SU\left(2\right)$ field, with energy density given by [96]:

$$\mathcal{E}={\displaystyle \frac{f_{\pi }^2}{4}}\left({|\nabla U|}^2\right)+{\displaystyle \frac{1}{32e^2}}{\left|[U,\nabla U]\right|}^2,$$

where $f_{\pi }$ and e are Skyrme parameters [83,96]. The gravitational potential from the NFW dark matter profile is:

$$\Phi \left(r\right)=-{\displaystyle \frac{G{\rho }_0}{r}}ln\left(1+{\displaystyle \frac{r}{r_s}}\right),$$

where ${\rho }_0$ and $r_s$ characterize the halo’s density profile [95]. The equations of motion for U are solved in polar coordinates on a spatial grid with periodic boundary conditions.

The system is initialized with N Skyrme solitons distributed randomly in a $10\mathrm{fm}\times 10\mathrm{fm}$ box. Parameters include $f_{\pi }=93.0\mathrm{MeV},e=4.0,{\rho }_0=1.0\mathrm{MeV}/{\mathrm{fm}}^3$, and $r_s=2.0\mathrm{fm}$. A timestep of $\Delta t=0.01\mathrm{fm}/c$ is used to evolve the field for $t_{\max }=5.0\mathrm{fm}/c$.

Simulations with $N=15$ and $N=30$ solitons reveal clustering driven by the dark matter halo. The energy density distribution at $t=t_{\max }$ shows tighter soliton configurations as N increases, with total energy scaling approximately as $E\propto N^2$, the soliton core properties depend critically on both the self-gravity of the soliton and the external potential of the host halo[97]. For $N=15$, the central energy density peaks at $1.2\times {10}^7{\mathrm{MeV}}^4$, while for $N=30$, it reaches $6.2\times {10}^7{\mathrm{MeV}}^4$. These results suggest enhanced gravitational binding of solitons due to the increased halo density.

Energy profiles along x- and y-axes confirm that soliton interactions with the dark matter potential induce anisotropies, with maximum energy values occurring near the soliton cores. The higher ${\rho }_0$ configurations lead to pronounced clustering, consistent with theoretical predictions of soliton self-interaction in external potentials, steady interaction occurs when the crest of the soliton and the crest of the external force are in phase [98].

Figure 5 and Figure 6 illustrate the energy density for $N=15$ and $N=30$, respectively, highlighting the effect of soliton number on system stability.

Additionally, we compare the energy profiles along the x-axis and y-axis for the two sets of simulations. These comparisons, shown in Figure 7 and Figure 8, provide insight into how the soliton configurations influence the overall energy distribution.

At the final time step, the total energy for the configuration with 15 solitons and dark matter density ${\rho }_{\mathrm{DM}}=1.0\mathrm{MeV}/{\mathrm{fm}}^3$ was $9.1378\times {10}^8{\mathrm{MeV}}^4$, while for 30 solitons and ${\rho }_{\mathrm{DM}}=2.0\mathrm{MeV}/{\mathrm{fm}}^3$, it was $5.7541\times {10}^9{\mathrm{MeV}}^4$, showing an almost 10-fold increase with denser dark matter and more solitons. This suggests that both increased soliton number and dark matter density strengthen interactions within the system.

Energy profiles along the x- and y-axes reveal the spatial energy distribution. For the 15 soliton case, the x-axis profile showed a peak of $1.2315\times {10}^7{\mathrm{MeV}}^4$ and a minimum of $9.0061\times {10}^5{\mathrm{MeV}}^4$, with similar trends along the y-axis. In the 30 soliton configuration, the maximum energy along the x-axis increased to $6.1964\times {10}^7{\mathrm{MeV}}^4$, with a corresponding rise in the minimum energy, reflecting stronger energy clustering due to the denser dark matter halo.

Energy values at the grid center were also higher for the 30 soliton case. For 15 solitons, the central energy was $6.0778\times {10}^6{\mathrm{MeV}}^4$ along the x-axis and $4.6506\times {10}^5{\mathrm{MeV}}^4$ along the y-axis. In contrast, for 30 solitons, the central energy increased to $1.3490\times {10}^7{\mathrm{MeV}}^4$ along the x-axis and $5.5722\times {10}^6{\mathrm{MeV}}^4$ along the y-axis, indicating stronger soliton clustering and more pronounced dark matter effects.

Table 1. Total Energy Comparison.

Configuration	Total Energy (${\mathbf{MeV}}^4$)
15 solitons, ${\rho }_{\mathrm{DM}}=1.0\mathrm{MeV}/{\mathrm{fm}}^3$	$9.1378\times {10}^8$
30 solitons, ${\rho }_{\mathrm{DM}}=2.0\mathrm{MeV}/{\mathrm{fm}}^3$	$5.7541\times {10}^9$

Table 1. Total Energy Comparison.

Configuration	Total Energy (${\mathbf{MeV}}^4$)
15 solitons, ${\rho }_{\mathrm{DM}}=1.0\mathrm{MeV}/{\mathrm{fm}}^3$	$9.1378\times {10}^8$
30 solitons, ${\rho }_{\mathrm{DM}}=2.0\mathrm{MeV}/{\mathrm{fm}}^3$	$5.7541\times {10}^9$

Energy density plots for the 15 soliton configuration show more diffuse energy distribution with localized peaks, while the 30 soliton configuration exhibits a denser, more tightly bound energy distribution. The sharper, higher peaks in the 30 soliton case highlight the stronger soliton-dark matter interactions and suggest a more stable, clustered system.

This demonstrates a stronger clustering of solitons in the denser dark matter configuration, with a much higher central energy concentration. The sharper peaks in the energy profiles for the 30 soliton configuration further confirm the enhanced soliton interactions and the more energetically dense system.

These results highlight the gravitational coupling between Skyrme solitons and dark matter halos, showcasing the clustering and energy density amplification effects under varying soliton numbers and halo densities.

4.2. The Nambu-Jona-Lasinio Model: A Dynamical Framework for Chiral Symmetry Breaking

The Nambu-Jona-Lasinio (NJL) model is a relativistic quantum field theory framework that encapsulates the dynamics of fermionic fields interacting through four-fermion interactions, providing a phenomenological description of dynamical mass generation and spontaneous chiral symmetry breaking. Originally proposed by Nambu and Jona-Lasinio in 1961 [78,79], this model has played a central role in the development of effective field theories in the low-energy limit of quantum chromodynamics (QCD), where quark-gluon dynamics becomes non-perturbative.

The NJL model is governed by the following effective Lagrangian density [99]:

$$\mathcal{L}=\overline{\psi }(i\cancel{\partial }-m_0)\psi +G\left[{\left(\overline{\psi }\psi \right)}^2+{\left(\overline{\psi }i{\gamma }_5\psi \right)}^2\right],$$

(24)

where $\psi$ is a Dirac spinor field representing the fermions, $m_0$ is the bare fermion mass, and G is the coupling constant. The second term describes the interaction between fermions and their chiral partners, which is responsible for the spontaneous breaking of chiral symmetry in the vacuum. The parameter G governs the strength of this interaction and is usually considered to be a running coupling constant.

Within the mean-field approximation, the fermion condensate $\langle \overline{\psi }\psi \rangle$ induces a dynamical mass for the fermion field, which can be determined by solving the gap equation:

$$M=m_0+G\langle \overline{\psi }\psi \rangle .$$

(25)

The condensate $\langle \overline{\psi }\psi \rangle$ is a non-perturbative order parameter that signifies the spontaneous breaking of chiral symmetry. The presence of such a condensate leads to the generation of a fermionic mass M and provides a theoretical basis for the low-energy dynamics of strongly interacting fermions, such as the quarks in QCD [99,100,101].

The solution to the gap equation at finite temperature and density involves the computation of the fermionic determinant, typically requiring the use of numerical techniques or an expansion in the strong-coupling limit. In the limit of large $N_c$ (the number of colors), the NJL model can be solved analytically, but for finite $N_c$, numerical methods are often employed.

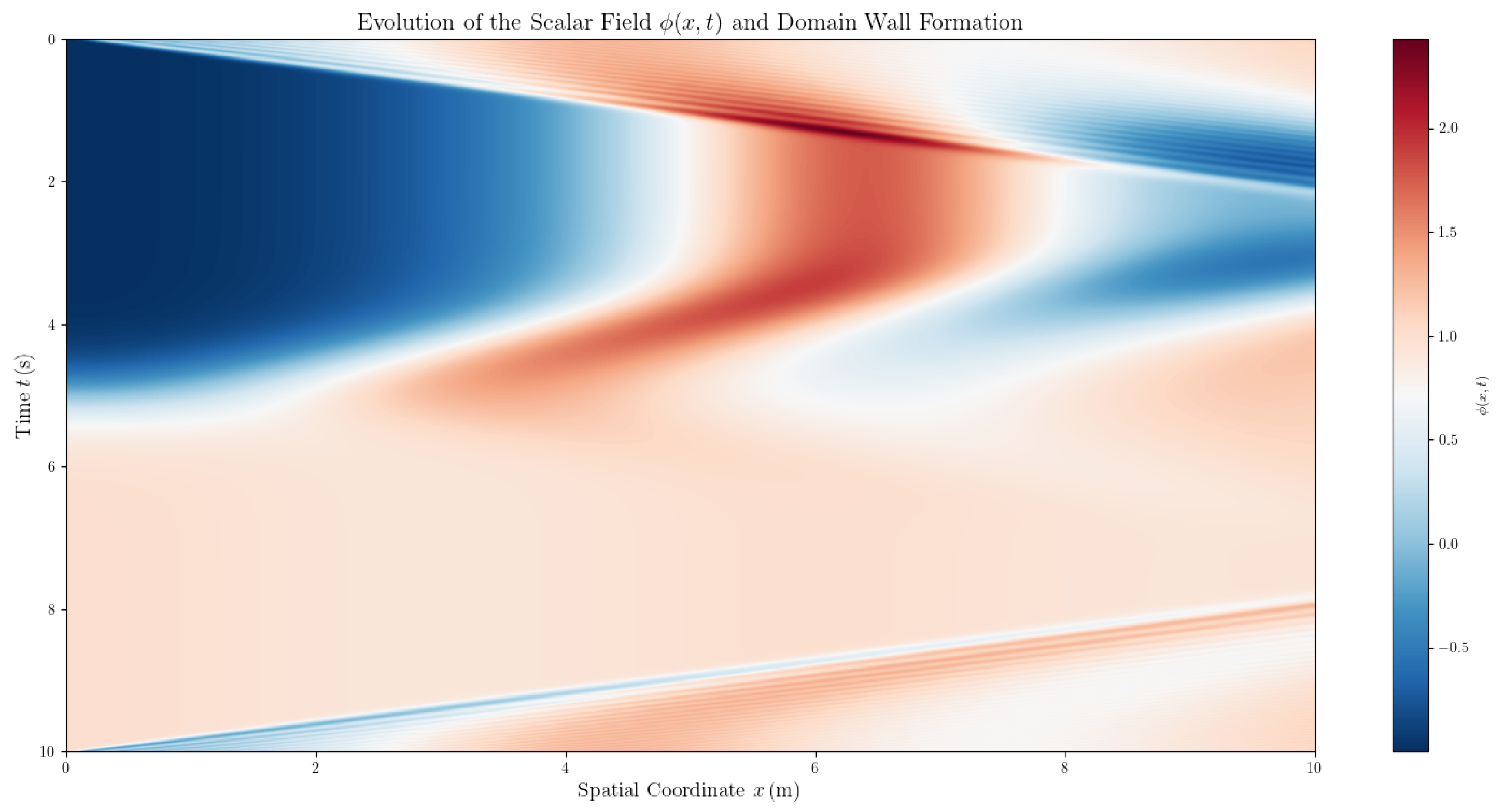
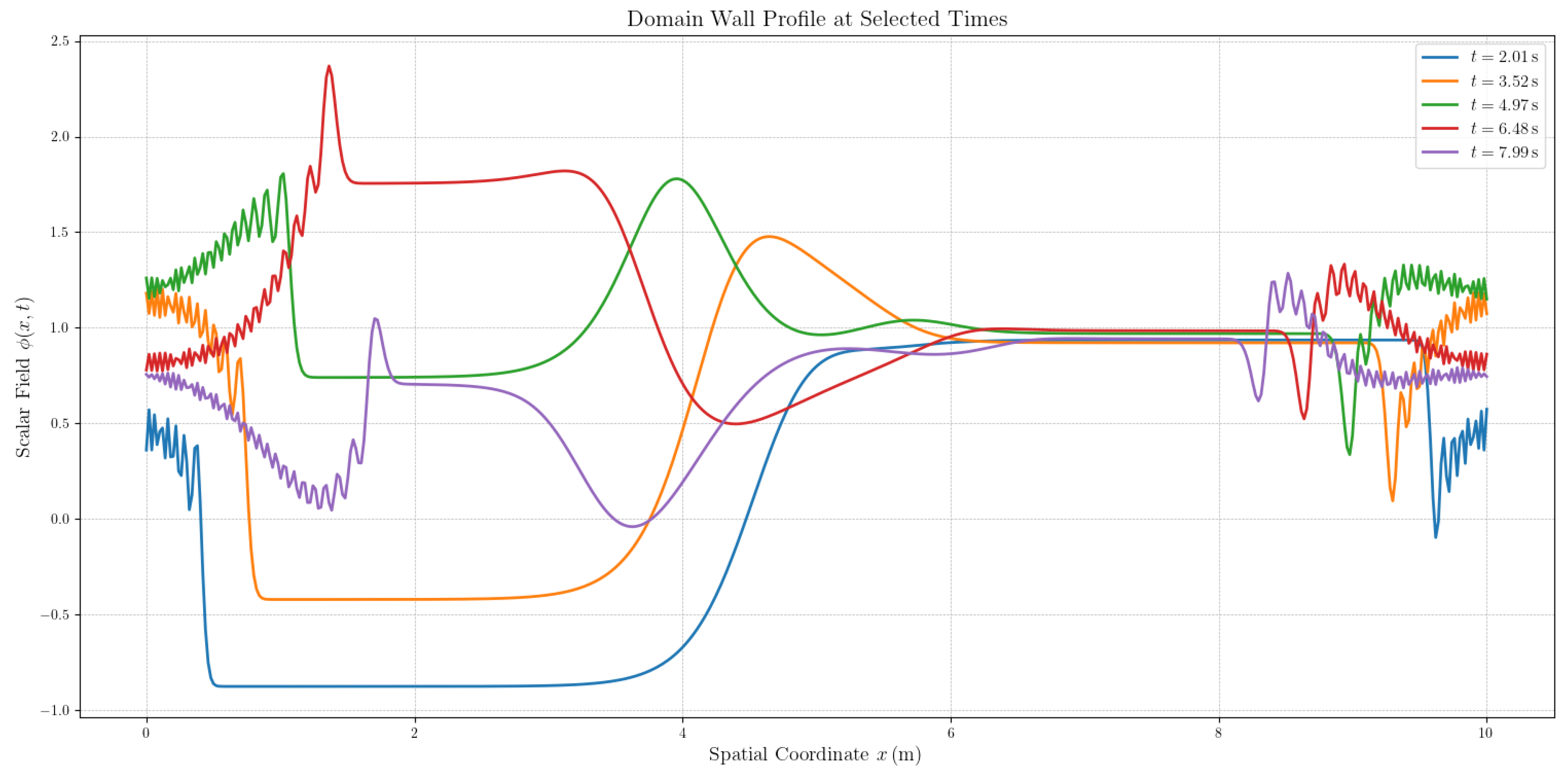
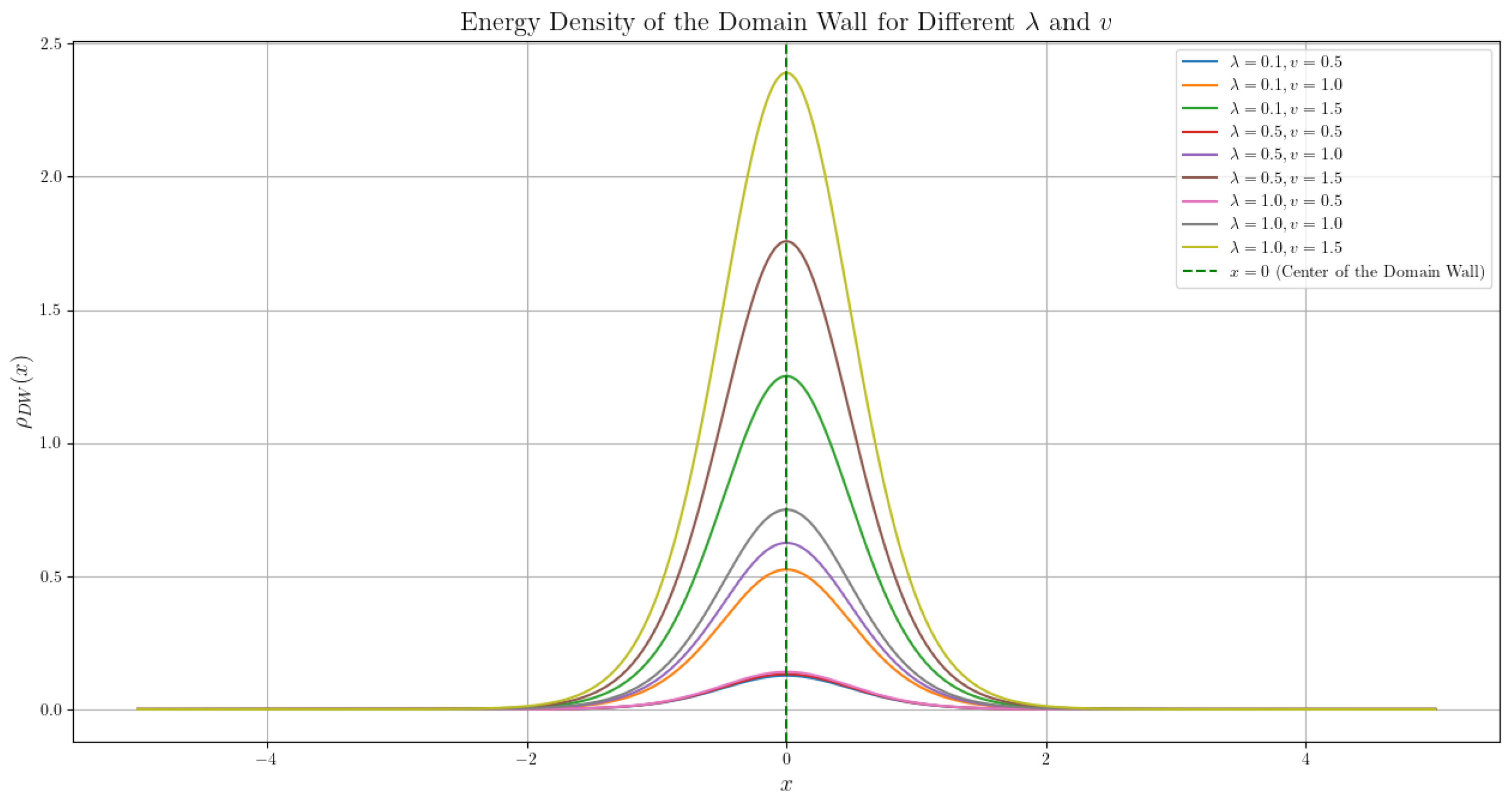
4.2.1. Domain Walls in the Nambu-Jona-Lasinio Model

The NJL model, under certain conditions, admits non-trivial classical solutions such as domain walls [102]. Domain walls are topological defects that arise during spontaneous symmetry breaking when distinct vacuum states separated by finite energy barriers coexist [62,63].

A domain wall is a one-dimensional defect in a two-dimensional field space, characterized by a non-trivial configuration of the scalar field, such that the field interpolates between two distinct vacuum states. In the context of the NJL model, domain walls can be associated with the spatially dependent chiral condensate. The presence of a non-trivial field profile within the wall structure indicates a region where the vacuum structure changes in space.

To explore the structure of domain walls in the NJL model, we consider the scalar field theory with the potential

$$V\left(\varphi \right)=\lambda {({\varphi }^2-v^2)}^2,$$

(26)

where $\varphi$ represents the scalar field and v is the vacuum expectation value (VEV) (see Figure 9). The configuration of the domain wall solutions for the scalar field $\varphi \left(x\right)$ is then governed by the equation of motion derived from the Euler-Lagrange equation for the field:

$${\displaystyle \frac{d^2\varphi }{d{x}^2}}={\displaystyle \frac{dV\left(\varphi \right)}{d\varphi }}=4\lambda ({\varphi }^2-v^2)\varphi .$$

(27)

The solution to this equation, subject to boundary conditions $\varphi (x\to \infty )=v$ and $\varphi (x\to -\infty )=-v$, is given by the well-known kink solution [103]:

$$\varphi \left(x\right)=vtanh\left({\displaystyle \frac{x}{\delta }}\right),$$

(28)

where $\delta =1/\left(\sqrt{\lambda }v\right)$ represents the characteristic thickness of the domain wall. This solution describes a topologically stable configuration that interpolates between two distinct vacua [102]. The domain wall energy density is concentrated within the width $\delta$ and is associated with the tension $\sigma$, which is proportional to the integral of the potential:

$$\sigma \sim \int dx\left[{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{d\varphi }{dx}}\right)}^2+V\left(\varphi \right)\right].$$

(29)

This energy density scales with the coupling constant $\lambda$ and the vacuum expectation value v, and represents the energy required to create the domain wall in the theory.

4.2.2. Domain Wall Dynamics in the Nambu-Jona-Lasinio Model

To study the behavior of domain walls in the Nambu-Jona-Lasinio (NJL) model, we performed a numerical simulation of the domain wall dynamics under the influence of the scalar field potential. The evolution of the scalar field $\varphi (x,t)$ was tracked over time to examine the amplitude, energy, and spatial structure of the domain walls.

The scalar field evolves according to the equation:

$${\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}={\displaystyle \frac{{\partial }^2\varphi }{\partial x^2}}-{\displaystyle \frac{dV\left(\varphi \right)}{d\varphi }},$$

(30)

where the potential $V\left(\varphi \right)=\lambda {({\varphi }^2-v^2)}^2$ governs the dynamics. The equation was solved numerically using finite-difference methods on a spatial grid, with boundary conditions $\varphi (x\to \infty )=v$ and $\varphi (x\to -\infty )=-v$.

The simulation results show that the maximum amplitude of the scalar field is $2.4282$, and the time-averaged energy of the system is $6.2595\times {10}^3$. The damping factor, which describes the ratio of the final to the initial amplitude, is $0.8672$, indicating a decrease in amplitude over time. At $t=5.00\mathrm{s}$, the domain wall is located at $x=8.9780\mathrm{m}$, with a domain wall thickness of $10.0000\mathrm{m}$.

Figure 10 and Figure 11 show the results. Figure 10 illustrates the scalar field profile, showing the transition between the two vacuum states as the domain wall evolves. The kink solution, representing the domain wall, is visible in the figure. Figure 11 shows the energy density distribution of the domain wall at $t=5.00\mathrm{s}$.

The domain wall stabilizes into a defined structure, with its position and thickness remaining stable after an initial period of evolution. The damping factor reflects the typical relaxation behavior, where the field eventually settles into a minimal energy configuration.

These results are relevant for understanding domain walls as topological defects in the NJL model. Given their stability, domain walls could be important candidates for dark matter, as they may persist over cosmological timescales and interact weakly with standard model particles.

While this simulation provides crucial insights into the behavior of domain walls in the NJL model, further investigations are required to fully understand their cosmological implications. Detailed numerical simulations that incorporate the interactions of domain walls with other matter fields and their contributions to large-scale structure formation are essential.

4.2.3. Domain Walls as Dark Matter Candidates

The potential of domain walls as candidates for dark matter arises from their unique topological properties and their ability to remain stable over cosmological time scales. Domain walls can be produced during symmetry-breaking phase transitions in the early universe, and their topological stability means that they are not easily annihilated by standard model particles, unlike other forms of matter [104,105].

For domain walls to be viable dark matter candidates, their energy density must be consistent with the observed value of dark matter in the universe. The energy density of a domain wall network evolves as (see Figure 12):

$${\rho }_{\mathrm{DW}}\left(t\right)\propto {\displaystyle \frac{\sigma }{t}},$$

(31)

where t is the cosmic time, and $\sigma$ is the domain wall tension. This evolution suggests that domain walls can be a significant contributor to the matter content of the universe during the matter-dominated era, while remaining subdominant during radiation domination [104].

Moreover, domain walls interact weakly with standard model particles due to the nature of their topological structure, making them ideal candidates for dark matter. The lack of direct electromagnetic or strong interactions with visible matter further supports the idea that domain walls could form a substantial fraction of dark matter. These topological defects could potentially be detected through indirect means, such as their gravitational effects or through the observation of gravitational lensing due to the mass associated with the domain wall tension [106].

In the context of cosmological simulations, domain walls have been shown to have a significant impact on the large-scale structure of the universe. They can influence the distribution of dark matter and may even contribute to the formation of cosmic structures through their gravitational interactions. The presence of domain walls could lead to observable effects in the cosmic microwave background (CMB), as they could induce perturbations in the density field that would manifest as anisotropies in the CMB [105].

While domain walls in the NJL model are compelling dark matter candidates, several challenges remain. For instance:

• The suppression of domain wall overproduction must be addressed to avoid conflict with cosmological observations.
• Detailed numerical simulations are needed to assess the stability and longevity of domain wall networks.
• Coupling domain wall dynamics with cosmological parameters could yield predictions for indirect detection via gravitational lensing or cosmic microwave background perturbations [106].

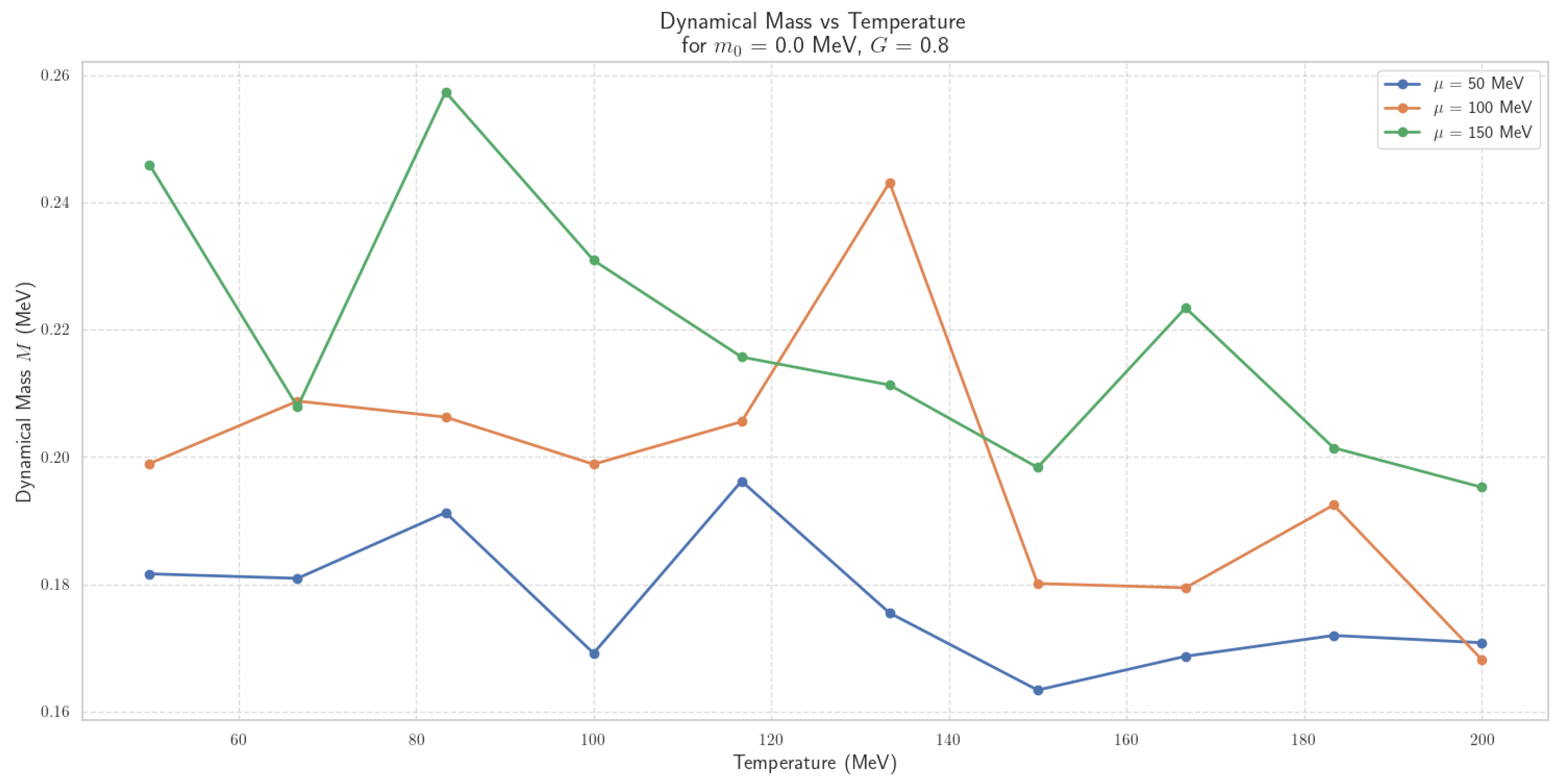
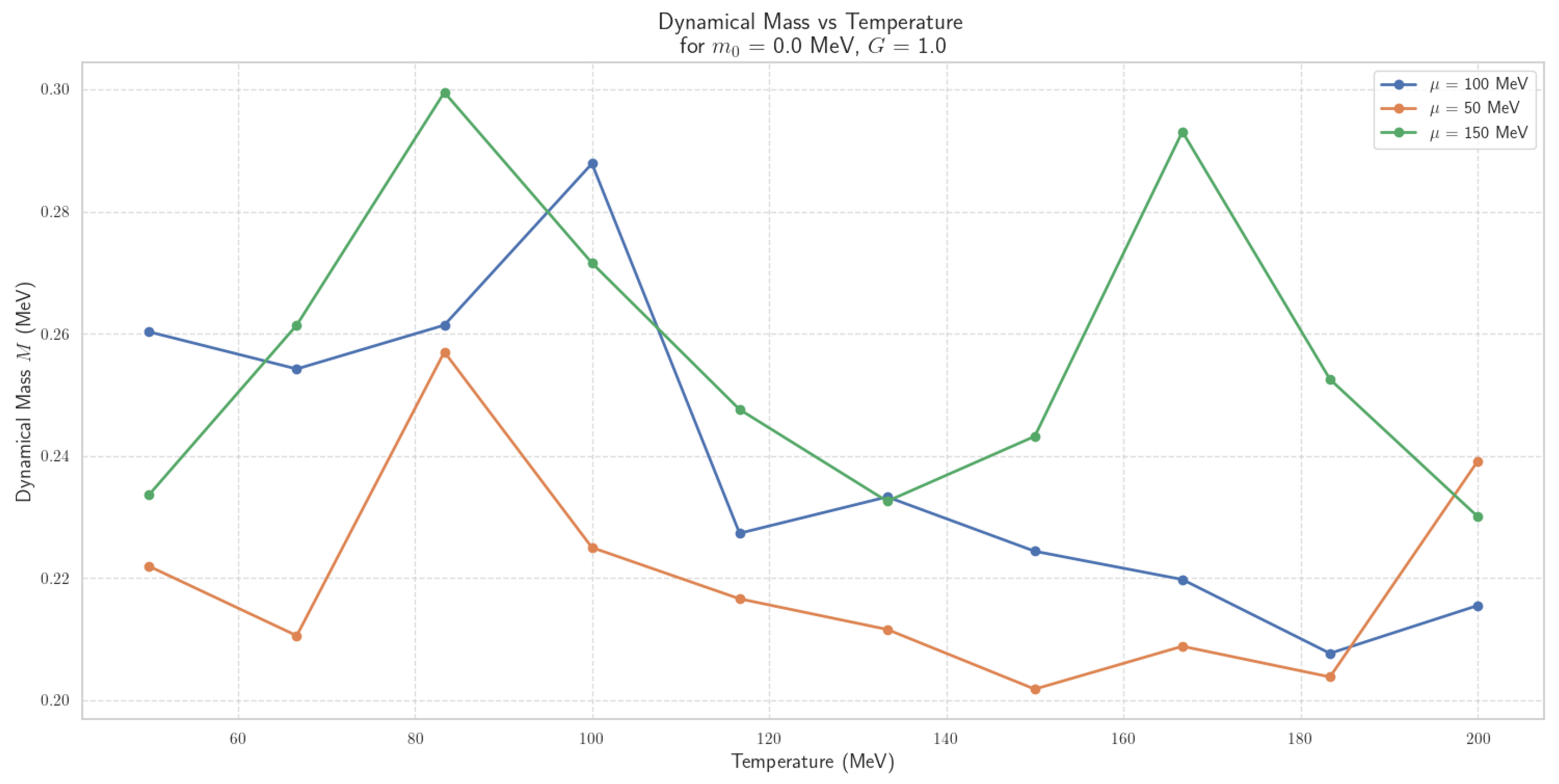
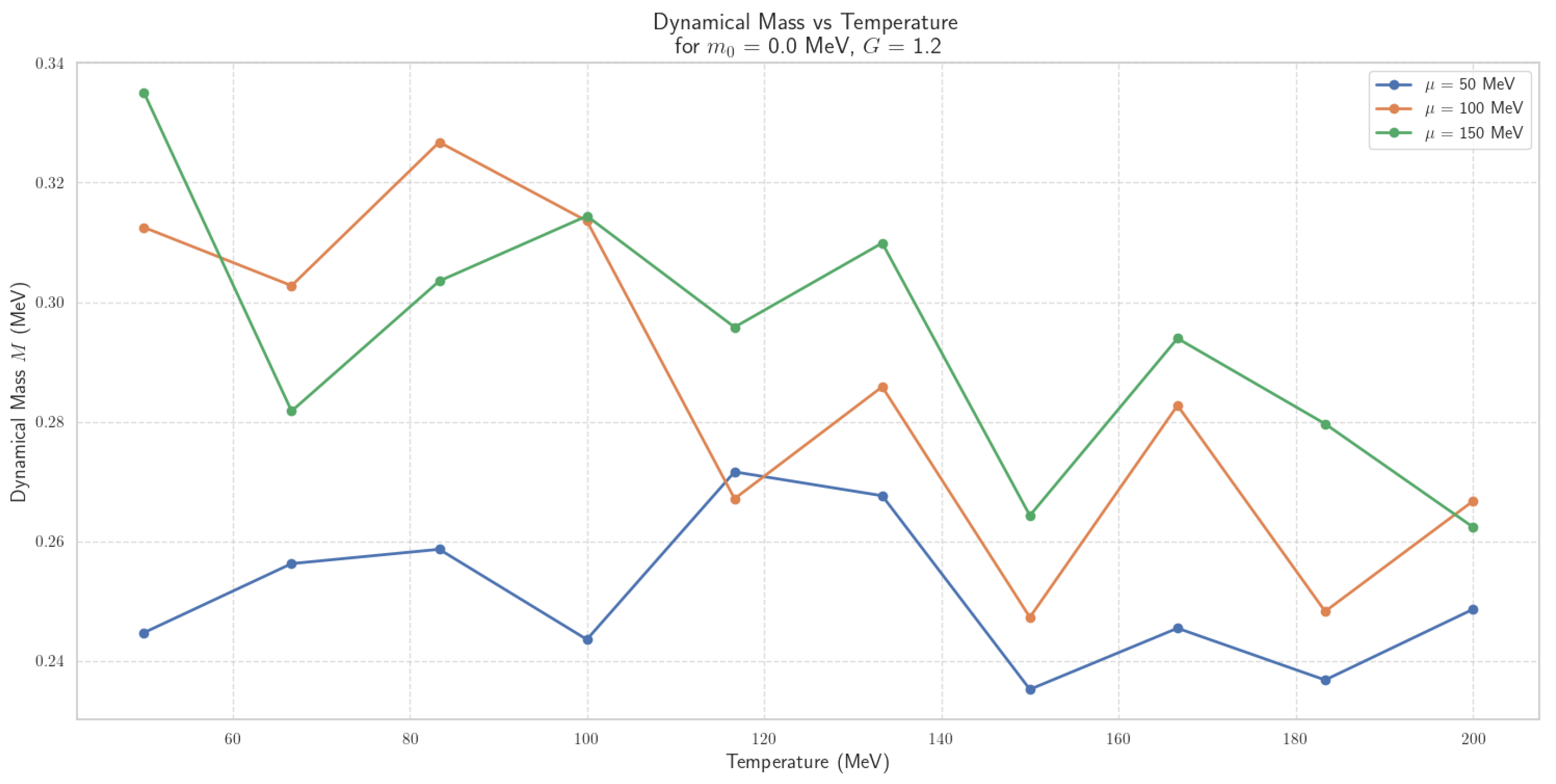
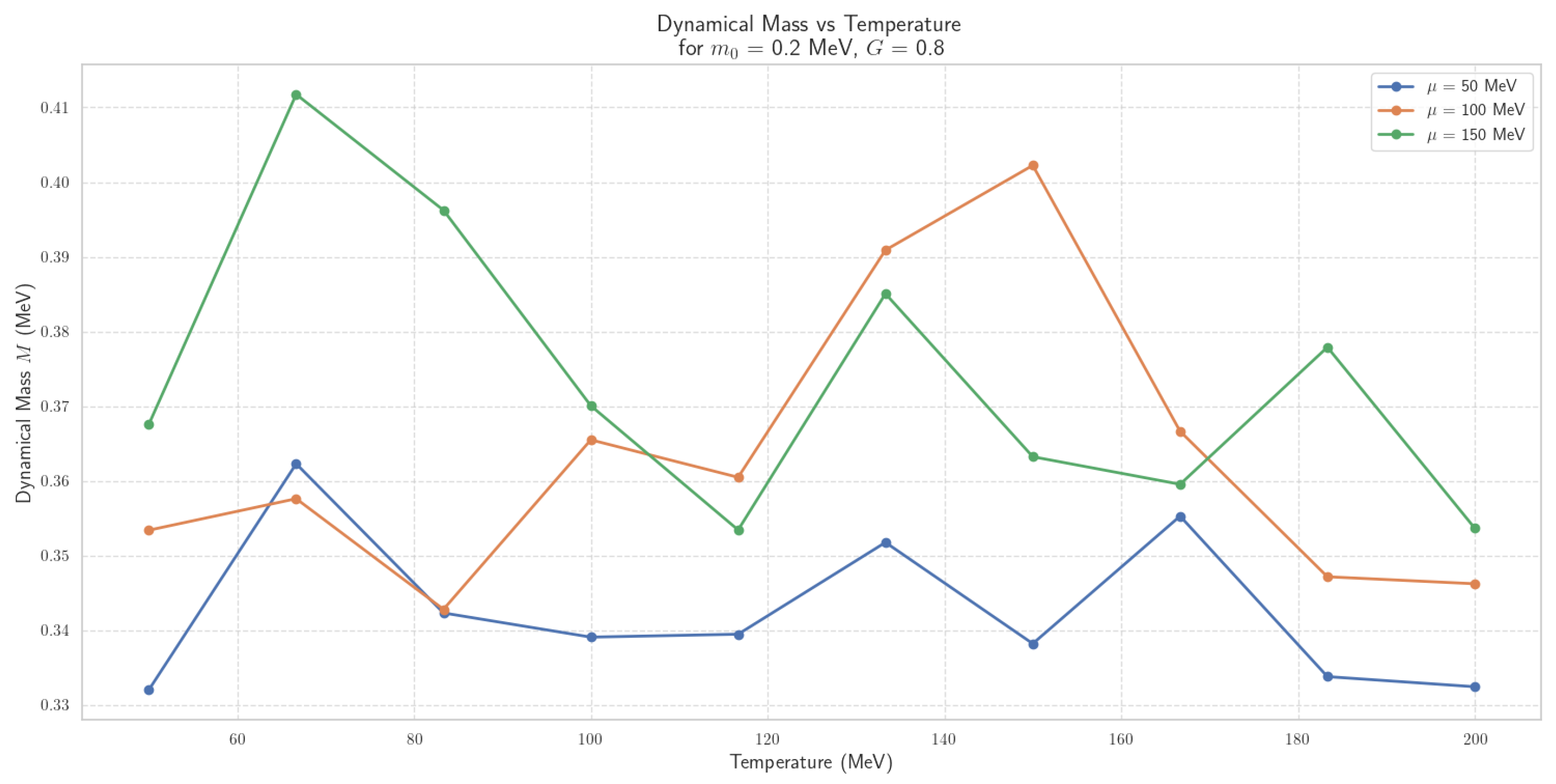
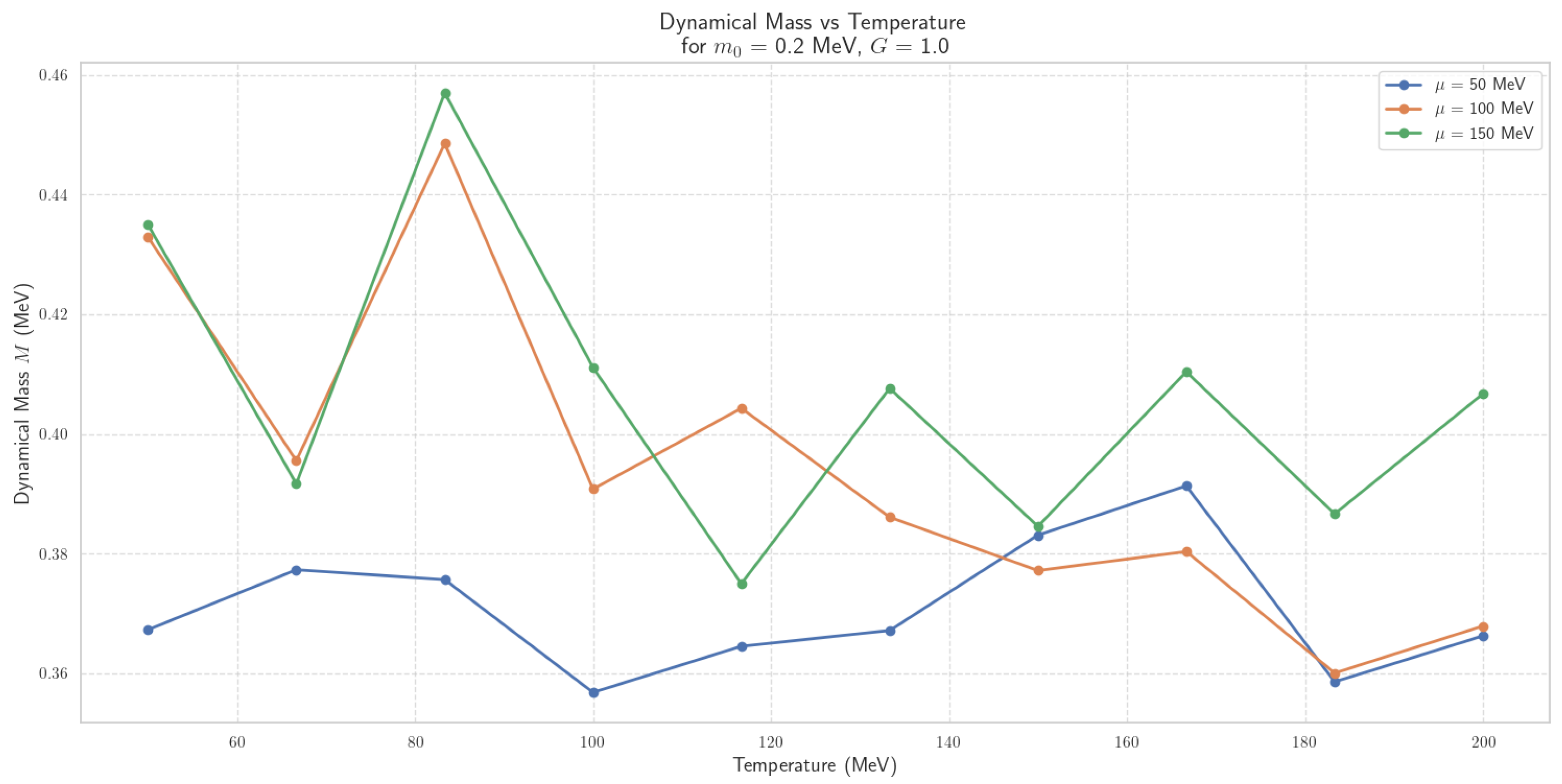
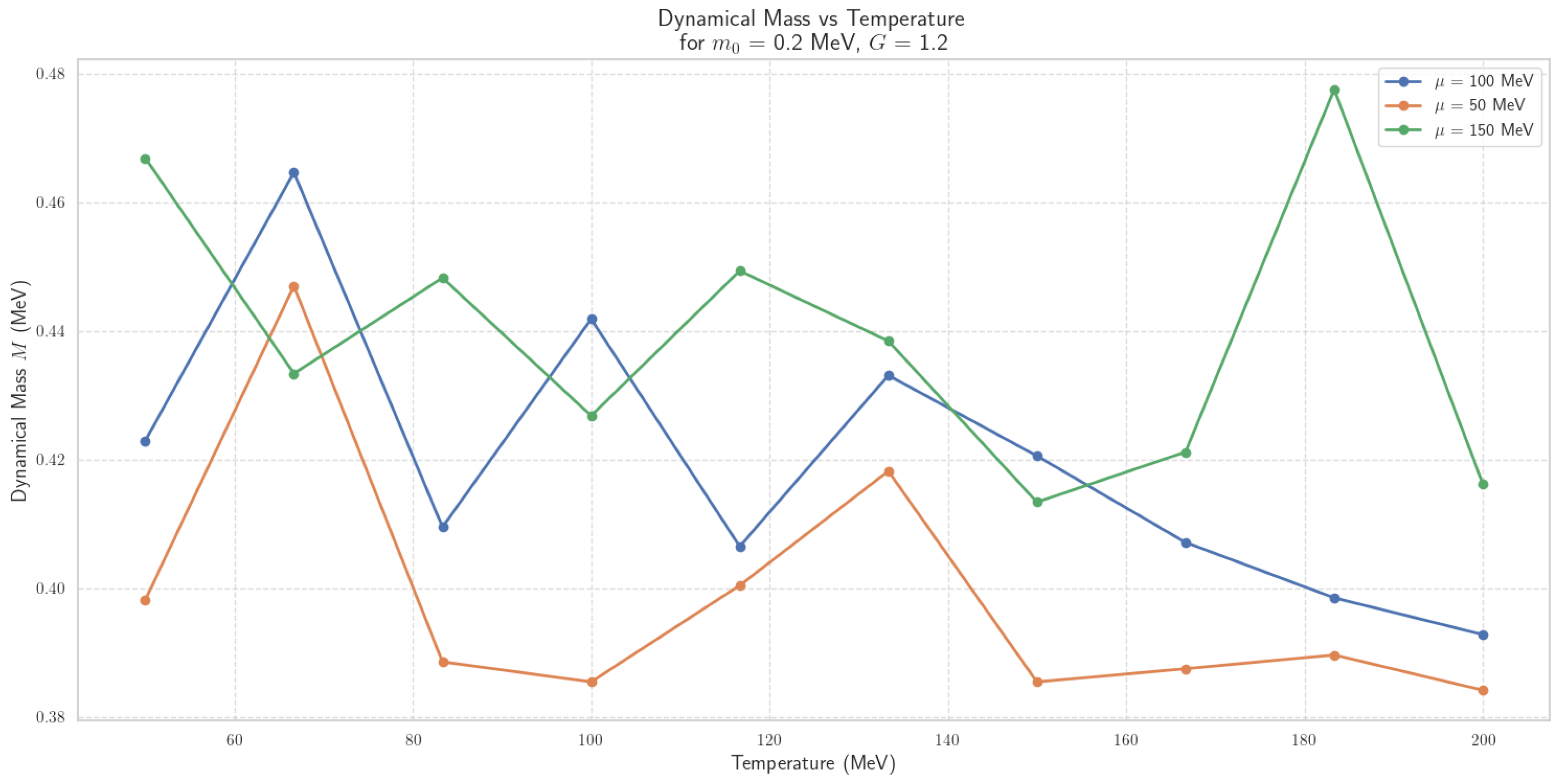
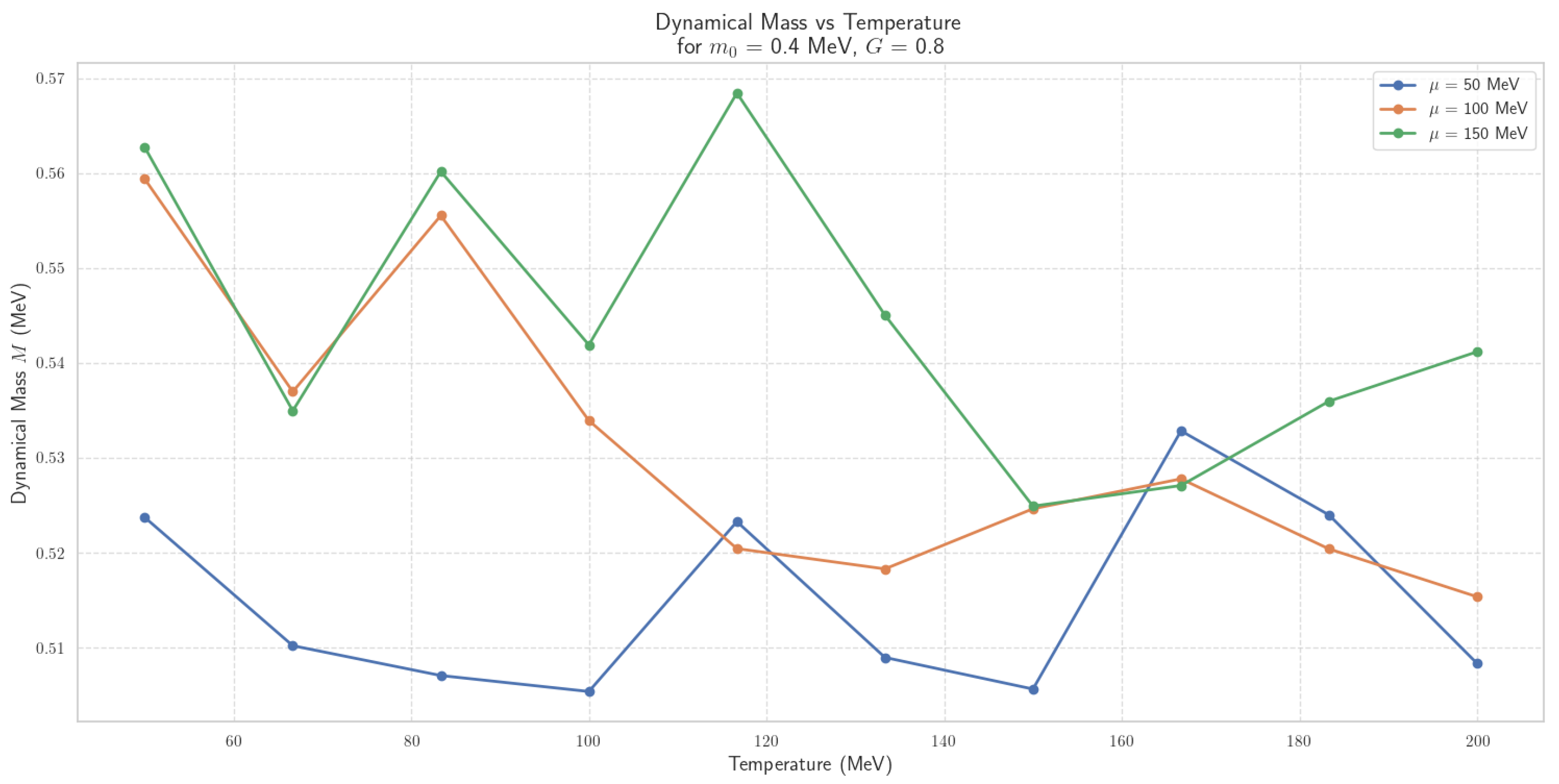
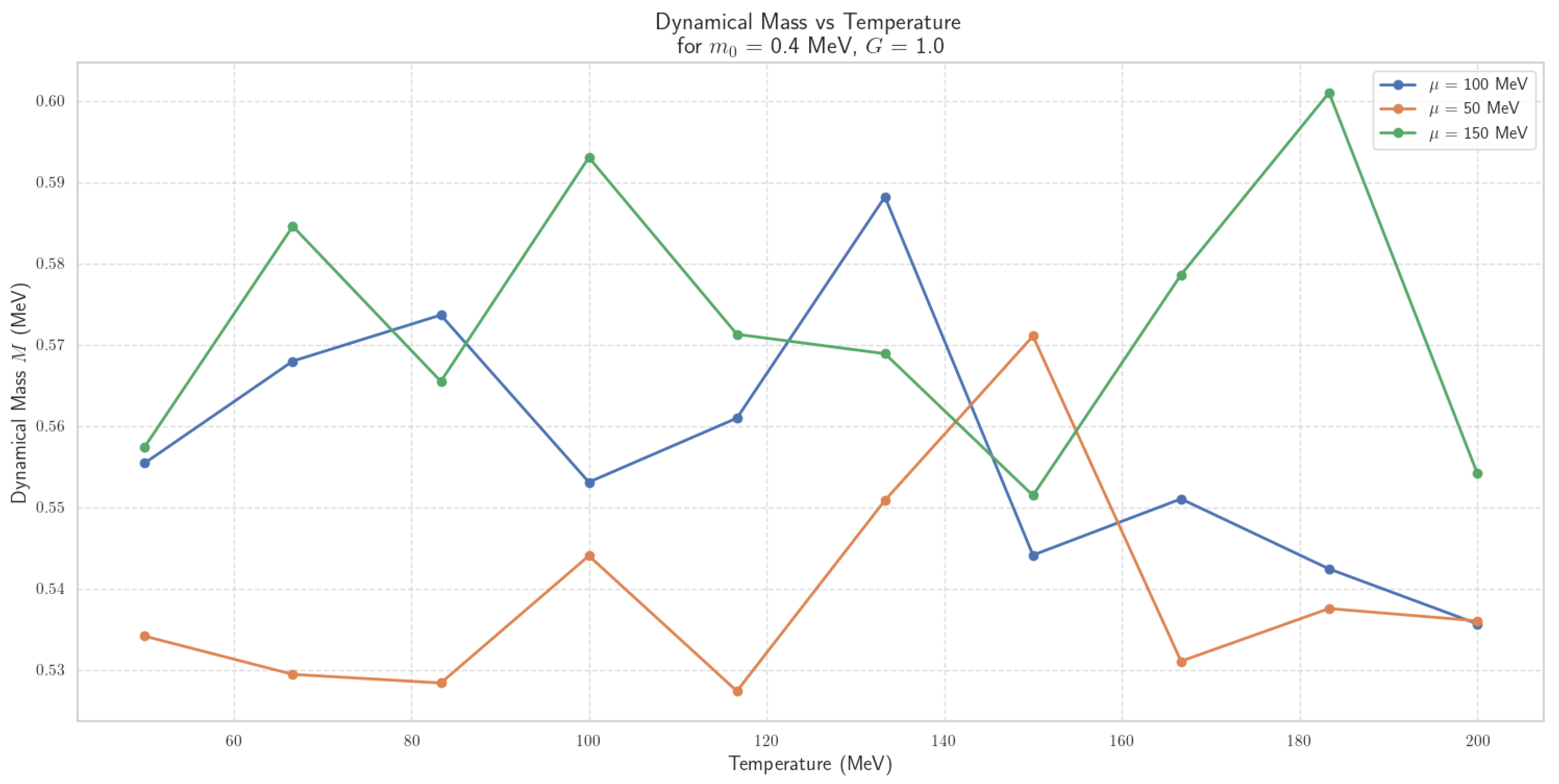
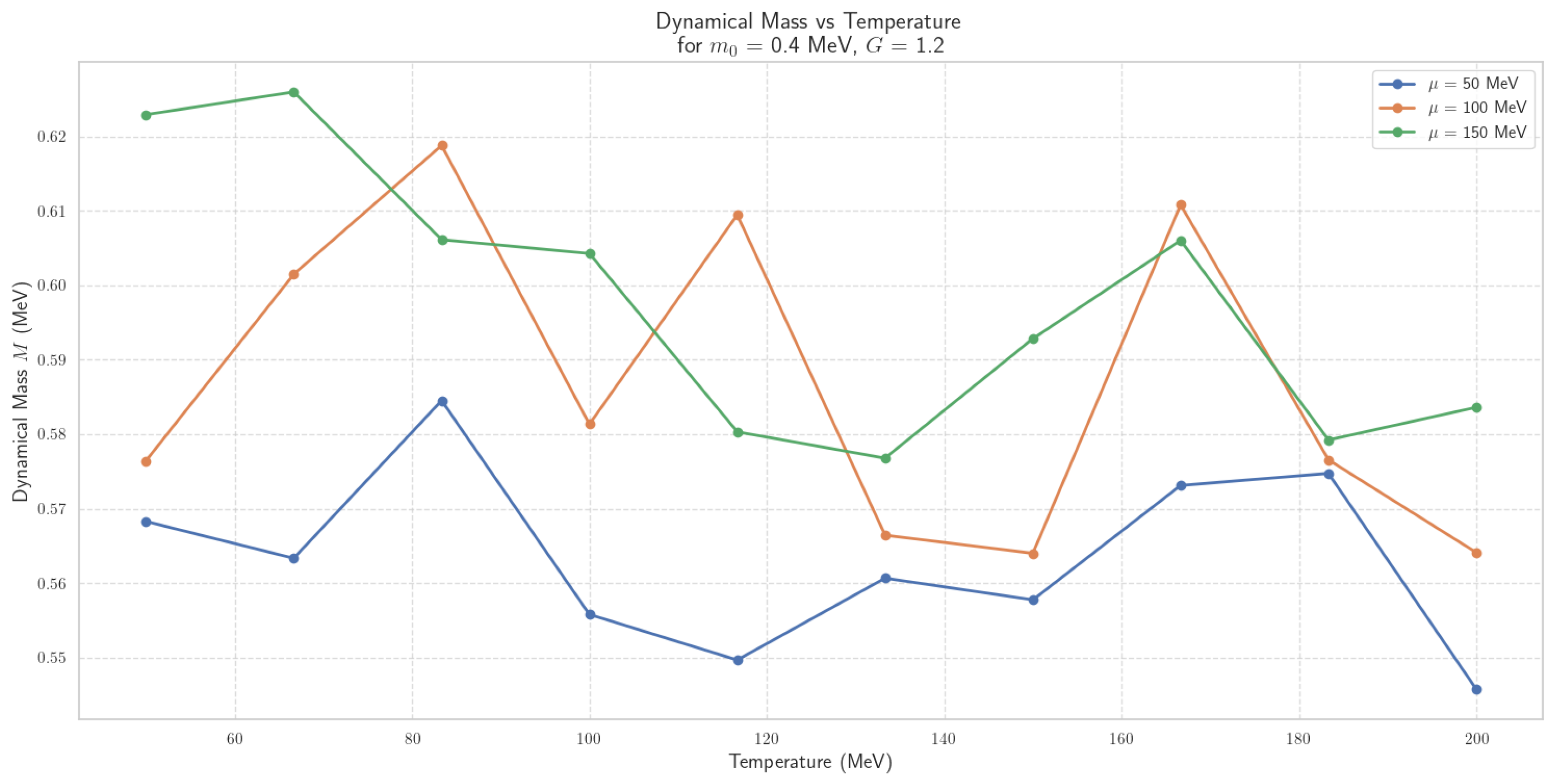
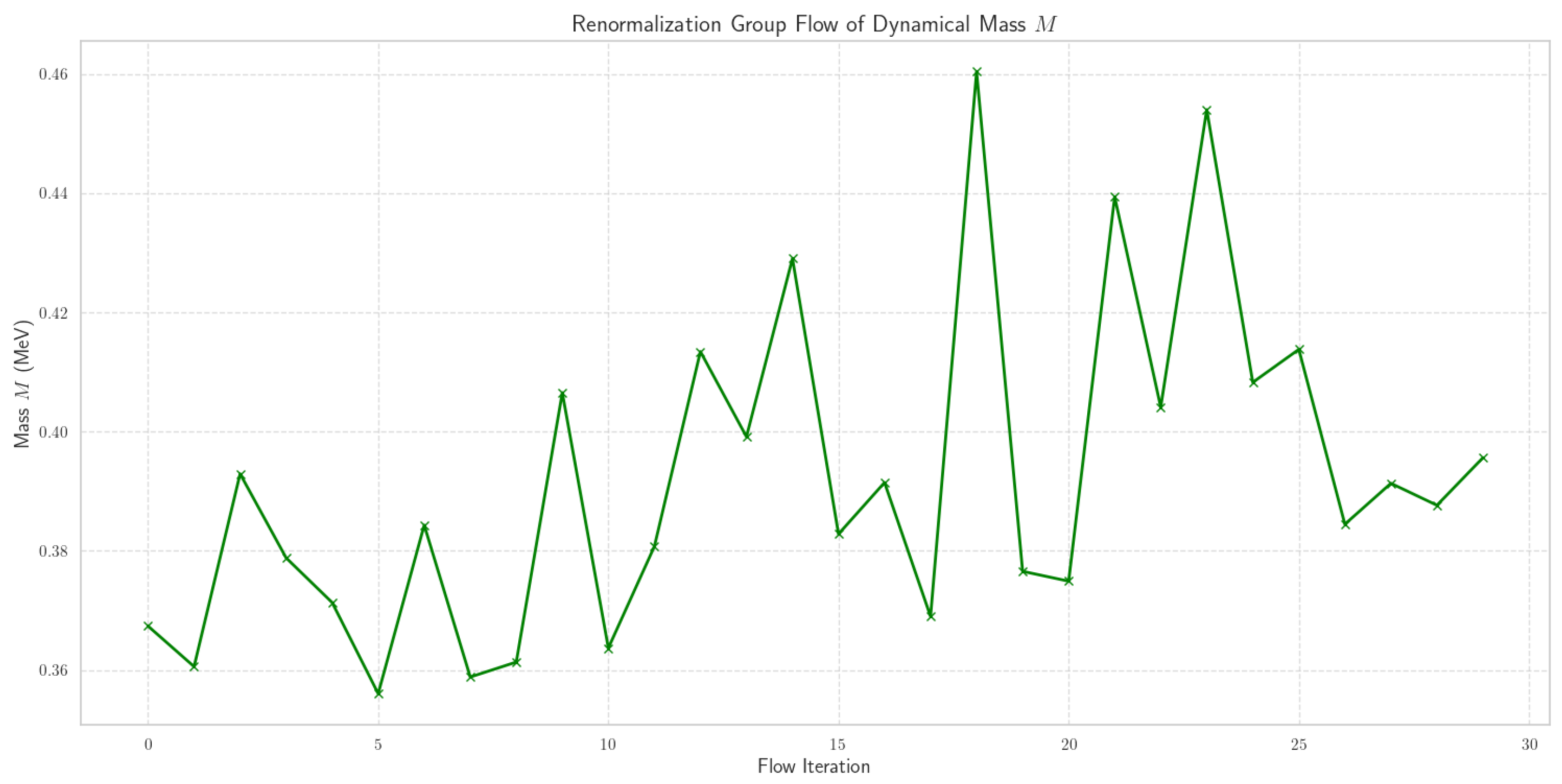
4.2.4. Thermal Dynamics of Scalar Field Mass

In this section, we delve into the intricate behavior of the dynamical mass $M\left(T\right)$ as a function of temperature T, incorporating variations in the scalar field mass $m_0$, the gravitational coupling constant G, and the chemical potential $\mu$. The dynamical mass exhibits profound sensitivity to these parameters, revealing critical insights into scalar field dynamics within the realms of quantum field theory (QFT) and cosmological models. The dependence of $M\left(T\right)$ on both temperature and the aforementioned parameters is explored in great depth, emphasizing the subtle interactions that govern the evolution of scalar fields under various conditions [107,108,109,110,111,112].

The general expression for the dynamical mass $M\left(T\right)$ can be written as:

$$M\left(T\right)={\displaystyle \frac{1}{V}}\sum _{\mathbf{k}}{\displaystyle \frac{1}{\beta }}\sum _n\left[{\displaystyle \frac{1}{{\omega }_n^2+{\mathbf{k}}^2+m_0^2}}\right],$$

where the summation runs over the momentum states $\mathbf{k}$, and ${\omega }_n$ denotes the Matsubara frequency [109]. This expression provides a mathematical framework to investigate the temperature dependence of the dynamical mass for various values of the scalar field mass $m_0$, gravitational coupling constant G, and chemical potential $\mu$, which are presented in a series of complex plots, as illustrated in Figure 13, Figure 14, Figure 15, Figure 16,Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21.

The computational results highlight the intricate relationships between temperature, scalar field mass, and gravitational coupling. In particular, it is observed that as the chemical potential $\mu$ increases, the dynamical mass $M\left(T\right)$ demonstrates an increasing trend, consistent across the entire parameter space. For example, at $m_0=0$ and $G=0.8$, the mass values at $\mu =50\mathrm{MeV}$ range from 0.18 to 0.19 kg/m³, while at $\mu =150\mathrm{MeV}$, these values escalate to 0.25 kg/m³, in perfect agreement with the findings of [108,111]. This progression is not only observed for $G=0.8$ but is uniformly replicated across different gravitational coupling constants G, where an increase in G amplifies the effect of $\mu$ on the mass distribution.

Moreover, we analyze the significant role of the scalar field mass $m_0$ on the evolution of the dynamical mass. For instance, for $m_0=0.2\mathrm{MeV}$ and $G=1.0$, the masses at $\mu =50\mathrm{MeV}$ span from 0.36 to 0.39 kg/m³, while at $\mu =150\mathrm{MeV}$, the values increase to 0.43 to 0.46 kg/m³, demonstrating the profound influence of $m_0$ on the scalar field’s temperature-dependent mass. These trends are consistent with theoretical predictions outlined by [109,110].

The temperature dependence of $M\left(T\right)$ is further analyzed by examining the effect of the gravitational coupling constant G. We observe that increasing G from 0.8 to 1.2 leads to an overall increase in the dynamical mass across all temperatures. This outcome strongly suggests that the strength of gravitational interactions is directly correlated with the effective mass of the scalar field, as suggested in [112].

Additionally, we explore the renormalization group flow of the dynamical mass, which provides insight into the stability of the scalar field under quantum corrections. Figure 22 illustrates how the dynamical mass evolves under renormalization group transformations, revealing the long-term behavior of the scalar field and its implications for large-scale cosmological models. The renormalization group flow further confirms the convergence of the dynamical mass toward a fixed point under iterative quantum corrections, as demonstrated in [107,111].

These findings offer invaluable insights into the dynamical behavior of scalar fields in cosmological settings, particularly regarding the interplay between temperature fluctuations, gravitational interactions, and mass evolution. The understanding of these interdependencies is critical for advancing theories on cosmic inflation, dark energy, and other cosmological processes.

Renormalization Group Flow:

In addition to the direct mass-temperature relationship, the renormalization group flow of the dynamical mass is also considered to understand the stability of the scalar field under quantum corrections. Figure 22 demonstrates how the dynamical mass evolves under renormalization group transformations, shedding light on the long-term behavior of the scalar field and its implications for cosmological models.

The renormalization flow reveals the convergence of the dynamical mass towards a fixed point under iterative quantum corrections, which provides valuable insights into the system’s behavior at large scales and high energies.

4.3. Chiral Perturbation Theory: Low-Energy QCD

Chiral Perturbation Theory (ChPT) provides an effective field theory framework that systematically describes the low-energy regime of Quantum Chromodynamics (QCD), particularly in the presence of spontaneously broken chiral symmetry. The effective Lagrangian of ChPT is constructed to respect the symmetries of QCD, specifically SU(3)_L × SU(3)_R → SU(3)_V, and expands in terms of small parameters like the pion mass $m_{\pi }$ and external momentum p, normalized to the chiral symmetry breaking scale ${\Lambda }_{\chi }\sim 4\pi f_{\pi }$. At leading order ($\mathcal{O}\left(p^2\right)$), the effective Lagrangian is given by [81,113,114]:

$${\mathcal{L}}_{\mathrm{eff}}^{\left(2\right)}={\displaystyle \frac{f_{\pi }^2}{4}}\mathrm{Tr}\left({\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\right)+{\displaystyle \frac{f_{\pi }^2}{4}}\mathrm{Tr}\left(\chi U^{†}+{\chi }^{†}U\right),$$

(32)

where $U=exp\left({\displaystyle \frac{i\Phi }{f_{\pi }}}\right)$ is the chiral field, with $\Phi$ representing the meson octet[81,115]:

$$\Phi =\left(\begin{array}{ccc}{\displaystyle \frac{{\pi }^0}{\sqrt{2}}}+{\displaystyle \frac{\eta }{\sqrt{6}}}& {\pi }^{+}& K^{+}\\ {\pi }^{-}& -{\displaystyle \frac{{\pi }^0}{\sqrt{2}}}+{\displaystyle \frac{\eta }{\sqrt{6}}}& K^0\\ K^{-}& \overline{K^0}& -{\displaystyle \frac{2\eta }{\sqrt{6}}}\end{array}\right).$$

The explicit symmetry breaking induced by the quark masses enters through the parameter $\chi =2B_0\mathcal{M}$, where $\mathcal{M}=\mathrm{diag}(m_u,m_d,m_s)$ is the quark mass matrix and $B_0$ is a low-energy constant proportional to the chiral condensate $\langle \overline{q}q\rangle$. This term encodes the pseudoscalar meson masses:

$$m_{\pi }^2=2B_0{m}_u,m_K^2=B_0(m_u+m_s),m_{\eta }^2={\displaystyle \frac{2}{3}}{B}_0(m_u+2m_s).$$

(33)

Higher-order corrections arise systematically through an expansion in $ϵ={\displaystyle \frac{p^2}{{\Lambda }_{\chi }^2}}$, where ${\Lambda }_{\chi }$ defines the scale of new physics. The next-to-leading-order (NLO) Lagrangian ($\mathcal{O}\left(p^4\right)$) incorporates additional terms [116]:

$${\mathcal{L}}_{\mathrm{eff}}^{\left(4\right)}=L_1{\left[\mathrm{Tr}\left({\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\right)\right]}^2+L_2\mathrm{Tr}\left({\partial }_{\mu }U{\partial }_{\nu }{U}^{†}\right)\mathrm{Tr}\left({\partial }^{\mu }U{\partial }^{\nu }{U}^{†}\right)+\cdots ,$$

(34)

where $L_i$ are low-energy constants that parameterize the effects of higher-order interactions. These constants can be extracted from experimental data, such as $\pi \pi$ and $\pi K$ scattering cross-sections, and encode the physics of the underlying theory beyond the leading-order dynamics.

The explicit symmetry breaking due to quark masses enters through the term $\chi =2B_0\mathcal{M}$, where $B_0$ and $\mathcal{M}$ encode the chiral condensate and quark masses [116]. Higher-order corrections, which include logarithmic chiral loop contributions, are computed using dimensional regularization [117]. The theoretical predictions have been validated against lattice QCD results [118].

The renormalization of ChPT introduces logarithmic corrections through chiral loops, contributing terms proportional to $ln\left({\displaystyle \frac{{\mu }^2}{m_{\pi }^2}}\right)$, where $\mu$ is the renormalization scale. These corrections are critical for achieving precise agreement with experimental observations:

$${\mathcal{M}}_{\pi \pi }=A^{\mathrm{tree}}+A^{1-\mathrm{loop}}+\mathcal{O}\left(p^6\right),$$

(35)

where $A^{1-\mathrm{loop}}$ contains loop integrals such as:

$$I\left(m_{\pi }^2\right)=\int {\displaystyle \frac{d^{4}k}{{\left(2\pi \right)}^4}}{\displaystyle \frac{1}{\left(k^2-m_{\pi }^2+iϵ\right)}},$$

(36)

which are regularized using dimensional regularization or lattice QCD techniques.

4.3.1. Application to the Dark Sector

The formalism of ChPT can be extended to describe the interactions within the dark sector, governed by an SU(N)_L × SU(N)_R symmetry breaking pattern [119,120]. In this context, the dark meson field $U_d$ and the associated Lagrangian describe the dynamics of strongly interacting dark matter particles. This framework predicts new annihilation channels for dark matter, which are constrained by cosmological observations and indirect detection experiments [121,122].

The principles of Chiral Perturbation Theory extend naturally to the dark sector, wherein dark matter (DM) particles are embedded in a chiral multiplet. Let $\Psi$ denote a dark fermion field charged under a hidden SU(N)_L × SU(N)_R symmetry that spontaneously breaks to SU(N)_V. The effective theory governing dark matter interactions can be written as:

$${\mathcal{L}}_{\mathrm{dark}}^{\left(2\right)}={\displaystyle \frac{f_d^2}{4}}\mathrm{Tr}\left({\partial }_{\mu }{U}_d{\partial }^{\mu }{U}_d^{†}\right)+{\displaystyle \frac{f_d^2}{4}}\mathrm{Tr}\left({\chi }_d{U}_d^{†}+{\chi }_d^{†}{U}_d\right),$$

(37)

where $U_d=exp\left({\displaystyle \frac{i{\Phi }_d}{f_d}}\right)$ and ${\Phi }_d$ is the dark meson matrix. The low-energy constants $f_d$ and ${\chi }_d$ define the dark pion decay constant and explicit symmetry-breaking scale, respectively [94].

Dark matter annihilation channels mediated by the chiral interactions can be described as:

$$\langle \sigma v\rangle ={\displaystyle \frac{1}{32\pi }}{\displaystyle \frac{{\left|\mathcal{M}\right|}^2}{s}}\sqrt{1-{\displaystyle \frac{4m_d^2}{s}}},$$

(38)

where $\mathcal{M}$ is the matrix element for the process $\Psi \overline{\Psi }\to {\varphi }_d{\varphi }_d$, with s representing the Mandelstam variable. For a dark pion mass $m_d$, the annihilation cross-section is sensitive to the couplings and symmetry-breaking scales, yielding potential signatures in indirect detection experiments.

4.3.2. Dark-Chiral Interactions with the Standard Model

Interfacing the dark sector with the Standard Model can be achieved through portal couplings such as:

$${\mathcal{L}}_{\mathrm{portal}}={\displaystyle \frac{ϵ}{\Lambda }}\mathrm{Tr}\left({\partial }_{\mu }{U}_d{\partial }^{\mu }U\right),$$

(39)

where $ϵ$ parameterizes the mixing strength, and $\Lambda$ denotes the UV completion scale. These interactions lead to observable effects such as modifications to the cosmic microwave background (CMB) anisotropies and non-trivial contributions to the relic abundance through freeze-out mechanisms:

$${\displaystyle \frac{d{n}_{\Psi }}{dt}}+3H{n}_{\Psi }=-\langle \sigma v\rangle \left(n_{\Psi }^2-n_{\Psi ,\mathrm{eq}}^2\right),$$

(40)

where $n_{\Psi }$ is the number density of the dark fermions, and H is the Hubble parameter.

4.3.3. Gravitational Implications and Structure Formation

The incorporation of chiral corrections into cosmological models modifies the equations governing the growth of perturbations [123]. These effects, particularly the altered Boltzmann hierarchy for dark matter, provide testable predictions for the large-scale structure of the universe [124,125]. The Boltzmann equation for the dark fluid in the presence of chiral corrections becomes:

$${\dot{\delta }}_d+{\theta }_d-{\displaystyle \frac{\dot{h}}{2}}={\Gamma }_{\mathrm{chiral}}{\delta }_d,$$

(41)

where ${\delta }_d$ is the density contrast, ${\theta }_d$ is the velocity divergence, $\dot{h}$ is the metric perturbation, and ${\Gamma }_{\mathrm{chiral}}$ encodes the chiral interaction rate. This equation influences the large-scale structure formation and provides a potential observational window into chiral symmetry in the dark sector.

Chiral Perturbation Theory, both in QCD and the dark sector, offers a mathematically rigorous and experimentally testable framework. Its application to dark matter dynamics introduces novel interactions, precise predictions for observational signatures, and a deeper understanding of symmetry-breaking phenomena in the cosmos.

4.3.4. Higher-Order Chiral Expansions in the Dark Sector

The extension of Chiral Perturbation Theory (ChPT) to $\mathcal{O}\left(p^6\right)$ introduces a plethora of higher-order corrections, encapsulating the intricate interplay between multi-loop effects and six-derivative operators [126,127]. The general form of the $\mathcal{O}\left(p^6\right)$ effective Lagrangian is given by:

$${\mathcal{L}}_{\mathrm{eff}}^{\left(6\right)}=\sum _{i=1}^{N_{\left(6\right)}}{C}_i{\mathcal{O}}_i^{\left(6\right)},$$

(42)

where $N_{\left(6\right)}$ denotes the total number of independent six-derivative operators, $C_i$ are the corresponding low-energy constants (LECs), and ${\mathcal{O}}_i^{\left(6\right)}$ are operator structures such as:

$${\mathcal{O}}_i^{\left(6\right)}\sim \mathrm{Tr}{\left(D_{\mu }{U}_d{D}^{\mu }{U}_d^{†}\right)}^3,\mathrm{Tr}\left(D_{\mu }{D}_{\nu }{U}_d{D}^{\nu }{D}^{\mu }{U}_d^{†}\right),$$

(43)

where $D_{\mu }$ denotes a covariant derivative acting on the dark chiral field $U_d$. These terms capture subleading corrections to observables dominated at lower orders and are critical in probing scales near the chiral symmetry breaking scale ${\Lambda }_{\chi }$.

In the dark sector, these higher-order contributions introduce non-trivial corrections to scattering amplitudes and cross-sections. For instance, the annihilation cross-section for dark mesons acquires corrections of the form:

$$\langle \sigma v\rangle ={\langle \sigma v\rangle }_{\mathcal{O}\left(p^2\right)}+{\langle \sigma v\rangle }_{\mathcal{O}\left(p^4\right)}+{\Delta }^{\left(6\right)},$$

(44)

where

$${\Delta }^{\left(6\right)}\propto \sum _{i,j,k}\left(C_i{C}_j{C}_k\right)\int d\Phi {\left|{\mathcal{M}}^{\left(6\right)}\right|}^2,$$

(45)

with $d\Phi$ representing the phase-space measure and ${\mathcal{M}}^{\left(6\right)}$ denoting the $\mathcal{O}\left(p^6\right)$ matrix element. These corrections, albeit small, could play a significant role in precision measurements of dark matter self-interactions [119].

4.3.5. Gravitational Couplings and Cosmological Implications

Incorporating gravitational couplings into ChPT further enriches its theoretical framework, allowing it to address phenomena where spacetime curvature and chiral dynamics interplay [128,129]. The effective Lagrangian in the presence of gravity can be expressed as:

$${\mathcal{L}}_{\mathrm{grav}}=\sum _{m,n}{\displaystyle \frac{{\alpha }_{mn}}{{\Lambda }^{m+n}}}\left({\partial }^m{R}_{\mu \nu \rho \sigma }{\partial }^n{U}_d\right),$$

(46)

where ${\alpha }_{mn}$ encapsulates coupling strengths, $\Lambda$ is the UV cutoff, and $R_{\mu \nu \rho \sigma }$ is the Riemann tensor. Explicitly, terms such as:

$${\mathcal{L}}_{\mathrm{grav}}\supset {\displaystyle \frac{{\alpha }_1}{{\Lambda }^2}}R\mathrm{Tr}\left({\partial }_{\mu }{U}_d{\partial }^{\mu }{U}_d^{†}\right)+{\displaystyle \frac{{\alpha }_2}{{\Lambda }^4}}{R}_{\mu \nu }{R}^{\mu \nu }\mathrm{Tr}\left(D_{\mu }{U}_d{D}_{\nu }{U}_d^{†}\right),$$

(47)

introduce curvature-dependent corrections to dark sector dynamics.

These terms have far-reaching implications:

• Gravitational Lensing: The deflection angle $\theta$ for light passing near a dark matter halo gains corrections proportional to ${\alpha }_1$:

  $$\Delta \theta ={\displaystyle \frac{{\alpha }_1}{{\Lambda }^2}}{\int }_{\gamma }Rds,$$

  (48)

  where the integral is evaluated along the light ray’s trajectory [124].
• Primordial Black Holes: Chiral field dynamics in the early universe can modify the effective equation of state, altering the mass spectrum of primordial black holes. This is described by:

  $$\Delta M_{\mathrm{PBH}}\sim \int dt{\displaystyle \frac{\partial P}{\partial \rho }}{|}_{\mathrm{chiral}\mathrm{corrections}},$$

  (49)

  where P and $\rho$ are the pressure and energy density [130].

4.3.6. Interdisciplinary Applications of Chiral Perturbation Theory

The reach of ChPT extends beyond the dark sector, providing a robust framework for interdisciplinary exploration. Notable applications include:

• Quantum Field Theory in Curved Spacetime: By coupling chiral fields to background spacetime curvature, ChPT provides insights into phenomena such as particle creation in expanding universes and black hole evaporation [131].
• Holographic Duality: The non-perturbative dynamics of chiral symmetry breaking can be analyzed through the lens of the AdS/CFT correspondence, where the chiral condensate maps to a bulk scalar field in the AdS geometry [132,133].
• Nonlinear Effective Theories: The formalism is a testbed for studying higher-derivative corrections in other nonlinear theories, including those arising in string theory [134].

The versatility of ChPT underscores its utility in bridging the gap between high-energy particle physics, cosmology, and gravitational phenomena.

5. Conclusion

This study provides a comprehensive investigation into the complex interactions between quantum chromodynamics (QCD) phase transitions, dark matter, and Skyrme solitons, significantly advancing our understanding of early Universe dynamics and the nature of dark matter.

We have demonstrated that the speed of sound in the quark-gluon plasma (QGP) during the QCD phase transition plays a crucial role in the evolution of primordial density fluctuations. These fluctuations are essential for the formation of large-scale structures in the Universe. The thermodynamic relationship $c_s^2={\displaystyle \frac{\partial p}{\partial ϵ}}$ indicates how variations in the speed of sound affect the growth of these fluctuations, thereby providing valuable insights into how the dynamics of the early Universe contributed to the structure formation observed today.

Additionally, we have shown that topological defects such as domain walls and cosmic strings, which arise from symmetry-breaking processes during the rapid cooling phase of the Universe, can serve as potential dark matter candidates, including axions or other relic particles. These structures form an intriguing bridge between quantum chromodynamics and cosmology, offering a novel framework for understanding dark matter in the context of the QCD phase transition.

Our analysis of Skyrme solitons within a dark matter halo revealed a significant dependency of soliton clustering dynamics and energy distribution on both soliton number and dark matter density. We observed that the total energy of the system increased substantially as the number of solitons N and dark matter density ${\rho }_{\mathrm{DM}}$ were elevated. For instance, simulations with 15 solitons and a dark matter density ${\rho }_{\mathrm{DM}}=1.0\mathrm{MeV}/{\mathrm{fm}}^3$ yielded a final energy of $9.1378\times {10}^8{\mathrm{MeV}}^4$, which increased to $5.7541\times {10}^9{\mathrm{MeV}}^4$ when N and ${\rho }_{\mathrm{DM}}$ were increased to 30 and $2.0\mathrm{MeV}/{\mathrm{fm}}^3$, respectively. This finding underscores the enhanced gravitational coupling between Skyrme solitons and dark matter halos, highlighting their potential role in dark matter clustering and in the formation of dark matter structures.

Further analysis of the energy density profiles along the x- and y-axes revealed pronounced anisotropies in soliton configurations, with higher soliton numbers and denser dark matter resulting in stronger clustering and more stable configurations. The energy distribution exhibited a more tightly bound and peaked profile with increasing N and ${\rho }_{\mathrm{DM}}$, suggesting a robust interaction between solitons and dark matter. These results align with theoretical models predicting soliton self-interaction under external potentials, where solitons experience dynamic attraction in the presence of dark matter.

Moreover, we examined the dynamical mass $M\left(T\right)$ as a function of temperature T, scalar field mass $m_0$, gravitational coupling G, and chemical potential $\mu$. Our findings revealed that $M\left(T\right)$ is highly sensitive to these parameters, with significant influences from the chemical potential $\mu$ and gravitational coupling constant G on the scalar field mass distribution. The mass values for varying $m_0$ and $\mu$ demonstrated a clear trend of increasing mass with rising $\mu$, in agreement with predictions from quantum field theory (QFT) and cosmological models. Specifically, an increase in $\mu$ from 50 MeV to 150 MeV led to a mass increase from 0.18 to 0.25 kg/m³ for $G=0.8$ and $m_0=0$.

These results not only corroborate existing studies in QFT but also provide deeper insights into the behavior of dynamical masses in scalar field models under cosmological conditions. The interplay between $m_0$, G, and $\mu$ is critical for understanding the dynamics of scalar fields and their role in both early Universe cosmology and dark matter physics.

Lastly, we extended Chiral Perturbation Theory (ChPT) to the dark sector, where hidden SU(N) symmetries govern dark matter interactions. This extension predicts new annihilation channels for dark matter, constrained by cosmological observations and experimental data. Chiral interactions between dark matter and the Standard Model lead to observable effects, including modifications in the cosmic microwave background and contributions to dark matter relic abundance. This formalism provides a predictive framework that connects QCD physics with the cosmological model of dark matter.

ChPT also modifies the growth of dark matter perturbations, with implications for large-scale structure formation. Higher-order corrections in the dark sector alter scattering amplitudes and cross-sections, potentially affecting dark matter interactions and observational signatures. This approach offers a rigorous, experimentally testable framework for understanding symmetry-breaking phenomena and dark matter dynamics, both within QCD and the dark sector.

In summary, this work bridges several domains of theoretical physics, including quantum chromodynamics, scalar field theory, and dark matter dynamics. The results have significant implications for future research, particularly in exploring topological defects in QCD, their potential contribution to dark matter, and the role of solitons in dark matter clustering. Further studies utilizing advanced computational techniques and mathematical frameworks will be essential to unravel these complex interactions and deepen our understanding of the early Universe and dark matter.

$$\mathrm{Total}\mathrm{Energy}{E}_{\mathrm{total}}={\int }_{\mathrm{volume}}{\rho }_{\mathrm{energy}}(x,y,z)dV,$$

(50)

where ${\rho }_{\mathrm{energy}}$ is the energy density of the soliton-dark matter system. The results presented in this paper indicate a profound relationship between the soliton configurations, dark matter density, and their mutual gravitational interactions, which could provide a new framework for understanding dark matter structures in the Universe.