Submitted:
02 April 2024
Posted:
03 April 2024
Read the latest preprint version here
Abstract
Keywords:
1. Prologue

2. Summary
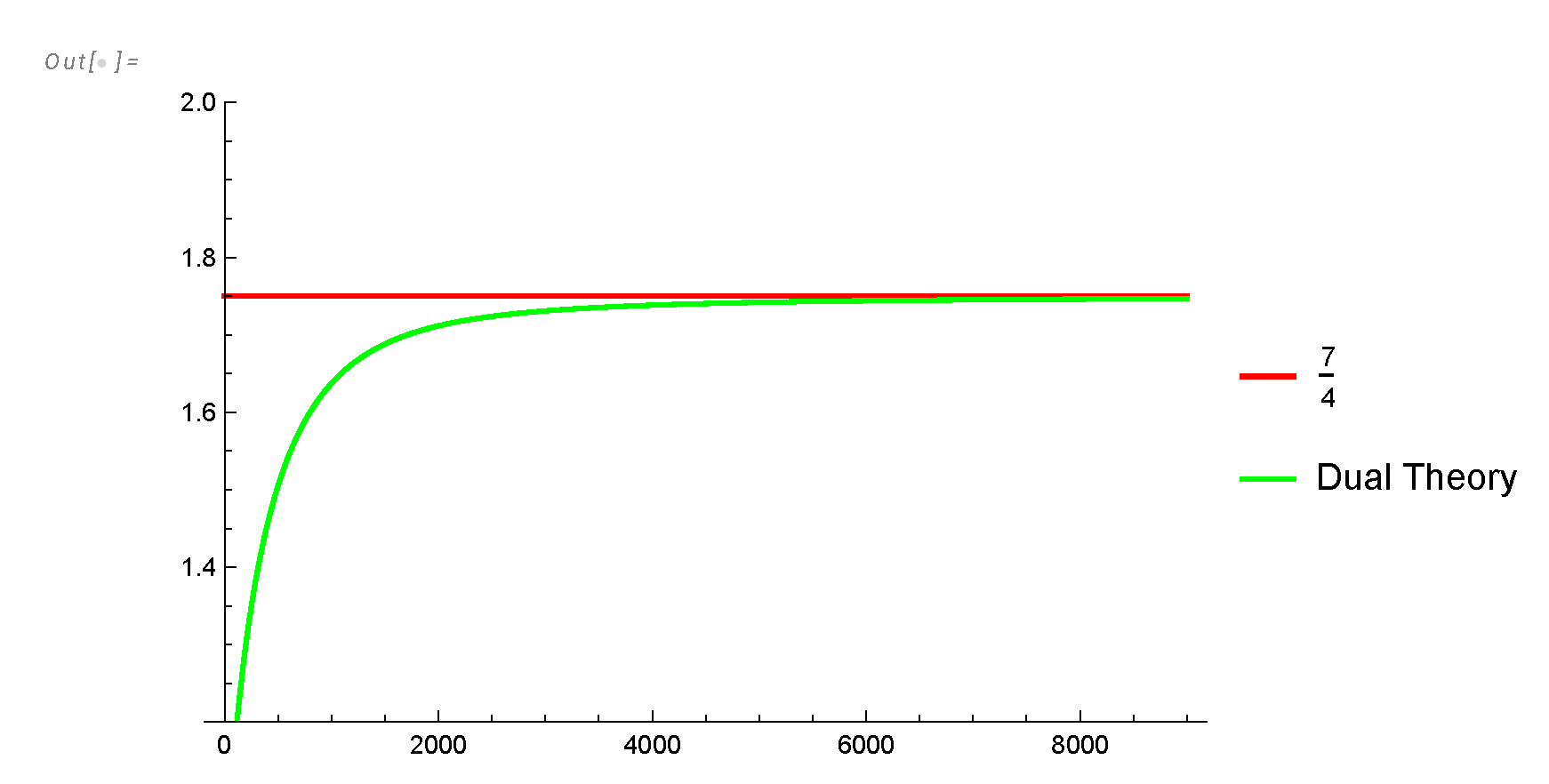
- We review the theory of Navier-Stokes loop equation, its relation to the Hopf functional equation, and the representation of the loop functional in terms of momentum loop.
- We present the solution of the loop equation in the inviscid limit of the three-dimensional Navier-Stokes theory in terms of the Euler ensemble. This ensemble consists of a one-dimensional ring of Ising spins in an external field related to random fractions of .
- We reduced the Markov process for the Euler ensemble in its fermionic representation (60) to the path integral.
- This path integral in the continuum limit is dominated by a complex classical trajectory (instanton), satisfying a nonlinear ODE (130).
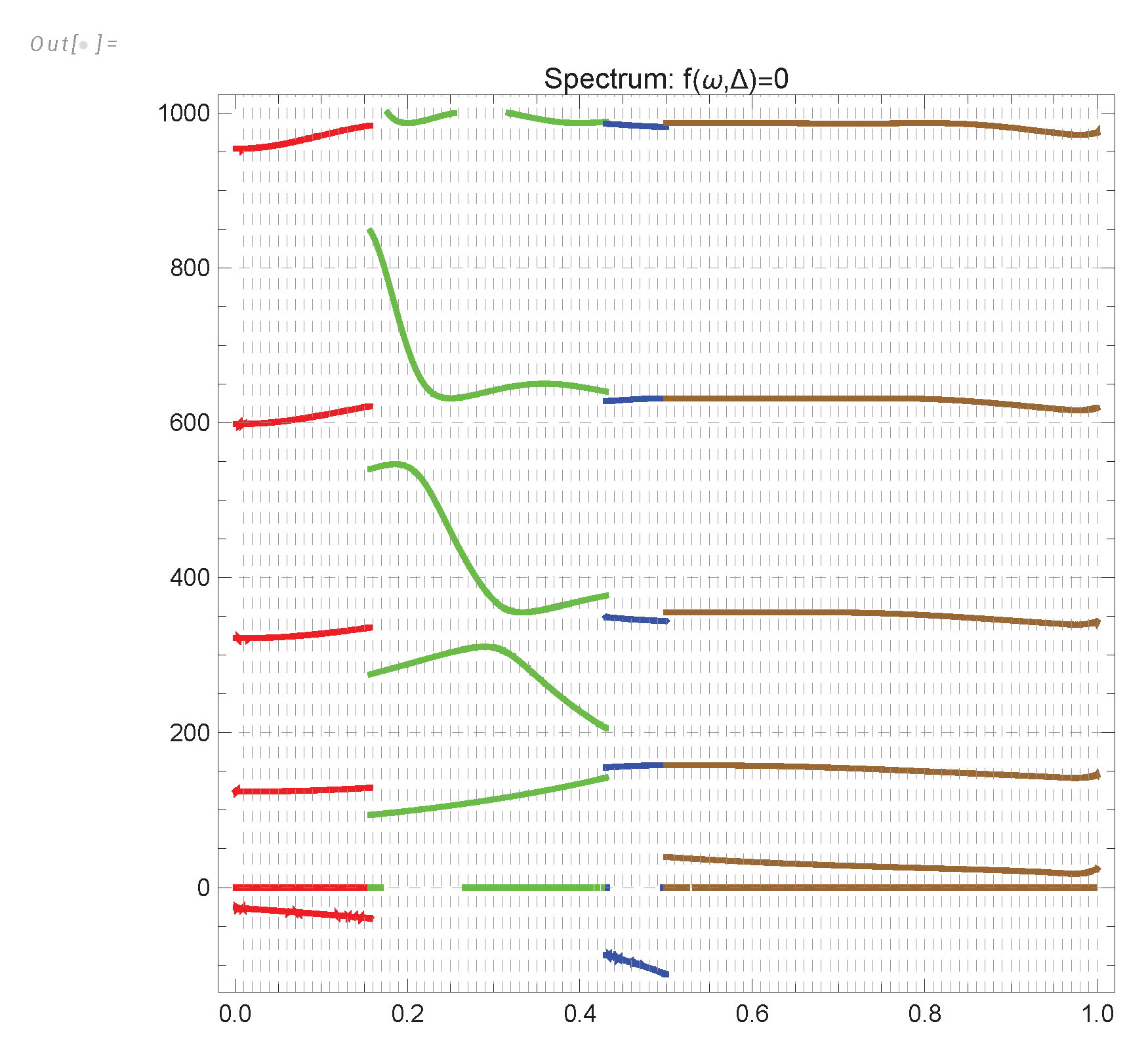
- We solved this classical equation corresponding to the vorticity correlation function and found the spectrum of the linear operator for small fluctuations around this solution.
- We computed the instanton’s contribution to the vorticity correlation function by using zeta regularization of the functional determinant of this linearized operator.
- The continuum limit of this solution, , corresponds to the inviscid limit of the decaying turbulence in the Navier-Stokes equation. Effective turbulent viscosity is . There are no quantum corrections to this instanton contribution in the turbulent limit.
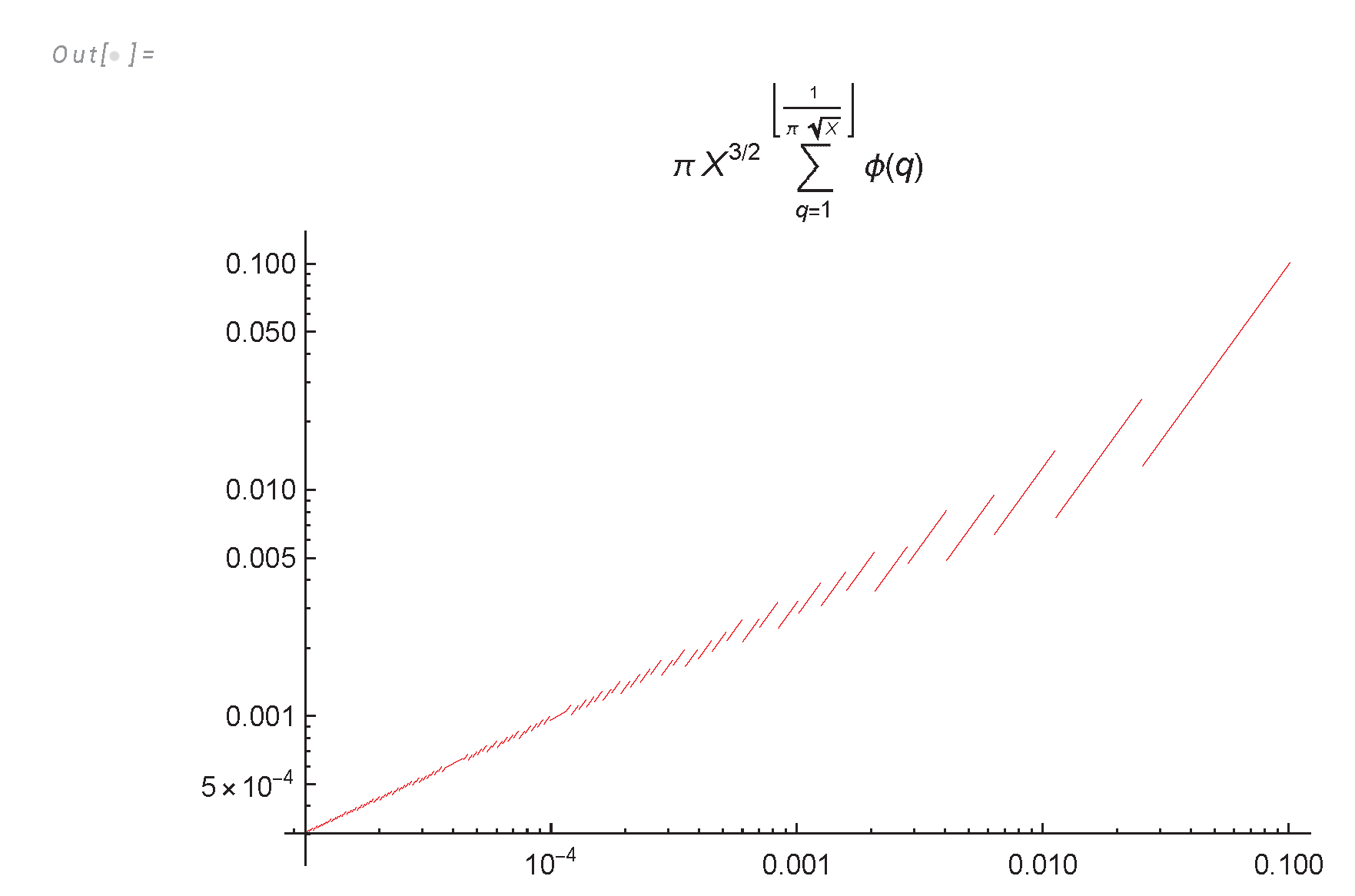
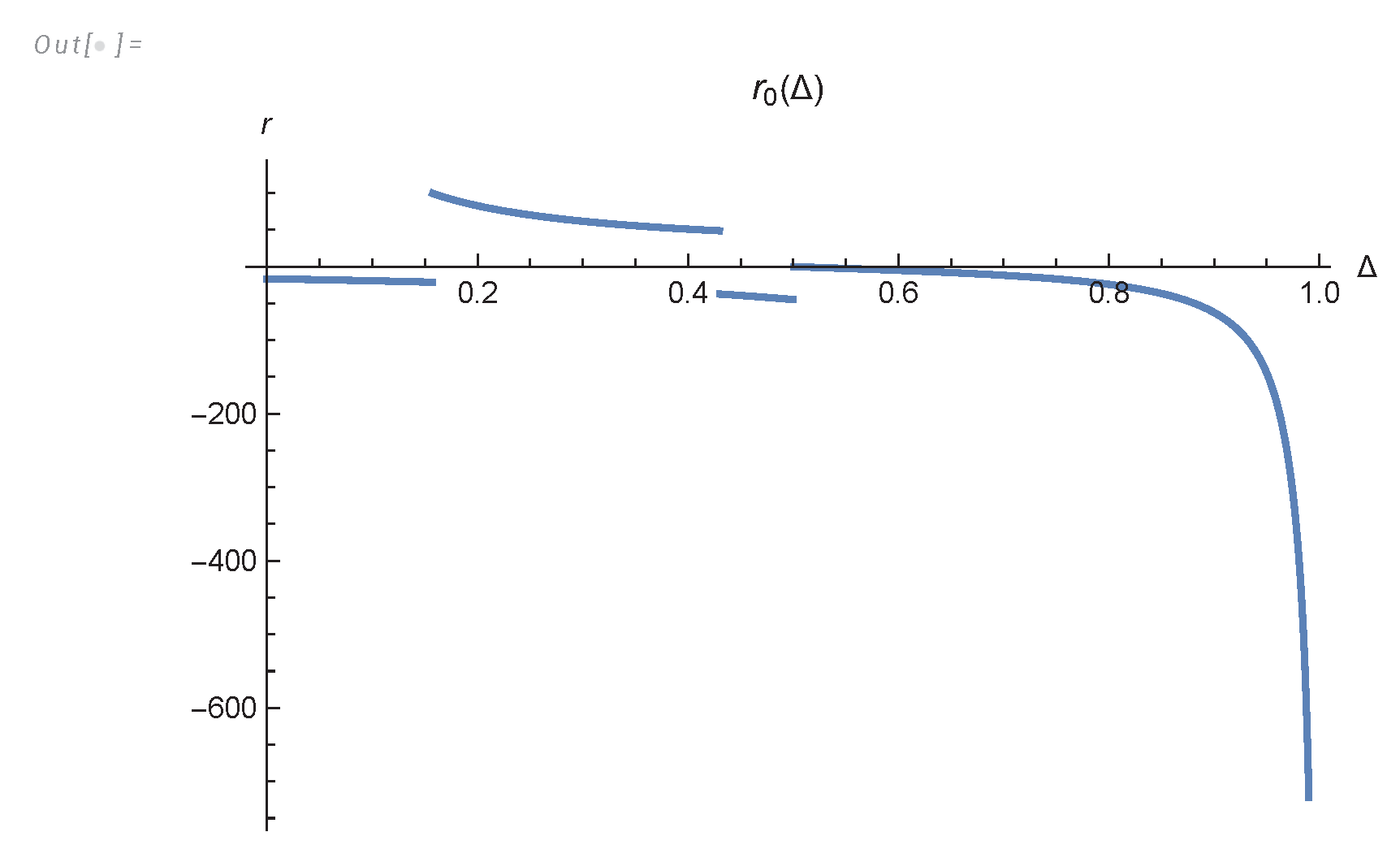
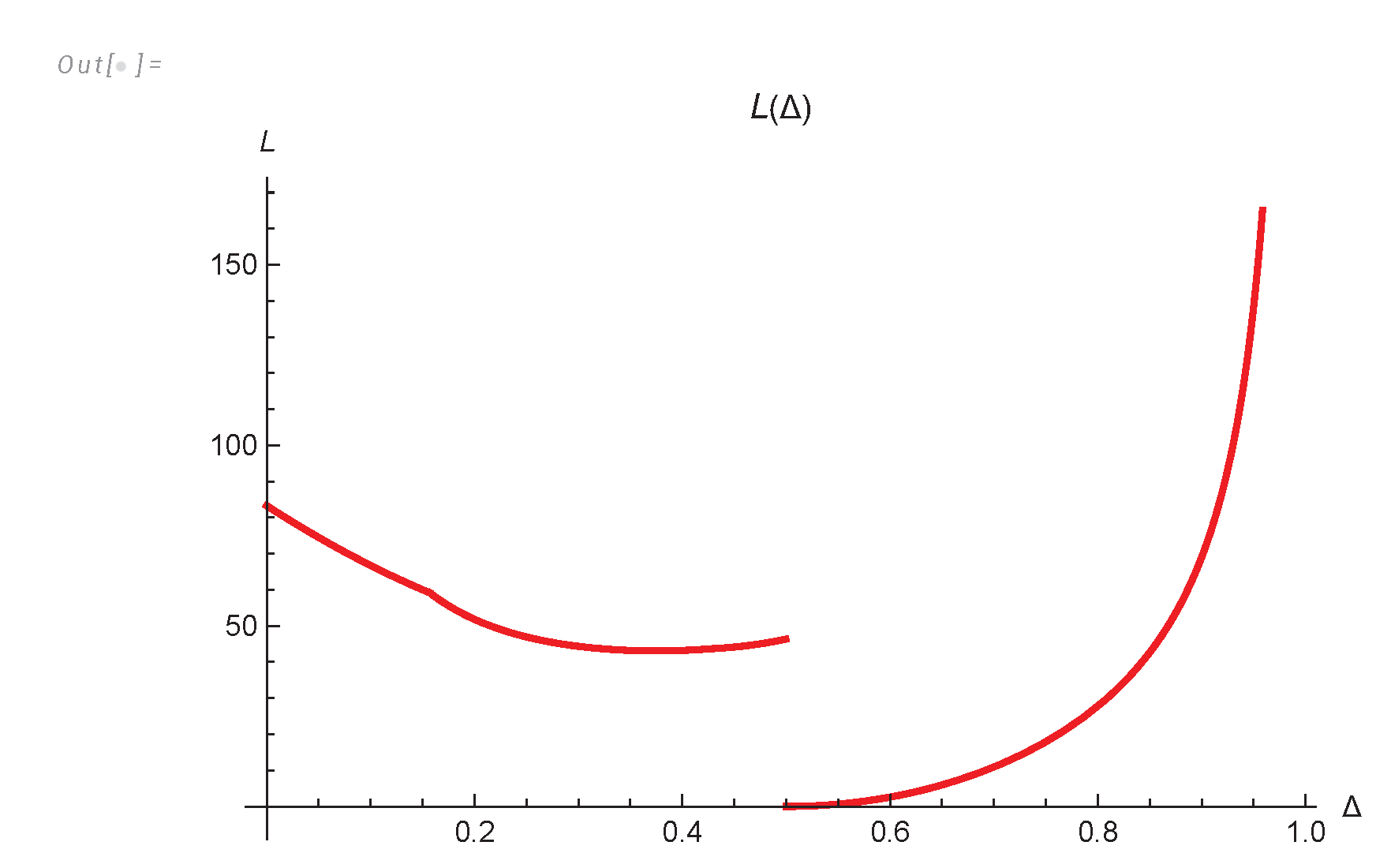
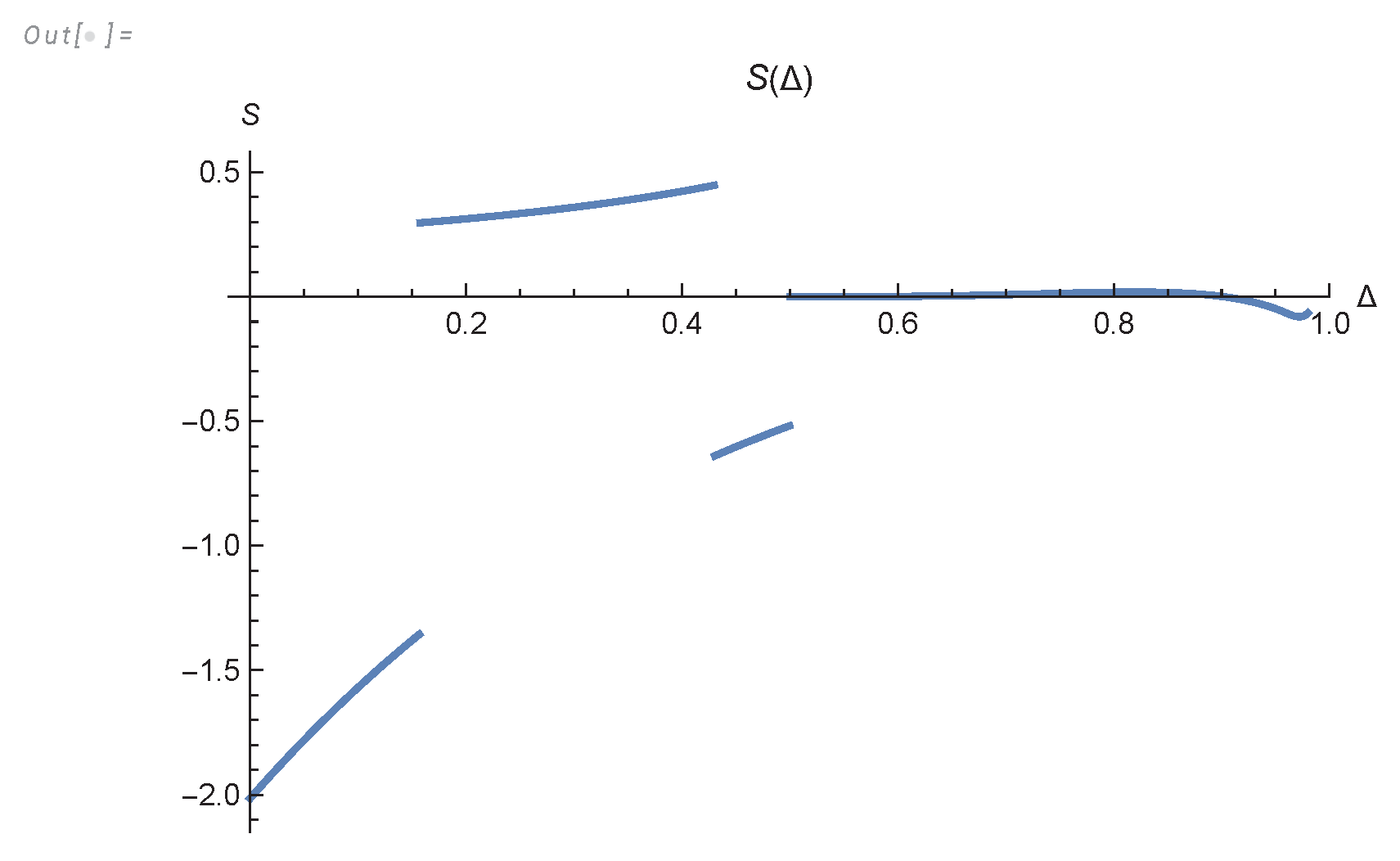
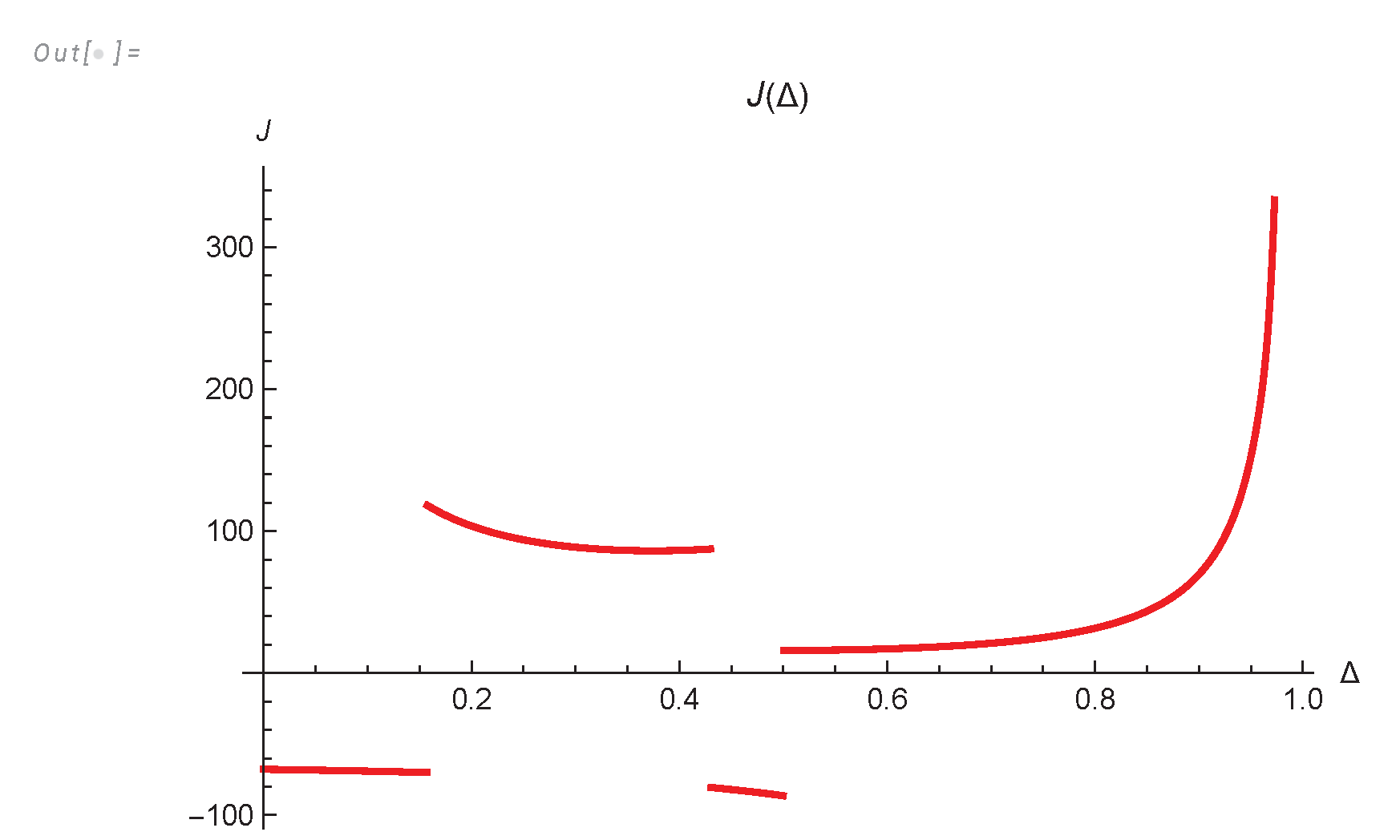
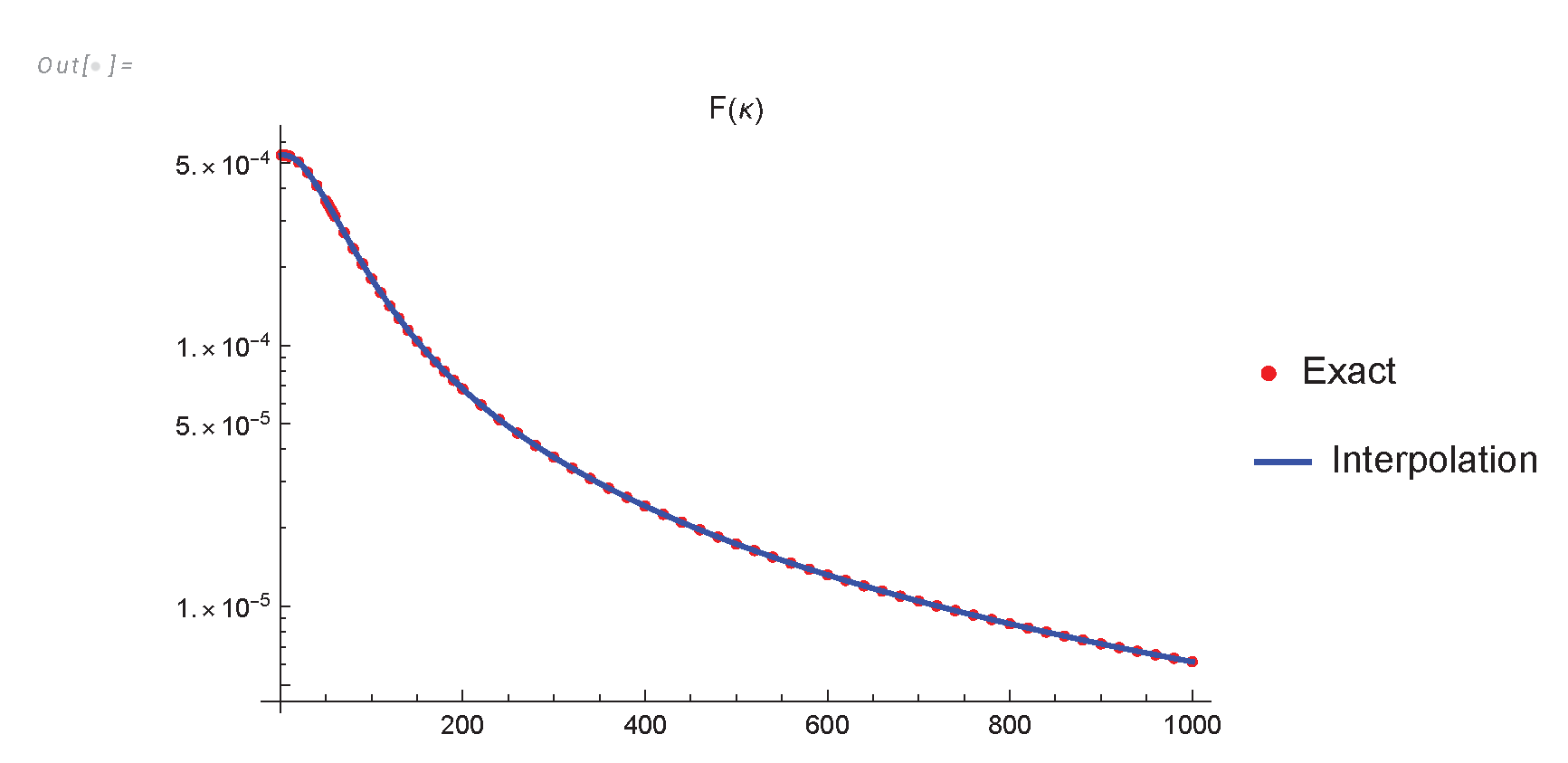
- We derived an analytic formula for energy spectrum and dissipation in finite system (233a), (233c), (233) and investigated it in Appendix A, Appendix B,Appendix C.
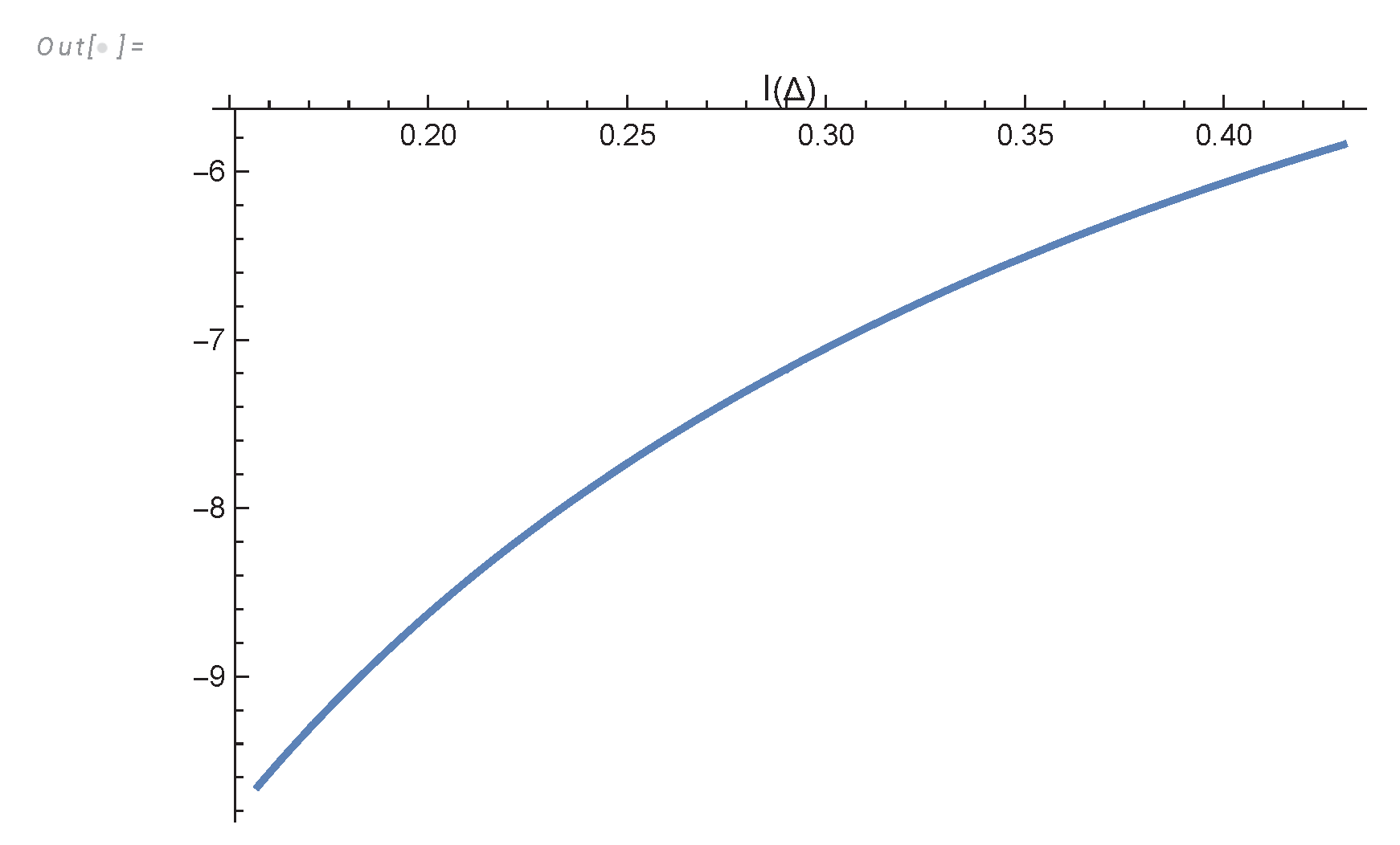
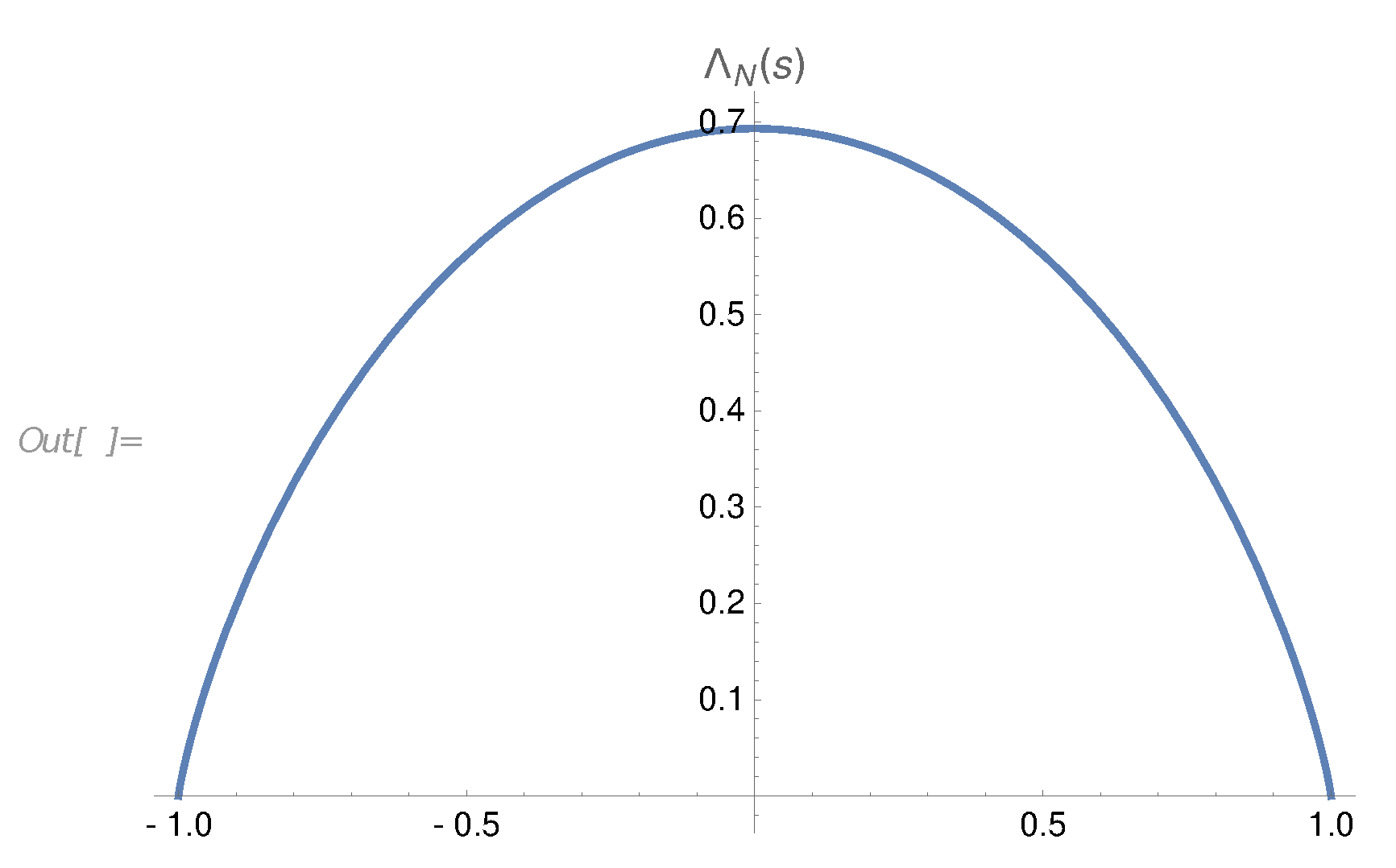
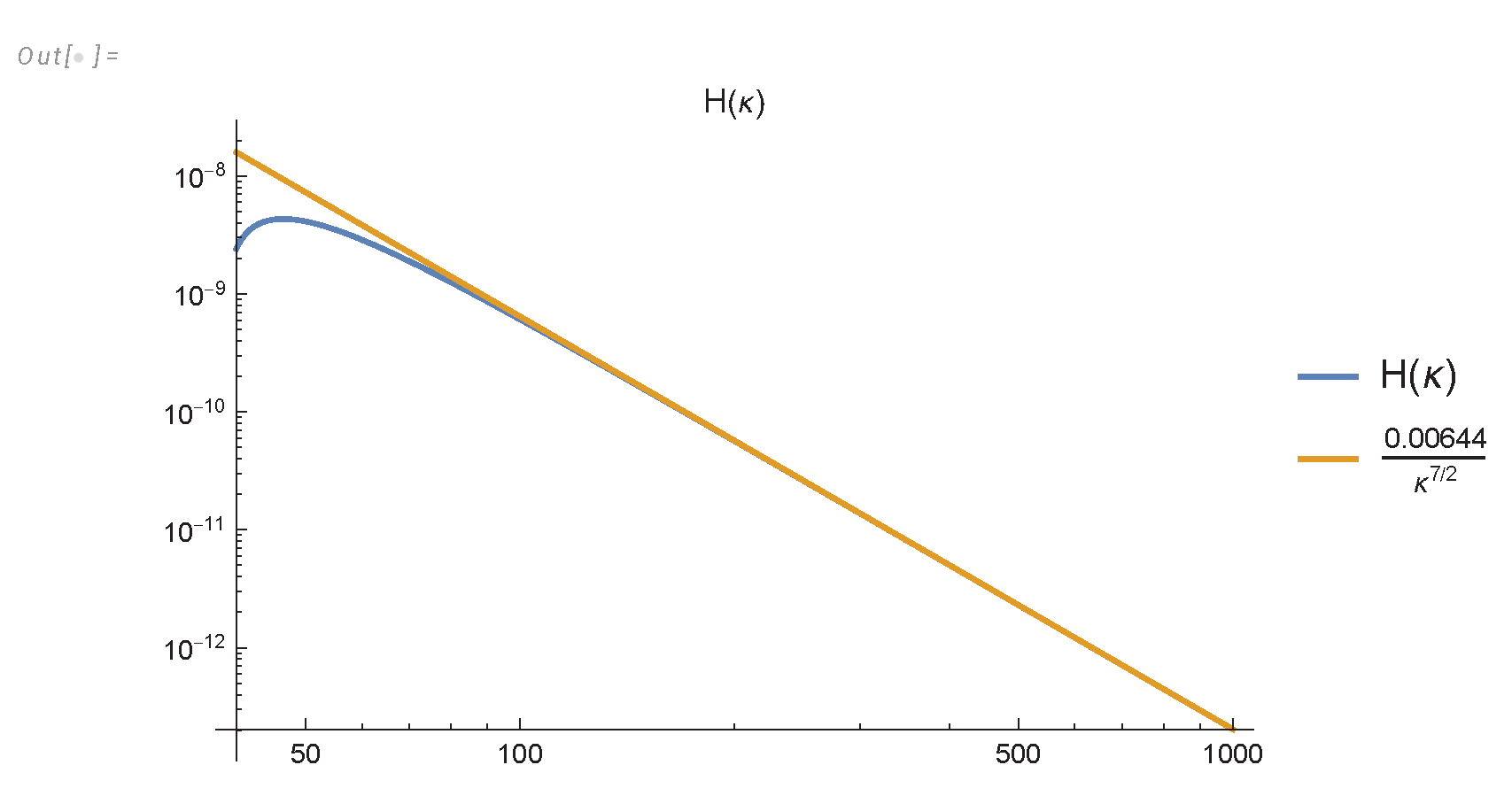
- The energy spectrum decays asymptotically aswhere and are imaginary parts of nontrivial zeros of the function.
- The total remaining energy decays as , but the effective index is a nontrivial function of approaching , see Figure 3).
3. Introduction
3.1. Physical Introduction. The Energy Flow and Random Vorticity Structures
3.2. Mathematical Introduction. The Loop Equation and Its Solution
- There is a fixed point for .
- The approach to this fixed point is exponential in , which is power-like in original time.
3.3. the Big and Small Euler Ensembles
4. The Markov Chain and Its Fermionic Representation
5. The Continuum Limit
5.1. Path Integral over Markov Histories
5.2. Matching Path Integral with Combinatorial Sums in Big Euler Ensemble
5.3. Small Euler Ensemble in Statistical Limit
5.4. Complex Classical Trajectory in the Path Integral
6. Dual Theory of Vorticity Correlation
6.1. Correlation Function and Path Integral
6.2. Turbulent Viscosity and the Local Limit
6.3. Functional Determinant in the Path Integral
6.4. The Fluctuation Term in
7. The Decaying Energy in Finite System
8. Discussion
8.1. Stochastic Solution of the Navier-Stokes Equation and Ergodic Hypothesis
8.2. The Physical Meaning of the Loop Equation and Dimensional Reduction
8.3. Classical Flow and Quantum Geometry
8.4. Stokes-Type Functionals and Vorticity Correlations
8.5. Relation of Our Solution to the Weak Turbulence
9. Remaining Problems
- We performed all the calculations up to numerical factors in the vorticity correlation function, which we recovered from the previously computed (see [21] ). It would be useful to compute all the normalization factors and thus double-check the solution.
- Our asymptotic energy spectrum contains calculable oscillations on top of power decay corrections (see Appendix B). These contributions scale as , and they oscillate due to factors where are imaginary parts of the zeros of the function. Computing the universal function in the intermediate region, connecting small and large expansions is a well-defined but difficult problem in Number Theory. Detecting these oscillations in experiments will require the next level of precision of the experimental/DNS data.
- The spectrum of indexes for deviations from our fixed trajectory [21] can be evaluated in the scaling limit, with finite . This will provide the solution for the vorticity correlations in the Navier-Stokes equation, perturbed by an infinitesimal random force.
Acknowledgments
Data Availability Statement
Appendix A. Computation of the Energy Spectrum
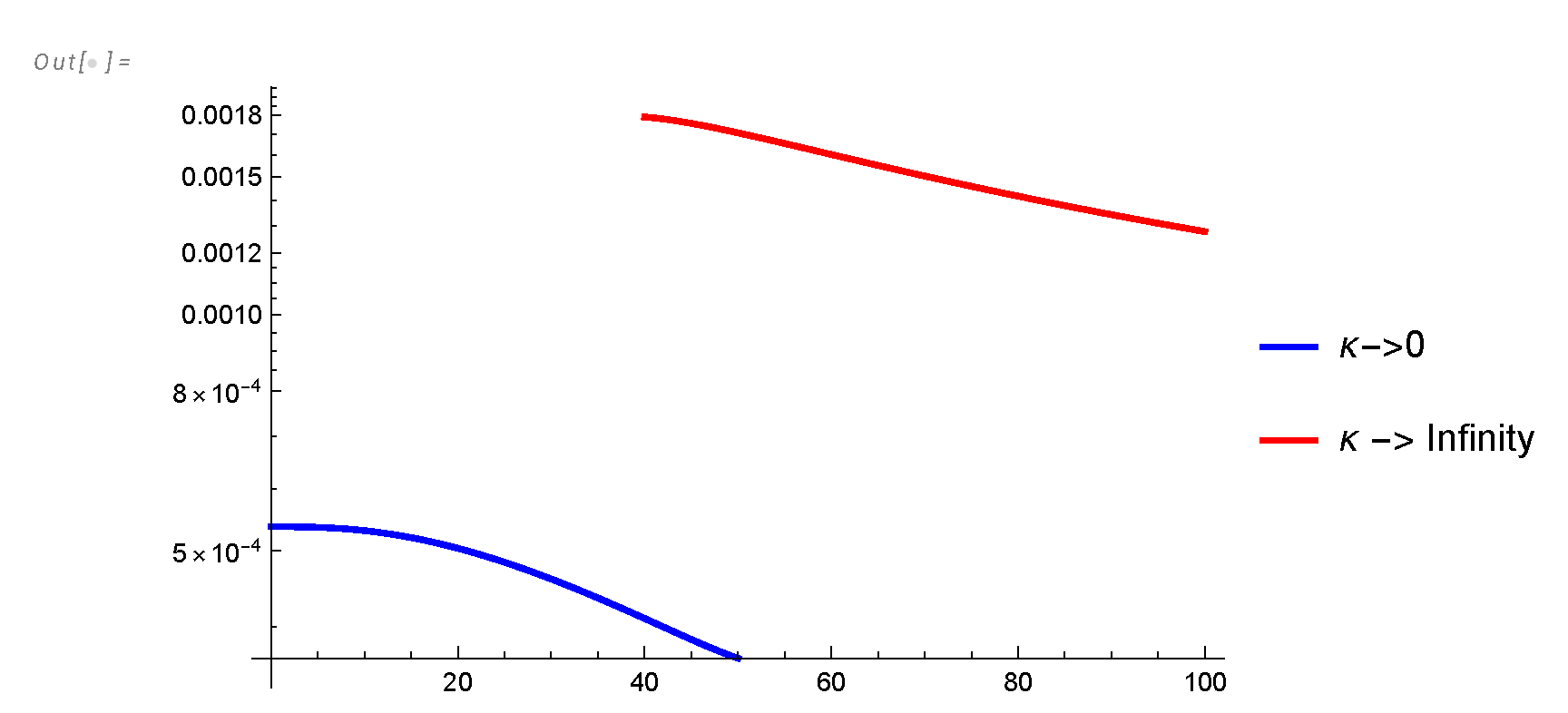
Appendix B. Sum over Riemann Zeta Zeros
Appendix C. Computation of the Energy Dissipation
References
- M.E. AGISHTEIN and A.A. MIGDAL. Simulations of four-dimensional simplicial quantum gravity as dynamical triangulation. Modern Physics Letters A, 07(12):1039–1061, 1992. [CrossRef]
- Peter D. Anderson and Martin Kruczenski. Loop equations and bootstrap methods in the lattice. Nuclear Physics B, 921:702–726, 2017. [CrossRef]
- Gabriel Apolinario, Luca Moriconi, Rodrigo Pereira, and Victor valadão. Vortex gas modeling of turbulent circulation statistics. PHYSICAL REVIEW E, 102:041102, 10 2020. [CrossRef]
- Abhay Ashtekar. New variables for classical and quantum gravity. Physical Review Letters, 57:2244–2247, 11 1986. [CrossRef]
- Debmalya Basak and Alexandru Zaharescu. Connections between number theory and the theory of turbulence, 2024. To be published.
- Maxim Bulatov and Alexander Migdal. Numerical simulation of euler ensemble. "unpublished", February 2024.
- Richard P Feynman, Robert B Leighton, and Matthew Sands. 3-7 how did it get that way? In Michael A. Gottlieb and Rudolf Pfeiffer, editors, The Feynman lectures on physics, Vol. I: Mainly mechanics, radiation, and heat, volume 1. Basic books, 2011.
- Clifford S Gardner, John M Greene, Martin D Kruskal, and Robert M Miura. Method for solving the korteweg-devries equation. Physical review letters, 19(19):1095, 1967. [CrossRef]
- G. H. Hardy and E. M. Wright. An introduction to the theory of numbers. Oxford University Press, Oxford, sixth edition, 2008. Revised by D. R. Heath-Brown and J. H. Silverman, With a foreword by Andrew Wiles.
- Kartik P Iyer, Sachin S Bharadwaj, and Katepalli R Sreenivasan. The area rule for circulation in three-dimensional turbulence. Proceedings of the National Academy of Sciences of the United States of America, 118(43):e2114679118, 10 2021. [CrossRef]
- Kartik P. Iyer, Katepalli R. Sreenivasan, and P. K. Yeung. Circulation in high reynolds number isotropic turbulence is a bifractal. Phys. Rev. X, 9:041006, 10 2019. [CrossRef]
- Vladimir Kazakov and Zechuan Zheng. Bootstrap for lattice Yang-Mills theory. Phys. Rev. D, 107(5):L051501, 2023. [CrossRef]
- Yu.M. Makeenko and A.A. Migdal. Exact equation for the loop average in multicolor qcd. Physics Letters B, 88(1):135–137, 1979. [CrossRef]
- T. Matsuzawa and W. Irvine. Realization of confined turbulence through multiple vortex ring collisions, 03/12/2019. "Talk at the Flatiron Conference Universality Turbulence Across Vast Scales".
- Takumi Matsuzawa, Noah P. Mitchell, Stéphane Perrard, and William T. Irvine. Creation of an isolated turbulent blob fed by vortex rings. Nature Physics, 19(8):1193–1200, 2023. [CrossRef]
- A. Migdal. Loop equations and expansion. Physics Reports, 201, 1983. [CrossRef]
- A.A. Migdal. Momentum loop dynamics and random surfaces in qcd. Nuclear Physics B, 265(4):594–614, 1986. [CrossRef]
- A.A. Migdal. Second quantization of the wilson loop. Nuclear Physics B - Proceedings Supplements, 41(1):151–183, 1995.
- Alexander Migdal. Loop equation and area law in turbulence. In Laurent Baulieu, Vladimir Dotsenko, Vladimir Kazakov, and Paul Windey, editors, Quantum Field Theory and String Theory, pages 193–231. Springer US, 1995.
- Alexander Migdal. Statistical equilibrium of circulating fluids. Physics Reports, 1011C:1–117, 2023. [CrossRef]
- Alexander Migdal. To the theory of decaying turbulence. Fractal and Fractional, 7(10):754, Oct 2023. [CrossRef]
- Alexander Migdal. Topological vortexes, asymptotic freedom, and multifractals. MDPI Fractals and Fractional, Special Issue, 2023.
- Alexander Migdal. "bernsum". "https://www.wolframcloud.com/obj/sasha.migdal/Published/BernSum.nb", 02 2024.
- Alexander Migdal. "instantoncomputations". "https://www.wolframcloud.com/obj/sasha.migdal/ Published/DualTheory1.nb", 03 2024.
- Alexander Migdal. "instantoncomputations". "https://www.wolframcloud.com/obj/sasha.migdal/ Published/DualTheory2.nb", 03 2024.
- Alexander Migdal. "instantoncomputations". "https://www.wolframcloud.com/obj/sasha.migdal/ Published/DualTheory3.nb", 03 2024.
- Alexander A. Migdal. Hidden symmetries of large N QCD. Prog. Theor. Phys. Suppl., 131:269–307, 1998. [CrossRef]
- Pieter Moree, Sumaia Saad Eddin, Alisa Sedunova, and Yuta Suzuki. Jordan totient quotients. Journal of Number Theory, 209:147–166, 2020. [CrossRef]
- MASATAKE MORI and TAKUYA OOURA. Double exponential formulas for fourier type integrals with a divergent integrand. In Contributions in Numerical Mathematics, pages 301–308. World Scientific, 1993.
- Nicolás P. Müller, Juan Ignacio Polanco, and Giorgio Krstulovic. Intermittency of velocity circulation in quantum turbulence. Phys. Rev. X, 11:011053, 03 2021. [CrossRef]
- James R. Norris. Markov chains. Cambridge Univ. Press, 2007.
- Nikita Nekrasov (private communication) suggested to me an algorithm of generating this solution as a set of adjacent triangles in complex 3-space and pointed out an invariant measure in phase space, made of lengths of shared sides and angles between them. Unfortunately, this beautiful construction does not guarantee real circulation, requiring further study.
- Koji Ohkitani. Study of the hopf functional equation for turbulence: Duhamel principle and dynamical scaling. Physical Review E, 101, 12 2019. [CrossRef]
- John Panickacheril John, Diego A Donzis, and Katepalli R Sreenivasan. Laws of turbulence decay from direct numerical simulations. Philos. Trans. A Math. Phys. Eng. Sci., 380(2218):20210089, March 2022. [CrossRef]
- G Parisi and U Frisch. On the singularity structure of fully developed turbulence turbulence and predictability. In R Benzi M Ghil and G Parisi, editors, Geophysical Fluid Dynamics: Proc. Intl School of Physics E. Fermi, pages 84–88. Amsterdam: North-Holland, 1985.
- Juan Ignacio Polanco, Nicolás P. Müller, and Giorgio Krstulovic. Vortex clustering, polarisation and circulation intermittency in classical and quantum turbulence. Nature Communications, 12(1):7090, Dec 2021. [CrossRef]
- Carlo Rovelli and Lee Smolin. Knot theory and quantum gravity. Phys. Rev. Lett., 61:1155–1158, 09 1988. [CrossRef]
| 1 | Nikita Nekrasov (private communication) suggested to me an algorithm of generating this solution as a set of adjacent triangles in complex 3-space and pointed out an invariant measure in phase space, made of lengths of shared sides and angles between them. Unfortunately, this beautiful construction does not guarantee real circulation, requiring further study. |

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





