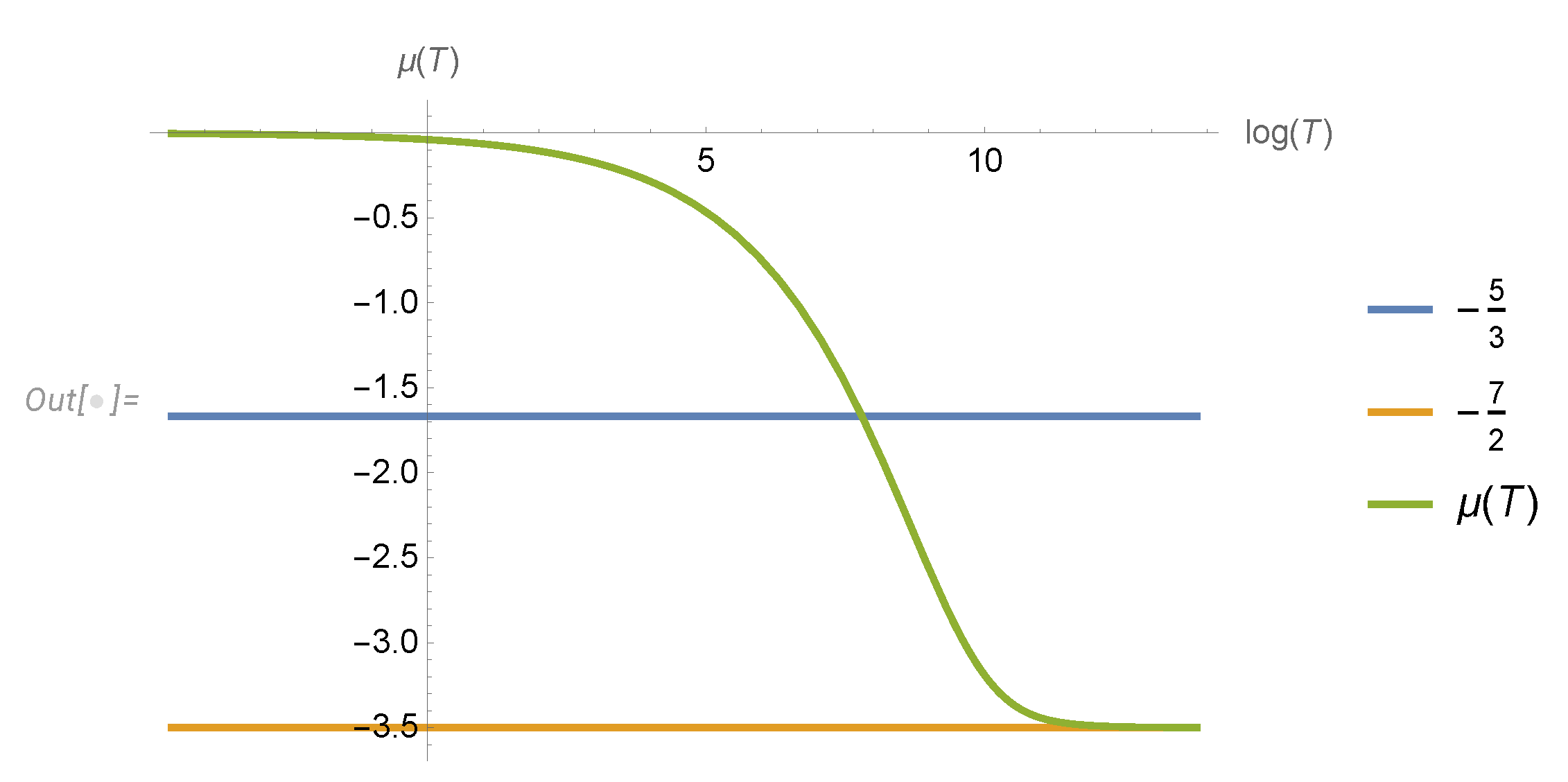Quantum Solution of Classical Turbulence Decaying Energy Spectrum

Alexander Migdal

doi:10.20944/preprints202312.1012.v11

Preprint

Article

Quantum Solution of Classical Turbulence Decaying Energy Spectrum

This version is not peer-reviewed.

Alexander Migdal^*

This version is not peer-reviewed.

Downloads

868

Views

421

Comments

Submitted:

03 May 2024

Posted:

06 May 2024

Read the latest preprint version here

A peer-reviewed article of this preprint also exists.

Abstract

This paper summarizes and elaborates on recently found \cite{migdal2023exact} exact reduction of decaying turbulence in the Navier-Stokes equation in $3 + 1$ dimensions to a Number Theory problem of the statistical limit of the Euler ensemble. We reformulate the Euler ensemble as a Markov chain and show the equivalence of this formulation to the \textbf{quantum} statistical theory of $N$ fermions on a ring, with an external field related to the random fractions of $\pi$. We find the solution of this system in the turbulent limit $N\to \infty, \nu \to 0$ in terms of a complex trajectory (instanton) providing a saddle point to the path integral over the density of these fermions. This results in an analytic formula for the observable correlation function of vorticity in wavevector space. This is a full solution of decaying turbulence from the first principle without approximations or fitted parameters. We compute resulting integrals in \Mathematica{} and present effective index $n(t) = -t E'(t)/E(t) $ for the energy decay as a function of time Fig.\ref{fig::NPlot} and $s(k)= -k\partial_k \log E(k,t) $ for the energy spectrum Fig.\ref{fig::SPIndex}. The asymptotic values are $n(\infty) = \frac{5}{4}, s(\infty) = \frac{7}{2}$, but the universal functions $n(t), s(t)$ are neither constant nor linear due to quantum effects (complex poles of the Mellin transform at zeros of Riemann zeta function). The theoretical value $n(\infty)=\sfrac{5}{4}$ matches the grid turbulence experiments \cite{GridTurbulence_1966} within experimental errors $\sim 2\%$.

Keywords:

turbulence

;

fractal

;

anomalous dissipation

;

fixed point

;

velocity circulation

;

loop equations

;

Euler Phi

;

prime numbers

;

fermi particles

;

instanton

Subject:

Physical Sciences - Fluids and Plasmas Physics

This preprints belongs to the Topic

Recent Trends in Nonlinear, Chaotic and Complex Systems

1. Prologue

Turbulence appears as an overwhelmingly complex phenomenon. As depicted in Figure 1 from a recent simulation [2], vortex lines of various shapes and sizes are entangled much like spaghetti. This visual complexity raises the question: How can such complexity be described analytically? Yet, it also sparks hope for a simplified statistical description.

Molecular dynamics, with its myriad interacting particles, similarly presents an intricate challenge. However, despite its complexity, a straightforward statistical description emerges that grows increasingly precise with the escalating complexity of the dynamical system. Maxwell, Boltzmann, and Gibbs demonstrated that Newton’s mechanics uniformly cover the energy surface over time, laying the groundwork for statistical mechanics—a robust theory, albeit sometimes computationally challenging, as in critical phenomena.

Why, then, should Navier-Stokes turbulence be any different?

Regrettably, no known analog of the Gibbs distribution exists for turbulent flows.

Therefore, a foundational element of turbulence theory must be to devise a substitute for the Gibbs distribution.

Hopf initiated this exploration in 1952 (see the recent review in [3]), formulating a functional equation that the probability distribution of the turbulent velocity field must satisfy. Through the iterative application of this equation to the nonlinear term in the Navier-Stokes equation, one can generate an expansion in inverse powers of viscosity. The core challenge of turbulence theory is solving the Hopf equation in the opposite limit of low viscosity.

This equation, as beautiful as it is, is mathematically as intricate as the vortex spaghetti depicted earlier. Such complexity places turbulence high within the hierarchy of physics theories, nestled between critical phenomena and the quark confinement problem.

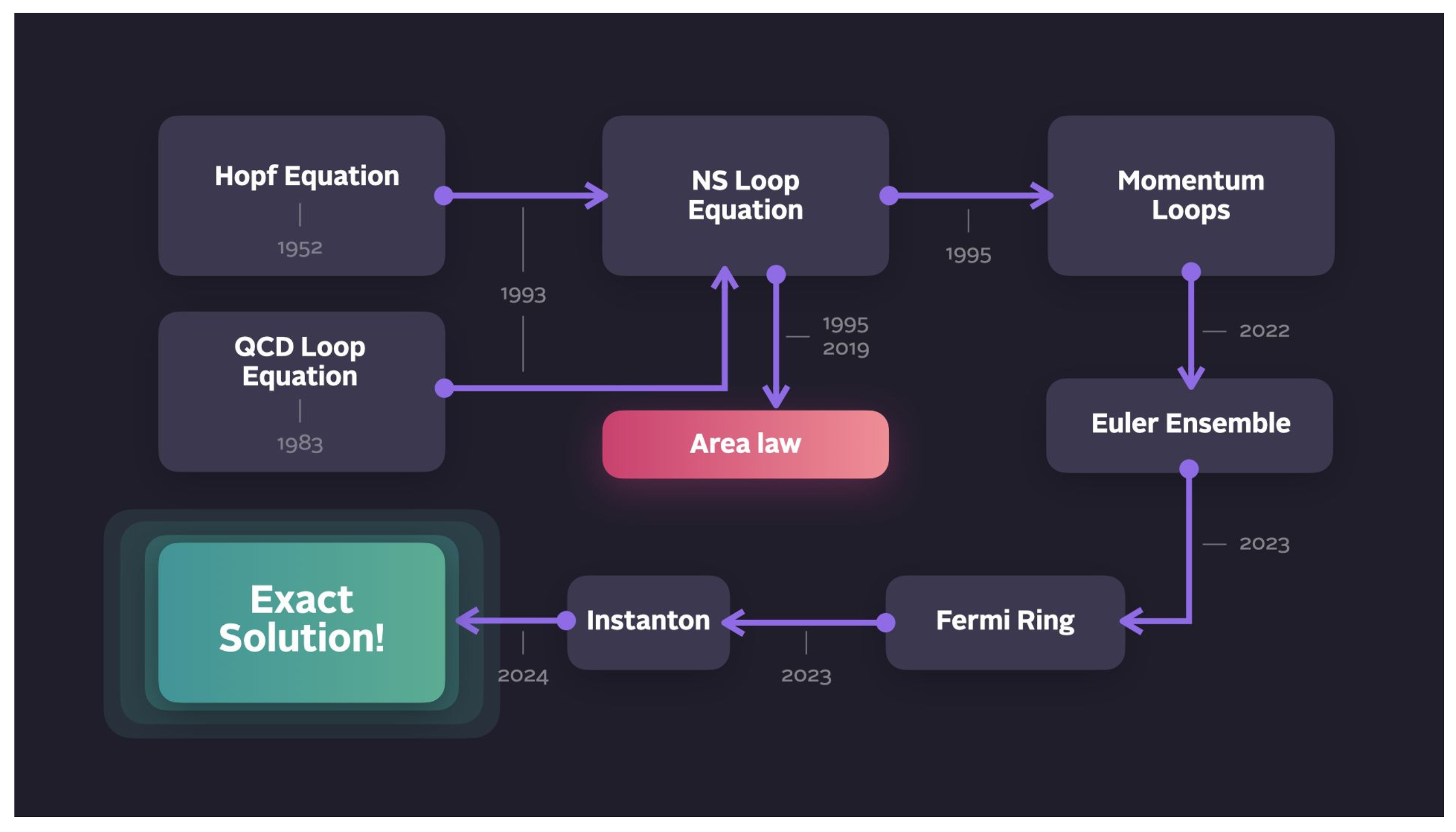
Our theory, initiated in 1993 (see Figure 2 for the historical outline), proposes a simpler variant of the Hopf equation—the loop equation—which suffices to define the statistics.

The loop equation corresponds to the Schrödinger equation in loop space. This profound analogy is not merely a poetic metaphor but a precise mathematical equivalence with significant implications, such as inducing quantum oscillations that alter the effective indexes in the scaling laws of classical turbulence.

Using the loop equation, we have identified a new instance of duality between the strong coupling phase of one theory (a fluctuating velocity field in three dimensions) and the weak coupling phase of another (a one-dimensional quantum ring of Fermi particles).

This weak coupling limit can be analytically solved, providing explicit formulas for observables in decaying turbulence, such as the energy dissipation decay index

n (t) = t \frac{E (t)}{E (t)}

The experimental data from decaying grid-turbulence (see Figure 3) corroborate our prediction that

n (\infty) = \frac{5}{4}

, within a 2% experimental error margin. We anticipate that more precise future measurements will validate the complete curves for

n (t), s (κ)

as forecasted by our theory.

2. Summary

Here are the main results reported in this paper.

We review the theory of Navier-Stokes loop equation, its relation to the Hopf functional equation, and the representation of the loop functional in terms of momentum loop.
We present the solution of the loop equation in the inviscid limit of the three-dimensional Navier-Stokes theory in terms of the Euler ensemble. This ensemble consists of a one-dimensional ring of Ising spins in an external field related to random fractions of $π$ .
The continuum limit of this solution, $N \to \infty$ , corresponds to the inviscid limit of the decaying turbulence in the Navier-Stokes equation. Effective turbulent viscosity is $\tilde{ν} = ν N^{2} \to const$ . There are no quantum corrections to this instanton contribution in the turbulent limit.
We derived an analytic formula for energy spectrum and dissipation in finite system (233a), (233c), (233) and investigated it in Appendix A.
The energy spectrum decays asymptotically as ${(\tilde{ν})}^{\frac{3}{2}} t^{- \frac{1}{2}} κ^{- \frac{7}{2}}$ where $κ = k \sqrt{\tilde{ν} t}$ .
The total remaining energy decays as $E (t) \propto t^{- \frac{5}{4}}$
Both effective indexes $n (t) = - \frac{d log E}{d log t}, μ (κ) = \frac{\partial log E (k, t)}{\partial log k}$ are nontrivial functions of the logarithm of scale and time, approaching $n (\infty) = \frac{5}{4}, μ (\infty) = - \frac{7}{2}$ , (see Figure 17, Figure 7).
The 1966 experimental values [1], Figure 3 of $n (\infty) \approx 1.25 \pm 0.02$ agree with our prediction.
The results of DNS for the energy spectrum in decaying turbulence (Figure 5 of the review paper [4]) shows the energy spectrum decaying faster than $k^{- \frac{5}{3}}$ . The shape of a log-parabolic curve in DNS matches our prediction Figure 6. The effective index $μ (t)$ approximately matches our theoretical curve at Figure 7.
We computed the spectrum of singularity indexes $p_{n}$ in the product $\vec{v} (0, t) \cdot \vec{v} (r, t) \sim \sum C_{n} (t) r^{p_{n}}$ , similar but different from the OPE in CFT. Some of these singularity indexes come in complex conjugate pairs related to the zeros of the Riemann $ζ$ function.

Figure 4. Green curve is the inverse energy

1 / E (t)

as a function of time. It slowly approaches from above its asymptotic law

1 / E (t) \propto t^{\frac{5}{4}}

shown in red.

Figure 4. Green curve is the inverse energy

1 / E (t)

as a function of time. It slowly approaches from above its asymptotic law

1 / E (t) \propto t^{\frac{5}{4}}

shown in red.

Figure 5. The log-log plot of deviation from K41 energy spectrum in decaying turbulence, taken from [4] with permission of the author. The observed curve approximately matches our theoretical curve in Figure 6. The K41 spectrum would correspond to a horizontal line, which is a total mismatch.

Figure 6. Log-log plot of the universal function

H (κ) κ^{\frac{5}{3}}

. It starts growing, reaches the maximum, then turns down, asymptotically decaying as

κ^{- \frac{11}{6}}

. This qualitatively matches the DNS plot at Figure 5. A larger DNS data at higher Reynolds numbers would be required to verify our theory with more precision.

Figure 6. Log-log plot of the universal function

H (κ) κ^{\frac{5}{3}}

. It starts growing, reaches the maximum, then turns down, asymptotically decaying as

κ^{- \frac{11}{6}}

. This qualitatively matches the DNS plot at Figure 5. A larger DNS data at higher Reynolds numbers would be required to verify our theory with more precision.

Figure 7. The theoretical plot of effective spectral index

μ (T) = k \partial_{k} log E (k, t)

as a function of

T = k^{2} \tilde{ν} t

. It starts at 0 and goes down to the limit

- \frac{7}{2}

. The DNS plot Figure 8 starts higher, at

μ = 2

, then goes down and stops at approximately

- 1

for accessible decay time t. The part from

- 0.5

- 1

qualitatively matches our curve, but clearly, more data at higher Reynolds numbers is required to verify this prediction of our theory.

Figure 7. The theoretical plot of effective spectral index

μ (T) = k \partial_{k} log E (k, t)

as a function of

T = k^{2} \tilde{ν} t

. It starts at 0 and goes down to the limit

- \frac{7}{2}

. The DNS plot Figure 8 starts higher, at

μ = 2

, then goes down and stops at approximately

- 1

for accessible decay time t. The part from

- 0.5

- 1

qualitatively matches our curve, but clearly, more data at higher Reynolds numbers is required to verify this prediction of our theory.

Figure 8. The DNS plot of spectral index

μ (t) = k \partial_{k} log E (k, t)

as a function of

log t

at fixed values of k. The curve goes from

μ = 2

μ \approx - 1

, which partly overlaps with our theoretical curve in Figure 7. Larger dataset with higher Reynolds numbers is needed for a quantitative match with our theory.

Figure 8. The DNS plot of spectral index

μ (t) = k \partial_{k} log E (k, t)

as a function of

log t

at fixed values of k. The curve goes from

μ = 2

μ \approx - 1

, which partly overlaps with our theoretical curve in Figure 7. Larger dataset with higher Reynolds numbers is needed for a quantitative match with our theory.

3. Introduction

This paper provides distinct pathways for understanding and applying the results of our study based on the reader’s background and interests. Our findings offer significant implications across various fields, including physics, mathematics, and engineering.

3.1. Introduction for Physicists

The physics introduction discusses the potential correspondence between our theoretical developments and decaying turbulence as observed in real-world or numerical experiments. For physicists, this theory offers a solution to the Hopf functional equation for the statistical distribution of the velocity field in the unforced Navier-Stokes equation. This distribution represents a much-needed analog of the Gibbs distribution for decaying turbulence. There are strong indications that our theory is relevant to one of the two universality classes observed in these experiments.

3.2. Introduction for Mathematicians

This section summarizes the mathematical framework behind the loop equation [6] and its solution [7] in terms of the Euler ensemble. Addressed to mathematicians, this introduction allows those with a focus on rigorous mathematical theory to bypass the more physically oriented discussions and delve directly into the ensemble as a novel Number Theory set with conjectured connections to decaying turbulence.

3.3. Guidance for Applied Mathematicians and Engineers

Applied mathematicians and engineers, primarily interested in practical applications rather than abstract theoretical constructs, are directed to the last Section 7 of this document. Here, they will find final formulas (233c), (233a), and accompanying Mathematica^®code [8,9] that facilitate the computation of both the energy spectrum and dissipation rates. These formulas can be compared with future (real or numerical) experiments.

3.4. Notes for the Curious and Skeptical

The fourth category of readers—those who are curious yet skeptical about the application of quantum mechanics to solve complex problems in classical physics—might still harbor doubts even after perusing the extensive computations presented in this paper. For them, we have dedicated the last Section 9, which aims to address some of their lingering questions and perhaps reassure their skepticism.

In the following sections, we explore each of these themes in depth, aiming to provide clarity and actionable insights for all readers, regardless of their specific area of expertise or interest.

3.5. Physical Introduction: The Energy Flow and Random Vorticity Structures

Decaying turbulence is an old topic, traditionally examined within a weak turbulence framework—utilizing a truncated perturbative expansion in inverse powers of viscosity

ν

in the forced Navier-Stokes equation. Various phenomenological models have also been aligned with experimental observations, as discussed in the recent review [4].

However, the comprehensive turbulence theory requires solving the Navier-Stokes equations in the strong coupling limit

ν \to 0

, the direct opposite of weak coupling. The universality of strong turbulence, with or without random forcing, poses the initial question in constructing such a theory.

Direct Numerical Simulation (DNS) data for energy decay in turbulent flows, detailed in [4], suggest a decay of the dissipation rate

E \sim t^{- n}

with

n \approx 1.25

1.60

depending on the initial conditions (finite total momentum or zero total momentum but finite total angular momentum, see [4]). Thus, two universality classes of decaying turbulence have been identified.

It remains unclear which, if any, of the data in [4] reached the homogeneous isotropic turbulence limit corresponding to our regime. Moreover, stochastic forces added to the Navier-Stokes equation in simulations might contaminate the natural decay of turbulence. These forces are intended to initiate and enhance the spontaneous stochasticity of turbulent flow. However, in our theory [7], this inherent stochasticity is related to a dual quantum system and is discrete.

The Gaussian forcing can distort these quantum stochastic phenomena by stirring the flow ubiquitously and constantly. When the forcing is switched off, allowing the turbulence to decay towards a universal stage, energy dissipation should occur within vorticity structures deeply embedded in the flow by the pure turbulent dynamics we study.

The forthcoming calculation supports the above relationship between singular vorticity distribution and energy flow. In the pure Navier-Stokes scenario, the energy balance reduces to energy dissipation by enstrophy within the bulk, counterbalanced by energy input from boundary forces (e.g., a large sphere encompassing the flow).

The general identity derived from the Navier-Stokes equations by multiplying both sides by

\vec{v}

and averaging over an infinite time interval is:

\begin{matrix} \int_{V} d^{3} r 〈ν {\vec{ω}}^{2}〉 = - \int_{V} d^{3} r \partial_{β} 〈v_{β} (p + \frac{1}{2} v_{α}^{2}) + ν v_{α} (\partial_{β} v_{α} - \partial_{α} v_{β})〉 \end{matrix}

(1)

Applying the Stokes theorem, the right side reduces to the flow through the boundary

\partial V

of the integration region V. The left side represents the dissipation within this volume:

\begin{matrix} E_{V} = - \int_{\partial V} d \vec{σ} \cdot 〈\vec{v} (p + \frac{1}{2} v_{α}^{2}) + ν \vec{ω} \times \vec{v}〉 \end{matrix}

(2)

This identity is valid for any volume, with the left side indicating viscous dissipation inside V and the right side representing the energy flow through the boundary

\partial V

Should a finite collection of vortex structures exist within the bulk, expanding this volume to infinite sphere results in the

\vec{ω} \times \vec{v}

term disappearing, as no vorticity persists at infinity.

Additionally, the velocity dictated by the Biot-Savart law diminishes as

| \vec{r} |^{- 3}

at infinity, so only the

\vec{v} p

term remains significant:

\begin{matrix} 〈E_{V}〉 \to - \int_{\partial V} d \vec{σ} \cdot 〈\vec{v} p〉 \end{matrix}

(3)

This representation of energy flow will remain finite even as the sphere expands if the pressure scales as

p \to - \vec{f} \cdot \vec{r}

, where

\vec{f}

is the local force at any given point on a large sphere:

\begin{matrix} 〈E〉 = f_{α} lim_{R \to \infty} R^{3} \int_{S_{2}} n_{α} n_{β} 〈v_{β} (R \vec{n})〉 \end{matrix}

(4)

What about the Kolmogorov energy flow? It persists within any finite volume surrounding the set of vortexes:

\begin{matrix} 〈E〉 = - \int_{V} d^{3} r 〈v_{β} \partial_{β} p + v_{α} v_{β} \partial_{β} v_{α}〉 = \\ - \int_{V} d^{3} r 〈v_{α} v_{β} \partial_{β} v_{α}〉 - \int_{\partial V} d \vec{σ} \cdot 〈\vec{v} p〉 \end{matrix}

(5)

The first term describes the Kolmogorov energy flow inside the volume V, and the second term represents the energy flow through the boundary.

Without a finite force

\vec{f}

acting on the boundary, such as with periodic boundary conditions, the boundary integral would be absent, and the Kolmogorov relation would be fully applicable:

\begin{matrix} 〈v_{α} v_{β} \partial_{β} v_{α}〉 = - 〈E〉 / V; \end{matrix}

(6)

This relation, alongside spatial symmetry properties in

R_{d}

, leads to the Kolmogorov three-point correlation:

\begin{matrix} 〈v_{α} ({\vec{r}}_{0}) v_{β} ({\vec{r}}_{0}) v_{γ} (\vec{r} + {\vec{r}}_{0})〉 = \frac{E}{(d - 1) (d + 2) V} (δ_{α γ} r_{β} + δ_{β γ} r_{α} - \frac{2}{d} δ_{α β} r_{γ}); \end{matrix}

(7)

In the conventional approach to the turbulence problem, periodic Gaussian random forces

\vec{f} (\vec{r}, t)

are added to the Navier-Stokes equations in the conventional approach, based on time averaging:

\begin{matrix} 〈E_{V}〉 = - \int_{V} d^{3} r 〈v_{β} \partial_{β} p - v_{β} f_{β} (\vec{r}, t) + v_{α} v_{β} \partial_{β} v_{α}〉 = \int_{V} d^{3} r 〈v_{β} f_{β} (\vec{r}, t)〉 \end{matrix}

(8)

As the force becomes uniformly distributed across space, we derive another definition with

E = \vec{f} \cdot \vec{P}

, where

\vec{P} = \int_{V} d^{3} r \vec{v}

is the total momentum.

The phenomenon of turbulence we study exhibits a universal spontaneous stochasticity that does not depend on boundary conditions.

As long as energy flows from the boundaries, confined turbulence in the middle will dissipate this energy through singular vortex tubes. This spontaneous stochasticity results from the random distribution of these singular tubes within the volume of the velocity flow [10]. The dual picture from our recent theory [7] represents these by random gaps in the momentum curve

\vec{P} (θ)

The relation between the energy pumping at the boundary and the distribution of vortex blobs in the bulk follows from the Biot-Savart integral:

\begin{matrix} \vec{v} (r) = - \vec{\nabla} \times \int d^{3} r^{'} \frac{\vec{ω} (r^{'})}{4 π | r - r^{'} |} \end{matrix}

(9)

Generally, a gradient of harmonic potential is added to the Biot-Savart integral, dependent on the boundary conditions. We consider the velocity decaying at infinity, thus not adding such a term.

The net linear momentum

〈\int d^{3} r \vec{v} (0) \cdot \vec{v} (\vec{r})〉

, generally, is not zero in our theory, as we impose no such restriction. This nonvanishing linear moment places our theory in the most general

k^{2}

(or Saffman) class.

On a large sphere

\partial V

with radius

R \to \infty

\begin{matrix} lim_{R \to \infty} R^{3} \vec{v} (R \vec{n}) \propto \\ \frac{1}{4 π} \sum_{blobs} \int_{blob} d^{3} r^{'} \vec{ω} (r^{'}) \times ({\vec{r}}^{'} - < \vec{r} >_{blob}); \end{matrix}

(10)

Here

< \vec{r} >_{blob}

is the geometric center of each blob. Substituting this into the identity (4), we directly relate the energy pumping with the forces at the boundary and the blob’s dipole moments of vorticity.

No forcing inside the flow is needed for this energy pumping; the energy flow starts at the boundary and propagates to numerous singular vorticity blobs, where it is finally dissipated. The distribution of these vorticity blobs is all we need for the turbulence theory. The forcing is required only as a boundary condition at infinity.

Another critical comment: with the velocity correlations growing with distance by the approximate K41 law, even the forcing at the remote boundary would influence the potential part of velocity in bulk. This boundary influence makes the energy cascade picture non-universal; it may depend upon the statistics of the random forcing.

Two asymptotic regimes manifesting this non-universality were observed for the energy spectrum

E (k, t)

: one for initial spectrum

E (k, 0) \propto k^{2}

and another for

E (k, 0) \propto k^{4}

. The potential velocity part differs for these regimes, as the first adds a constant velocity to the Biot-Savart integral. In the general case, it will be a harmonic potential flow with certain boundary conditions at infinity, with explicit continuous dependence of the boundary forces. The most general case is the

k^{2}

class, which does not require any restrictions.

Only the statistics of the rotational part of velocity, i.e., vorticity, could reach some universal regime independent of the boundary conditions at infinity. Certain discrete universality classes could exist as it is common in critical phenomena.

Unlike the potential part of velocity, vorticity is localized in singular regions—tubes and sheets, sparsely filling the space, as observed in numerical simulations. The potential part of velocity drops in the loop equations, and the remaining stochastic motion of the velocity circulation is equivalent to the vorticity statistics. Therefore, our solutions [7] of the loop equations [6,11] describe the internal stochastization of the decaying turbulence by a dual discrete system.

3.6. Mathematical Introduction. The Loop Equation and Its Solution

We derived a functional equation for the so-called loop average or Wilson loop in turbulence a while ago. All the references to our previous works can be found in a recent review paper [11].

The path to an exact solution by a dimensional reduction in this equation was proposed in the 1993 paper but has just been explored (see Figure 2). At the time, we could not compare a theory with anything but crude measurements in physical and numerical experiments at modest Reynolds numbers. All these experiments agreed with the K41 scaling, so the exotic equation based on unjustified methods of quantum field theory was premature. The specific prediction of the Loop equation, namely the Area law, could not be verified in DNS at the time with existing computer power.

The situation has changed over the last decades. No alternative microscopic theory based on the Navier-Stokes equation emerged, but our understanding of the strong turbulence phenomena grew significantly. On the other hand, the loop equations technology in the gauge theory also advanced over the last decades. The correspondence between the loop space functionals and the original vector fields was better understood, and various solutions to the gauge loop equations were found. In particular, the momentum loop equation was developed, similar to our momentum loop used below [12,13]. Recently, some numerical methods were found to solve loop equations beyond perturbation theory [14,15,16]. The loop dynamics was extended to quantum gravity, where it was used to study nonperturbative phenomena [17,18].

All these old and new developments made loop equations a major nonperturbative approach to gauge field theory. So, it is time to revive the hibernating theory of the loop equations in turbulence, where these equations are much simpler. The latest DNS [19,20,21,22] with Reynolds numbers of tens of thousands revealed and quantified violations of the K41 scaling laws. These numerical experiments are in agreement with so-called multifractal scaling laws [23].

Theoretically, we studied the loop equation in the confinement region (large circulation over large loop C) and justified the Area law suggested in ’93 on heuristic arguments. This law says that the tails of velocity circulation PDF in the confinement region are functions of the minimal area inside this loop. It was verified in DNS a few years ago [19], which triggered the further development of the geometric theory of turbulence [11,21,22]. In particular, the Area law was justified for flat and quadratic minimal surfaces, and an exact scaling law in confinement region

Γ \propto \sqrt{A r e a}

was derived [11]. The area law was verified with better precision in [20].

In the previous paper, [7], we have found a family of exact solutions of the loop equation for decaying turbulence [6,11]. This family describes a fixed trajectory of solutions with the universal time decay factor. The solutions are formulated in terms of the Wilson loop or loop average

\begin{matrix} Ψ [γ, C] = {〈exp (\frac{ı γ}{ν} \oint d \vec{C} (θ) \cdot \vec{v} (\vec{C} (θ)))〉}_{i n i t}; \end{matrix}

(11)

\begin{matrix} Ψ [γ, C] \Rightarrow {〈exp (\frac{ı γ}{ν} \oint d \vec{C} (θ) \vec{P} (θ))〉}_{E}; \end{matrix}

(12)

In the first equation (the definition), the averaging

〈\dots〉

goes over initial data for the solutions of the Navier-Stokes equation for velocity field

\vec{v} (\vec{r})

. In the second one (the solution), the averaging goes over the space of solutions

\vec{P} (θ)

of the loop equation [7]. We choose in this paper the parametrization of the loop with

ξ = \frac{θ}{2 π}

to match with the fermionic coordinates below (the parametrization is arbitrary, in virtue of parametric invariance of the loop dynamics).

The loop equation for the momentum loop

\vec{P} (θ)

follows from the Navier-Stokes equation for

\vec{v}

\begin{matrix} \partial_{t} v_{α} = ν \partial_{β} ω_{β α} - v_{β} ω_{β α} - \partial_{α} (p + \frac{v_{β}^{2}}{2}); \end{matrix}

(13)

\begin{matrix} \partial_{α} v_{α} = 0; \end{matrix}

(14)

\begin{matrix} ω_{β α} = \partial_{β} v_{α} - \partial_{α} v_{β} \end{matrix}

(15)

After some transformations, replacing velocity and vorticity with the functional derivatives of the loop functional, we found the following momentum loop equation in [7,11]

\begin{matrix} ν \partial_{t} \vec{P} = - γ^{2} {(Δ \vec{P})}^{2} \vec{P} + Δ \vec{P} (γ^{2} \vec{P} \cdot Δ \vec{P} + ı γ (\frac{{(\vec{P} \cdot Δ \vec{P})}^{2}}{Δ {\vec{P}}^{2}} - {\vec{P}}^{2})); \end{matrix}

(16)

\begin{matrix} \vec{P} (θ) \equiv \frac{\vec{P} (θ^{+}) + \vec{P} (θ^{-})}{2}; \end{matrix}

(17)

\begin{matrix} Δ \vec{P} (θ) \equiv \vec{P} (θ^{+}) - \vec{P} (θ^{-}); \end{matrix}

(18)

The momentum loop has a discontinuity

Δ \vec{P} (θ)

at every parameter

0 < θ \leq 1

, making it a fractal curve in complex space

C_{d}

. The details can be found in [7,11]. We will skip the arguments

t, θ

in these loop equations, as there is no explicit dependence of these equations on either of these variables. This Anzatz represents a plane wave in loop space, solving the loop equation for the Wilson loop due to the lack of direct dependence of the loop operator on the shape of the loop.

The superposition of these plane wave solutions would solve the Cauchy problem in loop space: find the stochastic function

\vec{P} (θ)

t = 0

, providing the initial velocity field distribution. Formally, the initial distribution

W_{0} [P]

of the momentum field

\vec{P} (θ)

is given by inverse functional Fourier transform.

\begin{matrix} W_{0} [P] = \int D C δ^{3} (\vec{C} [0]) Ψ {[C, γ]}_{t = 0} exp (- \frac{ı γ}{ν} \int d \vec{C} (θ) \cdot \vec{P} (θ)) \end{matrix}

(19)

This path integral was computed in [7,11] for a special stochastic solution of the Navier-Stokes equation: the global rotation with Gaussian random rotation matrix. The initial velocity distribution is Gaussian, with a slowly varying correlation function. The corresponding loop field reads (we set

γ = 1

for simplicity in this section)

\begin{matrix} Ψ_{0} [C] \equiv Ψ {[C, 1]}_{t = 0} = exp (- \frac{1}{2 ν^{2}} \int_{C} d \vec{C} (θ) \cdot d \vec{C} (θ^{'}) f (\vec{C} (θ) - \vec{C} (θ^{'}))) \end{matrix}

(20)

where

f (\vec{r})

is the velocity correlation function

〈v_{α} (r) v_{β} (r^{'})〉 = (δ_{α β} - \partial_{α} \partial_{β} \partial_{μ}^{- 2}) f (r - r^{'})

(21)

The potential part drops out in the closed loop integral. The correlation function varies at the macroscopic scale, which means that one could expand it in the Taylor series

f (r - r^{'}) \to f_{0} - f_{1} {(r - r^{'})}^{2} + \dots

(22)

The first term

f_{0}

is proportional to initial energy density,

\frac{1}{2} 〈v_{α}^{2}〉 = \frac{d - 1}{2} f_{0}

(23)

and the second one is proportional to initial energy dissipation rate

E_{0}

f_{1} = \frac{E_{0}}{2 d (d - 1) ν}

(24)

where

d = 3

is the dimension of space. The constant term in (22) as well as

r^{2} + r^{' 2}

terms drop from the closed loop integral, so we are left with the cross-term

r r^{'}

, which reduces to a full square

\begin{matrix} Ψ_{0} [C] \to exp (- \frac{f_{1}}{ν^{2}} {(\oint d C_{α} (θ) C_{β} (θ))}^{2}) \end{matrix}

(25)

This distribution is almost Gaussian: it reduces to Gaussian one by extra integration

\begin{matrix} Ψ_{0} [C] \to const \int (d ϕ) exp (- ϕ_{α β}^{2}) exp (2 ı \frac{\sqrt{f_{1}}}{ν} ϕ_{μ ν} \oint d C_{μ} (θ) C_{ν} (θ)) \end{matrix}

(26)

The integration here involves all

\frac{d (d - 1)}{2} = 3

independent

α < β

components of the antisymmetric tensor

ϕ_{α β}

. Note that this is ordinary integration, not the functional one.

This distribution can be translated into the momentum loop space. Here is the resulting stochastic function

\vec{P} (θ)

, defined by the Fourier expansion on the circle

\begin{matrix} P_{α} (θ) = \sum_{odd n = 1}^{\infty} P_{α, n} e^{ı n θ} + {\bar{P}}_{α, n} e^{- ı n θ}; \end{matrix}

(27)

\begin{matrix} P_{α, n} = N (0, 1); \end{matrix}

(28)

\begin{matrix} {\bar{P}}_{α, n} = \frac{4 \sqrt{f_{1}}}{n ν} ϕ_{α β} P_{β, n}; \end{matrix}

(29)

\begin{matrix} ϕ_{α β} = - ϕ_{β α}; \end{matrix}

(30)

\begin{matrix} ϕ_{α β} = N (0, 1) \forall α < β; \end{matrix}

(31)

At fixed tensor

ϕ

the correlations are

\begin{matrix} {〈P_{α, n} P_{β, m}〉}_{t = 0} = \frac{4 \sqrt{f_{1}}}{m ν} δ_{n m} ϕ_{α β}; \end{matrix}

(32)

\begin{matrix} {〈P_{α} (θ) P_{β} (θ^{'})〉}_{t = 0} = 2 ı \frac{\sqrt{f_{1}}}{ν} ϕ_{α β} sign (θ^{'} - θ); \end{matrix}

(33)

\begin{matrix} Ψ_{0} [C] = {〈exp (\frac{ı}{ν} \oint d \vec{C} (θ) \vec{P} (θ))〉}_{P, ϕ} \end{matrix}

(34)

Though this special solution does not describe isotropic turbulence, it helps understand the mathematical properties of the loop technology. In particular, it shows the significance of the discontinuities of the momentum loop

\vec{P} (θ)

Rather than solving the Cauchy problem, we are looking for an attractor: the fixed trajectory for

\vec{P} (θ, t)

with some universal probability distribution related to the decaying turbulence statistics.

The following transformation reveals the hidden scaling invariance of decaying turbulence

\begin{matrix} \vec{P} = \sqrt{\frac{ν}{2 (t + t_{0})}} \frac{\vec{F}}{γ} \end{matrix}

(35)

The new vector function

\vec{F}

satisfies an equation

\begin{matrix} 2 \partial_{τ} \vec{F} = (1 - {(Δ \vec{F})}^{2}) \vec{F} + Δ \vec{F} (γ^{2} \vec{F} \cdot Δ \vec{F} + ı γ (\frac{{(\vec{F} \cdot Δ \vec{F})}^{2}}{Δ {\vec{F}}^{2}} - {\vec{F}}^{2})); \end{matrix}

(36)

\begin{matrix} τ = log (t + t_{0}) \end{matrix}

(37)

This equation is invariant under translations of the new variable

τ = log (t + t_{0})

, corresponding to the rescaling/translation of the original time.

\begin{matrix} t \Rightarrow λ t + (λ - 1) t_{0} \end{matrix}

(38)

There are two consequences of this invariance.

There is a fixed point for $\vec{F}$ .
The approach to this fixed point is exponential in $τ$ , which is power-like in original time.

Both of these properties were used in [7]: the first one was used to find a fixed point, and the second one was used to derive the spectral equation for the anomalous dimensions $λ_{i}$ of decay $t^{- λ_{i}}$ of the small deviations from these fixed points. In this paper, we only consider the fixed point, leaving the exciting problem of the spectrum of anomalous dimensions for future research.

3.7. The Big and Small Euler Ensembles

Let us remember the basic properties of the fixed point for

\vec{F}

in [7]. It is defined as a limit

N \to \infty

of the polygon

{\vec{F}}_{0} \dots {\vec{F}}_{N} = {\vec{F}}_{0}

with the following vertices

\begin{matrix} {\vec{F}}_{k} = \frac{\{cos (α_{k}), sin (α_{k}), i cos (\frac{β}{2})\}}{2 sin (\frac{β}{2})}; \end{matrix}

(39)

\begin{matrix} θ_{k} = \frac{k}{N}; β = \frac{2 π p}{q}; N \to \infty; \end{matrix}

(40)

\begin{matrix} α_{k + 1} = α_{k} + σ_{k} β; σ_{k} = \pm 1, β \sum σ_{k} = 2 π p r; \end{matrix}

(41)

The parameters

\hat{Ω}, p, q, r, σ_{0} \dots σ_{N} = σ_{0}

are random, making this solution for

\vec{F} (θ)

a fixed manifold rather than a fixed point. We suggested calling this manifold the big Euler ensemble of just the Euler ensemble.

It is a fixed point of (36) with the discrete version of discontinuity and principal value:

\begin{matrix} Δ \vec{F} \equiv {\vec{F}}_{k + 1} - {\vec{F}}_{k}; \end{matrix}

(42)

\begin{matrix} \vec{F} \equiv \frac{{\vec{F}}_{k + 1} + {\vec{F}}_{k}}{2} \end{matrix}

(43)

Both terms of the right side (36) vanish; the term proportional to

Δ \vec{F}

and the term proportional to

\vec{F}

. Otherwise, we would have

\vec{F} ‖ Δ \vec{F}

, leading to zero vorticity [7]. The ensemble of all the different solutions is called the big Euler ensemble. The integer numbers

σ_{k} = \pm 1

came as the solution of the loop equation, and the requirement of the rational

\frac{p}{q}

came from the periodicity requirement.

We can use integration (summation) by parts to write the circulation as follows (in virtue of periodicity):

\begin{matrix} \oint d \vec{C} (θ) \cdot \vec{P} (θ) = - \oint d \vec{P} (θ) \cdot \vec{C} (θ); \end{matrix}

(44)

\begin{matrix} \sum_{k} Δ C_{k} {\vec{P}}_{k} = - \oint Δ {\vec{P}}_{k} \cdot {\vec{C}}_{k}; \end{matrix}

(45)

A remarkable property of this solution

\vec{P} (θ, t)

of the loop equation is that even though it satisfies the complex equation and has an imaginary part, the resulting circulation (44) is real! The imaginary part of the

\vec{P} (θ, t)

does not depend on

θ

and thus drops from the integral

\oint d \vec{P} (θ, t) \cdot \vec{C} (θ)

There is, in general, a larger manifold of periodic solutions to the discrete loop equation, which has all three components of

{\vec{F}}_{k}

complex and varying along the polygon.

We could not find a global parametrization of such a solution1. Instead, we generated it numerically by taking a planar closed polygon and evolving its vertices

{\vec{F}}_{k}

by a stochastic process in the local tangent plane to the surface of the equations in multi-dimensional complex space.

We could not submit such a solution to an extra restriction

Im {\vec{F}}_{k} = const

needed to make circulation real. We cannot prove that such a general solution does not exist but rather take the Euler ensemble as a working hypothesis and investigate its properties.

This ensemble can be solved analytically in the statistical limit and has nice physical properties, matching the expected behavior of the decaying turbulence solution.

We assign equal weights to all elements of this set; we call this conjecture the ergodic hypothesis. This prescription is similar to assigning equal weights to each triangulation of curved space with the same topology in dynamically triangulated quantum gravity [24]. Mathematically, this is the most symmetric weight assignment, and there are general expectations that various discrete theories converge into the same symmetry classes of continuum theories in the statistical limit. This method works remarkably well in two dimensions [25,26,27], providing the same correlation functions as continuum gravity (Liouville theory [28]).

The fractions

\frac{p}{q}

with fixed denominator are counted by Euler totient function

φ (q)

[29]

\begin{matrix} φ (q) = \sum_{\begin{matrix} p = 1 \\ (p, q) \end{matrix}}^{q - 1} 1 = q \prod_{p | q} (1 - \frac{1}{p}); \end{matrix}

(46)

For example

φ (16) = 8

and

φ (17) = 16

In some cases, one can analytically average over spins

σ

in the big Euler ensemble, reducing the problem to computations of averages over the small Euler ensemble

E (N) : N, p, q, r

with the measure induced by averaging over the spins in the big Euler ensemble.

In this paper, we perform this averaging over

σ

analytically, without any approximations, reducing it to a partition function of a certain quantum mechanical system with Fermi particles. This partition function is calculable using a WKB approximation in the statistical limit

N \to \infty

4. The Markov Chain and Its Fermionic Representation

Here is a new representation of the Euler ensemble, leading us to the exact analytic solution below.

We start by replacing independent random variables

σ

with fixed sum by a Markov process, as suggested in [7]. We start with n random values of

σ_{i} = 1

and remaining

N - n

values of

σ_{i} = - 1

. Instead of averaging over all of these values simultaneously, we follow a Markov process of picking

σ_{N}, \dots σ_{1}

one after another. At each step, there will be

M = N, \dots 0

remaining

σ

. We get a transition

n \Rightarrow n - 1

with probability

\frac{n}{M}

and

n \Rightarrow n

with complementary probability.

Multiplying these probabilities and summing all histories of the Markov process is equivalent to the computation of the product of the Markov matrices

\begin{matrix} \prod_{M = 1}^{N} Q (M); \end{matrix}

(47)

\begin{matrix} Q (M) | n 〉 = \frac{M - n}{M} | n 〉 + \frac{n}{M} | n - 1 〉; \end{matrix}

(48)

This Markov process will be random until

n = 0

. After that, all remaining

σ_{k}

will have negative signs and be taken with probability 1, keeping

n = 0

The expectation value of some function

X (\{σ\})

reduces to the matrix product

\begin{matrix} P [X] = \sum_{n = 0}^{N_{+}} 〈n| (\prod_{M = 1}^{N} \hat{Q} (M)) \cdot X \cdot |N_{+}〉; \end{matrix}

(49)

\begin{matrix} \hat{Q} (M) \cdot X | n 〉 = \frac{n}{M} X (σ_{M} \to 1) | n - 1 〉 + \frac{M - n}{M} X (σ_{M} \to - 1) | n 〉 \end{matrix}

(50)

Here

N_{+} = (N + \sum σ_{l}) / 2 = (N + q r) / 2

is the number of positive sigmas. The operator

\hat{Q} (M)

sets in

X | n 〉

the variable

σ_{M}

to 1 with probability

\frac{n}{M}

and to

- 1

with complementary probability. The generalization of the Markov matrix

Q (M)

to the operator

\hat{Q} (M)

will be presented shortly.

Once the whole product is applied to X, all the sigma variables in all terms will be specified so that the result will be a number.

This Markov process is implemented as a computer code in [30], leading to a fast simulation with

O (N^{0})

memory requirement.

Now, we observe that quantum Fermi statistics can represent the Markov chain of Ising variables. Let us construct the operator

\hat{Q} (M)

with Fermionic creation and annihilation operators, with occupation numbers

ν_{k} = (1 + σ_{k}) / 2 = (0, 1)

. These operators obey (anti)commutation relations, and they create/annihilate

σ = 1

state as follows (with Kronecker delta

δ [n] \equiv δ_{n, 0}

\begin{matrix} {[a_{i}, a_{j}^{†}]}_{+} = δ_{i j}; \end{matrix}

(51)

\begin{matrix} {[a_{i}, a_{j}]}_{+} = {[a_{i}^{†}, a_{j}^{†}]}_{+} = 0; \end{matrix}

(52)

\begin{matrix} a_{n}^{†} | σ_{1}, \dots, σ_{N} 〉 = δ [σ_{n} + 1] | σ_{1}, \dots, σ_{n} \to 1, \dots σ_{N} 〉; \end{matrix}

(53)

\begin{matrix} a_{n} | σ_{1}, \dots, σ_{N} 〉 = δ [σ_{n} - 1] | σ_{1}, \dots, σ_{n} \to - 1, \dots σ_{N} 〉; \end{matrix}

(54)

\begin{matrix} {\hat{ν}}_{n} = a_{n}^{†} a_{n}; \end{matrix}

(55)

\begin{matrix} {\hat{ν}}_{n} | σ_{1}, \dots, σ_{N} 〉 = δ [σ_{n} - 1] | σ_{1}, \dots, σ_{N} 〉 \end{matrix}

(56)

The number

n (M)

of positive sigmas

\sum_{l = 1}^{M} δ [σ_{l} - 1]

coincides with the occupation number of these Fermi particles.

\begin{matrix} \hat{n} (M) = \sum_{l = 1}^{M} {\hat{ν}}_{l}; \end{matrix}

(57)

This relation leads to the representation

\begin{matrix} \hat{Q} (M) = {\hat{ν}}_{M} \frac{\hat{n} (M)}{M} + (1 - {\hat{ν}}_{M}) \frac{M - \hat{n} (M)}{M}; \end{matrix}

(58)

The variables

σ_{l}

can also be expressed in terms of this operator algebra by using

\begin{matrix} {\hat{σ}}_{l} = 2 {\hat{ν}}_{l} - 1 . \end{matrix}

(59)

The Wilson loop in (11) can now be represented as an average over the small Euler ensemble

E (N)

of a quantum trace expression

\begin{matrix} Ψ [γ, C] = & \frac{{〈tr (\hat{Z} (q r) exp (\frac{i γ}{ν} \sum_{l} Δ {\vec{C}}_{l} \cdot \hat{Ω} \cdot {\vec{P}}_{l} (t)) \prod_{M = 1}^{N} \hat{Q} (M))〉}_{\hat{Ω}, E (N)}}{{〈tr (\hat{Z} (q r) \prod_{M = 1}^{N} \hat{Q} (M))〉}_{E (N)}}, \end{matrix}

(60)

\begin{matrix} \hat{Z} (s) = & \oint \frac{d ω}{2 π} exp (ı ω (\sum_{l} {\hat{σ}}_{l} - s)); \end{matrix}

(61)

\begin{matrix} Δ {\vec{C}}_{l} = & \vec{C} (\frac{l + 1}{N}) - \vec{C} (\frac{l}{N}), \end{matrix}

(62)

\begin{matrix} {\vec{P}}_{l} (t) = & \sqrt{\frac{ν}{2 (t + t_{0})}} \frac{{\vec{F}}_{l}}{γ}, \hat{Ω} \in O (3), \end{matrix}

(63)

\begin{matrix} {\vec{F}}_{l} = & \frac{\{cos ({\hat{α}}_{l}), sin ({\hat{α}}_{l}), 0\}}{2 sin (\frac{β}{2})}, \end{matrix}

(64)

\begin{matrix} E (N) : & p, q, r \in Z with 0 < p < q < N, \gcd (p, q) = 1, - N \leq q r \leq N, \end{matrix}

(65)

\begin{matrix} {\hat{α}}_{l} = & β \sum_{k = 1}^{l - 1} (2 {\hat{ν}}_{k} - 1); \end{matrix}

(66)

The last component of the vector

{\vec{F}}_{l}

is set to 0 as this component does not depend on l and yields zero in the sum over the loop

\sum_{l} Δ {\vec{C}}_{l} = 0

The proof of equivalence to the combinatorial formula with an average over

σ_{l} = \pm 1

can be given using the following Lemma (obvious for a physicist).

Lemma 1.

The operators

{\hat{ν}}_{l}

all commute with each other.

Proof.

Using commutation relations, we can write

\begin{matrix} {\hat{ν}}_{l} {\hat{ν}}_{n} = a_{l}^{†} (δ_{l n} - a_{n}^{†} a_{l}) a_{n} = a_{l}^{†} a_{n} δ_{l n} - a_{l}^{†} a_{n}^{†} a_{l} a_{n} \end{matrix}

(67)

Interchanging indexes

l, n

in this relation, we see that the first term does not change due to Kronecker delta, and the second term does not change because

a_{l}^{†}, a_{n}^{†}

anti-commute, as well as

a_{l}, a_{n}

, so the second term is symmetric as well. Therefore,

{\hat{ν}}_{l} {\hat{ν}}_{n} = {\hat{ν}}_{n} {\hat{ν}}_{l}

□

Theorem 1.

The trace formula (60) equals the expectation value of the momentum loop ansatz (12), (35), (39) in the big Euler ensemble.

Proof.

As all the operators

{\hat{ν}}_{l}

commute with each other, the operators

\hat{Q} (M)

can be applied in arbitrary order to the states

Σ = | σ_{1}, \dots σ_{N} 〉

involved in the trace. The same is true about individual terms in the circulation in the exponential of the Wilson loop. These terms

{\vec{F}}_{l}

involve the operators

{\hat{α}}_{l}

, which commute with each other and with each

\hat{Q} (M)

. Thus, we can use the ordered product of the operators

{\hat{G}}_{l} = \hat{Q} (l) exp (ı ω {\hat{σ}}_{l} + \frac{i γ}{ν} Δ {\vec{C}}_{l} \cdot {\vec{P}}_{l} (t))

. Each of the operators

{\hat{G}}_{l}

acting in turn on arbitrary state

Σ

will create two terms with

δ [σ_{l} \pm 1]

. The exponential in

{\hat{G}}_{l}

will involve

{\hat{σ}}_{k}, k \leq l

. As a result of the application of the operator

{\hat{Z}}_{l} = \prod_{k = 1}^{l} {\hat{G}}_{k}

to the state vector

Σ

we get

2^{l}

terms with

Σ \prod_{k = 1}^{l} δ [σ_{k} - η_{k}], η_{k} = \pm 1

. The factors

{\hat{Z}}_{l}

will involve only

{\hat{σ}}_{k}, k \leq l

, which are all reduced to

η_{k}, k \leq l

in virtue of the product of the Kronecker deltas. Multiplying all operators

{\hat{G}}_{M}

will lead to superposition

{\hat{Π}}_{N}

2^{N}

terms, each with product

\prod_{M = 1}^{N} δ [σ_{M} - η_{M}]

with various choices of the signs

η_{i} = \pm 1

for each i. Furthermore, the product of Kronecker deltas will project the total sum of

2^{N}

combinations of the states

Σ

in the trace

tr \dots

to a single term corresponding to a particular history

η_{1}, \dots η_{N}

of the Markov process. The product of Kronecker deltas in each history will be multiplied by the same state vector

Σ

, by the product of Markov transition probabilities, and by the exponential

exp (\frac{i γ}{ν} \sum_{l} Δ {\vec{C}}_{l} \cdot \hat{Ω} \cdot {\vec{P}}_{l} (t))

with the operators

\hat{σ}

{\vec{P}}_{k} (t)

replaced by numbers

η

leading to the usual numeric

{\vec{P}}_{l} (t)

. The transition probabilities of the Markov process are designed to reproduce combinatorial probabilities of random sigmas, adding up to one after summation over histories [31]. The integration over

ω

will produce

δ [\sum_{l} {\hat{η}}_{l} - s]

. This delta function will reduce the trace to the required sum over all histories of the Markov process with a fixed

\sum_{l} η_{l}

. □

We have found a third vertex of the triangle of equivalent theories: the decaying turbulence in three-dimensional space, the fractal curve in complex space, and Fermi particles on a ring. By degrees of freedom, this is a one-dimensional Fermi-gas in the statistical limit

N \to \infty

. However, there is no local Hamiltonian in this quantum partition function, just a trace of certain products of operators in Fock space. So, an algebraic (or quantum statistical) problem remains to find the continuum limit of this theory of the fermion ring.

This problem is addressed in the next section.

5. The Continuum Limit

As we shall shortly see, in the continuum limit

N \to \infty

, the accumulated numbers of Fermi particles

ν_{k} = 1

and Dirac holes

ν_{k} = 0

tend to some classical functions of "position"

ξ = \frac{k}{N}

, leading to the exact solution.

5.1. Path Integral over Markov Histories

Let us represent the product

Π_{N}

of the transitional probabilities of the particular history of the Markov processes as follows (with

n_{\pm} \equiv n_{\pm} (l), Δ n_{\pm} = - 1

)

\begin{matrix} Π_{N} = exp (N Λ_{N}); \end{matrix}

(68)

\begin{matrix} Λ_{N} = \frac{1}{N} \sum_{l} (Δ n_{+} log (\frac{n_{+}}{n_{+} + n_{-}}) + Δ n_{-} log (\frac{n_{-}}{n_{+} + n_{-}})); \end{matrix}

(69)

\begin{matrix} n_{+} = \sum_{k \leq l} ν_{k}; \end{matrix}

(70)

\begin{matrix} n_{-} = \sum_{k \leq l} (1 - ν_{k}); \end{matrix}

(71)

These

n_{\pm}

are net numbers of

η = \pm 1

in terms of Ising spins or occupation numbers

ν_{k} = (1, 0)

in the Fermi representation. There is an extra constraint on the Markov process

\begin{matrix} n_{+} + n_{-} = l; \forall l \end{matrix}

(72)

which follows from the above definition in terms of the occupation numbers. We can redefine

n_{\pm}

as N times the piecewise constant functions.

\begin{matrix} n_{\pm} = N f_{\pm} (ξ); \end{matrix}

(73)

\begin{matrix} f_{\pm} (ξ) = \sum_{k = 1}^{N ξ} \frac{ν_{k}}{N}; \end{matrix}

(74)

\begin{matrix} f_{\pm}^{'} (ξ) = \sum_{l = 1}^{N} δ (ξ - \frac{l}{N}) \sum_{k = 1}^{l} \frac{ν_{k}}{N}; \end{matrix}

(75)

\begin{matrix} 0 < ξ < 1; \end{matrix}

(76)

The sums can be rewritten as Lebesgue integrals

\begin{matrix} Λ_{N} = \int_{1}^{0} (d f_{+} (ξ) log (\frac{f_{+} (ξ)}{ξ}) + d f_{-} (ξ) log (\frac{f_{-} (ξ)}{ξ})) \end{matrix}

(77)

The sum over histories of the Markov process will become a path integral over the difference

ϕ = f_{+} (ξ) - f_{-} (ξ)

\begin{matrix} \sum_{η_{.} = \pm 1} exp (N (Λ_{N} + ı Λ_{N}^{(1)})) \to \int D ϕ exp (N (Λ_{N} + ı Λ_{N}^{(1)})) \end{matrix}

(78)

This path integral will be dominated by the "classical history," maximizing the product of transitional probabilities if such a classical trajectory exists.

The first term (without the circulation term) brings the variational problem

\begin{matrix} max_{ϕ} Λ_{N} [ϕ]; \end{matrix}

(79)

\begin{matrix} Λ_{N} [ϕ] = \int_{1}^{0} d ξ (\frac{d f_{+}}{d ξ} log (\frac{f_{+}}{ξ}) + \frac{d f_{-}}{d ξ} log (\frac{f_{-}}{ξ})); \end{matrix}

(80)

\begin{matrix} f_{\pm} (ξ) = \frac{1}{2} (ξ \pm ϕ (ξ)); \end{matrix}

(81)

\begin{matrix} f_{\pm} (ξ) \geq 0; \end{matrix}

(82)

This problem is, however, a degenerate one, as the functional reduces to the integral of the total derivative:

\begin{matrix} \frac{δ Λ_{N} [ϕ]}{δ ϕ (ξ)} = 0; \\ Λ_{N} [ϕ] = \int_{1}^{0} d (f_{+} log f_{+} + f_{-} log f_{-}) + 1 + \int_{0}^{1} d ξ log ξ = \end{matrix}

(83)

\begin{matrix} - \frac{1}{2} (1 - s) log (1 - s) - \frac{1}{2} (1 + s) log (1 + s) + log (2); \end{matrix}

(84)

It depends on the boundary condition

ϕ (0) = 0, ϕ (1) = s

but not on the shape of

ϕ (ξ)

This expression matches the Stirling formula for the logarithm of the binomial coefficient in the combinatorial solution [7] for the Euler ensemble

\begin{matrix} lim_{N \to \infty} \frac{log (\binom{N}{N (1 + s) / 2})}{N} = - \frac{1}{2} (1 - s) log (1 - s) - \frac{1}{2} (1 + s) log (1 + s) + log (2) \end{matrix}

(85)

This

Λ (s) = Λ_{\infty} (s)

is a smooth even function of s taking positive values from

Λ (\pm 1) = 0

to the maximal value

Λ (0) = log (2)

(see Figure 9).

Now, let us add the circulation term to the exponential of the partition function (60). This term can be directly expressed in terms of the difference between our two densities

N ϕ (ξ) = N f_{+} (ξ) - N f_{-} (ξ)

\begin{matrix} ı N Λ_{N}^{(1)} [ϕ, C_{Ω}] = \frac{ı}{\sqrt{2 ν t}} \int_{0}^{1} d {\vec{C}}_{Ω} (ξ) \cdot \vec{F} (ξ); \end{matrix}

(86)

\begin{matrix} \vec{F} (ξ) = \frac{\{sin (β N ϕ (ξ)), cos (β N ϕ (ξ)), 0\}}{2 sin (β / 2)}; \end{matrix}

(87)

\begin{matrix} {\vec{C}}_{Ω} (θ) = \hat{Ω} \cdot \vec{C} (θ); \end{matrix}

(88)

The key assumption is, of course, the existence of the smooth limit of the charge density

ϕ (ξ)

of these fermions when they are densely covering this loop.

We are working with

α (ξ) = β N ϕ (ξ)

in the following.

The measure for paths

[D α]

is undetermined. The derivatives of these alphas were quantized in the original Fermi theory: each step

α^{'} (ξ) \approx N Δ α = N β σ = \pm N β

As we demonstrate below, in continuum theory, this discrete distribution can be replaced by a Gaussian distribution with the same mean square

\begin{matrix} \sum_{α^{'} = \pm N β} \leftrightarrow \int d α^{'} exp (- \frac{{(α^{'})}^{2}}{2 N^{2} β^{2}}) \end{matrix}

(89)

To demonstrate that, we consider in the critical region

β^{2} \sim N^{- 1} \to 0

the most general term that arises in the moments of the circulation in (86) (see [32] for some exact computations of these moments)

\begin{matrix} 2^{- N} \sum_{σ_{i} = \pm 1} exp (ı β \sum_{i} k_{i} σ_{i}) = \prod_{i} cos β k_{i} \to exp (- β^{2} / 2 \sum_{i} k_{i}^{2}) \end{matrix}

(90)

where

k_{i}

are some integers. With a large number N of these integers, the sum in the exponential becomes an integral, which is equivalent to a Gaussian integral

\begin{matrix} exp (- β^{2} / 2 \sum_{i} k_{i}^{2}) = \prod_{i} \int_{- \infty}^{\infty} \frac{d σ_{i}}{\sqrt{2 π}} exp (- σ_{i}^{2} / 2) exp (ı β k_{i} σ_{i}) \to exp (- N β^{2} / 2 \int_{0}^{1} d ξ k {(ξ)}^{2}) \end{matrix}

(91)

We arrive at the standard path integral measure

\begin{matrix} \int [D α] = \int D α (ξ) exp (- \int_{0}^{1} d ξ \frac{{(α^{'})}^{2}}{2 N β^{2}}); \end{matrix}

(92)

\begin{matrix} \frac{\int [D α] exp (ı N \int_{0}^{1} d ξ α (ξ) K (ξ))}{\int [D α]} = exp (- \frac{1}{2} N^{2} \int \int d ξ_{1} d ξ_{2} K (ξ_{1}) K (ξ_{2}) G (ξ_{1}, ξ_{2})); \end{matrix}

(93)

\begin{matrix} G (ξ_{1}, ξ_{2}) = 〈α (ξ_{1}) α (ξ_{2})〉; \end{matrix}

(94)

The next section will compute this Green’s function

G (ξ_{1}, ξ_{2})

Thus, we arrive at the following path integral in the continuum limit

\begin{matrix} Ψ [C] = \frac{\sum_{p < q; (p, q)} \int_{Ω \in O (3)} d Ω \int [D α] exp (ı \frac{\int_{0}^{1} d ξ Im (C_{Ω}^{'} (ξ) exp (ı α (ξ)))}{2 sin (π p / q) \sqrt{2 ν (t + t_{0})}})}{\sum_{p < q; (p, q)} | O (3) | \int [D α]}; \end{matrix}

(95a)

\begin{matrix} C_{Ω} (θ) = \vec{C} (θ) \cdot \hat{Ω} \cdot {ı, 1, 0}; \end{matrix}

(95b)

We get the

U (1)

statistical model with the boundary condition

α (1) = α (0) + β N s

. The period

β N s = 2 π p r

is a multiple of

2 π

, which is irrelevant at

N \to \infty

. The effective potential for this theory is a linear function of the loop slope

{\vec{C}}^{'} (ξ)

This model is yet another representation of the Euler ensemble, suitable for the continuum limit.

5.2. Matching Path Integral with Combinatorial Sums in Big Euler Ensemble

The results of the path integration over

α

must match the combinatorial calculations with

σ_{l} = \pm 1

in the limit of large N. Without the interaction provided by the circulation term in (95a), this path integral is dominated by a linear trajectory

\begin{matrix} α_{c l} (ξ) = β N ξ s; \end{matrix}

(96)

We already saw the match between the classical Action

Λ_{N} [ϕ (ξ) = ξ s]

and the asymptotic value of the logarithm of the Binomial coefficient of the combinatorial solution for the sum over

σ

variables.

Let us verify some examples of the expectation values over

σ

. The simplest is (with

n \neq m

)

\begin{matrix} {〈σ_{n} σ_{m}〉}_{\sum σ = N s} \end{matrix}

(97)

The direct calculation using methods of [7,32] leads to

\begin{matrix} {〈σ_{n} σ_{m}〉}_{\sum σ = N s} = - \oint \frac{d ω}{2 π Z} e^{ı ω N s} cos ((N - 2) ω) {sin}^{2} (ω) = \frac{(1 - N s^{2})}{2^{N - 3} Z N (1 - s^{2})} (\binom{N - 2}{\frac{1}{2} (N + N s - 2)}); \end{matrix}

(98)

\begin{matrix} Z = \oint \frac{d ω}{2 π} e^{ı ω N s} cos (N ω) = 2^{- N} (\binom{N}{\frac{1}{2} (s N + N)}) \end{matrix}

(99)

Using Gamma function properties, this ratio simplifies to

\begin{matrix} \frac{N s^{2} - 1}{N - 1} \end{matrix}

(100)

This result can be derived from symmetry without any integration.

\begin{matrix} {〈σ_{n} σ_{m}〉}_{\sum σ = N s} = A (N, s) (1 - δ_{n m}) + δ_{n m}; \end{matrix}

(101)

\begin{matrix} \sum_{n, m} {〈σ_{n} σ_{m}〉}_{\sum σ = N s} = s^{2} N^{2} = A (N, s) N (N - 1) + N \end{matrix}

(102)

\begin{matrix} A (N, s) = \frac{N s^{2} - 1}{N - 1} \end{matrix}

(103)

The same limit

A (\infty, s) = s^{2}

follows from the classical trajectory

\begin{matrix} {〈σ_{n} σ_{m}〉}_{\sum σ = N s} \to \frac{α_{c l}^{'} (ξ)}{β N} \frac{α_{c l}^{'} (ξ^{'})}{β N} = s^{2} \end{matrix}

(104)

Let us consider less trivial example [7,32]

\begin{matrix} U_{n, m} \to \sum_{k = n}^{m - 1} exp (ı α_{k, n}); \end{matrix}

(105)

\begin{matrix} α_{k, n} = β \sum_{\begin{matrix} l = 0 \\ l \neq n \end{matrix}}^{k} σ_{l}; \end{matrix}

(106)

We shall set

s = 0

, as this is the leading contribution to the partition function. The expectation value of

U_{n, m}

in our continuum limit becomes

\begin{matrix} 〈U_{n, m}〉 = N \int_{ξ_{1}}^{ξ_{2}} d ξ 〈exp (ı α (ξ))〉 = N \int_{ξ_{1}}^{ξ_{2}} d ξ exp (- \frac{1}{2} G (ξ, ξ)) \end{matrix}

(107)

Here

G (ξ_{1}, ξ_{2})

is the Green’s function corresponding to a 1D particle on a line interval

ξ \in (0, 1)

, introduced in the previous section. It satisfies the equation, which follows from our Gaussian Action

\begin{matrix} \partial_{ξ}^{2} G (ξ, ξ^{'}) = - β^{2} N δ (ξ - ξ^{'}); \end{matrix}

(108)

\begin{matrix} G (0, ξ^{'}) = G (ξ, 0) = 0; \end{matrix}

(109)

The solution is

\begin{matrix} G (ξ, ξ^{'}) = \frac{1}{2} β^{2} N (ξ + ξ^{'} - | ξ - ξ^{'} |) \end{matrix}

(110)

Thus, we find

\begin{matrix} 〈U_{n, m}〉 = N \int_{ξ_{1}}^{ξ_{2}} d ξ exp (- \frac{1}{2} β^{2} N ξ) = \frac{2}{β^{2}} (exp (- y / 2) - exp (- x / 2)); \end{matrix}

(111)

\begin{matrix} x = β^{2} N ξ_{1}; \end{matrix}

(112)

\begin{matrix} y = β^{2} N ξ_{2}; \end{matrix}

(113)

in agreement with [7,32] in the critical region

N \to \infty, β^{2} \sim 1 / N

. Finally, the expectation value

\begin{matrix} 〈U_{n, m} {\bar{U}}_{n, m}〉 = \sum_{l = n}^{m - 1} \sum_{k = n}^{m - 1} 〈exp (ı α_{k n} - ı α_{l n})〉 \end{matrix}

(114)

Here, the Gaussian path integration yields

\begin{matrix} 〈U_{n, m} {\bar{U}}_{n, m}〉 \to N^{2} \int_{ξ_{1}}^{ξ_{2}} d ξ \int_{ξ_{1}}^{ξ_{2}} d ξ^{'} exp (- \frac{1}{2} (G (ξ, ξ) + G (ξ^{'}, ξ^{'}) - 2 G (ξ, ξ^{'}))) = \\ N^{2} \int_{ξ_{1}}^{ξ_{2}} d ξ \int_{ξ_{1}}^{ξ_{2}} d ξ^{'} exp (\frac{1}{2} β^{2} N | ξ - ξ^{'} |) = \frac{4}{β^{4}} (2 exp ((y - x) / 2) + x - y - 2) \end{matrix}

(115)

This result also agrees with combinatorial computations in [7,32].

5.3. Small Euler Ensemble in Statistical Limit

The remaining problem is averaging over the variables

N, p, q, r

of the small Euler ensemble.

The variable

s = \frac{q r}{N}

is distributed between

- 1, 1

with the binomial weight [7,32]

(\binom{N}{N (1 + s) / 2})

peaked at

s = 0

. There is a finite term coming from

r = 0

plus a continuum spectrum coming from large r

\begin{matrix} W (r) = \{\begin{matrix} 1 & if r = 0; \\ \frac{\sqrt{2 π N}}{q} exp (- \frac{{(q r)}^{2}}{2 N}) & otherwise; \end{matrix} \end{matrix}

(116)

As it was conjectured in [7] and supported by rigorous estimates in [32], the

r = 0

term dominates the sums, after which the variables

y, x

can be treated as continuous variables.

The variable p at fixed q has a discrete distribution

\begin{matrix} f_{p} (p ∣ q) = \frac{\sum_{\begin{matrix} p = 1 \\ (p, q) \end{matrix}}^{q - 1} δ (p - n)}{φ (q)} \end{matrix}

(117)

As we shall see, rather than p, we would need an asymptotic distribution of a scaling variable

\begin{matrix} X (p, q) = \frac{1}{q^{2}} {cot}^{2} (\frac{π p}{q}) \end{matrix}

(118)

This distribution for

X (p, q)

at fixed

q \to \infty

can be found analytically, using newly established relations for the cotangent sums (see Appendix in [7], and Mathematica^® notebook [33]). Asymptotically, at large q, these relations read

\begin{matrix} 〈X^{n}〉 \equiv lim_{q \to \infty} \frac{\sum_{\begin{matrix} p = 1 \\ (p, q) \end{matrix}}^{q - 1} X {(p, q)}^{n}}{q} = δ_{n, 0} + \frac{2 π^{- 2 n} ζ (2 n)}{(2 n + 1) ζ (2 n + 1)} \end{matrix}

(119)

This relation can be transformed further as

\begin{matrix} 〈X^{n}〉 = \{\begin{matrix} 1 & if n = 0 \\ \frac{2 \sum_{k = 1}^{\infty} φ (k) k^{- (2 n + 1)}}{(2 n + 1) π^{2 n}} & if n > 0 \end{matrix} \end{matrix}

(120)

The Mellin transform of these moments leads to the following singular distribution

\begin{matrix} 〈X^{n}〉 = \int_{0}^{\infty} f_{X} (X) d X X^{n}; \end{matrix}

(121)

(122)

\begin{matrix} \frac{2 π}{5} \sum_{1}^{\infty} Φ (k) (\frac{1}{{(π k)}^{5}} - \frac{1}{{(π (k + 1))}^{5}}) = \frac{2}{5 π^{4}} \sum_{1}^{\infty} \frac{φ (k)}{k^{5}} = \frac{1}{225 ζ (5)} \end{matrix}

(123)

where

Φ (n)

is the totient summatory function

\begin{matrix} Φ (q) = \sum_{n = 1}^{q} φ (n) \end{matrix}

(124)

The distribution can also be rewritten as an infinite sum

\begin{matrix} \int d x f_{X} (x) F (x) = (1 - α) F (0) + π \sum_{n = 1}^{\infty} φ (n) \int_{0}^{\frac{1}{π^{2} n^{2}}} x^{\frac{3}{2}} d x F (x) \end{matrix}

(125)

The normalization of this distribution comes out 1 as it should, with factor

1 - α

in front of the delta function.

The upper limit of X

\begin{matrix} X_{m a x} = X (q - 1, q) \to \frac{1}{π^{2}} \end{matrix}

(126)

Our distribution (121) is consistent with this upper limit, as the argument

⌊ \frac{1}{π \sqrt{X}} ⌋

becomes zero at

X π^{2} > 1

. It is plotted in Figure 10.

Once we are zooming into the tails of the

p, q

distribution, we also must recall that

\begin{matrix} P (q < y N) = \frac{Φ (⌊ N y ⌊)}{Φ (N)} \to y^{2}; \end{matrix}

(127)

\begin{matrix} f_{y} (y) = \frac{\sum_{q = 2}^{N} δ (y - \frac{q}{N}) φ (q)}{Φ (N)} \end{matrix}

(128)

5.4. Complex Classical Trajectory in the Path Integral

This classical equation for our path integral reads:

\begin{matrix} α^{''} = - ı κ (C_{Ω}^{'} exp (ı α) + {(C_{Ω}^{'})}^{★} exp (- ı α)); \end{matrix}

(129)

\begin{matrix} κ = \frac{1}{2 π y \sqrt{X} \sqrt{2 ν (t + t_{0})}} \end{matrix}

(130)

The parameter

κ

is distributed according to the above distributions for

y, X

in a small Euler ensemble in the statistical limit.

This complex equation leads to a complex classical solution (instanton). It simplifies for

z = exp (ı α)

\begin{matrix} z^{''} = \frac{{(z^{'})}^{2}}{z} + κ (C_{Ω}^{'} z^{2} + {(C_{Ω}^{'})}^{★}); \end{matrix}

(131)

\begin{matrix} z (0) = z (1) = 1 \end{matrix}

(132)

This equation cannot be analytically solved for arbitrary periodic function

C_{Ω}^{'} (ξ)

The weak and strong coupling expansions by

κ

are straightforward.

At small

κ

\begin{matrix} z (ξ) \to 1 + 2 κ (- A ξ + \int_{0}^{ξ} Re C_{Ω} (ξ^{'}) d ξ^{'}) + O (κ^{2}); \end{matrix}

(133)

\begin{matrix} A = \int_{0}^{1} Re C_{Ω} (ξ^{'}) d ξ^{'} \end{matrix}

(134)

At large

κ

\begin{matrix} z (ξ) \to ı exp (- ı arg C_{Ω}^{'} (ξ)) = ı \frac{|C_{Ω}^{'} (ξ)|}{C_{Ω}^{'} (ξ)} \end{matrix}

(135)

This solution is valid at intermediate

ξ

, not too close to the boundaries

ξ = (0, 1)

. In the region near the boundaries

ξ (1 - ξ) ≪ \frac{1}{\sqrt{κ}}

, the following asymptotic agrees with the classical equation

\begin{matrix} z \to 1 \pm ı ξ \sqrt{2 κ Re C_{Ω}^{'} (0)} + O (ξ^{2}); \end{matrix}

(136)

\begin{matrix} z \to 1 \pm ı (1 - ξ) \sqrt{2 κ Re C_{Ω}^{'} (1)} + O ({(1 - ξ)}^{2}); \end{matrix}

(137)

One can expand in small or large values of

κ

and use the above distributions for

X, y

term by term.

As it was noticed in the previous paper [7], the viscosity

ν = \frac{\tilde{ν}}{N^{2}} \to 0

in our theory. This limit makes

κ \sim N \to \infty

, justifying the strong coupling limit for the Wilson loop solution.

The classical limit of the circulation in exponential of (Section 5.1)

\begin{matrix} \int_{0}^{1} d ξ Im (C_{Ω}^{'} (ξ) exp (ı α (ξ))) \to \int_{0}^{1} d ξ |C_{Ω}^{'} (ξ)| \end{matrix}

(138)

becomes a positive definite function of the rotation matrix

Ω

. At large

κ

the leading contribution will come from the rotation matrix minimizing this functonal.

It is an interesting problem to compute the Wilson loop for a specific loop, say the circle, but there is a simpler quantity, which is directly observed in grid turbulence experiments [1] more than half a century ago.

In the next section we are considering an important calculable case of the vorticity correlation function, where the full solution in quadratures is available. This function was observed since then in numerous real experiments and numerical simulations [4].

6. Dual Theory of Vorticity Correlation

The simplest observable quantity we can extract from the loop functional is the vorticity correlation function [11], corresponding to the loop C backtracking between two points in space

{\vec{r}}_{1} = 0, {\vec{r}}_{2} = \vec{r}

, (see [7] for details and the justification).

The vorticity operators are inserted at these two points. Let us outline an analytical solution. We shift the time variable by

t + t_{0} \Rightarrow t

to simplify the formulas.

The correlation function reduces to the following average over the big Euler ensemble

E

of our random curves in complex space [7]

\begin{matrix} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{r})〉 = \int_{O (3)} \frac{d Ω}{4 t^{2} | O (3) |} \sum_{0 \leq n < m < N} {〈{\vec{ω}}_{m} \cdot {\vec{ω}}_{n} e^{ı \vec{ρ} \cdot \hat{Ω} \cdot ({\vec{S}}_{n, m} - {\vec{S}}_{m, n})}〉}_{E}; \end{matrix}

(139)

\begin{matrix} {\vec{S}}_{n, m} = \frac{\sum_{k = n}^{m - 1} {\vec{F}}_{k}}{m - n (mod N)}; \end{matrix}

(140)

\begin{matrix} {\vec{ω}}_{k} = \{0, 0, \frac{ı σ_{k}}{2} cot (\frac{β}{2})\}; \end{matrix}

(141)

\begin{matrix} \vec{ρ} = \frac{\vec{r}}{2 \sqrt{ν t}}; \end{matrix}

(142)

\begin{matrix} {〈X [σ . . .]〉}_{p, q, r} \equiv \frac{\sum_{E} X [σ . . .] δ [q r - \sum σ]}{\sum_{E} δ [q r - \sum σ]}; \end{matrix}

(143)

Integrating the global rotation matrix

O (3)

is part of the ensemble averaging.

6.1. Correlation Function and Path Integral

Let us apply our path integral to the expectation value over spins

σ = \pm 1

in the big Euler ensemble, with the distribution of

q, X

established in the previous section. In the continuum limit, we replace summation with integration. We arrive at the following expression for the correlation function:

\begin{matrix} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{r})〉 \propto \frac{\sum_{even q < N} \sum_{p; (p | q)} \frac{{cot}^{2} (π p / q)}{{(p / q)}^{2}} \int_{0 < ξ_{1} < ξ_{2} < 1} d ξ_{1} d ξ_{2} \int_{O (3)} d Ω \int [D α] α^{'} (ξ_{1}) α^{'} (ξ_{2}) e^{ı \frac{\vec{r} \cdot \hat{Ω} \cdot Im \vec{V} (ξ_{1}, ξ_{2})}{\sqrt{ν t}}}}{t^{2} Φ (N) | O (3) | \int [D α]}; \end{matrix}

(144)

\begin{matrix} \vec{V} (ξ_{1}, ξ_{2}) = q \sqrt{X} \{ı, 1, 0\} (S (ξ_{1}, ξ_{2}) - S (ξ_{2}, 1 + ξ_{1})); \end{matrix}

(145)

\begin{matrix} S (a, b) = \frac{\int_{a}^{b} d ξ e^{ı α (ξ)}}{b - a}; \end{matrix}

(146)

Here and in the following, we skip all positive constant factors, including powers of N. Ultimately, we restore the correct normalization of the vorticity correlation using its value at

\vec{r} = 0

computed in previous work [7].

The computations significantly simplify in Fourier space.

\begin{matrix} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{k})〉 = \int d^{3} \vec{r} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{r})〉 exp (- ı \vec{k} \cdot \vec{r}) \propto \\ \frac{\sum_{even q < N} \sum_{p; (p | q)} \frac{{cot}^{2} (π p / q)}{{(p / q)}^{2}} \int_{0 < ξ_{1} < ξ_{2} < 1} d ξ_{1} d ξ_{2} \int_{O (3)} d Ω \int [D α] α^{'} (ξ_{1}) α^{'} (ξ_{2}) δ (\frac{\vec{r} \cdot \hat{Ω} \cdot Im \vec{V} (ξ_{1}, ξ_{2})}{\sqrt{ν t}} - \vec{k})}{t^{2} Φ (N) | O (3) | \int [D α]}; \end{matrix}

(147)

The angular integration

\int d Ω

yields

\begin{matrix} \int_{O (3)} d Ω δ (\frac{\hat{Ω} \cdot Im \vec{V} (ξ_{1}, ξ_{2})}{\sqrt{ν t}} - \vec{k}) \propto \frac{\sqrt{ν t}}{{\vec{k}}^{2}} δ (|Im \vec{V} (ξ_{1}, ξ_{2})| - | \vec{k} | \sqrt{ν t}) \end{matrix}

(148)

Now, using the Lagrange multiplier

λ

for this condition, and shifting integration over

λ

to the real axis, we have to minimize effective action

\begin{matrix} A [α, λ] = \frac{π y^{2} X}{2} \int_{ξ_{1}}^{1 + ξ_{1}} {(α^{'})}^{2} + λ y \sqrt{X} |\frac{\int_{ξ_{1}}^{ξ_{2}} d ξ e^{ı α}}{ξ_{2} - ξ_{1}} - \frac{\int_{ξ_{2}}^{1 + ξ_{1}} d ξ e^{ı α}}{1 + ξ_{1} - ξ_{2}}|; \end{matrix}

(149)

\begin{matrix} \partial_{λ} A [α, λ] = | \vec{k} | \sqrt{ν t}; \end{matrix}

(150)

This variational problem reduces to two pendulum equations

\begin{matrix} α_{1}^{''} + \frac{r}{ξ_{2} - ξ_{1}} sin α_{1} = 0; \forall ξ_{1} < ξ < ξ_{2} \end{matrix}

(151)

\begin{matrix} α_{2}^{''} + \frac{r}{ξ_{2} - ξ_{1} - 1} sin α_{2} = 0; \forall ξ_{2} < ξ < 1 + ξ_{1} \end{matrix}

(152)

\begin{matrix} r = \frac{λ}{π y \sqrt{X} I (r)}; \end{matrix}

(153)

\begin{matrix} I (r) = |\frac{\int_{ξ_{1}}^{ξ_{2}} d ξ e^{ı α_{1}}}{ξ_{2} - ξ_{1}} - \frac{\int_{ξ_{2}}^{1 + ξ_{1}} d ξ e^{ı α_{2}}}{1 + ξ_{1} - ξ_{2}}|; \end{matrix}

(154)

The well-known solution is Jacobi amplitude

am (x ∣ u)

\begin{matrix} α_{1} (ξ) = 2 am (\frac{ξ - α_{2}}{2} a_{1} ∣ \frac{r}{a_{1}^{2} (ξ_{2} - ξ_{1})}); \end{matrix}

(155a)

\begin{matrix} α_{2} (ξ) = 2 am (\frac{ξ - α_{2}}{2} a_{2} ∣ - \frac{r}{a_{2}^{2} (1 - ξ_{2} + ξ_{1})}); \end{matrix}

(155b)

The free parameters

a_{1}, a_{2}, α_{1}, α_{2}

satisfy four equations

\begin{matrix} α_{1} (ξ_{2}) = α_{2} (ξ_{2}); \end{matrix}

(156a)

\begin{matrix} α_{1}^{'} (ξ_{2}) = α_{2}^{'} (ξ_{2}); \end{matrix}

(156b)

\begin{matrix} α_{1} (ξ_{1}) = α_{2} (1 + ξ_{1}); \end{matrix}

(156c)

\begin{matrix} α_{1}^{'} (ξ_{1}) = α_{2}^{'} (1 + ξ_{1}); \end{matrix}

(156d)

together with the constraint following from the variation of the Lagrange multiplier

λ

\begin{matrix} I (r) = \frac{| \vec{k} | \sqrt{ν t}}{y \sqrt{X}} \end{matrix}

(157)

6.2. Turbulent Viscosity and the Local Limit

These five equations, in general, are quite complex, but there is one simplifying property. In the local limit

N \to \infty

, the remaining effective action at the extremum

\begin{matrix} N A [α_{c}, λ_{c}] = \frac{π N y^{2} X}{2} (\int_{ξ_{1}}^{ξ_{2}} d ξ {(α_{1}^{'} (ξ))}^{2} + \int_{ξ_{2}}^{1 + ξ_{1}} d ξ {(α_{2}^{'} (ξ))}^{2}) \end{matrix}

(158)

grows as N, unless both

α_{1} (ξ) \sim α_{2} (ξ) \sim N^{- \frac{1}{2}} \to 0

. In this case, the above constraint can be expanded in

α_{1}, α_{2}

. As we show in [34], the leading constant and linear terms both cancel so that the quadratic term remains

\begin{matrix} \frac{2 | \vec{k} | \sqrt{ν t}}{y \sqrt{X}} = |\int_{ξ_{1}}^{ξ_{2}} \frac{d ξ α_{1}^{2} (ξ)}{ξ_{2} - ξ_{1}} - \int_{ξ_{2}}^{1 + ξ_{1}} \frac{d ξ α_{2}^{2} (ξ)}{1 + ξ_{1} - ξ_{2}}| \sim \frac{1}{N} \end{matrix}

(159)

This estimate then requires vanishing viscosity in the local limit, at fixed turbulent viscosity

\begin{matrix} \tilde{ν} = ν N^{2} \to const . \end{matrix}

(160)

This phenomenon of renormalization of viscosity by a factor of

N^{2}

was already observed in our first paper [7]. Our Euler ensemble in the local limit

N \to \infty

can only solve the inviscid limit of the Navier-Stokes decaying turbulence, with finite

\tilde{ν}

acting as a turbulent viscosity.

The desired anomalous dissipation phenomenon takes place in this limit of our theory.

Returning to the elliptic function solution, we rewrite it in the linearized case at

a_{1} \sim a_{2} \to 0

. This linearization is equivalent to replacing

sin (α) \to α

in the differential equation and studying the resulting linear ODE as a boundary problem. We choose different parametrizations in this linear case

\begin{matrix} α_{1} (ξ) = a (cos (K_{1} (ξ - ξ_{2})) + \frac{b}{K_{1}} sin (K_{1} (ξ - ξ_{2}))); \end{matrix}

(161)

\begin{matrix} α_{2} (ξ) = a (cos (K_{2} (ξ - ξ_{2})) + \frac{b}{K_{2}} sin (K_{2} (ξ - ξ_{2}))); \end{matrix}

(162)

\begin{matrix} K_{1} = \sqrt{\frac{r}{Δ}}; \end{matrix}

(163)

\begin{matrix} K_{2} = \sqrt{\frac{r}{Δ - 1}}; \end{matrix}

(164)

\begin{matrix} Δ = ξ_{2} - ξ_{1}; \end{matrix}

(165)

In the physical region

0 < Δ < 1, r < 0

K_{2}

is real, and

K_{1}

imaginary, but the solution stays real. The matching conditions at

α_{1} (ξ_{2}) = α_{2} (ξ_{2}), α_{1}^{'} (ξ_{2}) = α_{2}^{'} (ξ_{2})

are identically satisfied with this Anzatz. The derivative match

α_{1}^{'} (ξ_{1}) = α_{2}^{'} (1 + ξ_{1})

can be solved exactly for b

\begin{matrix} b = \frac{\sqrt{\frac{r}{Δ - 1}} sin ((1 - Δ) \sqrt{\frac{r}{Δ - 1}}) + \sqrt{\frac{r}{Δ}} sin (Δ \sqrt{\frac{r}{Δ}})}{cos ((Δ - 1) \sqrt{\frac{r}{Δ - 1}}) - cos (Δ \sqrt{\frac{r}{Δ}})} \end{matrix}

(166)

The remaining matching condition

α_{1} (ξ_{1}) = α_{2} (1 + ξ_{1})

reduces to the root of the function

\begin{matrix} g (r, Δ) = \frac{(2 Δ - 1) sin (\sqrt{(Δ - 1) r}) sin (\sqrt{Δ r})}{\sqrt{(Δ - 1) Δ}} + 2 cos (\sqrt{(Δ - 1) r}) cos (\sqrt{Δ r}) - 2 \end{matrix}

(167)

This function has multiple roots, but we are looking for the real root

r_{0} (Δ)

with minimal value of the action at given

Δ

\begin{matrix} A_{c} (r, Δ) = \int_{ξ_{1}}^{ξ_{2}} d ξ α_{1}^{'} {(ξ)}^{2} + \int_{ξ_{2}}^{1 + ξ_{1}} d ξ α_{2}^{'} {(ξ)}^{2} \end{matrix}

(168)

This integral is elementary, but the expression is too long to be presented here. It can be found in the Mathematica^® notebook [34], where it is used to select the roots

r_{0} (Δ)

g (r, Δ)

, minimizing

A_{c} (r_{0} (Δ), Δ)

for a given value of

Δ \in (0, 1)

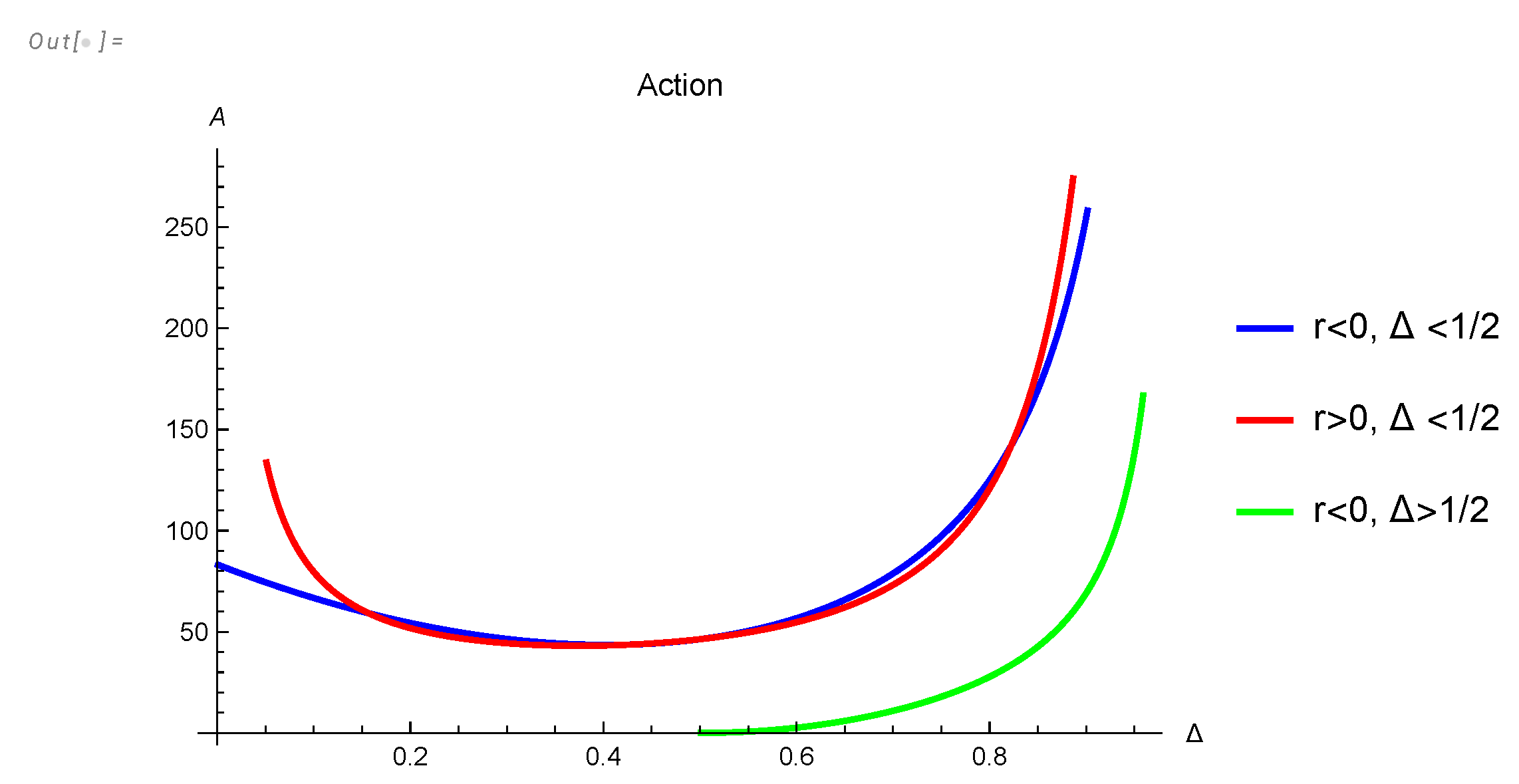
This lowest action root is plotted in Figure 11. The corresponding value of minimal action

L (Δ) = A_{c} (r_{0} (Δ), Δ)

is plotted in Figure 15.

There are phase transitions at

\begin{matrix} Δ = \{Δ_{1}, Δ_{2}, Δ_{3}\}; \end{matrix}

(169)

\begin{matrix} Δ_{1} = 0.157143; \end{matrix}

(170)

\begin{matrix} Δ_{2} = 0.43015; \end{matrix}

(171)

\begin{matrix} Δ_{3} = \frac{1}{2}; \end{matrix}

(172)

These branch points in

Δ

correspond to the switch of the lowest action solution. At small positive

Δ - \frac{1}{2}

\begin{matrix} r_{0} (Δ) \to - 48 (Δ - \frac{1}{2}) - \frac{1536 {(Δ - \frac{1}{2})}^{3}}{7} + \dots; \end{matrix}

(173)

\begin{matrix} A_{0} (r_{0} (Δ), Δ) \to 256 {(Δ - \frac{1}{2})}^{2} + \dots \end{matrix}

(174)

Δ \to 1

all solutions go to

- \infty

\begin{matrix} r_{n} (Δ) \to - \frac{6}{1 - Δ} + O (1) \end{matrix}

(175)

This behavior matches numerical computations in Mathematica^® [34].

The constraint (159) is also reduced to elementary functions, too lengthy to quote here (see [34]).

This constraint yields the quadratic relation for the last unknown parameter a in our solution

\begin{matrix} a^{2} = \frac{| \vec{k} | \sqrt{ν t}}{S (Δ) y \sqrt{X}}; \end{matrix}

(176)

with universal function

S (Δ)

presented in [34] and shown in Figure 12).

The resulting integral (up to the pre-exponential factor Q) is equal to

\begin{matrix} \int [D α] α^{'} (ξ_{1}) α^{'} (ξ_{2}) δ (|Im \vec{V} (ξ_{1}, ξ_{2})| - | \vec{k} | \sqrt{ν t}) \propto \\ Q 〈α^{'} (ξ_{1}) α^{'} (ξ_{2})〉 exp (- y \sqrt{X} | \vec{k} | \sqrt{\tilde{ν} t} \frac{π L (Δ)}{2 | S (Δ) |}) \end{matrix}

(177)

The factor

〈α^{'} (ξ_{1}) α^{'} (ξ_{2})〉

contains two terms :

\begin{matrix} 〈α^{'} (ξ_{1}) α^{'} (ξ_{2})〉 = α_{1}^{'} (ξ_{1}) α_{1}^{'} (ξ_{2}) + 〈δ α^{'} (ξ_{1}) δ α^{'} (ξ_{2})〉 \end{matrix}

(178)

The first term is the contribution of the classical solution we have just found, and the second term comes from Gaussian fluctuations

δ α (ξ)

around this solution.

The classical term is calculable (see [34])

\begin{matrix} α_{1}^{'} (ξ_{1}) α_{1}^{'} (ξ_{2}) = \frac{| \vec{k} | \sqrt{\tilde{ν} t}}{N y \sqrt{X}} \frac{J (Δ)}{| S (Δ) |}; \end{matrix}

(179)

\begin{matrix} J (Δ) = {\frac{r A (r, Δ) B (r, Δ)}{Δ (Δ - 1) C {(r, Δ)}^{2}}|}_{r = r_{0} (Δ)}; \end{matrix}

(180)

\begin{matrix} A (r, Δ) = Δ sin (\sqrt{(Δ - 1) r}) - \sqrt{(Δ - 1) Δ} sin (\sqrt{Δ r}); \\ B (r, Δ) = Δ sin (\sqrt{(Δ - 1) r}) cos (\sqrt{Δ r}) - \end{matrix}

(181)

\begin{matrix} \sqrt{(Δ - 1) Δ} sin (\sqrt{Δ r}) cos (\sqrt{(Δ - 1) r}); \end{matrix}

(182)

\begin{matrix} C (r, Δ) = cos (\sqrt{(Δ - 1) r}) - cos (\sqrt{Δ r}); \end{matrix}

(183)

(see Figure 14).

Figure 11. Log plot of

r_{0} (Δ)

Figure 11. Log plot of

r_{0} (Δ)

Figure 12. Plot of

S (Δ)

Figure 12. Plot of

S (Δ)

Figure 13. Plot of

A_{c} (r_{0} (Δ), Δ)

for the three real solutions of the equation

g (r, Δ) = 0

. At

Δ = Δ_{1}

and

Δ = Δ_{2}

, the action curves intersect; at

Δ = \frac{1}{2}

, there is a gap between the lowest action (

= 0

) and the lowest of the other two. So, there are second-order phase transitions at

Δ_{1}, Δ_{2}

and the first-order phase transition at

Δ = \frac{1}{2}

Figure 13. Plot of

A_{c} (r_{0} (Δ), Δ)

for the three real solutions of the equation

g (r, Δ) = 0

. At

Δ = Δ_{1}

and

Δ = Δ_{2}

, the action curves intersect; at

Δ = \frac{1}{2}

, there is a gap between the lowest action (

= 0

) and the lowest of the other two. So, there are second-order phase transitions at

Δ_{1}, Δ_{2}

and the first-order phase transition at

Δ = \frac{1}{2}

Figure 14. Plot of universal function

J (Δ)

.the four corves correspond to four phases (solutions for

r_{0} (Δ)

Figure 14. Plot of universal function

J (Δ)

.the four corves correspond to four phases (solutions for

r_{0} (Δ)

Figure 15. Log plot of

L (Δ) = A_{c} (r_{0} (Δ), Δ)

Figure 15. Log plot of

L (Δ) = A_{c} (r_{0} (Δ), Δ)

The fluctuation term

〈δ α^{'} (ξ_{1}) δ α^{'} (ξ_{2})〉

is also proportional to

1 / N

, therefore we must keep this term as well.

As for the pre-exponential factor Q in the saddle point integral, it is given by the functional determinant of the operator

\hat{L}

corresponding to linearized effective action (168) in the vicinity of the saddle point

λ_{c}, α_{c} (ξ)

\begin{matrix} A [α_{c} + δ α, λ_{c} + δ λ] \to A [α_{c}, λ_{c}] + \frac{1}{2} tr (V^{†} ∣ \hat{L} ∣ V); \end{matrix}

(184)

\begin{matrix} V = \{δ λ, δ α\}; \end{matrix}

(185)

\begin{matrix} Q (Δ, τ) = exp {(- \frac{1}{2} tr (\frac{log \hat{L}}{{\hat{L}}^{α}}))}_{α \to 0}; \end{matrix}

(186)

\begin{matrix} τ = y \sqrt{X}; \end{matrix}

(187)

The fluctuation correction reduces to the inverse operator

\hat{L}

, which we compute in the next section.

Now, we can reduce multiple sum/integral in (147) to the following

\begin{matrix} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{k})〉 = \frac{{\tilde{ν}}^{\frac{3}{2}} H (k \sqrt{\tilde{ν} t})}{\sqrt{t}}; \end{matrix}

(188)

\begin{matrix} H (κ) = \frac{1}{Z} \sum_{n = 1}^{\infty} φ (n) \int_{0}^{1 / n} d τ (τ^{5} / n^{5} - τ^{10}) \int_{0}^{1} d Δ (1 - Δ) G (Δ, τ, κ); \end{matrix}

(189)

\begin{matrix} G (Δ, τ, κ) = Q (Δ, τ) (\frac{κ}{N τ} \frac{J (Δ)}{| S (Δ) |} + 〈δ α^{'} (ξ_{1}) δ α^{'} (ξ_{2})〉) exp (- \frac{τ κ L (Δ)}{2 π | S (Δ) |}) \end{matrix}

(190)

where

Z

is the normalization constant to be determined later.

6.3. Functional Determinant in the Path Integral

As we have discussed in the previous section, in the limit

a \to 0

the classical solution

α_{1, 2} (ξ) \propto a \to 0

This observation simplifies the linearized theory corresponding to this quadratic form

〈V ∣ \hat{L} ∣ V〉

. First, integrate the fluctuations

δ λ

λ

around the saddle point solution.

The Lagrange multiplier at the saddle point vanishes, as we show in [34]

\begin{matrix} λ_{0} = τ r_{0} (Δ) I (r_{0} (Δ)) = 0 \end{matrix}

(191)

The quadratic term comes from the first derivatives

I_{λ} = \partial_{λ} I, I_{r} = \partial_{r} I, λ_{r} = \partial_{r} λ

, which can be simplified by switching to

λ (r) = τ t I (r)

\begin{matrix} A_{λ λ} = τ I_{λ} = \frac{τ I_{r}}{λ_{r}} = \frac{τ I_{r}}{τ r I_{r}} = \frac{1}{r} \end{matrix}

(192)

The bilinear term

λ δ α

also simplifies

\begin{matrix} A_{α λ} (δ α) = ı τ δ λ F [δ α]; \end{matrix}

(193)

\begin{matrix} F [δ α] = \int_{ξ_{1}}^{ξ_{2}} \frac{d ξ δ α (ξ)}{ξ_{2} - ξ_{1}} - \int_{ξ_{2}}^{1 + ξ_{1}} \frac{d ξ δ α (ξ)}{1 + ξ_{1} - ξ_{2}} \end{matrix}

(194)

We can integrate out

λ

, producing the extra pre-exponential factor

Q_{λ} = \sqrt{| r_{0} (Δ) |} / \sqrt{N}

The bilinear term in the exponential after

λ

integration leads to the following effective quadratic Action for

δ α

\begin{matrix} A_{e f f} [δ α] = \frac{τ^{2}}{2} \int_{ξ_{1}}^{1 + ξ_{1}} δ α^{' 2} + \frac{r_{0} (Δ) τ^{2}}{2} F {[δ α]}^{2}; \end{matrix}

(195)

There is a zero-mode

δ α (ξ) = const

, related to translational invariance of

A_{e f f} [δ α]

. Naturally, this zero-mode must be eliminated from the spectrum when we compute the functional determinant and the resolvent below.

After discarding the zero-mode, this effective action becomes a positive definite functional of

δ α

only in the region of

Δ

where

r_{0} (Δ) > 0

, i.e., for

Δ_{1} < Δ < Δ_{2}

As we shall see below, the spectrum of fluctuations is positive only in this region. Therefore, we restrict our integration to this region.

The

{(δ α)}^{2}

term corresponds to the linear eigenvalue equation with

f_{1, 2} = δ α_{1, 2}

\begin{matrix} f_{1, 2}^{''} (ξ) - μ_{1, 2} F [f] = - ω f_{1, 2} (ξ); \end{matrix}

(196)

\begin{matrix} μ_{1, 2} = \{\frac{r}{Δ}, \frac{r}{Δ - 1}\}; \end{matrix}

(197)

\begin{matrix} ϵ = ω τ^{2}; \end{matrix}

(198)

\begin{matrix} r = r_{0} (Δ); \end{matrix}

(199)

The solution matching with first derivative at

ξ = ξ_{2}, ξ = (ξ_{1}, 1 + ξ_{1})

is built the same way as in (166). Equations for

f_{1, 2}

being linear homogeneous, we can fix the normalization as

F [f] = 1

\begin{matrix} f_{1} (x) = a sin (\sqrt{ω} (ξ_{-} ξ_{2})) + B_{1} cos (\sqrt{ω} (ξ_{-} ξ_{2})) + \frac{r}{ω Δ}; \end{matrix}

(200)

\begin{matrix} f_{2} (ξ) = a sin (\sqrt{ω} (ξ_{-} ξ_{2})) + B_{2} cos (\sqrt{ω} (ξ_{-} ξ_{2})) + \frac{r}{ω (Δ - 1)}; \end{matrix}

(201)

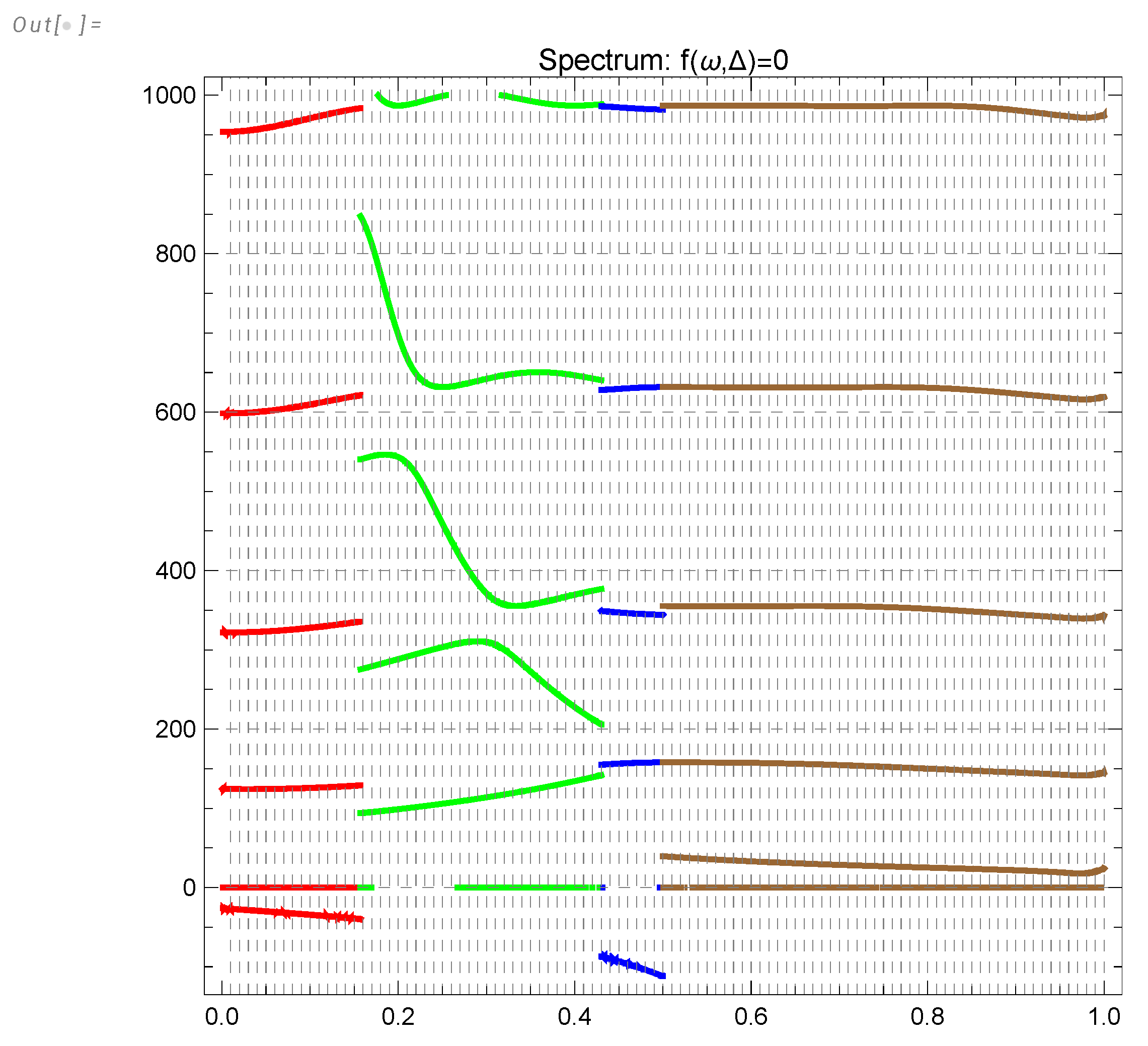
The spectrum

ω = ω_{n}

is defined by the transcendental equation (the discriminant of this linear system of equations), which we found in [34]

\begin{matrix} f (ω_{n}, Δ) = 0; \\ f (ω, Δ) = (Δ - 1) Δ \sqrt{ω} sin (\frac{\sqrt{ω}}{2}) ((Δ - 1) Δ ω + r) + \end{matrix}

(202)

\begin{matrix} r cos (\frac{1}{2} (1 - 2 Δ) \sqrt{ω}) - r cos (\frac{\sqrt{ω}}{2}); \end{matrix}

(203)

\begin{matrix} r = r_{0} (Δ); \end{matrix}

(204)

The spectrum is positive in the interval

Δ_{1} < Δ < Δ_{2}

where

r_{0} (Δ) > 0

so that the solution for

ω_{n} (Δ)

is stable. In the following, we only select the stable region with positive

r_{0} (Δ)

Figure 16. The first levels of the spectrum satisfying equation

f (ω, Δ) = 0

. The colored lines correspond to four phases. Red:

0 < Δ < Δ_{1}

, Green:

Δ_{1} < Δ < Δ_{2}

, Blue:

Δ_{2} < Δ < \frac{1}{2}

, Brown:

\frac{1}{2} < Δ < 1

. The green zone is left as stable, and others are eliminated because

r_{0} (Δ) < 0

in these zones. Naturally, we eliminate the zero-mode

ϵ_{0} = 0

corresponding to translational invariance of the effective Action.

Figure 16. The first levels of the spectrum satisfying equation

f (ω, Δ) = 0

. The colored lines correspond to four phases. Red:

0 < Δ < Δ_{1}

, Green:

Δ_{1} < Δ < Δ_{2}

, Blue:

Δ_{2} < Δ < \frac{1}{2}

, Brown:

\frac{1}{2} < Δ < 1

. The green zone is left as stable, and others are eliminated because

r_{0} (Δ) < 0

in these zones. Naturally, we eliminate the zero-mode

ϵ_{0} = 0

corresponding to translational invariance of the effective Action.

The functional determinant, resulting from the WKB approximation to the

α

path integral, would be related to the infinite product of positive eigenvalues

ϵ_{n} = τ^{2} ω_{n}

, which can be written using a contour integral

\begin{matrix} Q_{α} (Δ, τ) = \prod_{ω_{n} > 0} {(τ^{2} ω_{n})}^{- \frac{1}{2}} = {exp (\frac{1}{2} \partial_{x} Im \oint_{Γ} \frac{f^{'} (ω)}{f (ω)} \frac{d ω}{2 π {(ω τ^{2})}^{x}})|}_{x \to 0}; \end{matrix}

(205)

and the integration contour

Γ

encircles anticlockwise the positive real poles of the meromorphic function

f^{'} (ω) / f (ω)

. The integral converges at

x > \frac{1}{2}

and should be analytically continued to

x = 0

For this purpose, let us introduce another function

\begin{matrix} Φ (ω) = \frac{f (ω)}{cos (\sqrt{ω} / 2)} ω^{- 3 / 2} \end{matrix}

(206)

We show in [34] that at large

ω = ı y

this function reaches finite limits

\begin{matrix} Φ (ı y) \to ı sign y {(Δ - 1)}^{2} Δ^{2} + \frac{(Δ - 1) Δ r}{| y |} \end{matrix}

(207)

The logarithmic derivative of the original function differs from

\frac{Φ^{'} (ω)}{Φ (ω)}

by the following meromorphic function

\begin{matrix} \frac{f^{'} (ω)}{f (ω)} - \frac{Φ^{'} (ω)}{Φ (ω)} = - \frac{tan (\frac{\sqrt{ω}}{2})}{4 \sqrt{ω}} + \frac{3}{2 ω} \end{matrix}

(208)

This difference produces a calculable contribution to our integral. By summing residues of the poles of the tangent, we get

\begin{matrix} \oint_{Γ} (- \frac{tan (\frac{\sqrt{ω}}{2})}{4 \sqrt{ω}} + \frac{3}{2 ω}) \frac{d ω}{2 π {(ω τ^{2})}^{x}} = ı (1 - 2^{2 x}) {(2 π τ)}^{- 2 x} ζ (2 x) \end{matrix}

(209)

The derivative at

x = 0

yields a constant

\begin{matrix} \frac{1}{2} \partial_{x} Im ı (1 - 2^{2 x}) {(2 π τ)}^{- 2 x} ζ (2 x) \to \frac{log (2)}{2} \end{matrix}

(210)

leading to an irrelevant renormalization of

Q_{α} (Δ, τ)

by a factor

\sqrt{2}

The remaining integral with

f (ω) \Rightarrow Φ (ω)

already converges at

Re α > - 1

, so that we can set

α = 0

and rotate the integration contour

Γ

parallel to the imaginary axis at

Re Γ = ϵ > 0

\begin{matrix} Q_{α} (Δ, τ) = \\ exp (\frac{1}{2} Im \int_{ϵ - ı \infty}^{ϵ + ı \infty} \frac{Φ^{'} (ω)}{Φ (ω)} \frac{log (ω τ^{2}) d ω}{2 π}) \end{matrix}

(211)

The remarkable property of this functional determinant is the factorization of the

τ

dependence

\begin{matrix} Q_{α} (Δ, τ) = τ^{μ (Δ)} Q_{α} (Δ, 1); \end{matrix}

(212)

\begin{matrix} μ (Δ) = Im \int_{ϵ - ı \infty}^{ϵ + ı \infty} \frac{Φ^{'} (ω)}{Φ (ω)} \frac{d ω}{2 π} \end{matrix}

(213)

The index

μ (Δ)

has a topological origin and can be computed analytically.

\begin{matrix} μ (Δ) = \frac{arg Φ (ı \infty) - arg Φ (- ı \infty)}{2 π} = \frac{1}{2} \end{matrix}

(214)

Our result for the correlation function is given by (188) with

\begin{matrix} Q (Δ, τ) = Q_{α} (Δ, 1) τ^{\frac{1}{2}} \sqrt{r_{0} (Δ)} \end{matrix}

(215)

and

Q_{α} (Δ, 1)

given by (211). All the constant factors we have omitted here are absorbed by the normalization factor

Z

, which we determine at the end of the next section.

6.4. The Fluctuation Term in $α^{'} (ξ_{1}) α^{'} (ξ_{2})$

The last missing term is the fluctuation contribution to

α^{'} (ξ_{1}) α^{'} (ξ_{2})

. In the Gaussian approximation, valid at

N \to \infty

, this term equals

\begin{matrix} 〈δ α^{'} (ξ_{1}) δ α^{'} (ξ_{2})〉 = \frac{- 1}{N τ^{2}} {[\partial_{ξ} \partial_{ξ^{'}} G (ξ, ξ^{'})]}_{ξ = ξ_{1}, ξ^{'} = ξ_{2}} \end{matrix}

(216)

where

G (ξ, ξ^{'})

is a resolvent for the effective quadratic Action (195). This resolvent satisfies the equation

\begin{matrix} \partial_{ξ}^{2} G (ξ, ξ^{'}) - μ (ξ) F [G] = δ (ξ - ξ^{'}); \end{matrix}

(217)

\begin{matrix} G (ξ_{1}, ξ^{'}) = G (ξ_{1} + 1, ξ^{'}) = 0; \end{matrix}

(218)

\begin{matrix} F [G] = \int_{ξ_{1}}^{ξ_{2}} \frac{d ξ G (ξ, ξ^{'})}{ξ_{2} - ξ_{1}} - \int_{ξ_{2}}^{1 + ξ_{1}} \frac{d ξ G (ξ, ξ^{'})}{1 + ξ_{1} - ξ_{2}}; \end{matrix}

(219)

\begin{matrix} μ (ξ) = \{\begin{matrix} \frac{r}{Δ} & if ξ_{1} \leq ξ < ξ_{2} \\ \frac{r}{Δ - 1} & if ξ_{2} \leq ξ < 1 + ξ_{1} \end{matrix} \end{matrix}

(220)

The solution of this equation, matching with the first derivative at

ξ = ξ_{2}

\begin{matrix} G (ξ, ξ^{'}) = \{\begin{matrix} A + \frac{| ξ - ξ^{'} |}{2} + B (ξ - ξ_{2}) + \frac{F [G] r {(ξ - ξ_{2})}^{2}}{2 Δ} & if ξ_{1} \leq ξ < ξ_{2} \\ A + \frac{| ξ - ξ^{'} |}{2} + B (ξ - ξ_{2}) + \frac{F [G] r {(ξ - ξ_{2})}^{2}}{2 (Δ - 1)} & if ξ_{2} \leq ξ < 1 + ξ_{1} \end{matrix} \end{matrix}

(221)

The linear functional

F [G]

on this solution becomes a linear function of these unknown parameters

A, B

. Two boundary conditions

G (ξ_{1}, ξ^{'}) = G (ξ_{1} + 1, ξ^{'}) = 0

fix these parameters as functions of

ξ_{1}, ξ_{2}, ξ^{'}

The result derived in [34] is too lengthy to present here. The desired quantity (216) is quite simple

\begin{matrix} \frac{1}{N τ^{2}} {[\partial_{ξ} \partial_{ξ^{'}} G (ξ, ξ^{'})]}_{ξ = ξ_{1}, ξ^{'} = ξ_{2}} = \frac{2 (r - 6)}{(r + 12) N τ^{2}} \end{matrix}

(222)

Finally, we get the following correlation (188) (absorbing the constant factors in

Z

)

\begin{matrix} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{k})〉 = \frac{{\tilde{ν}}^{\frac{3}{2}} H (k \sqrt{\tilde{ν} t})}{\sqrt{t}}; \end{matrix}

(223a)

\begin{matrix} H (κ) = \int_{Δ_{1}}^{Δ_{2}} d Δ (1 - Δ) \sum_{n = 1}^{\infty} φ (n) \int_{0}^{1 / n} \frac{d τ}{τ^{\frac{5}{2}}} (τ^{5} / n^{5} - τ^{10}) G (Δ, τ κ); \end{matrix}

(223b)

\begin{matrix} G (Δ, x) = \frac{Q_{α} (Δ, 1) \sqrt{r_{0} (Δ)}}{Z} (x \frac{J (Δ)}{S (Δ)} + \frac{2 (r_{0} (Δ) - 6)}{(12 + r_{0} (Δ))}) exp (- \frac{x L (Δ)}{2 π S (Δ)}) \end{matrix}

(223c)

7. The Decaying Energy in Finite System

The vorticity correlation in Fourier space doubles as an energy spectrum

\begin{matrix} E (k, t) = 4 π {\vec{k}}^{2} 〈\vec{v} \cdot {\vec{v}}_{k}〉 = 4 π 〈\vec{ω} \cdot {\vec{ω}}_{k}〉 \end{matrix}

(224)

The energy spectrum in a finite system with size L is bounded from below. At low

| \vec{k} | \leq π / L

, the spectrum is no longer related to the turbulence but is given by the energy pumping by external forces at the boundaries.

This energy pumping [4] takes place at

t < t_{0}

, after which the pumping stops. At this moment, the energy spectrum is growing with wavevector by one of two possible laws (with P being the net momentum of the fluid and M being the rotation moment)

\begin{matrix} \{\begin{matrix} E (k, t_{0}) \propto P k^{2} \\ E (k, t_{0}) \propto M k^{4} \end{matrix} \end{matrix}

(225)

t > t_{0}

, without the forcing, the pumped energy dissipates at large k corresponding to smaller spatial scales of the hierarchy of vortex structures of all scales, ending with dissipative scales, or wavevectors

k ≫ π / L

. After sufficient time, the universal regime kicks in, corresponding to the decaying turbulence. It is implied that a large amount of energy was pumped in, so it takes a long time to reach this decaying regime, corresponding to some fixed trajectory.

Our solution does not impose any restrictions on the net momentum an thus applies to the most general, first regime with

k^{2}

spectrum at small k and some universal decay at large k, reflecting these distributed vortex structures. This issue requires more investigation.

The decaying energy, given by the part of the spectrum

k > k_{0} \sim 1 / L

, has the following form

\begin{matrix} E (t) = \int_{k_{0}}^{\infty} d k E (k, t) = \frac{4 π \tilde{ν}}{t} \int_{k_{0} \sqrt{\tilde{ν} t}}^{\infty} H (κ) d κ \end{matrix}

(226)

On top of the trivial decrease

\frac{\tilde{ν}}{t}

, as prescribed by dimensional counting in an infinite system, there is some extra decrease related to the increase of the lower limit.

The energy in our theory does not have a finite statistical limit as the integral in (226) diverges at the lower limit when

k_{0} \to 0

. Thus, we compute the energy as

\begin{matrix} E (t) = \int_{t}^{\infty} E (t^{'}) d t^{'} \end{matrix}

(227)

This energy dissipation rate

E (t^{'})

is calculable

\begin{matrix} E (t) = 4 π ν \int d k k^{2} 〈\vec{ω} (\vec{0}) \cdot \vec{ω} (\vec{k})〉 = 4 π \frac{\tilde{ν}}{t^{2}} \int_{k_{0} \sqrt{\tilde{ν} t}}^{\infty} κ^{2} H (κ) d κ \end{matrix}

(228)

In our theory, this integral has a finite limit in an infinite system (

k_{0} = 0

This limit was computed in [7] in a slightly different grand canonical ensemble, where N was fluctuating with the weight

exp (- μ N), μ \to 0

With our current ensemble of fixed even

N \to \infty

the results of [7] read:

\begin{matrix} E_{\infty} (t) = \frac{\tilde{ν}}{t^{2}} \frac{π^{2}}{864 ζ (3)}; \end{matrix}

(229)

In our present theory, the same quantity is given by the above integral at

k_{0} = 0

\begin{matrix} E_{\infty} (t) = 4 π \frac{\tilde{ν}}{t^{2}} \int_{0}^{\infty} κ^{2} H (κ) d κ \end{matrix}

(230)

Comparing these two expressions, we get the normalization of

H (κ)

\begin{matrix} 4 π \int_{0}^{\infty} κ^{2} H (κ) d κ = \frac{π^{2}}{864 ζ (3)} \end{matrix}

(231)

The integral on the left can be further reduced [34] to the following normalization condition:

\begin{matrix} Z = \frac{276480 ζ (3) ζ (\frac{15}{2})}{119 ζ (\frac{17}{2})} \\ \int_{Δ_{1}}^{Δ_{2}} d Δ \frac{(1 - Δ) \sqrt{r_{0} (Δ)} S (Δ) Q_{α} (Δ, 1) (π J (Δ) (r_{0} (Δ) + 12) + L (Δ) (r_{0} (Δ) - 6))}{L {(Δ)}^{2} (r_{0} (Δ) + 12)} \end{matrix}

(232)

This normalization constant

Z

can be used in equation (226) for the energy decay in a finite system. All the functions of

Δ

were defined above.

As for the energy spectrum, this is not an independent function in our theory. Comparing the two expressions (224) and (228), we arrive at the following relation

\begin{matrix} t^{2} E (t) = 4 π \tilde{ν} F (k_{0} \sqrt{\tilde{ν} t}); \end{matrix}

(233a)

\begin{matrix} F (κ) = \int_{κ}^{\infty} H (x) x^{2} d x, \end{matrix}

(233b)

\begin{matrix} \sqrt{t} E (k, t) = 4 π \tilde{ν} \sqrt{\tilde{ν}} H (k \sqrt{\tilde{ν} t}); \end{matrix}

(233c)

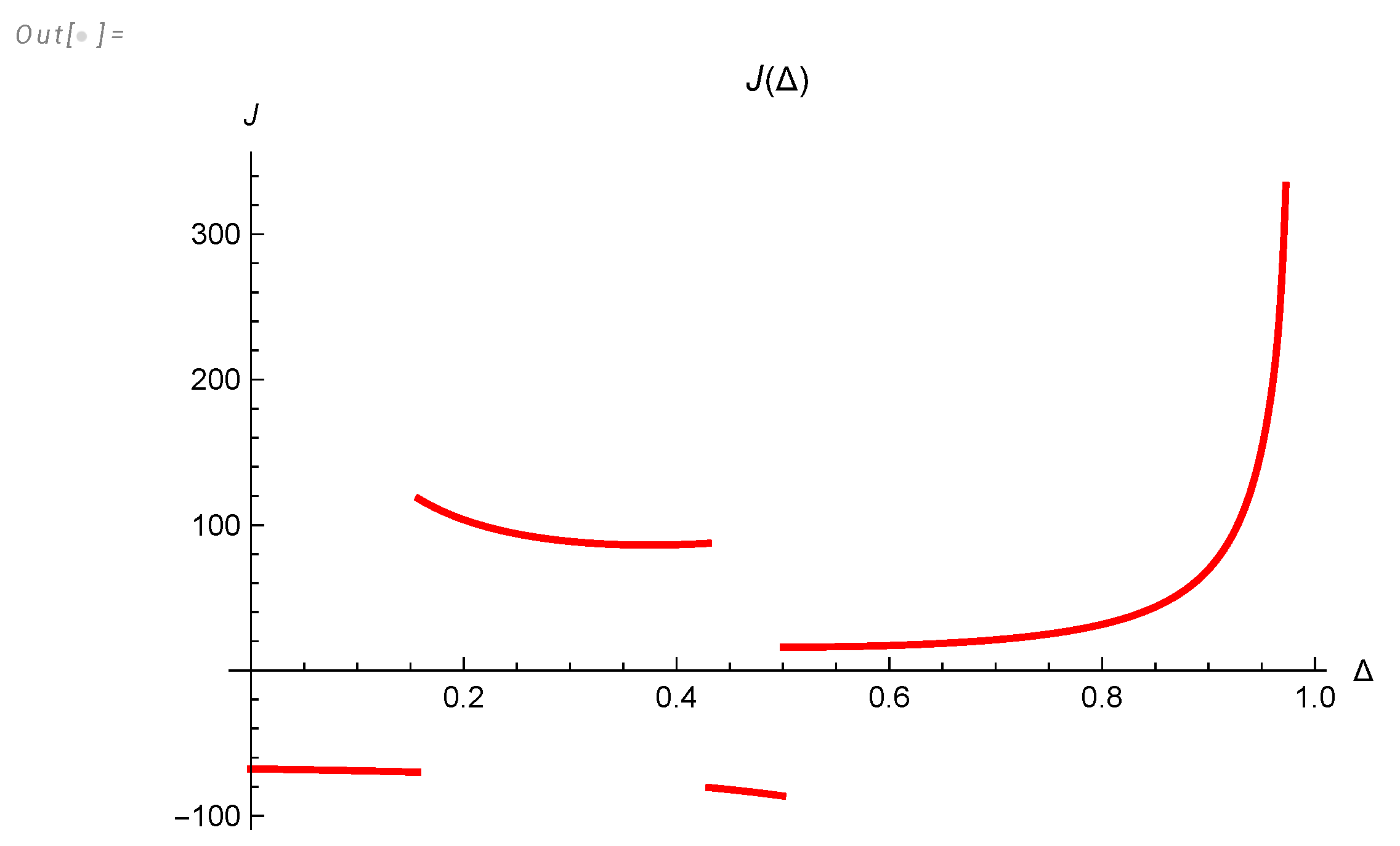
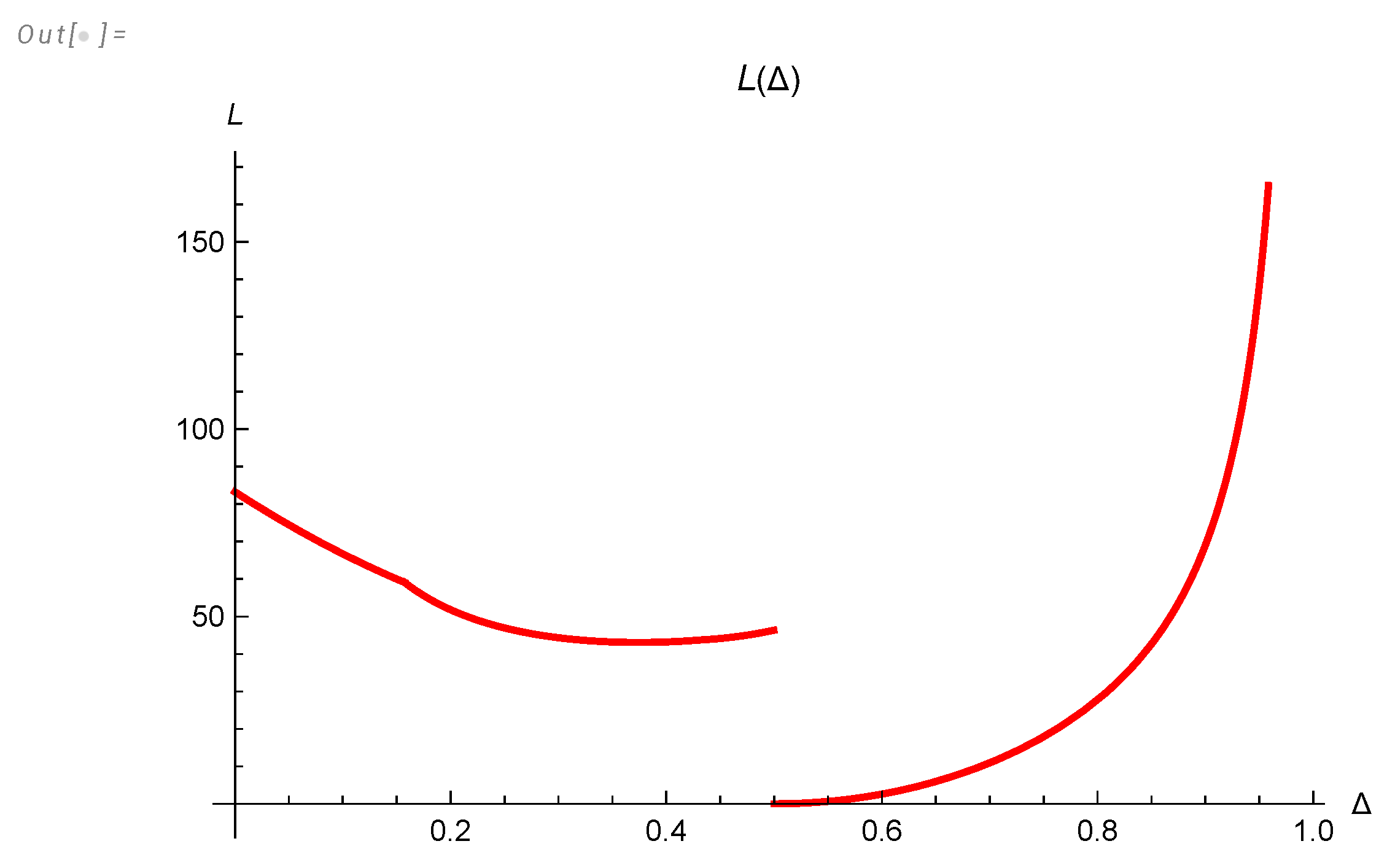
Both the energy dissipation and the energy spectrum are related to the same function

H (κ)

, but the energy spectrum related to this function at large argument

κ = k \sqrt{\tilde{ν} t}

, whereas the energy dissipation is related to integral of this function from small argument

κ = k_{0} \sqrt{\tilde{ν} t}

to infinity.

We computed this function in the Appendix A and numerically integrated it to obtain

F (κ), κ = k \sqrt{\tilde{ν} t}

. Asymptotically, at large t

\begin{matrix} E (k, t) \propto \frac{\tilde{ν} \sqrt{\tilde{ν}}}{\sqrt{t}} {(k \sqrt{\tilde{ν} t})}^{- \frac{7}{2}}; \end{matrix}

(234)

\begin{matrix} E (t) \propto t^{- \frac{9}{4}}; \end{matrix}

(235)

\begin{matrix} E (t) = \int_{t}^{\infty} E (t^{'}) d t^{'} \propto t^{- \frac{5}{4}} \end{matrix}

(236)

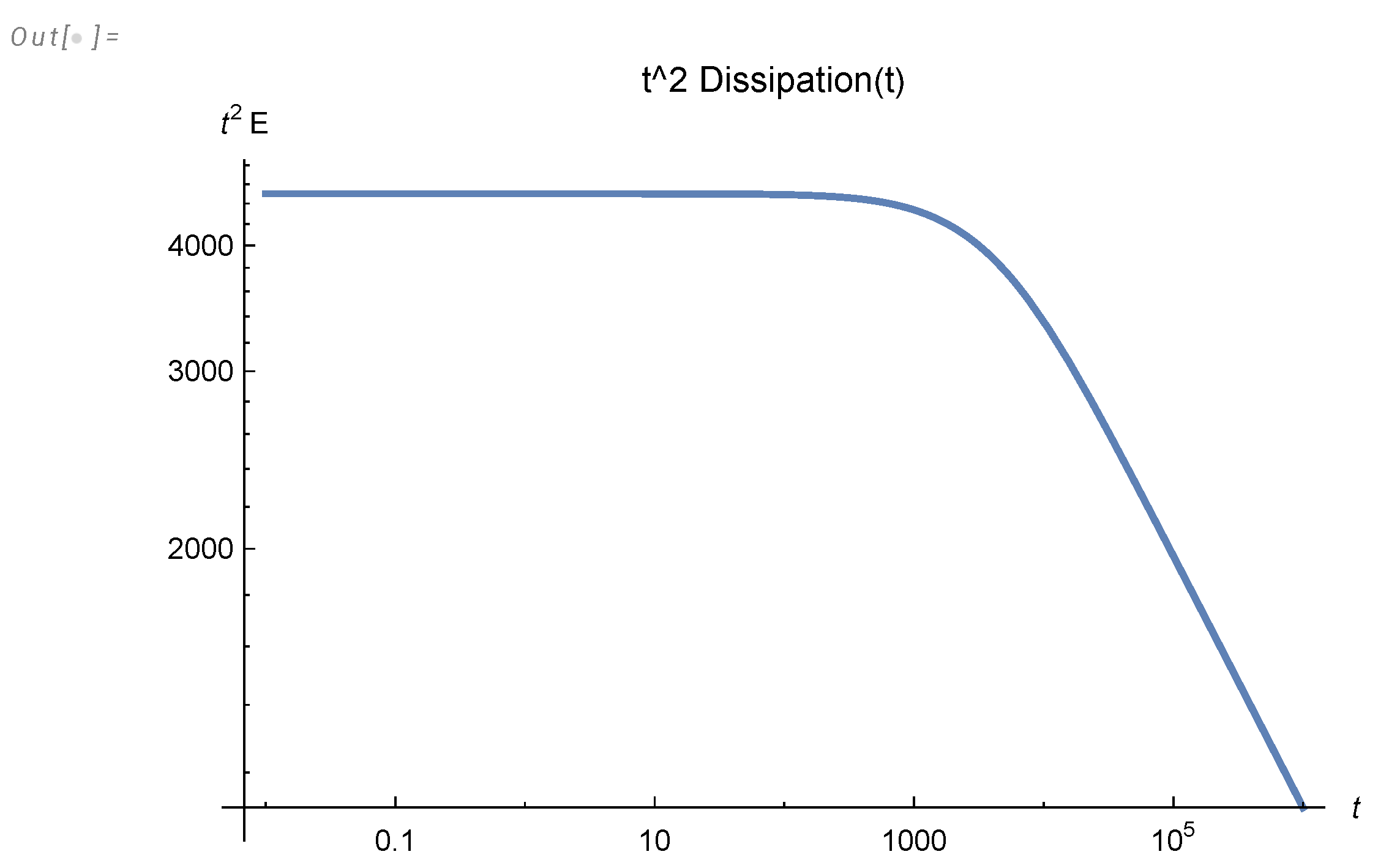
We computed the effective critical indexes

\begin{matrix} n (t) = - t \partial_{t} log E = - \frac{t E (t)}{E (t)}; \end{matrix}

(237)

\begin{matrix} s (κ) = - κ \partial_{κ} log H (κ) \end{matrix}

(238)

numerically in the Appendix A, using Mathematica^®. The accuracy is just 4-5 digits, but it can be easily improved by taking more CPU time once experimental data gets more precise. These curves are universal, and they change the regime before approaching their limits from below

n (\infty) = \frac{5}{4}, s (\infty) = \frac{7}{2}

. These regime changes are due to the quantum effects (complex zeros of the zeta function contributing to the energy spectrum’s Mellin transform, as shown in Appendix A).

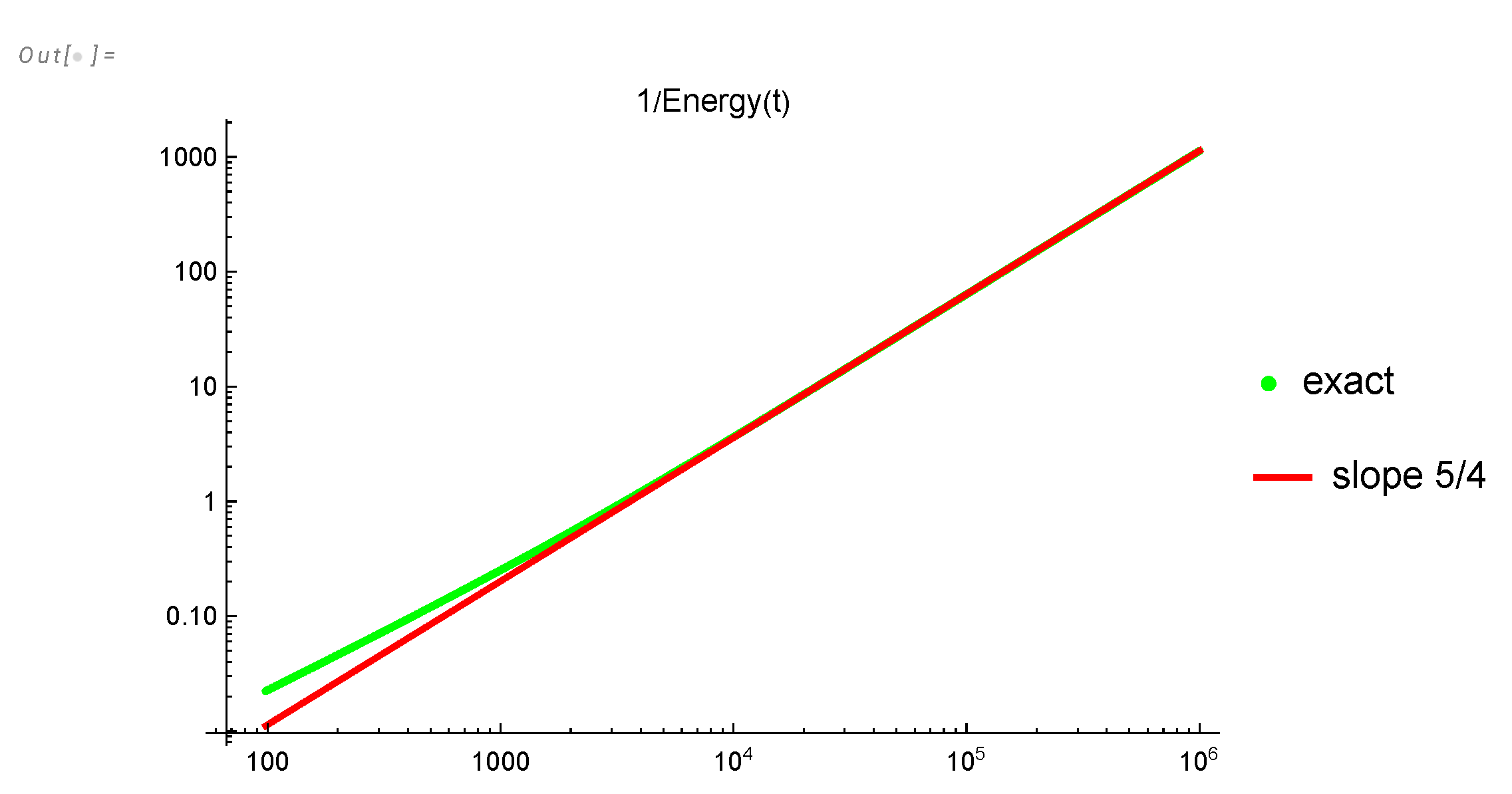
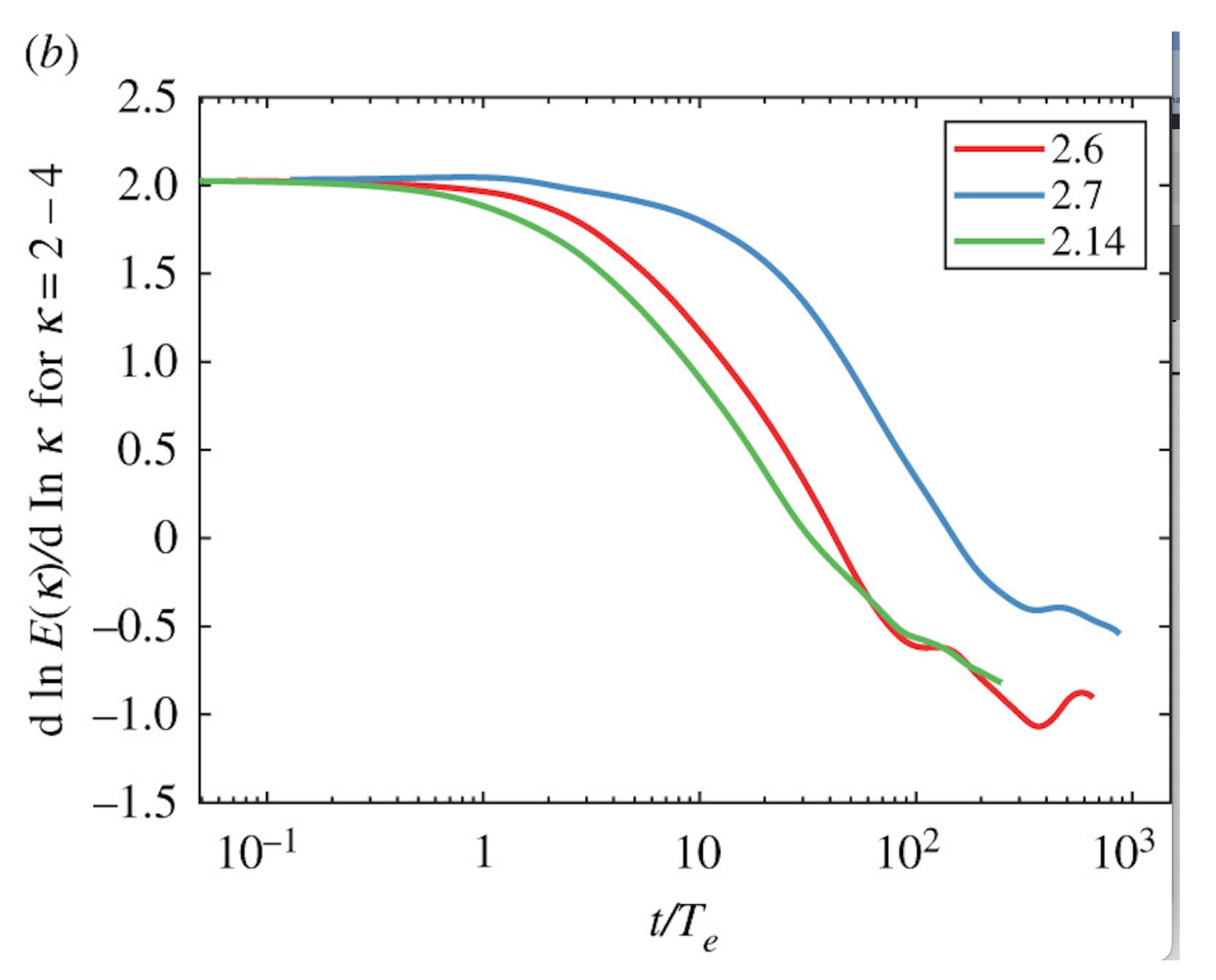
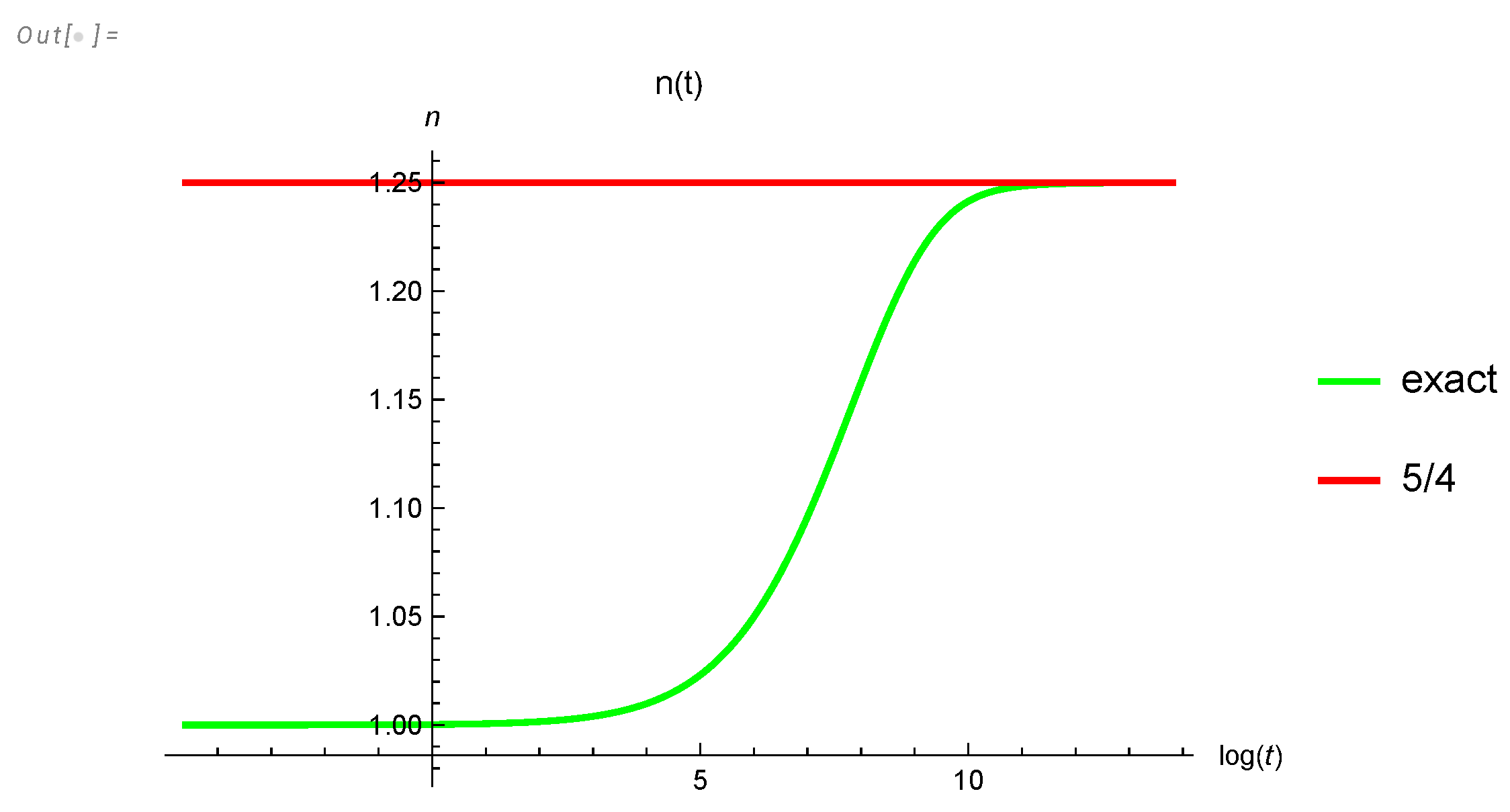
The experimental data [1] yields

n (\infty) \approx 1.25 \pm 0.02

, which agrees with our theoretical prediction in Figure 17.

Figure 17. The effective index

n (t) = - \frac{t E (t)}{E (t)}

compared with asymptotic value

n (\infty) = \frac{5}{4}

Figure 17. The effective index

n (t) = - \frac{t E (t)}{E (t)}

compared with asymptotic value

n (\infty) = \frac{5}{4}

Our universal curves for

n (t), s (κ)

were computed directly from the analytic solution of the loop equation in the turbulent limit without any fitting parameters. It will be very interesting to compare these curves with more precise experiments (real or numerical).

8. The Spectrum of Critical Indexes

In addition to numerically computing the energy spectrum and plotting effective critical indexes, we can go one step further in the mathematical analysis of the concept of the scaling laws in turbulence.

In a scale-invariant theory, the Mellin transform of the correlation function in coordinate or momentum space is a meromorphic function. The spectrum of critical indexes is given by the positions of poles of this function in a complex plane. In the theory of critical phenomena, which is described by a Conformal Field Theory (CFT), the whole spectrum of critical indexes is real.

As we shall prove below, our theory is scale-invariant by this definition, but it is not a CFT. In particular, some of the critical indexes come in complex conjugate pairs, reflecting the dissipative nature of our turbulence theory.

8.1. The Energy Spectrum

The spectral density

H (κ)

is in (223). The Mellin transform is the following transformation, assuming our function decreases at infinity.

\begin{matrix} H (κ) = \int_{- ϵ - ı \infty}^{- ϵ + ı \infty} \frac{d p}{2 π ı} h (p) κ^{p}; \end{matrix}

(239)

\begin{matrix} h (p) = \int_{0}^{\infty} \frac{d κ}{κ} κ^{- p} H (κ) \end{matrix}

(240)

We change the sign of p in conventional definition to better describe our functions.

The pure power law of decay would correspond to the Mellin transform

h (p)

having a single pole in the left semi-plane. The position

p = - a

of this pole becomes an index of the power law.

\begin{matrix} H (κ) \propto κ^{- a} \end{matrix}

(241)

The next level of complexity would be a function, depending on an extra parameter n, such that the Mellin transform has a simple pole, moving with this parameter

p = - a (n)

. This will produce multifractal scaling laws

\begin{matrix} κ^{- a (n)} \end{matrix}

(242)

Our energy spectrum has a more complex singularity structure in its Mellin transform

\begin{matrix} h (p) = \frac{f (p) ζ (p + \frac{15}{2}) Γ (- p)}{(2 p + 7) (2 p + 17) ζ (p + \frac{17}{2})}; \end{matrix}

(243)

\begin{matrix} f (p) = 20 \int_{Δ_{1}}^{Δ_{2}} d Δ (1 - Δ) C^{p - 1} (A C - B p) \end{matrix}

(244)

where

A, B, C

are some smooth positive functions of

Δ

varying in finite limits (see Appendix A). Given these properties, it is simple to prove that the Taylor series of

f (p)

at the origin converges as the expansion coefficients decrease as a factorial of the expansion order.

This makes this function an entire function without any finite singularities. The values of

C (Δ)

are bounded by two positive limits

\begin{matrix} 0.0541984 < C < 0.0630755, \forall Δ_{1} < Δ < Δ_{2} \end{matrix}

(245)

Therefore, the entire function

f (p)

decreases as

e^{- 2.76342 p}

in the right semiplane and grows as

e^{- 2.9151 p}

in the left semiplane. It oscillates along an imaginary axis, which is our integration path. Theoretically,

f (p)

could vanish at one or more positions of the poles of the remaining meromorphic function, eliminating these poles. We computed

f (p)

at the lowest poles and made sure it is far from zero. However, the cancellation of some higher poles by the root of

f (p)

remains an open problem.

The singularities of the Mellin transform

h (p)

for the energy spectrum

H (κ)

are given by the following table of simple poles

(246)

Here

\pm t_{n}

are imaginary parts of zeros of the

ζ

function on the critical line

z = \frac{1}{2} + ı t

. About

10^{13}

zeros are already known, though the Riemann hypothesis (that there are no other complex zeros) is still unproven. These poles are shown in Figure 18.

Figure 18. Complex poles of the Mellin transform

h (p)

H (κ)

in (243) defining the critical indexes of the energy spectrum as a function of

κ = | \vec{k} | \sqrt{\tilde{ν} t}

Figure 18. Complex poles of the Mellin transform

h (p)

H (κ)

in (243) defining the critical indexes of the energy spectrum as a function of

κ = | \vec{k} | \sqrt{\tilde{ν} t}

Only poles with negative real parts contribute to the power expansion at

κ \to \infty

. The real negative poles yield decaying power terms, but the infinite series of complex poles at Riemann zeros adds the oscillations in log scale

\begin{matrix} | W_{n} | κ^{- 8} cos (t_{n} log κ + arg W_{n}) \end{matrix}

(247)

These slow oscillations are visible as regime change in the log-log plots of effective indexes in Figure 17, Figure ??.

As we already discussed above, the energy spectrum decays as

t^{- \frac{9}{4}} k^{- \frac{7}{2}}

. The wavelength decay at fixed time is faster than K41

k^{- \frac{5}{3}}

. There is no theoretical reason for K41 in decaying turbulence, as the dissipation

E (t)

is not a constant to be used as a single scaling parameter.

8.2. The Energy Decay

The energy

E (t)

is related to the same function

\begin{matrix} E (t) = \int_{t}^{\infty} d t E (t) = 4 π \tilde{ν} \int_{t}^{\infty} \frac{d T}{T^{2}} \int_{k_{0} \sqrt{\tilde{ν} T}}^{\infty} H (x) x^{2} d x \end{matrix}

(248)

Substituting the Mellin transform for

H (x)

and integrating twice, we get the Mellin transform for the energy

\begin{matrix} E (t) = \int_{- 1 - ϵ - ı \infty}^{- 1 - ϵ + ı \infty} \frac{d q}{2 π ı} e (q) {(k_{0}^{2} \tilde{ν} t)}^{q}; \end{matrix}

(249a)

\begin{matrix} e (q) = 2 π k_{0}^{2} {\tilde{ν}}^{2} \frac{h (2 q - 1)}{q (q + 1)} \end{matrix}

(249b)

The table of complex poles of this function is

(250)

These poles are shown in Figure 19. The leading pole is at

p = - \frac{5}{4}

, corresponding to the asymptotic decay we compared to the grid turbulence decay data. Only poles with negative real parts contribute to the power expansion at

t \to \infty

Figure 19. Complex poles of the Mellin transform

e (q)

E (t)

in (Section 8.2) defining the spectrum of critical indexes of remaining energy as a function of time.

Figure 19. Complex poles of the Mellin transform

e (q)

E (t)

in (Section 8.2) defining the spectrum of critical indexes of remaining energy as a function of time.

Figure 20. The spectrum of (complex) indexes of the power expansion of the velocity correlation function. The poles in the right semiplane determine the small-distance expansion of the correlation function

\vec{v} (0) \cdot \vec{v} (r) \sim \sum_{n} O_{n} {| \vec{r} |}^{p_{n}}

\vec{v} (0) \cdot \vec{v} (r) \sim \sum_{n} O_{n} {| \vec{r} |}^{p_{n}}

8.3. The Velocity Correlation Function in Coordinate Space

Let us transform the velocity correlation back to coordinate space from wavevector space

\begin{matrix} 〈{(\vec{v} (\vec{r}, t) - \vec{v} ({\vec{r}}^{'}, t))}^{2}〉 = 2 \int \frac{d^{3} k}{{(2 π)}^{3}} (1 - exp (ı \vec{k} \cdot (\vec{r} - {\vec{r}}^{'}))) \frac{{〈ω \cdot \vec{ω}〉}_{k}}{{\vec{k}}^{2}} = \\ \frac{\tilde{ν}}{π^{2} t} \int_{- ϵ - ı \infty}^{- ϵ + ı \infty} \frac{d p}{2 π ı} {(\frac{| \vec{r} - {\vec{r}}^{'} |}{\sqrt{\tilde{ν} t}})}^{p} cos (\frac{π p}{2}) Γ (- p - 1) h (- 1 - p); \end{matrix}

(251)

The Mellin transform simplifies to

\begin{matrix} 〈{(\vec{v} (\vec{r}, t) - \vec{v} ({\vec{r}}^{'}, t))}^{2}〉 = \frac{\tilde{ν}}{t} \int_{- ϵ - ı \infty}^{- ϵ + ı \infty} \frac{d p}{2 π ı} V (p) {(\frac{| \vec{r} - {\vec{r}}^{'} |}{\sqrt{\tilde{ν} t}})}^{p}; \end{matrix}

(252)

\begin{matrix} V (p) = - \frac{f (- 1 - p) ζ (\frac{13}{2} - p) sin (\frac{π p}{2}) Γ (p) Γ (p + 1)}{π^{2} (2 p - 15) (2 p - 5) ζ (\frac{15}{2} - p)} \end{matrix}

(253)

The poles of this function in the right semiplane represent the indexes of the power singularities of the velocity correlation function at coinciding points

(0, \vec{r})

. Should our theory be a CFT (which it is not), this spectrum would be related to the spectrum of anomalous dimensions

Δ_{n}

in the OPE:

CFT : \vec{v} (0) \cdot \vec{v} (r) \sim \sum_{n} O_{n} {| r |}^{p_{n}}; p_{n} = 2 Δ_{v} - Δ_{n};

We have such an expansion with

\frac{| \vec{r} |}{\sqrt{\tilde{ν} t}}

in place of

| r |

and a factor

\frac{\tilde{ν}}{t}

in front. The spectrum of these scaling indexes

p_{n}

(unrelated to any dilatation operator) is given in the following table:

(254)

We have no CFT but a calculable spectrum of scaling dimensions. Unlike the CFT in three dimensions, this spectrum is complex. Only poles with positive real parts contribute to the power expansion at

| \vec{r} | \to 0

As we already mentioned in relation to the energy spectrum, there is no K41 scaling index

p = \frac{2}{3}

. This is not a contradiction, as K41 does not apply to decaying turbulence.

One more turbulence puzzle solved: these "anomalous dimensions" are related to the Riemann

ζ

function zeros. The way to measure experimentally the next to the leading pole in the Mellin transform of the energy decay is to measure the combination

\begin{matrix} E_{1} (t) = E (t) - \frac{4}{5} t E (t) \end{matrix}

(255)

According to our theory, this combination decays as

t^{- \frac{11}{4}}

, so that

\begin{matrix} t^{\frac{11}{4}} E_{1} (t) \to const; \end{matrix}

(256)

\begin{matrix} t E_{1}^{'} (t) \to - \frac{11}{4} E_{1} (t) \end{matrix}

(257)

9. Discussion

This section aims to reconcile traditional perspectives on turbulence phenomena, including enduring beliefs and myths, with the new mathematical frameworks of the quantum theory we have developed.

Portions of the upcoming discussion have been previously included in my paper [7]. We have significantly modified these sections to reflect our deepened grasp of this theory.

9.1. Myth and Reality of Turbulent Scaling Laws

More than eighty years ago, Kolmogorov and Obukhov made a pivotal breakthrough in the theory of turbulence by establishing the relation (7) for the three-point correlation function of the velocity field in turbulent flow. This formula, by taking two coincident points, only selects the potential part of the triple velocity correlation function. When taking the curl, we get zero:

〈v_{α} ({\vec{r}}_{0}) v_{β} ({\vec{r}}_{0}) ω_{γ} (\vec{r} + {\vec{r}}_{0})〉 = 0

This indicates no constraints on the rotational part concerning triple vorticity correlations and sheds no light on the scale invariance of turbulence theory.

The K41 scaling law was a phenomenological model, not intended to replace the missing microscopic theory. It was predicated on the assumption of non-fluctuating local dissipation density—a limitation well understood by its creators, who later proposed a log-normal distribution for this variable. However, this model did not claim any microscopic justification either.

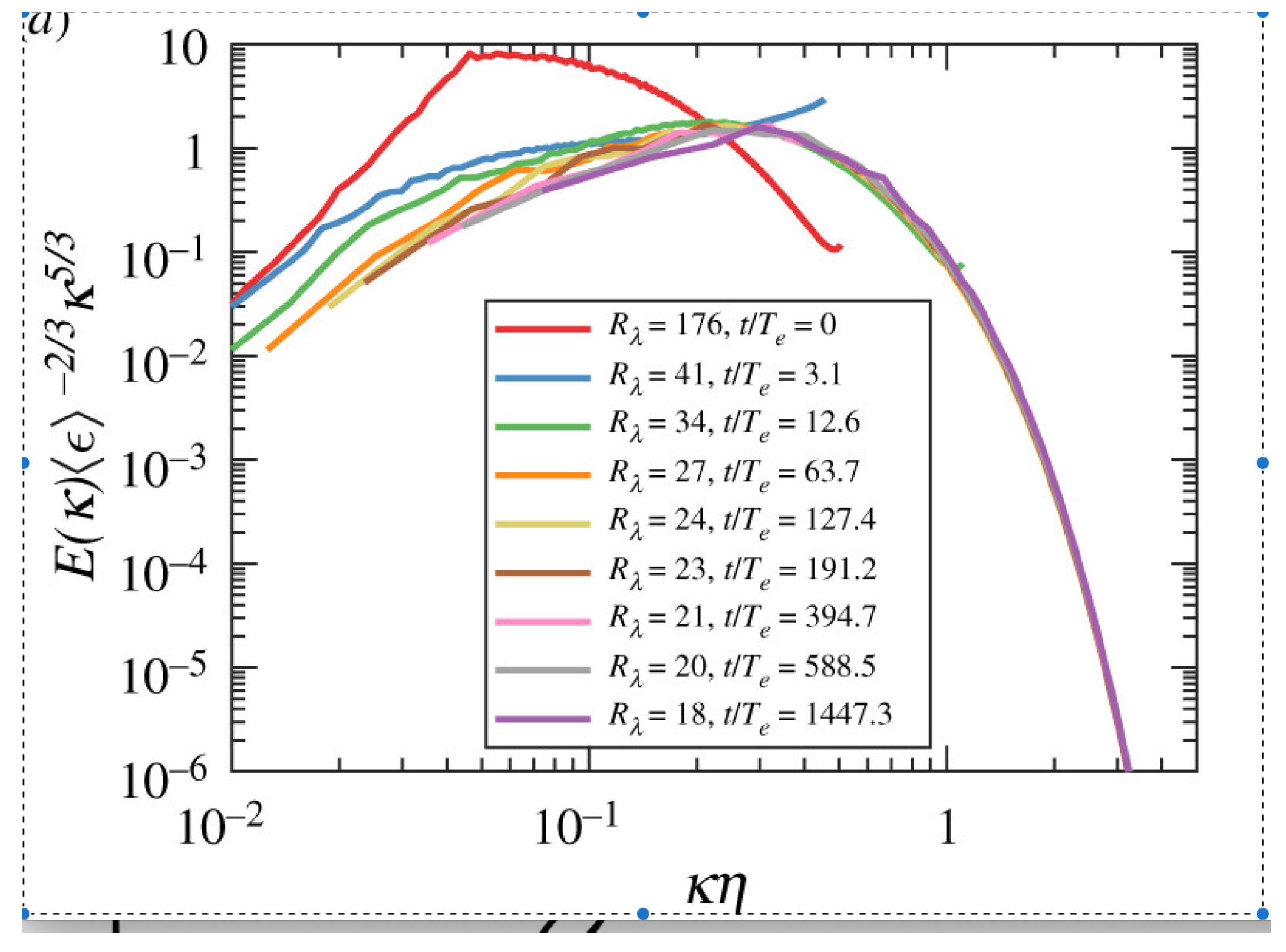
Subsequent experiments and DNS [35,36,37] have invalidated the K41 scaling law over the past thirty years. Regarding decaying turbulence, the Kolmogorov scaling laws have consistently diverged from experimental realities despite attempts to align DNS data with these scaling laws. We highlight significant deviations—six orders of magnitude—from the

k^{- \frac{5}{3}}

scaling in Figure 5.

A broader assumption posited that power laws with anomalous dimensions might exist in the inertial range. This analogy to critical phenomena led to the proposal of multifractal scaling laws [23], which, as a phenomenological model, successfully described observed deviations from the K41 laws [36,37].

However, there are no theoretical grounds for expecting conformal symmetry in turbulence, especially since the ’current conservation’ conditions

\partial_{α} v_{α} = 0, \partial_{γ} ω_{γ} = 0

in the CFT prescribe both velocity and vorticity dimensions of

d - 1 = 2

, contradicting the fact that vorticity is a curl of velocity.

Dismissing scaling and multifractal laws suggest that correlation functions are nonlinear on a log-log scale, as indicated by the data in Figure 5. Here, energy spectra for various parameters converge into a universal curve on the decreasing part of the spectrum, which is curved on the log-log scale, indicating that it cannot be described by a simple power law. Instead, it is a nontrivial universal function of

log k

, spanning several decades.

Our recent paper [10] discussed the possibility of violating scaling laws due to logarithmic divergences in a model of a dilute gas of vortex filaments. This model included logarithmic terms in the effective energy for the filament, leading to violations of scaling laws akin to asymptotic freedom in QCD.

Despite the apparent lack of conformal symmetry, the present theory for the second moment of velocity, discussed in Section 8, retains a critical aspect of CFT. The Mellin transform of the vorticity field’s correlation function in coordinate space is a meromorphic function of the Mellin parameter p. This characteristic implies some underlying scale invariance with an infinite discrete spectrum of complex anomalous dimensions.

Consequently, our theory extends the multifractal scaling laws by accommodating an infinite spectrum of discrete scaling dimensions, which diverges from traditional scaling models such as those proposed by Kolmogorov and Saffman. According to recent DNS results [5], our predictions align with observed slopes, thereby distinguishing them from conventional scaling predictions.

This reevaluation suggests that experiments and DNS in decaying turbulence should be conducted at larger scales and higher Reynolds numbers, fitting the data for logarithms of the spectrum and energy dissipation decay as nonlinear functions of the logarithm of the wavevector and time, as our theory provides a universal function framework for this comparison.

9.2. Stochastic Solution of the Navier-Stokes Equation and Ergodic Hypothesis

Richard Feynman wrote about turbulence in his Lectures in Physics: "Nobody in physics has really been able to analyze it mathematically satisfactorily in spite of its importance to the sister sciences. It is the analysis of circulating or turbulent fluids". [38]. We address this problem by seeking a stochastic solution to the Navier-Stokes equation, which asymptotically spans a universal manifold over an infinite time. Our approach reveals singularities in correlation functions, which emerge after averaging across this manifold in the statistical limit as its dimension approaches infinity. These singularities originate from the infinite time required to cover this manifold uniformly.

We identify this manifold (the Euler ensemble) by solving the loop equation—a subset of the Hopf functional equation for the generating functional of velocity field probabilities. Notably, none of the solutions within this manifold experiences finite-time blow-ups. Instead, we encounter singularities from the fixed trajectory of the loop equation, not from its finite-time solutions.

We adopt the most natural invariant measure from the perspective of number theory: each element of the Euler ensemble is weighted equally, an assumption we term the quantum ergodic hypothesis. This hypothesis isn’t necessary for solving the loop (i.e., Hopf) equation, as any linear superposition of the solutions would satisfy it.

Using this invariant measure, the Euler ensemble stands out because the loop functional is equal to the trace of the evolution operator in a quantum system—the Fermi particles on a ring interacting with a quantum field made of fractions of

π

. Every distinct state, including every distinct fraction, contributes equally to the quantum trace in this discrete system. For our purposes, this means treating every element in the Euler ensemble with equal weight.

Our quantum ergodic hypothesis thus stipulates an exact equivalence between the loop functional and the quantum trace of an evolution operator

tr exp (- ı \hat{H} τ)

for the one-dimensional ring of Fermi particles. This quantum analogy has paved the way for an analytical solution in the turbulent limit, akin to the quasiclassical limit of this Fermi system, where viscosity acts like Planck’s constant, and the inverse Reynolds number functions as a weak coupling constant of the dual theory.

Surprisingly, this theory leads to a dimensional reduction from 3 to 1, where the one-dimensional quantum system mirrors the three-dimensional decaying turbulence. This equivalence could not be achieved through local relationships between the dynamical variables of these systems; instead, it requires a nonlocal connection through the loop average.

A mathematical transformation that links the quantum amplitude with the turbulent probability differs from the typical analytic continuation to imaginary time in ordinary quantum statistics. Instead, it involves a Fourier transformation from the probability distribution of velocity circulation to the loop functional.

In the same way as the classical ergodic hypothesis in Newton’s mechanics without dissipation may be provable mathematically, we hope our quantum ergodic hypothesis can be proven from the Navier-Stokes equation. If confirmed, this hidden quantum mechanics of classical turbulence may become a law of Nature rather than a computational method.

Like the classical ergodic hypothesis, this may take another hundred years. Theoretical physics does not wait for rigorous proof but rather explores the consequences of the conjectured theory and compares them with physical and numerical experiments.

9.3. The Physical Meaning of the Loop Equation and Dimensional Reduction

The long-term evolution of Newton’s dynamical system with many particles eventually covers the energy surface (microcanonical ensemble). The ergodic hypothesis (accepted in Physics but still not proven mathematically) states that this energy surface is covered uniformly. The Turbulence theory aims to find a replacement of the microcanonical ensemble for the Navier-Stokes equation. This surface would also take part in the decay in the pure Navier-Stokes equation without artificial forcing. In both cases, Newton and Navier-Stokes, the probability distribution must satisfy the Hopf equation, which follows from the dynamics without specification of the mechanism of the stochastization. Indeed, the Gibbs, as well as the microcanonical distributions in Newton’s dynamics, satisfy the Hopf equation in a rather trivial way: It reduces to the conservation of the probability measure (Liouville theorem), which suggests the energy surface as the only additive integral of motion to use in the exponent of the fixed point distribution.

The loop technology was thoroughly discussed in the last few decades in the gauge theories, including QCD [12,14,15,16,39] where the loop equations were derived first [40,41].

In the case of the decaying turbulence, the loop equations represent a closed subset of the Hopf equations, which subset is still sufficient to generate the statistics of vorticity. In this case, the exact solution we have found for the loop functional also follows from the integrals of motion, this time, the conservation laws in the loop space.

The loop space Hamiltonian we have derived from the unforced Navier-Stokes equation does not have any potential terms (those with explicit dependence upon the shape of the loop). The Schrödinger equation with only kinetic energy in the Hamiltonian conserves the momentum. The corresponding wave function is a superposition of the plane waves

exp (ı \vec{p} \cdot \vec{x})

. This is the solution we have found, except the dot product

\vec{p} \cdot \vec{x}

becomes a symplectic form

\oint \vec{P} (θ) \cdot d \vec{C} (θ)

in the loop space. Our momentum

\vec{P} (θ, t)

is not an integral of motion, but simple scaling properties of the pure Navier-Stokes equation lead to the solution with

\vec{P} (θ, t) \propto \vec{F} (θ) / \sqrt{t}

, with

\vec{F} (θ)

being the integral of motion at large time (i.e. a fixed point). The rest is a purely technical task: substituting this scaling solution into the Navier-Stokes equation and solving the resulting universal equation for a fixed point

\vec{F} (θ)

This equation led us to the Fermi ring in the quasiclassical limit. The solution of the Fermi ring in this limit resulted in the energy spectrum and dissipation in a finite system found in the Section 7.

9.4. Classical Flow and Quantum Mechanics

Our computations heavily rely on number theory, particularly Jordan’s multitotients,

φ_{l} (q)

, which extend the Euler totient function [42]. What could number theory possibly have in common with turbulent flow? The quantization of parameters in the fixed manifold of decaying turbulence originates from the quantum correspondence discovered back in the nineties [6]. The statistical distribution of a nonlinear classical Navier-Stokes (NS) PDE is precisely related to the wave functional of a linear Schrödinger equation in loop space.

This relationship is indirect: the loop functional, a Fourier transform of the classical probability distribution for circulation, equals the complex quantum amplitude of the loop space theory, represented by a Fermi ring. Probability is real and positive, yet its Fourier transform is complex, illustrating no contradiction between classical and quantum mechanics.

The mechanism of quantization mirrors that found in conventional quantum mechanics: the solution’s periodicity.

For an expert in traditional approaches to turbulence, the fractal curve in complex momentum space,

\vec{P} (θ) \in C_{3}

, or Fermi-particles on a circle might appear unrelated to a velocity field in physical space,

\vec{v} (\vec{r}) \in R_{3}

. Is this a miracle or a mirage?

The equivalence of a strong coupling phase of the fluctuating vector field to a weak coupling phase of quantum geometry in a different dimension is a well-established duality phenomenon in gauge theory (the ADS/CFT duality). This represents more than a method to compute correlation functions of a strongly fluctuating vector field: it is a secret second identity of the original theory.

The fluctuations of the charge density in the quantum Fermi ring we discovered disappear in the turbulent limit, while in the original theory, the fluctuations are so intense that the vorticity field ceases to exist. Arguably, this Fermi ring is the true identity of decaying turbulence, as it is described by a smooth classical function: the instanton solution for the charge density we have identified.

The most appropriate answer to a hypothetical turbulence expert questioning this is that this mirage is a portal to a mirror universe, where familiar phenomena appear completely different. Duality applies to the correlation functions of two theories with different dynamical variables; while these variables may not correspond directly, their functions are equal.

Mathematical physics sometimes presents alternative languages for the same phenomena; examples include the duality between Schrödinger wave equation and Heisenberg’s matrix mechanics, and between matrix models [26,27,43] and Liouville theory [28,44] in 2D quantum gravity.

Long ago, in the eighties, the author conjectured [45] that QCD in the so-called large-N limit would manifest as a string theory, incorporating fermion degrees of freedom on the world sheet of the string. This hypothesis, based on the QCD loop equations [40], represented an early attempt to establish duality in gauge theory. However, this conjecture was later proven wrong due to the instability of the string theory in four dimensions.

Remarkably, a similar conjecture in the present theory involving comparable fermion degrees of freedom provides a physical solution to the loop equations in decaying turbulence. This revitalizes the idea of hidden fermions in loop dynamics and, unlike its predecessor, appears to be correct, aligning well with experimental results.

Additional complexities in gauge theory arise from short-distance singularities related to the infinite number of fluctuating degrees of freedom in quantum field theory. Wilson loop functionals in coordinate space are singular in gauge field theory and cannot be multiplicatively renormalized.

Perturbatively, there are no short-distance divergences in Navier-Stokes equations or the NS loop dynamics. The Euler equations represent the singular limit, which, as we argued, should be resolved using singular topological solitons regularized by the Burgers vortex. In this current theory, we encounter no singularities in coordinate space. Anomalous dissipation is achieved in our solution through a completely different mechanism: many finite discontinuities of the fractal curve. However, these singularities only occur in the inviscid limit,

ν \propto 1 / N^{2} \to 0

, and correspond to Euler singularities, such as line vortices, which are regularized by finite viscosity, just like our singularities.

9.5. Renormalizability of the Inviscid Limit of the Loop Equation

Let us examine the relationship

ν N^{2} = const

between diminishing viscosity and the increasing number of discontinuities on the momentum loop

\vec{P} (θ)

The Navier-Stokes (Navier-Stokes) equation is essentially an idealization of molecular dynamics, where the nonlocal theory is approximated by a truncated expansion in powers of gradients.

In the case of laminar flow, this truncated expansion poses no issues. However, in our solution for the loop equation, the velocity field becomes singular in the local limit.

Mathematically, velocity and vorticity are not ordinary functions in

R_{3}

but stochastic variables, with

Δ \vec{v} \sim {(Δ \vec{r})}^{α}

Fractal Calculus [46] was introduced to generally describe such fields. Yet, this alone does not account for turbulence, particularly since the more general power laws with multifractal dimensions

〈{(Δ \vec{v})}^{n}〉 \sim {(Δ \vec{r})}^{ζ_{n}}

cannot be explained in this manner.

In our theory, there is a universal function for the velocity correlation function as a function of the separation

\vec{r}

. However, the

\vec{r}

dependence is not defined by a single power: the Mellin transform of this function reveals infinitely many poles in the complex plane. The absence of the branch cuts supports the idea of scale invariance, but here is where the analogy with CFT ends.

Our solution characterizes a fractal vorticity field, yet this field does not conform to known fractal types. The fractal curve

\vec{P} (θ)

is not merely a random walk on a circle: dynamic restrictions, such as periodicity, lead to nontrivial critical behavior not describable by any finite set of fractal power laws.

We define the turbulent limit of the velocity field distribution by discretizing the loop equation (replacing the continuum loop with a polygon with an increasing number of vertices).

The relation between vanishing viscosity and an increasing number of degrees of freedom parallels the renormalization group (RG) relation between the bare coupling constant

g_{0}

and the lattice spacing a in QCD:

a \propto g_{0}^{α} exp (- β / g_{0}^{2})

The naive local limit

a \to 0, g_{0} = const

does not exist in QCD, but the RG limit effectively describes the strong interaction of hadrons.

Similarly, in our approach, renormalizability is present. The dissipation rate remains finite as

\tilde{ν} = ν N^{2} \to const

. Furthermore, the entire energy spectrum, expressed in terms of

\tilde{ν}

, remains finite in the local limit. Thus, akin to renormalizable quantum field theory (QFT), a "dimensional transmutation" occurs where infinities are absorbed into the dimensional parameter

\tilde{ν}

, defining the time scale.

9.6. Relation of Our Solution to Weak Turbulence

The solution of the loop equation with finite area derivative, satisfying the Bianchi constraint, belongs to the category of Stokes-type functionals [40], similar to the Wilson loop for gauge theory and fluid dynamics.

The Navier-Stokes (NS) Wilson loop represents a case of the Abelian loop functional, characterized by commuting components of the vector field

\vec{v}

. As extensively discussed in [11,40,41], any Stokes-type functional

Ψ [γ, C]

that satisfies the boundary condition at a shrunk loop

Ψ [0] = 1

and solves the loop equation can be iterated in the nonlinear term in the NS equations. This iteration is applicable in conditions of high viscosity.

The resulting expansion in inverse powers of viscosity (representing weak turbulence) coincides with the standard perturbation expansion of the NS equations for the velocity field, averaged over the distribution of initial data.

We have shown in [6,11] (and also here, in Section 3.6) how the velocity distribution for random uniform vorticity in the fluid was reproduced by a singular momentum loop

\vec{P} (θ)

The solution for

\vec{P} (θ)

at this specific fixed point of the loop equation was complex and had slowly decreasing Fourier coefficients, leading to a discontinuity

sign (θ - θ^{'})

in a pair correlation function (32). The corresponding Wilson loop is equated to the Stokes-type functional (25).

Using this example, we demonstrated how a discontinuous random momentum loop describes the vorticity distribution in the stochastic NS flow. Here, the vorticity acts as a global random variable corresponding to a random uniform fluid rotation—a well-known exact solution of the NS equation.

This example corresponds to a special fixed point for the loop equation. Although not general enough to describe turbulent flow, it serves as an ideal mathematical model for loop technology. It illustrates how the momentum loop solution aggregates all terms of the

1 / ν

expansion in the NS equation.

In our general solution, with the Euler ensemble, the summation of a divergent perturbation expansion occurs at an extreme level, leading to a universal fixed point in the limit of vanishing viscosity.

Given initial conditions, after a finite time, the solution will still depend on viscosity and the initial conditions. We expect no singularities for a smooth initial velocity field.

Over longer durations, however, it will converge to our universal fixed manifold and (presumably, for random initial data) cover it uniformly, according to the Euler ensemble measure.

Thus, the

ν \to 0, N \to \infty

limit of our solution for the fixed point

\vec{F} (θ)

corresponds to the

ν \to 0, t \to \infty

limit of the solution for the time-dependent loop equation.

10. Remaining problems

We performed all the calculations up to numerical factors in the vorticity correlation function, which we recovered from the previously computed $〈{\vec{ω}}^{2}〉$ (see [7]). It would be useful to compute all the normalization factors and thus double-check the solution.
The loop functional for the circular loop is the simplest object in this theory. It can be computed using the methods developed in this paper, with even simpler results. In this case, the classical equation is trivial, so the computations reduce to the functional determinant and the resolvent. On the other hand, this is an observable quantity, and one could measure it in DNS. It would be an interesting problem to solve and compare with the DNS.
The higher moments of circulation or velocity differences are calculable from this general WKB approximation for the path integral at $ν \to 0, N \to \infty$ . The nth moment of $Δ \vec{v} = \int d^{3} k \frac{ı \vec{k} \times {\vec{ω}}_{k}}{{\vec{k}}^{2}} (exp (ı \vec{k} \cdot \vec{r}) - exp (ı \vec{k} \cdot {\vec{r}}^{'}))$ reduces to the loop functional for the same backtracking "hairpin" traversed n times, with vorticity inserted n times at the ends. This computation will produce analytical results for the multifractal scaling laws for velocity moments.
The spectrum of indexes for deviations from our fixed trajectory [7] can be evaluated in the scaling limit, with finite $\tilde{ν}$ . This computation will produce results for the vorticity correlation functions in the Navier-Stokes equation, perturbed by an infinitesimal random force.

11. Conclusion

We have derived an analytical solution for decaying turbulence directly from the Navier-Stokes loop equation, deliberately eschewing reliance on models or approximations. This solution unveils a duality between decaying classical turbulence in 3+1 dimensions and a solvable one-dimensional quantum theory of Fermi particles on a ring. Notably, the coupling constant in this theory is related to random fractions of

π

, thereby establishing a substantive link to Number Theory. This discovery exposes a hidden alter ego of decaying turbulence and suggests a novel and significant bridge between classical and quantum physical frameworks.

Data Availability Statement

The Mathematica^®notebooks used to verify equations and compute some functions are available for download in [8,9,33,34,47].

Acknowledgments

Maxim Bulatov helped me with mathematical suggestions and discussions. He also participated in an unpublished paper [30] where we simulated the Euler ensemble as a Markov chain. The strong cancellations in the vorticity correlation function prevented this simulation from producing reliable numerical results. I filled the gaps in my knowledge of Number Theory in discussions of the Euler ensemble with Peter Sarnak, Alexandru Zaharesku, Konstantin Khanin, and Debmalya Basak. Yang-Hui and I discussed Euler’s totients at the Cambridge University workshop, where this theory was first reported in November 2023. His comments helped me derive the asymptotic distribution for scaling variables. I am also grateful to the organizers and participants of the "Field Theory and Turbulence " workshop at ICTS in Bengaluru, India, where this work was advanced in December 2023. Discussions with Katepalli Sreenivasan, Rahul Pandit, and Gregory Falkovich were especially useful. They helped me understand the physics of decaying turbulence in a finite system and match my solution with the DNS data. Recently, this work was discussed at the "Conformal Field Theory, Integrability, and Geometry" conference in Stony Brook in March 11-15, 2024. I am very grateful to Nikita Nekrasov, Sasha Polyakov, Sasha Zamolodchikov, Dennis Sullivan and other participants for deep and inspiring discussions. Finally, this work was thoroughly discussed for a week at the Perimeter Institute for Theoretical Physics, where I spoke at a colloquium on April 3. I received many interesting questions and comments, reflected in the last section, "Discussion," of this paper. I thank Davide Gaiotto, Luis Lehner, Sabrina Pastersky, Sergey Sibiryakov, Lee Smolin, and Andrey Shkerin for inspiring discussions. The help from Zechuan Zheng in Mathematica computations of the energy spectrum was also very useful. The most important help and support came from Sreeni, who, for the last year, discussed the physics of decaying turbulence with me and guided me through the maze of inconsistent DNS and physical experiment data. We concluded that the reliable subset of this data did not agree with old models (Kolmogorov, Loitzansky, and Saffman) but matched the present theory. This research was supported by a Simons Foundation award ID 686282 at NYU Abu Dhabi.

Appendix A. Mellin integral for the energy spectrum and energy decay

The spectral function

H (κ)

can be computed as follows. Let us represent the theta function as inverse Mellin transform (at

n > 0, τ > 0

)

\begin{matrix} θ (1 - n τ) = \int_{+ 0 - ı \infty}^{+ 0 + ı \infty} \frac{d p}{2 π ı p} n^{- p} τ^{- p} \end{matrix}

(A1)

Substituting this representation into our integral in (Section 6.4), and interchanging summations/integrations, we find

\begin{matrix} H (κ) = \int_{Δ_{1}}^{Δ_{2}} d Δ (1 - Δ) \int_{+ 0 - ı \infty}^{+ 0 + ı \infty} \frac{d p}{2 π ı p} \sum_{n = 1}^{\infty} \frac{φ (n)}{n^{p}} \int_{0}^{\infty} d t (\frac{t^{5 / 2}}{n^{5}} - t^{15 / 2}) t^{- p} (A + B t κ) e^{- C t κ}; \end{matrix}

(A2)

\begin{matrix} A = \frac{Q_{α} (Δ, 1) \sqrt{r_{0} (Δ)}}{Z} \frac{2 (r_{0} (Δ) - 6)}{(12 + r_{0} (Δ))}; \end{matrix}

(A3)

\begin{matrix} B = \frac{Q_{α} (Δ, 1) \sqrt{r_{0} (Δ)}}{Z} \frac{J (Δ)}{S (Δ)}; \end{matrix}

(A4)

\begin{matrix} C = \frac{L (Δ)}{2 π S (Δ)}; \end{matrix}

(A5)

The last integral reduces to Gamma functions and powers of n, after which the sum over n reduces to the ratio of two zeta functions

\begin{matrix} H (κ) = \int_{Δ_{1}}^{Δ_{2}} d Δ (1 - Δ) \int_{- 2 - ı \infty}^{- 2 + ı \infty} \frac{d z κ^{z}}{2 π ı} \frac{20 C^{z - 1} (A C - B z) ζ (z + \frac{15}{2}) Γ (- z)}{(2 z + 7) (2 z + 17) ζ (z + \frac{17}{2})} \end{matrix}

(A6)

According to the Riemann hypothesis, the function

ζ (w), w = z + \frac{17}{2}

in the denominator has trivial zeros at negative even points

z = - 2, - 4, \dots

and nontrivial zeros at the critical line

Re w = \frac{1}{2}

There is also a contribution from the poles at

z + \frac{15}{2} = 1, (2 z + 7) = 0, (2 z + 17) = 0

We are not going to sum the residues in these poles, but rather integrate along the line

z = - 2 + ı y

, where the integrand exponentially decreases as

exp (- \frac{π | y |}{2})

in both directions.

Figure A1. The log-log plot energy dissipation

t^{2} E (t)

as a function of t has a regime change due to quantum effects. It starts as constant at small t and asymptotically decays as

t^{2} E \propto t^{- \frac{1}{4}}

Figure A1. The log-log plot energy dissipation

t^{2} E (t)

as a function of t has a regime change due to quantum effects. It starts as constant at small t and asymptotically decays as

t^{2} E \propto t^{- \frac{1}{4}}

There are oscillations on top of this exponential decrease. The integrals can be computed with arbitrary accuracy in Mathematica^®using the "DoubleExponentialOscillatory" integration method. Each integration takes a fraction of a second. The remaining integral over

Δ

was performed by computing the table of (positive) values of integrand

I (Δ)

on a grid with step

δ Δ = \frac{Δ_{2} - Δ_{1}}{100}

, and interpolating

log (I (Δ))

between these values by fifth order polynomial

P_{5} (Δ)

. Integral of the exponential of this polynomial

\int d Δ (1 - Δ) exp (P_{5} (Δ))

yields good enough accuracy (floating precision

10^{- 8}

This process was repeated for all M =1000 values of

κ = 0.1 {(1000 / 0.1)}^{n / M}, n = 0, \dots, M

, corresponding to equidistant log grid. This table was computed in parallel in Mathematica^® in [9], which took just a few minutes. Here is the resulting function

H (κ) κ^{\frac{5}{3}}

(see Figure 6). It shows strong deviations from K41 spectrum, in agreement with the DNS at Figure 5.

The asymptotic behavior of this function is

\begin{matrix} H (κ) \propto κ^{- \frac{7}{2}} \end{matrix}

(A7)

The effective index

μ (κ) = \frac{d log H (κ)}{d log κ}

slowly decreases reaching

μ (\infty) = - \frac{7}{2}

, as shown on Figure 7.

The function

F (κ) = \int_{κ}^{\infty} x^{2} H (x) d x

was obtained by numerical integration of exponential of interpolated function as before, with asymptotic tail

H (κ) \to c o n s t κ^{- \frac{7}{2}}

integrated analytically.

The log-log plot of the energy dissipation as a function of time is shown in Figure A1, and it is curved in the log-log scale due to the quantum effects (complex poles of Mellin transform at Riemann

ζ

function zeros).

Notes

Nikita Nekrasov (private communication) suggested to me an algorithm of generating this solution as a set of adjacent triangles in complex 3-space and pointed out an invariant measure in phase space, made of lengths of shared sides and angles between them. Unfortunately, this beautiful construction does not guarantee real circulation, requiring further study.

References

Comte-Bellot, G.; Corrsin, S. The use of a contraction to improve the isotropy of grid-generated turbulence. Journal of Fluid Mechanics 1966, 25, 657–682. [Google Scholar] [CrossRef]
Polanco, J.I.; Müller, N.P.; Krstulovic, G. Vortex clustering, polarisation and circulation intermittency in classical and quantum turbulence. Nature Communications 2021, 12, 7090. [Google Scholar] [CrossRef]
Ohkitani, K. Study of the Hopf functional equation for turbulence: Duhamel principle and dynamical scaling. Physical Review E 2020, 101, 013104. [Google Scholar] [CrossRef]
Panickacheril John, J.; Donzis, D.A.; Sreenivasan, K.R. Laws of turbulence decay from direct numerical simulations. Philos. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20210089. [Google Scholar] [CrossRef] [PubMed]
Sreenivasan, K. Decaying Turbulence. https://youtu.be/Ghr3-mZJ9I8?si=DrRdu4rDQkaUHomH, 2023. [Field Theory and Turbulence 2023 DISCUSSION MEETING : FIELD THEORY AND TURBULENCE ; accessed 04-February-2024].
Migdal, A. Loop Equation and Area Law in Turbulence. In Quantum Field Theory and String Theory; Baulieu, L.; Dotsenko, V.; Kazakov, V.; Windey, P., Eds.; Springer US, 1995; pp. 193–231. [CrossRef]
Migdal, A. To the Theory of Decaying Turbulence. Fractal and Fractional 2023, 7, 754, [arXiv:physics.flu-dyn/2304.13719]. [Google Scholar] [CrossRef]
Migdal, A. "InstantonComputations". "https://www.wolframcloud.com/obj/sasha.migdal/Published/DualTheory3.nb", 2024.
Migdal, A. "ABC". "https://www.wolframcloud.com/obj/sasha.migdal/Published/ABCInterpolator.m.nb", 2024.
Migdal, A. Topological Vortexes, Asymptotic Freedom, and Multifractals. MDPI Fractals and Fractional, Special Issue, 2023; arXiv:physics.flu-dyn/2212.13356. [Google Scholar]
Migdal, A. Statistical Equilibrium of Circulating Fluids. Physics Reports 2023, 1011C, 1–117, [arXiv:physics.flu-dyn/2209.12312]. [Google Scholar] [CrossRef]
Migdal, A. Momentum loop dynamics and random surfaces in QCD. Nuclear Physics B 1986, 265, 594–614. [Google Scholar] [CrossRef]
Migdal, A. Second quantization of the Wilson loop. Nuclear Physics B - Proceedings Supplements 1995, 41, 151–183. [Google Scholar] [CrossRef]
Anderson, P.D.; Kruczenski, M. Loop equations and bootstrap methods in the lattice. Nuclear Physics B 2017, 921, 702–726. [Google Scholar] [CrossRef]
Kazakov, V.; Zheng, Z. Bootstrap for lattice Yang-Mills theory. Phys. Rev. D 2023, 107, L051501, [arXiv:hep-th/2203.11360]. [Google Scholar] [CrossRef]
Kazakov, V.; Zheng, Z. Bootstrap for Finite N Lattice Yang-Mills Theory, 2024. [arXiv:hep-th/2404.16925].
Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244–2247. [Google Scholar] [CrossRef] [PubMed]
Rovelli, C.; Smolin, L. Knot Theory and Quantum Gravity. Phys. Rev. Lett. 1988, 61, 1155–1158. [Google Scholar] [CrossRef] [PubMed]
Iyer, K.P.; Sreenivasan, K.R.; Yeung, P.K. Circulation in High Reynolds Number Isotropic Turbulence is a Bifractal. Phys. Rev. X 2019, 9, 041006. [Google Scholar] [CrossRef]
Iyer, K.P.; Bharadwaj, S.S.; Sreenivasan, K.R. The area rule for circulation in three-dimensional turbulence. Proceedings of the National Academy of Sciences of the United States of America 2021, 118, e2114679118. [Google Scholar] [CrossRef] [PubMed]
Apolinario, G.; Moriconi, L.; Pereira, R.; valadão, V. Vortex Gas Modeling of Turbulent Circulation Statistics. PHYSICAL REVIEW E 2020, 102, 041102. [Google Scholar] [CrossRef] [PubMed]
Müller, N.P.; Polanco, J.I.; Krstulovic, G. Intermittency of Velocity Circulation in Quantum Turbulence. Phys. Rev. X 2021, 11, 011053. [Google Scholar] [CrossRef]
Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence Turbulence and Predictability. Geophysical Fluid Dynamics: Proc. Intl School of Physics E. Fermi; M Ghil, R.B.; Parisi, G., Eds. Amsterdam: North-Holland, 1985, pp. 84–88.
AGISHTEIN, M.; MIGDAL, A. SIMULATIONS OF FOUR-DIMENSIONAL SIMPLICIAL QUANTUM GRAVITY AS DYNAMICAL TRIANGULATION. Modern Physics Letters A 1992, 07, 1039–1061. [Google Scholar] [CrossRef]
Gross, D.J.; Migdal, A.A. Nonperturbative two-dimensional quantum gravity. Physical Review Letters 1990, 64, 127. [Google Scholar] [CrossRef] [PubMed]
Brézin, E.; Kazakov, V. Exactly solvable field theories of closed strings. Physics Letters B 1990, 236, 144–150. [Google Scholar] [CrossRef]
Douglas, M.R.; Shenker, S.H. Strings in less than one dimension. Nuclear Physics B 1990, 335, 635–654. [Google Scholar] [CrossRef]
Knizhnik, V.; Polyakov, A.; Zamolodchikov, A. FRACTAL STRUCTURE OF 2d—QUANTUM GRAVITY. Modern Physics Letters A 1988, 03, 819–826. [Google Scholar] [CrossRef]
Hardy, G.H.; Wright, E.M. An introduction to the theory of numbers, sixth ed.; Oxford University Press, Oxford, 2008; pp. xxii+621. Revised by D. R. Heath-Brown and J. H. Silverman, With a foreword by Andrew Wiles.
Bulatov, M.; Migdal, A. Numerical Simulation of Euler ensemble. "unpublished".
Norris, J.R. Markov chains; Cambridge Univ. Press, 2007.
Basak, D.; Zaharescu, A. Connections between Number Theory and the theory of Turbulence, 2024. To be published.
Migdal, A. "BernSum". "https://www.wolframcloud.com/obj/sasha.migdal/Published/BernSum.nb", 2024.
Migdal, A. "InstantonComputations". "https://www.wolframcloud.com/obj/sasha.migdal/Published/DualTheory1.nb", 2024.
Yakhot, V.; Zakharov, V. Hidden conservation laws in hydrodynamics; energy and dissipation rate fluctuation spectra in strong turbulence. Physica D: Nonlinear Phenomena 1993, 64, 379–394. [Google Scholar] [CrossRef]
Yakhot, V.; Sreenivasan, K. Towards a dynamical theory of multifractals in turbulence. Physica A: Statistical Mechanics and its Applications 2004, 343, 147–155. [Google Scholar] [CrossRef]
Sreenivasan, K.R.; Yakhot, V. Dynamics of three-dimensional turbulence from Navier-Stokes equations. Phys. Rev. Fluids 2021, 6, 104604. [Google Scholar] [CrossRef]
Feynman, R.P.; Leighton, R.B.; Sands, M. 3-7 How did it get that way? In The Feynman lectures on physics, Vol. I: Mainly mechanics, radiation, and heat; Gottlieb, M.A.; Pfeiffer, R., Eds.; Basic books, 2011; Vol. 1.
Migdal, A.A. Hidden symmetries of large N QCD. Prog. Theor. Phys. Suppl. 1998, 131, 269–307. [Google Scholar] [CrossRef]
Makeenko, Y.; Migdal, A. Exact equation for the loop average in multicolor QCD. Physics Letters B 1979, 88, 135–137. [Google Scholar] [CrossRef]
Migdal, A. Loop equations and $\frac{1}{N}$ expansion. Physics Reports 1983, 201. [Google Scholar]
Moree, P.; Saad Eddin, S.; Sedunova, A.; Suzuki, Y. Jordan totient quotients. Journal of Number Theory 2020, 209, 147–166. [Google Scholar] [CrossRef]
Gross, D.J.; Migdal, A.A. Nonperturbative two-dimensional quantum gravity. Phys. Rev. Lett. 1990, 64, 127–130. [Google Scholar] [CrossRef] [PubMed]
Polyakov, A.M. Quantum Geometry of Bosonic Strings. Phys. Lett. B 1981, 103, 207–210. [Google Scholar] [CrossRef]
Migdal, A. QCD=Fermi string theory. Nuclear Physics B 1981, 189, 253–294. [Google Scholar] [CrossRef]
Golmankhaneh, A.K. Fractal Calculus and its Applications; WORLD SCIENTIFIC, 2022; [https://worldscientific.com/doi/pdf/10.1142/12988]. [CrossRef]
Migdal, A. "InstantonComputations". "https://www.wolframcloud.com/obj/sasha.migdal/Published/DualTheory2.nb", 2024.

Figure 1. The three-dimensional vortices in turbulent flow, from [2].

Figure 2. The path to the microscopic theory.

Figure 3. The experimental data [1] for decaying turbulence behind the oscillating grid. The two lines correspond to log-log plots of

1 / v_{⊥}^{2}, 1 / v_{‖}^{2}

for the flow behind the grid. The total inverse kinetic energy i

K = 2 / (v_{⊥}^{2} + v_{‖}^{2})

, would have the the mean slope

(1.24 + 1.27) / 2 \approx 1.255 \pm 0.02

in agreement with our prediction

n (\infty) = \frac{5}{4}

. This plot was shown by K.R.Sreenivasan at the ICTS in Dec’23 in Bangalore, India [5] as the most reliable experimental data. Other measurements and simulations, at different conditions reviewed in [4], provide mismatching data influenced by initial and boundary conditions. The only large-scale DNS [4] covering three time decades yields a close value of

1.27

Figure 3. The experimental data [1] for decaying turbulence behind the oscillating grid. The two lines correspond to log-log plots of

1 / v_{⊥}^{2}, 1 / v_{‖}^{2}

for the flow behind the grid. The total inverse kinetic energy i

K = 2 / (v_{⊥}^{2} + v_{‖}^{2})

, would have the the mean slope

(1.24 + 1.27) / 2 \approx 1.255 \pm 0.02

in agreement with our prediction

n (\infty) = \frac{5}{4}

1.27

Figure 9. The plot of the function

Λ (s)

. As required, it is positive, takes a maximal value

log (2)

s = 0

, and vanishes at both ends

s = \pm 1

of the physical region.

Figure 9. The plot of the function

Λ (s)

. As required, it is positive, takes a maximal value

log (2)

s = 0

, and vanishes at both ends

s = \pm 1

of the physical region.

Figure 10. The log-log-plot of the distribution

f_{X} (X)

. It is equals

π Φ (k) X \sqrt{X}

at each internal

\frac{1}{π^{2} {(k + 1)}^{2}} < X < \frac{1}{π^{2} k^{2}}

with positive integer k. Asymptotically

f_{X} (X) \to \frac{3 \sqrt{X}}{π^{3}}

X \to 0

Figure 10. The log-log-plot of the distribution

f_{X} (X)

. It is equals

π Φ (k) X \sqrt{X}

at each internal

\frac{1}{π^{2} {(k + 1)}^{2}} < X < \frac{1}{π^{2} k^{2}}

with positive integer k. Asymptotically

f_{X} (X) \to \frac{3 \sqrt{X}}{π^{3}}

X \to 0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

868

Views

421

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Solution of Classical Turbulence Decaying Energy Spectrum

Abstract

Keywords:

Subject:

1. Prologue

2. Summary

3. Introduction

3.1. Introduction for Physicists

3.2. Introduction for Mathematicians

3.3. Guidance for Applied Mathematicians and Engineers

3.4. Notes for the Curious and Skeptical

3.5. Physical Introduction: The Energy Flow and Random Vorticity Structures

3.6. Mathematical Introduction. The Loop Equation and Its Solution

3.7. The Big and Small Euler Ensembles

4. The Markov Chain and Its Fermionic Representation

5. The Continuum Limit

5.1. Path Integral over Markov Histories

5.2. Matching Path Integral with Combinatorial Sums in Big Euler Ensemble

5.3. Small Euler Ensemble in Statistical Limit

5.4. Complex Classical Trajectory in the Path Integral

6. Dual Theory of Vorticity Correlation

6.1. Correlation Function and Path Integral

6.2. Turbulent Viscosity and the Local Limit

6.3. Functional Determinant in the Path Integral

6.4. The Fluctuation Term in α ′ ( ξ 1 ) α ′ ( ξ 2 )

7. The Decaying Energy in Finite System

8. The Spectrum of Critical Indexes

8.1. The Energy Spectrum

8.2. The Energy Decay

8.3. The Velocity Correlation Function in Coordinate Space

9. Discussion

9.1. Myth and Reality of Turbulent Scaling Laws

9.2. Stochastic Solution of the Navier-Stokes Equation and Ergodic Hypothesis

9.3. The Physical Meaning of the Loop Equation and Dimensional Reduction

9.4. Classical Flow and Quantum Mechanics

9.5. Renormalizability of the Inviscid Limit of the Loop Equation

9.6. Relation of Our Solution to Weak Turbulence

10. Remaining problems

11. Conclusion

Data Availability Statement

Acknowledgments

Appendix A. Mellin integral for the energy spectrum and energy decay

Notes

References

MDPI Initiatives

Important Links

Subscribe

6.4. The Fluctuation Term in $α^{'} (ξ_{1}) α^{'} (ξ_{2})$