Quantum Solution of Classical Turbulence Decaying Energy Spectrum

1. Prologue

Turbulence seems a hopelessly complex problem. Here is a picture from a recent simulation [3] that produced vortex lines of various shapes and sizes tangled like spaghetti.

How could something so complex be described analytically?

The sheer complexity of this picture raises hopes of a simple statistical description.

Molecular dynamics with a large number of bodies is also hopelessly complex. Still, there is a simple statistical description that becomes increasingly accurate as the complexity of the original dynamical problem increases.

Figure 1. The three-edimensional vortices in turbulent flow, from [3].

Figure 1. The three-edimensional vortices in turbulent flow, from [3].

Figure 2. The path to the microscopic theory.

Figure 2. The path to the microscopic theory.

As Maxwell, Boltzmann, and Gibbs discovered, Newton’s mechanics cover the energy surface uniformly, given enough time. The rest of the statistical mechanics is a well-defined theory, though sometimes computations are difficult, like critical phenomena.

So, why not use the same approach in case of the Navier-Stokes turbulence?

Unfortunately, there is no known analog of the Gibbs distribution in the case of the turbulent flow.

So, the cornerstone of the turbulence theory must be a replacement for the Gibbs distribution.

Hopf made the first step in this direction in 1952 (see the recent review in [4]). He wrote down a functional equation satisfied by the probability distribution of the turbulent velocity field. Iterations of this equation in the nonlinear term in the Navier-Stokes equation generate expansion in inverse powers of viscosity, which is the opposite of our goal.

Our theory, which started in 1993 (see Figure 2 for the history), says there is a much simpler version of the Hopf equation (the loop equation), still sufficient to determine the statistics.

This equation is beautiful but mathematically as complex as the above picture of the vortex spaghetti. This apparent complexity placed the turbulence high in a hierarchy of physics theories, somewhere between the critical phenomena and the quark confinement problem.

The loop equation is equivalent to the Schrödinger equation in loop space. This deep analogy is not a poetic metaphor but a precise mathematical equivalence with far-reaching consequences, such as quantum oscillations resulting in regime changes of the effective indexes in scaling laws of classical turbulence.

We will present here and investigate the one-dimensional quantum statistical system satisfying the loop equation of the classical three-dimensional Navier-Stokes theory.

We have found a new example of duality between the strong coupling phase of one theory (a fluctuating velocity field in three dimensions) and the weak coupling of another (a one-dimensional quantum ring of Fermi particles).

This weak coupling limit is analytically solvable, yielding explicit formulas for observables in decaying turbulence, such as the energy dissipation decay index $n\left(t\right)=-t\frac{\mathcal{E}\left(t\right)}{E\left(t\right)}$

The experimental data for the decaying grid-turbulence (see Figure 3) agree with our prediction $n(\infty )=\frac{5}{4}$ within experimental error $\sim 2\%$. We hope more precise future measurements will verify the whole curve for $n\left(t\right)$ in our theory.

2. Summary

Here are the main results reported in this paper.

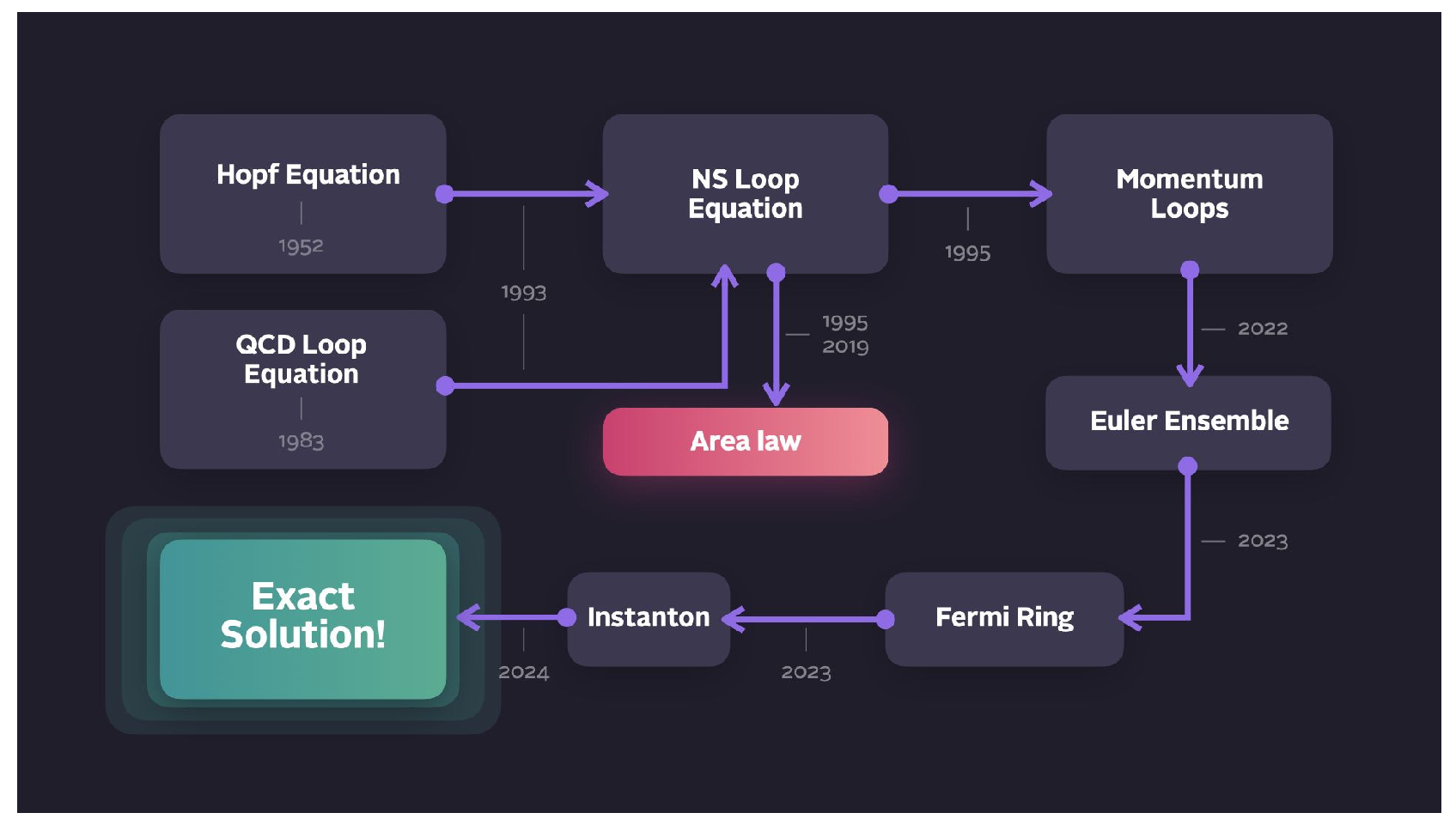
• We review the theory of Navier-Stokes loop equation, its relation to the Hopf functional equation, and the representation of the loop functional in terms of momentum loop.
• We present the solution of the loop equation in the inviscid limit of the three-dimensional Navier-Stokes theory in terms of the Euler ensemble. This ensemble consists of a one-dimensional ring of Ising spins in an external field related to random fractions of $\pi$.
• We reduced the Markov process for the Euler ensemble in its fermionic representation (60) to the path integral.

  

  Figure 3. The experimental data [2] for decaying turbulence behind the grid yield $n=1.25\pm 0.02$ which agrees with our prediction. This plot was shown by K.R.Sreenivasan at the ICTS in Dec’23 in Bangalore, India as the most reliable experimental data. Other measurements, at different conditions reviewed in [5], provide mismatching data, apparently reflecting a lack of the universal regime.

  Figure 3. The experimental data [2] for decaying turbulence behind the grid yield $n=1.25\pm 0.02$ which agrees with our prediction. This plot was shown by K.R.Sreenivasan at the ICTS in Dec’23 in Bangalore, India as the most reliable experimental data. Other measurements, at different conditions reviewed in [5], provide mismatching data, apparently reflecting a lack of the universal regime.

  

  

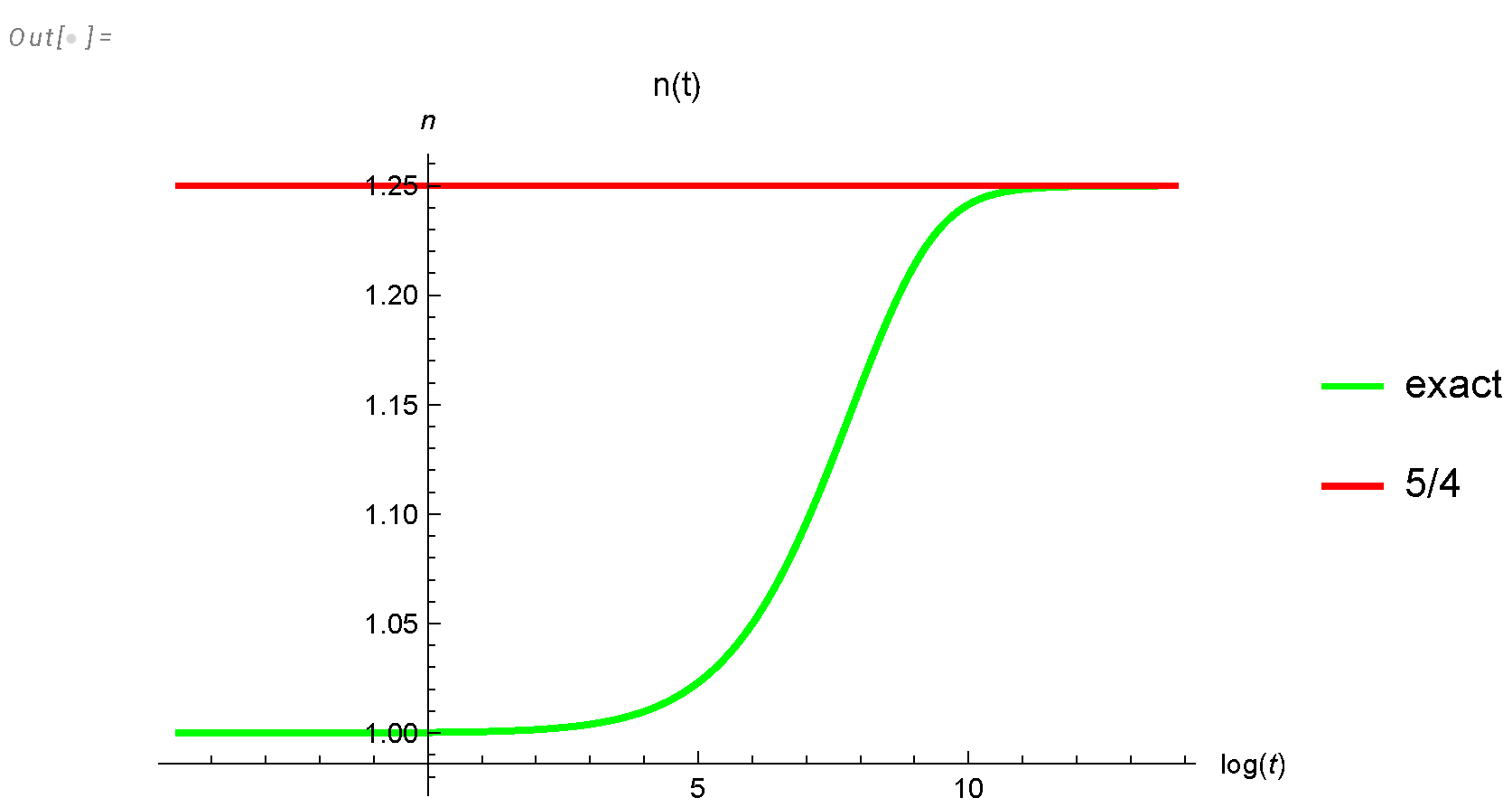
  Figure 4. Green curve is the inverse energy $1/E\left(t\right)$ as a function of time. It slowly rises to its asymptotic law $1/E\left(t\right)\propto t^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$ shown in red.

  Figure 4. Green curve is the inverse energy $1/E\left(t\right)$ as a function of time. It slowly rises to its asymptotic law $1/E\left(t\right)\propto t^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$ shown in red.

  
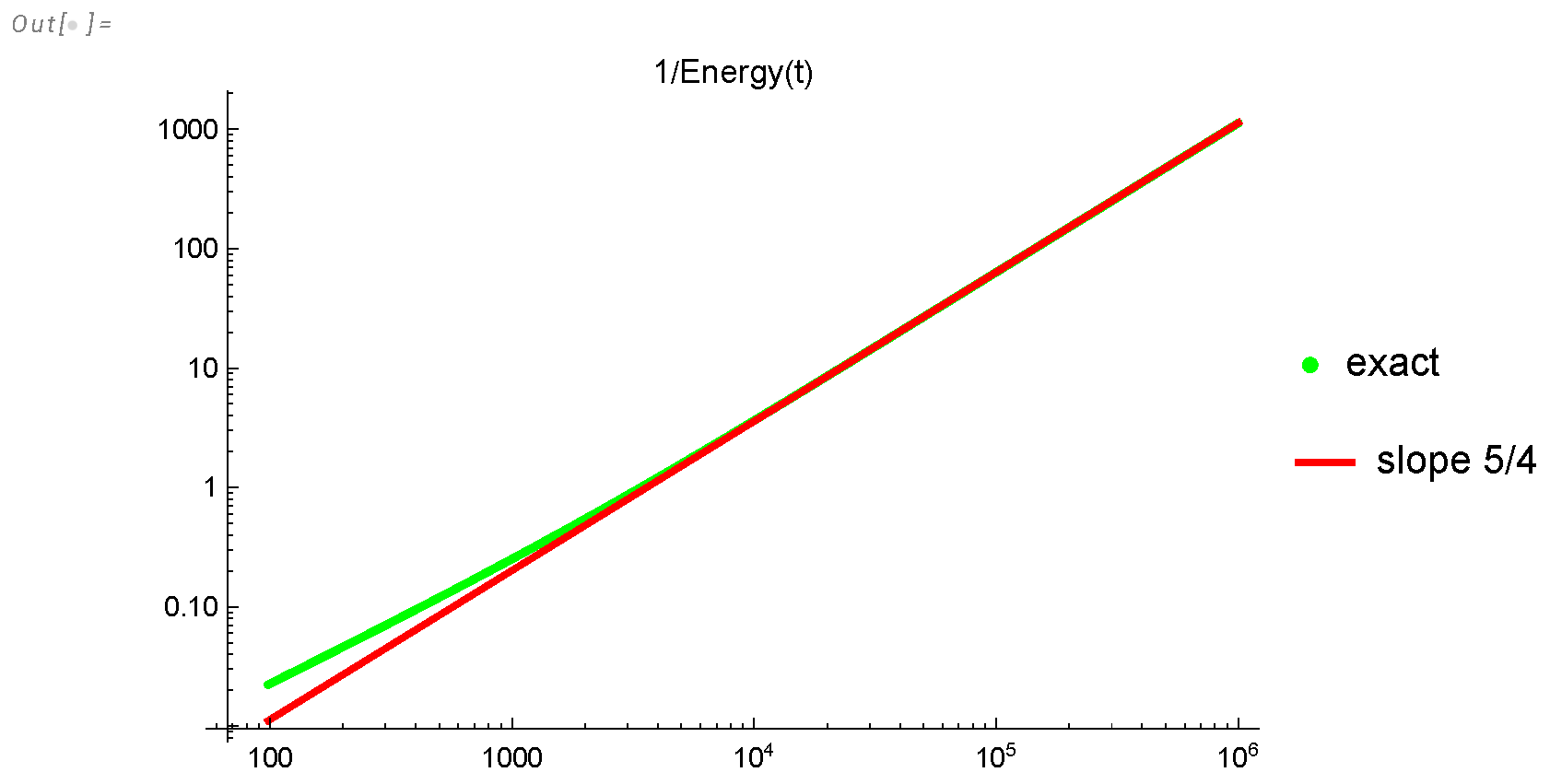
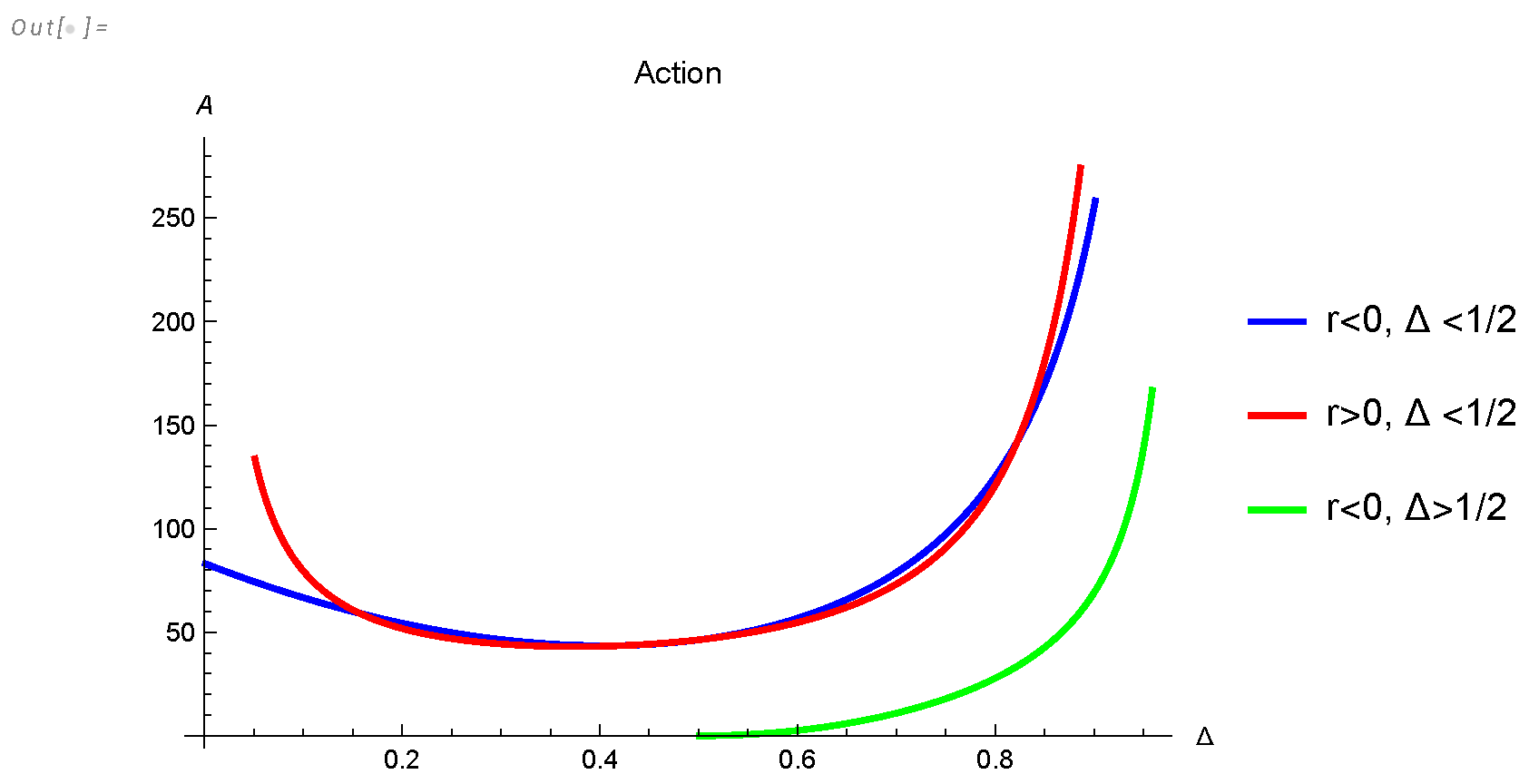
• This path integral in the continuum limit is dominated by a complex classical trajectory (instanton), satisfying a nonlinear ODE (130).
• We solved this classical equation corresponding to the vorticity correlation function and found the spectrum of the linear operator for small fluctuations around this solution.
• We computed the instanton’s contribution to the vorticity correlation function by using zeta regularization of the functional determinant of this linearized operator.
• The continuum limit of this solution, $N\to \infty$, corresponds to the inviscid limit of the decaying turbulence in the Navier-Stokes equation. Effective turbulent viscosity is $\tilde{\nu }=\nu N^2\to \mathit{const}$. There are no quantum corrections to this instanton contribution in the turbulent limit.
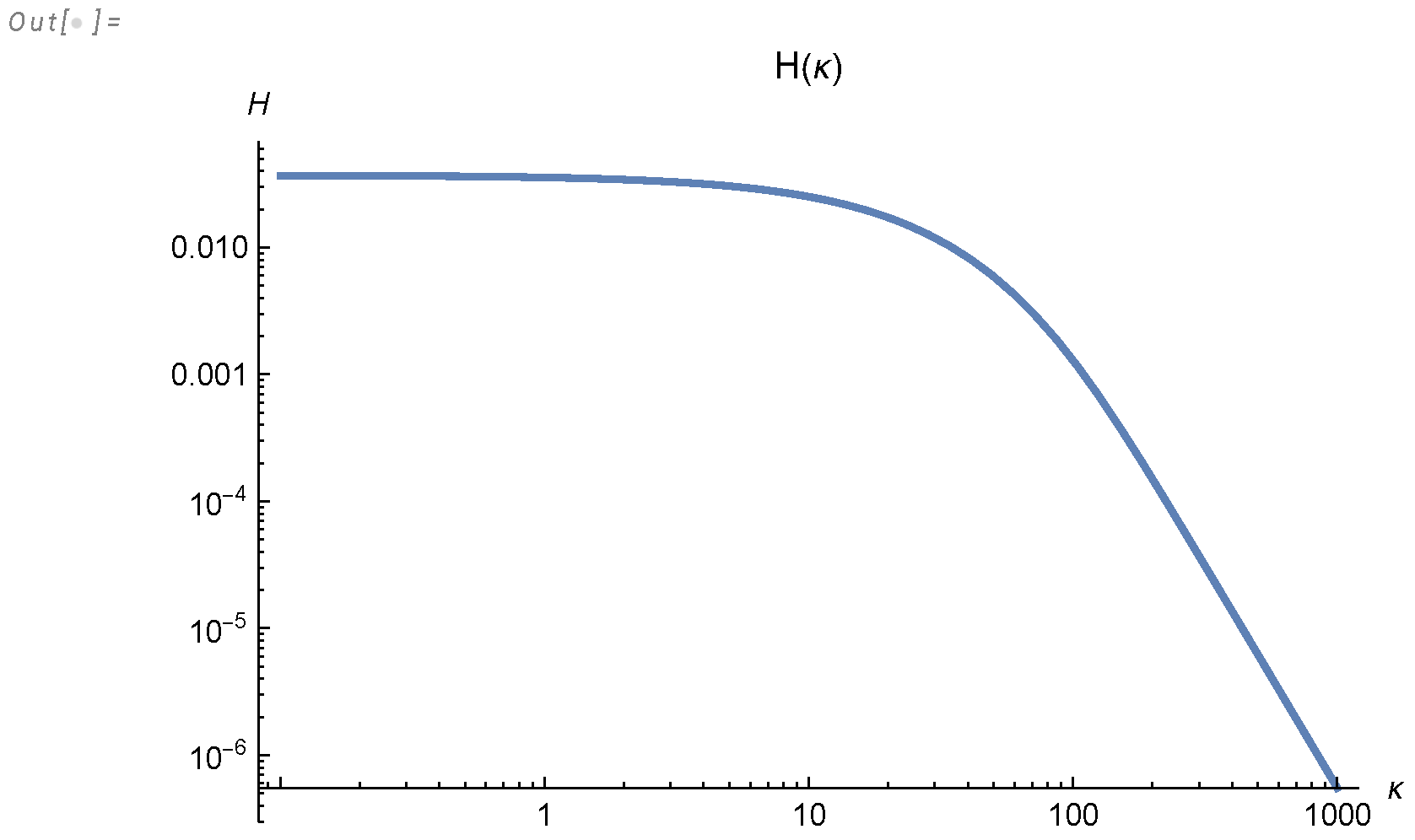
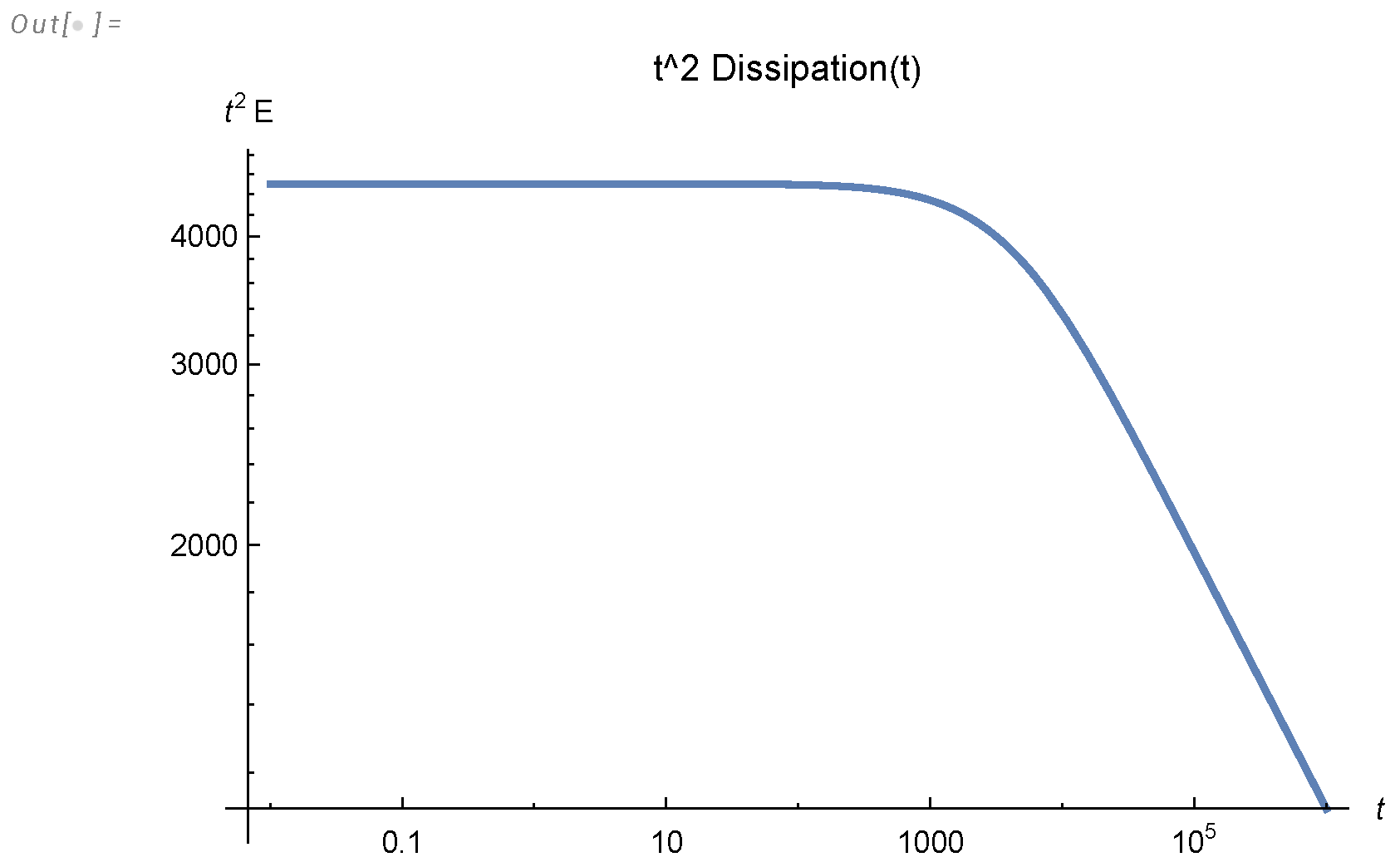
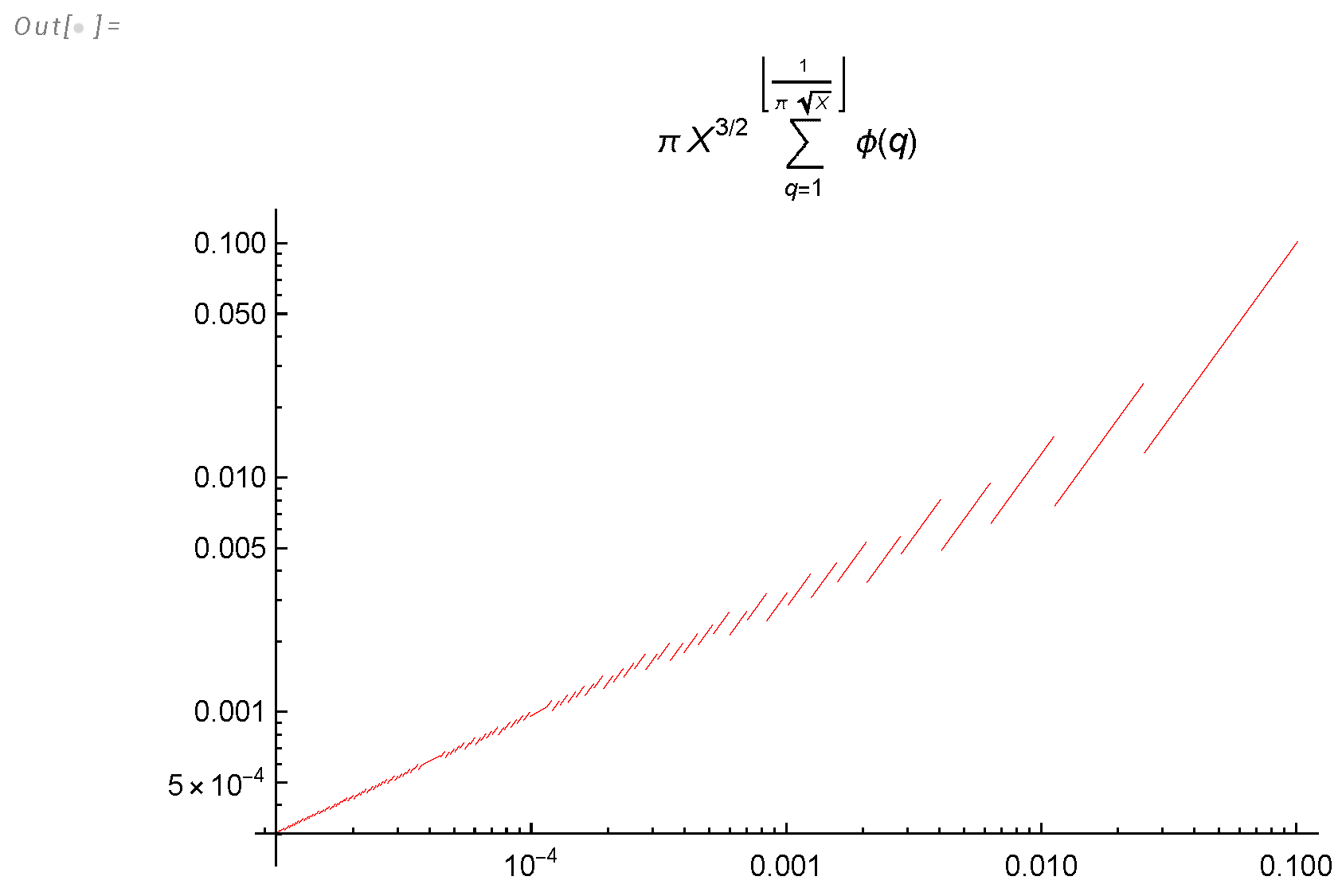
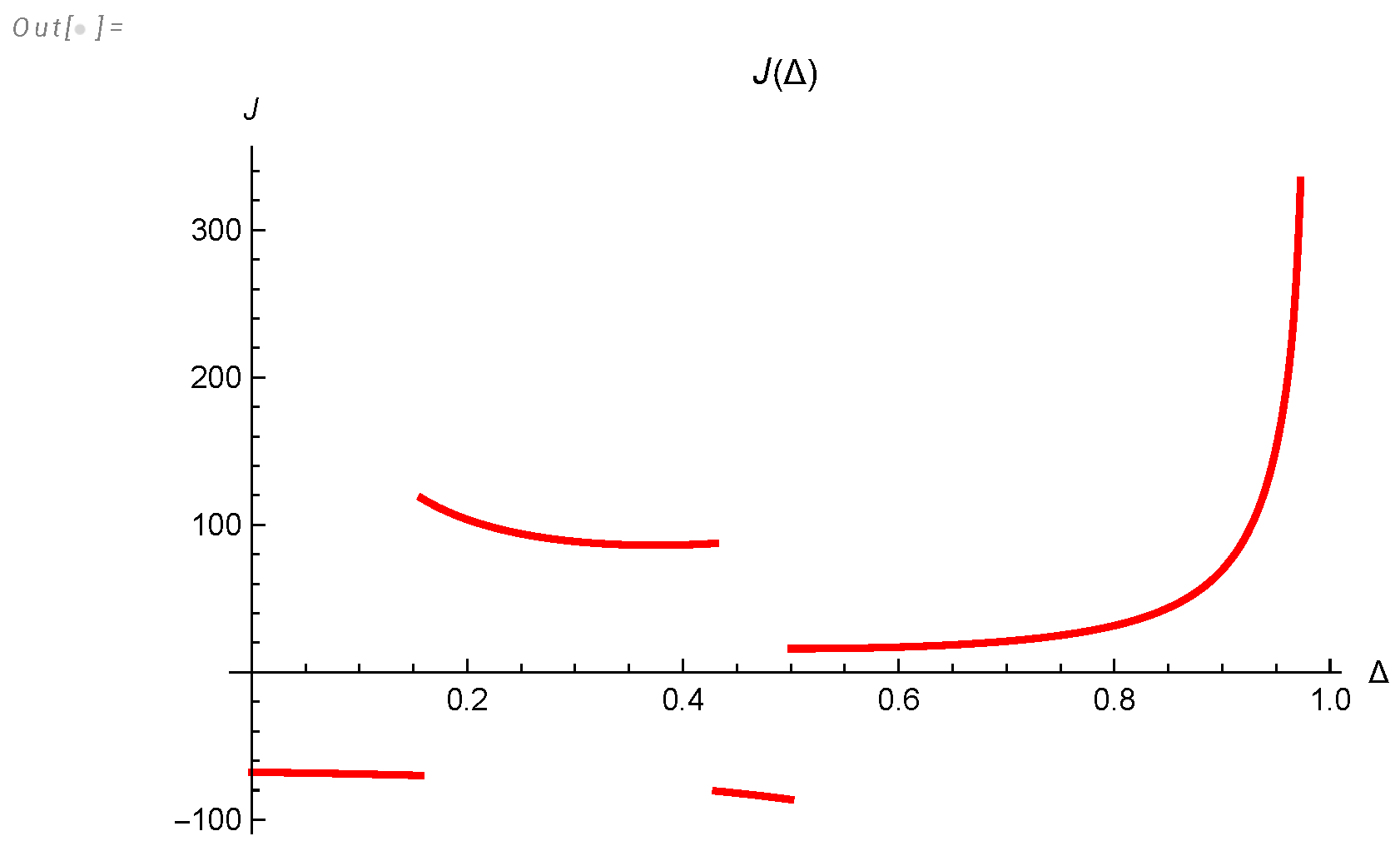
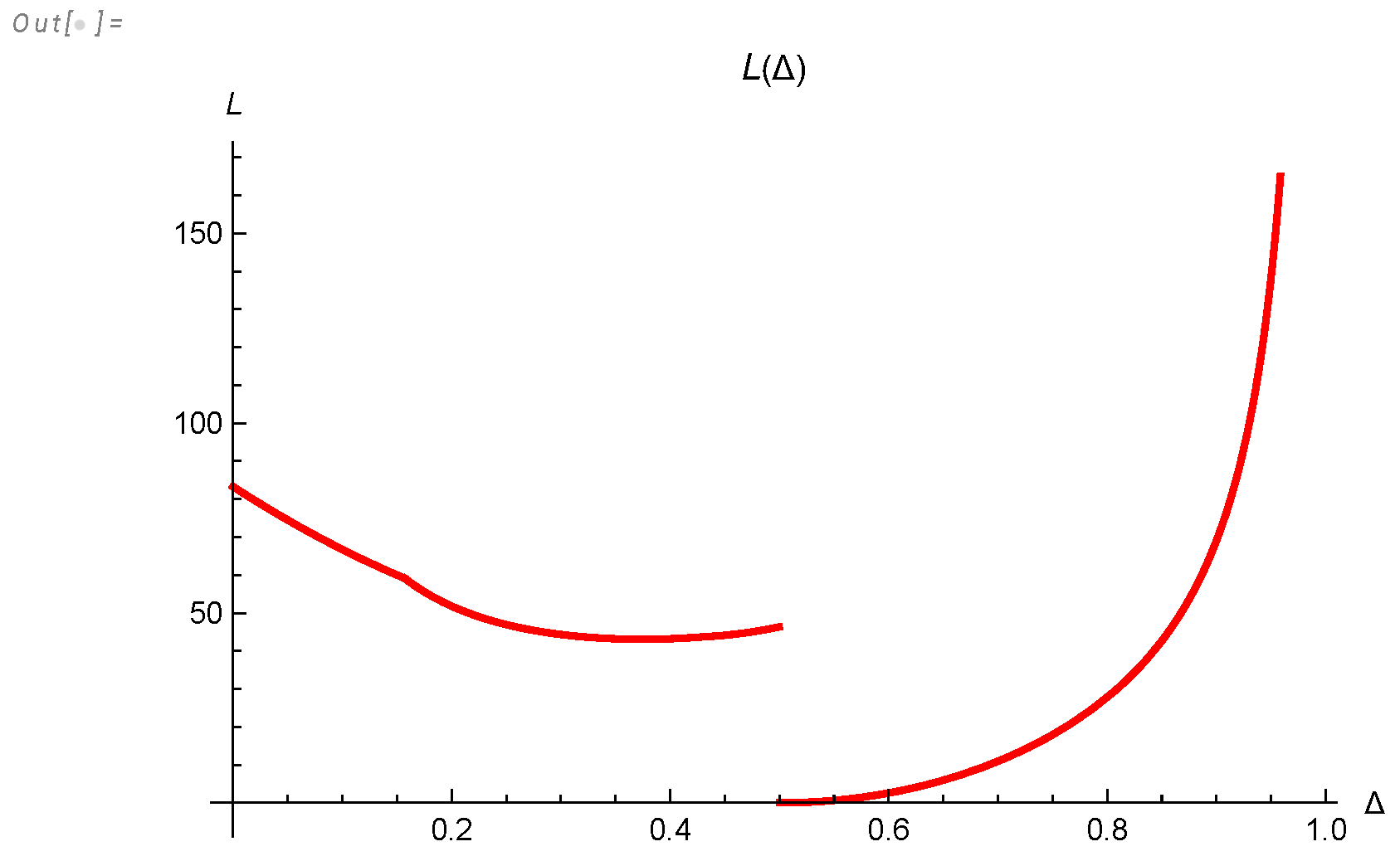
• We derived an analytic formula for energy spectrum and dissipation in finite system (233a), (233c), (223) and investigated it in Appendix A.
• The energy spectrum decays asymptotically as

  $$\frac{{\left(\tilde{\nu }\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\sqrt{t}}{\kappa }^{-\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

  where $\kappa =k\sqrt{\tilde{\nu }t}$.
• The total remaining energy decays as $E\left(t\right)\propto t^{-\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$
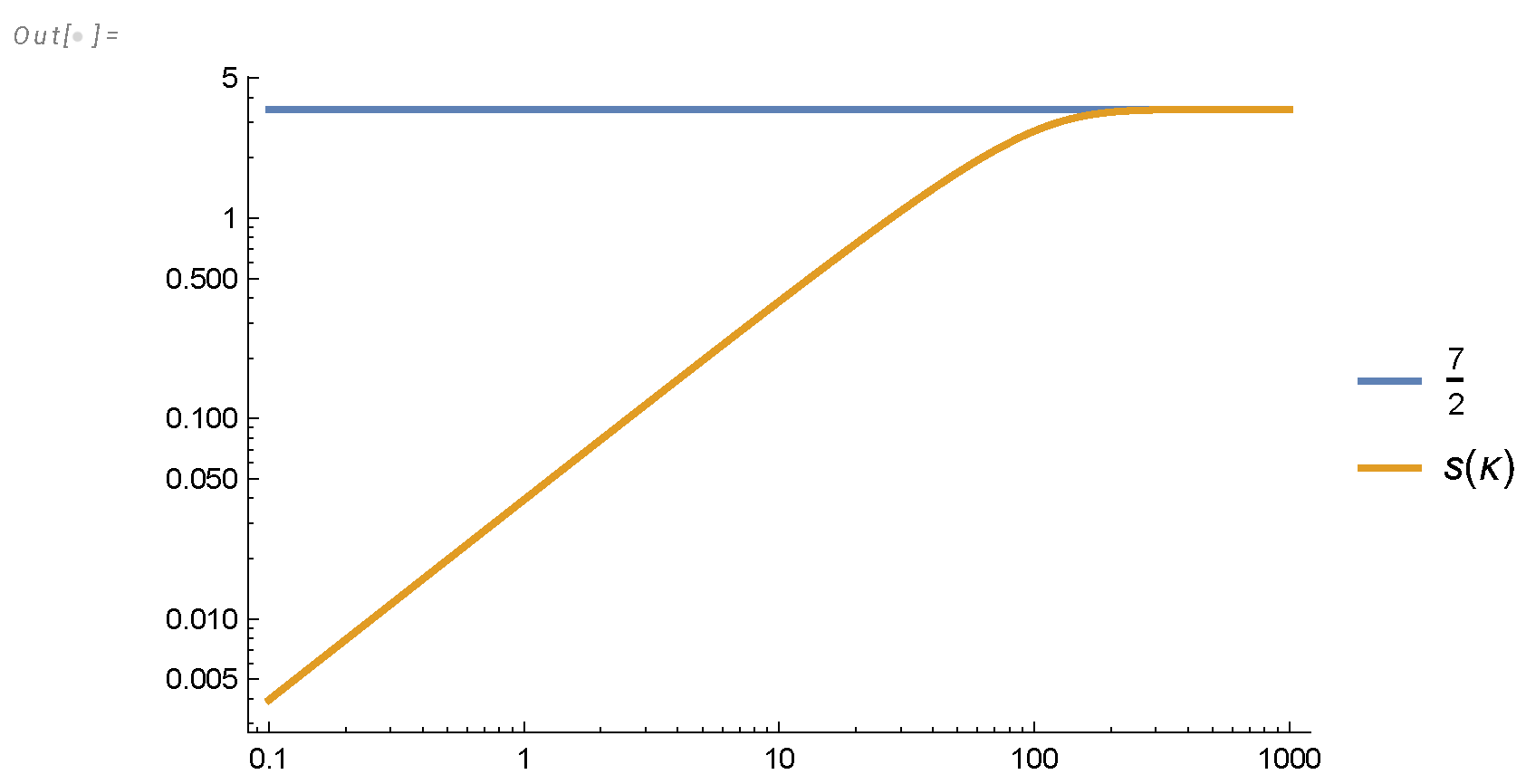
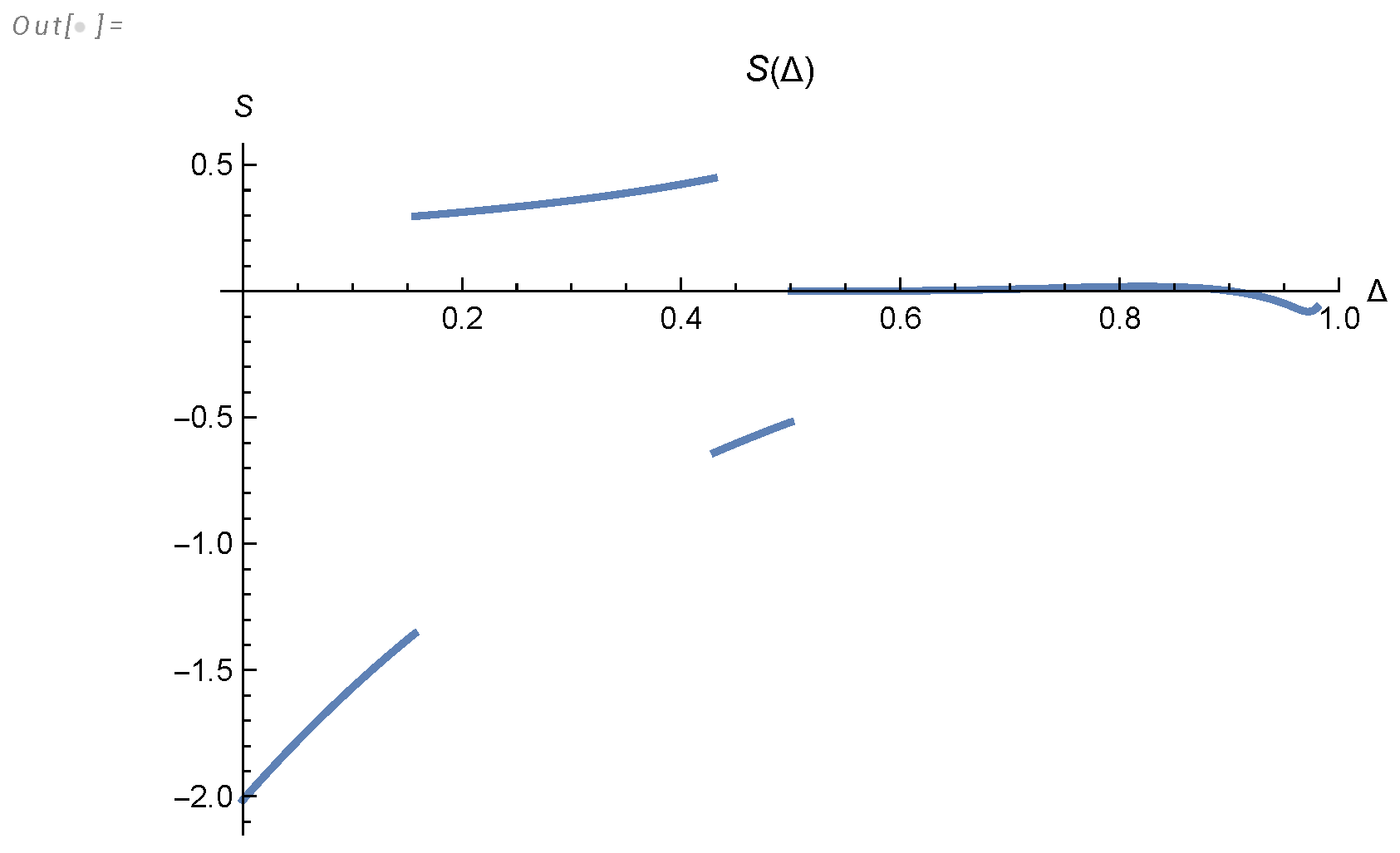
• Both effective indexes $n\left(t\right)=-\frac{dlogE}{dlogt},s\left(\kappa \right)=-\frac{\partial logE(k,t)}{\partial logk}$ are nontrivial functions of the logarithm of scale and time, approaching $n(\infty )=\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.,s(\infty )=\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, (see Figure 14, Figure 5).
• The 1966 experimental values [2], Figure 3 of $n(\infty )\approx 1.25\pm 0.02$ agree with our prediction.
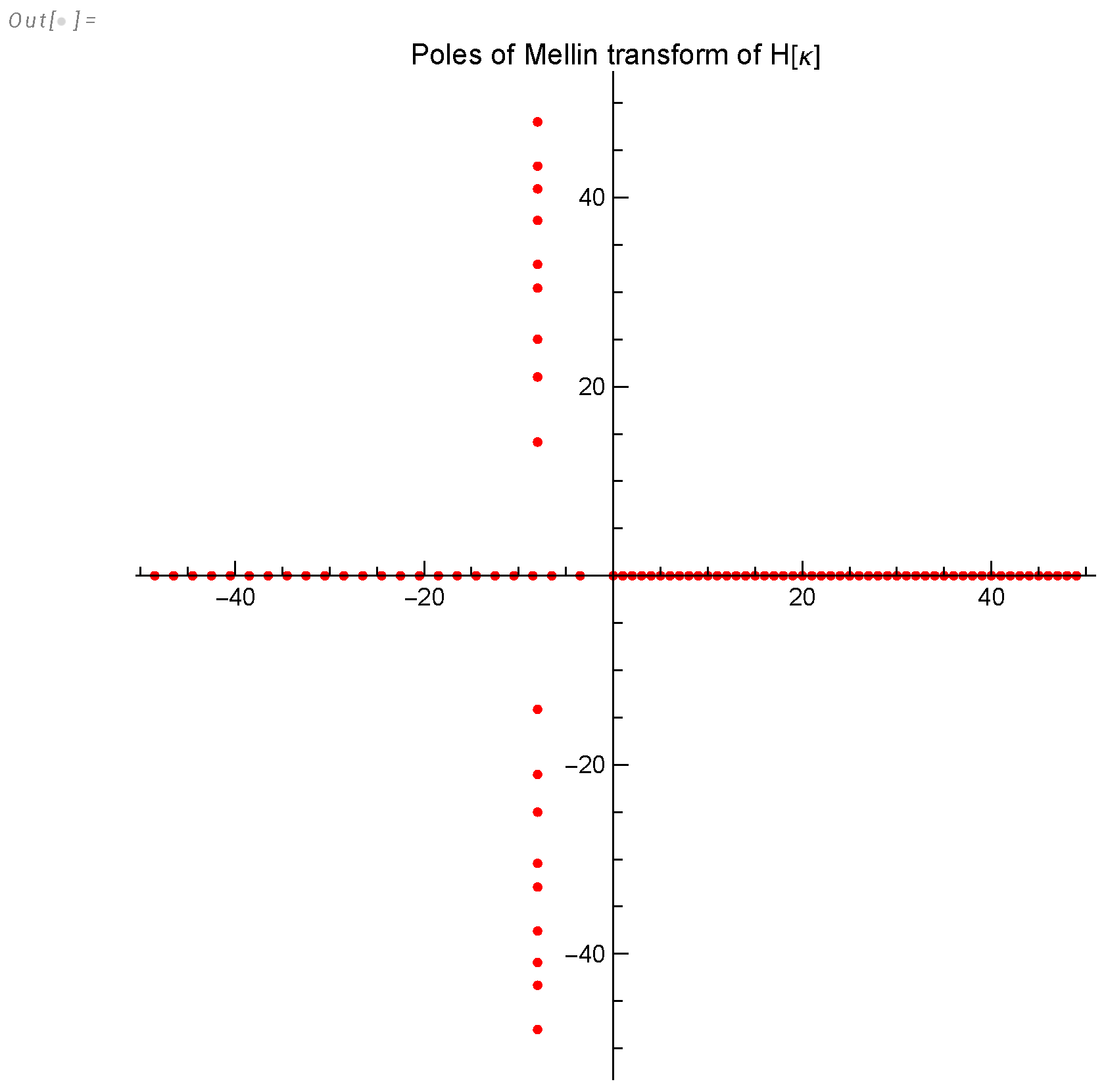
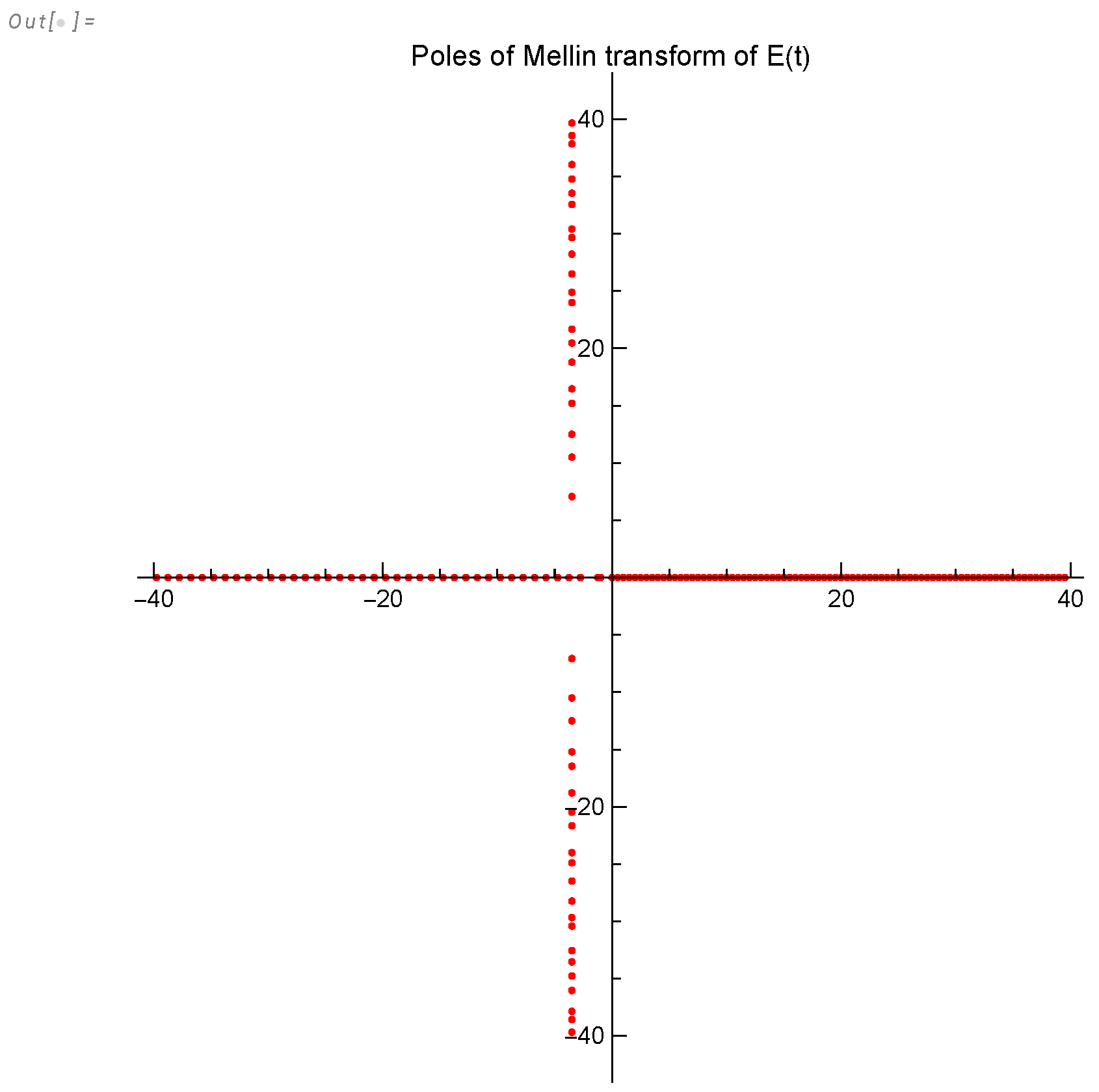
• The predicted oscillation of the effective decay indexes in classical turbulence demonstrates the quantum effects in our solution (singularities in the Mellin transform of the energy spectrum, related to complex zeros of the Riemann $\zeta$ function).

3. Introduction

Our paper will have two introductions: one for physicists and another for mathematicians.

The physics introduction discusses the possible correspondence between our theory and decaying turbulence as observed in real or numerical experiments. For a physicist, this theory provides a solution of the Hopf functional equation for the statistical distribution of velocity field in the unforced Navier-Stokes equation. This distribution provides a missing analog of the Gibbs distribution in decaying turbulence. There are strong indications that our theory applies to one of the two universality classes observed in these experiments.

The second introduction summarizes the mathematics behind the loop equation [6] and its solution [1] in terms of the Euler ensemble. This introduction is addressed to mathematicians, who can skip the first introduction and study this ensemble as a new Number Theory set with a conjectured relation to the decaying turbulence.

There is a third category of readers: applied mathematicians and engineers who are not interested in abstract theories but want to have data or formulas to compute the energy decay curve. These readers could go directly to the last Section 7 where they will find final formulas (233c),(233a) and the Mathematica^®code [7,8], which allows them to compute both the spectrum and the dissipation.

The fourth category (my favorite) is curious but skeptical readers who doubt that quantum tricks can solve the hardest problem of classical physics. These readers would still have questions, even after reviewing this paper’s lengthy computations. There is the last section 9, where some of their questions are answered.

3.1. Physical Introduction. The Energy Flow and Random Vorticity Structures

The decaying turbulence is an old subject addressed before within a weak turbulence framework (truncated perturbative expansion in inverse powers of viscosity $\nu$ in the forced Navier-Stokes equation). Some phenomenological models were also fitted to the experiments: see the recent review of these models and the experimental data in [5].

The perturbative approach is inadequate for the turbulence theory, which must be built by solving the Navier-Stokes equations in the strong coupling limit $\nu \to 0$, opposite to the weak coupling. The problem of universality of the strong turbulence with and without random forcing is the first question to ask when building such a theory.

The experimental data for the energy decay in turbulent flows, fitted in [5] suggest the decay of the dissipation rate $E\sim t^{-n}$ with $n\approx 1.25$ or $1.60$ depending on initial conditions (finite total momentum or zero total momentum but finite total angular momentum , see [5]). So, two universality classes of decaying turbulence were observed in these experiments.

It is unclear which data in [5] (if any) reached the strong turbulence limit corresponding to our regime. It is also possible that the stochastic forces added to the Navier-Stokes equation in simulations pollute the decaying turbulence. By design, these forces were supposed to trigger and amplify the spontaneous stochasticity of the turbulent flow. However, in our theory [1], this natural stochasticity is related to a dual quantum system and is discrete.

The Gaussian forcing with a continuous wavevector spectrum can distort these quantum stochastic phenomena as these forces stir the flow "with a large dirty spoon" all over the space at every moment. With forcing turned off at some moment and the turbulence reaching the universal stage in its subsequent decay, the energy dissipation would occur in vorticity structures deep inside the volume by the pure turbulent dynamics we are studying.

Some recent DNS reviewed in [5] used such a setup, with forcing turned off. They observed subsequent energy dissipation, apparently reaching one of the two universal regimes (with spectrum starting as $k^2$ or $k^4$), presumably due to these random vorticity structures. The cleanest experiment, according to Sreeni [5] was the decaying grid-turbulence in [2] (see Figure 3). The slope $n(\infty )=1.25\pm 0.02$ agrees with our prediction.

The following calculation supports the above relation between singular vorticity distribution and the energy flow. The energy balance in the pure Navier-Stokes reduces to the energy dissipation by the enstrophy in the bulk, compensated by the energy pumping by forces from the boundary (say, the large sphere around the flow).

The general identity, which follows from the Navier-Stokes if one multiplies both sides by $\overrightarrow{v}$ and averages over an infinite time interval, reads:

$$\begin{array}{c}\hfill {\int }_V{d}^{3}r〈\nu {\overrightarrow{\omega }}^2〉=-{\int }_V{d}^{3}r{\partial }_{\beta }〈v_{\beta }\left(p+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.v_{\alpha }^2\right)+\nu v_{\alpha }({\partial }_{\beta }{v}_{\alpha }-{\partial }_{\alpha }{v}_{\beta })〉\end{array}$$

(1)

By the Stokes theorem, the right side reduces to the flow through the boundary $\partial V$ of the integration region V. The left side is the dissipation in this volume, so we find:

$$\begin{array}{c}\hfill {\mathcal{E}}_V=-{\int }_{\partial V}d\overrightarrow{\sigma }·〈\overrightarrow{v}\left(p+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.v_{\alpha }^2\right)+\nu \overrightarrow{\omega }\times \overrightarrow{v}〉\end{array}$$

(2)

This identity holds for an arbitrary volume. The left side represents the viscous dissipation inside V, while the right represents the energy flow through the boundary $\partial V$.

If there is a finite collection of vortex structures in the bulk, we can expand this volume to an infinite sphere; in this case, the $\overrightarrow{\omega }\times \overrightarrow{v}$ term drops as there is no vorticity at infinity.

Furthermore, the velocity in the Biot-Savart law decreases as $|\overrightarrow{r}{|}^{-3}$ at infinity, so that only the $\overrightarrow{v}p$ term survives

$$\begin{array}{c}\hfill 〈{\mathcal{E}}_V〉\to -{\int }_{\partial V}d\overrightarrow{\sigma }·〈\overrightarrow{v}p〉\end{array}$$

(3)

This energy flow on the right side will stay finite in the limit of the expanding sphere in case the pressure grows as $p\to -\overrightarrow{f}·\overrightarrow{r}$, where $\overrightarrow{f}$ is the local force at a given point on a large sphere.

$$\begin{array}{c}\hfill 〈\mathcal{E}〉=f_{\alpha }\underset{R\to \infty }{lim}{R}^3{\int }_{S_2}{n}_{\alpha }{n}_{\beta }〈v_{\beta }\left(R\overrightarrow{n}\right)〉\end{array}$$

(4)

Where did we lose the Kolmogorov energy flow? It is still there for any finite volume surrounding the vortex sheet

$$\begin{array}{ccc}& & 〈\mathcal{E}〉=-{\int }_V{d}^{3}r〈v_{\beta }{\partial }_{\beta }p+v_{\alpha }{v}_{\beta }{\partial }_{\beta }{v}_{\alpha }〉=\hfill \\ & & -{\int }_V{d}^{3}r〈v_{\alpha }{v}_{\beta }{\partial }_{\beta }{v}_{\alpha }〉-{\int }_{\partial V}d\overrightarrow{\sigma }·〈\overrightarrow{v}p〉\hfill \end{array}$$

(5)

The first term is the Kolmogorov energy flow inside the volume V, and the second is the energy flow through the boundary.

Without finite force $\overrightarrow{f}$ acting on the boundary, say, with periodic boundary conditions, the boundary integral would be absent, and we would recover the Kolmogorov relation.

$$\begin{array}{c}\hfill 〈v_{\alpha }{v}_{\beta }{\partial }_{\beta }{v}_{\alpha }〉=-〈\mathcal{E}〉/V;\end{array}$$

(6)

This relation, together with space symmetry properties in ${\mathbb{R}}_d$ leads to the Kolmogorov three-point correlation

$$\begin{array}{ccc}& & 〈v_{\alpha }\left({\overrightarrow{r}}_0\right)v_{\beta }\left({\overrightarrow{r}}_0\right)v_{\gamma }(\overrightarrow{r}+{\overrightarrow{r}}_0)〉=\frac{\mathcal{E}}{(d-1)(d+2)V}\left({\delta }_{\alpha \gamma }{r}_{\beta }+{\delta }_{\beta \gamma }{r}_{\alpha }-\frac{2}{d}{\delta }_{\alpha \beta }{r}_{\gamma }\right);\hfill \end{array}$$

(7)

In the conventional approach, based on the time averaging of the Navier-Stokes equations, the periodic Gaussian random force $\overrightarrow{f}(\overrightarrow{r},t)$ is added to the right side. In this case, with periodic boundary conditions

$$\begin{array}{c}\hfill 〈{\mathcal{E}}_V〉=-{\int }_V{d}^{3}r〈v_{\beta }{\partial }_{\beta }p-v_{\beta }{f}_{\beta }(\overrightarrow{r},t)+v_{\alpha }{v}_{\beta }{\partial }_{\beta }{v}_{\alpha }〉={\int }_V{d}^{3}r〈v_{\beta }{f}_{\beta }(\overrightarrow{r},t)〉\end{array}$$

(8)

In the limit when the force becomes uniform in space, we recover another definition with $\mathcal{E}=\overrightarrow{f}·\overrightarrow{P}$, where $\overrightarrow{P}={\int }_V{d}^{3}r\overrightarrow{v}$ is a total momentum.

The turbulence phenomenon we study is a universal spontaneous stochasticity independent of the boundary conditions.

As long as there is an energy flow from the boundaries, the confined turbulence in the middle would dissipate this flow in singular vortex tubes. The spontaneous stochasticity results from the random distribution of these singular tubes inside the volume in the velocity flow picture [9]. In the dual picture of our recent theory [1], these are the random gaps in the momentum curve $\overrightarrow{P}\left(\theta \right)$ (see below).

The relation between the energy pumping on the large sphere and the distribution of the vortex blobs in bulk follows from the Biot-Savart integral

$$\begin{array}{c}\hfill \overrightarrow{v}\left(r\right)=-\overrightarrow{\nabla }\times \int d^3{r}^{\prime }\frac{\overrightarrow{\omega }\left(r^{\prime }\right)}{4\pi |r-r^{\prime }|}\end{array}$$

(9)

In the general case, a gradient of harmonic potential will be added to the Biot-Savart integral, depending upon the boundary conditions. We are considering the velocity decaying at infinity so that we do not add such a term.

The net linear momentum $〈\int d^{3}r\overrightarrow{v}\left(0\right)·\overrightarrow{v}\left(\overrightarrow{r}\right)〉$, in general, is not zero in our theory, as we impose no such restriction. This places our theory into the most general $k^2$ (or Saffman) class.

On a large sphere $\partial V$ with radius $R\to \infty$,

$$\begin{array}{ccc}& & \underset{R\to \infty }{lim}{R}^3\overrightarrow{v}\left(R\overrightarrow{n}\right)\propto \hfill \\ & & \frac{1}{4\pi }\sum _{\mathrm{blobs}}\underset{\mathrm{blob}}{\int }{d}^3{r}^{\prime }\overrightarrow{\omega }\left(r^{\prime }\right)\times \left({\overrightarrow{r}}^{\prime }-<\overrightarrow{r}{>}_{\mathrm{blob}}\right);\hfill \end{array}$$

(10)

Here $<\overrightarrow{r}{>}_{\mathrm{blob}}$ is the geometric center of each blob. Substituting this into the identity (4), we directly relate the energy pumping with the forces at the boundary and the blob’s dipole moments of vorticity.

No forcing inside the flow is needed for this energy pumping; the energy flow starts at the boundary and propagates to numerous singular vorticity blobs, where it is finally dissipated. The distribution of these vorticity blobs is all we need for the turbulence theory. The forcing is required only as a boundary condition at infinity.

These assumptions about confined turbulence as stochastic dynamics of isolated vortex structures were confirmed in a beautiful experimental work by William Irvine and collaborators at Chicago University ([10]). The energy was pumped in by vortex rings flying from eight corners of a large glass cube and colliding in the center, making a turbulent blob.

They measured the (approximately) Kolmogorov energy spectrum, proving that periodic boundary conditions were unnecessary.

The latest paper [11] also observed how the singular vortex structures move and reconnect inside this confined turbulence.

As for the decaying turbulence, these authors observed (William Irvine, private communication) two distinct decay regimes, not just a single power law like the old works [5].

Another critical comment: with the velocity correlations growing with distance by the approximate K41 law, even the forcing at the remote boundary would influence the potential part of velocity in bulk. This boundary influence makes the energy cascade picture non-universal; it may depend upon the statistics of the random forcing.

Two asymptotic regimes manifesting this non-universality were observed for the energy spectrum $E(k,t)$: one for initial spectrum $E(k,0)\propto k^2$ and another for $E(k,0)\propto k^4$. The potential velocity part differs for these regimes, as the first adds a constant velocity to the Biot-Savart integral. In the general case, it will be a harmonic potential flow with certain boundary conditions at infinity, with explicit continuous dependence of the boundary forces. The most general case is the $k^2$ class, as it doesn’t require any restrictions.

Only the statistics of the rotational part of velocity, i.e., vorticity, could reach some universal regime independent of the boundary conditions at infinity. Certain discrete universality classes could exist as it is common in critical phenomena.

Unlike the potential part of velocity, the vorticity is localized in singular regions – tubes and sheets, sparsely filling the space, as observed in numerical simulations. The potential part of velocity drops in the loop equations, and the remaining stochastic motion of the velocity circulation is equivalent to the vorticity statistics. Therefore, our solutions [1] of the loop equations [6,12] describe the internal stochastization of the decaying turbulence by a dual discrete system.

3.2. Mathematical Introduction. The Loop Equation and Its Solution

We derived a functional equation for the so-called loop average or Wilson loop in turbulence a while ago. All the references to our previous works can be found in a recent review paper [12].

The path to an exact solution by a dimensional reduction in this equation was proposed in the 1993 paper but has just been explored (see Figure 2). At the time, we could not compare a theory with anything but crude measurements in physical and numerical experiments at modest Reynolds numbers. All these experiments agreed with the K41 scaling, so the exotic equation based on unjustified methods of quantum field theory was premature. The specific prediction of the Loop equation, namely the Area law, could not be verified in DNS at the time with existing computer power.

The situation has changed over the last decades. No alternative microscopic theory based on the Navier-Stokes equation emerged, but our understanding of the strong turbulence phenomena grew significantly. On the other hand, the loop equations technology in the gauge theory also advanced over the last decades. The correspondence between the loop space functionals and the original vector fields was better understood, and various solutions to the gauge loop equations were found. In particular, the momentum loop equation was developed, similar to our momentum loop used below [13,14]. Recently, some numerical methods were found to solve loop equations beyond perturbation theory [15,16]. The loop dynamics was extended to quantum gravity, where it was used to study nonperturbative phenomena [17,18].

All these old and new developments made loop equations a major nonperturbative approach to gauge field theory. So, it is time to revive the hibernating theory of the loop equations in turbulence, where these equations are much simpler. The latest DNS [19,20,21,22] with Reynolds numbers of tens of thousands revealed and quantified violations of the K41 scaling laws. These numerical experiments are in agreement with so-called multifractal scaling laws [23].

Theoretically, we studied the loop equation in the confinement region (large circulation over large loop C) and justified the Area law suggested in ’93 on heuristic arguments. This law says that the tails of velocity circulation PDF in the confinement region are functions of the minimal area inside this loop. It was verified in DNS a few years ago [19], which triggered the further development of the geometric theory of turbulence[12,21,22]. In particular, the Area law was justified for flat and quadratic minimal surfaces, and an exact scaling law in confinement region $\mathsf{\Gamma }\propto \sqrt{Area}$ was derived [12]. The area law was verified with better precision in [20].

In the previous paper, [1], we have found a family of exact solutions of the loop equation for decaying turbulence [6,12]. This family describes a fixed trajectory of solutions with the universal time decay factor. The solutions are formulated in terms of the Wilson loop or loop average

$$\begin{array}{ccc}\hfill & & \mathsf{\Psi }[\gamma ,C]={〈exp\frac{\iota \gamma }{\nu }\oint d\overrightarrow{C}\left(\theta \right)·\overrightarrow{v}\left(\overrightarrow{C}\left(\theta \right)\right)〉}_{init};\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & & \mathsf{\Psi }[\gamma ,C]\Rightarrow {〈exp\frac{\iota \gamma }{\nu }\oint d\overrightarrow{C}\left(\theta \right)\overrightarrow{P}\left(\theta \right)〉}_{\mathbb{E}};\hfill \end{array}$$

(12)

In the first equation (the definition), the averaging $〈\dots 〉$ goes over initial data for the solutions of the Navier-Stokes equation for velocity field $\overrightarrow{v}\left(\overrightarrow{r}\right)$. In the second one (the solution), the averaging goes over the space of solutions $\overrightarrow{P}\left(\theta \right)$ of the loop equation [1]. We choose in this paper the parametrization of the loop with $\xi =\frac{\theta }{2\pi }$ to match with the fermionic coordinates below (the parametrization is arbitrary, in virtue of parametric invariance of the loop dynamics).

The loop equation for the momentum loop $\overrightarrow{P}\left(\theta \right)$ follows from the Navier-Stokes equation for $\overrightarrow{v}$

$$\begin{array}{ccc}& & {\partial }_t{v}_{\alpha }=\nu {\partial }_{\beta }{\omega }_{\beta \alpha }-v_{\beta }{\omega }_{\beta \alpha }-{\partial }_{\alpha }\left(p+\frac{v_{\beta }^2}{2}\right);\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& & {\partial }_{\alpha }{v}_{\alpha }=0;\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & {\omega }_{\beta \alpha }={\partial }_{\beta }{v}_{\alpha }-{\partial }_{\alpha }{v}_{\beta }\hfill \end{array}$$

(15)

After some transformations, replacing velocity and vorticity with the functional derivatives of the loop functional, we found the following momentum loop equation in [1,12]

$$\begin{array}{ccc}\hfill & & \nu {\partial }_t\overrightarrow{P}=-{\gamma }^2{(\Delta \overrightarrow{P})}^2\overrightarrow{P}+\Delta \overrightarrow{P}\left({\gamma }^2\overrightarrow{P}·\Delta \overrightarrow{P}+\iota \gamma \left(\frac{{(\overrightarrow{P}·\Delta \overrightarrow{P})}^2}{\Delta {\overrightarrow{P}}^2}-{\overrightarrow{P}}^2\right)\right);\hfill \end{array}$$

(16)

$$\begin{array}{ccc}& & \overrightarrow{P}\left(\theta \right)\equiv \frac{\overrightarrow{P}\left({\theta }^{+}\right)+\overrightarrow{P}\left({\theta }^{-}\right)}{2};\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & \Delta \overrightarrow{P}\left(\theta \right)\equiv \overrightarrow{P}\left({\theta }^{+}\right)-\overrightarrow{P}\left({\theta }^{-}\right);\hfill \end{array}$$

(18)

The momentum loop has a discontinuity $\Delta \overrightarrow{P}\left(\theta \right)$ at every parameter $0<\theta \le 1$, making it a fractal curve in complex space ${\mathbb{C}}_d$. The details can be found in [1,12]. We will skip the arguments $t,\theta$ in these loop equations, as there is no explicit dependence of these equations on either of these variables.

This Anzatz represents a plane wave in loop space, solving the loop equation for the Wilson loop due to the lack of direct dependence of the loop operator on the shape of the loop.

The superposition of these plane wave solutions would solve the Cauchy problem in loop space: find the stochastic function $\overrightarrow{P}\left(\theta \right)$ at $t=0$, providing the initial velocity field distribution. Formally, the initial distribution $W_0\left[P\right]$ of the momentum field $\overrightarrow{P}\left(\theta \right)$ is given by inverse functional Fourier transform.

$$\begin{array}{ccc}& & W_0\left[P\right]=\int DC{\delta }^3\left(\overrightarrow{C}\left[0\right]\right)\mathsf{\Psi }{[C,\gamma ]}_{t=0}exp-\frac{\iota \gamma }{\nu }\int d\overrightarrow{C}\left(\theta \right)·\overrightarrow{P}\left(\theta \right)\hfill \end{array}$$

(19)

This path integral was computed in [1,12] for a special stochastic solution of the Navier-Stokes equation: the global rotation with Gaussian random rotation matrix. The initial velocity distribution is Gaussian, with a slowly varying correlation function. The corresponding loop field reads (we set $\gamma =1$ for simplicity in this section)

$$\begin{array}{ccc}& & {\mathsf{\Psi }}_0\left[C\right]\equiv \mathsf{\Psi }{[C,1]}_{t=0}=exp-\frac{1}{2{\nu }^2}{\int }_{C}d\overrightarrow{C}\left(\theta \right)·d\overrightarrow{C}\left({\theta }^{\prime }\right)f\left(\overrightarrow{C}\left(\theta \right)-\overrightarrow{C}\left({\theta }^{\prime }\right)\right)\hfill \end{array}$$

(20)

where $f\left(\overrightarrow{r}\right)$ is the velocity correlation function

$$〈v_{\alpha }\left(r\right)v_{\beta }\left(r^{\prime }\right)〉=\left({\delta }_{\alpha \beta }-{\partial }_{\alpha }{\partial }_{\beta }{\partial }_{\mu }^{-2}\right)f(r-r^{\prime })$$

(21)

The potential part drops out in the closed loop integral. The correlation function varies at the macroscopic scale, which means that one could expand it in the Taylor series

$$f(r-r^{\prime })\to f_0-f_1{(r-r^{\prime })}^2+\dots$$

(22)

The first term $f_0$ is proportional to initial energy density,

$$\frac{1}{2}〈v_{\alpha }^2〉=\frac{d-1}{2}{f}_0$$

(23)

and the second one is proportional to initial energy dissipation rate ${\mathcal{E}}_0$

$$f_1=\frac{{\mathcal{E}}_0}{2d(d-1)\nu }$$

(24)

where $d=3$ is the dimension of space. The constant term in (22) as well as $r^2+r^{\prime 2}$ terms drop from the closed loop integral, so we are left with the cross-term $r{r}^{\prime }$, which reduces to a full square

$$\begin{array}{ccc}\hfill & & {\mathsf{\Psi }}_0\left[C\right]\to exp-\frac{f_1}{{\nu }^2}{\left(\oint d{C}_{\alpha }\left(\theta \right)C_{\beta }\left(\theta \right)\right)}^2\hfill \end{array}$$

(25)

This distribution is almost Gaussian: it reduces to Gaussian one by extra integration

$$\begin{array}{ccc}& & {\mathsf{\Psi }}_0\left[C\right]\to \mathit{const}\int \left(d\varphi \right)exp-{\varphi }_{\alpha \beta }^{2}exp2\iota \frac{\sqrt{f_1}}{\nu }{\varphi }_{\mu \nu }\oint d{C}_{\mu }\left(\theta \right)C_{\nu }\left(\theta \right)\hfill \end{array}$$

(26)

The integration here involves all $\frac{d(d-1)}{2}=3$ independent $\alpha <\beta$ components of the antisymmetric tensor ${\varphi }_{\alpha \beta }$. Note that this is ordinary integration, not the functional one.

This distribution can be translated into the momentum loop space. Here is the resulting stochastic function $\overrightarrow{P}\left(\theta \right)$, defined by the Fourier expansion on the circle

$$\begin{array}{ccc}& & P_{\alpha }\left(\theta \right)=\sum _{\mathrm{odd}n=1}^{\infty }{P}_{\alpha ,n}{e}^{\iota n\theta }+{\overline{P}}_{\alpha ,n}{e}^{-\iota n\theta };\hfill \end{array}$$

(27)

$$\begin{array}{ccc}& & P_{\alpha ,n}=\mathcal{N}(0,1);\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & {\overline{P}}_{\alpha ,n}=\frac{4\sqrt{f_1}}{n\nu }{\varphi }_{\alpha \beta }{P}_{\beta ,n};\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& & {\varphi }_{\alpha \beta }=-{\varphi }_{\beta \alpha };\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& & {\varphi }_{\alpha \beta }=\mathcal{N}(0,1)\forall \alpha <\beta ;\hfill \end{array}$$

(31)

At fixed tensor $\varphi$ the correlations are

$$\begin{array}{ccc}& & {〈P_{\alpha ,n}{P}_{\beta ,m}〉}_{t=0}=\frac{4\sqrt{f_1}}{m\nu }{\delta }_{nm}{\varphi }_{\alpha \beta };\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill & & {〈P_{\alpha }\left(\theta \right)P_{\beta }\left({\theta }^{\prime }\right)〉}_{t=0}=2\iota \frac{\sqrt{f_1}}{\nu }{\varphi }_{\alpha \beta }sign({\theta }^{\prime }-\theta );\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& & {\mathsf{\Psi }}_0\left[C\right]={〈exp\frac{\iota }{\nu }\oint d\overrightarrow{C}\left(\theta \right)\overrightarrow{P}\left(\theta \right)〉}_{P,\varphi }\hfill \end{array}$$

(34)

Though this special solution does not describe isotropic turbulence, it helps understand the mathematical properties of the loop technology. In particular, it shows the significance of the discontinuities of the momentum loop $\overrightarrow{P}\left(\theta \right)$.

Rather than solving the Cauchy problem, we are looking for an attractor: the fixed trajectory for $\overrightarrow{P}(\theta ,t)$ with some universal probability distribution related to the decaying turbulence statistics.

The following transformation reveals the hidden scaling invariance of decaying turbulence

$$\begin{array}{c}\hfill \overrightarrow{P}=\sqrt{\frac{\nu }{2(t+t_0)}}\frac{\overrightarrow{F}}{\gamma }\end{array}$$

(35)

The new vector function $\overrightarrow{F}$ satisfies an equation

$$\begin{array}{ccc}\hfill & & 2{\partial }_{\tau }\overrightarrow{F}=\left(1-{(\Delta \overrightarrow{F})}^2\right)\overrightarrow{F}+\Delta \overrightarrow{F}\left({\gamma }^2\overrightarrow{F}·\Delta \overrightarrow{F}+\iota \gamma \left(\frac{{(\overrightarrow{F}·\Delta \overrightarrow{F})}^2}{\Delta {\overrightarrow{F}}^2}-{\overrightarrow{F}}^2\right)\right);\hfill \end{array}$$

(36)

$$\begin{array}{ccc}& & \tau =log(t+t_0)\hfill \end{array}$$

(37)

This equation is invariant under translations of the new variable $\tau =log(t+t_0)$, corresponding to the rescaling/translation of the original time.

$$\begin{array}{c}\hfill t\Rightarrow \lambda t+(\lambda -1)t_0\end{array}$$

(38)

There are two consequences of this invariance.

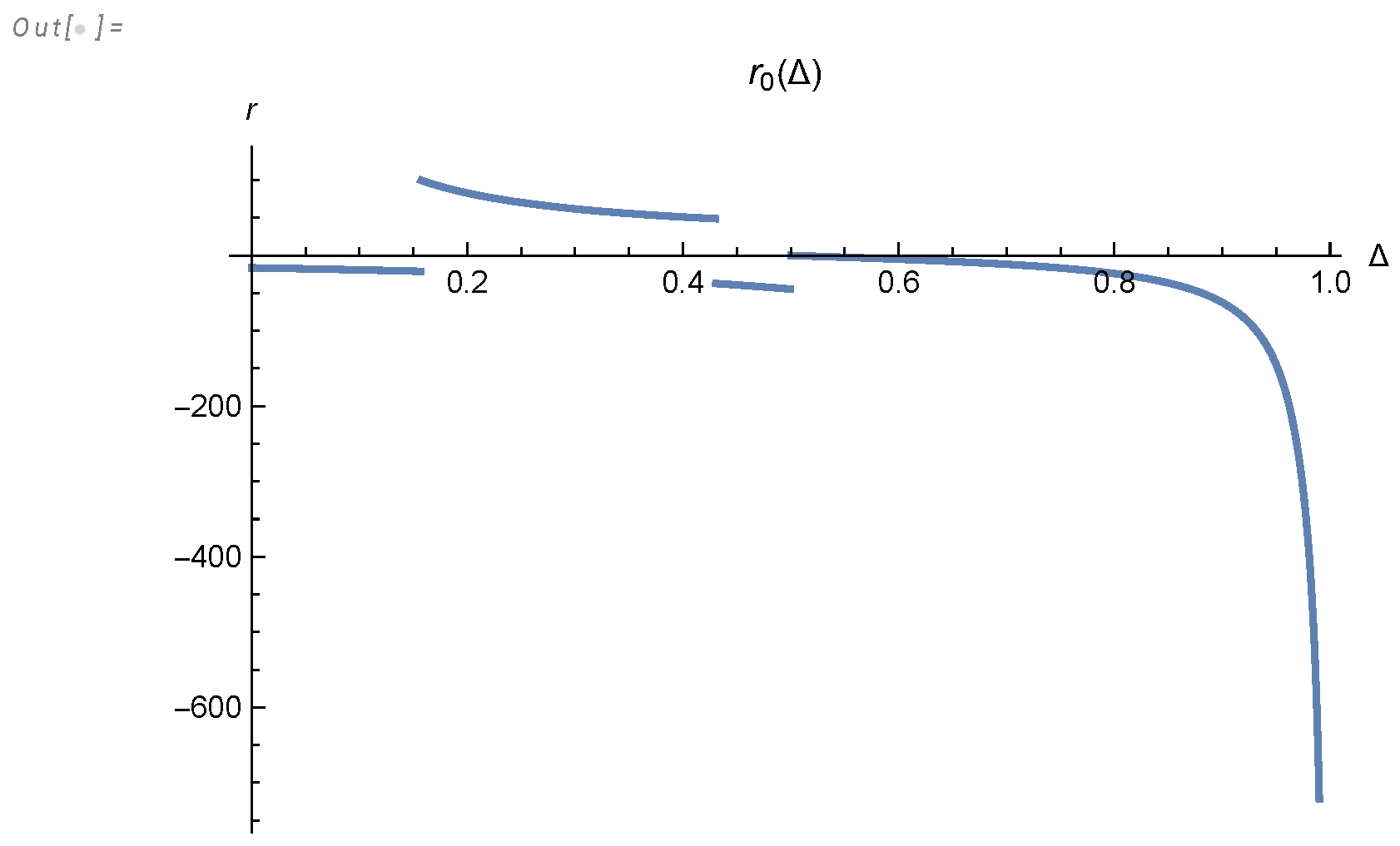
• There is a fixed point for $\overrightarrow{F}$.
• The approach to this fixed point is exponential in $\tau$, which is power-like in original time.

Both of these properties were used in [1]: the first one was used to find a fixed point, and the second one was used to derive the spectral equation for the anomalous dimensions ${\lambda }_i$ of decay $t^{-{\lambda }_i}$ of the small deviations from these fixed points. In this paper, we only consider the fixed point, leaving the exciting problem of the spectrum of anomalous dimensions for future research.

3.3. The Big and Small Euler Ensembles

Let us remember the basic properties of the fixed point for $\overrightarrow{F}$ in [1]. It is defined as a limit $N\to \infty$ of the polygon ${\overrightarrow{F}}_0\dots {\overrightarrow{F}}_N={\overrightarrow{F}}_0$ with the following vertices

$$\begin{array}{ccc}\hfill & & {\overrightarrow{F}}_k=\frac{\left\{cos\left({\alpha }_k\right),sin\left({\alpha }_k\right),icos\left(\frac{\beta }{2}\right)\right\}}{2sin\left(\frac{\beta }{2}\right)};\hfill \end{array}$$

(39)

$$\begin{array}{ccc}& & {\theta }_k=\frac{k}{N};\beta =\frac{2\pi p}{q};N\to \infty ;\hfill \end{array}$$

(40)

$$\begin{array}{ccc}& & {\alpha }_{k+1}={\alpha }_k+{\sigma }_k\beta ;{\sigma }_k=\pm 1,\beta \sum {\sigma }_k=2\pi pr;\hfill \end{array}$$

(41)

The parameters $\widehat{\mathsf{\Omega }},p,q,r,{\sigma }_0\dots {\sigma }_N={\sigma }_0$ are random, making this solution for $\overrightarrow{F}\left(\theta \right)$ a fixed manifold rather than a fixed point. We suggested calling this manifold the big Euler ensemble of just the Euler ensemble.

It is a fixed point of (36) with the discrete version of discontinuity and principal value:

$$\begin{array}{ccc}& & \Delta \overrightarrow{F}\equiv {\overrightarrow{F}}_{k+1}-{\overrightarrow{F}}_k;\hfill \end{array}$$

(42)

$$\begin{array}{ccc}& & \overrightarrow{F}\equiv \frac{{\overrightarrow{F}}_{k+1}+{\overrightarrow{F}}_k}{2}\hfill \end{array}$$

(43)

Both terms of the right side (36) vanish; the term proportional to $\Delta \overrightarrow{F}$ and the term proportional to $\overrightarrow{F}$. Otherwise, we would have $\overrightarrow{F} \Vert \Delta \overrightarrow{F}$, leading to zero vorticity [1]. The ensemble of all the different solutions is called the big Euler ensemble. The integer numbers ${\sigma }_k=\pm 1$ came as the solution of the loop equation, and the requirement of the rational $\frac{p}{q}$ came from the periodicity requirement.

We can use integration (summation) by parts to write the circulation as follows (in virtue of periodicity):

$$\begin{array}{ccc}\hfill & & \oint d\overrightarrow{C}\left(\theta \right)·\overrightarrow{P}\left(\theta \right)=-\oint d\overrightarrow{P}\left(\theta \right)·\overrightarrow{C}\left(\theta \right);\hfill \end{array}$$

(44)

$$\begin{array}{ccc}& & \sum _k\Delta C_k{\overrightarrow{P}}_k=-\oint \Delta {\overrightarrow{P}}_k·{\overrightarrow{C}}_k;\hfill \end{array}$$

(45)

A remarkable property of this solution $\overrightarrow{P}(\theta ,t)$ of the loop equation is that even though it satisfies the complex equation and has an imaginary part, the resulting circulation (44) is real! The imaginary part of the $\overrightarrow{P}(\theta ,t)$ does not depend on $\theta$ and thus drops from the integral $\oint d\overrightarrow{C}\left(\theta \right)·\overrightarrow{P}(\theta ,t)$.

There is, in general, a larger manifold of periodic solutions to the discrete loop equation, which has all three components of ${\overrightarrow{F}}_k$ complex and varying along the polygon.

We could not find a global parametrization of such a solution1. Instead, we generated it numerically by taking a planar closed polygon and evolving its vertices ${\overrightarrow{F}}_k$ by a stochastic process in the local tangent plane to the surface of the equations in multi-dimensional complex space.

We could not submit such a solution to an extra restriction $\Im {\overrightarrow{F}}_k=\mathit{const}$ needed to make circulation real. We cannot prove that such a general solution does not exist but rather take the Euler ensemble as a working hypothesis and investigate its properties.

This ensemble can be solved analytically in the statistical limit and has nice physical properties, matching the expected behavior of the decaying turbulence solution.

We assign equal weights to all elements of this set; we call this conjecture the ergodic hypothesis. This prescription is similar to assigning equal weights to each triangulation of curved space with the same topology in dynamically triangulated quantum gravity [24]. Mathematically, this is the most symmetric weight assignment, and there are general expectations that various discrete theories converge into the same symmetry classes of continuum theories in the statistical limit. This method works remarkably well in two dimensions [? ? ? ], providing the same correlation functions as continuum gravity (Liouville theory [25]).

The fractions $\frac{p}{q}$ with fixed denominator are counted by Euler totient function $\phi \left(q\right)$ [26]

$$\begin{array}{ccc}\hfill & & \phi \left(q\right)=\sum _{\begin{array}{c}p=1\\ (p,q)\end{array}}^{q-1}1=q\prod _{p|q}\left(1-\frac{1}{p}\right);\hfill \end{array}$$

(46)

For example $\phi \left(16\right)=8$ and $\phi \left(17\right)=16$.

In some cases, one can analytically average over spins $\sigma$ in the big Euler ensemble, reducing the problem to computations of averages over the small Euler ensemble $\mathcal{E}\left(N\right):N,p,q,r$ with the measure induced by averaging over the spins in the big Euler ensemble.

In this paper, we perform this averaging over $\sigma$ analytically, without any approximations, reducing it to a partition function of a certain quantum mechanical system with Fermi particles. This partition function is calculable using a WKB approximation in the statistical limit $N\to \infty$.

4. The Markov Chain and Its Fermionic Representation

Here is a new representation of the Euler ensemble, leading us to the exact analytic solution below.

We start by replacing independent random variables $\sigma$ with fixed sum by a Markov process, as suggested in [1]. We start with n random values of ${\sigma }_i=1$ and remaining $N-n$ values of ${\sigma }_i=-1$. Instead of averaging over all of these values simultaneously, we follow a Markov process of picking ${\sigma }_N,\dots {\sigma }_1$ one after another. At each step, there will be $M=N,\dots 0$ remaining $\sigma$. We get a transition $n\Rightarrow n-1$ with probability $\frac{n}{M}$ and $n\Rightarrow n$ with complementary probability.

Multiplying these probabilities and summing all histories of the Markov process is equivalent to the computation of the product of the Markov matrices

$$\begin{array}{ccc}& & \prod _{M=1}^{N}Q\left(M\right);\hfill \end{array}$$

(47)

$$\begin{array}{ccc}& & Q\left(M\right)|n\rangle =\frac{M-n}{M}|n\rangle +\frac{n}{M}|n-1\rangle ;\hfill \end{array}$$

(48)

This Markov process will be random until $n=0$. After that, all remaining ${\sigma }_k$ will have negative signs and be taken with probability 1, keeping $n=0$.

The expectation value of some function $X\left(\left\{\sigma \right\}\right)$ reduces to the matrix product

$$\begin{array}{ccc}& & \mathbb{P}\left[X\right]=\sum _{n=0}^{N_{+}}\left.〈n\right|\left(\prod _{M=1}^N\widehat{Q}\left(M\right)\right)·X·\left|N_{+}\right.〉;\hfill \end{array}$$

(49)

$$\begin{array}{ccc}& & \widehat{Q}\left(M\right)·X|n\rangle =\frac{n}{M}X\left({\sigma }_M\to 1\right)|n-1\rangle +\frac{M-n}{M}X\left({\sigma }_M\to -1\right)|n\rangle \hfill \end{array}$$

(50)

Here $N_{+}=(N+\sum {\sigma }_l)/2=(N+qr)/2$ is the number of positive sigmas. The operator $\widehat{Q}\left(M\right)$ sets in $X|n\rangle$ the variable ${\sigma }_M$ to 1 with probability $\frac{n}{M}$ and to $-1$ with complementary probability. The generalization of the Markov matrix $Q\left(M\right)$ to the operator $\widehat{Q}\left(M\right)$ will be presented shortly.

Once the whole product is applied to X, all the sigma variables in all terms will be specified so that the result will be a number.

This Markov process is implemented as a computer code in [27], leading to a fast simulation with $O\left(N^0\right)$ memory requirement.

Now, we observe that quantum Fermi statistics can represent the Markov chain of Ising variables. Let us construct the operator $\widehat{Q}\left(M\right)$ with Fermionic creation and annihilation operators, with occupation numbers ${\nu }_k=(1+{\sigma }_k)/2=(0,1)$. These operators obey (anti)commutation relations, and they create/annihilate $\sigma =1$ state as follows (with Kronecker delta $\delta \left[n\right]\equiv {\delta }_{n,0}$):

$$\begin{array}{ccc}& & {\left[a_i,a_j^{†}\right]}_{+}={\delta }_{ij};\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& & {\left[a_i,a_j\right]}_{+}={\left[a_i^{†},a_j^{†}\right]}_{+}=0;\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& & a_n^{†}|{\sigma }_1,\dots ,{\sigma }_N\rangle =\delta [{\sigma }_n+1]|{\sigma }_1,\dots ,{\sigma }_n\to 1,\dots {\sigma }_N\rangle ;\hfill \end{array}$$

(53)

$$\begin{array}{ccc}& & a_n|{\sigma }_1,\dots ,{\sigma }_N\rangle =\delta [{\sigma }_n-1]|{\sigma }_1,\dots ,{\sigma }_n\to -1,\dots {\sigma }_N\rangle ;\hfill \end{array}$$

(54)

$$\begin{array}{ccc}& & {\widehat{\nu }}_n=a_n^{†}{a}_n;\hfill \end{array}$$

(55)

$$\begin{array}{ccc}& & {\widehat{\nu }}_n|{\sigma }_1,\dots ,{\sigma }_N\rangle =\delta [{\sigma }_n-1]|{\sigma }_1,\dots ,{\sigma }_N\rangle \hfill \end{array}$$

(56)

The number $n\left(M\right)$ of positive sigmas ${\sum }_{l=1}^M\delta [{\sigma }_l-1]$ coincides with the occupation number of these Fermi particles.

$$\begin{array}{ccc}& & \widehat{n}\left(M\right)=\sum _{l=1}^M{\widehat{\nu }}_l;\hfill \end{array}$$

(57)

This relation leads to the representation

$$\begin{array}{ccc}& & \widehat{Q}\left(M\right)={\widehat{\nu }}_M\frac{\widehat{n}\left(M\right)}{M}+(1-{\widehat{\nu }}_M)\frac{M-\widehat{n}\left(M\right)}{M};\hfill \end{array}$$

(58)

The variables ${\sigma }_l$ can also be expressed in terms of this operator algebra by using

$$\begin{array}{c}\hfill {\widehat{\sigma }}_l=2{\widehat{\nu }}_l-1.\end{array}$$

(59)

The Wilson loop in (11) can now be represented as an average over the small Euler ensemble $\mathcal{E}\left(N\right)$ of a quantum trace expression

$$\begin{array}{ccc}\hfill \mathsf{\Psi }[\gamma ,C]=& & \frac{{\displaystyle {〈\mathrm{tr}\left(\widehat{Z}\left(qr\right)exp\frac{i\gamma }{\nu }\sum _l\Delta {\overrightarrow{C}}_l·\widehat{\mathsf{\Omega }}·{\overrightarrow{\mathcal{P}}}_l\left(t\right)\prod _{M=1}^N\widehat{Q}\left(M\right)\right)〉}_{\widehat{\mathsf{\Omega }},\mathcal{E}\left(N\right)}}}{{〈\mathrm{tr}\left(\widehat{Z}\left(qr\right){\prod }_{M=1}^N\widehat{Q}\left(M\right)\right)〉}_{\mathcal{E}\left(N\right)}},\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill \widehat{Z}\left(s\right)=& & \oint \frac{d\omega }{2\pi }exp\iota \omega \left(\sum _l{\widehat{\sigma }}_l-s\right);\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill \Delta {\overrightarrow{C}}_l=& & \overrightarrow{C}\left(\frac{l+1}{N}\right)-\overrightarrow{C}\left(\frac{l}{N}\right),\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill {\overrightarrow{\mathcal{P}}}_l\left(t\right)=& & \sqrt{\frac{\nu }{2\left(t+t_0\right)}}\frac{{\overrightarrow{\mathcal{F}}}_l}{\gamma },\widehat{\mathsf{\Omega }}\in O\left(3\right),\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill {\overrightarrow{\mathcal{F}}}_l=& & \frac{\left\{cos\left({\widehat{\alpha }}_l\right),sin\left({\widehat{\alpha }}_l\right),0\right\}}{2sin\left(\frac{\beta }{2}\right)},\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill \mathcal{E}\left(N\right):& & p,q,r\in \mathbb{Z}\mathrm{with}0<p<q<N,\mathbf{gcd}(p,q)=1,-N\le qr\le N,\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_l=& & \beta \sum _{k=1}^{l-1}(2{\widehat{\nu }}_k-1);\hfill \end{array}$$

(66)

The last component of the vector ${\overrightarrow{\mathcal{F}}}_l$ is set to 0 as this component does not depend on l and yields zero in the sum over the loop ${\sum }_l\Delta {\overrightarrow{C}}_l=0$.

The proof of equivalence to the combinatorial formula with an average over ${\sigma }_l=\pm 1$ can be given using the following Lemma (obvious for a physicist).

Lemma 1.

The operators ${\widehat{\nu }}_l$ all commute with each other.

Proof. 

Using commutation relations, we can write

$$\begin{array}{c}\hfill {\widehat{\nu }}_l{\widehat{\nu }}_n=a_l^{†}({\delta }_{ln}-a_n^{†}{a}_l)a_n=a_l^{†}{a}_n{\delta }_{ln}-a_l^{†}{a}_n^{†}{a}_l{a}_n\end{array}$$

(67)

Interchanging indexes $l,n$ in this relation, we see that the first term does not change due to Kronecker delta, and the second term does not change because $a_l^{†},a_n^{†}$ anti-commute, as well as $a_l,a_n$, so the second term is symmetric as well. Therefore, ${\widehat{\nu }}_l{\widehat{\nu }}_n={\widehat{\nu }}_n{\widehat{\nu }}_l$ □

Theorem 1.

The trace formula (60) equals the expectation value of the momentum loop ansatz (12), (35), (39) in the big Euler ensemble.

Proof. 

As all the operators ${\widehat{\nu }}_l$ commute with each other, the operators $\widehat{Q}\left(M\right)$ can be applied in arbitrary order to the states $\mathsf{\Sigma }=|{\sigma }_1,\dots {\sigma }_N\rangle$ involved in the trace. The same is true about individual terms in the circulation in the exponential of the Wilson loop. These terms ${\overrightarrow{\mathcal{F}}}_l$ involve the operators ${\widehat{\alpha }}_l$, which commute with each other and with each $\widehat{Q}\left(M\right)$. Thus, we can use the ordered product of the operators ${\widehat{G}}_l=\widehat{Q}\left(l\right)exp\iota \omega {\widehat{\sigma }}_l+\frac{i\gamma }{\nu }\Delta {\overrightarrow{C}}_l·{\overrightarrow{\mathcal{P}}}_l\left(t\right)$. Each of the operators ${\widehat{G}}_l$ acting in turn on arbitrary state $\mathsf{\Sigma }$ will create two terms with $\delta [{\sigma }_l\pm 1]$. The exponential in ${\widehat{G}}_l$ will involve ${\widehat{\sigma }}_k,k\le l$. As a result of the application of the operator ${\widehat{Z}}_l={\prod }_{k=1}^l{\widehat{G}}_k$ to the state vector $\mathsf{\Sigma }$ we get $2^l$ terms with $\mathsf{\Sigma }{\prod }_{k=1}^l\delta [{\sigma }_k-{\eta }_k],{\eta }_k=\pm 1$. The factors ${\widehat{Z}}_l$ will involve only ${\widehat{\sigma }}_k,k\le l$, which are all reduced to ${\eta }_k,k\le l$ in virtue of the product of the Kronecker deltas. Multiplying all operators ${\widehat{G}}_M$ will lead to superposition ${\widehat{\mathsf{\Pi }}}_N$ of $2^N$ terms, each with product ${\prod }_{M=1}^N\delta [{\sigma }_M-{\eta }_M]$ with various choices of the signs ${\eta }_i=\pm 1$ for each i. Furthermore, the product of Kronecker deltas will project the total sum of $2^N$ combinations of the states $\mathsf{\Sigma }$ in the trace $\mathrm{tr}\dots$ to a single term corresponding to a particular history ${\eta }_1,\dots {\eta }_N$ of the Markov process. The product of Kronecker deltas in each history will be multiplied by the same state vector $\mathsf{\Sigma }$, by the product of Markov transition probabilities, and by the exponential $exp\frac{i\gamma }{\nu }{\sum }_l\Delta {\overrightarrow{C}}_l·\widehat{\mathsf{\Omega }}·{\overrightarrow{P}}_l\left(t\right)$ with the operators $\widehat{\sigma }$ in ${\overrightarrow{\mathcal{P}}}_k\left(t\right)$ replaced by numbers $\eta$ leading to the usual numeric ${\overrightarrow{P}}_l\left(t\right)$. The transition probabilities of the Markov process are designed to reproduce combinatorial probabilities of random sigmas, adding up to one after summation over histories [28]. The integration over $\omega$ will produce $\delta \left[{\sum }_l{\widehat{\eta }}_l-s\right]$. This delta function will reduce the trace to the required sum over all histories of the Markov process with a fixed ${\sum }_l{\eta }_l$. □

We have found a third vertex of the triangle of equivalent theories: the decaying turbulence in three-dimensional space, the fractal curve in complex space, and Fermi particles on a ring. By degrees of freedom, this is a one-dimensional Fermi-gas in the statistical limit $N\to \infty$. However, there is no local Hamiltonian in this quantum partition function, just a trace of certain products of operators in Fock space. So, an algebraic (or quantum statistical) problem remains to find the continuum limit of this theory of the fermion ring.

This problem is addressed in the next section.

5. The Continuum Limit

As we shall shortly see, in the continuum limit $N\to \infty$, the accumulated numbers of Fermi particles ${\nu }_k=1$ and Dirac holes ${\nu }_k=0$ tend to some classical functions of "position" $\xi =\frac{k}{N}$, leading to the exact solution.

5.1. Path Integral over Markov Histories

Let us represent the product ${\mathsf{\Pi }}_N$ of the transitional probabilities of the particular history of the Markov processes as follows (with $n_{\pm }\equiv n_{\pm }\left(l\right),\Delta n_{\pm }=-1$)

$$\begin{array}{ccc}& & {\mathsf{\Pi }}_N=expN{\mathsf{\Lambda }}_N;\hfill \end{array}$$

(68)

$$\begin{array}{ccc}& & {\mathsf{\Lambda }}_N=\frac{1}{N}\sum _l\left(\Delta n_{+}log\left(\frac{n_{+}}{n_{+}+n_{-}}\right)+\Delta n_{-}log\left(\frac{n_{-}}{n_{+}+n_{-}}\right)\right);\hfill \end{array}$$

(69)

$$\begin{array}{ccc}& & n_{+}=\sum _{k\le l}{\nu }_k;\hfill \end{array}$$

(70)

$$\begin{array}{ccc}& & n_{-}=\sum _{k\le l}(1-{\nu }_k);\hfill \end{array}$$

(71)

These $n_{\pm }$ are net numbers of $\eta =\pm 1$ in terms of Ising spins or occupation numbers ${\nu }_k=(1,0)$ in the Fermi representation. There is an extra constraint on the Markov process

$$\begin{array}{c}\hfill n_{+}+n_{-}=l;\forall l\end{array}$$

(72)

which follows from the above definition in terms of the occupation numbers. We can redefine $n_{\pm }$ as N times the piecewise constant functions.

$$\begin{array}{ccc}& & n_{\pm }=N{f}_{\pm }\left(\xi \right);\hfill \end{array}$$

(73)

$$\begin{array}{ccc}& & f_{\pm }\left(\xi \right)=\sum _{k=1}^{N\xi }\frac{{\nu }_k}{N};\hfill \end{array}$$

(74)

$$\begin{array}{ccc}& & f_{\pm }^{\prime }\left(\xi \right)=\sum _{l=1}^N\delta \left(\xi -\frac{l}{N}\right)\sum _{k=1}^l\frac{{\nu }_k}{N};\hfill \end{array}$$

(75)

$$\begin{array}{ccc}& & 0<\xi <1;\hfill \end{array}$$

(76)

The sums can be rewritten as Lebesgue integrals

$$\begin{array}{ccc}& & {\mathsf{\Lambda }}_N={\int }_1^0\left(d{f}_{+}\left(\xi \right)log\left(\frac{f_{+}\left(\xi \right)}{\xi }\right)+d{f}_{-}\left(\xi \right)log\left(\frac{f_{-}\left(\xi \right)}{\xi }\right)\right)\hfill \end{array}$$

(77)

The sum over histories of the Markov process will become a path integral over the difference $\varphi =f_{+}\left(\xi \right)-f_{-}\left(\xi \right)$

$$\begin{array}{ccc}\hfill & & \sum _{{\eta }_{.}=\pm 1}expN({\mathsf{\Lambda }}_N+\iota {\mathsf{\Lambda }}_N^{\left(1\right)})\to \int D\varphi expN({\mathsf{\Lambda }}_N+\iota {\mathsf{\Lambda }}_N^{\left(1\right)})\hfill \end{array}$$

(78)

This path integral will be dominated by the "classical history," maximizing the product of transitional probabilities if such a classical trajectory exists. The first term (without the circulation term) brings the variational problem

$$\begin{array}{ccc}& & \underset{\varphi }{max}{\mathsf{\Lambda }}_N\left[\varphi \right];\hfill \end{array}$$

(79)

$$\begin{array}{ccc}& & {\mathsf{\Lambda }}_N\left[\varphi \right]={\int }_1^{0}d\xi \left(\frac{d{f}_{+}}{d\xi }log\left(\frac{f_{+}}{\xi }\right)+\frac{d{f}_{-}}{d\xi }log\left(\frac{f_{-}}{\xi }\right)\right);\hfill \end{array}$$

(80)

$$\begin{array}{ccc}& & f_{\pm }\left(\xi \right)=\frac{1}{2}\left(\xi \pm \varphi \left(\xi \right)\right);\hfill \end{array}$$

(81)

$$\begin{array}{ccc}& & f_{\pm }\left(\xi \right)\ge 0;\hfill \end{array}$$

(82)

This problem is, however, a degenerate one, as the functional reduces to the integral of the total derivative:

$$\begin{array}{ccc}\hfill & & \frac{\delta {\mathsf{\Lambda }}_N\left[\varphi \right]}{\delta \varphi \left(\xi \right)}=0;\hfill \\ & & {\mathsf{\Lambda }}_N\left[\varphi \right]={\int }_1^{0}d\left(f_{+}log{f}_{+}+f_{-}log{f}_{-}\right)+1+{\int }_0^{1}d\xi log\xi =\hfill \end{array}$$

(83)

$$\begin{array}{ccc}& & -\frac{1}{2}(1-s)log(1-s)-\frac{1}{2}(1+s)log(1+s)+log\left(2\right);\hfill \end{array}$$

(84)

It depends on the boundary condition $\varphi \left(0\right)=0,\varphi \left(1\right)=s$ but not on the shape of $\varphi \left(\xi \right)$.

This expression matches the Stirling formula for the logarithm of the binomial coefficient in the combinatorial solution [1] for the Euler ensemble

$$\begin{array}{ccc}& & \underset{N\to \infty }{lim}\frac{log\left({\displaystyle \genfrac{}{}{0pt}{}{N}{N(1+s)/2}}\right)}{N}=-\frac{1}{2}(1-s)log(1-s)-\frac{1}{2}(1+s)log(1+s)+log\left(2\right)\hfill \end{array}$$

(85)

This $\mathsf{\Lambda }\left(s\right)={\mathsf{\Lambda }}_{\infty }\left(s\right)$ is a smooth even function of s taking positive values from $\mathsf{\Lambda }(\pm 1)=0$ to the maximal value $\mathsf{\Lambda }\left(0\right)=log\left(2\right)$ (see Figure 6).

Now, let us add the circulation term to the exponential of the partition function (60). This term can be directly expressed in terms of the difference between our two densities $N\varphi \left(\xi \right)=N{f}_{+}\left(\xi \right)-N{f}_{-}\left(\xi \right)$:

$$\begin{array}{ccc}\hfill & & \iota N{\mathsf{\Lambda }}_N^{\left(1\right)}[\varphi ,C_{\mathsf{\Omega }}]=\frac{\iota }{\sqrt{2\nu t}}{\int }_0^{1}d{\overrightarrow{C}}_{\mathsf{\Omega }}\left(\xi \right)·\overrightarrow{F}\left(\xi \right);\hfill \end{array}$$

(86)

$$\begin{array}{ccc}& & \overrightarrow{F}\left(\xi \right)=\frac{\left\{sin\left(\beta N\varphi \right(\xi \left)\right),cos\left(\beta N\varphi \right(\xi \left)\right),0\right\}}{2sin(\beta /2)};\hfill \end{array}$$

(87)

$$\begin{array}{ccc}& & {\overrightarrow{C}}_{\mathsf{\Omega }}\left(\theta \right)=\widehat{\mathsf{\Omega }}·\overrightarrow{C}\left(\theta \right);\hfill \end{array}$$

(88)

The key assumption is, of course, the existence of the smooth limit of the charge density $\varphi \left(\xi \right)$ of these fermions when they are densely covering this loop.

We are working with $\alpha \left(\xi \right)=\beta N\varphi \left(\xi \right)$ in the following.

The measure for paths $\left[D\alpha \right]$ is undetermined. The derivatives of these alphas were quantized in the original Fermi theory: each step ${\alpha }^{\prime }\left(\xi \right)\approx N\Delta \alpha =N\beta \sigma =\pm N\beta$.

As we demonstrate below, in continuum theory, this discrete distribution can be replaced by a Gaussian distribution with the same mean square

$$\begin{array}{c}\hfill \sum _{{\alpha }^{\prime }=\pm N\beta }\leftrightarrow \int d{\alpha }^{\prime }exp-\frac{{\left({\alpha }^{\prime }\right)}^2}{2N^2{\beta }^2}\end{array}$$

(89)

To demonstrate that, we consider in the critical region ${\beta }^2\sim N^{-1}\to 0$ the most general term that arises in the moments of the circulation in (86) (see [29] for some exact computations of these moments)

$$\begin{array}{ccc}& & 2^{-N}\sum _{{\sigma }_i=\pm 1}exp\iota \beta \sum _i{k}_i{\sigma }_i=\prod _{i}cos\beta k_i\to exp-{\beta }^2/2\sum _i{k}_i^2\hfill \end{array}$$

(90)

where $k_i$ are some integers. With a large number N of these integers, the sum in the exponential becomes an integral, which is equivalent to a Gaussian integral

$$\begin{array}{ccc}& & exp-{\beta }^2/2\sum _i{k}_i^2=\prod _i{\int }_{-\infty }^{\infty }\frac{d{\sigma }_i}{\sqrt{2\pi }}exp-{\sigma }_i^2/2exp\iota \beta k_i{\sigma }_i\to exp-N{\beta }^2/2{\int }_0^{1}d\xi k{\left(\xi \right)}^2\hfill \end{array}$$

(91)

We arrive at the standard path integral measure

$$\begin{array}{ccc}& & \int \left[D\alpha \right]=\int D\alpha \left(\xi \right)exp-{\int }_0^{1}d\xi \frac{{\left({\alpha }^{\prime }\right)}^2}{2N{\beta }^2};\hfill \end{array}$$

(92)

$$\begin{array}{ccc}& & \frac{\int \left[D\alpha \right]exp\iota N{\int }_0^{1}d\xi \alpha \left(\xi \right)K\left(\xi \right)}{\int \left[D\alpha \right]}=exp-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.N^2\int \int d{\xi }_{1}d{\xi }_{2}K\left({\xi }_1\right)K\left({\xi }_2\right)G({\xi }_1,{\xi }_2);\hfill \end{array}$$

(93)

$$\begin{array}{ccc}& & G({\xi }_1,{\xi }_2)=〈\alpha \left({\xi }_1\right)\alpha \left({\xi }_2\right)〉;\hfill \end{array}$$

(94)

The next section will compute this Green’s function $G({\xi }_1,{\xi }_2)$.

Thus, we arrive at the following path integral in the continuum limit

$$\begin{array}{ccc}\hfill & & \mathsf{\Psi }\left[C\right]=\frac{{\displaystyle \sum _{p<q;(p,q)}\underset{\mathsf{\Omega }\in O\left(3\right)}{\int }d\mathsf{\Omega }\int \left[D\alpha \right]exp\iota \frac{{\int }_0^{1}d\xi \Im \left({\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\left(\xi \right)exp\iota \alpha \left(\xi \right)\right)}{2sin(\pi p/q)\sqrt{2\nu (t+t_0)}}}}{{\displaystyle \sum _{p<q;(p,q)}\left|O\left(3\right)\right|\int \left[D\alpha \right]}};\hfill \end{array}$$

(95)

$$\begin{array}{ccc}& & {\mathcal{C}}_{\mathsf{\Omega }}\left(\theta \right)=\overrightarrow{C}\left(\theta \right)·\widehat{\mathsf{\Omega }}·\{\iota ,1,0\};\hfill \end{array}$$

(96)

We get the $U\left(1\right)$ statistical model with the boundary condition $\alpha \left(1\right)=\alpha \left(0\right)+\beta Ns$. The period $\beta Ns=2\pi pr$ is a multiple of $2\pi$, which is irrelevant at $N\to \infty$. The effective potential for this theory is a linear function of the loop slope ${\overrightarrow{C}}^{\prime }\left(\xi \right)$.

This model is yet another representation of the Euler ensemble, suitable for the continuum limit.

5.2. Matching Path Integral with Combinatorial Sums in Big Euler Ensemble

The results of the path integration over $\alpha$ must match the combinatorial calculations with ${\sigma }_l=\pm 1$ in the limit of large N. Without the interaction provided by the circulation term in (95), this path integral is dominated by a linear trajectory

$$\begin{array}{c}\hfill {\alpha }_{cl}\left(\xi \right)=\beta N\xi s;\end{array}$$

(97)

We already saw the match between the classical Action ${\mathsf{\Lambda }}_N[\varphi \left(\xi \right)=\xi s]$ and the asymptotic value of the logarithm of the Binomial coefficient of the combinatorial solution for the sum over $\sigma$ variables.

Let us verify some examples of the expectation values over $\sigma$. The simplest is (with $n\ne m$)

$$\begin{array}{c}\hfill {〈{\sigma }_n{\sigma }_m〉}_{\sum \sigma =Ns}\end{array}$$

(98)

The direct calculation using methods of [1,29] leads to

$$\begin{array}{ccc}& & {〈{\sigma }_n{\sigma }_m〉}_{\sum \sigma =Ns}=-\oint \frac{d\omega }{2\pi Z}{e}^{\iota \omega Ns}cos\left((N-2)\omega \right){sin}^2\left(\omega \right)=\frac{(1-N{s}^2)}{2^{N-3}ZN(1-s^2)}\left({\displaystyle \genfrac{}{}{0pt}{}{N-2}{\frac{1}{2}(N+Ns-2)}}\right);\hfill \end{array}$$

(99)

$$\begin{array}{ccc}& & Z=\oint \frac{d\omega }{2\pi }{e}^{\iota \omega Ns}cos\left(N\omega \right)=2^{-N}\left(\genfrac{}{}{0pt}{}{N}{\frac{1}{2}(sN+N)}\right)\hfill \end{array}$$

(100)

Using Gamma function properties, this ratio simplifies to

$$\begin{array}{c}\hfill \frac{N{s}^2-1}{N-1}\end{array}$$

(101)

This result can be derived from symmetry without any integration.

$$\begin{array}{ccc}& & {〈{\sigma }_n{\sigma }_m〉}_{\sum \sigma =Ns}=A(N,s)(1-{\delta }_{nm})+{\delta }_{nm};\hfill \end{array}$$

(102)

$$\begin{array}{ccc}& & \sum _{n,m}{〈{\sigma }_n{\sigma }_m〉}_{\sum \sigma =Ns}=s^2{N}^2=A(N,s)N(N-1)+N\hfill \end{array}$$

(103)

$$\begin{array}{ccc}& & A(N,s)=\frac{N{s}^2-1}{N-1}\hfill \end{array}$$

(104)

The same limit $A(\infty ,s)=s^2$ follows from the classical trajectory

$$\begin{array}{c}\hfill {〈{\sigma }_n{\sigma }_m〉}_{\sum \sigma =Ns}\to \frac{{\alpha }_{cl}^{\prime }\left(\xi \right)}{\beta N}\frac{{\alpha }_{cl}^{\prime }\left({\xi }^{\prime }\right)}{\beta N}=s^2\end{array}$$

(105)

Let us consider less trivial example [1,29]

$$\begin{array}{ccc}& & U_{n,m}\to \sum _{k=n}^{m-1}exp\iota {\alpha }_{k,n};\hfill \end{array}$$

(106)

$$\begin{array}{ccc}& & {\alpha }_{k,n}=\beta \sum _{\begin{array}{c}l=0\\ l\ne n\end{array}}^k{\sigma }_l;\hfill \end{array}$$

(107)

We shall set $s=0$, as this is the leading contribution to the partition function. The expectation value of $U_{n,m}$ in our continuum limit becomes

$$\begin{array}{ccc}& & 〈U_{n,m}〉=N{\int }_{{\xi }_1}^{{\xi }_2}d\xi 〈exp\iota \alpha \left(\xi \right)〉=N{\int }_{{\xi }_1}^{{\xi }_2}d\xi exp-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.G(\xi ,\xi )\hfill \end{array}$$

(108)

Here $G({\xi }_1,{\xi }_2)$ is the Green’s function corresponding to a 1D particle on a line interval $\xi \in (0,1)$, introduced in the previous section. It satisfies the equation, which follows from our Gaussian Action

$$\begin{array}{ccc}& & {\partial }_{\xi }^{2}G(\xi ,{\xi }^{\prime })=-{\beta }^{2}N\delta (\xi -{\xi }^{\prime });\hfill \end{array}$$

(109)

$$\begin{array}{ccc}& & G(0,{\xi }^{\prime })=G(\xi ,0)=0;\hfill \end{array}$$

(110)

The solution is

$$\begin{array}{c}\hfill G(\xi ,{\xi }^{\prime })=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }^{2}N\left(\xi +{\xi }^{\prime }-|\xi -{\xi }^{\prime }|\right)\end{array}$$

(111)

Thus, we find

$$\begin{array}{ccc}& & 〈U_{n,m}〉=N{\int }_{{\xi }_1}^{{\xi }_2}d\xi exp-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }^{2}N\xi =\frac{2}{{\beta }^2}\left(exp-y/2-exp-x/2\right);\hfill \end{array}$$

(112)

$$\begin{array}{ccc}& & x={\beta }^{2}N{\xi }_1;\hfill \end{array}$$

(113)

$$\begin{array}{ccc}& & y={\beta }^{2}N{\xi }_2;\hfill \end{array}$$

(114)

in agreement with [1,29] in the critical region $N\to \infty ,{\beta }^2\sim 1/N$. Finally, the expectation value

$$\begin{array}{c}\hfill 〈U_{n,m}{\overline{U}}_{n,m}〉=\sum _{l=n}^{m-1}\sum _{k=n}^{m-1}〈exp\iota {\alpha }_{kn}-\iota {\alpha }_{ln}〉\end{array}$$

(115)

Here, the Gaussian path integration yields

$$\begin{array}{ccc}\hfill & & 〈U_{n,m}{\overline{U}}_{n,m}〉\to N^2{\int }_{{\xi }_1}^{{\xi }_2}d\xi {\int }_{{\xi }_1}^{{\xi }_2}d{\xi }^{\prime }exp-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left(G(\xi ,\xi )+G({\xi }^{\prime },{\xi }^{\prime })-2G(\xi ,{\xi }^{\prime })\right)=\hfill \\ & & N^2{\int }_{{\xi }_1}^{{\xi }_2}d\xi {\int }_{{\xi }_1}^{{\xi }_2}d{\xi }^{\prime }exp\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\beta }^{2}N|\xi -{\xi }^{\prime }|=\frac{4}{{\beta }^4}\left(2exp(y-x)/2+x-y-2\right)\hfill \end{array}$$

(116)

This result also agrees with combinatorial computations in [1,29].

5.3. Small Euler Ensemble in Statistical Limit

The remaining problem is averaging over the variables $N,p,q,r$ of the small Euler ensemble.

The variable $s=\frac{qr}{N}$ is distributed between $-1,1$ with the binomial weight [1,29] $\left({\displaystyle \genfrac{}{}{0pt}{}{N}{N(1+s)/2}}\right)$ peaked at $s=0$. There is a finite term coming from $r=0$ plus a continuum spectrum coming from large r

$$\begin{array}{c}\hfill W\left(r\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}r=0;\hfill \\ \frac{\sqrt{2\pi N}}{q}exp-\frac{{\left(qr\right)}^2}{2N}\hfill & \mathrm{otherwise};\hfill \end{array}\right.\end{array}$$

(117)

As it was conjectured in [1] and supported by rigorous estimates in [29], the $r=0$ term dominates the sums, after which the variables $y,x$ can be treated as continuous variables.

The variable p at fixed q has a discrete distribution

$$\begin{array}{c}\hfill f_p(p\mid q)=\frac{{\displaystyle \sum _{\begin{array}{c}p=1\\ (p,q)\end{array}}^{q-1}\delta (p-n)}}{\phi \left(q\right)}\end{array}$$

(118)

As we shall see, rather than p, we would need an asymptotic distribution of a scaling variable

$$\begin{array}{c}\hfill X(p,q)=\frac{1}{q^2}{cot}^2\left(\frac{\pi p}{q}\right)\end{array}$$

(119)

This distribution for $X(p,q)$ at fixed $q\to \infty$ can be found analytically, using newly established relations for the cotangent sums (see Appendix in [1], and Mathematica^® notebook [30]). Asymptotically, at large q, these relations read

$$\begin{array}{c}\hfill 〈X^n〉\equiv \underset{q\to \infty }{lim}\frac{{\displaystyle \sum _{\begin{array}{c}p=1\\ (p,q)\end{array}}^{q-1}X{(p,q)}^n}}{q}={\delta }_{n,0}+\frac{2{\pi }^{-2n}\zeta \left(2n\right)}{(2n+1)\zeta (2n+1)}\end{array}$$

(120)

This relation can be transformed further as

$$\begin{array}{c}\hfill 〈X^n〉=\left\{\begin{array}{cc}1\hfill & \mathrm{if}n=0\hfill \\ \frac{{\displaystyle 2\sum _{k=1}^{\infty }\phi \left(k\right)k^{-(2n+1)}}}{(2n+1){\pi }^{2n}}\hfill & \mathrm{if}n>0\hfill \end{array}\right.\end{array}$$

(121)

The Mellin transform of these moments leads to the following singular distribution

$$\begin{array}{ccc}\hfill & & 〈X^n〉={\int }_0^{\infty }{f}_X\left(X\right)dX{X}^n;\hfill \end{array}$$

(122)

$$\begin{array}{ccc}\hfill & & f_X\left(X\right)=(1-\alpha )\delta \left(X\right)+\pi X\sqrt{X}\mathsf{\Phi }\left(\lfloor \frac{1}{\pi \sqrt{X}}\rfloor \right);\hfill \\ & & \alpha =\pi {\int }_0^{\infty }X\sqrt{X}dX\mathsf{\Phi }\left(\lfloor \frac{1}{\pi \sqrt{X}}\rfloor \right)=\hfill \end{array}$$

(123)

$$\begin{array}{ccc}& & \frac{2\pi }{5}\sum _1^{\infty }\mathsf{\Phi }\left(k\right)\left(\frac{1}{{\left(\pi k\right)}^5}-\frac{1}{{\left(\pi (k+1)\right)}^5}\right)=\frac{2}{5{\pi }^4}\sum _1^{\infty }\frac{\phi \left(k\right)}{k^5}=\frac{1}{225\zeta \left(5\right)}\hfill \end{array}$$

(124)

where $\mathsf{\Phi }\left(n\right)$ is the totient summatory function

$$\begin{array}{c}\hfill \mathsf{\Phi }\left(q\right)=\sum _{n=1}^q\phi \left(n\right)\end{array}$$

(125)

The distribution can also be rewritten as an infinite sum

$$\begin{array}{c}\hfill \int dx{f}_X\left(x\right)F\left(x\right)=(1-\alpha )F\left(0\right)+\pi \sum _{n=1}^{\infty }\phi \left(n\right)\underset{0}{\overset{\frac{1}{{\pi }^2{n}^2}}{\int }}{x}^{\frac{3}{2}}dxF\left(x\right)\end{array}$$

(126)

The normalization of this distribution comes out 1 as it should, with factor $1-\alpha$ in front of the delta function.

The upper limit of X

$$\begin{array}{c}\hfill X_{max}=X\left(q-1,q\right)\to \frac{1}{{\pi }^2}\end{array}$$

(127)

Our distribution (122) is consistent with this upper limit, as the argument $\lfloor \frac{1}{\pi \sqrt{X}}\rfloor$ becomes zero at $X{\pi }^2>1$. It is plotted in Figure 7.

Once we are zooming into the tails of the $p,q$ distribution, we also must recall that

$$\begin{array}{ccc}& & \mathbb{P}(q<yN)=\frac{\mathsf{\Phi }\left(\lfloor Ny\rfloor \right)}{\mathsf{\Phi }\left(N\right)}\to y^2;\hfill \end{array}$$

(128)

$$\begin{array}{ccc}\hfill & & f_y\left(y\right)=\frac{{\displaystyle \sum _{q=2}^N\delta \left(y-\frac{q}{N}\right)\phi \left(q\right)}}{\mathsf{\Phi }\left(N\right)}\hfill \end{array}$$

(129)

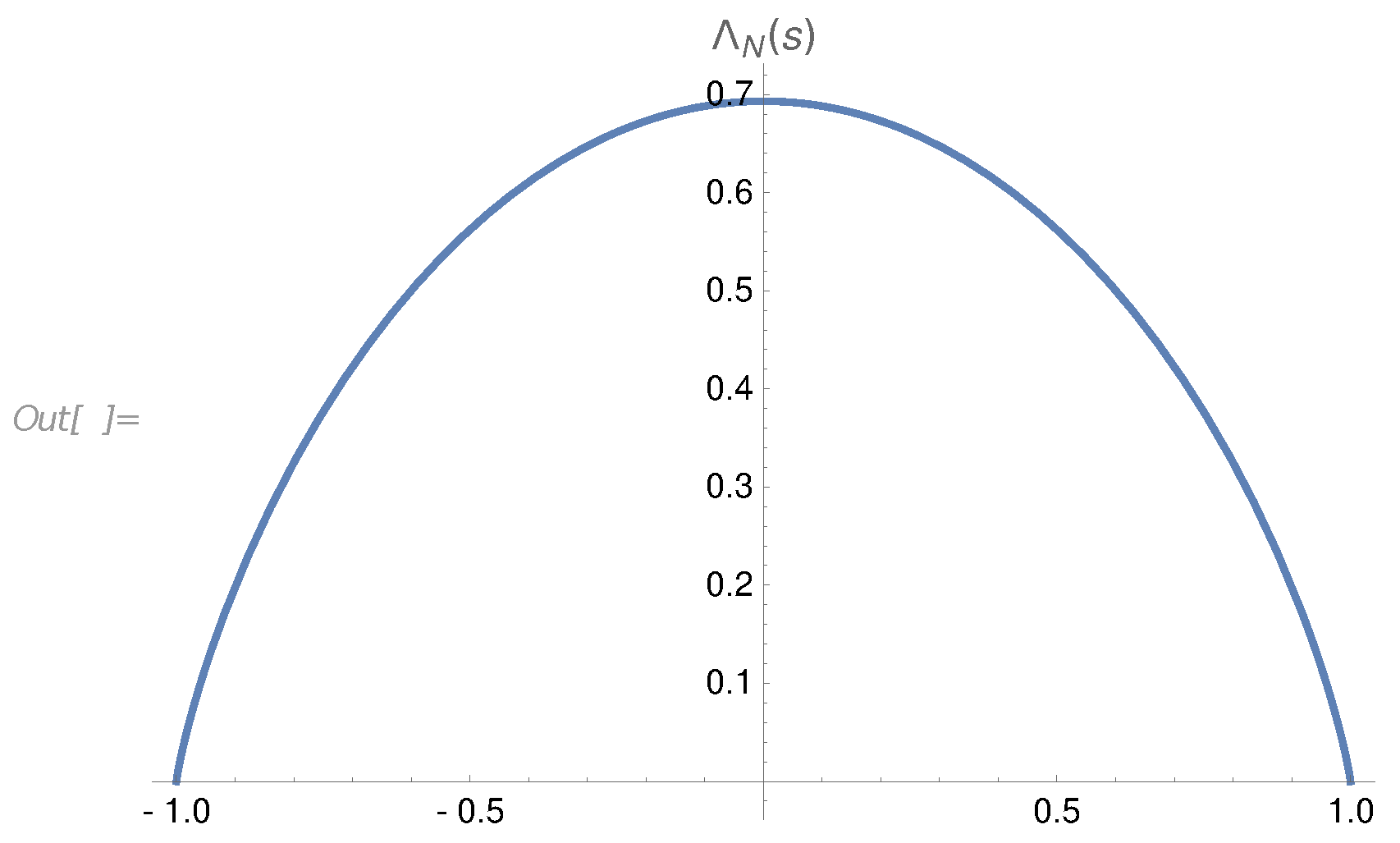
5.4. Complex Classical Trajectory in the Path Integral

This classical equation for our path integral reads:

$$\begin{array}{ccc}\hfill & & {\alpha }^{″}=-\iota \kappa \left({\mathcal{C}}_{\mathsf{\Omega }}^{\prime }exp\iota \alpha +{\left({\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\right)}^{★}exp-\iota \alpha \right);\hfill \end{array}$$

(130)

$$\begin{array}{ccc}& & \kappa =\frac{1}{2\pi y\sqrt{X}\sqrt{2\nu (t+t_0)}}\hfill \end{array}$$

(131)

The parameter $\kappa$ is distributed according to the above distributions for $y,X$ in a small Euler ensemble in the statistical limit.

This complex equation leads to a complex classical solution (instanton). It simplifies for $z=exp\iota \alpha$:

$$\begin{array}{ccc}& & z^{″}=\frac{{\left(z^{\prime }\right)}^2}{z}+\kappa \left({\mathcal{C}}_{\mathsf{\Omega }}^{\prime }{z}^2+{\left({\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\right)}^{★}\right);\hfill \end{array}$$

(132)

$$\begin{array}{ccc}& & z\left(0\right)=z\left(1\right)=1\hfill \end{array}$$

(133)

This equation cannot be analytically solved for arbitrary periodic function $C_{\mathsf{\Omega }}^{\prime }\left(\xi \right)$.

The weak and strong coupling expansions by $\kappa$ are straightforward.

At small $\kappa$

$$\begin{array}{ccc}& & z\left(\xi \right)\to 1+2\kappa \left(-A\xi +{\int }_0^{\xi }\Re {\mathcal{C}}_{\mathsf{\Omega }}\left({\xi }^{\prime }\right)d{\xi }^{\prime }\right)+O\left({\kappa }^2\right);\hfill \end{array}$$

(134)

$$\begin{array}{ccc}& & A={\int }_0^1\Re {\mathcal{C}}_{\mathsf{\Omega }}\left({\xi }^{\prime }\right)d{\xi }^{\prime }\hfill \end{array}$$

(135)

At large $\kappa$

$$\begin{array}{ccc}& & z\left(\xi \right)\to \iota exp-\iota arg{\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\left(\xi \right)=\iota \frac{\left|{\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\left(\xi \right)\right|}{{\mathcal{C}}_{\mathsf{\Omega }}^{\prime }\left(\xi \right)}\hfill \end{array}$$

(136)

This solution is valid at intermediate $\xi$, not too close to the boundaries $\xi =(0,1)$. In the region near the boundaries $\xi (1-\xi )\ll \frac{1}{\sqrt{\kappa }}$, the following asymptotic agrees with the classical equation

$$\begin{array}{ccc}& & z\to 1\pm \iota \xi \sqrt{2\kappa \Re C_{\mathsf{\Omega }}^{\prime }\left(0\right)}+O\left({\xi }^2\right);\hfill \end{array}$$

(137)

$$\begin{array}{ccc}& & z\to 1\pm \iota (1-\xi )\sqrt{2\kappa \Re C_{\mathsf{\Omega }}^{\prime }\left(1\right)}+O\left({(1-\xi )}^2\right);\hfill \end{array}$$

(138)

One can expand in small or large values of $\kappa$ and use the above distributions for $X,y$ term by term.

As it was noticed in the previous paper [1], the viscosity $\nu =\frac{\tilde{\nu }}{N^2}\to 0$ in our theory. This limit makes $\kappa \sim N\to \infty$, justifying the strong coupling limit for the Wilson loop solution. In the next section we are considering an important calculable case of the vorticity correlation function, where the full solution in quadratures is available.

6. Dual Theory of Vorticity Correlation

The simplest observable quantity we can extract from the loop functional is the vorticity correlation function [12], corresponding to the loop C backtracking between two points in space ${\overrightarrow{r}}_1=0,{\overrightarrow{r}}_2=\overrightarrow{r}$, (see [1] for details and the justification).

The vorticity operators are inserted at these two points. Let us outline an analytical solution. We shift the time variable by $t+t_0\Rightarrow t$ to simplify the formulas.

The correlation function reduces to the following average over the big Euler ensemble $\mathbb{E}$ of our random curves in complex space [1]

$$\begin{array}{ccc}\hfill & & 〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{r}\right)〉={\int }_{O\left(3\right)}\frac{d\mathsf{\Omega }}{4t^2\left|O\left(3\right)\right|}\sum _{0\le n<m<N}{〈{\overrightarrow{\omega }}_m·{\overrightarrow{\omega }}_n{e}^{\iota \overrightarrow{\rho }·\widehat{\mathsf{\Omega }}·\left({\overrightarrow{S}}_{n,m}-{\overrightarrow{S}}_{m,n}\right)}〉}_{\mathbb{E}};\hfill \end{array}$$

(139)

$$\begin{array}{ccc}& & {\overrightarrow{S}}_{n,m}=\frac{{\sum }_{k=n}^{m-1}{\overrightarrow{F}}_k}{m-n(modN)};\hfill \end{array}$$

(140)

$$\begin{array}{ccc}& & {\overrightarrow{\omega }}_k=\left\{0,0,\frac{\iota {\sigma }_k}{2}cot\left(\frac{\beta }{2}\right)\right\};\hfill \end{array}$$

(141)

$$\begin{array}{ccc}& & \overrightarrow{\rho }=\frac{\overrightarrow{r}}{2\sqrt{\nu t}};\hfill \end{array}$$

(142)

$$\begin{array}{ccc}& & {〈X[\sigma ...]〉}_{p,q,r}\equiv \frac{{\sum }_{\mathbb{E}}X[\sigma ...]\delta [qr-\sum \sigma ]}{{\sum }_{\mathbb{E}}\delta [qr-\sum \sigma ]};\hfill \end{array}$$

(143)

Integrating the global rotation matrix $O\left(3\right)$ is part of the ensemble averaging.

6.1. Correlation Function and Path Integral

Let us apply our path integral to the expectation value over spins $\sigma =\pm 1$ in the big Euler ensemble, with the distribution of $q,X$ established in the previous section. In the continuum limit, we replace summation with integration. We arrive at the following expression for the correlation function:

$$\begin{array}{ccc}& & 〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{r}\right)〉\propto \frac{{\displaystyle \sum _{\mathrm{even}q<N}\sum _{p;\left(p\right|q)}\frac{{cot}^2(\pi p/q)}{{(p/q)}^2}\underset{0<{\xi }_1<{\xi }_2<1}{\int }d{\xi }_{1}d{\xi }_2{\int }_{O\left(3\right)}d\mathsf{\Omega }\int \left[D\alpha \right]{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)e^{\iota \frac{\overrightarrow{r}·\widehat{\mathsf{\Omega }}·\Im \overrightarrow{V}({\xi }_1,{\xi }_2)}{\sqrt{\nu t}}}}}{t^2\mathsf{\Phi }\left(N\right)\left|O\left(3\right)\right|\int \left[D\alpha \right]};\hfill \end{array}$$

(144)

$$\begin{array}{ccc}& & \overrightarrow{V}({\xi }_1,{\xi }_2)=q\sqrt{X}\left\{\iota ,1,0\right\}\left(S({\xi }_1,{\xi }_2)-S({\xi }_2,1+{\xi }_1)\right);\hfill \end{array}$$

(145)

$$\begin{array}{ccc}& & S(a,b)=\frac{{\int }_a^{b}d\xi e^{\iota \alpha \left(\xi \right)}}{b-a};\hfill \end{array}$$

(146)

Here and in the following, we skip all positive constant factors, including powers of N. Ultimately, we restore the correct normalization of the vorticity correlation using its value at $\overrightarrow{r}=0$ computed in previous work [1].

The computations significantly simplify in Fourier space.

$$\begin{array}{ccc}\hfill & & 〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{k}\right)〉=\int d^3\overrightarrow{r}〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{r}\right)〉exp-\iota \overrightarrow{k}·\overrightarrow{r}\propto \hfill \\ & & \frac{{\displaystyle \sum _{\mathrm{even}q<N}\sum _{p;\left(p\right|q)}\frac{{cot}^2(\pi p/q)}{{(p/q)}^2}\underset{0<{\xi }_1<{\xi }_2<1}{\int }d{\xi }_{1}d{\xi }_2{\int }_{O\left(3\right)}d\mathsf{\Omega }\int \left[D\alpha \right]{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)\delta \left(\frac{\overrightarrow{r}·\widehat{\mathsf{\Omega }}·\Im \overrightarrow{V}({\xi }_1,{\xi }_2)}{\sqrt{\nu t}}-\overrightarrow{k}\right)}}{t^2\mathsf{\Phi }\left(N\right)\left|O\left(3\right)\right|\int \left[D\alpha \right]};\hfill \end{array}$$

(147)

The angular integration $\int d\mathsf{\Omega }$ yields

$$\begin{array}{ccc}& & {\int }_{O\left(3\right)}d\mathsf{\Omega }\delta \left(\frac{\widehat{\mathsf{\Omega }}·\Im \overrightarrow{V}({\xi }_1,{\xi }_2)}{\sqrt{\nu t}}-\overrightarrow{k}\right)\propto \frac{\sqrt{\nu t}}{{\overrightarrow{k}}^2}\delta \left(\left|\Im \overrightarrow{V}({\xi }_1,{\xi }_2)\right|-\left|\overrightarrow{k}\right|\sqrt{\nu t}\right)\hfill \end{array}$$

(148)

Now, using the Lagrange multiplier $\lambda$ for this condition, and shifting integration over $\lambda$ to the real axis, we have to minimize effective action

$$\begin{array}{ccc}& & A[\alpha ,\lambda ]=\frac{\pi y^{2}X}{2}{\int }_{{\xi }_1}^{1+{\xi }_1}{\left({\alpha }^{\prime }\right)}^2+\lambda y\sqrt{X}\left|\frac{{\displaystyle {\int }_{{\xi }_1}^{{\xi }_2}d\xi e^{\iota \alpha }}}{{\xi }_2-{\xi }_1}-\frac{{\displaystyle {\int }_{{\xi }_2}^{1+{\xi }_1}d\xi e^{\iota \alpha }}}{1+{\xi }_1-{\xi }_2}\right|;\hfill \end{array}$$

(149)

$$\begin{array}{ccc}\hfill & & {\partial }_{\lambda }A[\alpha ,\lambda ]=\left|\overrightarrow{k}\right|\sqrt{\nu t};\hfill \end{array}$$

(150)

This variational problem reduces to two pendulum equations

$$\begin{array}{ccc}& & {\alpha }_1^{″}+\frac{r}{{\xi }_2-{\xi }_1}sin{\alpha }_1=0;\forall {\xi }_1<\xi <{\xi }_2\hfill \end{array}$$

(151)

$$\begin{array}{ccc}& & {\alpha }_2^{″}+\frac{r}{{\xi }_2-{\xi }_1-1}sin{\alpha }_2=0;\forall {\xi }_2<\xi <1+{\xi }_1\hfill \end{array}$$

(152)

$$\begin{array}{ccc}\hfill & & r=\frac{\lambda }{\pi y\sqrt{X}I\left(r\right)};\hfill \end{array}$$

(153)

$$\begin{array}{ccc}& & I\left(r\right)=\left|\frac{{\displaystyle {\int }_{{\xi }_1}^{{\xi }_2}d\xi e^{\iota {\alpha }_1}}}{{\xi }_2-{\xi }_1}-\frac{{\displaystyle {\int }_{{\xi }_2}^{1+{\xi }_1}d\xi e^{\iota {\alpha }_2}}}{1+{\xi }_1-{\xi }_2}\right|;\hfill \end{array}$$

(154)

The well-known solution is Jacobi amplitude $\mathrm{am}(x\mid u)$,

$$\begin{array}{ccc}& & {\alpha }_1\left(\xi \right)=2\mathrm{am}\left(\frac{\xi -{\alpha }_2}{2}{a}_1\mid \frac{r}{a_1^2({\xi }_2-{\xi }_1)}\right);\hfill \end{array}$$

(155a)

$$\begin{array}{ccc}& & {\alpha }_2\left(\xi \right)=2\mathrm{am}\left(\frac{\xi -{\alpha }_2}{2}{a}_2\mid -\frac{r}{a_2^2(1-{\xi }_2+{\xi }_1)}\right);\hfill \end{array}$$

(155b)

The free parameters $a_1,a_2,{\alpha }_1,{\alpha }_2$ satisfy four equations

$$\begin{array}{ccc}& & {\alpha }_1\left({\xi }_2\right)={\alpha }_2\left({\xi }_2\right);\hfill \end{array}$$

(156a)

$$\begin{array}{ccc}& & {\alpha }_1^{\prime }\left({\xi }_2\right)={\alpha }_2^{\prime }\left({\xi }_2\right);\hfill \end{array}$$

(156b)

$$\begin{array}{ccc}& & {\alpha }_1\left({\xi }_1\right)={\alpha }_2(1+{\xi }_1);\hfill \end{array}$$

(156c)

$$\begin{array}{ccc}& & {\alpha }_1^{\prime }\left({\xi }_1\right)={\alpha }_2^{\prime }(1+{\xi }_1);\hfill \end{array}$$

(156d)

together with the constraint following from the variation of the Lagrange multiplier $\lambda$:

$$\begin{array}{ccc}& & I\left(r\right)=\frac{|\overrightarrow{k}|\sqrt{\nu t}}{y\sqrt{X}}\hfill \end{array}$$

(157)

6.2. Turbulent Viscosity and the Local Limit

These five equations, in general, are quite complex, but there is one simplifying property. In the local limit $N\to \infty$, the remaining effective action at the extremum

$$\begin{array}{ccc}& & NA[{\alpha }_c,{\lambda }_c]=\frac{\pi N{y}^{2}X}{2}\left({\int }_{{\xi }_1}^{{\xi }_2}d\xi {\left({\alpha }_1^{\prime }\left(\xi \right)\right)}^2+{\int }_{{\xi }_2}^{1+{\xi }_1}d\xi {\left({\alpha }_2^{\prime }\left(\xi \right)\right)}^2\right)\hfill \end{array}$$

(158)

grows as N, unless both ${\alpha }_1\left(\xi \right)\sim {\alpha }_2\left(\xi \right)\sim N^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\to 0$. In this case, the above constraint can be expanded in ${\alpha }_1,{\alpha }_2$. As we show in [31], the leading constant and linear terms both cancel so that the quadratic term remains

$$\begin{array}{ccc}\hfill & & \frac{2|\overrightarrow{k}|\sqrt{\nu t}}{y\sqrt{X}}=\left|{\int }_{{\xi }_1}^{{\xi }_2}\frac{d\xi {\alpha }_1^2\left(\xi \right)}{{\xi }_2-{\xi }_1}-{\int }_{{\xi }_2}^{1+{\xi }_1}\frac{d\xi {\alpha }_2^2\left(\xi \right)}{1+{\xi }_1-{\xi }_2}\right|\sim \frac{1}{N}\hfill \end{array}$$

(159)

This estimate then requires vanishing viscosity in the local limit, at fixed turbulent viscosity

$$\begin{array}{c}\hfill \tilde{\nu }=\nu N^2\to \mathit{const}.\end{array}$$

(160)

This phenomenon of renormalization of viscosity by a factor of $N^2$ was already observed in our first paper [1]. Our Euler ensemble in the local limit $N\to \infty$ can only solve the inviscid limit of the Navier-Stokes decaying turbulence, with finite $\tilde{\nu }$ acting as a turbulent viscosity.

The desired anomalous dissipation phenomenon takes place in this limit of our theory.

Returning to the elliptic function solution, we rewrite it in the linearized case at $a_1\sim a_2\to 0$. This linearization is equivalent to replacing $sin\left(\alpha \right)\to \alpha$ in the differential equation and studying the resulting linear ODE as a boundary problem. We choose different parametrizations in this linear case

$$\begin{array}{ccc}& & {\alpha }_1\left(\xi \right)=a\left(cos\left(K_1(\xi -{\xi }_2)\right)+\frac{b}{K_1}sin\left(K_1(\xi -{\xi }_2)\right)\right);\hfill \end{array}$$

(161)

$$\begin{array}{ccc}& & {\alpha }_2\left(\xi \right)=a\left(cos\left(K_2(\xi -{\xi }_2)\right)+\frac{b}{K_2}sin\left(K_2(\xi -{\xi }_2)\right)\right);\hfill \end{array}$$

(162)

$$\begin{array}{ccc}& & K_1=\sqrt{\frac{r}{\Delta }};\hfill \end{array}$$

(163)

$$\begin{array}{ccc}& & K_2=\sqrt{\frac{r}{\Delta -1}};\hfill \end{array}$$

(164)

$$\begin{array}{ccc}& & \Delta ={\xi }_2-{\xi }_1;\hfill \end{array}$$

(165)

In the physical region $0<\Delta <1,r<0$, $K_2$ is real, and $K_1$ imaginary, but the solution stays real. The matching conditions at ${\alpha }_1\left({\xi }_2\right)={\alpha }_2\left({\xi }_2\right),{\alpha }_1^{\prime }\left({\xi }_2\right)={\alpha }_2^{\prime }\left({\xi }_2\right)$ are identically satisfied with this Anzatz. The derivative match ${\alpha }_1^{\prime }\left({\xi }_1\right)={\alpha }_2^{\prime }(1+{\xi }_1)$ can be solved exactly for b

$$\begin{array}{c}\hfill b=\frac{\sqrt{\frac{r}{\Delta -1}}sin\left((1-\Delta )\sqrt{\frac{r}{\Delta -1}}\right)+\sqrt{\frac{r}{\Delta }}sin\left(\Delta \sqrt{\frac{r}{\Delta }}\right)}{cos\left((\Delta -1)\sqrt{\frac{r}{\Delta -1}}\right)-cos\left(\Delta \sqrt{\frac{r}{\Delta }}\right)}\end{array}$$

(166)

The remaining matching condition ${\alpha }_1\left({\xi }_1\right)={\alpha }_2(1+{\xi }_1)$ reduces to the root of the function

$$\begin{array}{ccc}& & g(r,\Delta )=\frac{(2\Delta -1)sin\left(\sqrt{(\Delta -1)r}\right)sin\left(\sqrt{\Delta r}\right)}{\sqrt{(\Delta -1)\Delta }}+2cos\left(\sqrt{(\Delta -1)r}\right)cos\left(\sqrt{\Delta r}\right)-2\hfill \end{array}$$

(167)

This function has multiple roots, but we are looking for the real root $r_0(\Delta )$ with minimal value of the action at given $\Delta$

$$\begin{array}{c}\hfill A_c(r,\Delta )={\int }_{{\xi }_1}^{{\xi }_2}d\xi {\alpha }_1^{\prime }{\left(\xi \right)}^2+{\int }_{{\xi }_2}^{1+{\xi }_1}d\xi {\alpha }_2^{\prime }{\left(\xi \right)}^2\end{array}$$

(168)

This integral is elementary, but the expression is too long to be presented here. It can be found in the Mathematica^® notebook[31], where it is used to select the roots $r_0(\Delta )$ of $g(r,\Delta )$, minimizing $A_c\left(r_0(\Delta ),\Delta \right)$ for a given value of $\Delta \in (0,1)$.

This lowest action root is plotted in Figure 8. The corresponding value of minimal action $L(\Delta )=A_c\left(r_0(\Delta ),\Delta \right)$ is plotted in Figure 12.

There are phase transitions at

$$\begin{array}{ccc}& & \Delta =\left\{{\Delta }_1,{\Delta }_2,{\Delta }_3\right\};\hfill \end{array}$$

(169)

$$\begin{array}{ccc}& & {\Delta }_1=0.157143;\hfill \end{array}$$

(170)

$$\begin{array}{ccc}& & {\Delta }_2=0.43015;\hfill \end{array}$$

(171)

$$\begin{array}{ccc}& & {\Delta }_3=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.;\hfill \end{array}$$

(172)

These branch points in $\Delta$ correspond to the switch of the lowest action solution. At small positive $\Delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$

$$\begin{array}{ccc}& & r_0(\Delta )\to -48(\Delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)-\frac{1536{(\Delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}^3}{7}+\dots ;\hfill \end{array}$$

(173)

$$\begin{array}{ccc}& & A_0(r_0(\Delta ),\Delta )\to 256{(\Delta -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}^2+\dots \hfill \end{array}$$

(174)

At $\Delta \to 1$ all solutions go to $-\infty$ as

$$\begin{array}{c}\hfill r_n(\Delta )\to -\frac{6}{1-\Delta }+O\left(1\right)\end{array}$$

(175)

This behavior matches numerical computations in Mathematica^® [31].

The constraint (159) is also reduced to elementary functions, too lengthy to quote here (see [31]).

This constraint yields the quadratic relation for the last unknown parameter a in our solution

$$\begin{array}{ccc}& & a^2=\frac{|\overrightarrow{k}|\sqrt{\nu t}}{S(\Delta )y\sqrt{X}};\hfill \end{array}$$

(176)

with universal function $S(\Delta )$ presented in [31] and shown in Figure 9).

The resulting integral (up to the pre-exponential factor Q) is equal to

$$\begin{array}{ccc}& & \int \left[D\alpha \right]{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)\delta \left(\left|\Im \overrightarrow{V}({\xi }_1,{\xi }_2)\right|-\left|\overrightarrow{k}\right|\sqrt{\nu t}\right)\propto \hfill \\ & & Q〈{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)〉exp-y\sqrt{X}\left|\overrightarrow{k}\right|\sqrt{\tilde{\nu }t}\frac{\pi L(\Delta )}{2\left|S\right(\Delta \left)\right|}\hfill \end{array}$$

(177)

The factor $〈{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)〉$ contains two terms :

$$\begin{array}{c}\hfill 〈{\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)〉={\alpha }_1^{\prime }\left({\xi }_1\right){\alpha }_1^{\prime }\left({\xi }_2\right)+〈\delta {\alpha }^{\prime }\left({\xi }_1\right)\delta {\alpha }^{\prime }\left({\xi }_2\right)〉\end{array}$$

(178)

The first term is the contribution of the classical solution we have just found, and the second term comes from Gaussian fluctuations $\delta \alpha \left(\xi \right)$ around this solution.

The classical term is calculable (see [31])

$$\begin{array}{ccc}& & {\alpha }_1^{\prime }\left({\xi }_1\right){\alpha }_1^{\prime }\left({\xi }_2\right)=\frac{|\overrightarrow{k}|\sqrt{\tilde{\nu }t}}{Ny\sqrt{X}}\frac{J\left(\Delta \right)}{\left|S\right(\Delta \left)\right|};\hfill \end{array}$$

(179)

$$\begin{array}{ccc}& & J\left(\Delta \right)={\left.\frac{rA(r,\Delta )B(r,\Delta )}{\Delta (\Delta -1)C{(r,\Delta )}^2}\right|}_{r=r_0(\Delta )};\hfill \end{array}$$

(180)

$$\begin{array}{ccc}& & A(r,\Delta )=\Delta sin\left(\sqrt{(\Delta -1)r}\right)-\sqrt{(\Delta -1)\Delta }sin\left(\sqrt{\Delta r}\right);\hfill \\ & & B(r,\Delta )=\Delta sin\left(\sqrt{(\Delta -1)r}\right)cos\left(\sqrt{\Delta r}\right)-\hfill \end{array}$$

(181)

$$\begin{array}{ccc}& & \sqrt{(\Delta -1)\Delta }sin\left(\sqrt{\Delta r}\right)cos\left(\sqrt{(\Delta -1)r}\right);\hfill \end{array}$$

(182)

$$\begin{array}{ccc}& & C(r,\Delta )=cos\left(\sqrt{(\Delta -1)r}\right)-cos\left(\sqrt{\Delta r}\right);\hfill \end{array}$$

(183)

(see Figure 11).

The fluctuation term $〈\delta {\alpha }^{\prime }\left({\xi }_1\right)\delta {\alpha }^{\prime }\left({\xi }_2\right)〉$ is also proportional to $1/N$, therefore we must keep this term as well.

As for the pre-exponential factor Q in the saddle point integral, it is given by the functional determinant of the operator $\widehat{L}$ corresponding to linearized effective action (168) in the vicinity of the saddle point ${\lambda }_c,{\alpha }_c\left(\xi \right)$.

$$\begin{array}{ccc}& & A[{\alpha }_c+\delta \alpha ,{\lambda }_c+\delta \lambda ]\to A[{\alpha }_c,{\lambda }_c]+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{tr}\left(V^{†}\mid \widehat{L}\mid V\right);\hfill \end{array}$$

(184)

$$\begin{array}{ccc}& & V=\left\{\delta \lambda ,\delta \alpha \right\};\hfill \end{array}$$

(185)

$$\begin{array}{ccc}& & Q(\Delta ,\tau )=exp{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\mathrm{tr}\left(\frac{log\widehat{L}}{{\widehat{L}}^{\alpha }}\right)}_{\alpha \to 0};\hfill \end{array}$$

(186)

$$\begin{array}{ccc}& & \tau =y\sqrt{X};\hfill \end{array}$$

(187)

The fluctuation correction reduces to the inverse operator $\widehat{L}$, which we compute in the next section.

Now, we can reduce multiple sum/integral in (147) to the following

$$\begin{array}{ccc}\hfill & & 〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{k}\right)〉=\frac{{\tilde{\nu }}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}H\left(k\sqrt{\tilde{\nu }t}\right)}{\sqrt{t}};\hfill \end{array}$$

(188)

$$\begin{array}{ccc}& & H\left(\kappa \right)=\frac{1}{\mathcal{Z}}\sum _{n=1}^{\infty }\phi \left(n\right){\int }_0^{1/n}d\tau \left({\tau }^5/n^5-{\tau }^{10}\right){\int }_0^{1}d\Delta (1-\Delta )G\left(\Delta ,\tau ,\kappa \right);\hfill \end{array}$$

(189)

$$\begin{array}{ccc}& & G\left(\Delta ,\tau ,\kappa \right)=Q\left(\Delta ,\tau \right)\left(\frac{\kappa }{N\tau }\frac{J\left(\Delta \right)}{\left|S\right(\Delta \left)\right|}+〈\delta {\alpha }^{\prime }\left({\xi }_1\right)\delta {\alpha }^{\prime }\left({\xi }_2\right)〉\right)exp-\frac{\tau \kappa L(\Delta )}{2\pi \left|S\right(\Delta \left)\right|}\hfill \end{array}$$

(190)

where $\mathcal{Z}$ is the normalization constant to be determined later.

6.3. Functional Determinant in the Path Integral

As we have discussed in the previous section, in the limit $a\to 0$ the classical solution ${\alpha }_{1,2}\left(\xi \right)\propto a\to 0$.

This observation simplifies the linearized theory corresponding to this quadratic form $〈V\mid \widehat{L}\mid V〉$. First, integrate the fluctuations $\delta \lambda$ of $\lambda$ around the saddle point solution.

The Lagrange multiplier at the saddle point vanishes, as we show in [31]

$$\begin{array}{c}\hfill {\lambda }_0=\tau r_0(\Delta )I\left(r_0(\Delta )\right)=0\end{array}$$

(191)

The quadratic term comes from the first derivatives $I_{\lambda }={\partial }_{\lambda }I,I_r={\partial }_{r}I,{\lambda }_r={\partial }_r\lambda$ , which can be simplified by switching to $\lambda \left(r\right)=\tau tI\left(r\right)$

$$\begin{array}{c}\hfill A_{\lambda \lambda }=\tau I_{\lambda }=\frac{\tau I_r}{{\lambda }_r}=\frac{\tau I_r}{\tau r{I}_r}=\frac{1}{r}\end{array}$$

(192)

The bilinear term $\lambda \delta \alpha$ also simplifies

$$\begin{array}{ccc}& & A_{\alpha \lambda }\left(\delta \alpha \right)=\iota \tau \delta \lambda F\left[\delta \alpha \right];\hfill \end{array}$$

(193)

$$\begin{array}{ccc}& & F\left[\delta \alpha \right]={\int }_{{\xi }_1}^{{\xi }_2}\frac{d\xi \delta \alpha \left(\xi \right)}{{\xi }_2-{\xi }_1}-{\int }_{{\xi }_2}^{1+{\xi }_1}\frac{d\xi \delta \alpha \left(\xi \right)}{1+{\xi }_1-{\xi }_2}\hfill \end{array}$$

(194)

We can integrate out $\lambda$, producing the extra pre-exponential factor $Q_{\lambda }=\sqrt{|r_0(\Delta )|}/\sqrt{N}$.

The bilinear term in the exponential after $\lambda$ integration leads to the following effective quadratic Action for $\delta \alpha$

$$\begin{array}{ccc}\hfill & & A_{eff}\left[\delta \alpha \right]=\frac{{\tau }^2}{2}{\int }_{{\xi }_1}^{1+{\xi }_1}\delta {\alpha }^{\prime 2}+\frac{r_0(\Delta ){\tau }^2}{2}F{\left[\delta \alpha \right]}^2;\hfill \end{array}$$

(195)

There is a zero-mode $\delta \alpha \left(\xi \right)=\mathit{const}$, related to translational invariance of $A_{eff}\left[\delta \alpha \right]$. Naturally, this zero-mode must be eliminated from the spectrum when we compute the functional determinant and the resolvent below.

After discarding the zero-mode, this effective action becomes a positive definite functional of $\delta \alpha$ only in the region of $\Delta$ where $r_0(\Delta )>0$, i.e., for ${\Delta }_1<\Delta <{\Delta }_2$.

As we shall see below, the spectrum of fluctuations is positive only in this region. Therefore, we restrict our integration to this region.

The ${\left(\delta \alpha \right)}^2$ term corresponds to the linear eigenvalue equation with $f_{1,2}=\delta {\alpha }_{1,2}$

$$\begin{array}{ccc}& & f_{1,2}^{″}\left(\xi \right)-{\mu }_{1,2}F\left[f\right]=-\omega f_{1,2}\left(\xi \right);\hfill \end{array}$$

(196)

$$\begin{array}{ccc}& & {\mu }_{1,2}=\left\{\frac{r}{\Delta },\frac{r}{\Delta -1}\right\};\hfill \end{array}$$

(197)

$$\begin{array}{ccc}& & ϵ=\omega {\tau }^2;\hfill \end{array}$$

(198)

$$\begin{array}{ccc}& & r=r_0(\Delta );\hfill \end{array}$$

(199)

The solution matching with first derivative at $\xi ={\xi }_2,\xi =({\xi }_1,1+{\xi }_1)$ is built the same way as in (166). Equations for $f_{1,2}$ being linear homogeneous, we can fix the normalization as $F\left[f\right]=1$,

$$\begin{array}{ccc}& & f_1\left(x\right)=asin\left(\sqrt{\omega }\left({\xi }_{-}{\xi }_2\right)\right)+B_{1}cos\left(\sqrt{\omega }\left({\xi }_{-}{\xi }_2\right)\right)+\frac{r}{\omega \Delta };\hfill \end{array}$$

(200)

$$\begin{array}{ccc}& & f_2\left(\xi \right)=asin\left(\sqrt{\omega }\left({\xi }_{-}{\xi }_2\right)\right)+B_{2}cos\left(\sqrt{\omega }\left({\xi }_{-}{\xi }_2\right)\right)+\frac{r}{\omega (\Delta -1)};\hfill \end{array}$$

(201)

The spectrum $\omega ={\omega }_n$ is defined by the transcendental equation (the discriminant of this linear system of equations), which we found in [31]

$$\begin{array}{ccc}\hfill & & f({\omega }_n,\Delta )=0;\hfill \\ & & f(\omega ,\Delta )=(\Delta -1)\Delta \sqrt{\omega }sin\left(\frac{\sqrt{\omega }}{2}\right)((\Delta -1)\Delta \omega +r)+\hfill \end{array}$$

(202)

$$\begin{array}{ccc}& & rcos\left(\frac{1}{2}(1-2\Delta )\sqrt{\omega }\right)-rcos\left(\frac{\sqrt{\omega }}{2}\right);\hfill \end{array}$$

(203)

$$\begin{array}{ccc}& & r=r_0(\Delta );\hfill \end{array}$$

(204)

The spectrum is positive in the interval ${\Delta }_1<\Delta <{\Delta }_2$ where $r_0(\Delta )>0$ so that the solution for ${\omega }_n(\Delta )$ is stable. In the following, we only select the stable region with positive $r_0(\Delta )$

Figure 13. The first levels of the spectrum satisfying equation $f(\omega ,\Delta )=0$. The colored lines correspond to four phases. Red: $0<\Delta <{\Delta }_1$, Green: ${\Delta }_1<\Delta <{\Delta }_2$, Blue: ${\Delta }_2<\Delta <\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, Brown: $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.<\Delta <1$. The green zone is left as stable, and others are eliminated because $r_0(\Delta )<0$ in these zones. Naturally, we eliminate the zero-mode ${ϵ}_0=0$ corresponding to translational invariance of the effective Action.

Figure 13. The first levels of the spectrum satisfying equation $f(\omega ,\Delta )=0$. The colored lines correspond to four phases. Red: $0<\Delta <{\Delta }_1$, Green: ${\Delta }_1<\Delta <{\Delta }_2$, Blue: ${\Delta }_2<\Delta <\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, Brown: $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.<\Delta <1$. The green zone is left as stable, and others are eliminated because $r_0(\Delta )<0$ in these zones. Naturally, we eliminate the zero-mode ${ϵ}_0=0$ corresponding to translational invariance of the effective Action.

The functional determinant, resulting from the WKB approximation to the $\alpha$ path integral, would be related to the infinite product of positive eigenvalues ${ϵ}_n={\tau }^2{\omega }_n$, which can be written using a contour integral

$$\begin{array}{ccc}\hfill & & Q_{\alpha }\left(\Delta ,\tau \right)=\prod _{{\omega }_n>0}{\left({\tau }^2{\omega }_n\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}={\left.exp\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\partial }_{\alpha }\Im {\oint }_{\mathsf{\Gamma }}\frac{f^{\prime }\left(\omega \right)}{f\left(\omega \right)}\frac{d\omega }{2\pi {\left(\omega {\tau }^2\right)}^{\alpha }}\right|}_{\alpha \to 0};\hfill \end{array}$$

(205)

and the integration contour $\mathsf{\Gamma }$ encircles anticlockwise the positive real poles of the meromorphic function $f^{\prime }\left(\omega \right)/f\left(\omega \right)$. The integral converges at $\alpha >\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and should be analytically continued to $\alpha =0$.

For this purpose, let us introduce another function

$$\begin{array}{c}\hfill \mathsf{\Phi }\left(\omega \right)=\frac{f\left(\omega \right)}{cos(\sqrt{\omega }/2)}{\omega }^{-3/2}\end{array}$$

(206)

We show in [31] that at large $\omega =\iota y$ this function reaches finite limits

$$\begin{array}{ccc}& & \mathsf{\Phi }\left(\iota y\right)\to \iota signy{(\Delta -1)}^2{\Delta }^2+\frac{(\Delta -1)\Delta r}{\left|y\right|}\hfill \end{array}$$

(207)

The logarithmic derivative of the original function differs from $\frac{{\mathsf{\Phi }}^{\prime }\left(\omega \right)}{\mathsf{\Phi }\left(\omega \right)}$ by the following meromorphic function

$$\begin{array}{ccc}& & \frac{f^{\prime }\left(\omega \right)}{f\left(\omega \right)}-\frac{{\mathsf{\Phi }}^{\prime }\left(\omega \right)}{\mathsf{\Phi }\left(\omega \right)}=-\frac{tan\left(\frac{\sqrt{\omega }}{2}\right)}{4\sqrt{\omega }}+\frac{3}{2\omega }\hfill \end{array}$$

(208)

This difference produces a calculable contribution to our integral. By summing residues of the poles of the tangent, we get

$$\begin{array}{ccc}& & {\oint }_{\mathsf{\Gamma }}\left(-\frac{tan\left(\frac{\sqrt{\omega }}{2}\right)}{4\sqrt{\omega }}+\frac{3}{2\omega }\right)\frac{d\omega }{2\pi {\left(\omega {\tau }^2\right)}^{\alpha }}=\iota \left(1-2^{2\alpha }\right){\left(2\pi \tau \right)}^{-2\alpha }\zeta \left(2\alpha \right)\hfill \end{array}$$

(209)

The derivative at $\alpha =0$ yields a constant

$$\begin{array}{c}\hfill \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\partial }_{\alpha }\Im \iota \left(1-2^{2\alpha }\right){\left(2\pi \tau \right)}^{-2\alpha }\zeta \left(2\alpha \right)\to \frac{log\left(2\right)}{2}\end{array}$$

(210)

leading to an irrelevant renormalization of $Q(\alpha ,\tau )$ by a factor $\sqrt{2}$.

The remaining integral with $f\left(\omega \right)\Rightarrow \mathsf{\Phi }\left(\omega \right)$ already converges at $\Re \alpha >-1$, so that we can set $\alpha =0$ and rotate the integration contour $\mathsf{\Gamma }$ parallel to the imaginary axis at $\Re \mathsf{\Gamma }=ϵ>0$:

$$\begin{array}{ccc}\hfill & & Q_{\alpha }\left(\Delta ,\tau \right)=\hfill \\ & & exp\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\Im {\int }_{ϵ-\iota \infty }^{ϵ+\iota \infty }\frac{{\mathsf{\Phi }}^{\prime }\left(\omega \right)}{\mathsf{\Phi }\left(\omega \right)}\frac{log\left(\omega {\tau }^2\right)d\omega }{2\pi }\hfill \end{array}$$

(211)

The remarkable property of this functional determinant is the factorization of the $\tau$ dependence

$$\begin{array}{ccc}& & Q_{\alpha }(\Delta ,\tau )={\tau }^{\mu (\Delta )}{Q}_{\alpha }(\Delta ,1);\hfill \end{array}$$

(212)

$$\begin{array}{ccc}\hfill & & \mu (\Delta )=\Im {\int }_{ϵ-\iota \infty }^{ϵ+\iota \infty }\frac{{\mathsf{\Phi }}^{\prime }\left(\omega \right)}{\mathsf{\Phi }\left(\omega \right)}\frac{d\omega }{2\pi }\hfill \end{array}$$

(213)

The index $\mu (\Delta )$ has a topological origin and can be computed analytically.

$$\begin{array}{c}\hfill \mu (\Delta )=\frac{arg\mathsf{\Phi }(\iota \infty )-arg\mathsf{\Phi }(-\iota \infty )}{2\pi }=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\end{array}$$

(214)

Our result for the correlation function is given by (188) with

$$\begin{array}{c}\hfill Q\left(\Delta ,\tau \right)=Q_{\alpha }\left(\Delta ,1\right){\tau }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{r_0(\Delta )}\end{array}$$

(215)

and $Q_{\alpha }(\Delta ,1)$ given by (211). All the constant factors we have omitted here are absorbed by the normalization factor $\mathcal{Z}$, which we determine at the end of the next section.

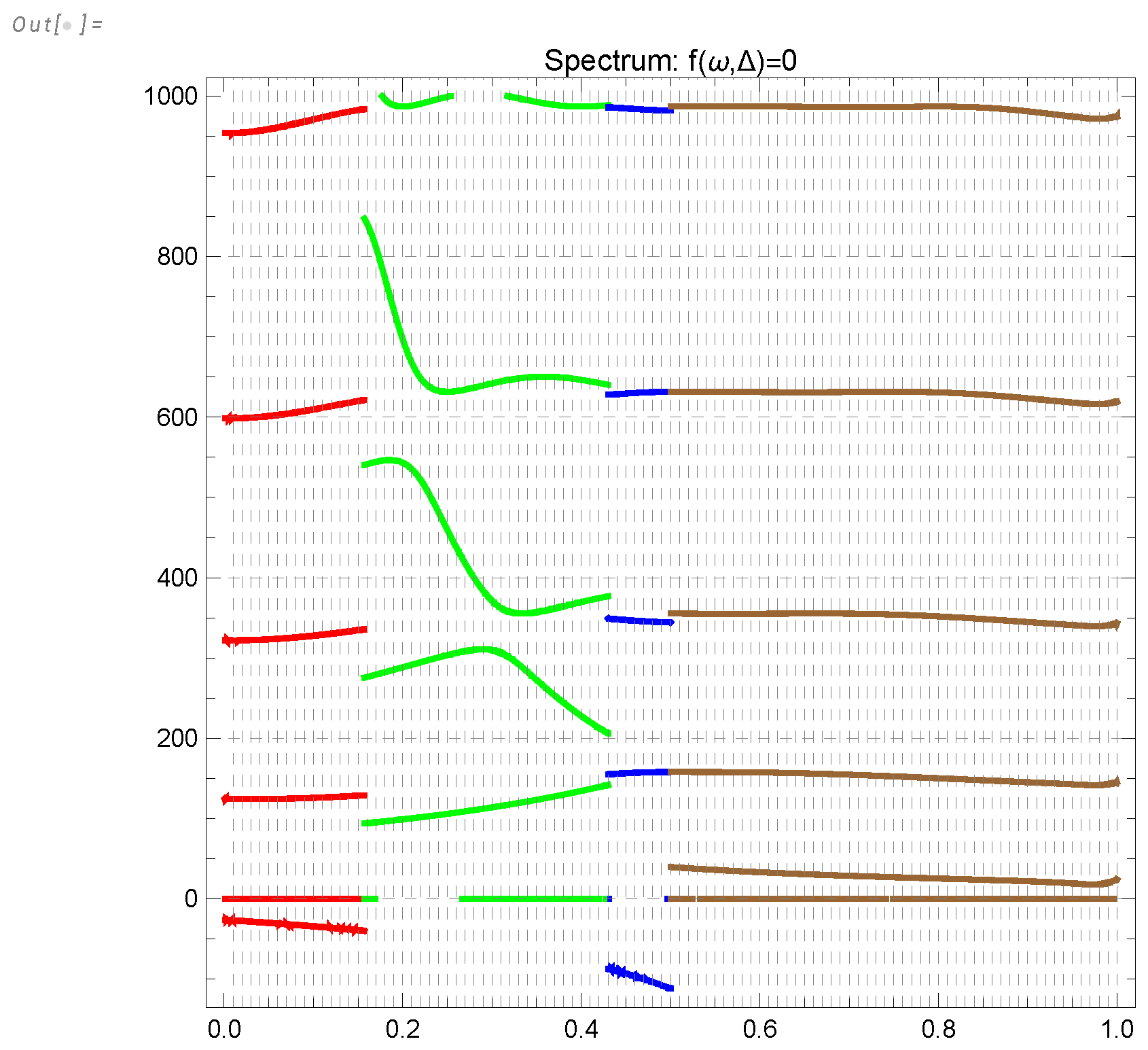
6.4. The Fluctuation Term in ${\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)$

The last missing term is the fluctuation contribution to ${\alpha }^{\prime }\left({\xi }_1\right){\alpha }^{\prime }\left({\xi }_2\right)$. In the Gaussian approximation, valid at $N\to \infty$, this term equals

$$\begin{array}{c}\hfill 〈\delta {\alpha }^{\prime }\left({\xi }_1\right)\delta {\alpha }^{\prime }\left({\xi }_2\right)〉=\frac{-1}{N{\tau }^2}{\left[{\partial }_{\xi }{\partial }_{{\xi }^{\prime }}G(\xi ,{\xi }^{\prime })\right]}_{\xi ={\xi }_1,{\xi }^{\prime }={\xi }_2}\end{array}$$

(216)

where $G(\xi ,{\xi }^{\prime })$ is a resolvent for the effective quadratic Action (195). This resolvent satisfies the equation

$$\begin{array}{ccc}& & {\partial }_{\xi }^{2}G(\xi ,{\xi }^{\prime })-\mu \left(\xi \right)F\left[G\right]=\delta (\xi -{\xi }^{\prime });\hfill \end{array}$$

(217)

$$\begin{array}{ccc}& & G({\xi }_1,{\xi }^{\prime })=G({\xi }_1+1,{\xi }^{\prime })=0;\hfill \end{array}$$

(218)

$$\begin{array}{ccc}& & F\left[G\right]={\int }_{{\xi }_1}^{{\xi }_2}\frac{d\xi G(\xi ,{\xi }^{\prime })}{{\xi }_2-{\xi }_1}-{\int }_{{\xi }_2}^{1+{\xi }_1}\frac{d\xi G(\xi ,{\xi }^{\prime })}{1+{\xi }_1-{\xi }_2};\hfill \end{array}$$

(219)

$$\begin{array}{ccc}& & \mu \left(\xi \right)=\left\{\begin{array}{cc}\frac{r}{\Delta }\hfill & \mathrm{if}{\xi }_1\le \xi <{\xi }_2\hfill \\ \frac{r}{\Delta -1}\hfill & \mathrm{if}{\xi }_2\le \xi <1+{\xi }_1\hfill \end{array}\right.\hfill \end{array}$$

(220)

The solution of this equation, matching with the first derivative at $\xi ={\xi }_2$ is

$$\begin{array}{c}\hfill G(\xi ,{\xi }^{\prime })=\left\{\begin{array}{cc}A+\frac{|\xi -{\xi }^{\prime }|}{2}+B(\xi -{\xi }_2)+\frac{F\left[G\right]r{(\xi -{\xi }_2)}^2}{2\Delta }\hfill & \mathrm{if}{\xi }_1\le \xi <{\xi }_2\hfill \\ A+\frac{|\xi -{\xi }^{\prime }|}{2}+B(\xi -{\xi }_2)+\frac{F\left[G\right]r{(\xi -{\xi }_2)}^2}{2(\Delta -1)}\hfill & \mathrm{if}{\xi }_2\le \xi <1+{\xi }_1\hfill \end{array}\right.\end{array}$$

(221)

The linear functional $F\left[G\right]$ on this solution becomes a linear function of these unknown parameters $A,B$. Two boundary conditions $G({\xi }_1,{\xi }^{\prime })=G({\xi }_1+1,{\xi }^{\prime })=0$ fix these parameters as functions of ${\xi }_1,{\xi }_2,{\xi }^{\prime }$.

The result derived in [31] is too lengthy to present here. The desired quantity (216) is quite simple

$$\begin{array}{c}\hfill \frac{1}{N{\tau }^2}{\left[{\partial }_{\xi }{\partial }_{{\xi }^{\prime }}G(\xi ,{\xi }^{\prime })\right]}_{\xi ={\xi }_1,{\xi }^{\prime }={\xi }_2}=\frac{2(r-6)}{(r+12)N{\tau }^2}\end{array}$$

(222)

Finally, we get the following correlation (188) (absorbing the constant factors in $\mathcal{Z}$)

$$\begin{array}{ccc}& & 〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{k}\right)〉=\frac{{\tilde{\nu }}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}H\left(k\sqrt{\tilde{\nu }t}\right)}{\sqrt{t}};\hfill \end{array}$$

(223a)

$$\begin{array}{ccc}& & {\displaystyle H\left(\kappa \right)={\int }_{{\Delta }_1}^{{\Delta }_2}d\Delta (1-\Delta )\sum _{n=1}^{\infty }\phi \left(n\right){\int }_0^{1/n}\frac{d\tau }{{\tau }^{\frac{5}{2}}}\left({\tau }^5/n^5-{\tau }^{10}\right)G\left(\Delta ,\tau \kappa \right);}\hfill \end{array}$$

(223b)

$$\begin{array}{ccc}& & G\left(\Delta ,x\right)=\frac{Q_{\alpha }\left(\Delta ,1\right)\sqrt{r_0(\Delta )}}{\mathcal{Z}}\left(x\frac{J\left(\Delta \right)}{S(\Delta )}+\frac{2(r_0(\Delta )-6)}{(12+r_0(\Delta ))}\right)exp-\frac{xL(\Delta )}{2\pi S(\Delta )}\hfill \end{array}$$

(223c)

7. The Decaying Energy in Finite System

The vorticity correlation in Fourier space doubles as an energy spectrum

$$\begin{array}{c}\hfill E(k,t)=4\pi {\overrightarrow{k}}^2〈\overrightarrow{v}·{\overrightarrow{v}}_k〉=4\pi 〈\overrightarrow{\omega }·{\overrightarrow{\omega }}_k〉\end{array}$$

(224)

The energy spectrum in a finite system with size L is bounded from below. At low $|\overrightarrow{k}| \le \pi /L$, the spectrum is no longer related to the turbulence but is given by the energy pumping by external forces at the boundaries.

This energy pumping [5] takes place at $t<t_0$, after which the pumping stops. At this moment, the energy spectrum is growing with wavevector by one of two possible laws (with P being the net momentum of the fluid and M being the rotation moment)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& E(k,t_0)\propto P{k}^2\hfill \\ & E(k,t_0)\propto M{k}^4\hfill \end{array}\right.\end{array}$$

(225)

At $t>t_0$, without the forcing, the pumped energy dissipates at large k corresponding to smaller spatial scales of the hierarchy of vortex structures of all scales, ending with dissipative scales, or wavevectors $k\gg \pi /L$. After sufficient time, the universal regime kicks in, corresponding to the decaying turbulence. It is implied that a large amount of energy was pumped in, so it takes a long time to reach this decaying regime, corresponding to some fixed trajectory.

Our solution does not impose any restrictions on the net momentum an thus applies to the most general, first regime with $k^2$ spectrum at small k and some universal decay at large k, reflecting these distributed vortex structures. This issue requires more investigation.

The decaying energy, given by the part of the spectrum $k>k_0\sim 1/L$, has the following form

$$\begin{array}{ccc}\hfill & & E\left(t\right)={\int }_{k_0}^{\infty }dkE(k,t)=\frac{4\pi \tilde{\nu }}{t}{\int }_{k_0\sqrt{\tilde{\nu }t}}^{\infty }H\left(\kappa \right)d\kappa \hfill \end{array}$$

(226)

On top of the trivial decrease $\frac{\tilde{\nu }}{t}$, as prescribed by dimensional counting in an infinite system, there is some extra decrease related to the increase of the lower limit.

The energy in our theory does not have a finite statistical limit as the integral in (226) diverges at the lower limit when $k_0\to 0$. Thus, we compute the energy as

$$\begin{array}{c}\hfill E\left(t\right)={\int }_t^{\infty }\mathcal{E}\left(t^{\prime }\right)d{t}^{\prime }\end{array}$$

(227)

This energy dissipation rate $\mathcal{E}\left(t^{\prime }\right)$ is calculable

$$\begin{array}{c}\hfill \mathcal{E}\left(t\right)=4\pi \nu \int dk{k}^2〈\overrightarrow{\omega }\left(\overrightarrow{0}\right)·\overrightarrow{\omega }\left(\overrightarrow{k}\right)〉=4\pi \frac{\tilde{\nu }}{t^2}{\int }_{k_0\sqrt{\tilde{\nu }t}}^{\infty }{\kappa }^{2}H\left(\kappa \right)d\kappa \end{array}$$

(228)

In our theory, this integral has a finite limit in an infinite system ($k_0=0$).

This limit was computed in [1] in a slightly different grand canonical ensemble, where N was fluctuating with the weight $exp-\mu N,\mu \to 0$.

With our current ensemble of fixed even $N\to \infty$ the results of [1] read:

$$\begin{array}{ccc}\hfill & & {\mathcal{E}}_{\infty }\left(t\right)=\frac{\tilde{\nu }}{t^2}\frac{{\pi }^2}{864\zeta \left(3\right)};\hfill \end{array}$$

(229)

In our present theory, the same quantity is given by the above integral at $k_0=0$

$$\begin{array}{c}\hfill {\mathcal{E}}_{\infty }\left(t\right)=4\pi \frac{\tilde{\nu }}{t^2}{\int }_0^{\infty }{\kappa }^{2}H\left(\kappa \right)d\kappa \end{array}$$

(230)

Comparing these two expressions, we get the normalization of $H\left(\kappa \right)$

$$\begin{array}{c}\hfill 4\pi {\int }_0^{\infty }{\kappa }^{2}H\left(\kappa \right)d\kappa =\frac{{\pi }^2}{864\zeta \left(3\right)}\end{array}$$

(231)

The integral on the left can be further reduced [31] to the following normalization condition:

$$\begin{array}{ccc}& & \mathcal{Z}=\frac{276480\zeta \left(3\right)\zeta \left(\frac{15}{2}\right)}{119\zeta \left(\frac{17}{2}\right)}{\int }_{{\Delta }_1}^{{\Delta }_2}d\Delta \frac{(1-\Delta )\sqrt{r_0(\Delta )}S(\Delta )Q_{\alpha }(\Delta ,1)\left(\pi J(\Delta )\left(r_0(\Delta )+12\right)+L(\Delta )\left(r_0(\Delta )-6\right)\right)}{L{(\Delta )}^2\left(r_0(\Delta )+12\right)}\hfill \end{array}$$

(232)

This normalization constant $\mathcal{Z}$ can be used in equation (226) for the energy decay in a finite system. All the functions of $\Delta$ were defined above.

As for the energy spectrum, this is not an independent function in our theory. Comparing the two expressions (224) and (228), we arrive at the following relation

$$\begin{array}{ccc}\hfill & & t^2\mathcal{E}\left(t\right)=4\pi \tilde{\nu }F\left(k_0\sqrt{\tilde{\nu }t}\right);\hfill \end{array}$$

(233a)

$$\begin{array}{ccc}& & F\left(\kappa \right)=\underset{\kappa }{\overset{\infty }{\int }}H\left(x\right)x^{2}dx,\hfill \end{array}$$

(233b)

$$\begin{array}{ccc}\hfill & & \sqrt{t}E(k,t)=4\pi \tilde{\nu }\sqrt{\tilde{\nu }}H\left(k\sqrt{\tilde{\nu }t}\right);\hfill \end{array}$$

(233c)

Both the energy dissipation and the energy spectrum are related to the same function $H\left(\kappa \right)$, but the energy spectrum related to this function at large argument $\kappa =k\sqrt{\tilde{\nu }t}$, whereas the energy dissipation is related to integral of this function from small argument $\kappa =k_0\sqrt{\tilde{\nu }t}$ to infinity.

We computed this function in the Appendix A and numerically integrated it to obtain $F\left(\kappa \right),\kappa =k\sqrt{\tilde{\nu }t}$. Asymptotically, at large t

$$\begin{array}{ccc}& & E(k,t)\propto \frac{\tilde{\nu }\sqrt{\tilde{\nu }}}{\sqrt{t}}{\left(k\sqrt{\tilde{\nu }t}\right)}^{-\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.};\hfill \end{array}$$

(234)

$$\begin{array}{ccc}& & \mathcal{E}\left(t\right)\propto t^{-\raisebox{1ex}{$9$}\!\left/ \!\raisebox{-1ex}{$4$}\right.};\hfill \end{array}$$

(235)

$$\begin{array}{ccc}& & E\left(t\right)={\int }_t^{\infty }\mathcal{E}\left(t^{\prime }\right)d{t}^{\prime }\propto t^{-\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}\hfill \end{array}$$

(236)

We computed the effective decay indexes

$$\begin{array}{ccc}& & n\left(t\right)=-t{\partial }_{t}logE=-\frac{t\mathcal{E}\left(t\right)}{E\left(t\right)};\hfill \end{array}$$

(237)

$$\begin{array}{ccc}& & s\left(\kappa \right)=-\kappa {\partial }_{\kappa }logH\left(\kappa \right)\hfill \end{array}$$

(238)

numerically in the Appendix A, using Mathematica^®. The accuracy is just 4-5 digits, but it can be easily improved by taking more CPU time once experimental data gets more precise. These curves are universal, and they change the regime before approaching their limits from below $n(\infty )=\frac{5}{4},s(\infty )=\frac{7}{2}$. These regime changes are due to the quantum effects (complex zeros of the zeta function contributing to the energy spectrum’s Mellin transform, as shown in Appendix A).

The experimental data [2] yields $n(\infty )\approx 1.25\pm 0.02$ which agrees with our theoretical prediction in Figure 14. Our universal curves for $n\left(t\right),s\left(\kappa \right)$ were computed directly from the analytic solution of the loop equation in the turbulent limit without any fitting parameters. It will be very interesting to compare these curves with more precise experiments (real or numerical).

8. The Spectrum of Decay Indexes in the Energy Spectrum

In addition to numerically computing the energy spectrum and plotting effective decay indexes, we can go one step further in the mathematical analysis of the concept of the scaling laws in turbulence.

The notion of power decay can be formulated in precise mathematical terms by studying the Mellin transform.

Namely, the spectrum of decay indexes is given by the positions of poles of the Mellin transform in the negative semiplane. We change the sign of p in conventional definition to better describe our functions.

In our case, there is a universal function $H\left(\kappa \right)$ in (223). The Mellin transform is the following transformation ( assuming our function decreases at infinity)

$$\begin{array}{ccc}& & H\left(\kappa \right)={\int }_{-ϵ-\iota \infty }^{-ϵ+\iota \infty }\frac{dp}{2\pi \iota }h\left(p\right){\kappa }^p;\hfill \end{array}$$

(239)

$$\begin{array}{ccc}& & h\left(p\right)={\int }_0^{\infty }\frac{d\kappa }{\kappa }{\kappa }^{-p}H\left(\kappa \right)\hfill \end{array}$$

(240)

The pure power law of decay would correspond to the Mellin transform $h\left(p\right)$ having a single pole in the left semi-plane. The position $p=-a$ of this pole becomes an index of the power law.

$$\begin{array}{ccc}& & H\left(\kappa \right)\propto {\kappa }^{-a}\hfill \end{array}$$

(241)

The next level of complexity would be a function, depending on an extra parameter n, such that the Mellin transform has a simple pole, moving with this parameter $p=-a\left(n\right)$. This will produce multifractal scaling laws

$$\begin{array}{c}\hfill {\kappa }^{-a\left(n\right)}\end{array}$$

(242)

Our energy spectrum has a more complex singularity structure in its Mellin transform

$$\begin{array}{ccc}\hfill & & h\left(p\right)=\frac{f\left(p\right)\zeta \left(p+\frac{15}{2}\right)\mathsf{\Gamma }(-p)}{(2p+7)(2p+17)\zeta \left(p+\frac{17}{2}\right)};\hfill \end{array}$$

(243)

$$\begin{array}{ccc}& & f\left(p\right)=20{\int }_{{\Delta }_1}^{{\Delta }_2}d\Delta (1-\Delta )C^{p-1}(AC-Bp)\hfill \end{array}$$

(244)

where $A,B,C$ are some smooth positive functions of $\Delta$ varying in finite limits (see Appendix A). Given these properties, it is simple to prove that the Taylor series of $f\left(p\right)$ at the origin converges as the expansion coefficients decrease as a factorial of the expansion order.

This makes this function an entire function without any finite singularities. The values of $C(\Delta )$ are bounded by two positive limits

$$\begin{array}{c}\hfill 0.0541984<C<0.0630755,\forall {\Delta }_1<\Delta <{\Delta }_2\end{array}$$

(245)

Therefore, the entire function $f\left(p\right)$ decreases as $e^{-2.76342p}$ in the right semiplane and grows as $e^{-2.9151p}$ in the left semiplane. It oscillates along imaginary axis, which is our integration path.

The singularities of the Mellin transform $h\left(p\right)$ are given by the following table of simple poles

(246)

Here $\pm t_n$ are imaginary parts of zeros of the $\zeta$ function on the critical line $z=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\iota t$. About ${10}^{13}$ zeros are already known, though the Riemann hypothesis (that there are no other complex zeros) is still unproven. These poles are shown in Figure 15

The real negative poles yield decaying power terms, but the infinite series of complex poles at Riemann zeros adds the oscillations in log scale

$$\begin{array}{c}\hfill |W_n|{\kappa }^{-8}cos\left(t_{n}log\kappa +arg{W}_n\right)\end{array}$$

(247)

These slow oscillations are visible as regime change in the log-log plots of effective indexes in Figure 14, Figure 5. The energy $E\left(t\right)$ is related to the same function

$$\begin{array}{ccc}& & E\left(t\right)={\int }_t^{\infty }dt\mathcal{E}\left(t\right)=4\pi \tilde{\nu }{\int }_t^{\infty }\frac{dT}{T^2}{\int }_{k_0\sqrt{\tilde{\nu }T}}^{\infty }H\left(x\right)x^{2}dx\hfill \end{array}$$

(248)

Substituting the Mellin transform for $H\left(x\right)$ and integrating twce we get the Mellin transform for the energy

$$\begin{array}{ccc}& & E\left(t\right)={\int }_{-1-ϵ-\iota \infty }^{-1-ϵ+\iota \infty }\frac{dq}{2\pi \iota }e\left(q\right){\left(k_0^2\tilde{\nu }t\right)}^q;\hfill \end{array}$$

(249a)

$$\begin{array}{ccc}& & e\left(q\right)=2\pi k_0^2{\tilde{\nu }}^2\frac{h(2q-1)}{q(q+1)}\hfill \end{array}$$

(249b)

The table of complex poles of this function is

(250)

These poles are shown at Figure 16

9. Discussion

Some parts of the following discussion were already published in my paper [1]. We use them with significant modifications, reflecting our increased understanding of this theory.

9.1. Stochastic Solution of the Navier-Stokes Equation and Quantum Hypothesis

Statistical "analysis of circulating or turbulent fluids" was defined by Feynman [32] as the last unsolved problem of classical physics. We are pursuing this problem by finding a stochastic solution of the Navier-Stokes equation, asymptotically covering a certain manifold at infinite time. Our singularities arise in correlation functions after averaging over this manifold in the statistical limit when the manifold’s dimension goes to infinity. However, the origin of singularities is an infinite time needed to cover this fixed manifold uniformly.

We find this manifold (Euler ensemble) by solving the loop equation (a subset of the Hopf functional equation for generating functional for the velocity field probability). None of the particular solutions in this manifold has a finite-time blow-up. We encounter a singularity of the fixed point of the loop equation rather than its solution for a finite time.

We take the most natural invariant measure from the point of the number theory: each element of the Euler ensemble enters with equal weight. We call it our ergodic hypothesis. This hypothesis is unnecessary to solve the loop (i.e., Hopf) equation, as any linear superposition of the found solutions would satisfy the loop equation. The singularities of our Euler ensemble at $N\to \infty$ remain in local variables such as enstrophy and its PDF, indicating singularities of the Navier-Stokes equation in the inviscid limit.

With this particular invariant measure, the Euler ensemble is singled out by its equivalence to the trace of the evolution operator of a quantum system: the Fermi particles on a ring in the external field related to random fractions of $\pi$. Every distinct state in the discrete quantum system enters a quantum trace with unit weight. In our case, this is equivalent to counting every element in the Euler ensemble with equal weight.

In other words, our ergodic hypothesis is equivalent to the requirement of exact equivalence of the loop functional to the quantum trace of the one-dimensional ring of Fermi particles. This quantum representation opened the way to the analytic solution in the turbulent limit, equivalent to the quasiclassical limit of this Fermi system. The viscosity acts as Planck’s constant, and the inverse Reynolds number acts as a weak coupling constant of the dual theory.

There is an unexpected gift of dimensional reduction. This quantum system is one-dimensional despite its equivalence to the three-dimensional decaying turbulence. Such equivalence would be impossible given the local relation between the dynamical variables of these two systems; however, with our nonlocal relation through the loop average, the duality becomes possible.

A mathematical transformation relates the quantum amplitude to the turbulent probability, but this is not an analytic continuation to imaginary time, like in ordinary quantum statistics. It is a Fourier transformation from the probability distribution of velocity circulation to the loop functional. This functional is dual to the trace of the evolution operator for a one-dimensional quantum system.

9.2. The Physical Meaning of the Loop Equation and Dimensional Reduction

The long-term evolution of Newton’s dynamical system with many particles eventually covers the energy surface (microcanonical ensemble). The ergodic hypothesis (accepted in Physics but still not proven mathematically) states that this energy surface is covered uniformly. The Turbulence theory aims to find a replacement of the microcanonical ensemble for the Navier-Stokes equation. This surface would also take part in the decay in the pure Navier-Stokes equation without artificial forcing. In both cases, Newton and Navier-Stokes, the probability distribution must satisfy the Hopf equation, which follows from the dynamics without specification of the mechanism of the stochastization. Indeed, the Gibbs, as well as the microcanonical distributions in Newton’s dynamics, satisfy the Hopf equation in a rather trivial way: It reduces to the conservation of the probability measure (Liouville theorem), which suggests the energy surface as the only additive integral of motion to use as a fixed point manifold.

In the case of the decaying turbulence, the loop equations represent a closed subset of the Hopf equations, which subset is still sufficient to generate the dynamics of vorticity. In this case, the exact solution we have found for the Hopf functional also follows from the integrals of motion, this time, the conservation laws in the loop space. The loop space Hamiltonian we have derived from the unforced Navier-Stokes equation does not have any potential terms (those with explicit dependence upon the shape of the loop). The Schrödinger equation with only kinetic energy in the Hamiltonian conserves the momentum. The corresponding wave function is the plane wave $exp\iota \overrightarrow{p}·\overrightarrow{x}$. This plane wave is the solution we have found, except the dot product $\overrightarrow{p}·\overrightarrow{x}$ becomes a symplectic form $\oint \overrightarrow{P}\left(\theta \right)·d\overrightarrow{C}\left(\theta \right)$ in the loop space. Our momentum $\overrightarrow{P}(\theta ,t)$ is not an integral of motion, but simple scaling properties of the pure Navier-Stokes equation lead to the solution with $\overrightarrow{P}(\theta ,t)\propto \overrightarrow{F}\left(\theta \right)/\sqrt{t}$, with $\overrightarrow{F}\left(\theta \right)$ being the integral of motion. The rest is a purely technical task: substituting this scaling solution into the Navier-Stokes equation and solving the resulting universal equation for a fixed point $\overrightarrow{F}\left(\theta \right)$.

This equation led us to the Fermi ring in the quasiclassical limit. This limit resulted in the energy spectrum and dissipation in a finite system found in the last Section 7.

9.3. Classical Flow and Quantum Mechanics

Our computations heavily rely on the number theory, particularly Jordan’s multitotients ${\phi }_l\left(q\right)$, generalizing [33] the Euler totient function. What could the number theory have in common with the turbulent flow? The quantization of parameters of the fixed manifold of decaying turbulence stems from the deep quantum correspondence we have discovered. The statistical distribution of a nonlinear classical Navier-Stokes PDE is exactly related to the wave functional of a linear Schrödinger equation in the loop space.

This relation is indirect: the loop functional, a Fourier transform of the classical probability distribution for circulation, equals the complex quantum amplitude of the loop space theory, as represented by a Fermion ring. Probability is real and positive, but its Fourier transform is complex, so there is no contradiction between classical and quantum mechanics.

The quantization mechanism is the same as in ordinary quantum mechanics; this requires the solution’s periodicity.

An expert in the traditional approach to turbulence may wonder why the loop equation’s solutions are related to the velocity field’s statistics in a decaying turbulent flow. How could this fractal curve in complex momentum space $\overrightarrow{P}\left(\theta \right)\in {\mathbb{C}}_3$ describe velocity field in a physical space $\overrightarrow{v}\left(\overrightarrow{r}\right)\in {\mathbb{R}}_3$? Is this a miracle or a mirage?

The equivalence of a strong coupling phase of the fluctuating vector field to quantum geometry is a well-known duality phenomenon in gauge theory (the ADS/CFT duality), ringing a bell to the modern theoretical physicist. In our case, this is a simpler quantum geometry: a fractal curve in complex space.

Miracles are known to happen in nonlinear PDE: some lucky nonlinear equations are related to linear problems in higher dimensions [34]. In our case, the Navier-Stokes equation is related to the linear problem in infinite-dimensional loop space. The miracle already happened when Hopf derived his linear functional equation. The loop equation is a reduced version of the Hopf equation, luckily solvable by a plane wave in loop space due to translational invariance.

The loop technology was thoroughly discussed in the last few decades in the gauge theories, including QCD[13,15,16,35] where the loop equations were derived first [36,37]. The short answer is that duality only applies to the correlation functions of two theories with different dynamical variables; there is no correspondence between these variables, but the correlation functions are identical.

Mathematical physics sometimes has alternative languages for the same phenomena; examples are the duality between Schrödinger wave equation and Heisenberg’s matrix mechanics, between dynamical triangulation and Liouville theory in 2D quantum gravity.

Extra complications in the gauge theory are the short-distance singularities related to the infinite number of fluctuating degrees of freedom in quantum field theory. The Wilson loop functionals in coordinate space are singular in the gauge field theory and cannot be multiplicatively renormalized.

Perturbatively, there is no short-distance divergence in the Navier-Stokes equations nor the Navier-Stokes loop dynamics. The Euler equations represent the singular limit, which, as we argued, should be resolved using singular topological solitons regularized by the Burgers vortex. In the present theory, we do not encounter any singularities in coordinate space. The anomalous dissipation is achieved in our solution via a completely different mechanism: large fluctuations of the fractal curve at $p\ll q$. However, these singularities only happen in the inviscid limit $\nu \propto 1/N^2\to 0$.

Therefore, these singularities correspond to the Euler singularities, such as line vortexes. Those vortexes are regularized by finite viscosity, just like our singularities.

9.4. Stokes-Type Functionals and Vorticity Correlations

The loop equation describes the gauge invariant sector of the gauge field theory. Therefore, the gauge degrees of freedom are lost in the loop functional. However, the gauge-invariant correlations of the field strength are recoverable from the solutions of the loop equation[36,37].

There is no gauge invariance regarding the velocity field in fluid dynamics (though there is such invariance in the Clebsch variables [12]). The longitudinal, i.e., a potential part of the velocity, has a physical meaning – it is responsible for pressure and energy pumping. This part is lost in the loop functional but is recoverable from the rotational part (the vorticity) using the Biot-Savart integral.

In the Fourier space, the correlation functions of the velocity field are algebraically related to those of vorticity ${\overrightarrow{v}}_k=\frac{\iota \overrightarrow{k}\times {\overrightarrow{\omega }}_k}{{\overrightarrow{k}}^2}$. Thus, the general solution for the Wilson loop functional $\mathsf{\Psi }[\gamma ,C]$ allows computing both vorticity and velocity correlation functions.

We demonstrated that by computing the moments of the enstrophy and resulting anomalous dissipation. This computation is nonperturbative: it corresponds to the extreme turbulent limit and cannot be expanded in inverse powers of viscosity.

9.5. Renormalizability of the Inviscid Limit of the Loop Equation

Let us discuss the relation $\nu N^2=\mathit{const}$ between the vanishing viscosity and growing number of discontinuities on the momentum loop $\overrightarrow{P}\left(\theta \right)$.

The Navier-Stokes equation itself is an idealization of the molecular dynamics: the nonlocal theory is approximated by truncated expansion in powers of gradients.

The laminar flow does not show any problems with this truncated expansion. However, the velocity field in our solution for the loop equation becomes singular in the local limit.

The mathematical statement is that the velocity and vorticity are not the ordinary functions in ${\mathbb{R}}_3$ but rather stochastic variables with $\Delta \overrightarrow{v}\sim {(\Delta \overrightarrow{r})}^{\alpha },\alpha \approx \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$.

The Fractal Calculus [38] was introduced for a general description of such fields. That, however, by itself does not explain turbulence: in particular, the more general power laws with multifractal dimensions $〈{(\Delta \overrightarrow{v})}^n〉\sim {(\Delta \overrightarrow{r})}^{{\zeta }_n}$ cannot be explained this way.

In our theory, there is a universal function for the expectation of Fourier components of vorticity as functions of the wavevector. Still, this relation is not a single power: the Mellin transform of this function has infinitely many poles in the complex plane.

Our solution describes a fractal vorticity field, but this is not a known fractal type. The fractal curve $\overrightarrow{P}\left(\theta \right)$ is not a simple random walk on a circle: dynamic restrictions (such as periodicity) lead to nontrivial critical behavior not describable by any fractal power laws.

Our discretization of the loop equation (replacement of continuum loop by a polygon with a growing number of vertices) defines the turbulent limit of the velocity field distribution.

The relation of the vanishing viscosity with the growing number of degrees of freedom is of the same nature as the RG relation between the bare coupling constant $g_0$ and the lattice spacing a in QCD: $a\propto g_0^{\alpha }exp-\beta /g_0^2$.

The naive local limit $a\to 0,g_0=const$ does not exist in $QCD$, but the RG limit describes the strong interaction of hadrons very well.

In the same way, as in QCD, there is renormalizability in our solution. The dissipation rate stays finite when $\tilde{\nu }=\nu N^2\to const$. Moreover, the whole energy spectrum is expressed in $\tilde{\nu }$ and stays finite in the local limit. So, like in the renormalizable QFT, there is a "dimensional transmutation": infinities can be hidden into the dimensional parameter $\tilde{\nu }$ defining the time scale.

9.6. Relation of Our Solution to the Weak Turbulence

The solution of the loop equation with finite area derivative, satisfying Bianchi constraint, belongs to the so-called Stokes-type functionals [36], the same as the Wilson loop for Gauge theory and fluid dynamics.

The Navier-Stokes Wilson loop is a case of the Abelian loop functional, with commuting components of the vector field $\overrightarrow{v}$. As we discussed in detail in [12,36,37], any Stokes-type functional $\mathsf{\Psi }[\gamma ,C]$ satisfying boundary condition at shrunk loop $\mathsf{\Psi }\left[0\right]=1$, and solving the loop equation can be iterated in the nonlinear term in the Navier-Stokes equations (which iterations would apply at large viscosity).

The resulting expansion in inverse powers of viscosity (weak turbulence) exactly coincides with the ordinary perturbation expansion of the Navier-Stokes equations for the velocity field, averaged over the distribution of initial data or boundary conditions at infinity.

We have demonstrated in [6,12] (and also here, in Section 3.2) how the velocity distribution for the random uniform vorticity in the fluid was reproduced by a singular momentum loop $\overrightarrow{P}\left(\theta \right)$.

The solution for $\overrightarrow{P}\left(\theta \right)$ in this special fixed point of the loop equation was random complex and had slowly decreasing Fourier coefficients, leading to a discontinuity $sign(\theta -{\theta }^{\prime })$ in a pair correlation function (33). The corresponding Wilson loop was equal to the Stokes-type functional (25).

Using this example, we demonstrated how a discontinuous momentum loop describes the vorticity distribution in the stochastic Navier-Stokes flow. In this example, the vorticity is a global random variable corresponding to a random uniform fluid rotation: a well-known exact solution of the Navier-Stokes equation.

This example corresponds to a special fixed point for the loop equation, not general enough to describe the turbulent flow but mathematically ideal as a toy model for the loop technology. It demonstrates how the momentum loop solution sums up all the terms of the $1/\nu$ expansion in the Navier-Stokes equation.

In our general solution, with the Euler ensemble, the summation of a divergent perturbation expansion occurs at an extreme level, leading to a universal fixed point in the limit of vanishing viscosity.

At a given initial condition, after a finite time, the solution will still depend on viscosity and initial condition. There will be no singularities for a smooth initial velocity field.

At the large time, though, it will approach our universal fixed manifold and (supposedly, for random initial data) cover it uniformly, according to the Euler ensemble measure.

So, the $\nu \to 0,N\to \infty$ limit of our solution for the fixed point corresponds to the limit $\nu \to 0,t\to \infty$ of the solution for the time-dependent loop equation.

The vorticity will become a random variable with a singular distribution in the local limit, corresponding to the inviscid limit of the Navier-Stokes equation.

10. Remaining Problems

• We performed all the calculations up to numerical factors in the vorticity correlation function, which we recovered from the previously computed $〈{\overrightarrow{\omega }}^2〉$ (see [1] ). It would be useful to compute all the normalization factors and thus double-check the solution.
• The loop functional for the circular loop is the simplest object in this theory. It can be computed using the methods developed in this paper, with even simpler results. In this case, the classical equation is trivial, so the computations reduce to the functional determinant and the resolvent. On the other hand, this is an observable quantity, and one could measure it in DNS. It would be an interesting problem to solve and compare with the DNS.
• The spectrum of indexes for deviations from our fixed trajectory [1] can be evaluated in the scaling limit, with finite $\tilde{\nu }$. This computation will produce results for the vorticity correlation functions in the Navier-Stokes equation, perturbed by an infinitesimal random force.