Submitted:
11 December 2023
Posted:
12 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Specimen Collection and Processing
2.1. Specimen Acquisition
2.2. Tensile Test Setup
2.2.1. Tensile Specimen Production
2.2.2. Test Procedure
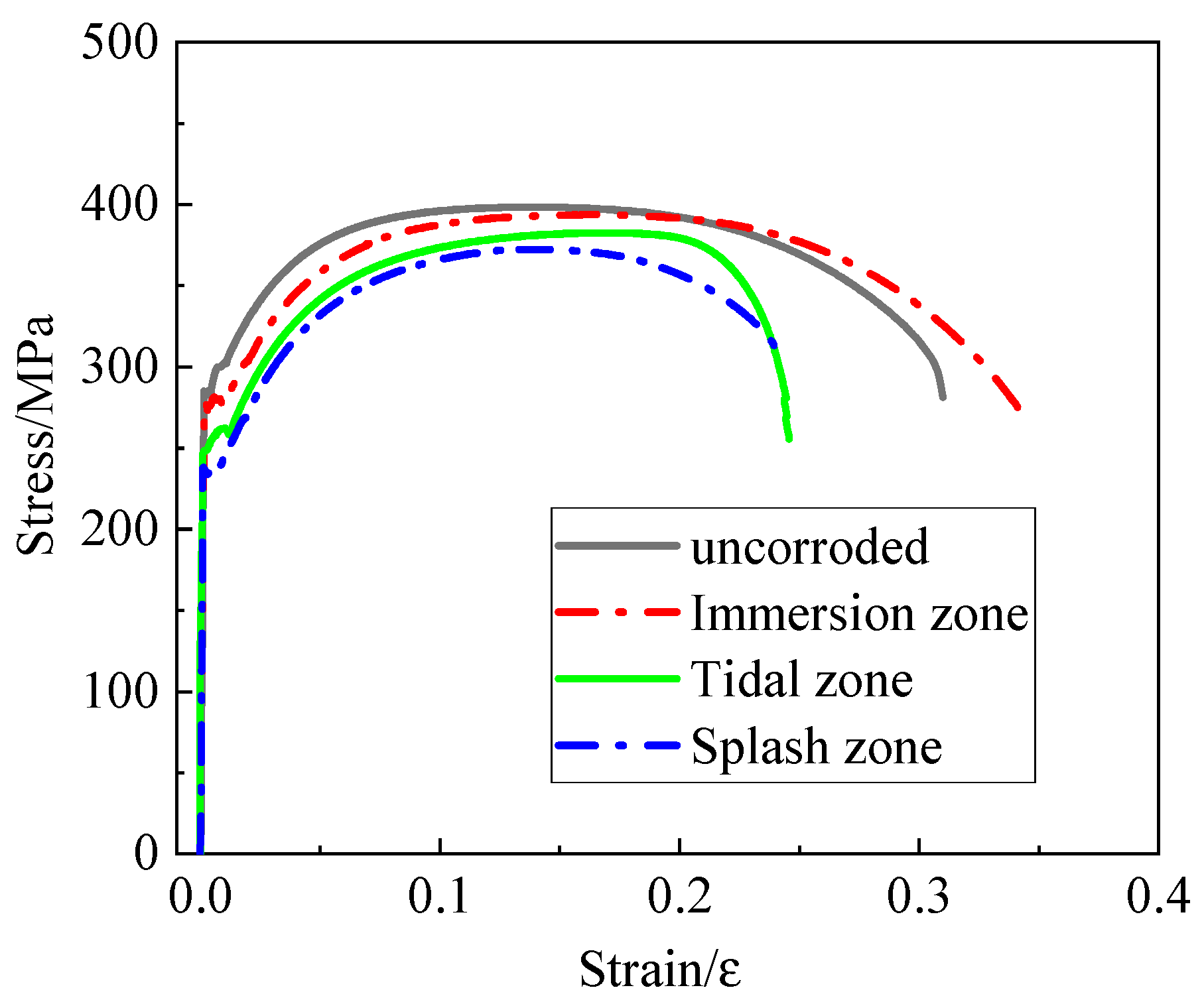
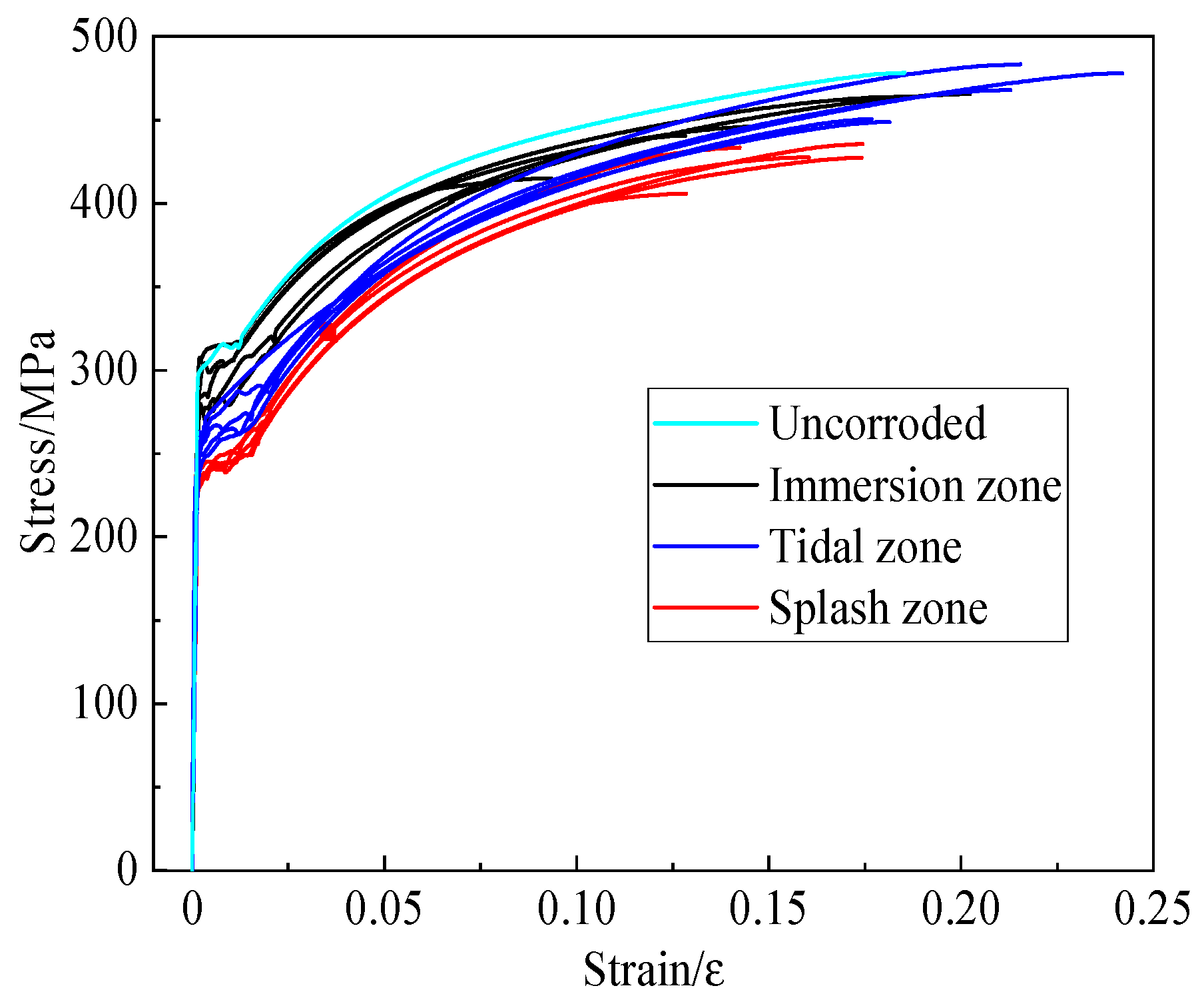
3. Strength Assessment
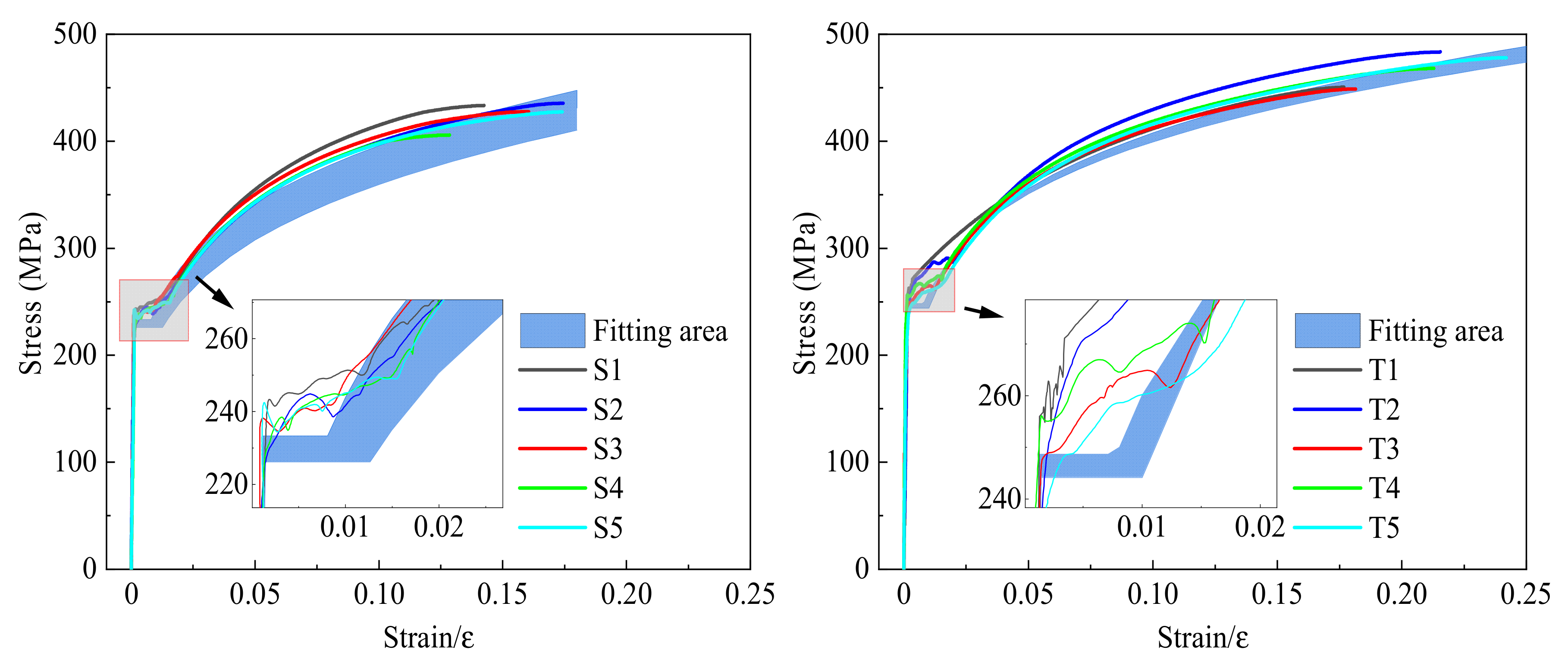
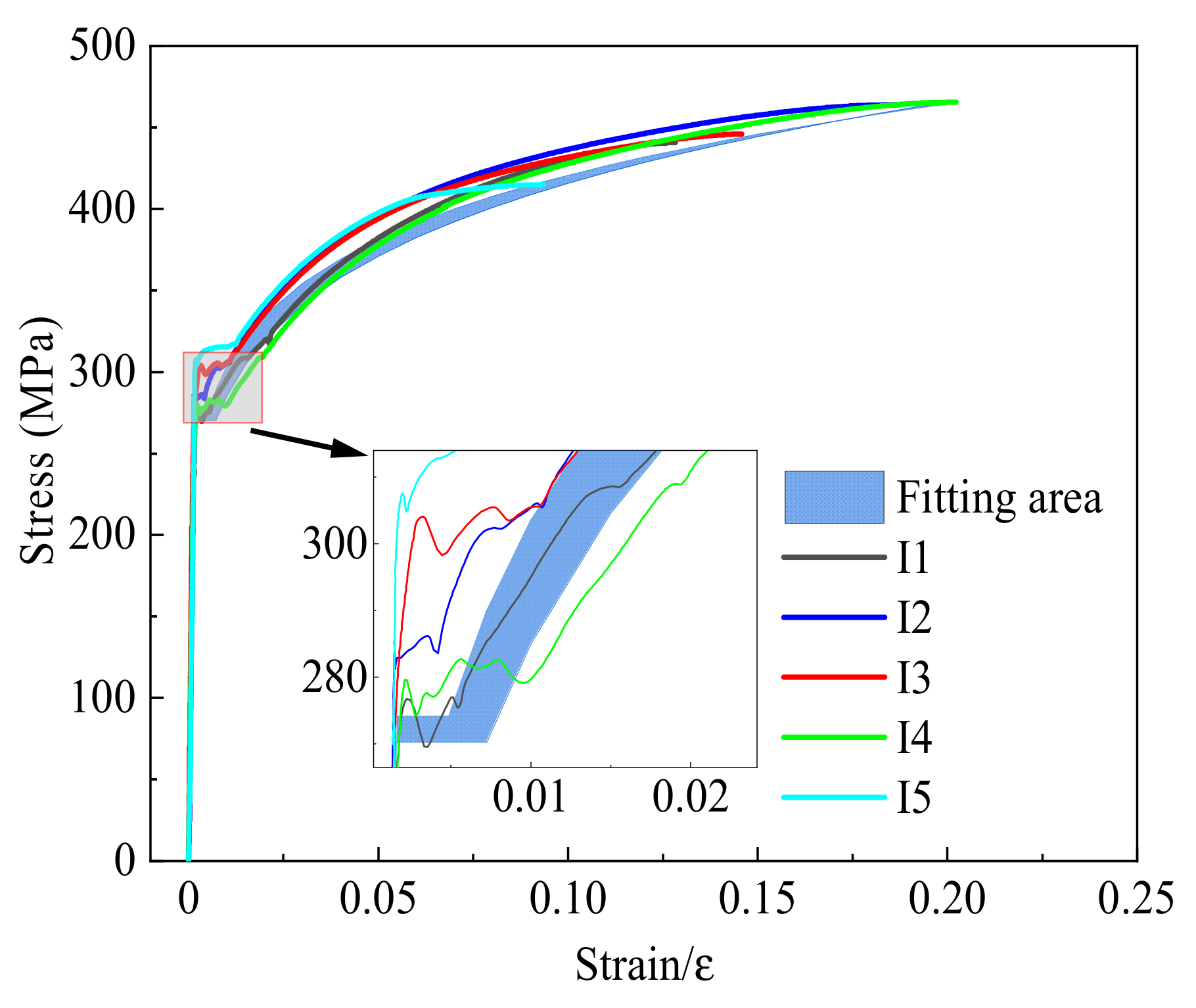
3.1. Stress-Strain Analysis
3.2. Mechanical Property Analysis
4. Stress-Strain Model
4.1. True Stress-Strain Model
4.2. Tri-Linear Constitutive Model
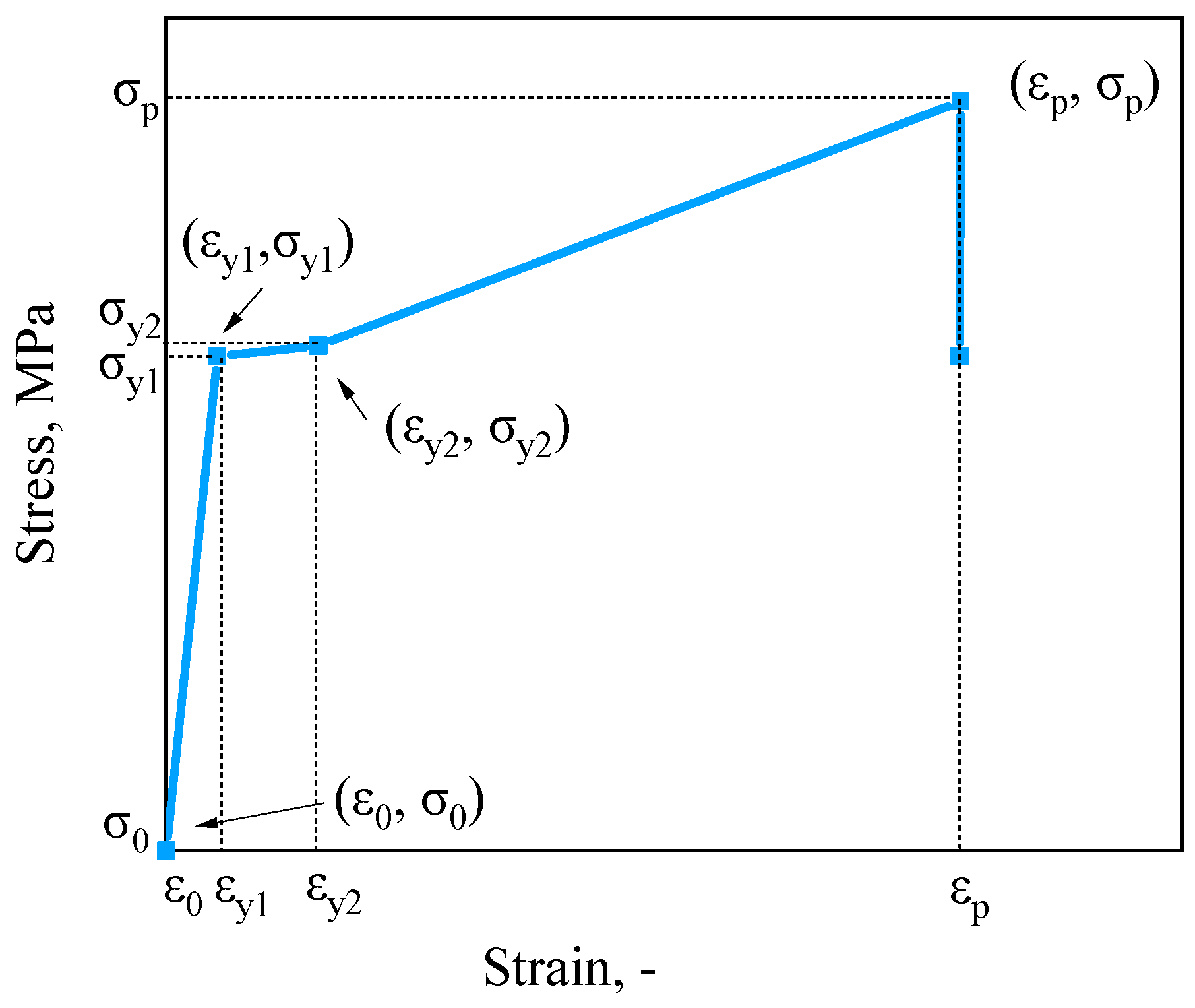
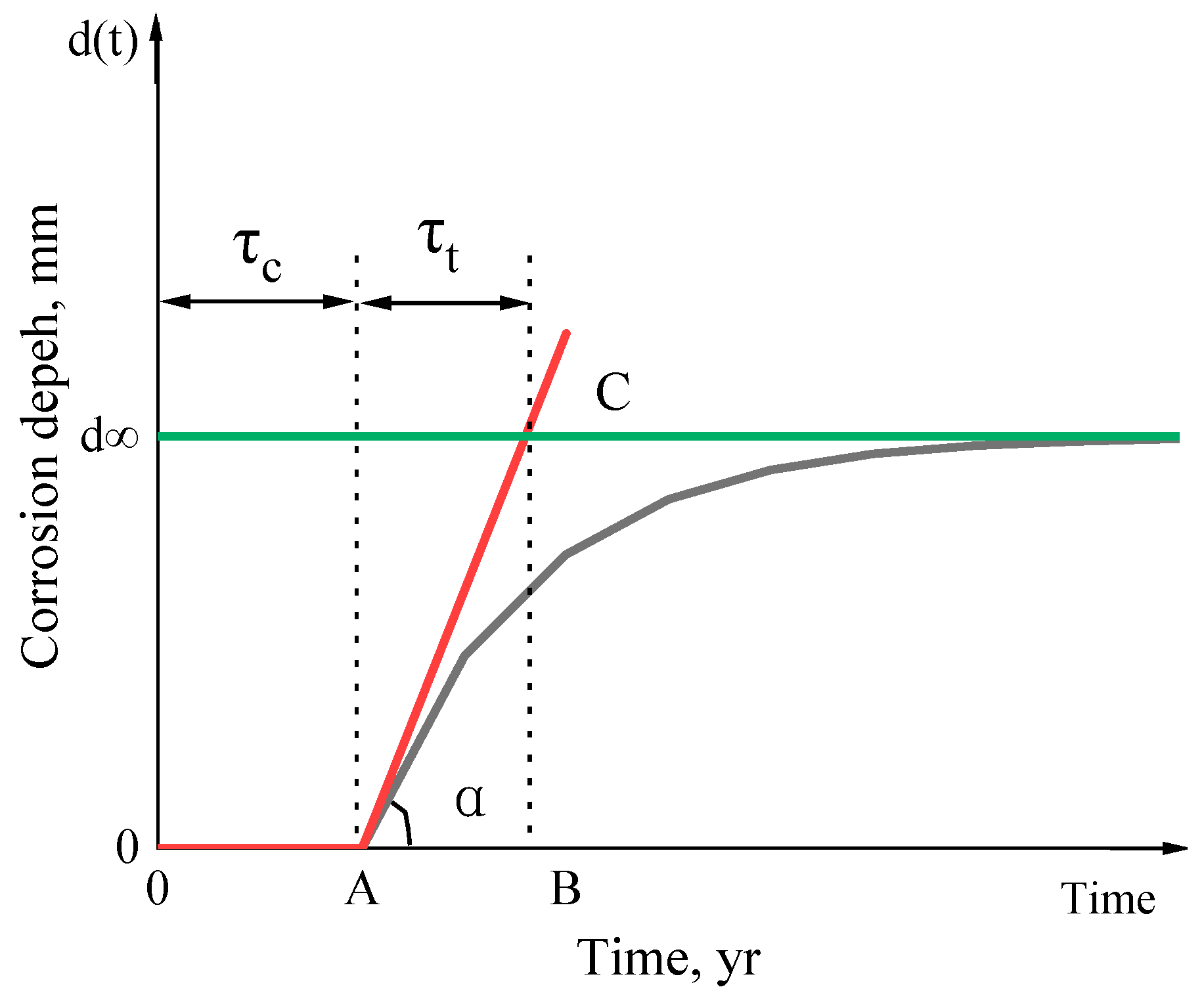
5. Corrosion degradation allowance
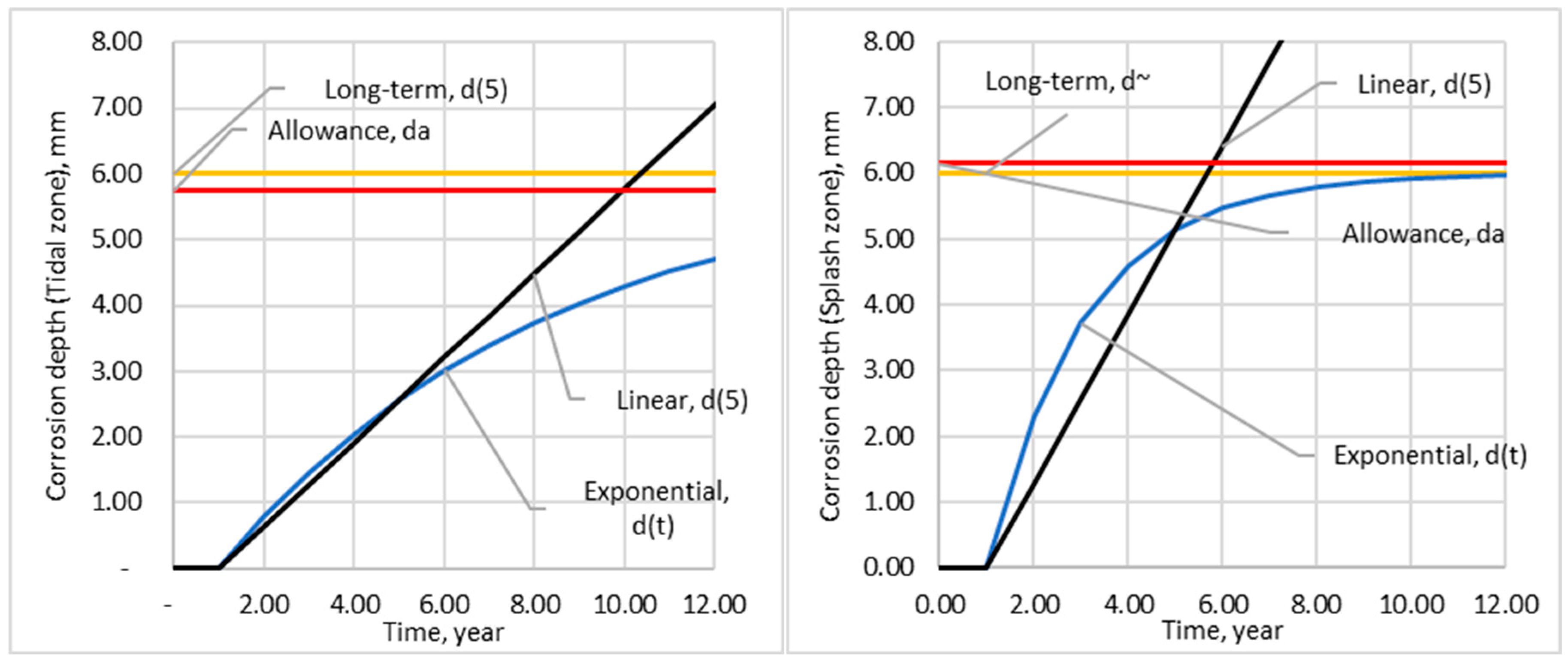
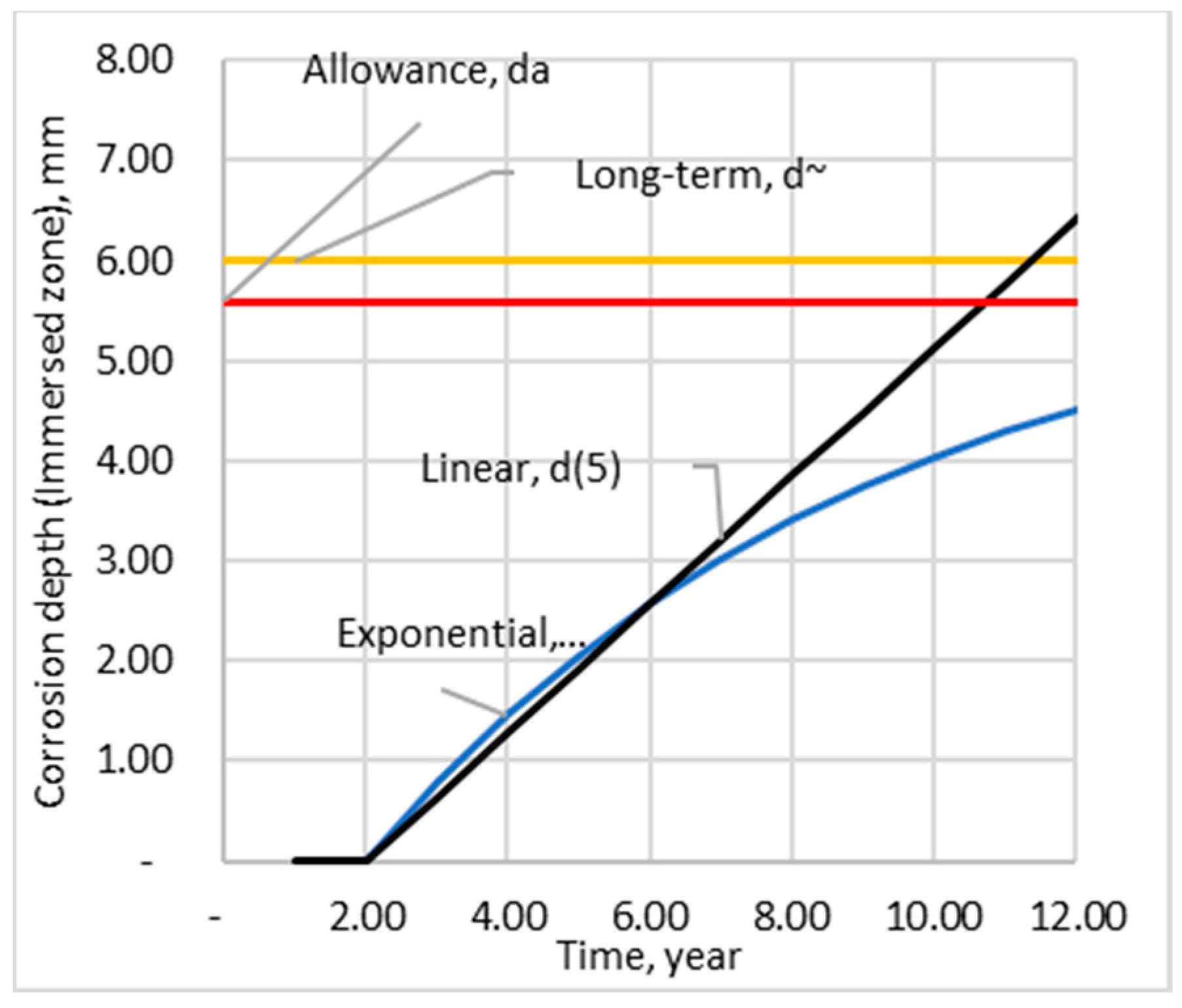
|
|
, years | |
|---|---|---|
| S-zone | 5.13 | 2.07 |
| T-zone | 2.65 | 7.17 |
| I-zone | 2.56 | 7.17 |
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wang, K.; Zhao, M. Mathematical model of homogeneous corrosion of steel pipe pile foundation for offshore wind turbines and corrosive action. Adv Mater Sci Eng. 2016, 9014317. [Google Scholar] [CrossRef]
- Alcántara, J.; Chico, B.; Simancas, J.; Díaz, I.; Morcillo, M. Marine atmospheric corrosion of carbon steel: a Review. Materials 2017, 10, 406. [Google Scholar] [CrossRef] [PubMed]
- Appuhamy, J.; Kaita, T.; Ohga, M.; Fujii, K. Prediction of residual strength of corroded tensile steel plates. Int J Steel Struct. 2011, 11, 65–79. [Google Scholar] [CrossRef]
- Garbatov, Y.; Guedes Soares, C.; Parunov, J.; Kodvanj, J. Tensile strength assessment of corroded small-scale specimens. Corros. Sci. 2014, 85, 296–303. [Google Scholar] [CrossRef]
- Garbatov, Y.; Parunov, J.; Kodvanj, J.; Saad-Eldeen, S.; Guedes Soares, C. Experimental assessment of tensile strength of corroded steel specimens subjected to sandblast and sandpaper cleaning. Marine Structures 2016, 49, 18–30. [Google Scholar] [CrossRef]
- Garbatov, Y.; Guedes Soares, C.; Parunov, J. Fatigue strength experiments of corroded small scale steel specimens. Int J Fatigue 2014, 59, 137–144. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Q.; Tu, S.; Wang, Y.; Li, Y.; Huang, Y. A study on a time-variant corrosion model for immersed steel plate elements considering the effect of mechanical stress. Ocean. Eng. 2016, 125, 134–146. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Q.; Tu, S.; Wang, Y.; Li, Y.; Huang, Y. Effects of inhomogeneous elastic stress on corrosion behaviour of Q235 steel in 3.5% NaCl solution using a novel multi-channel electrode technique. Corros. Sci. 2016, 110, 1–14. [Google Scholar] [CrossRef]
- Sheng, J.; Xia, J. Effect of simulated pitting corrosion on the tensile properties of steel. Constr. Build. Mater. 2017, 131, 90–100. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, X.H.; Guedes Soares, C. Experimental analysis of residual ultimate strength of stiffened panels with pitting corrosion under compression. Eng Struct. 2017, 152, 70–86. [Google Scholar] [CrossRef]
- Jia, C.; Shao, Y.; Guo, L.; Liu, Y. Incipient corrosion behaviour and mechanical properties of low-alloy steel in simulated industrial atmosphere. Constr. Build. Mater. 2018, 187, 1242–1252. [Google Scholar] [CrossRef]
- Gathimaba, N.; Kitane, Y.; Yoshida, T.; Itoh, Y. Surface roughness characteristics of corroded steel pipe piles exposed to marine environment. Constr. Build. Mater. 2019, 203(10), 267–281. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, L.; Zhang, Z.; Wang, Y.; Qiu, L. Study on tensile properties of Q235nh after corrosion. Steel Construction (Chinese & English), 2019; 37, 1–7. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, Y.; Xing, Y.; Jiao, J.; Fu, B.; Wang, Y. Experimental and numerical analysis of mechanical behaviours of long-term atmospheric corroded Q235 steel. Structures 2022, 39, 115–131. [Google Scholar] [CrossRef]
- Xia, R.; Jia, C.; Liu, C.; Liu, P.; Zhang, S. Non-uniform corrosion characteristics of the steel pipe pile exposed to marine environments. Ocean. Eng. 2023, 272, 113873. [Google Scholar] [CrossRef]
- Woloszyk, K.; Garbatov, Y.; Klosowski, P. Stress–strain model of lower corroded steel plates of normal strength for fitness-for-purpose analyses. Constr. Build. Mater. 2022, 323, 126560. [Google Scholar] [CrossRef]
- Woloszyk, K.; Garbatov, Y. Random field modelling of mechanical behaviour of corroded thin steel plate specimens. Eng Struct 2020, 212, 110544. [Google Scholar] [CrossRef]
- Garbatov, Y.; Guedes Soares, C. Spatial Corrosion Wastage Modeling of Steel Plates Exposed to Marine Environments. J Offshore Mech Arct. 2019, 141, 031602. [Google Scholar] [CrossRef]
- Woloszyk, K.; Garbatov, Y. Advanced numerical modelling for predicting residual compressive strength of corroded stiffened plates. Thin Wall Struct. 2023, 183, 110380. [Google Scholar] [CrossRef]
- Garbatov, Y. Fatigue strength assessment of ship structures accounting for a coating life and corrosion degradation. International Journal of Structural Integrity 2016, 7, 305–322. [Google Scholar] [CrossRef]
- Garbatov, Y.; Sisci, F.; Ventura, M. Risk-based framework for ship and structural design accounting for maintenance planning. Ocean. Eng. 2018, 166, 12–25. [Google Scholar] [CrossRef]
- Zayed, A.; Garbatov, Y.; Guedes Soares, C. Corrosion degradation of ship hull steel plates accounting for local environmental conditions. Ocean. Eng. 2018, 163, 299–306. [Google Scholar] [CrossRef]
- Gong, M. Metal corrosion theory and corrosion control. Chemical Industry Press, 2018.
- Removal of Corrosion Products from Corrosion Specimens of Metals and Alloys: GB/T 16545-2015. Beijing: Standards Press of China, 2015.
- Carbon Structural Steel: GB/T 700-2006. Beijing: Standards Press of China, 2006.
- Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature: GB/T 228.1—2010. Beijing: Standards Press of China, 2010.
- Garbatov, Y.; Guedes Soares, C. Experimental evaluation of ageing marine structures. SNAME Maritime Convention and 5th World Maritime Technology Conference 2015, D021S005R008. [Google Scholar] [CrossRef]
- Bai, P.; Ni, Y.; Lei, D. Measurement of true stress-strain relationship of stainless steel based on digital image correlation technique. Science Technology and Engineering 2020, 20, 5240–5246. [Google Scholar] [CrossRef]
- Chen, R.; 2022. Research on the degradation of steel structures for the needs of structural life-cycle design and time-dependent reliability in corrosive environment. Southeast University, 2022. [CrossRef]
- Woloszyk, K.; Garbatov, Y. Advances in Modelling and Analysis of Strength of Corroded Ship Structures. J. Mar. Sci. Eng. 2022, 10, 807. [Google Scholar] [CrossRef]
- Marchese, S.S.; Epasto, G.; Crupi, V.; Garbatov, Y. Tensile Response of Fibre-Reinforced Plastics Produced by Additive Manufacturing for Marine Applications. J. Mar. Sci. Eng. 2023, 11, 334. [Google Scholar] [CrossRef]
- Garbatov, Y.; Saad-Eldeen, S.; Guedes Soares, C.; Parunov, J.; Kodvanj, J. Tensile test analysis of corroded cleaned aged steel specimens. Corrosion Eng Sci Techn. 2018, 54, 154–162. [Google Scholar] [CrossRef]
- Melchers, R. Probabilistic Modelling of Marine Corrosion of Steel Specimens. In Proceedings of the 5th International Offshore and Polar Engineering Conference; 1995; pp. 204–210. [Google Scholar]
- Melchers, R.E. Modelling of Marine Corrosion of Steel Specimens. Corrosion Testing in Natural Waters 1997, 2, 20–23. [Google Scholar]
- Yamamoto, N.; Ikagaki, K. A Study on the Degradation of Coating and Corrosion on Ship´s Hull Based on the Probabilistic Approach. J Offshore Mech Arct. 1998, 120, 121–128. [Google Scholar] [CrossRef]
- Melchers, R.E. Probabilistic Modelling of Immersion Marine Corrosion. In Structural Safety and Reliability; Shiraishi, N., Shinozuka, M., Wen, Y., Eds.; Balkema, 1998; pp. 1143–1149. [Google Scholar]
- Yamamoto, N.; Yao, T. Hull girder strength of a tanker under longitudinal bending considering strength diminution due to corrosion. In Proceedings of the Structural Safety and Reliability, 8th International Conference (ICOSSAR2001); 2001. [Google Scholar]
- Zayed, A.; Garbatov, Y.; Guedes Soares, C. Corrosion modelling of single hull crude oil tanker subjected to multiple deterioration environments. In Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering; 2007; p. Paper OMAE2007-29741. [Google Scholar]
- Silva, J.E.; Garbatov, Y.; Guedes Soares, C. Reliability assessment of a steel plate subjected to distributed and localised corrosion wastage. Eng Struct 2014, 59, 13–20. [Google Scholar] [CrossRef]
- Jurišić, P.; Parunov, J.; Garbatov, Y. Aging Effects on Ship Structural Integrity. Brodogradnja 2017, 68, 15–28. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Garbatov, Y. Reliability of maintained, corrosion-protected plates subjected to non-linear corrosion and compressive loads. Mar. Struct. 1999, 12, 425–445. [Google Scholar] [CrossRef]
- Rackwitz, R. First order reliability theories and stochastic models. In Proceedings of the International conference ICOSSAR’77I, Munich, Germany, 19–21 September 1977. [Google Scholar]
- Gollwitzer, S.; Rackwitz, R. First-Order System Reliability of Structural Systems. In Proceedings of the 4th International Conference on Structural Safety and Reliability, Kobe, Japan, 27–29 May 1985; pp. 171–218. [Google Scholar]
- Garbatov, Y. Risk-based corrosion allowance of oil tankers. Ocean. Eng. 2020, 213, 107753. [Google Scholar] [CrossRef]





| Characteristic | Value |
|---|---|
| Mean tidal range, m | 4.3 |
| Water temperature, °C | 19.4 |
| Maximum water velocity, m/s | 2.23 |
| Average water velocity, m/s | 1.03 |
| Dissolved oxygen saturation, % | 95-100 |
| PH | 8.1-8.3 |
| Salinity, % | 3.0-3.2% |
| Average wind velocity, m/s | 6.9 |
| Tidal cycle, times/day | 2 |
| The most enormous wave height in history, m | 16 |
| Composition | C | Si | Mn | P | S |
|---|---|---|---|---|---|
| Content/% | 0.176 | 0.198 | 0.5 | 0.023 | 0.019 |
| GB/T 700-2006 | ≤0.20 | ≤0.35 | ≤1.40 | ≤0.045 | ≤0.045 |
| Zone | Specimen | , mm | , % | Mean, mm/ Var, mm2 |
|---|---|---|---|---|
| Splash | S-1 | 6.972 | 58.1 | 57.24/ 0.0143 |
| S-2 | 6.979 | 58.2 | ||
| S-3 | 6.877 | 57.3 | ||
| S-4 | 6.691 | 55.8 | ||
| S-5 | 6.815 | 56.8 | ||
| Tidal | T-1 | 9.367 | 78.1 | 77.92/ 0.0233 |
| T-2 | 9.496 | 79.1 | ||
| T-3 | 9.094 | 75.8 | ||
| T-4 | 9.356 | 78.0 | ||
| T-5 | 9.428 | 78.6 | ||
| Immersion | I-1 | 9.422 | 78.5 | 78.64/ 0.0004 |
| I-2 | 9.451 | 78.8 | ||
| I-3 | 9.429 | 78.6 | ||
| I-4 | 9.464 | 78.9 | ||
| I-5 | 9.413 | 78.4 | ||
| Intact | P-1 | 4.003 | - | - |
| No. | , MPa | Mean, MPa/ Var, MPa2 |
, MPa | Mean, MPa/ Var, MPa2 |
, % | Mean, %/ Var, - |
105, MPa | Mean, 105 MPa/ Var, MPa2 |
|---|---|---|---|---|---|---|---|---|
| S-1 | 248.81 | 237.40/ 42.005 |
382.01 | 371.51/ 52.161 |
20.38 | 22.68/ 9.853 |
1.67 | 1.67/0.001 |
| S-2 | 236.51 | 373.06 | 22.65 | 1.68 | ||||
| S-3 | 233.90 | 372.46 | 24.10 | 1.70 | ||||
| S-4 | 233.95 | 362.70 | 19.16 | 1.63 | ||||
| S-5 | 233.81 | 367.33 | 27.12 | 1.65 | ||||
| T-1 | 254.43 | 263.00/ 104.467 |
384.82 | 390.16/ 59.854 |
25.40 | 29.35/ 23.300 |
1.71 | 1.78/0.010 |
| T-2 | 279.48 | 402.60 | 35.00 | 1.93 | ||||
| T-3 | 258.37 | 382.68 | 24.58 | 1.71 | ||||
| T-4 | 266.15 | 390.60 | 33.90 | 1.83 | ||||
| T-5 | 256.56 | 390.12 | 27.86 | 1.70 | ||||
| I-1 | 268.62 | 285.12/ 229.482 |
392.41 | 392.33/ 27.420 |
28.5 | 29.68/ 3.367 |
1.73 | 1.80/0.009 |
| I-2 | 282.41 | 398.54 | 30.99 | 1.94 | ||||
| I-3 | 296.93 | 392.89 | 24.53 | 1.76 | ||||
| I-4 | 273.46 | 393.77 | 34.56 | 1.85 | ||||
| I-5 | 304.17 | 384.04 | 29.83 | 1.72 | ||||
| P-1 | 310.13 | 407.18 | 33.3 | 2.08 |
| No. | loss rate, % | Mean, %/ Var, - |
loss rate, % | Mean, %/ Var, - |
loss rate, % | Mean %/ Var, - |
loss rate, % | Mean %/ Var, - |
|---|---|---|---|---|---|---|---|---|
| S-1 | 19.77 | 23.45/ 4.370 |
6.18 | 8.76/ 3.145 |
38.80 | 31.89/ 88.829 |
19.71 | 19.90/ 1.682 |
| S-2 | 23.74 | 8.38 | 31.98 | 19.23 | ||||
| S-3 | 24.58 | 8.53 | 27.63 | 18.27 | ||||
| S-4 | 24.56 | 10.92 | 42.46 | 21.63 | ||||
| S-5 | 24.61 | 9.79 | 18.56 | 20.67 | ||||
| T-1 | 17.96 | 15.20/ 10.866 |
5.49 | 4.18/ 3.619 |
23.72 | 11.87/ 210.164 |
17.79 | 14.64/ 23.933 |
| T-2 | 9.88 | 1.12 | -5.11 | 7.21 | ||||
| T-3 | 16.69 | 6.02 | 26.19 | 17.89 | ||||
| T-4 | 14.18 | 4.07 | -1.80 | 12.02 | ||||
| T-5 | 17.27 | 4.19 | 16.34 | 18.27 | ||||
| I-1 | 13.38 | 8.06/ 23.838 |
3.63 | 3.65/ 1.653 |
14.41 | 10.87/ 120.531 |
16.83 | 13.46/20.230 |
| I-2 | 8.94 | 2.12 | 6.94 | 6.73 | ||||
| I-3 | 4.26 | 3.51 | 26.34 | 15.38 | ||||
| I-4 | 11.82 | 3.29 | -3.78 | 11.06 | ||||
| I-5 | 1.92 | 5.68 | 10.42 | 17.31 |
| Zone | Average loss |
Average loss |
Average loss |
Average loss |
|---|---|---|---|---|
| S-zone | 23.45% | 8.76% | 31.89% | 19.90% |
| T-zone | 15.20% | 4.18% | 11.87% | 14.63% |
| I-zone | 8.06% | 3.65% | 10.87% | 13.46% |
| S-zone | 0.514 | 0.722 | 0.851 |
| T-zone | 0.474 | 0.770 | 0.578 |
| I-zone | 0.592 | 0.515 | 0.794 |
| Eqn | R2 | Eqn | R2 | Eqn | R2 | Eqn | R2 | |
|---|---|---|---|---|---|---|---|---|
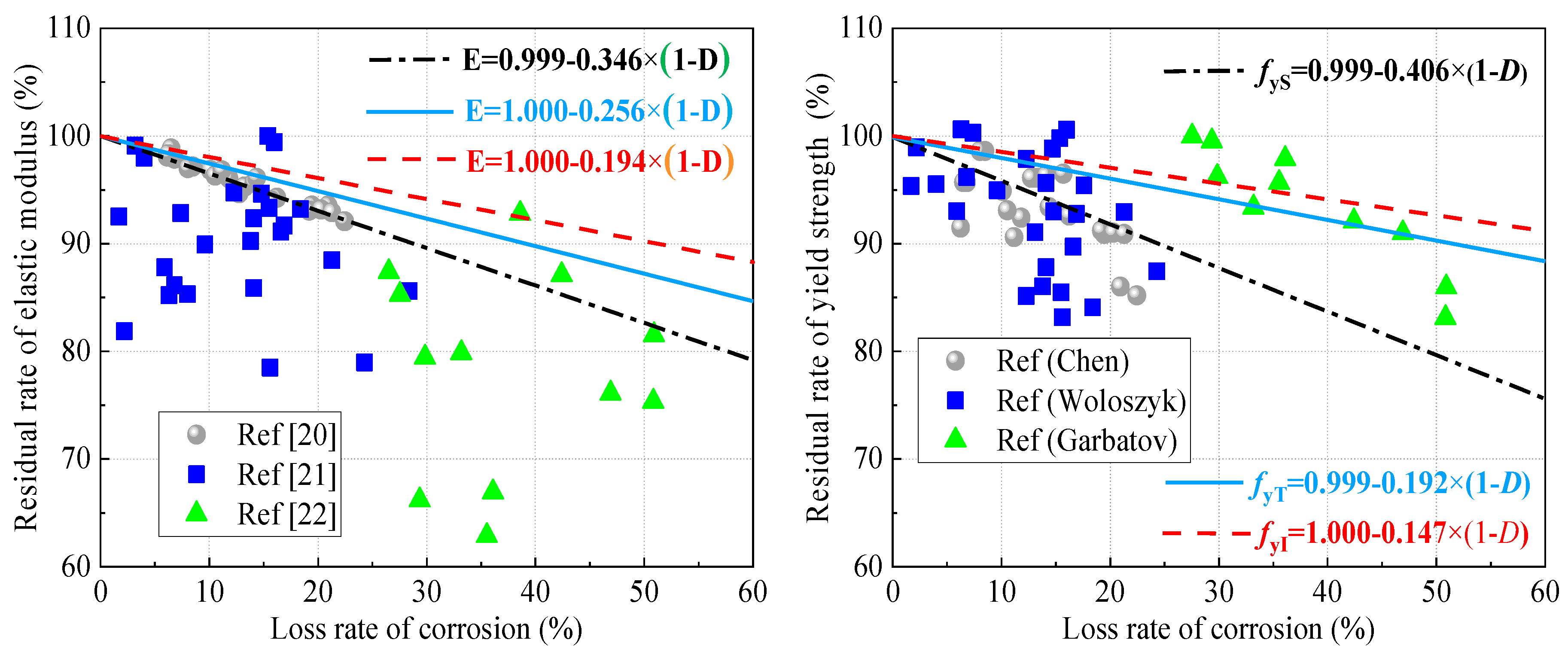
| S-zone | (4) | 0.539 | (7) | 0.350 | (12) | 0.164 | (15) | 0.181 |
| T-zone | (5) | 0.189 | (8) | 0.225 | (13) | 0.154 | (16) | 0.195 |
| I-zone | (6) | 0.724 | (9) | 0.197 | (14) | 0.286 | (17) | 0.391 |
| S-zone | 6.1487 | 1.0165 | 1.0082 |
| T-zone | 5.7386 | 1.0139 | 1.0151 |
| I-zone | 5.7207 | 1.0157 | 1.0102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





