Submitted:
01 December 2023
Posted:
04 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. BBN and updated constraints on electron neutrino-sterile neutrino oscillations parameters
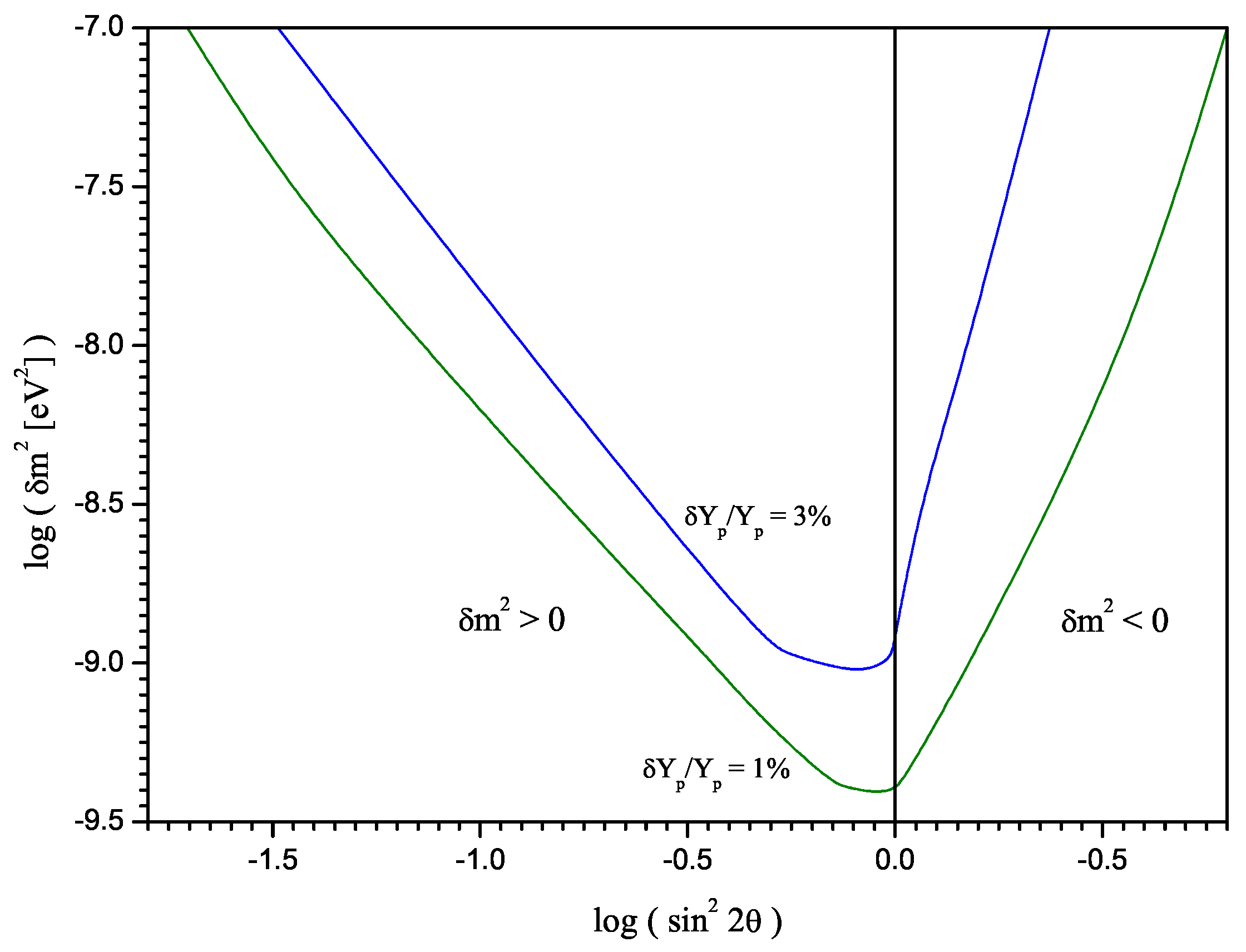
2.1. BBN with electron-sterile neutrino oscillations. BBN constraints on neutrino oscillations parameters in case of zero initial population of the sterile neutrino.
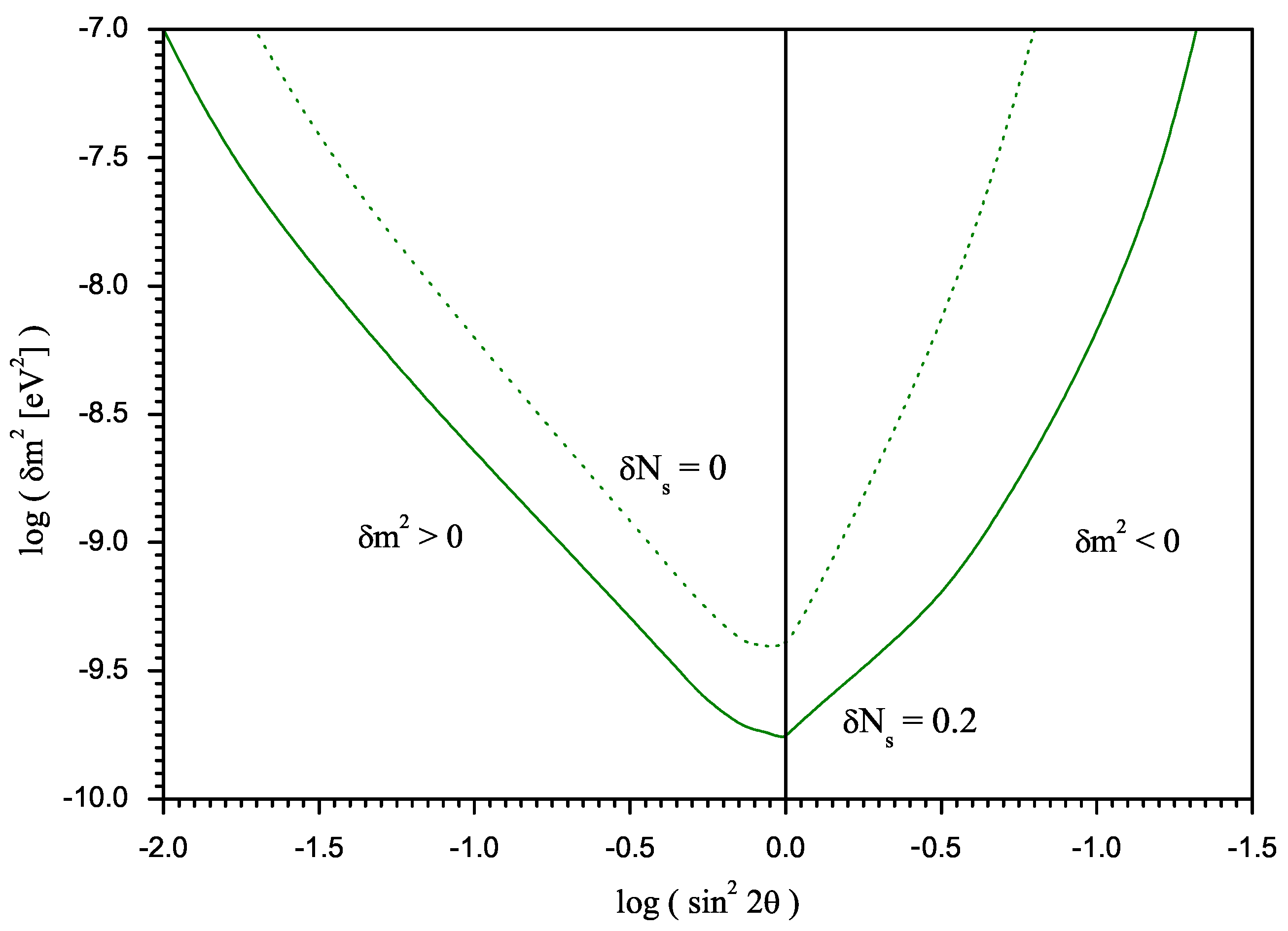
2.2. BBN constraints on electron-sterile neutrino oscillations in case of non-zero initial population of the sterile neutrino
3. BBN with lepton asymmetry and neutrino oscillations
3.1. L and the possible solution of the dark radiation puzzle
3.2. Discussion on L and the Hubble tension
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSM: | Beyond Standard Model |
| BBN: | Big Bang Nucleosynthesis |
| DR: | Dark Radiation |
References
- Kirilova, D. BBN Cosmological Constraints on Beyond Standard Model Neutrino, inPoS CORFU2018, 2019, 48 Corfu Summer Institute, Aug 31 - Sep 9, 2018.
- Kirilova, D., Chizhov, E. IJ Mod. Phys. A, 2019, 34, N11, 1950065.
- Kirilova, D. , Panayotova, M., Chizhov, E. Proceedings of Science, 11th International Conference of the Balkan Physical Union (BPU11), 2022, 28 August - 1 September, Belgrade, Serbia.
- Kirilova, D., Panayotova, M., Chizhov, E. Several cosmological nucleosynthesis constraints on neutrino and new neutrino physics Proc. of XIII Bulgarian-Serbian Astronomical Conference, Vellingrad, Bulgaria, Oct.3-7, 2023.
- Kirilova, D. JCAP , 2012, 06, 007.
- Kirilova, D. Hyperfine Interactions,2013, 215, 111.
- Angulo, C. , et al. Nucl. Phys. A 1999, 656, 3. [Google Scholar] [CrossRef]
- Xu, Y. , et al. Nucl. Phys. A 2013, 918, 61. [Google Scholar] [CrossRef]
- Pisanti, O. , et al. Comput. Phys. Commun. 2008, 178, 956. [Google Scholar] [CrossRef]
- Consiglio, et al. 2017, arXiv 1712.04378. ???
- Arbey, A. Comput. Phys. Commun. 2012, 183, 1822. [CrossRef]
- Pitrou, C. , Coc A., Uzan, J-P. and Vangioni, E. Physics Reports , 2018, 04, 005. [Google Scholar]
- Mangano, G. , Miele, G., Pastor, S., Pisanti, O., Sarikas, S. JCAP, 2011, 11, 035. [Google Scholar] [CrossRef]
- Serebrov, et al. PDG,2017,2022 ???
- Aver, E. , Olive, K., Skillman, E. JCAP 2015, 7, 011. [Google Scholar] [CrossRef]
- Cooke, R., Pettini, M., Steidel C. Astrophysical Journal, 2017, Volume 855, Issue 2, article id. 102.
- Fields, et al. PDG2022, Big Bang Nucleosynthesis, Particle Data Group ???
- Cooke, R., Fumagalli, M. Nature Astronomy 2018, 15 October.
- Balashev, et al. MNRAS, 2016, 458, 2, 2188. ???
- Aver, E., et. al. JCAP, 2021, 3, 027.
- Hsyu, T., et.al. arXiv:2005.12290 accepted ApJ 2020.
- Valerdi, M., et. al. Astrophys.J.2019, 876 2, 98.
- Dolgov, A. Sov. J. Nucl. Phys. 1981, 33, 700.
- Barbieri, R. , Dolgov, A. Phys. Lett.B , 1990, 237, 440. [Google Scholar] [CrossRef]
- Barbieri, R. , Dolgov, A. Nucl. Phys.B, 1991, 349, 743. [Google Scholar] [CrossRef]
- Kirilova, D. JINR 1988,preprint E2-88-301.
- Kirilova, D. , Chizhov, M. in Neutrino96, 1996,478.
- Kirilova, D. , Chizhov, M. Phys. Lett. B, 1997, 393, 375. [Google Scholar] [CrossRef]
- Kirilova, D., Chizhov, M. Nucl. Phys. B, 1998b, 534, 447.
- Kirilova, D., Chizhov, M. Phys.Rev.D,1998a, 58, 073004,.
- Kirilova, D., Chizhov, M. Nucl.Phys.B , 2000b, 591, 457.
- Dolgov, A. D., Villante, F. Nucl. Phys. B ,2004, 679 pp 261.
- Kirilova, D., Panayotova, M. JCAP ,2006, 12 pp 014.
- Gariazzo, S., et. al. JHEP, 2017 , 06 pp 135.
- Kopp, J., Maltoni, M., Schwetz, T. Phys. Rev. Lett., 2011, 107:091801.
- Dentler, M., et. al. High Energ. Phys., 2018, pp 10.
- Aartsen, M., et. al. Phys. Rev. Lett., 2020, 125(14) pp 141801.
- Gouvêa, A. , Sánchez, G.J., Kelly, K.J. Physical Review D, 2022, 106. pp 055025. [Google Scholar]
- Yeh Tsung-Han, Shelton, J. , Olive, K., Fields, JCAP, 2022, 10:046 ??? [Google Scholar]
- Fields et al.: , JCAP, 2020, 3, 010; Field s et al. :JCAP, 2020, 11, E02. ???
- Kirilova, D. , Panayotova, M. JCAP, 2006, 12. pp 014. [Google Scholar]
- Kirilova, D. Int. J. Mod. Phys. D, 2004, 13. pp 831.
- Kirilova, D. IJMPD,2007, 16 7 pp 1197.
- Wagoner, R. , Fowler, W. , Hoyle, F. Astrophys. J.Supp. 1967, 148, 3. [Google Scholar] [CrossRef]
- Dolgov, A. , et al. Nucl. Phys B 2002, 632, 363. [Google Scholar] [CrossRef]
- Mangano, G. , Serpico, P. Phys.Lett.B, 2011, 701, 296. [Google Scholar] [CrossRef]
- Foot, R. , Volkas, R. Phys.Rev.Lett., 1995, 75, 4350. [Google Scholar] [CrossRef] [PubMed]
- Mirizzi, A. , et al. PRD, 2012, 86, 053009. [Google Scholar] [CrossRef]
- Hannestad, S. , Tamborra, I., Tram, T. JCAP, 2012, 1207, 025. [Google Scholar] [CrossRef]
- Kirilova, D. On lepton asymmetry neutrino oscillations interplay, BBN and the problem of dark radiation, in proceedings of 53rd Rencontres de Moriond, Very High Energy Phenomena in the Universe, 2018 p. 379, La Thuile, Italy, March 17-24.
- Matsumoto, A. , et al. EMPRESS VIII: Astrophys. J. 2022, 941. no. 2 167, arXiv 2203.09617. [Google Scholar]
- Kawasaki, M. , Murai, K. Lepton asymmetric universe, JCAP2022 08, no. 08 041, arXiv:2203.09713].
- Burns, A.-K. , Tait, T. M. P., and Valli, M. Indications for a Nonzero Lepton Asymmetry from Extremely Metal-Poor Galaxies, Phys. Rev. Lett. 2023 130, no. 13 131001, arXiv:2206.00693].
- Seto, O. , Toda, Y. Phys. Rev. D 2021, 104, 063019. [Google Scholar] [CrossRef]
- Aghanim, N. , et al. [Planck], Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Serebrov, A. , et al. The result of the Neutrino-4 experiment, sterile neutrinos and dark matter, the fourth neutrino and the Hubble constant, arXiv:2302.09958 ???
| 1 | In BBN with fast proceeding before active neutrino decoupling oscillations can bring into equilibrium the sterile neutrino state and thus lead to higher expansion rate of the Universe, which refflects into higher production of He-4. This is the well known dynamical effect of active-sterile neutrino oscillations [23,24,25]. |
| 2 | Namely, several small base line experiments: reactor experiments, LSND, MiniBooNe, Gallium expt, SAGE and recently Ice Cube and NU4 hint to a presence of sterile neutrino participating into oscillations with flavor neutrinos with large mixing and squared mass difference in the range eV2 to several eV2. [35] [34,36] [37,38,56] |
| 3 | This result is in agreement with our preliminary analysis, discussed in ref. [3] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




