On Some Properties of a Complete Quadrangle

1. Introduction

In the paper [12] we started with the study of the complete quadrangle in the Euclidean plane. We continue in the same style in this paper. In [12] we have shown how to choose suitable coordinate system that allows us easily to prove some known statements, but also to obtain some new results (Theorem 8, Theorem 14). If four points are joined in pairs by six distinct lines, they are called the vertices of a complete quadrangle, and the lines are its six sides. Two sides are said to be opposite if they have no common vertex. In this paper we study properties of a complete quadrangle using rectangular coordinates symmetrically on four vertices and four parameters $a,b,c,d$. In [12] we have proved:

Lemma 1. 

Each quadrangle for which the opposite sides are not perpendicular, the rectangular hyperbola can be circumscribed.

2. Materials and Methods

Let $ABCD$ be a complete quadrangle and $\mathcal{H}$ a rectangular hyperbola circumscribed to it. With the suitable choice of the coordinate system it can be achieved that $\mathcal{H}$ has the equation $xy=1$ and the vertices of the quadrangle are of the form

$$A=\left(a,\frac{1}{a}\right),B=\left(b,\frac{1}{b}\right),C=\left(c,\frac{1}{c}\right),D=\left(d,\frac{1}{d}\right),$$

(1)

where $a,b,c,d\ne 0$.

Let $s,q,r,p$ be elementary symmetric functions in four variables $a,b,c,d$:

$$\begin{array}{c}\hfill s=a+b+c+d,q=ab+ac+bc+cd,\\ \hfill r=abc+abd+acd+bcd,p=abcd.\end{array}$$

The centroid of the quadrangle $ABCD$ is of the form

$$G=\left(\frac{s}{4},\frac{r}{4p}\right).$$

(2)

The sides of $ABCD$ have the equations:

$$\begin{array}{c}\hfill AB\cdots x+aby=a+b,AC\cdots x+acy=a+c,AD\cdots x+ady=a+d\\ \hfill BC\cdots x+bcy=b+c,BD\cdots x+bdy=b+d,CD\cdots x+cdy=c+d.\end{array}$$

(3)

3. Results

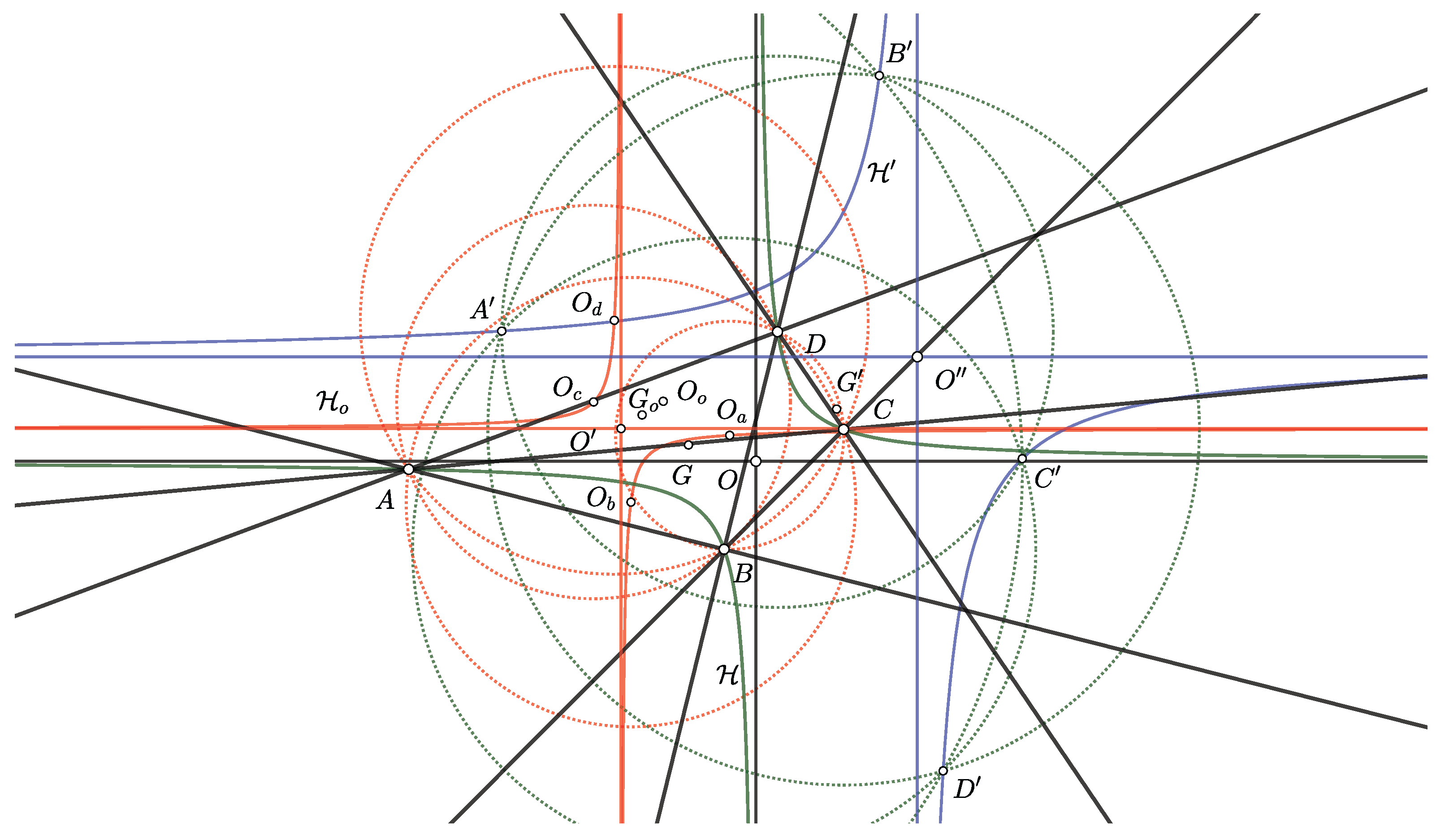
3.1. The center and anticenter of the quadrangle $ABCD$

In this section we study Euler circles of four triangles of the quadrangle $ABCD$, and define its center and anticenter. The circle with the equation

$$2abc\left(x^2+y^2\right)+\left[1-abc\left(a+b+c\right)\right]x-\left(a^2{b}^2{c}^2-ab-ac-bc\right)y=0$$

passes through the midpoint $(\frac{1}{2}(a+b),\frac{1}{2ab}(a+b))$ of points A and B. Similarly, it passes through the midpoints of $A,C$, i.e. $B,C$, so it is Euler’s circle ${\mathcal{N}}_d$ of the triangle $ABC$. It obviously passes through the origin O. Analogously, the same is valid for Euler’s circles ${\mathcal{N}}_c$, ${\mathcal{N}}_b$ and ${\mathcal{N}}_a$ of the triangles $ABD$, $ACD$, and $BCD$. Hence, we proved the following statement from [3]:

Theorem 1. 

Euler’s circles of the triangles $BCD$, $ACD$, $ABD$, $ABC$ of the complete quadrangle with circumscribed rectangular hyperbola passes through the center of the hyperbola.

There are several names for the point O in the literature, and we will call it the center of the quadrangle $ABCD$. The point $O^{\prime }=(\frac{s}{2},\frac{r}{2p})$, symmetric to the point O with respect to the centroid G we will call an anticenter of the quadrangle $ABCD$. The asymptotes $\mathcal{X}$ and $\mathcal{Y}$ of the hyperbola $\mathcal{H}$ we will call the axes of the quadrangle $ABCD$.

The center $N_d$ of the circle ${\mathcal{N}}_d$, i. e. Euler’s center of the triangle $ABC$, is the point

$$N_d=\left(\frac{1}{4}\left(a+b+c-\frac{1}{abc}\right),\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-abc\right)\right).$$

(4)

The Euler’s centers $N_a,N_b,N_c$ of the triangles $BCD$, $ACD$, $ABD$ are of similar forms. The distance from $N_d$ to the origin O fulfills

$$\begin{array}{ccc}\hfill O{N_d}^2& =& {\left(\frac{1}{4abc}\right)}^2{\left[abc(a+b+c)-1\right]}^2+{(ab+ac+bc-a^2{b}^2{c}^2)}^2\hfill \\ & =& {\left(\frac{1}{4abc}\right)}^2(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1).\hfill \end{array}$$

Hence, Euler’s circle of the triangle $ABC$ has the radius

$\frac{1}{4}\left|\frac{d}{p}\right|\sqrt{(a^2{b}^2+1)(a^2{c}^2+1)(b^2{c}^2+1)}$. The other three radii of the Euler’s circles of the other three triangles look like similarly, see [11]. Because of that, the radius ${\rho }_d$ of the circumscribed circle of the triangle $ABC$ is given within following analogous formulae

$${\rho }_a=\frac{1}{2}\left|\frac{a}{p}\right|\sqrt{{\lambda }^{\prime }{\mu }^{\prime }{\nu }^{\prime }},{\rho }_b=\frac{1}{2}\left|\frac{b}{p}\right|\sqrt{{\lambda }^{\prime }\mu \nu },{\rho }_c=\frac{1}{2}\left|\frac{c}{p}\right|\sqrt{\lambda {\mu }^{\prime }\nu },{\rho }_d=\frac{1}{2}\left|\frac{d}{p}\right|\sqrt{\lambda \mu {\nu }^{\prime }},$$

where ${\rho }_a,{\rho }_b,{\rho }_c$ are the radii of the circumscribed circles of the triangles $BCD$, $ACD$, $ABD$ using the following notations

$$\begin{array}{ccc}\hfill \lambda =a^2{b}^2+1,& \mu =a^2{c}^2+1,& \nu =a^2{d}^2+1,\hfill \\ \hfill {\lambda }^{\prime }=c^2{d}^2+1,& {\mu }^{\prime }=b^2{d}^2+1,& {\nu }^{\prime }=b^2{c}^2+1,\hfill \end{array}$$

(5)

where $\lambda ,\mu ,\nu ,{\lambda }^{\prime },{\mu }^{\prime },{\nu }^{\prime }>0$. The parameters (5) appear in formulae for lengths of sides of the quadrangle $ABCD$. Indeed, for the points A and B we get

$${AB}^2={(a-b)}^2+{\left(\frac{1}{a}-\frac{1}{b}\right)}^2={\left(\frac{a-b}{ab}\right)}^2(a^2{b}^2+1)={\left(\frac{a-b}{ab}\right)}^2\lambda ,$$

i.e. $AB=\left|\frac{a-b}{ab}\right|\sqrt{\lambda }$. The other five analogous statements are also valid

$$AC=\left|\frac{a-c}{ac}\right|\sqrt{\mu },AD=\left|\frac{a-d}{ad}\right|\sqrt{\nu },BC=\left|\frac{b-c}{bc}\right|\sqrt{{\nu }^{\prime }},BD=\left|\frac{b-d}{bd}\right|\sqrt{{\mu }^{\prime }},CD=\left|\frac{c-d}{cd}\right|\sqrt{{\lambda }^{\prime }}.$$

From these equalities the next equalities follow

$$\begin{array}{c}\hfill AB·CD=\left|\frac{(a-b)(c-d)}{p}\right|\sqrt{\lambda {\lambda }^{\prime }},AC·BD=\left|\frac{(a-c)(b-d)}{p}\right|\sqrt{\mu {\mu }^{\prime }},\end{array}$$

(6)

$$\begin{array}{c}\hfill AD·BC=\left|\frac{(a-d)(b-c)}{p}\right|\sqrt{\nu {\nu }^{\prime }}.\end{array}$$

(7)

For coordinates of the point $N_d$ from (4) it proves that

$$\left(x-\frac{s}{4}\right)\left(y-\frac{r}{4p}\right)=\frac{1}{16p}{(p+1)}^2.$$

The same is valid for $N_a,N_b,N_c$ as well. Therefore, we have proved the result given in [7] and [11]:

Theorem 2. 

The centroid G of the quadrangle $ABCD$ is the center of the quadrangle $N_a{N}_b{N}_c{N}_d$, where $N_a,N_b,N_c,N_d$ are centers of Euler circles $BCD$, $ACD$, $ABD$, $ABC$, respectively, and the quadrangles $ABCD$ and $N_a{N}_b{N}_c{N}_d$ have the parallel axes.

Because the midpoints $AD,BD,CD$ are symmetric to the midpoints $BC,AC,AB$ with respect to the centroid G, the circle incident to the midpoints of $AD,BD,CD$ is symmetric to the Euler circle ${\mathcal{N}}_d$ of the triangle $ABC$ with respect to the centroid G. Hence, that circle is incident to anticenter $O^{\prime }$ because the circle ${\mathcal{N}}_d$ is incident to O. We have proved the following:

Theorem 3. 

Circles incident to the midpoints of three sides $AD,BD,CD$; $AC,BC,CD$; $AB,BC,BD$; $AB,AC,AD$ are passing through $O^{\prime }$.

The result is given in [1] and [10] as well.

The line $AB$ has the slope $-\frac{1}{ab}$, and connecting line of the origin and the midpoint of $AB$ has the slope $\frac{1}{ab}$, so these lines are antiparallel with respect to coordinate axes. The same is valid for any side of the quadrangle $ABCD$. We showed the result given in [3] and [13]:

Theorem 4. 

The angle of any two sides of the quadrangle is opposite to the angle of connecting lines of the midpoints of these sides and the center of $ABCD$.

Let us study the points

$$H_a=\left(-\frac{1}{bcd},-bcd\right),H_b=\left(-\frac{1}{acd},-acd\right),H_c=\left(-\frac{1}{abd},-abd\right),H_d=\left(-\frac{1}{abc},-abc\right).$$

(8)

The line with the equation $abx-y=abc-\frac{1}{c}$ is perpendicular to the line $AB$ from (3) and it is incident to C and $H_d$, so the line $C{H}_d$ is height from C of the triangle $ABC$. Similarly, the lines $A{H}_d$ and $B{H}_d$ are heights from the vertices A and B of the triangle $ABC$. Therefore, $H_d$ is the orthocenter of that triangle. Hence, see [3]:

Theorem 5. 

The orthocenters $H_a,H_b,H_c,H_d$ of the triangles $BCD,ACD,ABD,ABC$, respectively, are incident to the rectangular hyperbola $\mathcal{H}$.

This statement proves the converse of Lemma 2 from [12].

As the orthocenters $H_a,H_b,H_c,H_d$ are incident to hyperbola $\mathcal{H}$, its center O is the center of the quadrangle $H_a{H}_b{H}_c{H}_d$. In [11] the following is proved:

Theorem 6. 

Quadrangles $ABCD$ and $H_a{H}_b{H}_c{H}_d$ have the same center.

If the point D coincides with $H_d$, then $d=\frac{1}{abc}$, $p=-1$, and the quadrangle $ABCD$ is the orthocentric quadrangle (see [12]).

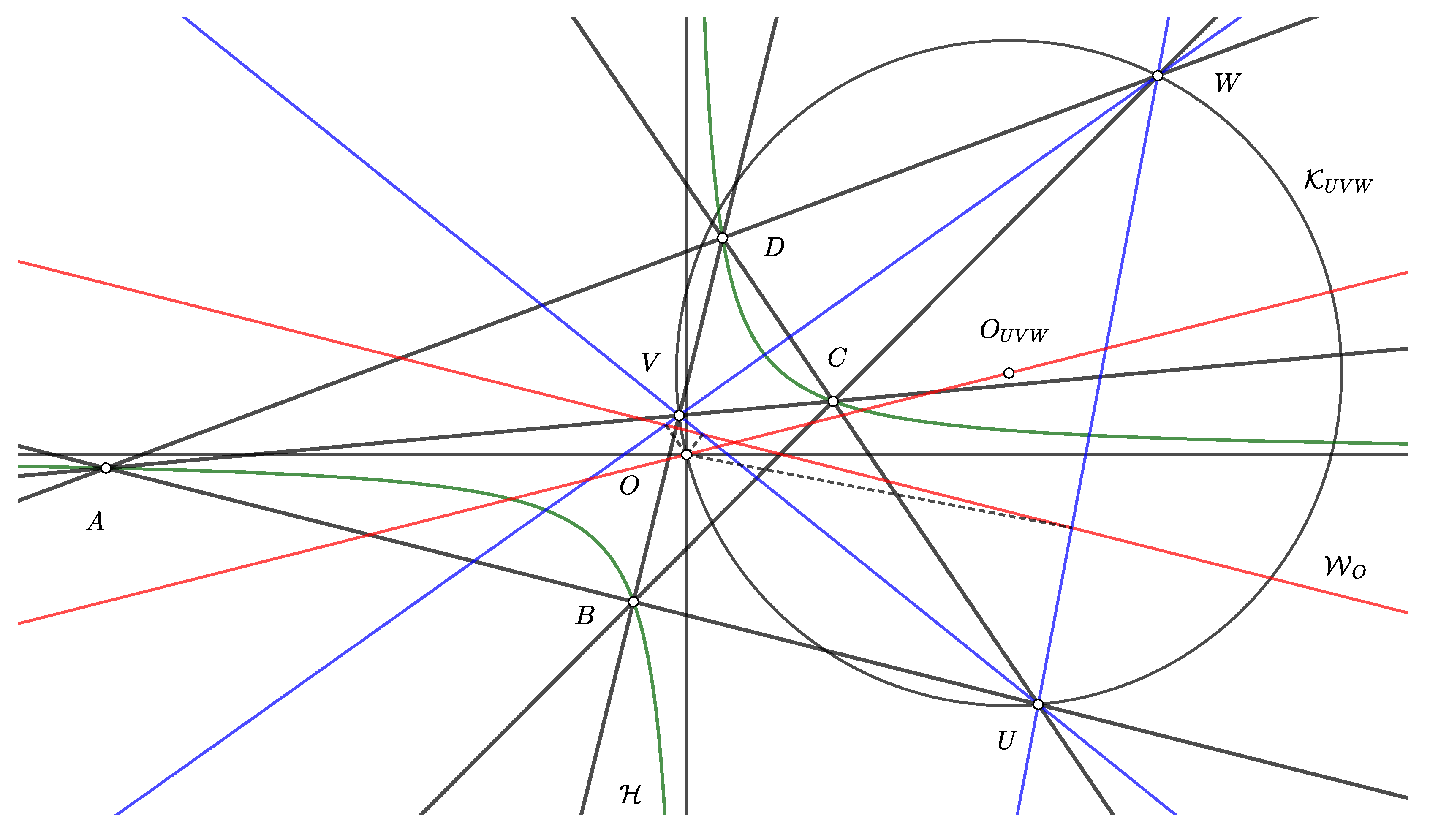
3.2. A diagonal triangle of the quadrangle $ABCD$

Diagonal points $U=AB\cap CD$, $V=AC\cap BD$, $W=AD\cap BC$ of the quadrangle $ABCD$ are given by

$$U=\left(\frac{ab(c+d)-cd(a+b)}{ab-cd},\frac{a+b-c-d}{ab-cd}\right),V=\left(\frac{ac(b+d)-bd(a+c)}{ac-bd},\frac{a+c-b-d}{ac-bd}\right),$$

$$W=\left(\frac{ad(b+c)-bc(a+d)}{ad-bc},\frac{a+d-b-c}{ad-bc}\right).$$

These points can be written in the shorter form

$$U=\left(\frac{u^{\prime }}{u},\frac{u^{\prime \prime }}{u}\right),V=\left(\frac{v^{\prime }}{v},\frac{v^{\prime \prime }}{v}\right),W=\left(\frac{w^{\prime }}{w},\frac{w^{\prime \prime }}{w}\right),$$

where

$$\begin{array}{ccc}\hfill u=ab-cd,& u^{\prime }=ab(c+d)-cd(a+b),& u^{\prime \prime }=a+b-c-d,\hfill \\ \hfill v=ac-bd,& v^{\prime }=ac(b+d)-bd(a+c),& v^{\prime \prime }=a+c-b-d,\hfill \\ \hfill w=ad-bc,& w^{\prime }=ad(b+c)-bc(a+d),& w^{\prime \prime }=a+d-b-c.\hfill \end{array}$$

The following equalities are valid

$$u^{\prime }{v}^{\prime \prime }+u^{\prime \prime }{v}^{\prime }=2uv,u^{\prime }{w}^{\prime \prime }+u^{\prime \prime }{w}^{\prime }=2uw,v^{\prime }{w}^{\prime \prime }+v^{\prime \prime }{w}^{\prime }=2vw.$$

Therefore, the lines $\mathcal{U}$, $\mathcal{V}$, $\mathcal{W}$ with equations

$$u^{\prime \prime }x+u^{\prime }y=2u,v^{\prime \prime }x+v^{\prime }y=2v,w^{\prime \prime }x+w^{\prime }y=2w$$

are incident to pairs of points $V,W$; $U,W$; $U,V$, respectively. So, they are the diagonals of the quadrangle $ABCD$. Hence, their equations are

$$\begin{array}{ccc}\hfill \mathcal{U}& \dots & (a+b-c-d)x+\left[ab\right(c+d)-cd(a+b\left)\right]y=2(ab-cd),\hfill \\ \hfill \mathcal{V}& \dots & (a+c-b-d)x+\left[ac\right(b+d)-bd(a+c\left)\right]y=2(ac-bd),\hfill \\ \hfill \mathcal{W}& \dots & (a+d-b-c)x+\left[ad\right(b+c)-bc(a+d\left)\right]y=2(ad-bc).\hfill \end{array}$$

The centroid $G_{UVW}$ of the triangle $UVW$ is the point

$$G_{UVW}=\left(\frac{u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }}{3uvw},\frac{u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }}{3uvw}\right).$$

The heights from vertices U and V of the diagonal triangle $UVW$ have the equations

$$u{u}^{\prime }x-u{u}^{\prime \prime }y={u^{\prime }}^2-{u^{\prime \prime }}^2,v{v}^{\prime }x-v{v}^{\prime \prime }y={v^{\prime }}^2-{v^{\prime \prime }}^2.$$

For their intersection point $(x,y)$ the equalities

$$\begin{array}{c}\hfill uv(u^{\prime }{v}^{\prime \prime }-u^{\prime \prime }{v}^{\prime })x={u^{\prime }}^{2}v{v}^{\prime \prime }-u{u}^{\prime \prime }{v^{\prime }}^2+u^{\prime \prime }{v}^{\prime \prime }(u{v}^{\prime \prime }-u^{\prime \prime }v),\\ \hfill uv(u^{\prime }{v}^{\prime \prime }-u^{\prime \prime }{v}^{\prime })y=u^{\prime }{v}^{\prime }(u^{\prime }v-u{v}^{\prime })+u{u}^{\prime }{v^{\prime \prime }}^2-{u^{\prime \prime }}^{2}v{v}^{\prime }\end{array}$$

are valid. However, it can be checked that

$$\begin{array}{ccc}\hfill u^{\prime }{v}^{\prime \prime }-u^{\prime \prime }{v}^{\prime }& =& 2(a-d)(b-c)w,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {u^{\prime }}^{2}v{v}^{\prime \prime }-u{u}^{\prime \prime }{v^{\prime }}^2& =& (a-d)(b-c)(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill u{v}^{\prime \prime }-u^{\prime \prime }v& =& (a-d)(b-c)w^{\prime \prime },\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill u^{\prime }v-u{v}^{\prime }& =& (a-d)(b-c)w^{\prime },\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill u{u}^{\prime }{v^{\prime \prime }}^2-{u^{\prime \prime }}^{2}v{v}^{\prime }& =& (a-d)(b-c)(u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime })\hfill \end{array}$$

are valid. Hence, the orthocenter of the triangle $UVW$ is the point

$$H_{UVW}=\left(\frac{u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }+u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime }}{2uvw},\frac{u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }+u^{\prime }{v}^{\prime }{w}^{\prime }}{2uw}\right).$$

The centroid, orthocenter and circumcenter $O_{UVW}$ of the triangle $UVW$ fulfill the equality $2O_{UVW}+H_{UVW}=3G_{UVW}$, out of which we get

$$O_{UVW}=\left(\frac{u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime }}{4uvw},\frac{u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime }{w}^{\prime }}{4uvw}\right).$$

Let us study now the circle ${\mathcal{K}}_{UVW}$ with the center $O_{UVW}$ and the equation

$$2uvw(x^2+y^2)-(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime })x-(u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime }{w}^{\prime })y=0.$$

(12)

We will show that is the circumscribed circle of the triangle $UVW$. That U is incident to this circle, it is proved by the equality

$$2vw({u^{\prime }}^2+{u^{\prime \prime }}^2)-(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime })u^{\prime }-(u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime }{w}^{\prime })u^{\prime \prime }=0$$

that can be written in the form

$$u^{\prime }w(u^{\prime }v-u{v}^{\prime })+u^{\prime }{w}^{\prime }(u^{\prime \prime }{v}^{\prime }-uv)-u^{\prime \prime }w(u{v}^{\prime \prime }-u^{\prime \prime }v)+u^{\prime \prime }{w}^{\prime \prime }(u^{\prime }{v}^{\prime \prime }-uv)=0$$

and it is valid because of (9) and (10) and the equalities

$$\begin{array}{ccc}\hfill u^{\prime \prime }{v}^{\prime }-uv& =& -(a-d)(b-c)w,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill u^{\prime }{v}^{\prime \prime }-uv& =& (a-d)(b-c)w.\hfill \end{array}$$

(14)

Theorem 7. 

The circumscribed circle of the diagonal triangle $UVW$ of the quadrangle $ABCD$ is incident to its center O.

The same result can be found in [2,3,6,8] and [10].

The line $\mathcal{U}$ has the equation $u^{\prime \prime }x+u^{\prime }y=2u$ and the normal from O to this line is given by $u^{\prime }x-u^{\prime \prime }y=0$. The intersection point of these two lines is the point

$$\left(\frac{2u{u}^{\prime \prime }}{{u^{\prime }}^2+{u^{\prime \prime }}^2},\frac{2u{u}^{\prime }}{{u^{\prime }}^2+{u^{\prime \prime }}^2}\right).$$

(15)

Out of the equalities (10) and (14), and (11) and (13) the next equalities follow

$$(u{v}^{\prime \prime }-u^{\prime \prime }v)w=(u^{\prime }{v}^{\prime \prime }-uv)w^{\prime \prime },(u{v}^{\prime }-u^{\prime }v)w=(u^{\prime \prime }{v}^{\prime }-uv)w^{\prime }$$

that can be written in the form

$$u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime \prime }{w}^{\prime \prime }=u^{\prime \prime }vw,u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime }{w}^{\prime }=u^{\prime }vw.$$

(16)

The expression

$$(u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime }{w}^{\prime })u^{\prime \prime }+(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime })u^{\prime }$$

can be written as

$$vw({u^{\prime }}^2+{u^{\prime \prime }}^2)+u^{\prime \prime }(u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime \prime }{w}^{\prime \prime })+u^{\prime }(u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime }{w}^{\prime }),$$

and because of (16) that is equal to $vw({u^{\prime }}^2+{u^{\prime \prime }}^2)+vw{u^{\prime \prime }}^2+vw{u^{\prime }}^2=2vw({u^{\prime }}^2+{u^{\prime \prime }}^2)$. It means that line with the equation

$${\mathcal{W}}_o\dots (u^{\prime \prime }vw+u{v}^{\prime \prime }w+uv{w}^{\prime \prime }-u^{\prime }{v}^{\prime }{w}^{\prime })x+(u^{\prime }vw+u{v}^{\prime }w+uv{w}^{\prime }-u^{\prime \prime }{v}^{\prime \prime }{w}^{\prime \prime })y=4uvw$$

(17)

is incident to the point (15), the pedal of the normal to the line $\mathcal{U}$ from the point O. Because of the symmetry, it is incident to the pedals of the normal to the line $\mathcal{V}$ and $\mathcal{W}$ from the point O, respectively. Hence, the line ${\mathcal{W}}_o$ in (17) is the Wallace’s line of the point O with respect to the triangle $UVW$. Therefore, the new statement is proved, see Figure 1.

Theorem 8. 

The Wallace’s line of the center O with respect to the diagonal triangle $UVW$ and the connecting line of the points $O_{UVW}$ and O form equal angles with the asymptotes $\mathcal{X}$ and $\mathcal{Y}$ of the hyperbola $\mathcal{H}$.

Namely, their slopes are opposite.

The line through the midpoint $(\frac{a+b}{2},\frac{a+b}{2ab})$ of the side $AB$ and parallel to the line $CD$ has the equation $x+cdy-\frac{a+b}{2ab}(ab+cd)=0$ and it is incident to the point

$$U_o=\left((ab+cd)\frac{u^{\prime \prime }}{2u},(ab+cd)\frac{u^{\prime }}{2pu}\right)$$

because

$$ab{u}^{\prime \prime }+u^{\prime }-(a+b)u=0.$$

(18)

Because of symmetry of coordinates of this point on pairs $a,b$ and $c,d$, it follows that the line incident to the midpoint of $CD$ and parallel to the side $AB$ is incident to $U_o$ as well. The midpoint of $AB$ and the point $U_o$ are lying on the circle given by

$$2pu(x^2+y^2)+[p(u^{\prime }-su)+u^{\prime }]x+[p^2{u}^{\prime \prime }+c^2{d}^2(c+d)-a^2{b}^2(a+b)]y=0.$$

This circle is incident to the midpoint of $CD$ and obviously to the point O. There are two more such circles obtained in analogously way. As it is stated in [1,3], the following is valid:

Theorem 9. 

The circles incident to the midpoints of $AB$, $CD$ and the point $U_o$; $AC$, $BD$, and $V_0$; $AD$, $BC$ and $W_0$ are incident to O.

The triangles $BCD$ and $ACD$ have centroids $G_a=\left(\frac{1}{3}(b+c+d),\frac{1}{3}(\frac{1}{b}+\frac{1}{c}+\frac{1}{d})\right)$, $G_b=\left(\frac{1}{3}(a+c+d),\frac{1}{3}(\frac{1}{a}+\frac{1}{c}+\frac{1}{d})\right)$ and their connecting line $G_a{G}_b$ has the equation $3cdx+3py=cds+ab(c+d)$. Analogously, the line $G_c{G}_d$ has the equation $3abx+3py=abs+cd(a+b)$. The intersection point $U_g=G_a{G}_b\cap G_c{G}_d$ is of the form

$$U_g=\left(\frac{s}{3}-\frac{u^{\prime }}{3u},\frac{c+d}{3cd}+\frac{u^{\prime }}{3abu}\right).$$

The orthocenters $H_a$ and $H_b$ from (8) have connecting line $H_a{H}_b$ with the equation $cdpx+y=-cd(a+b)$, and analogously the line $H_c{H}_d$ have the equation $abpx+y=-ab(c+d)$. The intersection point $U_h=H_a{H}_b\cap H_c{H}_d$ is

$$U_h=\left(-\frac{u^{\prime }}{pu},-\frac{p{u}^{\prime \prime }}{u}\right).$$

Let us remind from [12] that the circumcenter of the triangle $ABC$ is the point

$$O_d=\left(\frac{1}{2}\left(a+b+c+\frac{1}{abc}\right),\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+abc\right)\right).$$

(19)

The circumcenters $O_a$ and $O_b$ with forms analogous to (19) have the connecting line $O_a{O}_b$ with the equation $cdx-y=\frac{1}{2cd}(c+d)(c^2{d}^2+1)$, and analogously the line $O_c{O}_d$ have the equation $abx-y=\frac{1}{2ab}(a+b)(a^2{b}^2+1)$. For the intersection point $U_o=O_a{O}_b\cap O_c{O}_d$ we get the form

$$U_o=\left(\frac{1}{2pu}(psu-p{u}^{\prime }+u^{\prime }),\frac{1}{2pu}[ab(c+d)u+cd{u}^{\prime }+p^2{u}^{\prime \prime }]\right).$$

Out of terms for $U_g,U_h$ and $U_o$ it is easy to check that the equality $U_h+2U_o=3U_g$ is valid, i.e. $U_h-U_g=2(U_g-U_o)$ or $U_g{U}_h=2U_o{U}_g$, i. e. $U_o{U}_g:U_g{U}_h=1:2$. The same iz valid for the analogous intersections. So, we have proved the result that can be found in [9], where Myakishev addressed it to J. Ganin:

Theorem 10. 

If $G_a,G_b,G_c,G_d$ are centroids, $H_a,H_b,H_c,H_d$ are orthocenters and $O_a,O_b,O_c,O_d$ are circumcenters of the triangles $BCD,ACD,ABD,ABC$ in the quadrangle $ABCD$ and if $U_g,V_g,W_g$; $U_h,V_h,W_h$ and $U_o,V_o,W_o$ represent diagonal points of the quadrangles $G_a{G}_b{G}_c{G}_d$, $H_a{H}_b{H}_c{H}_d$ and $O_a{O}_b{O}_c{O}_d$, respectively then triples of points $U_g,U_h,U_o$; $V_g,V_h,V_o$; $W_g,W_h,W_o$ are collinear and $U_o{U}_g:U_g{U}_h=V_o{V}_g:V_g{V}_h=W_o{W}_g:W_g{W}_h=1:2$ is valid.

3.3. Isogonality with respect to the triangles $BCD$, $ACD$, $ABD$, $ABC$

If two lines $\mathcal{L}$ and ${\mathcal{L}}^{\prime }$ have slopes $\frac{m}{n}$ and $\frac{m^{\prime }}{n^{\prime }}$, then for the oriented angle $\angle (\mathcal{L},{\mathcal{L}}^{\prime })$ the following formula is valid

$$tg\angle (\mathcal{L},{\mathcal{L}}^{\prime })=\frac{m^{\prime }n-m{n}^{\prime }}{m{m}^{\prime }+n{n}^{\prime }}.$$

(20)

The lines $AB,AC,AD$ have slopes $-\frac{1}{ab},-\frac{1}{ac},-\frac{1}{ad}.$ Let $D^{\prime }$ be point isogonal to the point D with respect to the triangle $ABC$ and let k be slope of $A{D}^{\prime }$. Then $\angle (AB,AD)=\angle (A{D}^{\prime },AC)$ and due to (20) we get

$$tg\angle (AB,AD)=\frac{ad-ab}{a^{2}bd+1},tg\angle (A{D}^{\prime },AC)=\frac{ack+1}{ac-k}.$$

Out of equality $\frac{ad-ab}{a^{2}bd+1}=\frac{ack+1}{ac-k}$ it follows

$$k=\frac{a^{2}bc-a^{2}bd-a^{2}cd-1}{a^{3}bcd+ab+ac-ad}.$$

(21)

We will show that the point

$$D^{\prime }=\left(\frac{d-a-b-c}{abcd-1},\frac{abd+acd+bcd-abc}{abcd-1}\right)$$

is isogonal point to the point D with respect to the triangle $ABC$. Because of symmetry on $a,b,c$ it is enough to show that the line $A{D}^{\prime }$ is isogonal to the line $AD$ with respect to the lines $AB$ and $AC$, i.e. that the line $A{D}^{\prime }$ have the slope k from (21). The points A and $D^{\prime }$ have the difference between coordinates

$$\begin{array}{ccc}\hfill a-\frac{d-a-b-c}{abcd-1}& =& \frac{1}{abcd-1}(a^{2}bcd+b+c-d),\hfill \\ \hfill \frac{1}{a}-\frac{abd+acd+bcd-abc}{abcd-1}& =& \frac{1}{a(abcd-1)(a^{2}bc-a^{2}bd-a^{2}cd-1)},\hfill \end{array}$$

so the line $A{D}^{\prime }$ have the slope k in (21). The point $D^{\prime }$ can be rewritten as

$$D^{\prime }=\left(\frac{2d-s}{p-1},\frac{r-2abc}{p-1}\right).$$

(22)

In the same way we can get the points $A^{\prime },B^{\prime },C^{\prime }$ isogonal to the points $A,B,C$ with respect to the triangles $BCD,ACD,ABD$, respectively. The centroid of these four points is the point

$$G^{\prime }=\left(-\frac{s}{2(p-1)},\frac{r}{2(p-1)}\right).$$

(23)

The point $D^{\prime }$ from (22) and its analogous point $C^{\prime }$ have the midpoint $(-\frac{a+b}{p-1},\frac{a+b}{p-1}cd)$ that lies on the line $AB$ from (3). The line $C^{\prime }{D}^{\prime }$ has the slope $ab$, hence it is perpendicular to the line $AB$. It means that $AB$ is the bisector of the line segment $C^{\prime }{D}^{\prime }$. Similarly, the same is valid for the analogous elements of the quadrangles $ABCD$ and $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$. Because, the sides $AB,AC,AD,BC,BD,CD$ of the quadrangle $ABCD$ are bisectors of sides $C^{\prime }{D}^{\prime },B^{\prime }{D}^{\prime },B^{\prime }{C}^{\prime },A^{\prime }{D}^{\prime },A^{\prime }{C}^{\prime },A^{\prime }{B}^{\prime }$, respectively. Out of earlier facts it follows that the points $A,B,C,D$ are the centers of the circles $B^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{B}^{\prime }{D}^{\prime }$, $A^{\prime }{B}^{\prime }{C}^{\prime }$, that can be directly proved analytically, because for the distance of the point $D^{\prime }$ from the point $A=(a,\frac{1}{a})$ we get

$$a^2{(p-1)}^{2}A{D^{\prime }}^2=a^2{(a^{2}bcd+b+c-d)}^2+{[a^2(nc-bd-cd)-1]}^2=(a^2{b}^2+1)(a^2{c}^2+1)(a^2{d}^2+1),$$

so by analogy we conclude that $A{D}^{\prime }=A{C}^{\prime }=A{B}^{\prime }$. We have proved the statement found in [2] and [13]:

Theorem 11. 

The points $A,B,C,D$ are the centers of the circles $B^{\prime }{C}^{\prime }{D}^{\prime }$, $A^{\prime }{C}^{\prime }{D}^{\prime }$,

$A^{\prime }{B}^{\prime }{D}^{\prime }$, $A^{\prime }{B}^{\prime }{C}^{\prime }$.

In [5] we find:

Theorem 12. 

The points $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$ are isogonal to the points $A,B,C,D$ with respect to the triangles $BCD,ACD,ABD,ABC$ if and only if the points $A,B,C,D$ are centers of the circles $B^{\prime }{C}^{\prime }{D}^{\prime },A^{\prime }{C}^{\prime }{D}^{\prime },A^{\prime }{B}^{\prime }{D}^{\prime },A^{\prime }{B}^{\prime }{C}^{\prime }$.

It means that the role of the quadrangle $ABCD$ for the the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ is the same as the role of the quadrangle $O_a{O}_b{O}_c{O}_d$ for the quadrangle $ABCD$. However, the points $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$ are isogonal to the points $A,B,C,D$ with respect to the triangles $BCD,ACD,ABD,ABC$. The following theorem stated in [2] and [4] is valid:

Theorem 13. 

The points $A,B,C,D$ are isogonal to the points $O_a,O_b,O_c,O_d$ with respect to the triangles $O_b{O}_c{O}_d$, $O_a{O}_c{O}_d$, $O_a{O}_b{O}_d$, $O_a{O}_b{O}_c$.

For the point $O_d$ from (19) the next equalities are valid

$$\begin{array}{ccc}\hfill x-\frac{s}{2}& =& \frac{1}{2}(\frac{1}{abc}-d)=-\frac{p-1}{2abc}\hfill \\ \hfill y-\frac{r}{2p}& =& y-\frac{1}{2}(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d})=\frac{1}{2}(abc-\frac{1}{d})=\frac{p-1}{2d},\hfill \\ \hfill (x-\frac{s}{2})(y-\frac{r}{2p})& =& -\frac{1}{4p}{(p-1)}^2.\hfill \end{array}$$

(24)

Hence, this point, as well as points $O_b,O_c,O_d$ are incident to the rectangular hyperbola ${\mathcal{H}}_0$ with the equation (24) and the center $O^{\prime }=(\frac{s}{2},\frac{r}{2p})$. Due to that, $O^{\prime }$ is the center of the quadrangle $O_a{O}_b{O}_c{O}_d$, and anticenter to $ABCD$. So, the following theorem is valid:

Theorem 14. 

The center $O^{\prime }$ of the quadrangle $O_a{O}_b{O}_c{O}_d$ is the anticenter of the quadrangle $ABCD$. The center O of this quadrangle is the anticenter of $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$.

Figure 2. The visualization of Theorem 12 and Theorem 14

Figure 2. The visualization of Theorem 12 and Theorem 14

Center of the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ is the point symmetric to the point O with respect to the centroid $G^{\prime }$ of this triangle, given by (23), so this center is the point $(-\frac{s}{p-1},\frac{r}{p-1})$. It is easy to see that the point $O_d$ from (19) and analogous points $O_a,O_b,O_c$ have the centroid $G_o=(\frac{s}{8p}(3p+1),\frac{r}{8p}(p+3))$. As $O^{\prime }=(\frac{s}{2},\frac{r}{2p})$ is the center of the quadrangle $O_a{O}_b{O}_c{O}_d$, the anticenter is the point symmetric to the point $O^{\prime }$ with respect to the point $G_o$ and that is the point $O_o=(\frac{s}{4p}(p+1),\frac{r}{4p}(p+1))$.

If we apply a translation for the vector $[\frac{s}{p-1},-\frac{r}{p-1}]$ on the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$, then e.g. the point $D^{\prime }$ from (22) transfers to the point $D^{\prime \prime }=(\frac{2d}{p-1},-\frac{2abc}{p-1})$. In the same way we can get the points $A^{\prime \prime },B^{\prime \prime },C^{\prime \prime }$. All the four points have the same product of the coordinates, so they are all incident to the rectangular hyperbola ${\mathcal{H}}^{\prime \prime }$ with the centre O and with the same asymptotes as the rectangular hyperbola $\mathcal{H}$. Hence, the point O is the center of the quadrangle $A^{\prime \prime }{B}^{\prime \prime }{C}^{\prime \prime }{D}^{\prime \prime }$, so the point $(-\frac{s}{p-1},\frac{r}{p-1})$ is the center of the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$. Symmetric point to the latter point with respect to the centroid $G^{\prime }$ from (23) of the quadrangle $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ is the point O.

4. Discussion

Putting the complete quadrangle into such a coordinate system that its circumscribed hyperbola is rectangular and has the equation $xy=1$ allows us to prove many known properties by the same method. Thereat we come across some more quadrangles related to the referent one with some old and new results given.

That enables us to prove even more results in rich geometry of a complete quadrangle like an isoptic point, some circles related to the quadrangle etc. planned to be presented in some future papers.