Submitted:
09 November 2023
Posted:
10 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
3. Results
3.1. The center and anticenter of the quadrangle
3.2. A diagonal triangle of the quadrangle
3.3. Isogonality with respect to the triangles , , ,
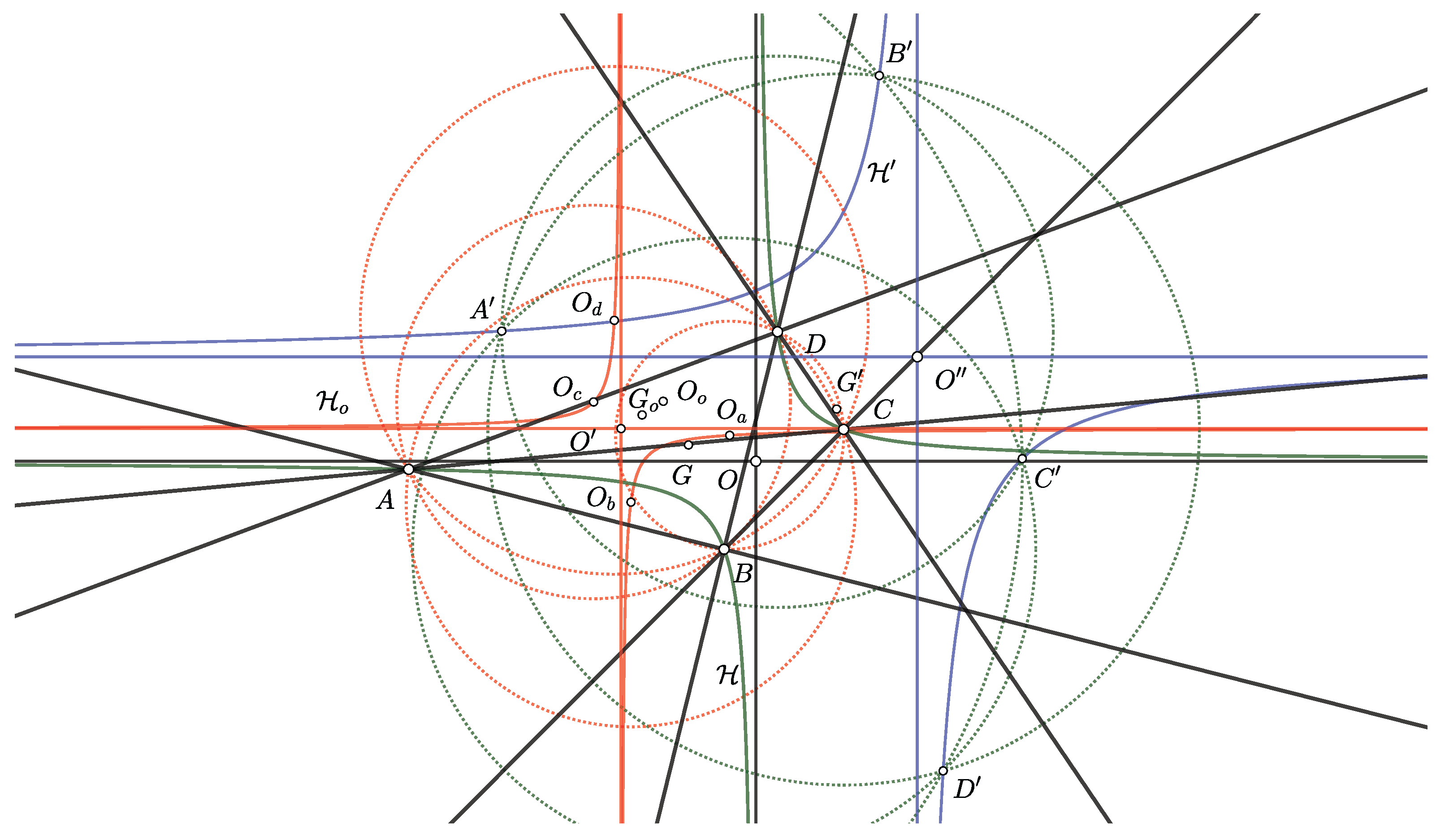
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Ayme, J.L. Le point d’Euler-Poncelet d’un quadrilatère, jl.ayme.pagesperso-orange.fr. Geometry 2010, 8, 133. [Google Scholar]
- Baumgartner, D.; Stärk, R. Ein merkwürdiger Punkt des Viereceks. Praxis Math. 2002, 44, 19–27. [Google Scholar]
- Brianchon, C. J.; Poncelet, J.V. Rechearches sur la détermination d’une hyperbole équilatère, au moyen de quatre conditions données. Ann. de Math. 1920-21, 11, 205–220. [Google Scholar]
- Cundy, H.M.; Parry, C.F. Geometrical properties of some Euler and circular cubics.PART 2. J. Geom 2000, 68, 58–75. [Google Scholar] [CrossRef]
- Grinberg, D. Isogonal conjugation with respect to a triangle. Unpublished notes September 23 2006, 56. Available online: https://www.cip.ifi.lmu.de/ grinberg/geometry2.html (accessed on September 7th 2023).
- Lawlor, J.H. Pedal circles. Math.Gaz. 1917, 9, 127–130. [Google Scholar] [CrossRef]
- Majo, A.de. Sur un point remarquable du quadrangle. Mathesis 1954, 63, 236–240. [Google Scholar]
- Mallison, H.V. Pedal circles and the quadrangle. Math. Gaz. 1958, 42, 17–20. [Google Scholar] [CrossRef]
- Myakishev, A. On two remarkable lines related to a quadrilateral. Forum Geom. 2006, 6, 289–295. [Google Scholar]
- Rolinek, M.; Dung, L.A. The Miquel points, pseudocircumcenter, and Euler-Poncelet point of a complete quadrilateral. Forum Geom. 2014, 14, 145–153. [Google Scholar]
- Schmidt, E. Euler-Gerade eines Vierecks. http://eckartschmidt.de/EULER.pdf, 2004, Theme 3, 12 S.
- Volenec, V. , Jurkin E., Šimić Horvath, M. On Quadruples of Orthopoles. Journal of Geometry 2023, 114, article–29. [Google Scholar] [CrossRef]
- Wood, P.W. Points isogonally conjugate with respect to a triangle. Math. Gaz. 1941, 25, 266–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



