Submitted:
17 April 2023
Posted:
17 April 2023
You are already at the latest version
Abstract
Keywords:
MSC: 51E20
1. Introduction and Motivation
2. The Singer Representation of PG(2,5)
| ω0=(1,0,0) | |||||
| ω1=(0,1,0) | ω2=(0,0,1) | ω3=(1,1,0) | ω4=(0,1,1) | ω5=(1,1,4) | ω6=(1,2,1) |
| ω7=(1,0,3) | ω8=(1,4,0) | ω9=(0,1,4) | ω10=(1,1,1) | ω11=(1,0,4) | ω12=(1,2,0) |
| ω13=(0,1,2) | ω14=(1,1,2) | ω15=(1,3,2) | ω16=(1,3,1) | ω17=(1,0,2) | ω18=(1,3,0) |
| ω19=(0,1,3) | ω20=(1,1,3) | ω21=(1,4,3) | ω22=(1,4,2) | ω23=(1,3,3) | ω24=(1,4,4) |
| ω25=(1,2,4) | ω26=(1,2,2) | ω27=(1,3,4) | ω28=(1,2,3) | ω29=(1,4,1) | ω30=(1,0,1) |

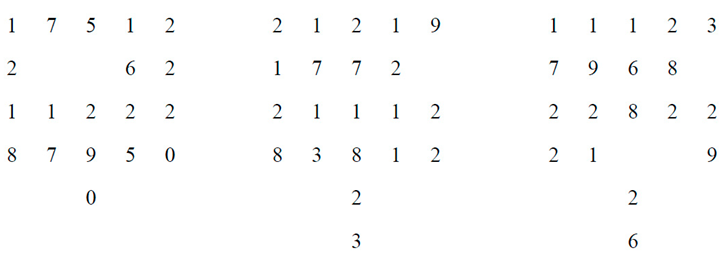
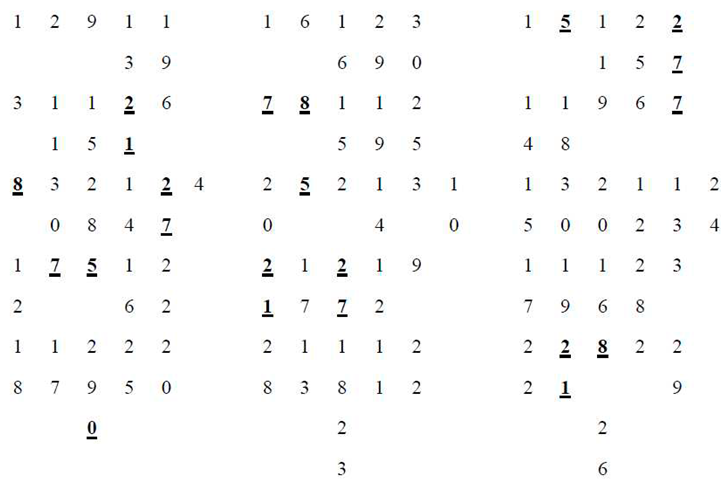
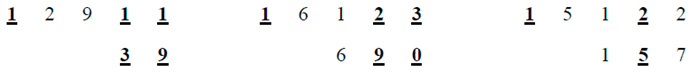
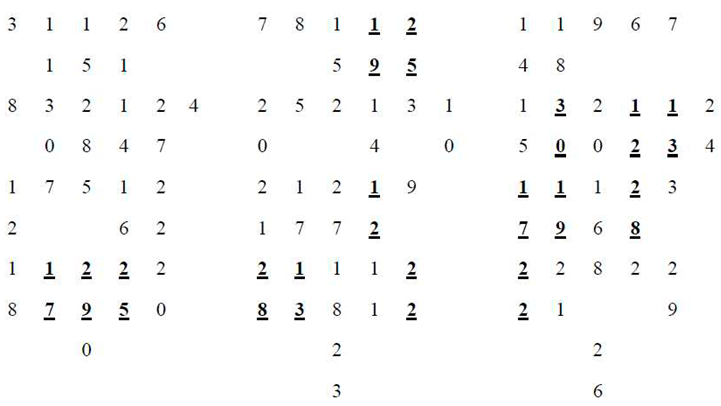
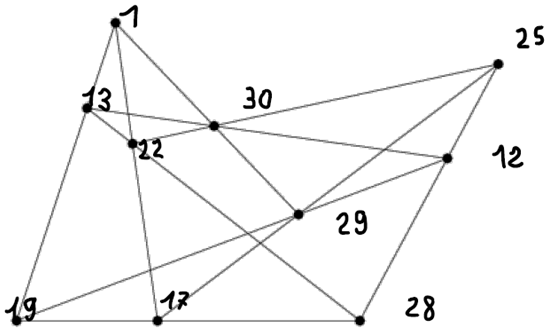
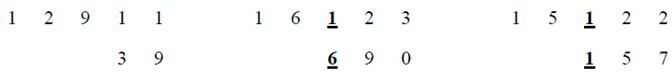

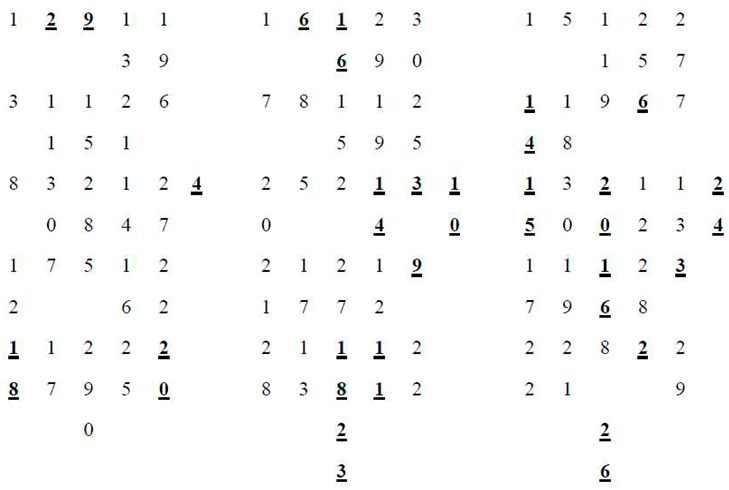

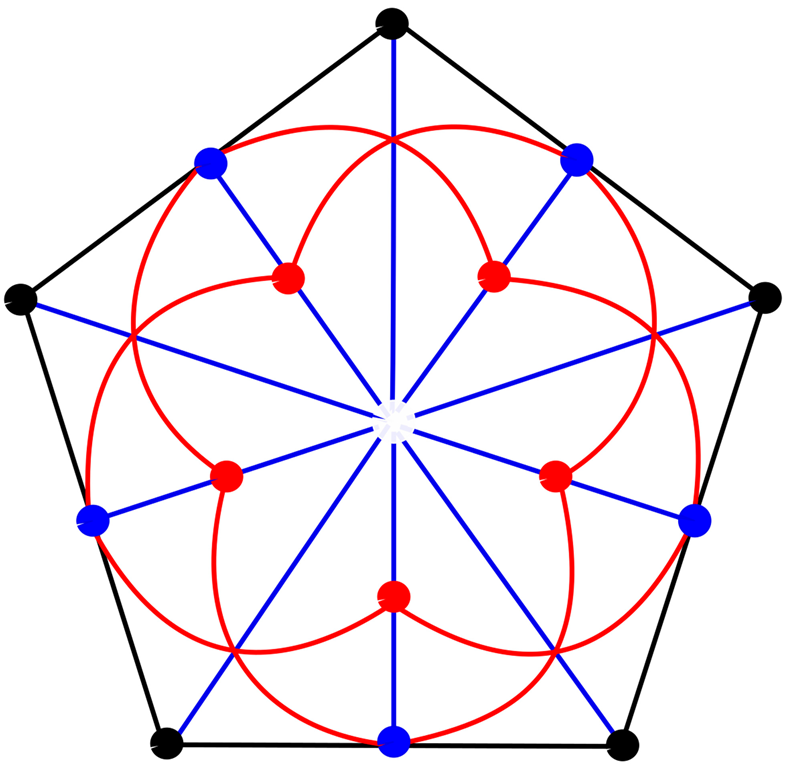
3. Conclusion
References
- Beutelspacher, A., A defense of the honour of an unjustly neglected little geometry or a combinatorial approach to the projective plane of order five. J. Geom. 30, 182-195 (1987). [CrossRef]
- Edge, W. L., 31-point Geometry, Math. Gaz. 39 (1955), 113-121.
- Havlicek, H., Lenz, H. Another simple proof for the existence of the small Witt design. Elem. Math. 56 89-94 (2001). [CrossRef]
- Hirschfeld, J. W. P., Projective geometries over finite fields, Clarendon Press, Oxford, Second Edition, 1998.
- Innamorati, S., Tondini, D., The yin-yang structure of the affine plane of order four, Ars Combin. 110 (2013), 193-197.
- Mancini, C., Zannetti, M., 21=9+12: PG(2,4)=AG(2,3)+DAG(2,3), Ars Combin. 135 (2017), 103-108.
- Saniga, M., Geometric Hyperplanes: Desargues Encodes Doily, HAL, Volume 2010, (2010) n. 0. http://gdmltest.u-ga.fr/item/hal-00550447/.
- Singer, J., A theorem in finite projective geometry and some applications to number theory, Trans. Am. Math. Soc. 43 (1938), 377-385.
- Tondini, D., An excursion in finite geometry, J. Interdiscip. Math. 22 (8) (2019), 1589-1595. [CrossRef]
- Tondini, D., The type of a point and a characterization of the set of external points of a conic in PG(2,q), q odd, J. Discrete Math. Sci. Cryptogr. 23 (5) (2020), 1077-1083. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




