1. Introduction
Chandrasekhar extensively analyzed the time-like and null-geodesic features of the Schwarzschild spacetime in his book [
1]. In addition, he has examined the orbital configurations of both the confined and unconfined trajectories using graphical representations. In addition, the authors in [
2] have examined the geodesic structures of the Schwarzschild anti-de Sitter spacetime. The researchers assessed both radial and non-radial paths for time-like and null geodesics. Additionally, they have demonstrated that the geodesic structures of this black hole exhibit distinct forms of motion that are not permitted by the Schwarzschild spacetime. The geometric framework of the Schwarzschild spacetime is also examined in [
3]. The Jacobi metric for time-like geodesics in static spacetimes has been examined in the reference [
4]. They have demonstrated that the unrestricted movement of large particles in stationary spacetimes is determined by the geodesics of a Riemannian metric that depends on the particle’s energy. This metric is similar to Jacobi’s metric in classical dynamics. When the mass of an object approaches zero, Jacobi’s metric becomes identical to the Fermat or optical metric, which does not depend on energy. In addition, they have provided a detailed account of the characteristics of the Jacobi metric pertaining to the motion of heavy particles beyond the event horizon of a Schwarzschild black hole. The authors of [
5] derived the Jacobi metric for different stationary metrics and developed the Jacobi-Maupertuis metric for time-dependent metrics by using the Eisenhart-Duval lift [
6,
7]. The authors in [
8] have documented the remarkable characteristics of the time-like geodesic structure when dark energy is present in an emergent gravity framework, specifically for the Barriola-Vilenkin metric [
9]. The K-essence emergent gravity metric is precisely correlated with the Barriola-Vilenkin (BV) metric for the Schwarzschild background, specifically for a certain form of K-essence scalar field [
10]. The researchers have analyzed the various paths that time-like geodesics can take in the presence of dark energy in the Barriola-Vilenkin spacetime [
8], which is equivalent to the Schwarzschild spacetime in terms of its fundamental structure. However, the permissible ranges for the maximum and minimum distances from the central object are significantly distinct. For a constant dark energy density, the orbits, both bound and unbound, are graphed.
In 1951, Vaidya proposed the first relativistic line element that properly represented the spacetime of a conceivable star [
11]. It extended the specific solution of Schwarzschild by depicting the emission of radiation for a mass that is not in a static state. The Schwarzschild solution describes the geometry of spacetime around a spherically symmetric, non-rotating, black object with a constant mass. Therefore, it is clear that the model is incapable of accurately depicting spacetime outside the confines of a star. The solution proposed by Vaidya [
11], known as the Vaidya spacetime or the radiating Schwarzschild metric, was introduced as a possible explanatory framework. The main distinction between the two metrics is that the Vaidya metric adds a time-dependent mass parameter, whereas the Schwarzschild metric uses a constant mass value. As a result, the spacetime in the Vaidya metric evolves with time. The Vaidya metric is primarily used to investigate gravitational collapse. The occurrence of gravitational collapse is widely acknowledged in the disciplines of general relativity and astrophysics, as demonstrated by the research conducted by Joshi et al. [
12,
13,
14,
15,
16,
17,
18,
21]. It plays a vital role in understanding several astrophysical aspects of our cosmos. The phenomenon of gravitational collapse provides useful insights into several elements of astronomy, including the evolution of structures, the features of stars, the genesis of black holes, and the construction of white dwarfs or neutron stars, among other events. Gravitational collapse refers to the phenomenon in which a star collapses as a result of its mass. The outcome of this collapse might vary depending on the exact beginning mass conditions, leading to distinct stages of collapse. Papapetrou [
19] was the first to demonstrate that the solution of a null dust fluid with spherical symmetry in gravitational collapse can lead to the creation of naked singularities. This statement presents a counterexample of the cosmic censorship hypothesis (CCH) as proposed by Penrose [
20]. The authors in [
14,
22] have provided a detailed account of the causal paths that connect the singularities in the continuing Vaidya scenario. Furthermore, a comprehensive classification of the non-spacelike geodesics that link the naked singularity in the past is presented, offering a rather thorough discussion of the restrictions involved. It is subsequently demonstrated to be a robust curvature singularity in a more significant manner.
The Vaidya solution, as a generalization, encompasses all the established solutions of Einstein’s field equations that include a mix of Type-I and Type-II matter fields [
23,
24,
25,
26,
27,
28]. The composition of this work is attributed to Husain [
29] and Wang & Wu [
30]. The extension of the Vaidya solution is sometimes referred to as the generalized Vaidya spacetime. The work performed in [
31] examines the gravitational collapse of the generalized Vaidya spacetime within the framework of the cosmic censorship theory. They demonstrated that the categories of generalized Vaidya mass functions had emerged in the situation, suggesting the end of collapse with a locally visible central singularity. The authors computed the magnitude of these singularities. A comprehensive mathematical framework was created to examine the requirements for the mass function for non-spacelike geodesics going towards the future to end at the singularity in the past. Furthermore, they demonstrated that, when considering a certain generalized Vaidya mass function, the ultimate outcome of the collapse can be precisely defined as either a black hole or a naked singularity. The work by Patil [
32] examines the phenomenon of gravitational collapse in higher dimensions within the context of the charged-Vaidya spacetime. It has been demonstrated that singularities occur in a charged null fluid in a higher dimension. These singularities consistently lack any form of covering, hence contradicting the strong CCH. This idea does not specifically pertain to weak cosmic censorship. The Vaidya metric has received significant attention in scholarly research, with several major contributions to our comprehension of this subject. The authors of the study [
33] examined the geometric properties of Vaidya’s spacetime while considering a white hole that undergoes a decrease in mass. They found that the white hole can either stabilize and transform into a black hole within a limited or indefinite amount of time, or entirely evaporate. The researchers have focused specifically on the scenario of total evaporation over an indefinite period of time. They have successfully demonstrated the presence of an asymptotic light-like singularity in the conformal curvature, which connects both the past space-like singularity and the future time-like infinity. Vertogradov [
34] conducted a study on the structure of the generalized Vaidya spacetime, specifically focusing on the case when the matter field of type-II follows the equation of state
. The findings of the study revealed the presence of an eternal naked singularity in this spacetime, which meets all energy conditions. Once formed, the singularity will remain perpetually uncovered by the apparent horizon. Nevertheless, the formation of the apparent horizon leads to the emergence of a white hole. Solanki et al. [
35] have derived precise mathematical equations that describe the changes in the photon sphere and the angular radius of the shadow in a certain Vaidya spacetime. The mass function
has been seen as a function of time that either increases or decreases linearly. The initial scenario can function as a basic representation of a black hole that is accumulating matter, whereas the subsequent scenario can be seen as an illustration of a black hole that is emitting radiation, as theorized by Hawking.
In the realm of K-essence geometry, Manna et al. [
36] were the first to establish a link between K-essence geometry and Vaidya spacetime. They achieved this by introducing a new definition of the generalized Vaidya mass function, which directly depends on the kinetic energy of the K-essence scalar field. Subsequently, Manna et al. [
37] demonstrated that the K-essence emergent gravity metric bears a strong resemblance to the recently found generalized Vaidya metrics for the collapse of a null fluid. This similarity arises from the presence of a k-essence emergent mass function. Notably, Manna’s analysis exclusively considers the K-essence scalar field as a function of either the advanced or the retarded time. The recently developed K-essence model, known as the K-essence emergent Vaidya spacetime, has successfully met all the necessary energy conditions. The presence of the centrally exposed singularity and the intensity and stability of the singularities in the K-essence emergent Vaidya metric yield intriguing results in their research. The evaporation of the dynamical horizon with the Hawking temperature in the K-essence Vaidya Schwarzschild spacetime was investigated by Manna et al. in [
38]. This study uses the dynamical horizon equation to quantify the reduction in mass caused by Hawking radiation. Additionally, the tunneling formalism, namely the Hamilton-Jacobi technique, is utilized to compute the Hawking temperature. In addition, Sawayama’s revised explanation of the dynamical horizon [
39] is utilized to demonstrate that the results obtained differ from the conventional Vaidya spacetime geometry. The authors have established by analytical measures that the mass of the black hole, denoted as
, in the K-essence emergent Schwarzschild-Vaidya spacetime, consistently decreases over time but does not fully evaporate.
The K-essence theory is a scalar field model that deviates from the canonical form. In this theory, the dominant energy component of the field is its kinetic energy, rather than its potential energy. This concept and related others have been extensively studied by several researchers [
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51]. The distinctions between the K-essence theory employing a non-canonical Lagrangian and the relativistic field theories utilizing a canonical Lagrangian are found in the sophisticated dynamical solutions of the K-essence equation of motion. These solutions not only spontaneously violate Lorentz invariance but also alter the metric for the perturbations around them. The disturbances propagate in the emergent or analogous curved spacetime, characterized by a metric distinct from the gravitational metric. The non-canonical Lagrangian may be expressed as
, where,
,
is the K-essence scalar field,
is the potential term. An alternate form of the Lagrangian, as described by Tian [
52], may be represented as
, where
,
and
are constants,
, and
and
are arbitrary functions. The functions
and
are unrestricted and can have any form. Furthermore, it is important to mention that there exist examples of K-essence theories that are not minimally linked, as mentioned in the Refs. [
53,
54,
55]. Nevertheless, this article only addresses the minimally coupled K-essence theory, as investigated by the Refs. [
40,
41,
42,
43,
44,
45,
46,
47,
48,
51]. In a general sense, the Lagrangian has the capacity to depend on any functions of
and
X. The K-essence theory offers the benefit of circumventing both the fine-tuning problem and the coincidence problem [
56] of the current universe. Additionally, it generates the negative pressure required for the universe’s acceleration only through the kinetic energy of the field. The kinetic term of the field dominates over the potential term. The article [
45] presents attractor solutions where the dynamics of the cosmos are governed by the scalar field of the models. During the radiation-dominated phase, the K-essence field mimicked the equation of state of radiation and had a constant ratio to the radiation density. The K-essence field was unable to replicate the dust-like equation of state (EOS) due to dynamical limits during the time dominated by dust. However, it rapidly reduced its energy value by many orders of magnitude and eventually reached a constant value. Subsequently, over a period approximately equivalent to the current age of the universe, the density of matter was diminished by the K-essence field, leading to the commencement of cosmic acceleration. The equation of state (EOS) of the K-essence theory ultimately converges to a value within the range of 0 to -1. Although in theory, it has the potential to extend beyond
. Another intriguing aspect of the K-essence idea is its potential to generate a type of dark energy where the speed of sound is consistently slower than that of light. This feature may mitigate the cosmic microwave background (CMB) disruptions on large angular scales [
57,
58,
59]. In this specific situation, Manna et al. [
8,
10,
36,
37,
38,
63,
64,
65,
66,
67,
68] have developed a fascinating emergent gravity metric referred to as
. This metric possesses distinct attributes in contrast to the standard gravitational metric
and is derived from the notions of the Dirac-Born-Infeld (DBI) type action, as outlined in the works [
71,
72,
73,
74]. Dirac et al. [
74] proposed a non-canonical Lagrangian in order to eliminate the infinite self-energy of the electron, as described in their work. The specific reasons and objectives for selecting the non-canonical theory, such as the K-essence theory, may be found in the Refs.[
69,
70]. The Planck collaborations’ findings, as shown in Refs. [
60,
61,
62], have examined the empirical evidence supporting the concept of K-essence with a DBI-type non-canonical Lagrangian, along with other modified theories. Furthermore, it has been noted that the K-essence theory may be applied in a model that combines dark energy and dark matter [
8,
10,
46,
63,
64,
65,
66], as well as from a purely gravitational perspective [
36,
37,
38,
67,
68].
This article is organized as follows: In
Section 2, we provided a concise explanation of the K-essence geometry and its connection to the conventional generalized Vaidya spacetime, which leads to the construction of a new generalized K-essence Vaidya spacetime.
Section 3 offers a comprehensive analysis of the geodesic structures observed in the generalized K-essence Vaidya spacetime. This analysis considers two forms of mass function while ensuring that the condition on the kinetic energy of the K-essence scalar field is maintained. This section also provides a detailed analysis of the radial and non-radial geodesics used to examine the structure of time-like and null geodesics in the given spacetime. This is achieved by solving the Euler-Lagrange equations. The graphical and numerical analysis is also done in this section. In
Section 4, we have wrapped up both the discussion and conclusion.
2. Brief of the relation between K-essence with generalized Vaidya spacetime
This section offers a short introduction to the geometry of K-essence and the generalized Vaidya spacetime. Initially, we present a brief summary of the geometric aspects related to the K-essence, as extensively explored in many scholarly references [
40,
41,
42,
43,
44,
45,
46,
47,
48,
51]. The action performed by this geometry is
where the expression
represents the canonical kinetic term, whereas
denotes the non-canonical Lagrangian. In this scenario, the conventional gravitational metric
has formed a minimum coupling with the K-essence scalar field (
).
The energy-momentum tensor that corresponds solely to the K-essence scalar field is:
where
and
is the covariant derivative defined with respect to the gravitational metric
.
The equation of motion (EOM) for the K-essence scalar field is
where
with
and
.
Following [
8,
10,
36,
37,
63], the inverse metric can be written as
The Eqs. (
4), (
5) have physical relevance when
is nonzero, assuming a positive definite
. Eq. (
5) states that the emergent metric, represented as
, differs in its conformal properties from the metric
when considering non-trivial configurations of the scalar field
. Like canonical scalar fields, the variable
exhibits diverse local causal structural properties. It also differs from those that are defined using
. The EOM, as stated in Eq. (
3), is valid even when taking into account the implicit relationship between
L and
. Then the EOM Eq. (
3) is:
This study addresses the Dirac-Born-Infeld (DBI) type non-canonical Lagrangian, which is represented as
[
8,
10,
36,
69,
70,
71,
72,
73,
74]:
The K-essence paradigm posits that the prevalence of kinetic energy over potential energy results in the exclusion of the potential term in the Lagrangian equation (
7) [
69,
70,
71]. The squared speed of sound, represented as
, is determined by the expression
. Therefore, the Eq. (
5) for the effective emergent metric is expressed as:
since
is a scalar.
The Christoffel symbol corresponding to the emergent gravity metric given by Eq. (
8) can be written as [
8,
10,
69,
70]:
where
is the usual Christoffel symbol associated with the gravitational metric
.
Hence, the geodesic equation governing the K-essence geometry may be expressed as:
where
is an affine parameter.
The covariant derivative
[
41,
69,
70] linked with the emergent metric
gives
and the inverse emergent metric is
such as
.
Therefore, considering the extensive behavior that defines the dynamics of K-essence and general relativity [
42,
69,
70], the Emergent Einstein’s Equation (EEE) may be formulated as:
where
is constant,
is Ricci tensor and
is the Ricci scalar. Moreover, the energy-momentum tensor
is linked to this emergent spacetime.
Now, we will provide a concise overview of the K-essence emergent generalized Vaidya spacetime. In the cited work [
37], the author has introduced the concept of K-essence emergent generalized Vaidya spacetime. This framework considers the background gravitational metric to be the typical generalized Vaidya metric [
29,
30], while also satisfying the necessary energy requirements. The line element for the emergent generalized Vaidya metric in K-essence theory is as follows:
with
.
They have defined the K-essence emergent Vaidya mass function
where
is the usual generalized Vaidya mass function and
(
) is the non-zero kinetic energy of the K-essence scalar field.
The above-mentioned mass function pertains to the gravitational energy associated with the K-essence emergent gravity within a specified radius
r. Here, we substitute the Eddington advanced time coordinate with the conventional time coordinate, without any loss of generality, denoted as
. In this study [
37], the author has examined the effective K-essence emergent metric, as denoted by Eq. (
8). Additionally, the author has calculated all the components of the EEE (Eq. (
12)) and the necessary energy conditions. It is important to mention that the assumption about
contradicts local Lorentz invariance since, in general, spherical symmetry only requires
. The inclusion of the assumption of the independence of
, denoted as
, suggests that beyond this specific frame selection, a spherically symmetric
is indeed a function of both
t and
r. The K-essence theory permits the occurrence of Lorentz violation due to the fact that the dynamic solutions of the K-essence equation of motion spontaneously break Lorentz invariance and alter the metric for the perturbations around these solutions.
Furthermore, the authors in [
36] have successfully established a connection between the geometry of K-essence and the Vaidya spacetime. The researchers have developed a model of the Vaidya spacetime with generalized K-essence, which takes into account any spherically symmetric static black hole as the underlying spacetime. The line element of the new geometry is (using Eq. (
8):
gives the mass function
In this article [
36], the authors also have calculated all the components of EEE and required energy conditions. If we consider
, i.e., the background physical spacetime is Schwarzschild spacetime, the mass function may be expressed as:
Again, if we select the function
,
Q represents the charge of the Reissner-Nordström (RN) black hole in the physical spacetime. In this case, the related mass function [
36] is modified as
It is important to mention that the values of
must be between 0 and 1. Otherwise, the metric (
13) and (
15) cannot be specified properly, and the presence of a dynamical horizon is also questionable [
36,
37]. In order to maintain the energy conditions, it is evident that the
must be a monotonically increasing function of
t, with the condition
. The admissible configurations for the K-essence scalar field in the generalized Vaidya solution, in order to have a dynamical horizon, are subject to a highly restrictive constraint. It is important to note that the metrics mentioned above represent dynamical horizons rather than isolated or event horizons, as explained extensively in Ref. [
36,
37].
It is also noted that the time dependence in the given mass functions (Eqs. (
17), (
18)) arises from the kinetic energy of the K-essence scalar field. However, in the mass function Eq. (
14), the time dependence comes from both the usual generalized Vaidya mass and the K-essence scalar fields. Thus, considering the above situations of the K-essence generalized Vaidya spacetime, we may conclude that the K-essence Vaidya mass function adheres to the general form specified in Eq. (
14). Therefore, we may conclude that the background metric can be chosen from any standard gravitational metric, with the only alteration being the replacement of their masses with a background mass, which likewise satisfies the EEE equation.
4. Discussion and Conclusion
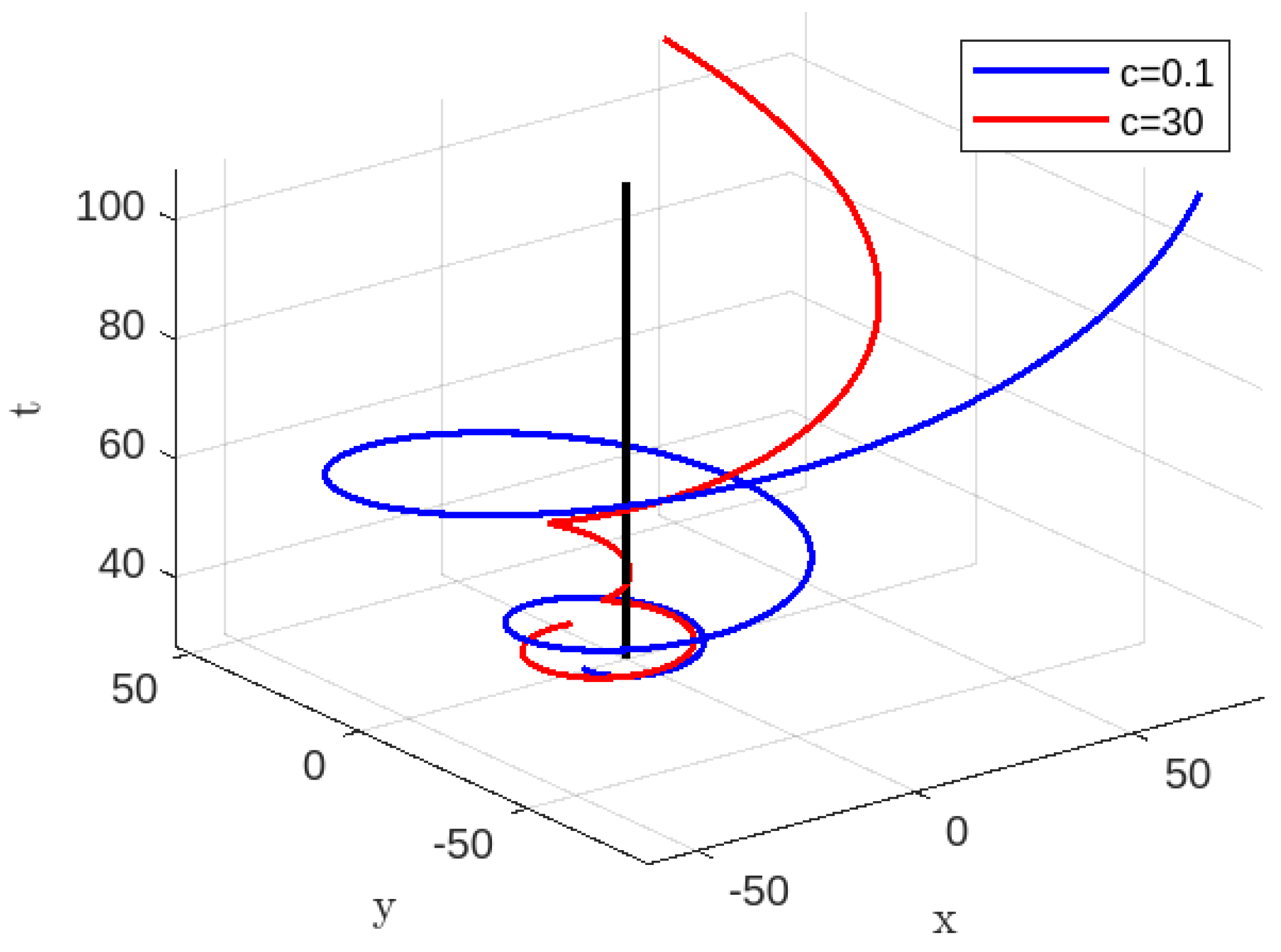
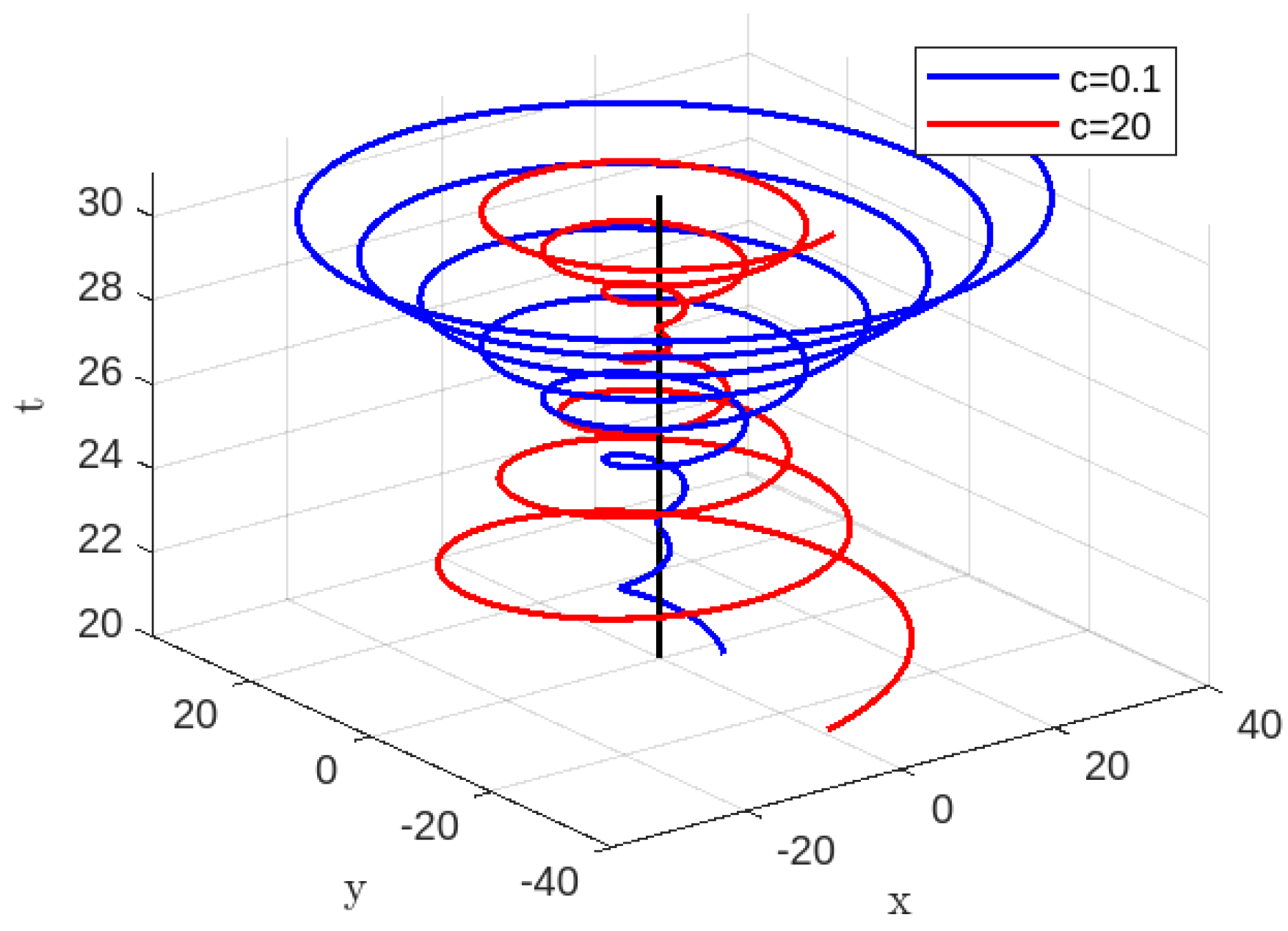
In the present investigation we have traced time-like geodesics and null geodesics for two different K-essence Vaidya Mass functions and on equatorial plane by using Euler-Lagrange equations. For both the cases, we observe that can be written in terms of energy . We have noticed that for the radial time-like and radial null geodesics for both the K-essence Vaidya masses, a particle having zero angular momentum starting from a finite distance takes a finite time to reach the singularity. For the first K-essence Vaidya mass function, there are two types of families for the time-like case that can be traced one for and the other for and similarly for the null case one for and the other for . But a bit of difference we observed for the second K-essence Vaidya mass function. There does exist only one type of family for the time-like case when and for the null case . For all the above-mentioned cases, for different finite value of arbitrary constants c, we have traced different kinds of orbits for both the generalized K-essence Vaidya mass function and the conclusions as follows:
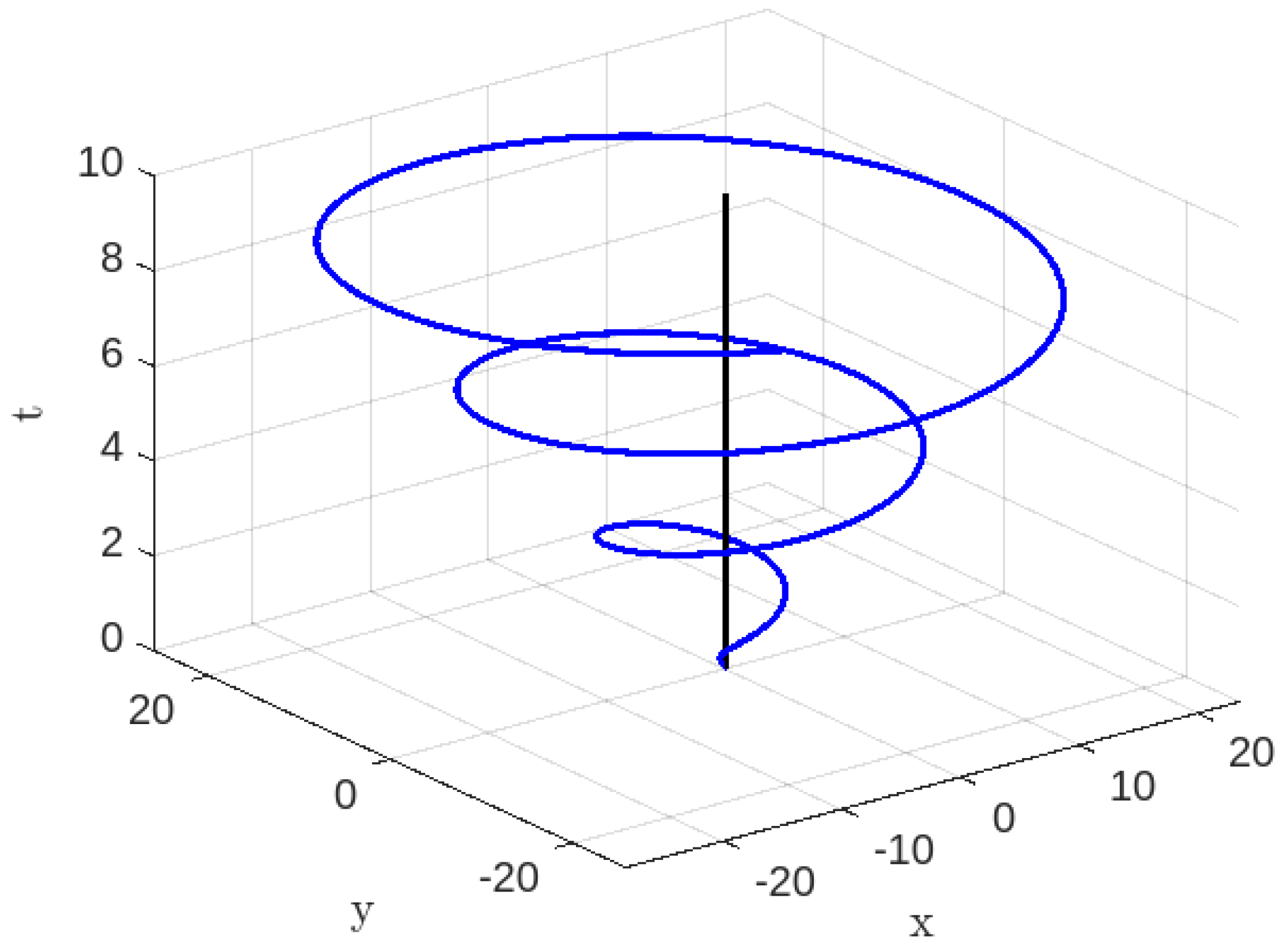
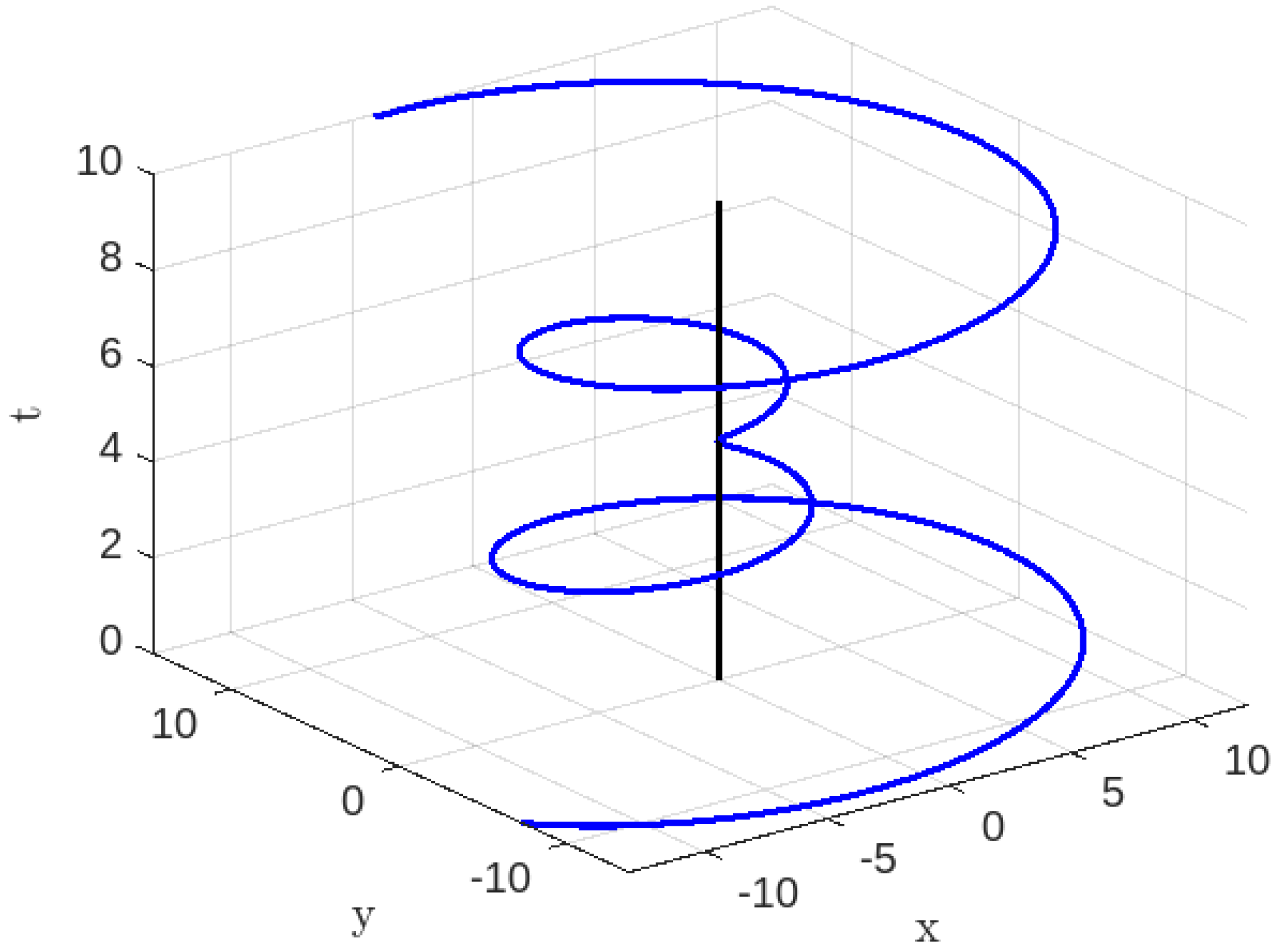
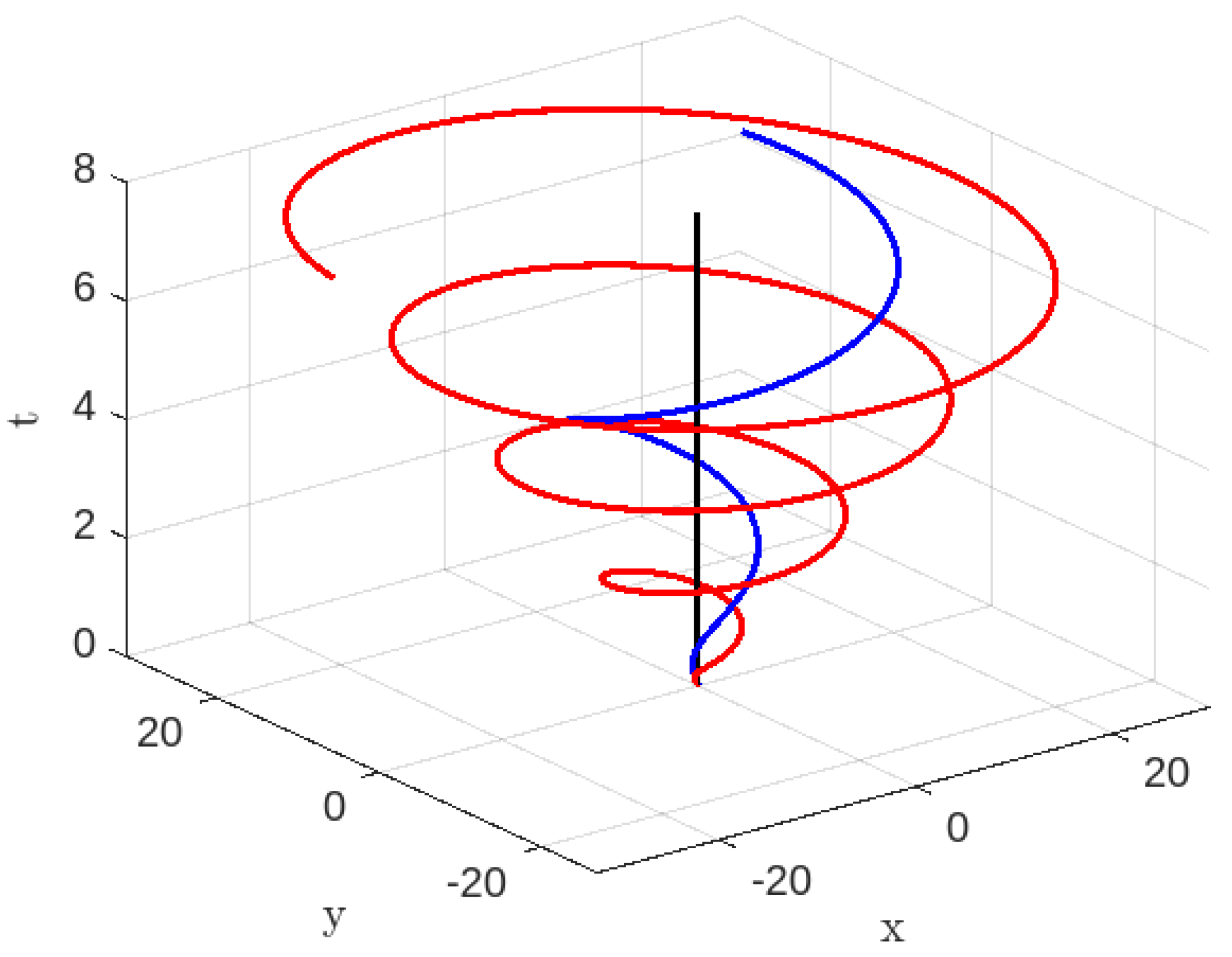
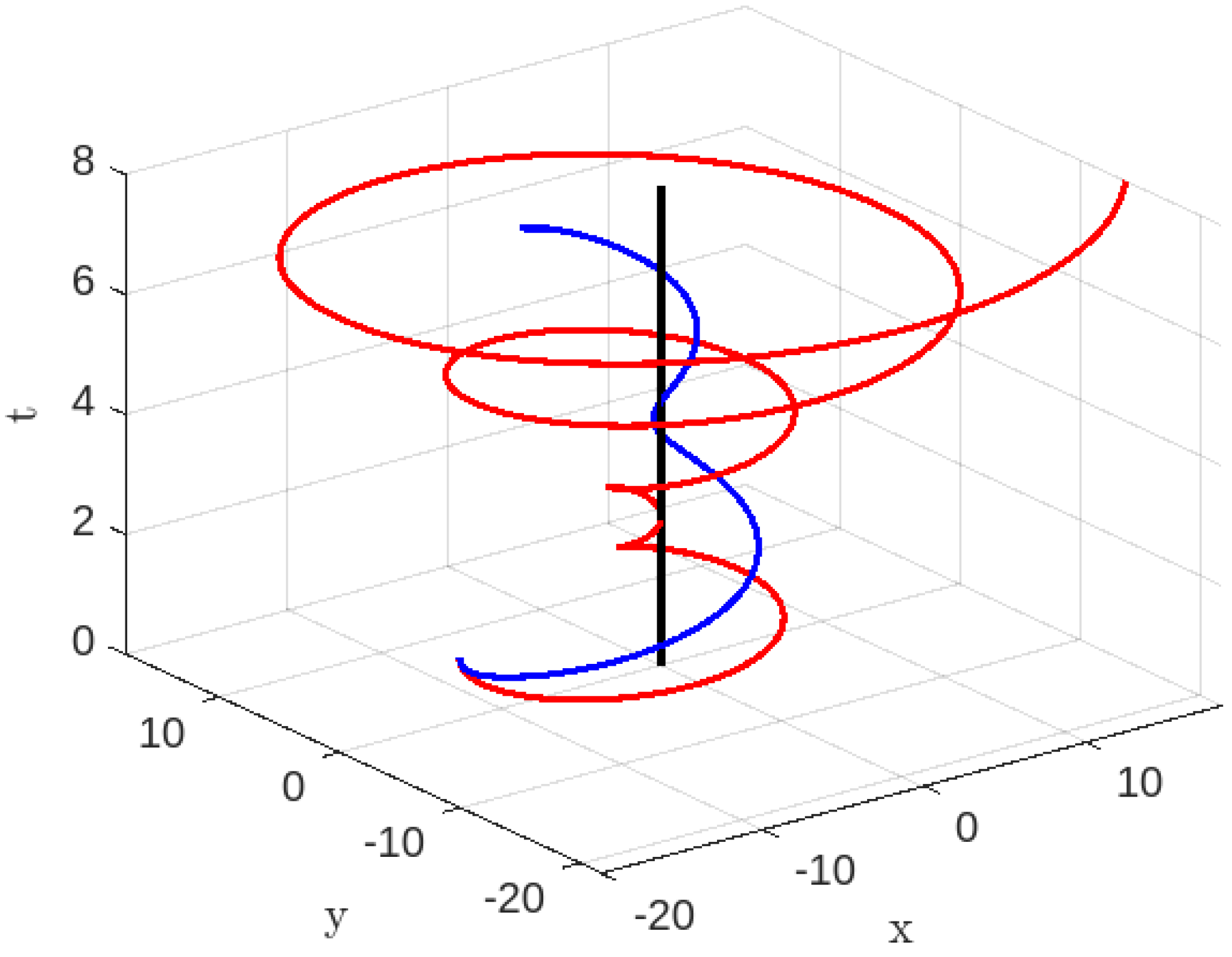
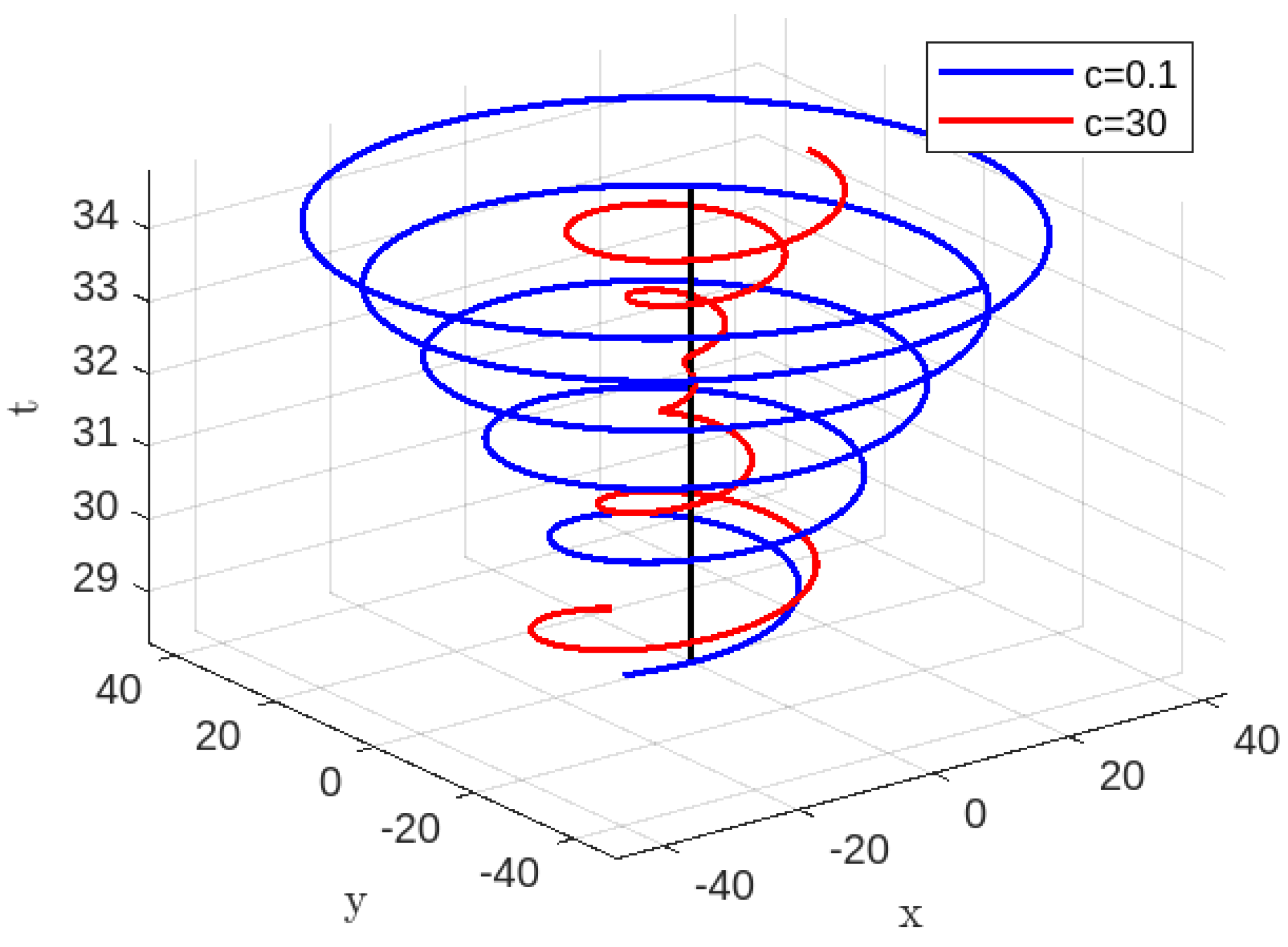
Based on
Figure 1, it may be inferred that a future observer will observe the particle approaching to the singularity within a finite amount of time, as previously stated. According to
Figure 2 –
Figure 4 it is evident that a future observer can watch the particle reaching at the singularity within a finite period and thereafter departing from it. Based on the information provided in
Figure 1,
Figure 2,
Figure 3,
Figure 4, for non-radial time-like geodesics of the generalized K-essence Vaidya spacetime (
13) with the first mass function (
17) or (
27), it can be inferred that there is a worry with the presence of a central singularity (where both
r and
t approach to 0). It is evident that the central singularity in the generalized Vaidya spacetime is defined by the limits
and
, as shown in [
21,
29,
31,
32,
37]. However, based on our analysis of the given data presented in
Figure 1,
Figure 2,
Figure 3,
Figure 4, we may conclude that when
r approaches zero,
t does not tend to zero. This phenomenon is also observed in the non-radial null geodesics with the same mass function but with varying finite time for different situations, as depicted in
Figure 5,
Figure 6,
Figure 7,
Figure 8. These phenomena can be explained as follows: a future observer is expected to see the particle approaching to the singularity and then moving away from it for a limited period of time (
51) or (
62) or (67) (non-radial time-like geodesic) and (
80) or (
95) or (
96) (non-radial null geodesic) in different situations. This observation could potentially indicate the presence of a wormhole during the extreme stages of spacetime, specifically the black hole and white hole, similar to the concept of the Einstein-Rosen bridge [
76,
77,
78,
79,
80,
81,
82,
83,
84,
85,
86,
87]. Regarding particles, it is clear that their signature is changed by the singularity. In this interesting scenario, it seems that the presence of a wormhole allows for the possibility of gravitational collapse resulting in either a naked singularity or a black hole and a white hole in the generalized
K-essence Vaidya spacetime with the given mass function (
27). Based on the analysis of collapsing scenarios in the generalized Vaidya spacetime, it has been established that there can be either a naked singularity or a black hole [
29,
37]. This is supported by the potential presence of a dynamical horizon, as discussed in [
88,
89,
90,
91]. On the other hand, Vertogradov [
34] has also addressed the issue and showed the presence of naked singularities as well as white holes within the framework of the usual generalized Vaidya spacetime in a different setting. However, in our case, the results are a bit different as we have already mentioned that there is the possibility of either a naked singularity or a black hole and a white hole. If we look at all the aforementioned figures with a closer view then it actually reveals the presence of a wormhole situation also in between the black hole and white hole scenarios. But here the conditions being extremal (
and
) we have a membrane-type wormhole instead of a tunnel as has been usually suggested. Alternatively, the previous explanation can also be elucidated as follows: Given that the particle reaches the point at
and then escapes from there within a certain period, it may be possible that a quantum tunneling event occurs at the vicinity of the central singularity. Since there is a finite time at the typical singular region at
, it follows that there is likewise a finite probability of escaping the region at
. We also have a finite time (
43) and (
73) to approach the singularity for a particle for the radial time-like and null geodesic situations.
On the other hand, we have the characteristics of the radial and non-radial time-like or null geodesics structures for the case of the second mass function (
97). Through an analysis of the radial properties of the time-like and null geodesics, we have determined that the particle ultimately approaches the singularity at
within a limited amount of time, as shown by Eqs. (
108) and (
130) respectively. To investigate the non-radial geodesics of the specified spacetime (
13) with the mass function (
97), we have not found a finite expression for time for a particle to reach the singularity at
. However, we have obtained a transcendental equation for different possibilities, namely Eqs. (
122) or (
127) for time-like geodesics and Eqs. (
143) or (149) for null geodesics. But from these transcendental equations, we have analyzed the non-radial time-like or null geodesics through numerical and graphical analysis. Based on the
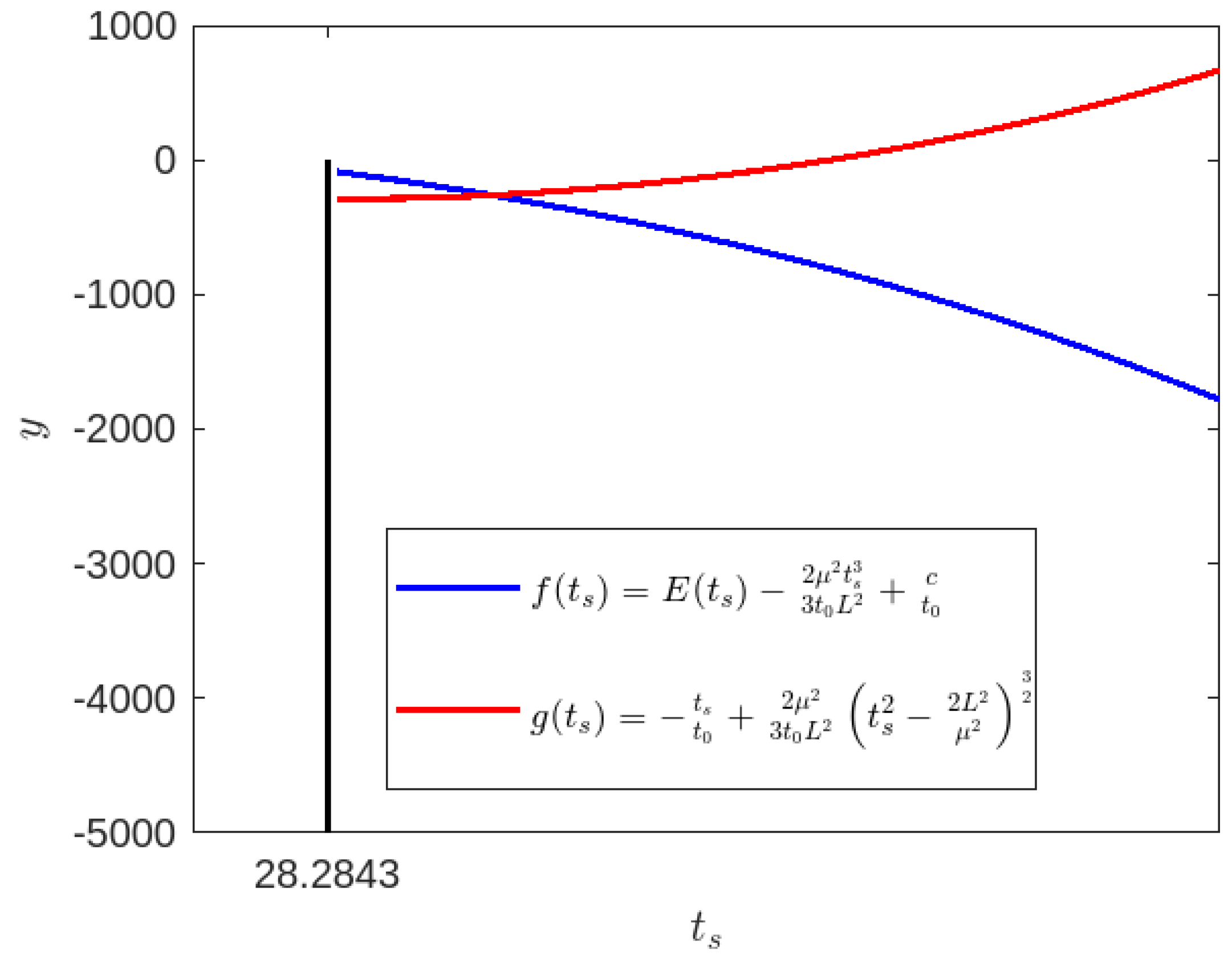
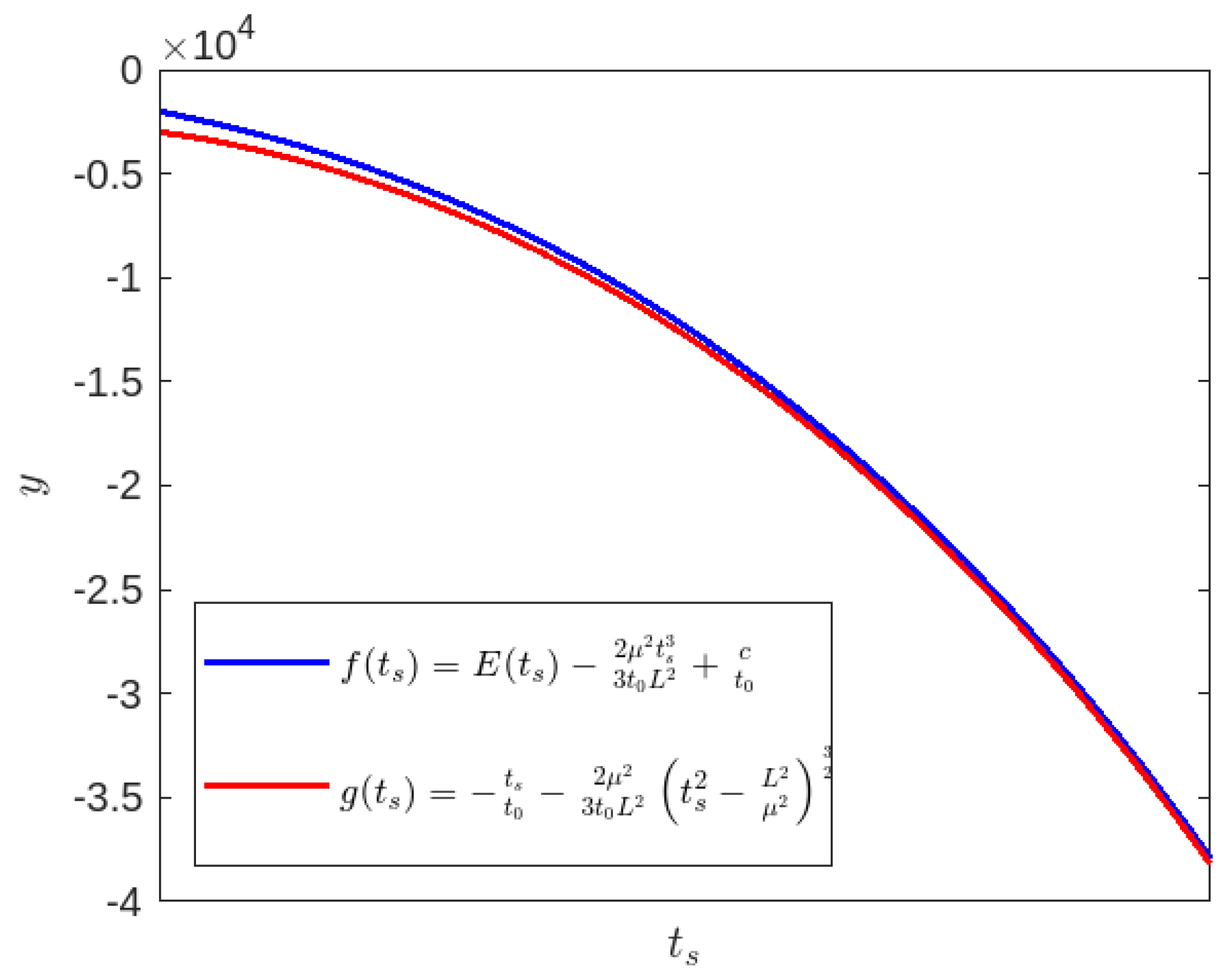
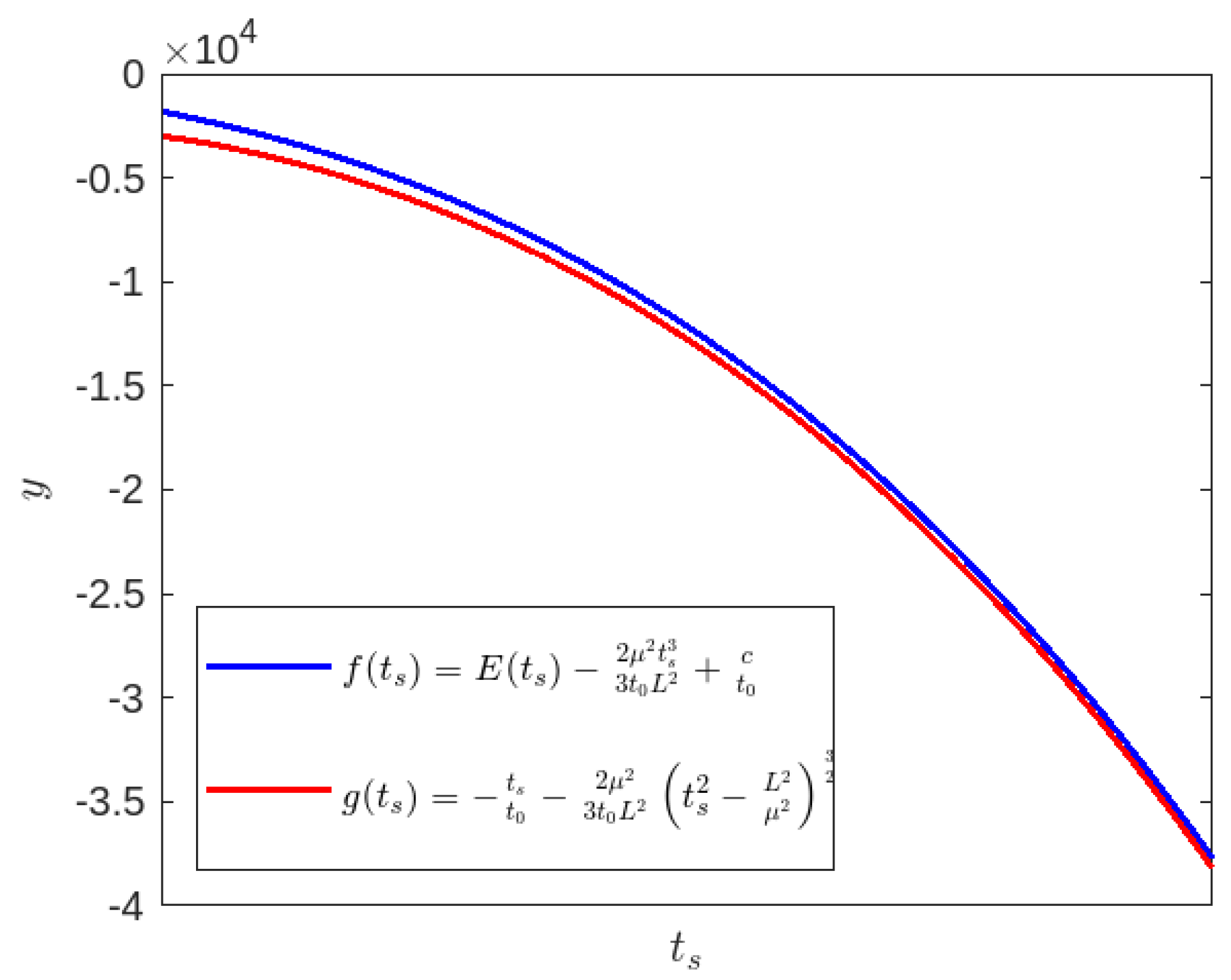
Figure 9 –
Figure 14, our investigation of non-radial time-like geodesics reveals that when
, the particle is unable to reach at the singularity at
(blue line). This phenomenon may be explained as follows: The presence of a black hole singularity with an event horizon might result in the spectator being unable to perceive the particle’s journey towards the singularity. Based on the aforementioned figures (red line), it has been observed that when the constant
is set to 30, the particle approaches to the singularity at
after a finite amount of time and subsequently moves away from it. Here, we also see the occurrence of a wormhole-like physical phenomenon or quantum tunneling effect near the singularity at
.
Regarding the non-radial null geodesic characteristics of the aforementioned spacetime and mass function (
97), we note that the transcendental Eqs. (
143) and (149) exhibit the same kind of solutions as Eq. (
131). In this situation also, we are yet unable to determine the expression for the time it takes to reach the singularity at
. After solving the transcendental equations using numerical analysis, we find the graphical solutions through the following figures, i.e.
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20 and
Figure 21. From
Figure 17, we have not found any tracing of the non-radial null geodesic structure for two choices of the constants
viz. and
though available for the choice of
, from
Figure 19 –
Figure 18. No traces of the non-radial null geodesic structure were noticed in the
Figure 17 for two different values of the constants, namely
and
. However, by setting
, as seen in
Figure 18, it is evident that the particle originates from a specific location and ultimately drops into the singularity. Alternatively, we have explored an additional solution to Eq. (
131) and its associated Eq. (149). We have analyzed the non-radial null geodesic structure and depicted it in
Figure 21. In this scenario, we note that for two specific values of the constants, namely
and
, the particle begins its trip from a fixed position and eventually reaches the singularity within a limited amount of time. After reaching at the singularity, the particle then escapes from it. This once again indicates the presence of a wormhole or the quantum tunneling effect.
Therefore, under the aforementioned discussion, we can conclude that in our specific model, we have investigated the existence of a wormhole during the extreme stages of spacetime, specifically the black hole and white hole, similar to the concept of the Einstein-Rosen bridge or quantum tunneling effect near the central singularity. This investigation was carried out in the comoving frame for the generalized K-essence Vaidya spacetime using two types of K-essence Vaidya mass functions. It is possible to argue that extra interactions between the K-essence scalar field and the usual gravity are the cause of this occurrence.
Moreover, based on the investigation of the present work, especially observations on the
Figure 2,
Figure 3,
Figure 4, one may raise the issue of the black holes and baby universes [
93] that whether there is any possibilities of such situations under the generalized
K-essence Vaidya spacetime. This obviously draws special attention and can be considered as a potential topic in the near future.
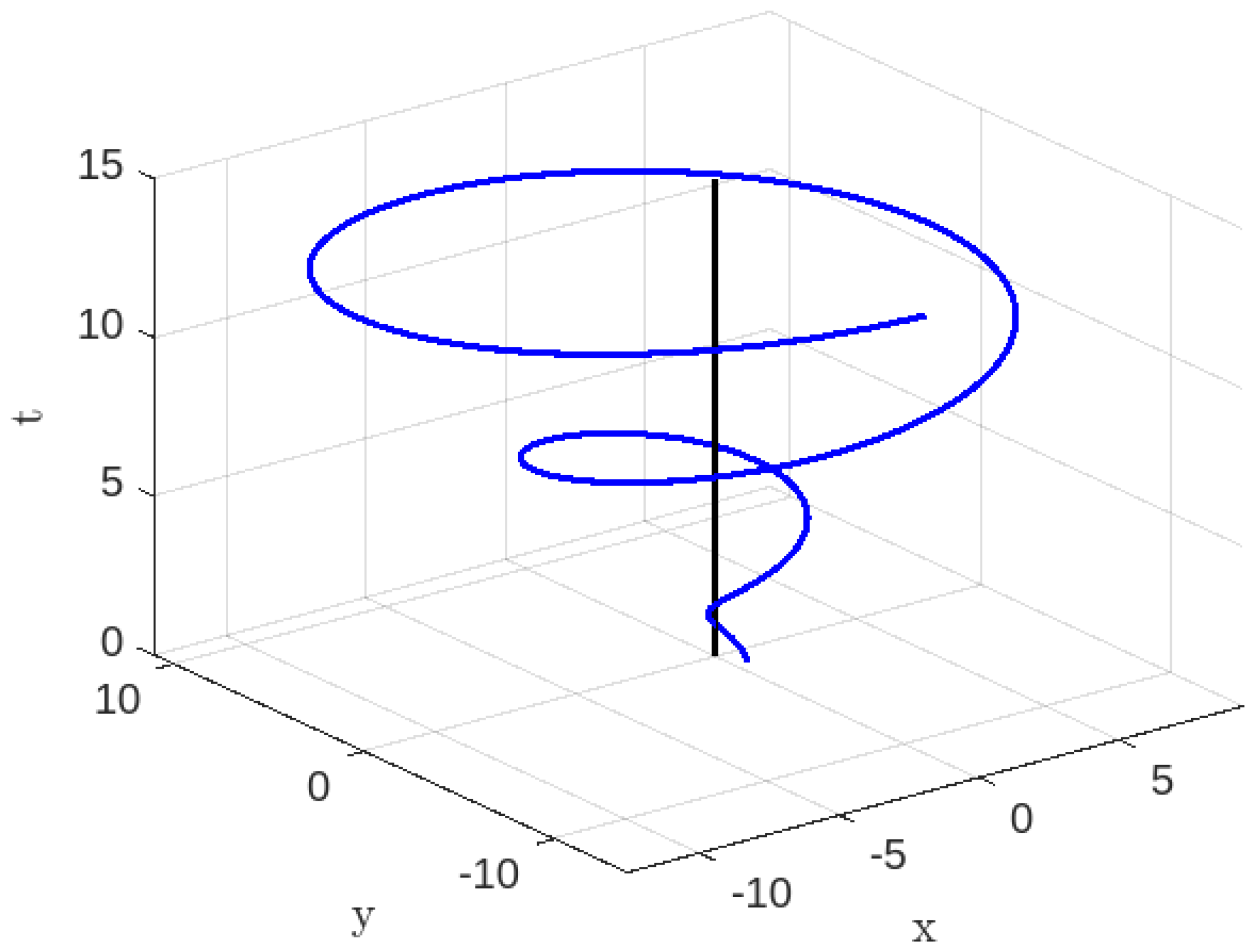
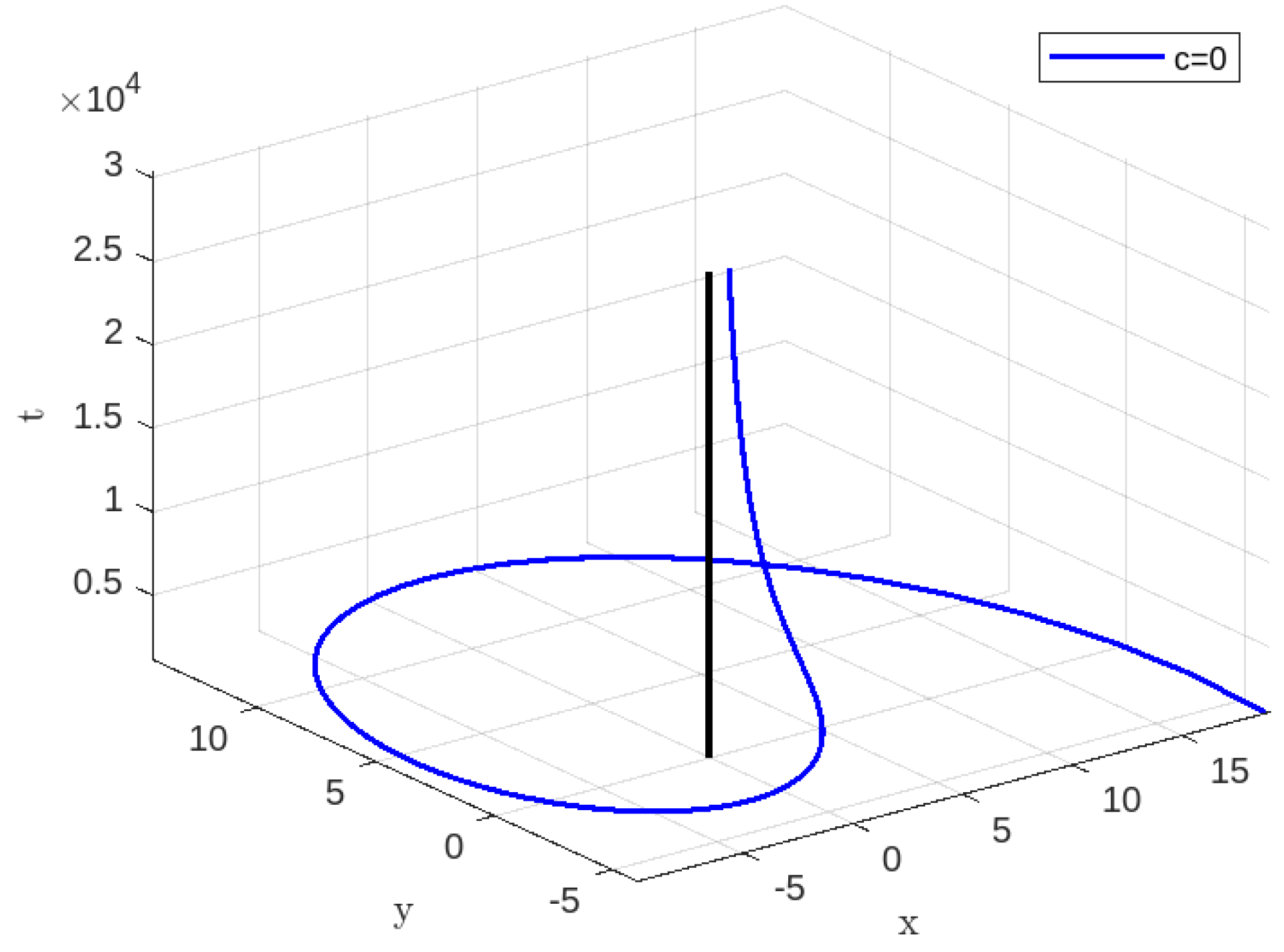
Figure 1.
Time-like geodesics for , , , .
Figure 1.
Time-like geodesics for , , , .
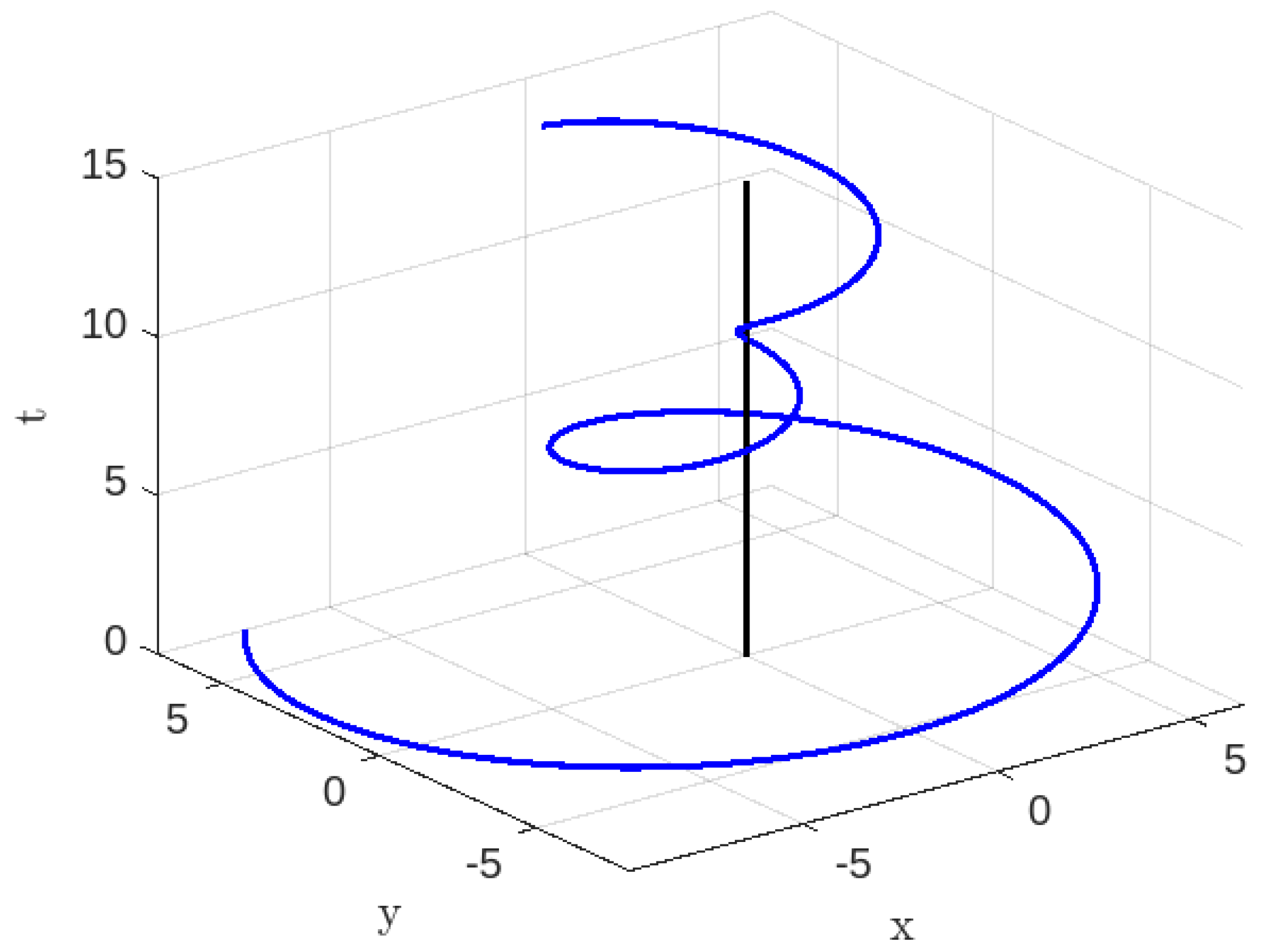
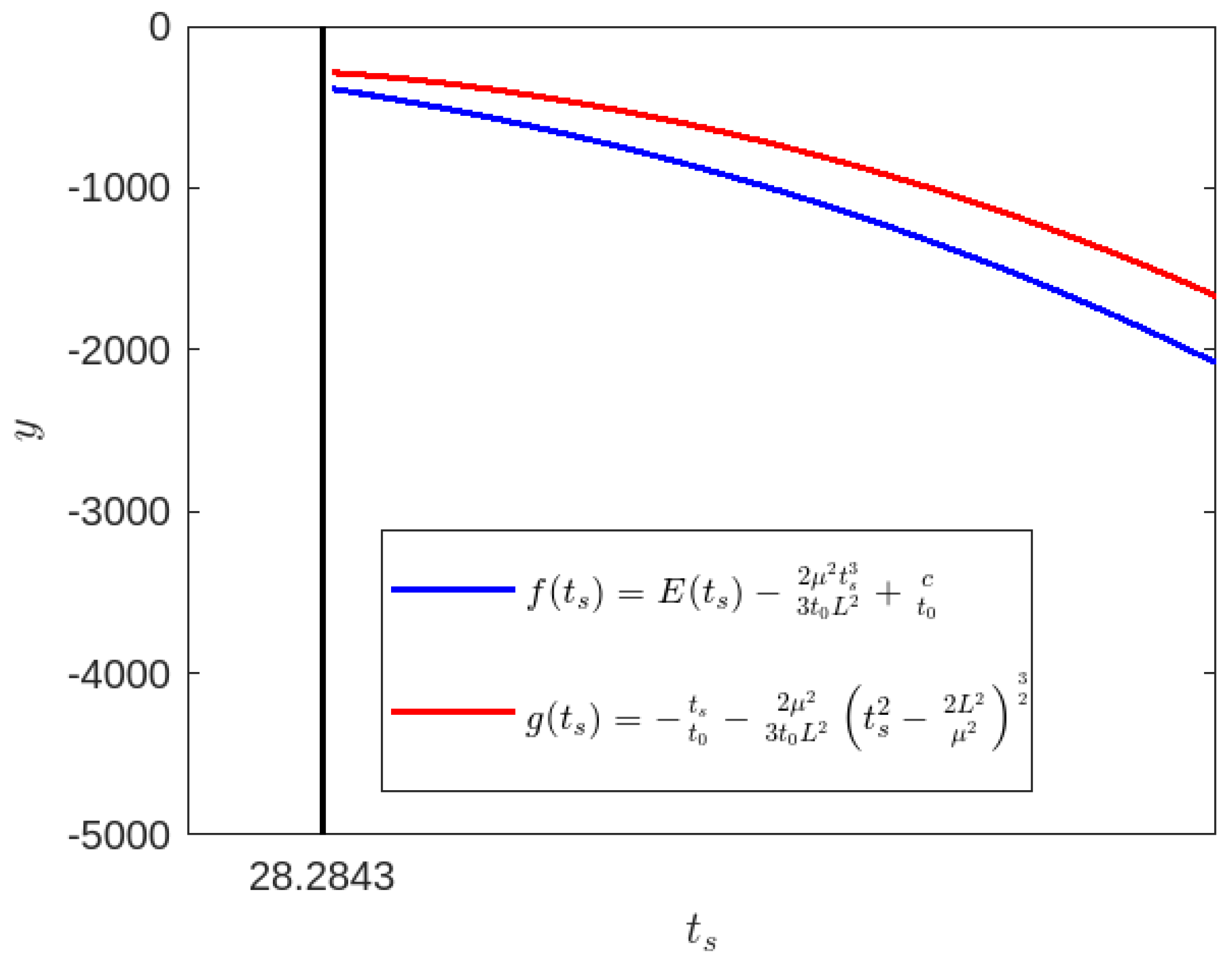
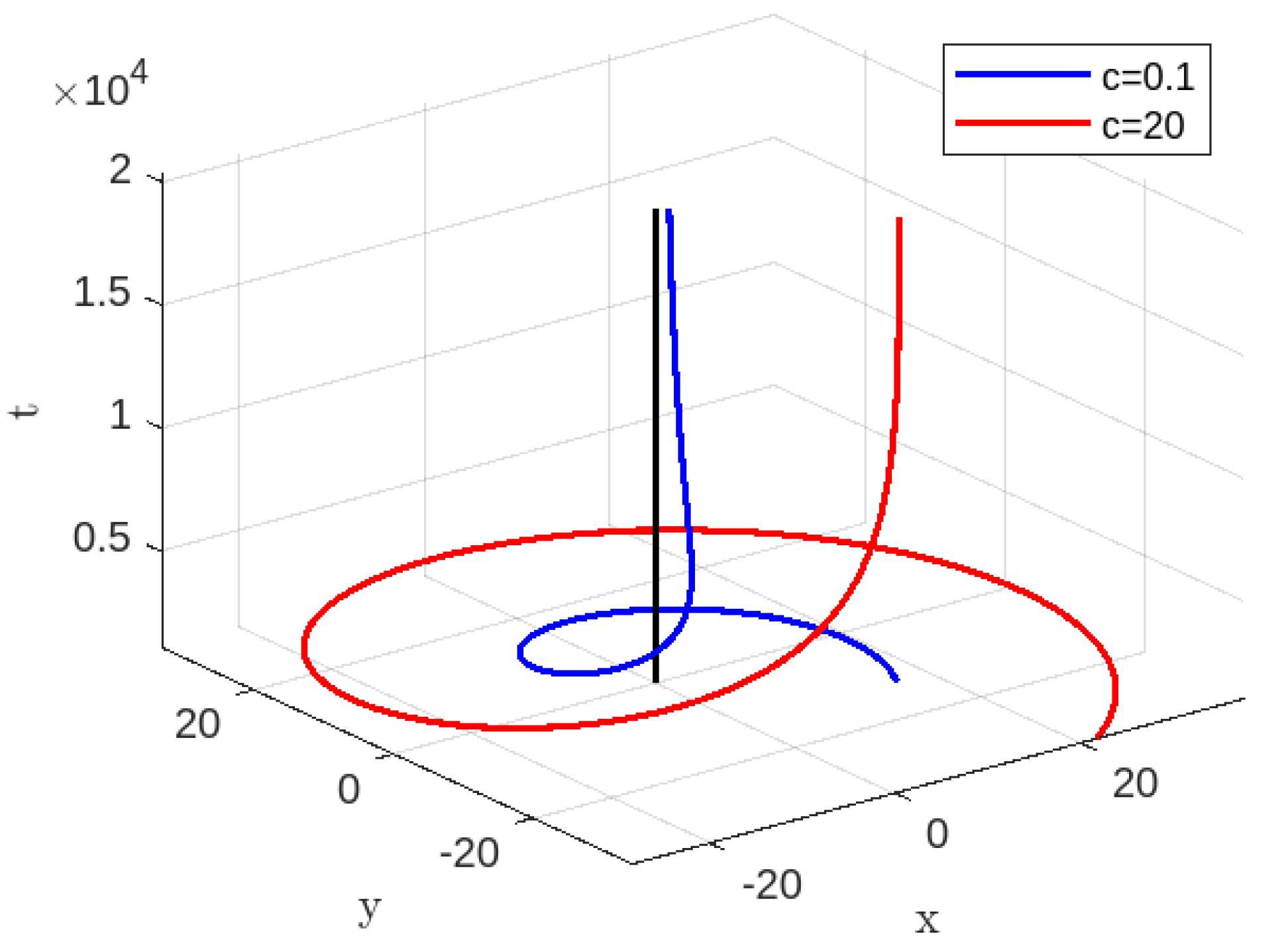
Figure 2.
Time-like geodesics for , , , .
Figure 2.
Time-like geodesics for , , , .
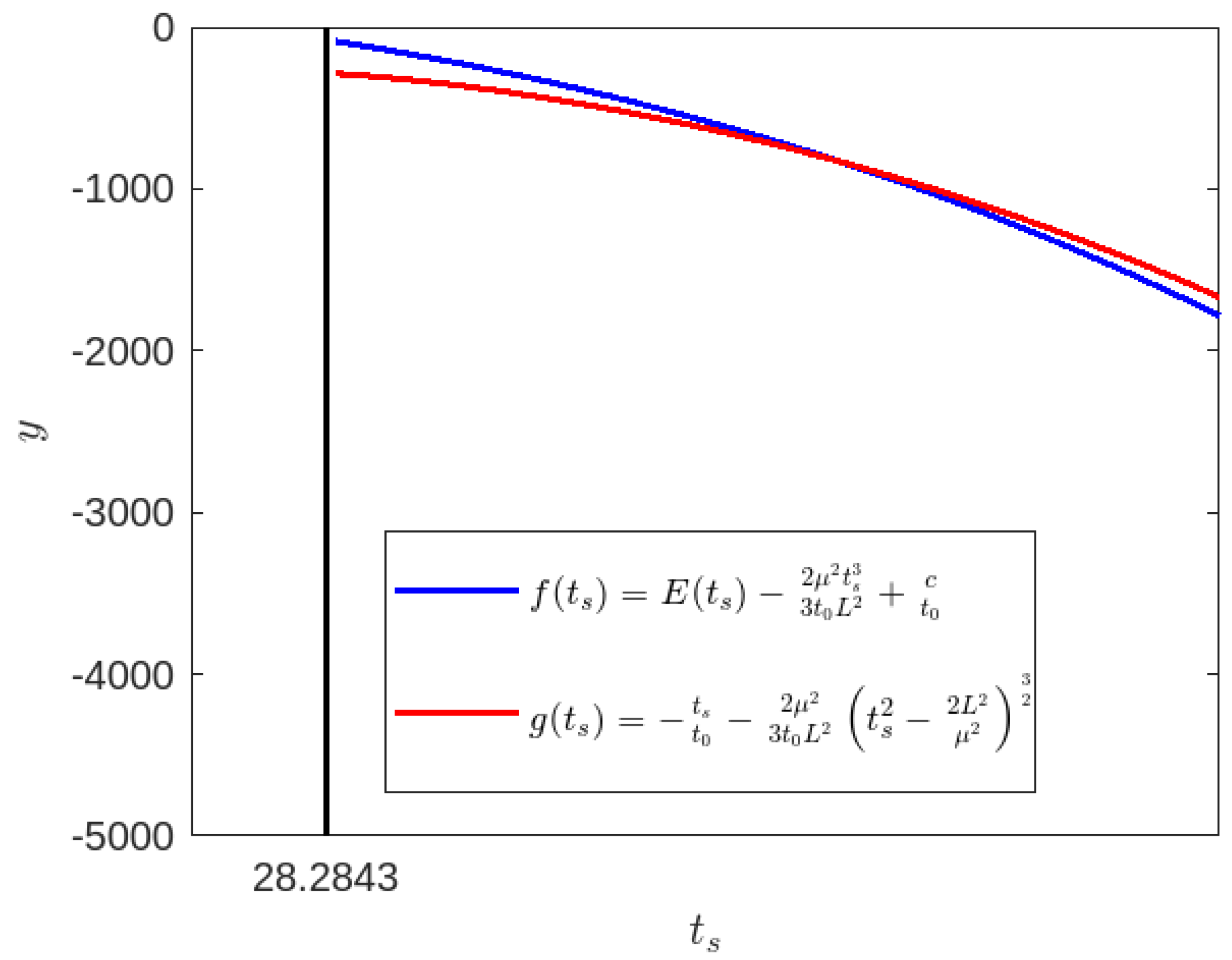
Figure 3.
Time-like geodesics for , , , : Blue Colour line for and Red colour line for
Figure 3.
Time-like geodesics for , , , : Blue Colour line for and Red colour line for
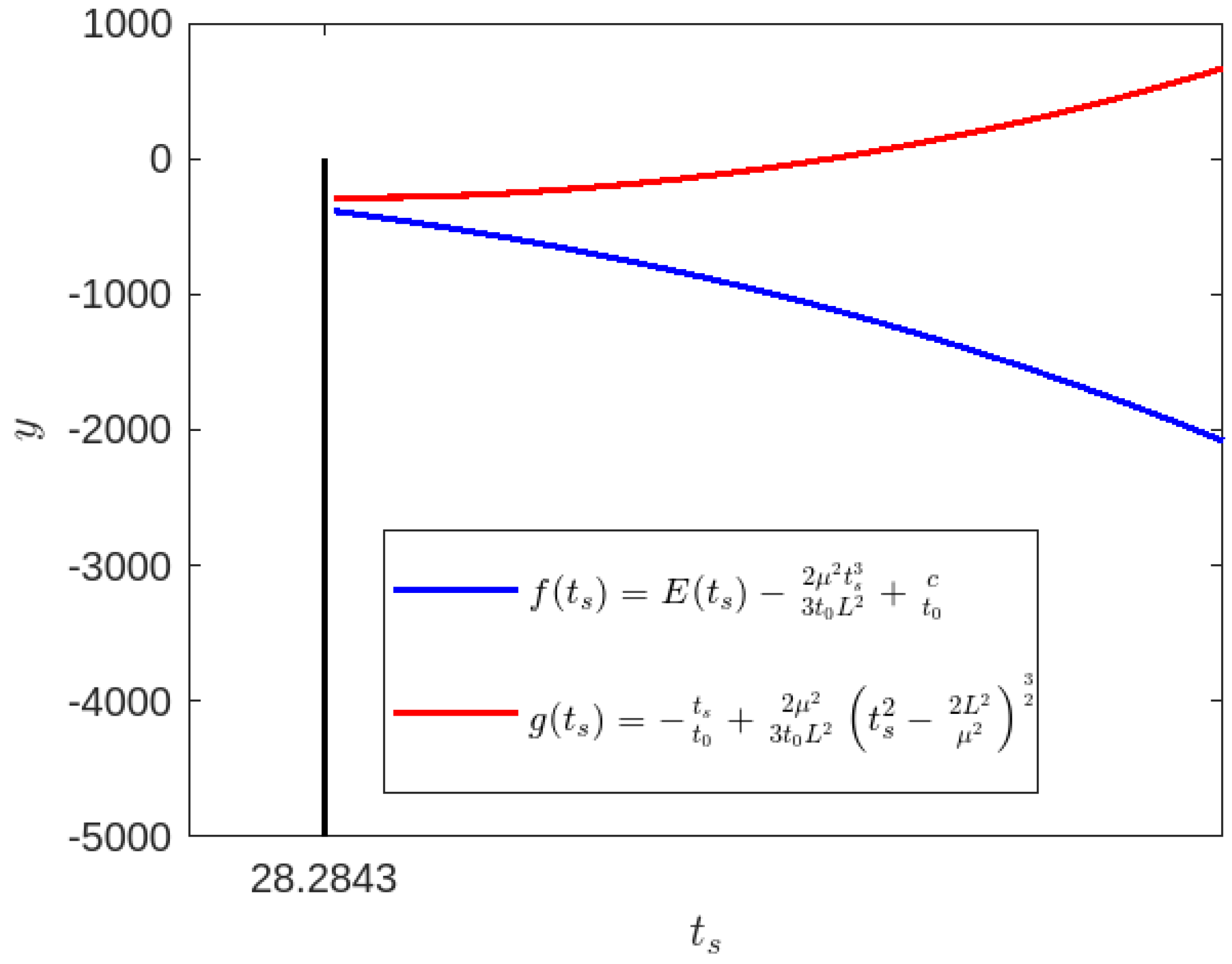
Figure 4.
Time-like geodesics for , , , : Blue Colour line for and Red colour line for
Figure 4.
Time-like geodesics for , , , : Blue Colour line for and Red colour line for
Figure 5.
Null geodesics for , , ,
Figure 5.
Null geodesics for , , ,
Figure 6.
Null geodesics for , , ,
Figure 6.
Null geodesics for , , ,
Figure 7.
Null geodesics for , , , : Blue Colour line for and Red colour line for
Figure 7.
Null geodesics for , , , : Blue Colour line for and Red colour line for
Figure 8.
Null geodesics for , , , : Blue Colour line for and Red colour line for
Figure 8.
Null geodesics for , , , : Blue Colour line for and Red colour line for
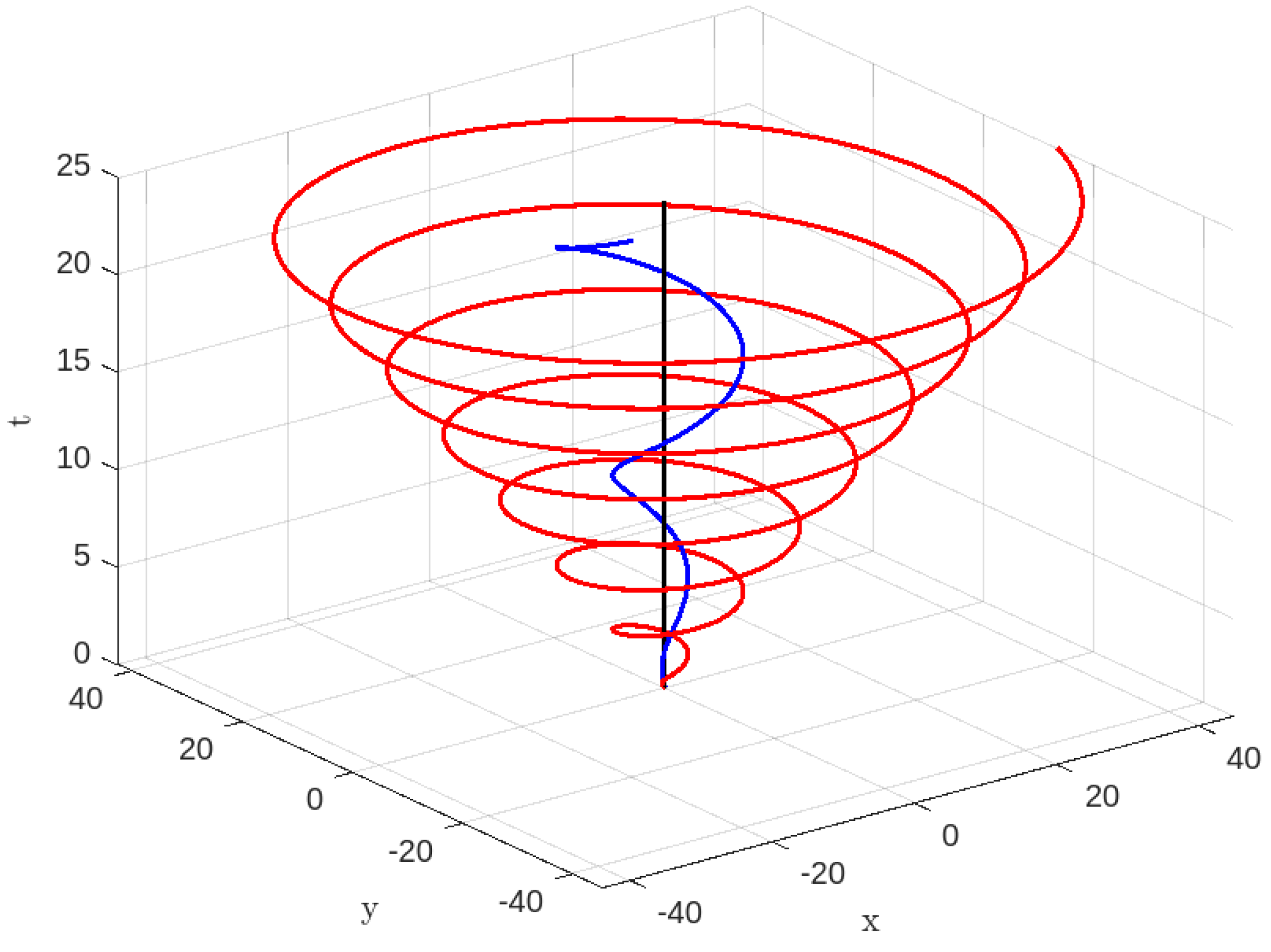
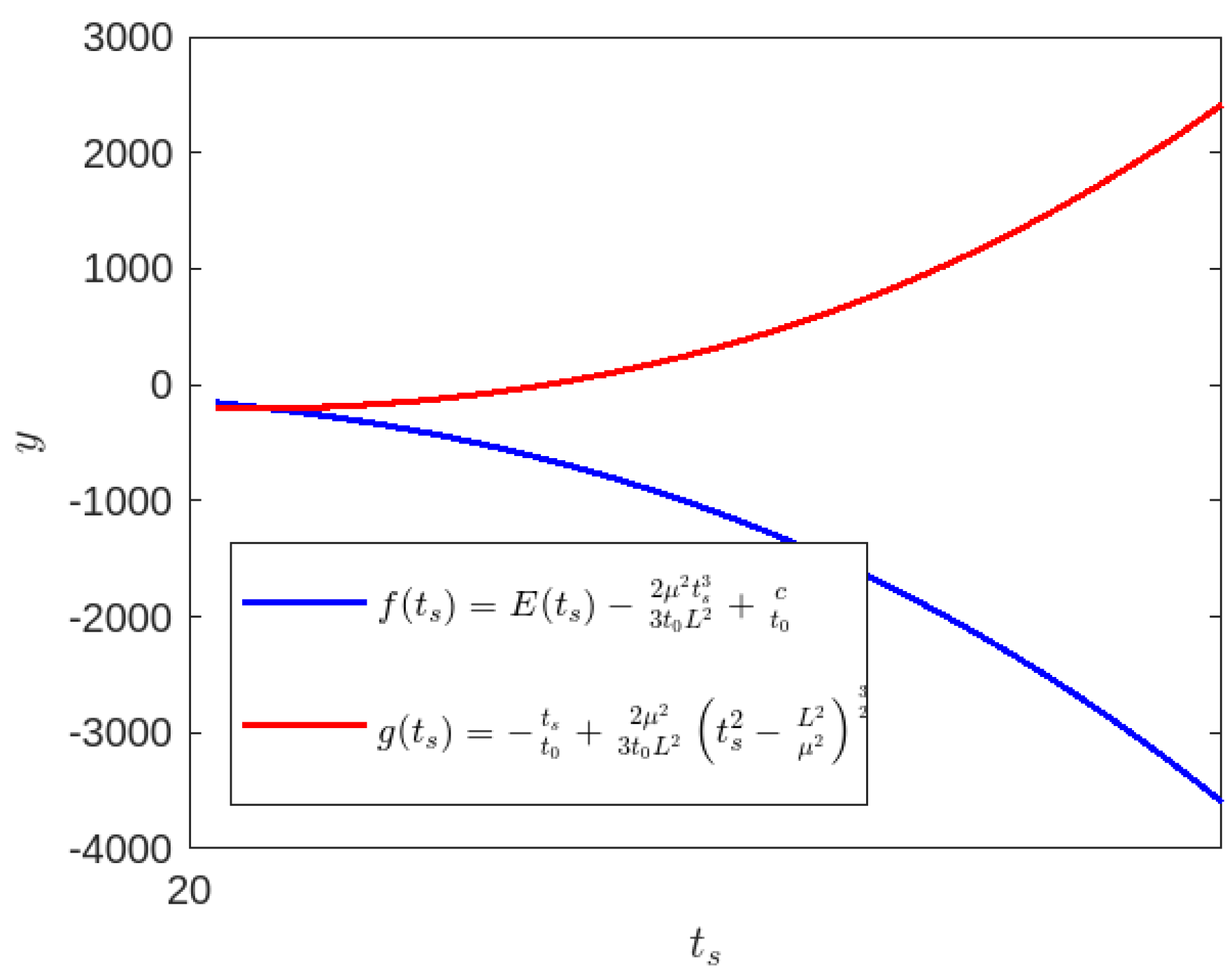
Figure 9.
, , and : Blue Colour line for and Red colour line for .
Figure 9.
, , and : Blue Colour line for and Red colour line for .
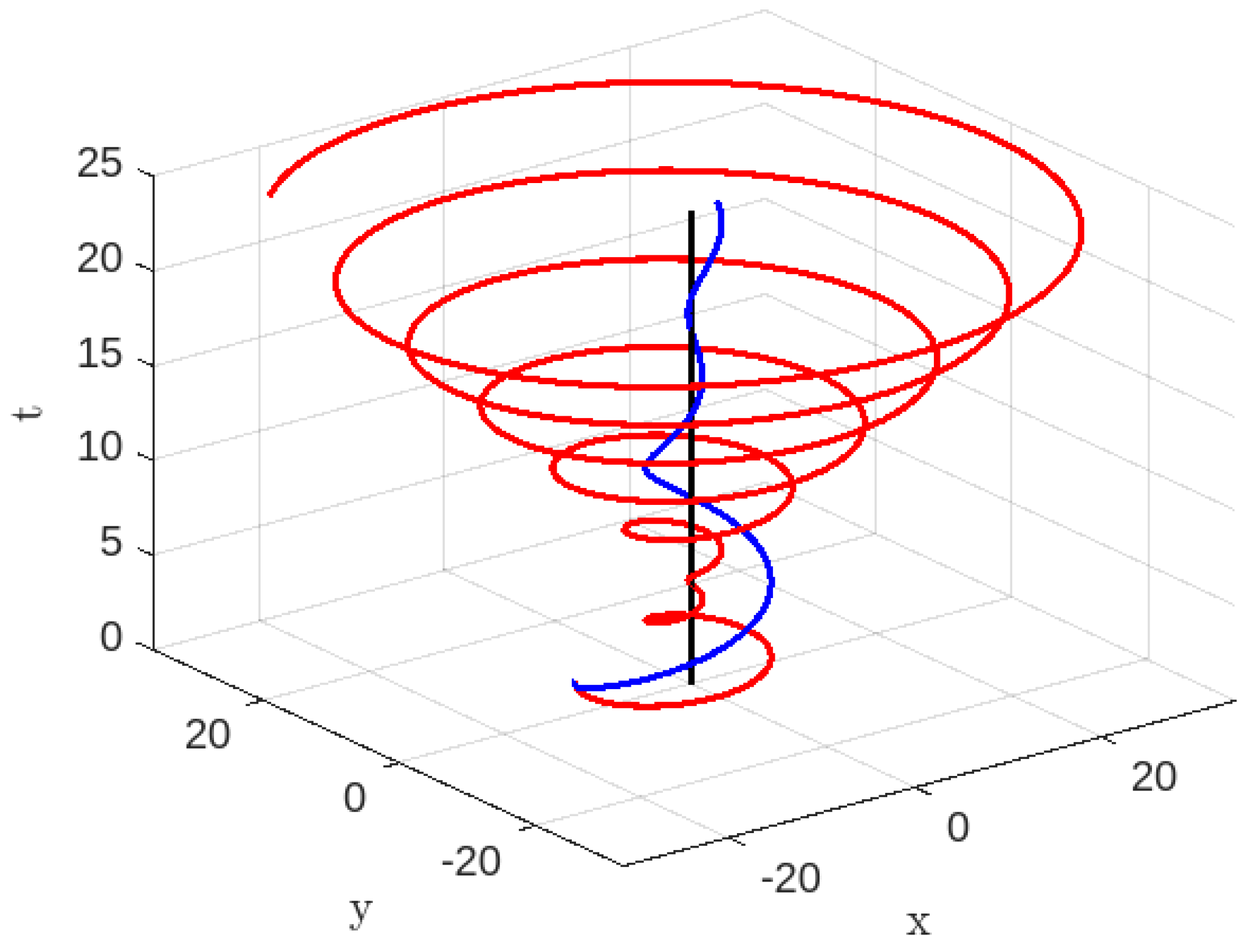
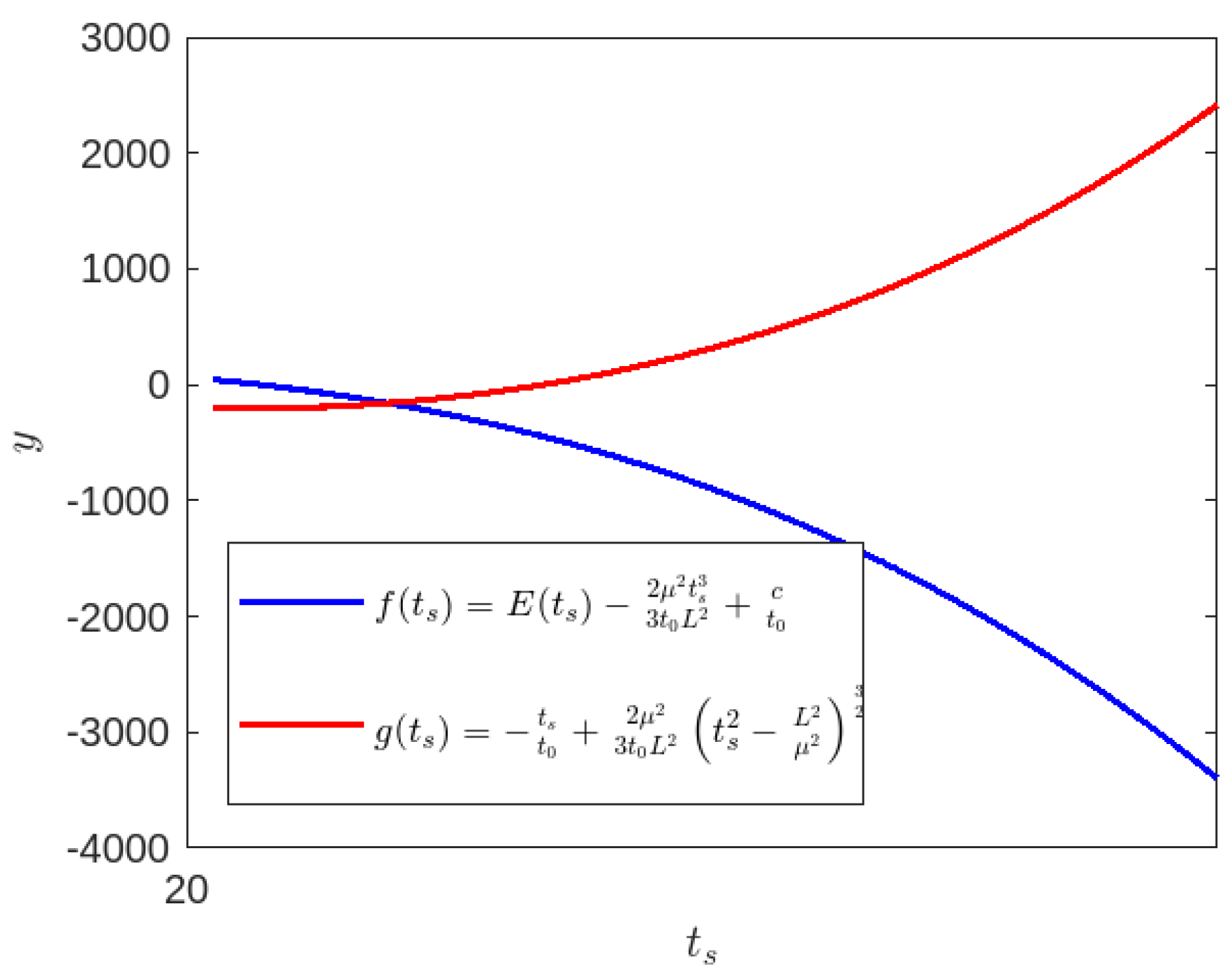
Figure 10.
, , and : Blue Colour line for and Red colour line for .
Figure 10.
, , and : Blue Colour line for and Red colour line for .
Figure 11.
Time-like geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 11.
Time-like geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 12.
, , and : Blue Colour line for and Red colour line for .
Figure 12.
, , and : Blue Colour line for and Red colour line for .
Figure 13.
, , and : Blue Colour line for and Red colour line for .
Figure 13.
, , and : Blue Colour line for and Red colour line for .
Figure 14.
Time-like geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 14.
Time-like geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 15.
, , and : Blue Colour line for and Red colour line for .
Figure 15.
, , and : Blue Colour line for and Red colour line for .
Figure 16.
, , and : Blue Colour line for and Red colour line for .
Figure 16.
, , and : Blue Colour line for and Red colour line for .
Figure 17.
Null geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 17.
Null geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 18.
Null geodesics for : When , , : Blue Colour line for .
Figure 18.
Null geodesics for : When , , : Blue Colour line for .
Figure 19.
, , and : Blue Colour line for and Red colour line for .
Figure 19.
, , and : Blue Colour line for and Red colour line for .
Figure 20.
, , and : Blue Colour line for and Red colour line for .
Figure 20.
, , and : Blue Colour line for and Red colour line for .
Figure 21.
Null geodesics for : When , , : Blue Colour line for and Red colour line for .
Figure 21.
Null geodesics for : When , , : Blue Colour line for and Red colour line for .