Alena Tensor and Its Possible Applications in Unification Theories

1. Introduction

The history of physics is also the history of unification. The past teaches us that after the stage of research on individual phenomena and obtaining a satisfactory description of them, comes the phase of unification, in which the scattered puzzles of descriptions are put together into one whole picture, which soon turns out to also be just a part of bigger picture.

Today, modern physicists are faced with many puzzles, most of which are huge pictures, entire sections of physics, composed of hundreds of smaller parts, the existence of which we owe to thousands of outstanding scientists. The largest and most famous descriptions of physical phenomena requiring unification are, of course, General Relativity (GR) and Quantum Field Theory (QFT), however, the unification cannot be simplified to finding a theory of quantum gravity. We cannot forget about other knowledge components (so fundamental that they are easy to miss), such as Continuum Mechanics or Thermodynamics, which are also being researched in the field of unification [1,2,3].

"In all the attempts at unification we encounter two distinct methodological approaches: a deductive-hypothetical and an empirical-inductive method." [4] where a good examples of the first approach are String Theory [5] and Supersymmetry [6] and the second one, Grand Unification [7] and, in a sense, the Standard Model itself. Part of the entire unification effort are dualistic theories [8], mainly adopting mentioned deductive-hypothetical approach. They are usually looking for a theoretical model in which existing descriptions can be reconciled and assume, that contradictions between existing descriptions may be apparent and in fact they are only different, equally valid ways of describing the same phenomena [9].

Considering the context of unification broadly, a dualistic solution to the puzzle may appear from a completely unexpected direction, as in the work of D. Grimmer describing topological redescription [10] and giving the possibility of changing the topology of space in a way similar to changing coordinate systems. When considering the unification of GR and Electrodynamics, unifying dualistic theory may come from a rather obvious direction [11], because it can be expected that there is a mathematical transformation between accelerated motion in flat spacetime and geodesic motion in curved spacetime for all accelerations due to known fields.

Dualistic descriptions are so widely used that we sometimes forget how controversial they once were. The main benefit of using such theories, apart from the cognitive value, seems to be the possibility of further, independent development and use of existing descriptions of reality, as well as, in many cases, the possibility of transforming the results between different descriptions.

For the reasons mentioned above, it is worth taking a look at a fairly new example of dualistic approach, called Alena Tensor, and discussing what new research perspectives it opens. Previous publications [12,13] have shown that Alena Tensor allows to obtain a coherent solution combining relativistic electrodynamics, QED and GR equations, so it is not just a purely theoretical, mathematical construction and seems worth further development. This method also indicates that the description of the physical system in curved spacetime and its description in flat spacetime with fields are equivalent, thanks to an appropriately constructed definition of the energy-momentum tensor which greatly facilitates further research.

Another and perhaps the most important reason to write this article is that the Alena Tensor is not an intuitive theory, requires some systematization and yet requires further research. A description of a physical theory usually begins with a description of the action and by varying it, one finds the equations of the theory, energy-momentum tensor and Lagrangians. In this case, however, such a line of reasoning would make it difficult to understand the unifying potential of this theory, which is why the action and the Lagrangian (derived in previously published papers) appear only later in this article.

When considering a curved spacetime, metrics are typically obtained from the solutions of the GR equations based on the symmetries used. In this article, the conclusions regarding the Einstein tensor will be presented in flat spacetime to reveal the meaning of the dualistic approach, which also breaks a certain accepted pattern and is not intuitive. However, such an analysis will reveal the meaning of the presented dualistic description without the need to significantly expand this article, especially since the methods of analyzing GR equations are quite well known.

Last part of the article will discuss the possibilities of further development and applications of Alena Tensor to analyze problems related to the broadly understood research on the unification of physical theories.

2. Alena Tensor and its properties

This chapter summarizes the state of knowledge about Alena Tensor based on recent publications and systematizes existing conclusions in the context of further applications. The authors use the Einstein summation convention, metric signature $(+,-,-,-)$ and commonly used notations.

Alena Tensor is the central object of the method described in [12] and [13]. It is a stress-energy tensor, which can be interpreted in flat and curved spacetime. The Alena Tensor $T^{\alpha \beta }$ has the following form

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-\left(c^2\varrho +{\Lambda }_{\rho }\right)\left(g^{\alpha \beta }-\xi h^{\alpha \beta }\right)$$

(1)

Designations used:

• $g^{\alpha \beta }$ is the metric tensor of spacetime in which the physical system is considered,
• $1/\xi \equiv \frac{1}{4}{g}_{\mu \nu }{h}^{\mu \nu }$ ,
• $\varrho \equiv {\varrho }_o\gamma$ where ${\varrho }_o$ is rest mass density and $\gamma$ is Lorentz gamma factor,
• $\varrho U^{\alpha }$ is four-momentum density in the system, in accordance with the postulate raised in the description to eq. (11) from publication [12],
• $h^{\alpha \beta }$ is the metric tensor of curved spacetime in which all motion takes place along geodesics and it is related to the field tensor, which will be explained next,
• ${\Lambda }_{\rho }$ is related to the invariant of the field tensor, which will be explained next.

The field present in the system is described by some field tensor, e.g. ${\mathbb{F}}^{\alpha \beta \gamma }$, which may be widely configured. To simplify the reasoning, it will be assumed that field is described by ${\mathbb{F}}^{\beta \gamma }$ representing electromagnetic field, but the properties described here are general and apply to the field in a broader sense.

For ${\mathbb{F}}^{\beta \gamma }$ understood as electromagnetic field tensor one gets the following relationships

$$h^{\alpha \beta }\equiv 2\frac{{\mathbb{F}}^{\alpha \delta }{g}_{\delta \gamma }{\mathbb{F}}^{\beta \gamma }}{\sqrt{{\mathbb{F}}^{\alpha \delta }{g}_{\delta \gamma }{\mathbb{F}}^{\beta \gamma }{g}_{\mu \beta }{\mathbb{F}}_{\alpha \eta }{g}^{\eta \xi }{\mathbb{F}}_{\xi }^{\mu }}}$$

(2)

which provides the property $h^{\alpha \beta }{g}_{\mu \beta }{h}_{\alpha }^{\mu }=4$, and

$${\Lambda }_{\rho }\equiv \frac{1}{4{\mu }_o}{\mathbb{F}}^{\alpha \mu }{g}_{\mu \gamma }{\mathbb{F}}^{\beta \gamma }{g}_{\alpha \beta }$$

(3)

where ${\mu }_o$ is vacuum magnetic permeability. The stress–energy tensor for electromagnetic filed, denoted as ${{\rm Y}}^{\alpha \beta }$ may be thus presented in a way that relates the field to the metric tensor of curved spacetime

$${{\rm Y}}^{\alpha \beta }\equiv {\Lambda }_{\rho }\left(g^{\alpha \beta }-\xi h^{\alpha \beta }\right)={\Lambda }_{\rho }{g}^{\alpha \beta }-\frac{1}{{\mu }_o}{\mathbb{F}}^{\alpha \delta }{g}_{\delta \gamma }{\mathbb{F}}^{\beta \gamma }$$

(4)

This connection of the field with the $h^{\alpha \beta }$ tensor opens up wide possibilities of unification, discussed later in the article.

The pressure p in the system is equal to

$$p\equiv c^2\varrho +{\Lambda }_{\rho }$$

(5)

where it was shown in [13] that p is negative. This allows (1) to be written as

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-\frac{p}{{\Lambda }_{\rho }}{{\rm Y}}^{\alpha \beta }$$

(6)

The remaining tensors that describe the system are defined as follows

$$R^{\alpha \beta }\equiv 2\varrho U^{\alpha }{U}^{\beta }-p{g}^{\alpha \beta }$$

(7)

its trace R

$$R\equiv R^{\alpha \beta }{g}_{\alpha \beta }=-2p-2{\Lambda }_{\rho }$$

(8)

and tensor $G^{\alpha \beta }$ as

$$G^{\alpha \beta }\equiv R^{\alpha \beta }-\frac{1}{2}R\xi h^{\alpha \beta }$$

(9)

which allows to rewrite (1) as

$$G^{\alpha \beta }-{\Lambda }_{\rho }{g}^{\alpha \beta }=2T^{\alpha \beta }+\varrho c^2\left(g^{\alpha \beta }-\xi h^{\alpha \beta }\right)$$

(10)

The above definitions allow to consider flat spacetime, curved spacetime, and all intermediate states, in which spacetime is partially curved and part of the motion results from the existence of residual fields. One may analyze boundary solutions: flat spacetime with fields and curved spacetime without fields.

2.1. Behavior of the system in curved spacetime

Considering $g^{\alpha \beta }$ as equal to $h^{\alpha \beta }$ one obtains that it yields $\xi =1$, therefore the whole part of Alena Tensor related to fields vanishes. It yields

$$T_{\alpha \beta }=\varrho U_{\alpha }{U}_{\beta }$$

(11)

The value of tensor $G_{\alpha \beta }$ becomes

$$G_{\alpha \beta }=R_{\alpha \beta }-\frac{1}{2}R{h}_{\alpha \beta }$$

(12)

and (10) reduces to

$$G_{\alpha \beta }-{\Lambda }_{\rho }{h}_{\alpha \beta }=2T_{\alpha \beta }$$

(13)

Therefore, in curved spacetime, $R_{\alpha \beta }$ acts as Ricci tensor and $G_{\alpha \beta }$ acts as Einstein curvature tensor, both with an accuracy of $\frac{4\pi G}{c^4}$ constant, where cosmological constant $\Lambda$ is related to the invariant of the field tensor

$$\Lambda =-\frac{4\pi G}{c^4}{\Lambda }_{\rho }$$

(14)

where ${\Lambda }_{\rho }$ has a negative value due to the adopted metric signature.

The above result gives a chance to solve the puzzle of the "smile of the Cheshire cat" [14] explaining the reason for the appearance of the cosmological constant in Einstein Field Equations. Since the first publication of General Relativity, this constant has appeared and disappeared in EFE like Cheshire cat from the book "Alice’s Adventures in Wonderland". The above equation indicates that its existence is necessary and proposes an explanation of its origin.

Eq. (13) can be further analyzed using known tools for considering metrics in General Relativity, taking into account the knowledge of the field tensor used to build the Alena Tensor. Since GR analysis is quite a well-known issue, interpretation of the obtained curvature tensors will be considered.

Since covariant four-divergences of $T_{\alpha \beta }$ and $G_{\alpha \beta }$ vanish, therefore they represent curvature tensors, related to corresponding four-force densities present in flat Minkowski spacetime. It is therefore worth taking a look at the four-force densities associated with these tensors in flat spacetime.

2.2. Behavior of the system in flat Minkowski spacetime

Considering $g^{\alpha \beta }$ as equal to ${\eta }^{\alpha \beta }$ Minkowski metric tensor, thanks to the amendment to the continuum mechanics explained in equations (13) - (21) of publication [12]

$${\partial }_{\alpha }{U}^{\alpha }=-\frac{d\gamma }{dt}\to {\partial }_{\alpha }\varrho U^{\alpha }=0$$

(15)

total four-force density $f^{\alpha }$ acting in the system is equal to

$$f^{\alpha }\equiv {\partial }_{\beta }\varrho U^{\alpha }{U}^{\beta }$$

(16)

and for considered system, it is the sum of electromagnetic ($f_{EM}^{\alpha }$), gravitational ($f_{gr}^{\alpha }$) and other ($f_{oth}^{\alpha }$) four-force densities, where

$$f^{\alpha }=\left\{\begin{array}{c}{f}_{EM}^{\alpha }\equiv {\partial }_{\beta }{{\rm Y}}^{\alpha \beta }\left(electromagnetic\right)\hfill \\ +\hfill \\ f_{gr}^{\alpha }\equiv \left({\eta }^{\alpha \beta }-\xi h^{\alpha \beta }\right){\partial }_{\beta }\varrho c^2\left(gravitational\right)\hfill \\ +\hfill \\ f_{oth}^{\alpha }\equiv \frac{\varrho c^2}{{\Lambda }_{\rho }}{f}_{EM}^{\alpha }\left(other\right)\hfill \end{array}\right.$$

(17)

The four-force density $f_{oth}$ is negligibly small for $-{\Lambda }_{\rho }>>\varrho c^2$ and it appears to act similar to Abraham–Lorentz force [15] (also called the radiation reaction force) or like the relativistic Stern-Gerlach force [16] (correction to the electromagnetic force, related to the magnetic moment of charged particle) since the existence of magnetic moment is expected for charged particles [17,18] and it influences the value of the electromagnetic force [19]. Later in the article it will be shown how these effects are taken into account in above forces and the issue of $f_{oth}$ will be discussed in the next two sections.

One may start by analyzing the gravitational force, since in the above description, the gravitational four-force density is not an interaction between bodies, but appears to result from the bending of the direction of electromagnetic field energy transport by the energy density gradient. Eq. (17) yields

$${\partial }_{\beta }{T}^{\alpha \beta }=0$$

(18)

and

$${\partial }_{\beta }{G}^{\alpha \beta }=f_{gr}^{\alpha }+f_{oth}^{\alpha }$$

(19)

The above result shows, that when using the Alena Tensor, it should be assumed that the Einstein tensor does not describe the curvature associated with gravity alone.

Neglecting other forces (as we currently do in known solutions for GR), one actually approximately obtains metric tensors responsible for gravity alone. However, the total value of the Einstein tensor corresponds to the curvature associated with the density of the four-forces from equation (19). This means that the above approach can be used to search for the causes of disturbances between observations and the expected motion resulting from gravitational equations, which is currently attributed entirely to Dark Matter [20]

One may also introduce an additional tensor ${\Pi }^{\alpha \beta }$ which turns out to play a role of deviatoric stress tensor [21]

$${\Pi }^{\alpha \beta }\equiv -c^2\varrho \xi h^{\alpha \beta }$$

(20)

To demonstrate this, Alena Tensor can be represented in flat Minkowski spacetime as

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-p{\eta }^{\alpha \beta }-{\Pi }^{\alpha \beta }+{\Lambda }_{\rho }\xi h^{\alpha \beta }$$

(21)

Now, vanishing four-divergence of the above

$$f^{\alpha }={\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }+f_{EM}^{\alpha }$$

(22)

express relativistic equivalence of Cauchy momentum equation (convective form) [22]. The above representation therefore allows for the analysis of the system using the tools of continuum mechanics. From this perspective, $f_{EM}$ appears as a body force, while the remaining forces are the effect of fluid dynamics [23] and could be modeled e.g. with help of Navier-Stokes Equations [24,25].

By imposing following condition on normalized Alena Tensor as described in [13]

$$0={\partial }_{\beta }\left(\frac{T^{\alpha \beta }}{{\eta }_{\mu \gamma }{T}^{\mu \gamma }}\right)+{\partial }^{\alpha }ln\left({\eta }_{\mu \gamma }{T}^{\mu \gamma }\right)$$

(23)

one obtains further simplification. Some gauge of electromagnetic four-potential denoted as ${\mathbb{A}}^{\mu }$ may be expressed as

$${\mathbb{A}}^{\mu }\equiv -\frac{{\Lambda }_{\rho }}{p}\frac{{\varrho }_o}{{\rho }_o}{U}^{\mu }$$

(24)

where ${\rho }_o$ denotes rest charge density in the system. It also simplifies Alena Tensor in flat Minkowski spacetime to

$$T^{\alpha \beta }=\frac{1}{{\mu }_o}{\mathbb{F}}^{\alpha \gamma }{\partial }^{\beta }{\mathbb{A}}_{\gamma }-{\Lambda }_{\rho }{\eta }^{\alpha \beta }$$

(25)

and leads to the explicit form of gravitational four-force density

$$f_{gr}^{\alpha }=\varrho \left(\frac{dln\left(p\right)}{d\tau }{U}^{\mu }-c^2{\partial }^{\mu }ln\left(p\right)\right)$$

(26)

Both Lagrangian density $\left(\mathcal{L}\right)$ and Hamiltonian density $(\mathcal{H}=T^{00})$ for the system appear to be related to invariant of the field tensor

$$\mathcal{L}=\mathcal{H}={\Lambda }_{\rho }$$

(27)

where it was shown in [13] that

$$\frac{\partial {\Lambda }_{\rho }}{\partial {\mathbb{A}}_{\alpha }}={\partial }_{\nu }\left(\frac{\partial {\Lambda }_{\rho }}{\partial \left({\partial }_{\nu }{\mathbb{A}}_{\alpha }\right)}\right)=-J^{\alpha }$$

(28)

In above $J^{\alpha }={\rho }_o\gamma U^{\alpha }$ is electric four-current and according to (15) its four-divergence vanishes.

Eq. (27) indicates, that in this solution there is no potential in the classical sense and dynamics of the system depends on itself. This is a clear analogy to main GR equation and something that should be expected from a GR-equivalent description of the system in flat spacetime.

2.3. Classical and quantum interpretation for continuous media in flat spacetime

At first, it is worth noting that the electromagnetic field energy density ${{\rm Y}}^{00}$ was calculated in [13] as

$${{\rm Y}}^{00}=\frac{{\Lambda }_{\rho }}{p}\left(\varrho c^2{\gamma }^2-{\Lambda }_{\rho }\right)$$

(29)

Denoting the magnetic field as $\overrightarrow{B}$, can therefore be written

$$\frac{B^2}{{\mu }_o}={\Lambda }_{\rho }+{{\rm Y}}^{00}=\frac{{\Lambda }_{\rho }}{p}{\varrho }_o{c}^2\left({\gamma }^3+\gamma \right)$$

(30)

This means that the four-potential of the electromagnetic field (24) can be simplified to

$${\rho }_o{\mathbb{A}}^{\mu }=-\frac{{ϵ}_o{B}^2}{{\gamma }^3+\gamma }{U}^{\mu }$$

(31)

where ${ϵ}_o$ is electric vacuum permittivity. For a particle at rest, the above reduces to a scalar $-\frac{1}{c}\frac{B^2}{2{\mu }_o}$ expressing classical value of magnetic energy density and zero vector, but completely stationary cases must be excluded, because they lead to $\overrightarrow{B}=\nabla \times \overrightarrow{A}=0$. The above equation also says that even in the absence of orbital angular momentum, the particle must vibrate or rotate and experience a magnetic field, because without the magnetic field, the entire four-potential vanishes.

Therefore, primary source of the electromagnetic field of quasi-stationary particles should be, accually, a magnetic moment caused by vorticity or spin (however since continuous media are considered here, the term magnetization should rather be used instead of the magnetic moment). The obtained four-potential must take into account, at least partially, the changes in magnetization caused by motion, because the magnetization itself seems to be the source of the electric field and it depends on $\gamma$, while the magnetic field depends on the rotation of the velocity (vorticity). Four-force density $f_{oth}$ is therefore only a correction complementing the above phenomenon and its meaning will be discussed in the next section.

The source of the electric field associated with the particle can now be represented, as reduced (compared to the classical value) magnetic energy density $u_B$

$$u_B\equiv \frac{1}{{\mu }_o}\frac{\overrightarrow{B}}{{\gamma }^2+1}·\overrightarrow{B}=-J_{\mu }{\mathbb{A}}^{\mu }$$

(32)

Although unintuitive, the above equation also means that the density of the electric field $u_E$ associated with the particle is increased compared to the classical description, because energy is not lost in nature. This means that charged elementary particles can be understood as a disturbance in the proportions of the electromagnetic field energy density distribution between the electric and magnetic fields. In the classical description, the denominator always has "2", so the difference for $\gamma \approx 1$ is almost imperceptible for non-relativistic solutions. Perhaps this is why only the QED revealed discrepancies in the measured values of the effects related to magnetic moment of particles.

In the above description, the $1+{\gamma }^2$ coefficient seems to play the role of volume magnetic susceptibility, and the electromagnetic four-force density, apart from the magnetic potential energy gradient, depends on other components, which, in this picture, should be understood as a contribution related to polarization. Therefore, the electromagnetic field associated with a charged particle will be most easily described as a propagating disturbance of magnetization and polarization, because the combination of magnetization and polarization also generates electric currents [26]. It will lead directly to the quantum interpretation seen in QED.

To clarify the above statement, one may introduce the symmetric energy-momentum tensor ${\Omega }^{\alpha \beta }$ associated with the particle understood as Polarization-Magnetization energy-momentum tensor [27]

$${\Omega }^{\alpha \beta }\equiv \varrho U^{\alpha }{U}^{\beta }-\frac{\varrho c^2}{{\Lambda }_{\rho }}{{\rm Y}}^{\alpha \beta }$$

(33)

what yields

$$T^{\alpha \beta }={\Omega }^{\alpha \beta }-{{\rm Y}}^{\alpha \beta }$$

(34)

Now, one obtains the classical equivalent of the description obtained in QED - a charged elementary particle understood as a certain spinor fields related to disturbances in magnetization and polarization, experiencing only electromagnetic field, which can be seen in below

$${\partial }_{\beta }{\Omega }^{\alpha \beta }={\partial }_{\beta }{{\rm Y}}^{\alpha \beta }=f_{EM}^{\alpha }$$

(35)

and what may be farther modeled by Jones matrices, vectors and symmetry groups [28,29] used to describe polarization and magnetization, analogously as it is done in QED.

In QED picture, if one considers solely the electromagnetic field within the system and substitutes (27) for the current Lagrangian density employed in QED

$${\mathcal{L}}_{QED}=\frac{1}{4{\mu }_o}{\mathbb{F}}^{\alpha \beta }{\mathbb{F}}_{\alpha \beta }=\frac{1}{2{\mu }_o}{\mathbb{F}}^{0\gamma }{\partial }^0{\mathbb{A}}_{\gamma }=\frac{1}{2}\overline{\psi }\left(i\hslash c[strikeout,draw]2D-m{c}^2\right)\psi$$

(36)

one simplifies currently used ${\mathcal{L}}_{QED}$ and derive equations that characterize the entire system involving the electromagnetic field, with the particle understood as analogous spinor fields. Remarkably, these equations will inherently encompass the system’s gravitational behavior. This is because, in the discussed approach, gravity naturally emerges within the system as an outcome of the presence of energy-momentum tensors associated with the fields present in Alena Tensor, and the resultant Lagrangian density duly incorporates this aspect. Four-forces $f_{gr}^{\alpha }$ and $f_{oth}^{\alpha }$ are now invisible in the equations, because they have been "absorbed" by the spinor-based description of the particle.

It’s very probable, that above explanation will clarify the challenging quest for identifying quantum gravity as a distinct interaction within Quantum Field Theory. It also explains the remarkable precision of QED’s predictions, provided it indeed characterizes the complete system involving the electromagnetic field.

Finally, it is worth analyzing what the factor $\left(1+\frac{\varrho c^2}{{\Lambda }_{\rho }}\right)$ is, occurring in the electromagnetic force

$$f_{EM}^{\alpha }+f_{oth}^{\alpha }=\left(1+\frac{\varrho c^2}{{\Lambda }_{\rho }}\right)f_{EM}^{\alpha }$$

(37)

In the limit for $\varrho c^2=0$ Alena Tensor simply becomes a tensor of the electromagnetic field $T^{\alpha \beta }={{\rm Y}}^{\alpha \beta }$, while in the limit $\varrho c^2=-{\Lambda }_{\rho }$ the field disappears, and therefore the forces caused by it also disappear. However, to check what the coefficient $\left(1+\frac{\varrho c^2}{{\Lambda }_{\rho }}\right)$ is, one needs to analyze the behavior of elementary particles.

2.4. Dynamics of point-like particles in flat spacetime

It was also shown in [13], that

$$H^{\beta }\equiv \left(\frac{H}{c},{\overrightarrow{p}}_H\right)\equiv -\frac{1}{c}\int T^{0\beta }{d}^{3}x$$

(38)

in flat spacetime acts as canonical four-momentum for the point-like particle, and for the system with electromagnetic field, four-divergence of $H^{\beta }$ vanishes due to the Poynting theorem. Hamiltonian for point-like particle is thus

$$H=-\int {\Lambda }_{\rho }{d}^{3}x$$

(39)

and the action S (Hamilton’s principal function) for the point-like particle was derived in [13] as

$$-S=H^{\beta }{X}_{\beta }=m{c}^2\tau +\int p{d}^{4}x=P^{\beta }{X}_{\beta }-m{c}^2\tau$$

(40)

where $P^{\beta }$ is four-momentum and $\tau$ is particle’s proper-time. One may denote in the above equation Pressure-Volume work (pressure potential energy) as $W_{PV}$

$$W_{PV}\equiv -\int p{d}^{3}x$$

(41)

and it has positive value. Denoting $F^{\beta }$ as total four-force acting on the particle one may notice that Lagrangian L for the particle may be understood as the Lagrangian for a particle of some perfect fluid [30]

$$-L=\frac{1}{\gamma }{F}^{\beta }{X}_{\beta }=\frac{m{c}^2}{\gamma }-W_{PV}$$

(42)

and may be also analyzed from the perspective of the laws of thermodynamics.

As one may notice, the action (40) vanishes for the inertial system. It clearly shows that inertial systems in this approach do not exist and should be considered as some abstract idealization. Considered system without fields and forces vanishes, what indicates that spacetime in this approach should be actually understood as some method to perceive the field.

Mentioned canonical four-momentum is equal to

$$H^{\mu }=P^{\mu }+V^{\mu }=-\frac{\gamma L}{c^2}{U}^{\mu }+{\mathbb{S}}^{\mu }$$

(43)

where L is Lagrangian for point-like particle, ${\mathbb{S}}^{\mu }$ due to its properties, seems to be some description of rotation or spin, and where $V^{\mu }$ describes the transport of energy due to the field. It can be expressed in a generalized way as

$$V^{\mu }=X_{\beta }{\partial }^{\mu }{P}^{\beta }-{\partial }^{\mu }m{c}^2\tau$$

(44)

For considered system with electromagnetic field it was calculated in [13] as

$$V^{\mu }=q{\mathbb{A}}^{\mu }+\frac{\varrho c^2{\gamma }^2}{p}{P}^{\beta }+\frac{\varrho c^2}{p}{\mathbb{S}}^{\mu }+Y^{\mu }$$

(45)

where $Y^{\mu }$ is the volume integral of the Poyinting four-vector

$$Y^{\beta }=\int {{\rm Y}}^{0\beta }{d}^{3}x$$

(46)

and

$${\mathbb{S}}^{\beta }=\int \frac{{ϵ}_o{\Lambda }_{\rho }}{\gamma c{\rho }_o}{\mathbb{F}}^{0\mu }{\partial }_{\mu }{U}^{\beta }{d}^{3}x$$

(47)

where ${ϵ}_o$ is electric vacuum permittivity. Using (39), (41), (43) and definition of the pressure (5) one may also notice, that

$$V^0=\frac{W_{PV}}{c}$$

(48)

which, as might be expected, relates the existence of negative pressure in the system to the energy of the field in the system.

It now becomes possible to interpret the correction for the electromagnetic force discussed in (37). It may be expressed as

$$1+\frac{\varrho c^2}{{\Lambda }_{\rho }}=1-\frac{mc\gamma }{H^0}=\frac{V^0}{H^0}$$

(49)

The increasing energy of an accelerated body cannot take energy from nowhere. Since energy is conserved in a closed system, this means that the increasing energy of the particle increases at the expense of decreasing field energy in the system. Therefore, force associated with this field must at some point decrease.

Above means, that discussed factor (49) upholds the principle of conservation of energy therefore it seems to be responsible for Abraham–Lorentz effect. The dependence of the four-potential on spin indicated in the previous chapter, together with the above should therefore be understood as a sum of Stern-Gerlach effect, Abraham–Lorentz effect and, actually, all other effects that we do not know yet. It is also worth noting that by including this force in the curvilinear description, non-physical effects such as black hole singularity must disappear, since four-force density (19) associated with the Einstein tensor in flat spacetime may be now expressed as

$${\partial }_{\beta }{G}^{\alpha \beta }=f_{gr}^{\alpha }+f_{oth}^{\alpha }={{\rm Y}}^{\alpha \beta }{\partial }_{\beta }\frac{V^0}{H^0}+\left(\frac{V^0}{H^0}-1\right)f_{EM}^{\alpha }$$

(50)

This can also be seen when analyzing solutions of (13) for the static, symmetric case, as these are smooth de Sitter solutions [31], free of singularities. However, this topic deserves to be developed in a separate article.

It is worth noting, that since in (43) $V^{\mu }$ is just "other gauge" of $-P^{\mu }$ thus in classical description for such a system occurs

$$F^{\alpha }=U_{\beta }\left({\partial }^{\beta }{P}^{\alpha }-{\partial }^{\alpha }{P}^{\beta }\right)=U_{\beta }\left({\partial }^{\alpha }{V}^{\beta }-{\partial }^{\beta }{V}^{\alpha }\right)$$

(51)

where $U_{\beta }{\partial }^{\alpha }{P}^{\beta }=0$ vanishes, due to the property of Minkowski metric ${\partial }^{\alpha }{U}_{\beta }{U}^{\beta }=0$.

To ensure compatibility with the equations of QM, one may perform a similar procedure as was done for QED in (34) and "absorb" everything except electromagnetism into the description of the particle. Assuming the description of the particle as ${\Sigma }^{\mu }$ and using (43) and (45) to define it

$${\Sigma }^{\mu }\equiv P^{\mu }+\frac{\varrho c^2{\gamma }^2}{p}{P}^{\beta }+\frac{\varrho c^2}{p}{\mathbb{S}}^{\mu }+Y^{\mu }$$

(52)

one obtains

$$H^{\mu }={\Sigma }^{\mu }+q{\mathbb{A}}^{\mu }$$

(53)

However, before continuing with the quantum description, one may explain the source of the mass of elementary particles. By associating the conserved energy of the system with the energy of the photon to which it corresponds and following the conclusions of this and previous section, individual energies can now be described and labeled:

• $E_{B\square }\equiv -cq{\mathbb{A}}^0$ is the energy of the magnetic field associated with the particle, according to (32),
• $E_{E\square }\equiv c{\Sigma }^0$ is thus the energy of the electric field associated with the charged particle,
• $E_{E\sim }$ is the energy of the electric field in the photon description, according to (39),
• $E_{B\sim }$ is the energy of the magnetic field in the photon description,
• ${\mathcal{E}}_{\sim }\equiv E_{E\sim }+E_{B\sim }$ is the energy of the electromagnetic field of the photon,
• ${\mathcal{E}}_{\square }\equiv E_{E\square }+E_{B\square }$ is the energy of the electromagnetic field associated with the charged particle.

where writing down the components of equation (53) one obtains conserved energy of the physical system as

$$H=c{H}^0=E_{E\sim }-E_{B\sim }=E_{E\square }-E_{B\square }$$

(54)

Adding $2E_{B\sim }=2E_{B\square }\left(1+{\gamma }^2\right)$ to both sides will get

$${\mathcal{E}}_{\sim }={\mathcal{E}}_{\square }+2{\gamma }^2{E}_{B\square }$$

(55)

Since no energy can be lost in nature, this means that this additional energy is simply the energy of the moving particle, which can be written as

$${\mathcal{E}}_{\sim }={\mathcal{E}}_{\square }+m{c}^2\gamma$$

(56)

Above yields

$$m{c}^2\frac{1}{\gamma }=2E_{B\square }$$

(57)

thus substituting into (42) will get

$$-L={\mathcal{E}}_{\sim }$$

(58)

Above explains the meaning of the relativistic Lagrangian for point-like particle, as potential energy resulting from the existence of the energy of the electromagnetic field.

Turning to the quantum description and introducing quantum wave function $\psi$ in form of

$$\psi \equiv e^{-i{K}^{\mu }{X}_{\mu }}$$

(59)

where $K^{\mu }$ is wave four-vector associated with a photon and related to canonical four-momentum

$$\hslash K^{\mu }\equiv H^{\mu }$$

(60)

one gets

$$i\hslash {\partial }^{\mu }\psi =H^{\mu }\psi ={\Sigma }^{\mu }\psi +q{\mathbb{A}}^{\mu }\psi$$

(61)

Assuming, that for a non-relativistic approximation it holds

$$\frac{p_H^2}{2m}\approx c{\Sigma }^0=E_{E\square }$$

(62)

above description with introduced quantum wave function $\psi$ is equivalent to Schrödinger equation in flat spacetime.

2.5. Generalization to other fields

One may also consider generalizing the Alena Tensor to other fields. At this point, however, it seems necessary to introduce a certain classification of fields that will explain the differences in the approach to their analysis in flat, curved spacetime and in quantum perspective.

For example, remaining with the previous notation, one may describe the field (e.g. electroweak field) in the system by some generalized field tensor ${\mathbb{F}}^{\alpha \beta \gamma }$ providing more degrees of freedom, and express Alena Tensor in flat spacetime as follows

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-\left(\frac{c^2\varrho }{{\Lambda }_{\rho }}+1\right)\left({\Lambda }_{\rho }{\eta }^{\alpha \beta }-{\mathbb{F}}^{\alpha \delta \gamma }{\mathbb{F}}_{\delta \gamma }^{\beta }\right)$$

(63)

where

$${\Lambda }_{\rho }\equiv \frac{1}{4}{\mathbb{F}}^{\alpha \beta \gamma }{\mathbb{F}}_{\alpha \beta \gamma }$$

(64)

$$\xi h^{\alpha \beta }\equiv \frac{{\mathbb{F}}^{\alpha \delta \gamma }{\mathbb{F}}_{\delta \gamma }^{\beta }}{{\Lambda }_{\rho }}$$

(65)

$$\xi \equiv \frac{4}{{\eta }_{\alpha \beta }{h}^{\alpha \beta }}$$

(66)

The Alena Tensor defined in this way retains most of properties described in the previous chapters, however, it now describes other four-force densities in the system. Total four-force density $f^{\alpha }$ can be now presented as

$$f^{\alpha }=\left\{\begin{array}{c}{f}_{fun}^{\alpha }\equiv -{\partial }_{\beta }{\mathbb{F}}^{\alpha \delta \gamma }{\mathbb{F}}_{\delta \gamma }^{\beta }\left(fundamentalforces\right)\hfill \\ +\hfill \\ f_{gr}^{\alpha }\equiv \left({\eta }^{\alpha \beta }-\xi h^{\alpha \beta }\right){\partial }_{\beta }\varrho c^2\left(relatedtogravity\right)\hfill \\ +\hfill \\ f_{sec}^{\alpha }\equiv \frac{\varrho c^2}{{\Lambda }_{\rho }}{f}_{fun}^{\alpha }\left(secondaryforces\right)\hfill \end{array}\right.$$

(67)

Therefore, interactions can be classified based on their properties as:

• fundamental interactions related to body forces $f_{fun}^{\alpha }$
• gravitational (or gravity with an additional field), related to $f_{gr}^{\alpha }$
• secondary interactions related to four-force density $f_{sec}^{\alpha }$

where each of above $f_i^{\alpha }$ four-force density should satisfy the condition

$$0=U_{\alpha }{f}_i^{\alpha }$$

(68)

Taking into account the conclusions from chapter Section 2.3, it can be assumed with high probability that the Electroweak Theory describes the particle in an analogous way as demonstrated in (34) for electromagnetic interactions, where now ${{\rm Y}}^{\alpha \beta }$ describes the energy-momentum tensor for the electroweak interactions, and ${\Omega }^{\alpha \beta }$ is still a spinor based description of the particle, this time describing disturbances in the propagation of this field.

This is not so obvious for QCD, due to the strong connection of these interactions with electromagnetism, and it would certainly require further research. However, it seems that the use of Alena Tensor opens up new possibilities in the study of these interactions both in the curvilinear and classical description, as well as in the regime of QFT mathematical apparatus.

3. Potential applications against the background of existing research

The properties of Alena Tensor presented in the previous chapter seem promising in terms of their further development. For this reason, it is worth analyzing the possibilities of using this tool in selected research areas related to unification.

3.1. Dark sector and perspectives for unification of interactions

The first topic discussed will be the issue of the dark sector, for which Alena Tensor brings new interpretation possibilities. Although Dark Energy and Dark Matter are concepts closely related to the General Relativity, their analysis is also carried out e.g. from the perspective of quantum theories and quantum cosmology [32,33,34].

The use of Alena Tensor indicates that the invariant of the field tensor is responsible for the vacuum energy and the associated cosmological constant [35]. This allows to replace "the worst theoretical prediction in the history of physics" [36] with an attempt to estimate the value of this field tensor invariant. This also means, that it becomes possible to search for the expected form of the field tensor based on the experimentally measured value of its invariant, and allows to look for an answer to the question of what fields, apart from the electromagnetic field, should constitute Alena Tensor.

An example of such an approach seems to be an attempt to estimate the values of magnetic and electric fields based on available background radiation data [37] and an attempt to determine the value of the invariant of the electromagnetic field tensor. Importantly, it also seems that field invariant in general does not have to be the constant [38,39], which would be particularly important for solving the Hubble tension problem [40]

Alena Tensor also introduces the possibility of a new interpretation of the forces attributed to Dark Matter. Therefore, it may also prove helpful for analysis of Maxwell’s equations with axion modifications [41] and attempts to explain Dark Matter based on these particles [42], especially in the context of the recent results regarding Sigma-8 tension [43].

Analyzing the possible directions of unification of interactions, it can also be noted that the Alena Tensor allows for testing hypotheses regarding the interconnections of fields and the connections of fields with gravity. Fields defined in the way presented in chapter (Section 2.5) allow for quite a lot of freedom in adapting them to the existing division of interactions that emerged in quantum mechanics: electroweak, strong and gravitational interactions.

Due to the fundamental importance of electroweak interaction (fermions are the building blocks of matter), it seems that the field strength tensor present in the system should be somehow related to this interaction, where the rest (related to gravity and secondary interactions) could be linked to gravity and to strong interactions and potentially to other fields [44]. It would be also supported by conclusions from research on Double Copy Theory [45,46,47], since it can be assumed that solutions should include perturbative duality between gauge theory and gravity. Thus it may be expected, that stong interactions play some role in the $f_{sec}$ four-force density. Perhaps this will shed new light on current work on the unification of these interactions [48,49,50].

Finally, when discussing the unification of interactions, it is impossible to ignore the importance of the Higgs field [51]. The adoption of an analysis model based on the Alena Tensor creates new possibilities for relating the geometry of spacetime with a field in general [52] and even based on the simple model presented in chapter Section 2.1, it is possible to analyze relationships between the Higgs field and the electromagnetic field [53,54]. Additionally, due to the possibility of analyzing the system based on the proposed Lagrangian and generalized canonical four-momentum, it becomes possible to study individual classes of fields in terms of their impact on the phenomenon of symmetry breaking [55,56].

When building theoretical models, however, one should remember about the limitations related to the adopted analysis method. In curved spacetime, the curvature described by the Einstein tensor will always be related to the four-force densities $f_{gr}^{\alpha }+f_{sec}^{\alpha }$. In flat spacetime, conditions (23), (27) and (38) still seem reasonable.

3.2. Quantum gravity

There is no universal agreement on the approach to developing quantum gravity [57] and so far research is being carried out using different methods in different directions. One of the research directions is canonical quantum gravity [58] with its attempt to quantify the canonical formulation of general relativity, the most promising example of which is Loop Quantum Gravity [59].

Work is also ongoing in the field of string theory, where M-theory [60] seems to be the leading area of research. There are also many other e.g. [61,62,63] less frequently cited studies that explore different, sometimes unusual [64] research areas

Against the background of the above research directions, the dualistic approach represented by Alena Tensor seems very promising because it changes the research paradigm in two ways.

The first paradigm shift is that, according to the conclusions presented earlier, in the description provided by Alena Tensor, the Einstein tensor is not exclusively related to gravity. The introduction of additional interactions into the system causes an additional spacetime curvature term related to secondary interactions to appear in the curved spacetime in the Einstein tensor. This means a change in assumptions and a completely new way of perceiving the prospect of unifying the remaining interactions with gravity.

The second paradigm shift results from the very nature of the dualistic approach and concerns the lack of need to search for quantization methods in curved spacetime. According to the reasoning presented earlier, if one describes the field in flat spacetime by some field tensor and enters it into the Alena Tensor in the appropriate way, the equations in curved spacetime will naturally turn into the Einstein Field Equations.

The second paradigm shift in particular seems to be extremely important from the point of view of research on quantum gravity phenomena. It also opens new possibilities for studying quantum phenomena in a strong gravitational fields.

Current research approaches to quantum problems in a strong gravitational field each time require the construction of an appropriate model in which the obtained results can be interpreted, either through careful selection of the observer [65], or making direct use of the principle of equivalence [66], or own, specific approach [67]. It also needed consideration of the specific quantum phenomena occurring in the vicinity of very massive objects, such as the Unruh effect [68] or Hawking radiation [69]. Thanks to the dualistic approach, such research can now be conducted in flat spacetime with fields and then the results can be easily analyzed in curved spacetime.

One of the natural directions of research seems to be the development of a field tensor that, in curved spacetime, provides the known metrics [70] used to describe gravity, extended by the term related to secondary interactions. The development of such a field tensor seems to be the first step towards building quantum gravity, this time - contrary to the direction described in the previous chapter - from the side of the General Relativity.

Interestingly, because the use of the Alena Tensor indicates the possibility of shaping the metric tensor of spacetime using a field, it also sheds new light on research on new drives [71], including the quantum effects [72] needed to analyze them. Although many QM and QFT problems seem unsolvable [73,74] using current paradigms, such as the Planck scale problems [75], previously mentioned paradigm shift can change this situation.

It also seems interesting to search for solutions to the problem of quantization of interactions related to the tensor (9) in various spacetimes, thus the problem of quantization should be addressed.

3.3. Quantization

To get a full picture of the applicability of the approach based on Alena Tensor, one may consider an example of its application to gravity quantization.

One may start with a choice of proper representation of a metric $g^{\alpha \beta }$ so that the interpretation of time in first quantization will be "natural". By "natural interpretation" of time, it is understood the approach in which, after the first quantization of Hamiltonian, one gets a proper definition of the time evolution operator in the ”Schrödinger representation”, in such a way that

$$U(t,t_0)=e^{-iH·(t-t_0)/\hslash }$$

(69)

fulfill classical conditions [76]

$$\begin{array}{cc}\hfill U^{†}(t,t_0)U(t,t_0)& =I\hfill \\ \hfill \left|\psi \right(t_0)\rangle & =U(t_0,t_0)|\psi \left(t_0\right)\rangle \hfill \\ \hfill U(t,t_0)& =U(t,t_1)U(t_1,t_0)\hfill \end{array}$$

(70)

This means that, in general, it should be possible to incorporate the Lagrangian formalism for the Gauge fields. Therefore, for the field strength tensor

$$F_{\mu \nu }^a={\partial }_{\mu }{A}_{\nu }^a-{\partial }_{\nu }{A}_{\mu }^a+g{f}^{abc}{A}_{\mu }^b{A}_{\nu }^c$$

(71)

one needs to define proper commutator

$$[t_a,t_b]=i{f}^{abc}{t}_c$$

(72)

As it was show in [77] this can be done by rewriting $g^{\alpha \beta }$ in the $(3+1)$-split in Geroch decomposition manner. This approach solves the proper initial value problem, since now spacetime can be interpreted as the evolution of space in time, with interpretation of time that is consistent with Quantum Mechanics: time as a distinguished, absolute, external, global parameter. A summary of full formalism has been presented many times, last and the modern one can be found in [78], where computation rules look as follows

$$\left\{{\gamma }_{ij},{\pi }^{kl}\right\}=\frac{1}{2}\left({\delta }_i^k{\delta }_j^l+{\delta }_j^k{\delta }_i^l\right){\delta }^{\left(3\right)}\left(x-y\right)$$

(73)

The above approach makes it possible to introduce gravity into Quantum Mechanics in form of canonical quantization and couple this field with other interactions in regular manner. In such picture gravity acts as just another quantum field that could be incorporated into the Standard Model Lagrangian and interact with other fields on the same principles. The only difference is that we are bound to only one representation of the metric $g^{\alpha \beta }$ with $(3+1)$-split Geroch decomposition. However, it may be transformed to other, more convenient coordinate systems when quantum phenomena can be negligible.

Presented approach opens a natural way to implement that representation of tensor $g^{\alpha \beta }$ into the Alena Tensor (1) for better understanding overall interpretation of GR in the big scale. From the other point of view, it opens the possibility to look for a quantum gravity phenomena on the small scale, where perturbation approach as quantum and gravity interaction are in the same level of magnitude. The most promising application of this approach could be implementing this calculations to Hawking radiation phenomena on the Planck scales, as the original calculations are questioned by other authors [79,80].

New observation methods allow to look for a quantum gravity phenomenon in the present or near future data that could test the boundaries of GR in the classical approach. One of the most promising directions in the present observation is the rise of gravitational wave (GW) astronomy. It might be worth investigating the post-merge echoes that occur because of the stimulated emission of Hawking radiation after compact binary merger events involving stellar black holes. This could be a promising way to search for deviations from General Relativity and could serve as evidence for the quantum structure of black hole horizons. Present methods used to model this phenomenon in modified theories of gravity are extremely challenging in Numerical Relativity and could provide inconclusive observation interpretations [81]. The approach presented in this paper may also help obtain results without using effective model echoes within the framework of linear perturbation theory.

4. Results and Discussion

As presented above, the possibility of using a new tool, Alena Tensor, seems to open up new research possibilities both in terms of searching for the relationship between QFT and GR [82], as well as in terms of connections between many phenomena previously analyzed separately: in quantum or classical description, curvilinear or in flat spacetime, or, for example, the possibility of combining the interpretation of fluid dynamics with field theory. 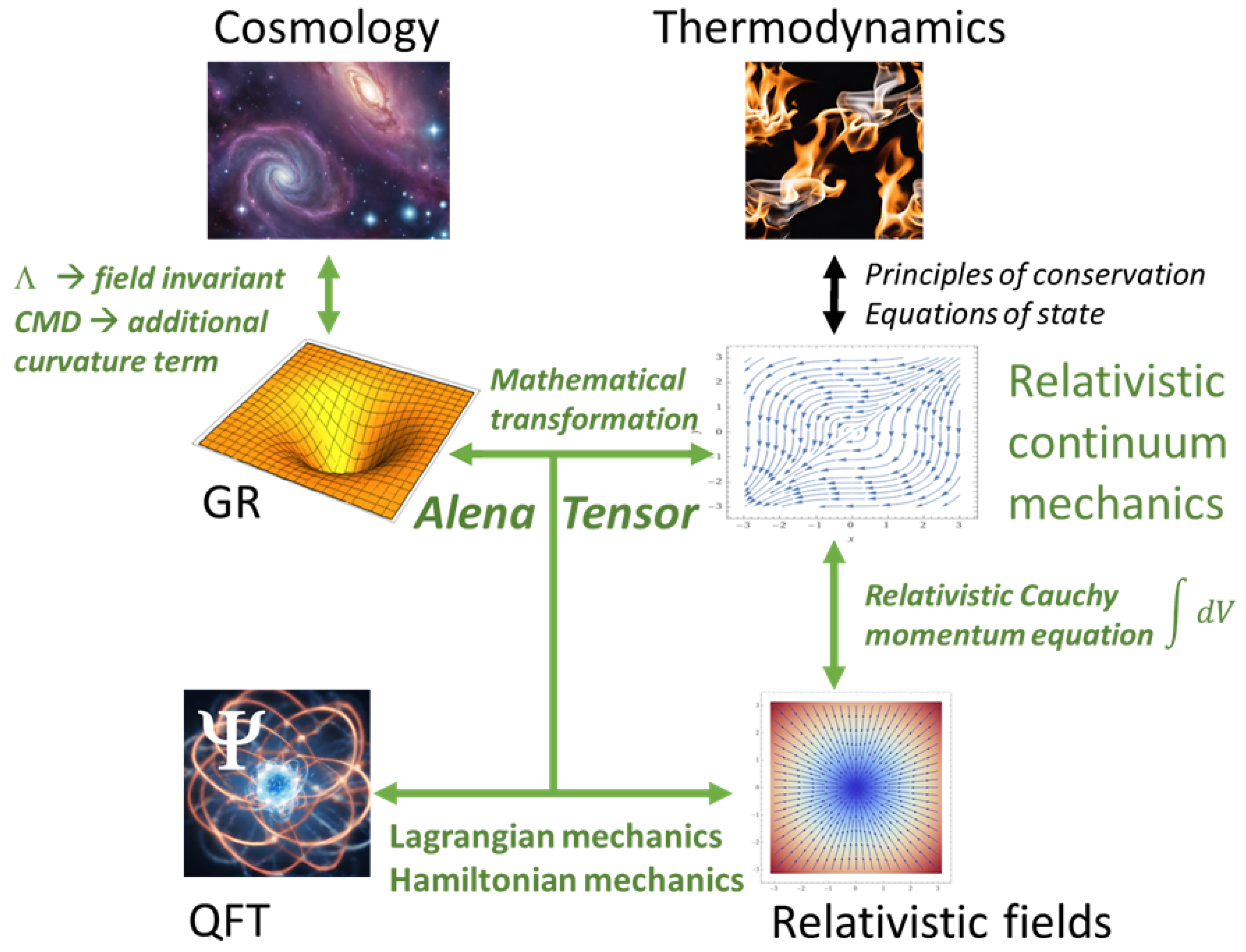Such an analysis may prove particularly interesting in the context of cosmology and the study of quantum phenomena in the early universe [83]. The lines of unification proposed by Alena Tensor can be visualized as in Figure 1 below.

By appropriately selecting field tensors and testing hypotheses regarding their relationship with the Einstein tensor in curved spacetime, it is possible to search for new interpretations for Dark Matter, as well as to analyze the relationships of the invariants of these field tensors with the cosmological constant. By adopting a new interpretation of the cosmological constant as an invariant of the field tensor, possibilities also open up to explain contradictory experimental data for cosmological phenomena, because the field tensor invariant does not have to be constant in time.

Due to the high flexibility of the Alena Tensor in the selection of fields, it also seems to be a very good tool for testing hypotheses regarding the unification of interactions. Such research can be conducted in the regime of the QFT mathematical apparatus and, importantly, thanks to a clear interpretation of the four-divergence of the field stress-energy tensor (four-force density), obtained results would also lead to obtaining an interpretation of quantum interactions in the classical description. It could be a major milestone in combining known QFT results with the classical description of interactions.

Finally, one can also seek a quantum description of gravity in new ways, taking advantage of the paradigm shift that Alena Tensor brings with it. This does not mean that the problems associated with quantizing fields in curved spacetime disappear and the behavior of quantum fields, when changing the metric tensor, will still require careful analysis. However, it seems that thanks to the dualistic description provided by Alena Tensor, these analysis may be much easier.

Further research on Alena Tensor may also lead to its important transformations and generalizations, as well as to the design of experiments in terms of the sought properties that match the experimental data. And all this has a chance to bring us one step closer to the next image that will connect the previously scattered puzzles of knowledge.

5. Statements

No datasets were generated or analysed during the current study.

During the preparation of this work the authors did not use generative AI or AI-assisted technologies, except for generating the elements of Figure 1.

Authors did not receive support from any organization for the submitted work.

Authors have no relevant financial or non-financial interests to disclose.

Both authors contributed equally.