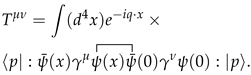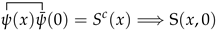2.1. The Lagrangian and Hamiltonian Systems with the Dynamical Constraints
The local axial gauge, , suffers from the residual gauge freedom. Hence, it demands the additional requirements to fix the remained gauge freedom. In the most of cases, the formulation of additional requirements is not a trivial task within the Lagrangian system. Indeed, if one demands simultaneously , the maximal gauge fixing is available only in a classical theory. In a quantum theory, the simultaneous conditions and as delta-function arguments in the corresponding functional integration (which lead to the effective Lagrangian with and ) result in the absence of the well-defined gauge propagator. It happens because the corresponding kinematical operator cannot be inverted. In this connection, it is necessary to develop an alternative method of gauge fixing compared to the “classical” approaches with the effective Lagrangian including both and . The contour gauge conception gives us such an alternative and effective method.
In order to understand all subtleties of the contour gauge, we remind the main stages of the Lagrangian (L-system) and Hamiltonian (H-system) approaches to the quantization of gauge fields (see, for example, [
50]). In this section, our efforts are concentrated on the demonstration that the H-system is the most adequate approach for our purposes. At the same time, due to the special role of a time-space in H-system, the L-system is more suitable for a practical use. In other words, we need the H-system as a convenient intermediate instrument to see how the contour gauge fixes uniquely the total gauge freedom. However, the main computation procedure has been formulated in terms of L-system related, of course, with the corresponding H-system.
Let us consider the H-system, defined by , where the phase space is formed by the generalized momenta and coordinates . In addition, we have constraints on and which have been imposed on the system. Traditionally, these constraints are denoted by and .
We suppose that the H-system has an equivalence orbit which is nothing but the gauge group orbit in the gauge theory. Since the phase space is overfilled by unphysical degrees, in the ideal case, we have to resolve all kinds of constraints. The additional constraints are necessary to fix uniquely the orbit representative. It is needed to quantize the H-system. From the pure theoretical viewpoint, after resolving all constraints we deal with the quantized H-system where the physical phase space of dimension is a subspace of the initial space of dimension . It is a fundament for H-system in terms of physical configurations, .
In the functional method of quantization, the amplitude between the initial
and the final
states takes the form of (modulo the unimportant normalization factors) [
1,
50]
where
denotes the Poisson brackets.
The delta-function
of Eqn. (
1) can be presented through the integration over the Lagrange factor
as
It gives the generalized Hamiltonian of system which reads
If we suppose that the constraint conditions (see the delta-function arguments) have somehow been resolved, the amplitude is given by
where only the physical generalized momenta and coordinates are forming the integration measure together with the Hamiltonian. The generating functional of (
4) corresponds to the H-system with the dynamical constraints which have been resolved. Therefore, there is no a (gauge) freedom associated with the arbitrary Lagrange factor
. It would be an ideal situation which cannot be realized practically in the most of cases. However, the contour gauge, as a class of nonlocal gauges, gives a possibility to realize the mentioned ideal situation. It is so because the contour gauge condition has a unique solution by construction, see below.
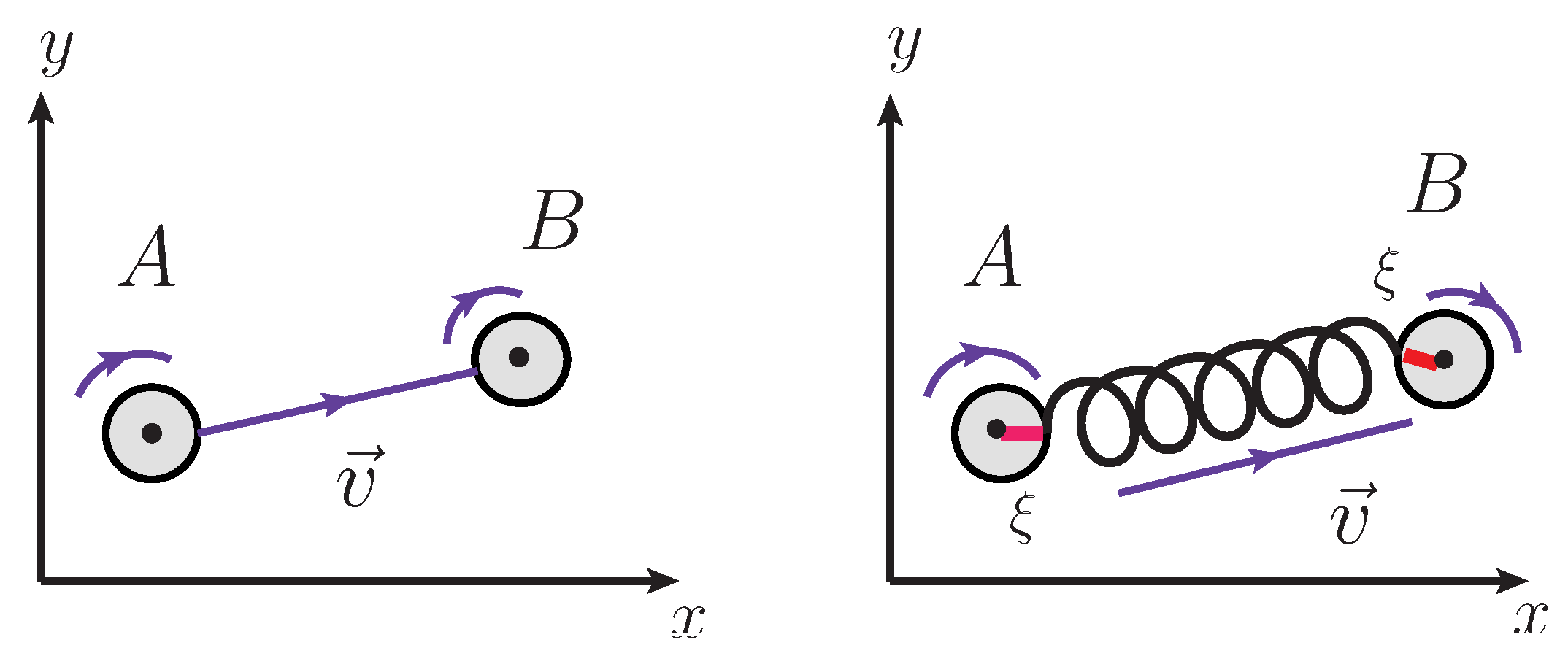
It is instructive to illustrate the difference between the H-system with unresolved and resolved constraint conditions. It can be done with the help of a trivial mechanical example, see
Figure 1. Consider the homogenous flat “ball” which moves from the point
A to the point
B. The ball has a spherical symmetry under the rotation around the inertia center. For the sake of simplicity, we focus on the ball rotation in a two-dimensional plane. Since the flat ball surface is homogenous, we do not have a chance to observe the rotation of the moving ball unless we mark some point on the surface. The invisible ball rotation around its center of inertia corresponds to the inner (gauge) transformations of the H-system. It does not affect much the trajectory provided the angle velocity is constant, see the left panel of
Figure 1. In this case, the inertia center plays a role of “physical” configurations of the H-system, while the moving of different sites on the flat ball surface is invisible and relates to the “unphysical” configurations.
If we mark the site on the flat ball surface by a dash, we break down the rotation symmetry. It means that we choose, so to say, the preferable site of the ball surface and the ball rotation becomes visible. In this case, we can describe the moving dash together with the inertia center as “physical” configurations of the H-system when the ball position varies from
A to
B, see the right panel of
Figure 1.
In the context of the contour gauge conception, the marked dash on the flat ball corresponds to the certain gauge function of the gauge transformations which has been fixed by the contour gauge condition. If we focus on the above mentioned ideal case of resolved constraints, we would merely deal with the gauge fields considered as a massless vector fields (transforming as a spinor of 2-rank under the Lorentz group) that are described by the Hamiltonian without the gauge transforms.
In both the Abelian and non-Abelian gauge theory, the correspondences between the canonical variables and the dynamical constraints (cf. Eqn. (
1)) can be expressed as
In the typical gauge theories, resolving the additional (or gauge) conditions is not a simple task. The gauge conditions, leading to the equation system for the gauge function , would have an unique solution . In fact, it might be practically impossible.
Within the frame of L-system, Faddeev and Popov have proposed the method (FP-method) to avoid the needs for finding the unique solution
. In FT-method, the infinite group orbit volume can be factorized out to the insubstantial normalization factor. It becomes thanks to the gauge invariance of the corresponding Lagrangian (or Hamiltonian) of theory [
1].
For the simplicity, let us dwell on
gauge theory. The H-system can be readily stemmed from the Lagrangian formalism of first order. The Lagrangian of first order is defined by
where
and
are supposed to be independent field configurations. The Lagrangian of Eqn. (
6) can be written in 3-dimensional form. We have
where
and
imply the generalized momenta and coordinates, respectively. Besides,
are the implicit variables in the integration measure, see below. From the Euler-Lagrange equations we can get the equations which do not include
. These equations give the constraint conditions written in the forms of
The gauge theory can be considered as the theory with the constraints which are applied on the field configurations. The constraint conditions of Eqn. (
8) have to be completed by the additional (or gauge) conditions. For example, they read
The full set of conditions defined by Eqns, (
8) and (
9) should eliminate all unphysical degrees of freedom for the correct quantization of H- (or L-) system.
Using the FP-method, we begin with the functional integration written for the L-system [
50]. We have
where the infinite group orbit volume given by
has been factorized out in the integration measure due to the gauge invariant action
and functional
.
The exact magnitude of the group volume prefactor,
i.e.
is irrelevant because the prefactor should be cancelled by the corresponding normalization of Green functions. In Eqn. (
11), the infinite group volume corresponds to the standard case of unresolved gauge conditions. The zero group volume appears in the case of resolved gauge conditions. Indeed, the integration measure
can be defined on the group manifold as an invariant measure,
denotes the product of the invariant measures defined on the structure group
G of fiber over each point of the Minkowski space. If the gauge function
is not fixed, we have the infinite integration over the group invariant measure, otherwise (that is, if the gauge function
is somehow fixed) the integration is equal zero for each point of the Minkowski space but the value of fixed
can vary from one point to another.
Returning to Eqn. (
10), it can be identically rewritten as
where the functional of action
is given by the Lagrangian of Eqn. (
6). In the three-dimensional forms, we obtain that
where
is now defined by Eqn. (
7). Integrations over
and
in Eqn. (
14) lead to the functional integral which is given by
where the Hamiltonian is
In Eqn. (
15), the gauge condition is chosen to be
.
On the other hand, Eqn. (
15) can be presented in the equivalent form. It reads
where the primary and secondary constraints together with the gauge conditions of Eqn. (
9) have been explicitly shown in the functional integrand. This representation of H-system resembles the functional integration presented by Eqn. (
1).
Notice that, in H-system, there are no problems to write all constraints through the delta functions. It is true because, in contrast to L-system which is forming the Feynman rules, we have no needs to invert the kinematical-like operator. At the same time, the H-system approach is not convenient for the practical computation in QFT.
This section is basically written in the textbook style. The basic reason for the usage of this style is that the section is preparing a reader for the main features of contour gauge uses. Indeed, we have reminded the differences between the H-systems with and without resolved additional dynamical constraints presenting the mechanical illustration in
Figure 1. Within the FP-method of L- and H-systems there is no need to find a unique solution of the additional (gauge) condition system with respect to the gauge function
. Thanks for the gauge invariance of Lagrangian (Hamiltonian) and functional
, the infinite group orbit volume defined by
has been factorized out in the corresponding functional integration measure giving a possibility to quantize the gauge theory modulo the residual gauge problems. However, if we resolve the additional (gauge) condition with respect to
, the group representative on each of orbits can be fixed uniquely. The factorized group integral defined through the Riemann summations should be equal to zero. Since the group volume has been cancelled by the corresponding normalization, it does not mean that the functional integration of Eqn. (
10) disappears. This case takes place if we use the contour gauge conception.
2.2. The Contour Gauge Conception
We now concentrate on the description of the contour gauge conception. It implies that the corresponding gauge condition can be formally resolved in order to find the unique gauge orbit representative. A few decades ago, the contour gauge had intensively been studied due to the fact that the quantum gauge theory should not suffer from the Gribov ambiguities (see, for example, [
46,
47,
51]).
It states that the gauge function can be completely fix (in the H-system, see Eqn. (
1)). In other words, the unphysical gluons can be eliminated (in the L-system, see Eqn. (
10)) if we demand the path dependent functional (Wilson path functional) to be equal to unity,
i.e.
where the path
between the points
and
x is fixed.
In QCD, the axial light-cone gauge,
, is a particular case of the reduced nonlocal contour gauge, see below, determined by Eqn. (
18) if the fixed path is given by the straightforward line connecting
with
x. By construction, the contour gauge does not possess the residual gauge freedom in the finite space. In [
2], it is shown that the possible residual gauge can be located at the corresponding boundary only. In what follows the boundary gluon configurations have assumed to be equal to zero. So, from the technical point of view, the contour gauge provides the simplest way to fix the gauge function completely.
The contour gauge conception is inspired by the path group formalism [
52,
53]. Also, it can be traced from the Mandelstam approach [
54]. For better understanding, it is worth to give a short introduction to the geometry of gluons where the gluon field has been treated as a connection on the principle fiber bundle
.
The principle fiber bundle
is one of main ingredients that forms a differential geometry basic. By definition, it is a combination of two sets,
and
together with the given transformations
between them. Moreover, the group structure
G is determined on the set
(strictly speaking, on each of fibers). The set
is named by a base of the fiber bundle. The base usually coincides with the Minkowski space. In the principle fiber bundle, we are able to define two directions. One direction is determined in the base
as the tangent vector of a curve going through the point
. The other direction is defined in the fiber and can be uniquely determined as the tangent subspace related to the parallel transport [
52,
53]. These two directions allow us to introduce the horizontal vector defined by
where
denotes the corresponding shift generator along the group fiber written in the differential form. The vector coefficients (connection of the principle fiber bundle),
, defines the algebraic vertical (tangent) vector field on the fiber [
52,
53]. The horizontal vector
is invariant under the structure group
G acting on the given representation of the fiber by construction.
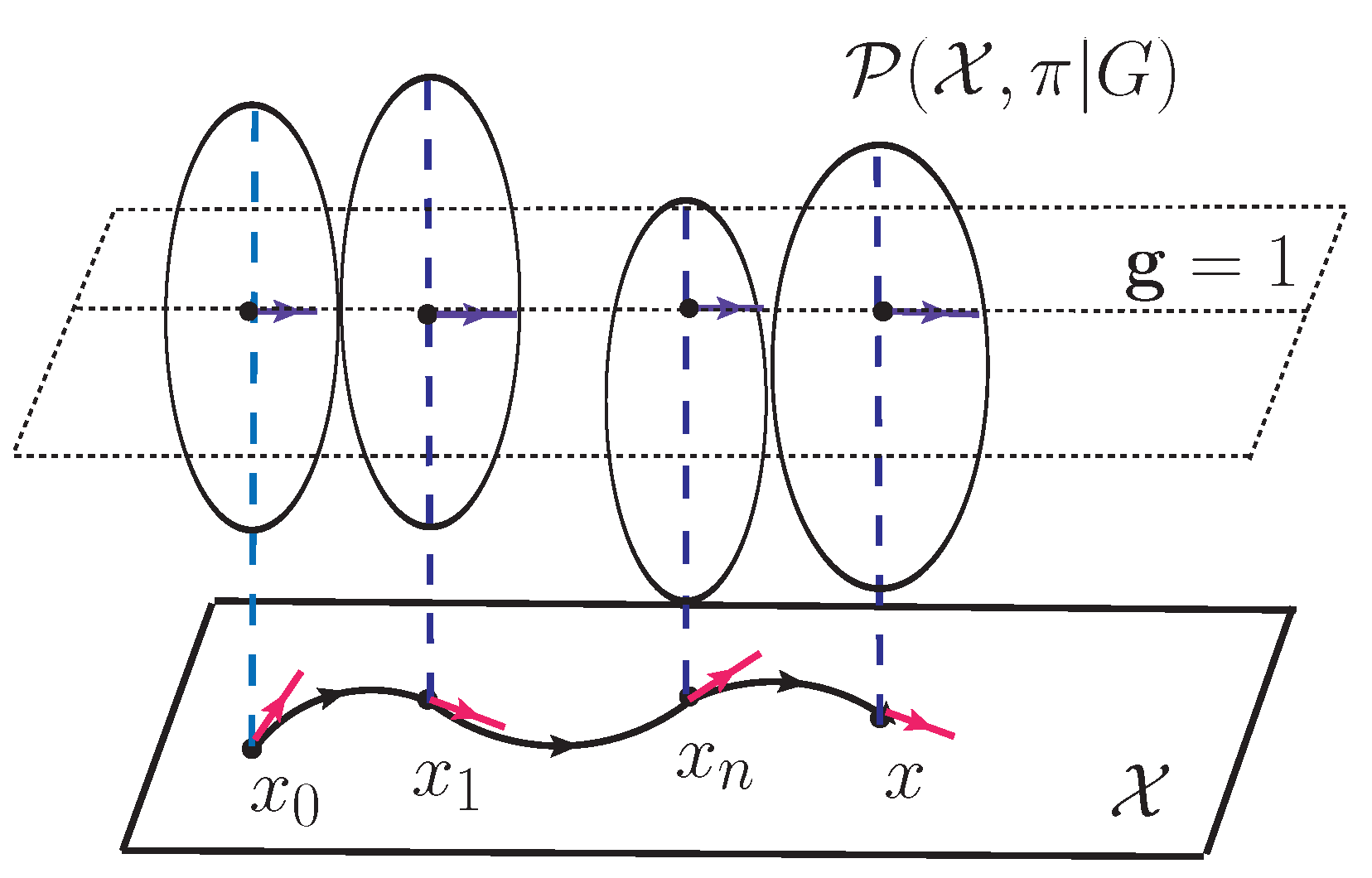
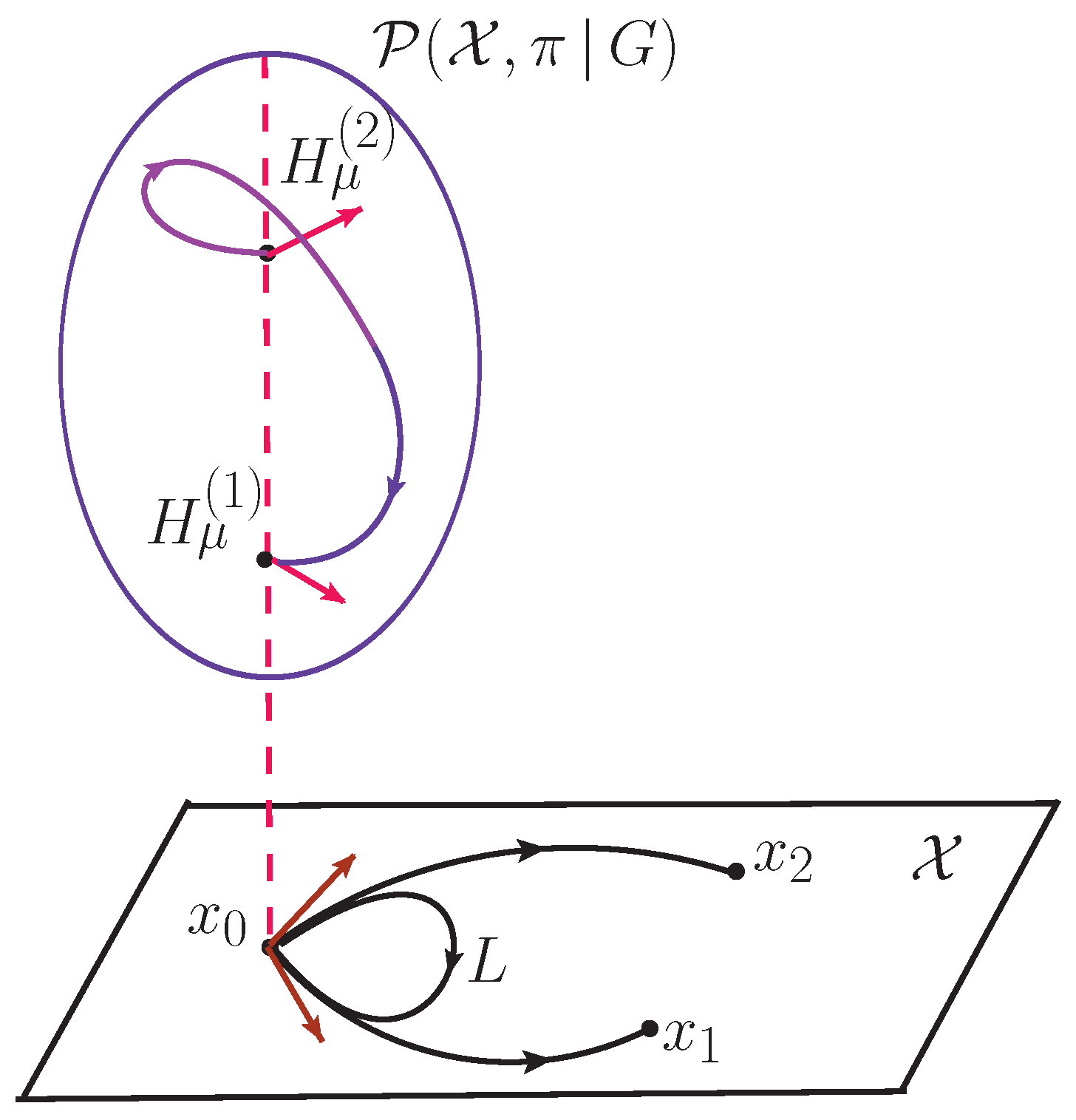
In
, the functional
of Eqn. (
18) is a solution of the parallel transport equation given by
where the fiber point
with the curve
parametrized by
s. Eqn. (
20) being a differential equation takes place even if
is fixed on the group. it is true because, in this case,
while
. In this connection, the condition presented by Eqn. (
18) implies that the full curve-linear integration goes to zero rather than the integrand itself.
It can be shown [
52,
53] that every of points belonging to the fiber bundle,
, has one and only one horizontal vector corresponding to the given tangent vector at
. We remind that the tangent vector at the point
x is uniquely determined by the given path passing through
x. In the frame of H-system based on the geometry of gluons the condition of Eqn. (
18) corresponds to the determining of the surface on
that is parallel to the base plane with the path. Moreover, it singles out the identity element,
, in every fibers of
, see
Figure 2. This choice can be traced to the Lagrange factor
which is formally fixed in H-system, see
Section 2.1. Roughly speaking, once the group (any) element of fiber is fixed, we deal with the Lagrange factor
of H-system which is also uniquely fixed. On the other hand, if we fix the group element of fiber we fix the function theta of gauge transforms as well. In this sense, we do not have the local gauge transforms (or the gauge freedom) anymore.
The path dependent functional given by the
l.h.s. of (
18) can be also gauge transformed. We have
where the local gauge function defined by
with the corresponding generator
. From this, one can see if the Minkowski space has been realized as a loop space, the path dependent functional becomes invariant under the local gauge transforms. In the general case of arbitrary paths, imposing the condition (
18) on the
r.h.s. of (
21), we are able to get the different contour gauge
with
, see (
22). From the theoretical point of view, this new contour gauge has the same status as the gauge of (
18). It would correspond to the different plane
in
Figure 2 which also transects the principle fiber bundle and, therefore, it generates the different contour gauge condition which, generally speaking, is related to the previous contour gauge by the local transform. However, from the practical point of view, the contour gauge given by
is not convenient to use for calculations because the representation of transverse gluon field through the strength tensor has a more complicated form compared to, for example, (
53). Of course, the physical quantities are independent on the contour gauge choice.
Notice that since the gauge condition given by Eqn. (
18) selects only the identity element of group
G on each fiber, it means that the gauge transforms have been reduced to the “global” gauge transforms. That is, the gauge function
becomes the coordinate independent and is fixed
. This situation is identical to that one can see in
Figure 1 of
Section 2.1. Namely, the red dash on the ball surface corresponds to one particular choice of the group element fixed by the given contour gauge. However, if we mark the line on the ball surface by the other dash, it would mean that we choose the other group element fixed by the different contour gauge. In both cases, we deal with the same description of H-system.
Since the functional
depends on the whole path in
, the contour gauge refers to the non-local class of gauges and generalises naturally the familiar local axial-type of gauges. It is also worth to notice that two different contour gauges can correspond to the same local (axial) gauge with the different fixing of residual gauges [
16,
17]. If we would consider the local gauge without the connection with the non-local gauge, the residual gauge freedom would require the extra conditions to fix the given freedom. This statement reflects the fact that, in contrast to the local axial gauge, the contour gauge does not possess the residual gauge freedom in the finite region of a space where the boundary gluon fields are absent [
2].
2.3. Comparison of Local and Nonlocal Gauge
The contour gauge as a nonlocal kind of gauges generalizes or extends the standard local gauge of axial type. Therefore, it is worth to discuss shortly the correspondence between the local and nonlocal gauge transforms.
Let us begin with the axial local gauge defined by
. The nonlocal gauge is given by Eqn. (
18) and the local gauge can be obtained from Eqn. (
18) if, as above-mentioned, the starting point is
and the path is fixed to be a straightforward line,
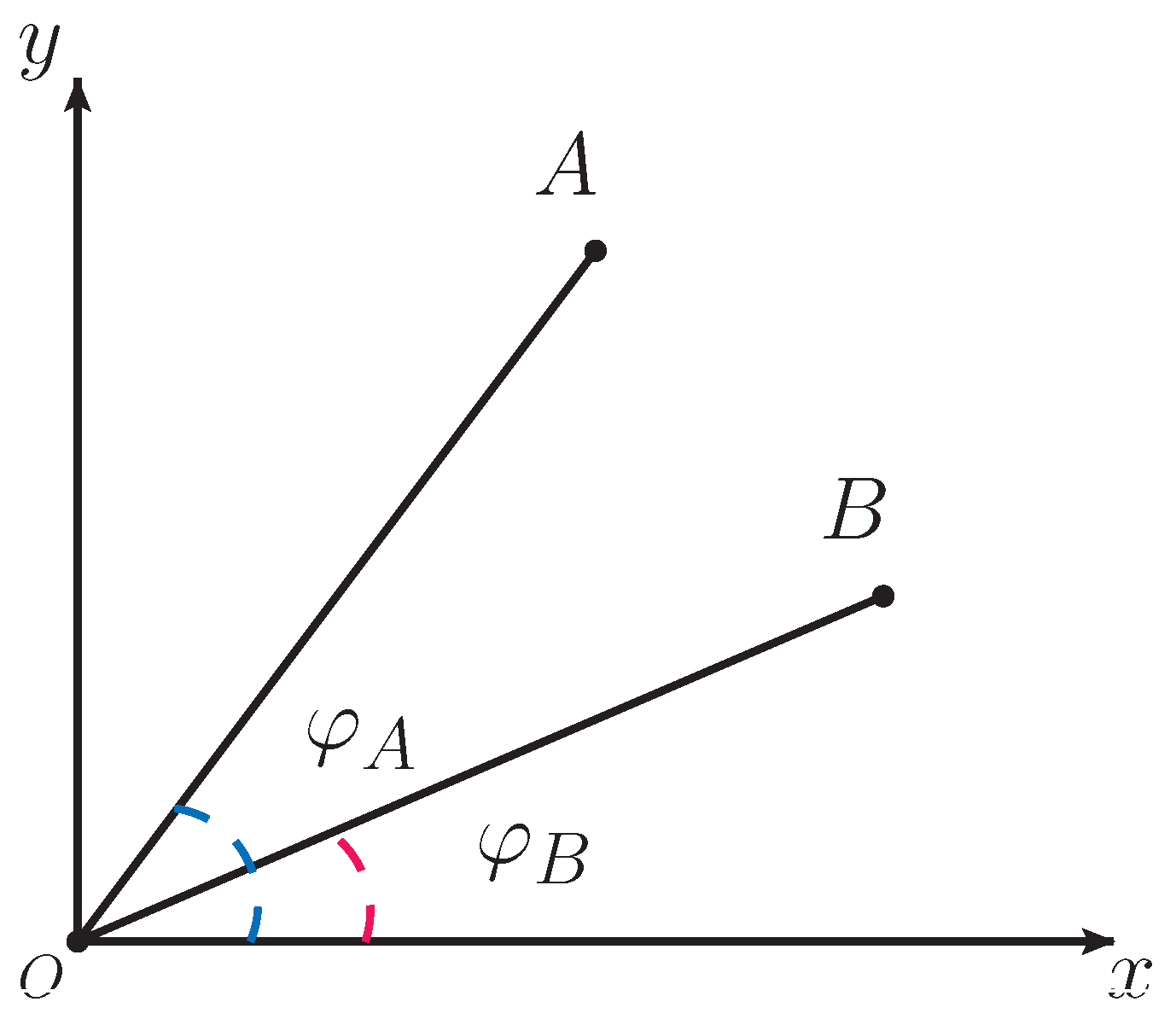
. The differences between the local and nonlocal gauges can symbolically be demonstrated by the following trivial example. Consider two different vectors
A and
B. We stress that they are different by construction. We now assume that these vectors have the same projection on the certain direction given by another vector
N. It is clear that if the vectors have the same projections on the vector
N, it does not mean the equivalence of vectors
A and
B,
i.e.
In this example, the different vectors
A and
B can be associated with two different contour nonlocal gauges,
While the local axial gauge plays a role of the projections on
N,
On the other hand, focusing on only the
N vector projection, there is no additional information to see from which vectors
A or
B the given projection has been performed.
We are coming back to the local axial gauge. The local axial gauge suffers from the residual gauge transformations which can lead to the spurious pole uncertainties. However, the preponderance of nonlocal (contour) gauge is that it fixes all the gauge freedom in the finite space (see for instance [
2]). To demonstrate it in the simplest way, we consider the local axial gauge as an equation on the gauge function
. We have
where
with
. We can readily find a solution of this equation which takes the form of the undetermined integration given by
At the same time, the solution
can be rewritten via the determined integration, it reads
Here,
is fixed and
is an arbitrary function which does not depend on
.
is given by
The arbitrariness of
C-function also reflects the fact that we deal with an arbitrary fixed starting point
.
Let us study the residual gauge freedom requiring both
and
, we then have
One can see that the function
C determines the residual gauge transforms. This situation takes place in the local axial gauge defined by the only condition
applied for (
28).
We go over to the nonlocal gauge which actually gives more information on the gauge fixing. The nonlocal (contour) gauge extends the local axial-type gauge and it demands that the full (curve-linear) integral in the exponential of Eqn. (
18) has to go to zero. We stress that in contrast to the local gauge where the corresponding exponential disappears thanks to that the integrand
goes to zero. One can demonstrate it on the example of solutions (
27) or (
28). Indeed, in the contour gauge the residual gauge function
can be related to the path dependent functionals with
and
which are also disappeared eliminating the gauge freedom and giving the physical gluon representation in the form of (134) (see [
18,
55] for details). That is, if we restore the full path in the path dependent functional for a given process, we can get that
Then, requiring the conditions as
we get that
In the contour gauge, Eqn. (
34) means that no the gauge freedom has left at all. We emphasize that the condition of (
32) demands that the integrand is zero, while the condition of (33) is imposed on the integration which leads to the corresponding representation for the transverse gluon field, see (
53), (54) and (134). Besides, the exact value of the fixed starting point
depends on the process under our consideration [
18].
The path dependent functional also defines the path dependent gauge transformation in the form of
where the starting point
is now fixed. Hence, having calculated the derivative of
in (
35), we get that (here, for the simplicity,
)
where
. If we are now focusing on the case of
, we readily obtain that the gluon representation reads
where the traditional notations
have been introduced. The representation given by (
37) is an important result for our further considerations.
So, in this section, we have demonstrated that the contour gauge gives a possibility to illuminate the unphysical gluon components, meanwhile the local axial gauge fixes the gauge partially leaving room for the residual gauge freedom.
2.4. The Advantages of the Contour Gauge Use
In the subsection, we concentrate our attention on the certain examples which, first, relate to the practical use of the contour gauge and, second, demonstrate the preponderance of the nonlocal gauges compared to the local gauges.
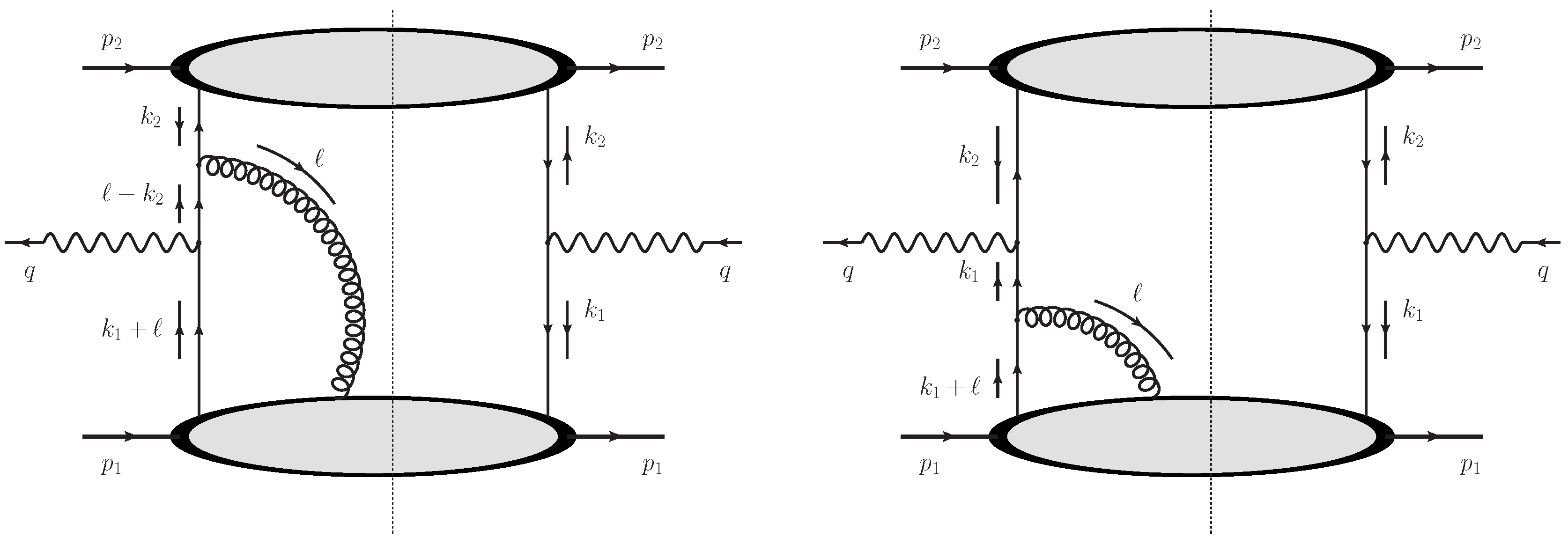
As discussed in [
16,
17,
55], the Drell-Yan-like processes with the polarized hadrons give the unique example where the contour gauge use shows the definite advantage from the practical point of view. In particular, the contour gauge use allows to find the new contributions to the Drell-Yan-like hadron tensor which restore and ensure the gauge invariance of the corresponding hadron tensors [
16,
17,
55]. It is important, however, to stress that the mentioned new contributions are invisible if we would work within the frame in the local gauge.
In the similar manner, due to the contour gauge conception the
-process of DVCS-amplitude which clarifies the gauge invariance of the non-forward processes takes the closed form again [
56]. From the practical point of view, it is instructive to consider the appearance of standard and non-standard diagrams contributing to the well-known deeply virtual Compton scattering (DVCS) amplitude in the frame of the factorization procedure. The gluons radiated from the internal quark of the hard subprocess generate the standard diagrams, while the non-standard diagrams are formed by the gluon radiations from the external quark of the hard subprocess (see [
56] for details).
In the most cases, it is sufficient to exponentiate only the longitudinal components of gluon field,
and
, which are related to the unphysical degrees. Indeed, the standard diagram contributions give the gauge invariant quark string operator which reads
where
and
stands for
-matrices the exact form of which is now irrelevant.
The non-standard diagram contributions result in the string operator defined as
where
Hence, using the contour gauge conception, we eliminate all the Wilson lines with the longitudinal gluon fields
and
demanding that
and
Eqns. (
45) and (
46) give rise to the local gauge conditions given by
and
.
With respect to the Wilson line with the transverse gluons , we remind that we work here within the factorization procedure applied for DVCS-amplitude. In this case, the Wilson lines with the transverse gluon fields are considered in the form of an expansion due to the fixed twist-order, and the transverse gluons correspond to the physical configurations of L-system.
Thus, the DVCS process gives us the example how the unphysical gluon degrees can be illuminated from the consideration with the help of contour gauge.
We are now going over to the Drell-Yan (DY) process with one transversely polarized hadron [
16]
where the virtual photon producing the lepton pair (
) has a large offshelness,
i.e. , while all the transverse momenta are small and integrated out in the corresponding cross-sections
. Here, the contour gauge use results in the gauge invariant hadron tensor and provides the new contributions to single spin asymmetries. Having considered this hadron tensor in the asymptotical regime associated with the very large
, the factorization theorem can be applied for the given hadron tensor as well as for the DVCS process. As a result, the DY hadron tensor takes a form of convolution as
where both the hard and soft parts should be independent of each other and are in agreement with the ultraviolet and infrared renormalizations. Moreover, the relevant single spin asymmetries (SSAs), which is a subject of experimental studies, can be presented as
where
and
are the lepton and hadron tensors, respectively. The hadron tensor
includes the the polarized hadron matrix element which takes a form of
where
stands for the Fourier transform between the coordinate space, formed by positions
, and the momentum space, realized by fractions
; the light-cone vector
is a dimensionful analog of
n. In Eqn. (
50), the parametrizing function
B describes the corresponding parton distribution.
In the studies, see for example [
7,
57,
58,
59], where the local light-cone gauge
has been used,
B-function of Eqn. (
50) is given by a purely real function. That is, we have
where the function
parametrizes the corresponding projection of
and obeys
.
In Eqn. (
51), the pole at
is treated as a principle value and it obviously leads to
. Indeed, within the local gauge
, the statement on that
B is the real function stems actually from the ambiguity in the solutions of the trivial differential equation, which is equivalent to the definition of
,
The formal resolving of Eqn. (
52) leads to two representations written as
We stress that within the approaches backed on the local axial gauge use, there are no evidences to think that Eqns. (
53) and (54) are not equivalent each other. That is, the local gauge
inevitably leads to the following logical scheme (see [
17] for details)
This equation demonstrates that the equivalence of Eqns. (
53) and (54) causes the representation of
B-function as in Eqn. (
51). The discussion on the boundary configurations can be found in [
17].
Regarding the DY process, the physical consequences of the use of
B presented by Eqn. (
51) are the problem with the photon gauge invariance of DY-like hadron tensors and the losing of significant contributions to SSAs [
16,
17]. Besides, based on the local gauge
, the representation of gluon field as a linear combination of Eqns. (
53) and (54) has been used in the different studies, see [
38,
45,
60].
In contrast to the local gauge
, as discussed in
Section 2.2, we can infer that the path dependent non-local gauge (see Eqn. (
18)) fixes unambiguously the representation of gluon field which is given by either Eqn. (
53) or Eqn. (54). Indeed, fixing the path
, a solution of Eqn. (
18) takes the form of (see [
16,
17,
61] for details)
where the boundary configuration
has assumed to be zero. By direct calculation, we can show that the non-local gauge
leads to the gluon filed representation of Eqn. (
53), while the non-local gauge
corresponds to the gluon field representation of Eqn. (54). Moreover, we can readily check that [
16,
17]
where
Notice that both the non-local contour gauges, i.e. and , can be projected into the same local gauge . As mentioned, the projection given by does not give a possibility to understand which of the non-local gauges generates the local gauge.
To conclude, we can state that, considering DY-like processes, the corresponding non-local gauge gives rise to the correct representation of
B-functions, see Eqn. (
58), which has the non-zero imaginary part. This enables us to find the new significant contributions to the hadron tensors that ensure ultimately the gauge invariance [
16,
17]. In a similar manner, with the help of Eqn. (
58) we can fix the prescriptions for the spurious singularities in the gluon propagators [
55].