Dark Energy and Dark Matter from Extra Dimensional Symmetry as Different Manifestations of Vacuum Energy

Preprint

Article

Dark Energy and Dark Matter from Extra Dimensional Symmetry as Different Manifestations of Vacuum Energy

Altmetrics

Downloads

375

Views

336

Comments

Kabir Umar^*

This version is not peer-reviewed

Submitted:

05 January 2024

Posted:

05 January 2024

Read the latest preprint version here

Alerts

Abstract

Dark energy and dark matter are described as different manifestations of vacuum energy using a newly developed framework of Extra Dimensional Symmetry (EDS) that doubles large spatial dimensions with microscopic partners. In this framework, the bare vacuum energy component exists in a gravitationally dark state where actual gravitational constant G_o= 0G, while real particles oscillate between this inert state and an active state where G_o = 2G. A small component of vacuum energy is constrained to exist in the gravitationally active state as dark energy due to energy density constraint and speed limit asymmetry determined by an asymmetry parameter . Furthermore, neutrinos induce small component of the gravitational constant in the dark state within a volume of space described by the wavelength, enabling the gravitation of virtual particles which manifests as dark matter. The resulting has oscillating light and heavy terms. The heavy term is usually inactive due to its suppression by negative pressure and becomes active for a lifetime once shear stress exceeds negative pressure threshold. This results in a light form of dark matter and a heavy form of dark matter that is detectable through its increased gravitational interaction and resulting acceleration.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

Dark energy is a mysterious energy component that has been observed to be driving the accelerated expansion of the universe, and have defied several explanations since its discovery in supernova observations [1]. Its existence has since been confirmed by several independent observations like the Planck measurements of the Cosmic Microwave Background (CMB), indicating that it accounts for about 68.3% of the gravitating energy content of the universe [2]. This is in addition to the older dark matter mystery [3] of a gravitationally attractive but invisible matter component constituting about 26.8% of the gravitating energy content of the universe. Only about 4.6% is in the form of visible baryonic matter.

The cosmological constant (Λ) earlier introduced into Einstein’s Field Equations, while being the simplest solution, results in a serious conflict between measured density of dark energy and the 120 orders of magnitude larger value predicted from quantum field theory [4]. The Λ problem has defied logical solution from supersymmetric cancellation approaches, relaxation of vacuum energy [5] and anthropic approach [6]. It also defies an approach that simply makes the spacetime metric insensitive to Λ [7].

Slowly evolving scalar field models like quintessence [8,9] is one of the many alternative approaches to solve the dark energy mystery without the Λ route. We also have modified gravity models [10] and unification of dark energy and dark matter [11]. See Ref. [12] for detailed review and Refs.[13, 14] for recent review.

The amount of theoretical and observational efforts that has been applied to understand dark energy and dark matter indicates that they require new physics beyond the existing standard model of cosmology and particle physics. Attempts to resolve the dark matter mystery can be mainly classified as either a modification of gravity or introduction of new particles beyond the standard model of particle physics. However, both approaches of modified gravity and particle dark matter tends to fail in providing consistent explanations to the dark matter mystery as each approach tends to succeed in explaining some observations and fail at some others.

There is an approach that explains dark matter as gravitational polarization of vacuum energy by baryonic matter without invoking new particle or modifying gravity in the traditional sense [15]. It is based on the idea that matter and antimatter have opposite gravitational charges which requires a violation of the Weak Equivalence Principle. Preliminary findings from measurements of antiproton to proton charge to mass ratio imply that matter and antimatter gravitate the same way [16]. Furthermore, the recent result from the ALPHA collaboration has ruled out the possibility of gravitationally repulsive antimatter [17].

In this paper, the dark energy and dark matter puzzle are approached using the new framework of Extra Dimension Symmetry (EDS) that doubles the number of large extra dimensions with microscopic partners. EDS provides a solution to the dark energy puzzle by placing the bare vacuum energy component in a gravitationally inert state where the actual gravitational constant G_o = 0G. Due to a speed limit asymmetry and energy density constraint, a nonzero component of vacuum energy is constrained to the gravitationally active state where G_o = 2G, manifesting as dark energy. For dark matter, it relies on the background effect of neutrinos which induces a nonzero gravitational constant in the inert state, enabling the gravitation of virtual particles which appears as dark matter. This neutrino substrate approach for dark matter doesn’t require the polarization of the quantum vacuum or opposite gravitational charges for particles and antiparticles like in [15].

This paper is organized as follows. Section 2 discusses the key dimensional symmetry in which spatial dimensions are grouped as a set of dimension(s) with dimensional partners having opposite dimension numbers that determines either a positive or negative response to the stress energy tensor. It also discusses the selective response of some other sets of dimension(s) to the components of the stress energy tensor. It further discusses the speed constraint, the two gravitationally inert and active states, their speed limit asymmetry and density constraint, which is then applied in Section 3 to provide a possible solution to the Λ problem of dark energy. Section 3 discusses the emergence of dark energy due to the speed limit asymmetry and energy density constraint discussed in Section 2. Section 4 discusses General Relativity in two set of these extra dimensions which has impact on the heavy term of neutrino induced gravitational constant. Section 5 discusses the neutrino induced gravitation of virtual particles which appears as dark matter. Discussion and conclusion follows in Section 6.

2. Extra Dimensional Symmetry Framework

In this framework, the number of spatial dimensions is described by the dimension number

S_{n}

with dimensionality d that can either be +1 or -1, such that,

S_{n} = (4 n - 1) d

(1)

where

n = 0, 1, 2, 3, \dots n = 0,

corresponds to

S_{n} = - 1 d

which is a time like spatial dimension that is invisible due to speed constraint discussed in Section 2.2.

n = 1,

corresponds to

S_{1} = 3 d

which is the visible set of spatial dimensions.

n = 2

, corresponds to

S_{2} = 7 d

. It is assumed that

d = + 1

in the present universe.

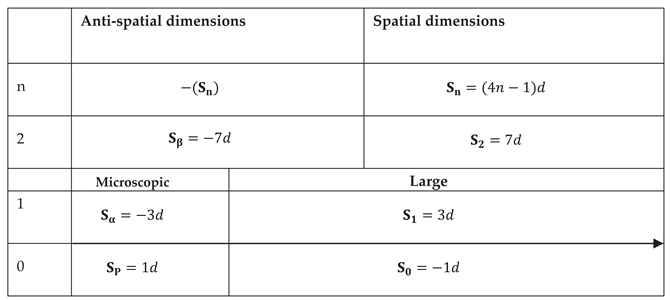
The EDS framework further doubles these set of spatial dimensions (-1, 3 and 7) with dimensional partners with opposite dimension numbers (anti-spatial dimensions) such that the total dimension number of the universe is zero as illustrated in Table 1. While the dimensional partner of S₀, is a Planck size

S_{P}

dimension, the dimensional partner of S₁ is denoted

S_{α}

and that of S₂ is denoted

S_{β}

The negative dimension numbers implies the inversion of the sign of the stress energy tensor in which expansion becomes contraction while contraction becomes expansion. As a result of this, the expansion of the large spatial dimensions S₁ and S₀ in the early universe is equivalent to the gravitational collapse of their dimensional partners. This is partly enabled by the selective response to the stress energy tensor discussed in Section 2.1. Any set of dimensions with

n > 1

, such as S₂ remain static neither able to expand, nor contract if they exist.

Table 1. Periodic table of spatial dimensions indicating dimension number symmetry between the sets of spatial and anti-spatial dimensions within the EDS framework. The direction of the arrow from left to right indicates a positive dimensionality d in which the large spatial dimensions expands while their microscopic dimensional partners collapse. S₂ and beyond are static neither able to expand, nor contract if they exist.

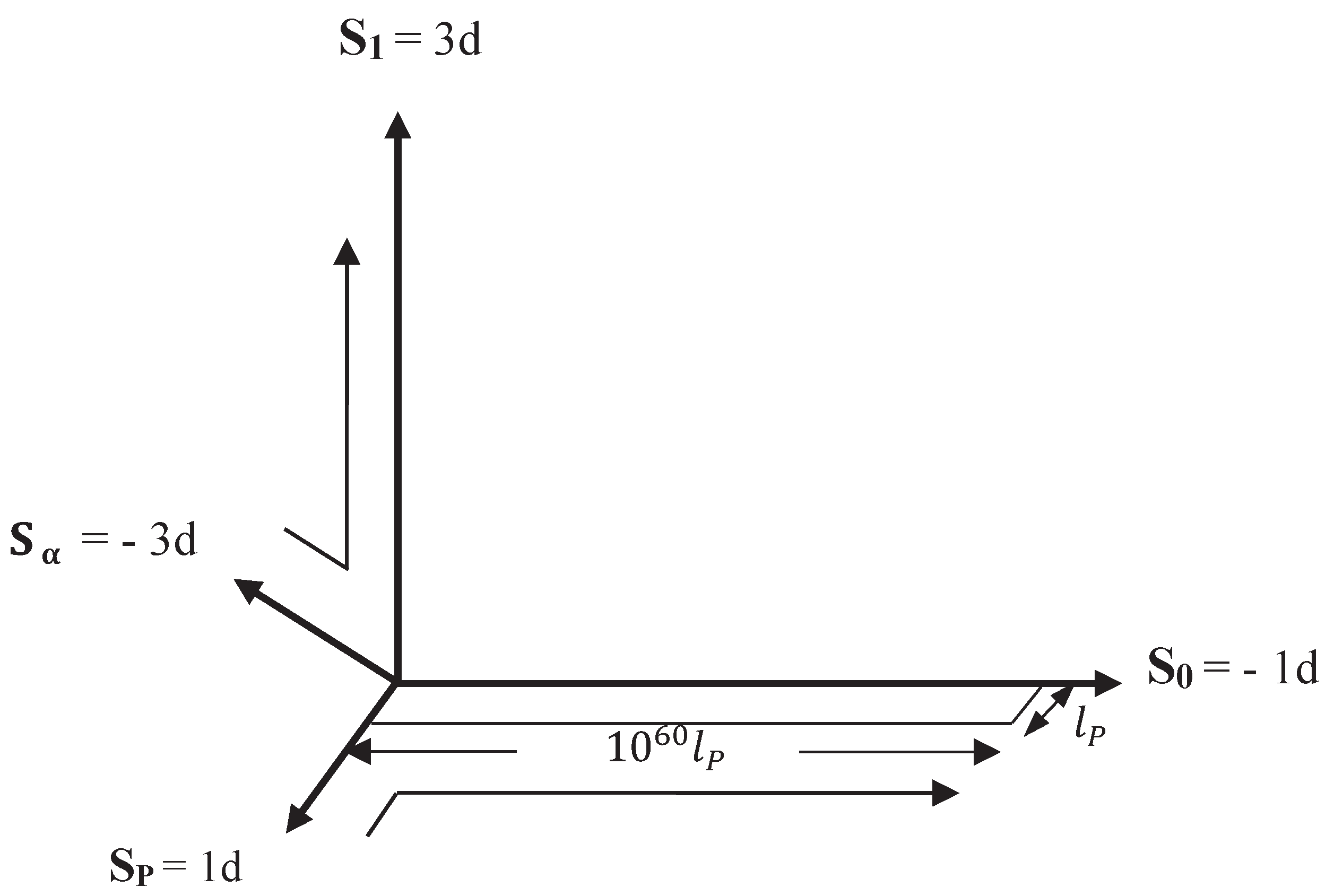
Figure 1. Large spatial dimensions S₁ and S₀ and their microscopic dimensional partners

S_{α}

and S_P. The opposite dimension numbers which inverts the sign of the stress energy tensor implies that S_P and S_α collapsed to their minimum microscopic sizes during the inflation of S₀ and S₁ in the early universe.

Figure 1. Large spatial dimensions S₁ and S₀ and their microscopic dimensional partners

S_{α}

In resolving the mysteries of dark energy and dark matter, this paper focuses on the large spatial dimensions S₁ and S₀, their microscopic dimensional partners

S_{α}

and S_P as well as some of their interactions with one another.

2.1. Selective Response to Components of the Stress Energy Tensor

In the EDS framework, while the S₀ dimension is unable to respond to shear stress due to its one spatial dimensionality, (shear stress requires at least two spatial dimensions), S_P doesn’t respond to negative pressure. Also, the

S_{α}

dimension is unable to respond to energy density, momentum flux and positive pressure. It only responds to shear stress and negative pressure.

2.2. Speed Constraint and Invisibility of S₀ Dimension

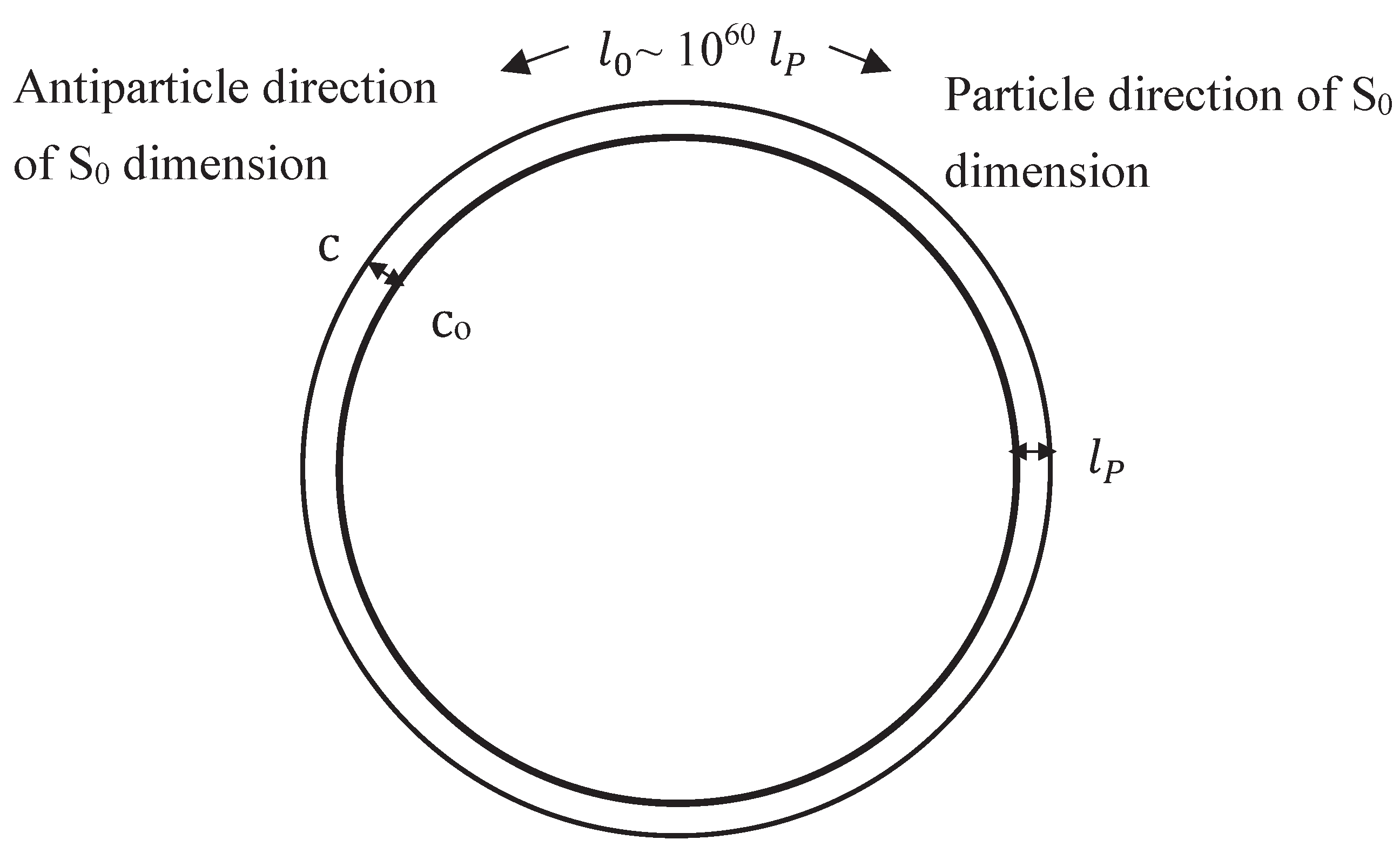
Despite its cosmic size, the S₀ dimension is invisible due to its time like behavior from the speed constraint illustrated in Equation (2). Consistent with Special Relativity, the speed constraint requires that a particle’s velocity must always equal the maximum speed limit c in the S₁ – S₀ dimensions.

Massless particles like photons have zero velocity component along S₀, while massive particles and antiparticles travel in opposite directions along S₀. This motion along S₀ is quantitatively equivalent to the passage of time such that,

c^{2} = μ^{2} + ν^{2} .

(2)

where µ is particle velocity along S₀, and ν is particle velocity along visible spatial dimension S₁.

When

ν \to 0,

for massive particles,

µ \to c

and conversely, when ν

= c

, for massless particles,

µ = 0

, to satisfy the speed constraint. This suggests that time can be an emergent temporal dimension driven by the velocity of a particle along S₀ dimension. How fast time appears to pass for a massive particle can be equivalent to the ratio of its S₀ component of velocity

µ

to the speed limit c as,

\frac{1}{γ^{*}} = \frac{μ}{c} .

(3)

where

γ^{*}

is the equivalent Lorentz factor for the S₀ dimension. Since

μ^{2} = c^{2} - ν^{2}

γ^{*} = \frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} .

(4)

2.3. Speed Limit Asymmetry

The asymmetry in speed limits c and c₀ is described by the asymmetry parameter

Γ

which is the ratio of the Planck size of S_P to the size of S₀ dimension, illustrated in Figure 2.

0 < Γ < 1

such that,

Γ = \frac{2 π}{l_{o}}

(5)

where

l_{o}

is the size of S₀ in Planck unit. And

l_{o} = Δ l_{o} + l_{f} .

(6)

where

l_{f} ~ 10^{60}

in Planck unit, is the value of

l_{o}

in flat spacetime. The increase in size

Δ l_{o}

is proportional to the gravitational potential

Φ

The asymmetry relationship between the two speed limits c and c₀, as shown in Figure 2 can be expressed as,

C_{o} = C [1 - Γ] .

(7)

2.4. Gravitational State Oscillation

In EDS, Standard Model particles oscillates between the two speed states which are also opposite gravitational on and off states. This is such that for a particle of energy E, the state life time

t_{s}

for such particle is,

t_{s} = \frac{4 π ℏ}{\sqrt{E_{P}^{2} - E^{2}}} .

(8)

where

ℏ

is the reduced Planck constant and

E_{P}

is the Planck energy.

The oscillation of Standard Model particles between the two gravitational states

G_{0} = 0 G

and

G_{0} = 2 G

, makes gravity discrete on microscopic spacetime scale. It however appears smooth on macroscopic spacetime scale with an average gravitational constant G. Furthermore, the value of the gravitational constant in both gravitationally active and inert state, is constrained such that,

G^{2} = \frac{G_{1}^{2} + G_{2}^{2}}{4}

(9)

where

G_{1}

and

G_{2}

are the gravitational constants in the active and the inert states respectively.

2.5. Energy Density Constraint

The energy density constraint essentially constrains the total energy density in a given volume of spacetime to always equal the upper limit of the Planck density

ρ_{P}

. This is only obtainable in the gravitational active state where the speed limit is c while the bare vacuum energy component exists in the inert state with lower speed limit and hence lower Planck density

ρ_{P 0} .

ρ_{P}^{2} = ρ_{m}^{2} + ρ_{v a c}^{2} .

(10)

where

ρ_{v a c}

is the vacuum energy density, and

ρ_{m}

is the total baryonic matter density. The key significance of this, is in the emergence of non zero Λ dark energy in Section 4. However, such energy density constraint implies a Planck density limit to the density of black holes like that suggested in [18], where Planck stars replace black hole singularities.

3. General Relativity in S₀ and $S_{α}$ Dimensions

3.1. General Relativity in S₀ Dimension

In -1+1 dimensionality, just as in 1+1 where the curvature term is zero [19], Einstein Field Equations can be expressed as,

Λ^{*} g_{μ ν} = \frac{8 π G}{c^{4}} T_{μ ν} .

(11)

where

Λ^{*}

is the equivalent cosmological constant in S₀ dimension,

g_{μ ν}

is the metric tensor and

T_{μ ν}

is the stress energy tensor. The negative one dimensionality of the S₀ dimension which inverts the sign of the stress energy tensor, confers on it some unique features such as:

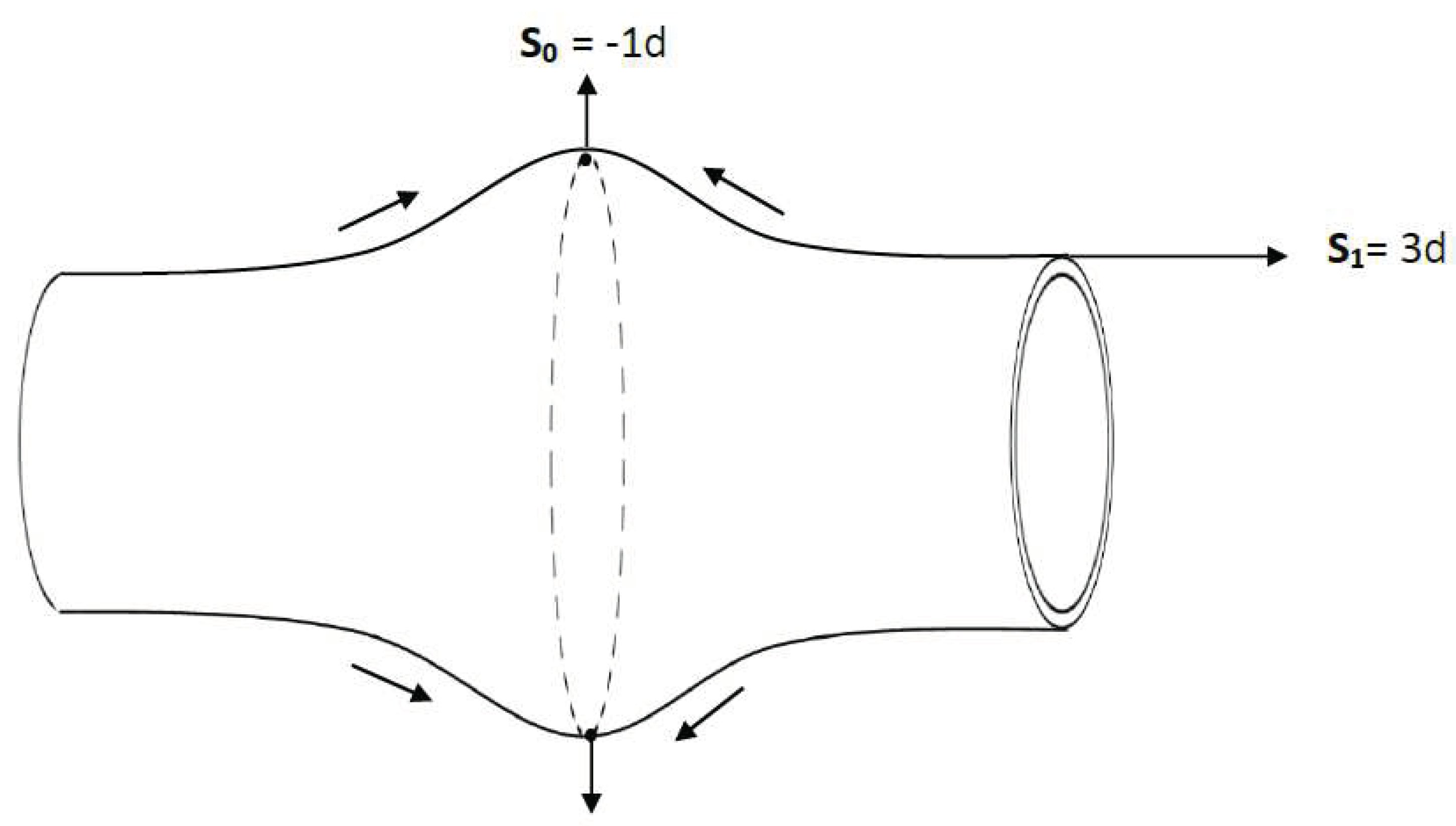
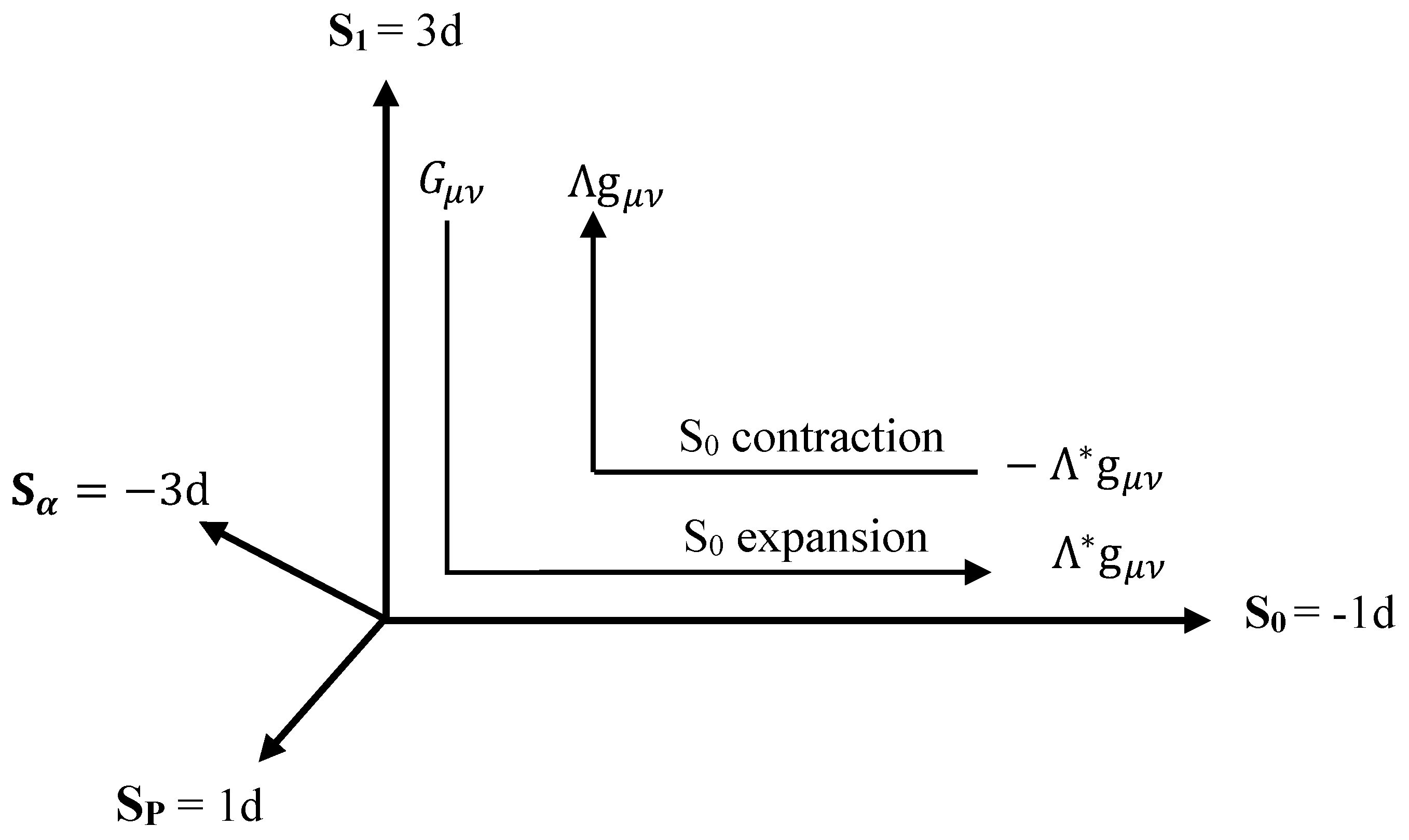
i.: Positive energy density in S₁ is equivalent to negative energy density everywhere in S₀.

An energy density associated with a given Planck volume of 3d space S₁ appears as an equivalent negative energy density everywhere along S₀ dimension associated with it as a positive cosmological constant as illustrated in Figure 3.

ii.: Positive pressure in S₁ is equivalent to negative pressure in S₀

Any form of positive pressure in S₁ appears as negative pressure in S₀ for the same reason of negative dimensionality. The result is a positive cosmological constant expansion of S₀.

iii.: Negative pressure in S₁ is equivalent to a positive pressure in S₀

The same negative dimensionality causes the inversion of negative pressure in S₁ appearing as positive pressure in S₀ driving its negative cosmological constant contraction. The result is that in the absence of shear stress component to which S₀ is insensitive to, as mentioned in Section 2.1, the curvature of S₁ (

G_{μ ν}

) is equivalent to the cosmological constant expansion of S₀ as illustrated in Figure 4, such that,

G_{μ ν} + Λ^{*} g_{μ ν} = 0,

(12)

and a positive cosmological constant term (

{Λ g}_{μ ν}

) in S₁ is equivalent to a negative cosmological constant term (

- Λ^{*} g_{μ ν}

) in S₀ such that,

{Λ g}_{μ ν} - Λ^{*} g_{μ ν} = 0 .

(13)

3.2. General Relativity in $S_{α}$ Dimensions

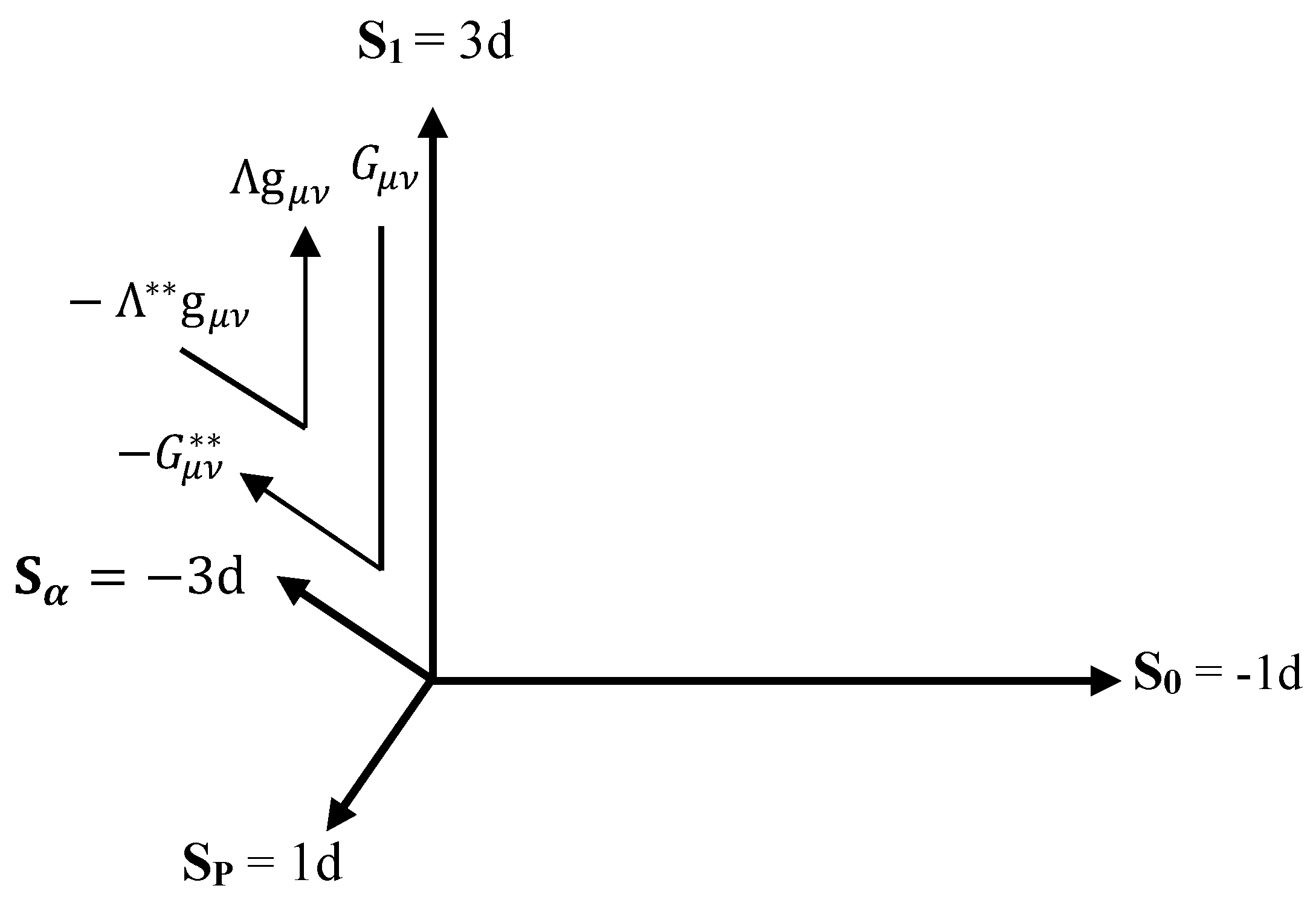
Unlike the one dimensionality of S₀ dimension where the Einstein tensor is zero, the three dimensionality of

S_{α}

dimensions ensures that the Einstein tensor is not zero. Furthermore, it only responds to shear stress and negative pressure due to selective response to the stress energy tensor as discussed in Section 2.1. The result is that the positive curvature effect (

G_{μ ν}

) of shear stress on

S_{1}

dimensions is equivalent to the negative curvature effect (

- G_{μ ν}^{* *}

) of shear stress on the

S_{α}

dimensions. Therefore,

G_{μ ν} - G_{μ ν}^{* *} = 0.

(14)

Furthermore, the positive cosmological constant (

Λ

) expansion of

S_{1}

due to negative pressure, can be equivalent to the negative cosmological constant (

- Λ^{* *}

) contraction of

S_{α}

{Λ g}_{μ ν} - Λ^{* *} g_{μ ν} = 0 .

(15)

The gravitational inversion of S₁ -

S_{α}

dimensions as illustrated in Figure 5 should be true until the size of the

S_{α}

dimension

l_{α}

falls to it characteristic minimum length scale of not less than

2 π

in Planck unit, and it can be as much as 137 Planck units depending on limits from geometrical considerations and other possible interactions that might be associated with it. Beyond this minimum length scale, the

S_{α}

dimension appears irresponsive to negative pressure as it becomes pinned down, unable to contract further or vibrate in response to weak gravitational wave oscillations. At this point it is only the cosmological constant contraction of S₀ that balances the cosmological constant expansion of S₁ as expressed in Equation (13).

4. Emergence of Nonzero Cosmological Constant

The asymmetry in speed limit described in Equation (7) between the two gravitational states also reflects in the values of their Planck densities such that

ρ_{P 0}^{2} = ρ_{P}^{2} [1 - Γ^{4}] .

(16)

where

ρ_{P 0}

is the lower Planck density in C₀ state and

ρ_{P}

is the Planck density in the C state.

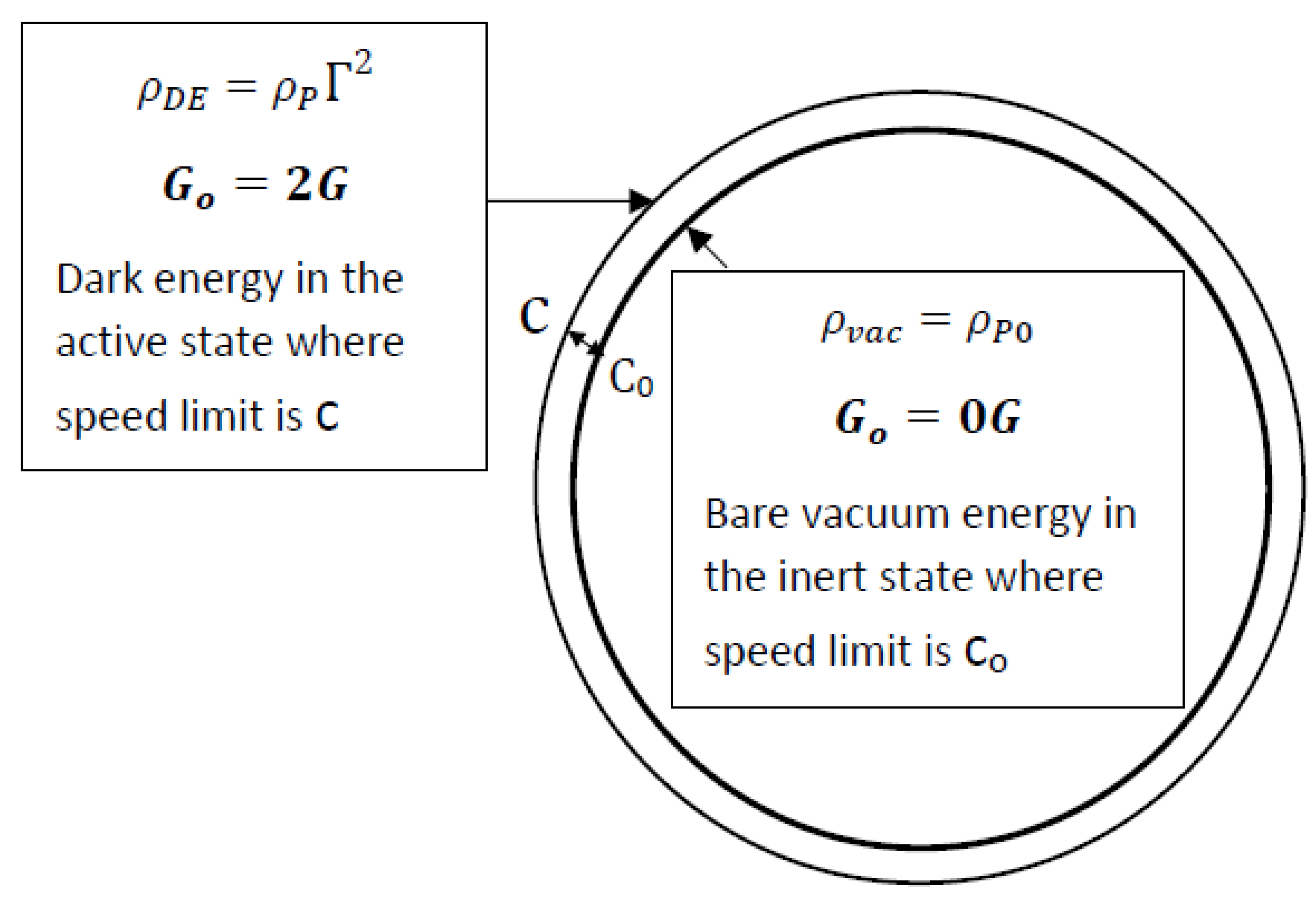
The existence of the bare vacuum energy component

ρ_{v a c}

in the lower C₀ state implies that

ρ_{v a c} = ρ_{P 0},

(17)

which is less than the Planck density and the energy density constraint in Section 2.5 requires that the total vacuum energy density should be equal to the Planck density in the absence of matter.

Since the gravitationally inert lower speed state lacks the capacity to contain all the vacuum energy components, a small component is therefore constrained to the gravitationally active state as dark energy

ρ_{D E}

as illustrated in Figure 6, such that,

ρ_{D E} = ρ_{P} Γ^{2} .

(18)

Since

Γ

is suppressed with the expansion of S₀ in the gravitational well of massive objects (Equation (5) and Figure 3), the density of this form of dark energy varies spatially according to this suppression by gravitational potential wells. The deeper the gravitational well the more the suppression. And substituting

Γ

from Equation (5),

ρ_{D E} = \frac{4 π^{2} ρ_{P}}{l_{0}^{2}}

(19)

where

l_{0}

is the size of S₀ dimension in Planck unit, which increases with the gravitational potential.

5. Dark Matter from Neutrino Enabled Gravitation of Virtual Particles

In the EDS framework, the existence of the bare vacuum energy component in the gravitationally dark state with actual gravitational constant

G_{0} = 0 G

ensures that virtual particles in such state are gravitationally inert. However, neutrinos can induce small component of the gravitational constant in this inert state as described by Equation (20). It enables virtual particles within a spatial volume determined by the neutrino wave length to gravitate with positive pressure and appear as dark matter.

G_{ν}^{2} = {(2 Γ^{2} β ϕ_{f} G)}^{2} + {(2 β ϕ G)}^{2} .

(20)

where

G_{ν}

is the neutrino induced gravitational constant in the inert state.

Γ

is the asymmetry parameter involved in the emergence of dark energy.

ϕ_{f}

is the dimensionless flavour parameter. It oscillates with neutrino flavour such that

0 < ϕ_{f} \leq 1

ϕ

is a dimensionless phase parameter that also oscillates between zero and one (

0 \leq ϕ \leq 1

), but gets dampened and constrained to zero by negative pressure. Once shear pressure exceeds negative pressure,

ϕ

oscillation resumes and remains in this active phase for a life time

t_{ϕ}

β

is a dimesionless energy scale parameter .

0 < β < 1

and it is described by,

β = \frac{E_{ν}}{E_{P}} .

(21)

where

E_{ν}

is neutrino energy and

E_{P}

is Planck energy.

Equation (20) consists of a usually inactive heavy term (

2 β ϕ G

) with

ϕ

constrained to its zero phase by negative pressure and an oscillating light term (

2 Γ^{2} β ϕ_{f} G

), lightened to the scale of dark energy by

Γ

. While the light term tends to produce the effect of light and hot dark matter, the heavy term produces the effect of heavy dark matter. Furthermore, such neutrinos can be significantly slowed down from the gravitational drag of the gravitationally enabled virtual particles appearing as cold dark matter.

5.1. Detectability

In terms of detectability, light dark matter can be quit thin and can only be detected through the CMB, gravitational lensing and dynamics of large stellar binaries, galactic and extra galactic structures. Heavy dark matter on the other hand, should in addition, be detectable through small scale mass and particle accelerations due to the strong gravitational interactions which also tends to increase neutrino interaction crossection. From Equation (20), an ultra high energy neutrino with 10^-16 eV energy and with

ϕ ~ 1

, should induce a gravitational constant

G_{ν} ~ 10^{- 12} G

for virtual particles to gravitate within the volume of space described by the neutrino wavelength. Such heavy term enabled gravitation of virtual particles produces the effect of heavy dark matter while active.

The key role of shear stress in activating the heavy term in Equation (20) by neutralizing the suppressive effect of negative pressure as indicated in Section 3.2, provides a means of activation and subsequent detection of heavy dark matter from relatively intense neutrino flux such as solar neutrino and even geoneutrinos. The life time

t_{ϕ}

can provide a way to determine the effective interaction distance

l_{e}

(from the point of shear activation), where

ϕ = 1

and the heavy term is at its heaviest. While the detailed dynamics of

t_{ϕ}

is yet to be fully worked out, it is expected to be inversely proportional to neutrino energy and negative pressure after shear activation of the heavy term. This can be worked out from future theoretical and experimental works.

6. Discussion and Conclusions

EDS provides a framework for the possible resolution of the mysteries of dark energy and dark matter. In doing so it provides potential insights into the dimensional structure of spacetime and gravity. Specifically, it places the bare vac.um energy component in a state where the gravitational field is switched off with actual gravitational constant G₀ = 0G, while real standard model particles, oscillate between this gravitationally inert state and the active state.

Due to an energy density constraint and a speed limit asymmetry described by an asymmetry parameter, a small component of vacuum energy is constrained to exist in the gravitationally active state and appear as dark energy. The asymmetry parameter is the ratio of the size of a large extra spatial dimension S₀ and its microscopic partner S_P. Furthermore, EDS describes dark matter as resulting from neutrino enabled gravitation of virtual particles, in which neutrinos induce non zero component of the gravitational constant in the gravitational dark state. The induced gravitational constant has an oscillating light term and a similarly oscillating heavy term that is suppressed by negative pressure but can be activated by shear stress. The result is a barely detectable light form of dark matter and a detectable heavy form dark matter. This neutrino substrate dependent form of dark matter should exhibit hybrid behaviour of particle dark matter and modified gravity form of dark matter like the gravitational polarization of vacuum energy approach [10] and superfluid dark matter [20]. The detailed dynamics of this form of dark matter shall be discussed in future papers.

Expected results from the trio of the JWST, Euclid and upcoming Nancy Grace Roman Telescope and Vera Rubin Observatory, are expected to provide precision measurements of dark energy density as well as the dynamics of dark matter. Such precision measurements should glean out the predicted suppression of dark energy density in the deep gravitational potential wells of baryonic matter like it apparently does to dark matter.

There are number of potential insights that can have interesting outcome but are beyond the scope of this article. For instance, a possible oscillation of dimensionality d in Equation (1) which can determine either a positive or negative response to the stress energy tensor might give rise to a cyclic universe scenario. This possibility and more, shall be explored in future works.

In conclusion, the EDS framework offers new physics explanations for dark energy and dark matter as different manifestations of vacuum energy that can be tested and provides potential insights into the dimensional structure of spacetime and gravity.

Author Contributions

Kabir Adinoyi Umar: Conceptualization, Investigation, Writing-original draft, Writing-review and editing, Resources. Benjamin Gbenga Ayatunji: Supervision.

Data Availability Statement

No data was used for the research described in the article

Acknowledgments

The author gratefully acknowledges Benjamin G. Ayatunji for his criticisms, encouragement and mentorship. The author is immensely grateful to Aminu M. Musa, Buhari M. Abubakar and Umar Sani Abdullahi. He is very grateful to S. X. K. Howusu for his inspiring advice and initial motivation for this work.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Riess, A.G.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998; 116, 1009–1038arXiv:astro-ph/9805201. [Google Scholar] [CrossRef]
Ade P, A.R. Planck 2013 results. XVI. cosmological parameters. 2013; arXiv:1303.5076[astro-ph.CO]. [Google Scholar]
Bertone, G.; Hooper, D. Hystory of dark matter. Rev. Mod. Phys. 2018; 90, 045002. [Google Scholar] [CrossRef]
Carroll, S.M. The cosmological constant. Living Rev. Rel. 2001; 4, arXiv:astro-ph/0004075. [Google Scholar]
Kachru, S.; et al. de Sitter vacua in string theory. Phys. Rev. 2003; D68, 046005arXiv:hep-th/0301240. [Google Scholar]
Banks, T.; et al. On anthropic solutions of the cosmological constant problem. JHEP, 2001; 0101, 031arXiv:hep-th/0007206. [Google Scholar] [CrossRef]
Arkani-Hamid, N. A small cosmological constant from a large extra dimension. Phys. Lett. h, 2000; B480, 193–199arXiv:hep-th/000197. [Google Scholar] [CrossRef]
Caroll, S.M. Quintessence and the rest of the world: suppressing long-range interactions. Phys. Rev. Lett. 1998, 81, 3067. [Google Scholar] [CrossRef]
Ratra, B.; Peebles, J. Cosmological consequences of a rolling homogenous scalar field. Phys. Rev. D 1988, 37, 321. [Google Scholar] [CrossRef]
Tsujikawa, S. Modified gravity models of dark energy. Lec. Notes Phys. 2010, 800, 99–145. [Google Scholar]
Bilic, N.; Tuper, G.B.; Viollier, R.D. Unification of dark matter and dark energy: The inhomogenous chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
Copeland, E.J. Dynamics of dark energy. Int. J. Mod. Phys. 2006; 1753–1936arXiv:hep-th/0603057. [Google Scholar]
Oks, E. Brief review of recent advances in understanding dark matter and dark energy. New Astron. Rev. 2021; 93, 101632arXiv:2111.00363[astro-ph.CO]. [Google Scholar] [CrossRef]
Arun, K.; et al. Dark matter, dark energy and alternate models: a review. Adv. Space Res. 2017; 60, 166–186arXiv:1704.06155[physics. [Google Scholar] [CrossRef]
Hajdukovic, D.S. Quantum vacuum and dark matter. Astrophys. Space Sci. 2012, 337, 9–14. [Google Scholar] [CrossRef]
Borchert, M.J.; Devlin, J.A.; Ulmer, S.; et al. , A 16 parts per trillion measurement of the antiproton to proton charge-mass ratio. Nature 2022, 601, 53–57. [Google Scholar] [CrossRef] [PubMed]
Anderson, E.K.; et al. Observation of the effect of gravity on the motion of antimatter. Nature 2023, 621, 716–722. [Google Scholar] [CrossRef] [PubMed]
Rovelli, C.; Vidoto, F. Planck Stars. Int. J. Mod. Phys. 2014; D23, 1442026arXiv:1401.6562. [Google Scholar] [CrossRef]
Boozer, A.D. General relativity in (1+1) dimension. Eur. J. Phys. 2008, 29, 319–333. [Google Scholar] [CrossRef]
Hossenfelder, S.; Mistele, T. The Milky Way’s rotation curve with superfluid dark matter. MNRAS, 2020; 498, 3484–349arXiv:2003.07324[astro-ph. [Google Scholar] [CrossRef]

Figure 2. Ring structure of S₀ - S_P dimensions with two slightly unequal speed limit states C and C₀, at the two ends of S_P dimension that can be seen as two brane surfaces. Traveling in opposite directions of S₀ represents particle and antiparticle states.

Figure 3. A gravitational well in S₁ is inverted into a gravitational hill with the expansion of S₀ by a test particle. The test particle is replicated over 10⁶⁰ times everywhere along S₀ dimension.

Figure 4. Gravitational inversion S₁-

S_{P}

dimensions. A positive cosmological constant expansion of S₀ is equivalent to curvature of S₁. Also, a negative cosmological constant contraction of S₀ is equivalent to a positive cosmological constant expansion of S₁.

Figure 4. Gravitational inversion S₁-

S_{P}

Figure 5. Gravitational inversion in S₁ -

S_{α}

dimensions. Positive curvature of S₁ resulting from shear stress, is equivalent to the negative curvature of

S_{α}

due to the same shear stress component. Also, a positive cosmological constant expansion of S₁ is equivalent to a negative cosmological constant contraction of

S_{α}

provided it has not reached it minimum length scale.

Figure 5. Gravitational inversion in S₁ -

S_{α}

dimensions. Positive curvature of S₁ resulting from shear stress, is equivalent to the negative curvature of

S_{α}

due to the same shear stress component. Also, a positive cosmological constant expansion of S₁ is equivalent to a negative cosmological constant contraction of

S_{α}

provided it has not reached it minimum length scale.

Figure 6. While the bare vacuum energy component occupy the gravitationally inert state C₀ to its limit, there has to be a component

ρ_{D E}

in the gravitationally active state C to satisfy the energy density constraint. The lower Planck density

ρ_{P 0}

is associated with speed state C₀.

Figure 6. While the bare vacuum energy component occupy the gravitationally inert state C₀ to its limit, there has to be a component

ρ_{D E}

in the gravitationally active state C to satisfy the energy density constraint. The lower Planck density

ρ_{P 0}

is associated with speed state C₀.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dark Energy and Dark Matter from Extra Dimensional Symmetry as Different Manifestations of Vacuum Energy

Abstract

1. Introduction

2. Extra Dimensional Symmetry Framework

2.1. Selective Response to Components of the Stress Energy Tensor

2.2. Speed Constraint and Invisibility of S0 Dimension

2.3. Speed Limit Asymmetry

2.4. Gravitational State Oscillation

2.5. Energy Density Constraint

3. General Relativity in S0 and S α Dimensions

3.1. General Relativity in S0 Dimension

3.2. General Relativity in S α Dimensions

4. Emergence of Nonzero Cosmological Constant

5. Dark Matter from Neutrino Enabled Gravitation of Virtual Particles

5.1. Detectability

6. Discussion and Conclusions

Author Contributions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.2. Speed Constraint and Invisibility of S₀ Dimension

3. General Relativity in S₀ and $S_{α}$ Dimensions

3.1. General Relativity in S₀ Dimension

3.2. General Relativity in $S_{α}$ Dimensions